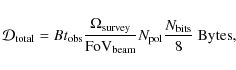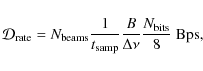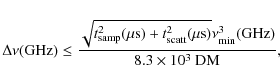Pulsar science with the Five hundred metre Aperture Spherical Telescope

R. Smits; D. R. Lorimer; M. Kramer; R. Manchester; B. Stappers; C. J. Jin; R. D. Nan; D. Li

doi:10.1051/0004-6361/200911939

Free Access

Issue		A&A Volume 505, Number 2, October II 2009


Page(s)		919 - 926
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/200911939
Published online		18 August 2009

Pulsar science with the Five hundred metre Aperture Spherical Telescope

R. Smits¹ - D. R. Lorimer^2,3 - M. Kramer^1,4 - R. Manchester⁵ - B. Stappers¹ - C. J. Jin⁶ - R. D. Nan⁶ - D. Li⁷

1 - Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, University of Manchester, Oxford Road, Manchester M13 9PL, UK
2 - Department of Physics, Hodges Hall, West Virginia University, Morgantown, WV 26506, USA
3 - National Radio Astronomy Observatory, Green Bank Observatory, PO Box 2, Green Bank, WV 24944, USA
4 - Max-Planck-Institut für Radioastronomie, Auf dem Huegel 69, 53121 Bonn, Germany
5 - Australia Telescope National Facility, CSIRO, PO Box 76, Epping NSW 1710, Australia
6 - National Astronomical Observatories, Chinese Academy of Sciences Chaoyang District, Datun Road, A.20, Beijing 100012, PR China
7 - Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Dr. Pasadena, CA 91109, USA

Received 24 February 2009 / Accepted 7 August 2009

Abstract
With a collecting area of 70 000 m², the Five hundred metre Aperture Spherical Telescope (FAST) will allow for great advances in pulsar astronomy. We have performed simulations to estimate the number of previously unknown pulsars FAST will find with its 19-beam or possibly 100-beam receivers for different survey strategies. With the 19-beam receiver, a total of 5200 previously unknown pulsars could be discovered in the Galactic plane, including about 460 millisecond pulsars (MSPs). Such a survey would take just over 200 days with eight hours survey time per day. We also estimate that, with about 80 six-hour days, a survey of M 31 and M 33 could yield 50-100 extra-Galactic pulsars. A 19-beam receiver would produce just under 500 MB of data per second and requires about 9 tera-ops to perform the major part of a real time analysis. We also simulate the logistics of high-precision timing of MSPs with FAST. Timing of the 50 brightest MSPs to a signal-to-noise of 500 would take about 24 h per epoch.

Key words: stars: neutron - stars: pulsars: general - telescopes

1 Introduction

FAST, the Five-hundred-metre Aperture Spherical Telescope, is an Arecibo-style telescope currently under construction in China. FAST will be located in a karst depression in Guizhou province at a latitude of about $+26\hbox{$^\circ$ }$ and is planned to be completed around 2014 (Nan 2006,2008). With an illuminated aperture of 300 m diameter, it will be an order of magnitude more sensitive than the steerable 100-m telescopes at Effelsberg and Green Bank and about twice as sensitive as Arecibo. Moreover, FAST will cover a frequency range of 70 MHz to 3 GHz and it will be able to observe at a zenith angle of 40 degrees without a significant loss in gain (Jin et al. 2008). By illuminating only part of the 300-m aperture the zenith angle can be extended even further; at a zenith angle of 60 degrees about half the aperture is still illuminated. With its sensitivity and its ability to see the majority of the sky, including a large part of the Galactic plane, FAST has excellent potential for finding radio pulsars (see also Nan et al. 2006).

Radio pulsars provide insights into a rich variety of physics and astrophysics. Applications to date (see e.g. Lorimer & Kramer 2005) include the study of the Milky Way, globular clusters, the evolution and collapse of massive stars, the formation and evolution of binary systems, the properties of super-dense matter, extreme plasma physics, tests of theories of gravity and as cosmological probes. A goal for the coming decade is the direct detection of low-frequency gravitational waves via high-precision timing of an array of millisecond pulsars (MSPs) (Jenet et al. 2005). Such an array would be greatly facilitated by further discoveries and timing of MSPs with FAST.

The aim of this paper is to investigate the possibilities of FAST for finding and timing radio pulsars. In Sect. 2 we present a simulation of a FAST survey of the pulsar sky, where we look into the survey speed and the number of pulsars that can be detected for different receivers. In Sect. 3 we present calculations to estimate the data rates and computational requirements for a pulsar survey with FAST. In Sect. 4 we look into the possibility for FAST to participate in a global pulsar timing array effort. Section 5 contains a discussion of the results, as well as a comparison between FAST and the Square Kilometre Array.

2 Survey simulation

In the past, the southern hemisphere has been the subject of extensive pulsar surveys (Lyne et al. 1998; Manchester et al. 2001,1996). FAST will be able to complement these surveys in the northern hemisphere with an even greater sensitivity. Initially, FAST will have a 19-beam receiver with a frequency range of 1.1-1.5 GHz and a system temperature of 20 K (not including the sky temperature). A possible future phased array feed (PAF) is planned to have over 100 beams (Jin et al. 2008) with the same frequency range and a system temperature of 30 K. Table 1 shows the parameters involved in the survey simulation. The number of beams will determine the speed of the survey and the dwell time per pointing. We therefore perform the simulations as a function of both frequency and field of view (FoV).

Table 1: Expected system parameters of FAST and the pulsar survey.

2.1 Simulation method

We performed Monte Carlo simulations following Lorimer et al. (2006) using the psrpop package (cf. Smits et al. 2009). In their study, Lorimer et al. (2006) used the results from recent surveys with the Parkes Multibeam system to derive an underlying population of pulsars with an optimal set of probability density functions for pulsar period (P), 1400-MHz radio luminosity (L), Galactocentric radius (R) and height above the Galactic plane (z). We make use of these results in our simulations described below which use as a starting point model C $^\prime$ from Lorimer et al. (2006).

Our simulation procedure begins by generating a population of normal pulsars which beam towards the Earth. Each pulsar is assigned a value of P, L, R and z based on the assumed probability density functions. For the distributions in P, R and z, we use the distributions from C $^\prime$ of Lorimer et al. (2006). To compute L, we adopt the log-normal distribution found by Faucher-Giguère & Kaspi (2006). This has the advantage of not requiring a specific lower bound in L, as is the case for the power-law luminosity models considered by Lorimer et al. (2006).

We compute intrinsic pulse widths using the following self-consistent approach. Assuming a simple geometry with circular beams of radius $\rho$ , the pulse width can be found from the inclination angle between the pulsar spin and magnetic axis, $\alpha$ , and the impact parameter between the magnetic axis and the line of sight, $\beta$ . Following Kramer et al. (1998), we use the empirical relationship between $\rho$ and spin period P (s) defined as follows:

$\begin{displaymath}\rho_{\rm model} = \left\{ \begin{array}{ll} 5.4^{\circ} P... ...} \\ 31.2^{\circ} & \mbox{otherwise}, \end{array} \right. \end{displaymath}$

where the angle of $31.2^{\circ}$ is the value of the above expression evaluated for P=30 ms. To model the scatter about this relationship (see, e.g., Fig. 3.5 from Lorimer & Kramer 2005), we use a Monte Carlo approach to find a dithered beam radius

$\begin{displaymath}\rho = 10^{\log_{10} (\rho_{\rm model}) + p}, \end{displaymath}$

(1)

where p is a random number drawn from a flat distribution in the range $-0.15 \leq p \leq 0.15$ . This, somewhat arbitrary, scheme dithers the beam radius logarithmically by a third of a decade and provides a good match to the observed scatter. The pulsar is assumed to be beaming towards us and the impact parameter $\beta$ is chosen from a simple flat distribution in the range $-\rho \leq \beta \leq \rho$ . Finally, we assume that the magnetic inclination angle $\alpha$ is randomly distributed, that is

$\begin{displaymath}\alpha = \arccos q, \end{displaymath}$

(2)

where q is a random number drawn from a flat distribution in the range 0<q<1. With these quantities defined, the observed pulse width W is found using the following geometrical relationship (see, e.g., Gil et al. 1984):

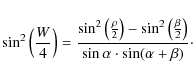$\begin{displaymath}\sin^2 \left( \frac{W}{4} \right) = \frac{ \sin^2 \left( \fr... ...2} \right) }{ \sin\alpha \cdot \sin ( \alpha + \beta ) }\cdot \end{displaymath}$

(3)

To compute the expected DM and scatter broadening effects on each pulse, we use the NE2001 electron density model (Cordes & Lazio 2002). Note that, since we are primarily concerned with the distant population of highly dispersed pulsars in these simulations, we do not attempt to account for interstellar scintillation. Finally, to allow us to extrapolate the 1400-MHz luminosities to other survey frequencies in the next step, we make the reasonable assumption that pulsar spectra can be approximated as a power law (Lorimer et al. 1995) and assign each pulsar a spectral index drawn from a normal distribution with mean of -1.6 and standard deviation 0.35.

As described by Lorimer et al. (2006), when generating the normal pulsar population according to the above criteria, we keep track of the number of pulsars detectable by the detailed model of the Parkes Multibeam Pulsar Surveys of the Galactic plane (Manchester et al. 2001) and at high latitudes (Burgay et al. 2006). Our simulations terminate when the numbers of model detectable normal pulsars matches the 1005 pulsars found by these surveys. This results in an underlying sample of 120 000 model pulsars.

To model the MSP population, we follow the same approach and assumptions as for the normal pulsars described above, but with two exceptions: (i) model z heights are chosen from an exponential distribution with a mean of 500 pc (Cordes & Chernoff 1997); (ii) the underlying period distribution used is taken from a recent study of the MSP population (Lorimer et al. 2009; in preparation). Note that implicit in this approach is the notion that the luminosity functions for normal pulsars and MSPs are identical; this is consistent with earlier results Lyne et al. (1998).

In addition to the Parkes Multibeam Surveys considered above for the normal pulsars, we also make use of the Parkes 70-cm pulsar survey of the southern sky (Lyne et al. 1998; Manchester et al. 1996) and two intermediate latitude surveys carried out by the Parkes multibeam system (Edwards et al. 2001; Jacoby et al. 2007). Our simulations are normalized such that they terminate when the total of 49 MSPs detected by these surveys is reached. This results in an underlying sample of 23 000 model MSPs.

Once the pulsar population was determined, we performed simulations to find the number of pulsars FAST would detect as a function of frequency. For this purpose, we allowed the centre frequency to range from 400 MHz to 1.4 GHz. The bandwidth was kept at one third of the centre frequency, the observation time per pointing was kept constant at 600 s and the gain was kept constant at 16.5 KJy^-1. The frequency-dependent sky temperature was added to the system temperature. Considering the beamwidth of about 3.4 arcmin at 1.4 GHz, we limited the surveys to Galactic latitudes of either between $\pm$ $5^\circ$ or between $\pm$ $10^\circ$ . Further, we simulated the number of pulsars FAST will detect as a function of observation time. All detected pulsars include already known pulsars.

2.2 Simulation results

Figure 1 shows the number of normal pulsars and MSPs that were detected in the simulation of the Galactic plane as a function of centre frequency. The figure shows that for both normal pulsars and MSPs, the number of detected pulsars is reasonably stable from centre frequencies of 1 to 1.4 GHz. Similar results are found for observation times of 120 and 1800 s.

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f01.eps} \end{figure}$

Figure 1:

Number of normal pulsars and MSPs detected in simulations of FAST surveys of the Galactic plane as a function of observation frequency. The surveys were limited in Galactic longitude by $20^\circ < {l}<90^\circ$ . The solid lines and the dotted lines show the number of normal pulsars and millisecond pulsars, respectively. The squares indicate a survey region limited in Galactic latitude by $\vert {b}\vert<5^\circ$ . The circles indicate a survey region limited in Galactic latitude by $\vert {b}\vert<10^\circ$ . The observation time was kept constant at 600 s and the bandwidth was kept at one third of the observation frequency.

Open with DEXTER

The number of detected pulsars as a function of observation time is shown in Fig. 2. This figure shows that, while the number of detected pulsars continues to climb with increasing observation time, the rate of increase slows significantly after times of about 600 s.

The 19 beams in the multibeam receiver of FAST have a total FoV of about 0.061 deg². A possible future PAF with over 100 beams will have a total FoV of 0.32 deg². Table 2 shows the total survey time for different observation times per pointing, for different survey regions for both a 19-beam and a 100-beam receiver. The total survey time is given in days assuming eight hours of observation time per day.

With the initial 19-beam receiver about 5200 previously unknown pulsars, including 460 MSPs, can be found by searching the region with $20^\circ <\rm {l}<90^\circ$ and $\vert {b}\vert<5^\circ$ , using 10-min pointings. This survey would take just over 200 days to complete. Using the 100-beam receiver to survey the same region with 30-min pointings, 5900 previously unknown pulsars can be found in 130 days, including about 540 MSPs. Doubling the survey area to $\vert {b}\vert<10^\circ$ will add about 1100 pulsars using 10-min pointings and about 1450 pulsars using 30-min pointing. The 100-beam receiver will also enable an all-sky survey. Using 2-min pointings, 4300 previously unknown pulsars can be found in 300 days, including about 440 MSP's.

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f02.eps} \end{figure}$

Figure 2:

Number of normal pulsars and MSPs detected in simulations of FAST surveys as a function of observation time per pointing. The surveys were limited in Galactic latitude and longitude by $\vert {b}\vert<10^\circ$ and $20^\circ < {l}<90^\circ$ . The solid line and the dotted line show the number of normal pulsars and MSPs, respectively. The centre frequency is 1.315 GHz with a bandwidth of 400 MHz.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=17cm,clip]{eps/11939f03.eps} \end{figure}$

Figure 3:

Distribution of detected normal pulsars and MSPs for different models. The top left plot shows the distribution of normal pulsars from models 1 (similar to model 3) and 5. The top right plot shows the distribution of normal pulsars from models 2 (similar to model 4) and 6. The two plots in the middle show the distribution of millisecond pulsars from the same models as the plot directly above. The bottom plot shows a Hammer-Aitoff projection of the distribution of normal pulsars and millisecond pulsars from model 7 in galactic coordinates. The black and white striped boxes mark the areas defined by $20^\circ < {l}<90^\circ$ , $\vert {b}\vert<5^\circ$ and $\vert {b}\vert<10^\circ$ .

Open with DEXTER

Figure 3 shows the distribution of detected pulsars for all the models. The top two plots show the normal pulsars that are detected in the models that are limited to the Galactic plane. The plots directly below show the millisecond pulsars that are detected in the same models. The bottom plot shows the all-sky survey.

2.3 Survey of M 31 and M 33

The great sensitivity of FAST will permit searches for pulsars in other galaxies. We can estimate the number of pulsars that FAST can detect in a survey of M 31 and M 33, both visible for about six hours per day from FAST. Table 3 shows the parameters of these galaxies.

Table 2: Total survey time for different FAST surveys.

Table 3: Parameters of M 31 and M 33.

The minimum detectable flux density of a pulsar in a survey is given by: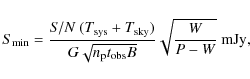

$\begin{displaymath}S_{\rm min}=\frac{{\it S/N}~(T_{\rm sys}+T_{\rm sky})} {G\sqrt{n_{\rm p}t_{\rm obs}B}}\sqrt{\frac{W}{P-W}}~ {\rm mJy}, \end{displaymath}$

(4)

where S/N is the signal-to-noise ratio required for a detection, $T_{\rm sys}$ is the system noise temperature (K), $T_{\rm sky}$ is the sky temperature (K), G is the gain of the telescope (K Jy^-1), $n_{\rm p}$ is the number of polarisations, $t_{\rm obs}$ is the observation length (s) per pointing, B is the observation bandwidth (MHz), P is the period of the pulsar (s) and W is the equivalent width (s) (Lorimer & Kramer 2005). For an observation frequency of 1.315 GHz and S/N = 9, $T_{\rm sys} = 20$ K, $T_{\rm sky} = 1.4$ K for M 31 and $T_{\rm sky}$ = 1.1 K for M 33, G = 16.5 K Jy^-1, $n_{\rm p} = 2$ , $t_{\rm obs} = 6$ h, B = 400 MHz and assuming an equivalent width of 5% of the period we obtain a minimum detectable flux density of 600 nJy. This leads to a minimum detectable luminosity of 360 and 560 mJy kpc² for a pulsar in M 31 and M 33, respectively. There are at least 55 pulsars known in our Galaxy with a higher luminosity at 1.4 GHz than 360 mJy kpc² and 32 pulsars higher than 560 mJy kpc². If we correct for the mass ratio between our Galaxy and the galaxies M 31 and M 33, then we can expect of order 80 pulsars to be detected by a FAST survey of M 31 and about 3 pulsars in M 33. However, the supernova rate per unit mass in our Galaxy is thought to be higher than in M 31 and considerably lower than in M 33 (Berkhuijsen 1984; Gordon et al. 1998). Also, since the angular extent of M 33 is about 1 quarter that of M 31, the number of pulsars found per pointing might not differ much between M 31 and M 33. We estimate that the total number of pulsars found in a FAST survey of both M 31 and M 33 would lie between 50 and 100. Finding such a number of pulsars would allow studies of the pulsar population in these galaxies and would provide a valuable probe of the inter-galactic medium. The combined angular extent of M 31 and M 33 is 3.8 deg², which means about 1500 beams are required. With a 19-beam receiver, this would require 79 pointings each of duration six hours, leading to a total of 470 h of observing time.

3 Data processing

The total amount of data from a FAST pulsar survey is given by

$\begin{displaymath}{\cal D}_{\rm total} = Bt_{\rm obs}\frac{\Omega_{\rm survey}}... ...FoV_{\rm beam}}}N_{\rm pol}\frac{N_{\rm bits}}{8}\rm {~Bytes}, \end{displaymath}$

(5)

where B is the bandwidth, $t_{\rm obs}$ is the observation time per pointing, FoV $_{\rm beam}$ is the FoV of 1 beam, $\Omega_{\rm survey}$ is the total field of the survey, $N_{\rm pol}$ is the number of polarisations and $N_{\rm bits}$ is the number of bits used in the digitisation.

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f08.eps} \end{figure}$

Figure 4:

Total amount of data from a FAST pulsar survey as a function of the total survey field. The calculation assumes a bandwidth of 400 MHz, a FoV $_{\rm beam}$ of 0.0025 deg², 1 polarisation and 2 bits per sample. The three different lines correspond to observation times of 120, 600 and 1800 s. The dotted vertical lines indicate from left to right the survey fields given by $20^\circ <\rm {l}<90^\circ$ and $\vert {b}\vert<5^\circ$ , $20^\circ <\rm {l}<90^\circ$ and $\vert {b}\vert<10^\circ$ and the entire visible sky.

Open with DEXTER

Figure 4 shows the total amount of data from a FAST pulsar survey as a function of the total survey field for different observation times. We have assumed a bandwidth of 400 MHz, a FoV $_{\rm beam}$ of 0.0025 deg², 1 polarisation and 2 bits per sample. Table 4 shows the total amount of data for the seven different survey models from Table 2.

Table 4: Total amount of data from different survey models (see Table 2). Except for model 7, the surveys are limited in Galactic longitude by $20^\circ <\rm {l}<90^\circ$ .

The data acquisition rate from a pulsar survey sampling the detected outputs of a filterbank of total bandwidth B and channel bandwidth $\Delta\nu$ is given by:

$\begin{displaymath}{\cal D}_{\rm rate} = N_{\rm beams}\frac{1}{t_{\rm samp}}\frac{B}{\Delta\nu}\frac{N_{\rm bits}}{8}{\rm ~Bps}, \end{displaymath}$

(6)

where $N_{\rm beams}$ is the number of beams in the receiver, $t_{\rm samp}$ is the sampling time and $N_{\rm bits}$ is the number of bits used in the digitisation. $\Delta\nu$ can be estimated by demanding that the dispersion smearing within the frequency channel does not exceed the effective time resolution, given by the sampling time and the scattering time:

$\begin{displaymath}\Delta\nu({\rm GHz}) \le \frac{\sqrt{t_{\rm samp}^2(\mu{\rm ... ...rm {s})}\nu_{\rm min}^3({\rm GHz})} {8.3\times10^3~{\rm DM}}, \end{displaymath}$

(7)

where $\nu_{\rm min}$ is the minimum (lowest) frequency in the observation frequency band, DM is the dispersion measure and $t_{\rm scatt}$ is the scattering time. Following Bhat et al. (2004), we relate $t_{\rm scatt}$ to the DM and observing frequency as follows:

$\displaystyle \log_{10}(t_{\rm scatt}(\rm {ms})) = -6.46 + 0.154\log_{10}({\rm DM})+1.07(\log_{10}~{\rm DM})^2 - 3.86 \log_{10}(\nu(\rm {GHz})).$

(8)

In practice, however, the scattering time can differ from this by a factor up to 100 (see Bhat et al. 2004). A smaller scattering time leads to the requirement of smaller - and thus more - frequency channels. To be on the safe side, we apply the highest frequency in the frequency band to Eq. (8) and divide the resulting scattering time by 100. Substituting $t_{\rm scatt}$ from Eqs. (8) in (7) and taking $\nu_{\rm min}= 1.115$ GHz, leads to a relationship between $\Delta\nu$ and DM with a minimum of 42 kHz (at DM = 428). This means that having a constant frequency channel width of 42 kHz over the frequency band will be sufficient for the pulsar survey. This leads to 9500 frequency channels for B=400 MHz.

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f09.eps} \end{figure}$	Figure 5: Amount of data per second from a FAST pulsar survey as a function of FoV. The calculation assumes a sampling time of 100 $\mu$ s, a frequency range of 1.115 to 1.515 GHz and 2 bits per sample. The dotted vertical lines indicate from left to right the FoV of 1, 19 and 100 beams, respectively.
Open with DEXTER

Figure 5 shows the data rate from a FAST pulsar survey as a function of FoV. We have assumed 100 $\mu$ s sampling time, a frequency range of 1.115 to 1.515 GHz and 2 bits per sample. For the initial 19-beam receiver, the data rate is just under 0.5 GB per second. For 100 beams it is about 2.4 GB per second.

The number of operations required to search these data for normal pulsars, millisecond pulsars and accelerated pulsars in binary systems is approximately

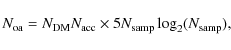$\begin{displaymath}N_{\rm oa}=N_{\rm DM}N_{\rm acc}\times5N_{\rm samp}\log_2(N_{\rm samp}), \end{displaymath}$

(9)

where $N_{\rm DM}$ is the number of DM-trial values and $N_{\rm acc}$ is the number of trial accelerations. Figure 6 shows the number of operations per second required to perform a real time analysis of a FAST pulsar survey, assuming 100 trial accelerations, a sampling time of 100 $\mu$ s, an observation time of 600 s and DM $_{\rm max} = 1000$ cm^-3 pc. $N_{\rm DM}$ was obtained numerically by demanding that the total time delay within the frequency band between two consecutive DM-trial values is equal to twice the effective time resolution, given by the sampling time and the scattering time of Eq. (8). This leads to $N_{\rm DM} = 4280$ . For the initial 19-beam receiver, the required computation power for real time analysis is 9 tera-ops. For 100 beams it becomes 48 tera-ops. Contributions from de-dispersion, harmonic folding and possibly other processes would increase these values by a factor less than two. However, it is not unreasonable to store all the data from a FAST pulsar survey and to perform the analysis off-line. This would reduce the required computation power significantly.

4 Timing

In addition to being a very powerful search machine, FAST will also excel in the high-precision timing of pulsars. For a given pulsar, the timing precision roughly scales with the S/N of the observed pulse profile (Lorimer & Kramer 2005), and hence with telescope sensitivity. Until the Square Kilometre Array comes on-line (Sect. 5) FAST will have the largest sensitivity of all existing radio telescopes and will also be able to see a larger fraction of the sky than the Arecibo telescope. Consequently, FAST will be the telescope of choice for a number of high-precision timing experiments. While the Northern location of FAST means that it is unlikely to contribute significantly to the timing of, say, the Double Pulsar (PSR J0737-3039A/B, Burgay et al. 2003; Lyne et al. 2004), a major contribution of FAST will be the participation in the global Pulsar Timing Array efforts.

High-precision timing of a network of pulsars allows detection of a gravitational wave background by correlating the timing residuals of the pulsars (e.g. Jenet et al. 2006). Current efforts include PPTA (Parkes Pulsar Timing Array), EPTA (European Pulsar Timing Array) and NANOGrav (North American Nanohertz Observatory for Gravitational Waves). In terms of combination of sky coverage and sensitivity, FAST will only be matched by the European LEAP efforts (Large European Array for Pulsars), where the European 100-m class telescopes are combined to obtain Arecibo-like sensitivity for pulsar timing. This effort, however, has to overcome the challenge of coherently combining the signals between telescopes up to 2000 kilometres apart.

$\begin{figure} \par\includegraphics[angle=-90,width=8.4cm]{eps/11939f10.eps} \end{figure}$

Figure 6:

Required computation power for real-time searching for possibly accelerated fast and slow pulsars in the data from a FAST pulsar survey as a function of FoV. The calculation assumes a sampling time of 100 $\mu$ s, a frequency range of 1.115 to 1.515 GHz, 2 bits per sample and a DM $_{\rm max}$ of 1000. The dotted vertical lines indicate from left to right the FoV of 1, 19 and 100 beams, respectively.

Open with DEXTER

4.1 Pulsar timing array experiment

Following earlier work by Detweiler (1979) and Kaspi et al. (1994), pulsar timing is now routinely used to constrain the amplitude of a gravitational wave (GW) background. Currently the most stringent limits have been placed by Jenet et al. (2006) from observations of seven MSPs with the Parkes 64-m radio telescope (cf. Manchester 2008) which constrain $\Omega_{\rm GW}$ , the ratio of the energy density of the GW background to the closure density to be $\Omega_{\rm GW}h^2 < 1.9\times 10^{-8}$ , where h is the dimensionless Hubble constant defined as $H_0\equiv h\times 100$ km s^-1 Mpc^-1. The sensitivity that is needed to achieve a GW detection depends on details of the Galaxy merger rate, since the GW background generated by an ensemble of super-massive black holes distributed throughout the Universe is expected to be the strongest signal to be detected. The signal originating from such sources is expected at a level of $\Omega_{\rm GW}h^2 \sim 2\times 10^{-10}$ (Enoki et al. 2004; Jaffe & Backer 2003; Wyithe & Loeb 2003). Simulations suggest that the timing of 20 pulsars with a timing precision of 100 ns over five years would lead to a sensitivity of $\Omega_{\rm GW}h^2 < 6.6\times 10^{-11}$ and hence to a first direct detection of a GW background (Jenet et al. 2006). While this is difficult with current technology, FAST will have the sensitivity and sky coverage to make a major contribution to achieving this goal.

Here we estimate the amount of time needed to time the brightest MSPs, found by FAST, to high precision. For this simulation we choose model 2 from Table 2, which provides us with 670 MSPs. We take the 50 brightest of these and calculate the amount of time required for a S/N of 500, taking into account a conservative profile stabilisation time of five minutes. This leads to 24 h to time all 50 pulsars once. These numbers do not include accompanying low-frequency observations to allow correction for variations in interstellar dispersion. As expected, we found that the FoV provided by 19 beams had no impact on the timing performance, as there was no instance where two or more pulsars could be timed simultaneously.

5 FAST versus the SKA

The Square Kilometre Array (SKA) is a planned multi-purpose radio telescope with a collecting area approaching 1 million square metres. Although the exact design is not yet determined, it is likely to consist of aperture arrays to cover frequencies from 70 MHz up to 500 or even 800 MHz and 15-m dishes for the higher frequencies. About half of the elements will be placed within a 5-kilometre core of the SKA, the rest will be placed on spiral arms extending several thousands of kilometres outwards. Smits et al. (2009) have studied the performance of the SKA concerning pulsar surveys and timing. Here we will discuss the differences between these findings and those of the current paper.

A pulsar survey with FAST is straightforward compared to an SKA pulsar survey. With the initial receiver, no beam-forming is required. The future PAF does require beam-forming, but it does not need the vast computational power of several peta-ops required for beam-forming the SKA. Another benefit for FAST is that the data do not need to be transported over long distances; the data processing can be performed close to the dish. Also, the data rates and required computation power for a real time acceleration search are much lower for the FAST survey. This is mostly due to the smaller FoV of FAST, which is 10 to 50 times less than the FoV for an SKA pulsar survey, but also because these data rates and computational power scale with the square of the telescope diameter. The diameter of FAST is given by the illuminated aperture of 300 m. For the SKA it is determined by the largest baselines between the elements used in the survey. Smits et al. (2009) estimate that the limits in computational power will restrict these baselines to 1 kilometre. Because of this limitation, the telescope sensitivity of a pulsar survey with the SKA is about 2000 m²K^-1 which is equal to that of FAST. However, the larger FoV of the SKA will not only enable a survey of a much larger portion of the sky, but also allow for a longer dwell time per pointing. The actual FoV of the SKA depends on the final design, but at the very least it will be equal to the FoV of the 15-m dishes which at 1.4 GHz is about 0.64 deg². For comparison, a reasonable assumption would be that an SKA survey has a dwell time of 40 min versus 10 min for a FAST survey. This makes the survey sensitivity of the SKA twice that of FAST. Compared to the initial 19-beam receiver of FAST, a pulsar survey with the SKA would be about 2.5 times faster, but with the 100-beam PAF, the survey speed of FAST would be twice that of the SKA. Moreover, because the elements of the SKA are fully steerable, the SKA will be able to survey a much larger part of the sky and with its latitude of about -30 $^\circ$ this includes almost the entire Galactic plane.

Timing pulsars with the SKA can be performed with a considerable fraction of the full collecting area, providing a sensitivity close to 10 000 m² K^-1. Also, the large FoV of the SKA allows timing of many pulsars simultaneously (but depending on the SKA design, this might not be the case when using the SKA for a pulsar timing array). Even the future 100-beam PAF of FAST only has a quarter of the FoV of 15-m dishes and should the SKA be equipped with PAFs or mid-frequency aperture arrays, its FoV increases significantly to 20 deg² or even 250 deg².

Given that FAST will be operational well ahead of the full SKA, it is likely to be the most powerful telescope to perform pulsar science in the next decade and will remain an outstanding instrument for pulsar science, complementing the SKA once it is operational.

6 Summary

The FAST pulsar survey simulation in Sect. 2 shows that, despite the small natural beam-size and limitations in zenith angle, FAST will be a formidable instrument for finding pulsars.

A tradeoff between the number of pulsars and total observation time can be determined from Table 2. With the initial 19-beam receiver about 5200 previously unknown pulsars, including 460 MSPs, can be found in a survey of about 230 days of the visible part of the Galactic plane with $\vert {b}\vert<5^\circ$ . With a 100-beam receiver 5900 previously unknown pulsars can be found in the same region in 130 days, including about 540 previously unknown MSPs. The 100-beam receiver will also enable an all-sky survey yielding 4300 previously unknown pulsars in 300 days. Further, we estimate that a 470-h survey of M 31 and M 33 would yield between 50 and 100 extra-Galactic pulsars.

A pulsar survey with the 19-beam receiver will produce just under 500 MB of data per second. Depending on the survey, this leads to a total of 17 or 33 peta-bytes. The major part of a real-time acceleration search of these data would require 9 tera-ops. After 2014, such data rates and processing power should be very feasible.

FAST will also be able to contribute to the existing efforts to detect a gravitational wave background by timing a large number of MSPs to high precision. Although the visible sky of FAST is limited to 58% of the entire sky, those pulsars that are visible to FAST can be timed to great precision very quickly. A simulation in Sect. 4 suggests that the 50 brightest MSPs, visible to FAST can be timed to a S/N of 500 in just 24 h.

Compared to a pulsar survey with the SKA, FAST will match the sensitivity of the SKA, but the large FoV of the SKA will allow for longer dwell times and make the survey faster, at least for the initial 19-beam configuration of FAST. Also, the SKA will be able to survey a much larger part of the sky. However, having a single dish rather than many elements spread over a large area significantly reduces the required data rates and computational power. When timing pulsars for a pulsar timing array, the SKA will have much more sensitivity than FAST, since the SKA can use almost the full collecting area in this case. Also, the larger FoV of the SKA will allow timing of many pulsars simultaneously, although this will probably not benefit the timing of the limited number of pulsars from the timing array. Given that FAST will be operational well ahead of the full SKA, it will provide the best prospects for pulsar science in the next decade.

Acknowledgements

We would like to thank the referee, Scott Ransom, for his useful suggestions and comments. The authors have made use of the ATNF Pulsar Catalogue which can be found at http://www.atnf.csiro.au/research/pulsar/psrcat. This effort/activity is supported by the European Community Framework Programme 6, Square Kilometre Array Design Studies (SKADS), contract No. 011938. D.R.L. is supported by a Research Challenge Grant from West Virginia EPSCoR.

References

Berkhuijsen, E. M. 1984, A&A, 140, 431 [NASA ADS]
Bhat, N. D. R., Cordes, J. M., Camilo, F., Nice, D. J., & Lorimer, D. R. 2004, ApJ, 605, 759 [NASA ADS] [CrossRef] (In the text)
Bonanos, A. Z., Stanek, K. Z., Kudritzki, R. P., et al. 2006, ApJ, 652, 313 [NASA ADS] [CrossRef]
Burgay, M., D'Amico, N., Possenti, A., et al. 2003, Nature, 426, 531 [NASA ADS] [CrossRef]
Burgay, M., Joshi, B. C., D'Amico, N., et al. 2006, MNRAS, 368, 283 [NASA ADS] (In the text)
Corbelli, E., & Salucci, P. 2000, MNRAS, 311, 441 [NASA ADS] [CrossRef]
Cordes, J. M., & Chernoff, D. F. 1997, ApJ, 482, 971 [NASA ADS] [CrossRef] (In the text)
Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv Astrophysics e-prints (In the text)
Detweiler, S. 1979, ApJ, 234, 1100 [NASA ADS] [CrossRef] (In the text)
Edwards, R. T., Bailes, M., van Straten, W., & Britton, M. C. 2001, MNRAS, 326, 358 [NASA ADS] [CrossRef]
Enoki, M., Inoue, K. T., Nagashima, M., & Sugiyama, N. 2004, ApJ, 615, 19 [NASA ADS] [CrossRef]
Faucher-Giguère, C.-A., & Kaspi, V. M. 2006, ApJ, 643, 332 [NASA ADS] [CrossRef] (In the text)
Gordon, S. M., Kirshner, R. P., Long, K. S., et al. 1998, ApJS, 117, 89 [NASA ADS] [CrossRef]
Jacoby, B. A., Bailes, M., Ord, S. M., Knight, H. S., & Hotan, A. W. 2007, ApJ, 656, 408 [NASA ADS] [CrossRef]
Jaffe, A. H., & Backer, D. C. 2003, ApJ, 583, 616 [NASA ADS] [CrossRef]
Jenet, F. A., Hobbs, G. B., Lee, K. J., & Manchester, R. N. 2005, ApJ, 625, L123 [NASA ADS] [CrossRef] (In the text)
Jenet, F. A., Hobbs, G. B., van Straten, W., et al. 2006, ApJ, 653, 1571 [NASA ADS] [CrossRef] (In the text)
Jin, C. J., Nan, R. D., & Gan, H. Q. 2008, in IAU Symp., 248, 178 (In the text)
Kaspi, V. M., Taylor, J. H., & Ryba, M. F. 1994, ApJ, 428, 713 [NASA ADS] [CrossRef] (In the text)
Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy (Cambridge University Press) (In the text)
Lorimer, D. R., Yates, J. A., Lyne, A. G., & Gould, D. M. 1995, MNRAS, 273, 411 [NASA ADS] (In the text)
Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] (In the text)
Lyne, A. G., Burgay, M., Kramer, M., et al. 2004, Science, 303, 1153 [NASA ADS] [CrossRef]
Lyne, A. G., Manchester, R. N., Lorimer, D. R., et al. 1998, MNRAS, 295, 743 [NASA ADS] [CrossRef]
Manchester, R. N. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, ed. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 584 (In the text)
Manchester, R. N., Lyne, A. G., D'Amico, N., et al. 1996, MNRAS, 279, 1235 [NASA ADS]
Manchester, R. N., Lyne, A. G., Camilo, F., et al. 2001, MNRAS, 328, 17 [NASA ADS] [CrossRef]
Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef]
Nan, R. 2006, Science in China Series G: Physics, Mechanics and Astronomy, 49, 2, 129
Nan, R. 2008, in SPIE Conf. Ser., 7012
Nan, R.-D., Wang, Q.-M., Zhu, L.-C., et al. 2006, Chinese J. Astron. Astrophys. Suppl., 6, 020000 (In the text)
Ribas, I., Jordi, C., Vilardell, F., et al. 2005, ApJ, 635, L37 [NASA ADS] [CrossRef]
Seigar, M. S., Barth, A. J., & Bullock, J. S. 2008, MNRAS, 389, 1911 [NASA ADS] [CrossRef]
Smits, R., Kramer, M., Stappers, B., et al. 2009, A&A, 493, 1161 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Wyithe, J. S. B., & Loeb, A. 2003, ApJ, 590, 691 [NASA ADS] [CrossRef]

Footnotes

... psrpop: http://psrpop.sourceforge.net

All Tables

Table 1: Expected system parameters of FAST and the pulsar survey.

Table 2: Total survey time for different FAST surveys.

Table 3: Parameters of M 31 and M 33.

Table 4: Total amount of data from different survey models (see Table 2). Except for model 7, the surveys are limited in Galactic longitude by $20^\circ <\rm {l}<90^\circ$ .

All Figures

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f01.eps} \end{figure}$	Figure 1: Number of normal pulsars and MSPs detected in simulations of FAST surveys of the Galactic plane as a function of observation frequency. The surveys were limited in Galactic longitude by $20^\circ < {l}<90^\circ$ . The solid lines and the dotted lines show the number of normal pulsars and millisecond pulsars, respectively. The squares indicate a survey region limited in Galactic latitude by $\vert {b}\vert<5^\circ$ . The circles indicate a survey region limited in Galactic latitude by $\vert {b}\vert<10^\circ$ . The observation time was kept constant at 600 s and the bandwidth was kept at one third of the observation frequency.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f02.eps} \end{figure}$	Figure 2: Number of normal pulsars and MSPs detected in simulations of FAST surveys as a function of observation time per pointing. The surveys were limited in Galactic latitude and longitude by $\vert {b}\vert<10^\circ$ and $20^\circ < {l}<90^\circ$ . The solid line and the dotted line show the number of normal pulsars and MSPs, respectively. The centre frequency is 1.315 GHz with a bandwidth of 400 MHz.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{eps/11939f03.eps} \end{figure}$	Figure 3: Distribution of detected normal pulsars and MSPs for different models. The top left plot shows the distribution of normal pulsars from models 1 (similar to model 3) and 5. The top right plot shows the distribution of normal pulsars from models 2 (similar to model 4) and 6. The two plots in the middle show the distribution of millisecond pulsars from the same models as the plot directly above. The bottom plot shows a Hammer-Aitoff projection of the distribution of normal pulsars and millisecond pulsars from model 7 in galactic coordinates. The black and white striped boxes mark the areas defined by $20^\circ < {l}<90^\circ$ , $\vert {b}\vert<5^\circ$ and $\vert {b}\vert<10^\circ$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f08.eps} \end{figure}$	Figure 4: Total amount of data from a FAST pulsar survey as a function of the total survey field. The calculation assumes a bandwidth of 400 MHz, a FoV $_{\rm beam}$ of 0.0025 deg², 1 polarisation and 2 bits per sample. The three different lines correspond to observation times of 120, 600 and 1800 s. The dotted vertical lines indicate from left to right the survey fields given by $20^\circ <\rm {l}<90^\circ$ and $\vert {b}\vert<5^\circ$ , $20^\circ <\rm {l}<90^\circ$ and $\vert {b}\vert<10^\circ$ and the entire visible sky.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.8cm]{eps/11939f09.eps} \end{figure}$	Figure 5: Amount of data per second from a FAST pulsar survey as a function of FoV. The calculation assumes a sampling time of 100 $\mu$ s, a frequency range of 1.115 to 1.515 GHz and 2 bits per sample. The dotted vertical lines indicate from left to right the FoV of 1, 19 and 100 beams, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.4cm]{eps/11939f10.eps} \end{figure}$	Figure 6: Required computation power for real-time searching for possibly accelerated fast and slow pulsars in the data from a FAST pulsar survey as a function of FoV. The calculation assumes a sampling time of 100 $\mu$ s, a frequency range of 1.115 to 1.515 GHz, 2 bits per sample and a DM $_{\rm max}$ of 1000. The dotted vertical lines indicate from left to right the FoV of 1, 19 and 100 beams, respectively.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.