| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 727 - 733 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911822 | |
| Published online | 03 August 2009 | |
CNO enrichment by rotating AGB stars in globular clusters
T. Decressin1,2 - C. Charbonnel1,3 - L. Siess4,5 - A. Palacios6 - G. Meynet1 - C. Georgy1
1 - Geneva Observatory, University of Geneva, 51 ch. des
Maillettes, 1290
Versoix, Switzerland
2 - Argenlader Institut für Astronomie (AIfA), Universität Bonn, Auf dem Hügel 71, 53121 Bonn,
Germany
3 - Laboratoire d'Astrophysique de Toulouse-Tarbes,
CNRS UMR 5572, Université de Toulouse, 14 Av. E. Belin, 31400 Toulouse, France
4 - Institut d'Astronomie et d'Astrophysique, Université Libre de
Bruxelles, ULB - CP 226, 1050 Brussels, Belgium
5 - Centre for Stellar and Planetary Astrophysics, School of
Mathematical Sciences, Monash University, Victoria 3800, Australia
6 - Groupe de Recherche en Astronomie et Astrophysique du Languedoc, UMR 5024, Université Montpellier II, CNRS, place Eugène Bataillon, 34095 Montpellier, France
Received 10 February 2009 / Accepted 14 July 2009
Abstract
Context. AGB stars have long been held responsible for the important star-to-star variations in light elements observed in Galactic globular clusters (GCs).
Aims. We analyse the main impacts of a first generation of rotating intermediate-mass stars on the chemical properties of second-generation GC stars. The rotating models were computed without magnetic fields and without the effects of internal gravity waves. They account for the transports by meridional currents and turbulence.
Methods. We computed the evolution of both standard and rotating stellar models with initial masses between 2.5 and 8 M![]() within the metallicity range covered by Galactic GCs.
within the metallicity range covered by Galactic GCs.
Results. During central He-burning, rotational mixing transports fresh CO-rich material from the core towards the hydrogen-burning shell, leading to the production of primary 14N. In stars more massive than M![]() 4 M
4 M![]() , the convective envelope reaches this reservoir during the second dredge-up episode, resulting in a large increase in the total C+N+O content at the stellar surface and in the stellar wind. The corresponding pollution depends on the initial metallicity. At low- and intermediate-metallicity (i.e., [Fe/H] lower than or equal to
, the convective envelope reaches this reservoir during the second dredge-up episode, resulting in a large increase in the total C+N+O content at the stellar surface and in the stellar wind. The corresponding pollution depends on the initial metallicity. At low- and intermediate-metallicity (i.e., [Fe/H] lower than or equal to ![]() - 1.2), it is at odds with the constancy of C+N+O observed among GC low-mass stars.
- 1.2), it is at odds with the constancy of C+N+O observed among GC low-mass stars.
Conclusions. With the given input physics, our models suggest that massive (i.e., ![]() 4 M
4 M![]() ) rotating AGB stars have not shaped the abundance patterns observed in low- and intermediate-metallicity GCs. Our non-rotating models, on the other hand, do not predict surface C+N+O enhancements, hence are in a better position as sources of the chemical anomalies in GCs showing the constancy of the C+N+O. However at the moment, there is no reason to think that intermediate-mass stars were not rotating. On the contrary there is observational evidence that stars in clusters have higher rotational velocities than in the field.
) rotating AGB stars have not shaped the abundance patterns observed in low- and intermediate-metallicity GCs. Our non-rotating models, on the other hand, do not predict surface C+N+O enhancements, hence are in a better position as sources of the chemical anomalies in GCs showing the constancy of the C+N+O. However at the moment, there is no reason to think that intermediate-mass stars were not rotating. On the contrary there is observational evidence that stars in clusters have higher rotational velocities than in the field.
Key words: stars: AGB and post-AGB - star: rotation - star: abundances - globular clusters: general
1 Introduction
While the abundances of heavy elements (i.e., Fe-group andWe now have compelling evidence that these peculiar chemical patterns were present in the intracluster gas from which second-generation (anomalous) low-mass stars formed, and that they resulted from the dilution of pristine material with the hydrogen-burning products ejected by a first generation of more massive and faster evolving GC stars (for a review see Prantzos et al. 2007).
Massive AGB stars that undergo efficient hot-bottom burning (HBB) during the thermal pulse phase (TP-AGB) have been proposed as the possible GC polluters in this so-called self-enrichment scenario (Ventura et al. 2001). The AGB hypothesis has been extensively discussed in the literature, first on a qualitative basis, and more recently with the help of custom-made standard (i.e., non-rotating) stellar models (Herwig 2004a; Ventura & D'Antona 2005b; Ventura et al. 2001; Ventura & D'Antona 2008b; Ventura et al. 2002; Ventura & D'Antona 2008a; Herwig 2004b; Ventura & D'Antona 2005c; Bekki et al. 2007; Denissenkov & Herwig 2003; Fenner et al. 2004; Ventura & D'Antona 2005a; Karakas & Lattanzio 2003). These studies point out several difficulties in building the observed chemical patterns in theoretical TP-AGB models. The main problem stems from the competition between the third dredge-up (3DUP) that contaminates the AGB envelope with the helium-burning ashes produced in the thermal pulse and HBB that modifies the envelope abundances via the CNO-cycle and the NeNa- and MgAl-chains. It is thus very difficult to obtain simultaneous O depletion and Na enrichment in the TP-AGB envelope, while keeping the C+N+O sum constant as required by the observations (see Charbonnel 2007, for more details and references).
To date, only AGB models in the mass range 5-6.5 M![]() have
managed to simultaneously achieve an encouraging agreement with
the observed O depletion and the Na enrichment
(Ventura & D'Antona 2008a). These models include the FST
formulation for convection (Canuto et al. 1996), which
strongly affects the O depletion once the stars enter the TP-AGB
(Ventura & D'Antona 2005b). Compared to the classical MLT
treatment, FST indeed leads to higher temperatures at the base of
the convective envelope (resulting in more advanced
nucleosynthesis) and induces higher surface luminosities resulting
in stronger mass loss and thus fewer thermal pulses and 3DUP
events. As shown by Ventura & D'Antona (2005b), some O depletion
can also be obtained with the MLT prescription, but only when the
free parameter
have
managed to simultaneously achieve an encouraging agreement with
the observed O depletion and the Na enrichment
(Ventura & D'Antona 2008a). These models include the FST
formulation for convection (Canuto et al. 1996), which
strongly affects the O depletion once the stars enter the TP-AGB
(Ventura & D'Antona 2005b). Compared to the classical MLT
treatment, FST indeed leads to higher temperatures at the base of
the convective envelope (resulting in more advanced
nucleosynthesis) and induces higher surface luminosities resulting
in stronger mass loss and thus fewer thermal pulses and 3DUP
events. As shown by Ventura & D'Antona (2005b), some O depletion
can also be obtained with the MLT prescription, but only when the
free parameter ![]() is arbitrarily and strongly modified with
respect to the value calibrated on the Sun. These models are also
able to produce a slight decrease in Mg accompanied with a large
increase in Al.
is arbitrarily and strongly modified with
respect to the value calibrated on the Sun. These models are also
able to produce a slight decrease in Mg accompanied with a large
increase in Al.
The Na enrichment is more difficult to estimate and requires
fine-tuning of the NeNa-cycle reaction rates. More precisely, an
increase in sodium is achieved in the most oxygen-poor ejecta of
the 5-6.5 M![]() models only when the maximum allowed values for
the 22Ne(p,
models only when the maximum allowed values for
the 22Ne(p,![]() ) rate are adopted. In summary, and as
clearly stated by Ventura & D'Antona (2008a), the AGB scenario is
viable from the nucleosynthesis point of view, provided that only
massive AGB stars of 5-6.5 M
) rate are adopted. In summary, and as
clearly stated by Ventura & D'Antona (2008a), the AGB scenario is
viable from the nucleosynthesis point of view, provided that only
massive AGB stars of 5-6.5 M![]() contribute to the GC
self-enrichment, and under the physical assumptions described
above.
contribute to the GC
self-enrichment, and under the physical assumptions described
above.
However the previously quoted models have only focused on physical uncertainties related to the TP-AGB phase, and their predictions have not been tested in different astrophysical contexts. In particular, the impact of rotation in our models on the nucleosynthesis predictions for AGB stars has never been investigated in the context of the GC self-enrichment scenario, although rotation is often invoked to understand a wide variety of observations (e.g., Maeder & Meynet 2000,2006; Chiappini et al. 2008, see Sect. 4). The present paper addresses this question for the first time, using up-to-date treatment for rotation-induced processes. As we shall see, the main signature of rotation on the chemical composition of the stellar envelope and winds of intermediate-mass stars already show up during the second dredge-up event and cannot be erased during the TP-AGB phase.
2 Physical input of the stellar models
Although only massive AGB stars in a very narrow mass range
between 5 and 6.5 M![]() are now suspected to play a role in the
self-enrichment scenario
(Ventura & D'Antona 2008a,b), we computed
standard and rotating models of 2.5, 3, 4, 5, 7 and 8 M
are now suspected to play a role in the
self-enrichment scenario
(Ventura & D'Antona 2008a,b), we computed
standard and rotating models of 2.5, 3, 4, 5, 7 and 8 M![]() stars
with the code STAREVOL (V2.75) (Siess 2006; Siess et al. 2000).
We present results for several metallicities, namely
Z = 4 x 10-3, 10-3,
5 x 10-4, 10-4 and 10-5(i.e.,
[Fe/H]
stars
with the code STAREVOL (V2.75) (Siess 2006; Siess et al. 2000).
We present results for several metallicities, namely
Z = 4 x 10-3, 10-3,
5 x 10-4, 10-4 and 10-5(i.e.,
[Fe/H] ![]() -0.66, - 1.26, - 1.56, - 2.26 and -3.26,
respectively)
-0.66, - 1.26, - 1.56, - 2.26 and -3.26,
respectively)![]() . The composition is scaled
solar according to the Grevesse & Sauval (1998) mixture and
enhancement in
. The composition is scaled
solar according to the Grevesse & Sauval (1998) mixture and
enhancement in ![]() -elements
([
-elements
([
![]() /Fe] = + 0.3 dex) is accounted for. All models were
evolved up to the completion of the 2DUP.
/Fe] = + 0.3 dex) is accounted for. All models were
evolved up to the completion of the 2DUP.
We used the OPAL opacity tables (Iglesias & Rogers 1996) above
T > 8000 K that account for C and O enrichments, and the
Ferguson et al. (2005) data at lower temperatures. We
followed the evolution of 53 chemical species from
![]() to
to
![]() using the NACRE nuclear reaction rates
(Angulo et al. 1999) by default and those by
Caughlan & Fowler (1988) otherwise
(see Siess & Arnould 2008). The treatment of convection is
based on the classical mixing length formalism with
using the NACRE nuclear reaction rates
(Angulo et al. 1999) by default and those by
Caughlan & Fowler (1988) otherwise
(see Siess & Arnould 2008). The treatment of convection is
based on the classical mixing length formalism with
![]() = 1.75, and no convective overshoot is included. The mass
loss rates are computed with Reimers (1975) formula (with
= 1.75, and no convective overshoot is included. The mass
loss rates are computed with Reimers (1975) formula (with
![]() = 0.5).
= 0.5).
For the treatment of rotation-induced processes we proceed as
follows. Solid-body rotation is assumed on the ZAMS and a typical
initial surface velocity of 300 km s-1 is chosen for all the
models. (The impact of this choice is discussed in
Sect. 3.3 where we present models computed with initial
rotation velocities ranging from 50 to 500 km s-1.) On the main
sequence, the evolution of the internal angular momentum profile
is accounted for with the complete formalism developed by
Zahn (1992) and Maeder & Zahn (1998) (see
Palacios et al. 2003; Decressin et al. 2009; Palacios et al. 2006
for a description of the implementation in STAREVOL), which takes
advection by meridional circulation and diffusion by shear
turbulence into account. The initial solid-body profile relaxes on
the main sequence on a short timescale of a few Myr and generates
differential rotation. For our most massive stellar models
(M![]() 4 M
4 M![]() ), the complete formalism for angular momentum
transport is applied up to the 2DUP. For the lower mass models,
however, the complete treatment is only applied up to the end of
the main sequence, while a more crude approach is used in the more
advanced evolution phases where angular momentum evolves only
through local conservation (i.e., only the structural changes
modify the angular momentum). This simplification is motivated by
the evolutionary timescale (i.e., the Kelvin-Helmholtz timescale
on the RGB) becoming shorter than the meridional circulation
timescale. We test this assumption by running a 5 and 7 M
), the complete formalism for angular momentum
transport is applied up to the 2DUP. For the lower mass models,
however, the complete treatment is only applied up to the end of
the main sequence, while a more crude approach is used in the more
advanced evolution phases where angular momentum evolves only
through local conservation (i.e., only the structural changes
modify the angular momentum). This simplification is motivated by
the evolutionary timescale (i.e., the Kelvin-Helmholtz timescale
on the RGB) becoming shorter than the meridional circulation
timescale. We test this assumption by running a 5 and 7 M![]() with and without the full treatment of rotational mixing and the
results show little difference, validating our approximation. In
all cases the transport of chemical species resulting from
meridional circulation and both vertical and horizontal turbulence
is computed as a diffusive process (Chaboyer & Zahn 1992)
throughout the evolution.
with and without the full treatment of rotational mixing and the
results show little difference, validating our approximation. In
all cases the transport of chemical species resulting from
meridional circulation and both vertical and horizontal turbulence
is computed as a diffusive process (Chaboyer & Zahn 1992)
throughout the evolution.
3 Signatures of rotation-induced mixing up to the early-AGB phase
3.1 Models at [Fe/H] = -1.56
Up to the beginning of the TP-AGB phase, the surface composition
of the standard models is only modified by the dredge-up event(s).
Let us note that only the 2.5 and 3 M![]() models undergo deep
enough first dredge-up so as to modify their surface abundances;
however, all stars experience to various extents the second
dredge-up (hereafter 2DUP) after central He-exhaustion. As
described below, in the rotating models the effects of additional
mixing become visible at the stellar surface during the quiescent
central He-burning phase.
models undergo deep
enough first dredge-up so as to modify their surface abundances;
however, all stars experience to various extents the second
dredge-up (hereafter 2DUP) after central He-exhaustion. As
described below, in the rotating models the effects of additional
mixing become visible at the stellar surface during the quiescent
central He-burning phase.
![\begin{figure}
{%
\par\includegraphics[width=18cm]{11822fg1} }
\end{figure}](/articles/aa/full_html/2009/38/aa11822-09/Timg27.png) |
Figure 1:
Chemical profiles (in mass fraction) at the end of central
He-burning in rotating (top) and standard (bottom) 5 M |
| Open with DEXTER | |
Figure 1 shows the abundance profiles (in mass
fraction) of
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
as well as the total sum C+N+O, at the end of central
He-burning and before the 2DUP, for standard (lower row) and
rotating (upper row) 5 M
,
as well as the total sum C+N+O, at the end of central
He-burning and before the 2DUP, for standard (lower row) and
rotating (upper row) 5 M![]() model.
model.
In the standard case, 14N steadily increases as one moves
inwards through the H-rich radiative layers down to the He-buffer
(located between
Mr ![]() 0.7 and 1.2 M
0.7 and 1.2 M![]() ) as a result of
CNO processing. Further inside, the stellar core has experienced
complete He-burning and is essentially made of
) as a result of
CNO processing. Further inside, the stellar core has experienced
complete He-burning and is essentially made of
![]() and
and
![]() .
In this 5 M
.
In this 5 M![]() model, during the 2DUP, the convective
envelope penetrates into the He-rich buffer (down to
Mr
model, during the 2DUP, the convective
envelope penetrates into the He-rich buffer (down to
Mr ![]() 0.85 M
0.85 M![]() ) as indicated by the hatched area.
This produces an envelope enrichment in H-burning ashes: the
surface abundances of
) as indicated by the hatched area.
This produces an envelope enrichment in H-burning ashes: the
surface abundances of
![]() and
and
![]() decrease, while
that of
decrease, while
that of
![]() and
and
![]() increase. The sum C+N+O, however,
remains constant, since only the H-burning products are dredged
up.
increase. The sum C+N+O, however,
remains constant, since only the H-burning products are dredged
up.
Rotation-induced mixing strongly modifies the internal chemical
structure. As shown in the upper-row panels of
Fig. 1, the abundance gradients are smoothed
out in the radiative envelope (i.e., the region above the He-rich
buffer up to the surface or the convective envelope) compared to
the standard case:
![]() produced in the internal H-burning
layers diffuses outwards, while the
produced in the internal H-burning
layers diffuses outwards, while the
![]() and
and
![]() present in the envelope are transported inwards. As a
consequence, during the whole central He-burning phase, rotational
mixing produces a continuous surface increase in
present in the envelope are transported inwards. As a
consequence, during the whole central He-burning phase, rotational
mixing produces a continuous surface increase in
![]() concomitant to a decrease in
concomitant to a decrease in
![]() and
and
![]() .
At the
same time, the products of central helium-burning, namely
.
At the
same time, the products of central helium-burning, namely
![]() and
and
![]() ,
also diffuse outwards in the He-rich
buffer (i.e., the region where He is the dominant species, between
0.6 and 1.4 M
,
also diffuse outwards in the He-rich
buffer (i.e., the region where He is the dominant species, between
0.6 and 1.4 M![]() in Fig. 1).
in Fig. 1).
The transport of chemical species is mainly driven by shear
turbulence (
Dshear ![]() 108 cm s-1) in the
radiative envelope and in the He-rich layer. At the interface of
these two regions, i.e., at the base of the hydrogen-burning shell
(HBS), the large mean molecular weight gradient strongly reduces
the efficiency of mixing (
Dshear
108 cm s-1) in the
radiative envelope and in the He-rich layer. At the interface of
these two regions, i.e., at the base of the hydrogen-burning shell
(HBS), the large mean molecular weight gradient strongly reduces
the efficiency of mixing (
Dshear ![]() 103 cm s-1),
thus preventing the transport of primary C, N and O from the
He-rich buffer to the HBS, hence thus to the surface during
central He-burning. At the same time, hydrogen from the envelope
is also transported inwards and rapidly captured by
103 cm s-1),
thus preventing the transport of primary C, N and O from the
He-rich buffer to the HBS, hence thus to the surface during
central He-burning. At the same time, hydrogen from the envelope
is also transported inwards and rapidly captured by
![]() and
and
![]() nuclei through CNO burning at high temperature. This
leads to the production of a peak of primary
nuclei through CNO burning at high temperature. This
leads to the production of a peak of primary
![]() at
the base of the HBS as seen in Fig. 1. The
resulting chemical profiles at the end of central He-burning thus
differ significantly from those obtained in the standard case
where
at
the base of the HBS as seen in Fig. 1. The
resulting chemical profiles at the end of central He-burning thus
differ significantly from those obtained in the standard case
where
![]() is only produced in the HBS from the
is only produced in the HBS from the
![]() and
and
![]() originally present in the star and is therefore of
secondary origin (Meynet & Maeder 2002). During the subsequent
2DUP, the convective envelope of the 5 M
originally present in the star and is therefore of
secondary origin (Meynet & Maeder 2002). During the subsequent
2DUP, the convective envelope of the 5 M![]() rotating model
reaches the polluted He-rich buffer (see
Fig. 1) producing a large increase in
rotating model
reaches the polluted He-rich buffer (see
Fig. 1) producing a large increase in
![]() .
Simultaneously the primary CNO and thus the overall
metallicity increases in the envelope.
.
Simultaneously the primary CNO and thus the overall
metallicity increases in the envelope.
In the 2.5 and 3 M![]() rotating models, the convective envelope
does not reach the contaminated He-buffer during the 2DUP. As a
consequence in these low-mass models, only the H-burning products
are dredged up to the surface:
rotating models, the convective envelope
does not reach the contaminated He-buffer during the 2DUP. As a
consequence in these low-mass models, only the H-burning products
are dredged up to the surface:
![]() strongly increases,
while
strongly increases,
while
![]() and
and
![]() decrease, but the sum C+N+O, as
well as the total metallicity, remain unchanged (see
Table 1).
decrease, but the sum C+N+O, as
well as the total metallicity, remain unchanged (see
Table 1).
![]() also diffuses outwards into the
radiative envelope leading to a surface
also diffuses outwards into the
radiative envelope leading to a surface
![]() -enhancement by
about 0.03 (in mass fraction) compared to non-rotating models.
-enhancement by
about 0.03 (in mass fraction) compared to non-rotating models.
Table 1 summarises the abundance variations after the
2DUP in all our standard and rotating models at
[Fe/H] = - 1.56.
The main signature of rotational mixing at the surface of massive
early-AGB stars (
![]() )
is a strong increase in He-burning
products, i.e., primary CNO (see also Fig. 2). As
all rotating models produce an enrichment of CNO elements inside
the He-buffer, the total increase of C+N+O at the surface of
rotating models mainly depends on the depth reached by the
convective envelope during the 2DUP. We thus obtain a stronger
variation with increasing stellar mass.
)
is a strong increase in He-burning
products, i.e., primary CNO (see also Fig. 2). As
all rotating models produce an enrichment of CNO elements inside
the He-buffer, the total increase of C+N+O at the surface of
rotating models mainly depends on the depth reached by the
convective envelope during the 2DUP. We thus obtain a stronger
variation with increasing stellar mass.
Table 1:
Surface abundance variations after the completion of the 2DUP
with respect to the initial composition
(
![]() )
for the models with initial value of
[Fe/H] = - 1.56.
)
for the models with initial value of
[Fe/H] = - 1.56.
3.2 Influence of metallicity
![\begin{figure}
{%
\par\includegraphics[width=8.8cm]{11822fg2} }
\end{figure}](/articles/aa/full_html/2009/38/aa11822-09/Timg29.png) |
Figure 2:
Surface C+N+O increase index (
|
| Open with DEXTER | |
The impact of rotation on stellar properties and stellar yields is
known to depend strongly on metallicity (see,
e.g., Meynet & Maeder 2002). The metallicity dependence of our
predictions is depicted in Fig. 1 showing the
internal profiles of
![]() ,
,
![]() ,
and
,
and
![]() at the
end of central He-burning in standard and rotating 5 M
at the
end of central He-burning in standard and rotating 5 M![]() models
at four different metallicities (
[Fe/H]
models
at four different metallicities (
[Fe/H] ![]() -1.26,
-1.56, -2.26 and -3.26). As previously explained, the C+N+O
profile outside the CO core is constant in the standard models,
while it strongly increases in the He-rich layers below the HBS in
the rotating models. This C+N+O step is higher in lower
metallicity stars, which results in a stronger CNO surface
enrichment after 2DUP in the most metal-poor stars as shown in
Fig. 2. The maximal depth reached by the
convective envelope for a given stellar mass hardly depends on
metallicity; e.g., it reaches 1.04 and 1.07 M
-1.26,
-1.56, -2.26 and -3.26). As previously explained, the C+N+O
profile outside the CO core is constant in the standard models,
while it strongly increases in the He-rich layers below the HBS in
the rotating models. This C+N+O step is higher in lower
metallicity stars, which results in a stronger CNO surface
enrichment after 2DUP in the most metal-poor stars as shown in
Fig. 2. The maximal depth reached by the
convective envelope for a given stellar mass hardly depends on
metallicity; e.g., it reaches 1.04 and 1.07 M![]() for the 7 M
for the 7 M![]() at
Z = 10-3 and
Z = 10-4.
at
Z = 10-3 and
Z = 10-4.
At
[Fe/H] = - 2.26, the envelope (and thus the wind) of all the
stars more massive than ![]() 5 M
5 M![]() undergo a C+N+O increase by
1 to 2 orders of magnitude, while an increase by a factor of 5 is
obtained at
[Fe/H] = - 1.26. When metallicity becomes
higher than
[Fe/H]
undergo a C+N+O increase by
1 to 2 orders of magnitude, while an increase by a factor of 5 is
obtained at
[Fe/H] = - 1.26. When metallicity becomes
higher than
[Fe/H] ![]() - 1, rotation-induced mixing
increases the total C+N+O by less than a factor 2-3, which is
undetectable with current observations (see Sect. 5).
The effect is null at
[Fe/H] = - 0.66.
- 1, rotation-induced mixing
increases the total C+N+O by less than a factor 2-3, which is
undetectable with current observations (see Sect. 5).
The effect is null at
[Fe/H] = - 0.66.
3.3 Influence of initial rotation velocity
![\begin{figure}{%
\par\includegraphics[width=8.8cm]{11822fg3} }
\end{figure}](/articles/aa/full_html/2009/38/aa11822-09/Timg30.png) |
Figure 3:
Top: enrichment in C+N+O after the 2DUP completion as a
function of the mean main sequence velocity for a 5 M |
| Open with DEXTER | |
We present several models for the 5 M![]() star at
Z = 0.0005(
[Fe/H] = - 1.56) with initial rotation velocities between
0 and 500 km s-1 as part of investigating the dependence of our
results on this parameter. As shown in Fig. 3,
the C+N+O enhancement increases with increasing initial rotation.
A higher initial velocity leads to a faster spinning core and to a
larger differential rotation at the core edge during central
He-burning. Since mixing stems mainly from shear turbulence and
scales as
(
star at
Z = 0.0005(
[Fe/H] = - 1.56) with initial rotation velocities between
0 and 500 km s-1 as part of investigating the dependence of our
results on this parameter. As shown in Fig. 3,
the C+N+O enhancement increases with increasing initial rotation.
A higher initial velocity leads to a faster spinning core and to a
larger differential rotation at the core edge during central
He-burning. Since mixing stems mainly from shear turbulence and
scales as
(![]()
![]() /
/![]() r)2(Talon & Zahn 1997), more CNO elements are stored in the He-rich
buffer and then revealed at the surface after 2DUP. In the model
with an initial velocity of 150 km s-1, the C+N+O rises by a
factor 3, while it increases by more than a factor 14 for an
initial velocity of 500 km s-1.
r)2(Talon & Zahn 1997), more CNO elements are stored in the He-rich
buffer and then revealed at the surface after 2DUP. In the model
with an initial velocity of 150 km s-1, the C+N+O rises by a
factor 3, while it increases by more than a factor 14 for an
initial velocity of 500 km s-1.
4 Discussion on the model uncertainties
4.1 Mean rotation velocity
As shown above, the total C+N+O enhancement depends on the assumed initial rotational velocity. We note that, for an initial (i.e., ZAMS) velocity of 300 km s-1, the time-averaged velocity of our models on the main sequence ranges between 220 and 256 km s-1 depending on the stellar mass and metallicity. What are the observational constraints on this ingredient?
Martayan et al. (2006,2007a) find mean vsin iof 161 ![]() 20 km s-1 and 155
20 km s-1 and 155 ![]() 20 km s-1 for SMC B-type stars of
2-5 M
20 km s-1 for SMC B-type stars of
2-5 M![]() (111 stars) and 5-10 M
(111 stars) and 5-10 M![]() (81 stars), respectively.
Accounting in a statistical way for the sin i effect (i.e.,
multiplying the averaged vsin i by 4/
(81 stars), respectively.
Accounting in a statistical way for the sin i effect (i.e.,
multiplying the averaged vsin i by 4/![]() supposing a random
distribution of the rotational axis), we obtain averaged values
for v between 197 and 205 km s-1 for B-type stars in the SMC. At
first glance, the main-sequence time-averaged velocity of our
models is slightly higher than the observed values for SMC stars.
However, the following points have to be considered:
supposing a random
distribution of the rotational axis), we obtain averaged values
for v between 197 and 205 km s-1 for B-type stars in the SMC. At
first glance, the main-sequence time-averaged velocity of our
models is slightly higher than the observed values for SMC stars.
However, the following points have to be considered:
- 1.
- The mean observed values quoted above do not account for Be-type
stars. Let us recall that Be stars are fast rotators that present
emission lines originating in an outward equatorial expanding disk
probably formed due to strong stellar rotation
(Martayan et al. 2007b). Therefore Be stars belong to the upper part
of the velocity distribution, and it is legitimate to incorporate them in
the estimate of the averaged velocities of B-type stars. Taking them into
account does enhance the observed average velocities. As an illustrative
example, the mean vsin i for SMC Be stars in the mass ranges
2-5,
5-10 M
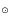 are
277
are
277 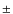 34 km s-1(14 stars) and
297
34 km s-1(14 stars) and
297 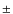 25 km s-1(81
stars), respectively. As can be seen in Fig. 3, our
assumptions on the stellar rotation velocities are thus totally
realistic.
25 km s-1(81
stars), respectively. As can be seen in Fig. 3, our
assumptions on the stellar rotation velocities are thus totally
realistic.
- 2.
- Martayan et al. (2007a) (see also Hunter et al. 2008b) find that, for both B and Be stars, the lower the metallicity, the higher the rotational velocities. This agrees with the finding by Maeder et al. (1999) and Wisniewski & Bjorkman (2006) that the fraction of Be stars with respect to the total number of B+Be stars increases when the metallicity decreases. Since the metallicities considered in this work are lower than that of the SMC, we may expect that the averaged velocities of the stars would be somewhat higher than the one quoted above for the SMC.
- 3.
- Last but not least, there is evidence that the rotation rates of stars are higher in clusters than in the field (Strom et al. 2005; Wolff et al. 2007; Huang & Gies 2005; Keller 2004; Dufton et al. 2006).
4.2 Treatment of rotation
Of course, rotating models are not free from uncertainties and their predictions should be carefully compared with well-observed features. The physics included in the present models is the same as the one that provides a good fit to the following observed features:- the surface enrichments in nitrogen in main-sequence B-type stars (Maeder et al. 2009), even if invoking binarity or magnetic fields is required to explain the whole observational pattern (Hunter et al. 2008a);
- the observed number ratio of blue to red supergiants in the SMC (Maeder & Meynet 2001);
- the variation with the metallicity of the number fraction of WR to O-type stars (Meynet & Maeder 2005,2003);
- the variation with metallicity of the number ratio of type Ibc to type II core collapse supernovae (Meynet & Maeder 2005);
- the lithium abundance patterns in A-type and early F-type dwarf stars, as well as in their subgiant descendants (Palacios et al. 2003; Charbonnel & Talon 1999).
4.3 Rotational rate of remnants
The present models have some difficulty, however, in accounting for the observed rotation rates of young pulsars and white dwarfs (see e.g., Suijs et al. 2008; Heger et al. 2005; Kawaler 1988). More precisely, they predict too fast rotation of the stellar cores in the advanced phases. This maybe stem from different causes that could lead to additional angular momentum loss from the central regions at different evolutionary phases:- already during the nuclear lifetime;
- at the time of the supernova explosion in the case of neutron stars or during the TP-AGB phase at the time of the superwind episode in the case of white dwarfs;
- by the neutron stars or the white dwarfs themselves shortly after their formation.
The study of the s-process nucleosynthesis in low-mass TP-AGB
stars could provide some hints to the rotational evolution of the
stellar core. At the moment the properties and the behaviour of
rotating TP-AGB stars are poorly known. Calculations using a
diffusive treatment for the transport of angular momentum by
Langer et al. (1999), Herwig et al. (2003) and
Siess et al. (2004) have shown that rotationally induced
instabilities provide enough mixing to trigger the 3DUPs. However,
a shear layer at the base of the convective envelope leads to an
efficient pollution of the
![]() pocket
pocket![]() (the neutron source) by
(the neutron source) by
![]() with the result of strongly inhibiting the
s-process nucleosynthesis.
This is at odds with the observations
of s-stars and tends to indicate that the modelling of rotation
used in these models needs to be improved and that angular
momentum must have been removed by the time the thermal pulses
start. Therefore, if the extraction of angular momentum occurs
before core He-burning, no CNO enrichment will be expected because
it relies on shear due to a fast spinning core. On the other hand,
if the extraction occurs during the early-AGB phase, it could
allow both the CNO enrichment of the He-buffer and the s-process
during the TP-AGB phase.
with the result of strongly inhibiting the
s-process nucleosynthesis.
This is at odds with the observations
of s-stars and tends to indicate that the modelling of rotation
used in these models needs to be improved and that angular
momentum must have been removed by the time the thermal pulses
start. Therefore, if the extraction of angular momentum occurs
before core He-burning, no CNO enrichment will be expected because
it relies on shear due to a fast spinning core. On the other hand,
if the extraction occurs during the early-AGB phase, it could
allow both the CNO enrichment of the He-buffer and the s-process
during the TP-AGB phase.
The mechanism frequently pointed to for removing angular momentum from the core is the magnetic field. For instance, Heger et al. (2005) have shown that magnetic coupling between the core and envelope can account for the rotation rates of young neutron stars. Suijs et al. (2008) also find that magnetic torques may be required to understand the slow spin rate of white dwarfs. However the dynamo model (Spruit 2002) on which the current rotating models with magnetic fields are based has recently been tested through hydrodynamical computations by Zahn et al. (2007), who do not find the amplification of the magnetic field as expected from the theory, casting some doubt on its validity. In view of the remaining theoretical uncertainties associated with the treatment of magnetic fields, it seems reasonable to stick to the present models whose predictions account for a broad variety of observations as described in Sect. 4.3.
Finally let us note that Talon & Charbonnel (2008) predict that angular momentum transport by internal gravity waves should be efficient in intermediate-mass stars during the early-AGB phase. If these waves were the culprit, then the predictions of the present models would be valid as far as the CNO enrichment is concerned since it builds up earlier in the life of the star.
5 Consequences for the self-enrichment scenario
5.1 Summary of the theoretical predictions
During central He-burning, rotational mixing efficiently
transports primary 12C and 16O outside the
convective core in the H-burning region where these elements are
processed by the CNO-cycle, resulting in an important production
of primary 14N. In the massive (M![]() 4 M
4 M![]() ) rotating
models, after central He-exhaustion, the convective envelope
penetrates into the layers affected by rotation-induced mixing. In
contrast to standard models, the 2DUP produces a large surface
enrichment in total C+N+O that cannot be erased by hot-bottom
(hydrogen) burning during the subsequent TP-AGB evolution. 3DUP
episodes further increase the total C+N+O mass fraction as they
bring the products of He-burning to the surface.
) rotating
models, after central He-exhaustion, the convective envelope
penetrates into the layers affected by rotation-induced mixing. In
contrast to standard models, the 2DUP produces a large surface
enrichment in total C+N+O that cannot be erased by hot-bottom
(hydrogen) burning during the subsequent TP-AGB evolution. 3DUP
episodes further increase the total C+N+O mass fraction as they
bring the products of He-burning to the surface.
As a consequence, if rotating massive AGB stars were responsible
for the abundance patterns observed in GCs, one would expect large
C+N+O differences between (O-rich and Na-poor) first-generation
stars and (O-poor and Na-rich) second-generation stars (see
e.g., Prantzos & Charbonnel 2006). Such differences would easily
amount to 1.6 dex in GCs with
[Fe/H] ![]() - 1.5, and to 2.2 dex
in the most metal-poor clusters with
[Fe/H]
- 1.5, and to 2.2 dex
in the most metal-poor clusters with
[Fe/H] ![]() - 2.2 for the
cases where the ejecta of the first-generation would not have been
diluted with pristine material. Diluting these ejecta with 10
times more pristine material would still give differences of 0.6
to 1.2 dex, well above the observed dispersion (see
Sect. 5.2). Actually, to maintain C+N+O constant would
require such a high dilution of the ejecta with the intracluster
matter that the O-Na and Mg-Al anticorrelations would be erased
and, as far as abundances are concerned, first- and
second-generation stars would be indistinguishable.
- 2.2 for the
cases where the ejecta of the first-generation would not have been
diluted with pristine material. Diluting these ejecta with 10
times more pristine material would still give differences of 0.6
to 1.2 dex, well above the observed dispersion (see
Sect. 5.2). Actually, to maintain C+N+O constant would
require such a high dilution of the ejecta with the intracluster
matter that the O-Na and Mg-Al anticorrelations would be erased
and, as far as abundances are concerned, first- and
second-generation stars would be indistinguishable.
5.2 Comparison with the observations
C, N and O abundances have been determined simultaneously in stars of several GCs. Up to now, no significant star-to-star variation of the total C+N+O has been detected, except in NGC 1851.
In the case of the most metal-rich GCs such as 47 Tuc (Carretta et al. 2005) and NGC 6712 (Yong et al. 2008), this C+N+O constancy is actually compatible with pollution by both standard and rotating AGB stars since the 2DUP CNO enrichment is found to be negligible in the most metal-rich rotating models. This is of course without considering possible C+N+O increase due to the 3DUP of He-processed material during the TP-AGB phase, which is beyond the scope of the present study.
In the case of intermediate-metallicity (
[Fe/H] ![]() - 1.2) GCs, such as NGC 288 and NGC 362 (Dickens et al. 1991) and M4
(Ivans et al. 1999; Smith et al. 2005), the total C+N+O is found
constant from star-to-star, within observational uncertainties
that amount to
- 1.2) GCs, such as NGC 288 and NGC 362 (Dickens et al. 1991) and M4
(Ivans et al. 1999; Smith et al. 2005), the total C+N+O is found
constant from star-to-star, within observational uncertainties
that amount to ![]() 0.25-0.3 dex. At this metallicity, the most
massive intermediate-mass rotating models (M
0.25-0.3 dex. At this metallicity, the most
massive intermediate-mass rotating models (M ![]() 5) predict a
C+N+O increase between 0.5 and 0.7 dex at odds with the
observations. The only exception is NGC 1851
5) predict a
C+N+O increase between 0.5 and 0.7 dex at odds with the
observations. The only exception is NGC 1851 ![]() -1.2]YongGrundahl2009, where variations in the total CNO
by 0.57
-1.2]YongGrundahl2009, where variations in the total CNO
by 0.57 ![]() 0.15 dex were found, which is compatible with the
CNO enrichment produced by our rotating models as shown in
Fig. 2. We note, however, that the stars observed
by Yong and collaborators in NGC 1851 are very bright objects. In
view of its position in the colour-magnitude diagram, the only
star with C+N+O exceeding the typical error bar could actually be
an AGB star. In that case, the high value of the total CNO may not
have been inherited at birth by the star, but may instead be due
to nuclear processes within the star itself. Being an AGB would
also explain why this star is the only one among the sample to
exhibit some enhancement in s-process elements. We note that in
this cluster a double subgiant branch has been detected by
photometric measurements (Milone et al. 2008) that can be
interpreted as caused by an age difference among cluster stars of
about 1 Gyr
0.15 dex were found, which is compatible with the
CNO enrichment produced by our rotating models as shown in
Fig. 2. We note, however, that the stars observed
by Yong and collaborators in NGC 1851 are very bright objects. In
view of its position in the colour-magnitude diagram, the only
star with C+N+O exceeding the typical error bar could actually be
an AGB star. In that case, the high value of the total CNO may not
have been inherited at birth by the star, but may instead be due
to nuclear processes within the star itself. Being an AGB would
also explain why this star is the only one among the sample to
exhibit some enhancement in s-process elements. We note that in
this cluster a double subgiant branch has been detected by
photometric measurements (Milone et al. 2008) that can be
interpreted as caused by an age difference among cluster stars of
about 1 Gyr ![]() . However, Cassisi et al. (2008) propose to fit
the double sequence assuming two coeval cluster stellar populations with a
C+N+O difference of a factor of 2. CNO measurements in NGC 1851 unevolved
stars (as done in most of the other clusters studied so far) are thus
crucial for settling the problem.
. However, Cassisi et al. (2008) propose to fit
the double sequence assuming two coeval cluster stellar populations with a
C+N+O difference of a factor of 2. CNO measurements in NGC 1851 unevolved
stars (as done in most of the other clusters studied so far) are thus
crucial for settling the problem.
Finally, the CNO predictions for the rotating most massive intermediate
mass models lead to increasing factors up to 10 (5 M![]() ) and 100 (7 M
) and 100 (7 M![]() )
at low-metallicity (
[Fe/H] = - 2.2), in clear contradiction with
the observations in the metal-poor clusters studied so far, i.e., M3 and
M13 (Smith et al. 1996; Cohen & Meléndez 2005), NGC 6752, and
NGC 6397(Carretta et al. 2005)
)
at low-metallicity (
[Fe/H] = - 2.2), in clear contradiction with
the observations in the metal-poor clusters studied so far, i.e., M3 and
M13 (Smith et al. 1996; Cohen & Meléndez 2005), NGC 6752, and
NGC 6397(Carretta et al. 2005)![]() . CNO measurements in other very metal-poor GCs like
M15 or M92 would be extremely valuable in this context.
. CNO measurements in other very metal-poor GCs like
M15 or M92 would be extremely valuable in this context.
6 Conclusions
In this paper we have investigated the effects of rotation in low-metallicity intermediate-mass stars during their evolution up to the completion of the 2DUP and arrival on the AGB. Our rotating stellar models include the complete formalism developed by Zahn (1992) and Maeder & Zahn (1998) and accounts for the transport of chemicals and angular momentum by meridional circulation and shear turbulence. With respect to standard models, the most important change concerning the nucleosynthesis is the large 14N production resulting from the diffusion of protons below the HBS in a region enriched with primary C and O during central He-burning. During the subsequent 2DUP, the convective envelope of massive AGB stars deepens in this region, producing a large surface increase in the total C+N+O, which irreversibly imprints the yields.
This behaviour is in sharp contrast to what is observed in low- and intermediate-metallicity GCs where the sum C+N+O is constant within the experimental errors. Our rotating models based on the Zahn (1992) formalism, which neglect the effects of magnetic fields and internal gravity waves, suggest that massive rotating AGB stars can be discarded as potential polluters in the self-enrichment scenario in GCs, unless the crowded environment prevented intermediate-mass stars from rotating. This latest hypothesis is highly improbable in view of the observations finding higher stellar rotation velocities in clusters than in the field.
Acknowledgements
We acknowledge financial support of the French Programme National de Physique Stellaire (PNPS) CNRS/INSU and of the Swiss National Science Foundation (FNS). L. S. is FNRS Research Associate and acknowledges financial support from the the Communauté française de Belgique - Actions de Recherche Concertées. We thank E. Carretta and A. Bragaglia for enlightening discussions.
References
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] (In the text)
- Bekki, K., Campbell, S. W., Lattanzio, J. C., & Norris, J. E. 2007, MNRAS, 377, 335 [NASA ADS] [CrossRef]
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] (In the text)
- Carretta, E., Gratton, R. G., Lucatello, S., Bragaglia, A., & Bonifacio, P. 2005, A&A, 433, 597 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] (In the text)
- Caughlan, G. R., & Fowler, W. A. 1988, At. Data Nucl. Data Tables, 40, 283 [NASA ADS] [CrossRef] (In the text)
- Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [NASA ADS] (In the text)
- Charbonnel, C. 2007, in Why Galaxies Care About AGB Stars: Their Importance as Actors and Probes, ed. F. Kerschbaum, C. Charbonnel, & R. F. Wing, ASP Conf. Ser., 378, 416 (In the text)
- Charbonnel, C., & Talon, S. 1999, A&A, 351, 635 [NASA ADS]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences]
- Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences]
- Cohen, J. G., & Meléndez, J. 2005, AJ, 129, 303 [NASA ADS] [CrossRef]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences]
- Denissenkov, P. A., & Herwig, F. 2003, ApJ, 590, L99 [NASA ADS] [CrossRef]
- Dickens, R. J., Croke, B. F. W., Cannon, R. D., & Bell, R. A. 1991, Nature, 351, 212 [NASA ADS] [CrossRef] (In the text)
- Dufton, P. L., Ryans, R. S. I., Simón-Díaz, S., Trundle, C., & Lennon, D. J. 2006, A&A, 451, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Fenner, Y., Campbell, S., Karakas, A. I., Lattanzio, J. C., & Gibson, B. K. 2004, MNRAS, 353, 789 [NASA ADS] [CrossRef]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] (In the text)
- Gratton, R. G. 2007, in From Stars to Galaxies: Building the Pieces to Build Up the Universe, ed. A. Vallenari, R. Tantalo, L. Portinari, & A. Moretti, ASP Conf. Ser., 374, 147 (In the text)
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef]
- Herwig, F. 2004a, ApJ, 605, 425 [NASA ADS] [CrossRef]
- Herwig, F. 2004b, ApJS, 155, 651 [NASA ADS] [CrossRef]
- Herwig, F., Langer, N., & Lugaro, M. 2003, ApJ, 593, 1056 [NASA ADS] [CrossRef] (In the text)
- Huang, W., & Gies, D. R. 2005, in Bull. Am. Astron. Soc., 1273
- Hunter, I., Brott, I., Lennon, D. J., et al. 2008a, ApJ, 676, L29 [NASA ADS] [CrossRef] (In the text)
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008b, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] (In the text)
- Ivans, I. I., Sneden, C., Kraft, R. P., et al. 1999, AJ, 118, 1273 [NASA ADS] [CrossRef]
- Johnson, C. I., Pilachowski, C. A., Simmerer, J., & Schwenk, D. 2008, ApJ, 681, 1505 [NASA ADS] [CrossRef]
- Karakas, A. I., & Lattanzio, J. C. 2003, PASA, 20, 279 [NASA ADS]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef]
- Keller, S. C. 2004, PASA, 21, 310 [NASA ADS]
- Langer, N., Heger, A., Wellstein, S., & Herwig, F. 1999, A&A, 346, L37 [NASA ADS] (In the text)
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Maeder, A., & Meynet, G. 2006, A&A, 448, L37 [NASA ADS] [CrossRef] [EDP Sciences]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] (In the text)
- Maeder, A., Grebel, E. K., & Mermilliod, J.-C. 1999, A&A, 346, 459 [NASA ADS] (In the text)
- Maeder, A., Meynet, G., Georgy, C., & Ekström, S. 2009, in IAU Symp., 259, 311 (In the text)
- Martayan, C., Frémat, Y., Hubert, A.-M., et al. 2006, A&A, 452, 273 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Martayan, C., Floquet, M., Hubert, A. M., et al. 2007a, A&A, 472, 577 [NASA ADS] [CrossRef] [EDP Sciences]
- Martayan, C., Frémat, Y., Hubert, A.-M., et al. 2007b, A&A, 462, 683 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [NASA ADS] [CrossRef] [EDP Sciences]
- Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] (In the text)
- Norris, J. E., & Da Costa, G. S. 1995, ApJ, 447, 680 [NASA ADS] [CrossRef]
- Palacios, A., Talon, S., Charbonnel, C., & Forestini, M. 2003, A&A, 399, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Palacios, A., Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453, 261 [NASA ADS] [CrossRef] [EDP Sciences]
- Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Prantzos, N., Charbonnel, C., & Iliadis, C. 2007, A&A, 470, 179 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Reimers, D. 1975, in Problems in Stellar Atmospheres and Envelopes, 229 (In the text)
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences]
- Siess, L., & Arnould, M. 2008, A&A, 489, 395 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS]
- Siess, L., Goriely, S., & Langer, N. 2004, A&A, 415, 1089 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Smith, G. H., Shetrone, M. D., Bell, R. A., Churchill, C. W., & Briley, M. M. 1996, AJ, 112, 1511 [NASA ADS] [CrossRef]
- Smith, V. V., Cunha, K., Ivans, I. I., et al. 2005, ApJ, 633, 392 [NASA ADS] [CrossRef]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Strom, S. E., Wolff, S. C., & Dror, D. H. A. 2005, AJ, 129, 809 [NASA ADS] [CrossRef]
- Suijs, M. P. L., Langer, N., Poelarends, A.-J., et al. 2008, A&A, 481, L87 [NASA ADS] [CrossRef] [EDP Sciences]
- Talon, S., & Charbonnel, C. 2008, A&A, 482, 597 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [NASA ADS] (In the text)
- Ventura, P., & D'Antona, F. 2005a, ApJ, 635, 149 [NASA ADS] [CrossRef]
- Ventura, P., & D'Antona, F. 2005b, A&A, 431, 279 [NASA ADS] [CrossRef] [EDP Sciences]
- Ventura, P., & D'Antona, F. 2005c, A&A, 439, 1075 [NASA ADS] [CrossRef] [EDP Sciences]
- Ventura, P., & D'Antona, F. 2008a, A&A, 479, 805 [NASA ADS] [CrossRef] [EDP Sciences]
- Ventura, P., & D'Antona, F. 2008b, MNRAS, 385, 2034 [NASA ADS] [CrossRef]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] (In the text)
- Ventura, P., D'Antona, F., & Mazzitelli, I. 2002, A&A, 393, 215 [NASA ADS] [CrossRef] [EDP Sciences]
- Walker, A. R. 1998, AJ, 116, 220 [NASA ADS] [CrossRef]
- Wisniewski, J. P., & Bjorkman, K. S. 2006, ApJ, 652, 458 [NASA ADS] [CrossRef] (In the text)
- Wolff, S. C., Strom, S. E., Dror, D., & Venn, K. 2007, AJ, 133, 1092 [NASA ADS] [CrossRef]
- Yong, D., Meléndez, J., Cunha, K., et al. 2008, ApJ, 689, 1020 [NASA ADS] [CrossRef] (In the text)
- Yong, D., Grundahl, F., D'Antona, F., et al. 2009, ApJ, 695, L62 [NASA ADS] [CrossRef]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] (In the text)
- Zahn, J.-P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... (GC)
![[*]](/icons/foot_motif.png)
- Except
 Cen (Norris & Da Costa 1995; Johnson et al. 2008).
Cen (Norris & Da Costa 1995; Johnson et al. 2008).
- ...
respectively)
![[*]](/icons/foot_motif.png)
- The models at
[Fe/H]
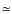 - 0.66 and -3.26 are actually from Maeder & Meynet (2001)
and Meynet & Maeder (2002), respectively. To check the
consistency of our predictions with those of the Geneva code, we
computed a 7 M
- 0.66 and -3.26 are actually from Maeder & Meynet (2001)
and Meynet & Maeder (2002), respectively. To check the
consistency of our predictions with those of the Geneva code, we
computed a 7 M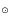 model at
Z = 10-5 with STAREVOL and found
excellent agreement in terms of both evolutionary and chemical
characteristics (see Fig. 2).
model at
Z = 10-5 with STAREVOL and found
excellent agreement in terms of both evolutionary and chemical
characteristics (see Fig. 2).
- ... pocket
![[*]](/icons/foot_motif.png)
- In this
framework, the
neutrons needed for the s-process are released in the
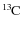 pocket
by
pocket
by
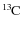 (
( ,n) reaction.
,n) reaction.
- ... 1 Gyr
![[*]](/icons/foot_motif.png)
- The hypothesis of two populations with similar age and [Fe/H] differing beyond the errorbars has been ruled out by the spectroscopic study of RGB stars by Yong et al. (2009) and by the photometric study of RR Lyrae by Walker (1998).
- ...(Carretta et al. 2005)
![[*]](/icons/foot_motif.png)
- NGC 6397
(
[Fe/H]
 -1.95) does not show a very extended O-Na
anticorrelation, a more modest C+N+O increase is expected in that
case.
-1.95) does not show a very extended O-Na
anticorrelation, a more modest C+N+O increase is expected in that
case.
All Tables
Table 1:
Surface abundance variations after the completion of the 2DUP
with respect to the initial composition
(
![]() )
for the models with initial value of
[Fe/H] = - 1.56.
)
for the models with initial value of
[Fe/H] = - 1.56.
All Figures
![\begin{figure}
{%
\par\includegraphics[width=18cm]{11822fg1} }
\end{figure}](/articles/aa/full_html/2009/38/aa11822-09/Timg27.png) |
Figure 1:
Chemical profiles (in mass fraction) at the end of central
He-burning in rotating (top) and standard (bottom) 5 M |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
{%
\par\includegraphics[width=8.8cm]{11822fg2} }
\end{figure}](/articles/aa/full_html/2009/38/aa11822-09/Timg29.png) |
Figure 2:
Surface C+N+O increase index (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}{%
\par\includegraphics[width=8.8cm]{11822fg3} }
\end{figure}](/articles/aa/full_html/2009/38/aa11822-09/Timg30.png) |
Figure 3:
Top: enrichment in C+N+O after the 2DUP completion as a
function of the mean main sequence velocity for a 5 M |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


