Acoustic oscillations in the field-free, gravitationally stratified cavities under solar bipolar magnetic canopies

D. Kuridze; T. V. Zaqarashvili; B. M. Shergelashvili; S. Poedts

doi:10.1051/0004-6361/200811484

Free Access

Issue		A&A Volume 505, Number 2, October II 2009


Page(s)		763 - 770
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361/200811484
Published online		15 June 2009

Acoustic oscillations in the field-free, gravitationally stratified cavities under solar bipolar magnetic canopies

D. Kuridze^1,2 - T. V. Zaqarashvili² - B. M. Shergelashvili^1,2,3 - S. Poedts¹

1 - Center for Plasma Astrophysics, K.U. Leuven, 200 B, 3001 Leuven, Belgium
2 - Georgian National Astrophysical Observatory at the Faculty of Physics and Mathematics, I. Chavchavadze State University, Al. Kazbegi ave. 2a, 0160 Tbilisi, Georgia
3 - Institute for Theoretical Physics, K.U. Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium

Received 8 December 2008 / Accepted 28 April 2009

Abstract
Aims. The main goal here is to study the dynamics of the gravitationally stratified, field-free cavities in the solar atmosphere, located under small-scale, cylindrical magnetic canopies, in response to explosive events in the lower-lying regions (due to granulation, small-scale magnetic reconnection, etc.).
Methods. We derive the two-dimensional Klein-Gordon equation for isothermal density perturbations in cylindrical coordinates. The equation is first solved by a standard normal mode analysis to obtain the free oscillation spectrum of the cavity. Then, the equation is solved in the case of impulsive forcing associated to a pressure pulse specified in the lower lying regions.
Results. The normal mode analysis shows that the entire cylindrical cavity of granular dimensions tends to oscillate with frequencies of 5-8 mHz and also with the atmospheric cut-off frequency. Furthermore, the passage of a pressure pulse, excited in the convection zone, sets up a wake in the cavity oscillating with the same cut-off frequency. The wake oscillations can resonate with the free oscillation modes, which leads to an enhanced observed oscillation power.
Conclusions. The resonant oscillations of these cavities explain the observed power halos near magnetic network cores and active regions.

Key words: Sun: photosphere - Sun: oscillations

1 Introduction

Observations show a high spectral power of oscillations ( $\nu>5$ mHz) in the vicinity of active regions. The observed velocity power maps are sometimes referred to as ``photospheric power halos'' (Braun et al. 1992; Brown et al. 1992; Hindman & Brown 1998; Jain & Haber 2002; Muglach et al. 2005; Moretti et al. 2007; Nagashima et al. 2007; Hanasoge 2008). The power enhancement is only observed in the Doppler velocity power maps and not in continuum intensity (Hindman & Brown 1998; Jain & Haber 2002; Muglach et al. 2005; Nagashima et al. 2007). The enhanced power spectra peak at the period of $\sim$ 3 min.

In addition, observations show that the chromospheric active regions and magnetic network elements are surrounded by ``magnetic shadows'', which lack oscillatory power in the higher frequency range (McIntosh & Judge 2001; Krijger et al. 2001; Vecchio et al. 2007). From the observations it seems reasonable to conclude that both the photospheric power halos and the chromospheric magnetic shadows reflect the same physical process.

In our previous paper (Kuridze et al. 2008), we proposed an explanation of the photospheric power halos as the effect of a magnetic canopy on the wave dynamics. We showed that the field-free cavity regions under the magnetic canopy can trap high-frequency acoustic oscillations, leading to the observed increased high-frequency power in the photosphere, while the lower-frequency oscillations are channeled upwards in the form of magneto-acoustic waves (Erdélyi et al. 2007; Srivastava et al. 2008). However, those calculations have been performed without taking the gravitational stratification into account, which is important at the photospheric level.

In the present paper, we study acoustic oscillations in the stratified, cylindrical field-free cavity regions under the magnetic canopy as a possible explanation of the power-halo phenomenon. There are various analytical and numerical investigations of the acoustic wave propagation in isothermal stratified atmospheres (e.g., Lamb 1908; Rae & Roberts 1982; Fleck & Schmitz 1991; Kalkofen et al. 1993; Sutmann et al. 1998; Roberts 2004). However, almost all these calculations involve simple 1D models (for vertically propagating acoustic waves), because 2D and 3D models necessarily include internal gravity waves, which considerably complicates the analysis. To avoid further complications from the gravity waves, it is possible, however, to only consider isothermal propagation, which automatically neglects gravity waves. This enables us to study the 2D propagation of only isothermal acoustic waves or pulses in a stratified atmosphere. Here, we study normal isothermal acoustic oscillations and the propagation of acoustic pulses in a cylindrical field-free cavity by solving the 2D Klein-Gordon equation in cylindrical geometry. Unlike the 1D case, the two-dimensional solution allows us to investigate the variation in the density/velocity perturbation amplitude in the azimuthal direction. First, we use a standard normal mode analysis to study the spectrum of possible acoustic oscillations in the cavity region. Then, we solve the Klein-Gordon equation with impulsive forcing in the photospheric region.

The outline of the paper is as follows. In Sect. 2 we present the basic hydrodynamic equations for the problem of the propagation of acoustic waves in a stratified cavity medium. Section 3 describes the normal mode approach and the resulting oscillation spectrum in the cavity. In Sects. 5 and 6 we analyze the response of the cavity region to a pressure pulse. The results obtained are discussed in Sect. 7.

2 The wave equation

We use the ideal hydrodynamic equations for a gravitationally stratified field-free cavity:

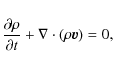$\begin{displaymath}{\partial \rho \over \partial t}+\nabla \cdot (\rho \vec{v})=0, \end{displaymath}$

(1)

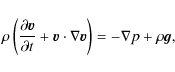$\begin{displaymath}\rho\left({\partial \vec{v} \over \partial t}+\vec{v}\cdot\nabla \vec{v} \right) =-\nabla p+\rho \vec{g}, \end{displaymath}$

(2)

$\begin{displaymath}{\partial p\over\partial t}+\vec{v} \cdot\nabla p+{\gamma p\nabla \cdot \vec{v}} =0, \end{displaymath}$

(3)

where $\vec{v}$ is the fluid velocity, p and $\rho$ denote the pressure and density, respectively, $\gamma$ is the ratio of specific heats, and $\vec{g}$ is the gravitational acceleration.

The considered acoustic cavity under the cylindrical magnetic canopy has a semicircular form (Fig. 1). Therefore, it is convenient to consider Eqs. (1-3) in a cylindrical coordinate system. For simplicity, we study the 2D case, i.e. perturbations polarized in the $(r,\phi)$ plane, where r is the radial coordinate and $\phi$ is the azimuthal angle.

In this cylindrical (or polar) coordinate system, the equilibrium pressure and density are related as

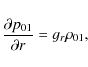$\begin{displaymath}{\partial p_{01}\over \partial r}=g_r\rho_{01}, \end{displaymath}$

(4)

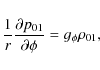$\begin{displaymath}{1 \over r}{\partial p_{01}\over \partial \phi}=g_{\phi}\rho_{01}, \end{displaymath}$

(5)

where p₀₁, $\rho_{01}$ denote the equilibrium pressure and density and

$\begin{eqnarray*}g_r&=&-g \sin\phi, \\ g_{\phi}&=&-g \cos\phi, \end{eqnarray*}$

are the r- and $\phi$ -components of the gravitational acceleration vector, $\vec{g}$ , respectively.

$\begin{figure} \par\includegraphics[width=7cm,clip]{11484fg1.eps} \end{figure}$	Figure 1: Simple schematic picture of small-scale magnetic canopy overlying a field-free cavity with gravitational stratification, g.
Open with DEXTER

Equations (4, 5) then easily lead to the equilibrium values of the pressure and the density in the cavity:

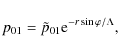$\begin{displaymath}p_{01}=\tilde{p}_{01}{\rm e}^{-r\sin \varphi /\Lambda}, \end{displaymath}$

(6)

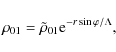$\begin{displaymath}\rho _{01}=\tilde{\rho }_{01}{\rm e}^{-r\sin \varphi /\Lambda}, \end{displaymath}$

(7)

where

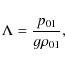$\begin{displaymath}\Lambda={p_{01}\over g\rho _{01}}, \end{displaymath}$

(8)

is the pressure-scale height. The atmosphere is considered to be isothermal. Therefore, this pressure scale height is constant.

In the considered cylindrical (polar) coordinate system, the linearized hydrodynamic equations for adiabatic fluctuations can be written as

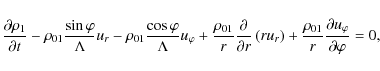$\begin{displaymath}\frac{\partial \rho _{1}}{\partial t}-\rho _{01}\frac{\sin \v... ...o _{01}}{r}\frac{\partial u_{\varphi }}{\partial \varphi }=0 , \end{displaymath}$

(9)

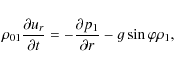$\begin{displaymath}\rho _{01}\frac{\partial u_{r}}{\partial t}=-\frac{\partial p_{1}}{\partial r% }-g\sin \varphi\rho _{1}, \end{displaymath}$

(10)

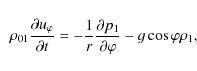$\begin{displaymath}\ \ \rho _{01} \frac{\partial u_{\varphi }}{\partial t}=-\fra... ...rac{\partial p_{1}}{\partial \varphi }-g\cos \varphi\rho _{1}, \end{displaymath}$

(11)

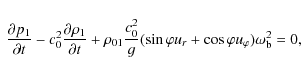$\begin{displaymath}\ \frac{\partial p_{1}}{\partial t}-c_{0}^{2}\frac{\partial \... ...rphi u_{r} +\cos \varphi u_{\varphi } )\omega _{\rm b}^{2}=0, \end{displaymath}$

(12)

where $c^2_0={\gamma p_{01}/\rho_{01}}$ is adiabatic uniform sound speed and $\omega_{\rm b}$ denotes the Brunt-Väisälä frequency:

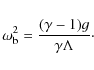$\begin{displaymath}\omega^2_{\rm b}={(\gamma-1)g\over \gamma \Lambda}\cdot \end{displaymath}$

(13)

These equations describe the acoustic and internal gravity waves propagating in a stratified atmosphere. In principle, the cavity under a magnetic canopy may trap both types of waves. Unfortunately, the simultaneous consideration of both wave types is very complicated, especially from an analytical point of view. However, by adopting specific approximations, we can consider each of the wave types separately. The limit of incompressibility, e.g., neglects the acoustic branch so only gravity waves remain in this case. On the other hand, the limit of isothermal propagation neglects the gravity branch of the spectrum, and in this case, only the acoustic branch remains. The latter limit means that the temperature exchange is so rapid that any temperature fluctuation in the perturbations is zero. This is achieved when $\gamma$ approaches unity.

We use the approximation/limit of isothermal propagation in the remaining part of this paper. For isothermal perturbations, Eqs. (9-12) lead to the following wave equation:

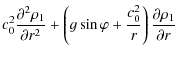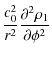$\displaystyle c_{0}^{2}\frac{\partial ^{2}\rho _{1}}{\partial r^{2}}+\left( g\sin \varphi +\frac{c_{0}^{2}}{r}\right) \frac{\partial \rho _{1}}{\partial r}$	+	$\displaystyle \frac{ c_{0}^{2}}{r^{2}}\frac{\partial ^{2}\rho _{1}}{\partial \phi ^{2}}$
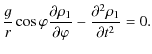	+	$\displaystyle \frac{g}{r}\cos \varphi \frac{\partial \rho _{1}}{\partial \varphi }- \frac{\partial ^{2}\rho _{1}}{\partial t^{2}} =0.$	(14)

Equation (14) can be written in a more convenient form by using the following transformation:

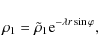$\begin{displaymath}{\rho }_{1}=\tilde{\rho} _{1}{\rm e}^{-\lambda r\sin \varphi }, \end{displaymath}$

(15)

where the parameter $\lambda$ can be chosen in such a way that the resulting wave equation has the form of a Klein-Gordon equation in the cylindrical/polar coordinate system. This procedure is analogous to the well-known transformation in a 1D Cartesian coordinate system (Kahn 1990; Sutmann et al. 1998).

By substituting Eq. (15) into Eq. (14) we obtain

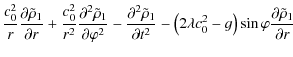$\displaystyle c_{0}^{2}\frac{\partial ^{2}\tilde{\rho }_{1}}{\partial r^{2}}$	+	$\displaystyle \frac{c_{0}^{2}}{r}\frac{\partial \tilde{\rho }_{1}}{\partial r}+... ...a c_{0}^{2}-g\right)\sin \varphi\frac{\partial \tilde{\rho }_{1}}{% \partial r}$
	-	$\displaystyle \left(2 \lambda c_{0}^{2}-g\right){\cos \varphi \over r}\frac{\pa... ...1}}{% \partial \phi}+(\lambda^{2}c_{0}^{2}-\lambda g) \tilde{\rho }% _{1}(r)=0,$	(16)

from which we find the following condition on $\lambda$

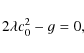$\begin{displaymath}2\lambda c_{0}^{2}-g=0, \end{displaymath}$

(17)

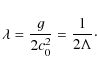$\begin{displaymath}\lambda={g \over 2c_{0}^{2}}={1\over 2\Lambda}\cdot \end{displaymath}$

(18)

Using this condition, we obtain

$\begin{displaymath}\frac{\partial ^{2}\tilde{\rho }_{1}}{\partial r^{2}}+{1\over... ... }_{1}}{\partial t^{2}}+\omega^2_{ac}\tilde{\rho_1}\right ]=0, \end{displaymath}$

(19)

where $\omega^2_{ac}$ refers to the acoustic cut-off frequency

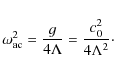$\begin{displaymath}\omega^2_{\rm ac}={g\over 4\Lambda}={c_0^2\over 4\Lambda^2}\cdot \end{displaymath}$

(20)

Equation (19) is the Klein-Gordon equation in cylindrical/polar coordinates. This equation governs the isothermal propagation of acoustic waves (and pulses) in the considered gravitationally stratified medium. The very dynamic convective layer located under the cavity can excite quasi-harmonic wave trains, as well as acoustic pulses. Clearly, the cavity will respond in different ways to these different types of perturbations. We study two different responses of the cavity to such different perturbations from below. First, we consider the cavity as a resonator for acoustic waves and, using the standard normal mode approach, we study the spectrum of possible wave harmonics trapped in the canopy. Next, we consider the propagation of a pressure pulse, which can be caused in the lower regions by the eruption of new granular cells or by some small-scale magnetic reconnection processes.

3 Normal mode analysis

A standard Fourier analysis of Eq. (19) with respect to time leads to the equation:

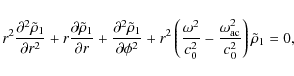$\begin{displaymath}r^{2}\frac{\partial ^{2}\tilde{\rho }_{1}}{\partial r^{2}}+r\... ...2}}-{\omega^2_{\rm ac}\over c^2_0}\right)\tilde{\rho }_{1} =0, \end{displaymath}$

(21)

$\begin{eqnarray*}\frac{\omega ^{2}}{c_{0}^{2}}-\frac{g}{4\Lambda c_{0}^{2}}\equiv k_1^2, \end{eqnarray*}$

which gives

$\begin{eqnarray*}\omega^2=k_1^2c_0^2+\omega^2_{\rm ac}. \end{eqnarray*}$

We consider the solution of Eq. (21) in three different cases depending on the size of the circular frequency $\omega$ with respect to $\omega_{\rm ac}$ .

When $\omega=\omega_{\rm ac}$ , Eq. (21) leads to the Laplace equation in cylindrical coordinates. The solution of this equation inside the canopy (i.e. inside the semicircle $r=r_{\rm c}$ , where $r_{\rm c}$ is the cavity/canopy boundary (see Fig. 1)) with the condition $\tilde\rho_1=\tilde\rho_{\rm c}(\phi)$ (i.e. a Dirichlet condition) along the boundary is given by (Morse & Feshbach 1953)

$\begin{displaymath}{\tilde\rho}_1=\sum_{m=0}^{\infty}[A_m\cos(m\phi)+B_m\sin(m\phi)]\left({r\over r_{\rm c}}\right)^m, \end{displaymath}$

(22)

where

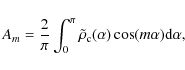$\begin{displaymath}A_m={2\over\pi}\int_{0}^{\pi}\tilde\rho_{\rm c}(\alpha)\cos(m\alpha){\rm d}\alpha, \end{displaymath}$

(23)

and

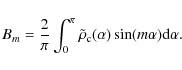$\begin{displaymath}B_m={2\over\pi}\int_{0}^{\pi}\tilde\rho_{\rm c}(\alpha)\sin(m\alpha){\rm d}\alpha. \end{displaymath}$

(24)

This means that one of the free oscillation modes in the cavity oscillates at the cut-off frequency for any m (which plays the role of azimuthal wave number). For the photospheric sound speed of 7.5 km s^-1, the acoustic cut-off frequency is on the order of 0.031 s^-1 with a corresponding period of $\sim$ 200 s.

In the case $\omega>\omega_{\rm ac}$ , Eq. (21), again after a Fourier analysis with respect to the azimuthal direction and with azimuthal wave number m, transforms to a Bessel equation with the general solution

$\begin{displaymath}{\tilde\rho}_1=c_{1}J_m(k_1r)+c_{2}Y_m(k_1r), \end{displaymath}$

(25)

where J_m and Y_m are the bessel functions of the first and second kinds, respectively, and c₁ and c₂ are arbitrary constants.

When $\omega<\omega_{\rm ac}$ , then a similar Fourier analysis transforms Eq. (21) to the modified Bessel equation, with the general solution

$\begin{displaymath}{\tilde\rho}_1=c_{3}I_m(k_1r)+c_4K_m(k_1r), \end{displaymath}$

(26)

where I_m and K_m are the modified Bessel functions of the first and second kinds, respectively, and c₃ and c₄ are arbitrary constants. The density perturbations must be finite at r=0, which yields the condition c₂=c₄=0. We also need a second condition at the upper boundary of the cavity in order to find a unique solution for Eq. (21). The correct approach is to find an analytical solution to the magnetohydrodynamic equations in the overlying magnetic canopy region and then merge it with the solution (25) at the canopy/cavity interface ( $r=r_{\rm c}$ ). This would yield the exact oscillation spectrum of the cavity, which may reveal some wave leakage. Unfortunately, we could not get an analytical solution to the complete cylindrical MHD equations for the gravitationally stratified plasma in the canopy region. However, we can exploit the quick decrease in density from the photosphere to the chromosphere. According to the VAL-C atmospheric model (Vernazza et al. 1981), there is the sharp density gradient in the low area of the chromosphere (Fontenla et al. 1990). Therefore, it is justified to approximate the sharp gradient between the photospheric and the chromospheric densities as a discontinuity at the canopy/cavity interface. The density is then much higher in the cavity than in the overlying magnetic canopy (Fig. 1). This allows the use of a free boundary condition, i.e. $\tilde \rho_1=0$ , at the cavity/canopy interface, which yields an approximate spectrum of acoustic oscillations in the cavity. The influence of overlying canopy can be studied by complete numerical simulations, but this is not the scope of the present paper and should be done in the future. The free boundary condition leads to the expressions:

$\begin{displaymath}c_1 J_m(k_1r_{\rm c})=0, \\ {\rm for} \\ \omega > \omega_{\rm ac}, \end{displaymath}$

(27)

$\begin{displaymath}c_3 I_m(k_1r_{\rm c})=0, \\ {\rm for} \\ \omega < \omega_{\rm ac}. \end{displaymath}$

(28)

The first condition gives oscillatory solutions (oscillating with respect to the r-coordinate), while the second is only satisfied when c₃=0. Therefore, Eq. (28) yields the trivial solution of Eq. (21), and in the following we concentrate on the oscillatory solution connected with only condition (27). The spectrum of acoustic oscillations in the cavity can then be deduced from the zeros of the solution J_m(z), which (as it is known from the theory of Bessel functions) are all real when $m\geq -1$ , and they can be easily found in tables (see e.g. Abramowitz & Stegun 1967).

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{11484fg2} \end{figure}$	Figure 2: The oscillation frequency, $\omega$ , versus the cavity radius, $r_{\rm c}$ , for the first zeros of the m=1 ( bottom line), m=2( middle line), and m=3 ( top line) harmonics.
Open with DEXTER

Figure 2 shows the dependence of the frequencies of the acoustic oscillations on the cavity radius, $r_{\rm c}$ , for the first zero of J_m(z) for the m=1,2,3 harmonics. It is evident from this figure that the frequency decreases with increasing $r_{\rm c}$ , as can be expected from physical considerations. This means that these cavities, with typical granular radii $r_{\rm c}=400{-}800\;$ km, support oscillations with frequencies in the range 0.07- $0.05\;$ s^-1(i.e. with periods of $1.5{-}2\;$ min). For considerably large cavity radii, the frequencies of all the harmonics tend to the cut-off value.

It seems that cylindrical cavities support higher frequency oscillations than typical quiet Sun regions, because in cylindrical cavities, the oscillations are partly along the $\phi$ -direction due to the small k₁ term for the first zero of Bessel function in Eq. (27), which prevents their leakage upwards and leads to their trapping in the cavities. On the other hand, the regions without overlying canopies (e.g., nonmagnetic quiet Sun regions outside the network cores) cannot trap the high frequency oscillations, because they may propagate upwards. Therefore, it is expected that the high-frequency oscillations are trapped around the magnetic network cores and active regions where the cylindrical magnetic canopies can be formed. The periods of the lower order harmonics in cavities with a radius of $1000\;$ km (Fig. 2) correspond to the observed spectrum of acoustic oscillations ( $5{-}8\;$ mHz) (Moretti et al. 2007, see their Fig. 1).

The free boundary condition, which is used to obtain the oscillation spectrum, does not lead to wave leakage in the canopy region. However, we may explore the problem using the wave propagation along a narrow sector around the vertical ( $\phi\approx\pi/2$ ) direction.

Let us first consider the unperturbed current-free cylindrical magnetic field in the canopy region expressed as $B_{\phi}=B_{\phi0}(r_{\rm c}/ r)$ (see Kuridze et al. 2008), where $B_{\phi0}$ is the magnetic field strength at canopy/cavity interface. For simplicity, we consider the zero- $\beta$ approximation ( $\beta=8\pi p_{02}/B^2_{\phi0}\approx 0$ ), where p₀₂ is the plasma pressure in the canopy. For this configuration, the solution to magnetohydrodynamic equations for the radial velocity is found in the form of the Hankel function of the first kind (Kuridze et al. 2008):

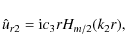$\begin{displaymath}{\hat u_{r2}}={\rm i}c_3rH_{m/2}(k_2r), \end{displaymath}$

(29)

where c₃ is an arbitrary constant and $k_2={{\omega}/{(2v_{\rm A})}}$ . Here, $v_{\rm A}= {B_{\phi0}/\sqrt{4\pi \rho_{02}}}$ is the Alfvén speed and $\rho_{02}$ the plasma mass density in the canopy area. The radial velocity component in the narrow sector around the vertical direction of the cavity can be obtained by combining Eqs. (10), (15), and (25) as

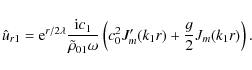$\begin{displaymath}{\hat u_{r1}}={\rm e}^{r/2\lambda}{{\rm i}c_{1}\over {\tilde\... ...}\left (c^2_{0}J^{\prime}_m(k_1r)+{g\over 2}J_m(k_1r)\right ). \end{displaymath}$

(30)

The continuity of the velocity and the total pressure perturbations at the canopy/cavity interface then leads to the following dispersion equation:

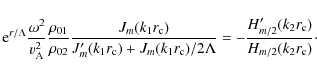$\begin{displaymath}{\rm e}^{r/\Lambda}{{\omega^2}\over v^2_{\rm A}}{\rho_{01}\ov... ...{m/2}^{\prime}(k_2r_{\rm c})}\over H_{m/2}(k_2r_{\rm c})}\cdot \end{displaymath}$

(31)

The dispersion relation (31) is a transcendental equation for the complex frequency $\omega$ . A non-vanishing imaginary part of $\omega$ indicates wave leakage from the field-free cavity into the overlying magnetic canopy. The question then arises as to how important this wave leakage is. The analytical solution of Eq. (31) is complicated, so we apply numerical techniques to solve it.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg3} \end{figure}$	Figure 3: Real $\omega _{\rm r}$ (m=1 bottom line, m=2 top line on the left panel) and imaginary $\omega _{\rm i}$ (m=1 top line, m=2 bottom line on the right panel) parts of wave frequency vs. the radius of field-free cavity $r_{\rm c}$ . The straight line in the left panel is the solution with the cut-off frequency.
Open with DEXTER

The numerical solution of Eq. (31) shows that the dispersion equation has a real solution with a cut-off frequency $\omega=\omega_{\rm ac}$ , and complex solutions with very small imaginary parts. Figure 3 shows the dependence of the real (left panel) and the imaginary (right panel) parts of the frequency on the cavity size $r_{\rm c}$ . The real part of the frequency decreases with increasing $r_{\rm c}$ , as expected. The damping time of the oscillations $t_{\rm d}=1/\omega_i \sim 10^3{-}10^5 ~ T_0$ ( $T_0=2\pi/\omega_r$ ) is very long, which indicates there is almost no wave leakage in the canopy region. This means that the first few harmonics are trapped in the cavity. It must be mentioned that the frequencies of first few harmonics (left panel of Fig. 3) are almost identical to the frequencies obtained with the free-boundary condition (Fig. 2). Thus, the oscillation spectrum does not depend significantly on the choice of the boundary conditions.

It is interesting to find out what happens if the cylindrical canopy is replaced by a horizontal magnetic field (as could be the case in the quiet Sun regions far from the network cores). We have analyzed the spectrum of the field free photospheric area under a horizontal magnetic canopy. In this configuration there are no trapped high-frequency ( $\omega>\omega_{\rm ac}$ ) oscillations along the vertical direction. The damping times of the vertically propagating waves are about $t_{\rm d}\sim 2{-}7\;T_0$ , which indicates their leaky nature. On the other hand, horizontally propagating waves (with large horizontal wave numbers) have real frequencies. But since their velocities are almost horizontal they cannot be seen in Doppler velocity power maps. Any initial pulse or wave train will quickly be dispersed in the horizontal direction. Therefore, these modes cannot form the observed high-frequency halos.

4 Excitation by a pressure pulse

The solar photosphere is very dynamic and contains many different types of impulsive sources. For example, the eruption of new granules, magnetic-field reconnection events just under the solar surface, and various other explosive events may take place there. Therefore, the excitation of pressure and velocity pulses seems to be quiet common under photospheric conditions. In this section, we study the propagation of such a pressure pulse (which corresponds to a density pulse in the isothermal approximation) in the cavity region. For simplicity, we assume that the pulse has a $\delta$ -function shape in space and time.

Mathematically this corresponds either to the solution of Eq. (19) with impulsive initial and boundary conditions or to the solution of that equation with an additional term modeling the impulsive external forcing. The equation can then be written as (with the driving force term in the righthand side)

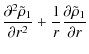$\displaystyle \frac{\partial ^{2}\tilde{\rho }_{1}}{\partial r^{2}}+{1\over r}\frac{ \partial \tilde{\rho }_{1}}{\partial r}$	+	$\displaystyle {1\over r^2} \frac{\partial ^{2}\tilde{\rho }_{1}}{\partial \phi^... ... ^{2}\tilde{\rho }_{1}}{\partial t^{2}}+\omega^2_{\rm ac}\tilde{\rho_1}\right]=$
	-	$\displaystyle {4\pi\delta(t-t_0)\delta(r-r_0)\delta(\phi-\phi_0)\over r},$	(32)

where r₀, $\phi_0$ denotes position of the source (Fig. 4). Equation (32) governs the propagation of the pulse, which is set at r=r₀, $\phi=\phi_0$ at the time t=t₀.

If we consider the case when

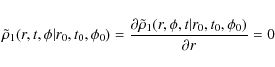$\begin{displaymath}\tilde\rho_1(r,t,\phi\vert r_0,t_0,\phi_0)={{\partial \tilde\rho_1(r,\phi,t\vert r_0,t_0,\phi_0)}\over \partial r}=0 \end{displaymath}$

(33)

for t<t₀, then $\tilde{\rho}_1$ is the Green's function for Eq. (32) and has the form (Morse & Feshbach 1953)

$\displaystyle \tilde\rho_1(r,t,\phi\vert r_0,t_0,\phi_0)={A_0\delta(t-t_0-R/c_0... ...^2-{(R/c_{0})^2}}\right]\over c_0 \sqrt{(t-t_0)^2-(R/c_{0})^2}} H(t-t_0-R/c_0),$

(34)

where A₀ is a constant,

$\begin{eqnarray*}R=\mid \vec{r}-\vec{r}_0 \mid=\sqrt{r^2+r^2_0-2rr_0\cos(\phi-\phi_0)}, \end{eqnarray*}$

and H denotes the Heaviside step function.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{11484fg4} \end{figure}$	Figure 4: Source point, observation point at t>t₀, and canopy/cavity interface.
Open with DEXTER

The first term on the right hand side in Eq. (34) describes the propagation of the pulse. It is followed by a wake which is given by the second term in Eq. (34). This is a demonstration of a well-known result (Rae & Roberts 1982; Fleck & Schmitz 1991; Kalkofen et al. 1993; Sutmann et al. 1998; Roberts 2004; Zaqarashvili & Skhirtladze 2008), viz. the presence of a wavefront that moves away from the point ( $r_0, \phi_0$ ) with speed c₀. The disturbance ahead of the wavefront is at rest, but behind the wavefront, the medium begins to oscillate at the cut-off frequency $\omega_{\rm ac}$ .

Using Eqs. (15), (18), and (34), the density perturbation for the wake oscillations takes the form (here t₀=0 is chosen without loss of generality):

$\begin{displaymath}\rho _{1}= -{A_0\omega_{\rm ac}{\rm e}^{-r\sin \varphi /2\Lam... ...eft[\omega_{\rm ac}\sqrt{t^2-{(R/ c_{0}})^2}\right]H(t-R/c_0). \end{displaymath}$

(35)

An asymptotic form of the density perturbation can be obtained using the expression of the Bessel function J₁ that holds for large arguments $(t\gg R/c_0)$ (Abramowitz & Stegun 1967). We then obtain

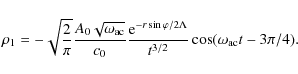$\begin{displaymath}\rho _{1}=-{\sqrt{2\over \pi}}{A_0\sqrt{\omega_{\rm ac}}\over... ...arphi /2\Lambda}\over {t^{3/2}}}\cos(\omega_{\rm ac}t-3\pi/4). \end{displaymath}$

(36)

After the passage of the pressure pulse, the medium density thus oscillates at the cut-off frequency and this oscillation decays asymptotically as 1/t^3/2. In fact, the pressure pulse will excite the wide spectrum of oscillations, but the higher frequencies harmonics escape upwards and the lower frequency harmonics are evanescent, so that only the oscillations at the cut-off frequency remain.

It is interesting to study what happens with the velocity perturbations in this asymptotic case ( $t\gg R/c_0$ ). Combining Eqs. (10), (11), and (34), we obtain

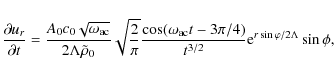$\begin{displaymath}{\partial u_r\over \partial t}={A_0c_0\sqrt{\omega_{\rm ac}}\... ...\pi/4)\over t^{3/2}}{\rm e}^{r\sin \varphi /2\Lambda}\sin\phi, \end{displaymath}$

(37)

and

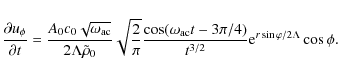$\begin{displaymath}{\partial u_{\phi}\over \partial t}={A_0c_0\sqrt{\omega_{\rm ... ...\pi/4)\over t^{3/2}}{\rm e}^{r\sin \varphi /2\Lambda}\cos\phi. \end{displaymath}$

(38)

The integration of Eqs. (37) and (38) with respect to time and using the conditions u_r=0 and $u_{\phi}=0$ for $t\rightarrow\infty$ , we obtain (see the Appendix for the detailed calculations):

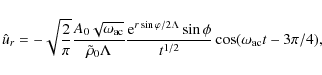$\begin{displaymath}\hat u_{r}=-\sqrt{{2\over\pi}}{A_0\sqrt{\omega_{\rm ac}}\over... ...\Lambda}\sin\phi\over {t^{1/2}}}\cos(\omega_{\rm ac}t-3\pi/4), \end{displaymath}$

(39)

and

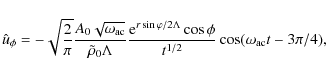$\begin{displaymath}\hat u_{\phi}=-\sqrt{{2\over\pi}}{A_0\sqrt{\omega_{\rm ac}}\o... ...\Lambda}\cos\phi\over {t^{1/2}}}\cos(\omega_{\rm ac}t-3\pi/4), \end{displaymath}$

(40)

where $\hat u_r=u_r/c_0$ and $\hat u_{\phi}=u_{\phi}/c_0$ . Therefore, the propagation of the pressure pulse also sets up a velocity wake oscillating with the cut-off frequency. This velocity oscillation decays with time as 1/t^1/2, i.e. much more slowly than the decay of the density wake. Thus the oscillations may easily persist during a few tens of cut-off periods (i.e. during $\sim$ 30- $60\;$ min), which is much longer than the expected time interval between consecutive pulses (which can be estimated as the granular lifetime, i.e. $\sim$ $10\;$ min). Therefore, these wakes of consecutive pulses may gradually strengthen the oscillations and thus may lead to the observed power halos.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg5} \end{figure}$	Figure 5: The density fluctuation after the propagation of pulse as a function of time and radial coordinate at $\phi =\pi /4$ . The time t is normalized by cut-off frequency and r is normalized by the photospheric scale height.
Open with DEXTER

Figure 5 shows a plot of the density fluctuation, given by Eq. (35) (the time is normalized to the cut-off frequency, $t'=t\omega_{\rm ac}$ , and the radial coordinate is normalized by the scale height, $r'=r/2\Lambda$ ). It is seen that the propagation of the pulse is followed by a weak amplitude wake that oscillates with the cut-off period. The amplitude of both the pulse and the wake decrease with height/time. However, it must be mentioned that the normalized perturbation of the density, $\rho_1/\rho_0$ , increases with r. The normalized amplitude of the density perturbation in the asymptotic form, can be written as

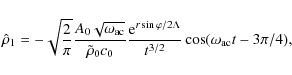$\begin{displaymath}\hat\rho_1=-{\sqrt{2\over \pi}}{A_0\sqrt{\omega_{\rm ac}}\ove... ...arphi /2\Lambda}\over {t^{3/2}}}\cos(\omega_{\rm ac}t-3\pi/4), \end{displaymath}$

(41)

where

$\begin{eqnarray*}\hat\rho_1={\rho_1\over \rho_0}\cdot \end{eqnarray*}$

The normalized amplitude of the asymptotic density perturbation depends on the direction of propagation (i.e. on the $\phi$ -coordinate). The wake has its maximum amplitude in the vertical direction (at $\phi=\pi/2$ ), and its amplitude decreases for inclined directions (see Fig. 6).

Figure 7 shows the dependence of the asymptotic velocity wake on the azimuthal angle, $\phi$ . It is clear that the radial component has a maximum amplitude in the vertical direction, while the azimuthal velocity component has a maximal amplitude close to $45^{\circ}$ .

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg6} \end{figure}$	Figure 6: Normalized asymptotic amplitude of the density wake versus the azimuthal angle $\phi$ at r'=2, t'=100 (the time t is normalized to the cut-off period and r is normalized to the scale height).
Open with DEXTER

5 The energy propagation

Our calculations show clearly that at t=0 the energy is concentrated in the initial pressure pulse and that it propagates away as time elapses. The initial pulse, which travels at the sound speed, carries most of the energy injected into the medium. We can write down an expression for the asymptotic total energy density for the wake oscillation, which is the sum of the kinetic and acoustic potential energy densities

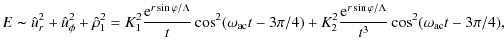$\displaystyle E\thicksim \hat{u}^2_r+\hat{u}^2_{\phi}+\hat\rho_1^2=K^2_1{{\rm e... ...{{\rm e}^{r\sin \varphi /\Lambda}\over {t^{3}}}\cos^2(\omega_{\rm ac}t-3\pi/4),$

(42)

where

$\begin{eqnarray*}K_1=\sqrt{{2\over\pi}}{A_0\sqrt{\omega_{\rm ac}}\over \tilde \rho_0 \Lambda}, \end{eqnarray*}$

and

$\begin{eqnarray*}K_2={\sqrt{2\over \pi}}{A_0\sqrt{\omega_{\rm ac}}\over \tilde\rho_0 c_0}\cdot \end{eqnarray*}$

It is clear from Eq. (42) that the potential part of the wake energy decays much faster than the kinetic part. Therefore, after some time only the velocity oscillations remain, while the density oscillations have decayed. Furthermore, the total energy is greatest in the vertical direction (at $\phi=\pi/2$ ) and the lowest in the horizontal direction (at $\phi=0$ ). It means that the energy of the wake oscillations is concentrated near the vertical direction (see Fig. 8). Therefore, the wake, which remains after the passage of the pressure pulse, tends to oscillate along the vertical direction. The same result was found by Bodo et al. (1999). The total energy of the wake decays in time as $\thicksim$ 1/t.

6 Discussion and conclusions

We have carried out a linear perturbation analysis of the two-dimensional wave propagation in a stratified, field-free cavity, which is located under a chromospheric cylindrical magnetic canopy. We considered the higher density in the cavity than in the overlying magnetic canopy region (due to the sharp density gradient between the photosphere and the chromosphere). Then the free boundary condition at canopy/cavity interface leads to the spectrum of acoustic oscillation in the cavity. We also examined the response of the cavity to the propagation of a pressure pulse, which can be excited in the lower regions by various sources, including small-scale magnetic reconnection events. It has been shown that the cavity, which has a radius comparable to the granular dimensions ( $\sim$ 500 km), supports trapped oscillations with periods of 1.5-2 min (cf. Figs. 2, 3). However, one of the oscillation modes in the cavity is the oscillation with the cut-off frequency. Furthermore, the frequency of the acoustic modes also has the tendency to approach the cut-off value for large-scale granular size (cf. Fig. 2). On the other hand, it has been shown that a pressure pulse propagating through the cavity sets up a wake, oscillating at the cut-off frequency. The wake oscillation will resonate with a free oscillating mode of the cavity, which may lead to an enhanced acoustic power at the same frequency.

There have been several different explanations of power halos in the literature: (i) the enhancement of acoustic emission by some unknown source (Braun et al. 1992; Brown et al. 1992; Jain & Haber 2002); (ii) incompressible oscillations, such as Alfvén waves or transverse kink waves, in magnetic tubes (Hindman & Brown 1998); (iii) the interaction of acoustic waves with the overlying magnetic canopy (Muglach et al. 2005; Kuridze et al. 2008); and (iv) a change of the spatial-temporal spectrum of the turbulent convection in the magnetic field (Jacoutot et al. 2008). However, observations show a lack of power halos in the intensity maps (Hindman & Brown 1998; Jain & Haber 2002; Muglach et al. 2005; Nagashima et al. 2007), which needs an adequate explanation. These observations challenge the model of the power halos as the result of acoustic waves. However, our model easily explains the discrepancy.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg7}\par\includegraphics[width=9cm,clip]{11484fg8} \end{figure}$	Figure 7: Normalized asymptotic amplitudes of the velocity perturbation components versus $\phi$ at r'=2, t'=100 (the time t is normalized to the cut-off period and r is normalized to the scale height).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg9} \end{figure}$	Figure 8: Normalized total energy density with respect to $\phi$ . It is clearly seen that the energy is concentrated near the vertical direction.
Open with DEXTER

We suggest that the surroundings of the magnetic network cores and the active regions consist of many small-scale, closed, magnetic-canopy structures (McIntosh & Judge 2001; Schrijver & Title 2003). Granular motions transport the magnetic field at the boundaries and consequently create field-free cylindrical cavity areas under the canopy (Fig. 1). The pressure pulses excited in a lower region propagate through the cavity and leave behind wakes oscillating at the cut-off frequency. These wake oscillations resonate with the free oscillation modes of the cavity. Therefore, the cavities accumulate acoustic oscillations with the observed frequency. However, the amplitude of the density perturbation in the wakes decreases in time faster (viz. as t^-3/2) than the amplitude of velocity perturbations (viz. as t^-1). Therefore, the density perturbations quickly decay leaving only the velocity oscillations. This explains why the power halos are only seen in the velocity power maps.

Thus, our model suggests that the high-frequency acoustic oscillations should be trapped around the magnetic network cores and the active regions, where acoustic cavities can be formed under small-scale cylindrical magnetic canopies. The deduced oscillation periods are within 1.5-2 min for cavities with granular sizes, but the cavities should also oscillate with the photospheric cut-off frequency. However, the picture will be different far away from the network cores and active regions, where the cylindrical bipolar magnetic fields are probably replaced by almost a horizontal magnetic canopy that has been used as a model for a long time (Evans & Roberts 1990). In this case, the higher frequency oscillations propagate upwards (only trapped cut-off modes appear) and, consequently, power halos cannot be formed. The oscillation at cut-off frequency should have a small amplitude there, as the rectangular vertical cavity does not have any oscillation mode with this frequency. The wake oscillating at cut-off frequency should be observed there, but with a smaller amplitude, as almost the whole initial energy is carried away by an initial pulse or a wave train. Therefore, it is the cylindrical structure of the field-free regions (see Fig. 1), that helps to trap acoustic waves as the oscillations occur partly along the $\phi$ -direction. This explains why the ``power halos'' and ``magnetic shadows'' are observed only near the quiet-Sun chromospheric magnetic network cores (McIntosh & Judge 2001; Krijger et al. 2001; Vecchio et al. 2007).

It must be noted that intensity halos are visible in the magnetic canopy regions in some observations (Moretti et al. 2007). However, this is consistent with our model. As mentioned before, our calculation does not include the exact solution in the overlying magnetic canopy region because of mathematical difficulties. On the other hand, the free oscillations of the cavity/canopy interface may excite oscillations in the overlying region as observed by Moretti et al. (2007). Likewise, the oscillations of the cavity may excite transverse waves in an overlying magnetic canopy, which can be checked by observations of the magnetic field oscillation in the power-halo regions.

Acknowledgements

This work was supported by Georgian National Science Foundation grant GNSF/ST06/4-098. D.K. is grateful for kind hospitality at the Center for Plasma Astrophysics, K.U. Leuven, during his visit when the significant parts of the work were developed. These results were obtained in the framework of the projects GOA/2009-009 (K.U. Leuven), G.0304.07 (FWO-Vlaanderen), and C 90347 (ESA Prodex 9). T.Z. acknowledges Austrian Fond zur Förderung der wissenschaftlichen Forschung (project P21197-N16).

Appendix A: Derivation of the velocity components

Integration of Eqs. (37) and (38) gives

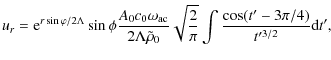$\displaystyle u_r ={\rm e}^{r\sin \varphi /2\Lambda}\sin\phi{A_0c_0\omega_{\rm ... ...bda\tilde \rho_0}\sqrt{2\over \pi}\int{\cos(t'-3\pi/4)\over t'^{3/2}}{\rm d}t',$			(A.1)
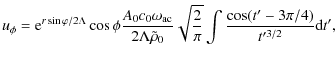$\displaystyle u_{\phi}={\rm e}^{r\sin \varphi /2\Lambda}\cos\phi{A_0c_0\omega_{... ...bda\tilde \rho_0}\sqrt{2\over \pi}\int{\cos(t'-3\pi/4)\over t'^{3/2}}{\rm d}t',$			(A.2)

where $t'=\omega_{\rm ac}t$ .

Integral in Eqs. (A.1), (A.2) can be solved as

I	=	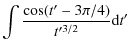$\displaystyle \int{\cos(t'-3\pi/4)\over t'^{3/2}}{\rm d}t'$
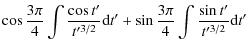	=	$\displaystyle \cos{3\pi\over 4}\int{{\cos t'\over t'^{3/2}}}{\rm d}t'+\sin{3\pi\over 4}\int{{\sin t'\over t'^{3/2}}}{\rm d}t'$
	=	$\displaystyle \cos{3\pi\over 4}\left[ -{2\cos t'\over t'^{1/2}}-2\sqrt{2\pi} S\left(\sqrt{2t'/\pi}\right)+F_1\right]$
		$\displaystyle +\sin{3\pi\over 4}\left[ -{2\sin t'\over t'^{1/2}}+2\sqrt{2\pi} C\left(\sqrt{2t'/\pi}\right)+F_2\right]$
	=	$\displaystyle -{2\over t'^{1/2}}\left[\cos{3\pi\over 4}\cos t'+\sin{3\pi\over 4}\sin t' \right]$
		$\displaystyle +2\sqrt{\pi}\left[S\left(\sqrt{2t'/\pi}\right)+C\left(\sqrt{2t'/\pi}\right)\right]+{\sqrt{2}\over 2}\left(F_2-F_1\right)$
	=	$\displaystyle -2{\cos(t'-3\pi/4)\over t'^{1/2}}+2\sqrt{\pi}\left[S\left(\sqrt{2t'/\pi}\right)+C\left(\sqrt{2t'/\pi}\right) \right]$
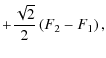		$\displaystyle +{\sqrt{2}\over 2}\left(F_2-F_1\right),$	(A.3)

where F₁, F₂ are the integration constants, and S and Care the Fresnel sine and cosine integral functions, respectively. Fresnel functions tend to 1/2 for large arguments, therefore we have

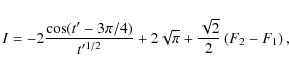$\begin{displaymath}I=-2{\cos(t'-3\pi/4)\over t'^{1/2}}+2\sqrt{\pi}+{\sqrt{2}\over 2}\left(F_2-F_1\right), \end{displaymath}$

(A.4)

where $u_r, u_{\phi}$ should tend to zero when $t'\rightarrow\infty$ ; therefore,

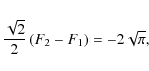$\begin{displaymath}{\sqrt{2}\over 2}\left(F_2-F_1\right)=-2\sqrt{\pi}, \end{displaymath}$

(A.5)

which gives

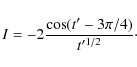$\begin{displaymath}I=-2{\cos(t'-3\pi/4)\over t'^{1/2}}\cdot \end{displaymath}$

(A.6)

Substitution of the expression (A.6) into Eqs. (A.1), (A.2) gives Eqs. (39) and (40).

References

Abramowitz, M., & Stegun, I. A. 1967, Handbook of Mathematical Functions (New York: Dover Publications) (In the text)
Bodo, G., Kalkofen, W., Massaglia, S., & Rossi, P. 2000, A&A, 354, 296 [NASA ADS]
Braun, D. C., Lindsey, C., Fan, Y., & Jefferies, S. M. 1992, ApJ, 392, 739 [NASA ADS] [CrossRef] (In the text)
Brown, T. M., Bogdan, T. J., Lites, B. W., & Thomas, J. H. 1992, ApJ, 394, 65 [NASA ADS] [CrossRef] (In the text)
Centeno, R., Socas-Navarro, H., Lites, B., et al. 2007, ApJ, 666, 137 [NASA ADS] [CrossRef]
de Wijn, A. G., Rutten, R. J., Haverkamp, E. M. W. P., & Sutterlin, P. 2005, A&A, 441, 1183 [NASA ADS] [CrossRef] [EDP Sciences]
Erdélyi, R., Malins, C., Toth, G., & de Pontieu, B. 2007, A&A, 461, 1299 [NASA ADS] [CrossRef] (In the text)
Evans, D. J., & Roberts, B. 1990, ApJ, 356, 704 [NASA ADS] [CrossRef] (In the text)
Fontenla, J. M., Avrett, E. H., & Loeser, R. 1990, ApJ, 355, 700 [NASA ADS] [CrossRef] (In the text)
Fleck B., & Schmitz, F. 1991, A&A, 250, 235 [NASA ADS] (In the text)
Jacoutot, L., Kosovichev, A. G., Wray, A., & Mansour, N. N. 2008, ApJ, 684, 51 [NASA ADS] [CrossRef] (In the text)
Jain, R., & Haber, D. 2002, A&A, 387, 1092 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hindman, B. W., & Brown, T.M. 1998, ApJ, 504, 1029 [NASA ADS] [CrossRef] (In the text)
Hanasoge, S. M. 2008, ApJ, 680, 1457 [NASA ADS] [CrossRef] (In the text)
Kahn, P.B. 1990, Mathematical Methods for Scientists and Engineers (John Wiley & Sons), 208 (In the text)
Kalkofen, W., Rossi, P., Bodo, G., & Massaglia, S. 1994, A&A, 279, 579
Krijger, J. M., Rutten, R. J., Lites, B. W., et al. 2001, A&A, 379, 1052 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kuridze, D., Zaqarashvili, T. V., Shergelashvili, B. M., & Poedts, S. 2008, Annales Geophysicae, 26, 10, 2983 (In the text)
Lamb, H. 1908, Proc. Lond. Math. Soc., Ser., 2, 7, 122 (In the text)
McIntosh, S. W., & Judge, P.G. 2001, ApJ, 561, 420 [NASA ADS] [CrossRef] (In the text)
Moretti, P. F., Jefferies, S. M., Armstrong, J. D., & Mc Intosh, S. W. 2007, A&A, 471, 961 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Morse P. M., & Feshbach H. 1953, Methods of Theoret. Physics Part I (New York: Mc Graw Hill) (In the text)
Muglach, K., Hofmann, A., & Staude, J. 2005, A&A, 437, 1055 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Nagashima, K., Sekii, T., Kosovichev, A. G., et al. 2007, PASJ, 59, 631 [NASA ADS] (In the text)
Rae I. C., & Roberts, B. 1982, ApJ, 256, 761 [NASA ADS] [CrossRef] (In the text)
Roberts, B. 2004, ESA SP-547, 1 (In the text)
Schrijver, C. J., & Title, A. M. 2003, ApJ, 597, L165 [NASA ADS] [CrossRef] (In the text)
Srivastava, A. K., Kuridze, D., Zaqarashvili, T. V., & Dwivedi B. N. 2008, A&A, 481, 95 [NASA ADS] [CrossRef] (In the text)
Sutmann, G., Musielak, Z. E., & Ulmschneider, P. 1998, A&A, 340, 556 [NASA ADS] (In the text)
Vecchio, A., Cauzzi, G., Reardon, K. P., Janssen, K., & Rimmele, T. 2007, A&A, 461, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] (In the text)
Zaqarashvili, T. V., & Skhirtladze, N. 2008, ApJ, 683, 91 [NASA ADS] [CrossRef] (In the text)

All Figures

$\begin{figure} \par\includegraphics[width=7cm,clip]{11484fg1.eps} \end{figure}$	Figure 1: Simple schematic picture of small-scale magnetic canopy overlying a field-free cavity with gravitational stratification, g.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{11484fg2} \end{figure}$	Figure 2: The oscillation frequency, $\omega$ , versus the cavity radius, $r_{\rm c}$ , for the first zeros of the m=1 ( bottom line), m=2( middle line), and m=3 ( top line) harmonics.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg3} \end{figure}$	Figure 3: Real $\omega _{\rm r}$ (m=1 bottom line, m=2 top line on the left panel) and imaginary $\omega _{\rm i}$ (m=1 top line, m=2 bottom line on the right panel) parts of wave frequency vs. the radius of field-free cavity $r_{\rm c}$ . The straight line in the left panel is the solution with the cut-off frequency.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{11484fg4} \end{figure}$	Figure 4: Source point, observation point at t>t₀, and canopy/cavity interface.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg5} \end{figure}$	Figure 5: The density fluctuation after the propagation of pulse as a function of time and radial coordinate at $\phi =\pi /4$ . The time t is normalized by cut-off frequency and r is normalized by the photospheric scale height.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg6} \end{figure}$	Figure 6: Normalized asymptotic amplitude of the density wake versus the azimuthal angle $\phi$ at r'=2, t'=100 (the time t is normalized to the cut-off period and r is normalized to the scale height).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg7}\par\includegraphics[width=9cm,clip]{11484fg8} \end{figure}$	Figure 7: Normalized asymptotic amplitudes of the velocity perturbation components versus $\phi$ at r'=2, t'=100 (the time t is normalized to the cut-off period and r is normalized to the scale height).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11484fg9} \end{figure}$	Figure 8: Normalized total energy density with respect to $\phi$ . It is clearly seen that the energy is concentrated near the vertical direction.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.