| Issue |
A&A
Volume 505, Number 1, October I 2009
|
|
|---|---|---|
| Page(s) | 339 - 350 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912367 | |
| Published online | 22 July 2009 | |
Stellar coronal magnetic fields and star-planet interaction
A. F. Lanza
INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
Received 22 April 2009 / Accepted 9 June 2009
Abstract
Context. Evidence of magnetic interaction between late-type stars and close-in giant planets is provided by the observations of stellar hot spots rotating synchronously with the planets and showing an enhancement of chromospheric and X-ray fluxes. Possible photospheric signatures of such an interaction have also been reported.
Aims. We investigate star-planet interaction in the framework of a magnetic field model of a stellar corona, considering the interaction between the coronal field and that of a planetary magnetosphere moving through the corona. This is motivated, among other reasons, by the difficulty of accounting for the energy budgets of the interaction phenomena with previous models.
Methods. A linear force-free model is applied to describe the coronal field and study the evolution of its total magnetic energy and relative helicity according to the boundary conditions at the stellar surface and the effects related to the planetary motion through the corona.
Results. The energy budget of the star-planet interaction is discussed, assuming that the planet may trigger a release of the energy of the coronal field by decreasing its relative helicity. The observed intermittent character of the star-planet interaction is explained by a topological change in the stellar coronal field, induced by a variation in its relative helicity. The model predicts the formation of many prominence-like structures in the case of highly active stars owing to the accumulation of matter evaporated from the planet inside an azimuthal flux rope in the outer corona. Moreover, the model can explain why stars accompanied by close-in planets have a higher X-ray luminosity than those with distant planets. It predicts that the best conditions for detecting radio emission from the exoplanets and their host stars are achieved when the field topology is characterized by field lines connected to the surface of the star, leading to a chromospheric hot spot rotating synchronously with the planet.
Conclusions. The main predictions of the model can be verified with current observational techniques, by a simultaneous monitoring of the chromospheric flux and X-ray (or radio) emission, and spectropolarimetric observations of the photospheric magnetic fields.
Key words: stars: planetary systems - stars: activity - stars: late-type - stars: magnetic fields - stars: general
1 Introduction
More than 350 extrasolar giant planets are presently
known![]() , among which
, among which ![]() 25 percent have a
projected orbital semimajor axis smaller than 0.1 AU. Such planets are expected
to interact with their host stars, not only through tides, but also
with other mechanisms, possibly associated with magnetic fields. Specifically, reconnection between the coronal field of the host star and the magnetic field of the planet is expected to release heat, produce hydromagnetic waves, and accelerated particles that may be conveyed onto the stellar chromosphere producing a localized enhanced emission (Cranmer & Saar 2007; Cuntz et al. 2000; Ip et al. 2004; Preusse et al. 2006; McIvor et al. 2006). Indeed, Shkolnik et al. (2005,2008) show that HD 179949 and
25 percent have a
projected orbital semimajor axis smaller than 0.1 AU. Such planets are expected
to interact with their host stars, not only through tides, but also
with other mechanisms, possibly associated with magnetic fields. Specifically, reconnection between the coronal field of the host star and the magnetic field of the planet is expected to release heat, produce hydromagnetic waves, and accelerated particles that may be conveyed onto the stellar chromosphere producing a localized enhanced emission (Cranmer & Saar 2007; Cuntz et al. 2000; Ip et al. 2004; Preusse et al. 2006; McIvor et al. 2006). Indeed, Shkolnik et al. (2005,2008) show that HD 179949 and ![]() Andromedae have chromospheric hot spots that rotate with the orbital periods of their inner planets. Two other stars,
HD 189733 and
Andromedae have chromospheric hot spots that rotate with the orbital periods of their inner planets. Two other stars,
HD 189733 and ![]() Bootis, show evidence of an excess of chromospheric variability, probably because of flaring that is modulated with the orbital periods of their respective planets (cf. also Walker et al. 2008).
Modelling such features can allow us to obtain information on the magnetic fields of the planets, although in an indirect way (cf. Shkolnik et al. 2008), which is very important for constraining their internal structure and evolution as well as for characterizing a possible habitability in the case of rocky planets.
Bootis, show evidence of an excess of chromospheric variability, probably because of flaring that is modulated with the orbital periods of their respective planets (cf. also Walker et al. 2008).
Modelling such features can allow us to obtain information on the magnetic fields of the planets, although in an indirect way (cf. Shkolnik et al. 2008), which is very important for constraining their internal structure and evolution as well as for characterizing a possible habitability in the case of rocky planets.
A recent step forward in the understanding of the star-planet magnetic interaction (hereinafter SPMI) is the work of Lanza (2008). It applies force-free and non-force-free coronal field models to accounting for the observed phase lags between planets and synchronous chromospheric hot spots. Moreover, it conjectures about the possible influence of a close-in planet on the hydromagnetic dynamo action occurring in its host star. In the present paper, we extend that work by discussing topology, total energy, and relative magnetic helicity of the coronal field and by investigating their role in the effects associated with the motion of a hot Jupiter inside a stellar corona. We propose a new mechanism to account for the energy budget of SPMI and its intermittent nature, as revealed by the latest observations (see Sect. 2). Moreover, we discuss how the different coronal field topologies and the presence of a planet embedded in the corona may affect the formation of prominence-like structures, as well as the X-ray and radio emissions of a star.
2 Observations
Evidence of SPMI was reported by Shkolnik et al. (2003,2005,2008), who observed chromospheric hot spots rotating with the orbital period of the planets in HD 179949 and ![]() And instead of their respective rotation periods. The spots were not located at the subplanetary point, i.e., along the line joining the centre of a star with its planet, but led the planet by
And instead of their respective rotation periods. The spots were not located at the subplanetary point, i.e., along the line joining the centre of a star with its planet, but led the planet by ![]()
![]() in the case of
HD 179949 and
in the case of
HD 179949 and ![]()
![]() in the case of
in the case of ![]() And.
The flux irradiated by the hot spot was greater in the case of HD 179949, with an excess power of
And.
The flux irradiated by the hot spot was greater in the case of HD 179949, with an excess power of ![]() 1020 W, corresponding to that of a large solar flare. The hot spot synchronized with the planet was observed in four out of six seasons in HD 179949, suggesting that it is not a steady phenomenon, but may have a lifetime not exceeding 300-400 days. A similarly intermittent interaction is suggested by the observations of
1020 W, corresponding to that of a large solar flare. The hot spot synchronized with the planet was observed in four out of six seasons in HD 179949, suggesting that it is not a steady phenomenon, but may have a lifetime not exceeding 300-400 days. A similarly intermittent interaction is suggested by the observations of ![]() And, leading Shkolnik et al. (2008) to propose that these on/off SPMI transitions are related to a variation in the configuration of the coronal magnetic field of the host stars, possibly connected to their activity cycles. For the planet hosts HD 189733 and HD 73256, Shkolnik et al. (2008) suggest a correlation of the amplitude of the intranight variability of the Ca II K line core flux with the orbital phase of the planet, with a maximum of activity leading the planet by
And, leading Shkolnik et al. (2008) to propose that these on/off SPMI transitions are related to a variation in the configuration of the coronal magnetic field of the host stars, possibly connected to their activity cycles. For the planet hosts HD 189733 and HD 73256, Shkolnik et al. (2008) suggest a correlation of the amplitude of the intranight variability of the Ca II K line core flux with the orbital phase of the planet, with a maximum of activity leading the planet by ![]()
![]() in the case of HD 189733. This may stem from some chromospheric flaring activity synchronized with the planet.
in the case of HD 189733. This may stem from some chromospheric flaring activity synchronized with the planet.
The X-ray flux coming from HD 179949 appears to be modulated with the orbital period of the planet with a variation of ![]() 30 percent (Saar et al. 2007).
A statistical analysis of a sample of late-type stars reveals that those hosting a hot Jupiter closer than 0.15 AU have, on the average, an X-ray flux
30 percent (Saar et al. 2007).
A statistical analysis of a sample of late-type stars reveals that those hosting a hot Jupiter closer than 0.15 AU have, on the average, an X-ray flux ![]() 3-4 times greater than stars hosting planets farther than 1.5 AU (Kashyap et al. 2008). This suggests that a close-in giant planet may increase the X-ray activity level of its host star.
3-4 times greater than stars hosting planets farther than 1.5 AU (Kashyap et al. 2008). This suggests that a close-in giant planet may increase the X-ray activity level of its host star.
Circumstantial evidence of planet-induced photospheric magnetic activity in stars hosting hot Jupiters has been reported in ![]() Bootis by Walker et al. (2008) and in CoRoT-2a and CoRoT-4a by Lanza et al. (2009a), Pagano et al. (2009), and Lanza et al. (2009b). For
Bootis by Walker et al. (2008) and in CoRoT-2a and CoRoT-4a by Lanza et al. (2009a), Pagano et al. (2009), and Lanza et al. (2009b). For ![]() Boo, there is evidence of an active region leading the planet by about
Boo, there is evidence of an active region leading the planet by about
![]() whose signatures have been observed both in the Ca II K line core flux and in the wide-band optical flux as monitored by the MOST (Microvariability and Oscillation of STars) satellite.
The region shows a rotational modulation of
whose signatures have been observed both in the Ca II K line core flux and in the wide-band optical flux as monitored by the MOST (Microvariability and Oscillation of STars) satellite.
The region shows a rotational modulation of ![]() 1 mmag. In 2004
it resembled a dark spot of variable depth, while in 2005 it varied between bright and dark.
Since
1 mmag. In 2004
it resembled a dark spot of variable depth, while in 2005 it varied between bright and dark.
Since ![]() Boo has an average rotation period of 3.3 days, synchronized with the orbital period of the planet, and displays a surface differential rotation comparable to that of the Sun (Catala et al. 2007), it is the constancy of the phase shift between the spot and the planet that supports a possible SPMI in this case. As a matter of fact, the hot spot can be traced back to 2001, thanks to a previous Ca II K line flux monitoring.
Boo has an average rotation period of 3.3 days, synchronized with the orbital period of the planet, and displays a surface differential rotation comparable to that of the Sun (Catala et al. 2007), it is the constancy of the phase shift between the spot and the planet that supports a possible SPMI in this case. As a matter of fact, the hot spot can be traced back to 2001, thanks to a previous Ca II K line flux monitoring.
The planet host CoRoT-4a as a spectral type similar to ![]() Boo and its rotation appears to be synchronized on the average with that of its planet. Modelling two months of uninterrupted CoRoT observations, Lanza et al. (2009b) found evidence of a persistent active region at the subplanetary longitude. Five months of observations of CoRoT-2a revealed a modulation of the total spotted area with a cycle close to ten synodic periods of the hot Jupiter with respect to the stellar rotation period (Lanza et al. 2009a), again suggesting some kind of SPMI.
Pagano et al. (2009) found that the variance of the stellar flux was modulated in phase with the planetary orbit, with minimum variance at phase 0.3-0.4 and maximum at phase 0.8-0.9.
Finally, Henry et al. (2002) found evidence of a photospheric spot in HD 192263 that in two observing seasons rotated with the orbital period of its planet for at least three rotation cycles (see Santos et al. 2003).
Boo and its rotation appears to be synchronized on the average with that of its planet. Modelling two months of uninterrupted CoRoT observations, Lanza et al. (2009b) found evidence of a persistent active region at the subplanetary longitude. Five months of observations of CoRoT-2a revealed a modulation of the total spotted area with a cycle close to ten synodic periods of the hot Jupiter with respect to the stellar rotation period (Lanza et al. 2009a), again suggesting some kind of SPMI.
Pagano et al. (2009) found that the variance of the stellar flux was modulated in phase with the planetary orbit, with minimum variance at phase 0.3-0.4 and maximum at phase 0.8-0.9.
Finally, Henry et al. (2002) found evidence of a photospheric spot in HD 192263 that in two observing seasons rotated with the orbital period of its planet for at least three rotation cycles (see Santos et al. 2003).
This preliminary evidence of photospheric cool spots synchronized with a hot Jupiter is impossible to explain in the framework of a magnetic reconnection model because reconnection leads to energy release and thus heating of the atmosphere. Conversely, it suggests that the planet may affect in some way the stellar dynamo action or the emergence of magnetic flux, as conjectured by Lanza (2008).
Spectropolarimetric observations can be applied to mapping photospheric fields outside starspots, and indeed for ![]() Boo a sequence of maps has been obtained that suggests that the magnetic activity cycle of the star is as short as
Boo a sequence of maps has been obtained that suggests that the magnetic activity cycle of the star is as short as ![]() 2 years, instead of 22 years as in the Sun
(Donati et al. 2008; Fares et al. 2009).
2 years, instead of 22 years as in the Sun
(Donati et al. 2008; Fares et al. 2009).
Solar system giant planets emit in the radio domain, mainly via the electron-cyclotron maser mechanism. Most of the power is coherently radiated near the cyclotron frequency
![]() MHz, where B is the intensity of the planet's magnetic field in Gauss. In the case of Jupiter, the maximum of the flux falls around 40 MHz. Solar system planets follow a scaling law that relates their emitted radio power to the power supplied by the impinging solar wind
at their magnetospheric boundary.
When generalizing that scaling law, it is possible to predict exoplanetary radio emission powers
(cf., e.g., Stevens 2005; Zarka 2007; Jardine & Collier Cameron 2008). For
MHz, where B is the intensity of the planet's magnetic field in Gauss. In the case of Jupiter, the maximum of the flux falls around 40 MHz. Solar system planets follow a scaling law that relates their emitted radio power to the power supplied by the impinging solar wind
at their magnetospheric boundary.
When generalizing that scaling law, it is possible to predict exoplanetary radio emission powers
(cf., e.g., Stevens 2005; Zarka 2007; Jardine & Collier Cameron 2008). For ![]() Boo and some other systems, fluxes between 30 and 300 mJy, i.e., within the detection limits of some of the largest radio telescopes, have been predicted for favourable conditions. Nevertheless, no positive detection has been reported yet, not only in the case of
Boo and some other systems, fluxes between 30 and 300 mJy, i.e., within the detection limits of some of the largest radio telescopes, have been predicted for favourable conditions. Nevertheless, no positive detection has been reported yet, not only in the case of ![]() Boo, observed at several epochs at 74 MHz with upper limits between 135 and 300 mJy (Lazio & Farrell 2007), but also for
Boo, observed at several epochs at 74 MHz with upper limits between 135 and 300 mJy (Lazio & Farrell 2007), but also for ![]() Eridani and HD 128311 at 150 MHz (George & Stevens 2007) for which tight upper limits of 10-20 mJy were derived, and for HD 189733, for which an upper limit of
Eridani and HD 128311 at 150 MHz (George & Stevens 2007) for which tight upper limits of 10-20 mJy were derived, and for HD 189733, for which an upper limit of ![]() 80 mJy was reached over the 307-347 MHz range (Smith et al. 2009). It is hoped that the next generation of low-frequency radio telescopes can lower those limits by at least one order of magnitude, allowing us to clarify whether the missed detections are due to a lack of sensitivity or a lack of emission from the exoplanets at those frequencies. As a matter of fact, if hot Jupiters have magnetic field strengths comparable to that of Jupiter, i.e.,
80 mJy was reached over the 307-347 MHz range (Smith et al. 2009). It is hoped that the next generation of low-frequency radio telescopes can lower those limits by at least one order of magnitude, allowing us to clarify whether the missed detections are due to a lack of sensitivity or a lack of emission from the exoplanets at those frequencies. As a matter of fact, if hot Jupiters have magnetic field strengths comparable to that of Jupiter, i.e.,
![]() G at the poles (with
G at the poles (with
![]() G at the planet's equator), most of their radio emission falls at lower frequencies than those of the above-mentioned surveys. Another possibility is that the emission is beamed out of the line of sight or that the stellar wind power (kinetic and/or magnetic) is significantly less than assumed.
G at the planet's equator), most of their radio emission falls at lower frequencies than those of the above-mentioned surveys. Another possibility is that the emission is beamed out of the line of sight or that the stellar wind power (kinetic and/or magnetic) is significantly less than assumed.
3 Coronal field model
We adopt a spherical polar coordinate frame having its origin at the baricentre of the host star and the polar axis along the stellar rotation axis. The radial distance from the origin is indicated with r, the colatitude measured from the North pole with ![]() ,
and the azimuthal angle with
,
and the azimuthal angle with ![]() .
The planet orbit is assumed circular with a semimajor axis a and lying in the equatorial plane of the star
.
The planet orbit is assumed circular with a semimajor axis a and lying in the equatorial plane of the star![]() .
.
Close to a star, the magnetic pressure in the corona is much greater than the plasma pressure and the gravitational force, so we can assume that the corona is in a force-free magnetohydrostatic balance, i.e., the current density ![]() is parallel everywhere to the magnetic field
is parallel everywhere to the magnetic field ![]() ,
viz.
,
viz.
![]() .
This means that
.
This means that
![]() ,
with the force-free parameter
,
with the force-free parameter ![]() constant along each field line (Priest 1982). If
constant along each field line (Priest 1982). If ![]() is uniform in the stellar corona, the field is called a linear force-free field, and it satisfies the vector Helmoltz equation
is uniform in the stellar corona, the field is called a linear force-free field, and it satisfies the vector Helmoltz equation
![]() .
Its solutions in spherical geometry have been studied by, e.g., Chandrasekhar (1956) and Chandrasekhar & Kendall (1957).
.
Its solutions in spherical geometry have been studied by, e.g., Chandrasekhar (1956) and Chandrasekhar & Kendall (1957).
Linear force-free fields are particularly attractive in view of their mathematical symplicity and their minimum-energy properties in a finite domain, as shown by Woltjer (1958). Specifically, in ideal magnetohydrodynamics, the minimum energy state of a magnetic field in a finite domain is a linear force-free state set according to the boundary conditions and the constraint posed by the conservation of the magnetic helicity. In a confined stellar corona, magnetic dissipation is localized within thin current sheets whose global effect is that of driving the field configuration toward the minimum energy state compatible with the conservation of the total helicity, the so-called Taylor's state, which is a linear force-free field (see, e.g., Berger 1985; Heyvaerts & Priest 1984, for details). Only in large flares is the total helicity not conserved because of strong turbulent dissipation and ejection of magnetized plasma.
The total helicity of a confined magnetic structure constrains its free energy, which is the energy that can be released in a magnetic dissipation process. It is the difference between the initial energy of the field, which is usually in a nonlinear force-free state (i.e., with a nonuniform ![]() ), and the energy of the linear force-free field satisfying the same boundary conditions and having the same total helicity (see, e.g., Régnier & Priest 2007). Therefore, a decrease in the total helicity produced by a change of the boundary conditions or a strong magnetic dissipation will in general make more free energy available for heating the corona.
), and the energy of the linear force-free field satisfying the same boundary conditions and having the same total helicity (see, e.g., Régnier & Priest 2007). Therefore, a decrease in the total helicity produced by a change of the boundary conditions or a strong magnetic dissipation will in general make more free energy available for heating the corona.
To model the magnetic interaction between the stellar coronal field and a close-in planet, we consider only the dipole-like component (i.e., with a radial order n=1) of the linear force-free solution of Chandrasekhar & Kendall (1957) because it has the slowest decay with distance from the star and therefore leads to the strongest interaction. Moreover, since the observations of star-planet interaction show a hot spot rotating with the orbital period of the planet and do not show the periodicity of stellar rotation, an axisymmetric field (i.e., with an azimuthal degree m=0) is a good approximation to describe the interaction, as discussed by Lanza (2008).
Our linear force-free field can be expressed in the formalism of Flyer et al. (2004) as
where
![\begin{displaymath}g (q) \equiv \frac{[b_{0} J_{-3/2}(q) + c_{0} J_{3/2}(q)]\sqr...
...{[b_{0} J_{-3/2}(q_{0}) + c_{0} J_{3/2}(q_{0})] \sqrt{q_{0}}},
\end{displaymath}](/articles/aa/full_html/2009/37/aa12367-09/img28.png) |
(2) |
where b0 and c0 are free constants, J-3/2 and J3/2 are Bessel functions of the first kind of order -3/2 and 3/2, respectively,
where
The magnetic field geometry specified by Eqs. (3) depends on two independent parameters, i.e., ![]() and
b0/c0. They can be derived from the boundary conditions at the stellar photosphere, i.e., knowing the magnetic field
and
b0/c0. They can be derived from the boundary conditions at the stellar photosphere, i.e., knowing the magnetic field
![]() on the surface at r=R. Using the orthogonality properties of the basic poloidal and toroidal fields (see Chandrasekhar 1961), we find
on the surface at r=R. Using the orthogonality properties of the basic poloidal and toroidal fields (see Chandrasekhar 1961), we find
where
The magnetic energy E of the field confined between the spherical surfaces r=R and
![]() can be found from Eq. (79) in Sect. 40 of Chandrasekhar (1961):
can be found from Eq. (79) in Sect. 40 of Chandrasekhar (1961):
where
The field obtained by changing the sign of
In the limit ![]() ,
i.e., close to the stellar surface, neglecting terms
of the order of O(q2), we find that
,
i.e., close to the stellar surface, neglecting terms
of the order of O(q2), we find that
![]() and
and
![]() ,
independently of b0 and c0. From Eqs. (3), we see that
,
independently of b0 and c0. From Eqs. (3), we see that
![]() and
and
![]() close to the star are similar to the analogous components of the potential dipole field with the same radial component at the surface.
close to the star are similar to the analogous components of the potential dipole field with the same radial component at the surface.
It is also interesting to study the limit
![]() of our force-free field. In this limit,
of our force-free field. In this limit,
![]() and the radial extension of the field grows without bounds. Nevertheless, the field tends to become indistinguishable from the corresponding potential field and
and the radial extension of the field grows without bounds. Nevertheless, the field tends to become indistinguishable from the corresponding potential field and
![]() .
In the same limit, the relative magnetic helicity grows without bounds because
.
In the same limit, the relative magnetic helicity grows without bounds because
![]() in Eq. (6), but the helicity density (i.e., the magnetic helicity per unit volume) tends to zero (see Zhang & Low 2005; Berger 1985, for a further description of this limit state).
in Eq. (6), but the helicity density (i.e., the magnetic helicity per unit volume) tends to zero (see Zhang & Low 2005; Berger 1985, for a further description of this limit state).
For a finite ![]() ,
,
![]() because the potential field has the minimum energy for a given
because the potential field has the minimum energy for a given
![]() .
If we consider all magnetic fields with one end of their field lines anchored at r=R and the other out to infinity, satisfying the same boundary conditions of our field at r=R, the field with the lowest possible energy is called the Aly field and its energy
.
If we consider all magnetic fields with one end of their field lines anchored at r=R and the other out to infinity, satisfying the same boundary conditions of our field at r=R, the field with the lowest possible energy is called the Aly field and its energy
![]() (see Flyer et al. 2004). We assume that the Aly energy is an upper bound for the energy of our field because it is the lowest energy allowing the field to open up all its lines of force out to infinity driving a plasma outflow similar to a solar coronal mass ejection.
(see Flyer et al. 2004). We assume that the Aly energy is an upper bound for the energy of our field because it is the lowest energy allowing the field to open up all its lines of force out to infinity driving a plasma outflow similar to a solar coronal mass ejection.
From a topological point of view, the fields obtained from Eqs. (3) can be classified into two classes. If the function g(q) decreases monotonously in the interval
![]() ,
all field lines are anchored at both ends on the boundary r=R. On the other hand, if the function has a relative minimum (and a relative maximum) in that interval, the field contains an azimuthal rope of flux located entirely in the r > R space and running around the axis of symmetry. The magnetic field configurations considered by Lanza (2008) to model SPMI are of the first kind; an example of a field configuration containing an azimuthal flux rope will be discussed in Sect. 4.2. An analogous topological classification holds in the case of the nonlinear force-free fields considered by Flyer et al. (2004).
,
all field lines are anchored at both ends on the boundary r=R. On the other hand, if the function has a relative minimum (and a relative maximum) in that interval, the field contains an azimuthal rope of flux located entirely in the r > R space and running around the axis of symmetry. The magnetic field configurations considered by Lanza (2008) to model SPMI are of the first kind; an example of a field configuration containing an azimuthal flux rope will be discussed in Sect. 4.2. An analogous topological classification holds in the case of the nonlinear force-free fields considered by Flyer et al. (2004).
The photospheric magnetic field components can be measured by means of spectropolarimetric techniques if the star rotates fast enough (
![]() -15 km s-1) as shown in the case of, e.g.,
-15 km s-1) as shown in the case of, e.g., ![]() Boo by Catala et al. (2007) and Donati et al. (2008).
Therefore, Eqs. (4) can be applied to derive the parameters of the coronal field model and its topology, by assuming that the field is force-free down to the photosphere, as we show in Sect. 4.2.
Boo by Catala et al. (2007) and Donati et al. (2008).
Therefore, Eqs. (4) can be applied to derive the parameters of the coronal field model and its topology, by assuming that the field is force-free down to the photosphere, as we show in Sect. 4.2.
4 Applications
In this section we consider some applications of the above model for the stellar coronal field to the phenomena introduced in Sect. 2.
4.1 Power dissipated in SPMI
The power needed to explain the excess flux from a chromospheric hot spot or an X-ray emission synchronous with the planet is of the order of 1020-1021 W. Magnetic reconnection between the stellar coronal field and the planetary field at the boundary of the planetary magnetosphere is not sufficient to account for such a power, as we show in Sect. 4.1.1. Therefore, we propose an interaction mechanism that may be capable of sustaining that level of power in Sect. 4.1.2.
4.1.1 A simple magnetic reconnection model
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg70.png) |
Figure 1:
The modulus of the magnetic field on the equatorial plane of the star normalized to its value at the surface vs. the radial distance from the star for
b0/c0=-1.1 and
|
| Open with DEXTER | |
The first mechanism proposed to account for the energy budget of SPMI is reconnection between the planetary and the stellar magnetic fields at the boundary of the planetary magnetosphere. This boundary is characterized by a balance between the magnetic pressure of the coronal field and the planetary field.
The ram pressure is negligible because the planet is inside the region where the stellar wind speed is subalfvenic (cf., e.g., Preusse et al. 2005), and the orbital velocity of the planet is about one order of magnitude lower than the Alfven velocity (Lanza 2008). Therefore, assuming a planetary field with a dipole geometry, the radius of the planetary magnetosphere ![]() ,
measured from the centre of the planet, is given by
,
measured from the centre of the planet, is given by
![\begin{displaymath}R_{\rm m} = R_{\rm pl} \left[ \frac{B(a, \frac{\pi}{2})}{B_{\rm pl}} \right]^{-\frac{1}{3}},
\end{displaymath}](/articles/aa/full_html/2009/37/aa12367-09/img72.png) |
(7) |
where
We specify our considerations for the SPMI model of HD 179949 developed by Lanza (2008) that assumes
b0/c0= -1.1 and
![]() to explaining the phase lag between the chromospheric hot spot and the planet. The magnetic field intensity vs. the distance from the star is plotted in Fig. 1. The field strength decreases as that of a potential dipole field close to the star, i.e., where
to explaining the phase lag between the chromospheric hot spot and the planet. The magnetic field intensity vs. the distance from the star is plotted in Fig. 1. The field strength decreases as that of a potential dipole field close to the star, i.e., where
![]() (cf. Sect. 3), then it decreases more slowly for r > (6-7) R because the decrease of g(q) becomes less steep (cf., e.g., Fig. 3).
(cf. Sect. 3), then it decreases more slowly for r > (6-7) R because the decrease of g(q) becomes less steep (cf., e.g., Fig. 3).
At the distance of the planet, i.e., a=7.72 R, the field is reduced by a factor of ![]() 300 with respect to its value at the stellar surface. Assuming a mean field at the surface
B0 = 10 G (cf. Donati et al. 2008), the field at the boundary of the planetary magnetosphere is
300 with respect to its value at the stellar surface. Assuming a mean field at the surface
B0 = 10 G (cf. Donati et al. 2008), the field at the boundary of the planetary magnetosphere is
![]() G. Adopting a planetary field
G. Adopting a planetary field
![]() G (cf., e.g., Grießmeier et al. 2004) and a radius of the planet equal to that of Jupiter, we find
G (cf., e.g., Grießmeier et al. 2004) and a radius of the planet equal to that of Jupiter, we find
![]() m. The power dissipated by magnetic reconnection can be estimated as
m. The power dissipated by magnetic reconnection can be estimated as
where
4.1.2 Magnetic energy release induced by a hot Jupiter
To solve the energy problem, it is important to note that the energy released at the reconnection site is only a fraction of the energy that is actually available. The emergence of magnetic flux from the convection zone and the photospheric motions lead to a continuous accumulation of energy in the coronal field, independently of the presence of any planet. Our conjecture is that a close-in planet triggers a release of such an accumulated energy, modulating the chromospheric and coronal heating with the orbital period of the planet.
As a matter of fact, the reconnection between the coronal and the planetary field lines has remarkable consequences for the topological structure of the coronal field. The final configuration of the coronal field after reconnection is in general a nonlinear force-free one; i.e., ![]() is no longer spatially uniform. This happens because the field must simultaneously satisfy the boundary conditions at the photosphere, which impose the value of
is no longer spatially uniform. This happens because the field must simultaneously satisfy the boundary conditions at the photosphere, which impose the value of ![]() close to the star, and those at the reconnection site close to the planet, which in general will not be compatible with a uniform value of
close to the star, and those at the reconnection site close to the planet, which in general will not be compatible with a uniform value of ![]() .
Since
.
Since ![]() must be constant along a given field line, the field re-arranges itself into a configuration with different values of
must be constant along a given field line, the field re-arranges itself into a configuration with different values of ![]() along different field lines to satisfy the boundary conditions. We know from the Woltjer theorem that the energy of the field in such a state is greater than that of the linear force-free field with the same magnetic helicity and boundary conditions at the stellar surface. In other words, some energy can be released if the field makes a transition to this linear force-free state, restoring its unperturbed configuration. Such a transition can be stimulated by the fact that the helicity in the region where the field has reconnected is lower than the initial helicity because reconnection processes lead to a steady dissipation of helicity. Considering the volume V(t) occupied at any given time t by the plasma where reconnection has just occurred, the rate of helicity change inside V(t) is given by Eq. (13) of
Heyvaerts & Priest (1984):
along different field lines to satisfy the boundary conditions. We know from the Woltjer theorem that the energy of the field in such a state is greater than that of the linear force-free field with the same magnetic helicity and boundary conditions at the stellar surface. In other words, some energy can be released if the field makes a transition to this linear force-free state, restoring its unperturbed configuration. Such a transition can be stimulated by the fact that the helicity in the region where the field has reconnected is lower than the initial helicity because reconnection processes lead to a steady dissipation of helicity. Considering the volume V(t) occupied at any given time t by the plasma where reconnection has just occurred, the rate of helicity change inside V(t) is given by Eq. (13) of
Heyvaerts & Priest (1984):
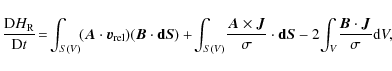 |
(9) |
where S(V) is the surface bounding the volume V(t),
where
We conjecture that, once a magnetic energy release is triggered by such a decrease in helicity in the reconnection volume, it extends to the whole flux tube connecting the planetary magnetosphere with the stellar surface and proceeds faster and faster thanks to a positive feedback between energy release and helicity dissipation. In other words, the fast and localized energy release produces a turbulent plasma that in turn enhances turbulent dissipation of magnetic energy and helicity, giving rise to a self-sustained process.
An order-of-magnitude estimate of the helicity dissipation rate can be based on Eq. (10), now considering turbulent dissipation. It can be recast in the approximate form:
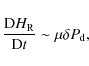 |
(11) |
where
In the above derivation, we have guessed the dissipated power from the available observations. For the mechanism to be at least plausible, we need to show that it is possible to sustain that level of dissipated power. This implies a computation of the energy stored in the nonlinear force-free field that is produced by the reconnection process, which is beyond the capability of our simple linear model. Nevertheless, we may estimate the energy available by means of a simplified argument that is by no means rigorous, but has the advantage of using our model for linear force-free configurations. Its results should only be regarded as an illustration of the plausibility of the proposed mechanism, deferring a more detailed and rigorous treatment to future studies.
To compute the available energy, we assume that the reconnection between the coronal and planetary fields produces a dissipation of the helicity of the initial field configuration, i.e., that unperturbed by the planet. Again, we specify our considerations for the case of HD 179949, adopting the linear force-free model of Lanza (2008). Therefore, we fix
![]() and
b0/c0=-1.1 in the initially unperturbed state, giving a total energy
and
b0/c0=-1.1 in the initially unperturbed state, giving a total energy
![]() and a relative helicity
and a relative helicity
![]() (cf. Eqs. (5) and (6)). The boundary conditions at the stellar surface specify the values of
(cf. Eqs. (5) and (6)). The boundary conditions at the stellar surface specify the values of
![]() and
and ![]() through Eqs. (4). The value of
through Eqs. (4). The value of ![]() depends on the radial and azimuthal field components at the surface and must be regarded as fixed. Conversely, the value of
b0/c0 is pratically independent of the value of
depends on the radial and azimuthal field components at the surface and must be regarded as fixed. Conversely, the value of
b0/c0 is pratically independent of the value of
![]() for
b0/c0 < -1.0. This is illustrated in Fig. 2 and is discussed further in Sect. 4.2. In other words, the ratio
b0/c0 is only marginally constrained by the boundary conditions and can be assumed to vary in order to decrease the total helicity of the field. The minimum helicity is obtained for
for
b0/c0 < -1.0. This is illustrated in Fig. 2 and is discussed further in Sect. 4.2. In other words, the ratio
b0/c0 is only marginally constrained by the boundary conditions and can be assumed to vary in order to decrease the total helicity of the field. The minimum helicity is obtained for
![]() ,
which gives
,
which gives
![]() while for the initial field configuration with
b0/c0= -1.1,
while for the initial field configuration with
b0/c0= -1.1,
![]() ,
corresponding to a variation in the boundary condition by only 0.13 percent. This state of the field has
,
corresponding to a variation in the boundary condition by only 0.13 percent. This state of the field has
![]() and
and
![]() ,
i.e., a helicity variation
,
i.e., a helicity variation
![]() with respect to the initial state. Assuming B0= 10 G and
with respect to the initial state. Assuming B0= 10 G and
![]() m, the transition from the initial state to this final state releases an energy
m, the transition from the initial state to this final state releases an energy
![]() J. A crucial point is the timescale for the release of
J. A crucial point is the timescale for the release of ![]() because it determines the power available to explain the observed phenomena. It depends on the timescale for the dissipation of the helicity and can be computed from the helicity dissipation rate as
because it determines the power available to explain the observed phenomena. It depends on the timescale for the dissipation of the helicity and can be computed from the helicity dissipation rate as
![]() s, where we make use of Eq. (12).
Therefore, the available maximum power, estimated from
s, where we make use of Eq. (12).
Therefore, the available maximum power, estimated from
![]() ,
turns out to be
,
turns out to be ![]()
![]() W, which is of the right order of magnitude to account for the chromospheric hot spot and the enhancement of X-ray flux.
W, which is of the right order of magnitude to account for the chromospheric hot spot and the enhancement of X-ray flux.
It is important to note that our argument provides us only with a lower limit for the energy that can be released because we approximate the process as a transition between two linear force-free fields. As a matter of fact, when the field is in a nonlinear force-free state, its energy is greater than the energy of the initially unperturbed linear force-free field, allowing the system to release more energy than we have estimated above. This can explain the modulation of the emitted flux with the orbital phase of the planet if only a portion of the stellar corona surrounding the flux tube connecting the planet with the star is involved in the energy release process at any given time.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f2.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg122.png) |
Figure 2:
The first derivative of the function g at the surface of the star (i.e., r=R) vs.
b0/c0 for
|
| Open with DEXTER | |
The initial field configuration needs to be restored on a timescale comparable to the orbital period of the planet to achieve a quasi-stationary situation in agreement with the observations.
An order of magnitude estimate of the helicity flux coming from the photospheric motions can be obtained from Eq. (11) of Heyvaerts & Priest (1984) as
where
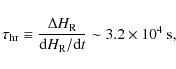 |
(14) |
where
It is interesting to note that the greater the magnetic field of a hot Jupiter, the more efficient the triggering of helicity dissipation in a stellar corona by the planet itself because the dissipated power scales as
![]() in Eqs. (8) and (10). However, even if the planetary magnetic field is negligible, we still expect some dissipation by the currents induced in the planetary conductive interior by its motion through the stellar coronal field (Laine et al. 2008) or by the currents associated with the Alfven waves excited by the motion of the planet through the stellar wind (Preusse et al. 2005,2006). The corresponding helicity dissipation rate in Eq. (10) is expected to be at least two orders of magnitude less than when the planet has a field
in Eqs. (8) and (10). However, even if the planetary magnetic field is negligible, we still expect some dissipation by the currents induced in the planetary conductive interior by its motion through the stellar coronal field (Laine et al. 2008) or by the currents associated with the Alfven waves excited by the motion of the planet through the stellar wind (Preusse et al. 2005,2006). The corresponding helicity dissipation rate in Eq. (10) is expected to be at least two orders of magnitude less than when the planet has a field
![]() of 5-10 G, essentially because the current dissipation is confined within a much smaller volume. Therefore, the efficiency of the proposed mechanism is likely to be significantly reduced when the planetary field vanishes.
of 5-10 G, essentially because the current dissipation is confined within a much smaller volume. Therefore, the efficiency of the proposed mechanism is likely to be significantly reduced when the planetary field vanishes.
4.2 The intermittent nature of SPMI
The fact that chromospheric hot spots rotating synchronously with the planetary orbit have not always been observed in HD 179949 and ![]() And (Shkolnik et al. 2008) can be interpreted by assuming that their activity cycles are very short, i.e., of the order of 1-2 years. If the large-scale dipole field cyclically reverses its direction, we have alternate phases of strong and weak interactions with the magnetic field of the planet (see Lanza 2008). Such a hypothesis has received some support from the observation of two consecutive field reversals in a couple of years in
And (Shkolnik et al. 2008) can be interpreted by assuming that their activity cycles are very short, i.e., of the order of 1-2 years. If the large-scale dipole field cyclically reverses its direction, we have alternate phases of strong and weak interactions with the magnetic field of the planet (see Lanza 2008). Such a hypothesis has received some support from the observation of two consecutive field reversals in a couple of years in ![]() Boo (Donati et al. 2008; Fares et al. 2009). Moreover, Cranmer & Saar (2007) and Shkolnik et al. (2009) build a statistical model for SPMI, based on the observations of the solar photospheric field along cycle 22 and its extrapolation to the corona by means of a potential field model, which predicts an intermittent interaction. The relative durations of the on and off phases depend on the phase of the solar cycle and generally agree with the few available observations reported in Sect. 2. Nevertheless, another interpretation is possible that does not require a global reversal of the magnetic field or a complex geometry of the coronal field, but only a change in the photospheric boundary conditions that induces a change in the global topology of the coronal field.
Boo (Donati et al. 2008; Fares et al. 2009). Moreover, Cranmer & Saar (2007) and Shkolnik et al. (2009) build a statistical model for SPMI, based on the observations of the solar photospheric field along cycle 22 and its extrapolation to the corona by means of a potential field model, which predicts an intermittent interaction. The relative durations of the on and off phases depend on the phase of the solar cycle and generally agree with the few available observations reported in Sect. 2. Nevertheless, another interpretation is possible that does not require a global reversal of the magnetic field or a complex geometry of the coronal field, but only a change in the photospheric boundary conditions that induces a change in the global topology of the coronal field.
We explore the effect of a change in the boundary conditions on the force-free configuration adopted by Lanza (2008) to model SPMI in the case of HD 179949. It assumes
![]() and
b0/c0 = -1.1. The mean of the meridional field component over the surface of the star
and
b0/c0 = -1.1. The mean of the meridional field component over the surface of the star
![]() in the righthand side of the second of Eqs. (4) fixes the value of
in the righthand side of the second of Eqs. (4) fixes the value of
![]() from which we can derive the model parameter
b0/c0. A plot of
from which we can derive the model parameter
b0/c0. A plot of
![]() vs.
b0/c0 is given in Fig. 2 for
vs.
b0/c0 is given in Fig. 2 for
![]() and shows that there is a large interval of
b0/c0 where the variation of
and shows that there is a large interval of
b0/c0 where the variation of
![]() is very small. In other words, a modest variation in the meridional field component produces a remarkable variation in
b0/c0. On the other hand, to significantly change the parameter
is very small. In other words, a modest variation in the meridional field component produces a remarkable variation in
b0/c0. On the other hand, to significantly change the parameter ![]() we need a remarkable change of the axisymmetric azimuthal field component over the surface of the star that can be achieved only on timescales comparable with the stellar activity cycle. Therefore, the dependence on the boundary conditions suggests to explore the modification of the field topology for a variable
b0/c0 helding
we need a remarkable change of the axisymmetric azimuthal field component over the surface of the star that can be achieved only on timescales comparable with the stellar activity cycle. Therefore, the dependence on the boundary conditions suggests to explore the modification of the field topology for a variable
b0/c0 helding ![]() fixed.
fixed.
The plots of the radial function g(q) and its first derivative
![]() vs. q are shown in Fig. 3 for several values of
b0/c0 and
vs. q are shown in Fig. 3 for several values of
b0/c0 and
![]() .
For
(b0/c0) < - 0.9745, the function g is monotonously decreasing and all the field lines have both ends anchored onto the photosphere. A sketch of the meridional section of the field lines is given in Fig. 1 of Lanza (2008) for
b0/c0 = -1.1. On the other hand, for
.
For
(b0/c0) < - 0.9745, the function g is monotonously decreasing and all the field lines have both ends anchored onto the photosphere. A sketch of the meridional section of the field lines is given in Fig. 1 of Lanza (2008) for
b0/c0 = -1.1. On the other hand, for
![]() ,
the derivative
,
the derivative
![]() vanishes at two points within the interval
vanishes at two points within the interval
![]() ,
and the field develops an azimuthal rope of flux centred around the maximum of g(q) and whose inner radius coincides with the minimum of g(q).
,
and the field develops an azimuthal rope of flux centred around the maximum of g(q) and whose inner radius coincides with the minimum of g(q).
![\begin{figure}
\par\includegraphics[width=8.8cm,height=12cm]{12367f3.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg133.png) |
Figure 3:
Upper panel: the radial function g vs. q for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f4.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg137.png) |
Figure 4:
Upper panel: the magnetic field energy as a fraction of the corresponding potential field energy vs.
b0/c0 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=12cm]{12367f5.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg140.png) |
Figure 5:
Meridional section of the magnetic field lines for
|
| Open with DEXTER | |
We have illustrated the dependences of
![]() ,
field energy and helicity on the parameter
b0/c0 for the particular case of
,
field energy and helicity on the parameter
b0/c0 for the particular case of
![]() ,
but their qualitative behaviours are the same for different values of
,
but their qualitative behaviours are the same for different values of ![]() .
Specifically, we have explored numerically the dependence of
.
Specifically, we have explored numerically the dependence of
![]() and
and
![]() in the rectangle
in the rectangle
![]() finding that they are always monotonously increasing functions of
b0/c0 for any fixed value of
finding that they are always monotonously increasing functions of
b0/c0 for any fixed value of ![]() .
.
In Sect. 4.1.2, we have assumed that the helicity of the stellar corona is determined by a dynamical balance between the opposite contributions of the emerging magnetic fields and photospheric motions that build it up, and the orbital motion of the planet that triggers a continuous dissipation of helicity and magnetic energy in the corona. Therefore, the photospheric boundary conditions that fix the value of the helicity in our model can be regarded as a result of those processes that rule the helicity balance of the stellar corona.
To explain the transition between states with and without a chromospheric hot spot, we assume that the helicity of the coronal field and the corresponding boundary conditions can vary on a shorter timescale than the stellar activity cycle. Specifically, the flux of helicity into the corona and the meridional component of the surface field are expected to vary as a result of the fluctuations characterizing turbulent hydromagnetic dynamos (cf., e.g., Brandenburg & Subramanian 2005). As a consequence, b0/c0 varies, spanning a certain range of values. If such a range is wide enough, the value of the parameter can sometimes cross the threshold b0/c0= -0.9745 for the transition to a flux rope topology, thus halting the SPMI mechanism described in Sect. 4.1.2. Conversely, when the parameter crosses the threshold in the reverse direction, SPMI is resumed. The relative durations of such on and off phases depend on the statistical distribution of the fluctuations of the meridional component of the surface field, which is presently unknown. However, an on/off transition can take place on a timescale as short as 105-106 s assuming the helicity fluxes and dissipation rates estimated in Sect. 4.1.2.
The phase lag
![]() between the planet and the chromospheric hot spot depends on
b0/c0 for a fixed
between the planet and the chromospheric hot spot depends on
b0/c0 for a fixed ![]() (see Lanza 2008, for the method to compute
(see Lanza 2008, for the method to compute
![]() ). We plot such a dependence in Fig. 6.
When the field has no flux rope, i.e.,
b0/c0 < -0.97,
). We plot such a dependence in Fig. 6.
When the field has no flux rope, i.e.,
b0/c0 < -0.97,
![]() only slightly depends on
b0/c0 varying only by
only slightly depends on
b0/c0 varying only by
![]() around the mean observed value of
around the mean observed value of ![]()
![]() ,
even for values of
b0/c0 as small as -3.0, i.e., well beyond the range considered to model the observations of HD 179949. The variation in
,
even for values of
b0/c0 as small as -3.0, i.e., well beyond the range considered to model the observations of HD 179949. The variation in
![]() only becomes steep when the field is very close to develop a flux rope. The inner radius of the flux rope reaches the distance of the planet (
r/R = 7.72) when
b0/c0= -0.908. We assume that the transition from, say,
b0/c0= -1.1 to -0.9 occurs on a timescale so short that it has no observable consequences on
only becomes steep when the field is very close to develop a flux rope. The inner radius of the flux rope reaches the distance of the planet (
r/R = 7.72) when
b0/c0= -0.908. We assume that the transition from, say,
b0/c0= -1.1 to -0.9 occurs on a timescale so short that it has no observable consequences on
![]() given the limited duty cycles of present ground-based observations.
given the limited duty cycles of present ground-based observations.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f6.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg145.png) |
Figure 6:
The phase lag between the planet and the synchronous chromospheric hot spot vs.
b0/c0 for
|
| Open with DEXTER | |
By increasing
b0/c0, the energy of the field grows up to the Aly limit where an instability opening the field lines may possibly be triggered. The magnetic field intensity vs. the distance from the star is plotted in Fig. 7 for a model with
![]() and the Aly energy.
and the Aly energy.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f7.eps} %
\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg146.png) |
Figure 7:
The modulus of the magnetic field on the equatorial plane of the star normalized to its value at the surface vs. the radial distance from the star for
b0/c0=-0.107 and
|
| Open with DEXTER | |
The explanation suggested above for the intermittent behaviour of SPMI can be tested by measuring the direction of
![]() ,
i.e., the meridional field component at the stellar surface, which is possible by means of spectropolarimetric techniques (cf. Donati et al. 2008; Moutou et al. 2007) if the star rotates fast enough (
,
i.e., the meridional field component at the stellar surface, which is possible by means of spectropolarimetric techniques (cf. Donati et al. 2008; Moutou et al. 2007) if the star rotates fast enough (
![]() -15 km s-1).
If the on/off SPMI transition is not associated with a reversal of
-15 km s-1).
If the on/off SPMI transition is not associated with a reversal of
![]() ,
the present explanation gains support. In principle, by measuring the surface components of the field and the angle
,
the present explanation gains support. In principle, by measuring the surface components of the field and the angle
![]() with sufficient accuracy, it is possible to estimate
b0/c0, thus constraining the model parameters during the SPMI on phases. Specifically, we can use the first and the third of Eqs. (4) to find B0 and
with sufficient accuracy, it is possible to estimate
b0/c0, thus constraining the model parameters during the SPMI on phases. Specifically, we can use the first and the third of Eqs. (4) to find B0 and ![]() ,
and then fix the range of
b0/c0 that reproduces the observed
,
and then fix the range of
b0/c0 that reproduces the observed
![]() (cf., e.g., Fig. 6). The second of Eqs. (4) can be used as an independent check of the accuracy of the linear force-free assumption because the resulting value of
(cf., e.g., Fig. 6). The second of Eqs. (4) can be used as an independent check of the accuracy of the linear force-free assumption because the resulting value of
![]() should be close to, e.g., -8 for
should be close to, e.g., -8 for
![]() ,
if our model is indeed applicable.
,
if our model is indeed applicable.
4.3 Azimuthal flux rope and planetary evaporation
An interesting property of the flux rope topology is the possibility of storing matter in the stellar corona. The evaporation of hot Jupiters under the action of the ionizing radiation of their host stars originates a flow of cool plasma at a temperature of ![]() 104 K that escapes from the planetary atmospheres into the stellar coronae (cf., e.g., Ehrenreich et al. 2008; Murray-Clay et al. 2009). The flux rope geometry keeps the evaporating plasma confined into a torus in the equatorial plane of the star, thus making its detection easier in the case of transiting hot Jupiters (Vidal-Madjar et al. 2003).
104 K that escapes from the planetary atmospheres into the stellar coronae (cf., e.g., Ehrenreich et al. 2008; Murray-Clay et al. 2009). The flux rope geometry keeps the evaporating plasma confined into a torus in the equatorial plane of the star, thus making its detection easier in the case of transiting hot Jupiters (Vidal-Madjar et al. 2003).
Considering a moderately active star and assuming a lifetime of ![]() 300 days for the flux rope configuration according to the duration of the off phases of chromospheric interaction,
the evaporated mass is of the order of
300 days for the flux rope configuration according to the duration of the off phases of chromospheric interaction,
the evaporated mass is of the order of
![]() kg (cf., e.g., Murray-Clay et al. 2009).
Such a material may eventually condense in the form of prominence-like structures around the minimum of the gravitational potential inside the flux rope, which is in the equatorial plane of the star, possibly closer to the star than the hot Jupiter (cf. Fig. 5).
It is unlikely that all the evaporated matter collects into a single condensation. The thermal instability of the plasma is expected to lead to many condensations with typical lengthscales of
108-109 m, comparable in order of magnitude to those observed in, e.g., solar prominences (Field 1965). Moreover, a high degree of inhomogeneity is expected inside each condensation, analogous to the filamentary structure of solar prominences, because the pressure scale height at a temperature of
kg (cf., e.g., Murray-Clay et al. 2009).
Such a material may eventually condense in the form of prominence-like structures around the minimum of the gravitational potential inside the flux rope, which is in the equatorial plane of the star, possibly closer to the star than the hot Jupiter (cf. Fig. 5).
It is unlikely that all the evaporated matter collects into a single condensation. The thermal instability of the plasma is expected to lead to many condensations with typical lengthscales of
108-109 m, comparable in order of magnitude to those observed in, e.g., solar prominences (Field 1965). Moreover, a high degree of inhomogeneity is expected inside each condensation, analogous to the filamentary structure of solar prominences, because the pressure scale height at a temperature of ![]() 104 K is only of the order of 105-106 m.
104 K is only of the order of 105-106 m.
Assuming a mass of 1 ![]() for the star and a radius
for the star and a radius
![]() ,
the gravitational potential energy of the whole prominence material is
,
the gravitational potential energy of the whole prominence material is ![]()
![]() J, for a mean radial distance of 7 R. It is only 1 percent of the magnetic energy of the coronal field, therefore it is not expected to perturb appreciably the field geometry.
J, for a mean radial distance of 7 R. It is only 1 percent of the magnetic energy of the coronal field, therefore it is not expected to perturb appreciably the field geometry.
On the other hand, in the case of a very active star, i.e., having an X-ray luminosity 2-3 orders of magnitude greater than the Sun (cf., e.g., Penz et al. 2008), the planet evaporation rate may increase by a factor of ![]() 100, leading to a potential energy of the whole prominence material of the order of 1027-1028 J. This can significantly perturb the field, whose configuration can no longer be assumed force-free. A non-force-free model may be applicable, such as that of Neukirch (1995), discussed by Lanza (2008). It gives rise to the same field topologies of the present force-free model because it is obtained from a linear force-free model by means of a linear transformation of the independent variable q of the radial function g(q) (cf. Lanza 2008).
A large amount of prominence material may help to stabilize the flux rope configuration, because lifting up the prominences to open or change the geometry of the magnetic field lines requires a comparable additional amount of energy. This may imply that the flux rope topology is the most stable in the case of very active stars, leading to a lower probability of observing a chromospheric hot spot synchronized with the planet.
100, leading to a potential energy of the whole prominence material of the order of 1027-1028 J. This can significantly perturb the field, whose configuration can no longer be assumed force-free. A non-force-free model may be applicable, such as that of Neukirch (1995), discussed by Lanza (2008). It gives rise to the same field topologies of the present force-free model because it is obtained from a linear force-free model by means of a linear transformation of the independent variable q of the radial function g(q) (cf. Lanza 2008).
A large amount of prominence material may help to stabilize the flux rope configuration, because lifting up the prominences to open or change the geometry of the magnetic field lines requires a comparable additional amount of energy. This may imply that the flux rope topology is the most stable in the case of very active stars, leading to a lower probability of observing a chromospheric hot spot synchronized with the planet.
Prominence-like structures have indeed been detected around some young and highly active dwarf stars, through the absorption transients migrating across their H![]() ,
Ca II H & K and Mg II h & k emission line profiles (e.g., Collier Cameron & Robinson 1989). Typical masses are in the range (2-
,
Ca II H & K and Mg II h & k emission line profiles (e.g., Collier Cameron & Robinson 1989). Typical masses are in the range (2-
![]() kg for the young (
kg for the young (![]() 50 Myr), single K0 dwarf AB Dor (Collier Cameron et al. 1990). We expect a remarkable increase in the number of such phenomena in highly active stars hosting evaporating hot Jupiters. Assuming a lifetime of
50 Myr), single K0 dwarf AB Dor (Collier Cameron et al. 1990). We expect a remarkable increase in the number of such phenomena in highly active stars hosting evaporating hot Jupiters. Assuming a lifetime of ![]() 300 days for the flux rope configuration, a total evaporated mass of
300 days for the flux rope configuration, a total evaporated mass of
![]() kg can lead to the formation of
kg can lead to the formation of
![]() 100 prominence-like structures akin to those observed in AB Dor.
100 prominence-like structures akin to those observed in AB Dor.
The most favourable geometrical conditions for their detection are found in transiting systems where the prominences are expected to transit across the disc of the host star. The radial distance of a condensation inside a flux rope is several stellar radii, in contrast to a minimum distance of a few stellar radii observed in the case of the prominences formed by evaporation from the chromosphere of the star (Collier Cameron & Robinson 1989). This implies that the transit times of the absorption features across the line profiles are shorter by a factor of 2-5 in the case of flux rope condensations.
On the other hand, the expected relative decrease in the intensity along the H![]() line profile is between 5 and 20 percent, with typical equivalent widths of the absorption features between 50 and 500 mÅ, as reported by Collier Cameron & Robinson (1989) for AB Dor, whose coronal parameters can be considered fairly typical of those of very active stars.
line profile is between 5 and 20 percent, with typical equivalent widths of the absorption features between 50 and 500 mÅ, as reported by Collier Cameron & Robinson (1989) for AB Dor, whose coronal parameters can be considered fairly typical of those of very active stars.
Finally, note that a prominence does not form at the distance of the planet when the field topology does not contain a flux rope because in that case all the evaporated matter will fall onto the star, except when the star rotates so fast that the centrifugal force reverses the effective gravity at the top of the loops interconnecting the planet with the star.
4.4 Consequences for X-ray emissions
In our model, all the magnetic field lines are closed, so the corona consists of closed loops. However, if we adopt a more realistic model, such as the nonlinear force-free model of Flyer et al. (2004), it is possible to have open field lines that may account for the configuration observed in solar coronal holes. Also in those nonlinear models we can have a coronal field with a large azimuthal flux rope that affects the topology of the coronal field lines close to the star. From a qualitative point of view, we can refer to Fig. 5 to show that all the magnetic structures at low and intermediate latitudes must have a closed configuration with a top height lower than ![]() 4-5 R, because they lie below the flux rope. This implies that open field configurations, akin to solar coronal holes, are not allowed at low latitudes when a sizeable flux rope has developed in the outer corona. Since closed magnetic configurations are characterized by X-ray fluxes up to
4-5 R, because they lie below the flux rope. This implies that open field configurations, akin to solar coronal holes, are not allowed at low latitudes when a sizeable flux rope has developed in the outer corona. Since closed magnetic configurations are characterized by X-ray fluxes up to ![]() 10-100 times greater than coronal holes, an azimuthal flux rope configuration is expected to be associated with a greater X-ray luminosity of the star than in the case of all magnetic field lines being connected to the photosphere. Of course, this is independent of the presence of any planet.
10-100 times greater than coronal holes, an azimuthal flux rope configuration is expected to be associated with a greater X-ray luminosity of the star than in the case of all magnetic field lines being connected to the photosphere. Of course, this is independent of the presence of any planet.
When a star is accompanied by a close-in planet, it may increase the dissipation of magnetic helicity and energy, as conjectured in Sect. 4.1.2. According to Kashyap et al. (2008), stars with a distant planet have an average X-ray luminosity
![]() W, while stars with a hot Jupiter have
W, while stars with a hot Jupiter have
![]() W.
Considering the model introduced in Sect. 4.1.2, the dissipated power is proportional to B02, where B0 is the photospheric magnetic field (see Sect. 3). This holds true either for a field topology with all field lines connected to the photosphere, or with an azimuthal flux rope. We find that for both field topologies an average photospheric field
W.
Considering the model introduced in Sect. 4.1.2, the dissipated power is proportional to B02, where B0 is the photospheric magnetic field (see Sect. 3). This holds true either for a field topology with all field lines connected to the photosphere, or with an azimuthal flux rope. We find that for both field topologies an average photospheric field
![]() G is sufficient to account for the enhancement of X-ray luminosity in stars with hot Jupiters. Since our model underestimates the free energy available in real nonlinear force-free fields, such a value of B0 should be regarded as an upper limit, thus our estimate agrees well with the available observations (e.g., Moutou et al. 2007).
G is sufficient to account for the enhancement of X-ray luminosity in stars with hot Jupiters. Since our model underestimates the free energy available in real nonlinear force-free fields, such a value of B0 should be regarded as an upper limit, thus our estimate agrees well with the available observations (e.g., Moutou et al. 2007).
4.5 Consequences for radio emission
The frequency of radio emission from exoplanets depends on the planetary magnetic field
(Zarka 2007).
According to the scaling laws adopted by Grießmeier et al. (2004), the magnetic moments of hot Jupiters are expected to be one order of magnitude smaller than that of Jupiter owing to tidal synchronization between their rotation and orbital motion. When adopting a surface field of 10 percent of Jupiter, i.e., 1.4 G, the cyclotron maser emission should peak at ![]() 4 MHz, which is impossible to detect because it falls below the plasma frequency cutoff (Jardine & Collier Cameron 2008). The situation is much more favourable if the magnetic fields of hot Jupiters are indeed as strong as predicted by the models of Christensen et al. (2009) in which the planetary dynamo is powered by the internal convective motions and the field intensity is pratically independent of the rotation rate of the planet. Assuming a field intensity at the surface of 25 G, the cyclotron maser emission peaks at frequencies around 70 MHz.
4 MHz, which is impossible to detect because it falls below the plasma frequency cutoff (Jardine & Collier Cameron 2008). The situation is much more favourable if the magnetic fields of hot Jupiters are indeed as strong as predicted by the models of Christensen et al. (2009) in which the planetary dynamo is powered by the internal convective motions and the field intensity is pratically independent of the rotation rate of the planet. Assuming a field intensity at the surface of 25 G, the cyclotron maser emission peaks at frequencies around 70 MHz.
In addition to the emission from the poles of the planet, we expect radio emission from the stellar corona. When the field lines are connected to the stellar surface, electrons accelerated at the reconnection sites travel down to the star producing emissions up to the GHz range from localized regions above photospheric spots with fields of 102-103 G. However, this is impossible when the field has a topology with an azimuthal flux rope. In this case, the coronal field intensity is of the order of 10-2 G and the emission peaks at very low frequencies, comparable to or below the plasma frequency; i.e., it is self-absorbed before escaping from the emitting region. In this case, we expect detectable radio emission only from the poles of the planet, i.e., from a highly localized region. The beaming of cyclotron-maser emission may additionally decrease the power toward the observer, thus explaining the lack of detection at frequencies of 50-100 MHz.
In conclusion, we expect that the best chances of detecting radio emission from exoplanets with the current instrumentation can be achieved when observing systems with a chromospheric hot spot synchronized with the planet. In this case, a fraction of the electrons accelerated at the reconnection sites inside the long loop connecting the star with the planet may be driven to the polar regions of the planet and to the stellar surface, increasing the irradiated power. In this case, the emission is expected to be strongly modulated with the orbital period of the planet.
5 Discussion
We have presented a model for the coronal magnetic field of late-type stars that allows us to investigate the magnetic interaction between a star and a close-in exoplanet. The same model was used by Lanza (2008) to explain the observed phase lags between chromospheric hot spots attributed to SPMI and the planets. We discussed the energy budget of SPMI and its intermittency on the basis of that model. We suggested that the coronal field evolution in a star hosting a hot Jupiter is ruled by a dynamical balance between the helicity coming up into the corona from the photosphere and that dissipated by the reconnection events triggered by the orbital motion of the planet. At any given time, most of the energy is dissipated in the loop connecting the planet with the stellar surface and in its neighbouring magnetic structures rather than at the boundary of the planetary magnetosphere.
This scenario is quite different from that characteristic of stars with distant planets, like our Sun. In that case the accumulation of magnetic helicity and energy in the corona leads to an instability of closed field structures that erupt as coronal mass ejections (CMEs), eliminating the excess of helicity (Zhang et al. 2006; Zhang & Low 2005). In the present model, in addition to the CME mechanism, the interaction between the coronal field and the planetary magnetosphere takes part in the helicity dissipation process. In principle, one expects that a large flare that extends over most of the stellar corona may sometimes occur thanks to the ability of the planet to trigger a large-scale helicity dissipation process. If most of the coronal helicity is dissipated during such an event, the maximum available energy can approach the difference between the Aly limit and the energy of the potential field with the same radial
component at the photosphere; i.e.,
![]() .
For the case of HD 179949 with an assumed photospheric field of B0=10 G, we have
.
For the case of HD 179949 with an assumed photospheric field of B0=10 G, we have
![]() J. Assuming a photospheric mean field B0=40 G and
J. Assuming a photospheric mean field B0=40 G and
![]() ,
as suggested by the observations of the K dwarf HD 189733 by Moutou et al. (2007), we get
,
as suggested by the observations of the K dwarf HD 189733 by Moutou et al. (2007), we get
![]() J. Such high energies may explain the superflares observed in some dwarf stars, supporting the conjecture by Rubenstein & Schaefer (2000).
J. Such high energies may explain the superflares observed in some dwarf stars, supporting the conjecture by Rubenstein & Schaefer (2000).
Processes like CMEs, i.e., capable of reducing the helicity of the stellar field, are required for the operation of a stellar hydromagnetic dynamo (Brandenburg & Subramanian 2005; Blackman & Brandenburg 2003). Therefore, a hot Jupiter may help the star to get rid of the helicity generated by its dynamo in the convection zone, increasing dynamo efficiency and the overall level of magnetic activity. This may ultimately explain the higher X-ray luminosity of stars with hot Jupiters. Moreover, shorter activity cycles may be expected (cf., e.g., Sect. 11.2.1 of Brandenburg & Subramanian 2005), which might account for the 2-year magnetic cycle suggested by the latest observations of ![]() Boo (Fares et al. 2009).
Boo (Fares et al. 2009).
The modulation of the helicity loss with the orbital period of the planet might account for the photospheric cool spots that appear to rotate synchronously with the planet, as conjectured by Lanza (2008). These spots are related to the emergence of magnetic flux from the convection zone that may contribute to the formation of hot spots in the chromosphere and in the corona by reconnecting with pre-existing fields, thus contributing to the energy budget of SPMI.
Our model predicts a field intensity that decreases slower than for a potential field far away from the star. In the case of the flux rope topology, the field decreases even more slowly than r-2 in the outer part of the closed corona. This may enhance the dynamical coupling between the star and the planet, as suggested by some preliminary computations of the angular momentum exchange between CoRoT-4a and its hot Jupiter having an orbital semimajor axis
![]() ,
where R is the stellar radius. They indicate that the rotation of the outer convection zone of the star may have been synchronized with the orbital motion of the planet if the surface field
,
where R is the stellar radius. They indicate that the rotation of the outer convection zone of the star may have been synchronized with the orbital motion of the planet if the surface field
![]() G
and the age of the system is
G
and the age of the system is ![]() 0.5 Gyr. These results may explain the tight synchronization observed in the CoRoT-4 system, which is impossible to understand with tidal models given the large distance of the hot Jupiter and its low mass
(
0.5 Gyr. These results may explain the tight synchronization observed in the CoRoT-4 system, which is impossible to understand with tidal models given the large distance of the hot Jupiter and its low mass
(![]() 0.7 M
0.7 M![]() ,
Lanza et al. 2009b).
,
Lanza et al. 2009b).
A limitation of the present approach is the use of a linear force-free model for the stellar coronal field. This mainly affects our energy estimates, while the main topological features of our linear model are shared by nonlinear models (cf., e.g., Zhang et al. 2006; Flyer et al. 2004). The latter can be useful to treat the contribution of the outer coronal fields because they can provide us with field configurations that extend to the infinity with a finite magnetic energy. However, given the much greater mathematical complexity of nonlinear force-free models, the present treatment is preferable for a first description of the most relevant physical effects.
Nonlinear models can also be useful for investigating the stability of coronal magnetohydrostatic configurations. In the framework of the adopted model, stability is warranted by the Woltjer theorem because a linear force-free configuration is the minimum-energy state for a given total helicity and boundary conditions (Berger 1985). However, the real coronal field that is in a nonlinear force-free state may become unstable before reaching the Aly energy limit by, e.g., kink modes, when it develops an azimuthal flux rope.
6 Conclusions
We have investigated the model proposed by Lanza (2008) further to interpret the observations of star-planet magnetic interaction. A linear force-free model of the stellar coronal field has been applied to addressing the energy budget of the interaction and understanding its intermittency. We propose that the magnetic helicity budget plays a fundamental role in the interaction. A hot Jupiter contributes to this budget by increasing the helicity dissipation that triggers an additional magnetic energy release in the stellar corona.
The transition between phases with and without a chromospheric hot spot rotating synchronously with the planet is interpreted as a consequence of a topological change in the coronal field induced by an accumulation of helicity. Its timescale depends on the mechanisms ruling the helicity fluctuations in the stellar hydromagnetic dynamo and the helicity budget of the stellar corona, which are presently poorly known. However, a timescale as short as 105-106 s should be possible (cf. Sect. 4.2).
The model can be tested in the case of sufficiently rapidly rotating stars, such as ![]() Boo or HD 189733, by combining spectropolarimetric measurements of the stellar photospheric fields with Ca II K line observations to determine the phase lag between a planet-induced hot spot and the planet. Such simultaneous measurements should be able to constrain the topology of the field by allowing us to estimate the parameters of the force-free field model as detailed at the end of Sect. 4.2.
Boo or HD 189733, by combining spectropolarimetric measurements of the stellar photospheric fields with Ca II K line observations to determine the phase lag between a planet-induced hot spot and the planet. Such simultaneous measurements should be able to constrain the topology of the field by allowing us to estimate the parameters of the force-free field model as detailed at the end of Sect. 4.2.
The present model also bears interesting consequences for the coronal emissions of stars hosting hot Jupiters. It may explain why stars with a close-in giant planet have, on the average, a higher X-ray luminosity than stars with a distant planet. Moreover, it suggests that the best chances of detecting radio emission from hot Jupiters or their host stars are found in systems showing a chromospheric hot spot rotating synchronously with the planet.
We also investigated the consequences of the different field topologies for confining and storaging the matter evaporated from a planetary atmosphere under the action of the radiation from the host star. When the field has an azimuthal rope of flux encircling the star, the evaporated matter can neither escape nor fall onto the star and is expected to condense in the outer corona forming several prominence-like structures. They can in principle be detected in the case of rapidly rotating and highly active stars through the observations of transient absorption features moving across the profile of their chromospheric emission lines.
Simultaneous optical, X-ray, and radio observations can prove the association between a chromospheric hot spot induced by a hot Jupiter and the X-ray and radio emission enhancements expected on the basis of our model because the energy is mainly released in the corona of the star and then conveyed along magnetic field lines to heat the lower chromospheric layers. Most of the coronal energy should be released within one stellar radius, where the magnetic field is stronger. Therefore, no large phase lags are expected between the chromospheric enhancement and the X-ray and radio enhancements varying in phase with the orbital motion of the planet. On the other hand, when there is no signature of SMPI in the chromosphere, we expect that the modulation of the X-ray flux with the orbital motion of the planet is also significantly reduced. No detectable radio emission is expected in this case, except when the planet has a polar field of at least 20-30 G. Finally, we expect to observe the signatures of several prominence-like condensations in the coronae of rapidly rotating (
![]() -50 km s-1), highly active stars (
-50 km s-1), highly active stars (
![]() -1023 W) hosting transiting hot Jupiters, if our assumption that coronal flux ropes have a typical lifetime of 200-300 days is true.
-1023 W) hosting transiting hot Jupiters, if our assumption that coronal flux ropes have a typical lifetime of 200-300 days is true.
Acknowledgements
The author wishes to thank an anonymous Referee for a careful reading of the manuscript and valuable comments. AFL is grateful to Drs. P. Barge, S. Dieters, C. Moutou, and I. Pagano for drawing his attention to the problem of star-planet magnetic interaction and for interesting discussions. This work has been partially supported by the Italian Space Agency (ASI) under contract ASI/INAF I/015/07/0, work package 3170. Active star research and exoplanetary studies at INAF-Catania Astrophysical Observatory and the Department of Physics and Astronomy of Catania University is funded by MIUR (Ministero dell'Istruzione, Università e Ricerca), and by Regione Siciliana, whose financial support is gratefully acknowledged. This research has made use of the ADS-CDS databases, operated at the CDS, Strasbourg, France.
References
- Blackman, E. G., & Brandenburg, A. 2003, ApJ, 584, L99 [NASA ADS] [CrossRef]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] (In the text)
- Berger, M. A. 1985, ApJS, 59, 433 [NASA ADS] [CrossRef]
- Collier Cameron, A., & Robinson R. D. 1989, MNRAS, 236, 57 [NASA ADS] (In the text)
- Collier Cameron, A., Duncan, D. K., Ehrenfreund, P., et al. 1990, MNRAS, 247, 415 [NASA ADS] (In the text)
- Catala, C., Donati, J.-F., Shkolnik, E., Bohlender, D., & Alecian, E. 2007, MNRAS, 374, L42 [NASA ADS] (In the text)
- Chandrasekhar, S. 1956, Proc. Natl. Acad. Sci. USA, 42, 1 [NASA ADS] [CrossRef] (In the text)
- Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (London: Oxford Univ. Press) (In the text)
- Chandrasekhar, S., & Kendall, P. C. 1957, ApJ, 126, 457 [NASA ADS] [CrossRef] (In the text)
- Christensen, U. R., Holzwarth, V., & Reiners, A. 2009, Nature, 457, 167 [NASA ADS] [CrossRef] (In the text)
- Cranmer, S. R., & Saar, S. H. 2007, [arXiv:astro-ph/0702530v1]
- Cuntz, M., Saar, S. H., & Musielak, Z. E. 2000, ApJ, 533, L151 [NASA ADS] [CrossRef]
- Donati, J.-F., Moutou, C., Farés, R., et al. 2008, MNRAS, 385, 1179 [NASA ADS] [CrossRef]
- Ehrenreich, D., Lecavelier des Etangs, A., Hébrard, G., et al. 2008, A&A, 483, 933 [NASA ADS] [CrossRef] [EDP Sciences]
- Fares, R., Donati, J.-F., Moutou, C., et al. 2009, MNRAS, in press[arXiv:0906.4515]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] (In the text)
- Flyer, N., Fornberg, B., Thomas, S., & Low, B. C. 2004, ApJ, 606, 1210 [NASA ADS] [CrossRef] (In the text)
- George, S. J., & Stevens, I. R. 2007, MNRAS, 382, 455 [NASA ADS] [CrossRef] (In the text)
- Grießmeier, J.-M., Stadelmann, A., Penz, T., et al. 2004, A&A, 425, 753 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Heyvaerts, J., & Priest, E. R. 1984, A&A, 137, 63 [NASA ADS]
- Henry, G. W., Donahue, R. A., & Baliunas, S. L. 2002, ApJ, 577, L111 [NASA ADS] [CrossRef] (In the text)
- Ip, W.-H., Kopp, A., & Hu, J.-H. 2004, ApJ, 602, L53 [NASA ADS] [CrossRef]
- Jardine, M., & Collier Cameron A. 2008, A&A, 490, 843 [NASA ADS] [CrossRef] [EDP Sciences]
- Kashyap, V. L., Drake J. J., & Saar S. H. 2008, ApJ, 687, 1339 [NASA ADS] [CrossRef] (In the text)
- Laine, R. O., Lin, D. N. C., & Dong, S. 2008, ApJ, 685, 521 [NASA ADS] [CrossRef] (In the text)
- Lanza, A. F. 2008, A&A, 487, 1163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lanza, A. F., Pagano, I., Leto, G., et al. 2009a, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lanza, A. F., Aigrain, S., Messina, S., et al. 2009b, A&A, in press [arXiv:0901.4618] (In the text)
- Lazio, T. J. W., & Farrell, W. M. 2007, ApJ, 668, 1182 [NASA ADS] [CrossRef] (In the text)
- Lecavelier des Etangs, A., Vidal-Madjar, A., McConnell, J. C., & Hébrard, G. 2004, A&A, 418, L1 [NASA ADS] [CrossRef] [EDP Sciences]
- McIvor, T., Jardine, M., & Holzwarth, V. 2006, MNRAS, 367, L1 [NASA ADS] [CrossRef]
- Moutou, C., Donati, J.-F., Savalle, R., et al. 2007, A&A, 473, 651 [NASA ADS] [CrossRef] [EDP Sciences]
- Murray-Clay, R. A., Chiang, E. I., & Murray, N. 2009, ApJ, 693, 23 [NASA ADS] [CrossRef]
- Neukirch, T. 1995, A&A, 301, 628 [NASA ADS] (In the text)
- Pagano, I., Lanza, A. F., Leto, G., et al. 2009, Earth, Moon and Planets, in press [arXiv:0905.3633] (In the text)
- Penz, T., Micela, G., & Lammer, H. 2008, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Preusse, S., Kopp, A., Büchner, J., & Motschmann, U. 2005, A&A, 434, 1191 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Preusse, S., Kopp, A., Büchner, J., & Motschmann, U. 2006, A&A, 460, 317 [NASA ADS] [CrossRef] [EDP Sciences]
- Priest, E. R. 1982, Solar magnetohydrodynamics (Dordrecht: D. Reidel Publ. Co.) (In the text)
- Priest, E. R. 2003, Adv. Space Res., 32, 1021 [NASA ADS] [CrossRef] (In the text)
- Régnier, S., & Priest, E. R. 2007, ApJ, 669, L53 [NASA ADS] [CrossRef] (In the text)
- Rubenstein, E. P., & Schaefer, B. E. 2000, ApJ, 529, 1031 [NASA ADS] [CrossRef] (In the text)
- Santos, N. C., Udry, S., Mayor, M., et al. 2003, A&A, 406, 373 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Saar, S. H., Cuntz, M., Kashyap, V. L., & Hall, J. C. 2007, in Exoplanets: Detection, Formation and Dynamics, ed. Y.-S. Sun, S. Ferraz-Mello, & J.-L. Zhou (Cambridge: Cambridge Univ. Press), IAU Symp., 249, 79 (In the text)
- Shkolnik, E., Walker, G. A. H., & Bohlender, D. A. 2003, ApJ, 597, 1092 [NASA ADS] [CrossRef]
- Shkolnik, E., Walker, G. A. H., Bohlender, D. A., Gu, P.-G., & Kürster M. 2005, ApJ, 622, 1075 [NASA ADS] [CrossRef]
- Shkolnik, E., Bohlender, D. A., Walker, G. A. H., & Collier Cameron A. 2008, ApJ, 676, 628 [NASA ADS] [CrossRef]
- Shkolnik, E., Aigrain, S., Cranmer, S., et al. 2009, Proceedings of the 15th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, AIP Conf. Proc., 1094, 275 [arXiv:0809.4482v1] (In the text)
- Smith, A. M. S., Collier Cameron, A., Greaves, J., et al. 2009, MNRAS, 395, 335 [NASA ADS] [CrossRef] (In the text)
- Stevens, I. R. 2005, MNRAS, 356, 1053 [NASA ADS] [CrossRef]
- Vidal-Madjar, A. Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] (In the text)
- Walker, G. A. H., Croll, B., Matthews, J. M., et al. 2008, A&A, 482, 691 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Woltjer, L. 1958, Proc. Nat. Sci., 44, 489 [NASA ADS] [CrossRef] (In the text)
- Zarka, P. 2007, Planetary and Space Science, 55, 598 [NASA ADS] [CrossRef]
- Zhang M., & Low, B. C. 2005, ARA&A, 43, 103 [NASA ADS] [CrossRef]
- Zhang, M., Flyer N., & Low B. C. 2006, ApJ, 644, 575 [NASA ADS] [CrossRef]
Footnotes
- ...
known
![[*]](/icons/foot_motif.png)
- See a web catalogue at: http://exoplanet.eu/
- ... star
![[*]](/icons/foot_motif.png)
- About 70 percent of the hot Jupiters within 0.1 AU from their host stars have a measured orbital eccentricity lower than 0.05, consistent with a circular orbit (see http://exoplanet.eu/).
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg70.png) |
Figure 1:
The modulus of the magnetic field on the equatorial plane of the star normalized to its value at the surface vs. the radial distance from the star for
b0/c0=-1.1 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f2.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg122.png) |
Figure 2:
The first derivative of the function g at the surface of the star (i.e., r=R) vs.
b0/c0 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=12cm]{12367f3.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg133.png) |
Figure 3:
Upper panel: the radial function g vs. q for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f4.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg137.png) |
Figure 4:
Upper panel: the magnetic field energy as a fraction of the corresponding potential field energy vs.
b0/c0 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=12cm]{12367f5.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg140.png) |
Figure 5:
Meridional section of the magnetic field lines for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f6.eps} %\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg145.png) |
Figure 6:
The phase lag between the planet and the synchronous chromospheric hot spot vs.
b0/c0 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm]{12367f7.eps} %
\end{figure}](/articles/aa/full_html/2009/37/aa12367-09/Timg146.png) |
Figure 7:
The modulus of the magnetic field on the equatorial plane of the star normalized to its value at the surface vs. the radial distance from the star for
b0/c0=-0.107 and
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}{\vec B} = \frac{1}{r \sin \theta} \left[ \frac{1}{r} \frac{\...
...rtial r} \hat{\vec \theta} + \alpha A \hat{\vec \phi} \right],
\end{displaymath}](/articles/aa/full_html/2009/37/aa12367-09/img24.png)
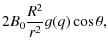
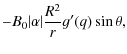
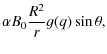
![\begin{displaymath}E = E_{\rm p} \left\{ 2 + q_{0} q_{\rm L} [g^{\prime}(q_{\rm ...
...^{2} - q_{0}^{2} [g^{\prime}(q_{0})]^{2} - q_{0}^{2} \right\},
\end{displaymath}](/articles/aa/full_html/2009/37/aa12367-09/img50.png)
![\begin{displaymath}H_{\rm R} = B_{0}^{2} R^{4} \left[ 2 g^{\prime}(q_{0}) + \fra...
...{q_{0} E_{\rm p}} \right] \frac{\vert\alpha\vert}{\alpha}\cdot
\end{displaymath}](/articles/aa/full_html/2009/37/aa12367-09/img54.png)
![\begin{displaymath}P_{\rm d} \simeq \gamma \frac{\pi}{\mu} \left[B\left(a, \frac{\pi}{2}\right)\right]^{2} R_{\rm m}^{2} v_{\rm rel},
\end{displaymath}](/articles/aa/full_html/2009/37/aa12367-09/img79.png)