| Issue |
A&A
Volume 505, Number 1, October I 2009
|
|
|---|---|---|
| Page(s) | 405 - 415 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200912127 | |
| Published online | 22 July 2009 | |
The initial conditions of stellar protocluster formation
I. A catalogue of Spitzer dark clouds![[*]](/icons/foot_motif.png)
N. Peretto - G. A. Fuller
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
Received 20 March 2009 / Accepted 18 June 2009
Abstract
Context. The majority of stars form in clusters. Therefore a comprehensive view of star formation requires understanding the initial conditions for cluster formation.
Aims. The goal of our study is to shed light on the physical properties of infrared dark clouds (IRDCs) and the role they play in the formation of stellar clusters. This article, the first of a series dedicated to the study of IRDCs, describes techniques developed to establish a complete catalogue of Spitzer IRDCs in the Galaxy.
Methods. We have analysed Spitzer GLIMPSE and MIPSGAL data to identify a complete sample of IRDCs in the region of Galactic longitude and latitude
![]() and
and
![]() .
From the 8
.
From the 8 ![]() m observations we have constructed opacity maps and used a newly developed extraction algorithm to identify structures above a column density of
m observations we have constructed opacity maps and used a newly developed extraction algorithm to identify structures above a column density of
![]() cm-2. The 24
cm-2. The 24 ![]() m data are then used to characterize the star formation activity of each extracted cloud.
m data are then used to characterize the star formation activity of each extracted cloud.
Results. A total of 11 303 clouds have been extracted. A comparison with the existing MSX based catalogue of IRDCs shows that 80![]() of these Spitzer dark clouds were previously unknown. The algorithm also extracts
of these Spitzer dark clouds were previously unknown. The algorithm also extracts ![]() 20 000 to 50 000 fragments within these clouds, depending on detection threshold used. A first look at the MIPSGAL data indicates that between 20% and 68% of these IRDCs show 24
20 000 to 50 000 fragments within these clouds, depending on detection threshold used. A first look at the MIPSGAL data indicates that between 20% and 68% of these IRDCs show 24 ![]() m point-like association. This new database provides an important resource for future studies aiming to understand the initial conditions of star formation in the Galaxy.
m point-like association. This new database provides an important resource for future studies aiming to understand the initial conditions of star formation in the Galaxy.
Key words: catalogs - stars: formation - ISM: clouds
1 Introduction
The majority of stars form in groups of a few tens to few hundreds objects (e.g. Lada & Lada 2003). So, understanding cluster formation is key to understanding the formation of stars. Clusters form from the gas located in the densest parts of molecular clouds, within structures called clumps (Blitz 1993). These clumps fragment into an assembly of protostellar cores which collapse to produce stars, forming ``protoclusters''. By definition, protoclusters are active star forming regions, with jets, flows and heating sources (e.g. Bally et al. 2006) which rapidly start to shape their surroundings. From the study of these protoclusters, it is therefore difficult to back track to the initial conditions of their formation. On the other hand, clumps which are on the verge of forming protostars, but which have not formed any yet, are structures unpolluted by star formation activity and must still reflect the initial conditions of the formation of protoclusters. Looking for, and studying such ``pre-protoclusters'' is crucial for our understanding of star formation processes.
![\begin{figure}
\par\includegraphics[angle=-90,width=14.5cm,clip]{12127fg1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg29.png) |
Figure 1:
These images show the GLIMPSE Spitzer 8 |
| Open with DEXTER | |
Only a tiny percentage of the material in any molecular cloud forms stars.
These star-forming regions are traced by various signposts of star formation
activity such as the presence of strong infrared sources, outflows, jets,
methanol and water masers and compact HII regions. The problem with
identifying pre-protoclusters is that by definition these signposts are not
yet present. Other means are thus necessary to find such objects. The two
infrared satellites ISO and MSX have been important tools for this
purpose. The large infrared surveys these satellites carried out
identified infrared dark structures, seen in absorption from 7 to 25 ![]() m
against the background emission (Perault et al. 1996; Simon et al. 2006a; Hennebelle et al. 2001; Egan et al. 1998) . Millimeter molecular lines (e.g. Pillai et al. 2006; Carey et al. 1998; Teyssier et al. 2002) and dust continuum observations
(e.g. Teyssier et al. 2002; Rathborne et al. 2006) have clearly demonstrated that
these infrared dark clouds are dense, cold structures, possibly being the
progenitors of protoclusters (Simon et al. 2006b). Rathborne et al. (2006) even
suggested that the dust continuum ``cores'' observed in these IRDCs are the
direct progenitors of massive stars. However, the wide range of mass and size of these IRDCs clearly suggests that they cannot all be evolving along the same evolutionary path and they must lead to the formation of a large range of different stellar contents.
m
against the background emission (Perault et al. 1996; Simon et al. 2006a; Hennebelle et al. 2001; Egan et al. 1998) . Millimeter molecular lines (e.g. Pillai et al. 2006; Carey et al. 1998; Teyssier et al. 2002) and dust continuum observations
(e.g. Teyssier et al. 2002; Rathborne et al. 2006) have clearly demonstrated that
these infrared dark clouds are dense, cold structures, possibly being the
progenitors of protoclusters (Simon et al. 2006b). Rathborne et al. (2006) even
suggested that the dust continuum ``cores'' observed in these IRDCs are the
direct progenitors of massive stars. However, the wide range of mass and size of these IRDCs clearly suggests that they cannot all be evolving along the same evolutionary path and they must lead to the formation of a large range of different stellar contents.
So far, the study of the earliest stages of the formation of
protoclusters have mostly focussed on the closest objects such as
![]() -Oph (e.g. André et al. 2007; Motte et al. 1998), Perseus
(Hatchell et al. 2005; Enoch et al. 2006), NGC2264
(e.g. Teixeira et al. 2006; Peretto et al. 2006). The results of these
studies set important constraints on models of star formation, but may
not be representative of the formation of stars throughout the Galaxy.
The only way to define such a representative view is through
studies of large unbiased samples of the precursors of stellar
clusters.
-Oph (e.g. André et al. 2007; Motte et al. 1998), Perseus
(Hatchell et al. 2005; Enoch et al. 2006), NGC2264
(e.g. Teixeira et al. 2006; Peretto et al. 2006). The results of these
studies set important constraints on models of star formation, but may
not be representative of the formation of stars throughout the Galaxy.
The only way to define such a representative view is through
studies of large unbiased samples of the precursors of stellar
clusters.
In this paper we identify and characterise the IRDCs detected using the Spitzer
GLIMPSE and MIPSGAL archive data. The high angular resolution of the Spitzer
data provides a detailed probe of the structure of these sources while the
high sensitivity of IRAC and MIPS allows us to detect previously unseen deeply embedded protostars/protoclusters. Section 2 of this paper presents the Spitzer archive data used for this study. Section 3 will discuss the
construction of 8 ![]() m opacity maps for IRDCs, while Sect. 4 will focus on the conversion from 8
m opacity maps for IRDCs, while Sect. 4 will focus on the conversion from 8 ![]() m opacity to H2 column density. The extraction
of structures within these maps will be discussed in Sect. 5. A comparison
with the MSX catalogue of IRDCs is in Sect. 6 while Sect. 7 summarizes our initial study. The nature of these dark clouds and their star formation
actively are discussed in more detail in subsequent papers (Peretto & Fuller, in preparation).
m opacity to H2 column density. The extraction
of structures within these maps will be discussed in Sect. 5. A comparison
with the MSX catalogue of IRDCs is in Sect. 6 while Sect. 7 summarizes our initial study. The nature of these dark clouds and their star formation
actively are discussed in more detail in subsequent papers (Peretto & Fuller, in preparation).
2 A large survey of infrared dark clouds: Spitzer archive data
IRDCs are seen in silhouette against the infrared background emission (see Fig. 1) and as a sample are likely to contain protoclusters and pre-protoclusters. Even when large scale (sub)millimetre surveys of the Galactic plane become available and these objects can be detected through their dust emission, IRDCs and studies of the absorption towards these sources will remain important. Not only can the IRDCs be studied at high angular resolution at infrared wavelengths, but unlike the (sub)millimetre emission, their column density can be measured from the absorption independent of the dust temperature.
Table 1: Properties of the first 30 out of the 11303 in the Spitzer dark cloud (SDC) catalogue. The full catalogue is available at the CDS.
The first large survey of IRDCs was undertaken by Simon et al. (2006a) using the mid-infrared data of the MSX satellite. In total, Simon et al. detected more than 10 000 IRDCs, with sizes larger than (36
![]() )2 and flux density more than 2 MJy/sr (>2 times the rms noise of the MSX images) below the mid-infrared radiation field. Within these IRDCs they extracted more than 12 000 IRDC ``cores''. Simon et al. (2006b) performed a follow up of a sub-sample of few hundreds sources for which they were able to determine distances. They found that these IRDCs are very similar to CO molecular clumps (e.g. Blitz 1993).
)2 and flux density more than 2 MJy/sr (>2 times the rms noise of the MSX images) below the mid-infrared radiation field. Within these IRDCs they extracted more than 12 000 IRDC ``cores''. Simon et al. (2006b) performed a follow up of a sub-sample of few hundreds sources for which they were able to determine distances. They found that these IRDCs are very similar to CO molecular clumps (e.g. Blitz 1993).
In the GLIMPSE and MIPSGAL surveys the Spitzer satellite has resurveyed a
large fraction of the Galactic plane at infrared wavelengths (
![]() ). These data have both better angular resolution
(2
). These data have both better angular resolution
(2
![]() vs. 20
vs. 20
![]() at 8
at 8 ![]() m) and sensitivity (0.3 MJy/sr vs
1.2 MJy/sr at 8
m) and sensitivity (0.3 MJy/sr vs
1.2 MJy/sr at 8 ![]() m) than the MSX data, as well as wider wavelength
coverage.The IRAC (3.6, 4.5, 5.8, 8
m) than the MSX data, as well as wider wavelength
coverage.The IRAC (3.6, 4.5, 5.8, 8 ![]() m) GLIMPSE and MIPS (24, 70, 160
m) GLIMPSE and MIPS (24, 70, 160 ![]() m) MIPSGAL observations provide a unique opportunity to shed light on the role of IRDCs during the earliest stages of star formation.
Despite a smaller coverage of the Galactic plane by Spitzer,
an initial comparison of the MSX IRDC catalogues with the Spitzer
observations indicated that the Spitzer data contained IRDCs undetected by MSX in the same region of the Galaxy. Therefore an unbiased search of the Spitzer GLIMPSE data has been undertaken to identify IRDCs.
m) MIPSGAL observations provide a unique opportunity to shed light on the role of IRDCs during the earliest stages of star formation.
Despite a smaller coverage of the Galactic plane by Spitzer,
an initial comparison of the MSX IRDC catalogues with the Spitzer
observations indicated that the Spitzer data contained IRDCs undetected by MSX in the same region of the Galaxy. Therefore an unbiased search of the Spitzer GLIMPSE data has been undertaken to identify IRDCs.
Many IRDCs can been seen in silhouette up to at least 24 ![]() m, providing a
wide wavelength range over which they can be studied in absorption. However
several factors affect the choice of the optimal wavelength at which to
identify and study the overall cloud properties. These include the strength
and uniformity of the background emission and the number of foreground and
background stars and in principle, the wavelength dependence of the dust
extinction law, although recent work suggests that from 4.5 to 8
m, providing a
wide wavelength range over which they can be studied in absorption. However
several factors affect the choice of the optimal wavelength at which to
identify and study the overall cloud properties. These include the strength
and uniformity of the background emission and the number of foreground and
background stars and in principle, the wavelength dependence of the dust
extinction law, although recent work suggests that from 4.5 to 8 ![]() m,
the three last bands observed by Spitzer/IRAC, the extinction is a
relatively flat function of wavelength
(Indebetouw et al. 2005; Román-Zúñiga et al. 2007; Lutz et al. 1996). The angular resolution of
the observations is highest at the shortest wavelengths, but in these bands a
very high density of stars is detected and a high degree of structure in the
relatively weak background emission makes analysis of the images at these
wavelengths complex. Overall, inspection of the Spitzer data shows that the
strength and relative smoothness of the background emission together with the
relatively low density of stars make the IRAC 8
m,
the three last bands observed by Spitzer/IRAC, the extinction is a
relatively flat function of wavelength
(Indebetouw et al. 2005; Román-Zúñiga et al. 2007; Lutz et al. 1996). The angular resolution of
the observations is highest at the shortest wavelengths, but in these bands a
very high density of stars is detected and a high degree of structure in the
relatively weak background emission makes analysis of the images at these
wavelengths complex. Overall, inspection of the Spitzer data shows that the
strength and relative smoothness of the background emission together with the
relatively low density of stars make the IRAC 8 ![]() m band the most suitable
for this initial study of a large sample of objects.
m band the most suitable
for this initial study of a large sample of objects.
The GLIMPSE and MIPSGAL data have been reduced and calibrated automatically to produce the so called post-basic calibrated data (PBCD). The typical flux
uncertainty for point-like sources is ![]() 2% at 8
2% at 8 ![]() m (Reach et al. 2005)
while the position uncertainty is less than 0.3
m (Reach et al. 2005)
while the position uncertainty is less than 0.3
![]() (IRAC manual V8.0:
http://ssc.spitzer.caltech.edu/documents/SOM/). However, because we are not looking at point-like sources but extended objects, a calibration factor has to be applied on the PBCD 8
(IRAC manual V8.0:
http://ssc.spitzer.caltech.edu/documents/SOM/). However, because we are not looking at point-like sources but extended objects, a calibration factor has to be applied on the PBCD 8 ![]() m images (Reach et al. 2005). This calibration factor, CF, is a function of the aperture radius,
m images (Reach et al. 2005). This calibration factor, CF, is a function of the aperture radius, ![]() ,
for the source under
investigation (http://ssc.spitzer.caltech.edu/irac/calib/extcal/). The
relation between CF and
,
for the source under
investigation (http://ssc.spitzer.caltech.edu/irac/calib/extcal/). The
relation between CF and ![]() in arcsec, at 8
in arcsec, at 8 ![]() m is CF
m is CF
![]() .
Because the typical size of the structure we
analyse is about one arcminute, in the analysis which follows we applied a
calibration factor of 0.8 to the PBCD 8
.
Because the typical size of the structure we
analyse is about one arcminute, in the analysis which follows we applied a
calibration factor of 0.8 to the PBCD 8 ![]() m images. A different
calibration factor would not change the opacities of the IRDCs we calculated, but would imply different related intensities (Table 1).
m images. A different
calibration factor would not change the opacities of the IRDCs we calculated, but would imply different related intensities (Table 1).
![\begin{figure}
\par\includegraphics[width=6cm,angle=270,clip]{12127fg2.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg46.png) |
Figure 2:
Schematic view a typical IRDC flux density profile. The variables described in the text are illustrated on this figure. In this figure,
|
| Open with DEXTER | |
3 Opacity distribution of IRDCs
3.1 Principle
Infrared dark clouds are structures seen in absorption against the background
emission. The strength of the absorption is directly related to the opacity
along the line of sight. Following the notation of Bacmann et al. (2000), the relation between the opacity
![]() and
the intensity at wavelength at
and
the intensity at wavelength at ![]() ,
emerging from the cloud
,
emerging from the cloud
![]() ,
is given by
,
is given by
where
The determination of
![]() is crucial to infer the spatial opacity
distribution of a given IRDC. To illustrate this point, we computed the
opacity of the cloud profile shown in Fig. 2 for three
different values of
is crucial to infer the spatial opacity
distribution of a given IRDC. To illustrate this point, we computed the
opacity of the cloud profile shown in Fig. 2 for three
different values of
![]() (Fig. 3). On this figure we
see that, with increasing
(Fig. 3). On this figure we
see that, with increasing
![]() ,
the opacity increases
significantly everywhere in the cloud, and even more sharply at the
peak. These opacity variations are even more drastic for shallower clouds.
It is therefore important to constrain
,
the opacity increases
significantly everywhere in the cloud, and even more sharply at the
peak. These opacity variations are even more drastic for shallower clouds.
It is therefore important to constrain
![]() when calculating the opacity distribution of an IRDC.
when calculating the opacity distribution of an IRDC.
![\begin{figure}
\par\includegraphics[width=6.0cm,angle=270,clip]{12127fg3.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg56.png) |
Figure 3:
Calculated opacity profiles of the IRDC plotted in
Fig.2 corresponding to 3 different assumptions on the
foreground intensity. The solid line shows
|
| Open with DEXTER | |
Of course it is also possible that at least some the IRDCs are saturated and their intensity profiles become flattened. In such cases, it becomes impossible to recover the central structure of the clouds through the extinction maps. Moreover, such flattening could lead to an incorrect interpretation of the final opacity profiles of IRDCs.
3.2 Constraining I
Comparison of the infrared extinction and millimeter emission can be used to
constrain the infrared foreground emission towards an IRDC by requiring that
both techniques give the same column density towards the source.
For this purpose we have used the 38 IRDC 1.2 mm dust continuum images
Rathborne et al. (2006) obtained with the IRAM 30 m telescope at 11
![]() angular resolution. The 1.2 mm emission can be translated into an 8
angular resolution. The 1.2 mm emission can be translated into an 8 ![]() m opacity,
m opacity,
![]() ,
using the equation
,
using the equation
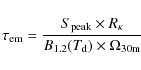 |
(3) |
where
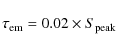 |
(4) |
with
![\begin{figure}
\par\includegraphics[width=9.cm,angle=270]{12127fg4.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg67.png) |
Figure 4:
Plot of the 8 |
| Open with DEXTER | |
Assuming that for starless cores the true 8 ![]() m opacity is given by
m opacity is given by
![]() ,
we can invert Eq. (2) to estimate the value of
,
we can invert Eq. (2) to estimate the value of
![]() in terms of
in terms of
![]() .
We did this calculation for every
starless core and plot the results in Fig. 5, I
.
We did this calculation for every
starless core and plot the results in Fig. 5, I
![]() being measured at the position of the core on the large scale emission map
(Sect. 3.3). A strong correlation is seen between
being measured at the position of the core on the large scale emission map
(Sect. 3.3). A strong correlation is seen between
![]() and
and
![]() .
The best linear fit to this correlation is given by
.
The best linear fit to this correlation is given by
with a standard deviation of 0.08, and a maximum deviation of a single point from the fit of 0.75. This relationship allows us to compute an average foreground emission towards any IRDC by just by estimating the mid-infrared radiation towards the cloud. Figure 6 shows
![\begin{figure}
\par\includegraphics[width=6.cm,angle=270]{12127fg5.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg71.png) |
Figure 5:
Plot of the 8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=270]{12127fg6.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg72.png) |
Figure 6:
Same as Fig. 4 but only for starless sources and with a 8 |
| Open with DEXTER | |
The relation in Eq. (5) gives us the maximum opacity (and
equivalent column density) we can probe before reaching saturation. Since the
rms noise level of the 8 ![]() m images (
m images (
![]() MJy/sr)
defines the minimum flux we can detect above the foreground emission. Below
this value, the dust in the cloud is absorbing all the background emission
and we cannot recover the true peak column density. This saturation opacity,
MJy/sr)
defines the minimum flux we can detect above the foreground emission. Below
this value, the dust in the cloud is absorbing all the background emission
and we cannot recover the true peak column density. This saturation opacity,
![]() ,
is given by
,
is given by
![]() ,
with
,
with
![]() .
The saturation opacity is calculated for every IRDC and given
in Table 1. We also note that we have
.
The saturation opacity is calculated for every IRDC and given
in Table 1. We also note that we have
![]() as also observed by Johnstone et al. (2003) and this suggests that most of the foreground emission originates from the same place as the
background emission and is local to the IRDC, and therefore the foreground
emission is independent of distance to the IRDC.
as also observed by Johnstone et al. (2003) and this suggests that most of the foreground emission originates from the same place as the
background emission and is local to the IRDC, and therefore the foreground
emission is independent of distance to the IRDC.
3.3 Construction of the opacity maps
To construct opacity maps of IRDCs all over the Galactic plane we
mosaiced the GLIMPSE 8 ![]() m and MIPSGAL 24
m and MIPSGAL 24 ![]() m images in blocks
of
m images in blocks
of ![]() in longitude by
in longitude by ![]() in latitude using the Montage
software (http://montage.ipac.caltech.edu/). To allow the
identification of IRDCs which cross the edges of these blocks and to
allow the extraction of regions large enough for our analysis around
clouds near the edges of these blocks, each consecutive block overlaps
adjacent blocks by 0.5
in latitude using the Montage
software (http://montage.ipac.caltech.edu/). To allow the
identification of IRDCs which cross the edges of these blocks and to
allow the extraction of regions large enough for our analysis around
clouds near the edges of these blocks, each consecutive block overlaps
adjacent blocks by 0.5![]() .
In principle this means our extraction
could miss IRDCs larger than about
.
In principle this means our extraction
could miss IRDCs larger than about ![]() in size. However the
largest cloud identified by Simon et al. (2006a) is 27
in size. However the
largest cloud identified by Simon et al. (2006a) is 27![]() long.
long.
The sensitivity of the Spitzer images is such that significant numbers of
stars and galaxies appear in them, even at 8 ![]() m. These need to be removed
in order to produce clean mid-infrared images and opacity maps of the
clouds. This has been done in two steps. First identifying the central
position of stars in the field using the IDL FIND task from the Astronomy
library. Second, the values in the pixels containing the star were replaced
with values calculated from an average gradient plane fit to the values of the pixels surrounding the star we want to remove. While this allowed the
recovery of some part of the structure of a cloud, it can also produce
artifacts.
m. These need to be removed
in order to produce clean mid-infrared images and opacity maps of the
clouds. This has been done in two steps. First identifying the central
position of stars in the field using the IDL FIND task from the Astronomy
library. Second, the values in the pixels containing the star were replaced
with values calculated from an average gradient plane fit to the values of the pixels surrounding the star we want to remove. While this allowed the
recovery of some part of the structure of a cloud, it can also produce
artifacts.
Once the 8 ![]() m stars were removed, we calculated the mid-infrared radiation field
m stars were removed, we calculated the mid-infrared radiation field
![]() by smoothing each 8
by smoothing each 8 ![]() m block by a normalised Gaussian of
m block by a normalised Gaussian of
![]()
![]() . This size is a compromise between several parameters: the typical size of an IRDC, the typical spatial scale of the 8
. This size is a compromise between several parameters: the typical size of an IRDC, the typical spatial scale of the 8 ![]() m emission of the Galactic plane and the computation time. Visual inspection of Spitzer images suggests that most of the clouds are filamentary with a minor axis which is not larger than a few arcminutes. The smoothing we have used is well matched to such clouds and our method will recover their exact structure. For
clouds which are larger than the smoothing length, but which are centrally
condensed, we will detect them but somewhat underestimate their opacity. On
the other hand shallow large clouds will be missed (Sects. 5 and 6). Using a
larger smoothing length would allow us to better detect these large clouds,
but at the cost of additional processing time and more significantly, the
introduction of spurious artificial clouds, especially where the background
emission is weak. In any case, distinguishing between a feature due to a
smooth lack of background emission or the presence of a large and low column
density cloud requires observations of tracers in addition to the inferred
mid-infrared extinction. We preferred to convolve the images with a Gaussian
rather than using a median filter in order to better recover potential clouds
adjacent to strong 8
m emission of the Galactic plane and the computation time. Visual inspection of Spitzer images suggests that most of the clouds are filamentary with a minor axis which is not larger than a few arcminutes. The smoothing we have used is well matched to such clouds and our method will recover their exact structure. For
clouds which are larger than the smoothing length, but which are centrally
condensed, we will detect them but somewhat underestimate their opacity. On
the other hand shallow large clouds will be missed (Sects. 5 and 6). Using a
larger smoothing length would allow us to better detect these large clouds,
but at the cost of additional processing time and more significantly, the
introduction of spurious artificial clouds, especially where the background
emission is weak. In any case, distinguishing between a feature due to a
smooth lack of background emission or the presence of a large and low column
density cloud requires observations of tracers in addition to the inferred
mid-infrared extinction. We preferred to convolve the images with a Gaussian
rather than using a median filter in order to better recover potential clouds
adjacent to strong 8 ![]() m emitting structures.
m emitting structures.
Having calculated
![]() we are able to compute both I
we are able to compute both I
![]() and I
and I
![]() images (Sect. 3.2). Then using Eq. (2)
we can construct the 8
images (Sect. 3.2). Then using Eq. (2)
we can construct the 8 ![]() m opacity image, but before doing so, we smoothed
the 8
m opacity image, but before doing so, we smoothed
the 8 ![]() m images with a 4
m images with a 4
![]() Gaussian in order to suppress high
frequency noise.
Gaussian in order to suppress high
frequency noise.
A series of artifacts, and spurious clouds may arise from our method. The
first one comes from potentially interpreting every decrease in the 8 ![]() m
emission on spatial scale smaller than
m
emission on spatial scale smaller than ![]()
![]() as being a potential
cloud. This effect is especially important at high latitudes where the
mid-infrared radiation field is weak. In these regions a small decrease in the intensity will be interpreted as a stronger increase in the opacity
than for a similar intensity drop in a high mid-infrared radiation field
environment. Identifying such spurious clouds is difficult, and only
follow-ups in other tracers in emission will give a definitive answer on the
nature of these sources. However, we have attempted to minimise such objects
by selecting a relatively high opacity detection threshold.
as being a potential
cloud. This effect is especially important at high latitudes where the
mid-infrared radiation field is weak. In these regions a small decrease in the intensity will be interpreted as a stronger increase in the opacity
than for a similar intensity drop in a high mid-infrared radiation field
environment. Identifying such spurious clouds is difficult, and only
follow-ups in other tracers in emission will give a definitive answer on the
nature of these sources. However, we have attempted to minimise such objects
by selecting a relatively high opacity detection threshold.
Another artifact can arise in regions with strong intensity gradients in the
initial 8 ![]() m block where the smoothing may artifially produce features
identified as clouds, although real clouds also exist in these environments
(Deharveng et al. 2009). To help identify possible spurious objects in regions of large 8
m block where the smoothing may artifially produce features
identified as clouds, although real clouds also exist in these environments
(Deharveng et al. 2009). To help identify possible spurious objects in regions of large 8 ![]() m intensity variations, our catalogue (Table 1)
m intensity variations, our catalogue (Table 1)![]() lists
lists
![]() ,
the normalised maximum variation of
,
the normalised maximum variation of
![]() within
the IRDC and defined as
within
the IRDC and defined as
![]() .
Our experience suggests that clouds with
.
Our experience suggests that clouds with
![]() have to be treated with caution. These clouds represent
14% of the total number of IRDCs included in our sample. Overall, after a
visual inspection of every IRDC and the removal of obviously spurious IRDCs, we believe that more than 90% of the catalogued objects are true IRDCs.
have to be treated with caution. These clouds represent
14% of the total number of IRDCs included in our sample. Overall, after a
visual inspection of every IRDC and the removal of obviously spurious IRDCs, we believe that more than 90% of the catalogued objects are true IRDCs.
The tools to automatically construct the maps were mainly constructed using IDL packages.
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{12127fg7.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg86.png) |
Figure 7:
8 |
| Open with DEXTER | |
4 From 8  m opacities to column densities
m opacities to column densities
The images resulting from the analysis described above provide the spatial 8 ![]() m opacity distribution towards IRDCs. However a more useful quantity is the H2 column density distribution of these clouds. To convert 8
m opacity distribution towards IRDCs. However a more useful quantity is the H2 column density distribution of these clouds. To convert 8 ![]() m
opacities to H2 column densities requires a knowledge of the properties of
the absorbing dust. Depending on the line of sight and on the structures
observed e.g. diffuse material or dense material, the dust chemical
composition and thus, the dust properties, are different. In dense clouds like IRDCs, it is believed that dust grains are larger than in the diffuse
interstellar medium due to coagulation and presence of icy mantles on the
grains. This is supported by ISO (Lutz et al. 1996), and more recently Spitzer
(Indebetouw et al. 2005; Román-Zúñiga et al. 2007), observations which have shown that
towards dense clouds, the extinction cannot be fitted by a single power-law
from the near-IR up to the mid-IR (Draine & Lee 1984). The recent work has shown that in dense clouds the extinction decreases from the near infrared to
m
opacities to H2 column densities requires a knowledge of the properties of
the absorbing dust. Depending on the line of sight and on the structures
observed e.g. diffuse material or dense material, the dust chemical
composition and thus, the dust properties, are different. In dense clouds like IRDCs, it is believed that dust grains are larger than in the diffuse
interstellar medium due to coagulation and presence of icy mantles on the
grains. This is supported by ISO (Lutz et al. 1996), and more recently Spitzer
(Indebetouw et al. 2005; Román-Zúñiga et al. 2007), observations which have shown that
towards dense clouds, the extinction cannot be fitted by a single power-law
from the near-IR up to the mid-IR (Draine & Lee 1984). The recent work has shown that in dense clouds the extinction decreases from the near infrared to
![]() 5
5 ![]() m and then reaches a plateau up to the silicate absorption band
around 9
m and then reaches a plateau up to the silicate absorption band
around 9 ![]() m. This behavior can be reproduced with dust models having
m. This behavior can be reproduced with dust models having
![]() (Weingartner & Draine 2001), implying larger dust grains (compared to the commonly used value
(Weingartner & Draine 2001), implying larger dust grains (compared to the commonly used value
![]() for diffuse interstellar medium).
for diffuse interstellar medium).
For the IRDCs we therefore adopt a value of
![]() (Indebetouw et al. 2005; Román-Zúñiga et al. 2007). To convert to the molecular hydrogen column density,
(Indebetouw et al. 2005; Román-Zúñiga et al. 2007). To convert to the molecular hydrogen column density,
![]() we adopt
we adopt
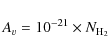 |
(6) |
from Bohlin et al. (1978), although the more recent work by Draine (2003), based on the observations of Rachford et al. (2002), suggests a 50% larger column density per magnitude of extinction. To account for this, and other uncertainties, the column densities in this (and subsequent papers), have been calculated from the 8
5 Identification of sources
Once the opacity maps have been constructed, we need to extract the information on the structures lying within them. For this purpose, we have developed a new code, largely inspired by the CLUMPFIND source extraction code of Williams et al. (1994). The operation of the code is described in Appendix A. The main differences compared to CLUMPFIND are how a source is defined and its properties determined. This new method does not assume that every pixel belongs to a source, but we define the boundaries of an object by the local minimum between closest neighbours. Then to estimate the size of the source we calculate the first and second order moments of the absorption distribution, and then we diagonalise the second order moment matrix (Appendix A).
5.1 IRDCs
In our maps, the IRDCs have been defined as connected structures lying above
an opacity,
![]() ,
of 0.35 with a peak above 0.7 and a diameter greater than 4
,
of 0.35 with a peak above 0.7 and a diameter greater than 4
![]() .
Therefore, using Eq. (7), these detection thresholds correspond to
.
Therefore, using Eq. (7), these detection thresholds correspond to
![]() cm-2 and
cm-2 and
![]() cm-2, respectively. With these parameters, we have
identified 11 303 IRDCs (see Fig. 7). Table 1
lists the first 30 IRDCs, giving their name, coordinates,
cm-2, respectively. With these parameters, we have
identified 11 303 IRDCs (see Fig. 7). Table 1
lists the first 30 IRDCs, giving their name, coordinates,
![]() in MJy/sr,
in MJy/sr,
![]() in MJy/sr,
in MJy/sr,
![]() (see Sect. 3.3),
(see Sect. 3.3),
![]() the major axis size in arcseconds,
the major axis size in arcseconds, ![]() the minor axis size in arcseconds,
the minor axis size in arcseconds, ![]() the position angle in degrees (see Appendix A for an exact definition of these parameters),
the position angle in degrees (see Appendix A for an exact definition of these parameters),
![]() the equivalent radius which corresponds to the radius of a disc having the same area as the IRDC in arcsec,
the equivalent radius which corresponds to the radius of a disc having the same area as the IRDC in arcsec,
![]() the 8
the 8 ![]() m peak opacity,
m peak opacity,
![]() the 8
the 8 ![]() m opacity averaged over the cloud,
m opacity averaged over the cloud,
![]() the saturation opacity as described in Sect. 3.2, the number of fragments within the IRDC (Sect. 5.2),
whether there is a 24
the saturation opacity as described in Sect. 3.2, the number of fragments within the IRDC (Sect. 5.2),
whether there is a 24 ![]() m star in the field/IRDC or not (Sect. 5.3), and
m star in the field/IRDC or not (Sect. 5.3), and
![]() the 24
the 24 ![]() m stellar density around the IRDC in number of stars per arcminute squared.
m stellar density around the IRDC in number of stars per arcminute squared.
5.2 IRDC fragments
Substructures are seen in almost every IRDC map (Fig. 7). Since column density peaks likely pinpoint the sites of the formation of the next generation of stars, identifying these peaks is crucial in identifying the initial conditions of star formation in IRDCs. We call these substructures identified within the IRDCs fragments. We prefer this name, rather than for example, cores, as they have been called in other papers (e.g. Rathborne et al. 2006). The term core has often been used to identify a substructure which forms one star or a small group of stars and we do not at this stage wish to imply any physical interpretation of these structures in IRDCs. Especially since we do not know the distance of the majority of the IRDCs, and so caution is needed in inferring the physical parameters such as the sizes and masses of the fragments/IRDCs.
To extract the IRDC fragments, we apply the same extraction code used
to identify the IRDCs (Appendix A). We applied different
values of
![]() in order to get a comprehensive picture
of the fragmentation in these IRDCs. In total we identified 20 000 to
50 000 fragments depending on
in order to get a comprehensive picture
of the fragmentation in these IRDCs. In total we identified 20 000 to
50 000 fragments depending on
![]() (from 0.1 to
0.35). For each of these fragments we have measured their positions,
sizes, peak and average opacity, and their 24
(from 0.1 to
0.35). For each of these fragments we have measured their positions,
sizes, peak and average opacity, and their 24 ![]() m star
association. As an indication of the degree of fragmentation Table
1 includes the number of fragments extracted in each IRDC
with
m star
association. As an indication of the degree of fragmentation Table
1 includes the number of fragments extracted in each IRDC
with
![]() .
The nature of these fragments is
discussed in detail in Peretto & Fuller (2009, in preparation).
.
The nature of these fragments is
discussed in detail in Peretto & Fuller (2009, in preparation).
Table 2:
Average properties of IRDCs and fragments (extracted with
![]() ).
).
5.3 24  m point-like sources association
m point-like sources association
In order to check for star formation activity associated with the IRDCs and
fragments, we analysed the 24 ![]() m MIPSGAL data, looking for point-like
sources. For this purpose we used the IDL FIND task of the IDL Astronomy
Library. As an initial indication of the the star formation activity of these IRDCs, we have identified all the 24
m MIPSGAL data, looking for point-like
sources. For this purpose we used the IDL FIND task of the IDL Astronomy
Library. As an initial indication of the the star formation activity of these IRDCs, we have identified all the 24 ![]() m stars lying within a box
(described as Field in Table 1 Col. 16) of twice the
calculated extent along the coordinate axes of each IRDC. Doing so, we find
that 32% of the IRDCs do not have any 24
m stars lying within a box
(described as Field in Table 1 Col. 16) of twice the
calculated extent along the coordinate axes of each IRDC. Doing so, we find
that 32% of the IRDCs do not have any 24 ![]() m point-like sources in such
a box
m point-like sources in such
a box![]() . On the
other hand, 20% of the IRDCs have a 24
. On the
other hand, 20% of the IRDCs have a 24 ![]() m source lying within their
boundaries (Table 1 Col. 17). Therefore, the percentage of active
star forming IRDCs is likely to be between 20% and 68%. A more detailed
analysis of the stellar content of IRDCs will be presented in a following
paper.
m source lying within their
boundaries (Table 1 Col. 17). Therefore, the percentage of active
star forming IRDCs is likely to be between 20% and 68%. A more detailed
analysis of the stellar content of IRDCs will be presented in a following
paper.
Concerning the fragments, between 1% and 6% have stars lying within their boundaries, depending on the parameters used to extract the fragments (Peretto & Fuller 2009, in preparation).
We have also calculated the 24 ![]() m stellar surface density around each IRDC extracted (Table 2 Col. 18). This number provides an idea of the crowding in the area around the IRDC.
m stellar surface density around each IRDC extracted (Table 2 Col. 18). This number provides an idea of the crowding in the area around the IRDC.
5.4 Uncertainties on the opacity estimates
The main source of uncertainty in the opacity maps arises from the
estimate of the foreground intensity
![]() .
As explained in
Sect. 3, we used the relation
.
As explained in
Sect. 3, we used the relation
![]() to calculate this quantity for every cloud. However, as
can be seen in Fig. 5 a dispersion of
to calculate this quantity for every cloud. However, as
can be seen in Fig. 5 a dispersion of ![]() 0.1 exists
on this relation with a maximum variation of
0.1 exists
on this relation with a maximum variation of ![]() 0.25. To assess the
impact of such variations on the calculated peak opacities of the
clouds we have computed for every cloud the ratio, K, of the peak
opacity inferred assuming
0.25. To assess the
impact of such variations on the calculated peak opacities of the
clouds we have computed for every cloud the ratio, K, of the peak
opacity inferred assuming
![]() where
0.25<Cf<0.75 to the peak opacity calculated with the fiducial
where
0.25<Cf<0.75 to the peak opacity calculated with the fiducial
![]() (Eq. (5); Cf=0.54). Figure 8
shows the median value of this ratio as a function of Cf. For each
value of Cf we also calculated the dispersion in K across the
entire sample of clouds. These dispersions were all <0.1, except
for the case Cf=0.75 where the dispersion in K reached 0.3. The
range in K shown on Fig. 8 provides an estimate of the
peak opacity uncertainty related to the choice/variation of
(Eq. (5); Cf=0.54). Figure 8
shows the median value of this ratio as a function of Cf. For each
value of Cf we also calculated the dispersion in K across the
entire sample of clouds. These dispersions were all <0.1, except
for the case Cf=0.75 where the dispersion in K reached 0.3. The
range in K shown on Fig. 8 provides an estimate of the
peak opacity uncertainty related to the choice/variation of
![]() .
In most cases this uncertainty is less than a factor
of 2, but can be as large as 10 for extreme cases. On the same
figure we also plot the fraction of saturated clouds as a function of
the adopted
.
In most cases this uncertainty is less than a factor
of 2, but can be as large as 10 for extreme cases. On the same
figure we also plot the fraction of saturated clouds as a function of
the adopted
![]() .
Naturally, the higher
.
Naturally, the higher
![]() ,
the higher the number of saturated clouds, reaching 80
,
the higher the number of saturated clouds, reaching 80![]() in the most
extreme case, but being less than 10% for
in the most
extreme case, but being less than 10% for
![]() .
In the case of
Cf = 0.54, the percentage of
saturated cloud is 3%. This is consistent with a visual inspection of the 8
.
In the case of
Cf = 0.54, the percentage of
saturated cloud is 3%. This is consistent with a visual inspection of the 8 ![]() m intensity profiles of a sample of clouds which indicates that less than 10% of the objects show a flattening in their inner regions, a
signature of possible saturation.
m intensity profiles of a sample of clouds which indicates that less than 10% of the objects show a flattening in their inner regions, a
signature of possible saturation.
Another source of uncertainty is the variation of the foreground
intensity relative to the background emission. Since we have shown
that on average the background emission is equal to the foreground
emission (Sect. 3.2), we assumed that the variations of
both quantities in front and behind a cloud have the same origin, and
so, the same variations. However, this assumption could be wrong. For
instance one could be constant over the extent of the cloud, more
likely the foreground, with the other one containing all the
variations observed in the mid-infrared radiation field. The impact of
such effects on the opacity estimate is similar to the one described
above. Clouds with small variations in
their mid-infrared radiation fields are thus better constrained than
the ones with high values of
![]() .
.
As mentioned in the previous section large clouds (>
![]() )
have
opacities which are likely to be underestimated, however this effect is minor
compared with those mentioned above. Overall, considering all the factors
which contribute to the uncertainty in opacity, we estimate the values
derived from the Spitzer data are uncertain by a factor of no more than
two. This result is consistent with the observations of a subset of clouds in
the 1.2 mm continuum emission from the dust (Fig. 6).
)
have
opacities which are likely to be underestimated, however this effect is minor
compared with those mentioned above. Overall, considering all the factors
which contribute to the uncertainty in opacity, we estimate the values
derived from the Spitzer data are uncertain by a factor of no more than
two. This result is consistent with the observations of a subset of clouds in
the 1.2 mm continuum emission from the dust (Fig. 6).
![\begin{figure}
\par\includegraphics[width=12.5cm,angle=270]{12127fg8.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg100.png) |
Figure 8: Top: correction factor to apply to peak opacities in order to correct for different foreground intensities than the one we used in this study. Bottom: fraction of saturated clouds as a function of the assumption made on the foreground intensity. |
| Open with DEXTER | |
6 Comparison with the MSX IRDC catalogue
Simon et al. (2006a) undertook a systematic survey of IRDCs using MSX
data. Their survey covers a larger area of the Galactic plane than ours due to the smaller coverage of GLIMPSE survey. In total, Simon et al. (2006a) have
extracted 6721 clouds between
![]() and
and
![]() .
For the same coverage we extracted 11 303 Spitzer dark clouds, which is roughly twice as many. However, the parameters of the two surveys are so different that a more detailed comparison is required than just a simple comparison of the numbers of clouds.
.
For the same coverage we extracted 11 303 Spitzer dark clouds, which is roughly twice as many. However, the parameters of the two surveys are so different that a more detailed comparison is required than just a simple comparison of the numbers of clouds.
![\begin{figure}
\par\includegraphics[width=17.9cm,angle=0,clip]{12127fg9.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg103.png) |
Figure 9:
In grey scale is the Spitzer 8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,angle=270,clip]{12127fg10.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg104.png) |
Figure 10:
Comparison of three IRDCs seen with Spitzer at 8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{12127fg11.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg105.png) |
Figure 11: Comparison of the latitude distribution of Spitzer and MSX dark clouds. |
| Open with DEXTER | |
As illustrated by Fig. 9, it appears that a minority of IRDCs are
common to both MSX and Spitzer catalogues. Actually, only 20![]() of the
Spitzer dark clouds appear in the MSX catalogue (corresponding to 25
of the
Spitzer dark clouds appear in the MSX catalogue (corresponding to 25![]() of
MSX clouds being associated with a Spitzer dark cloud). Based on this
comparison we define 3 categories of clouds: Spitzer only, which are
clouds appearing only in our catalogue; MSX only, which are clouds
appearing only in Simon et al. catalogue; and both, which are clouds
appearing in both catalogues. Figure 10 shows an example of an
IRDC in each of these categories.
of
MSX clouds being associated with a Spitzer dark cloud). Based on this
comparison we define 3 categories of clouds: Spitzer only, which are
clouds appearing only in our catalogue; MSX only, which are clouds
appearing only in Simon et al. catalogue; and both, which are clouds
appearing in both catalogues. Figure 10 shows an example of an
IRDC in each of these categories.
Of the Spitzer only clouds, 51% do not meet the size criteria,
![]() ,
imposed by Simon et al. (2006a) to identify the MSX IRDCs, explaining why they are not in the MSX catalogue. The remaining
,
imposed by Simon et al. (2006a) to identify the MSX IRDCs, explaining why they are not in the MSX catalogue. The remaining ![]() 30% of Spitzer only IRDCs result from the difference in the method used to estimate the background. Using a median filter of 30
30% of Spitzer only IRDCs result from the difference in the method used to estimate the background. Using a median filter of 30![]() diameter, Simon et al. (2006a) underestimated the background almost everywhere in the inner
diameter, Simon et al. (2006a) underestimated the background almost everywhere in the inner
![]() of the Galactic plane. As a consequence, the inferred background reaches a similar value to that in an IRDC itself, and
therefore, an IRDC is not detected. This artifact can be seen when ploting the source fraction as a function of the Galactic latitude
(Fig. 11). We see a significant difference between the
distributions of MSX and Spitzer IRDCs. The MSX IRDCs have a rather flat
distribution in a central 1
of the Galactic plane. As a consequence, the inferred background reaches a similar value to that in an IRDC itself, and
therefore, an IRDC is not detected. This artifact can be seen when ploting the source fraction as a function of the Galactic latitude
(Fig. 11). We see a significant difference between the
distributions of MSX and Spitzer IRDCs. The MSX IRDCs have a rather flat
distribution in a central 1![]() region whereas the Spitzer IRDC distribution has a clear central peak decreasing sharply on both sides of it. We believe than this difference arises from the difference in the background construction.
region whereas the Spitzer IRDC distribution has a clear central peak decreasing sharply on both sides of it. We believe than this difference arises from the difference in the background construction.
On the other hand the MSX only clouds have
very low contrast (opacity peaks) and are particularly large. The
detection of such clouds in the MSX data has been possible due to
the large background smoothing length, and the low contrast
threshold used by Simon et al. (2006a). In order to investigate this
effect and see whether our method could recover these clouds when
using a larger Gaussian, we smoothed the block shown in
Fig 9 to 20![]() ,
and performed the extraction of IRDCs
on the resulting opacity map. Doing so, we find twice as many clouds
(40%) which are in both catalogues, but in parallel 35% of Spitzer
clouds which were initially detected using a smaller Gaussian are
lost. The remaining MSX only clouds are just too shallow to be
identified given the opacity threshold we used, 0.7. In
addition, looking at their 8
,
and performed the extraction of IRDCs
on the resulting opacity map. Doing so, we find twice as many clouds
(40%) which are in both catalogues, but in parallel 35% of Spitzer
clouds which were initially detected using a smaller Gaussian are
lost. The remaining MSX only clouds are just too shallow to be
identified given the opacity threshold we used, 0.7. In
addition, looking at their 8 ![]() m emission it is not clear
whether many of these clouds are real, or just a decrease in the
background of the Galactic plane.
m emission it is not clear
whether many of these clouds are real, or just a decrease in the
background of the Galactic plane.
Overall, we can say that 80% of our catalogue comprises IRDCs which
were previously unknown and constitutes the most complete catalogue
available of such objects with column density peaks above
![]() cm-2.
cm-2.
7 Summary
This paper, the first of a series dedicated to the study of infrared dark
clouds, describes the techniques developed to establish a complete catalogue
of Spitzer dark clouds. We analysed the full data set of the 8 ![]() m GLIMPSE
Galactic plane to look for IRDCs. We extracted 11303 of these clouds,
obtaining column density maps for each of them, and characterizing their
physical properties. A similar analysis of 10 IRDCs has recently been carried out by Butler & Tan (2009). We also identify the substructures, fragments, lying within these clouds, extracting up to
m GLIMPSE
Galactic plane to look for IRDCs. We extracted 11303 of these clouds,
obtaining column density maps for each of them, and characterizing their
physical properties. A similar analysis of 10 IRDCs has recently been carried out by Butler & Tan (2009). We also identify the substructures, fragments, lying within these clouds, extracting up to ![]() 50 000 fragments. Table 2 presents a summary of the average and range of properties of both the clouds and the fragments. The full table of the properties of the clouds and fragments plus images and opacity maps are available from an online
database
50 000 fragments. Table 2 presents a summary of the average and range of properties of both the clouds and the fragments. The full table of the properties of the clouds and fragments plus images and opacity maps are available from an online
database![]() . In subsequent papers we will exploit the tremendous quantity of information concerning the initial
conditions for the formation of stars in the Galaxy contained within this set
of IRDC column density maps.
. In subsequent papers we will exploit the tremendous quantity of information concerning the initial
conditions for the formation of stars in the Galaxy contained within this set
of IRDC column density maps.
Acknowledgements
This work was supported in part by the PPARC and STFC grants. We thank Hannah Stacey for her work in the early stages of identifying some of the IRDCs. We also thank Jim Jackson, Robert Simon, and Jill Rathborne for providing us with the IRAM 30 m dust continuum images published in Rathborne et al. (2006) This research made use of Montage, funded by the National Aeronautics and Space Administration's Earth Science Technology Office, Computation Technologies Project, under Cooperative Agreement Number NCC5-626 between NASA and the California Institute of Technology. Montage is maintained by the NASA/IPAC Infrared Science Archive.
Appendix A: Method for extracting sources
![\begin{figure}
\par\includegraphics[width=6.cm,angle=270,clip]{12127fg12.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg108.png) |
Figure A.1:
Illustration of our extraction method. This figure shows the opacity profile of a typical IRDC. The bottom dashed line shows the opacity threshold beneath which structures are ignored. The dotted lines show the different slices through the cloud, every slice being separated by
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=270]{12127fg13.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg109.png) |
Figure A.2:
8 |
| Open with DEXTER | |
We developed a new code to extract sources from our opacity maps. The first
part of our algorithm is mainly based on the same principle as the one
developed by Williams et al. (1994) for CLUMPFIND. We set two main parameters
which are the lowest contour level under which we do not consider any
structure,
![]() ,
and a step in unit of the map,
,
and a step in unit of the map,
![]() .
Then we look at every local peak between two consecutive
levels, up to the maximum of our image. The number of local peaks gives us the
number of fragments we will extract from the image, unless the final estimated
size is lower than the final angular resolution or the amplitude between the
peak of the fragment and its external boundary is less than
.
Then we look at every local peak between two consecutive
levels, up to the maximum of our image. The number of local peaks gives us the
number of fragments we will extract from the image, unless the final estimated
size is lower than the final angular resolution or the amplitude between the
peak of the fragment and its external boundary is less than
![]() .
Then we have to determine the pixels we associate to each
local peak. For this, for every peak, we go down, level by level, and check if
the local peak we are looking at is the only one in this contour. If yes, we
look at the following contour and do the same job. If there is more than one
local peak within the contour we look for the local minimum between these two
peaks,
.
Then we have to determine the pixels we associate to each
local peak. For this, for every peak, we go down, level by level, and check if
the local peak we are looking at is the only one in this contour. If yes, we
look at the following contour and do the same job. If there is more than one
local peak within the contour we look for the local minimum between these two
peaks,
![]() .
The pixels lying above
.
The pixels lying above
![]() and
associated with the considered peak define the extent of the fragment.
and
associated with the considered peak define the extent of the fragment.
In order to measure the size of the clouds and fragments, we did not want to
assume any particular shape for the source. So, once we have identify all the
pixels associated with a given peak, we estimate first the center of gravity
of the cores,
(XCG,YCG), using
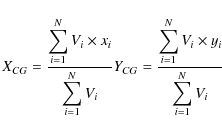 |
(A.1) |
where Vi is the value of the ith pixel, xi and yi its coordinates, and N is the number of pixels. Then, we calculate the matrix of moment of inertia, I:
![\begin{displaymath}I=\left[\begin{array}{cc}
I_{xx}&I_{xy}\\
I_{yx}&I_{yy}\\
\end{array}\right]
\end{displaymath}](/articles/aa/full_html/2009/37/aa12127-09/img112.png) |
(A.2) |
with
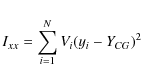 |
(A.3) |
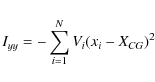 |
(A.4) |
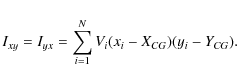 |
(A.5) |
Finally, we diagonalize I in order to obtain its two eigenvalues and eigenvectors. From this we can easily calculate the position angle
![\begin{displaymath}\sigma_X^2 \!=\!\! \displaystyle\sum_{i\!=\!1}^N \left(\left[...
...{CG} \cos(\alpha) \!-\! Y_{CG} \sin(\alpha) \right] \right)^2~
\end{displaymath}](/articles/aa/full_html/2009/37/aa12127-09/img116.png) |
(A.6) |
![\begin{displaymath}\sigma_Y^2\! =\!\! \displaystyle\sum_{i=1}^N \left(\left[ x_i...
...} \sin(\alpha)\! +\! Y_{CG}
\cos(\alpha) \right] \right)^2\!.~
\end{displaymath}](/articles/aa/full_html/2009/37/aa12127-09/img117.png) |
(A.7) |
The sizes are then estimated by
The three values, ![]() ,
,
![]() and
and ![]() ,
are given for every
IRDC in Table 1.
,
are given for every
IRDC in Table 1.
References
- André, P., Belloche, A., Motte, F., et al. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences]
- Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [NASA ADS] (In the text)
- Bally, J., Walawender, J., Luhman, K. L., et al. 2006, AJ, 132, 1923 [NASA ADS] [CrossRef] (In the text)
- Blitz, L. 1993, in Protostars and Planets III, ed. E. H. Levy, & J. I. Lunine, 125 (In the text)
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] (In the text)
- Butler, M. J., & Tan, J. C. 2009, ApJ, 696, 484 [NASA ADS] [CrossRef] (In the text)
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721 [NASA ADS] [CrossRef]
- Deharveng, L., Zavagno, A., Schuller, F., et al. 2009, A&A, 496, 177 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef] (In the text)
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, L199 [NASA ADS] [CrossRef]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [NASA ADS] [CrossRef]
- Hatchell, J., Richer, J. S., Fuller, G. A., et al. 2005, A&A, 440, 151 [NASA ADS] [CrossRef] [EDP Sciences]
- Hennebelle, P., Pérault, M., Teyssier, D., et al. 2001, A&A, 365, 598 [NASA ADS] [CrossRef] [EDP Sciences]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef]
- Johnstone, D., Fiege, J. D., Redman, R. O., Feldman, P. A., & Carey, S. J. 2003, ApJ, 588, L37 [NASA ADS] [CrossRef]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] (In the text)
- Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269 [NASA ADS]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS]
- Perault, M., Omont, A., Simon, G., et al. 1996, A&A, 315, L165 [NASA ADS]
- Peretto, N., André, P., & Belloche, A. 2006, A&A, 445, 979 [NASA ADS] [CrossRef] [EDP Sciences]
- Pillai, T., Wyrowski, F., Carey, S. J., et al. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences]
- Rachford, B. L., Snow, T. P., Tumlinson, J., et al. 2002, ApJ, 577, 221 [NASA ADS] [CrossRef] (In the text)
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [NASA ADS] [CrossRef]
- Reach, W. T., Megeath, S. T., Cohen, M., et al. 2005, PASP, 117, 978 [NASA ADS] [CrossRef] (In the text)
- Román-Zúñiga, C. G., Lada, C. J., Muench, A., et al. 2007, ApJ, 664, 357 [NASA ADS] [CrossRef]
- Simon, R., Jackson, J. M., Rathborne, J. M., et al. 2006a, ApJ, 639, 227 [NASA ADS] [CrossRef]
- Simon, R., Rathborne, J. M., Shah, R. Y., Jackson, J. M., & Chambers, E. T. 2006b, ApJ, 653, 1325 [NASA ADS] [CrossRef] (In the text)
- Teixeira, P. S., Lada, C. J., Young, E. T., et al. 2006, ApJ, 636, L45 [NASA ADS] [CrossRef]
- Teyssier, D., Hennebelle, P., & Pérault, M. 2002, A&A, 382, 624 [NASA ADS] [CrossRef] [EDP Sciences]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] (In the text)
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... clouds
![[*]](/icons/foot_motif.png)
- The complete version of the catalogue (Table 1) is available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/505/405
- ...
![[*]](/icons/foot_motif.png)
- This size corresponds to (pixel size)
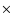 28.
28.
- ...)
![[*]](/icons/foot_motif.png)
- The complete version of Table 1 can be found on CDS. Moreover, images of all clouds are available online at: http://www.irdarkclouds.org or http://www.manchester.ac.uk/jodrellbank/sdc
- ... box
![[*]](/icons/foot_motif.png)
- In Table 1 Cols. 16 and 17 y stands for yes and indicates the presence of a star within the field (and/or the cloud), while n indicates there are no such stars.
- ...
database
![[*]](/icons/foot_motif.png)
- The database is available at http://www.irdarkclouds.org or http://www.manchester.ac.uk/jodrellbank/sdc
All Tables
Table 1: Properties of the first 30 out of the 11303 in the Spitzer dark cloud (SDC) catalogue. The full catalogue is available at the CDS.
Table 2:
Average properties of IRDCs and fragments (extracted with
![]() ).
).
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=14.5cm,clip]{12127fg1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg29.png) |
Figure 1:
These images show the GLIMPSE Spitzer 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270,clip]{12127fg2.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg46.png) |
Figure 2:
Schematic view a typical IRDC flux density profile. The variables described in the text are illustrated on this figure. In this figure,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.0cm,angle=270,clip]{12127fg3.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg56.png) |
Figure 3:
Calculated opacity profiles of the IRDC plotted in
Fig.2 corresponding to 3 different assumptions on the
foreground intensity. The solid line shows
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.cm,angle=270]{12127fg4.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg67.png) |
Figure 4:
Plot of the 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.cm,angle=270]{12127fg5.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg71.png) |
Figure 5:
Plot of the 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=270]{12127fg6.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg72.png) |
Figure 6:
Same as Fig. 4 but only for starless sources and with a 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,angle=270]{12127fg7.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg86.png) |
Figure 7:
8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm,angle=270]{12127fg8.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg100.png) |
Figure 8: Top: correction factor to apply to peak opacities in order to correct for different foreground intensities than the one we used in this study. Bottom: fraction of saturated clouds as a function of the assumption made on the foreground intensity. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.9cm,angle=0,clip]{12127fg9.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg103.png) |
Figure 9:
In grey scale is the Spitzer 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.7cm,angle=270,clip]{12127fg10.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg104.png) |
Figure 10:
Comparison of three IRDCs seen with Spitzer at 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{12127fg11.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg105.png) |
Figure 11: Comparison of the latitude distribution of Spitzer and MSX dark clouds. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.cm,angle=270,clip]{12127fg12.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg108.png) |
Figure A.1:
Illustration of our extraction method. This figure shows the opacity profile of a typical IRDC. The bottom dashed line shows the opacity threshold beneath which structures are ignored. The dotted lines show the different slices through the cloud, every slice being separated by
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=270]{12127fg13.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12127-09/Timg109.png) |
Figure A.2:
8 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



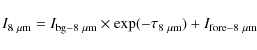
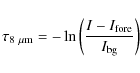
![\begin{displaymath}N_{\rm {H_2}} = \tau_{8\mu\rm {m}} \times 3[\pm1] \times10^{22} \rm {cm}^{-2}
\end{displaymath}](/articles/aa/full_html/2009/37/aa12127-09/img92.png)