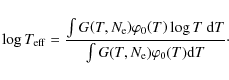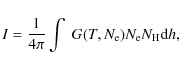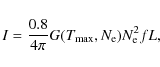| Issue |
A&A
Volume 505, Number 1, October I 2009
|
|
|---|---|---|
| Page(s) | 307 - 318 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912114 | |
| Published online | 27 July 2009 | |
Solar transition region above sunspots![[*]](/icons/foot_motif.png)
H. Tian1,2 - W. Curdt1 - L. Teriaca1 - E. Landi3 - E. Marsch1
1 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 - School of Earth and Space Sciences, Peking University, PR China
3 - Naval Research Laboratory, Washington D.C., USA
Received 19 March 2009 / Accepted 10 June 2009
Abstract
Aims. We study the transition region (TR) properties above sunspots and the surrounding plage regions, by analyzing several sunspot reference spectra obtained by the SUMER (Solar Ultraviolet Measurements of Emitted Radiation) instrument in March 1999 and November 2006.
Methods. We compare the SUMER spectra observed in the umbra, penumbra, plage, and sunspot plume regions. The hydrogen Lyman line profiles averaged in each of the four regions are presented. For the sunspot observed in 2006, the electron densities, differential emission measure (DEM), and filling factors of the TR plasma in the four regions are also investigated.
Results. The self-reversals of the hydrogen Lyman line profiles are almost absent in sunspots at different locations (at heliocentric angles of up to ![]() )
on the solar disk. In the sunspot plume, the Lyman lines are also not reversed, whilst the lower Lyman line profiles observed in the plage region are obviously reversed, a phenomenon found also in the normal quiet Sun. The TR densities of the umbra and plume are similar and one order of magnitude lower than those of the plage and penumbra. The DEM curve of the sunspot plume exhibits a peak centered at
)
on the solar disk. In the sunspot plume, the Lyman lines are also not reversed, whilst the lower Lyman line profiles observed in the plage region are obviously reversed, a phenomenon found also in the normal quiet Sun. The TR densities of the umbra and plume are similar and one order of magnitude lower than those of the plage and penumbra. The DEM curve of the sunspot plume exhibits a peak centered at
![]() ,
which exceeds the DEM of other regions by one to two orders of magnitude at these temperatures. We also find that more than 100 lines, which are very weak or not observed anywhere else on the Sun, are well observed by SUMER in the sunspot, especially in the sunspot plume.
,
which exceeds the DEM of other regions by one to two orders of magnitude at these temperatures. We also find that more than 100 lines, which are very weak or not observed anywhere else on the Sun, are well observed by SUMER in the sunspot, especially in the sunspot plume.
Conclusions. We suggest that the TR above sunspots is higher and probably more extended, and that the opacity of the hydrogen lines is much lower above sunspots, compared to the TR above plage regions. Our result indicates that the enhanced TR emission of the sunspot plume is probably caused by a large filling factor. The strongly enhanced emission at TR temperatures and the reduced continuum ensure that many normally weak TR lines are clearly distinctive in the spectra of sunspot plumes.
Key words: Sun: UV radiation - Sun: transition region - sunspots - line: profiles
1 Introduction
The solar transition region (TR, between ![]() 104 K and 106 K)
is the interface between the chromosphere and corona, where the
temperature and density change dramatically. Most of the TR emission
occurs in the VUV (vacuum ultraviolet) range of the electromagnetic
radiation (Wilhelm et al. 2007). Thus, ultraviolet emission lines can
provide ample information about the magnetic structures and plasma
properties of the TR.
104 K and 106 K)
is the interface between the chromosphere and corona, where the
temperature and density change dramatically. Most of the TR emission
occurs in the VUV (vacuum ultraviolet) range of the electromagnetic
radiation (Wilhelm et al. 2007). Thus, ultraviolet emission lines can
provide ample information about the magnetic structures and plasma
properties of the TR.
Earlier ultraviolet observations such as those made by the Naval Research Laboratory (NRL) S082-B EUV spectrograph onboard the Skylab space station (Bartoe et al. 1977), and NRL High-Resolution Telescope Spectrograph (HRTS) flown on some rockets and Spacelab2 (Brueckner & Bartoe 1983; Brueckner et al. 1977,1986), provided much valuable information about the TR. These earlier results were reviewed by Mariska (1992).
Our knowledge of the TR has been enhanced greatly since the SUMER (Solar Ultraviolet Measurements of Emitted Radiation) instrument (Wilhelm et al. 1995; Lemaire et al. 1997) onboard SOHO (Solar and Heliospheric Observatory) began to observe in 1996. Because of its high spectral, spatial, and temporal resolutions, and the wide wavelength coverage, many more TR line profiles than in the past were obtained, identified, and used in intensive studies (Curdt et al. 2004,2001). In addition, the CDS (Coronal Diagnostic Spectrometer) instrument (Harrison et al. 1995) onboard SOHO has also increased significantly our understanding of the TR structures and dynamics. For a review of these recent progresses, we refer to Wilhelm et al. (2007).
Gabriel (1976) proposed a magnetic network model, in which the TR emission originates in funnels diverging with height from the underlying supergranular boundary. A decade later, Dowdy et al. (1986) proposed a modified model in which only a fraction of the network flux opens, in the shape of funnels, into the corona, while the remainder of the network is occupied by a population of low-lying loops with lengths less than 10 Mm. Based on SUMER observations, Peter (2001) suggested a new picture for the structure of the TR, in which the funnels are either connected to the solar wind or just the legs of large loops.
Table 1: Observational parameters of the 5 reference spectra of sunspots.
All the models mentioned above refer to the average structures in the TR. However, the solar atmosphere is very inhomogeneous and characterized by different large and small-scale structures. Moreover, studies have shown that the TR is not thermally stratified but strongly nonuniform and magnetically structured (Feldman 1983,1987; Marsch et al. 2006). The SUMER instrument is well suited to study the difference in TR structures in different regions of the Sun. By combing the technique of magnetic field extrapolation with SUMER observations, it has been found that the TR in coronal holes is higher and more extended than in the quiet Sun (Tian et al. 2008b; Tu et al. 2005b,a; Tian et al. 2008a).
An active region is an area with an especially strong magnetic field, where sunspots and plages are frequently formed. Our current empirical knowledge and physical understanding of sunspots were reviewed by Solanki (2003). The sunspot spectra obtained by SUMER reveal some distinct properties (Curdt et al. 2001). For instance, some spectral lines which are not observed in other areas of the Sun stick out in the sunspot spectra. Moreover, in contrast to the quiet Sun, the hydrogen Lyman line profiles in the sunspot are not reversed. Until now, little has been done to understand these phenomena.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12114f1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg21.png) |
Figure 1:
Averaged profiles of Ly-2 ( upper panels) and Ly-3 ( lower panels) in the sunspot observed on 16th (
|
| Open with DEXTER | |
Spectral lines with formation temperatures between ![]() 105 K and
106 K (upper-TR) often have significantly enhanced intensities at
locations overlying sunspot umbrae (Foukal et al. 1974). These features
are usually termed sunspot plumes (Foukal 1976). A sunspot plume
usually has one end point anchored in the umbra and the other can
reach far from the sunspot. It is regarded as nothing more than the
common footpoints of several active region loops (Dammasch et al. 2008).
Although sunspot plumes have been studied extensively, the reason
why the plume emission is so prominent at upper-TR temperatures is
still unknown.
105 K and
106 K (upper-TR) often have significantly enhanced intensities at
locations overlying sunspot umbrae (Foukal et al. 1974). These features
are usually termed sunspot plumes (Foukal 1976). A sunspot plume
usually has one end point anchored in the umbra and the other can
reach far from the sunspot. It is regarded as nothing more than the
common footpoints of several active region loops (Dammasch et al. 2008).
Although sunspot plumes have been studied extensively, the reason
why the plume emission is so prominent at upper-TR temperatures is
still unknown.
Some work has been done to study the plasma properties of sunspot
plumes. The electron density,
![]() ,
of
the TR plasma in sunspot plumes is about 10 (Doyle & Madjarska 2003; Doyle et al. 1985).
The sunspot plumes seem to be associated with downflows of TR plasma
(Dammasch et al. 2008; Marsch et al. 2004; Foukal 1976; Brynildsen et al. 2001; Brosius & Landi 2005).
The emission measure (EM) curve based on S-055 spectra of sunspot
plumes revealed two peaks at
,
of
the TR plasma in sunspot plumes is about 10 (Doyle & Madjarska 2003; Doyle et al. 1985).
The sunspot plumes seem to be associated with downflows of TR plasma
(Dammasch et al. 2008; Marsch et al. 2004; Foukal 1976; Brynildsen et al. 2001; Brosius & Landi 2005).
The emission measure (EM) curve based on S-055 spectra of sunspot
plumes revealed two peaks at
![]() and 6.1,
respectively (Noyes et al. 1985), while a more recent study showed that
the plume's differential emission measure (DEM) exhibited only one
peak centered at
and 6.1,
respectively (Noyes et al. 1985), while a more recent study showed that
the plume's differential emission measure (DEM) exhibited only one
peak centered at
![]() or 5.8
(Brosius & Landi 2005). More work is needed to compare the
properties of sunspot plumes and other regions.
or 5.8
(Brosius & Landi 2005). More work is needed to compare the
properties of sunspot plumes and other regions.
![\begin{figure}
\par\includegraphics[width=12.5cm]{12114f2.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg24.png) |
Figure 2: The sunspot observed on 14th of November, 2006. (A) The SUMER slit is located on the image of the 1600 Å passband of TRACE. The TRACE image was obtained at 00:32 on November 14, 2006. (B) The intensities of continuum around 1045 Å (solid line) and O VI (1031.9 Å, dotted line) along the slit. Four segments corresponding to the plage, penumbra, umbra, and sunspot plume are marked in grey. The O VI intensity has been divided by 600. |
| Open with DEXTER | |
In this paper, we present a more complete analysis, by analyzing more sunspot spectra obtained with SUMER at different locations of the Sun , and compare the Lyman line (of main quantum number n higher than 2) profiles, electron densities, DEM curves, and filling factors of the sunspot plume, umbra, penumbra, and the surrounding plage regions. Our results have important physical conclusions for the TR properties above the sunspot and the surrounding plage region.
2 Observation and data reduction
We selected five reference spectra of two sunspots observed by
SUMER. One sunspot was observed at different locations of the solar
disk during March 16-19, 1999. The reference spectrum of the other
sunspot was obtained between 23:58 on November 13 and 02:52 of the
next day in 2006. The observational details are listed in
Table 1. The pointing in x and y is given in arcseconds
and refers to the slit center at the central time of the
observation. ![]() is the heliocentric angle.
is the heliocentric angle.
The standard procedures for correcting the SUMER data were applied, including local-gain correction, dead-time correction, flat-field correction, and image destretching.
In the earlier work of Curdt et al. (2000), the 1999 sunspot was
analyzed. However, only the reference spectrum obtained on March 18
was used. This spectrum was also used to produce the sunspot atlas,
and both the context image and slit position can be found in
Curdt et al. (2001). Here we extend the earlier work by analyzing four
reference spectra of this sunspot obtained at different solar
locations. Because of the solar rotation, this sunspot rotated from
the central meridian towards the limb, and its heliocentric angle
increases from ![]() to
to ![]() .
Thus, we can study the
center to limb variation in the Lyman line profiles of the sunspot,
as shown in Fig. 1.
.
Thus, we can study the
center to limb variation in the Lyman line profiles of the sunspot,
as shown in Fig. 1.
The sunspot observed in 2006 was large in size, and several reference spectra for it were obtained, all near the disk center. For this reason, we analyze only one reference spectrum of this sunspot. During this observation, TRACE (Transition Region and Corona Explorer) obtained an image of the 1600 Å passband at 00:32 on November 14, 2006. The sunspot image observed by TRACE is shown in panel (A) of Fig. 2. Also shown there is the approximate location of the SUMER slit. The SUMER instrument also scanned this sunspot region by using several typical TR lines (N IV, O IV, Si IV, O III), and the relevant results were published in Teriaca et al. (2008). Although the scans were completed at different times, and a temporal variation may have occurred in the sunspot region, their Fig. 1 still provides an impression of the TR emission from the sunspot and the surrounding plage regions.
3 Hydrogen Lyman line profiles
Hydrogen is the most abundant element in the solar atmosphere and its resonance lines play an important role in the overall radiative energy transport of the Sun (Fontenla et al. 1988). Profiles of hydrogen Lyman series can also be used to diagnose nonthermal effects in solar flares (Fang et al. 1995; Xu et al. 2005).
Line profiles of the full hydrogen Lyman series can be acquired by
SUMER at high spectral resolution. It has been found that the
average profiles for Ly![]() (n = 2) through Ly
(n = 2) through Ly![]() (n = 5)
are self-reversed and stronger in the red horns, while the higher H Lyman series lines (from Ly
(n = 5)
are self-reversed and stronger in the red horns, while the higher H Lyman series lines (from Ly![]() to Ly
to Ly![]() ,
(
,
(
![]() )) are flat-topped (Warren et al. 1998; Xia 2003; Xia et al. 2004). Higher Lyman
lines obtained near the limb were analysed by Marsch et al. (1999) and
Marsch et al. (2000), in which the authors found an increase in the line
width with decreasing main quantum number and an unexpectedly flat
hydrogen-temperature gradient. The Ly
)) are flat-topped (Warren et al. 1998; Xia 2003; Xia et al. 2004). Higher Lyman
lines obtained near the limb were analysed by Marsch et al. (1999) and
Marsch et al. (2000), in which the authors found an increase in the line
width with decreasing main quantum number and an unexpectedly flat
hydrogen-temperature gradient. The Ly![]() profiles in the quiet Sun
were obtained by SUMER through several non-routine observations, by
closing the aperture door of SUMER to reduce the incoming photon
flux to a 20%-level (Curdt et al. 2008; Tian et al. 2009). The average
Ly
profiles in the quiet Sun
were obtained by SUMER through several non-routine observations, by
closing the aperture door of SUMER to reduce the incoming photon
flux to a 20%-level (Curdt et al. 2008; Tian et al. 2009). The average
Ly![]() profile was found to be strongly reversed and have a stronger
blue horn. It is believed that the opposite asymmetries in the
average profiles of Ly
profile was found to be strongly reversed and have a stronger
blue horn. It is believed that the opposite asymmetries in the
average profiles of Ly![]() and higher Lyman lines are probably caused
by the combined effect of flows in the different layers of the solar
atmosphere and opacity differences of the lines (Tian et al. 2009; Gunár et al. 2008).
and higher Lyman lines are probably caused
by the combined effect of flows in the different layers of the solar
atmosphere and opacity differences of the lines (Tian et al. 2009; Gunár et al. 2008).
The Lyman series are important for diagnosing the variation in the thermodynamic conditions in prominences (Vial 2007). Prominence thread models including multi-level non-LTE transfer calculations have shown that the profiles of Lyman lines are more reversed when seen across than along the magnetic field lines (Heinzel et al. 2005). This behaviour was confirmed in a prominence observation by Schmieder et al. (2007).
In sunspot regions, the Lyman line profiles exhibit properties that are different from the average profiles. The sunspot atlas of SUMER reveals that the Lyman line profiles observed in the sunspot are almost not reversed (Curdt et al. 2001). However, the authors did not mention this phenomenon in that paper. Here we extend this earlier work by analyzing four reference spectra of this sunspot obtained at different solar locations. Since the magnetic field lines in sunspots are almost vertical, we can use the 4 spectra to study the properties of the Lyman line profiles in sunspots and the dependence of their self-reversals on the orientation of field lines.
The Lyman line profiles in the four spectra are all not or only
slightly reversed, similar to those in off-limb coronal hole
observations (Marsch et al. 2000). This result suggests that the TR
plasma of the sunspot is almost optically thin, regardless of the
location where the sunspot is observed. Since it is known that the
higher order Lyman lines are optically thinner than lower order
Lyman lines, radiative transfer effects, if present, should be more
pronounced in lower order Lyman lines than in higher order Lyman
lines. Thus, we present only the Ly-2 and Ly-3 profiles averaged
over the sunspot (umbra) portion of the slit in Fig. 1.
Note that there are some blends with the Lyman lines
(Curdt et al. 2001). From an inspection of Fig. 1, it seems
that profiles begin to reverse when the vertical field lines of the
sunspot make an angle of about ![]() with respect to the line
of sight. This phenomenon seems to be similar to the observational
result for prominences, namely that the Lyman profiles are more
reversed when seen across the field lines than along the field lines
(Schmieder et al. 2007). However, from
with respect to the line
of sight. This phenomenon seems to be similar to the observational
result for prominences, namely that the Lyman profiles are more
reversed when seen across the field lines than along the field lines
(Schmieder et al. 2007). However, from
![]() to
to
![]() ,
it is difficult to say whether or not there is a
trend in the shapes of the top parts of the profiles.
,
it is difficult to say whether or not there is a
trend in the shapes of the top parts of the profiles.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12114f3.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg32.png) |
Figure 3: The dashed, dot-dashed, dotted, and solid lines represent the average profiles of the Lyman lines (from Lyman-2 to Lyman-9) observed in the plage, penumbra, umbra, and plume for the 2006 data set. Note that the profiles of the umbra were multiplied by a factor of two. |
| Open with DEXTER | |
The sunspot observed in 2006 is a large one, and the SUMER slit also caught part of a sunspot plume and the surrounding plage region. Figure 2 shows the intensities of the continuum around 1045 Å and of the O VI (1031.9 Å) line along the slit, and the resulting curves clearly show the umbra, penumbra, and plage regions as well as part of the sunspot plume. In this paper, the term intensity is regarded as being equivalent to radiance. The sunspot plume shows enhanced radiance in typical TR lines, which corresponds to the slit segment with the highest intensities of O VI in our reference spectra. We selected four portions of the slit, which are marked in grey in Fig. 2 and correspond to the umbra, penumbra, plage, and plume locations. The average Lyman line profiles (from Ly-2 to Ly-9) of the four parts are presented in Fig. 3. For the blends with the Lyman lines, we refer to Curdt et al. (2001).
Our results show that the self-reversals of all the hydrogen Lyman line profiles are absent in the umbra and plume regions. The lower Lyman line profiles observed in the plage region are obviously reversed, a phenomenon similar to the normal quiet Sun (one can refer to the atlas presented in Curdt et al. 2001). The profiles in the penumbra are not so peaked as those in the umbra and plume, and not so reversed as those in the plage. We also note that the Lyman line profiles observed in the plage have a very strong red-horn asymmetry (the red horn is much stronger than the blue horn), which might be at least partly caused by the strong red shift observed in the TR. The asymmetries of the lower Lyman line profiles in the penumbra seem to be opposite to those of the plage, which might indicate a different pattern of flows in the upper atmosphere of the two regions.
Unfortunately, so far SUMER has not been used to complete
Ly![]() observations of the sunspot. We note that Fontenla et al. (1988)
presented a Ly
observations of the sunspot. We note that Fontenla et al. (1988)
presented a Ly![]() profile (see Fig. 12 in the paper) of a sunspot
observed by the Ultraviolet Spectrometer and Polarimeter on the
SMM (Solar Maximum Mission) spacecraft. As mentioned in that
paper, the emission suffered from geocoronal absorption. After
correcting for this effect, their Ly
profile (see Fig. 12 in the paper) of a sunspot
observed by the Ultraviolet Spectrometer and Polarimeter on the
SMM (Solar Maximum Mission) spacecraft. As mentioned in that
paper, the emission suffered from geocoronal absorption. After
correcting for this effect, their Ly![]() profile seems to be
flat-topped, which is very different from the strongly reversed
Ly
profile seems to be
flat-topped, which is very different from the strongly reversed
Ly![]() profiles in the quiet Sun (Curdt et al. 2008; Tian et al. 2009).
profiles in the quiet Sun (Curdt et al. 2008; Tian et al. 2009).
The above results indicate that the opacity is strongly reduced
above the sunspot, with respect to the surrounding plage region. By
analysing the emission lines of H2 in the sunspot as well as
the quiet Sun, Jordan et al. (1978) and Bartoe et al. (1979) concluded that
the opacity over the sunspot is about an order of magnitude lower
than in the quiet Sun. The different opacities above sunspots and
plages are confirmed by the intensity ratio between Ly![]() and Ly
and Ly![]() ,
which is about 200 in the sunspot umbra and 130 in the plage. In the
sunspot, the profiles are only weakly absorbed. In the plage, the
opacity is higher and thus the absorption is enhanced. Since
Ly
,
which is about 200 in the sunspot umbra and 130 in the plage. In the
sunspot, the profiles are only weakly absorbed. In the plage, the
opacity is higher and thus the absorption is enhanced. Since
Ly![]() has a larger opacity, its absorption will be stronger than
Ly
has a larger opacity, its absorption will be stronger than
Ly![]() ,
which will lead to a lower observed value of the intensity
ratio. However, we note that the Ly
,
which will lead to a lower observed value of the intensity
ratio. However, we note that the Ly![]() line was recorded on the
attenuator, so the measurement of its intensity is highly uncertain
and we do not consider it in detail here.
line was recorded on the
attenuator, so the measurement of its intensity is highly uncertain
and we do not consider it in detail here.
Table 2:
Electron density (
![]() ))
measurements, for the sunspot observed in 2006.
))
measurements, for the sunspot observed in 2006.
Since the Lyman line profiles in the plage are quite similar to those observed in the normal quiet Sun, we may expect a similar opacity in both regions. This similarity might be the result of the similar magnetic structures. In both regions, magnetic loops reaching different heights are the dominant structures. The emission sources of Lyman lines are located mainly in loops that reach the layers of chromosphere and TR. When the chromospheric Lyman line photons travel through the upper atmosphere, they will be initially absorbed by the hydrogen atoms in upper-chromospheric and TR loops, and further absorbed in coronal loops. Since the density decreases and the temperature increases with height above the temperature minimum, there are more hydrogen atoms, and the absorption is much stronger in the upper chromosphere and lower-TR layers than at higher layers. In the plage region and quiet Sun, the Lyman line emission originates by a large fraction in the chromosphere and are strongly absorbed in the upper chromosphere and lower TR, leading to a strong absorption at the center of the Lyman line profiles.
The scenario seems to differ in sunspot regions. The almost Gaussian-shaped profiles suggest a weak absorption of the Lyman line emission. This observational result seems to favor a scenario where there is less chromospheric plasma above sunspots, which might be the case because the sunspot is much cooler than the surrounding regions. In this case, the ratio of the chromospheric to TR contributions of the Lyman line radiation is lower in sunspots than in plage regions. As a result, the chromospheric emission will only be weakly absorbed because there is little absorbing material in the upper chromosphere. Moreover, the absorption of the TR emission is weak because of the lower density above the emission sources.
Sunspot plumes often show greatly enhanced emission at upper-TR
temperatures (![]() 105 and 106 K), while at lower or higher
temperatures the emission is rather weak
(e.g., Foukal et al. 1974; Brosius & Landi 2005). Sunspot plumes are
frequently reported to be associated with TR downflows
(e.g., Dammasch et al. 2008; Marsch et al. 2004). Observational results seem to
reveal that plasmas at TR temperatures dominate in plumes. Thus, the
ratio of TR to chromospheric contributions to the Lyman line
emissions may be significantly higher in plumes. These plume loops
are large in size (and far reaching) and the overlying corona is
insufficiently dense to cause an obvious dip at the center of the
Lyman line profiles.
105 and 106 K), while at lower or higher
temperatures the emission is rather weak
(e.g., Foukal et al. 1974; Brosius & Landi 2005). Sunspot plumes are
frequently reported to be associated with TR downflows
(e.g., Dammasch et al. 2008; Marsch et al. 2004). Observational results seem to
reveal that plasmas at TR temperatures dominate in plumes. Thus, the
ratio of TR to chromospheric contributions to the Lyman line
emissions may be significantly higher in plumes. These plume loops
are large in size (and far reaching) and the overlying corona is
insufficiently dense to cause an obvious dip at the center of the
Lyman line profiles.
The above explanations are based mainly on a static stratified atmosphere. However, it is well known that the real solar atmosphere, especially the TR over sunspots, is rather inhomogeneous and dynamic (Brynildsen et al. 1999b,a). It has been found that the Lyman line profiles can be modified by TR flows in the quiet Sun (Curdt et al. 2008; Tian et al. 2009). In sunspot regions, both significant upflows and downflows have been frequently reported (e.g., Teriaca et al. 2008; Kjeldseth-Moe et al. 1988). Thus, we should not exclude the possibility that additional effects, such as the presence of velocities and radiation penetrating from the sides in the inhomogeneous plasma, may alter the source functions of the Lyman lines and also affect the Lyman line profiles.
4 Electron densities
Based on the assumption that the plasma is in ionization equilibrium, one can calculate the electron density from line-ratio observations (for a review, see Wilhelm et al. 2004; Xia 2003). Density-sensitive line pairs usually include two emission lines within the same ion. In the de-excitation process, the relative importance of radiative decay to collisional de-excitation is different for the two lines.
There are several density-sensitive line pairs in the SUMER spectral
range (Wilhelm et al. 1995). However, some of these lines are either
severely blended with other lines and difficult to decompose, or too
weak for a reliable calculation. We selected as many lines as
possible to calculate the densities for the sunspot observed in
2006. All of these line pairs have a weak dependence on the electron
temperature. Fortunately, the few density-sensitive lines are close
in wavelength, so that the effects of temporal variations on the
measured densities are minimized. By applying the method of single-
or multi-Gaussian fitting to the profiles of these lines averaged in
the plage, umbra, penumbra, and plume, we were able to obtain the
intensities. The theoretical relations between intensity ratios of
line pairs and electron densities were taken from the CHIANTI data
base (Dere et al. 1997; Landi et al. 2006). The details of the line pairs and
density calculations are listed in Table 2. Here
![]() represents the formation temperature of the ion. We
attempted to measure the electron density in all temperature
regimes, but accurate measurements could only be carried out for the
lower-temperature region; the available coronal lines allow us to
derive only broad estimates. We assume a 15% uncertainty in the
determination of the line intensities. This error finally propagates
into the uncertainties for the densities listed in
Table 2.
represents the formation temperature of the ion. We
attempted to measure the electron density in all temperature
regimes, but accurate measurements could only be carried out for the
lower-temperature region; the available coronal lines allow us to
derive only broad estimates. We assume a 15% uncertainty in the
determination of the line intensities. This error finally propagates
into the uncertainties for the densities listed in
Table 2.
The most accurate measurements are obtained in the transition region from [ O iv] and [ O v]. The O IV 1401.16 Å line is blended by the chromospheric line S I 1401.51 Å, and the O IV 1407.39 Å line is blended with two second order O III lines (703.845 Å, 703.85 Å). However, both of these blends can be resolved by a two-component Gaussian fitting, and thus we are able to obtain reliable intensities of the O IV 1407.39 Å and O IV 1401.16 Å lines.
The electron densities derived by using O V line pairs show a
general consistency. In the plage and penumbra regions, the value of
![]() is around 11, which is one order of
magnitude larger than in the umbra and plume regions. The derived
density in the sunspot plume here is consistent with those derived
by Doyle et al. (1985) and Doyle & Madjarska (2003). In Doyle et al. (1985), the
authors used the ratio of O V 760 Å/630 Å obtained by
the S-055 EUV spectrometer onboard Skylab and derived a
density of
is around 11, which is one order of
magnitude larger than in the umbra and plume regions. The derived
density in the sunspot plume here is consistent with those derived
by Doyle et al. (1985) and Doyle & Madjarska (2003). In Doyle et al. (1985), the
authors used the ratio of O V 760 Å/630 Å obtained by
the S-055 EUV spectrometer onboard Skylab and derived a
density of
![]() .
Doyle & Madjarska (2003)
measured the density of the sunspot plumes observed by SUMER on
March 18, 1999. By using the same O V line pairs as we did,
they obtained a density of
.
Doyle & Madjarska (2003)
measured the density of the sunspot plumes observed by SUMER on
March 18, 1999. By using the same O V line pairs as we did,
they obtained a density of
![]() .
The
O V 759.43 line is suggested to be blended by
S IV 759.34 (Curdt et al. 2001). However, the measurement of
Doyle & Madjarska (2003) indicates that this blend should not be significant.
Our result confirms this finding.
.
The
O V 759.43 line is suggested to be blended by
S IV 759.34 (Curdt et al. 2001). However, the measurement of
Doyle & Madjarska (2003) indicates that this blend should not be significant.
Our result confirms this finding.
The average umbra and plume densities derived by using the
O IV line pairs seem to be higher than in the O V
results. However, the differences are within the uncertainties. We
found that the intensity of the plume part seen in O IV is
not as strong as that seen in O V, which indicates that the
strongest part of the plume emission might not have been caught by
the slit, or that the plume was less prominent at the observation
time of the O IV line pairs. By using the ratio of
O IV 625 Å/790 Å from the S-055 sunspot plume
spectrum, Doyle et al. (1985) derived a density of
![]() ,
which is very close to our
plume density at the same temperature. However, by using the line
pair of O IV 625.8 Å/554.5 Å measured by CDS,
Brosius & Landi (2005) derived relatively low values
(
,
which is very close to our
plume density at the same temperature. However, by using the line
pair of O IV 625.8 Å/554.5 Å measured by CDS,
Brosius & Landi (2005) derived relatively low values
(
![]() )
of plume density.
However, the line of O IV 625.8 Å was rather weak and
blended with Mg X 624.9 Å in the red wing, so the derived
densities were highly uncertain.
)
of plume density.
However, the line of O IV 625.8 Å was rather weak and
blended with Mg X 624.9 Å in the red wing, so the derived
densities were highly uncertain.
The [ C iii] and [ Si iii] measurements only provide lower
limits to the electron density. The [ C iii] values agree with
the TR values from the oxygen ions, while [ Si iii] infers a
higher density than the oxygen ions in the umbra and plume. This
might suggest the presence of a significant density gradient in the
umbra and in the plume from the chromosphere to the lower TR, which
would indicate a decrease in the plasma pressure, if we calculate
the pressure to be
![]() .
However, possible
strong temperature gradients on one side, and opacity effects in the
[ C iii] and [ Si iii] on the other, cast huge uncertainties
on the presence of a density and pressure gradient in the umbra and
the plume.
.
However, possible
strong temperature gradients on one side, and opacity effects in the
[ C iii] and [ Si iii] on the other, cast huge uncertainties
on the presence of a density and pressure gradient in the umbra and
the plume.
In the corona, [ Mg viii] and [ Fe xii] provide only very rough estimates of or upper limits to the electron densities, which are consistent with almost any value measured in the corona in quiescent conditions. In this case, our SUMER dataset is unable to provide significant constraints.
The umbra and plume densities derived here are similar to, or
slightly larger than, the density of the normal quiet Sun, which has
an upper limit of
![]() at
at
![]() in Griffiths et al. (1999). A similar result
is also obtained by Brosius & Landi (2005), in which the densities
of plumes and quiet Sun areas are estimated to be around
in Griffiths et al. (1999). A similar result
is also obtained by Brosius & Landi (2005), in which the densities
of plumes and quiet Sun areas are estimated to be around
![]() and
and
![]() ,
respectively, by using the same
line pair of O IV 625.8 Å/554.5 Å as observed by the
CDS instrument.
,
respectively, by using the same
line pair of O IV 625.8 Å/554.5 Å as observed by the
CDS instrument.
By analyzing the EUV data obtained by the Harvard spectrometer on the Apollo telescope mount, Foukal et al. (1974) measured a significant decrease in the gas density of the umbra relative to the surrounding plage. Here we confirm this result by finding that the densities of the umbra and plume at TR temperatures are about a factor of 10 lower than of the plage. Our measurements seem to indicate that the sunspot plasma emitting at TR temperatures is higher and probably more extended than in the surrounding plage region. Since the density of the solar atmosphere decreases almost exponentially with height above the photosphere, this scenario naturally leads to a much lower density in the TR above sunspots, as compared to the TR above the surrounding plage. This scenario also implies that the sunspot TR temperature is much lower than the surrounding temperature at the same heights. Our scenario predicts a temperature structure of sunspots as that proposed by Nicolas et al. (1982). Our conclusion is also consistent with that of Guo et al. (2009), in which the authors suggested that stronger magnetic fields correspond to higher formation heights of VUV lines.
We note that this TR scenario is similar to that for a coronal hole,
since the TR in the coronal hole is also found to be higher and more
extended than the TR in the quiet Sun
(Tian et al. 2008b; Tu et al. 2005b,a; Tian et al. 2008a). The average Ly![]() and Ly-3
profiles in the coronal hole atlas are not reversed, a phenomenon
similar to the sunspot, whilst they are obviously reversed in the
quiet Sun (Curdt et al. 2001). Moreover, solar wind flows out along
magnetic funnels in coronal holes (Tu et al. 2005a; Esser et al. 2005), and the
signature of upflows associated with open field lines was also found
in sunspots (Marsch et al. 2004). These results infer a similarity
between the properties of the TR above sunspots/plages and the TR in
CH/QS (coronal hole and quiet Sun).
and Ly-3
profiles in the coronal hole atlas are not reversed, a phenomenon
similar to the sunspot, whilst they are obviously reversed in the
quiet Sun (Curdt et al. 2001). Moreover, solar wind flows out along
magnetic funnels in coronal holes (Tu et al. 2005a; Esser et al. 2005), and the
signature of upflows associated with open field lines was also found
in sunspots (Marsch et al. 2004). These results infer a similarity
between the properties of the TR above sunspots/plages and the TR in
CH/QS (coronal hole and quiet Sun).
It was suggested that the downflow of TR plasma is essential to the
existence of plumes (Foukal 1976; Brynildsen et al. 2001). However, it
remains debated whether this is achieved by siphon flows along far
reaching loops (Doyle & Madjarska 2003; Brosius 2005; Brynildsen et al. 2001) or by
cooling and condensing coronal plasma falling downward along the
``cold surface'' of the plume
(Dammasch et al. 2008; Noyes et al. 1985; Brosius & Landi 2005). A siphon flow is possibly
driven by a strong asymmetric heating and the resulting pressure
difference in two loop legs (McClymont & Craig 1987; Spadaro et al. 1991; Mariska 1988). This type of
flow may cause a blue shift in one leg and red shift in the other.
Brynildsen et al. (2001) concluded that the inflow of plasma at TR
temperatures from locations well outside the sunspots is a necessary
requirement for the sunspot plume to occur. This hypothesis seems to
be supported by the observational result of Brosius (2005), in
which a significantly higher density
(
![]() ,
compared to
,
compared to
![]() in the plume, in an upflow
region outside the sunspot was observed by CDS. Doyle & Madjarska (2003) also
measured higher densities (with
in the plume, in an upflow
region outside the sunspot was observed by CDS. Doyle & Madjarska (2003) also
measured higher densities (with
![]() ranging from 10.20 to 10.45) in nearby quiet regions (their QS1might be a plage region) than in the plume
(
ranging from 10.20 to 10.45) in nearby quiet regions (their QS1might be a plage region) than in the plume
(
![]() ), and suggested that the gas
pressure difference might be sufficient to drive siphon flows from
outside the spot into the umbra. Our measured densities in different
regions also seem to support this idea. It is generally believed
that sunspot plumes are associated with loops in which one leg is
anchored in the umbra and the other anchored outside the sunspot,
probably in the plage region. Our measurement shows that the
densities at TR temperatures are one order of magnitude lower in the
umbra and plume than in the plage. This pressure difference is
certainly sufficient to initiate a siphon flow in the loop.
), and suggested that the gas
pressure difference might be sufficient to drive siphon flows from
outside the spot into the umbra. Our measured densities in different
regions also seem to support this idea. It is generally believed
that sunspot plumes are associated with loops in which one leg is
anchored in the umbra and the other anchored outside the sunspot,
probably in the plage region. Our measurement shows that the
densities at TR temperatures are one order of magnitude lower in the
umbra and plume than in the plage. This pressure difference is
certainly sufficient to initiate a siphon flow in the loop.
5 Differential emission measure
5.1 Method
The plasma in the upper solar atmosphere can usually be assumed to be optically thin, although this assumption does not hold for the coldest ions observed in the SUMER spectra, such as neutrals and singly ionized species. In the optically thin case, the radiance of
a line can be written as
where
![\begin{figure}
\par\mbox{\includegraphics[angle=90,width=8.5cm]{12114f41.eps}\in...
...2114f43.eps}\includegraphics[angle=90,width=8.5cm]{12114f44.eps} }\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg72.png) |
Figure 4: DEM curves for the four regions. Top left: umbra; top right: penumbra; bottom left: plage; Bottom right: plume. |
| Open with DEXTER | |
The contribution function includes all the atomic physics involved in the process of line formation, and can be computed as a function of temperature and density using spectral codes that include all the atomic parameters necessary to calculate the contribution function. In the present work we will use version 5.2.1 of the CHIANTI database (Dere et al. 1997; Landi et al. 2006), the ion fraction dataset of Mazzotta et al. (1998), and the photospheric abundances of Grevesse & Sauval (1998).
The
![]() term beneath the sign of the integral on the
right-hand side of Eq. (1) includes plasma
conditions involved in the process of line formation. It is an
important quantity when studying the thermal structure of the solar
corona and comparing predictions from theoretical models with
observations. When the plasma is multi-thermal and there is a
continuous relationship between the amount of plasma and
temperature, then Eq. (1) can be rewritten by
defining the Differential Emission Measure (DEM) function
term beneath the sign of the integral on the
right-hand side of Eq. (1) includes plasma
conditions involved in the process of line formation. It is an
important quantity when studying the thermal structure of the solar
corona and comparing predictions from theoretical models with
observations. When the plasma is multi-thermal and there is a
continuous relationship between the amount of plasma and
temperature, then Eq. (1) can be rewritten by
defining the Differential Emission Measure (DEM) function
![]() as
as
where the DEM indicates the amount of material in the plasma as a function of temperature. Several methods have been developed to determine
A new
| (5) |
and then interpolating the results over temperatures to provide a continuous function. The resulting
5.2 DEM curves
We adopted an electron density of
![]() for the umbra and the plume,
and
for the umbra and the plume,
and
![]() for the penumbra and plage,
to calculate the contribution functions to be used for DEM
diagnostics. The DEM curves determined using the spectral lines
listed in Table 5 are shown in Fig. 4. To obtain those
curves, it was necessary to complete an additional selection of the
spectral lines to be used, as well as to modify the adopted element
abundances.
for the penumbra and plage,
to calculate the contribution functions to be used for DEM
diagnostics. The DEM curves determined using the spectral lines
listed in Table 5 are shown in Fig. 4. To obtain those
curves, it was necessary to complete an additional selection of the
spectral lines to be used, as well as to modify the adopted element
abundances.
When we applied the DEM diagnostic technique to all the listed
lines at once, very large disagreements were found between lines of
the same ion, and between lines of different ions with similar
![]() .
These disagreements occurred in all four regions, and
made it impossible to calculate a DEM curve for each region because:
1) the correction curves
.
These disagreements occurred in all four regions, and
made it impossible to calculate a DEM curve for each region because:
1) the correction curves
![]() never converged
to unity and showed an oscillatory behavior; and 2) even when they
were close to unity, the disagreements between different ions and
between lines of the same ion were so large that the resulting DEM
curve was meaningless.
never converged
to unity and showed an oscillatory behavior; and 2) even when they
were close to unity, the disagreements between different ions and
between lines of the same ion were so large that the resulting DEM
curve was meaningless.
The causes of these problems are probably numerous: atomic physics problems in the level population calculation within each ion; inaccurate ion abundances; opacity effects (for the coldest lines in the dataset); non-photospheric element abundances; or temporal variability. Opacity effects can be ruled out for all the listed lines, except for the strongest lines belonging to the ions formed at lowest temperatures. The intensities of all other cold lines are too weak to provide significant self-absorption. Moreover, Brooks et al. (2000) ruled out opacity effects for many of the coldest ions, although they showed that there may be significant opacity effects for [ C ii] and [ C iii]. Atomic physics problems can be ruled out as the discrepancies between lines of the same ions are much larger than any effect of inaccurate collisional or radiative excitation rates. The same can be said for ion abundances, unless non-equilibrium conditions are present in the emitting plasma. The most likely cause of the problems that we encountered is the temporal variability of the plasma. Any temporal changes in the physical properties of the plasma directly affect our DEM results because the SUMER data were taken over several hours, and the transition region plasma is known to be changing even within a few minutes.
To minimize the effects of temporal variability, we restricted our analysis to lines that were emitted within about 20 min. Since SUMER scans its wavelength range by shifting the reference wavelength by fixed amounts from one exposure to the next, the selected time frame in our observations corresponds to 120 Å. The optimal spectral range including the highest number of lines and ions in the widest temperature range within 120 Å for detector B is the shortest wavelength range of 670-790 Å. To further sample the corona, we also included the two [ Fe xii] lines 1241.95 Å and 1349.43 Å, even though they are far apart from the selected interval. This choice makes some sense since coronal lines might experience less temporal variation than the TR ones, so they might still be representative of the corona.
We have applied the DEM diagnostic technique to the lines observed
between 670 Å and 790 Å in first order, and this time the
solutions converged to the curves displayed in Fig. 4.
However, there was one last correction necessary to determine the
final DEM curves: the abundances of the low-FIP elements (those with
a First Ionization Potential lower than 10 eV) needed to be
increased by a factor of 10. This huge factor is 2.5 times higher
than the the factor required by the normal FIP effect. This
correction only affects the corona, since below
![]() all the ions belong to high-FIP elements; in
contrast, all coronal ions except [ Ne viii] belong to low-FIP
elements. This correction was required to ensure agreement between
results derived for the [ Mg viii] and [ Ne viii] lines, whose
temperatures of formation are very similar. It is important to note
that [ Ne viii] belongs to the lithium isoelectronic sequence.
This sequence has been found to overestimate theoretical
emissivities relative to those of the other elements, leading to EM
and DEM measurements lower by a factor
all the ions belong to high-FIP elements; in
contrast, all coronal ions except [ Ne viii] belong to low-FIP
elements. This correction was required to ensure agreement between
results derived for the [ Mg viii] and [ Ne viii] lines, whose
temperatures of formation are very similar. It is important to note
that [ Ne viii] belongs to the lithium isoelectronic sequence.
This sequence has been found to overestimate theoretical
emissivities relative to those of the other elements, leading to EM
and DEM measurements lower by a factor ![]() 2 than those of
elements formed at similar temperatures (Landi et al. 2002; Dupree 1972). If
we take this systematic effect into account for [ Ne viii], the
effective increase in the abundance of low-FIP elements is a factor
of 5, much closer to the standard FIP effect commonly measured in
the corona (i.e., Feldman & Laming 2000).
2 than those of
elements formed at similar temperatures (Landi et al. 2002; Dupree 1972). If
we take this systematic effect into account for [ Ne viii], the
effective increase in the abundance of low-FIP elements is a factor
of 5, much closer to the standard FIP effect commonly measured in
the corona (i.e., Feldman & Laming 2000).
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{12114f51.eps}\par\includegraphics[angle=90,width=8cm,clip]{12114f52.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg90.png) |
Figure 5: Comparison of the DEM curves from the four regions. Upper: absolute values; lower: normalized values. |
| Open with DEXTER | |
All the DEM curves that we measured exhibited an enhanced peak at
![]() ,
in the upper transition region. The
only exception is the plume DEM, which peaks at lower temperatures,
,
in the upper transition region. The
only exception is the plume DEM, which peaks at lower temperatures,
![]() .
The peak of the plume DEM curve exceeds the
DEM of other regions by one to two orders of magnitude at these
temperatures. All the curves are able to reproduce the observed
lines, but some scatter is still present among the measurements
provided by each line. It is difficult to say whether the DEM curves
have a coronal component beyond
.
The peak of the plume DEM curve exceeds the
DEM of other regions by one to two orders of magnitude at these
temperatures. All the curves are able to reproduce the observed
lines, but some scatter is still present among the measurements
provided by each line. It is difficult to say whether the DEM curves
have a coronal component beyond
![]() ,
because the
restricted dataset of lines we used does not include real coronal
lines formed at temperatures higher than one million degrees. The
only exceptions are the two [ Fe xii] lines, but their
contribution function has a low temperature tail that is strongly
influenced by the colder plasma. Its emission measure is so large,
that the
,
because the
restricted dataset of lines we used does not include real coronal
lines formed at temperatures higher than one million degrees. The
only exceptions are the two [ Fe xii] lines, but their
contribution function has a low temperature tail that is strongly
influenced by the colder plasma. Its emission measure is so large,
that the
![]() of the [ Fe xii] lines is lower than
the temperature of maximum abundance for [ Fe xii]. The curves
that we determined are compared with each other in Fig. 5.
In absolute units (upper panel of Fig. 5), the curves are
rather similar, the only exception being the plume curve, whose peak
is at lower temperatures. When normalized to their value at
of the [ Fe xii] lines is lower than
the temperature of maximum abundance for [ Fe xii]. The curves
that we determined are compared with each other in Fig. 5.
In absolute units (upper panel of Fig. 5), the curves are
rather similar, the only exception being the plume curve, whose peak
is at lower temperatures. When normalized to their value at
![]() ,
the slope of all four curves is approximately
the same up to
,
the slope of all four curves is approximately
the same up to
![]() .
This behavior was noted by
Feldman et al. (2009). If we approximate the DEM curves below
.
This behavior was noted by
Feldman et al. (2009). If we approximate the DEM curves below
![]() as
as
| (6) |
the slope a of the DEM is similar to the values found by Feldman et al. (2009) in coronal hole, quiet Sun, and active region spectra. We note that in Brosius & Landi (2005) the DEM at lower temperatures (less than
The plume DEM curve that we measured and the one determined by
Brosius & Landi (2005) are compared in Fig. 6.
Brosius & Landi (2005) measured the DEM of a plume in two different
days, and found similar results: their DEM curves were broad and
stretched in the entire
![]() temperature range. They also measured the DEM of the quiet Sun in
both days, and those curves, with a very narrow peak in the
temperature range. They also measured the DEM of the quiet Sun in
both days, and those curves, with a very narrow peak in the
![]() range, are also shown in Fig. 6
for comparison. The plume DEM we measured (solid line in
Fig. 6) has a much narrower peak at slightly lower
temperatures. One reason for these differences can of course be an
intrinsic variability in the sunspot plume thermal structure.
Unfortunately, to the best of our knowledge no other DEM
measurements of plumes have been made, so this conclusion needs to
be confirmed. Another cause of discrepancy might be that
Brosius & Landi (2005) used CDS spectra to determine the curves in
Fig. 6. In these spectra, many more lines formed at
range, are also shown in Fig. 6
for comparison. The plume DEM we measured (solid line in
Fig. 6) has a much narrower peak at slightly lower
temperatures. One reason for these differences can of course be an
intrinsic variability in the sunspot plume thermal structure.
Unfortunately, to the best of our knowledge no other DEM
measurements of plumes have been made, so this conclusion needs to
be confirmed. Another cause of discrepancy might be that
Brosius & Landi (2005) used CDS spectra to determine the curves in
Fig. 6. In these spectra, many more lines formed at
![]() were present, so that the coronal component
of the DEM was better constrained than in the present work. The
presence of a larger coronal component than in our plume curve might
alter the shape of the DEM at temperatures higher than
were present, so that the coronal component
of the DEM was better constrained than in the present work. The
presence of a larger coronal component than in our plume curve might
alter the shape of the DEM at temperatures higher than
![]() .
In general, we can say that the main signature
of sunspot plumes is a greatly enhanced DEM at transition region
temperatures, while at
.
In general, we can say that the main signature
of sunspot plumes is a greatly enhanced DEM at transition region
temperatures, while at
![]() the slope of the DEM
curve is similar to that of any other region in the Sun, indicating
that the thermal structures across this temperature range are fairly
similar.
the slope of the DEM
curve is similar to that of any other region in the Sun, indicating
that the thermal structures across this temperature range are fairly
similar.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{12114f6.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg102.png) |
Figure 6: Comparison of the plume DEM curve with the results of Brosius & Landi (2005). |
| Open with DEXTER | |
We have to mention that the density and DEM calculations are based on the assumption of ionization equilibrium. In the TR with the strong temperature gradient and presence of significant flows, this assumption is not necessarily valid (Wilhelm et al. 2004). This, as well as the inhomogeneity and variability of the TR plasma, might be important to the determination of electron densities and DEM. However, recent investigations using 3-D model indicated that the assumption of ionization equilibrium might not be too bad in the coronal and TR plasma (Peter et al. 2006,2004). The calculations in Peter et al. (2006) showed that the ionization and recombination times are at least not (much) longer and often shorter than the typical hydrodynamic timescales. Peter et al. (2006) also found that flows with typical values of 10 km s-1 lead to a more shallow temperature gradient and thus help to maintain an ionization equilibrium. Thus, the approximation of ionization equilibrium in our study should not be too bad.
6 Filling factor
Although it is well known that the emission of sunspot plumes is greatly enhanced at TR temperatures, the reason for the enhanced intensity remains unknown.
Our measurement reveals a higher intensity in the plume than in the sunspot umbra, penumbra, and the surrounding plage region. The enhanced intensity cannot result from a higher density, since the derived TR densities of the plume are similar to those of the umbra and even much lower than those of the penumbra and plume. It might therefore be an effect of filling factor or temperature, or both.
By using temperature-sensitive line pairs, Doyle et al. (1985) derived the electron temperatures in sunspot plumes. They concluded that the ions are shifted to lower temperatures in the sunspot plume. In our reference spectra, we have no suitable temperature-sensitive line pairs that were observed simultaneously. Thus, this conclusion cannot be examined. However, our DEM analysis clearly reveals that the emitting material of the sunspot plume is concentrated at lower temperatures (higher peak at low T), which is indicative of a lower plume temperature, compared to that of the surrounding plasma.
With the measurements of line intensities and electron densities, we
are able to calculate the filling factor. As mentioned in
Dere (2008), the observed intensity of a spectral line emitted by
a coronal loop is
where G(T),
![]() ,
,
![]() ,
and
,
and ![]() represent the contribution function, electron density, hydrogen
density, and the differential of the integration, respectively.
Based on the assumption of an isothermal emission feature, we can
evaluate the contribution function at its peak temperature
represent the contribution function, electron density, hydrogen
density, and the differential of the integration, respectively.
Based on the assumption of an isothermal emission feature, we can
evaluate the contribution function at its peak temperature
![]() .
The ratio of the hydrogen density relative to the
electron density is about 0.8 in a completely ionized plasma of
cosmic composition (Landi & Landini 1997). Usually a loop is not completely
filled with emitting plasma, thus a volumetric filling factor should
be introduced to account for this. Taking into account these
considerations, Eq. (7) can be rewritten as
.
The ratio of the hydrogen density relative to the
electron density is about 0.8 in a completely ionized plasma of
cosmic composition (Landi & Landini 1997). Usually a loop is not completely
filled with emitting plasma, thus a volumetric filling factor should
be introduced to account for this. Taking into account these
considerations, Eq. (7) can be rewritten as
where f is the filling factor and L is the length of the integration path.
We used four O V lines to determine the filling factor of the
sunspot plume. The O V 774.51 Å line is density
independent, and the other three lines have been used to measure the
electron densities. Table 3 lists the calculation details
from Eq. (8). Here the intensity refers to that
averaged over the plume part along the slit and was converted into
energy units by using the procedure of radiometry.pro in
SSW (SolarSoft). The contribution function at its peak
temperature
![]() is density dependent and was calculated
at the corresponding density from the CHIANTI database. The factor
is density dependent and was calculated
at the corresponding density from the CHIANTI database. The factor
![]() is included in the
is included in the
![]() calculation.
calculation.
It is difficult to estimate L. However, we may be able to provide
an upper and a lower limit to this parameter. In the case of
ionization equilibrium, the major part of the O V emission
comes from plasmas in the range of
![]() .
By using a new model of quiet-Sun chromosphere and transition
region, Avrett and Loeser (2008) determined the distribution of temperature
with height. Using their results, the span of the plasma in the
range of
.
By using a new model of quiet-Sun chromosphere and transition
region, Avrett and Loeser (2008) determined the distribution of temperature
with height. Using their results, the span of the plasma in the
range of
![]() is around 500 km. We
assumed this value to be the lower limit to L. Since plumes might
be related to the high-arching loops observed in ARs (active
regions), we may use the extension of the O V emission in
cross-limb AR loop observations as the upper limit to L. An
example of this type of observation can be found in
Brekke et al. (1997), where the AR loop width is about
10
is around 500 km. We
assumed this value to be the lower limit to L. Since plumes might
be related to the high-arching loops observed in ARs (active
regions), we may use the extension of the O V emission in
cross-limb AR loop observations as the upper limit to L. An
example of this type of observation can be found in
Brekke et al. (1997), where the AR loop width is about
10
![]() .
Thus, we adopted a value of 7 Mm as the upper
limit.
.
Thus, we adopted a value of 7 Mm as the upper
limit.
Table 3: The details of the filling factor calculations, for the O V emission of the sunspot plume observed in 2006.
The derived filling factors turn out to be relatively large, which
might explain the very strong TR emission of sunspot plumes. To
compare the filling factor of the plume with those of other
features, we can assume that the integration paths in various
regions are the same, although this assumption might not be
realistic due to a possible difference in their thermal and magnetic
structures. Again we obtained the average intensities of the four
regions, and calculated
![]() at corresponding densities
by using the CHIANTI database. The ratios of the filling factors in
the four regions are listed in Table 4.
at corresponding densities
by using the CHIANTI database. The ratios of the filling factors in
the four regions are listed in Table 4.
Table 4: The ratios of the filling factors in the four regions, for the O V emission in the 2006 data set.
The results show that the filling factor of the sunspot plume at TR temperatures is between one and three orders of magnitude higher than for the surrounding regions. The difference is so large that it seems safe to conclude that the strong TR emission of sunspot plumes is mainly the result of a large filling factor. However, we should not exclude the possibility that other effects, e.g., the region emitting TR lines being much thicker in sunspot plumes, might also play a role in producing the strong emission.
7 Peculiar lines in the sunspot
As mentioned in our earlier paper (Curdt et al. 2000), more than 100
``peculiar'' lines including several H2 lines are present in the
sunspot reference spectra obtained on March 18, 1999. These lines
are also found in the sunspot atlas presented by Curdt et al. (2001).
Most of these lines are upper-TR lines with a temperature range of
![]() 6.0, corresponding to 4 to 8-fold
ionized species. Here we confirm that these ``peculiar'' lines are
also present in all of the 5 analyzed data sets. These lines are
weak or not observed in either the quiet Sun and or corona. Some of
them may be present in streamer spectra.
6.0, corresponding to 4 to 8-fold
ionized species. Here we confirm that these ``peculiar'' lines are
also present in all of the 5 analyzed data sets. These lines are
weak or not observed in either the quiet Sun and or corona. Some of
them may be present in streamer spectra.
Many of these ``peculiar'' lines correspond to forbidden transitions. Thus, we may speculate that an extremely low density might be responsible for their formation. However, as we mentioned previously, the umbra and plume densities derived here are similar to, or slightly higher than the density of the normal quiet Sun. This means that the sunspot plasma density is not extremely low and the above explanation is questionable.
Through a visual inspection of the spectra analyzed here and several other sunspot reference spectra, we found that the ``peculiar'' lines seem more likely to be associated with plumes, rather than the umbrae. One possible reason why these lines are present in the umbra (Curdt et al. 2001) is that part of the sunspot plumes are just located above the umbra and the sample of the sunspot emission might be a mixture of the plume and umbra emissions. Since the plume emission is much stronger than the umbra emission at TR temperatures, the average sunspot spectrum in Curdt et al. (2001) is dominated by the plume spectrum.
The reason why these ``peculiar'' lines are so distinctive in the sunspot plume is probably a combination of two effects. First, the plume emission is strongest at upper-TR temperatures. Second, the continuum emission of the plume is much weaker than that of the plage.
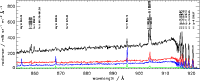 |
Figure 7: Part of the spectra observed in the plage, penumbra, umbra and plume for the 2006 data set. The black, red, green and blue lines correspond to the plage, penumbra, umbra and plume spectra. |
| Open with DEXTER | |
We list these ``peculiar'' lines in Table 6. As an example, in Fig. 7 we show part of the spectra observed in the plage, penumbra, umbra, and plume for the 2006 data set. We see that several forbidden lines (e.g., Mg VII 854.75 Å, Mg VII 868.24 Å, Ne VII 895.19 Å) become very prominent in the plume spectrum. Here, we also see in the umbra spectrum the enhanced forbidden lines, which are not so enhanced as in the plume and might be due to contamination from the plume emission at the formation temperatures of these lines. However, the strongly reduced continuum emission of the umbra may also cause the forbidden lines to be distinctive.
The H2 emission is extremely weak in the quiet Sun (Sandlin et al. 1986). It was also observed in flares (Bartoe et al. 1979) and microflares in the active region plage (Innes 2008). In sunspot regions, the H2 emission is distinctive and relatively strong (Jordan et al. 1978; Curdt et al. 2001; Schühle et al. 1999). Several lines of the H2 Werner bands are within the SUMER spectral range. These lines are believed to be excited by resonance fluorescence through the strong O VI 1031.9 Å line. In our data, the emission of these lines is clearly detected in the umbra and plume regions, which might be related to the reduced opacity above the sunspot. The O VI 1031.9 Å emission is able to reach the chromosphere and excite the H2 lines if the opacity is low.
8 Summary
By analyzing sunspot reference spectra taken by the SUMER instrument, we have shown that the TR above sunspots has some distinctive properties compared to the surrounding plage regions.
We have found that the hydrogen Lyman line profiles are not reversed
in sunspots at different locations (heliocentric angle up to
![]() )
on the solar disk. The Lyman lines are also not reversed
in sunspot plumes. In the plage region, the lower Lyman line
profiles are obviously reversed, a phenomenon also found in the
normal quiet Sun. Line-pair diagnostics yields an electron density
of
)
on the solar disk. The Lyman lines are also not reversed
in sunspot plumes. In the plage region, the lower Lyman line
profiles are obviously reversed, a phenomenon also found in the
normal quiet Sun. Line-pair diagnostics yields an electron density
of
![]() for the umbra and the
plume, and
for the umbra and the
plume, and ![]() 11.0 for the penumbra and plage, at TR
temperatures. To explain these results, we suggest that the TR above
sunspots is higher and probably more extended, and the opacity above
sunspots is much lower than in the TR above plage regions.
11.0 for the penumbra and plage, at TR
temperatures. To explain these results, we suggest that the TR above
sunspots is higher and probably more extended, and the opacity above
sunspots is much lower than in the TR above plage regions.
We also completed a DEM analysis for the sunspot observed in 2006.
To the best of our knowledge, this is the first time that SUMER
spectra have been used for the DEM diagnostics of a sunspot. The DEM
curve of the plume is obviously different from those of other
regions. It peaks at a lower temperature of around
![]() ,
which exceeds the DEM of other regions by one
to two orders of magnitude at these temperatures. At
,
which exceeds the DEM of other regions by one
to two orders of magnitude at these temperatures. At
![]() ,
the slope of the DEM curve is similar in the four regions,
indicating that the thermal structure in this temperature range is
fairly similar everywhere in and around the sunspots.
,
the slope of the DEM curve is similar in the four regions,
indicating that the thermal structure in this temperature range is
fairly similar everywhere in and around the sunspots.
The reason why the plume emission is so strong at upper-TR temperatures has been investigated for the first time. Our calculations seem to indicate that the enhanced TR emission of the sunspot plume is very likely to be the result of a large filling factor.
More than 100 lines that are rather weak or not observed anywhere else on the Sun, are well observed by SUMER in the sunspot, especially in the sunspot plume. We propose that it is the combination of strongly enhanced emission at TR temperatures and reduced continuum cause these normally weak lines to be clearly distinctive in the spectra of sunspot plumes.
Acknowledgements
The SUMER project is financially supported by DLR, CNES, NASA, and the ESA PRODEX Programme (Swiss contribution). SUMER is an instrument onboard SOHO, a mission operated by ESA and NASA. We thank Dr. D. E. Innes and Dr. H. Peter for the helpful comments.Hui Tian is supported by the IMPRS graduate school run jointly by the Max Planck Society and the Universities of Göttingen and Braunschweig. The work of Hui Tian's group at PKU is supported by the National Natural Science Foundation of China (NSFC) under contract 40874090. Enrico Landi acknowledges support from the NNG06EA14I, NNH06CD24C NASA grants.
References
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [NASA ADS] [CrossRef] (In the text)
- Bartoe, J.-D. F., Brueckner, G. E., Purcell, J. D., et al. 1977, Appl. Opt., 16, 879 [NASA ADS] (In the text)
- Bartoe, J.-D. F., Brueckner, G. E., Nicolas, K. R., et al. 1979, MNRAS, 187, 463 [NASA ADS] (In the text)
- Brekke, P., Kjeldseth-Moe, O., & Harrison, R. A. 1997, Sol. Phys., 175, 511 [NASA ADS] [CrossRef] (In the text)
- Brooks, D. H., Fischbacher, G. A., Fludra, A., et al. 2000, A&A, 357, 697 [NASA ADS] (In the text)
- Brosius, J. W. 2005, ApJ, 622, 1216 [NASA ADS] [CrossRef]
- Brosius, J. W., & Landi, E. 2005, ApJ, 632, 1196 [NASA ADS] [CrossRef]
- Brynildsen, N., Maltby, P., Brekke, P., Haugan, S. V. H., & Kjeldseth-Moe, O. 1999a, Sol. Phys., 186, 141 [NASA ADS] [CrossRef]
- Brynildsen, N., Maltby, P., Leifsen, T., Kjeldseth-Moe, O., & Wilhelm, K. 1999b, Sol. Phys., 191, 129 [NASA ADS] [CrossRef]
- Brynildsen, N., Maltby, P., Fredvik, T., et al. 2001, Sol. Phys., 198, 89 [NASA ADS] [CrossRef]
- Brueckner, G. E., & Bartoe, J.-D. F. 1983, ApJ, 272, 329 [NASA ADS] [CrossRef]
- Brueckner, G. E., Bartoe, J.-D. F., & VanHoosier, M. E. 1977, in Proc. OSO-8 Workshop, ed. E. Hansen, & S. Schaffner (Boulder: Univ. Colorado Press), 380
- Brueckner, G. E., Bartoe, J.-D. F., Cook, J. W., Dere, K. P., & Socker, D. G. 1986, Adv. Space Res., 6, 263 [NASA ADS] [CrossRef]
- Curdt, W., Dwivedi, B. N, & Feldman, U. 2000, A&A, 21, 397 (In the text)
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A 375, 591
- Curdt, W., Landi, E., & Feldman, U. 2004, A&A, 427, 1045 [NASA ADS] [CrossRef] [EDP Sciences]
- Curdt, W., Tian, H., Teriaca, L., Schühle, U., & Lemaire, P. 2008, A&A, 492, L9 [NASA ADS] [CrossRef] [EDP Sciences]
- Dammasch, I. E., Curdt, W., Dwivedi, B. N., et al. 2008, Ann. Geophys., 26, 2955 [NASA ADS] (In the text)
- Dere, K. P. 2008, A&A, 491, 561 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dere, K. P., Landi, E., Mason, H. E., et al. 1997, A&ASS, 125, 149 [NASA ADS] [CrossRef]
- Dowdy, J. F., Jr., Rabin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35 [NASA ADS] [CrossRef] (In the text)
- Doyle, J. G., & Madjarska, M. S. 2003, A&A, 407, L29 [NASA ADS] [CrossRef] [EDP Sciences]
- Doyle, J. G., Raymond, J. C., Noyes, R. W., et al. 1985, ApJ, 297, 816 [NASA ADS] [CrossRef]
- Dupree, A. K. 1972, ApJ, 178, 527 [NASA ADS] [CrossRef]
- Ekberg, J. O., & Feldman, U. 2003, ApJS, 148, 567 [NASA ADS] [CrossRef] (In the text)
- Esser, R., Lie-Svendsen, Ø, Janse, Å. M., et al. 2005, ApJ, 629, L61 [NASA ADS] [CrossRef]
- Fang, C., Feautrier, N., & Hénoux, J.-C. 1995, A&A, 297, 854 [NASA ADS] (In the text)
- Feldman, U. 1983, ApJ, 275, 367 [NASA ADS] [CrossRef]
- Feldman, U. 1987, ApJ, 320, 426 [NASA ADS] [CrossRef]
- Feldman, U., & Laming, J. M. 2000, Phys. Scr., 61, 222 [NASA ADS] [CrossRef] (In the text)
- Feldman, U., Behring, W. E., Curdt, W., et al. 1997, ApJS, 113, 195 [NASA ADS] [CrossRef]
- Feldman, U., Dammasch, I. E., & Landi, E. 2009, ApJ, 693, 1474 [NASA ADS] [CrossRef] (In the text)
- Fontenla, J. M., Reichmann, E. J., & Tandberg-Hanssen, E. 1988, ApJ, 329, 464 [NASA ADS] [CrossRef] (In the text)
- Foukal, P. V. 1976, ApJ, 210, 575 [NASA ADS] [CrossRef] (In the text)
- Foukal, P. V., Huber, M. C. E., Noyes, R. W., et al. 1974, ApJ, 193, L143 [NASA ADS] [CrossRef] (In the text)
- Gabriel, A. H. 1976, Philos. Trans. R. Soc. London A, 281, 575 (In the text)
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Griffiths, N. W., Fisher, G. H., Woods, D. T., et al. 1999, ApJ, 512,992 (In the text)
- Gunár, S., Heinzel, P., Anzer, U., et al. 2008, A&A, 490, 307 [NASA ADS] [CrossRef] [EDP Sciences]
- Guo, Y., Ding, M. D., Jin, M., et al. 2009, ApJ, 696, 1526 [NASA ADS] [CrossRef] (In the text)
- Harrison, R. A., & Thompson, A. M. 1992, Intensity integral inversion techniques: a study in preparation for the SOHO mission, RAL-91-092, Rutherford Appleton Laboratory (In the text)
- Harrison, R. A., Sawyer, E. C., Carter, M. K., et al. 1995, Sol. Phys.,1995, 162, 233 (In the text)
- Heinzel, P., Anzer, U., & Gunár, S. 2005, A&A, 442, 331 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Innes, D. E. 2008, A&A, 481, L41 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jordan, C., Brueckner, G. E., Bartoe, J.-D. F., et al. 1978, ApJ, 226, 687 [NASA ADS] [CrossRef] (In the text)
- Kjeldseth-Moe, O., Brynildsen, N., Brekke, P., et al. 1988, ApJ, 334, 1066 [NASA ADS] [CrossRef]
- Landi, E., & Landini, M. 1997, A&A, 327, 1230 [NASA ADS] (In the text)
- Landi, E., Feldman, U., & Dere, K. P. 2002, ApJS, 139, 281 [NASA ADS] [CrossRef]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef]
- Lemaire, P., Wilhelm, K., Curdt, W., et al. 1997, Sol. Phys., 170, 105 [NASA ADS] [CrossRef]
- Mariska, J. T. 1988, ApJ, 334, 489 [NASA ADS] [CrossRef]
- Mariska, J. T. 1992, The Solar Transition Region (Cambridge: Cambridge Univ. Press) (In the text)
- Marsch, E., Tu, C.-Y., Heinzel, P., Wilhelm, K., & Curdt, W. 1999, A&A, 347, 676 [NASA ADS] (In the text)
- Marsch, E., Tu, C.-Y., & Wilhelm, K. 2000, A&A, 359, 381 [NASA ADS] (In the text)
- Marsch, E., Wiegelmann, T., & Xia L.-D. 2004, A&A, 428, 629 [NASA ADS] [CrossRef] [EDP Sciences]
- Marsch, E., Zhou, G.-Q., He, J.-S., et al. 2006, A&A, 457, 699 [NASA ADS] [CrossRef] [EDP Sciences]
- McClymont, A. N., & Craig, I. J. D. 1987, ApJ, 312, 402 [NASA ADS] [CrossRef]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., et al. 1998, A&AS, 133, 197 [CrossRef] [EDP Sciences] (In the text)
- Nicolas, K. R., Kjeldseth-Moe, O., Bartoe, J.-D. F., et al. 1982, Sol. Phys., 81, 253 [NASA ADS] [CrossRef] (In the text)
- Noyes, R. W., Raymond, J. C., Doyle, J. G., et al. 1985, ApJ, 297, 805 [NASA ADS] [CrossRef] (In the text)
- Peter, H. 2001, A&A, 374,1108 (In the text)
- Peter, H., Gudiksen, B., & Nordlund, Å. 2004, ApJ, 617, L85 [NASA ADS] [CrossRef]
- Peter, H., Gudiksen, B., & Nordlund, Å. 2006, ApJ, 638, 1086 [NASA ADS] [CrossRef]
- Phillips, K. J. H., Feldman, U., & Landi, E. 2008, Ultraviolet and X-ray spectroscopy of the solar atmosphere, Cambridge Astrophysics Series 44 (Cambridge University Press) (In the text)
- Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team (2008), NIST Atomic Spectra Database (version 3.1.5). http://physics.nist.gov/asd3. National Institute of Standards and Technology, Gaithersburg, MD
- Sandlin, G. D., Bartoe, J.-D. F., & Brueckner, G. E. 1986, ApJS, 61, 801 [NASA ADS] [CrossRef] (In the text)
- Schmieder, B., Gunár, S., Heinzel, P., et al. 2007, Sol. Phys. 241, 53 (In the text)
- Schühle, U., Brown, C. M., Curdt, W., et al. 1999, in Proc. SOHO 8, ESA SP-446, 617
- Solanki, S. K. 2003, Astron. Astrophys. Rev., 11, 153 [NASA ADS] [CrossRef] (In the text)
- Spadaro, D., Antiochos, S. K., & Mariska, J. T. 1991, ApJ 382, 338
- Tian, H., Marsch, E., Tu, C.-Y., Xia, L.-D., & He, J.-S. 2008a, A&A, 482, 267 [NASA ADS] [CrossRef] [EDP Sciences]
- Tian, H., Xia, L.-D., He, J.-S., Tan, B., & Yao, S. 2008b, Chin. J. Astron. Astrophys., 8, 6 [CrossRef], 732
- Tian, H., Curdt, W., Marsch, E., Schühle, U. 2009, A&A, 504, 239 [NASA ADS] [CrossRef] [EDP Sciences]
- Teriaca, L., Curdt, W., & Solanki, S. K. 2008, A&A, 491, L5 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tu, C.-Y., Zhou, C., Marsch, E., et al. 2005a, Science, 308, 519 [NASA ADS] [CrossRef]
- Tu, C.-Y., Zhou, C., Marsch, E., et al. 2005b, ApJ, 624, L133 [NASA ADS] [CrossRef]
- Vial, J. C., Ebadi, H., & Ajabshirizadeh, A. 2007, Sol. Phys. 246, 327 (In the text)
- Warren, H. P., Mariska, J. T., & Wilhelm, K. 1998, ApJS 119, 105
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys. 162, 189
- Wilhelm, K., Dviwedi, B. N., Marsch, E., et al. 2004, Space Sci. Rev., 111, 415 [NASA ADS] [CrossRef]
- Wilhelm, K., Marsch, E., Dviwedi, B. N., et al. 2007, Space Sci. Rev., 133, 103 [NASA ADS] [CrossRef] (In the text)
- Xia, L.-D. 2003, Ph.D. Thesis (Göttingen: Georg-August-Univ.)
- Xia, L.-D., Marsch, E., & Wilhelm, K. 2004, A&A, 424, 1025 [NASA ADS] [CrossRef] [EDP Sciences]
- Xu, Z., Fang, C., & Gan, W.-Q. 2005, Chin. J. Astron. Astrophys., 5, 519 [NASA ADS] [CrossRef] (In the text)
Online Material
Table 5:
List of lines used for DEM diagnostics. The values of intensities (in the unit of
![]() )
of the four regions are also shown.
)
of the four regions are also shown.
Table 6:
List of ``peculiar'' lines identified in SUMER spectra of the sunspot.
![]() is the Einstein coefficient taken from NIST Atomic Spectral Database (Ralchenko et al. 2008) and Chianti Database (Dere et al. 1997; Landi et al. 2006). If available, unidentified lines are
characterized by the temperature classification of Feldman et al. (1997) (a):
is the Einstein coefficient taken from NIST Atomic Spectral Database (Ralchenko et al. 2008) and Chianti Database (Dere et al. 1997; Landi et al. 2006). If available, unidentified lines are
characterized by the temperature classification of Feldman et al. (1997) (a):
![]() K, (b):
K, (b):
![]() K,
(c):
K,
(c):
![]() K, (d):
K, (e):
K, (d):
K, (e):
![]() K, (f):
K, (f):
![]() K. The line intensities are given in the unit of
.
References in last column: (0) Curdt et al. (Curdt et al. (2001)), (1) Ekberg & Feldman (Ekberg & Feldman (2003)), (2) Sandlin et al. (Sandlin et al. (1986)) (3) New identification.
K. The line intensities are given in the unit of
.
References in last column: (0) Curdt et al. (Curdt et al. (2001)), (1) Ekberg & Feldman (Ekberg & Feldman (2003)), (2) Sandlin et al. (Sandlin et al. (1986)) (3) New identification.
Footnotes
- ... sunspots
![[*]](/icons/foot_motif.png)
- Tables 5 and 6 are only available in electronic form at http://www.aanda.org
All Tables
Table 1: Observational parameters of the 5 reference spectra of sunspots.
Table 2:
Electron density (
![]() ))
measurements, for the sunspot observed in 2006.
))
measurements, for the sunspot observed in 2006.
Table 3: The details of the filling factor calculations, for the O V emission of the sunspot plume observed in 2006.
Table 4: The ratios of the filling factors in the four regions, for the O V emission in the 2006 data set.
Table 5:
List of lines used for DEM diagnostics. The values of intensities (in the unit of
![]() )
of the four regions are also shown.
)
of the four regions are also shown.
Table 6:
List of ``peculiar'' lines identified in SUMER spectra of the sunspot.
![]() is the Einstein coefficient taken from NIST Atomic Spectral Database (Ralchenko et al. 2008) and Chianti Database (Dere et al. 1997; Landi et al. 2006). If available, unidentified lines are
characterized by the temperature classification of Feldman et al. (1997) (a):
is the Einstein coefficient taken from NIST Atomic Spectral Database (Ralchenko et al. 2008) and Chianti Database (Dere et al. 1997; Landi et al. 2006). If available, unidentified lines are
characterized by the temperature classification of Feldman et al. (1997) (a):
![]() K, (b):
K, (b):
![]() K,
(c):
K,
(c):
![]() K, (d):
K, (e):
K, (d):
K, (e):
![]() K, (f):
K, (f):
![]() K. The line intensities are given in the unit of
.
References in last column: (0) Curdt et al. (Curdt et al. (2001)), (1) Ekberg & Feldman (Ekberg & Feldman (2003)), (2) Sandlin et al. (Sandlin et al. (1986)) (3) New identification.
K. The line intensities are given in the unit of
.
References in last column: (0) Curdt et al. (Curdt et al. (2001)), (1) Ekberg & Feldman (Ekberg & Feldman (2003)), (2) Sandlin et al. (Sandlin et al. (1986)) (3) New identification.
All Figures
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12114f1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg21.png) |
Figure 1:
Averaged profiles of Ly-2 ( upper panels) and Ly-3 ( lower panels) in the sunspot observed on 16th (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm]{12114f2.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg24.png) |
Figure 2: The sunspot observed on 14th of November, 2006. (A) The SUMER slit is located on the image of the 1600 Å passband of TRACE. The TRACE image was obtained at 00:32 on November 14, 2006. (B) The intensities of continuum around 1045 Å (solid line) and O VI (1031.9 Å, dotted line) along the slit. Four segments corresponding to the plage, penumbra, umbra, and sunspot plume are marked in grey. The O VI intensity has been divided by 600. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12114f3.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg32.png) |
Figure 3: The dashed, dot-dashed, dotted, and solid lines represent the average profiles of the Lyman lines (from Lyman-2 to Lyman-9) observed in the plage, penumbra, umbra, and plume for the 2006 data set. Note that the profiles of the umbra were multiplied by a factor of two. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=90,width=8.5cm]{12114f41.eps}\in...
...2114f43.eps}\includegraphics[angle=90,width=8.5cm]{12114f44.eps} }\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg72.png) |
Figure 4: DEM curves for the four regions. Top left: umbra; top right: penumbra; bottom left: plage; Bottom right: plume. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{12114f51.eps}\par\includegraphics[angle=90,width=8cm,clip]{12114f52.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg90.png) |
Figure 5: Comparison of the DEM curves from the four regions. Upper: absolute values; lower: normalized values. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{12114f6.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12114-09/Timg102.png) |
Figure 6: Comparison of the plume DEM curve with the results of Brosius & Landi (2005). |
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Part of the spectra observed in the plage, penumbra, umbra and plume for the 2006 data set. The black, red, green and blue lines correspond to the plage, penumbra, umbra and plume spectra. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.