| Issue |
A&A
Volume 505, Number 1, October I 2009
|
|
|---|---|---|
| Page(s) | 299 - 306 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200912069 | |
| Published online | 24 July 2009 | |
No first ionization potential fractionation in the active stars AR Piscium and AY Ceti![[*]](/icons/foot_motif.png)
J. Sanz-Forcada1 - L. Affer2 - G. Micela2
1 - Laboratorio de Astrofísica Estelar y Exoplanetas,
Centro de Astrobiología / CSIC-INTA, LAEFF Campus, PO Box 78,
28691 Villanueva de la
Cañada, Madrid, Spain
2 -
INAF - Osservatorio Astronomico di Palermo
G. S. Vaiana, Piazza del Parlamento, 1, 90134 Palermo, Italy
Received 13 March 2009 / Accepted 1 July 2009
Abstract
Context. The comparison of coronal and photospheric abundances in cool stars is an essential question to resolve. In the Sun an enhancement of the elements with low first ionization potential (FIP) is observed in the corona with respect to the photosphere. Stars with high levels of activity seem to show a depletion of elements with low FIP when compared to solar standard values; however, the few cases of active stars in which photospheric values are available for comparison lead to confusing results, and an enlargement of the sample is mandatory for solving this longstanding problem.
Aims. We calculate in this paper the photospheric and coronal abundances of two well known active binary systems, AR Psc and AY Cet, to get further insight into the complications of coronal abundances.
Methods. Coronal abundances of 9 elements were calculated by means of the reconstruction of a detailed emission measure distribution, using a line-based method that considers the lines from different elements separately. Photospheric abundances of 8 elements were calculated using high-resolution optical spectra of the stars.
Results. The results once again show a lack of any FIP-related effect in the coronal abundances of the stars. The presence of metal abundance depletion (MAD) or inverse FIP effects in some stars could stem from a mistaken comparison to solar photospheric values or from a deficient calculation of photospheric abundances in fast-rotating stars.
Conclusions. The lack of FIP fractionation seems to confirm that Alfvén waves combined with pondermotive forces are dominant in the corona of active stars.
Key words: stars: coronae - stars: abundances - stars: individual: AR Psc - X-rays: stars - line: identification - stars: individual: AY Cet
1 Introduction
One of the most debated issues in stellar astrophysics is whether the
coronal abundances are similar to the photospheric counterparts in
cool stars. A different composition in the corona and the
photosphere would indicate a physical process taking place
somewhere between the cooler photospheric material and the hotter
corona. Such a process should be capable of distinguishing between
different elements based on a certain physical variable. A
pattern related to that variable would help understanding the
physical processes taking place in the coronal loops.
Such a pattern has been observed in the Sun, which shows, on average,
an enhancement of elements with a low first ionization potential (FIP)
in the corona with respect to the photosphere. The so called ``FIP
effect'' is actually observed in the solar corona and slow wind, but
is absent in coronal holes or fast wind (Laming et al. 1995; Feldman & Laming 2000).
Stars similar to the Sun, such as ![]() Cen, show a
similar FIP effect (Raassen et al. 2003; Drake et al. 1997).
Less active stars, such as Procyon (F4IV),
do not show any fractionation (Raassen et al. 2002; Sanz-Forcada et al. 2004).
Intermediate-activity stars,
like
Cen, show a
similar FIP effect (Raassen et al. 2003; Drake et al. 1997).
Less active stars, such as Procyon (F4IV),
do not show any fractionation (Raassen et al. 2002; Sanz-Forcada et al. 2004).
Intermediate-activity stars,
like ![]() Eri, 36 Oph or 70 Oph present a much lower FIP effect,
if any is present (Laming et al. 1996; Wood & Linsky 2006; Ness & Jordan 2008; Sanz-Forcada et al. 2004).
Eri, 36 Oph or 70 Oph present a much lower FIP effect,
if any is present (Laming et al. 1996; Wood & Linsky 2006; Ness & Jordan 2008; Sanz-Forcada et al. 2004).
For the most active stars,
the results are more uncertain. Their coronal
composition is relatively easy to determine once high spectral
resolution is available. But their high rotation rates
hamper the measurements of photospheric composition due to line
broadening, making the comparison more difficult.
The photospheric composition can only be well
calculated for stars with low projected rotational
velocity (![]() ).
Initial studies of
active stars made with XMM-Newton and Chandra high-resolution spectra
found a very different pattern from the Sun (e.g. Güdel 2004, and references
therein). The elements with low FIP would
actually be underabundant in the corona, a ``metal abundance
depletion'' (``MAD syndrome'', Schmitt et al. 1996), or alternatively,
the elements with high FIP would
be enhanced in the corona (the ``inverse FIP effect'', Brinkman et al. 2001).
A caveat of many of the active stars is that
their coronal abundances are actually compared to the solar photosphere,
which at least yields to risky conclusions (Favata & Micela 2003). Moreover, most
active stars with photospheric abundances calculated have large
).
Initial studies of
active stars made with XMM-Newton and Chandra high-resolution spectra
found a very different pattern from the Sun (e.g. Güdel 2004, and references
therein). The elements with low FIP would
actually be underabundant in the corona, a ``metal abundance
depletion'' (``MAD syndrome'', Schmitt et al. 1996), or alternatively,
the elements with high FIP would
be enhanced in the corona (the ``inverse FIP effect'', Brinkman et al. 2001).
A caveat of many of the active stars is that
their coronal abundances are actually compared to the solar photosphere,
which at least yields to risky conclusions (Favata & Micela 2003). Moreover, most
active stars with photospheric abundances calculated have large
![]() ,
with broad photospheric lines.
As a result, their abundances determination could actually
carry some hidden errors not assessed well by formal
calculations. This is the case for II Peg, AB Dor, or AR Lac (see
Table 1).
,
with broad photospheric lines.
As a result, their abundances determination could actually
carry some hidden errors not assessed well by formal
calculations. This is the case for II Peg, AB Dor, or AR Lac (see
Table 1).
Table 1: Fractionation effects in other stars with known photospheric and coronal abundances.
Theoretical explanations of the FIP effect are found in Laming (2004). The authors also propose that Alfvén waves, combined with pondermotive forces, would explain the observed FIP effect on the Sun, pointing towards the disappearance of any fractionation of stars with lower or higher activity levels. The same mechanism could also explain the inverse FIP effect, if such exists, by reflecting the Alfvén waves in the chromosphere. Alfén waves are also being suggested in recent years as responsible for the energy transportation between the outer convective layers of the star and the much hotter corona (e.g. De Pontieu et al. 2007; Erdélyi & Fedun 2007, and references therein), one of the most important problems unresolved in stellar astrophysics. Both questions, the energy transportation and the FIP fractionation, could actually be connected.
It is thus essential to understand whether active stars suffer an
inverse FIP effect or just no significant fractionation with respect
to the photospheric composition. Given the problems measuring the
photospheric abundances, we should mainly trust
those results for stars with low ![]() .
Sanz-Forcada et al. (2004)
showed the case of two active stars,
.
Sanz-Forcada et al. (2004)
showed the case of two active stars, ![]() And and V851 Cen,
for which coronal and photospheric abundances are consistent, and no
effect related to FIP would be present. Stars such as Capella
(which shows solar photospheric abundances, Argiroffi et al. 2003; Brickhouse et al. 2000; Audard et al. 2003)
show no inverse FIP effect either, although their
photospheric abundance is poorly known
= -0.16,][]mcw90. Other cases of active stars
with no sign of an inverse FIP effect, which are compared to poorly
known photospheric iron abundances, are
And and V851 Cen,
for which coronal and photospheric abundances are consistent, and no
effect related to FIP would be present. Stars such as Capella
(which shows solar photospheric abundances, Argiroffi et al. 2003; Brickhouse et al. 2000; Audard et al. 2003)
show no inverse FIP effect either, although their
photospheric abundance is poorly known
= -0.16,][]mcw90. Other cases of active stars
with no sign of an inverse FIP effect, which are compared to poorly
known photospheric iron abundances, are ![]() CrB
(Suh et al. 2005), EK Dra (Telleschi et al. 2005), and YY Men
(Audard et al. 2004)
CrB
(Suh et al. 2005), EK Dra (Telleschi et al. 2005), and YY Men
(Audard et al. 2004)![]() .
The present situation is still confusing given the few cases described
in the literature with both photospheric and coronal abundances
well-calculated. In this
work we present the results for two more RS CVn systems known to have
narrow photospheric lines despite their high rotation and activity
level.
.
The present situation is still confusing given the few cases described
in the literature with both photospheric and coronal abundances
well-calculated. In this
work we present the results for two more RS CVn systems known to have
narrow photospheric lines despite their high rotation and activity
level.
![\begin{figure}
\par\mbox{\includegraphics[angle=90,width=8cm]{12069f1a.ps} \includegraphics[angle=90,width=8cm]{12069f1b.ps} }
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg10.png) |
Figure 1: Light curves of AR Psc (using all EPIC detectors) and AY Cet (using order +1 and -1 of LETGS) in X-rays. Upper axis indicate the orbital phase, assuming that secondary star is located behind the primary star at phase 0. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=18cm]{12069f2a.ps}\par\hspace{5mm}
\par\includegraphics[angle=270,width=18cm]{12069f2b.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg11.png) |
Figure 2: AR Psc and AY Cet X-ray spectra. The dashed line represents the continuum predicted by the EMD. |
| Open with DEXTER | |
Following Sanz-Forcada et al. (2004) we have chosen two active stars that are observed
with their pole on, and therefore have low ![]() .
Thus, their optical spectra display narrow
lines, allowing us to measure the photospheric abundances better. The
two RS CVn binaries are well known X-ray emitters. Their emission
is attributed to coronal activity, powered by the fast rotation forced
by the close binariety. AR Psc (G7V/K1IV,
.
Thus, their optical spectra display narrow
lines, allowing us to measure the photospheric abundances better. The
two RS CVn binaries are well known X-ray emitters. Their emission
is attributed to coronal activity, powered by the fast rotation forced
by the close binariety. AR Psc (G7V/K1IV,
![]() km s-1, Nordström et al. 2004)
and AY Cet (WD/G5III,
km s-1, Nordström et al. 2004)
and AY Cet (WD/G5III,
![]() km s-1, Massarotti et al. 2008)
were observed with the
Extreme Ultraviolet Explorer Observatory (EUVE), giving a
first glimpse of its coronal emission (Sanz-Forcada et al. 2003a).
Optical spectra also indicate a high level of chromospheric activity
(Montes et al. 1997). Their EMD is similar to other active
stars, either showing an inverse FIP effect, like AB Dor
(Sanz-Forcada et al. 2003b; García-Alvarez et al. 2005,2008), or no
FIP-related fractionation, such as
km s-1, Massarotti et al. 2008)
were observed with the
Extreme Ultraviolet Explorer Observatory (EUVE), giving a
first glimpse of its coronal emission (Sanz-Forcada et al. 2003a).
Optical spectra also indicate a high level of chromospheric activity
(Montes et al. 1997). Their EMD is similar to other active
stars, either showing an inverse FIP effect, like AB Dor
(Sanz-Forcada et al. 2003b; García-Alvarez et al. 2005,2008), or no
FIP-related fractionation, such as ![]() And (Sanz-Forcada et al. 2004). In the case of
AY Cet, it is not expected that its white dwarf
companion contributes substantially to the X-rays band.
Photospheric abundances were calculated by Ottmann et al. (1998) for AY Cet in
only three elements: [Fe/H] = -0.32, [Mg/H] = -0.22, and [Si/H] = -0.32,
with Asplund et al. (2005) values as reference. Shan et al. (2006) finds a low iron
abundance in AR Psc, but no information is provided on the reference
system used in the calculations.
And (Sanz-Forcada et al. 2004). In the case of
AY Cet, it is not expected that its white dwarf
companion contributes substantially to the X-rays band.
Photospheric abundances were calculated by Ottmann et al. (1998) for AY Cet in
only three elements: [Fe/H] = -0.32, [Mg/H] = -0.22, and [Si/H] = -0.32,
with Asplund et al. (2005) values as reference. Shan et al. (2006) finds a low iron
abundance in AR Psc, but no information is provided on the reference
system used in the calculations.
The paper is divided as follows: in Sect. 2 the observations are described. Results are given in Sect. 3, with discussion in Sect. 4, to finish with the conclusions.
2 Observations
Time was awarded (P.I. J. Sanz-Forcada) for observing high-resolution X-rays spectra of AY Cet and AR Psc. The Chandra Low Energy Transmission Grating Spectrograph (LETGS) (
Optical spectra (Fig. 3) were acquired on 27 and 28 November 2002 to
calculate the photospheric abundances of the two stars, as part of a
wider observational campaign. The detailed instrumental setup and
observations are described well in Affer et al. (2005), so only a short
description is given here. We used the high-resolution cross-dispersed echelle
spectrograph SOFIN, mounted on the Cassegrain focus of the 2.56 m Nordic Optical
Telescope (NOT) located at the Observatorio del Roque de Los Muchachos (La
Palma, Spain). Exposure times ranged from 4 to 20 min,
resulting in high S/N per pixel (![]() 0.025 Å/px)
averaging at about 280. A
spectrum of a Th-Ar lamp was obtained following each stellar spectrum, ensuring
accurate wavelength calibration.
The total spectral range is 3900-9900 Å, and the resolving power
is
0.025 Å/px)
averaging at about 280. A
spectrum of a Th-Ar lamp was obtained following each stellar spectrum, ensuring
accurate wavelength calibration.
The total spectral range is 3900-9900 Å, and the resolving power
is
![]() .
The spectra were
reduced with the standard software available
within the CCDRED and ECHELLE packages of IRAF
.
The spectra were
reduced with the standard software available
within the CCDRED and ECHELLE packages of IRAF![]() . The analysis includes overscan
subtraction, flat-fielding, removal of scattered light, extraction of
one-dimensional spectra, wavelength calibration, and continuum
normalization (see Affer et al. 2005, for further details). The
EWs were measured using the SPLOT task in
IRAF, assuming a Gaussian profile for weak or moderately strong lines (
. The analysis includes overscan
subtraction, flat-fielding, removal of scattered light, extraction of
one-dimensional spectra, wavelength calibration, and continuum
normalization (see Affer et al. 2005, for further details). The
EWs were measured using the SPLOT task in
IRAF, assuming a Gaussian profile for weak or moderately strong lines (
![]() mÅ) and a Voigt profile for stronger lines. The accuracy (absolute
error) is harder to assess. It almost certainly contains a systematic error due
to the continuum location, because of the presence of interference
fringes (which could not be completely removed) in the redder part of
the stellar spectra, which cause a modulation of
the local continuum. This error could be particularly important for
the weak lines.
mÅ) and a Voigt profile for stronger lines. The accuracy (absolute
error) is harder to assess. It almost certainly contains a systematic error due
to the continuum location, because of the presence of interference
fringes (which could not be completely removed) in the redder part of
the stellar spectra, which cause a modulation of
the local continuum. This error could be particularly important for
the weak lines.
3 Results
Light curves of AR Psc and AY Cet (Fig. 1) show no flares in these observations, although variability up to a
![\begin{figure}
\par\includegraphics[width=8.8cm]{12069f3.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg25.png) |
Figure 3: AR Psc and AY Cet optical spectra. |
| Open with DEXTER | |
The photospheric abundances (Fig. 6,
Table 5) were calculated
through the analysis of the
optical spectra, in which we select a group of lines that are free
of blends, as explained in Affer et al. (2005) and Morel et al. (2003).
To avoid the difficulty in defining the continuum in
the blue part of the spectra, only lines with
![]() Å were
selected. Lines that appeared
asymmetric or showed an unusually large width were assumed to be blended with
unidentified lines so were discarded from the initial sample.
To obtain information on individual abundances from the spectral
lines of various elements, one must first
determine the parameters that characterize the atmospheric model; i.e., the
effective temperature (
Å were
selected. Lines that appeared
asymmetric or showed an unusually large width were assumed to be blended with
unidentified lines so were discarded from the initial sample.
To obtain information on individual abundances from the spectral
lines of various elements, one must first
determine the parameters that characterize the atmospheric model; i.e., the
effective temperature (
![]() ), the surface gravity (
), the surface gravity (![]() ),
the microturbulent velocity (
),
the microturbulent velocity (![]() ), and the
iron abundance. They were calculated in an iterative process from the
comparison of the observed spectra and the model for a given set of
parameters.
The atmospheric parameters and metal
abundances were determined using the measured EWs and a standard
local thermodynamic equilibrium (LTE) analysis with the most recent
version of the line abundance code
MOOG (Sneden 1973) and a grid of Kurucz (1993) ATLAS9 atmospheres,
computed without the overshooting option and with a mixing length to
pressure scale height ratio
), and the
iron abundance. They were calculated in an iterative process from the
comparison of the observed spectra and the model for a given set of
parameters.
The atmospheric parameters and metal
abundances were determined using the measured EWs and a standard
local thermodynamic equilibrium (LTE) analysis with the most recent
version of the line abundance code
MOOG (Sneden 1973) and a grid of Kurucz (1993) ATLAS9 atmospheres,
computed without the overshooting option and with a mixing length to
pressure scale height ratio
![]() .
Assumptions made in the models include: the
atmosphere is plane-parallel and in hydrostatic equilibrium, the
total flux is constant, the source function
is described by the Planck function, the populations of different excitation
levels and ionization stages are governed by LTE.
The abundances were derived from theoretical curves of growth, computed
by MOOG, using model atmospheres
and atomic data (wavelength,
excitation potential, gf values). The input model was constructed using as
atmospheric parameters the average values of previous determinations
found in the literature and solar metallicity.
Further details on the iterative process followed, and the errors
determination is described in Affer et al. (2005).
For an elemental abundance derived
from many lines, the uncertainty of the atmospheric parameters is the dominant
error, while for an abundance derived from a few lines, the uncertainty in the
equivalent widths may be more significant.
In our case, the atmospheric parameters calculated are
.
Assumptions made in the models include: the
atmosphere is plane-parallel and in hydrostatic equilibrium, the
total flux is constant, the source function
is described by the Planck function, the populations of different excitation
levels and ionization stages are governed by LTE.
The abundances were derived from theoretical curves of growth, computed
by MOOG, using model atmospheres
and atomic data (wavelength,
excitation potential, gf values). The input model was constructed using as
atmospheric parameters the average values of previous determinations
found in the literature and solar metallicity.
Further details on the iterative process followed, and the errors
determination is described in Affer et al. (2005).
For an elemental abundance derived
from many lines, the uncertainty of the atmospheric parameters is the dominant
error, while for an abundance derived from a few lines, the uncertainty in the
equivalent widths may be more significant.
In our case, the atmospheric parameters calculated are
![]() K,
K,
![]() [cm s-2] ,
and
[cm s-2] ,
and
![]() km s-1 for AR Psc, and
km s-1 for AR Psc, and
![]() K,
K,
![]() [cm s-2], and
[cm s-2], and
![]() km s-1
for AY Cet. In the case of AY Cet, these parameters are in good
agreement with Ottmann et al. (1998) except for lower gravity in our
case; iron abundance agrees with that of Ottman et al., but Mg and Si
are substantially higher (-0.22 and -0.32 in their case, respectively).
km s-1
for AY Cet. In the case of AY Cet, these parameters are in good
agreement with Ottmann et al. (1998) except for lower gravity in our
case; iron abundance agrees with that of Ottman et al., but Mg and Si
are substantially higher (-0.22 and -0.32 in their case, respectively).
Table 4: Emission measure distribution of the target stars.
The coronal abundances are compared to the photosphere of the same
stars (Fig. 5), using the solar photospheric values
as scale. There is no proof of
MAD or any inverse FIP effect in either of the two cases.
The best calculated values, the abundance of Fe, Ni and Mg,
show consistent coronal and photospheric abundances.
Some metal depletion seems to take place for Si and O in AY Cet.
It must be noticed that photospheric
abundances of elements other than Fe are calculated with fewer lines, so
we are less confident about their values.
These results confirm those of ![]() And and V851 Cen
(Sanz-Forcada et al. 2004), displayed here for easier comparison
(Fig. 7, Table 5.
It is also worth checking the abundance ratio [Ne/O] in the
corona. Drake & Testa (2005) find that an average value of [Ne/O] = 0.41,
calculated in the corona of nearby stars, would help for solving the
``solar model problem'' (see also discussion in Schmelz et al. 2005). The
ratios in the coronae of AR Psc and AY Cet are consistent with the
value observed by Drake & Testa (2005). An upwards correction of the Ne solar abundance, as proposed by these authors, would not affect our
results since we compared coronal and photospheric abundances of the
same star.
And and V851 Cen
(Sanz-Forcada et al. 2004), displayed here for easier comparison
(Fig. 7, Table 5.
It is also worth checking the abundance ratio [Ne/O] in the
corona. Drake & Testa (2005) find that an average value of [Ne/O] = 0.41,
calculated in the corona of nearby stars, would help for solving the
``solar model problem'' (see also discussion in Schmelz et al. 2005). The
ratios in the coronae of AR Psc and AY Cet are consistent with the
value observed by Drake & Testa (2005). An upwards correction of the Ne solar abundance, as proposed by these authors, would not affect our
results since we compared coronal and photospheric abundances of the
same star.
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm]{12069f4a.eps} \includegraphics[width=8.8cm]{12069f4b.eps} }
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg65.png) |
Figure 4: Emission measure distribution (EMD) of AR Psc and AY Cet. Thin lines represent the relative contribution function for each ion (the emissivity function multiplied by the EMD at each point). Small numbers indicate the ionization stages of the species. Also plotted are the observed-to-predicted line flux ratios for the ion stages in the upper figure. The dotted lines denote a factor of 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12069f5a.eps}
\includegraphics[width=7.6cm,clip]{12069f5b.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg66.png) |
Figure 5: Coronal abundances of AR Psc and AY Cet, in increasing order of FIP. Filled circles are coronal values and open circles represent photospheric values. A dashed line indicates the adopted solar photospheric abundance (Asplund et al. 2005). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12069f6a.eps}
\includegraphics[width=7.6cm,clip]{12069f6b.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg67.png) |
Figure 6: Photospheric abundances of AR Psc and AY Cet. A dashed line indicates the adopted solar photospheric abundance (Asplund et al. 2005). |
| Open with DEXTER | |
4 Discussion
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{12069f7a.eps} \includegraphics[width=8.5cm]{12069f7b.eps} }
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg68.png) |
Figure 7:
Same as in Fig. 5, but for
|
| Open with DEXTER | |
Table 5: Coronal and photospheric abundances of the elements ([X/H], solar units) in the target stars.
The results are suggestive of a lack of MAD effect.
We see once again that coronal
abundances of active stars, once they are compared with their own
photospheric values instead of the solar photosphere, show no sign of
inverse FIP effect or MAD. So far, all the active stars with inverse FIP effect observed (we discard those compared to solar photosphere) have
a high projected rotational velocity
(Table 1). A large ![]() broadens the
lines observed in the optical wavelengths, those usually employed to
calculate photospheric abundances.
The broadening of lines might yield erroneous measurements of equivalent
widths (blends are included in the measurements, and continuum is more
difficult to place), and
therefore wrong photospheric abundances.
All active stars are fast rotators, but only the cases with high projected
rotational velocity will
affect the measurements of lines. Ottmann et al. (1998) note that values of
broadens the
lines observed in the optical wavelengths, those usually employed to
calculate photospheric abundances.
The broadening of lines might yield erroneous measurements of equivalent
widths (blends are included in the measurements, and continuum is more
difficult to place), and
therefore wrong photospheric abundances.
All active stars are fast rotators, but only the cases with high projected
rotational velocity will
affect the measurements of lines. Ottmann et al. (1998) note that values of
![]() km s-1 yield wrong results. We therefore are more inclined
to believe that the inverse FIP effect is an observational effect,
rather than a real fact. Thus, from now on we will interpret the
results in this basis, insisting that more observations are needed in order to
clarify how real the inverse FIP effect is.
km s-1 yield wrong results. We therefore are more inclined
to believe that the inverse FIP effect is an observational effect,
rather than a real fact. Thus, from now on we will interpret the
results in this basis, insisting that more observations are needed in order to
clarify how real the inverse FIP effect is.
Assuming that no inverse FIP effect exists among active stars, the observations suits the coronal model explained by Laming (2004). The works carried out in the Sun in past years have strengthened the idea of the Alfvén waves as the main force responsible for the energy transportation between chromosphere and corona of the Sun. Recent observations with the mission Hinode (De Pontieu et al. 2007; Erdélyi & Fedun 2007) support this idea. In the model described by Laming (2004), the Alfvén waves, combined with pondermotive forces, would be responsible for part of the energy transportation in the corona.
Their model explains
the observed abundances pattern in the solar corona: either the
low FIP in the coronal active regions and the slow wind or the
absence of FIP effect in coronal holes or fast wind.
According to this
model, the stars earlier than the Sun, like Procyon, would behave more
like coronal holes, because they have shallower convective zones
yielding smaller coronal magnetic fields. Their chromospheric Alfvén
waves are stronger than the coronal fields, similar to a
coronal hole. In stars later than the Sun, but not very active yet,
there is a deeper convection, yielding lower frequency chromospheric
waves and higher coronal magnetic fields.
The wave transmission is less
efficient and this would yield a
reduced FIP effect.
This is the case
for ![]() Eri or
Eri or
![]() Cen.
Cen.
Following the same reasoning, it makes sense to find that Alfvén waves are more inefficient for the more active stars, yielding no FIP fractionation for stars such as AR Psc or AY Cet. Some arguments have been proposed by Laming (2004) to explain why an inverse FIP effect could be present in active stars, such as AB Dor: wave reflection in the chromosphere (more likely for stars with lower gravity), or turbulence introduced by differential rotation.
A more complete census of active stars with well measured photospheric and coronal abundances would be necessary to confirm the results, but if we assume that the cases with inverse FIP effect observed are a product of observational effects, the model proposed by Laming (2004) could actually explain the observed abundances patterns in both low and high activity stars.
5 Conclusions
The results suggest that metal abundance depletion, or
inverse FIP effect, are not present in these two stars. This
agrees with results for other active stars with
well-known photospheric abundances, such as ![]() And or
V851 Cen. Stars with observed inverse FIP effect have their
photospheric lines broadened by the high rotation of the stars,
hampering their photospheric measurements. The results observed in
AR Psc and AY Cet suit the expected behavior in active stars
according to the model of Laming (2004), which combines the use of
pondermotive forces with Alfvén waves. The same model is also able to
explain both the FIP effect in the solar corona and slow wind and the
absence of FIP fractionation in solar coronal holes and fast wind.
Further measurements in active
stars with low projected rotational velocity would help to assure this
confirmation of the model.
And or
V851 Cen. Stars with observed inverse FIP effect have their
photospheric lines broadened by the high rotation of the stars,
hampering their photospheric measurements. The results observed in
AR Psc and AY Cet suit the expected behavior in active stars
according to the model of Laming (2004), which combines the use of
pondermotive forces with Alfvén waves. The same model is also able to
explain both the FIP effect in the solar corona and slow wind and the
absence of FIP fractionation in solar coronal holes and fast wind.
Further measurements in active
stars with low projected rotational velocity would help to assure this
confirmation of the model.
Acknowledgements
We acknowledge support by the Ramón y Cajal Program ref. RYC-2005-000549, financed by the Spanish Ministry of Science. J.S. wants to thank Aitor Ibarra for his aid in the treatment of XMM data. This research has also made use of NASA's Astrophysics Data System Abstract Service and the SIMBAD Database, operated at CDS, Strasbourg (France).
References
- Affer, L., Micela, G., Morel, T., Sanz-Forcada, J., & Favata, F. 2005, A&A, 433, 647 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [NASA ADS] [CrossRef] (In the text)
- Argiroffi, C., Maggio, A., & Peres, G. 2003, A&A, 404, 1033 [NASA ADS] [CrossRef] [EDP Sciences]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 (In the text)
- Audard, M., Güdel, M., Sres, A., Raassen, A. J. J., & Mewe, R. 2003, A&A, 398, 1137 [NASA ADS] [CrossRef] [EDP Sciences]
- Audard, M., Telleschi, A., Güdel, M., et al. 2004, ApJ, 617, 531 [NASA ADS] [CrossRef] (In the text)
- Ball, B., Drake, J. J., Lin, L., et al. 2005, ApJ, 634, 1336 [NASA ADS] [CrossRef]
- Brickhouse, N. S., Dupree, A. K., Edgar, R. J., et al. 2000, ApJ, 530, 387 [NASA ADS] [CrossRef]
- Brinkman, A. C., Behar, E., Güdel, M., et al. 2001, A&A, 365, L324 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007, Science, 318, 1574 [NASA ADS] [CrossRef]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Drake, J. J., & Testa, P. 2005, Nature, 436, 525 [NASA ADS] [CrossRef] (In the text)
- Drake, J. J., Laming, J. M., & Widing, K. G. 1997, ApJ, 478, 403 [NASA ADS] [CrossRef]
- Erdélyi, R., & Fedun, V. 2007, Science, 318, 1572 [NASA ADS] [CrossRef]
- Favata, F., & Micela, G. 2003, Space Sci. Rev., 108, 577 [NASA ADS] [CrossRef] (In the text)
- Feldman, U., & Laming, J. M. 2000, Phys. Scr., 61, 222 [NASA ADS] [CrossRef]
- García-Alvarez, D., Drake, J. J., Lin, L., Kashyap, V. L., & Ball, B. 2005, ApJ, 621, 1009 [NASA ADS] [CrossRef]
- García-Alvarez, D., Drake, J. J., Kashyap, V. L., Lin, L., & Ball, B. 2008, ApJ, 679, 1509 [NASA ADS] [CrossRef]
- Güdel, M. 2004, A&ARv, 12, 71 [NASA ADS] (In the text)
- Huenemoerder, D. P., Canizares, C. R., & Schulz, N. S. 2001, ApJ, 559, 1135 [NASA ADS] [CrossRef]
- Huenemoerder, D. P., Canizares, C. R., Drake, J. J., & Sanz-Forcada, J. 2003, ApJ, 595, 1131 [NASA ADS] [CrossRef]
- Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data, ed. R. L. Kurucz (In the text)
- Laming, J. M. 2004, ApJ, 614, 1063 [NASA ADS] [CrossRef] (In the text)
- Laming, J. M., Drake, J. J., & Widing, K. G. 1995, ApJ, 443, 416 [NASA ADS] [CrossRef]
- Laming, J. M., Drake, J. J., & Widing, K. G. 1996, ApJ, 462, 948 [NASA ADS] [CrossRef]
- Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [NASA ADS] [CrossRef] (In the text)
- McWilliam, A. 1990, ApJS, 74, 1075 [NASA ADS] [CrossRef]
- Montes, D., Fernandez-Figueroa, M. J., de Castro, E., & Sanz-Forcada, J. 1997, A&AS, 125, 263 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Morel, T., Micela, G., Favata, F., Katz, D., & Pillitteri, I. 2003, A&A, 412, 495 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ness, J.-U., & Jordan, C. 2008, MNRAS, 385, 1691 [NASA ADS] [CrossRef]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ottmann, R., Pfeiffer, M. J., & Gehren, T. 1998, A&A, 338, 661 [NASA ADS] (In the text)
- Raassen, A. J. J., Mewe, R., Audard, M., et al. 2002, A&A, 389, 228 [NASA ADS] [CrossRef] [EDP Sciences]
- Raassen, A. J. J., Ness, J.-U., Mewe, R., et al. 2003, A&A, 400, 671 [NASA ADS] [CrossRef] [EDP Sciences]
- Randich, S., Gratton, R., & Pallavicini, R. 1993, A&A, 273, 194 [NASA ADS]
- Sanz-Forcada, J., Brickhouse, N. S., & Dupree, A. K. 2003a, ApJS, 145, 147 [NASA ADS] [CrossRef] (In the text)
- Sanz-Forcada, J., Maggio, A., & Micela, G. 2003b, A&A, 408, 1087 [NASA ADS] [CrossRef] [EDP Sciences]
- Sanz-Forcada, J., Favata, F., & Micela, G. 2004, A&A, 416, 281 [NASA ADS] [CrossRef] [EDP Sciences]
- Schmelz, J. T., Nasraoui, K., Roames, J. K., Lippner, L. A., & Garst, J. W. 2005, ApJ, 634, L197 [NASA ADS] [CrossRef] (In the text)
- Schmitt, J. H. M. M., Stern, R. A., Drake, J. J., & Kuerster, M. 1996, ApJ, 464, 898 [NASA ADS] [CrossRef] (In the text)
- Shan, H., Liu, X., & Gu, S. 2006, New Astron., 11, 287 [NASA ADS] [CrossRef] (In the text)
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] (In the text)
- Sneden, C. A. 1973, Ph.D. thesis, The University of Texas at Austin (In the text)
- Suh, J. A., Audard, M., Güdel, M., & Paerels, F. B. S. 2005, ApJ, 630, 1074 [NASA ADS] [CrossRef] (In the text)
- Telleschi, A., Güdel, M., Briggs, K., et al. 2005, ApJ, 622, 653 [NASA ADS] [CrossRef] (In the text)
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] (In the text)
- Wood, B. E., & Linsky, J. L. 2006, ApJ, 643, 444 [NASA ADS] [CrossRef]
Online Material
Table 2: XMM/RGS line fluxes of AR Psca.
Table 3: Chandra/LETG line fluxes of AY Ceta.
Footnotes
- ... Ceti
![[*]](/icons/foot_motif.png)
- Tables 2 and 3 are only available in electronic form at http://www.aanda.org
- ...(Audard et al. 2004)
![[*]](/icons/foot_motif.png)
- Although the authors claim that coronal iron is depleted in YY Men, the values in the corona and photosphere of the star are actually consistent, once reasonable uncertainties of 0.2 dex are considered for the photospheric iron, calculated from a low-resolution spectrum by Randich et al. (1993).
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF (Image Reduction and Analysis Facility) is distributed by National Optical Astronomy Observatories, operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
- ... measured
![[*]](/icons/foot_motif.png)
- We then measured fluxes
for interstellar medium absorption (ISM), using
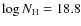 (AY Cet) and
(AY Cet) and
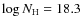 (AR Psc), although it
is only important in a few lines.
(AR Psc), although it
is only important in a few lines.
All Tables
Table 1: Fractionation effects in other stars with known photospheric and coronal abundances.
Table 4: Emission measure distribution of the target stars.
Table 5: Coronal and photospheric abundances of the elements ([X/H], solar units) in the target stars.
Table 2: XMM/RGS line fluxes of AR Psca.
Table 3: Chandra/LETG line fluxes of AY Ceta.
All Figures
![\begin{figure}
\par\mbox{\includegraphics[angle=90,width=8cm]{12069f1a.ps} \includegraphics[angle=90,width=8cm]{12069f1b.ps} }
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg10.png) |
Figure 1: Light curves of AR Psc (using all EPIC detectors) and AY Cet (using order +1 and -1 of LETGS) in X-rays. Upper axis indicate the orbital phase, assuming that secondary star is located behind the primary star at phase 0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=18cm]{12069f2a.ps}\par\hspace{5mm}
\par\includegraphics[angle=270,width=18cm]{12069f2b.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg11.png) |
Figure 2: AR Psc and AY Cet X-ray spectra. The dashed line represents the continuum predicted by the EMD. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{12069f3.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg25.png) |
Figure 3: AR Psc and AY Cet optical spectra. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm]{12069f4a.eps} \includegraphics[width=8.8cm]{12069f4b.eps} }
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg65.png) |
Figure 4: Emission measure distribution (EMD) of AR Psc and AY Cet. Thin lines represent the relative contribution function for each ion (the emissivity function multiplied by the EMD at each point). Small numbers indicate the ionization stages of the species. Also plotted are the observed-to-predicted line flux ratios for the ion stages in the upper figure. The dotted lines denote a factor of 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12069f5a.eps}
\includegraphics[width=7.6cm,clip]{12069f5b.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg66.png) |
Figure 5: Coronal abundances of AR Psc and AY Cet, in increasing order of FIP. Filled circles are coronal values and open circles represent photospheric values. A dashed line indicates the adopted solar photospheric abundance (Asplund et al. 2005). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12069f6a.eps}
\includegraphics[width=7.6cm,clip]{12069f6b.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg67.png) |
Figure 6: Photospheric abundances of AR Psc and AY Cet. A dashed line indicates the adopted solar photospheric abundance (Asplund et al. 2005). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{12069f7a.eps} \includegraphics[width=8.5cm]{12069f7b.eps} }
\end{figure}](/articles/aa/full_html/2009/37/aa12069-09/Timg68.png) |
Figure 7:
Same as in Fig. 5, but for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


