| Issue |
A&A
Volume 505, Number 1, October I 2009
|
|
|---|---|---|
| Page(s) | 361 - 371 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200811416 | |
| Published online | 22 July 2009 | |
Fast and robust segmentation of solar EUV images: algorithm and results for solar cycle 23
V. Barra1 - V. Delouille2 - M. Kretzschmar3 - J.-F. Hochedez2
1 - LIMOS, UMR 6158, Univ. Blaise Pascal, Campus des Cézeaux, 63173 Aubière, France
2 -
Royal Observatory of Belgium, Circular Avenue 3, 1180 Brussels, Belgium
3 -
LPC2E, UMR 6115 CNRS - Univ. d'Orléans, 3A av. de la recherche scientifique, 45071 Orléans, France
Received 25 November 2008 / Accepted 4 June 2009
Abstract
Context. The study of the variability of the solar corona and the monitoring of coronal holes, quiet sun and active regions are of great importance in astrophysics as well as for space weather and space climate applications.
Aims. In a previous work, we presented the spatial possibilistic clustering algorithm (SPoCA). This is a multi-channel unsupervised spatially-constrained fuzzy clustering method that automatically segments solar extreme ultraviolet (EUV) images into regions of interest. The results we reported on SoHO-EIT images taken from February 1997 to May 2005 were consistent with previous knowledge in terms of both areas and intensity estimations. However, they presented some artifacts due to the method itself.
Methods. Herein, we propose a new algorithm, based on SPoCA, that removes these artifacts. We focus on two points: the definition of an optimal clustering with respect to the regions of interest, and the accurate definition of the cluster edges. We moreover propose methodological extensions to this method, and we illustrate these extensions with the automatic tracking of active regions.
Results. The much improved algorithm can decompose the whole set of EIT solar images over the 23rd solar cycle into regions that can clearly be identified as quiet sun, coronal hole and active region. The variations of the parameters resulting from the segmentation, i.e. the area, mean intensity, and relative contribution to the solar irradiance, are consistent with previous results and thus validate the decomposition. Furthermore, we find indications for a small variation of the mean intensity of each region in correlation with the solar cycle.
Conclusions. The method is generic enough to allow the introduction of other channels or data. New applications are now expected, e.g. related to SDO-AIA data.
Key words: techniques: image processing - Sun: corona - Sun: activity - Sun: rotation - Sun: UV radiation
1 Introduction
Solar extreme ultraviolet (EUV) flux plays a major role in Solar-Terrestrial relationships since it is the main source of the diurnal ionosphere. Understanding its variability is thus an important issue for space weather and climate applications. Towards this goal, an accurate monitoring of coronal holes (CH), quiet sun (QS) and active regions (AR) would provide a key element e.g. in building a solar EUV flux model. Moreover, catalogs of ARs and CHs in the EUV are desirable. Indeed, a catalog of ARs describing key parameters such as their location, shape, area, mean and integrated intensity, or more complex parameters such as the fractal dimension would allow one to relate those properties to the occurence of flares. On the other hand, a catalog of CHs would allow one to compare their properties to those of fast solar wind streams.
In this paper, we propose a method that separates at the same time the CH, AR, and QS, thereby providing a monitoring of the three zones. We show how the algorithm can produce catalogs of regions of interests. Our procedure is based on fuzzy clustering. It is fast, stable in time and space, allows for multichannel inputs, and separates in an optimal way coronal holes, quiet sun and active regions even though the boundaries of these regions are not always well defined.
The problem of coronal image segmentation in general and the detection and tracking of regions of interest in solar images in particular has been addressed in many ways in the last decade. Following the classical dichotomy of image segmentation methods, we briefly review the main approaches in three broad categories: region-based methods, edge-based methods and hybrid approaches.
Region-based methods seek a partition of the image satisfying an homogeneity criterion (on mono-, multi-spectral gray levels or higher level attributes such as texture or feature vectors modeling pixels and their neighborhood). Several processes of this family have been successfully applied in solar image processing, including simple or dynamical thresholding techniques, possibly linked to post processings using e.g. mathematical morphology, for the detection of sunspots (Steinegger et al. 1997; Pettauer & Brandt 1997), active regions (Steinegger et al. 1998), bright points (Brajsa et al. 2001), filaments and plage regions (Wagstaff et al. 2003; Bornmann et al. 1996), photospheric structures (Ortiz 2005; Berrili et al. 2005) or chromospheric structures (Worden et al. 1999); region growing methods for the segmentation of filaments (Gao et al. 2002; Aboudarham et al. 2008), sunspots (Preminger et al. 1997; Zharkov et al. 2004) active regions (Hill et al. 2001; Benkhalil et al. 2003) and coronal holes when coupled with a watershed approach (Nieniewski 2002); or classification schemes in some relevant feature space, in their Bayesian interpretation (Turmon et al. 2002), supervised (Dudok de Wit 2006; Zharkova & Schetinin 2003) or unsupervised (Barra et al. 2005) version.
The dual edge-based approaches aim at characterising image discontinuities, and thus locating region boundaries. Primal edge-based methods look for the maximum of intensity gradients, using either spatial or frequency filters, or zeros in the Laplacian of the image, often pre processed by a low pass Gaussian filtering, due to the Laplacian sensitivity to noise. Such methods have been used for the extraction of umbral and penumbral areas of sunspots, (Steinegger et al. 1997) or for the automatic segmentation of flares from
![]() full-disk images (Veronig et al. 2000), or simply as pre-processing techniques for image enhancement, before e.g. a region-growing procedure allowing an efficient segmentation of filaments in
full-disk images (Veronig et al. 2000), or simply as pre-processing techniques for image enhancement, before e.g. a region-growing procedure allowing an efficient segmentation of filaments in
![]() spectroheliograms (Fuller et al. 2005). Some extended and dedicated edge-based methods have also been proposed, using for example the Hough transform (Robbrecht et al. 2006) or a multiscale edge detector (Young et al. 2003).
spectroheliograms (Fuller et al. 2005). Some extended and dedicated edge-based methods have also been proposed, using for example the Hough transform (Robbrecht et al. 2006) or a multiscale edge detector (Young et al. 2003).
The hybrid methods either consider a cooperation between region and contour approaches (Veronig et al. 2001), or process some other original method such as simulated annealing (Bratsolis & Sigelle 1998), multiscale approaches such as the ``a trous'' algorithm (Portier-Fozzani et al. 2001) or the continuous wavelet transform (Antoine et al. 2002), multiresolution schemes allowing a fast and accurate segmentation of filaments (Qahwaji 2003).
This paper builds upon a previous work (Barra et al. 2008,2005), where we presented the first spatial possibilistic clustering algorithm (SPoCA). This is a multi-channel unsupervised spatially-constrained fuzzy clustering method that segments EUV images into regions of interest. Although the results we reported on EIT images (Delaboudiniere et al. 1995) taken from February 1997 until May 2005 were interesting and globally consistent with previous works, we noted several artifacts induced by the method itself: misclassification of some pixels (particularly those located in the surroundings of active regions and near the limb), complex shape of active region edges, and gathering of filaments and coronal holes in a single class. As a consequence, the time series extracted from the segmentation (such as the area occupied by AR, CH, and QS) also showed some artifacts and were difficult to interpret. Here, we propose a new fast and reliable segmentation of EUV images that overcomes the above mentioned limitations.
After recalling the original SPoCA algorithm in Sect. 2, we detail in Sect. 3 the improvements of our new algorithm: first, we present an oversegmentation scheme to optimally separate active regions from the quiet sun. Second, we propose a limb correction process to remove the discontinuity introduced by the enhanced brightness of the limb. Third, we show how to apply a regularization scheme for the edges of active regions. A sensor data fusion process is then introduced in order to separate filaments from coronal holes in the segmentation, and finally we show how to track regions of interest through time.
In Sect. 5, the new method is applied to the same dataset as in Barra et al. (2008). From the segmentation, we derived time series such as the area, mean intensity, and integrated intensity of AR, QS, and CH. An analysis of these time series is performed and compared to previous results from the literature.
2 Spatial possibilistic clustering algorithm (SPoCA)
The spatial possibilistic clustering algorithm (SPoCA) (Barra et al. 2008) is a fuzzy unsupervised clustering algorithm, allowing the fast and automatic segmentation of coronal holes (CH), quiet sun (QS) and active regions (AR) from multispectral solar EUV images. We only introduce here the notations necessary for this paper, and we refer the reader either to Barra et al. (2008) or to Appendix A which fully details the algorithm.
If each pixel
![]() is described by a p-dimensional feature vector
is described by a p-dimensional feature vector
![]() ,
representing for example its gray-levels in the multispectral dataset, SPoCA is an iterative algorithm that searches for C compact clusters gathering in
,
representing for example its gray-levels in the multispectral dataset, SPoCA is an iterative algorithm that searches for C compact clusters gathering in
![]() the xjs by computing both a fuzzy partition matrix
the xjs by computing both a fuzzy partition matrix
![]() ,
,
![]() being the membership degree of xj to class i, and unknown cluster centers
being the membership degree of xj to class i, and unknown cluster centers
![]() .
.
The description of the segmentation process in terms of fuzzy logic was motivated by the facts that information provided by an EUV solar image is uncertain (Poisson and readout noise, cosmic ray hits) and subject to both observational biases (line-of-sight integration of a transparent volume) and interpretation (the apparent boundary between regions is a matter of convention). Size, shape, and precise location of areas of interest are then not easy to determine with only a single piece of information, and we capture this complexity through matrix U.
In this article, we chose p=2, and xj was set as the 2D-vector of pixel j whose components were the gray-level values of EIT 17.1 nm and 19.5 nm images, calibrated with eit_prep. The introduction of additional information (e.g. 28.4 nm image) is very easy through the concept of feature vector.
3 The new algorithm
Although results we reported on SoHO-EIT images taken from February 1997 until May 2005 were interesting and globally consistent with previous works, the original SPoCA method induced several problems in the final segmentation:
- areas surrounding the active regions were classified as quiet sun, mainly because the definition of AR only concerns their cores;
- the limb was always misclassified;
- the edges of the regions of interest were fractal-shaped;
- some false positives were observed, particularly in the CH class, where filaments were clustered as coronal holes.
3.1 Limb correction
Since the solar corona is optically thin, and since the intensity in EUV images is obtained through an integration along the line of sight, there is a limb brightening effect in those images, which may hinder the segmentation process. Therefore, we first process the EUV images so as to lower the enhanced brightness and the discontinuity at the limb.
Some authors have studied the use of a limb brightening factor correction, assuming for example a hydrostatic, isothermal and spherical atmosphere (Andretta et al. 2003). We propose to first apply a polar transform to represent the image I in a
![]() plane, with the origin at the solar disc center. The polar transform is a conformal mapping from points in the Cartesian plane (x,y) to points in this polar plane, described by
plane, with the origin at the solar disc center. The polar transform is a conformal mapping from points in the Cartesian plane (x,y) to points in this polar plane, described by
![]() .
.
We then compute the integral
![]() ,
which specifies the intensity distribution as a function of
,
which specifies the intensity distribution as a function of ![]() .
Denoting
.
Denoting ![]() the median value of intensities on the on-disc part of the Sun, we propose to correct for the enhanced brightness at the limb as follows:
the median value of intensities on the on-disc part of the Sun, we propose to correct for the enhanced brightness at the limb as follows:
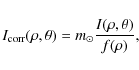 |
(1) |
where
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[height=40mm]{11416f1.eps...
...eps}\\
(c) Vertical profile & (d) Horizontal profile
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg17.png) |
Figure 1: a) Original image. The vertical line and the horizontal line show the location of profile. b) Image with limb brightness enhancement corrected. c) The intensity along the vertical profile before and after correction. d) The intensity along the horizontal profile before and after correction. |
| Open with DEXTER | |
3.2 Sursegmentation and optimal clustering
Image segmentation is a crucial step in many image processing applications, but it is difficult to assess whether one algorithm produces more accurate results than another, or to evaluate the optimal parameters of a given algorithm. The most common method for assessing the effectiveness of a segmentation method is subjective evaluation, in which an expert visually compares the segmentation results for different segmentation algorithms or different sets of parameters. This is often a tedious process which, moreover, intrinsically limits the evaluation to a relatively small number of cases. Another way to assess segmentation results is to use a supervised evaluation scheme, in which a segmented image is compared against a manually segmented (or a reference image), referred to as the ``ground truth''. Both approaches are not feasible for our purpose. Indeed, we were primarly interested in finding the best number of clusters without having either a manual intervention (because of the large number of images to be processed) or a ground truth (inaccessible). We thus chose a sursegmentation method whose steps are outlined in Algorithm 1. Sursegmentation consists of segmenting the image into a number of classes strictly superior to the intuitively expected number of classes in the image, and then finding an aggregation criterion of the resulting partition that shows the relevant classes.
![\includegraphics[width=10cm,clip]{algo1.eps}](/articles/aa/full_html/2009/37/aa11416-08/img18.png) |
This method finds the best gathering of points in the feature space X with respect to a cluster quality objective function. It thus relies on both an unsupervised, quantitative and objective evaluation of a clustering result, and on an analysis of the feature vectors spreading in X.
3.2.1 The ASSESS procedure
The literature offers a wide range of evaluation methods for both inter-segmenter comparisons (Sahoo et al. 1988; Chabrier et al. 2004; Zhang et al. 2008a; Borsotti et al. 1998; Weszka & Rosenfeld 1978) and cluster quality evaluation (Halkidi et al. 2001; Rezaee et al. 1998; Zhang et al. 2008b). We focused on and adapted here a cluster validity function to be minimized, first proposed by Xie & Beni (1991) (with the parameter m=2) and generalized by Pal & Bezdek (1995)
This validity index focused on geometrical properties of the clusters in the feature space, through two quantitative indexes:
- separation
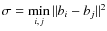 ,
,
- compactness
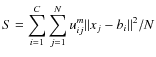 .
.
The numerator
![]() of (3) indicates the compactness of the fuzzy partition, while the denominator indicates the strength of the separation between clusters.
of (3) indicates the compactness of the fuzzy partition, while the denominator indicates the strength of the separation between clusters.
Note that a good partition may produce a small value for the compactness, and that well-separated bi s will produce a high value for the separation.
Hence in order to produce the best clustering performance for the data set X, an optimal
number of clusters can be found by solving the optimization problem:

The upper bound N-1 on the value of the number of cluster c corresponds to the trivial case where each feature vector is treated as a cluster. This upper bound may be replaced with an application-driven empirical bound
3.2.2 The MERGE procedure
Compactness and separation can also be processed for each cluster i separately. An individual validity index can be defined for each cluster by:
The merging process then consists of aggregating the two closest clusters having the largest (i.e. worst) individual validity index. These clusters are geometrically defined either by a huge spreading of their points and/or a close distance to their immediate neighbors.
Figures 2 and 3 present results of this algorithm on a 19.5 nm image, taken on August 03, 2000 during maximal activity (denoted as I2 in the following) with
![]() (including background).
(including background).
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=34mm]{11416f5.eps...
...1416f10.eps}\\
$c^*=3, V = 9885.71$\space & (a)\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg32.png) |
Figure 2: Sursegmentation and merging process, illustrated on image I2. The limb correction was not applied, both to compare results with Barra et al. (2008) and to see the impact of optimal clustering on the final result. a) shows the direct SPoCA segmentation with 3 classes. |
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=42mm]{11416f11.ep...
...degraphics[width=42mm]{11416f12.eps}\\
(a) & (b)\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg33.png) |
Figure 3: Direct SPoCA segmentation with 3 classes a) and improved b) segmentation, illustrated on AR edges in image I2 (detail). |
| Open with DEXTER | |
3.3 Smoothing of region edges
Previous works (Benkhalil et al. 2005; McAteer et al. 2005; Meunier 1999) showed that any segmentation of active regions based on thresholds only creates edges whose shape are very dependent on the value of the chosen threshold. In Barra et al. (2008), we proposed a first alternative to improve the AR edge shape by incorporating a spatial regularization term. Results however were sometimes of poor quality (Fig. 4a), because of the smooth transitions between AR and their surroundings, which generates fractal-shaped edges.
Hence we propose to automatically post-process our segmentation results using morphological operations, see Serra (1983). More precisely, we applied to the initial contour a conditional morphological opening, with a circular isotropic element of size one (see Appendix B for an introduction to mathematical morphology). If
![]() is the image of AR edges stemming from the segmentation of image I, the conditional morphological opening preserves the general shape of AR, and the main geometric structures of AR edges, while smoothing the contours in
is the image of AR edges stemming from the segmentation of image I, the conditional morphological opening preserves the general shape of AR, and the main geometric structures of AR edges, while smoothing the contours in
![]() ,
cutting the narrow ismuthes, and suppressing the small islands and the sharp capes of AR, see Fig. 4b.
The conditional property moreover ensures that the final edge contains pixels whose gray levels are all within the same range of values.
,
cutting the narrow ismuthes, and suppressing the small islands and the sharp capes of AR, see Fig. 4b.
The conditional property moreover ensures that the final edge contains pixels whose gray levels are all within the same range of values.
![\begin{figure}
\par\includegraphics[width=84mm]{11416f13.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg35.png) |
Figure 4: Edge smoothing on image I2. The segmentation of the region of interest is magnified without a) and with b) the smoothing process. |
| Open with DEXTER | |
3.4 Accurately segmenting the coronal holes: using a sensor data fusion process
Separating CH from a filament using EUV intensity only is a challenging task, since both zones have similar temperature, and similar emissivity. Since SPoCA relies here on intensity values only, both CH and filaments have the same signature as defined by the algorithm. The resulting ``CH'' fuzzy map then contains both CH zones and filaments. Separating CH from filaments in this map cannot be performed easily, even with the addition of some topological and morphological constraints that take into account information such as filaments being thin elongated structures.
We propose here a non-real time solution for the accurate segmentation of CH, using a sensor data fusion process. Given a daytime t and a corresponding set of EIT images It (Fig. 5a), an H-alpha image from the Kanzelhoehe observatory taken at t (Fig. 5b) was used to accurately separate filaments from the CH map. Images were roughly spatially registered, using information extracted from their header, by first translating the center of the Sun, then by scaling with respect to the ratio of solar radius. The H-alpha image was then processed to extract filaments (Fig. 5c). Since filaments are dark, well contrasted and thin-elongated structures in this image, a simple method was proposed that allows a fast and reproducible segmentation. We first compute a mean curvature image, by assessing for each pixel (x,y) the trace of the local Hessian matrix H(x,y). A simple empirical threshold (set as 80% of the maximum mean curvature) then allows us to select points with high curvatures, and a search for connected components was begun to suppress isolated pixels. A region growing procedure was finally applied on the resulting image to highlight filaments, which were then reported on the CH fuzzy map. Finally, a region growing technique was applied on the CH fuzzy map to fully extract these components.
![\begin{figure}
\par\mbox{\subfigure[EIT image, taken on 2000-01-20]{
\includegr...
...{
\includegraphics[width = 42mm]{11416f16.eps} }\hspace*{2.1cm}}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg36.png) |
Figure 5: The sensor data fusion process and the extraction of filaments from the CH fuzzy map. |
| Open with DEXTER | |
3.5 Automatic tracking of regions of interest
Since the new version of the SPoCA allows us to accurately segment the regions of interest, we propose to extend this algorithm to the automatic tracking of any region of interest in the on-disc part of the Sun. We illustrate this extension with the automatic tracking of active regions. The idea of the algorithm is to find connected components in a AR fuzzy map, and to follow their mass center in subsequent images. The corresponding algorithm is given in Algorithm 2.
![\includegraphics[width=10cm,clip]{algo2.eps}](/articles/aa/full_html/2009/37/aa11416-08/img37.png) |
Suppose we want to track the biggest active region. Let
![]() denote the AR fuzzy map at date t (
denote the AR fuzzy map at date t (
![]() ). The FindLargestCC procedure finds ARt, the largest connected component (in pixels) in
). The FindLargestCC procedure finds ARt, the largest connected component (in pixels) in
![]() .
The FindCC method is a growing region technique to process the connected region seeded with a given point. The ComputeCenterMass is an easy-to-compute isobarycenter, and the Forecast method applies a translation of a point with a given vector. More precisely, the center of mass Gt-1 of ARt-1 is translated to Gt, such that the vector with start point Gt-1 and end point Gt is equal to the displacement field, denoted vG, observed at pixel Gt-1.
The displacement field between images It-1 and It is estimated with the opticalFlow procedure, which
uses a multi-resolution Lucas and Kanade optical flow scheme (Lucas & Kanade 1981), see Appendix C.
This procedure is simple and fast, and hence allows for a real-time tracking of AR.
.
The FindCC method is a growing region technique to process the connected region seeded with a given point. The ComputeCenterMass is an easy-to-compute isobarycenter, and the Forecast method applies a translation of a point with a given vector. More precisely, the center of mass Gt-1 of ARt-1 is translated to Gt, such that the vector with start point Gt-1 and end point Gt is equal to the displacement field, denoted vG, observed at pixel Gt-1.
The displacement field between images It-1 and It is estimated with the opticalFlow procedure, which
uses a multi-resolution Lucas and Kanade optical flow scheme (Lucas & Kanade 1981), see Appendix C.
This procedure is simple and fast, and hence allows for a real-time tracking of AR.
Although we can suppose that because of the slow motion between It-1 and It, Gt will lie in the trace of ARt-1 in It (and thus a region growing technique may be sufficient, directly starting from Gt in It), we use the optical flow for handling non successive images It and
![]() ,
and also for computing some velocity parameters of the active regions such as the magnitude, the phase, etc, and to allow the tracking of small regions of interest such as coronal bright points.
,
and also for computing some velocity parameters of the active regions such as the magnitude, the phase, etc, and to allow the tracking of small regions of interest such as coronal bright points.
Figure 6 presents an example of an AR tracking on a sequence of images, taken from 2000-08-01 to 2000-08-10. This method is generic enough to be applicable to the tracking of any connected components of a fuzzy map: ARs, but also CHs of any size, or even bright points which can be extracted in the QS after a second iteration of the algorithm.
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width = 26mm]{11416f1...
...mm]{11416f22.eps}\\
2000-08-07&2000-08-08&2000-08-09
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg41.png) |
Figure 6: Example of an AR tracking process. The tracking was performed on an active region detected on 2000-08-04 until 2000-08-09. |
| Open with DEXTER | |
4 Dataset
We applied our segmentation procedure on a set of EIT images taken from February 14th 1997 until April 30th 2005, thus spanning more than 8 years of the 11-year solar cycle. During these 8 years, there were two extended periods without data: from 25 June up to 12 October 1998, and during the whole month of January 1999. Outside these two periods, we consider for almost every day one set of 2 images (17.1 nm, 19.5 nm) taken less than 30 min apart. These images do not contain telemetry missing blocks.
We analyze the on-disc part of these EIT images, which is defined as the disk centered on the Sun and having a radius equal to
![]() ,
,
![]() being the solar radius.
The images have been preprocessed using the standard eit_prep procedure of the
solar software (ssw) library. They are photometrically corrected with the MgII index until May 2005. Image intensities were moreover normalized by their median value.
being the solar radius.
The images have been preprocessed using the standard eit_prep procedure of the
solar software (ssw) library. They are photometrically corrected with the MgII index until May 2005. Image intensities were moreover normalized by their median value.
As in Barra et al. (2008), we compute several parameters of interest. From the multichannel segmentation, we obtain the area covered by each zone (CH, QS, AR), see Fig. 7. Next, for both the 17.1 nm and 19.5 nm channel, we compute the mean (Fig. 8) and integrated (Fig. 9) intensity of each zone. from the multichannel segmentation results (the CH, QS and AR maps behave as masks for both channels). Note that in order to ease the analysis of these time series, we use a cubic interpolation to replace the missing values.
5 Results and discussion
We first show the results of our improved segmentation on one image. We then analyse the time series built with the parameters extracted from the segmentation.
5.1 Segmented image
Figures 2 and 3 show the overlays of our multichannel segmentation procedures on image I2. They show the comparison between the segmentation proposed in Barra et al. (2005,2008) and the improved segmentation described above.
One can see that in the new segmentation, the AR also contains the diffuse regions around them, and as a result the QS is not contaminated by the surroundings of the AR, as was the case in the first version of SPoCA.
Moreover, since we correct for the limb discontinuity and perform segmentation up to
![]() ,
we have a more complete and precise account of the area covered by the different zones.
,
we have a more complete and precise account of the area covered by the different zones.
5.2 Time series of segmented images
![\begin{figure}
\par\includegraphics[height=60mm]{11416f23.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg44.png) |
Figure 7: Results of improved SPoCA: Areas covered by coronal holes (CH), quiet sun (QS), and active regions (AR). |
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[height=60mm]{11416f24.ep...
... \includegraphics[height=60mm]{11416f25.eps}\\ (b)
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg45.png) |
Figure 8: Quantities computed from the improved SPoCA segmentation a) Mean intensity at 17.1 nm b) Mean intensity at 19.5 nm. |
| Open with DEXTER | |
5.2.1 Variability analysis
We now analyse the variations over the solar cycle of the area, mean, and total intensity of the three zones.
We first look at the variation of the relative areas (normalized to the whole surface) in Fig. 7. These areas have been computed with the multichannel procedure, thus using the information at both 17.1 nm and 19.5 nm. In particular, the 19.5 nm channel contains hot temperature information (>10 MK). With no surprise, the area of solar surface occupied by active regions is positively correlated with the solar cycle. The area of coronal holes is small (<![]() )
but still exhibits an anti correlated behavior with respect to the solar cycle; indeed, the presence of many active regions restricts the possibility of regions with open field-lines. The area of the quiet sun is anti-correlated with that of active regions (the correlation coefficient is equal to -0.96). All areas exhibit a very strong modulation due to the solar rotation.
)
but still exhibits an anti correlated behavior with respect to the solar cycle; indeed, the presence of many active regions restricts the possibility of regions with open field-lines. The area of the quiet sun is anti-correlated with that of active regions (the correlation coefficient is equal to -0.96). All areas exhibit a very strong modulation due to the solar rotation.
![\begin{figure}
\par\includegraphics[height=65mm]{11416f26.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg47.png) |
Figure 9: Intensity of CH, QS and AR divided by the total flux, at 17.1 nm and at 19.5 nm. |
| Open with DEXTER | |
Next, the segmentation provided by the improved SPoCA can be used as a mask on 17.1 nm and 19.5 nm images to extract the integrated intensity and the mean for CH, QS and AR.
Figure 9 shows the relative contributions of, respectively, quiet regions, coronal holes, and active regions integrated intensity to the whole solar flux,
for the two bandpasses. Clearly, the coronal hole contribution is very small and becomes still smaller at the maximum of activity when active regions occupy most of the surface. The contribution of active regions ranges from almost zero at the minimum (even at low activity we find that about ![]() of the solar surface looks ``active'') to about 40%
for
of the solar surface looks ``active'') to about 40%
for
![]() and
and ![]() for
for
![]() at the maximum. The stronger contribution of active regions at
at the maximum. The stronger contribution of active regions at
![]() reflects the fact that this line is emitted by a hotter plasma and is thus more sensistive to activity. It is noticeable that only at 19.5 nm, and only at the maximum of solar activity, does the contribution of active region become greater than 50% of the whole solar flux in this waveband.
reflects the fact that this line is emitted by a hotter plasma and is thus more sensistive to activity. It is noticeable that only at 19.5 nm, and only at the maximum of solar activity, does the contribution of active region become greater than 50% of the whole solar flux in this waveband.
Next, we evaluate the time variability along the solar cycle: we compute the variance
of the integrated intensity for, respectively, CH, QS, and AR, and then the ratio of each of these variances to the total variance (defined as the sum of the three variances). These ratios
reveal that AR contributes to ![]() (resp.
(resp. ![]() )
to the total time variability in the 19.5 nm (resp. 17.1 nm) bandpass.
One may wonder if this variability is caused only by the appearance of active regions, or if other zones also exhibit an enhanced intensity. To investigate these issues, we study the variation of the mean intensity for the three regions.
)
to the total time variability in the 19.5 nm (resp. 17.1 nm) bandpass.
One may wonder if this variability is caused only by the appearance of active regions, or if other zones also exhibit an enhanced intensity. To investigate these issues, we study the variation of the mean intensity for the three regions.
A first look at the mean intensities of the quiet areas, the coronal hole and the active regions shows that they are constant over the solar cycle. The fact that the mean intensity of the three extracted features is roughly constant validates both the existence of these features over the solar cycle and our algorithm. In particular, it indicates that the regions we have found are well defined and that there is no contamination of active regions in the quiet area and coronal hole. It is also noticeable that the mean intensity of active region seems constant over the solar cycle. This is consistent with the idea that we can model the solar EUV variation by ``decomposing'' the solar surface into regions of various intensity. The intensity in quiet areas is about three times higher than in coronal holes, both at 17.1 nm and 19.5 nm. These values correspond to a contrast that is slightly larger than the factor two generally accepted (Vernazza & Reeves 1978), but since it is constant over the whole solar cycle we think it is a robust result. The ratio between the active and quiet region intensities equals on average 2.38 for 17.1 nm and 2.58 for 19.5 nm. Here again, these ratios do not change with the solar activity. The higher contrast for the 19.5 nm waveband reflects the fact that this line is formed by a hotter plasma.
![\begin{figure}
\par\includegraphics[height=80mm]{11416f27.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg54.png) |
Figure 10: Zoom on variation of the mean intensity. This small variation is correlated with the solar cycle for each zone. The curve was averaged using a 27-day windows. |
| Open with DEXTER | |
However, a close-up look at these curves show a small variation for both lines and for the three regions, see Fig. 10, where the mean time series have been smoothed with a 27-day windows in order to remove the solar rotation periodic component. This variation is very similar both in amplitude and shape for the two lines and for QS and CH intensities, while it is slightly higher for ARs, see Fig. 9. Furthermore, and very interestingly, it is correlated with the solar cycle in all cases. For the QS and CH, an artefact could explain this increase: the ARs are more tightly constrained in the new SPoCA compared to the previous one. Thus, some material that was previously labeled as AR is now labeled as QS and CH and, as the solar cycle varies, what was previously thought of as AR material is being considered in the QS and CH classes. Indeed, the inspection of temporal evolution (not shown) of the area of the sub-classes that compose the quiet Sun (colored blue, green, and yellow in Fig. 2) reveals that the area of the yellow sub-class -which is the nearest to the actual active regions- increases with the solar activity, while the total quiet sun area decreases. This confirms the previous scenario as a possible explanation for the increase of the mean QS and CH intensity, while the increase of the mean intensity of ARs looks more real. However, it should be noted that the mean intensities of all the sub-classes, yellow one included, also exhibit the same small increase correlated with the solar cycle. This clearly needs to be confirmed by other studies but it suggests that the increase of the intensity is not strictly confined in active regions and that each point on the solar surface contributes to the whole irradiance enhancement. Such a result has been proposed by Schühle et al. (2000), but has not been confirmed since them; in particular Kretzschmar et al. (2004) has shown that it is difficult to identify rigourously a variation of the quiet-Sun intensities with the solar cycle because of the already high intrinsic variability of the quiet solar areas. Both studies were made with SOHO/SUMER data. The results presented here support the idea that the mean intensities of the quiet areas, at least as usually defined e.g. without removing bright points first, do increase with the increasing solar activity, and shows for the first time an increase of the coronal hole and active region intensities. Although this increase is best seen in the active regions, this could be caused by some kind of diffuse magnetic activity occurring everywhere and whose typical size (if any) is not resolved with the current resolution. For example this could be associated with some increase of ``nanoflaring activity'', that is, an increase of the rate of small amplitude power law distributed reconnection events. However, since nanoflaring is not the only mechanism for coronal heating, another explanation for these observations could be that the dissipation by wave turbulence is stronger at solar maximum.
This contribution of each point remains small (a few percent: ![]() for 17.1 nm and
for 17.1 nm and ![]() for 19.5 nm) in comparison with the increasing number of active regions appearing on the solar surface with the solar cycle.
for 19.5 nm) in comparison with the increasing number of active regions appearing on the solar surface with the solar cycle.
5.2.2 Periodicity analysis
In order to assess nonstationary phenomena and find periodicities in the time series of Figs. 7-9, we perform a Morlet wavelet analysis. The Morlet wavelet coefficients were computed with the toolbox Yet Another Wavelet toolbox (YAWtb) (http://rhea.tele.ucl.ac.be/yawtb/), while the cone of influence and contours indicating significant coefficients (assuming a red noise background) were obtained with the wavelet software provided by Torrence & Compo (1998).
We compute the global wavelet spectrum (or energy spectrum) by summing, for each
periodicity ![]() ,
the modulus of wavelet coefficients present at
,
the modulus of wavelet coefficients present at ![]() .
Local maxima of the energy spectrum then give the characteristic periodicities of the time series.
.
Local maxima of the energy spectrum then give the characteristic periodicities of the time series.
Within the cone of influence (COI), we look at significant wavelet coefficients at the 95% confidence level in order to determine the significiant characteristic periodicities.
The main periodicities found with this method are related to the solar differential rotation, see Table 1. Apart from the case of mean intensity values in 17.1 nm, the periodicities found for ARs are smaller than for CH and QS. This is consistent with the general fact that ARs are located at lower latitudes than CHs, and hence turn faster.
Besides the solar rotation period, we found two other periodicities. First, the area of ARs shows between 2000 and 2003 a periodicity of 495 days (1.3 year), see Fig. 11a. This could be related to the 1.3y periodicity observed in sunspot time series in Krivova & Solanki (2002) in many datasets (including geophysics), or it might be a casual effect due to the presence of the two local maxima (around 2001 and 2002) in the corresponding time series. Second, we observe a 495 day period in the time series of AR area, and a transient periodicity of 416 days between 1999 and 2002 for the CH mean observed in 17.1 nm. These two periodicities might represent a multiple of the 26 days rotation period.
Table 1: Main periodicities (in days) of the area covered by coronal holes (CH), quiet sun (QS), and active regions (AR).
![\begin{figure}
\begin{tabular}{c}
\includegraphics[height=70mm,clip]{11416f28....
...udegraphics[height=70mm,clip]{11416f29.eps}\\ (b)
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg60.png) |
Figure 11:
Periodicity analysis for a) area of AR and b) mean intensity of CH in 17.1 nm.
The white horizontal lines indicate the solar rotation period (
|
| Open with DEXTER | |
6 Conclusion and future work
We proposed in this paper a segmentation procedure for EUV images. Our algorithm is stable over time, corrects for limb brightening effects, computes an optimal clustering with respect to the regions of interest using a quality criterion, and proposes an accurate definition of the cluster edges.
We applied our procedure on 8 years of EIT data in order to separate AR, CH, QS, and we analyzed extracted time series of area, mean and integrated intensity evolution for each zone. Area and integrated intensity evolution is consistent with previous knowledge. In addition, we show that there exists a small variation of the mean intensity that is similar in shape and amplitude for the three zones, and that is correlated with the solar cycle. These results support the idea that the mean intensities of all solar areas increase with the increasing solar activity, although more work is needed to establish this more clearly for QS and CH (even if Veselovsky et al. 2001 have already demonstrated the QS variability). In a forthcoming paper, we plan to analyze in more detail the properties of this small variation.
We now enumerate some future applications for our segmentation procedure.
First, note that by computing a segmentation of the quiet sun zone alone, it is possible to isolate bright points. The aim would then be e.g. to study the evolution of their density during the solar cycle. Second, the segmentation procedure is generic enough to be applicable to transformed data such as DEM maps. In this case, SPoCA will determine for a given temperature, zones of similar emission measure.
Finally, we will adapt the algorithm to deal with SDO/AIA data at full resolution. It would then be of interest to monitor e.g. the evolution of pertinent active regions properties, especially before a flare. We saw that filament channels seen in coronal EUV passbands are often erroneously classified as ``coronal holes'' in the segmentation. Taking into account all AIA channels, and in particular the ones sampling the Transition Region and the hot corona, should provide a solution to the separation problem, e.g., via an absorption analysis (Daw et al. 1995).
Acknowledgements
Funding of V.D. and J.F.H. by the Belgian Federal Science Policy Office (BELSPO) through the ESA/PRODEX LYRA and SIDC Data Exploitation programs is hereby appreciatively acknowledged. The authors thank Francesca Zucharello for providing the Himage from Kanzelhohe, and SIDC for the data exploitation.
Appendix A: Mathematical background of the SPoCA
Let I=(Ij) be the image to be processed,
SPoCA is an iterative algorithm that searches for C compact clusters
in X by computing both a fuzzy partition matrix
![]() ,
,
![]() being the membership degree of
being the membership degree of ![]() to class i, and unknown cluster centers
to class i, and unknown cluster centers
![]() .
It uses iterative optimizations to find the minimum of a constrained objective function:
.
It uses iterative optimizations to find the minimum of a constrained objective function:
subject for all
![]() to
to
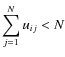 ,
for all
,
for all
![]() to
to
![]() ,
where m>1 is a fuzzification parameter (Bezdek et al. 1997), and
,
where m>1 is a fuzzification parameter (Bezdek et al. 1997), and
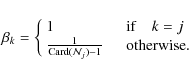 |
(A.2) |
Parameter

The first term in (A.1) is the total fuzzy intra-cluster variance, while the second term prevents the trivial solution U=0 and relaxes the probabilistic constraint
 ,
,
We showed in Barra et al. (2008) that U and B could be computed as

SPoCA provides thus fuzzy maps Ui=(uij) for
In order to ensure the temporal stability of the method, we first determined the class centers B by clustering with the improved SPoCA a subset sampling representative EIT images. We picked one day per month, from November 1997 to May 2005 (except during the July-September 1998 period and in January 1999), and we kept one (17.1 nm, 19.5 nm) acquisition in these days. This gives 95 images in each channel; this image dataset is denoted SampleSet in the following. We ran SPoCA with a subset of SampleSet, containing M images and always starting in November 1997. We then plotted the evolution of each class center component
![]() as a function of M for each class i,
as a function of M for each class i,
![]() ,
and we retain for each channel the cluster centers corresponding to stable bi values with respect to an increasing M, and we use the corresponding B for the full SPoCA analysis described below.
,
and we retain for each channel the cluster centers corresponding to stable bi values with respect to an increasing M, and we use the corresponding B for the full SPoCA analysis described below.
Appendix B: An introduction to mathematical morphology
Mathematical morphology is a set-theoretic method of signal and image analysis providing a quantitative description of geometrical structures (Serra 1983). Most of the morphological operations are based on simple expanding and shrinking operations on binary or quantitized signals and images. In the following, we only address the mathematical morphology applied to 2D grey-level images, and we denote AR the binary image of AR edges stemming from the segmentation of image I.
The two basic morphological set transformations are erosion and dilation, which involve the interactions between an image I and a structuring
set ![]() ,
called the structuring element. Typically
,
called the structuring element. Typically ![]() is a circular disc in the plane, but it can be of any shape, the choice being driven by the application.
Let
is a circular disc in the plane, but it can be of any shape, the choice being driven by the application.
Let ![]() be two subsets of
be two subsets of
![]() .
The dilation of I by
.
The dilation of I by ![]() is the set
is the set

where
The erosion of I by ![]() is the set
is the set
Roughly speaking, dilation is used to increase the size of objects in I, conditional to the shape of the structuring element
Dilation and erosion are duals of each other with respect to set complementation and reflection. Erosion and dilation can be used in a variety of ways, in parallel and series, to give other transformations including thickening, thinning, skeletonisation and many others. Two very important transformations are opening and closing. If, intuitively, dilation expands an image object and erosion shrinks it, opening generally smooths a contour in an image, breaking narrow isthmuses and eliminating thin protrusions, whereas closing tends to narrow smooth sections of contours, fusing narrow breaks and long thin gulfs, eliminating small holes, and filling gaps in contours.
More precisely, the opening of I by ![]() is defined by
is defined by
and the closing is defined by
A classical morphological opening is defined by
Appendix C: The optical flow algorithm
A fundamental problem in vision and image processing is the measurement of image velocity, or image flow, which consists of computing an approximation of a 2D motion field, projection of the 3D velocities of surface points onto the imaging surface, from spatiotemporal images. Many methods have been proposed to address this issue, and we applied in this article a differential technique first developed in Lucas & Kanade (1981).
Differential techniques compute velocities from spatiotemporal derivatives of image intensities, or low-pass or band pass filtered version of the image. If I(x,y,t) denotes the gray-level of pixel (x,y) at date t, they require this function to be differentiable, and assume the conservation of image intensities through time. This leads to an under-determined problem
where
where
where W(x,y) denotes a window function that gives more influence to constraints at the center of the neighborhood than those at the surroundings. The solution of (C.2) is given by
where for n points

and so
![]() .
.
In this paper, we applied a multiresolution version of this algorithm: the images were downsampled to a given lowest resolution, then the optical flow algorithm was computed for this resolution, and serves as an initialization for the computation of optical flow at the next resolution. This process was iteratively applied until the initial resolution was reached. This allows a coarse-to-fine estimation of velocities.
References
- Aboudarham, J., Scholl, I., Fuller, N., et al. 2008, Annales Geophysicae, 26, 243 [NASA ADS]
- Andretta, V., Del Zanna, G., & Jordan, S. D. 2003, A&A, 400, 737 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Antoine, J., Demanet, L., Hochedez, J., et al. 2002, Physicalia magazine, 24, 93 (In the text)
- Barra, V., Delouille, V., Hochedez, J., & Chainais, P. 2005, in Proceedings of the 11th European Solar Physics Meeting, The Dynamic Sun: Challenges for Theory and Observations, ESA SP-600, 77.1 (In the text)
- Barra, V., Delouille, V., & Hochedez, J. 2008, Adv. Space Res., 42, 917 [NASA ADS] [CrossRef]
- Benkhalil, A., Zharkova, V., Zharkov, S., & Ipson, S. 2003, in Proceedings of the AISB'03 Symposium on Biologically-inspired Machine Vision, Theory and Application, 66
- Benkhalil, A., Zharkova, V., Ipson, S., & Zharkov, S. 2005, Int. J. Comput. Appl., 12, 21
- Berrili, F., Moro, D. D., & Russo, S. 2005, ApJ, 632, 677 [NASA ADS] [CrossRef]
- Bezdek, J., Hall, L. O., Clark, M., Goldof, D., & Clarke, L. 1997, Statistical Methods in Medical Research, 6, 191 [CrossRef] (In the text)
- Bornmann, P., Winkelman, D., & Kohl, T. 1996, in Proceedings of the solar terrestrial predictions workshop (Japan: Hitachi), 23
- Borsotti, M., Campadelli, P., & Schettini, R. 1998, Pattern Recognition Letters, 19, 741 [CrossRef]
- Brajsa, R., Wöhl, H., Vrsnak, B., et al. 2001, A&A, 374, 309 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bratsolis, E., & Sigelle, M. 1998, A&AS, 131, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chabrier, S., Emile, B., Laurent, H., Rosenberger, C., & Marche, P. 2004, in ICPR '04: Proceedings of the Pattern Recognition, 17th International Conference on (ICPR'04) Volume 1 (Washington, DC, USA: IEEE Computer Society), 576
- Daw, A., Deluca, E. E., & Golub, L. 1995, ApJ, 453, 929 [NASA ADS] [CrossRef] (In the text)
- Delaboudiniere, J.-P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] (In the text)
- Dudok de Wit, T. 2006, Sol. Phys., 239, 519 [NASA ADS] [CrossRef]
- Fuller, N., Aboudarham, J., & Bentley, R. 2005, Sol. Phys., 227, 61 [NASA ADS] [CrossRef] (In the text)
- Gao, J., Zhou, M., & Wang, H. 2002, Sol. Phys., 205, 93 [NASA ADS] [CrossRef]
- Halkidi, M., Batistakis, Y., & Vazirgiannis, M. 2001, in SSDBM '01: Proceedings of the Thirteenth International Conference on Scientific and Statistical Database Management (Washington, DC, USA: IEEE Computer Society), 3
- Hill, M., Castelli, V., Chu-Sheng, L., et al. 2001, in Proceedings of the IEEE International Conference on Image Processing, 834
- Kretzschmar, M., Lilensten, J., & Aboudarham, J. 2004, A&A, 419, 345 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Krishnapuram, R., & Keller, J. 1993, IEEE Transactions on Fuzzy Systems, 1, 98 [CrossRef] (In the text)
- Krivova, N. A., & Solanki, S. K. 2002, A&A, 394, 701 [NASA ADS] [CrossRef] [EDP Sciences]
- Lucas, B., & Kanade, T. 1981, in Proceedings of Imaging understanding workshop, 121 (In the text)
- McAteer, R. T. J., Gallagher, P. T., & Ireland, J. 2005, ApJ, 631, 628 [NASA ADS] [CrossRef]
- Meunier, N. 1999, ApJ, 515, 801 [NASA ADS] [CrossRef]
- Nieniewski, M. 2002, in Proceedings of the SOHO 11 Symposium on From Solar Min to Max: Half a Solar Cycle with SOHO, ed. N. E. P. D. A. Wilson, Noordwijk, 323 (In the text)
- Ortiz, A. 2005, Adv. Space Res., 35, 350 [NASA ADS] [CrossRef]
- Pal, N., & Bezdek, J. 1995, IEEE Trans. Fuzzy Systems, 3, 370 [CrossRef] (In the text)
- Pettauer, T., & Brandt, P. 1997, Sol. Phys., 175, 197 [NASA ADS] [CrossRef]
- Portier-Fozzani, F., Vandame, B., Bijaoui, A., Maucherat, A., & the EIT team. 2001, Sol. Phys., 201, 271 [NASA ADS] [CrossRef] (In the text)
- Preminger, D., Walton, S., & Chapman, G. 1997, Sol. Phys., 171, 303 [CrossRef]
- Qahwaji, R. 2003, in Proceedings of the Solar image recognition workshop (Brussels, Belgium) (In the text)
- Rezaee, M. R., Lelieveldt, B. B., & Reiber, J. H. 1998, Pattern Recognition Letters, 19, 237 [CrossRef]
- Robbrecht, E., Berghmans, D., & der Linden, R. V. 2006, Adv. Space Res., 38, 475 [NASA ADS] [CrossRef] (In the text)
- Sahoo, P. K., Soltani, S., Wong, A. K., & Chen, Y. C. 1988, Computer Vision Graphics and Image Processing, 41, 233 [CrossRef]
- Schühle, U., Wilhelm, K., Hollandt, J., & Lemaire, P. 2000, A&A, 354 (In the text)
- Serra, J. 1983, Image Analysis and Mathematical Morphology (Orlando, FL, USA: Academic Press, Inc.) (In the text)
- Steinegger, M., Bonet, J., & Vazquez, M. 1997, Sol. Phys., 171, 303 [NASA ADS] [CrossRef]
- Steinegger, M., Bonet, J., Vazquez, M., & Jimenez, A. 1998, Sol. Phys., 177, 279 [NASA ADS] [CrossRef] (In the text)
- Torrence, C., & Compo, G. 1998, Bulletin of the American Meteorological Society, 79, 61 [NASA ADS] [CrossRef], http://atoc.colorado.edu/research/wavelets/ (In the text)
- Turmon, M., Pap, J., & Mukhtar, S. 2002, ApJ, 568, 396 [NASA ADS] [CrossRef] (In the text)
- Vernazza, J. E., & Reeves, E. M. 1978, ApJS Series, 37, 485 [CrossRef] (In the text)
- Veronig, A., Steinegger, M., Otruba, W., et al. 2000, in Proceedings of the 1st Solar and Space Weather Euroconference, ed. N. E. P. D. A. Wilson, Noordwijk, 455 (In the text)
- Veronig, A., Steinegger, M., Otruba, W., et al. 2001, Harvard Observatory Bulletin, 195 (In the text)
- Veselovsky, I. S., Zhukov, A. N., Dmitriev, A. V., et al. 2001, Sol. Phys., 201, 27 [NASA ADS] [CrossRef] (In the text)
- Wagstaff, K., Rust, D. M., LaBonte, B. J., & Bernasconi, P. N. 2003, in Proceedings of the Solar image recognition workshop (Brussels, Belgium)
- Weszka, J. S., & Rosenfeld, A. 1978, IEEE Transactions on Systems, Man, and Cybernetics, SMC-8(8), 622
- Worden, J., Woods, T., Neupert, W., & Delaboudiniere, J. 1999, ApJ, 965 (In the text)
- Xie, X. L., & Beni, G. 1991, IEEE Transactions on Pattern Analysis and Machine Intelligence, 13, 841 [CrossRef] (In the text)
- Young, C., Gallagher, P., & Myers, D. 2003, AGU Fall Meeting Abstracts, B543 (In the text)
- Zhang, H., Fritts, J. E., & Goldman, S. A. 2008a, Computer Vision and Image Understanding, 110, 260 [CrossRef]
- Zhang, Y., Wang, W., Zhang, X., & Li, Y. 2008b, Information Science, 178, 1205 [CrossRef]
- Zharkov, S., Zharkova, V., Ipson, S., & Benkhalil, A. 2004, in Proceedings of the 8th International Conference on Knowledge-Based Intelligent Information and Engineering Systems (KES2004), 446
- Zharkova, V., & Schetinin, V. 2003, in Proceedings of the seventh International Conference on Knowledge-Based Intelligent Information and Engineering Systems (KES-03), 148
All Tables
Table 1: Main periodicities (in days) of the area covered by coronal holes (CH), quiet sun (QS), and active regions (AR).
All Figures
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[height=40mm]{11416f1.eps...
...eps}\\
(c) Vertical profile & (d) Horizontal profile
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg17.png) |
Figure 1: a) Original image. The vertical line and the horizontal line show the location of profile. b) Image with limb brightness enhancement corrected. c) The intensity along the vertical profile before and after correction. d) The intensity along the horizontal profile before and after correction. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=34mm]{11416f5.eps...
...1416f10.eps}\\
$c^*=3, V = 9885.71$\space & (a)\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg32.png) |
Figure 2: Sursegmentation and merging process, illustrated on image I2. The limb correction was not applied, both to compare results with Barra et al. (2008) and to see the impact of optimal clustering on the final result. a) shows the direct SPoCA segmentation with 3 classes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=42mm]{11416f11.ep...
...degraphics[width=42mm]{11416f12.eps}\\
(a) & (b)\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg33.png) |
Figure 3: Direct SPoCA segmentation with 3 classes a) and improved b) segmentation, illustrated on AR edges in image I2 (detail). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=84mm]{11416f13.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg35.png) |
Figure 4: Edge smoothing on image I2. The segmentation of the region of interest is magnified without a) and with b) the smoothing process. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\subfigure[EIT image, taken on 2000-01-20]{
\includegr...
...{
\includegraphics[width = 42mm]{11416f16.eps} }\hspace*{2.1cm}}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg36.png) |
Figure 5: The sensor data fusion process and the extraction of filaments from the CH fuzzy map. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[width = 26mm]{11416f1...
...mm]{11416f22.eps}\\
2000-08-07&2000-08-08&2000-08-09
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg41.png) |
Figure 6: Example of an AR tracking process. The tracking was performed on an active region detected on 2000-08-04 until 2000-08-09. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=60mm]{11416f23.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg44.png) |
Figure 7: Results of improved SPoCA: Areas covered by coronal holes (CH), quiet sun (QS), and active regions (AR). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[height=60mm]{11416f24.ep...
... \includegraphics[height=60mm]{11416f25.eps}\\ (b)
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg45.png) |
Figure 8: Quantities computed from the improved SPoCA segmentation a) Mean intensity at 17.1 nm b) Mean intensity at 19.5 nm. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=65mm]{11416f26.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg47.png) |
Figure 9: Intensity of CH, QS and AR divided by the total flux, at 17.1 nm and at 19.5 nm. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=80mm]{11416f27.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg54.png) |
Figure 10: Zoom on variation of the mean intensity. This small variation is correlated with the solar cycle for each zone. The curve was averaged using a 27-day windows. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\begin{tabular}{c}
\includegraphics[height=70mm,clip]{11416f28....
...udegraphics[height=70mm,clip]{11416f29.eps}\\ (b)
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/37/aa11416-08/Timg60.png) |
Figure 11:
Periodicity analysis for a) area of AR and b) mean intensity of CH in 17.1 nm.
The white horizontal lines indicate the solar rotation period (
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



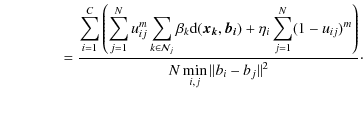
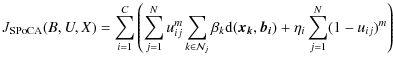
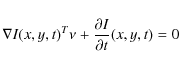
![\begin{displaymath}\displaystyle\sum_{(x,y)\in\Omega} W^2(x,y)\left [\nabla I(x,y,t)^T\nu + \frac{\partial I}{\partial t}(x,y,t)\right ]^2
\end{displaymath}](/articles/aa/full_html/2009/37/aa11416-08/img95.png)