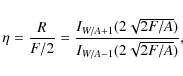| Issue |
A&A
Volume 504, Number 3, September IV 2009
|
|
|---|---|---|
| Page(s) | L5 - L8 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200912746 | |
| Published online | 18 August 2009 | |
LETTER TO THE EDITOR
Accurate rate coefficients for models of interstellar gas-grain chemistry
I. Lohmar1 - J. Krug1 - O. Biham2
1 - Institute for Theoretical Physics, University of Cologne, Cologne, Germany
2 - Racah Institute of Physics, The Hebrew University, Jerusalem 91904, Israel
Received 22 June 2009 / Accepted 28 July 2009
Abstract
Aims. The methodology for modeling grain-surface chemistry has been greatly improved by taking into account the grain size and fluctuation effects. However, the reaction rate coefficients currently used in all practical models of gas-grain chemistry are inaccurate by a significant amount. We provide expressions for these crucial rate coefficients that are both accurate and easy to incorporate into gas-grain models.
Methods. We use exact results obtained in earlier work, where the reaction rate coefficient was defined by a first-passage problem, which was solved using random walk theory.
Results. The approximate reaction rate coefficient presented here is easy to include in all models of interstellar gas-grain chemistry. In contrast to the commonly used expression, the results that it provides are in perfect agreement with detailed kinetic Monte Carlo simulations. We also show the rate coefficient for reactions involving multiple species.
Key words: astrochemistry - ISM: clouds - ISM: molecules - dust, extinction - molecular processes
1 Introduction
The chemistry in interstellar clouds of gas and dust is very complex, consisting of reactions taking place in the gas phase as well as on the surfaces of dust grains (Herbst 1995). Of the latter reactions, the formation of molecular hydrogen (Hollenbach et al. 1971) is of particular importance, but many more processes have been identified (Hasegawa et al. 1992). Modeling of these complex gas-grain chemical networks is important to the understanding of the observed chemical complexity in interstellar clouds and the effects of those molecules on gravitational collapse and star formation (Herbst 1995; Hartquist & Williams 1995; Tielens 2005).
While for gas-phase reactions, rate equations are widely used and fully appropriate, for grain surface chemistry they were found to be inaccurate for a wide range of astrophysically relevant conditions (Lederhendler & Biham 2008; Biham et al. 2005; Biham & Lipshtat 2002; Tielens 1995; Caselli et al. 1998; Lohmar & Krug 2006). To address this problem, modified rate equations were proposed (Stantcheva et al. 2001; Caselli et al. 1998; Garrod 2008). They were found to provide improved results, but involve ad-hoc and uncontrolled approximations. The master equation, describing the time evolution in the probability distribution of the number of reactants on the grain, provides a complete and accurate description of the reactions on grain surfaces (Biham & Lipshtat 2002; Biham et al. 2001; Green et al. 2001).
The surface chemistry was also studied using stochastic simulations (Charnley 2001; Tielens & Hagen 1982). Kinetic Monte Carlo simulations (KMC) have been developed for different surface morphologies (Cuppen & Herbst 2005; Chang et al. 2005).
An important advantage of approaches based on differential equations is that they can easily be coupled to the rate equations of gas-phase chemistry. The difficulty with the master equation is that the number of equations quickly proliferates as the number of reactive species on the grains increases, thus approximations are needed (Stantcheva & Herbst 2003; Stantcheva et al. 2002). From the master equation, it is possible to construct a set of moment equations that account correctly for the reaction rates on grain surfaces (Barzel & Biham 2007b,a; Lipshtat & Biham 2003).
Here we consider the form of the rate coefficients that enter the models. Apart from KMC simulations, all approaches to grain-surface chemistry feature the sweeping rate A as a crucial parameter. This rate coefficient governs the reaction rate on the surface, where there is competition between diffusion-mediated reaction and desorption. Without a precise definition of A, the expression A=a/S is widely used, where a is the hopping rate between adjacent adsorption sites and S is the number of these sites on the grain. This expression does not account for the competition between reaction and desorption. It also does not account for the peculiarities of two-dimensional diffusion.
Lohmar & Krug (2006) introduced a proper definition of the rate coefficient A in terms of the two-particle encounter probability. These authors evaluated it exactly for a single-species reaction on a closed two-dimensional surface where the adsorption sites form a regular lattice (Lohmar & Krug 2006,2009). The result was compared to the conventional approximation for A, which was found to deviate significantly. However, the exact expression contains a large sum of terms, which is costly to evaluate in practice.
In this letter, we present an expression for the reaction rate coefficient that is both accurate and easy to evaluate. We compare the reaction rates obtained using this expression to those obtained from KMC simulations and find perfect agreement. We also generalize the expression to the case of reactions involving multiple species.
2 Review of earlier results
There is no need here to elaborate on the various analytical approaches to grain-surface reaction kinetics, which we cited before. Throughout, we consider a system of S adsorption sites arranged in a two-dimensional quadratic square lattice with periodic boundaries, onto which atoms impinge at a certain homogeneous flux F=fS. They perform nearest-neighbor hops with (undirected) rate a and desorb at a rate ![]() .
The sweeping rate A then appears in all approaches as the pre-factor in the recombination term and the corresponding production rate. For example, the rate equation for the mean number of particles on the grain,
.
The sweeping rate A then appears in all approaches as the pre-factor in the recombination term and the corresponding production rate. For example, the rate equation for the mean number of particles on the grain,
![]() ,
reads
,
reads
![]() ,
with a production rate
,
with a production rate
![]() of molecules. In the master equation and the moment equations, the latter rate becomes
instead
of molecules. In the master equation and the moment equations, the latter rate becomes
instead
![]() (Biham & Lipshtat 2002; Lipshtat & Biham 2003, e.g.), where the moments
(Biham & Lipshtat 2002; Lipshtat & Biham 2003, e.g.), where the moments
![]() ,
and P(N) is the probability of having N particles on the grain at a given time. Any adsorbed atom may end up either reacting (with rate A) or desorbing (with rate W). Therefore, the probability for an atom to end up reacting
is given by p=A/(A+W). With this, we can define A by means of (Lohmar & Krug 2006)
,
and P(N) is the probability of having N particles on the grain at a given time. Any adsorbed atom may end up either reacting (with rate A) or desorbing (with rate W). Therefore, the probability for an atom to end up reacting
is given by p=A/(A+W). With this, we can define A by means of (Lohmar & Krug 2006)
where p is the encounter probability that two specific particles present on the grain meet before one of them desorbs. If atoms only react with a certain probability upon encounter, p is simply multiplied by this probability. In Sect. 5 below, we derive the corresponding relation in the context of multi-species reactions, and also show how the encounter probability generalizes to that case.
The encounter probability has been studied in great detail (Lohmar & Krug 2006,2009). Generally, it features two regimes: the ``small-grain'' regime, where ![]() and encounter is almost sure,
and encounter is almost sure,
![]() ,
and the ``large-grain'' regime, where
,
and the ``large-grain'' regime, where ![]() and encounters are rare,
and encounters are rare, ![]() .
The best model at hand is given by a discrete-time random walk analysis. Well-known results then yield p in terms of a single sum, and the asymptotic behavior is given by (Lohmar & Krug 2009)
.
The best model at hand is given by a discrete-time random walk analysis. Well-known results then yield p in terms of a single sum, and the asymptotic behavior is given by (Lohmar & Krug 2009)
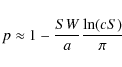 |
(2) |
(with a numerical constant
Using Eq. (1) thus yields the small-grain asymptotic
and for large grains,
This behavior is largely independent of the precise model used to obtain p, the latter only affecting the pre-factor inside the logarithm (Lohmar & Krug 2009). The logarithmic factor in Eqs. (4) and (5) reflects the return probability of a two-dimensional random walker (``back diffusion'') and as such, is also typical of other two-dimensional diffusion problems (Krug 2003).
3 Practical approximation
The exact expressions for p are typically complicated, but the asymptotic results for the sweeping rate of interest are fairly simple. Moreover, its functional form is the same in both regimes, only differing in the argument to the logarithm, which naturally suggests an interpolation formula.
We first considered to simply use the minimal argument to the logarithm, making the dependence continuous and producing the correct limiting behavior in both regimes. While this appears to be natural and is very easy to implement, it also introduces a cusp to the dependence, and it is an arbitrary choice: any function of cS and 8a/W that approaches the smaller argument in the corresponding limit could be used as well. We thus tested
![]() instead. Evidently, this has the proper limits for n>0, and the exponent can be used to tune the behavior in-between; the minimum function corresponds to
instead. Evidently, this has the proper limits for n>0, and the exponent can be used to tune the behavior in-between; the minimum function corresponds to
![]() .
For several values of
.
For several values of ![]() ,
we ``visually'' tuned the exponent to yield the smallest relative deviation from the exact values, and ended up at values
,
we ``visually'' tuned the exponent to yield the smallest relative deviation from the exact values, and ended up at values
![]() ,
which decrease the maximum deviation with respect to the exact result from between 3-7% (for
the min function) to
,
which decrease the maximum deviation with respect to the exact result from between 3-7% (for
the min function) to
![]() th of this value. Numerically, this however is an extraordinary complication. Being so close to unity, n=1 is a feasible choice instead, and this still decreases the maximum deviation by a factor of about 1/6 in the examples shown below. Consequently, we propose the approximation
th of this value. Numerically, this however is an extraordinary complication. Being so close to unity, n=1 is a feasible choice instead, and this still decreases the maximum deviation by a factor of about 1/6 in the examples shown below. Consequently, we propose the approximation
where
3.1 Comparison
In Fig. 1, we present the exact sweeping rate together with the approximate expression in Eq. (6), both normalized by the conventional approximation a/S.
The approximation proposed above is in perfect agreement with the exact result. Using thermal activation of rates with activation energies for amorphous carbon as given by Katz et al. (1999),
W/a=10-3 occurs at
![]() ,
and the other values at
,
and the other values at
![]() and
and
![]() ,
respectively. The discrepancy with respect to the conventional approximation is
found to be most pronounced for large grains. We note that even for the smallest grains, where the correction is least severe, the factor is still well below unity.
,
respectively. The discrepancy with respect to the conventional approximation is
found to be most pronounced for large grains. We note that even for the smallest grains, where the correction is least severe, the factor is still well below unity.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12746fg1.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12746-09/Timg27.png) |
Figure 1:
Ratio between the correct sweeping rate A and the
conventional approximation a/S, as obtained from the exact expression for A (solid lines) and from the approximate form (circles) given by Eq. (6), for three different
values of |
| Open with DEXTER | |
3.2 Lattice-type effects
In the above, we considered the case of a quadratic square lattice. The restriction to the quadratic case, in which the lattice extends to the same lengths in both dimensions, is not easily removed; indeed, rectangular lattices exhibit a more complex behavior than desired for a simple model (Lohmar & Krug 2009). Different lattice types can be examined rather easily however, and we also considered the triangular lattice. For the exact expressions, the effect on the encounter probability p as well as the sweeping rate A has been shown to be minute throughout (Lohmar & Krug 2006,2009). In the approximation presented herein, the triangular lattice simply amounts to a change in the pre-factors in Eq. (6), namely
![\begin{displaymath}%
A \approx \frac{a}{S} \cdot \frac{2\pi}{\sqrt{3}}
\left[ \ln \frac{1}{1/(\tilde cS)+W/(12a)} \right]^{-1},
\end{displaymath}](/articles/aa/full_html/2009/36/aa12746-09/img28.png) |
(7) |
where now
3.3 Langmuir-Hinshelwood rejection
Expressions for the encounter probability given so far include coinciding initial positions of both particles. The question of whether Langmuir-Hinshelwood rejection should be accounted for on the
``global'' level of the surface-chemistry model is beyond the scope of this Letter; most likely, it is relevant only for H and D atoms. Irrespective of this, we are interested here in the most accurate numerical value for the reaction rate coefficient as opposed to a consistent theoretical framework (e.g., one may even use rate equations in the end). Consequently, one might want to use
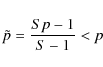 |
(8) |
for the encounter probability, which does not permit coinciding initial positions (Lohmar & Krug 2009). The implied change in the sweeping rate is given by
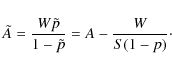 |
(9) |
We evaluate this for both regimes separately. For small grains,
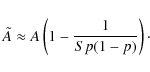 |
(10) |
Here,
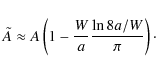 |
(11) |
Since both S as well as a/W can safely be assumed to be larger than a few hundred, the relative corrections to A are below
4 Kinetic Monte Carlo simulations
We now show that using the approximation in Eq. (6) in analytical approaches is in excellent agreement with KMC simulations. In our context, we restrict ourselves to a proof-of-principle comparison, hence we treat only the case of single-species recombination. We also use the master equation approach as the most precise model, to avoid discrepancies that might arise from factors unrelated to our approximations. In practice, one would use an approximation such as the moment equations (Lipshtat & Biham 2003), which have been shown to produce accurate results for a broad range of conditions, and to be applicable to large-scale astrochemistry simulations (Barzel & Biham 2007b,a).
The single-species master equation admits a stationary solution (Biham & Lipshtat 2002; Green et al. 2001). The efficiency ![]() of the process is then given by the production rate R (molecules produced on the grain per unit time) normalized by the influx, and one obtains
of the process is then given by the production rate R (molecules produced on the grain per unit time) normalized by the influx, and one obtains
where
Our KMC simulations use a standard algorithm (described, e.g., in Chang et al. 2005), which has been suitably optimized for the peculiarities of our system, and the code has been tested extensively. Atoms impinging onto occupied sites are rejected by the Langmuir-Hinshelwood mechanism, while we do not account for this process in the analytical treatment - this illustrates that the framework presented here is fully appropriate for moderate coverages (i.e., for the high-temperature drop in efficiency). We also wait for a long enough time to establish steady-state conditions, and follow the system for 108 impingements.
Surface parameters are chosen as found experimentally for amorphous carbon surfaces (Katz et al. 1999), with thermal activation energies
![]() ,
,
![]() ,
and an attempt frequency
,
and an attempt frequency
![]() .
With experimentally determined site
densities and assuming standard gas phase conditions (hydrogen atom density of
.
With experimentally determined site
densities and assuming standard gas phase conditions (hydrogen atom density of
![]() at a temperature of
at a temperature of
![]() ), one obtains an H influx f=7.3
), one obtains an H influx f=7.3 ![]()
![]() (Biham et al. 2001). For these conditions and a grain temperature of
(Biham et al. 2001). For these conditions and a grain temperature of
![]() ,
the results of the KMC simulations are compared to the master equation steady-state efficiency in Eq. (12) using either the approximation to A given by Eq. (6) or the conventional
,
the results of the KMC simulations are compared to the master equation steady-state efficiency in Eq. (12) using either the approximation to A given by Eq. (6) or the conventional
![]() in Fig. 2. Evidently, the agreement is perfect using the approximation of A given in Eq. (6), while the conventional approximation is in significant disagreement.
in Fig. 2. Evidently, the agreement is perfect using the approximation of A given in Eq. (6), while the conventional approximation is in significant disagreement.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12746fg2.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12746-09/Timg51.png) |
Figure 2: Recombination efficiency versus grain size, as obtained from KMC simulations (circles), from the master equation using Eq. (6) (solid line) and using the conventional approximation a/S (dashed line). |
| Open with DEXTER | |
5 Generalization to multi-species reactions
Our method has been formulated for single-species reactions exclusively. As speculated by Lohmar & Krug (2006), we now show that it can easily be generalized to multi-species reactions.
We use X and Y to denote two different species of particles. First, we consider the two-particle problem to find the encounter probability
![]() of an X and a Y particle on a translationally invariant lattice. So far, we have been concerned with two particles, each with a (undirected) hopping rate a and desorption rate W; this situation can be mapped onto a single walker moving and desorbing at rates 2a and 2W, respectively. Both rates can then be
rescaled to their old values, since only their ratio is relevant (Lohmar & Krug 2006,2009).
For two species X and Y, and the corresponding rates
of an X and a Y particle on a translationally invariant lattice. So far, we have been concerned with two particles, each with a (undirected) hopping rate a and desorption rate W; this situation can be mapped onto a single walker moving and desorbing at rates 2a and 2W, respectively. Both rates can then be
rescaled to their old values, since only their ratio is relevant (Lohmar & Krug 2006,2009).
For two species X and Y, and the corresponding rates ![]() ,
,
![]() and
and
![]() ,
,
![]() ,
we map to one walker moving with rate
,
we map to one walker moving with rate
![]() and desorbing at a rate
and desorbing at a rate
![]() .
The rescaling argument is not applicable for arbitrary rates. However, it is evident that we may simply substitute each a in the
single-species p (Sect. 2) by
.
The rescaling argument is not applicable for arbitrary rates. However, it is evident that we may simply substitute each a in the
single-species p (Sect. 2) by
![]() now, and each W by
now, and each W by
![]() .
This yields the encounter probability
.
This yields the encounter probability
![]() of a given pair of X and Y particles.
of a given pair of X and Y particles.
Second, we derive the relation between the encounter probability
![]() and the sweeping rate
and the sweeping rate
![]() ,
following Lohmar & Krug (2006). We start from the production rate of XY molecules,
,
following Lohmar & Krug (2006). We start from the production rate of XY molecules,
| (13) |
in an analogous way to the single-species situation. This means that the reaction reduces the number of XY pairs at a rate
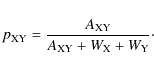 |
(14) |
Consequently,
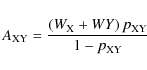 |
(15) |
is the definition for the reaction rate coefficient of
Since the right-hand side has the same form as for the single-species reaction with the substitution
![]() (and hopping rates do not occur here), the sum of desorption rates cancels with the factor of the
(and hopping rates do not occur here), the sum of desorption rates cancels with the factor of the
![]() asymptotics just as it does for the single-species case. Using Eq. (6), we thus obtain the approximation
asymptotics just as it does for the single-species case. Using Eq. (6), we thus obtain the approximation
![\begin{displaymath}%
A_{\rm XY} \approx \frac{a_{\rm X}+a_{\rm Y}}{S} \pi \left[...
...rac{W_{\rm X}+W_{\rm Y}}{8(a_{\rm X}+a_{\rm Y})}} \right]^{-1}
\end{displaymath}](/articles/aa/full_html/2009/36/aa12746-09/img65.png) |
(16) |
for the reaction rate coefficient of
6 Conclusions
We have used exact results for the sweeping rate in diffusion-mediated reactions on dust grain surfaces to provide an approximate formula for the crucial reaction rate coefficient. This expression is numerically accurate, and easy and efficient to implement even in complex gas-grain reaction networks. For single-species reactions, the expression was employed in the exact analytical master equation framework, and comparison with KMC simulations shows excellent agreement throughout. The results were also generalized to reactions of multiple species. We strongly advocate the incorporation of the reaction rate coefficients presented here into all models of interstellar gas-grain chemistry. This could be easily achieved and, in stark contrast to the commonly used approximation, it provides accurate results at virtually no additional computational cost. This is an important step towards an accurate modeling of the fascinating chemistry of interstellar clouds.
Acknowledgements
This work was supported by DFG within SFB/TR-12 Symmetries and Universality in Mesoscopic Systems. J.K. acknowledges the gracious hospitality of Hebrew University and the Lady Davis Fellowship Trust.
References
- Barzel, B., & Biham, O. 2007a, ApJ, 658, Ll37
- Barzel, B., & Biham, O. 2007b, J. Chem. Phys., 127, 144703 [NASA ADS] [CrossRef]
- Biham, O., & Lipshtat, A. 2002, Phys. Rev. E, 66, 056103 [NASA ADS] [CrossRef]
- Biham, O., Furman, I., Pirronello, V., & Vidali, G. 2001, ApJ, 553, 595 [NASA ADS] [CrossRef]
- Biham, O., Krug, J., Lipshtat, A., & Michely, T. 2005, Small, 1, 502 [CrossRef]
- Caselli, P., Hasegawa, T. I., & Herbst, E. 1998, ApJ, 495, 309 [NASA ADS] [CrossRef]
- Chang, Q., Cuppen, H. M., & Herbst, E. 2005, A&A, 434, 599 [NASA ADS] [CrossRef] [EDP Sciences]
- Charnley, S. B. 2001, ApJ, 562, L99 [NASA ADS] [CrossRef]
- Cuppen, H. M., & Herbst, E. 2005, MNRAS, 361, 565 [NASA ADS] [CrossRef]
- Garrod, R. T. 2008, A&A, 491, 239 [NASA ADS] [CrossRef] [EDP Sciences]
- Green, N. J. B., Toniazzo, T., Pilling, M. J., et al. 2001, A&A, 375, 1111 [NASA ADS] [CrossRef] [EDP Sciences]
- Hartquist, T. W., & Williams, D. A. 1995, The Chemically Controlled Cosmos (Cambridge University Press)
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] (In the text)
- Herbst, E. 1995, Annu. Rev. Phys. Chem., 46, 27 [CrossRef] (In the text)
- Hollenbach, D. J., Werner, M. W., & Salpeter, E. E. 1971, ApJ, 163, 165 [NASA ADS] [CrossRef] (In the text)
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] (In the text)
- Krug, J. 2003, Phys. Rev. E, 67, 065102(R) [NASA ADS] [CrossRef] (In the text)
- Lederhendler, A., & Biham, O. 2008, Phys. Rev. E, 78, 041105 [NASA ADS] [CrossRef]
- Lipshtat, A., & Biham, O. 2003, A&A, 400, 585 [NASA ADS] [CrossRef] [EDP Sciences]
- Lohmar, I., & Krug, J. 2006, MNRAS, 370, 1025 [NASA ADS]
- Lohmar, I., & Krug, J. 2009, J. Stat. Phys., 134, 307 [NASA ADS] [CrossRef]
- Stantcheva, T., & Herbst, E. 2003, MNRAS, 340, 983 [NASA ADS] [CrossRef]
- Stantcheva, T., Caselli, P., & Herbst, E. 2001, A&A, 375, 673 [NASA ADS] [CrossRef] [EDP Sciences]
- Stantcheva, T., Shematovich, V. I., & Herbst, E. 2002, A&A, 391, 1069 [NASA ADS] [CrossRef] [EDP Sciences]
- Tielens, A. G. G. M. 1995, unpublished
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge University Press)
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [NASA ADS]
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12746fg1.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12746-09/Timg27.png) |
Figure 1:
Ratio between the correct sweeping rate A and the
conventional approximation a/S, as obtained from the exact expression for A (solid lines) and from the approximate form (circles) given by Eq. (6), for three different
values of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12746fg2.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12746-09/Timg51.png) |
Figure 2: Recombination efficiency versus grain size, as obtained from KMC simulations (circles), from the master equation using Eq. (6) (solid line) and using the conventional approximation a/S (dashed line). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



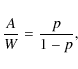
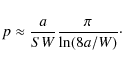
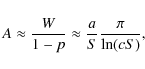
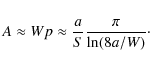
![\begin{displaymath}%
A \approx \frac{a}{S}\cdot\pi
\left[ \ln \frac{1}{1/(cS)+W/(8a)} \right]^{-1},
\end{displaymath}](/articles/aa/full_html/2009/36/aa12746-09/img23.png)