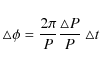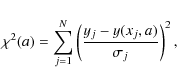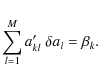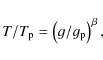Spectroscopic modeling of oscillating Algol-type stars

A. Tkachenko; H. Lehmann; D. E. Mkrtichian

doi:10.1051/0004-6361/200911949

Free Access

Issue		A&A Volume 504, Number 3, September IV 2009


Page(s)		991 - 1001
Section		Stellar atmospheres
DOI		https://doi.org/10.1051/0004-6361/200911949
Published online		22 July 2009

I. RZ Cassiopeia

A. Tkachenko¹ - H. Lehmann¹ - D. E. Mkrtichian²

1 - Thüringer Landessternwarte, 07778 Tautenburg, Germany
2 - Crimean Astrophysical Observatory, Nauchny, Crimea 98409, Ukraine

Received 25 February 2009 / Accepted 18 June 2009

Abstract
Aims. Based on time series of high-resolution spectra, we investigate the oEA star (i.e., Algol-type eclipsing binary with an oscillating primary component) RZ Cas to derive precise system and atmospheric parameters and search for phases of rapid mass-transfer and its effects on various system parameters at different epochs of observations.
Methods. We combine a variety of methods including the KOREL program to decompose the components of the spectra and determine the orbital solution, the SynthV program to analyze the disentangled spectra by computing synthetic spectra based on atmosphere models, and the newly developed program Shellspec07_inverse to compute optimized stellar parameters from composite line profiles at all orbital phases.
Results. Based on spectra taken in 2006, the RZ Cas system can be modeled accurately by assuming that only two stars are present. For spectra acquired in 2001, we obtained an improved solution by adding a light attenuating accretion annulus surrounding the primary, but were unable to model remaining structures in the O-C value distribution. The primary of RZ Cas is a normal A-type star that shows no $\lambda$ Boo signatures, both components have close to solar abundance. The derived mass of the primary and the separation of the components are slightly smaller than previously assumed. The effective temperature of the primary of 8900 K, is 300 K higher than derived before. The Roche-lobe-filling secondary is assumed to have a large cool spot on its surface pointing towards the primary. We confirm the increase in the orbital period by 2 s between years 2001 and 2006, but not the previously assumed decrease in the orbital radial velocity amplitudes.
Conclusions. With the new Shellspec07_inverse program, we obtained precise stellar parameters of RZ Cas. Results clearly point to the occurrence of a transient phase of rapid mass transfer of RZ Cas in 2001, while in 2006 the system was in a quiet state.

Key words: stars: binaries: eclipsing - stars: variables: general - stars: individual: RZ Cas - stars: oscillations

1 Introduction

RZ Cas (HD 17138, HIP 13133) belongs to the new class of oEA stars, i.e., Algol-type systems with mass transfer, where the mass-accreting primary exhibits $\delta$ Scuti-like oscillations (Mkrtichian et al. 2002,2004). Investigations of members of this class are important for at least three reasons. First, because of the mass transfer in the Algol-type systems, we can study stellar evolution on a short timescale. Second, due to the change in the excited oscillation modes during and after phases of rapid mass transfer, the changing structure of the outer layers of the gainer star can be investigated by asteroseismic methods. And third, observations can infer the basic principles of interaction between the magnetic activity cycle of the cool secondary, the occurrence of rapid mass transfer episodes, and the excitation of different non-radial pulsation modes of the mass-accreting primary. The oEA stars are eclipsing binaries and basic stellar and system parameters can be directly obtained by combining photometry and spectroscopy. During primary eclipse, we also observe the so-called spatial filtration effect, which means that at these orbital phases the secondary acts as a spatial filter and produces specific amplitude and phase changes in brightness and line profiles, depending on the observed oscillation modes (Gamarova et al. 2003). This effect can help us to identify the modes in terms of l and m numbers.

RZ Cas (spectral type A3 V+K0 IV) is a short-period ( $P=1\hbox{$.\!\!^{\rm d}$ }1953$ ) Algol-type system and one of the most well studied oEA stars. During primary minimum, a partial eclipse is observed (Narusawa et al. 1994). Olson (1982) and Varricatt et al. (1998) found evidence of circumstellar matter surrounding the primary. Single-peaked emission originating from a structure located between the two stars was detected by Richards & Albright (1999). These spectra and Doppler tomography (Richards 2004) indicate that a gas stream was visible during the observations in 1994. The presence of a gas stream was also assumed by Rodriguez et al. (2004). Based on extended photometric observations in 1999, the authors proposed a hot spot that was present where this stream impacts the surface of the primary star. The discovery that RZ Cas is also both an X-ray source (McCluskey & Kondo 1984) and a variable radio source (Drake et al. 1986) was explained by Umana et al. (1999) as being caused by the strong coronal activity of the cool secondary.

RZ Cas was found by Ohshima et al. (1998,2001) to exhibit short-period light variability. They found a dominant oscillation mode of the primary with a frequency of 64.2 c d^-1 and this frequency was later confirmed by means of dedicated photometric campaigns by both Mkrtichian et al. (2003) and Rodriguez et al. (2004). From photometric observations acquired until 2000, an apparently mono-periodic behavior with a dominant frequency of 64.2 c d^-1 was observed. Lehmann & Mkrtichian (2004, Paper I hereinafter) identified multi-periodic behavior in spectra taken in 2001 with two dominant modes of 56.600 and 64.189 c d^-1, both in agreement with the photometric findings by Mkrtichian et al. (2003), who also found that the photometric amplitudes of the principal modes were lower than in 1997-2000. A detailed investigation of the photometric amplitude variability of the principal modes of RZ Cas showed an increase in the amplitude of the 64.189 c d^-1 mode in 2001-2006 (Mkrtichian et al. 2007).

In 2006, the star changed its pulsation pattern again: Lehmann & Mkrtichian (2008, Paper II hereinafter) found at least three pulsation frequencies of 64.270, 56.761, and 62.406 c d^-1, where the last was observed for the first time. By comparing spectra taken in 2001 and 2006, the authors observed a changing asymmetry in the Rossiter-McLaughlin effect, a much stronger amplitude modulation of the non-radial pulsation modes related to the spatial filtration effect in 2006, and a change in both the orbital period and the pulsation pattern. The authors concluded that RZ Cas has undergone a transient phase of rapid mass transfer in 2001, whereas it was in a quiet state in 2006.

Stellar and system parameters for RZ Cas were derived e.g., by Maxted et al. (1994) from combined spectroscopy and UBVphotometry (Chambliss 1976), by Varricatt et al. (1998) from UBV (Chambliss 1976) and J and K band photometry, by Rodriguez et al. (2004) from Stroemgren photometry, by Soydugan et al. (2006) from combined spectroscopy and B and V band photometry, and by us (Papers I and II) from spectroscopy. From the color indices, the effective temperature of the primary was derived by Rodriguez et al. (2004) to be 8600 K, in agreement with Maxted et al. (1994), whereas Varricatt et al. (1998) adopted a higher temperature of 8720 K. The mass ratio is given as q=0.331 by Maxted et al. (1994). Soydugan et al. (2006) analyzed both the light and radial velocity (RV hereinafter) curves based on photometric observations from 2002 and spectral data from 2003/2004 by using the Wilson-Devinney program (Wilson & Devinney 1971; van Hamme & Wilson 2003). For a fixed surface temperature of the primary of 8600 K, the authors derived the temperature of the secondary to be 4480 K, the mass ratio to be 0.338, the orbital separation to be 6.87 $R_\odot$ , and the orbital inclination to be 81 $.\!\!^\circ$ 98. Varricatt et al. (1998) mentioned that the best-fit model of the J band light curve is obtained by assuming a dark spot exists on the secondary.

The present article is our third paper in a series based on a large number of high-resolution spectra of RZ Cas taken in 2001 and in 2006. Whereas Paper I described the spectroscopic detection of $\delta$ Sct-like oscillations in RZ Cas, we investigated in Paper II the differences in the results obtained during the two epochs of observations such as the different pulsation patterns, the development of the Rossiter effect, or the different strengths of the amplitude modulation of the pulsation modes with orbital phase. We also attempted to model the observed line profile variations in RZ Cas based on a very simple model with two spherical stars and Gaussian intrinsic line profiles. Based on spectra obtained in 2006, the resulting distribution of the O-C values with orbital phase was very smooth, except for a region around the secondary minimum where the calculated line profiles were of greater amplitude than the observed ones. We interpreted this as the attenuation effect caused by an accretion annulus around the gainer. However, the model completely failed in the case of the spectra taken in 2001. The corresponding O-C distribution with orbital phase showed a complex structure pointing to the necessity for an improvement in the model by taking typical Algol-type effects, such as circumprimary matter and a gas stream, into account.

Table 1: Journal of observations.

The aim of the present work is to apply a new computer program called Shellspec07_inverse. This program can model the composite line profiles of eclipsing binary stars in a more robust way by considering intrinsic line profiles computed from atmosphere models as well as the non-sphericity of the Roche lobe filling, cool secondary, and corresponding gravity darkening. By applying Shellspec07_inverse to RZ Cas we attempt to derive precise stellar and system parameters and model effects that we could not explain in Paper II. We start by using the KOREL program (Hadrava 2004b) to compute the disentangled spectra of the components and an orbital solution that includes both stars (Sect. 3). A detailed analysis of the disentangled spectra using synthetic spectra calculated with the SynthV program (Tsymbal 1996) then infers the chemical abundances of the components as well as the starting values of stellar and system parameters (Sect. 4), which are fine-tuned by Shellspec07_inverse (Sect. 5). The model for RZ Cas is described in Sect. 6, and our discussion and conclusions are given in Sects. 7 and 8.

2 Observations and spectra reduction

Data sets containing 951 and 512 spectra of RZ Cas were obtained with the Coude-Echelle-Spectrograph at the 2-m telescope at TLS in 2001 and 2006, respectively. The spectra have a spectral resolution of 33 000 and cover the wavelength range from 4760 Å to 7400 Å. Table 1 gives the journal of observations, where N is the number of spectra obtained in different nights.

Spectrum reduction was completed using standard MIDAS packages, including bias and stray-light subtraction, filtering of cosmic rays, flat fielding, wavelength calibration by a ThAr lamp, and normalization to the local continuum. All spectra were corrected in wavelength for individual instrumental shifts by using a large number of telluric O₂ lines.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11949fg1.eps} \end{figure}$	Figure 1: RVs of RZ Cas determined with KOREL, folded with the corresponding periods.
Open with DEXTER

3 KOREL analysis

We used KOREL (Hadrava 2004b), a Fourier-transform-based program, that, from a time series of spectra calculates simultaneously the optimized orbital elements and the mean disentangled spectra of the components. The program also considers the variation in the line strengths of the components with orbital phase. From both data sets, we selected all spectra of RZ Cas with S/N>60 and used the wavelength range 4950-5680 Å. The conversion from wavelengths to the RV scale produced 8192 bins of width 5 km s^-1, corresponding to a spectral two-pixel resolution of 30 000.

3.1 Orbital solutions

We started by separately analyzing the two data sets from 2001 and 2006, assuming circular orbits and allowing for variable line strengths in the solution. The first two panels in Fig. 1 show the RVs of the primary (black) and the secondary (red) derived from spectra taken in 2001 and 2006 and folded with the corresponding periods. The solid curves show the calculated orbital solutions, zero phase corresponds to the phase of maximum separation. The bottom panel shows the RVs of both components for the data obtained in 2001 (black) and 2006 (red) folded with the period observed in 2006. The Rossiter effect in the RVs of the primary is clearly evident. For both 2001 and 2006, a stronger deviation in the RVs from those expected on the basis of Keplerian motion can be seen in a broad region around secondary minimum. This region is too extended to be caused by the Rossiter effect during secondary eclipse. We discuss in more detail the underlying effect in Sect. 6. Besides this large-scale deviation, the RVs obtained from the spectra taken in 2001 show deviations over short ranges in orbital phase that cannot be found in the data from 2006.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11949fg2.eps} \end{figure}$	Figure 2: Line strength variations of primary (small amplitude) and secondary (large amplitude) calculated with KOREL.
Open with DEXTER

Table 2: Orbital elements derived with KOREL.

Figure 2 shows the variation in relative line strengths in both epochs of observation. The increase in the line strength of the secondary during primary eclipse can be seen as it is expected, whereas its decrease during secondary eclipse covers a region in orbital phase that is much broader than the duration of the eclipse and resembles the region of the RV deviations discussed before.

The derived orbital elements are listed in Table 2 where T refers to the time of primary minimum (2 450 000+). The results obtained in Paper II are given for comparison. The version of KOREL that we used did not allow us to determine the errors in the deduced parameters. Thus, we applied a separate program based on the method of differential corrections to the RVs derived with KOREL to estimate the errors in the orbital elements. They are given in Table 2 in parentheses, in units of the last digits.

The values derived for the orbital period in the two epochs of observation differ significantly, which is similar to the results of Paper II where we determined the RVs of only the primary from cross-correlation with a template spectrum. We checked this additionally by computing the orbital solution with KOREL from the combined 2001 and 2006 data allowing for a linear trend in orbital period and RV semi-amplitudes. We inferred a rate of period change of $\dot{P}=0.66\pm0.39$ s y^-1 and $\dot{K}=0.104\pm87$ km s^-1 y^-1 for the change in RV amplitudes (Table 2). We assume that the low accuracy in determining $\dot{P}$ results from the short time base (7 d) of the observations in 2001 (see also the large error in P obtained from the 2001 data) and, in contrast to the results obtained in Paper II, that the variation in K-values is non-significant. The difference of 1583 d in the observed epochs suggests that the total orbital period changed over the 5-yr interval by ( $2.9\pm 1.7$ ) s.

Alternatively, the period change can also be determined by using phase shift information. In this case, the accuracy depends not on the duration of the observation periods but on the time span $\triangle t$ between the two epochs. In our case, the period change can be determined in this way far more precisely. If we observe in 2001 an orbital period of P and in 2006 one of $P+\triangle P$ but fold the RVs measured from both epochs with $P+\triangle P$ , we obtain a phase shift of

$\begin{displaymath}\triangle\phi = \frac{\displaystyle2\pi}{\displaystyle P}\frac{\displaystyle\triangle P}{\displaystyle P}~\triangle t \end{displaymath}$

(1)

between the RVs from 2006 and 2001. It follows that

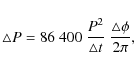$\begin{displaymath}\triangle P = 86~400~\frac{\displaystyle P^2}{\displaystyle\triangle t}~\frac{\triangle\phi}{\displaystyle2 \pi}, \end{displaymath}$

(2)

where $\triangle P$ is in seconds and both the period and epoch difference are in days. In the bottom panel of Fig. 1, we folded all RVs in this way using the period from 2006. We observe a phase shift of $\frac{\displaystyle\triangle\phi}{\displaystyle2\pi}=0.026$ . Assuming an error in the derived phase shift of 0.001 and an error in the epoch difference of 10% of the longer period of observations (29 d in 2006), we deduce an orbital period change of ( $2.0\pm0.1$ ) s or ( $0.47\pm0.02$ ) s y^-1.

3.2 Spectral disentangling

We used all spectra not acquired during the primary eclipse in 2006 to identify the spectrum of the primary, and all spectra outside secondary eclipse in case of the secondary. In each case, we assigned the orbital elements according to the KOREL solution for that data set. We did not use the spectra from 2001, since they are assumed to be distorted by accretion structures and chromospheric emission from the secondary due to the active phase of RZ Cas in this epoch. For the secondary, we also rejected all spectra with a deviation of the individual RVs from the orbital curve of larger than 7 km s^-1. In this way, we obtained 470 measurements for the primary and 247 measurements for the secondary at our disposal.

KOREL yields decomposed spectra normalized to the common continuum of both stars. Normalization to the individual continua was completed by using the uvby luminosities derived from Stroemgren photometry of RZ Cas (Mkrtichian et al. 2009). From an interpolation of the uvby luminosity ratios (WD solution with hot spot), we derived

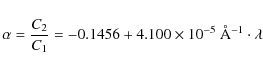$\begin{displaymath}\alpha = \frac{\displaystyle C_2}{\displaystyle C_1} = -0.1456 + 4.100\times 10^{-5}~\AA^{-1}\cdot\lambda \end{displaymath}$

(3)

for the wavelength dependence of the ratio of the continua of both stars. Normalization of the disentangled spectra R_i' was achieved by applying

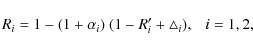$\begin{displaymath}R_i = 1-(1+\alpha_i)~(1-R_i'+\triangle_i),~~~i=1,2, \end{displaymath}$

(4)

where $\alpha_1=\alpha$ for the primary and $\alpha_2=\alpha^{-1}$ for the secondary, and $\triangle_i$ are the a priori unknown shifts of the disentangled KOREL spectra, which were first adapted to provide the best (most reliable) local continua and fine-tuned in a later step of the analysis.

4 Spectrum analysis with SynthV

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{11949fg3a.eps}\vspace{2mm} \includegraphics[width=8.9cm,clip]{11949fg3b.eps} \end{figure}$	Figure 3: Observed (thick) and calculated (thin) spectra of the primary ( top) and secondary ( bottom) of RZ Cas.
Open with DEXTER

Synthetic spectra of the stars were calculated with SynthV (Tsymbal 1996) and used to derive chemical abundances of the components and initial values for $v\sin{i}$ , $\xi_{\rm turb}$ , and $T_{\rm eff}$ for the stars. Atomic line lists were taken from the VALD database (Kupka et al. 2000). Model atmospheres for the hot primary were calculated with LLmodels (Shulyak et al. 2004). For the cool secondary, we used MARCS atmospheres (Gustafsson et al. 2008) and included an additional molecular line list taken from Kurucz CDs (Kurucz 1995). For both primary and secondary, $\log{g}$ was fixed to the values obtained from photometry (see Paper II). We used $T_{\rm eff}$ , $v\sin{i}$ , and elemental abundances as free parameters. In the case of the primary, we also iterated the value of the microturbulence, whereas it was impossible to disentangle the values of $v\sin{i}$ and $\xi_{\rm turb}$ for the secondary with its non-spherical configuration and not so well determined continuum. For the secondary, we therefore fixed $\xi_{\rm turb}$ to 2 km s^-1. To correct for the previously mentioned unknown shifts $\triangle_i$ in a more secure way than described above, we allowed the shift of the continua of the disentangled spectra to be an additional free parameter in the least-squares fit of the calculated by the observed spectra. Results showed that these additional shifts have always been very small, so in principle they could be neglected.

Figure 3 shows the observed and calculated spectra. In the case of the secondary, the fit is not as good as in the case of the primary because of the more uncertain continuum of this late type star. Moreover, the normalization of the observed spectrum to the assumed local continuum is not perfect, even though we included the full molecular line list and used MARCS atmosphere models. In addition, the values obtained from the best fit are not as well constrained because the Fe I lines that dominate the spectrum have only a low sensitivity to temperature changes in this temperature range of 4500 to 5000 K. For the primary, we obtained $v\sin{i}$ = ( $66.0\pm 0.5$ ) km s^-1, $\xi_{\rm turb}$ = ( $3.0\pm0.2$ ) km s^-1, and $T_{\rm eff}$ = ( $8850\pm25$ ) K, with $\log{g}$ = 4.35 (fixed). Table 3 lists the differences in the derived abundances from solar, and the mean error in the measurement is 0.03. The derived abundances are approximately solar, while Si is underabundant by a factor of 2.5. For the secondary, we found that $v\sin{i}$ = ( $81\pm 2$ ) km s^-1 and $T_{\rm eff}$ = ( $4800\pm 100$ ) K with $\log{g}$ = 3.5 (fixed). In this case, the derived abundances are close to solar (Table 3), Fe is underabundant by a factor of 2.6, and Cr by a factor of 4. The mean error of the measurement is 0.1.

Table 3: Derived abundances of RZ Cas relative to standard solar values.

5 Calculation of the synthetic composite spectrum

Our first attempt to model the composite stellar spectra of spectroscopic eclipsing binaries described in Paper II, was based on simple approximations, such as spherical stars and Gaussian intrinsic line profiles. For the next stage, we decided to use subroutines from the computer program ``Shellspec07'' written by Budaj & Richards (2004) for the computation of synthetic composite line profiles of the stars and the products of Roche overflow (see also Budaj et al. 2005). Hereby we make use of the capabilities of Shellspec07 to compute such spectra for arbitrary orbital phases including eclipse mapping by taking the non-spherical shapes and gravity darkening of the components into account. Moreover, Shellspec07 is well suited to our planned analysis of the distribution of circumbinary matter in different mass-transfer stages since the program can include an optical thin accretion disk and a gas stream and compute the corresponding effects on the resulting spectrum.

The Shellspec07 code is used as a basis for an iterative procedure even though it was not originally meant to solve for individual parameters. Our new program called Shellspec07_inverse solves the non-linear optimization problem by using the Levenberg-Marquardt algorithm. The core of Shellspec07 was implemented as central subroutine for calculating the Roche geometry of the cool secondary, for applying the necessary coordinate transformations in different orbital phases, and for integrating the fluxes from the visible stellar surfaces. For the calculation of intrinsic line profiles we used the SynthV program (Tsymbal 1996). Furthermore, we converted the Shellspec07 program code from Fortran77 to Fortran90 and declared the dynamical arrays to avoid problems with memory allocation.

Shellspec07 calculates the position of the local continuum using a straight line between the outermost points of the considered spectral region. We use SynthV to calculate the line fluxes as well as the continuum fluxes. In this way, the calculation of intensities normalized to the local continuum in Shellspec07_inverse is a trivial task and we do not need any artificial assumption about the continuum location.

5.1 Non-linear optimization of stellar parameters

For solving the inverse problem, i.e., the optimization of stellar parameters based on the observed spectra, we use the Levenberg-Marquardt algorithm (Marquardt 1963). It determines the parameters a of a function y = y(x,a) by minimizing the $\chi ^2$ merit function

$\begin{displaymath}\chi^2(a) = \sum_{j=1}^N\left(\frac{y_j-y(x_j,a)}{\sigma_j}\right)^2, \end{displaymath}$

(5)

where $\sigma_j$ represents the error in the measurement of y_j. In each step of the iterative procedure, the increments $\delta a_l$ are found by solving the system of linear equations

$\begin{displaymath}\sum_{l=1}^M a'_{kl}~\delta a_l = \beta_k . \end{displaymath}$

(6)

Where a'_kl represents a Hessian matrix with modified main diagonal $a'_{jj} = a_{jj}~(1+\lambda)$ , which is also called the curvature matrix, while $\beta_k$ is proportional to the Jacobian matrix of the first partial derivatives. The damping parameter $\lambda$ influences both the direction and the size of the increments $\delta a_l$ . If $\lambda$ is high, the Levenberg-Marquardt algorithm operates in a similar way to the steepest descent method and to the Gauss-Newton method if its value is small.

We used a modified, fast version of the Levenberg-Marquardt algorithm developed by Piskunov & Kochukhov (2002) that additionally optimizes $\lambda$ within each iteration keeping the right-hand side of Eq. (6) and the Hessian matrix a_klunchanged. We used the described algorithm and modified routines taken from Shellspec07, and made some additional changes as described in the next subsections to optimize basic stellar and orbital parameters, such as the effective temperatures of the binary components T₁ and T₂, $v_1\sin{i}$ for the primary (for the cool secondary we assume synchronized rotation), RV semi-amplitudes K₁ and K₂, the $\gamma$ -velocity of the system, and also the orbital inclination and the radius of the primary (the secondary is assumed to fill its Roche lobe). To improve the efficiency of the calculations, we used all out-of-eclipse phases to optimize the six first aforementioned parameters, and eclipse phases for the last two.

5.2 Intrinsic line profiles and limb darkening

To compute the intrinsic, rotationally unbroadened, stellar line profiles, we used the program SynthV (Tsymbal 1996) and the atomic line list from the VALD database. Atmosphere models for the more massive, hot primary were computed with the program LLmodels (Shulyak et al. 2004), while we used MARCS atmosphere models for the cool secondary.

Shellspec07 assumes constant intrinsic profiles and calculates the center-to-limb variation by using a linear limb-darkening law

$\begin{displaymath}I(\theta) = I_{0}(1 - u + u\cos\theta), \end{displaymath}$

(7)

where the limb darkening coefficient u describes the center to limb variation of the specific intensity. This is a rough approximation since it assumes that the variation over the disk is described by a constant value of u that is independent of line depth. In reality, the limb darkening coefficient strongly varies with line depth and can even reach negative values at the line centers, as shown by Townsend (1997) for the Balmer line cores. Instead of this law, we used SynthV to calculate the profiles for nine different values of $\Theta$ (angle between the line of sight and normal to the stellar surface) on the visible stellar disk and interpolate between them according to the exact position for which the profile has to be calculated. If we calculate the limb darkening coefficient as defined by Eq. (7) with our procedure, we can clearly see that it varies with line depths over a wide range. Figures 4 and 5 show an example calculated from the Fe I 4957 Å doublet and the atmospheric parameters that were finally derived for the primary of RZ Cas. A second advantage of our limb darkening calculation is that we are not restricted to spherical disks but can also calculate the intensity variations produced by different optical depths along the line of sight in the case of non-spherical secondary.

$\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11949fg4.eps} \end{figure}$	Figure 4: Fe I 4957 Å intrinsic line profiles calculated with SynthV at the center of the stellar disk (solid) and at the limb (dashed). Intensity is given in erg cm^-2 s^-1 Hz^-1 rad^-1.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11949fg5.eps} \end{figure}$	Figure 5: Limb darkening coefficient for different line depths, derived from the blue (solid curve) and from the red (dotted curve) components of the doublet shown in Fig. 4.
Open with DEXTER

5.3 Gravity darkening

Besides the limb darkening of both components, we have to take the gravity darkening of the Roche-lobe filling secondary into account. It results from the variation in the effective temperature with local gravity on the surface of the non-spherical star according to

$\begin{displaymath}T/T_{\rm p} = \left(g/g_{\rm p}\right)^{\beta}, \end{displaymath}$

(8)

where $T_{\rm p}$ and $g_{\rm p}$ are temperature and gravity at the pole and $\beta$ is the gravity darkening exponent. Theory predicts values of $\beta =0.08$ for stars with convective envelopes (Lucy 1967), and $\beta=0.25$ for those in hydrostatic and radiative equilibrium (von Zeipel 1924). In its original version, Shellspec07 applies a gravity darkening factor to the surface intensity that is assumed for the pole of the star. This factor is calculated from the ratio of the Planck functions, $f=B_\nu(T)/B_\nu(T_{\rm p})$ . Here, we see almost the same case as for limb darkening because the code assumes that this ratio does not depend on line depth. Instead of using such a factor, we use SynthV to calculate the intrinsic line profiles for each point on the stellar surface for exactly the required temperature as given by Eq. (8), where the local gravity is calculated by Shellspec07 according to the Roche geometry. To speed up the computations, we used a library of pre-calculated MARCS atmosphere models. The assumed values for $\beta$ are discussed in Sect. 6.

6 Spectroscopic modeling of RZ Cas

6.1 Application to the spectra from 2006

In this phase of the analysis we used the Shellspec07_inverse code described in Sect. 5. According to the conclusion drawn in Paper II that the star was in a quiet state in 2006, we started by analyzing the spectra taken in 2006 using a model that includes only the two stars without considering any effects from circumbinary matter. The deviation of the primary from a spherical shape can be neglected, whereas the secondary fills its Roche lobe. The model assumes a circular orbit and synchronized rotation for the secondary.

$\begin{figure} \par\mbox{\includegraphics[angle=-90,scale=0.242]{11949fg6a.eps}\... ...ace{2mm} \includegraphics[angle=-90,scale=0.242]{11949fg6c.eps} } \end{figure}$	Figure 6: Time series of observed ( left) and calculated ( center) Fe I 4957 Å line profiles taken in 2006, folded with the orbital period. The right panel shows the $\chi ^2$ -distribution of the fit.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=-90,scale=0.62]{11949fg7.eps} \end{figure}$

Figure 7:

Left column: surface intensity distributions of the secondary based on $\beta =0.08$ a), $\beta =0.50$ c), and on a combination of these values e). Middle colum: corresponding O-C values for the spectra from 2006 folded with the orbital period. Right column: O-C values for the spectra from 2001, based on the final solution for 2006 (i), including a homogeneous disk (ii), and assuming a disk of variable density (iii).

Open with DEXTER

For the analysis, we averaged the 512 spectra into 100 orbital phase bins based on the derived orbital period and focused our investigations on the four most unblended, stronger metal lines: Fe I 4957, 5056, 5616, and 5625 Å. Figure 6 shows the phase-binned observed profiles of one of these lines folded with the orbital period. For each position in phase, the Shellspec07_inverse program computes a synthetic line profile as shown in the middle panel of the figure. The Rossiter effect caused by a primary eclipse is clearly evident in both panels as the S-shaped distortion of the line profile of the primary. The right panel shows the two-dimensional distribution of the O-C values normalized to the individual errors in the measurement (the terms that enter the sum in Eq. (5) to compute $\chi ^2$ ). This normalized distribution used to determine the goodness of fit is much smoother than the O-C distributions shown in Fig. 7. This is because of the strong variation of the signal-to-noise of the observed profiles with orbital phase, caused by the different number of averaged single observations per phase bin and the lower amount of light during primary eclipse e.g., as seen from the noisy region around phase 0.25 in Fig. 7f. We note that we shifted the primary eclipse to this phase for clearer visualization.

Figure 7 shows the results obtained by using different gravity darkening exponents for the cool secondary. We give the surface intensity distribution in the left row of panels (intensity is in erg/cm²/s/Hz/rad on a logarithmic scale, distances are in units of the separation of the components), the O-C line intensity residuals for the Fe I 4957 Å profiles from 2006 (center row) and from 2001 (right row). For the gravity darkening exponent of the Roche lobe filling secondary, we first assumed the value of $\beta =0.08$ as predicted by theory in the case of a star with a convective envelope. The assumed model gives a smooth solution for all orbital phases except for a larger region around secondary minimum, which appears to be brighter (the calculated line of the secondary is stronger than the observed one). This brightening, covering about one fifth of the orbit, corresponds to an attenuation of the line of the secondary, as already found for the same region in Paper II and that can also be seen in the form of a deviation of the RVs from our KOREL solution (Fig. 1). The $\chi ^2$ of the Levenberg-Marquardt solution including all orbital phases is 2.21.

Table 4: Comparison of parameters of the RZ Cas system from literature and obtained with Shellspec07_inverse (see text for a detailed explanation).

In the next step, we tried to model the observed deviations in the region around secondary minimum assuming that they are caused by some intrinsic property of the secondary itself. From our point of view, the most reliable explanation is that the star shows a different temperature distribution over the surface than we assumed in our model. Unno et al. (1994) found that the secondary of RZ Cas can be modeled only by assuming an unusually large value of the gravity darkening exponent of 0.53 and inferred that dark spots were present on the front and back sides of the secondary with respect to the primary. Therefore, we examined whether an ultra-high value of $\beta$ could effectively simulate large, cool spots and improve the $\chi ^2$ of our spectroscopic solution. The resulting model (Fig. 7c, d) fits the observed line profiles in the region around secondary minimum well but completely fails at phases near primary eclipse, where the calculated line profiles are much too weak and a dark region in the O-C frame appears. The resulting $\chi ^2$ of 2.56 is higher than the value derived for $\beta$ = 0.08.

Finally, we divided the stellar surface of the secondary into two regions by applying $\beta=0.5$ to the hemisphere pointing towards the primary and the normal value of $\beta =0.08$ to the opposite side (Fig. 7e). The previously bright region around secondary minimum was then almost perfectly fitted and no difference with respect to the first solution ( $\beta =0.08$ for the entire surface) can be seen in the O-C distribution around primary minimum (Fig. 7f). The resulting $\chi ^2$ is 1.93. The remaining, faint structures in the O-C distribution are caused by the outermost parts of the wings of the lines of the primary where the observations show a slightly smoother transition than the calculated profiles whose shapes are dominated by rotational broadening.

Furthermore, we used Shellspec07_inverse to derive for the primary $K_1=(71.41\pm0.15)$ km s^-1 and $v_1\sin{i} =(68.45\pm0.31)$ km s^-1, and for the secondary $K_2=(206.13 \pm0.80)$ km s^-1. The values of the other determined parameters are listed in the last row of Table 4 and used in Sect. 7 when compared with previously obtained values from the literature. The value given there for the radius of the secondary is in our case derived from the orbital period and $v\sin{i}$ , obtained from the analysis of the KOREL decomposed spectra and represents some mean value of the secondary radius. Figure 8 shows, for a smaller number of selected phase bins, a comparison between the observed and calculated line profiles based on this solution (line profiles are shifted by a constant value for a clearer visualization).

6.2 Application to the spectra from 2001

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{11949fg8.eps} \end{figure}$	Figure 8: Comparison between observed (solid) and calculated (dashed) Fe I 4957 Å line profiles. The orbital phase is marked to the right.
Open with DEXTER

In a next step, we applied the derived model to the spectra taken in 2001, first without changing any of the parameter values. Figure 7i shows the resulting O-C distribution. We see that the line profile of the primary observed in 2001 is weaker than in 2006, and there is a strong general attenuation along the full orbit.

The residuals represented in Fig. 7ii correspond to the solution obtained by adding attenuating circumprimary matter of disk-like structure and both constant temperature and density to the model. The density of $3.0\times 10^{-9}$ g cm^-3 and disk temperature of 1050 K were taken from an unpublished 3D hydrodynamic simulation of mass-transfer in the RZ Cas system (Mkrtichian et al. 2009) computed with a program written by Nazarenko (Nazarenko et al. 2001).

The radial extension and thickness of the disk were adjusted manually. Finally, we assumed a disk with a thickness of 3 $R_\odot$ (comparable to the diameter of the primary) and a radial extension from 1.6 $R_\odot$ (close to the surface of the primary) to 3 $R_\odot$ . This model allows us to adjust the mean line strength of the primary for all orbital phases in a far more reliable way, although many structures remain, as can be seen from Fig. 7ii. Most obvious is the difference in line strength of the primary between the two half-orbits around first and second quadrature.

Finally, Fig. 7iii shows the solution obtained by assuming two different values of the density of the circumprimary disk of $6.5\times 10 ^{-9}$ g cm^-3 for the ``bright'' line profiles of the primary and $3.0\times 10^{-9}$ g cm^-3 for the ``dark'' part (Mkrtichian et al. 2009). The large-scale differences in line strength were in this way reduced. However, small-scale, regional structures of high contrast in the residuals remain.

We confirmed the two suggestions in Paper II that: (i) RZ Cas has undergone a transient phase of rapid mass-transfer; (ii) an accretion annulus around the primary was formed at this epoch. Our model including an attenuating annulus around the gainer significantly improves the solution, compared to that for the model including only the two stars. However, small-scale, regional structures of high contrast in the residuals remain, caused probably by the complex hydrodynamic structure of the circumprimary matter which cannot be modeled with Shellspec07_inverse in its current form.

7 Discussion

By combining several methods based on the KOREL, SynthV and Shellspec07_inverse programs, we have reinvestigated the RZ Cas system based on time series of spectroscopic observations taken in 2001 and 2006. We used the KOREL program mainly to decompose the spectra of the RZ Cas components for spectrum analysis. In this way we also obtained new spectroscopic orbits, based on a different method than those applied in Papers I and II. As is is evident from the type of input data, the method combines the measurement of the RVs of both components (as in Paper I for the centroids of selected lines of both components) with the use of a wider spectral range (Paper II, cross-correlation with a template, but only primary). We now also consider the full range in orbital phase, and KOREL weights the data according to the derived relative line strengths. Our new solution does not reach the formal accuracy of the orbital elements derived from cross-correlation (Paper II). On the other hand, the full information about the composite lines formed in all orbital phases is used. The analysis includes for the first time the secondary based on the spectra from 2006, and allows a comparison of mass ratio and shape of the RV curves derived from the data from 2001 and 2006. These results are compared below with those obtained from Shellspec07_inverse.

Based on the observed phase shift between the two epochs of observation, we can determine the difference in orbital period very precisely to ( $2.0\pm0.1$ ) seconds. In Paper II, we also discussed a decrease in the RV semi-amplitudes by 0.6 km s^-1 between the years 2001 and 2006. We showed that a decrease by such an amount cannot be explained by mass transfer effects and suggested that the decrease is feigned by distortions in the RVs measured in the active phase of RZ Cas in 2001. We have now confirmed this assumption, whether or not the KOREL solution or the Shellspec07_inverse results show significantly different K values between the 2001 and 2006 data.

The analysis of the decomposed spectra of the components using SynthV resulted in a close fit between the observed spectrum of the primary and the computed synthetic spectrum, whereas the spectrum of the secondary could not be modeled perfectly. One reason for this, besides the lower S/N and the less clearly defined continuum of the fainter, cool-type star is that the SynthV analysis was based on the assumption of a spherical star.

From the spectrum analysis, we did not find any strong metal underabundance of iron peak elements or $\lambda$ Boo signatures of the primary component as reported by Narusawa et al. (2006), who found Cr, Ti, Mg and Fe underabundances of -0.95, -0.45, -0.55 and -0.63 dex, respectively. Both Cr and Ti have solar abundance within the errors of measurement. The abundances of Mg (+0.14 dex) and Fe (-0.16 dex) can also be considered to be close to solar values. The only remarkable deficiency of -0.39 dex was found for Si (-0.59 dex by Narusawa). We conclude that the primary component of RZ Cas is a normal A-type star of nearly solar abundance

Our first application of Shellspec07_inverse to derive stellar and system parameters of RZ Cas from a non-linear optimization using time series of line profiles was successful in the case of the relatively undistorted spectra obtained in the quiet phase of RZ Cas in 2006. In the following, we compare the results obtained from different methods. The spectra decomposed with KOREL represent the mean spectra of the components from all out-of-eclipse phases. Its analysis using SynthV is based on the assumption of spherical configurations of both stars. Shellspec07_inverse includes the composite spectra from all orbital phases and considers Roche geometry and gravity darkening of the secondary. And it is able to derive the orbital inclination and the radius of the primary directly from the observed spectra. Since it considers synchronized rotation and Roche-lobe filling of the secondary, it will not give values for the radius of the secondary or its $v\sin{i}$ , however. These values are implicit values depending on the derived mass ratio, orbital separation, and inclination. A special case are the effective temperatures of the two stars derived by Shellspec07_inverse. They were derived from the analysis of only four Fe I lines. In a narrow sense, they represent only mean line strength scaling factors for these special lines. Effective temperatures of the same physical meaning as derived from the decomposed spectra could be obtained with Shellspec07_inverse only, if we investigated a wider spectral region as we did in the decomposition. We plan to explore this much more computer-intensive application using the least-squares deconvolution (LSD, Donati et al. 1997) of profiles computed over wide spectral ranges.

The following comparison of derived system parameters is based on Table 4. It lists the derived system parameters and compares them with values from literature. The sources are A) Maxted et al. (1994), B)Varricatt et al. (1998), C) Rodriguez et al. (2004), D)Soydugan et al. (2006), E) this paper, spectra from 2006. Values that were assumed but not derived by the authors are given in brackets. Errors in units of the last digit are given in parentheses. Our value of $T_{\rm eff}$ for the primary of 8907 K is only slightly higher than those derived from the analysis of the disentangled spectrum but more than 300 K higher than the value of 8600 K derived by both Maxted et al. (1994) and Rodriguez et al. (2004); in contrast, Varricatt et al. (1998) found a value of 8720 K. Based on our model, we can exclude these lower temperatures from both the Shellspec07_inverse application and from the analysis of the decomposed spectrum. For the secondary, we obtain $T_{\rm eff}$ = 4800 K. Although it was derived from only four lines, it resembles the value derived from the decomposed spectrum. However, we note that it represents the effective temperature of the non-spherical secondary only at the pole. The temperature over most of the surface is lower because of the assumed gravity darkening (see discussion below).

RV semi-amplitudes or K-values derived from RVs measured from line centroids are based on a model that does not include any non-sphericity effects or effects that occur during the eclipses (Rossiter effect). KOREL derives the orbital solution from RVs weighted by the derived line strengths and suppresses in this way the influence of the Rossiter effect on the orbital solution, but does not also consider non-sphericity effects. Shellspec07_inverse derives the RV semi-amplitudes or K-values by considering the effects of non-sphericity on line shapes as well as the line asymmetries during the eclipses (eclipse mapping). Thus, it should provide the most reliable mass ratio of the stars that we determined to be $0.343\pm0.002$ . This value is clearly higher than the values between 0.331 and 0.338 determined by previous authors. The derived mass of the secondary agrees within the errors of measurement with the values derived by other authors except for Soydugan et al. (2006). Thus, the higher value of the mass ratio is caused by the lower value of the mass of the primary of ( $2.01\pm0.02$ ) $M_\odot$ that we obtained, and the smaller separation of ( $6.59\pm0.03$ ) $R_\odot$ . The derived radius of the primary of ( $1.61\pm0.01$ ) $R_\odot$ and the orbital inclination of ( $82.0\pm0.3$ ) $^\circ$ agree well with the values derived by Soydugan et al. (2006).

Comparing the rotational period of the primary of ( $1.190\pm0.013$ ) d derived from the radius and $v\sin{i}$ with the orbital one, we find, to within the errors of measurement, that the primary rotates synchronously.

If we assume that the surface intensity distribution of the secondary is only influenced by limb and gravity darkening, the most accurate solution is found by applying a gravity darkening exponent of 0.5 to the hemisphere of the secondary pointing towards the primary, and the usual value of 0.08 to the opposite hemisphere. Of course, we are aware that we derived such an exotic value of $\beta=0.5$ because we tried to model some inhomogeneous surface intensity distribution that may arise e.g., from the presence of spots by applying a law that describes a completely different physical effect. The improved modeling of the observations provided by this high value of $\beta$ suggests the presence of a large dark spot that dominates the surface region pointing to the primary and that may have a smooth transition to the other parts of the surface. If the reflection effect is taken into account, we expect to measure an even higher value of the gravity darkening exponent since this effect would brighten in particular the surface covered by the dark spot. These findings partly in agree with those by Unno et al. (1994), where authors found a gravity darkening exponent of $\beta=0.53$ . They concluded that spots on the front and back sides of the surface of the secondary (pointing towards and away from the primary) are formed as the result of mass-outflow. However, we found no evidence of such a cool dark spot on the back side of the secondary as also suggested by Varricatt et al. (1998).

The application of the model derived from the spectra taken in 2006 to those from 2001 showed a strong attenuation of the line of the primary, inferring that there is dense circumprimary matter and that a transient phase of rapid mass-transfer occurred shortly before the observing period in 2001 as already suggested in Paper II. The attempt to model this attenuation by introducing optically thin circumprimary matter of disk-like structure in Shellspec07 provided a significantly improved solution. The $\chi ^2$ of the solution decreases in this case and decreases even more if we assume different densities of the disk in two different regions of the orbit. Complex structures in the O-C distribution however remain.

8 Conclusions

The new Shellspec07_inverse program has been successfully applied to time series of spectra of the oscillating Algol-type star RZ Cas obtained during its quiet state in 2006. The derived mass of the primary and the separation of the components are slightly smaller than previously obtained from photometry and spectroscopy, whereas the temperatures of both components are slightly higher. All other system parameters agree with at least one of the previous determinations. Shellspec07_inverse takes the full spectroscopic information from line profiles in all orbital phases including eclipse mapping as well as the non-sphericity of the Roche lobe filling secondary and an improved modeling of gravity and limb darkening into account. For these reasons and the large number of spectra analyzed, we believe that the stellar and system parameters of RZ Cas derived in this work are the most precise spectroscopically derived so far.

We have detected a distortion over a broad range of phases around secondary minimum that we interpret as the effect of a dark spot on the surface of the secondary pointing towards the primary. This effect can be seen in the RVs obtained with KOREL as well as in the corresponding line strengths and residuals of the Shellspec07_inverse solution, assuming normal gravity darkening. Since the surface intensity distribution of the secondary can be modeled well by assuming a very high value of the gravity darkening exponent, a very large dark spot must be present that has a smooth transition to the surrounding stellar atmosphere.

We also determined the abundances of the components and conclude that both components have approximately solar abundance with a slight underabundance of Si for the primary and of both Cr and Ni for the secondary. From the orbital solutions, we derive a precise value of the increase in the orbital period of ( $2.0\pm0.1$ ) s between the two epochs of observations in 2001 and 2006, in agreement with the photometric findings (for a detailed discussion of period changes see Paper II).

The application of Shellspec07_inverse to the spectra obtained in 2001 shows that the system cannot be described by including only the two stars into the model. The situation is improved by adding an attenuating accretion annulus surrounding the primary but complex structures in the 2D O-C distribution remain. This result confirms our conclusion drawn in Paper II that the star had undergone a transient episode of rapid mass transfer shortly before the observations in 2001. It also shows, however, that a very detailed map of the circumbinary gas distribution is needed to ensure more robust modeling.

In the future, we plan to work with Shellspec07_inverse also on LSD profiles calculated from wider spectral regions so that the results for atmospheric parameters such as $T_{\rm eff}$ are more representative. We also plan to develop a more detailed model of the structure of circumbinary matter during active phases, and to apply the program to other Algol-type stars.

Acknowledgements

We would like to thank Jan Budaj for providing us with the latest version of the Shellspec07 program and for his help in software usage. We are grateful to Vadim Tsymbal for providing us with the SynthV code and to Oleg Khochukov for the modified version of the Levenberg-Marquardt algorithm as well as for their steady help and useful comments. We want to thank the referee, Mercedes Richards, for her substantial comments that helped us to improve the article considerably.

References

Budaj, J., & Richards, M. T. 2004, Contrib. Astron. Obs. Skalnate Pleso, 34, 167 [NASA ADS] (In the text)
Budaj, J., Richards, M. T., & Miller, B. 2005, ApJ, 623, 411 [NASA ADS] [CrossRef] (In the text)
Chambliss, C. R. 1976, PASP, 88, 22 [NASA ADS] [CrossRef] (In the text)
Donati, J.-F., Semel, M., Carter, B. D., et al. 1997, MNRAS, 291, 658 [NASA ADS] (In the text)
Drake, S. A., Simon, T., & Linsky, J. L. 1986, AJ, 91, 1229 [NASA ADS] [CrossRef]
Gamarova, A. Yu., Mkrtichian, D. E., & Rodriguez, E. 2003, ASPC, 292, 369 [NASA ADS] (In the text)
Giuricin, G., Mardirossian, F., & Fredolin, F. 1980, Ap&SS, 73, 389 [NASA ADS] [CrossRef]
Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hadrava, P. 2004a, Publ. Astron. Inst. ASCR, 92, 1
Hadrava, P. 2004b, Publ. Astron. Inst. ASCR, 92, 15 (In the text)
Kim, S.-L., Lee, J. W., Kwon, S.-G., et al. 2003, A&A, 405, 231 [NASA ADS] [CrossRef] [EDP Sciences]
Kupka, F., Ryabchikova, T. A., Piskunov N. E., et al. 2000, Baltic Astron., 9, 590 [NASA ADS] (In the text)
Kurucz, R. L. 1995, ASPC, 78, 205 [NASA ADS] (In the text)
Kusakin, A. V., Mkrtichian, D. E., & Gamarova, A. Yu. 2001, Inf. Bull. Variable Stars, No. 5106
Lehmann, H., & Mkrtichian, D. E. 2004, A&A, 413, 293 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lehmann, H., & Mkrtichian, D. E. 2008, A&A, 480, 247 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lehmann, H., Mkrtichian, D. E., & Tkachenko, A. 2008a, J. Phys.: Conf. Ser., 118, 012062 [NASA ADS] [CrossRef]
Lucy, L. B. 1967, Zs. f. Ap., 65, 89 [NASA ADS] (In the text)
Marquardt, D. 1963, SIAM J. Appl. Math., 11, 431 [CrossRef] (In the text)
Maxted, P. F. L., Hill, G., & Hilditch, R. R. 1994, A&A, 282, 821 [NASA ADS] (In the text)
McCluskey, G. E., Jr., & Kondo, Y. 1984, PASP, 96, 817 [NASA ADS] [CrossRef] (In the text)
Mkrtichian, D. E., Kusakin, A. V., Gamarova, A. Yu., et al. 2002, PASPC, 259, 96 [NASA ADS] (In the text)
Mkrtichian, D. E., Nazarenko, V., Gamarova, A. Yu., et al. 2003, PASPC, 292, 113 [NASA ADS] (In the text)
Mkrtichian, D. E., Kusakin, A. V., Rodriguez, E., et al. 2004, A&A, 419, 1015 [NASA ADS] [CrossRef] [EDP Sciences]
Mkrtichian, D. E., Kim, S.-L., & Rodriguez, E. 2007, ASP Conf. Ser., 370, 194 [NASA ADS]
Mkrtichian D. E., et al. 2009, in preparation (In the text)
Narusawa, S. Y., Nakamura, Y., & Yamasaki, A. 1994, AJ, 107, 1141 [NASA ADS] [CrossRef] (In the text)
Narusawa, S. Y., Ozaki, S., Kambe, E., & Sadakane, K. A. 1994, PASPJ, 58, 617 [NASA ADS] (In the text)
Nazarenko, V. V., & Glazunova, L. V. 2006, ARep, 50, 369 [NASA ADS]
Nazarenko, V. V., Glazunova, L. V., & Karetnikov, V. G. 2001, ARep, 45, 452 [NASA ADS] (In the text)
Ohshima, O., Narusawa, S., Akazawa, H., et al. 1998, IBVS, 4581 (In the text)
Ohshima, O., Narusawa, S.-Y., Akazawa, H., et al. 2001, AJ, 122, 418 [NASA ADS] [CrossRef]
Olson, E. C. 1982, ApJ, 259, 702 [NASA ADS] [CrossRef] (In the text)
Piskunov, N., & Kochukhov, O. 2002, A&A, 381, 736 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Richards, M. T. 2004, AN, 325, 229 [NASA ADS] (In the text)
Richards, M. T., & Albright, G. E. 1999, ApJS, 123, 537 [NASA ADS] [CrossRef] (In the text)
Rodriguez, E., Gracia, J. M., Mkrtichian, D. E., et al. 2004, MNRAS, 347, 1317 [NASA ADS] [CrossRef] (In the text)
Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef]
Shulyak, D., Tsymbal, V., Ryabchikova, T., et al. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Soydugan, E., Soydugan, F., Ibanoglu, C., et al. 2006, Astron. Nachr., 327, 905 [NASA ADS] [CrossRef] (In the text)
Townsend, R. H. D. 1997, Non-radial pulsation in early-type stars, Ph.D. Thesis, University of London (In the text)
Tsymbal, V. 1996, ASP Conf. Ser., 108, 198 [NASA ADS] (In the text)
Umana, G., Leto, P., Trigilio, C., et al. 1999, A&A, 342, 709 [NASA ADS] (In the text)
Unno, W., Kuguchi, M., & Kitamura, M. 1994, Publ. Astron. Japan, 46, 613 [NASA ADS] (In the text)
van Hamme, W., & Wilson, R. E. 2003, ASP Conf. Ser., 298, 323 [NASA ADS] (In the text)
Varricatt, W. P., Ashok, N. M., & Chandrasekhar, T. 1998, AJ, 116, 1447 [NASA ADS] [CrossRef] (In the text)
von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] (In the text)
Wilson, R. E., & Devinney, R. G. 1971, APJ, 166, 606 [NASA ADS] [CrossRef] (In the text)

Footnotes

... Cassiopeia: Based on observations with the 2-m Alfred Jensch telescope at the Thüringer Landessternwarte (TLS) Tautenburg.

All Tables

Table 1: Journal of observations.

Table 2: Orbital elements derived with KOREL.

Table 3: Derived abundances of RZ Cas relative to standard solar values.

Table 4: Comparison of parameters of the RZ Cas system from literature and obtained with Shellspec07_inverse (see text for a detailed explanation).

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{11949fg1.eps} \end{figure}$	Figure 1: RVs of RZ Cas determined with KOREL, folded with the corresponding periods.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11949fg2.eps} \end{figure}$	Figure 2: Line strength variations of primary (small amplitude) and secondary (large amplitude) calculated with KOREL.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{11949fg3a.eps}\vspace{2mm} \includegraphics[width=8.9cm,clip]{11949fg3b.eps} \end{figure}$	Figure 3: Observed (thick) and calculated (thin) spectra of the primary ( top) and secondary ( bottom) of RZ Cas.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11949fg4.eps} \end{figure}$	Figure 4: Fe I 4957 Å intrinsic line profiles calculated with SynthV at the center of the stellar disk (solid) and at the limb (dashed). Intensity is given in erg cm^-2 s^-1 Hz^-1 rad^-1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{11949fg5.eps} \end{figure}$	Figure 5: Limb darkening coefficient for different line depths, derived from the blue (solid curve) and from the red (dotted curve) components of the doublet shown in Fig. 4.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[angle=-90,scale=0.242]{11949fg6a.eps}\... ...ace{2mm} \includegraphics[angle=-90,scale=0.242]{11949fg6c.eps} } \end{figure}$	Figure 6: Time series of observed ( left) and calculated ( center) Fe I 4957 Å line profiles taken in 2006, folded with the orbital period. The right panel shows the $\chi ^2$ -distribution of the fit.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,scale=0.62]{11949fg7.eps} \end{figure}$	Figure 7: Left column: surface intensity distributions of the secondary based on $\beta =0.08$ a), $\beta =0.50$ c), and on a combination of these values e). Middle colum: corresponding O-C values for the spectra from 2006 folded with the orbital period. Right column: O-C values for the spectra from 2001, based on the final solution for 2006 (i), including a homogeneous disk (ii), and assuming a disk of variable density (iii).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.9cm,clip]{11949fg8.eps} \end{figure}$	Figure 8: Comparison between observed (solid) and calculated (dashed) Fe I 4957 Å line profiles. The orbital phase is marked to the right.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.