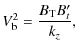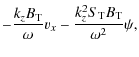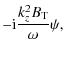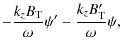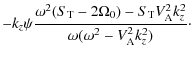| Issue |
A&A
Volume 504, Number 2, September III 2009
|
|
|---|---|---|
| Page(s) | 309 - 320 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200912272 | |
| Published online | 09 July 2009 | |
Turbulent resistivity evaluation in magnetorotational instability generated turbulence
G. Lesur1 - P.-Y. Longaretti2
1 - Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences,
Wilberforce Road, Cambridge CB3 0WA, UK
2 -
Laboratoire d'Astrophysique, UJF CNRS, BP 53, 38041 Grenoble Cedex 9, France
Received 3 April 2009 / Accepted 26 June 2009
Abstract
Context. MRI turbulence is a leading mechanism for the generation of an efficient turbulent transport of angular momentum in an accretion disk through a turbulent viscosity effect. It is believed that the same process could also transport large-scale magnetic fields in disks, reshaping the magnetic structures in these objects. This process, known as turbulent resistivity, has been suggested and used in several accretion-ejection models and simulations to produce jets. Still, the efficiency of MRI-driven turbulence to transport large-scale magnetic fields is largely unknown.
Aims. We present new analytical and numerical results aiming at quantifying the turbulent resistivity produced by MRI-driven turbulence in accretion disks.
Methods. We investigate this problem both analytically and numerically. We introduce a linear calculation of the MRI in the presence of a spatially inhomogeneous mean magnetic field. We show that, in this configuration, MRI modes lead to an efficient magnetic field transport, on the order of the angular momentum transport. We next use fully non linear simulations of MRI turbulence to compute the turbulent resistivity in several magnetic configurations.
Results. We find that the turbulent resistivity is on the order of the turbulent viscosity in all our simulations, although somewhat lower. The variations in the turbulent resistivity are correlated with the variation in the turbulent viscosity as a function of the imposed mean field. Finally, the turbulent resistivity tensor is found to be highly anisotropic with a diffusion coefficient 3 times greater in the radial direction than in the vertical direction.
Conclusions. These results support the possibility of driving jets from turbulent disks; the resulting jets may not be steady.
Key words: accretion, accretion disks - turbulence - magnetohydrodynamics (MHD)
1 Introduction
After several decades of debate, and in spite of significant
progress, the origin and efficiency of angular momentum transport
remains a central problem in accretion disks physics. Turbulence is
one of the major physical mechanism through which the
observationally well-constrained anomalous transport can be
achieved; indeed, the first ![]() model (Shakura & Sunyaev 1973) already
assumed a strong level of turbulence, leading to an effective
viscosity orders of magnitude higher than molecular viscosity.
However, the physical origin of this turbulence in disks is still
largely discussed.
model (Shakura & Sunyaev 1973) already
assumed a strong level of turbulence, leading to an effective
viscosity orders of magnitude higher than molecular viscosity.
However, the physical origin of this turbulence in disks is still
largely discussed.
Various sources of turbulence, both hydrodynamical and magneto-hydrodynamical, have been proposed. Subcritical turbulence (Richard & Zahn 1999, and references therein), if present, is too inefficient (Ji et al. 2006; Lesur & Longaretti 2005). Convection is also too inefficient and transports angular momentum in the wrong direction (Stone & Balbus 1996; Cabot 1996). Two-dimensional turbulence driving by small-scale, incoherent gravitational instabilities (Gammie 1996) or baroclinic instabilities (Klahr & Bodenheimer 2003) is a possible option, although the last one is still highly controversial (Petersen et al. 2007; Johnson & Gammie 2006).
In a seminal paper, Balbus & Hawley (1991) indentify an MHD instability, the magnetorotational instability (MRI) that drives turbulence in the nonlinear regime. This instability provides the most extensively studied transport mechanism, mainly with the help of local unstratified (Hawley et al. 1995) and stratified (Stone et al. 1996) 3D simulations, and global (Hawley 2000) disk simulations. These simulations have shown that MRI turbulence is an efficient way to transport angular momentum, although the role of microphysical processes has largely been underestimated (Lesur & Longaretti 2007; Fromang et al. 2007).
MRI turbulence may also produce resistive transport![]() (transport of magnetic fields through a ``turbulent
resistivity'' process) in disks. This transport is a key ingredient
of accretion-ejection models (see, e.g., Ferreira 1997; Casse & Ferreira 2000, and
references therein). The related turbulent resistivity
(transport of magnetic fields through a ``turbulent
resistivity'' process) in disks. This transport is a key ingredient
of accretion-ejection models (see, e.g., Ferreira 1997; Casse & Ferreira 2000, and
references therein). The related turbulent resistivity
![]() is
parameterized with the Shakura-Sunyaev ansatz as
is
parameterized with the Shakura-Sunyaev ansatz as
![]() (
(![]() is the Alfvén speed based on
the mean field); stationary accretion ejection models require an
anisotropy of the turbulent resistivity transport of few; furthermore,
a very efficient turbulent transport with
is the Alfvén speed based on
the mean field); stationary accretion ejection models require an
anisotropy of the turbulent resistivity transport of few; furthermore,
a very efficient turbulent transport with
![]() is required to produce stationary
structures. Less efficient transport would not prevent the
launching of jets from disks, but these structures would then be
nonstationary. The question of whether turbulent resistivity is
an adequate source of field line slippage through the gas to
launch a jet is still controversial in the literature, and is
further discussed in the concluding section of this paper.
is required to produce stationary
structures. Less efficient transport would not prevent the
launching of jets from disks, but these structures would then be
nonstationary. The question of whether turbulent resistivity is
an adequate source of field line slippage through the gas to
launch a jet is still controversial in the literature, and is
further discussed in the concluding section of this paper.
In any case, turbulent resistivity is an issue in its own right, and in this paper, we present new numerical results aimed at quantifying more precisely the resistive transport due to MRI turbulence. Our approach differs from the method recently introduced by Brandenburg, Rädler, Schrinner and coworkers to compute the turbulent resistivity tensor (see Schrinner et al. 2005; Brandenburg et al. 2008, and references therein). Their method relies on an expansion of the mean electromotive force with respect to the mean field and its derivatives, and makes use of appropriately chosen test field, whose evolution is computed along with the turbulent flow. Our approach is also different from the one used by Guan & Gammie (2009), in which a magnetic structure is imposed as an initial condition, and the resistive properties of the background turbulent flow are deduced from the decay time of this structure. The method we adopt here is described in Sect. 2, and the physical content of the two methods is discussed there. More generally, Sect. 2 describes the physics and the numerical methods we have used to study turbulent resistivity in disks. Section 3 presents a linear analysis of the model, which sheds some light on the numerical findings described in Sect. 4. Section 5 discusses the astrophysical implications of these results along with some future line of work.
2 Shearing-box equations and numerical method
MRI-related turbulence has been extensively studied in the literature, but little attention has been devoted to the question of turbulent-driven resistivity yet. One of the major advances of the recent years has been the realization that an accurate determination of turbulent transport properties requires an accurate representation of all scales down to the dissipation scales (Lesur & Longaretti 2007; Fromang et al. 2007), although this accuracy has not yet been achieved for astrophysically relevant magnetic Prandtl and Reynolds numbers regimes. We do not imply that actual astrophysical Reynolds numbers need to be resolved in simulations to obtain reliable results, an obviously hopeless task anyway; but for large enough Reynolds and magnetic Reynolds numbers, one expects the dissipation scale to be decoupled from the transport scales, in which case one could use a closure model without resolving the dissipation scales. However, today simulations don't seem to have reached this regime yet.
Shearing box simulations offer a particularly convenient setting to quantify turbulent resistivity; however, the boundary conditions prevent the existence of the large scale gradients of mean magnetic field required for characterizing the transport of this mean field produced by turbulence. We bypass this difficulty by a prescription whose physical motivation and formulation will be described later on in this section. For the time being, we briefly recall the basic equations for the shearing-box model, which has been largely studied and used in the literature. The reader may consult Hawley et al. (1995), Balbus (2003) and Regev & Umurhan (2008) for an extensive discussion of the properties and limitations of this model.
Since MHD turbulence in disks is essentially subsonic, we will work in the incompressible approximation, which allows us to eliminate sound waves and density waves from the problem. Although density waves are excited in shearing box turbulence (Heinemann & Papaloizou 2008b) they should not have a big impact on the turbulence spectrum itself or on turbulent transport as their amplitude decays exponentially fast when one goes to small scales (Heinemann & Papaloizou 2008a). This has also been confirmed by direct comparison between incompressible and compressible simulations (Fromang et al. 2007). We also neglect vertical stratification, consistently with the local shearing-box model (Regev & Umurhan 2008). Explicit molecular viscosity and resistivity are included in our description.
The shearing box equations follow from a local approximation. We
chose a Cartesian box centered at r=R0, rotating with the disk
at angular velocity
![]() and having dimensions
(Lx,Ly,Lz) with
and having dimensions
(Lx,Ly,Lz) with
![]() .
Assuming
.
Assuming
![]() and
and
![]() ,
one eventually obtains the shearing
box equations:
,
one eventually obtains the shearing
box equations:
The boundary conditions associated with this system are periodic in the x and z direction and shearing-periodic in the ydirection (Hawley et al. 1995). In these equations, we have defined the mean shear
The steady-state solution to these equations is the local
Keplerian profile
![]() .
In this paper, we will
consider only the turbulent deviations from this Keplerian
profile. These may be written as
.
In this paper, we will
consider only the turbulent deviations from this Keplerian
profile. These may be written as
![]() ,
leading to the following equations for
,
leading to the following equations for ![]() :
:
Following Hawley et al. (1995), one can integrate the induction Eq. (6) over the volume of the box, leading to:
where
To numerically solve the shearing-box equations, we use a spectral
Galerkin representation of Eqs. (5)-(8) in the sheared frame
(see Lesur & Longaretti 2005). This frame allows us to use a Fourier
decomposition since the shearing-sheet boundary conditions are
transformed into perfectly periodic boundary conditions. Moreover,
this decomposition allows us to conserve magnetic flux to machine
precision without any modification, which is an advantage compared
to finite-difference or finite-volume methods (the total magnetic
flux created during one simulation is typically 10-11).
Equations (7) and (8) are enforced to
machine precision using a spectral projection (Peyret 2002). The
nonlinear terms are computed with a pseudospectral method, and
aliasing is prevented using the 3/2 rule. To always compute the
physically relevant scales in the sheared frame, we use a remap
method similar to the one described by Umurhan & Regev (2004). This routine
redefines the sheared frame every
![]() and we have checked that none of the behaviour we describe in this
paper was related to this numerical timescale. Since spectral
methods are very little dissipative by nature, we check that
numerical dissipation is kept to very small values, computing the
total energy budget at each time step (see Lesur & Longaretti 2005, for a discussion
of this procedure). We therefore ensure that numerical
dissipation is responsible for less than
and we have checked that none of the behaviour we describe in this
paper was related to this numerical timescale. Since spectral
methods are very little dissipative by nature, we check that
numerical dissipation is kept to very small values, computing the
total energy budget at each time step (see Lesur & Longaretti 2005, for a discussion
of this procedure). We therefore ensure that numerical
dissipation is responsible for less than ![]() of the total
dissipative losses occurring in these simulations.
of the total
dissipative losses occurring in these simulations.
To quantify the dissipation processes in the simulations, we use dimensionless numbers defined as:
- the Reynolds number,
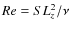 ,
comparing the nonlinear advection term to the viscous dissipation;
,
comparing the nonlinear advection term to the viscous dissipation;
- the magnetic Reynolds number,
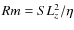 ,
comparing magnetic field advection to the Ohmic resistivity;
,
comparing magnetic field advection to the Ohmic resistivity;
- the magnetic Prandtl number, defined as the ratio of the two previous quantities
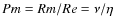 ,
which
measures the relative importance of the dissipation processes,
and, correlatively, is related to the ratio of the viscous and
resistive dissipation scales.
,
which
measures the relative importance of the dissipation processes,
and, correlatively, is related to the ratio of the viscous and
resistive dissipation scales.
2.1 Turbulent resistivity definition
Our aim is to test to which extent the effect of MRI turbulence on
the mean field can be modelled as a turbulent resistivity on large
scales, and characterize inasmuch as possible the resulting
turbulent resistivity tensor. We therefore distinguish the large
scale mean field
![]() and velocity
and velocity
![]() and the fluctuating (turbulent) fields
and the fluctuating (turbulent) fields
![]() and
and ![]() .
We assume
.
We assume
![]() and
and
![]() where
where
![]() denotes an
ensemble (or time, under the ergodic hypothesis) average. The
induction equation reads:
denotes an
ensemble (or time, under the ergodic hypothesis) average. The
induction equation reads:
where we have defined the mean electromotive force (EMF)
Our main objective is to test and quantify this assumption. We keep no term proportional to
At this point, two different routes are open to study the turbulent diffusion of the magnetic field.
- In the first one, Eq. (11) is assumed.
One can split Eq. (6) into an equation for the mean field
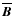 and one for the deviation from the mean
and one for the deviation from the mean  .
As the induction equation is linear in the field, b formally depends on the mean and turbulent velocity fields and mean
magnetic field only. One
then introduces extraneous magnetic fields
bpq, whose equation of
evolution is the same as for
.
As the induction equation is linear in the field, b formally depends on the mean and turbulent velocity fields and mean
magnetic field only. One
then introduces extraneous magnetic fields
bpq, whose equation of
evolution is the same as for  ,
except for the mean field
,
except for the mean field
 which is replaced
by a ad hoc test field
which is replaced
by a ad hoc test field
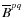 .
It is then possible to derive the EMF associated
to this test field
.
It is then possible to derive the EMF associated
to this test field
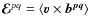 .
.
One can deduce some of the components of
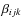 using several test fields and computing
the correlations between
using several test fields and computing
the correlations between
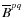 and
and
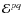 .
By construction, this method
probes the velocity field
.
By construction, this method
probes the velocity field 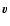 with a test field
with a test field
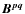 which is different from
the real field
which is different from
the real field 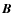 entering in the Lorentz force. Therefore, one assumes implicitly
that the properties of
entering in the Lorentz force. Therefore, one assumes implicitly
that the properties of
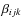 don't depend on the topological properties of
don't depend on the topological properties of 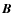 ,
which might not be true for subcritical dynamos (see e.g. Lesur & Ogilvie 2008) or turbulence driven through the Lorentz force like MRI turbulence.
This method is detailed in Schrinner et al. (2005) and Brandenburg et al. (2008) and references therein.
,
which might not be true for subcritical dynamos (see e.g. Lesur & Ogilvie 2008) or turbulence driven through the Lorentz force like MRI turbulence.
This method is detailed in Schrinner et al. (2005) and Brandenburg et al. (2008) and references therein.
- Alternatively, one can impose the constancy of some large
scale component of the magnetic field gradient throughout
the evolution and test if Eq. (11) accurately represents
the effect of turbulence on field diffusion. As in the previous approach,
adequate choices of the imposed field configuration allow us to characterize various
elements of the diffusivity tensor. This approach is adopted here and specified
in more detail in the following subsection.
In practice, we chose field configurations such that only one
component of the field gradient is non vanishing at any given
time, so that the current is directly proportional to this
non-vanishing gradient. In this situation, one can dispense with
the third order tensor and use
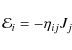 |
(12) |
instead, where
To keep in line with the logic of the ![]() parameterization as
adapted to an incompressible fluid (see Lesur & Longaretti 2007), one may
introduce an
parameterization as
adapted to an incompressible fluid (see Lesur & Longaretti 2007), one may
introduce an ![]() tensor relating to the turbulent
tensor relating to the turbulent ![]() tensor:
tensor:
With our choice of units (S=1 and Lz=1), one has
2.2 Numerical protocol
To compute the turbulent resistivity, one needs a mean current,
which is not present in local (shearing box) simulations. We
obtain this current by imposing a large scale and non
homogeneous field in the box. This is done with the help of our
Galerkin representation by forcing the largest Fourier mode in one
direction to a constant value
![]() .
To trigger the MRI, we
impose a mean field B0 which can be either azimuthal or
vertical. The aspect ratio is
.
To trigger the MRI, we
impose a mean field B0 which can be either azimuthal or
vertical. The aspect ratio is
![]() where
where ![]() ,
y=-r and z=z. The
factor 2 in Ly allow us to trigger more easily secondary
instabilities in the strong mean vertical field cases (see
Goodman & Xu 1994; and Bodo et al. 2008). The resolution used is
,
y=-r and z=z. The
factor 2 in Ly allow us to trigger more easily secondary
instabilities in the strong mean vertical field cases (see
Goodman & Xu 1994; and Bodo et al. 2008). The resolution used is
![]() ,
similar in cell size to the one used in
Lesur & Longaretti (2007). The Reynolds number is kept constant at Re=1600 as
well as the magnetic Prandtl number, which is fixed at unity:
Pm=1. This corresponds to a Elsasser number
,
similar in cell size to the one used in
Lesur & Longaretti (2007). The Reynolds number is kept constant at Re=1600 as
well as the magnetic Prandtl number, which is fixed at unity:
Pm=1. This corresponds to a Elsasser number
![]() for B0=0.1 and
for B0=0.1 and
![]() for
B0=0.025. Each simulation is integrated over 500 shear times
(to obtain meaningful time averages), and the average are computed
from 400 last shear times (to avoid initial conditions artifacts).
for
B0=0.025. Each simulation is integrated over 500 shear times
(to obtain meaningful time averages), and the average are computed
from 400 last shear times (to avoid initial conditions artifacts).
To postprocess the results, we first compute the time average of
![]() and
and
![]() .
We then use a script which
extracts the mean current and compute the correlation with the
emfs, giving in the end one component of the
.
We then use a script which
extracts the mean current and compute the correlation with the
emfs, giving in the end one component of the ![]() tensor for one
run. Note that using this procedure, we can compute resistivity
associated with Bz(y) (radially varying vertical field),
Bx(y) (radially varying azimuthal field) and Bx(z)(vertically varying azimuthal field) configurations. Imposing a
constant radial field By would lead to a linear growth of the
azimuthal field Bx, which may not have any physical meaning. We
cannot compute turbulent resistivity associated with non
axisymmetric structures because of the shearing-sheet boundary
conditions.
tensor for one
run. Note that using this procedure, we can compute resistivity
associated with Bz(y) (radially varying vertical field),
Bx(y) (radially varying azimuthal field) and Bx(z)(vertically varying azimuthal field) configurations. Imposing a
constant radial field By would lead to a linear growth of the
azimuthal field Bx, which may not have any physical meaning. We
cannot compute turbulent resistivity associated with non
axisymmetric structures because of the shearing-sheet boundary
conditions.
The runs we have performed do not test all the dependencies of the dimensionless turbulent resistive transport with respect to all the dimensionless parameters of the problem, but only a subset of them, namely:
- the role of the mean field orientation B0, and of the
orientation the imposed field varying component
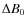 ;
;
- the role of the relative amplitude of the mean and imposed
varying field components
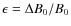 .
In the
process, only a few components of the turbulent resistivity tensor
are probed;
.
In the
process, only a few components of the turbulent resistivity tensor
are probed;
- the role of the relative mean field amplitude,
characterized by
![[*]](/icons/foot_motif.png)
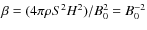 (the
last equality follows from our choice of units).
(the
last equality follows from our choice of units).
Our local simulation box physical size is on the order of the
scale height at most. As such, one would expect to mimic the
effect of large scale gradients of the magnetic field by small
values of ![]() .
However sizeable (but of limited extent)
local field gradients may also be present in disks as a result of
the dynamics, and it is of some interest to explore values of
.
However sizeable (but of limited extent)
local field gradients may also be present in disks as a result of
the dynamics, and it is of some interest to explore values of
![]() of order unity as well.
of order unity as well.
3 Analytic results
It is of some interest to look into the linear behavior of the instability first, as it does provide some insight into the turbulent problem that we discuss in the next section. Indeed, there is evidence that the channel mode (both a linear and nonlinear solution to the incompressible equations) plays some role in the overall transport properties of the MRI-driven turbulent states.
For this reason, we want to test the turbulent resistivity
hypothesis (Eqs. (10) and (11)) in the linear
regime. This is done assuming the fluctuations v and b are
infinitely small compared to the averaged fields. We then
calculate v and b by a classical linear analysis and deduce
the EMF
![]() which is a quadratic quantity in this
limit
which is a quadratic quantity in this
limit![]() . The same procedure can be used for Maxwell and
Reynolds stresses, allowing one to compute ``effective'' transport
coefficients in the linear regime.
. The same procedure can be used for Maxwell and
Reynolds stresses, allowing one to compute ``effective'' transport
coefficients in the linear regime.
To make comparisons easier, we investigate one of the configurations which is
simulated in the next section of this paper, namely we impose a
vertical mean field of the form
where
Assuming that the development of the instability is fast compared
to the viscous and resistive time-scales, we neglect the
corresponding terms in Eqs. (5) and (6)
in this linear analysis. Under this approximation, the system
Eq. (5) to (7) admits a simple equilibrium
with constant pressure and varying equilibrium azimuthal
velocity![]() profile to balance the magnetic
pressure gradient:
profile to balance the magnetic
pressure gradient:
This leads us to introduce the total shear
It turns out that only channel-like mode present correlations of the EMF that behave as expected under the resistivity hypothesis, so we specialize from the onset to that type of modes. First order linear deviations from the mean stationary solution described above are referred to as
where
It is useful to distinguish the poloidal and toroidal components
of the velocity and magnetic fields:
Because, of the assumed axisymmetry, on can introduce potential fields
All variables can be expressed in terms of
where
The magnetic field
We have solved Eq. (22) numerically with periodic radial boundary conditions
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12272f1.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg121.png) |
Figure 1:
Mean emfs and best fit with the current for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12272f2.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg122.png) |
Figure 2:
Ratio of the mean emf |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{12272f3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg123.png) |
Figure 3:
Zeroth and first order components of the poloidal magnetic and velocity fields for the fastest growing channel mode ( |
| Open with DEXTER | |
Solutions in the
![]() limit are the usual MRI modes, i.e.
simple sinusoidal modes
limit are the usual MRI modes, i.e.
simple sinusoidal modes
![]() .
Solutions for arbitrary
.
Solutions for arbitrary ![]() generalize these modes. It
turns out that only the nodeless mode (ky=0) produces a mean
emf that correlates with the imposed current
generalize these modes. It
turns out that only the nodeless mode (ky=0) produces a mean
emf that correlates with the imposed current![]() , and in
the following, only these modes are studied.
, and in
the following, only these modes are studied.
For definiteness, we show results pertaining to the fastest
growing mode, for ![]() and
and
![]() .
Similar results
are obtained for other sets of parameters, and for other purely
vertical modes.
.
Similar results
are obtained for other sets of parameters, and for other purely
vertical modes.
Following the quasi-linear analysis procedure, we define the
quadratic emf as:
![\begin{displaymath}\langle\vec{\mathcal{E}}(y)\rangle=\frac{1}{2}\Re \Big[ \vec{v \times b^\dagger} \Big]
\end{displaymath}](/articles/aa/full_html/2009/35/aa12272-09/img127.png) |
(30) |
where
It is of some interest to compare the efficiency of the
``resistive'' and ``viscous'' transport due to the instability,
i.e., the value of
![]() deduced here to
the value of
deduced here to
the value of
![]() due to the same mode. This is shown in
Fig. 2 for the same mode and for two different values of
due to the same mode. This is shown in
Fig. 2 for the same mode and for two different values of
![]() and a range of values of
and a range of values of ![]() .
Note that this ratio
is constant throughout the growth of the mode. The analytic result
for this ratio in the limit of small
.
Note that this ratio
is constant throughout the growth of the mode. The analytic result
for this ratio in the limit of small ![]() is
is
![]() .
Apparently, the
relative efficiency of resistive and viscous transports due to the
instability are of similar magnitude, more or less independently
of the amplitude of the imposed field variation and mean field
strength.
.
Apparently, the
relative efficiency of resistive and viscous transports due to the
instability are of similar magnitude, more or less independently
of the amplitude of the imposed field variation and mean field
strength.
The comparable efficiency of the two transport effects due to the channel mode comes somewhat as a surprise. From a thermodynamical point of view, the instability sets in because of the imposed velocity shear and tries to restore a thermodynamical equilibrium by transporting momentum to reduce this shear. At first sight, there is no reason that it should also try to suppress a gradient in magnetic field with about the same efficiency.
However, if one considers the second-order correlation approximation
used in mean field electrodynamic, one finds (e.g. Rädler & Rheinhardt 2007):
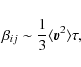 |
(31) |
where
The analytic results as well as the preceding argument imply that
the motion and magnetic field deviations due to the varying field
should be coupled. An illustration of the efficiency of these
couplings leading to this high resistive transport can be obtained
from the analytic solution in the small ![]() limit. In this
limit, the correlation arises from the correlation of zeroth and
first order quantities in
limit. In this
limit, the correlation arises from the correlation of zeroth and
first order quantities in ![]() ,
,
![]() .
Figure 3 shows the four involved poloidal fields for the
most unstable channel mode (
.
Figure 3 shows the four involved poloidal fields for the
most unstable channel mode (![]() ,
,
![]() ). Direct
inspection indeed shows that the relevant fields do exhibit a
significant level of correlation.
). Direct
inspection indeed shows that the relevant fields do exhibit a
significant level of correlation.
Having gained this understanding of the transport due to the linear modes of the instability, we now turn to the full nonlinear problem.
4 Numerical results
We have simulated three different configurations, which combine a mean vertical and/or azimuthal field with a varying field component in the vertical or azimuthal direction, the direction of variation being either vertical or radial. This allows us to characterize a number of components of the turbulent resistivity tensor.
To classify our numerical results, we use the following naming convention: the first letter indicates the direction of the mean field, the second letter indicates the direction of the varying field and the third letter corresponds to the direction of the spatial dependency. We finally add a number to identify the simulations done in the same configuration but with different field intensity. For instance, run XZY7 have a mean field in the x direction, a varying field in the z direction with a spatial dependency in the y direction.
The various configurations and results are presented in the corresponding subsections. They are then compared in the concluding subsection.
4.1 Vertical field with radial dependency Bz(y)
In this case, we force the following structure for the mean magnetic field:
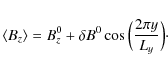 |
(32) |
The mean current is then written:
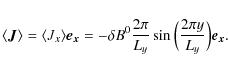 |
(33) |
We are therefore looking for a correlation between Jx and
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f4a.eps}\hspace*{8mm}
\includegraphics[width=8.45cm,clip]{12272f4b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg143.png) |
Figure 4:
Mean field ( left) and Emfs ( right) from run ZZY4 (Bz(y) case) with a mean vertical field Bz0=0.1 and
|
| Open with DEXTER | |
Table 1: Main results from the Bz(y) (vertical field with a radial dependency) case in the presence of a mean vertical field Bz0.
The extraneous EMF component was already present at the linear level, as noted in the previous section, but with the opposite sign. We have not been able to understand the significance of this sign difference. In our simulations, this component plays no physical role (its rotational vanishes). This may not be a generic feature, in particular in more complex stratified settings. This component shows anyway that the turbulent state is anisotropic.
One may note a decrease of the turbulence efficiency in models
ZZY4-ZZY5, which may be due to the fact that increasing
![]() to high values leads to strong modification of the background
field. Since Bz0=0.1 corresponds to the maximum of the growth
rate for the
to high values leads to strong modification of the background
field. Since Bz0=0.1 corresponds to the maximum of the growth
rate for the
![]() mode, increasing
mode, increasing
![]() always
weakens the instability, which might explain these results. As
expected, this effect is not observed in
Bz0=0.025 models, for
which this explanation doesn't hold.
always
weakens the instability, which might explain these results. As
expected, this effect is not observed in
Bz0=0.025 models, for
which this explanation doesn't hold.
According to these results, and anticipating on the result of the
last subsection where the correlations are compared in detail, we
point out that, on average
| (34) |
The resulting ratio
4.2 Toroidal field with a radial dependency Bx(y)
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f5a.eps}\hspace*{8mm}
\includegraphics[width=8.9cm,clip]{12272f5b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg175.png) |
Figure 5:
Mean field ( left) and emfs ( right) from run ZXY5 (Bx(y) case) with a mean vertical field Bz0=0.1 and
|
| Open with DEXTER | |
In this case, we impose the following field:
| |
= | Bz0, | (35) |
| = | (36) |
The mean current is then defined by:
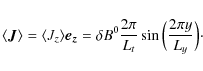 |
(37) |
As in the previous case, we look for a correlation between Jzand
Table 2: Main results from the Bx(y) (toroidal field with a radial dependency) case for several toroidal and vertical mean fields Bj0.
Comparing turbulent transport coefficient turbulent resistivity with the Bz(y) case,
we note that no turbulence weakening occurs in the present case, consistently with the linear
justification (the expected linear growth rate is not modified by a varying toroidal field).
Although other experiments for larger values of
![]() would allow a better determination of the resistivity, we
can still approximate
would allow a better determination of the resistivity, we
can still approximate
| (38) |
with a mean vertical field and
| (39) |
with a mean toroidal field.
4.3 Toroidal field with a vertical dependency Bx(z)
We define the mean field by:
| |
= | Bz0, | (40) |
| = | (41) |
The mean current is then found to be:
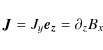 |
(42) |
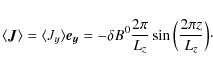 |
(43) |
Looking for a correlation between Jy and
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f6a.eps}\hspace*{8mm}
\includegraphics[width=8.42cm,clip]{12272f6b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg208.png) |
Figure 6:
Mean field ( left) and emfs ( right) for a case with Bz0=0.1 and
|
| Open with DEXTER | |
These complications induce the existence of off-diagonal
components of the resistivity tensor, which cannot be quantified
with the simple method adopted in this paper. Nevertheless, in
spite of these difficulties, the procedure used in the previous
subsections yields reasonable results for the diagonal component,
as can be seen in Fig. 6:
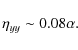 |
(44) |
This value of
Table 3: Main results from the Bx(z) (toroidal field with a vertical dependency) case with a mean vertical field Bz0.
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f7a.eps}\hspace*{8mm}
\includegraphics[width=8.65cm,clip]{12272f7b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg224.png) |
Figure 7:
Mean field ( left) and emfs ( right) for a case with a mean toroidal flux Bx0=0.1, Bz0=0,
|
| Open with DEXTER | |
The value of ![]() is more precisely derived when Bz0=0which prevent channel flow formation. We present in
Fig. 7 an example of the profiles obtained from such a
simulation and the resistivity values for several runs in
Table 4.
is more precisely derived when Bz0=0which prevent channel flow formation. We present in
Fig. 7 an example of the profiles obtained from such a
simulation and the resistivity values for several runs in
Table 4.
Table 4: Main results from the Bx(z) (toroidal field with a vertical dependency) case for various toroidal Bx0.
Interestingly, ![]() seems to be constant although
seems to be constant although ![]() varies significantly, contrarily to previous cases. We can still
approximate:
varies significantly, contrarily to previous cases. We can still
approximate:
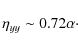 |
(45) |
We note however that this relation doesn't mean that the diffusive process is very strong in the vertical direction compared to that in the horizontal direction, as the turbulence intensity is weaker with a mean toroidal field than with a mean vertical field (compare for instance the values of
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{12272f8.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg234.png) |
Figure 8:
Dependence of the turbulent diffusivity tensor components that we were
able to measure on |
| Open with DEXTER | |
4.4 Parameter and configuration dependence of the turbulent resistivity tensor
It is of interest to compare the effect of the field configuration and magnitude on the various turbulent resistivity tensor components that we have characterized, most notably concerning the radial and vertical diffusion of vertical and azimuthal field components. To this effect, the various dependencies have been represented in Fig. 8.
The most significant trend is due to the direction of the mean field. As for turbulent viscous transport (but somewhat less dramatically), the turbulent resistive transport in the radial direction is substantially reduced when the mean field is azimuthal with respect to a vertical mean field, by nearly an order of magnitude; however, and somewhat surprisingly, no such trend is visible for the diffusion in the vertical direction (bottom left subplot). Our simulations with a mean toroidal field may suffer (as all others) from a lack of resolution of the relevant small scale modes, a point that has apparently never been adequately checked in the literature.
Another important trend, and the most critical one for the issue of jet driving from accretion disks, concerns the relative efficiency in the radial diffusion of vertical and azimuthal field components (top right subplot). The diffusion of the azimuthal field is more efficient by a factor of order 2 to 3.
There is apparently some influence of the magnitude on the mean
field on the efficiency of transport in the radial direction (top
left subplot). This trend is the same as for the turbulent viscous
transport, as shown on the bottom right subplot. The simplest
explanation for this trend is that the transport is magnetically
driven, whereas the usual adimensionalization of quantities (which
we have more or less followed in our definitions) scales transport
with the sound speed and the scale height: within factors of order
unity,
![]() and similarly
for the various
and similarly
for the various ![]() components. With this scaling, the various
simulations available in the literature imply that
components. With this scaling, the various
simulations available in the literature imply that
![]() .
If a scaling with the Alfveén speed were chosen
instead, i.e.,
.
If a scaling with the Alfveén speed were chosen
instead, i.e.,
![]() ,
the characteristic
dimensionless number
,
the characteristic
dimensionless number
![]() is independent of
is independent of ![]() (at
least until B0 is so weak that the zero mean field MRI dynamo
process takes over). It has been noted in the first subsection
that the decrease with
(at
least until B0 is so weak that the zero mean field MRI dynamo
process takes over). It has been noted in the first subsection
that the decrease with ![]() for the largest value of
for the largest value of ![]() is most likely a saturation process linked to the fact that this
choice of
is most likely a saturation process linked to the fact that this
choice of ![]() is close to the marginal stability limit of the
instability.
is close to the marginal stability limit of the
instability.
The last subplot (bottom right) indicates that ![]() (amplitude
of the mean field) and
(amplitude
of the mean field) and ![]() (amplitude of the field
variation) influence in much the same way the turbulent resistive
and turbulent transport. To some extent, this is also true of the
spatial orientation of the underlying quantities, and not only
their magnitudes. Overall, the turbulent resistive transport has
an efficiency which is smaller but comparable to the turbulent
viscous one, within a factor of order 2 or 3.
(amplitude of the field
variation) influence in much the same way the turbulent resistive
and turbulent transport. To some extent, this is also true of the
spatial orientation of the underlying quantities, and not only
their magnitudes. Overall, the turbulent resistive transport has
an efficiency which is smaller but comparable to the turbulent
viscous one, within a factor of order 2 or 3.
5 Discussion
We have presented a systematic method to determine the turbulent resistivity associated with MRI turbulence in accretion disks. We have exemplified this method in the configuration radially and vertically varying vertical magnetic fields, using nonlinear spectral simulations of turbulence. We have also analyzed the resistive transport due to channel modes in the linear limit, in the presence of a radially varying vertical fields. Both the linear calculations and the fully nonlinear simulations show that the turbulent resistive transport is large, comparable to the turbulent viscous transport, albeit a factor of 2 to 4 smaller. This feature contradicts the heuristic model developed by Shu and coworkers (Shu et al. 2007) for turbulent resistive transport in YSOs accretion disks, thereby removing an obstacle to the launching of jets by accretion disks.
More precisely, we find that the turbulent resistivity
![]() is
largely correlated to the turbulent viscosity
is
largely correlated to the turbulent viscosity
![]() over a wide
range of variations of the dimensionless parameters of the problem
(but we have not explored the dependency on the dissipation
numbers, which needs an extensive study in itself). As a matter of
fact, we may define a turbulent Prandtl number
over a wide
range of variations of the dimensionless parameters of the problem
(but we have not explored the dependency on the dissipation
numbers, which needs an extensive study in itself). As a matter of
fact, we may define a turbulent Prandtl number
![]() ,
which is found to be on the order of 2-5.
Second, we find that the turbulent resistivity is an anisotropic
tensor. In particular, the toroidal field (Bx) diffuses about 3
times more rapidly than the poloidal field (Bz), in the radial
as well as the vertical directions. We also find that non diagonal
terms of the turbulent resistivity tensor are non zero. As shown
by Lesur & Ogilvie (2008), such terms might play an important role for disk
dynamos and large scale magnetic field generation.
,
which is found to be on the order of 2-5.
Second, we find that the turbulent resistivity is an anisotropic
tensor. In particular, the toroidal field (Bx) diffuses about 3
times more rapidly than the poloidal field (Bz), in the radial
as well as the vertical directions. We also find that non diagonal
terms of the turbulent resistivity tensor are non zero. As shown
by Lesur & Ogilvie (2008), such terms might play an important role for disk
dynamos and large scale magnetic field generation.
It is often argued that a turbulent Prandtl number
![]() on the order of R/H is required for turbulent disks to be able
to launch jets (see van Ballegooijen in Belvedere 1989, and
Lubow et al. 1994). In fact, because the accretion velocity in
jet-driving disks is larger than in standard accretion disks, this
requirement overestimates the necessary turbulent resistivity,
which turns out to be comparable to the turbulent viscosity in
self-consistent accretion-ejection models (see e.g. Casse & Ferreira 2000; see also Rothstein & Lovelace 2008 and Lovelace et al. 2009, for a
simplified version of the same argument). This large turbulent
Prandtl number argument is also often invoked to justify that an
outer standard disk cannot transform into an inner jet-launching
one in the accretion process, but the validity of this conclusion
relies heavily on the assumed vertical structure of the models
considered (in particular the magnetic structure of the corona), a
point that has not been appropriately taken into account in the
literature up to now.
on the order of R/H is required for turbulent disks to be able
to launch jets (see van Ballegooijen in Belvedere 1989, and
Lubow et al. 1994). In fact, because the accretion velocity in
jet-driving disks is larger than in standard accretion disks, this
requirement overestimates the necessary turbulent resistivity,
which turns out to be comparable to the turbulent viscosity in
self-consistent accretion-ejection models (see e.g. Casse & Ferreira 2000; see also Rothstein & Lovelace 2008 and Lovelace et al. 2009, for a
simplified version of the same argument). This large turbulent
Prandtl number argument is also often invoked to justify that an
outer standard disk cannot transform into an inner jet-launching
one in the accretion process, but the validity of this conclusion
relies heavily on the assumed vertical structure of the models
considered (in particular the magnetic structure of the corona), a
point that has not been appropriately taken into account in the
literature up to now.
On the basis of these results, it seems quite plausible that accretion disks have the ability to launch non stationary jets. Although the turbulent resistivity we find is somewhat too weak to allow for the existence of stationary accretion-ejection structure, the anisotropy is in the right range. Nevertheless, further work is required to get a complete characterization of the turbulent resistivity. In particular, the correlation with turbulent viscous transport needs to be more precisely studied, as well as the impact of the (molecular) Prandtl number, which is known to be strong on the momentum transport efficiency (Lesur & Longaretti 2007).
While we were writing this paper, a similar study in shearing box
with the ZEUS code has appeared on the astro-ph ArXiV by Guan and
Gammie (Guan & Gammie 2009), and some discussion of the connection between
the two investigations is in order. In their paper, they impose of
mean toroidal field, wait for turbulence to reach a stationary
state. They superimpose then a sinusoidally varying field
component whose decay rate is used to quantify the turbulent
resistivity. Instead, we impose a constant sinusoidal component of
the field and study the correlation between the resulting emf and
the current in the insuing statistically stationary turbulent
regime. Guan and Gammie have also made some resolution studies,
which we have not performed, as previous experience with the
dimensionless numbers used in this work has shown us that the
dissipation scales are adequately resolved with our adopted
resolution. Finally, Guan and Gammie have looked into the effect
of the box aspect ratio, which was held fixed here. Conversely,
our parameter study is somewhat more extensive than theirs for the
type of configurations we have looked into. The majority of the
runs performed by Guan and Gammie have been made for vertical
sinusoidal component superimposed on the mean toroidal field, a
configuration we have not investigated, so that these runs are not
directly comparable to ours. Note however that using a mean
vertical field instead of a mean toroidal one is more relevant to
the question of flux diffusion for accretion-ejection models.
Nevertheless, some of the runs of Guan & Gammie (2009) have been performed
with both the mean and sinusoidal component in the azimuthal
direction, which are comparable to the ones presented here in
Sect. 4.3. Their turbulent resistivity and viscosity values are
systematically larger than ours, but note that their ![]() parameter in these runs is four times larger than the larger one
we have used (and believe to be more relevant to disk physics). As
there is a clear trend towards a significant increase of the
turbulent resistivity and viscosity with increasing
parameter in these runs is four times larger than the larger one
we have used (and believe to be more relevant to disk physics). As
there is a clear trend towards a significant increase of the
turbulent resistivity and viscosity with increasing ![]() at
the larger values of
at
the larger values of ![]() shown in Table 4, we conclude that
the two results are reasonably compatible. More generally
speaking, in order of magnitude, both studies are rather
complementary and agree on the fact that the turbulent resistivity
and viscosity are comparable, but runs in similar settings would
be required to make a full comparison between the two methods.
shown in Table 4, we conclude that
the two results are reasonably compatible. More generally
speaking, in order of magnitude, both studies are rather
complementary and agree on the fact that the turbulent resistivity
and viscosity are comparable, but runs in similar settings would
be required to make a full comparison between the two methods.
Acknowledgements
The majority of the simulations presented in this paper were performed using the Darwin Supercomputer of the University of Cambridge High Performance Computing Service (http://www.hpc.cam.ac.uk/), provided by Dell Inc. using Strategic Research Infrastructure Funding from the Higher Education Funding Council for England. G.L. acknowledges support by STFC. Other simulations have been performed on the SCCI cluster of the Observatoire de Grenoble.We thank our referee, Jim Stone, for his detailed comments on this work.
References
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] (In the text)
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] (In the text)
- Belvedere, G., 1989, Astrophysics and Space Science Library, 156, Accretion disks and magnetic fields in astrophysics, Proceedings of the European Physical Society Study Conference, Noto, Italy, June 16-21, 1988 (In the text)
- Bodo, G., Mignone, A., Cattaneo, F., Rossi, P., & Ferrari, A. 2008, A&A, 487, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brandenburg, A., Rädler, K.-H., Rheinhardt, M., & Käpylä, P. J. 2008, ApJ, 676, 740 [NASA ADS] [CrossRef] (In the text)
- Cabot, W. 1996, ApJ, 465, 874 [NASA ADS] [CrossRef]
- Casse, F., & Ferreira, J. 2000, A&A, 353, 1115 [NASA ADS]
- Dubrulle, B., Dauchot, O., Daviaud, F., et al. 2005, Phys. Fluids, 17, 095103 [NASA ADS] [CrossRef] (In the text)
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] (In the text)
- Goodman, J., & Xu, G. 1994, ApJ, 432, 213 [NASA ADS] [CrossRef] (In the text)
- Guan, X., & Gammie, C. F. 2009, ApJ, 697, 1901 [NASA ADS] [CrossRef] (In the text)
- Hawley, J. F. 2000, ApJ, 528, 462 [NASA ADS] [CrossRef] (In the text)
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] (In the text)
- Heinemann, T., & Papaloizou, J. C. B. 2008a, MNRAS, 397, 52 [NASA ADS] [CrossRef] (In the text)
- Heinemann, T., & Papaloizou, J. C. B. 2008b, MNRAS, 397, 64 [NASA ADS] [CrossRef] (In the text)
- Ji, H., Burin, M., Schartman, E., & Goodman, J. 2006, Nature, 444, 343 [NASA ADS] [CrossRef]
- Johnson, B. M., & Gammie, C. F. 2006, ApJ, 636, 63 [NASA ADS] [CrossRef]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] (In the text)
- Lesur, G., & Longaretti, P.-Y. 2005, A&A, 444, 25 [NASA ADS] [CrossRef] [EDP Sciences]
- Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef]
- Lesur, G., & Ogilvie, G. I. 2008, A&A, 488, 451 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lovelace, R. V. E., Bisnovatyi-Kogan, G. S., & Rothstein, D. M. 2009, Nonlinear Processes in Geophysics, 16, 77 [NASA ADS] (In the text)
- Lubow, S. H., Papaloizou, J. C. B., & Pringle, J. E. 1994, MNRAS, 267, 235 [NASA ADS] (In the text)
- Petersen, M. R., Stewart, G. R., & Julien, K. 2007, ApJ, 658, 1252 [NASA ADS] [CrossRef]
- Peyret, R. 2002, Spectral Methods for Incompressible Viscous Flow (Springer) (In the text)
- Rädler, K.-H., & Rheinhardt, M. 2007, Geophysical and Astrophysical Fluid Dynamics, 101, 117 [NASA ADS] [CrossRef] (In the text)
- Regev, O., & Umurhan, O. M. 2008, A&A, 481, 21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Richard, D., & Zahn, J. 1999, A&A, 347, 734 [NASA ADS] (In the text)
- Rothstein, D. M., & Lovelace, R. V. E. 2008, ApJ, 677, 1221 [NASA ADS] [CrossRef] (In the text)
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. 2005, Astron. Nachr., 326, 245 [NASA ADS] [CrossRef] (In the text)
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
- Shu, F. H., Galli, D., Lizano, S., & Cai, M. J. 2007, in IAU Symp. 243, ed. J. Bouvier, & I. Appenzeller, 249 (In the text)
- Stone, J. M., & Balbus, S. A. 1996, ApJ, 464, 364 [NASA ADS] [CrossRef]
- Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] (In the text)
- Umurhan, O. M., & Regev, O. 2004, A&A, 427, 855 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... transport
![[*]](/icons/foot_motif.png)
- In this paper, a transport process refers to any physical mechanism by which a magnetic field line is moved from one place to another, without assuming anything about flux-freezing conditions.
- ... by
![[*]](/icons/foot_motif.png)
- Our
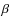 parameter is akin to the
usual plasma beta parameter, as both differ only by a factor of
order unity in a stratified disk in vertical hydrostatic
equilibrium.
parameter is akin to the
usual plasma beta parameter, as both differ only by a factor of
order unity in a stratified disk in vertical hydrostatic
equilibrium.
- ...
limit
![[*]](/icons/foot_motif.png)
- For this reason, this approach is also called ``quasi-linear''.
- ...
velocity
![[*]](/icons/foot_motif.png)
- An actual disk is indeed expected to react to the presence of a superimposed magnetic pressure gradient at some initial time by first adjusting its velocity profile instead of its gas pressure profile. Nevertheless, we have also explored the converse situation, where the magnetic pressure variation is balanced by a variation of the gas pressure, without modification of the Keplerian profile (a behavior expected in an incompressible fluid). This change of equilibrium has little effect on the results reported in this section.
- ... conditions
![[*]](/icons/foot_motif.png)
- No boundary condition is implied vertically so that the modes are not discretized in this direction. In this section, the unit of length is set to Ly, but this has no incidence on the results or on the rest of the paper.
- ... current
![[*]](/icons/foot_motif.png)
- The reason
for this can be understood by looking at the equation for the
first order correction
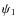 ,
which shows that the correct
radial behavior for coupling occurs only in this case.
,
which shows that the correct
radial behavior for coupling occurs only in this case.
All Tables
Table 1: Main results from the Bz(y) (vertical field with a radial dependency) case in the presence of a mean vertical field Bz0.
Table 2: Main results from the Bx(y) (toroidal field with a radial dependency) case for several toroidal and vertical mean fields Bj0.
Table 3: Main results from the Bx(z) (toroidal field with a vertical dependency) case with a mean vertical field Bz0.
Table 4: Main results from the Bx(z) (toroidal field with a vertical dependency) case for various toroidal Bx0.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12272f1.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg121.png) |
Figure 1:
Mean emfs and best fit with the current for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12272f2.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg122.png) |
Figure 2:
Ratio of the mean emf |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{12272f3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg123.png) |
Figure 3:
Zeroth and first order components of the poloidal magnetic and velocity fields for the fastest growing channel mode ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f4a.eps}\hspace*{8mm}
\includegraphics[width=8.45cm,clip]{12272f4b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg143.png) |
Figure 4:
Mean field ( left) and Emfs ( right) from run ZZY4 (Bz(y) case) with a mean vertical field Bz0=0.1 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f5a.eps}\hspace*{8mm}
\includegraphics[width=8.9cm,clip]{12272f5b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg175.png) |
Figure 5:
Mean field ( left) and emfs ( right) from run ZXY5 (Bx(y) case) with a mean vertical field Bz0=0.1 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f6a.eps}\hspace*{8mm}
\includegraphics[width=8.42cm,clip]{12272f6b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg208.png) |
Figure 6:
Mean field ( left) and emfs ( right) for a case with Bz0=0.1 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,clip]{12272f7a.eps}\hspace*{8mm}
\includegraphics[width=8.65cm,clip]{12272f7b.eps} }
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg224.png) |
Figure 7:
Mean field ( left) and emfs ( right) for a case with a mean toroidal flux Bx0=0.1, Bz0=0,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{12272f8.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12272-09/Timg234.png) |
Figure 8:
Dependence of the turbulent diffusivity tensor components that we were
able to measure on |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



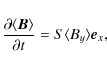
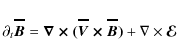
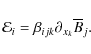
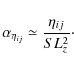
![\begin{displaymath}
B_T(y)= B_0\left[1+\epsilon\cos(k_0 y)\right],
\end{displaymath}](/articles/aa/full_html/2009/35/aa12272-09/img90.png)
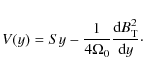
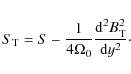
![$\displaystyle (\omega^2 - V_{\rm A}^2k_z^2)\psi'' - 2 V_{\rm b}^2k_z^3\psi'
+ \...
...S_{\rm T} V_{\rm A}^2 k_z^2}{\omega^2
-V_{\rm A}^2k_z^2}\right] k_z^2 \psi = 0,$](/articles/aa/full_html/2009/35/aa12272-09/img107.png)