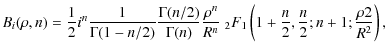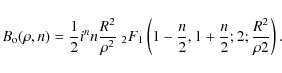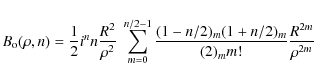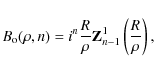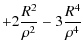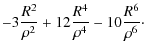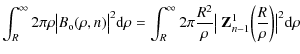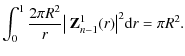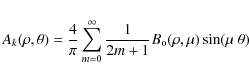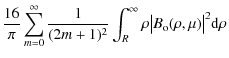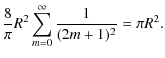| Issue |
A&A
Volume 504, Number 2, September III 2009
|
|
|---|---|---|
| Page(s) | 663 - 671 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912067 | |
| Published online | 09 July 2009 | |
Phase mask coronagraphy using a Mach-Zehnder interferometer
A. Carlotti - G. Ricort - C. Aime
Université de Nice Sophia-Antipolis, Centre National de la Recherche Scientifique, Laboratoire Fizeau, Observatoire de la Côte d'Azur, Parc Valrose, 06108 Nice Cedex, France
Received 13 March 2009 / Accepted 9 June 2009
Abstract
Aims. We report results obtained with a four-quadrant and an eight-octant phase-mask coronagraphs (4QC and 8OC) produced using amplitude masks inside a Mach-Zehnder interferometer (MZI). We describe the laboratory implementation of these coronagraphs operated in laser light and provide a detailed comparison between theory and experiment.
Methods. The +1 and -1 (![]() phase) amplitude transmissions required to produce a 4QC or an 8OC were obtained using complementary binary-masks (transmission of 1 or 0 for quadrants of similar parities) in the two arms of a MZI, taking advantage of the achromatic
phase) amplitude transmissions required to produce a 4QC or an 8OC were obtained using complementary binary-masks (transmission of 1 or 0 for quadrants of similar parities) in the two arms of a MZI, taking advantage of the achromatic ![]() phase shift between the two paths. In one output of the MZI, the reconstructed image of the focal plane is similar to those obtained for sectorised phase-masks coronagraphs, and the image of the aperture corresponds to the characteristic patterns of the 4QC/8OC coronagraphs.
phase shift between the two paths. In one output of the MZI, the reconstructed image of the focal plane is similar to those obtained for sectorised phase-masks coronagraphs, and the image of the aperture corresponds to the characteristic patterns of the 4QC/8OC coronagraphs.
Results. Observations are compared with the theory published by other authors and developed further here. The expressions for the light diffracted outside the aperture image are simplified using the Zernike radial polynomials
![]() instead of the rapidly diverging hypergeometric functions otherwise used. Experimental results are found to be in very good agreement with the theory. With the present laboratory experiment, about 99
instead of the rapidly diverging hypergeometric functions otherwise used. Experimental results are found to be in very good agreement with the theory. With the present laboratory experiment, about 99![]() of the light is rejected outside the Lyot stop and the contrast obtained beyond
of the light is rejected outside the Lyot stop and the contrast obtained beyond
![]() is higher than 105 for both the 4QC and 8OC. As expected, the 8OC is less affected by a pointing error than the 4QC, but more sensitive to an aperture central obstruction. Incidently, the loss of transmission for a planet crossing two phase masks is given theoretically as a function of the Lyot stop size, in agreement with observations.
is higher than 105 for both the 4QC and 8OC. As expected, the 8OC is less affected by a pointing error than the 4QC, but more sensitive to an aperture central obstruction. Incidently, the loss of transmission for a planet crossing two phase masks is given theoretically as a function of the Lyot stop size, in agreement with observations.
Key words: instrumentation: high angular resolution - methods: laboratory - techniques: high angular resolution - techniques: interferometric
1 Introduction
The four-quadrant phase mask coronagraph (4QC) proposed by Rouan et al. (2000) is among the most amazing optical systems developed for the direct observation of an exoplanet, with the closely related optical vortex coronagraph proposed by Mawet et al. (2005b). The efficiency of the four-quadrant phase mask (4QC) to fully reject the light of an on-axis point source outside the geometrical image of a circular aperture was first demonstrated by Gay (2002) and published independently by Abe et al. (2003) and Lloyd et al. (2003). Making use of the analytical solution of Mawet et al. (2005b) for the optical vortex coronagraph, a more general demonstration of this remarkable property was given by Jenkins (2008).
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=0.55\textwidth]{1...
...includegraphics[width=0.35\textwidth]{12067fg2.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg8.png) |
Figure 1: The general optical layout of the experiment with details inside the MZI showing the two additive and subtractive output and the binary masks. |
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8cm]{12067fg3.eps}...
....eps}\\
\includegraphics[width=8cm]{12067fg5.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg9.png) |
Figure 2: Top: image plane reformed in one arm of the interferometer (representation: power law scale). Center and bottom: constructive output for the 4QC and the 8OC. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{12067fg6.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg10.png) |
Figure 3: Close-up of the internal region limited to the aperture for the 8OC of Fig. 5 showing an offset probably due to a residual unbalance of transmissions between the two arms of the MZI. |
| Open with DEXTER | |
The light rejection of the 4QC is sensitive to small pointing errors, and this coronagraph is not well suited to detecting a planet orbiting a resolved star. This condition may be relaxed with the eight-octant phase mask coronagraph (8OC), as shown by Murakami et al. (2008). The main difficulty is chromaticity. A solution was proposed by Abe et al. (2001) using two orthogonal phase knives. Another possibility is to use multiple layers to create phase masks (see Riaud et al. 2001; Abe et al. 2007). Rouan et al. (2007) proposed multi-stages 4QC, each of them being designed for a particular wavelength. The annular groove phase mask and the four-quadrant zeroth order grating (see Mawet et al. 2005b,a) are also two achromatic 4QC's relatives. To address this problem, we proposed to couple amplitude binary masks and a Mach-Zehnder interferometer to form an achromatic 4QC. The experiment was implemented using simple binary masks (Aime et al. 2007, in French). We report in the present paper the results obtained in laser light with an improved version of the first experiment. For that, precise sector masks have been fabricated for the 4QC and 8OC.
We present the experimental device in Sect. 2 and our results are given in Sect. 3. Our observations are strengthened by a theoretical approach given in two appendices. One is devoted to the generalization of Gay (2002)'s approach to the 8OC. The second, based on the work of Mawet et al. (2005b) and Jenkins (2008), makes it possible to obtain a practicable expression for the full diffraction pattern of sector mask coronagraphs.
2 Optical setup of the experiment
The optical setup is a new version of the experiment used by Carlotti et al. (2008) for interferometric apodization of telescope apertures, and where the ability of the MZI to work as an addition-subtraction instrument was described. A few general improvements were made, among them a piezoelectric remote control of the optical mounts of the mirrors and a stabilization of the temperature of the working environment. The setups of the two experiments essentially differ inside the arms of the MZI: in the former study, the aperture plane was imaged onto phase masks, while in the present experiment, the focal plane is imaged onto amplitude masks.
A drawing of the optical setup is made in Fig. 1. The source is a polarized He-Ne Laser (632.8 nm). After a beam expander, a mirror M0 reflects the collimated beam towards the MZI. A slight tilt of M0 is used to produce an off-axis source. A pupil mask and a lens constitute a telescope whose focus is located inside the MZI. To remove unwanted phase terms, the pupil mask is set in the object focal plane of the lens. At the exits to the interferometer, the recombination of the beams is done and two series of lenses reform the pupil plane and the focal plane. The binary complementary masks are placed in the two image focal planes of the telescope, inside the MZI. The destructive output is the one used for coronagraphy, where a Lyot stop of 93% of the pupil's diameter is placed in the reimaged pupil plane.
The system is correctly tuned when the two optical axes inside the MZI perfectly coincide and the path lengths are the same within a fraction of a wavelength. In practice, setting the device is mainly a geometrical problem. One must check that the focal images and the aperture images seen through the two arms of the interferometer are both correctly superimposed. When this geometrical result is obtained, the fringes are clearly visible, and a fine tuning must then be completed to obtain a bright and a dark uniform output.
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8cm]{12067fg7.eps}\\
\includegraphics[width=8cm]{12067fg8.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg11.png) |
Figure 4: Experimental (full line) and theoretical (dashed lines) curves corresponding to the intensity inside circles of various radii r (in units of telescope radius), for the 4QC ( top) and the 8OC ( bottom). |
| Open with DEXTER | |
A first generation of masks was produced by manual assembly
on a microscope thin metallic plates. They were good enough to
prove the principle of the experiment, as reported in
Aime et al. (2007), but it was found that their quality had to be improved. Several attempts were made to achieve this. Masks made with a
wire-EDM technique were tested, but the quality of their edges, in
particular at the mask center, was not satisfying. The masks
that we now use were manufactured by the firm Optimask and
were obtained by deposing a thin metallic layer on a
parallel window. We have two sets of masks, one for the 4QC and
the other for the 8OC. The geometric precision of the deposit is
of the order of ![]() m on the entire surface, including the
central (and most important) part of the mask. The quality of
these masks is good enough not to limit the extinction of the
coronagraph. The residual errors that we still observe come mainly from
other optical components (lens, mirrors, beamsplitters) and the
recombination of the images through the MZI.
m on the entire surface, including the
central (and most important) part of the mask. The quality of
these masks is good enough not to limit the extinction of the
coronagraph. The residual errors that we still observe come mainly from
other optical components (lens, mirrors, beamsplitters) and the
recombination of the images through the MZI.
The adjustment of the masks inside the MZI is a delicate
operation. It is mandatory to obtain a high quality recontructed
image of the focal plane. We proceed as follows. A mask is set
in one arm of the MZI in the focal plane at the center of the Airy
pattern produced by the lens. With the other arm of the MZI
obscured, the image obtained by the camera appears as shown in
Fig. 2 for a 4QC mask. The other mask is then set in
the second arm of the MZI. A superposition of the two images can
be seen in the additive and subtractive outputs. Adjustment
errors appear more clearly in the subtractive output, for example
Fresnel fringes can be seen there when the mask is out of focus.
The first mask being fixed, a fine tuning of the second mask, in
transverse position and orientation, makes it possible to obtain a
fair complementarity using a trial and error procedure. Defaults
are clearly visible in Fig. 2 as bright and dark lines
redrawing the lines of the masks. These defaults are of the order
of between 5 and 10 ![]() m, the Airy spot being about 400
m, the Airy spot being about 400 ![]() m in size.
Residual Fresnel fringes are also visible there, which is indicative of slightly out-of-focus masks.
m in size.
Residual Fresnel fringes are also visible there, which is indicative of slightly out-of-focus masks.
3 Experimental results and comparison with theory
3.1 Diffracted intensity in the Lyot stop plane
The 4QC and 8OC should theoretically have the same complete null inside the aperture as shown in Appendices A and B. In practice, this is not observed. Experimental images of the aperture after the MZI and before the Lyot stop are shown in Fig. 5 (top curves) on a power law scale. The data are recorded with two 16-bit cameras set on the two outputs of the MZI; to optimize the dynamic range, exposure times used ranged from 0.04 s to 2 s, depending on the observations.
The observations are in fairly good agreement with the theoretical
expectations (Fig. 5, bottom curves). Analytic
expressions are computed in Appendix B, based on
the works of Mawet et al. (2005b) and Jenkins (2008). Combining
Eqs. (B.6) and (B.9) in the Appendix, the amplitude can be expressed in polar coordinates as the function:
where R is the radius of the circular aperture, n=k(2m+1)/2, and
The experimental images are corrupted by various interference patterns. Light inside the image of the aperture is not as low as expected. This is probably because of various causes, such as the quality of the optics or an imperfect recombination of the images in the two arms of the MZI. A close-up linear representation of the residual light inside the aperture for the 8OC is given in Fig. 3. The 3D representation highlights the uniformity of the light left inside the aperture. This offset may indicate a slight imbalance between the transmissions of the two paths of our experiment, probably coming from the beamsplitters.
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=7.6cm]{12067fg9.e...
....eps} &
\includegraphics[width=7.6cm]{12067f12.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg17.png) |
Figure 5:
Images of the aperture plane inside the coronagraph before the Lyot stop for the 4QC ( left) and the 8OC ( right). Top: experimental curves. Bottom: theoretical expression for the intensity
|
| Open with DEXTER | |
In Fig. 4, we have compared experimental and theoretical results for the intensity flux contained within a disk of variable radius and centered on the center of the aperture. Experimental results were normalized to fit the theoretical curves as closely as possible. The dark ring visible in the 8OC image produces a step in these curves. There is a more concentrated light concentration for the 4QC than for the 8OC, and one may conclude that the 8OC is more sensitive than the 4QC to a central obstruction of the telescope.
Depending on the chosen diameter of the pupil (with a Lyot stop diameter equal to 100% and 80% of the pupil diameter, respectively), in the 4QC case the value of this ratio ranges between 50 and 100, whereas in the 8OC case it ranges between 60 and 120. One should however consider that the rejection rate is underestimated: the intensity on the image only represents about 0.9 (for the 4QC) and 0.8 (for the 8OC) of the whole intensity. Therefore, one can estimate the rejection factor to be equal to 110 (for the 4QC) and 150 (for the 8OC).
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=7cm]{12067f13.eps...
...5.eps} &
\includegraphics[width=7cm]{12067f16.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg18.png) |
Figure 6:
Images observed at the output of the coronagraphs: 4QC ( left) and 8OC ( right). Top: on-axis source. Bottom: off-axis source tilted by
|
| Open with DEXTER | |
3.2 Reconstructed images of the focal plane
The figures obtained in the interferometric output of the MZI for
the 4QC and 8OC masks are shown in Fig. 6 for an
on-axis source and a source tilted by just 1 ![]() .
The size
of the Lyot stop is 93% of the aperture. The integration
time for the on-axis image is about 30 times as long as the
off-axis one. Unwanted spurious reflections, whose origins are not
clearly understood, are still visible in the figures (there are no
simulated planets).
.
The size
of the Lyot stop is 93% of the aperture. The integration
time for the on-axis image is about 30 times as long as the
off-axis one. Unwanted spurious reflections, whose origins are not
clearly understood, are still visible in the figures (there are no
simulated planets).
Another comparison of the on-axis and off-axis responses is given
in Fig. 9. The curves represent radial cuts of the
focal images for the high and low throughput axes of the
coronagraphs. In this example, the off-axis source, situated at
about 10.5 ![]() from the center, is represented here as being
re-shifted to the center of the image. A partial angular average
is calculated in both cases (about
from the center, is represented here as being
re-shifted to the center of the image. A partial angular average
is calculated in both cases (about ![]() for the 4QC and
for the 4QC and ![]() for
the 8OC). The high throughput region is the relevant curve since
we expect the planet to be there. The 4QC on-axis curve presents
an increase in the first ring of the diffraction image clearly
visible in the 2D image of Fig. 6.
for
the 8OC). The high throughput region is the relevant curve since
we expect the planet to be there. The 4QC on-axis curve presents
an increase in the first ring of the diffraction image clearly
visible in the 2D image of Fig. 6.
3.3 Inner working angles
The throughput of the 4QC and 8OC was measured for several
off-axis positions of the source (along the high-throughput axes).
In the case of the 4QC, there are 11 positions from 0.64
![]() to 7.9
to 7.9 ![]() ,
and in the case of the
8OC, 13 positions from 0.21
,
and in the case of the
8OC, 13 positions from 0.21 ![]() to 10.4
to 10.4 ![]() .
We also
tilted the source along the low-throughput axes (behind the phase
transition axes): the throughput was measured at 3 different
positions in the case of the 4QC and 7 for the 8OC. Results are
shown in Fig. 7. For each position, we integrate the
light inside a disk equal in size to the central part of the diffraction
pattern after the Lyot stop.
.
We also
tilted the source along the low-throughput axes (behind the phase
transition axes): the throughput was measured at 3 different
positions in the case of the 4QC and 7 for the 8OC. Results are
shown in Fig. 7. For each position, we integrate the
light inside a disk equal in size to the central part of the diffraction
pattern after the Lyot stop.
Our results are in accordance with the transmission maps
calculated by Murakami et al. (2008). In the same way as performed in
their paper, we also define the mask's angular inner limitation to be
the angular distance for which the planet's intensity decreases to
half of its maximum value. In the case of the 4QC, this angle is
![]() ,
whereas it is
,
whereas it is
![]() for the 8OC
along the high throughput axes.
for the 8OC
along the high throughput axes.
Rejections obtained with the 8OC and the 4QC are roughly similar. The 8OC is less sensitive to the star angular diameter, with the drawback of having twice as many transition zones of low throughput for the planet, which reduces the discovery space. Along the low throughput axes, we measured a transmission for the planet that is lower by a factor of about 5, than the theoretical value of 5.5 computed in Appendix B. We show there that it may be as low as 3 for a perfect experiment using a Lyot stop of the size of the entrance aperture.
3.4 Error in the position measurement
The maximum of flux within the Airy spot may also define the
position of the off-axis image. When looking at the coronagraphic
image plane, the photocenter of the ``planet'' is not at the same
distance from the center of the mask as the true ``planet'' is. For
example in the image plane of the 8OC, an off-axis source at a distant
from the mask of
![]() appears to be at a distance of
appears to be at a distance of
![]() :
the part of the PSF that is closer to the masks is
indeed more attenuated than the other part, and this shifts the
photocenter in a direction opposite to the center of the mask.
Once this effect is known, one can take it into account when correcting
the positions. The contrasts are therefore computed for a given
list of positions (the one of the photocenters) but they are
associated with a different list of positions. The closer to the
masks, the stronger the apparent translation. We note that the true
position of the off-axis source is measured in our experiment by
the additive output, but this would not be possible when observing a
real planetary system.
:
the part of the PSF that is closer to the masks is
indeed more attenuated than the other part, and this shifts the
photocenter in a direction opposite to the center of the mask.
Once this effect is known, one can take it into account when correcting
the positions. The contrasts are therefore computed for a given
list of positions (the one of the photocenters) but they are
associated with a different list of positions. The closer to the
masks, the stronger the apparent translation. We note that the true
position of the off-axis source is measured in our experiment by
the additive output, but this would not be possible when observing a
real planetary system.
Figure 8 shows how much the photocenter of the
``planet'' is shifted away from its true position. The distance from
the center of the mask at which this effect reaches a maximum is higher
in the case of the 8OC than in the case of the 4QC. In the latter case,
it becomes unnoticeable beyond
![]() ,
whereas it is visible until
,
whereas it is visible until
![]() for the 8OC.
for the 8OC.
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8.5cm]{12067f17.ep...
....eps}\\
\includegraphics[width=8.5cm]{12067f19.eps} \end{tabular} \end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg24.png) |
Figure 7:
Top: coronagraphic PSF. Center: normalized attenuation factor of the off-axis light. Bottom: contrast ratio as a function of the distance between the ``planet'' and the center of the masks. A continuous line corresponds to the 4QC, a dashed line to the 8OC. The upper curves refer to a translation of the PSF along a high throughput axis, whereas the lower curves refer to a translation along a low throughput axis. The horizontal axes are in units of
|
| Open with DEXTER | |
| |
Figure 8: Differences due to the action of the masks between the distances measured in the coronagraphic output and in the second output. Left: case of the 4QC, right: case of the 8OC. |
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8.5cm]{12067f22.ep...
...ps}\\
\includegraphics[width=8.5cm]{12067f24.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg26.png) |
Figure 9: Contrasts achieved by the 4QC and the 8OC. Top: case of the high throughput axes. Bottom: case of the low throughput axes. Black curve: non-coronagraphic PSF: red: 4QC PSF, blue: 8OC PSF. Directions along which the source is moved. Path 1 corresponds to one of the high-throughput axes, and Path 2 corresponds to one of the phase separation axes. |
| Open with DEXTER | |
4 Discussion
We have shown that a Mach-Zehnder interferometer
could be used to obtain the ![]() phase shift of sector mask
coronagraphs. The experiment has provided interesting results,
which however remain preliminary. The results have been obtained in laser
light. Our next step will be to test our layout for white
light using a supercontinuum source. To do so several major
improvements will have to be tested, for example substituting the
lenses with mirrors, replacing the current beamsplitters by cubes.
The faces of our beamsplitters are not parallel and
introduce a small prismatic effect. The current masks might have
to be replaced by freestanding ones. The present experiment has
inferred integrated rejection factors of the order of 100 or so. The
residual intensity in the image of the aperture is rather
uniform, and can be interpreted as being caused by an unbalance between the
transmission of the two arms of the interferometer. A system of
amplitude compensation between the two arms will probably be very
useful.
phase shift of sector mask
coronagraphs. The experiment has provided interesting results,
which however remain preliminary. The results have been obtained in laser
light. Our next step will be to test our layout for white
light using a supercontinuum source. To do so several major
improvements will have to be tested, for example substituting the
lenses with mirrors, replacing the current beamsplitters by cubes.
The faces of our beamsplitters are not parallel and
introduce a small prismatic effect. The current masks might have
to be replaced by freestanding ones. The present experiment has
inferred integrated rejection factors of the order of 100 or so. The
residual intensity in the image of the aperture is rather
uniform, and can be interpreted as being caused by an unbalance between the
transmission of the two arms of the interferometer. A system of
amplitude compensation between the two arms will probably be very
useful.
Aside from the laboratory experiment, theoretical developments have been given in two appendices. It appears that the number of sectors must be a multiple of 4 and not a power of 2 as one can read in the literature (Rouan et al. 2007). However, the most useful result is probably the expression of the amplitude diffracted by a sector mask as a sum of Zernike polynomials, applied to the wave itself and not its phase. This approach may be able to be developed in the analysis of sector mask coronagraphs.
Acknowledgements
We wish to thank the anonymous referee for his detailed analysis of the paper and helpful suggestions, in particular concerning Appendix A.
Appendix A: Expected null for the 8OC inside the aperture via a direct 2D Fourier approach
The efficiency of the 4QC to fully reject the light of an on axis
point source outside the geometrical image of a circular aperture
was first demonstrated by Gay (2002) and reported by
Abe et al. (2003). They computed the 2D Fourier transform of the
focal plane image. The mask
M4(x,y) and its transform
![]() are written as
are written as
where sgn(x) is the sign function which is equal to -1 for x<0 and +1 for x>0, and whose Fourier transform is
A key point in the mathematical approach of Abe et al. (2003) is the convolution of the circular aperture and the 2D transform of the mask. To prove the existence of the theoretical null inside the aperture image, they used a geometrical relation known as the circle power. Independently, Lloyd et al. (2003) provided a similar geometrical demonstration using the similarity of the triangles generated by the chords of a circle.
A similar procedure can be used for the 8OC. The eight-octant mask could be naturally expressed as the product of two four-quadrant rotated by ![]() with respect to one another
with respect to one another
Computing the direct 2D Fourier transform of this function is not straightforward, because the product of functions of x (or y), in the transform domain, infer convolutions that are difficult to handle. To overcome this difficulty, it is convenient to write M8(x,y) in the form of a function of x and y, multiplied by a function of y
where
The second step is to take the transform of y in v. Here there is a product of two functions of y leading to a convolution in the transform domain. The transform of
an expression that seems quite different from
The 4QC divides the
Appendix B: Expression for the full diffraction pattern of a sector masks coronagraph
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=7cm]{12067f25.eps...
...f27.eps} &
\includegraphics[width=7cm]{12067f28.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg45.png) |
Figure B.1: Amplitude in the pupil plane in the case of: a phase knife ( top left), 4QC ( top right), 8OC ( bottom left), 12 sectors coronagraph ( bottom right). When the function goes from -1 to 1, the color function goes from the blue to the red through green and yellow. |
| Open with DEXTER | |
The intensity diffracted by a 4QC was given analytically by Jenkins (2008), by applying the results of Mawet et al. (2005b). We briefly recall a few relations drawn from these papers that will permit us to derive a simpler general expression. The 4QC, expressed as an exponential Fourier series, is interpreted to be the sum of evenly charged vortex phase masks, each of them corresponding to a null inside the circular aperture. This approach also makes it possible to reproduce analytically the transmitted light in the entire re-imaged pupil plane.
Generalizing the approach of Jenkins (2008) and
Murakami et al. (2008), a mask of k sectors can be written as the
Fourier expansion
where with this notation we directly have, for example, k=4 for a 4QC and k=8 for a 8OC. For the 4QC, the phase coefficients correspond to vortex phase masks of even charges of the form 4m+2, i.e., 2, 6, 10,... For the 8OC, the coefficients corresponds to the even charges 8m+4, i.e., 4,12, 20, ...
Since the Fourier transform of a sum is the sum of the Fourier
transforms, the solution for a k sector mask reduces to the
transform of vortex phase masks, a question treated by
Mawet et al. (2005b). The problem in its general form is to find the
Fourier transform of an Airy pattern distorted by a phase term
![]() ,
where n is an integer.
According to Mawet et al. (2005b), the amplitude
,
where n is an integer.
According to Mawet et al. (2005b), the amplitude
![]() at the pupil plane image can be written as
at the pupil plane image can be written as
where we have multiplied the amplitude with the area of the aperture
The amplitude in the re-imaged aperture plane takes a different
form inside or outside the aperture. We give thereafter the
expressions C7 of Mawet et al. (2005b) after correction of a few
typos. Inside the aperture,
![]() takes the form
takes the form
where
Outside the aperture image,
![]() can be written as
can be written as
A simplification of the hypergeometric function can be made because of the particular values of its first argument. For n=2, the function
where (a)m is the Pochhammer symbol equal to
where
One can verify that for any even value of n the light rejected outside the aperture image exactly equals the incoming flux
We return to the 4Q and 8O phase masks. The diffracted amplitude of a mask of k sectors in the pupil plane can be evaluated by substituting the effects of the phase terms in the Fourier series expression of the mask. We have
with
We can verify that the light rejected outside the aperture still
equals the incoming flux in the aperture. This can be achieved by summing
![]() for
for ![]() varying from R to
varying from R to ![]() and
and ![]() varying from 0 to 2
varying from 0 to 2![]() .
The modulus squared of the
sum can be expressed as a double sum. Because of the orthogonality
property of the sine function, cross terms with different
.
The modulus squared of the
sum can be expressed as a double sum. Because of the orthogonality
property of the sine function, cross terms with different ![]() values cancel after the angular integration. The computation
reduces to a simple sum that can be easily computed using the
above results for a single vortex. We have
values cancel after the angular integration. The computation
reduces to a simple sum that can be easily computed using the
above results for a single vortex. We have
In practice, we limit the number of terms in the theoretical expression of
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12067f29.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg82.png) |
Figure B.2: Evolution in the residual intensity as a function of the diameter of the Lyot stop for a phase knife. |
| Open with DEXTER | |
Illustrations for the amplitude diffracted by various sector masks (k=2, 4, 8 and 12) are given in Fig. B.1. For the 4, 8, and 12 sectors, the mask transmissions are even functions, andthe amplitude is real, symmetric, and alternatively positive and negative around the diffraction pattern. For the phase knife, the amplitude is imaginary and anti-symmetric. The complexity of the images increases with the number of sectors in successive rings. As already experimentally observed, the spread of the pattern increases with k.
In Fig. B.2 we give the normalized intensity flux left by a phase mask for a Lyot stop of variable diameter. For a 4QC or an 8OC, this indicates the level of the light for a planet crossing exactly the border that divides two quadrants. Our Lyot stop has a diameter that is 93% of the pupil diameter, and theoretically induces an attenuation that is approximately equal to 0.16 times the original intensity. In practice the measured attenuation is 0.2 which can be explained by a slight misalignment of the PSF's center over the axes. For a perfect instrument, a Lyot stop exactly equal to the aperture, 2/3 of the light is lost when a faint companion crosses exactly a sector of the mask far from the center. This corresponds to a loss of about 1.2 mag, which is much less than generally expected (Rouan et al. 2007).
References
- Abe, L., Vakili, F., & Boccaletti, A. 2001, A&A, 374, 1161 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Abe, L., Domiciano de Souza, Jr., A., Vakili, F., & Gay, J. 2003, A&A, 400, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Abe, L., Beaulieu, M., Vakili, F., et al. 2007, A&A, 461, 365 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions (New York: Dover) (In the text)
- Aime, C., Carlotti, A., & Ricort, G. 2007, Comptes Rendus Physique, 8, 961 [NASA ADS] [CrossRef] (In the text)
- Carlotti, A., Ricort, G., Aime, C., El Azhari, Y., & Soummer, R. 2008, A&A, 477, 329 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ferrari, A. 2007, ApJ, 657, 1201 [NASA ADS] [CrossRef] (In the text)
- Gay, J. 2002, private communication (In the text)
- Jenkins, C. 2008, MNRAS, 384, 515 [NASA ADS] [CrossRef] (In the text)
- Lloyd, J. P., Gavel, D. T., Graham, J. R., et al. 2003, in SPIE Conf. Ser. 4860, ed. A. B. Schultz, 171 (In the text)
- Mawet, D., Riaud, P., Absil, O., Baudrand, J., & Surdej, J. 2005a, in SPIE Conf. Ser. 5905, ed. D. R. Coulter, 502
- Mawet, D., Riaud, P., Absil, O., & Surdej, J. 2005b, ApJ, 633, 1191 [NASA ADS] [CrossRef] (In the text)
- Murakami, N., Uemura, R., Baba, N., et al. 2008, PASP, 120, 1112 [NASA ADS] [CrossRef] (In the text)
- Riaud, P., Boccaletti, A., Rouan, D., Lemarquis, F., & Labeyrie, A. 2001, PASP, 113, 1145 [NASA ADS] [CrossRef] (In the text)
- Rouan, D., Riaud, P., Boccaletti, A., Clénet, Y., & Labeyrie, A. 2000, PASP, 112, 1479 [NASA ADS] [CrossRef] (In the text)
- Rouan, D., Baudrand, J., Boccaletti, A., et al. 2007, Comptes Rendus Physique, 8, 298 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... form
![[*]](/icons/foot_motif.png)
- Another way of achieving this result is to express the mask directly in polar coordinates, as indicated to us by the anonymous referee.
All Figures
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=0.55\textwidth]{1...
...includegraphics[width=0.35\textwidth]{12067fg2.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg8.png) |
Figure 1: The general optical layout of the experiment with details inside the MZI showing the two additive and subtractive output and the binary masks. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8cm]{12067fg3.eps}...
....eps}\\
\includegraphics[width=8cm]{12067fg5.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg9.png) |
Figure 2: Top: image plane reformed in one arm of the interferometer (representation: power law scale). Center and bottom: constructive output for the 4QC and the 8OC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12067fg6.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg10.png) |
Figure 3: Close-up of the internal region limited to the aperture for the 8OC of Fig. 5 showing an offset probably due to a residual unbalance of transmissions between the two arms of the MZI. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8cm]{12067fg7.eps}\\
\includegraphics[width=8cm]{12067fg8.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg11.png) |
Figure 4: Experimental (full line) and theoretical (dashed lines) curves corresponding to the intensity inside circles of various radii r (in units of telescope radius), for the 4QC ( top) and the 8OC ( bottom). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=7.6cm]{12067fg9.e...
....eps} &
\includegraphics[width=7.6cm]{12067f12.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg17.png) |
Figure 5:
Images of the aperture plane inside the coronagraph before the Lyot stop for the 4QC ( left) and the 8OC ( right). Top: experimental curves. Bottom: theoretical expression for the intensity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=7cm]{12067f13.eps...
...5.eps} &
\includegraphics[width=7cm]{12067f16.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg18.png) |
Figure 6:
Images observed at the output of the coronagraphs: 4QC ( left) and 8OC ( right). Top: on-axis source. Bottom: off-axis source tilted by
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8.5cm]{12067f17.ep...
....eps}\\
\includegraphics[width=8.5cm]{12067f19.eps} \end{tabular} \end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg24.png) |
Figure 7:
Top: coronagraphic PSF. Center: normalized attenuation factor of the off-axis light. Bottom: contrast ratio as a function of the distance between the ``planet'' and the center of the masks. A continuous line corresponds to the 4QC, a dashed line to the 8OC. The upper curves refer to a translation of the PSF along a high throughput axis, whereas the lower curves refer to a translation along a low throughput axis. The horizontal axes are in units of
|
| Open with DEXTER | |
| In the text | |
| |
Figure 8: Differences due to the action of the masks between the distances measured in the coronagraphic output and in the second output. Left: case of the 4QC, right: case of the 8OC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=8.5cm]{12067f22.ep...
...ps}\\
\includegraphics[width=8.5cm]{12067f24.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg26.png) |
Figure 9: Contrasts achieved by the 4QC and the 8OC. Top: case of the high throughput axes. Bottom: case of the low throughput axes. Black curve: non-coronagraphic PSF: red: 4QC PSF, blue: 8OC PSF. Directions along which the source is moved. Path 1 corresponds to one of the high-throughput axes, and Path 2 corresponds to one of the phase separation axes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=7cm]{12067f25.eps...
...f27.eps} &
\includegraphics[width=7cm]{12067f28.eps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg45.png) |
Figure B.1: Amplitude in the pupil plane in the case of: a phase knife ( top left), 4QC ( top right), 8OC ( bottom left), 12 sectors coronagraph ( bottom right). When the function goes from -1 to 1, the color function goes from the blue to the red through green and yellow. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12067f29.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa12067-09/Timg82.png) |
Figure B.2: Evolution in the residual intensity as a function of the diameter of the Lyot stop for a phase knife. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




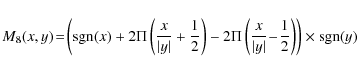
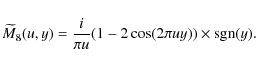
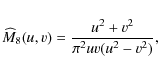

=B(\rho,n)\times {\rm e}^{{\rm i} n \theta},
\end{displaymath}](/articles/aa/full_html/2009/35/aa12067-09/img49.png)