| Issue |
A&A
Volume 504, Number 2, September III 2009
|
|
|---|---|---|
| Page(s) | 451 - 460 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200911762 | |
| Published online | 15 July 2009 | |
Supersonic cloud collision - II
S. Anathpindika1,2
1 - School Of Astronomy & Physics, Cardiff University, 5-The Parade, UK
2 -
Indian Institute Of Astrophysics, 2nd Block - Koramangala, Bangalore 560 034, India
Received 31 January 2009 / Accepted 27 May 2009
Abstract
Aims. In this second paper of the sequel of two papers, we continue to investigate the problem of molecular cloud (MC) collision. The companion paper to this one considered highly supersonic cloud collisions and examined the effect of bending and shearing instabilities on the shocked gas slab. We now consider moderately supersonic cloud collisions (precollision cloud velocities from 1.2 km s-1 to 2.4 km s-1).
Methods. In the current paper, we present five SPH simulations of fast head-on and/or off-centre cloud collisions to study the evolution of a ram-pressure confined gas slab. The relevant thermodynamical details of the problem have been simplified by adopting a simple barytropic equation of state. We explore the parameter space by varying the pre-collision velocity and the temperature of the post collision gas slab.
Results. Slab temperature appears to play a key role in its dynamical evolution. The pressure-confined gas slab becomes Jeans unstable if the average sound crossing time,
![]() ,
of putative clumps condensing out of it is much longer than their respective freefall time,
,
of putative clumps condensing out of it is much longer than their respective freefall time,
![]() .
Self gravitating clumps may spawn multiple/larger N-body star clusters. Warmer gas slabs are less likely to fragment and may simply end up as diffuse gas clouds.
.
Self gravitating clumps may spawn multiple/larger N-body star clusters. Warmer gas slabs are less likely to fragment and may simply end up as diffuse gas clouds.
Key words: instabilities - stars: formation - ISM: clouds - shock waves
1 Introduction
Potential star-forming clouds move randomly with velocities in the range of a few km s-1 to a few tens of km s-1 (e.g. Larson 1981; Elmegreen 1997, 2000). Having investigated the paradigm of high-velocity cloud collisions in our earlier paper (Anathpindika 2009, hereafter referred to as Paper I), we now proceed to explore the low-velocity cloud collisions. In Paper I, we suggested that high velocity cloud collisions produced approximately isothermal, cold shocked slabs dominated by internal shear, irrespective of whether the collision was head-on or off-centre. The shocked slab evolved through a complex interplay between the hydrodynamical instabilities and the gravitational instability. Our simulations show that, generally the latter is suppressed by the former.
Internal shear leads to mixing between slab layers and, apparently, makes it susceptible to the non linear thin shell instability (NTSI) and the Kelvin-Helmholtz (KH) instability. This is a dominant mechanism for dissipation of internal energy, causing the shocked slab to collapse and form a thin, long filament, aligned with the collision axis. This is quite similar to the integral filament in Orion. While all but one of our high velocity cloud collision models finally yielded a filamentary structure, we consider such collisions, a viable mechanism to explain the observed filamentary structure in giant molecular clouds (GMCs). As a corollary to this problem, below we present an investigation of the evolution of gas slabs confined by ram pressure.
We demonstrate that such slabs could be a result of moderately supersonic (precollision Mach number of order unity) cloud collisions. It has been suggested by, for instance, Whitworth et al. (1994), Clarke (1999), and Boyd & Whitworth (2005), among others, that cold, isothermal pressure confined slabs may undergo gravitational fragmentation. If sufficiently massive, clumps formed in this way may become self gravitating. This is, therefore, a particularly interesting when considering the formation of small multiple systems or even larger star clusters. Observations of various star forming regions have shown that, stars seldom form in isolation and are usually a part of multiple systems or larger N-body clusters. The orbital dynamics of clusters have enabled observers to estimate various physical properties of multiples such as orbital eccentricities, orbital stability, and stellar masses. Star clusters have reasonably homogeneous environs and therefore, are useful regions for studying stellar evolution (e.g. Clarke et al. 2000; Pudritz 2002).
A related problem is that of the correspondence between the dense core mass function (DCMF) and the stellar initial mass function (IMF) (cf. Nutter & Ward-Thompson 2007). An understanding of possible core formation mechanisms might help us better understand any correlation between the DCMF and the IMF. The mechanisms of star formation may be broadly classified into two paradigms, the quiescent mode of star formation - the cloud - core picture (Hoyle 1953; Whitworth et al. 1996) and the dynamical mode - also called triggered star formation. The former picture is elucidated by self-gravitating MCs. Potential star forming clouds may become self-gravitating due to internal perturbations or may be compressed either by shock waves or galactic density waves. Such theories are encouraged by spatial correlation between between star formation and the spiral arms of disk galaxies. Gravitational perturbations grow in regions that become Toomre unstable and the surface density in star-forming regions,
![]() ,
is supposedly related to the star formation rate (SFR),
,
is supposedly related to the star formation rate (SFR),
![]() ,
through the Schmidt-Kennicutt power-law
,
through the Schmidt-Kennicutt power-law
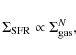
where
This paradigm, however, suffers on two counts. First, it inevitably leads to a correlation between the SFR and the density wave amplitude; however, there is no corroborative observational evidence (e.g. Elmegreen & Elmegreen 1986; Kennicutt 1989). Second, this paradigm fails to reconcile the observations of star formation in those spirals, which have a small density wave amplitude (e.g. Block et al. 1994). This suggests that the density waves and disk instabilities are not quintessential to star formation. We may therefore have to explore certain aspects of the second paradigm stated above. Tan (2000), for instance, invoked cloud collision in the SFR calculations for a galactic disk and arrived at a power-law similar to the Schmidt-Kennicutt correlation.
Triggered star formation is elucidated by dynamical interaction between fluid flows within GMCs. Colliding flows produce gas slabs that are dynamically unstable (e.g. Klessen et al. 1998; Klessen & Burkert 2000). For instance, dense gas shells swept up by expanding ionising fronts from massive star clusters are also dynamically unstable and may fragment to produce a number of potential star-forming clouds and filaments (e.g. Wada et al. 2000; Dale et al. 2007; Furuya et al. 2008; Lefloch et al. 2008). The other model suggested and investigated further in the present work, is that of gravitational fragmentation of an external pressure confined gas slab; see for e.g. Elmegreen & Elmegreen (1978), Whitworth et al. (1994), Clarke (1999), and Boyd & Whitworth (2005). These slabs result from clouds colliding with relatively small precollision Mach numbers (e.g. Chapman et al. 1992; Bhattal et al. 1998).
Below, we present five simulations, which include two each of fast (precollision velocity ![]() 1.2 km s-1 to
1.2 km s-1 to ![]() 2.4 km s-1) head-on and off-centre cloud collisions, respectively. The remaining one is the case of a slow head-on cloud collision, which leads to a continuous (C) shock rather than a jump (J) shock, such as the one in the previous four cases. In this paper, we attempt to contrast the evolution of a shocked slab, discussed in Paper I, with that of a pressure-confined slab. The plan of the paper is as follows. In Sect. 2 below we briefly introduce the numerical scheme employed for our work and the code used. In Sect. 3 we describe the initial conditions and list the simulations performed. The results are discussed in Sect. 4 and we conclude in Sect. 5. The column density is measured in
2.4 km s-1) head-on and off-centre cloud collisions, respectively. The remaining one is the case of a slow head-on cloud collision, which leads to a continuous (C) shock rather than a jump (J) shock, such as the one in the previous four cases. In this paper, we attempt to contrast the evolution of a shocked slab, discussed in Paper I, with that of a pressure-confined slab. The plan of the paper is as follows. In Sect. 2 below we briefly introduce the numerical scheme employed for our work and the code used. In Sect. 3 we describe the initial conditions and list the simulations performed. The results are discussed in Sect. 4 and we conclude in Sect. 5. The column density is measured in ![]() pc-2 and all the column density plots presented here are plotted on a logarithmic scale since they span about six orders of magnitude. The spatial coordinates are marked in parsecs.
pc-2 and all the column density plots presented here are plotted on a logarithmic scale since they span about six orders of magnitude. The spatial coordinates are marked in parsecs.
Table 1: List of simulations performed with relevant physical details.
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12cm,clip]{Figure 16:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg18.png) |
Figure 1: A column density plot of the time (measured in Myr) sequence of cloud collision in model 1. Cloud collision results in the formation of a pressure confined gas slab, which then expands and terminates in a diffuse gas cloud, as can be seen in the last snapshot (t = 3.49 Myr). |
| Open with DEXTER | |
2 Numerical method and code
We use the smoothed particle hydrodynamics (SPH) numerical method for our simulations. This scheme treats the fluid under investigation as an ensemble of particles. The simulations presented here, were performed using an extensively tested SPH code, DRAGON (Goodwin et al. 2004). It uses the Barnes-Hut octal spatial tree (Barnes & Hut 1986) to search nearest neighbours and, evaluate the net force on a SPH particle. The critical cell opening angle of a leaf cell used is
![]() 0.45, and each particle has
0.45, and each particle has ![]() neighbours. In order to improve the accuracy of force calculations, the code also includes quadrupole moments of remote leaf cells. The code employs the multiple particle time-stepping scheme (Makino 1991).
neighbours. In order to improve the accuracy of force calculations, the code also includes quadrupole moments of remote leaf cells. The code employs the multiple particle time-stepping scheme (Makino 1991).
An extremely dense agglomeration of particles in the simulation is replaced by a sink particle. The sink is characterised by two physical variables viz. the sink radius,
![]() ,
and the sink density,
,
and the sink density,
![]() ,
both of which are predefined (Bate et al. 1995). We set
,
both of which are predefined (Bate et al. 1995). We set
![]() = 10-12 g cm-3 in all the simulations presented here. The sink radius is so chosen, that the initial mass of a sink particle is comparable to the minimum resolvable mass,
= 10-12 g cm-3 in all the simulations presented here. The sink radius is so chosen, that the initial mass of a sink particle is comparable to the minimum resolvable mass,
![]() ,
in the simulation, which is essentially the same as the Bate-Burkert mass (Bate & Burkert 1997). We may remind our reader that an identical prescription was adopted in Paper I (refer Sect. 2 therein). In the present work, protostellar cores are modelled as sinks.
,
in the simulation, which is essentially the same as the Bate-Burkert mass (Bate & Burkert 1997). We may remind our reader that an identical prescription was adopted in Paper I (refer Sect. 2 therein). In the present work, protostellar cores are modelled as sinks.
3 Initial conditions and numerical experiments
We model MCs as unconfined Bonnor-Ebert spheres. Thus, there is no external pressure on the cloud edges. Individual clouds are assembled in the same way as described in Paper I. We compromise with the intercloud medium in these simulations to permit more gas particles in each cloud.
In the first four models tested here, we adopted the same equation of state (EOS) as in Paper I, albeit with appropriate changes in the density switches. Using the (temperature) jump condition, we calculated the post shock temperature,
![]() ,
for each model. In the first two simulations, we cool the gas downstream of the shock down to the original precollision cloud temperature,
,
for each model. In the first two simulations, we cool the gas downstream of the shock down to the original precollision cloud temperature,
![]() ,
while in the next two, the gas is cooled even further, to 10 K. The EOS employed is
,
while in the next two, the gas is cooled even further, to 10 K. The EOS employed is
![\begin{displaymath}%
\frac{P}{\rho} = (k_{\rm B}/\bar{m})
\left\{ \begin{array}...
...\Big];~\rho > 10^{-18}~\textrm{g cm}^{-3}.
\end{array} \right.
\end{displaymath}](/articles/aa/full_html/2009/35/aa11762-09/img25.png) |
(1) |
Here
By virtue of the adiabatic nature of a C-shock, we employed a slightly stiffer EOS to model it. Thus, in model 5, the gas temperature is determined according to the equation below
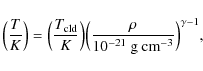 |
(2) |
where all the symbols have their usual meanings and the adiabatic gas constant,
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.7cm,clip]{Figure 12:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg30.png) |
Figure 2: Column density plot showing a time (measured in Myr) sequence tracking model 2. This sequence shows the colliding clouds, formation of the post-collision gas slab, and then its expansion. |
| Open with DEXTER | |
4 Discussion
The question of gravitational instability in cold, semi-infinite planar gas slabs has been extensively studied in the past. However, most of these analyses were restricted to slabs with no external pressure on them; see for instance, McKee (1999) and Larson (1985). On the other hand, stability analysis of cold, external pressure-confined isothermal slabs by Elmegreen & Elmegreen (1978) and Elmegreen (1989) suggests that the minimum mass of a fragment condensing out of such a slab increases with the age of that slab as it continues to accrete matter. The monotonic growth period of the shortest unstable mode in such a slab is ![]() 0.25
0.25
![]() (Elmegreen 1989), where
(Elmegreen 1989), where
![]() is the average density of the post-shock gas slab.
is the average density of the post-shock gas slab.
Expressions for the length of the fastest growing mode, the timescale of growth of this mode and the minimum mass of the fragment condensing out of the slab have been derived by (Whitworth et al. 1994) and Boyd & Whitworth (2005). Below we discuss the models tested in the present work and compare the results of models 3 and 4 with the analytic findings of the latter group of authors.
4.1 Fast cloud collision (T0 = T
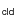 ;
models 1 and 2)
;
models 1 and 2)
In model 1, MCs of mass 50 ![]() each collide head-on with each other at a pre-collision velocity of
each collide head-on with each other at a pre-collision velocity of ![]() 1.3 km s-1 (
1.3 km s-1 (
![]() = 3). Individual clouds are thermally supported against self gravity. The post-collision thermodynamics in this model is governed by the EOS, defined by Eq. (1) above. The clouds collide and form a planar gas slab confined by ram pressure. The time sequence of colliding clouds and their evolution after collision is shown in Fig. 1. We treat the gas slab as approximately isothermal and hold it at the original pre-collision cloud temperature. Our assumption of a somewhat lower post collision temperature,
= 3). Individual clouds are thermally supported against self gravity. The post-collision thermodynamics in this model is governed by the EOS, defined by Eq. (1) above. The clouds collide and form a planar gas slab confined by ram pressure. The time sequence of colliding clouds and their evolution after collision is shown in Fig. 1. We treat the gas slab as approximately isothermal and hold it at the original pre-collision cloud temperature. Our assumption of a somewhat lower post collision temperature,
![]() ,
is unlikely to have any significant effect on the final state of the gas slab for
,
is unlikely to have any significant effect on the final state of the gas slab for
![]() ,
calculated using the jump condition will only be higher, making the slab even warmer.
,
calculated using the jump condition will only be higher, making the slab even warmer.
The post-shock gas slab in this model does not fragment. After formation, it simply expands and ends up as a diffuse gas cloud (t = 3.49 Myr in Fig. 1). The gas slab in this case is not massive enough, or in other words, it is not cold enough (for the mass that it has) to support the Jeans instability. According to Whitworth et al. (1994), the length of the fastest growing unstable mode is
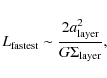 |
(3) |
which is roughly a few parsecs for the present case, at least an order of magnitude greater than the slab thickness.
Unlike those reported in Paper I, the slab in this model does not seem to develop any bending modes. However, gas elements within the slab are non static and dissipate mechanical energy via shocking, facilitated by the artificial viscosity. The gas slab in this case seems to evolve via an interplay between gravity and thermal pressure. There are two phases in this evolution. In the first, thermal pressure builds up in the slab after collision; in the next phase as we permit the gas to cool, thermal pressure within the slab rapidly diminishes. The slab is too warm to become Jeans unstable and simply expands. The expansion may seem similar to that of the shocked slabs reported in Paper I; however, unlike those slabs, the one in this case does not collapse to form an elongated object along the collision axis. This suggests that gravity and thermal pressure attain a state of dynamic equilibrium.
In model 2, we maintain physical conditions identical to those in the previous case, except now the cloud collision is off-centre. The impact parameter, b, is a fourth of the cloud radius,
![]() .
The time sequence of colliding clouds in this model is shown in Fig. 2. The cloud collision results in an oblique shocked slab unlike a planar slab in model 1. After formation, the slab tumbles about the z-axis and eventually expands, as in model 1. This can be seen in the snapshot corresponding to t = 1.89 Myr in Fig. 2.
.
The time sequence of colliding clouds in this model is shown in Fig. 2. The cloud collision results in an oblique shocked slab unlike a planar slab in model 1. After formation, the slab tumbles about the z-axis and eventually expands, as in model 1. This can be seen in the snapshot corresponding to t = 1.89 Myr in Fig. 2.
As in model 1, the gas slab in this case also evolves through an interplay between gravity and thermal pressure. Contrary to intuition, the slabs in either case evolve on a similar timescale. This suggests that the expansion of the oblique slab also commences at a similar epoch to the planar slab. In fact, the oblique slab expands slightly faster than the planar slab of model 1. This is presumably because of axial transfer of angular momentum as the far ends of the oblique slab move outward (see snapshot corresponding to t = 1.89 Myr in Fig. 2). The terminal state in this case is similar to case 1.
Equation (3) is still valid in this case, as we chose a rather small impact parameter, b. The length of the fastest growing mode,
![]() ,
calculated using this equation for the present model is much longer than the slab thickness. The gas slab in this case as well fails to become Jeans unstable. Such a scenario (as in models 1 and 2) will thus simply lead to formation of diffuse clouds in the ISM. These clouds may spawn star formation only when they have been sufficiently squeezed.
,
calculated using this equation for the present model is much longer than the slab thickness. The gas slab in this case as well fails to become Jeans unstable. Such a scenario (as in models 1 and 2) will thus simply lead to formation of diffuse clouds in the ISM. These clouds may spawn star formation only when they have been sufficiently squeezed.
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.5cm,clip]{Figure 10:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg36.png) |
Figure 3: A time (measured in Myr) sequence of column density plots showing the commencement of gravitational fragmentation, formation of clumps, and finally the fragmented planar gas slab, in model 3. |
| Open with DEXTER | |
4.2 Fast cloud collision (T0 = 10 K; models 3 and 4)
We now repeat the simulations preformed in models 1 and 2 in our next two cases, 3 and 4 respectively, but with one change. We now allow the post-shock gas slab to cool down to 10 K. As discussed above, we intend to explore the effect of cooling on the dynamical evolution of the gas slab. We noted in models 1 and 2 above, that the gas slab at temperature,
![]() ,
did not support gravitational instability.
,
did not support gravitational instability.
However, in model 3 where the MCs collide head-on, we observe that the post-collision gas slab undergoes gravitational fragmentation. In Fig. 3, we present a time sequence of the gas slab after its formation, as seen face-on. As the gravitational instability starts growing, the slab shows signs of flocculation (t = 0.65 Myr, t = 0.7 Myr in Fig. 3), and clumps in the slab eventually condense out. Some of the smaller clumps merge to form larger clumps, while others lie embedded in filamentary structures. Because most of the clumps are spheroidal, appear non circular in the projection maps (see Fig. 4 above).
The gravitational instability grows on a timescale that is much smaller than the free fall time of the individual precollision clouds, or even the cloud crushing time,
![]()
![]() . We now compare observations from this model with corresponding analytic predictions. In our simulation we observe that the clump formation commences after about 0.65 Myr. This is the time required for the growth of the unstable mode,
. We now compare observations from this model with corresponding analytic predictions. In our simulation we observe that the clump formation commences after about 0.65 Myr. This is the time required for the growth of the unstable mode,
![]() ,
leading to condensation of a clump and defined as
,
leading to condensation of a clump and defined as
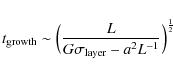 |
(4) |
(Whitworth et al. 1994).
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12cm,clip]{Figure 14:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg40.png) |
Figure 4: Column density plot (t = 0.85 Myr) of the fragmented slab in model 3. Density contours have been overlayed to facilitate identification of the structure in it. |
| Open with DEXTER | |
Here L,
![]() ,
and
,
and
![]() are the size of the clump, average surface density of the slab, and the average sound speed in the slab, respectively. Plugging in the appropriate values from the simulation, we get
are the size of the clump, average surface density of the slab, and the average sound speed in the slab, respectively. Plugging in the appropriate values from the simulation, we get
![]() = 0.6 Myr, which agrees with the epoch observed in the simulation. We again note that clump formation commences after about 0.65 Myr. Thereafter the gravitational instability grows quickly and the slab fragments into a number of clumps. The minimum mass of a fragment is given by
= 0.6 Myr, which agrees with the epoch observed in the simulation. We again note that clump formation commences after about 0.65 Myr. Thereafter the gravitational instability grows quickly and the slab fragments into a number of clumps. The minimum mass of a fragment is given by
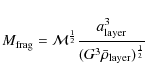 |
(5) |
(Whitworth et al. 1994). Here
The fragmentation of this slab results in the formation of 36 big and small clumps. Figure 4 shows a close-up of the fragmented slab. At this epoch a few clumps have already become self-gravitating, while a few others oscillate for some time before collapsing under self gravity. The column density plot in Fig. 5 shows a closer view of the central region of this slab. A few other small clumps merge with similar clumps and form larger clumps and filaments. To facilitate identification of the structure in the slab, we have overlayed the density contours on the column density plot in this figure.
![\begin{figure}
\par\includegraphics[origin=rb,width=9cm,clip]{Figure 9:11762.eps} \end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg46.png) |
Figure 5: Column density plot showing a closer view of the central region of the fragmented slab in model 3. The (three) black dots are the (three) sinks formed in various clumps. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.5cm,clip]{Figure 11:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg47.png) |
Figure 6: A time (measured in Myr) sequence of column density plots of the oblique slab in model 4. A face-on view of the slab has been shown in these plots. We can see that as the slab grows old, it shows signs of flocculation (t = 0.82 Myr) and subsequently fragments (right hand plot in the third row, t = 1.6 Myr). The last plot shows a network of filaments and clumps embedded in the filaments. |
| Open with DEXTER | |
The slab as seen in Figs. 4 and 5 is fairly evolved and, at this epoch, the gravitational instability has fully grown. Almost all the gas in the slab ends up in density structures. The average density of the structure in the slab is ![]() 10-18 g cm-3, which then suggests that the growth period of the instability, as defined by Elmegreen (1989) and quoted above, is
10-18 g cm-3, which then suggests that the growth period of the instability, as defined by Elmegreen (1989) and quoted above, is ![]() 0.8 Myr. This is comparable to the epoch (0.85 Myr) when the instability has fully grown.
0.8 Myr. This is comparable to the epoch (0.85 Myr) when the instability has fully grown.
According to Nakamura et al. (1993), the characteristic length scale of a filamentary structure is
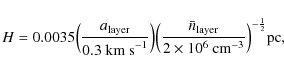 |
(6) |
where all the symbols have their usual meanings. The average temperature of the densest regions in the slab is about 10 K, while
Next, in model 4 the cloud collision produces an oblique gas slab confined by ram pressure. As in the previous case (model 3), this slab also undergoes gravitational fragmentation. However, the fragmentation observed here is somewhat different from what Chapman et al. (1992) and Pongracic et al. (1992) report. According to these authors, the oblique gas slab tumbles about a direction perpendicular to the plane of collision and breaks into two blobs, which then undergo secondary fragmentation to form multiple systems. The initial fragmentation, reported by these authors, resembles a bar-mode instability. In the present case, although the oblique slab exhibits a similar tumbling motion, the final outcome is different from what is reported by the respective authors. Also, the reported simulations were performed with only a few thousand particles, so it is likely that their simulations suffered from lack of resolution.
Another possible reason for this observed difference in the unstable mode could be a shorter Jeans length in the present case. Since our clouds are more massive, their collision produces a slab with higher surface density, which shortens the Jeans length and enhances its growth rate. In this eventuality, the gravitational instability will dominate the other unstable modes of the tumbling slab, notably the bar mode. The fragmentation of the slab after its formation can be seen in Fig. 6, a time sequence of column density plots of the gas slab, as seen face-on. The nature of fragmentation observed here is in consonance with the predictions of Whitworth et al. (1994) for an off-centre cloud collision, with a small impact parameter.
![\begin{figure}
\par\includegraphics[origin=rb,width=12.5cm,clip]{Figure 13:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg55.png) |
Figure 7: A column density plot (t = 1.4 Myr) showing a close view of the oblique slab in model 4. Fragmentation of the slab leads to formation of a number of clumps and elongated structures as can be seen with the aid of density contours overlayed on the column density plot. The circled region shows a fragmenting clump. |
| Open with DEXTER | |
As in the previous case, we calculated the dynamical properties for this slab, using Eqs. (3), (4), and (5). The length of the fastest growing unstable mode in the slab,
![]() ,
defined by Eq. (3) above is, indeed much shorter than the radial extent of the slab. Clumping in the slab commences after
,
defined by Eq. (3) above is, indeed much shorter than the radial extent of the slab. Clumping in the slab commences after ![]() 0.4 Myr, while the smallest clump has mass
0.4 Myr, while the smallest clump has mass ![]() 12
12 ![]() and size
and size ![]() 0.1 pc. Corresponding analytic calculations yield 0.4 Myr, 11
0.1 pc. Corresponding analytic calculations yield 0.4 Myr, 11 ![]() ,
and 0.12 pc, respectively. The calculated values thus seem to be in good agreement with those observed in the simulation.
,
and 0.12 pc, respectively. The calculated values thus seem to be in good agreement with those observed in the simulation.
Once the slab becomes unstable, it develops floccules and soon fragments. The final state of the slab, post-fragmentation, can be seen in Fig. 7, which is a column density plot of the slab as seen face-on. The clumps and filaments in it have density of ![]() 10-19 g cm-3, and density contours overlayed on this plot elucidate the structure in it. The average smoothing of SPH particles in these simulations is at least an order of magnitude less than
10-19 g cm-3, and density contours overlayed on this plot elucidate the structure in it. The average smoothing of SPH particles in these simulations is at least an order of magnitude less than
![]() .
We therefore think that the observed fragmentation of gas slabs is likely to be physical.
.
We therefore think that the observed fragmentation of gas slabs is likely to be physical.
We find that fragmentation of a cold gas slab leads to clump formation, and self-gravitating clumps may spawn a single or multiple stellar system, a view that has also been advanced by numerous workers before: Chapman et al. (1992), Bhattal et al. (1994) and Clarke (1999), among others. Here we can see that fragmenting gas slabs also produce dense filaments. In fact, Burkert & Hartmann (2004) performed 2-d grid simulations of self-gravitating, finite gas sheets with different geometries. It makes an interesting comparison between two of their models viz. the ``static circular sheet'' and the ``rotating elliptical sheet'', with the respective gas slabs in models 3 and 4 discussed in this section.
While the formation of the outer ring-like structure in the gas slab of model 3 (see Fig. 4), looks similar to the structure in their collapsing circular sheet, but unlike the global collapse observed in their model, the gas slab discussed here undergoes gravitational fragmentation. However, the reason behind formation of this ring, that of edge material initially piling up, might still be valid. Similarly, the Burkert & Hartmann (2004) model of collapsing elliptical gas sheet leading to the formation of a filament is at variance with the result of model 4, discussed here. This obviously is the result of the faster growth rate of the gravitational instability, as compared to the global collapse time of the gas slab. However, the shocked slab (both planar and oblique), where the gravitational instability is apparently suppressed by hydrodynamical instabilities, undergoes global collapse (see Paper I). Hartmann & Burkert (2007) have, in fact, proposed a rotating elliptical sheet model to explain the formation of the Orion integral filament. Observational evidence for similar occurrences have been reported, for instance by Lada et al. (1999), and Elmegreen (2002) about a star cluster embedded in an elongated region, IC 546. This cluster is thought to have been formed because of some external trigger, i.e. feedback from some nearby star-forming region.
4.3 Slow cloud collision
Finally, we examine the case of a very low-velocity head-on cloud collision. As discussed above, an adiabatic EOS, given by Eq. (2) with
![]() is used to model the weak shock in this case. Figure 8 shows a time sequence of column density plots of the colliding clouds. Post-collision, the clouds merge and form a prolate gas cloud (t = 1.42 Myr in Fig. 8). The cloud is thermally supported against self gravity with a non isotropic thermal pressure gradient in its interiors, on account of its spheroidal shape.
is used to model the weak shock in this case. Figure 8 shows a time sequence of column density plots of the colliding clouds. Post-collision, the clouds merge and form a prolate gas cloud (t = 1.42 Myr in Fig. 8). The cloud is thermally supported against self gravity with a non isotropic thermal pressure gradient in its interiors, on account of its spheroidal shape.
Post-collision, as material from the colliding clouds streams into the gas cloud, it progressively becomes denser and therefore warmer, as dictated by the stiff EOS employed in this model. This builds up a thermal reservoir within it, and the cloud therefore starts expanding along the collision axis (t = 1.96 Myr, t = 2.62 Myr, and t = 2.96 Myr in Fig. 8). During this process it flattens, and the expansion continues until the thermal pressure along the y-axis arrests the lateral collapse. This observation in the simulation is in consonance with the analytic predictions of Ramsay (1961) and Mestel (1965). This cloud is not self-gravitating, and the lateral collapse is just a phenomenon involving gravo-thermal balance.
From the snapshots in Fig. 8, we can also see that some material is ejected, also called jets, from the top and bottom ends of the cloud. The qualitative feature of this model is similar to that of models 1 and 2 discussed above. However, the post collision gas cloud evolves on a much larger timescale than in cases 1 and 2. This is yet another scenario that could lead to the formation of diffuse clouds in the ISM. Star formation can commence in such clouds only when they become sufficiently dense and begin collapsing under self gravity.
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.5cm,clip]{Figure 15:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg57.png) |
Figure 8: A time (measured in Myr) sequence of column density plots in model 5. Collision of clouds, followed by the formation of a prolate gas cloud (t = 1.07 Myr), and finally its expansion is evident from these plots. The expansion of the post-collision gas cloud terminates in a diffuse cloud (t = 2.96 Myr). Material squirting from the top and bottom ends (jets) of the slab are also visible in these plots. |
| Open with DEXTER | |
5 Conclusions
Colliding clouds dissipate kinetic energy and produce gas slabs that may fragment, leading to the formation of density structures of various shapes and sizes. Some of these structures may collapse and form stars, while others may suffer tidal disruption. This model does not demand injection of turbulence to trigger star formation, and stellar feedback from one episode of star formation may lead to other such events in the neighbourhood.
Numerical simulations by Clarke & Gittins (2006), for instance, have shown that a burst event creates local perturbations in the galactic disk, which in turn generate spiral patterns in it. Interference of many such perturbations may create a complex structure that might evolve on the timescale of a rotation period. The evolution of a galaxy essentially depends on the global star formation rate. Starburst events also play an important role in the chemistry of the intercloud medium. Powerful winds from young star clusters drive shock fronts and, while the abundance of molecular species may suffer attrition following the post shock ionisation, the pool of heavier elements will be replenished via stellar evolution. Cloud collision is a prominent mechanism of triggered star formation and, supposedly also plays a pivotal role in the distribution of prestellar core masses and stellar population, in the ISM (McKee 1999; Tan 2000).
In the present work, we explored the paradigm of low-velocity cloud collisions, and also tried to ascertain the importance of post-shock cooling, albeit in a rather crude manner, upon the dynamical evolution of the pressure confined slab. Our simple investigation shows that, gas slabs become Jeans unstable under suitable physical conditions and may fragment to produce clumps and filaments. We conclude that colder slabs are more likely to fragment, otherwise the slab simply expands and ends up as a diffuse cloud in dynamical equilibrium. The former scenario is more interesting from the perspective of forming either multiple or larger N-body stellar systems. Density perturbations in the gas slab grow purely from white noise and therefore do not require any external trigger. In the latter scenario, however, the diffuse gas clouds may become self gravitating, but only when crushed by sufficient external pressure, otherwise such clouds of various shapes are not uncommon in the ISM.
Models 1, 2, and 5 in the present work belong to this latter paradigm, and models 3 and 4 to the former. Figures 4 and 7 respectively show the fragmented gas slabs in models 3 and 4. Clumps and well-defined, elongated density structures are evident in both. Indeed, a few clumps in either slab have become self-gravitating by the time respective calculations were terminated. The collapse of individual clumps, however, could no longer be followed because of limited resources. However, fragmentation of gas slabs is evidently a propitious mode of clump formation. Clumps may eventually spawn stars and some of the larger clumps may even be the wombs to larger star clusters.
The results of our off-centre cloud collision experiments (both models 2 and 4) differ significantly from similar experiments performed by Lattanzio et al. (1985), Chapman et al. (1992) and Bhattal et al. (1998), among others. These authors report a bar-mode fragmentation of the post-collision, oblique, pressure-compressed slab, which is different from the fragmentation observed in our model. On the contrary, we observe that the oblique gas slab either simply expands to finally produce a diffuse gas cloud (model 2) or fragments gravitationally to form clumps and filaments (model 4). We attribute this difference to the mass of the slab, which in our simulation is at least an order of magnitude greater than in the work cited above. As a result of higher mass, hence higher column density, the length of the unstable mode is shortened and grows much faster. Also, the SPH simulations reported by those authors were performed using only a few thousand particles so, it is unlikely that any dynamical instabilities would have been resolved.
We admit that the investigation presented here is too simplified and that it dwells solely on a gravo-thermal treatment of the problem. At best, we have a skewed picture before us, nevertheless, essential in any further investigation of the problem. For an elaborate study of the subject, magnetic field needs to be included and post-shock radiative cooling needs to be more thoroughly treated (cf. Vázquez-Semadeni et al. 2007). Also, collapsing clumps can be followed to higher densities by employing a radiative transfer scheme (cf. Stamatellos et al. 2007), rather than the simple barytropic EOS used here.
Acknowledgements
This work was completed as part of post graduate research and funded through a studentship (DSW/Edu/Inf/2004/6283(35)) awarded by the State Government Of Maharashtra, India. All the column density plots presented here were prepared using the publicly available graphics package, SPLASH prepared by Dr. D. Price (Price 2007). Dr. S. V. Anathpindika particularly thanks Dr. Simon Goodwin for providing the latest version of his SPH code, DRAGON. Useful comments and suggestions by an anonymous referee and the editors are greatly appreciated.
References
- Anathpindika, S. 2009, A&A, 504, 437 [CrossRef] [EDP Sciences] (In the text)
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] (In the text)
- Bate, M., Bonnell, I., & Price, N. 1995, MNRAS, 277, 362 [NASA ADS] (In the text)
- Boyd, D., & Whitworth, A. 2005, A&A, 430, 1059 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bhattal, A. S., Francis, N., Watkins, S. J., & Whitworth, A. P. 1998, MNRAS, 297, 435 [NASA ADS] [CrossRef] (In the text)
- Block, D. L., Bertin, G., Stockton, A., et al. 1994, A&A, 288, 365 [NASA ADS] (In the text)
- Burkert, A., & Hartmann, L. 2004, ApJ, 616, 288 [NASA ADS] [CrossRef] (In the text)
- Chapman, S., Pongracic, H., Disney, M., et al. 1992, Nature, 359, 207 [NASA ADS] [CrossRef] (In the text)
- Clarke, C. 1999, MNRAS, 307, 328 [NASA ADS] [CrossRef] (In the text)
- Clarke, C., & Gittins, D. 2006, MNRAS, 371, 530 [NASA ADS] [CrossRef] (In the text)
- Clarke, C., Bonnell, I., & Hillenbrand, L. 2000, Protostars And Planets iv, ed. V., Mannings, A., Boss, & S., Russell (Arizona Press) (In the text)
- Curry, C. 2002, ApJ, 576, 849 [NASA ADS] [CrossRef]
- Dale, J., Bonnell, I., & Whitworth, A. 2007, MNRAS, 375, 1291 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. 1989, ApJ, 340, 786 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. 1997, ApJ, 477, 196 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. 2000, ApJ, 530, 277 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. 2002, Extragalactic Star Clusters, ed. D., Geisler, E., Grebel, & D., Minniti, IAU Symp. Ser., 207 (In the text)
- Elmegreen, B., & Elmegreen, D. 1978, ApJ, 220, 1051 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, D., & Elmegreen, B. 1986, ApJ, 311, 554 [NASA ADS] [CrossRef] (In the text)
- Furuya, R., Kitamura, Y., & Shinnaga, H. 2008, PASJ, 60, 421 [NASA ADS] (In the text)
- Goodwin, S., Whitworth, A., & Ward-Thompson, D. 2004, MNRAS, 414, 633 [NASA ADS] (In the text)
- Hartmann, L., & Burkert, A. 2007, ApJ, 654, 988 [NASA ADS] [CrossRef] (In the text)
- Hoyle, F. 1953, ApJ, 118, 513 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, R. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, R. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] (In the text)
- Klessen, R., & Burkert, A. 2000, ApJS, 128, 287 [NASA ADS] [CrossRef] (In the text)
- Klessen, R., Burkert, A., & Bate, M. 1998, ApJ, 501, L205 [NASA ADS] [CrossRef] (In the text)
- Lada, C., Alves, J., & Lada, B. 1999, ApJ, 512, 250 [NASA ADS] [CrossRef] (In the text)
- Larson, R. 1981, MNRAS, 194, 809 [NASA ADS] (In the text)
- Larson, R. 1985, MNRAS, 214, 379 [NASA ADS] (In the text)
- Lattanzio, J. C., Monaghan, J. J., Pongracic, H., & Schwarz, M. P. 1985, MNRAS, 215, 125 [NASA ADS] (In the text)
- Lefloch, B., Cernicharo, J., & Pardo, J. 2008, A&A, 489, 157 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Makino, J. 1991, PASJ, 43, 859 [NASA ADS] (In the text)
- McKee, C. 1999, Conf. Proc. The Physics Of Star Formation & Early Stellar Evolution, [arXiv:astro-ph/9901370] (In the text)
- Mestel, L. 1965, QJRAS, 6, 161 [NASA ADS] (In the text)
- Nakamura, F., Hanawa, T., & Nakano, T. 1993, PASJ, 45, 551 [NASA ADS] (In the text)
- Nutter, D., & Ward-Thompson, D. 2007, MNRAS, 374, 1413 [NASA ADS] [CrossRef] (In the text)
- Pongracic, H., Chapman, S. J., Davies, J. R., et al. 1992, MNRAS, 256, 291 [NASA ADS] (In the text)
- Price, D. 2007, PASA, 24(3), 159
- Pudritz, R. 2002, Science, 295, 68 [NASA ADS] [CrossRef] (In the text)
- Ramsay, A. 1961, Theory Of Newtonian Attraction (Cambridge University Pub.) (In the text)
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] (In the text)
- Stamatellos, D., Whitworth, A. P., Bisbas, T., Goodwin, S. 2007, A&A, 475, 37 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tan, J. 2000, ApJ, 536, 173 [NASA ADS] [CrossRef] (In the text)
- Vàzquez-Semadeni, et al. 2007, ApJ, 657, 780 [NASA ADS] (In the text)
- Wada, K., Spaans, M., & Kim, S. 2000, ApJ, 540, 797 [NASA ADS] [CrossRef] (In the text)
- Whitworth, A. P., Bhattal, A. S., Chapman, S. J., Disney, M. J., & Turner, J. A. 1994, A&A, 290, 421 [NASA ADS] (In the text)
- Whitworth, A. P., Bhattal, A. S., Francis, N., & Watkins, S. J. 1996, MNRAS, 283, 1061 [NASA ADS] (In the text)
- Wyse, R. 1986, ApJ, 311, L41 [NASA ADS] [CrossRef]
- Wyse, R., & Silk, J. 1989, ApJ, 339, 700 [NASA ADS] [CrossRef]
Footnotes
- ...
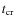
![[*]](/icons/foot_motif.png)
-
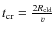 ,
where v is the precollision speed of a cloud and
,
where v is the precollision speed of a cloud and
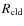 is its radius.
is its radius.
All Tables
Table 1: List of simulations performed with relevant physical details.
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12cm,clip]{Figure 16:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg18.png) |
Figure 1: A column density plot of the time (measured in Myr) sequence of cloud collision in model 1. Cloud collision results in the formation of a pressure confined gas slab, which then expands and terminates in a diffuse gas cloud, as can be seen in the last snapshot (t = 3.49 Myr). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.7cm,clip]{Figure 12:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg30.png) |
Figure 2: Column density plot showing a time (measured in Myr) sequence tracking model 2. This sequence shows the colliding clouds, formation of the post-collision gas slab, and then its expansion. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.5cm,clip]{Figure 10:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg36.png) |
Figure 3: A time (measured in Myr) sequence of column density plots showing the commencement of gravitational fragmentation, formation of clumps, and finally the fragmented planar gas slab, in model 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12cm,clip]{Figure 14:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg40.png) |
Figure 4: Column density plot (t = 0.85 Myr) of the fragmented slab in model 3. Density contours have been overlayed to facilitate identification of the structure in it. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[origin=rb,width=9cm,clip]{Figure 9:11762.eps} \end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg46.png) |
Figure 5: Column density plot showing a closer view of the central region of the fragmented slab in model 3. The (three) black dots are the (three) sinks formed in various clumps. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.5cm,clip]{Figure 11:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg47.png) |
Figure 6: A time (measured in Myr) sequence of column density plots of the oblique slab in model 4. A face-on view of the slab has been shown in these plots. We can see that as the slab grows old, it shows signs of flocculation (t = 0.82 Myr) and subsequently fragments (right hand plot in the third row, t = 1.6 Myr). The last plot shows a network of filaments and clumps embedded in the filaments. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[origin=rb,width=12.5cm,clip]{Figure 13:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg55.png) |
Figure 7: A column density plot (t = 1.4 Myr) showing a close view of the oblique slab in model 4. Fragmentation of the slab leads to formation of a number of clumps and elongated structures as can be seen with the aid of density contours overlayed on the column density plot. The circled region shows a fragmenting clump. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,origin=rb,width=12.5cm,clip]{Figure 15:11762.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11762-09/Timg57.png) |
Figure 8: A time (measured in Myr) sequence of column density plots in model 5. Collision of clouds, followed by the formation of a prolate gas cloud (t = 1.07 Myr), and finally its expansion is evident from these plots. The expansion of the post-collision gas cloud terminates in a diffuse cloud (t = 2.96 Myr). Material squirting from the top and bottom ends (jets) of the slab are also visible in these plots. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


