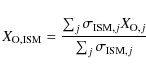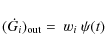| Issue |
A&A
Volume 504, Number 2, September III 2009
|
|
|---|---|---|
| Page(s) | 373 - 388 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200911756 | |
| Published online | 09 July 2009 | |
The evolution of the mass-metallicity relation in galaxies of different morphological types
F. Calura1 - A. Pipino2 - C. Chiappini3,4 - F. Matteucci1,4 - R. Maiolino5
1 - Dipartimento di Astronomia, Universitá di Trieste,
via G.B. Tiepolo 11, 34143 Trieste, Italy
2 -
Department of Physics & Astronomy, University of Southern California, Los Angeles 90089-0484, USA
3 -
Observatoire de Genève, Universitè de Genève, 51 Chemin des Maillettes, 1290 Sauverny, Switzerland
4 -
INAF - Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
5 -
INAF - Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
Received 30 January 2009 / Accepted 31 March 2009
Abstract
Aims. By means of chemical evolution models for ellipticals, spirals, and irregular galaxies, we aim at investigating the physical meaning and the redshift evolution of the mass-metallicity relation, as well as how this relation is connected with galaxy morphology.
Methods. Our models distinguish among different morphological types through the use of different infall, outflow, and star formation prescriptions. We assume that galaxy morphologies do not change with cosmic time. We present a method accounting for a spread in the epochs of galaxy formation and refining the galactic mass grid. To do that, we extracted the formation times randomly and assumed an age dispersion
![]() .
We compared our predictions to observational results obtained for galaxies between redshifts 0.07 and 3.5.
.
We compared our predictions to observational results obtained for galaxies between redshifts 0.07 and 3.5.
Results. We reproduce the mass-metallicity (MZ) relation mainly by means of an increasing efficiency of star formation with mass in galaxies of all morphological types, without any need to invokegalactic outflows favoring the loss of metals in the less massive galaxies. Our predictions can help constraining the slope and the zero point of the observed local MZ relation, both affected by uncertainties related to the use of different metallicity calibrations. We show how, by considering the MZ, the O/H vs. star formation rate (SFR), and the SFR vs. galactic mass diagrams at various redshifts, it is possible to constrain the morphology of the galaxies producing these relations. Our results indicate that the galaxies observed at z=3.5 should be mainly proto-ellipticals, whereas at z=2.2 the observed galaxies consist of a morphological mix of proto-spirals and proto-ellipticals. At lower redshifts, the observed MZ relation is reproduced by considering both spirals and irregulars. Galaxies with different star formation histories may overlap in the MZ diagram, but measures of abundance ratios such as [O/Fe] can help to break this degeneracy. Predictions for the MZ relations for other elements (C, N, Mg, Si, Fe) are also presented, with largest dispersions predicted for elements produced in considerable amounts by Type Ia SNe, owing to the long lifetimes of their progenitors.
Key words: galaxies: abundances - ISM: abundances - galaxies: high-redshift
1 Introduction
In the past few years, several observational projects have been devoted to studying the relation between galactic stellar mass and metallicity in star-forming galaxies. In particular, the study of the redshift evolution of the mass-metallicity (hereinafter MZ) relation has provided us with crucial information on the cosmic evolution of star formation, as well as on the temporal evolution of the chemical properties of the stellar populations. Various observational studies of the MZ relation have outlined that across a wide redshift range, i.e. between z=3.5 and z=0, in the high-mass, high-metallicity part of the MZ plot, galaxies tend to form a plateau, whereas at lower masses the MZ plot shows an increase in metallicity with mass. Moreover, both the zero point and the slope of the MZ relation are a function of redshift, as shown in a recent paper by Maiolino et al. (2008). Therefore, the metallicity evolution is stronger for low-mass galaxies than for high-mass galaxies.Various theoretical explanations of the MZ relation have been proposed so far.
One interpretation is linked to starburst-induced galactic outflows, more efficient in expelling metal-enriched gas in dwarf galaxies than in giant galaxies, owing to the shallow gravitational potential wells of the former (Larson 1974; Dekel & Silk 1986; Tremonti et al. 2004; De Lucia et al. 2004; Kobayashi et al. 2007; Finlator & Davé 2008). Alternatively, the dilution caused by infall can act in a way similar to the presence of outflows, once one assumes longer infall times in lower mass galaxies (Dalcanton et al. 2004). Another possibility is that low-mass galaxies are less evolved than large galaxies. In this picture, while large galaxies have formed the bulk of their stars by means of an intense event at high redshift, quickly enriching their ISM to solar or over-solar metallicities, dwarf galaxies, characterised by lower star formation efficiencies (i.e. star formation rates per unit mass of gas) have sub-solar interstellar metallicities. This interpretation is supported by several chemical evolution models (Lequeux et al. 1979; Matteucci 1994), by cosmological N-body simulations (Brooks et al. 2007; Mouhcine et al. 2008; Tassis et al. 2008) and by hydrodynamical simulations (Tissera et al. 2005; De Rossi et al. 2007). A third interpretation of the MZ relation is linked to the initial mass function. Köppen et al. (2007) show how the MZ relation can be explained by a higher upper-mass cutoff in the initial mass function (IMF) in more massive galaxies. However, none of these theoretical studies have investigated how the MZ relation is connected with galaxy morphology, as well as the role played by the star formation histories of galaxies of different morphological types.
In this paper, our aim is to investigate these aspects, as well as to understand the physical meaning of the MZ relation for different galaxies. To perform this task, we use detailed chemical evolution models for elliptical, spiral, and irregular galaxies. These models have proven to reproduce the main chemical properties of elliptical (e.g. Pipino & Matteucci 2004), spirals (Chiappini et al. 2001, 2003; Cescutti et al. 2007), and irregular galaxies (e.g. Lanfranchi & Matteucci 2003), as well as other observational constraints, such as the gas-to-light ratios, the supernova rates as a function of morphological type (Calura & Matteucci 2006a), and the cosmic evolution of the luminosity density (Calura & Matteucci 2003; Calura et al. 2004).
This paper is organised as follows. In Sect. 2, we present our models and our methods of
investigating the MZ relation. In Sect. 3, we describe the set of observational data used
in this work and we present our results. Finally, in Sect. 4 we draw some conclusions.
Throughout the paper, we adopt a concordance ![]() -cold dark matter cosmology, characterised by
-cold dark matter cosmology, characterised by
![]() ,
,
![]() and h=0.7.
and h=0.7.
2 Chemical evolution models
In this paper, we use chemical evolution
models for elliptical, spiral and irregular galaxies that have already been tested
against various local observational constraints. In general, in chemical evolution models,
the time-evolution of the fractional mass of the element i
in the gas within a galaxy, Gi, is described by the basic
equation:
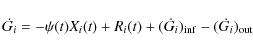 |
(1) |
where
The nucleosynthesis prescriptions are common to all models.
For massive stars and Type Ia SNe, we adopt the empirical yields suggested by François et al. (2004),
which are based on Woosley & Weaver (1995) for massive stars and on the Type Ia SNe yields of Iwamoto et al. (1999).
Fow low and intermediate mass stars, the adopted prescriptions are the ones by van den Hoeck ![]() Groenewegen (1997). The Type Ia SN rate computation is based on the single-degenerate model and follows the Matteucci & Recchi (2001) prescriptions.
The SFR
Groenewegen (1997). The Type Ia SN rate computation is based on the single-degenerate model and follows the Matteucci & Recchi (2001) prescriptions.
The SFR ![]() is a
Schmidt (1959) law expressed as
is a
Schmidt (1959) law expressed as
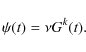 |
(2) |
The quantity
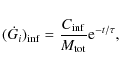 |
(3) |
with
In all our models, the instantaneous recycling approximation (IRA) is relaxed.
This means that the chemical abundances are computed by taking into account
the stellar lifetimes.
We assume that interstellar abundances are not affected by dust depletion.
This assumption is motivated by the fact that the observational abundances considered here are measured
in H![]() regions, where dust grains are destroyed by intense the UV radiation fields generated by massive stars
(Okada et al. 2008).
Quantitative estimates of the effects of dust on metallicity measures in H
regions, where dust grains are destroyed by intense the UV radiation fields generated by massive stars
(Okada et al. 2008).
Quantitative estimates of the effects of dust on metallicity measures in H![]() regions indicate that
the presence of dust grains does not introduce large errors into the global metallicity indicators being
the uncertainty in the metallicity due to dust effects in any case
regions indicate that
the presence of dust grains does not introduce large errors into the global metallicity indicators being
the uncertainty in the metallicity due to dust effects in any case ![]() 0.2 dex (Shields & Kennicutt 1996).
Furthermore, local depletion measurements in different environments indicate that O should not be considered as a strongly
refractory element (Jensen et al. 2005). This provides further support to our assumption of neglecting dust-depletion effects in MZ studies.
0.2 dex (Shields & Kennicutt 1996).
Furthermore, local depletion measurements in different environments indicate that O should not be considered as a strongly
refractory element (Jensen et al. 2005). This provides further support to our assumption of neglecting dust-depletion effects in MZ studies.
We assume that galaxy morphology does not change with redshift. When discussing different galaxy types at high redshift, it may seem inappropriate to use the classification in terms of ellipticals, spirals, and irregulars, as we observe them today. For this reason, when discussing our results at any redshift, with the expressions ``ellipticals'', ``spirals'' or ``irregulars'' we refer to the high-redshift counterparts of each morphological type, or more appropriately to proto-ellipticals, proto-spirals, and proto-irregulars.
2.1 Elliptical galaxies
For the chemical evolution of elliptical galaxies, we adopt the one-zone model of Pipino &
Matteucci (2004).
Here we assume that all spheroids, i.e.
elliptical galaxies, spiral bulges, and halos, are included in the same category, described in this section.
Here we recall the main assumptions:
ellipticals form by means of a rapid infall of pristine gas, which triggers an intense starburst.
Star formation is assumed to halt when
the energy of the ISM, heated by stellar winds and supernova (SN) explosions,
exceeds the binding energy of the gas (Dekel & Silk 1986).
At this time a galactic wind occurs, sweeping away almost all of
the residual gas present at that time. After the SF has stopped,
the galactic wind is maintained by Type Ia SNe, which continue exploding until the present time,
and its duration
depends on the balance between this heating source and the gas cooling.
The binding energy of the gas is strongly
influenced by assumptions concerning the presence and distribution of dark
matter (Matteucci 1992). For the model adopted here, a diffuse
(
![]() ,
where
,
where
![]() is the effective radius of the galaxy and
is the effective radius of the galaxy and ![]() is the radius
of the dark matter core), but a
massive (
is the radius
of the dark matter core), but a
massive (
![]() )
dark halo has
been assumed (see Bertin et al. 1992).
)
dark halo has
been assumed (see Bertin et al. 1992).
The outflow rate
![]() is the
same order of magnitude (in general within a factor of 2) of
the value taken by the SFR just before the galactic wind (Pipino et al. 2005).
This result agrees with the indications from
the observations of starburst galaxies (e.g. Heckman 2002). For further details, see Pipino et al. (2005).
is the
same order of magnitude (in general within a factor of 2) of
the value taken by the SFR just before the galactic wind (Pipino et al. 2005).
This result agrees with the indications from
the observations of starburst galaxies (e.g. Heckman 2002). For further details, see Pipino et al. (2005).
We assume that the efficiency of star formation is higher in more massive objects that evolve faster than less massive ones (inverse-wind scenario, Matteucci 1994, otherwise called ``downsizing''). This implies that the galactic wind develops after a timescale varying with the galactic mass, with more massive galaxies experiencing earlier outflows. This mechanism allows us to reproduce the observed increase in [Mg/Fe] with galactic mass in ellipticals (see Matteucci 1994; Pipino & Matteucci 2004). It is also worth noting that this wind mechanism is the opposite of what was originally proposed by Larson (1974) to explain the MZ-relation in ellipticals. In fact, in Larson's model the galactic wind develops later in more massive systems due to an assumed constant efficiency of star formation with galactic mass. Matteucci (1994) obtained the ``inverse-wind'' scenario simply by assuming an increasing efficiency of star formation with mass and such an assumption can preserve the MZ-relation as well.
A Salpeter (1955) IMF constant in space and time is adopted, with lower limit
![]() and upper limit
and upper limit
![]() .
The choice of such an IMF for ellipticals and S0 galaxies assures that
several observational constraints such as the average stellar abundances and the colour-magnitude diagram
(see Pipino & Matteucci 2004), are reproduced, as well as the metal content in clusters of galaxies (see Renzini 2004; Calura et al. 2007).
We consider three elliptical galaxy models of three different luminous masses:
.
The choice of such an IMF for ellipticals and S0 galaxies assures that
several observational constraints such as the average stellar abundances and the colour-magnitude diagram
(see Pipino & Matteucci 2004), are reproduced, as well as the metal content in clusters of galaxies (see Renzini 2004; Calura et al. 2007).
We consider three elliptical galaxy models of three different luminous masses:
![]() and
and
![]() .
The infall is assumed to occurr on an extremely short timescale (<0.5 Gyr).
In Table 1 we list the initial baryonic mass,
the effective radius, the star formation efficiency
.
The infall is assumed to occurr on an extremely short timescale (<0.5 Gyr).
In Table 1 we list the initial baryonic mass,
the effective radius, the star formation efficiency ![]() ,
the infall timescale
,
the infall timescale
![]() ,
and the IMF adopted for each galaxy.
In Fig. 1, we show the predicted time evolution of the star formation rates, Type Ia, Type II SNe rates and interstellar
metallicity, represented by the O abundance (in units of
,
and the IMF adopted for each galaxy.
In Fig. 1, we show the predicted time evolution of the star formation rates, Type Ia, Type II SNe rates and interstellar
metallicity, represented by the O abundance (in units of ![]() O/H) for the three elliptical galaxy models used in this paper.
O/H) for the three elliptical galaxy models used in this paper.
Table 1: Elliptical models: parameters.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11756f1.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg54.png) |
Figure 1:
From top left corner, clockwise: SFR, interstellar O abundance (in units log(O/H)+12), Type II SNR,
and Type Ia SNR vs. time for the three elliptical galaxy models used in this paper.
The solid, dotted and dashed lines are the predictions for the models with total baryonic
mass
|
| Open with DEXTER | |
2.2 Spiral galaxies
To model spiral galaxies, we use a single-infall model designed to describe the evolution of the thin disc of the Milky Way galaxy (Chiappini et al. 2001). By using this model, we make the implicit assumption that the baryonic mass of any spiral galaxy is dominated by a thin disc of stars and gas in analogy with the Milky Way. The model used for spiral discs is a multi-zone one. The disc is approximated by several independent rings, 2 kpc wide, without exchange of matter between them. The timescale for the disc formation is assumed to increase with the galactocentric distance, thus producing an ``inside-out'' scenario for the disc formation (Matteucci & Francois 1989; Chiappini et al. 2001; Cescutti et al. 2007).
In this work, we use three spiral models representing galaxies of different masses. One model is designed to reproduce the main features of the M101 spiral galaxy (see Chiappini et al. 2003), representing the most massive spiral disc. The MW disc is used to represent a spiral galaxy of intermediate mass. Finally, a model for a low-mass spiral has been developed, characterised by a star formation efficiency and a mass surface density lower than the ones of the Milky Way (see Table 2).
Each model is characterised by a particular infall law and a star formation efficiency.
Our main assumption here is that larger discs evolve faster than smaller ones (Boissier et al. 2001),
in analogy with ellipticals and in agreement with observations.
For the mass-surface density of each spiral disc, we assume an exponential profile
![]() .
The SFR surface density is a
Kennicutt (1998) law expressed as
.
The SFR surface density is a
Kennicutt (1998) law expressed as
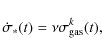 |
(4) |
with k=1.5. As for ellipticals, the SF efficiency
Table 2: Spiral models: parameters.
An important indication about the IMF in spiral discs also comes from chemical evolution models (see Chiappini et al. 1997, 2001), which clearly
indicate that, to reproduce the main features of the solar neighbourhood and the whole disc of the Milky Way,
a Scalo-like IMF (constant during the entire disc evolution) is
preferred, and that the Salpeter IMF would overestimate the solar abundances (see Romano et al. 2005, for a detailed discussion on this point).
In Table 2 we list the adopted values for the central surface mass density ![]() ,
the scaling radius
,
the scaling radius ![]() ,
the star formation efficiency
,
the star formation efficiency ![]() ,
the infall timescale
,
the infall timescale
![]() and the IMF for spirals of different masses.
In Fig. 2, we show the time evolution of the star formation rates, Type Ia, Type II SNe rates and interstellar
O abundance
for the three spiral galaxy models used in this paper.
In spiral discs, to compute the interstellar O abundance by means of our multi-zone models,
we calculated the mass-weighted interstellar O abundance on the whole disc
and the IMF for spirals of different masses.
In Fig. 2, we show the time evolution of the star formation rates, Type Ia, Type II SNe rates and interstellar
O abundance
for the three spiral galaxy models used in this paper.
In spiral discs, to compute the interstellar O abundance by means of our multi-zone models,
we calculated the mass-weighted interstellar O abundance on the whole disc
(see Calura & Matteucci 2004), where the
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11756f2.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg74.png) |
Figure 2:
From top left corner, clockwise: SFR, interstellar O abundance (in units log(O/H)+12), Type II SNR,
and Type Ia SNR vs. time for the three spiral galaxy models used in this paper.
The solid, dotted and dashed lines are the predictions for the models with central surface density
|
| Open with DEXTER | |
2.3 Irregular galaxies
For the irregulars we assume a one-zone model with instantaneous and complete mixing of gas inside this zone. Irregular galaxies assemble all their mass by means of a continuous infall of pristine gas. The SFR is continuous, with SF efficiency values lower than the ones used to describe ellipticals and spirals. In fact, as suggested by Calura & Matteucci (2006a), the main features of local galaxies of different morphological types may be reproduced by interpreting the Hubble sequence as a sequence of decreasing SF efficiency from early types to late types, i.e. from ellipticals to irregulars.
Also in this case, the star formation can trigger a galactic wind if the thermal energy of the gas exceeds its binding energy (Bradamante et al. 1998; Recchi et al. 2002). As for elliptical galaxies, for Irr the adopted IMF is the one of Salpeter (1955). This choice is consistent with the results by Calura & Matteucci (2004), who have showed that the adoption of a steeper IMF in dwarf irregulars leads to underestimating their average metallicity.
The rate of gas loss via galactic winds for each element i
is assumed to be proportional to the star formation rate at
time t:
where wi is a free parameter that describes the efficiency of the galactic wind for a given element i, and it is the same for all the elements. In irregular galaxies, the parameter wi, is fixed in order to reproduce the present-day gas fraction observed in dwarf irregulars. The assumption of wi=0.25 allows us to account for the correct fraction of neutral gas in irregulars (Calura & Matteucci 2006a).
Also in this case, we model irregular galaxies of three different luminous masses:
![]() and
and
![]() .
These values should bracket the baryonic masses of the most massive typical dwarf irregular galaxies (Lee et al. 2006), and
are compatible with the lowest stellar masses of the observational data samples used in this work.
Table 3 shows our adopted values for the initial baryonic mass, the luminous radius, the star formation efficiency
.
These values should bracket the baryonic masses of the most massive typical dwarf irregular galaxies (Lee et al. 2006), and
are compatible with the lowest stellar masses of the observational data samples used in this work.
Table 3 shows our adopted values for the initial baryonic mass, the luminous radius, the star formation efficiency ![]() ,
the infall timescale, and the IMF for each galaxy. For all irregulars, we assume a luminous radius of 1 kpc.
In Fig. 3, we show the time evolution of the star formation rates, Type Ia, Type II SNe rates, and interstellar O abundance for the three dwarf galaxy models used in this paper.
,
the infall timescale, and the IMF for each galaxy. For all irregulars, we assume a luminous radius of 1 kpc.
In Fig. 3, we show the time evolution of the star formation rates, Type Ia, Type II SNe rates, and interstellar O abundance for the three dwarf galaxy models used in this paper.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11756f3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg79.png) |
Figure 3:
From top left corner, clockwise: SFR, O abundance the gas (in units log(O/H)+12), Type II SNR,
and Type Ia SNR vs. time for the three irregular galaxy models used in this paper.
The solid, dotted and dashed lines are the predictions for the models with baryonic mass
|
| Open with DEXTER | |
Table 3: Irregular models: parameters.
2.4 Different galaxy formation epochs
As we have just seen, for each galactic morphological type we adopt a set of three models
correponding to fixed initial baryonic masses.
These models are designed to reproduce the main chemical features
of galaxies of different morphological types.
In general, in chemical evolution studies, the galaxies are all considered coeval
in the sense that, to compare any prediction
with local observations, in general one assumes that ellipticals, spirals and irregulars
have today an age comparable to the one of the Universe, i.e. ![]() 13.5 Gyr.
This is justified by the observational fact that the majority of galaxies contain stars as old as the Universe. This is certainly true for the ellipticals and spirals, although spiral discs are generally younger than stellar halos and have ages in the range 8-11 Gyr, whereas this is less clear for the irregulars.
Then, one considers the model outputs at this age,
which are compared with observations at z=0.
13.5 Gyr.
This is justified by the observational fact that the majority of galaxies contain stars as old as the Universe. This is certainly true for the ellipticals and spirals, although spiral discs are generally younger than stellar halos and have ages in the range 8-11 Gyr, whereas this is less clear for the irregulars.
Then, one considers the model outputs at this age,
which are compared with observations at z=0.
However, in a more realistic picture,
one should allow for some differences among the times at which star formation started,
to take into account a possible intrinsic spread in the MZ-relation.
For elliptical galaxies, a realistic age formation spread is 3 Gyr as indicated by studies of field ellipticals (Bernardi et al. 1998),
with the cluster ellipticals showing an even narrower spread of 2 Gyr (Bower et al. 1992).
For the spirals the situation is less clear: we tentatively assume a spread of 5 Gyr on the basis of the fact that
discs take a longer time to assemble by gas accretion than spheroids. As we see later (Sect. 3.4), such age dispersion values are
compatible with other age estimates for spirals present in the literature.
Concerning irregulars, in principle, the
age spread could be as long as ![]() 10 Gyr, i.e. comparable to a Hubble time.
10 Gyr, i.e. comparable to a Hubble time.
In this section, we describe how we simulate a population of non-coeval galaxies
and how we create a finer mass grid.
First of all, we define as galaxy-formation epoch the time at which star formation starts in a given galaxy.
For each morphological type, we choose a mean
redshift of formation ![]() and an age dispersion
and an age dispersion
![]() ,
relative to the spread in the galaxy formation time.
If the mean redshift of formation is
,
relative to the spread in the galaxy formation time.
If the mean redshift of formation is ![]() and t(z) is the age of the Universe at a given redshift z,
galaxies are allowed to form across
the cosmic time interval
and t(z) is the age of the Universe at a given redshift z,
galaxies are allowed to form across
the cosmic time interval
![]() ,
i.e. this means that galaxies may start forming at a redshift greater than
,
i.e. this means that galaxies may start forming at a redshift greater than ![]() .
If
.
If ![]() is the redshift of observation of a particular galactic observable,
the ages (defined as the times elapsed since the beginning of star formation)
of the galaxies at
is the redshift of observation of a particular galactic observable,
the ages (defined as the times elapsed since the beginning of star formation)
of the galaxies at ![]() are allowed to vary between two values
are allowed to vary between two values
![]() and
and
![]() ,
depending on
,
depending on ![]() and
the assumed values of
and
the assumed values of ![]() and
and
![]() :
:
- if
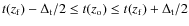 ,
i.e. if galaxies are still forming at the redshift of observation,
,
i.e. if galaxies are still forming at the redshift of observation,
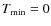 and
and
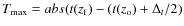 (Cases 1 and 2 in Fig. 4);
(Cases 1 and 2 in Fig. 4);
- if
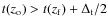 ,
i.e. galaxies have stopped forming at the redshift
,
i.e. galaxies have stopped forming at the redshift 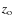 ,
then
,
then
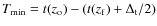 and
and
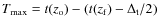 (Case 3 in Fig. 4)
(Case 3 in Fig. 4)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11756f4.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg94.png) |
Figure 4:
In cases 1 and 2, galaxies are still forming at the redshift of observation, i.e.
|
| Open with DEXTER | |
In Fig. 5, we show an example of the application of this technique:
the predicted MZ relation for ellipticals, spirals, and irregulars, obtained
assuming
![]() ,
,
![]() Gyr and computed at a redshft
Gyr and computed at a redshft
![]() .
The discontinuity predicted for elliptical galaxies (lower panel of Fig. 5) stems from
the steep increase in the metallicity in the first evolutionary phases, i.e. within the first 0.1 Gyr
(see Fig. 1). Also the evolution of the stellar mass density is fast, hence small variations
in the extracted times correspond to large variations for both the mass and the metallicity.
.
The discontinuity predicted for elliptical galaxies (lower panel of Fig. 5) stems from
the steep increase in the metallicity in the first evolutionary phases, i.e. within the first 0.1 Gyr
(see Fig. 1). Also the evolution of the stellar mass density is fast, hence small variations
in the extracted times correspond to large variations for both the mass and the metallicity.
The method described in this section will be used to generate mass-metallicity plots for galaxies of various morphological types, to be compared with observational data obtained at various redshifts.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f5.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg95.png) |
Figure 5:
Predicted MZ relation for galaxies of various morphological types.
In each panel, the curves represent the evolutionary
tracks of individual galaxies of various baryonic masses. The grey areas are the
predictions obtained by means
of our method to create an almost-continuous galaxy formation and a finer stellar mass grid (see Sect. 2.4). In this case, we assumed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11756f6.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg96.png) |
Figure 6: Predicted MZ-relation at z=0 for spirals and irregulars. The figure also shows the best fit to the local MZ-relation derived by Maiolino et al. (2008) from the data of Kewley & Ellison (2008). The open squares are the data by Lee et al. (2006), who measured the MZ relation in a sample of local dwarf galaxies. |
| Open with DEXTER | |
3 Results
In Fig. 6, we show the predicted MZ-relations at the present time for spirals and irregulars and compare them with the best fit of the MZ-relation obtained by Maiolino et al. (2008) from an analithical fit to the local observations (Kewley & Ellison 2008) and to the data of Lee et al. (2006), who determined the MZ relation in a sample of local dwarf galaxies. The agreement between our predictions and the observations is quite good. It is worth stressing that we do not show the results for local ellipticals since in this paper we are comparing gas abundances at various redshifts in star-forming galaxies, so we cannot compare the predicted present time MZ-relation for the gas in ellipticals with the data, since these galaxies stopped forming stars several Gyrs ago. On the other hand, local ellipticals show a definite MZ-relation, based on the abundances of their stellar populations, which is well-fitted by our models (see Pipino & Matteucci 2004).
Figure 6 shows that the local MZ relation can be naturally explained by assuming a lower star formation efficiency for less massive galaxies, irrespective of the galactic morphological type and that galactic winds are not needed to explain it. In fact, our models for spirals do not include galactic winds. The reason for this choice is that galactic winds are not required to explain the main features of disc galaxies, as shown by Tosi et al. (1998). We consider galactic winds in dwarf irregulars, since they are observed in these systems. However, these winds do not carry away large amounts of matter, in agreement with the fact that irregulars are gas-rich systems.
It is worth noting that Dalcanton (2007) reinterprets the observed MZ-relation in terms of infall/outflow in galaxies by means of simple models with IRA and concludes that only gas-rich systems with low star formation rates can produce and maintain low effective yields. This result shows the importance of assuming a lower star formation efficiency in lower mass systems.
The flattening of the MZ relation observed at
![]() is accounted for by our models and
comes from the assumed SF efficiencies of the high-mass spiral disc models.
The adopted SF efficiencies cause a
steep evolution of the (O/H) vs. time relation (see Fig. 2).
For larger galaxies, their present-day metallicity is reached at earlier times.
In fact, for the M101 model, very little evolution in the
(O/H)- time diagram is predicted at cosmic times greater than
is accounted for by our models and
comes from the assumed SF efficiencies of the high-mass spiral disc models.
The adopted SF efficiencies cause a
steep evolution of the (O/H) vs. time relation (see Fig. 2).
For larger galaxies, their present-day metallicity is reached at earlier times.
In fact, for the M101 model, very little evolution in the
(O/H)- time diagram is predicted at cosmic times greater than ![]() 5 Gyr. The growth of the metallicity for the MW model is slightly slower than the one
predicted for M101. This is because the adopted SF efficiencies are comparable.
On the other hand, the model for small discs has a SF efficiency lower by almost one order of magnitude,
hence the growth of metallicity with time is slower, and the present-day metallicity is much lower than the ones of the MW and of M101.
5 Gyr. The growth of the metallicity for the MW model is slightly slower than the one
predicted for M101. This is because the adopted SF efficiencies are comparable.
On the other hand, the model for small discs has a SF efficiency lower by almost one order of magnitude,
hence the growth of metallicity with time is slower, and the present-day metallicity is much lower than the ones of the MW and of M101.
In conclusion, the observed flattening of the MZ relation for large discs indicates that in the past, their SF efficiences must have been similar. This is also consistent with the similarity of the O gradients observed in the MW and in M101, although M101 is more massive (see Chiappini et al. 2003).
3.1 The calibration of the mass-metallicity at redshift zero
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f7.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg98.png) |
Figure 7: Predicted mass-metallicity for spiral galaxies (red contours) and irregular galaxies (blue contours) at z=0.07. The solid lines of different colours are best-fit relations calculated by Kewley & Ellison (2008) using different metallicity calibrations. KK04: Kobulnicky & Kewley (2004); KD02: Kewley & Dopita (2002); D02: Denicoló (2002); PP04: Pettini & Pagel (2004); P05: Pilyugin & Thuan (2005). |
| Open with DEXTER | |
In Fig. 7 we show the predicted MZ relation for local star forming galaxies, compared with a set of observational MZ relations at z=0.07. In our models, only spirals and irregulars experience star formation at z=0.07. This is supported by several observational studies, which have shown that local ellipticals are dominated by old stellar populations (de Freitas Pacheco et al. 2003, and references therein). The filled contours in Fig. 7 are the predicted MZ relation computed at z=0.07 for spirals and irregulars, whereas the lines are fits to the observed local mass-metallicity relation as reported by Kewley & Ellison (2008), obtained by assuming different metallicity calibrations.
Kewley & Ellison consider ![]() 28 000 star-forming galaxies of the SDSS
with derived stellar masses.
They applied 10 different metallicity calibrations to the emission lines of the spectra of this sample,
in order to investigate
the effect of the calibration on the MZ relation. Some calibrations are based on a direct method for determining
metallicity. This method, often referred to as the ``
28 000 star-forming galaxies of the SDSS
with derived stellar masses.
They applied 10 different metallicity calibrations to the emission lines of the spectra of this sample,
in order to investigate
the effect of the calibration on the MZ relation. Some calibrations are based on a direct method for determining
metallicity. This method, often referred to as the ``![]() '' method,
is based on the measure of the ratio of two lines, such as
the O4363 auroral line and the [OIII]
'' method,
is based on the measure of the ratio of two lines, such as
the O4363 auroral line and the [OIII]![]() 5007 lines and allows an estimate of the electron temperature of
the interstellar gas, finally used to determine the metallicity.
Some other calibrations are empirical, and are obtained by fitting the relation between direct
5007 lines and allows an estimate of the electron temperature of
the interstellar gas, finally used to determine the metallicity.
Some other calibrations are empirical, and are obtained by fitting the relation between direct ![]() metallicities and strong
line ratios for H
metallicities and strong
line ratios for H![]() regions, such as [NII]
regions, such as [NII]![]() 6584/H
6584/H![]() .
Finally, in other cases, mostly at high metallicity, where
.
Finally, in other cases, mostly at high metallicity, where ![]() is not measurable,
photoionization models are used to compute strong-line ratios.
Is it important to point out that each of these calibrations are valid in relatively narrow metallicity intervals (Kewley & Ellison 2008).
is not measurable,
photoionization models are used to compute strong-line ratios.
Is it important to point out that each of these calibrations are valid in relatively narrow metallicity intervals (Kewley & Ellison 2008).
In Fig. 7, the curves labeled KK04 (Kobulnicky & Kewley 2004), KD02 (Kewley & Dopita 2002) are based on theoretical methods,
the curves labeled PP04 (Pettini & Pagel 2004) and P05 (Pilyugin & Thuan 2005)
are based on empirical methods, while the D02 (Denicolo et al. 2002)
curve has been derived by means of a combined method. The sample of D02
is composed by a set of H![]() regions, some of which
have metallicities derived using the
regions, some of which
have metallicities derived using the ![]() method, while others have
empirical or theoretical metallicities.
method, while others have
empirical or theoretical metallicities.
As can be seen in Fig. 7, the choice of the metallicity calibration
plays an important role in observationally determining
the MZ relation. Kewley & Ellison (2008) outline that different calibrations
can produce very different results, concerning both
the zero-point and the slope of the observational MZ relation, as well as the location of the plateau for high-mass galaxies.
For the particular cases reported in Fig. 7, including the most extreme calibrations,
one can see that the zero point of the observed MZ relation can vary by ![]() 0.4 dex, whereas
the high-mass plateau position may vary by
0.4 dex, whereas
the high-mass plateau position may vary by ![]() 0.3 dex, without considering the extreme calibration
by Pilyugin & Thuan (2005), leading to an almost flat MZ.
0.3 dex, without considering the extreme calibration
by Pilyugin & Thuan (2005), leading to an almost flat MZ.
Concerning the predictions, here we have assumed
![]() and
and
![]() Gyr for spirals, and
Gyr for spirals, and
![]() and
and
![]() Gyr for irregulars.
However, as we will see later, for spirals and irregulars the parameters
Gyr for irregulars.
However, as we will see later, for spirals and irregulars the parameters ![]() and
and
![]() have little effect on the zero point and on the slope of the predicted
mass-metallicity relation, whereas they mostly influence the predicted dispersion of the stellar masses and of the O abundances.
As discussed in Sect. 2,
the models used for spirals and irregulars are calibrated to reproduce a large set of
chemical evolution constraints from local observations, such as the abundances observed in stars
of the Milky Way, the stellar metallicity distribution in the solar neighbourhood (Chiappini et al. 2001),
the abundance gradients in the MW and in M101 (Chiappini et al. 2003),
as well as the stellar abundances and stellar metallicity distributions
in local dwarf galaxies (Lanfranchi & Matteucci 2003). Since our models can reproduce
local independent observations, it seems appropriate to use them to find some constraints
on the best calibration method for the local observational MZ relation.
Among the different calibrations considered here, our predictions are compatible
with the MZ relations obtained by adopting the calibrations KD02, D02 and PP04.
have little effect on the zero point and on the slope of the predicted
mass-metallicity relation, whereas they mostly influence the predicted dispersion of the stellar masses and of the O abundances.
As discussed in Sect. 2,
the models used for spirals and irregulars are calibrated to reproduce a large set of
chemical evolution constraints from local observations, such as the abundances observed in stars
of the Milky Way, the stellar metallicity distribution in the solar neighbourhood (Chiappini et al. 2001),
the abundance gradients in the MW and in M101 (Chiappini et al. 2003),
as well as the stellar abundances and stellar metallicity distributions
in local dwarf galaxies (Lanfranchi & Matteucci 2003). Since our models can reproduce
local independent observations, it seems appropriate to use them to find some constraints
on the best calibration method for the local observational MZ relation.
Among the different calibrations considered here, our predictions are compatible
with the MZ relations obtained by adopting the calibrations KD02, D02 and PP04.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11756f8.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg102.png) |
Figure 8:
Redshift evolution of the MZ relation as a function of morphological type. The black points are the observations
at various redshifts. The blue and red contours repesent the regions where 100% and 75% of our predictions lie, respectively.
In the first, second and third column
the results for ellipticals, spirals and irregulars are shown, respectively.
From top to bottom and for each morphological type,
predictions and observations at four different redshifts are shown: z=0.07, z=0.7, z=2.2, z=3.5.
In this case, we have assumed a redshift of formation
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11756f9.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg103.png) |
Figure 9:
Redshift evolution of the MZ relation as a function of morphological type. Symbols and contours as in Fig. 8.
In this case, we have assumed a redshift of formation
|
| Open with DEXTER | |
The possibility to use our models to constrain the metallicity calibrations is motivated by the fact that most of the observables cited above and used to tune our models have typical errors much lower than the calibration uncertainty. For instance, the abundances observed in local stars have typical errors of 0.05-0.1 dex, in extremely rare cases greater than 0.2 dex (Cayrel et al. 2004; Spite et al. 2005). Similar uncertainties are also typical of abundances observed in the stars of local dwarf spheroidal galaxies (Shetrone et al. 2003), blue compact galaxies (Izotov & Thuan 1999), and in local early type galaxies (Thomas et al. 2005).
Concerning the calibration method used by Lee et al. (2006) for the data reported in Fig. 6,
the ![]() method was used for most
of the objects, consistent with the one of Maiolino et al. (2008) for the metallicity
range investigated by Lee et al. (2006). For a very limited number of systems, Lee et al. (2006) use the strong line method.
Given the uncertainties of various calibration methods in particular at metallicities
method was used for most
of the objects, consistent with the one of Maiolino et al. (2008) for the metallicity
range investigated by Lee et al. (2006). For a very limited number of systems, Lee et al. (2006) use the strong line method.
Given the uncertainties of various calibration methods in particular at metallicities
![]() ,
we neglect this difference and use the data by Lee et al. (2006) at face value.
,
we neglect this difference and use the data by Lee et al. (2006) at face value.
3.2 The observational data used in this work
The observational data for the MZ relation at redshits z=0.07,
z=0.7, z=2.2, and z=3.5 are taken from Kewley & Ellison (2008),
Savaglio et al. (2005), Erb et al. (2006a), and Maiolino et al. (2008),
respectively. These are all MZ relations for the gas phase metallicity,
and include only star-forming galaxies. In fact, active star formation is required
to ionize the gas which produce the nebular lines used for the metallicity
determination. In these works different diagnostics and
calibrations have been adopted, which affect the zero point and slope
of the MZ relation. This issue is discussed extensively by
Kewley & Ellison (2008), who also propose a criterion for interlacing
different calibrations. However, each of these calibration is appropriate
in different, relatively narrow metallicity ranges.
Maiolino et al. (2008) point out that the metallicy range spanned by galaxies
through the cosmic epochs is so wide (
![]() )
that no single
metallicity calibration method is appropriate to cover it. As a consequence,
Maiolino et al. (2008) define a new calibration that adopts
the electron temperature method at low metallicities (
)
that no single
metallicity calibration method is appropriate to cover it. As a consequence,
Maiolino et al. (2008) define a new calibration that adopts
the electron temperature method at low metallicities (
![]() )
and the photionization models by Kewley & Dopita (2002) at high
metallicities (
)
and the photionization models by Kewley & Dopita (2002) at high
metallicities (
![]() ). Details on this method and
the appropriateness of this calibration scale are given in Maiolino et al.
(2008). To have the metallicities of all galaxies at the various redshifts
sampled by the different studies on a consistent metallicity scale,
Maiolino et al. (2008) re-determined the
metallicities of the previous works at lower redshifts by using the new
calibrations inferred by them. Maiolino et al. (2008) also correct the
stellar masses of different studies to the same IMF.
In the following section, we will use the same data as the ones
used by Maiolino et al. (2008), together with SFR determinations at various redshifts.
As we will see later, the combined use of observational mass-metallicity measured and of SFR determinations
will allow us to put some constraints on the morphologies of the galaxies populating the observed MZ relation
at various redshifts.
). Details on this method and
the appropriateness of this calibration scale are given in Maiolino et al.
(2008). To have the metallicities of all galaxies at the various redshifts
sampled by the different studies on a consistent metallicity scale,
Maiolino et al. (2008) re-determined the
metallicities of the previous works at lower redshifts by using the new
calibrations inferred by them. Maiolino et al. (2008) also correct the
stellar masses of different studies to the same IMF.
In the following section, we will use the same data as the ones
used by Maiolino et al. (2008), together with SFR determinations at various redshifts.
As we will see later, the combined use of observational mass-metallicity measured and of SFR determinations
will allow us to put some constraints on the morphologies of the galaxies populating the observed MZ relation
at various redshifts.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11756f10.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg107.png) |
Figure 10:
Predicted redshift evolution of the MZ, (O/H) vs. SFR, and SFR vs. mass plots for ellipticals (green contours),
spirals (red contours), and irregulars (blue contours)
and as observed by various authors at z=0.07, z=0.7, z=2.2, z=3.5.
For the predictions, we have assumed a redshift of formation
|
| Open with DEXTER | |
3.3 The evolution of the mass-metallicity relation
In Fig. 8 we show
the observed redshift evolution of the MZ relation in star-forming
galaxies, as well as the predicted MZ relation for various
galactic morphological types used in this work.
The predicted MZ relations for ellipticals, spirals, and irregulars were
computed by assuming zf=3,
![]() Gyr.
From this plot, it is clear how galaxies of various morphological types occupy different regions of the MZ plot.
At any redshift, in general, elliptical galaxies present the highest stellar masses and the highest
metallicities, whereas the irregulars are the least massive galaxies,
characterised by the lowest O abundances. In this case, ellipticals appear only
at z=3.5 and at z=2.2 since, with the age dispersion of 3 Gyr as chosen here, these galaxies become passive
at redshift
Gyr.
From this plot, it is clear how galaxies of various morphological types occupy different regions of the MZ plot.
At any redshift, in general, elliptical galaxies present the highest stellar masses and the highest
metallicities, whereas the irregulars are the least massive galaxies,
characterised by the lowest O abundances. In this case, ellipticals appear only
at z=3.5 and at z=2.2 since, with the age dispersion of 3 Gyr as chosen here, these galaxies become passive
at redshift ![]() 1.4.
From Fig. 8, we can see that the majority of ellipticals show
metallicities higher than the observations, both at z=3.5 and at z=2.2.
This fact concerns only ellipticals and may
come from the growth of (O/H) vs. time being very steep for elliptical galaxies.
We investigate this
issue later in deeper detail, in Sect. 3.5. On the other hand, spiral galaxies show
metallicities that are always comparable to the values observed at various redshifts.
Irregular galaxies have low star formation rates and at high redshift their stellar masses are very small,
in general
1.4.
From Fig. 8, we can see that the majority of ellipticals show
metallicities higher than the observations, both at z=3.5 and at z=2.2.
This fact concerns only ellipticals and may
come from the growth of (O/H) vs. time being very steep for elliptical galaxies.
We investigate this
issue later in deeper detail, in Sect. 3.5. On the other hand, spiral galaxies show
metallicities that are always comparable to the values observed at various redshifts.
Irregular galaxies have low star formation rates and at high redshift their stellar masses are very small,
in general
![]() at
at ![]() .
The observed masses of the galaxies populating
the MZ relation at these redshifts are in general higher than
.
The observed masses of the galaxies populating
the MZ relation at these redshifts are in general higher than
![]() ,
hence
there is poor overlap between the observational MZ relations and our predictions for irregulars at
,
hence
there is poor overlap between the observational MZ relations and our predictions for irregulars at ![]() .
At z=0.07, the SDSS catalogue also contains a lot of galaxies with stellar masses
.
At z=0.07, the SDSS catalogue also contains a lot of galaxies with stellar masses
![]() .
The galaxies with these stellar mass values overlap with our predictions for irregular galaxies.
At
.
The galaxies with these stellar mass values overlap with our predictions for irregular galaxies.
At ![]() ,
we also note that the chosen value for the age dispersion does not allow us to
reproduce the observed data dispersion. Also this aspect will be investigated in more detail later on.
,
we also note that the chosen value for the age dispersion does not allow us to
reproduce the observed data dispersion. Also this aspect will be investigated in more detail later on.
A comparison between Figs. 8 and 9 is useful for appreciating
the effects of our parameter
![]() on our predictions for the MZ relation as a function of redshift.
The results for spirals and irregulars
are fairly insensitive to the assumption of the redshift of
formation
on our predictions for the MZ relation as a function of redshift.
The results for spirals and irregulars
are fairly insensitive to the assumption of the redshift of
formation ![]() ,
whereas for ellipticals the assumption of an high
formation redshift, such as
,
whereas for ellipticals the assumption of an high
formation redshift, such as
![]() in Fig. 9, leads to a population
of extremely high-metallicity ellipticals at z=2.2, which does not
match the MZ relation observed at this redshift by Erb et al. (2006a).
in Fig. 9, leads to a population
of extremely high-metallicity ellipticals at z=2.2, which does not
match the MZ relation observed at this redshift by Erb et al. (2006a).
It may be worth stressing that the contours are not linked to the comoving densities
of galaxies of various morphological types present at any redshift.
Such a prediction would require adopting a galaxy luminosity function or a stellar mass function as a function of redshift.
In this case, the predictions represent the number of galaxies present in each M-Z bin, normalised to the total amount of simulated
galaxies.
The blue contours enclose the region where at least 1 galaxy is present. On the other hand, the red contours
enclose the region where the total number of galaxies is 0.75 times the total number of simulated galaxies.
In order to rely on a robust statistics, we simulated ![]() 105 galaxies,
i.e. performed
105 galaxies,
i.e. performed ![]() 105 interpolations on the mass and metallicity grids according to the method described in Sect. 2.4.
However, we have verified that, in most cases, the shape of the contour plots does not strongly depend on the adopted number of simulated galaxies.
The adopted number of simulated galaxies may have some effects in regions of the plots where galaxies are rare, corresponding to
the discontinuities visible in the contours. An example is the peculiar ``comb'' feature present in the M-Z plots of elliptical galaxies
in Fig. 8, on the left bottom side of the plot.
105 interpolations on the mass and metallicity grids according to the method described in Sect. 2.4.
However, we have verified that, in most cases, the shape of the contour plots does not strongly depend on the adopted number of simulated galaxies.
The adopted number of simulated galaxies may have some effects in regions of the plots where galaxies are rare, corresponding to
the discontinuities visible in the contours. An example is the peculiar ``comb'' feature present in the M-Z plots of elliptical galaxies
in Fig. 8, on the left bottom side of the plot.
As shown by Calura et al. (2009), the use of a cosmological galaxy formation model can provide directly galaxy abundances in the MZ plot, but no indication on the galaxy morphology. In the following, we present a method to constrain the morphology of galaxies, starting from the assumption that morphology does not change with redshift.
3.4 The mass-metallicity relation of star-forming galaxies: constraints on their morphology
In this section, we focus on the observed evolution of the mass-metallicity relation for star-forming galaxies, also considering their star formation rates. The SFR provides us with a fundamental information, since, as we will see, it allows us to have further hints to the nature of the galaxies building the MZ relation. Furthermore, a study of a 3-dimensional plot linking mass, metallicity, and SFR is a crucial test of our models, which should be able to reproduce at the same time all of these properties at any redshift.
In Fig. 10, we show the observed and predicted MZ, (O/H)-SFR and SFR-Mass plots for all morphological types as a function of reshift. At each redshift, the observed quantities are compared to theoretical predictions, obtained for ellipticals, spirals, and irregular galaxies as explained in Sect. 2.4. For the observational SFRs, at z=0.07 we use the values derived for SDSS galaxies by Brinchmann et al. (2004). At z=0.7 we use observations by Maier et al. (2005) and Juneau et al. (2005), at z=2.2 we use the values by Erb et al. (2006b), and at z=3.5 we use the data by Maiolino et al. (2008). It is important to note that, at z=0.07, z=0.7, and z=3.5 we use metallicities, stellar masses, and SFRs estimated observationally for individual galaxies. In particular, at z=0.7, we use metallicity measurements only for those galaxies whose SFRs are available. At z=2.2, the measurements of O/H for the individual galaxies are not available. The only data available are represented by the rebinned MZ relation as published by Erb et al. (2006a). On the other hand, the SFRs for individual galaxies are available (Erb et al. 2006b). For these galaxies, we calculate the metallicity from the stellar mass by means of the relation found by Maiolino et al. (2008) for star-forming galaxies at z=2.2, which basically represents an analithical fit to the data of Erb et al. (2006a).
For the parameters ![]() and
and
![]() ,
we investigated several cases, in the ranges
,
we investigated several cases, in the ranges
![]() and 2 Gyr
and 2 Gyr
![]() Gyr.
In Fig. 10, we show the case computed with the fiducial set of the parameters, i.e.
Gyr.
In Fig. 10, we show the case computed with the fiducial set of the parameters, i.e.
![]() for all galaxies,
for all galaxies,
![]() Gyr for elliticals,
Gyr for elliticals,
![]() Gyr for spirals, and
Gyr for spirals, and
![]() Gyr for irregulars. It is worth noting that for irregulars and spirals, the assumption of a smaller
Gyr for irregulars. It is worth noting that for irregulars and spirals, the assumption of a smaller
![]() does not change
the shape of the MZ relation, of the O/H vs. SFR, and of the SFR vs. M* relations, but only only the predicted dispersion.
This plot shows how most of the observational constraints considered in this work
are satisfactorily reproduced once all morphological types are included.
In this figure, the predictions for ellipticals, spirals, and irregulars are shown with different colours.
At z=3.5, the observed MZ, metallicity vs. SFR and SFR vs. stellar mass plots are reproduced by our
models for elliptical galaxies, whereas the spirals and irregulars present considerably lower SFRs than the observations.
This indicates that the galaxies
observed by Maiolino et al. (2008) are likely proto-ellipticals observed during the starburst phase.
does not change
the shape of the MZ relation, of the O/H vs. SFR, and of the SFR vs. M* relations, but only only the predicted dispersion.
This plot shows how most of the observational constraints considered in this work
are satisfactorily reproduced once all morphological types are included.
In this figure, the predictions for ellipticals, spirals, and irregulars are shown with different colours.
At z=3.5, the observed MZ, metallicity vs. SFR and SFR vs. stellar mass plots are reproduced by our
models for elliptical galaxies, whereas the spirals and irregulars present considerably lower SFRs than the observations.
This indicates that the galaxies
observed by Maiolino et al. (2008) are likely proto-ellipticals observed during the starburst phase.
At z=2.2, a morphological mix of spirals and ellipticals can reproduce the MZ relation, the (O/H)-SFR and the SFR-Mass plots as observed by Erb et al. (2006a,b). However, the figure indicates that there is a limited number of observational points that are compatible with both predictions for ellipticals and spirals. This leads us to a degeneracy concerning interpretation of the observational results. A possible way to break this degeneracy is suggested later in Sect. 3.6.
At z=0.7, we slightly underestimate the metallicities in the MZ and in the
(O/H) vs. SFR plots by means of the models for spirals;
however, given the uncertainties due to calibration discussed in Sect. 3.1, we do not
consider this as a major issue.
On the other hand, we predict a positive correlation between
M* and the SFR.
The observational data seem to suggest a weaker correlation between M* and the SFR.
Furthermore, several observed SFRs are higher than the values we predict for spiral galaxies.
This discrepancy could be partly reduced by considering larger age dispersions for spirals.
For spirals, assuming a redshift of formation
![]() ,
an age dispersion of
,
an age dispersion of
![]() Gyr implies present ages
between 8.86 Gyr and one Hubble time.
Independent estimates of the present ages of spiral galaxies indicate values ranging from 5-6 Gyr up to one Hubble time
(Bell & de Jong 2000; Boissier et al. 2001), with low-mass spirals younger than high-mass discs.
This indicates
that the assumed age dispersion for spirals may be slightly underestimated, in particular for low-mass spirals.
However, the observed SFRs may be higher owing to episodic
starbursts,
possibly triggered by a dynamical process such as galaxy interactions (Alonso-Herrero et al. 1998).
These events, which are of random nature and which are not taken into account by our models, could
be the cause of the weak correlation between SFR and M* as observed at
Gyr implies present ages
between 8.86 Gyr and one Hubble time.
Independent estimates of the present ages of spiral galaxies indicate values ranging from 5-6 Gyr up to one Hubble time
(Bell & de Jong 2000; Boissier et al. 2001), with low-mass spirals younger than high-mass discs.
This indicates
that the assumed age dispersion for spirals may be slightly underestimated, in particular for low-mass spirals.
However, the observed SFRs may be higher owing to episodic
starbursts,
possibly triggered by a dynamical process such as galaxy interactions (Alonso-Herrero et al. 1998).
These events, which are of random nature and which are not taken into account by our models, could
be the cause of the weak correlation between SFR and M* as observed at ![]() .
For this reason, this explanation may be the most likely for
the discrepancy between our predictions and the observed SFRs at z=0.7.
.
For this reason, this explanation may be the most likely for
the discrepancy between our predictions and the observed SFRs at z=0.7.
At z=0.07, we can reproduce the shape of the observed MZ relation. However, the dispersion
of the data is larger than what our predictions indicate.
For spirals, by assuming
![]() Gyr, we predict a maximum dispersion of 0.2 dex.
The observed dispersion cannot be reproduced even assuming the unrealistic value of
Gyr, we predict a maximum dispersion of 0.2 dex.
The observed dispersion cannot be reproduced even assuming the unrealistic value of
![]() Gyr, i.e. equal to an Hubble time.
Also in this case,
this discrepancy
could come from the star formation histories considered here for spirals and irregulars
not taking stochastic events into account such as
episodic starburtsts, which could increase the dispersion of the observed metallicities.
However, this does not represent a major concern since, as shown in Kewley & Ellison (2008),
the dispersion also depends on the calibration.
The use of the metallicity calibration of KD02, along with some others (e.g. Pilyugin & Thuan 2005),
produce dispersions in the local MZ relation of
Gyr, i.e. equal to an Hubble time.
Also in this case,
this discrepancy
could come from the star formation histories considered here for spirals and irregulars
not taking stochastic events into account such as
episodic starburtsts, which could increase the dispersion of the observed metallicities.
However, this does not represent a major concern since, as shown in Kewley & Ellison (2008),
the dispersion also depends on the calibration.
The use of the metallicity calibration of KD02, along with some others (e.g. Pilyugin & Thuan 2005),
produce dispersions in the local MZ relation of ![]() 0.6 dex, whereas with
other calibrations the degree of dispersion in the data is lower (
0.6 dex, whereas with
other calibrations the degree of dispersion in the data is lower (![]() 0.4 dex or lower, Kewey & Ellison 2008).
For this reason, in this study,
the observed y-axis dispersion in the MZ or (O/H) vs. SFRs cannot be considered as a key-constraint to our models.
0.4 dex or lower, Kewey & Ellison 2008).
For this reason, in this study,
the observed y-axis dispersion in the MZ or (O/H) vs. SFRs cannot be considered as a key-constraint to our models.
Also at z=0.07, a large number of observed galaxies present higher SFRs than what our predictions
for spirals indicate.
However, the observed correlation between SFR and M* is reproduced by our predictions.
Interestingly, at z=0.07 the data indicate even higher SFRs than those observed at z=0.7.
Locally, very high SFR may be measured in
luminous infrared galaxies or in galaxies experiencing episodic starbursts, but not considered here.
However, it is possible that the star formation rates may be overestimated for some galaxies.
In fact, by comparing to other data of star-forming galaxies observed in the AEGIS field (Noeske et al. 2007),
the maximum observed SFRs are
![]() SFR/
SFR/![]() /yr
/yr
![]() in the lowest redshift bin, consistent with our values predicted for spirals,
whereas the SFRs of the SDSS data may be as high as
in the lowest redshift bin, consistent with our values predicted for spirals,
whereas the SFRs of the SDSS data may be as high as
![]() SFR/
SFR/![]() /yr
/yr
![]() or, in a very few cases, even higher. We suggest here that the discrepancy
may be due to different dust extinction corrections. This aspect will be investigated in detail with next release of the SDSS data.
or, in a very few cases, even higher. We suggest here that the discrepancy
may be due to different dust extinction corrections. This aspect will be investigated in detail with next release of the SDSS data.
3.5 A possible dust-obscuration bias at z = 3.5
In Sect. 3.3, when discussing the MZ relation at z=3.5,
we have seen that our predictions for ellipticals, i.e. the best candidates for the galaxies observed at z=3.5 by Maiolino et al. (2008),
indicate metallicity values higher by ![]() 0.5 dex than the observed ones.
This difference is higher than the offset due to different calibrations discussed in Sect. 3.1, since the metallicity
calibration we use in this paper provides metallicities very close to the ones of Kewley & Dopita (2002),
one of the calibrations providing
the highest metallicities in the set analysed by Kewley & Ellison (2008).
This fact concerns only the predictions for ellipticals galaxies.
The discrepancy between the metallicities predicted for most ellipticals at z=3.5 and the observed values
may be partly due to dust obscuration.
To investigate this issue, we used chemical evolution models for ellipticals
including also dust grain production and destruction.
The method of modelling dust evolution in galaxies is described in
Calura et al. (2008a).
Dust grains are produced in low-mass stars, Type Ia and Type II SNe, destroyed by SN shocks and the grain cores, are allowed to accrete mantles,
i.e. to grow by mass, during the starburst, when large reservoirs of molecular H are available for star formation. For further details on the formalism built to handle dust evolution in galaxies of different morphological types, we refer the reader to Calura et al. (2008a).
0.5 dex than the observed ones.
This difference is higher than the offset due to different calibrations discussed in Sect. 3.1, since the metallicity
calibration we use in this paper provides metallicities very close to the ones of Kewley & Dopita (2002),
one of the calibrations providing
the highest metallicities in the set analysed by Kewley & Ellison (2008).
This fact concerns only the predictions for ellipticals galaxies.
The discrepancy between the metallicities predicted for most ellipticals at z=3.5 and the observed values
may be partly due to dust obscuration.
To investigate this issue, we used chemical evolution models for ellipticals
including also dust grain production and destruction.
The method of modelling dust evolution in galaxies is described in
Calura et al. (2008a).
Dust grains are produced in low-mass stars, Type Ia and Type II SNe, destroyed by SN shocks and the grain cores, are allowed to accrete mantles,
i.e. to grow by mass, during the starburst, when large reservoirs of molecular H are available for star formation. For further details on the formalism built to handle dust evolution in galaxies of different morphological types, we refer the reader to Calura et al. (2008a).
In this case, we are interested in the dust surface density at various evolutionary phases.
In ellipticals, the dust surface mass density
![]() is
is
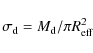 |
(7) |
where
A study of the amount of dust present in proto-ellipticals at various evolutionary stages is interesting because of the link between
dust mass and obscuration (Calzetti 2001). Stages characterised by higher dust surface densities
correspond to more dust-obscuration, hence in principle to phases more difficult to observe.
However, as pointed out before, owing to the intense UV radiation field present in H![]() regions,
dust depletion is not likely to affect the measured metallicities (Okada et al. 2008).
regions,
dust depletion is not likely to affect the measured metallicities (Okada et al. 2008).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f11.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg124.png) |
Figure 11:
Upper panel: SFR vs. stellar mass plot at z=3.5. Green, magenta and cyan regions as above.
The three dashed lines are isochrones at 0.05 Gyr, 0.1 Gyr, and 0.2 Gyr, from the
left to the right of the plot. The three solid lines are the evolutionary tracks for the three
baseline models for ellipticals considered in this paper.
Lower panel: MZ plot at z=3.5 as predicted for elliptical galaxies and as observed by Maiolino
et al. (2008). The green, cyan, and magenta regions represents our predictions for ellipticals with
dust surface mass densities in the ranges
|
| Open with DEXTER | |
In Fig. 11, we show the predictions for the MZ plot and the SFR vs. mass plot
for ellipticals at z=3.5 grouped in three different
regions, depending on the dust column density at various evolutionary stages.
In the MZ plot, most of the data points overlap with the predictions
computed for ellipticals at the earlier phases,
characterised by the lowest dust surface densities.
The fact that some stellar masses are underestimated by our predictions
may be due to the uncertainties affecting the
spectro-photometric models used to determine the observational M*. In this case, we plot the stellar
masses obtained by Maiolino et al. (2008) by adopting the spectral synthesis models of
Bruzual & Charlot (2003).
Maiolino et al. (2008) have also published stellar masses obtained with the Maraston (2005)
spectral synthesis models, in general producing stellar masses lower by ![]() 0.1 dex or less.
The use of these stellar masses would reduce the discrepancy between our predictions and the observations.
0.1 dex or less.
The use of these stellar masses would reduce the discrepancy between our predictions and the observations.
In the SFR-mass plot, most of the observations, plotted with their error bars, overlap with predictions for galaxies with intermediate dust-surface densities. An important caveat concerning the observed SFRs we should keep in mind is that, in most cases, it is likely that the observed SFRs may represent underestimations to the real values. In general, in observational studies of high-redshift galaxies, the SFRs and the ages are very uncertain parameters. The SFRs are determined from the UV luminosity by assuming that the age of each galaxy is greater than 50 Myr. By removing this constraint, the estimated SFRs may be higher by a factor of 3 for the youngest objects. As a consequence, all the points would move upwards, towards regions characterised by lower dust surface density, hence less dust-obscured.
The evolution of the ellipticals is very quick within the first 0.2 Gyr (see Fig. 1),
such as the accumulation of a large dust mass.
Figure 11 indicates that, if the AMAZE sample at z=3.5 is composed
primarily of the progenitors of ellipticals, most of these galaxies may remain
observable for times ![]() 0.2 Gyr, considering also the uncertainties
in the observed SFRs. After 0.2 Gyr, the bulk of galaxies
may become
heavily dust-obscured and cannot be detected by current surveys in the optical-UV bands.
0.2 Gyr, considering also the uncertainties
in the observed SFRs. After 0.2 Gyr, the bulk of galaxies
may become
heavily dust-obscured and cannot be detected by current surveys in the optical-UV bands.
A population of extremely dust-obscured and vigorously star-forming galaxies is represented by the SCUBA galaxies (Clements et al. 2008), very luminous in the far infrared and sub-millimetric bands owing to massive dust reprocessing, but intrinsically faint in the optical band. Schurer et al. (2009) have used the same elliptical models as described in this work to compute the photometric properties of galaxies, by taking into account both the chemical and the spectro-photometric evolution of silicate and carbon dust grains. Schurer et al. (2009) show that the general shape of the spectral energy distribution and the observed amount of dust reprocessing of SCUBA galaxies are correctly reproduced by means of our models.
In summary, for ellipticals we predict higher metallicities than the observations owing to the very fast evolution of our galaxies. A possible way to reduce the predicted metallicities could invoke longer infall times for the ellipticals. A longer infall timescale would cause a longer star formation period in each galaxy and lower star formation rates, consequently a slower growth of the metallicity versus time. Another possibility could invoke stronger outflows in the elliptical models, or metal-enhanced ouflows, where the metallicity of the ejected matter is higher than the one of the ISM. However, this would require introducing additional parameters in the elliptical model.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{11756f12.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg125.png) |
Figure 12:
Predicted MZ relations for various elements in spiral galaxies.
Here we have assumed
|
| Open with DEXTER | |
3.6 MZ relation for various elements and interstellar abundance ratios
In Fig. 12, we show our predictions for the MZ relations
for spiral galaxies, considering various chemical elements:
O, C, N, Mg, Si, Fe. Here we have assumed
![]() and
and
![]() Gyr.
These elements are produced by different stellar sources and restored into the ISM
on different timescales (see Matteucci 2001; Calura & Matteucci 2006b).
C and N are mainly produced by low and intermediate mass stars of
mass <
Gyr.
These elements are produced by different stellar sources and restored into the ISM
on different timescales (see Matteucci 2001; Calura & Matteucci 2006b).
C and N are mainly produced by low and intermediate mass stars of
mass <
![]() ,
and Mg, Si, and O are produced by massive stars, dying as Type II SNe.
However, Mg and Si are also produced by Type Ia SNe in a non negligible amount.
Finally, the bulk of Fe is produced by Type Ia SNe.
The maximum dispersion of the predicted MZ relations (i.e. the dispersion at stellar masses
,
and Mg, Si, and O are produced by massive stars, dying as Type II SNe.
However, Mg and Si are also produced by Type Ia SNe in a non negligible amount.
Finally, the bulk of Fe is produced by Type Ia SNe.
The maximum dispersion of the predicted MZ relations (i.e. the dispersion at stellar masses
![]() )
reflect the different production timescales of the elements and the lifetimes of the stars where they are synthesised.
The smallest dispersion is of
)
reflect the different production timescales of the elements and the lifetimes of the stars where they are synthesised.
The smallest dispersion is of ![]() 0.2 dex, visible for O.
Dispersions of
0.2 dex, visible for O.
Dispersions of ![]() 0.22-0.25 dex are predicted for C, N, and Mg.
The largest dispersions are predicted for the elements Si (
0.22-0.25 dex are predicted for C, N, and Mg.
The largest dispersions are predicted for the elements Si (![]() 0.3 dex) and Fe (
0.3 dex) and Fe (![]() 0.4 dex), produced in considerable amounts
by Type Ia SNe. This is related to the
lifetimes of stars exploding as Type Ia SNe spanning a very wide range, from 0.03 Gyr for
the highest masses (
0.4 dex), produced in considerable amounts
by Type Ia SNe. This is related to the
lifetimes of stars exploding as Type Ia SNe spanning a very wide range, from 0.03 Gyr for
the highest masses (
![]() )
up to a Hubble time for the lowest mass stars.
The reason for the larger scatter in the elements produced by Type Ia SNe
with respect to the
)
up to a Hubble time for the lowest mass stars.
The reason for the larger scatter in the elements produced by Type Ia SNe
with respect to the ![]() elements can be understood by looking at Fig. 2. While the Type II SN rate, scaling with the rate of production of the
elements can be understood by looking at Fig. 2. While the Type II SN rate, scaling with the rate of production of the
![]() elements, presents a peak at early times and then decreases progressively, the Type Ia SN rate presents a monotonic increase with cosmic time;
therefore, the massive production of the Fe-peak elements lasts for a longer time than the
elements, presents a peak at early times and then decreases progressively, the Type Ia SN rate presents a monotonic increase with cosmic time;
therefore, the massive production of the Fe-peak elements lasts for a longer time than the ![]() -element production.
-element production.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f13.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg129.png) |
Figure 13:
Predicted [O/Fe] vs. [Fe/H] at z=3.5 ( lower panel) and at z=2.2 ( upper panel)
for elliptical galaxies (blue areas), spirals (cyan areas), and irregulars (magenta areas).
Here we have assumed
|
| Open with DEXTER | |
3.7 The importance of abundance ratios
In Sect. 3.3, we have seen that, in the MZ, O/H vs. SFR, and SFR vs. Mass plots,
the predictions for ellipticals and spirals overlap, thus making it difficult to interpret
the observational data.
A way to overcome this issue
is to consider diagrams which involve abundance ratios between two different chemical
elements.
The abundance ratios between two chemical
elements synthesised on
different timescales
can be used as ``cosmic clocks'', providing us with information on the relative
roles of various stellar sources in the chemical enrichment of the interstellar medium (Matteucci 2001).
In particular, the study of the [![]() /Fe]
/Fe]![]() is of major importance,
owing to the difference in the timescales for
is of major importance,
owing to the difference in the timescales for ![]() -elements and Fe production.
-elements and Fe production.
In Fig. 13, we show the predicted [O/Fe] plots computed
at z=3.5 and at z=2.2 for ellipticals, spirals, and irregulars.
As one can see, in both plots the three morphological
types occupy very distinct regions. This effect stems primarily from the
star formation histories: ellipticals galaxies form quickly, by means of intense starbursts.
For this reason,
the enrichment of their ISM is dominated at low metallicity (e.g. [Fe/H![]() )
by
)
by ![]() -elements, produced by short-living massive stars.
Owing to their short and strong
starbursts, ellipticals reach high metallicities very quickly by means of Type II SNe, thus having high [
-elements, produced by short-living massive stars.
Owing to their short and strong
starbursts, ellipticals reach high metallicities very quickly by means of Type II SNe, thus having high [![]() /Fe] ratios for a wide range of [Fe/H].
On the other hand, spirals and irregulars have lower star formation
rates and more prolonged star formation histories. For this reason, they reach
high metallicities at later times, when the contribution of Type Ia SNe, producing
the bulk of Fe and exploding on long timescales, becomes important.
In principle, if measures of interstellar Fe abundances in high-redshift star-forming galaxies were accessible,
it would be possible
thanks to our chemical evolution models
to find out more about the morphology of these objects.
/Fe] ratios for a wide range of [Fe/H].
On the other hand, spirals and irregulars have lower star formation
rates and more prolonged star formation histories. For this reason, they reach
high metallicities at later times, when the contribution of Type Ia SNe, producing
the bulk of Fe and exploding on long timescales, becomes important.
In principle, if measures of interstellar Fe abundances in high-redshift star-forming galaxies were accessible,
it would be possible
thanks to our chemical evolution models
to find out more about the morphology of these objects.
The measure of metal abundances in high-redshift star-forming galaxies has become accessible in recent years, thanks to the use of 10 m telescopes for spectroscopic studies, for which bright Lyman-break galaxies observed at z>2 are particularly valuable tools. Unfortunately, in these objects the measure of abundances other than O are hampered by weak emission lines, depletion uncertainties, and unknown ionization corrections (Pettini 2004; Leitherer 2005). More promising objects for interstellar abundance ratio studies are damped-Lyman alpha galaxies, observed in absorption in the spectra of background quasars. For these systems, the use of high-resolution spectrographs allows access to weak interstellar lines, which lead to precise determination of interstellar abundances for various elements (Dessauges-Zavadsky et al. 2007). Recently, an attempt to study the possible existence of a mass-metallicity relation also in damped Lyman alpha systems has been suggested in a pioneer work by Ledoux et al. (2006). The interpretation of these data by means of models, such as the ones presented in this paper, will represent the next step in cosmic chemical evolution studies.
4 Conclusions
In this paper, we have performed a study of the evolution of the MZ relation in galaxies of different morphological types and compared our results with the most recent observational data. We used various observations achieved by several different authors, adopting a common metallicity calibration suited to our study. The measured metallicities of the galaxies, observed at redshifts from 0.07 to 3.5, span a wide range of values. We used chemical evolution models for ellipticals, spirals, and irregular galaxies. The models used here are able to reproduce the main properties of local galaxies. For each morphological type, we used three baseline models of different present-day stellar masses. We assumed that galaxy morphologies do not change with cosmic time. We developed a method to take a possible spread in the epochs of galaxy formation into account, namely in the times at which different galaxies start forming stars.Our main results can be summarised as follows.
- 1.
- Previous papers have interpreted the observed MZ-relation in terms of the simple model of galactic chemical
evolution.
In this model, the main quantity linked to the galactic metal content is the ``effective yield''
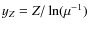 ,
where
,
where
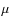 is the gas fraction.
In reality, galaxies will suffer infall/outflow and the true yield will be lower than the effective one.
The strongest assumption about the simple model is the instantaneous recycling approximation,
and if other elements than O were
considered, such as N or Fe, this hypothesis would be very poor, since both N and Fe are mainly produced
by low and intermediate mass stars on long timescales. For O, the IRA can still be acceptable.
Therefore, interpreting the MZ-relation in terms of the simple model has led several authors to conclude
that larger galaxies should have a larger true yield than less massive ones. This can be achieved in several
ways: i) by varying the IMF; ii) by decreasing the importance of outflows in more massive galaxies; and iii) by decreasing the importance of infall in more massive galaxies. In this paper, we have shown that
an MZ-relation naturally arises if less massive galaxies experience a lower star formation efficiency
(i.e. the star formation rate per unit mass of gas),
irrespective of the galactic morphological type. Galactic winds in less massive galaxies are therefore
not needed to explain the MZ-relation.
is the gas fraction.
In reality, galaxies will suffer infall/outflow and the true yield will be lower than the effective one.
The strongest assumption about the simple model is the instantaneous recycling approximation,
and if other elements than O were
considered, such as N or Fe, this hypothesis would be very poor, since both N and Fe are mainly produced
by low and intermediate mass stars on long timescales. For O, the IRA can still be acceptable.
Therefore, interpreting the MZ-relation in terms of the simple model has led several authors to conclude
that larger galaxies should have a larger true yield than less massive ones. This can be achieved in several
ways: i) by varying the IMF; ii) by decreasing the importance of outflows in more massive galaxies; and iii) by decreasing the importance of infall in more massive galaxies. In this paper, we have shown that
an MZ-relation naturally arises if less massive galaxies experience a lower star formation efficiency
(i.e. the star formation rate per unit mass of gas),
irrespective of the galactic morphological type. Galactic winds in less massive galaxies are therefore
not needed to explain the MZ-relation.
From the observational point of view, it is not clear whether the effective yield decreases or increases with galactic mass (see Tremonti et al. 2004; Erb et al. 2006a). New data on the redshift evolution of the gas fractions and of the effective yields have recently become available (Calura et al. 2008b; Mannucci et al. 2009). A forthcoming paper will focus on the study of the redshift evolution of both the gas fractions and of effective yields, considering galaxies of various morphological types.
- 2.
- At z=0.07, the slope and the zero point of the observed
MZ relation are affected by uncertainties related to the use of different metallicity calibration methods.
Our predictions, obtained with
models able to reproduce a large set of independent chemical evolution constraints for spirals and irregulars,
may be useful for constraining the best calibration method.
By means of our predictions, we suggest
the best calibrations methods for use by observers to derive gas metallicities.
Our results are consistent with the MZ relations obtained by means of the calibration
of Kewley & Dopita (2002), Denicolo et al. (2002), and Pettini & Pagel (2004).
- 3.
- From the redshift evolution of the MZ relation,
we have seen how galaxies of various morphological types
occupy different regions in the MZ plots at various redshifts. However, in these plots,
in some cases, predictions for different galaxies tend to overlap.
For this reason, the MZ plot alone cannot be used to constrain the morphology
of the observed galaxies.
- 4.
- To constrain the morphological type of the observed galaxies,
a very helpful method is to consider the
O/H vs. SFR and SFR vs. mass diagrams beside the MZ plot.
We tested how the adoption of different values for
the parameters used in this study,
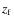 and
and
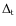 ,
influences the predictions at various redshifts.
At z=3.5, z=2.2 and z=0.7, our models can reproduce both
the metallicities and the SFRs of the observed galaxies by assuming
an average redshift of formation of
,
influences the predictions at various redshifts.
At z=3.5, z=2.2 and z=0.7, our models can reproduce both
the metallicities and the SFRs of the observed galaxies by assuming
an average redshift of formation of
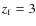 for all galaxies.
An age dispersion of
for all galaxies.
An age dispersion of
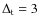 Gyr for ellipticals, compatible with the values
coming from photometric studies of the Colour-magnitude relations of early-type galaxies
in clusters and in the field,
Gyr for ellipticals, compatible with the values
coming from photometric studies of the Colour-magnitude relations of early-type galaxies
in clusters and in the field,
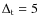 Gyr for spirals and
Gyr for spirals and
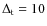 irregulars, allows
us to reproduce most of the observational constraints considered in this work.
irregulars, allows
us to reproduce most of the observational constraints considered in this work.
- 5.
- The contribution of each type of star-forming
galaxy to the MZ relation is a fuction of redshift.
At z=3.5, the observed stellar masses, metallicities and SFRs are reproduced by our models
for elliptical galaxies.
At z=2.2, the observed metallicities and SFRs indicate that the galaxies are likely to
represent a morphological mix, partly composed of spirals (or proto-spirals) and partly of
(proto-)ellipticals.
At z=0.7, we slightly underestimate the observed metallicities.
Furthermore, we tend to overestimate the observed SFRs, which, plotted against the stellar mass M*,
show a weaker correlation than our predictions.
At z=0.07, we reproduce the shape of the observed MZ relation. However, the dispersion
of the data is larger than what our predictions indicate. The discrepancies between predictions and observations
at z=0.7 and z=0.07 could be due to the fact that, in our chemical
evolution models, the star formation histories do not take into account stochastic events such as
episodic starbursts. Such events could increase the dispersion of the observed metallicities and make the
real star formation histories more irregular than the predicted ones.
In any case, this does not represent a major concern since, as shown in Kewley & Ellison (2008),
the dispersion also depends on the calibration.
Our predicted SFRs are compatible with the observed values of the SDSS galaxies, although this sample
includes objects with very high SFRs, up to
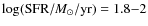 ,
which we cannot reproduce and which are sometimes
even higher than the values observed at z=0.7 in the GEMINI Deep Deep Survey (Juneau et al. 2005). A possible reason for such high SFRs could
be overestimated dust attenuation in the SDSS sample (Brinchmann, private communication).
,
which we cannot reproduce and which are sometimes
even higher than the values observed at z=0.7 in the GEMINI Deep Deep Survey (Juneau et al. 2005). A possible reason for such high SFRs could
be overestimated dust attenuation in the SDSS sample (Brinchmann, private communication).
- 6.
- At z=3.5, the majority of the predicted metallicity
values for the ellipticals are higher than the observed ones by
 0.5 dex.
This difference is greater than the offset due to the use of different calibrations.
By computing the dust-surface mass densities for our elliptical models,
we show that,
if the AMAZE sample is composed mainly of
the progenitors of local ellipticals,
most of these galaxies may remain
observable for times
0.5 dex.
This difference is greater than the offset due to the use of different calibrations.
By computing the dust-surface mass densities for our elliptical models,
we show that,
if the AMAZE sample is composed mainly of
the progenitors of local ellipticals,
most of these galaxies may remain
observable for times 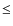 0.2 Gyr, also considering the uncertainties
in the observed SFRs. After 0.2 Gyr, the bulk of galaxies
may become
heavily dust-obscured and hardly detectable by current surveys in the optical-UV bands.
0.2 Gyr, also considering the uncertainties
in the observed SFRs. After 0.2 Gyr, the bulk of galaxies
may become
heavily dust-obscured and hardly detectable by current surveys in the optical-UV bands.
- 7.
- Our study of the MZ relation for various elements in spirals
shows that the predicted dispersion at the lowest stellar masses
depends on the lifetimes of the stellar progenitors
producing the elements. The largest dispersions in the MZ plot are predicted
for Si and Fe, which are produced by Type Ia SNe in considerable amounts.
- 8.
- An analysis of the predicted [O/Fe] plots computed at z=3.5 and at z=2.2 for ellipticals, spirals, and irregulars shows that, if interstellar Fe abundances in high-redshift star-forming galaxies were measurable, thanks to our chemical evolution models, it would be possible to have strong hints on the morphology of these objects.
It is also worth noting that Fe abundances can be obtained in absorption in gas-rich galaxies observed in the spectra of high-redshift QSOs, such as Damped-Lyman Alpha galaxies, together with the abundances of various other elements. A seminal work of Ledoux et al. (2006) points towards a possible mass-metallicity relation also in DLAs. In the future, this issue, which needs to be confirmed by further observations, will be an interesting subject for forthcoming theoretical chemical evolution studies.
Acknowledgements
G. De Lucia is acknowledged for interesting discussions. An anonymous referee is acknowledged for useful suggestions.This work was partially supported by the Italian Space Agency through contract ASI-INAF I/016/07/0. F.C. and F.M. acknowledge financial support from PRIN2007, Prot.2007JJC53X_001. C.C. acknowledgs financial support from the Swiss National Science Foundation (SNF).
References
- Alonso-Herrero, A., Rieke, M. J., & Rieke, G. H. 1998, Ap&SS, 263, 131 [NASA ADS] [CrossRef] (In the text)
- Bell, E. F., & de Jong, R. S. 2000, MNRAS, 312, 497 [NASA ADS] [CrossRef] (In the text)
- Bernardi, M., Ponman, T. J., Brown, R. J. N., et al. 1998, ApJ, 508, L43 [NASA ADS] [CrossRef] (In the text)
- Bertin, G., Saglia, R. P., & Stiavelli, M. 1992, ApJ, 384, 423 [NASA ADS] [CrossRef] (In the text)
- Boissier, S., Boselli, A., Prantzos, N., & Gavazzi, G. 2001, MNRAS, 321, 733 [NASA ADS] [CrossRef] (In the text)
- Bower, R. G., Lucey, J. R., & Ellis, R. S. 1992, MNRAS, 254, 613 [NASA ADS] (In the text)
- Bradamante, F., Matteucci, F., & D'Ercole, A. 1998, A&A, 337, 338 [NASA ADS] (In the text)
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] (In the text)
- Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] (In the text)
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
- Calura, F., & Matteucci, F. 2003, ApJ, 596, 734 [NASA ADS] [CrossRef] (In the text)
- Calura, F., & Matteucci, F. 2004, MNRAS, 350, 351 [NASA ADS] [CrossRef]
- Calura, F., & Matteucci, F. 2006a, ApJ, 652, 889 [NASA ADS] [CrossRef] (In the text)
- Calura, F., & Matteucci, F. 2006b, MNRAS, 369, 465 [NASA ADS] [CrossRef] (In the text)
- Calura, F., Matteucci, F., & Menci, N. 2004, MNRAS, 353, 500 [NASA ADS] [CrossRef]
- Calura, F., Matteucci, F., & Tozzi, P. 2007, MNRAS, 378, L11 [NASA ADS] (In the text)
- Calura, F., Pipino, A., & Matteucci, F. 2008a, A&A, 479, 669 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Calura, F., Jimenez, R., Panter, B., Matteucci, F., & Heavens, A. F. 2008b, ApJ, 682, 252 [NASA ADS] [CrossRef] (In the text)
- Clements, D. L., Vaccari, M., Babbedge, T., et al. 2008, MNRAS, 387, 247 [NASA ADS] [CrossRef] (In the text)
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] (In the text)
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] (In the text)
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] (In the text)
- Chiappini, C., Romano, D., & Matteucci, F. 2003, MNRAS, 339, 63 [NASA ADS] [CrossRef] (In the text)
- Cescutti, G., Matteucci, F., François, P, & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dalcanton, J. J. 2007, ApJ, 658, 941 [NASA ADS] [CrossRef] (In the text)
- Dalcanton, J. J., Yoachim, P., & Bernstein, R. A. 2004, ApJ, 608, 189 [NASA ADS] [CrossRef] (In the text)
- de Freitas Pacheco, J. A., Michard, R., & Mohayaee, R. 2003, in Recent Research Developments in Astronomy and Astrophysics, in press [arXiv:astro-ph/0301248] (In the text)
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] (In the text)
- De Lucia, G., Kauffman, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef] (In the text)
- Denicoló, G., Terlevich, R., & Terlevich, E. 2002, MNRAS, 330, 69 [NASA ADS] [CrossRef] (In the text)
- de Rossi, M. E., Tissera, P. B., & Scannapieco, C. 2007, MNRAS, 374, 323 [NASA ADS] [CrossRef] (In the text)
- Dessauges-Zavadsky, M., Calura, F., Prochaska, J. X., D'Odorico, S., & Matteucci, F. 2007, A&A, 470, 431 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006a, ApJ, 644, 813 [NASA ADS] [CrossRef] (In the text)
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006b, ApJ, 646, 107 [NASA ADS] [CrossRef] (In the text)
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] (In the text)
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef]
- Halliday, C. 2008, A&A, 479, 417 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Heckman, T. M. 2002, in Extragalactic Gas at Low Redshift, ed. J. S. Mulchaey, & J. Stocke (San Francisco: ASP), ASP Conf. Proc., 254, 292 (In the text)
- Izotov, Y. I., & Thuan, T. X. 1999, ApJ, 511, 639 [NASA ADS] [CrossRef] (In the text)
- Jensen, A. G., Rachford, B. L., & Snow, T. P. 2005, ApJ, 619, 891 [NASA ADS] [CrossRef] (In the text)
- Juneau, S., Glazebrook, K., Crampton, D., et al. 2005, ApJ, 619, L135 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] (In the text)
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] (In the text)
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] (In the text)
- Kobayashi, C., Springel, V., & White, S. D. M. 2007, MNRAS, 376, 1465 [NASA ADS] [CrossRef] (In the text)
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [NASA ADS] [CrossRef] (In the text)
- Köppen, J., Weidner, C., & Kroupa, P. 2007, MNRAS, 375, 673 [NASA ADS] [CrossRef] (In the text)
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] (In the text)
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] (In the text)
- Lanfranchi, G. A., & Matteucci, F. 2003, MNRAS, 345, 71 [NASA ADS] [CrossRef] (In the text)
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lee, H., Skillman, E. D., Cannon, J. M., et al. 2006, ApJ, 647, 970 [NASA ADS] [CrossRef] (In the text)
- Leitherer, C. 2005, in From Lithium to Uranium, ed. V. Hill, P. François, & F. Primas (Cambridge: CUP), IAU Symp., 228, 551 (In the text)
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] (In the text)
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, in press[arXiv:0902.2398] (In the text)
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] (In the text)
- Matteucci, F. 1992, ApJ, 397, 32 [NASA ADS] [CrossRef] (In the text)
- Matteucci, F. 1994, A&A, 288, 57 [NASA ADS] (In the text)
- Matteucci, F. 2001, The Chemical Evolution of the Galaxy (Dordrecht: Kluwer), ASSL, 253, 293 (In the text)
- Matteucci, F., & François, P. 1989, MNRAS, 239, 885 [NASA ADS] (In the text)
- Matteucci, F., & Recchi, S. 2001, ApJ, 558, 351 [NASA ADS] [CrossRef] (In the text)
- Maier, C., Lilly, S. J., Carollo, C. M., Stockton, A., & Brodwin, M. 2005, ApJ, 634, 849 [NASA ADS] [CrossRef] (In the text)
- Mouhcine, M., Gibson, B. K., Renda, A., Kawata, D. 2008, A&A, 486, 711 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [NASA ADS] [CrossRef] (In the text)
- Okada, Y., Onaka, T., Miyata, T., et al. 2008, ApJ, 682, 416 [NASA ADS] [CrossRef] (In the text)
- Pettini, M. 2004, in Cosmochemistry: The Melting Pot of the Elements, ed. C. Esteban et al. (Cambridge: Cambridge Univ. Press), 257 (In the text)
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] (In the text)
- Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] (In the text)
- Pipino, A., & Matteucci, F. 2004, MNRAS, 347, 968 [NASA ADS] [CrossRef] (In the text)
- Pipino, A., Kawata, D., Gibson, B. K., & Matteucci, F. 2005, A&A, 434, 553 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Recchi, S., Matteucci, F., D'Ercole, A., & Tosi, M. 2002, A&A, 384, 799 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Renzini, A. 2005, in The Initial Mass Function 50 Years Later, ed. E. Corbelli, & F. Palla, ASSL Conf. Ser. (Dordrecht: Springer), 327, 221
- Rix, S. A., Pettini, M., Leitherer, C., et al. 2004, ApJ, 615, 98 [NASA ADS] [CrossRef]
- Romano, D., Chiappini C., Matteucci F., & Tosi, M. 2005, A&A, 430, 491 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
- Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] (In the text)
- Scalo, J. M. 1986, FCPh, 11, 1 [NASA ADS] (In the text)
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] (In the text)
- Schurer, A., Calura, F., Silva, L., et al. 2009, MNRAS, 394, 2001 [NASA ADS] [CrossRef] (In the text)
- Shetrone, M., Venn, K. A., Tolstoy, E., & Primas, F. 2003, AJ, 125, 684 [NASA ADS] [CrossRef] (In the text)
- Shields, J. C., & Kennicutt, R. C., Jr. 1995, ApJ, 454, 807 [NASA ADS] [CrossRef]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [CrossRef] [EDP Sciences] (In the text)
- Tassis, K., Kravtsov, A. V., & Gnedin, N. Y. 2008, ApJ, 672, 888 [NASA ADS] [CrossRef] (In the text)
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] (In the text)
- Tinsley, B. M. 1980, FCPh, 5, 287 [NASA ADS]
- Tissera, P. B., De Rossi, M. E., & Scannapieco, C. 2005, MNRAS, 364, L38 [NASA ADS] (In the text)
- Tosi, M., Steigman, G., Matteucci, F., & Chiappini, C. 1998, ApJ, 498, 226 [NASA ADS] [CrossRef] (In the text)
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] (In the text)
- Van den Hoeck, L. B. & Groenwegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
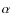 /Fe]
/Fe]![[*]](/icons/foot_motif.png)
- All the abundances between two different elements X and Y
are expressed as
![$\rm [X/Y]=\log(X/Y)-\log(X/Y)_{\odot}$](/articles/aa/full_html/2009/35/aa11756-09/img130.png) ,
where (X/Y) and (X/Y)
,
where (X/Y) and (X/Y)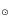 are
the ratios between the mass fractions of X and Y in the ISM and in the sun, respectively.
We use the set of solar abundances as determined by Grevesse et al. (2007).
are
the ratios between the mass fractions of X and Y in the ISM and in the sun, respectively.
We use the set of solar abundances as determined by Grevesse et al. (2007).
All Tables
Table 1: Elliptical models: parameters.
Table 2: Spiral models: parameters.
Table 3: Irregular models: parameters.
All Figures
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11756f1.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg54.png) |
Figure 1:
From top left corner, clockwise: SFR, interstellar O abundance (in units log(O/H)+12), Type II SNR,
and Type Ia SNR vs. time for the three elliptical galaxy models used in this paper.
The solid, dotted and dashed lines are the predictions for the models with total baryonic
mass
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11756f2.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg74.png) |
Figure 2:
From top left corner, clockwise: SFR, interstellar O abundance (in units log(O/H)+12), Type II SNR,
and Type Ia SNR vs. time for the three spiral galaxy models used in this paper.
The solid, dotted and dashed lines are the predictions for the models with central surface density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11756f3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg79.png) |
Figure 3:
From top left corner, clockwise: SFR, O abundance the gas (in units log(O/H)+12), Type II SNR,
and Type Ia SNR vs. time for the three irregular galaxy models used in this paper.
The solid, dotted and dashed lines are the predictions for the models with baryonic mass
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11756f4.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg94.png) |
Figure 4:
In cases 1 and 2, galaxies are still forming at the redshift of observation, i.e.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f5.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg95.png) |
Figure 5:
Predicted MZ relation for galaxies of various morphological types.
In each panel, the curves represent the evolutionary
tracks of individual galaxies of various baryonic masses. The grey areas are the
predictions obtained by means
of our method to create an almost-continuous galaxy formation and a finer stellar mass grid (see Sect. 2.4). In this case, we assumed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11756f6.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg96.png) |
Figure 6: Predicted MZ-relation at z=0 for spirals and irregulars. The figure also shows the best fit to the local MZ-relation derived by Maiolino et al. (2008) from the data of Kewley & Ellison (2008). The open squares are the data by Lee et al. (2006), who measured the MZ relation in a sample of local dwarf galaxies. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f7.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg98.png) |
Figure 7: Predicted mass-metallicity for spiral galaxies (red contours) and irregular galaxies (blue contours) at z=0.07. The solid lines of different colours are best-fit relations calculated by Kewley & Ellison (2008) using different metallicity calibrations. KK04: Kobulnicky & Kewley (2004); KD02: Kewley & Dopita (2002); D02: Denicoló (2002); PP04: Pettini & Pagel (2004); P05: Pilyugin & Thuan (2005). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11756f8.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg102.png) |
Figure 8:
Redshift evolution of the MZ relation as a function of morphological type. The black points are the observations
at various redshifts. The blue and red contours repesent the regions where 100% and 75% of our predictions lie, respectively.
In the first, second and third column
the results for ellipticals, spirals and irregulars are shown, respectively.
From top to bottom and for each morphological type,
predictions and observations at four different redshifts are shown: z=0.07, z=0.7, z=2.2, z=3.5.
In this case, we have assumed a redshift of formation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{11756f9.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg103.png) |
Figure 9:
Redshift evolution of the MZ relation as a function of morphological type. Symbols and contours as in Fig. 8.
In this case, we have assumed a redshift of formation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11756f10.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg107.png) |
Figure 10:
Predicted redshift evolution of the MZ, (O/H) vs. SFR, and SFR vs. mass plots for ellipticals (green contours),
spirals (red contours), and irregulars (blue contours)
and as observed by various authors at z=0.07, z=0.7, z=2.2, z=3.5.
For the predictions, we have assumed a redshift of formation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f11.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg124.png) |
Figure 11:
Upper panel: SFR vs. stellar mass plot at z=3.5. Green, magenta and cyan regions as above.
The three dashed lines are isochrones at 0.05 Gyr, 0.1 Gyr, and 0.2 Gyr, from the
left to the right of the plot. The three solid lines are the evolutionary tracks for the three
baseline models for ellipticals considered in this paper.
Lower panel: MZ plot at z=3.5 as predicted for elliptical galaxies and as observed by Maiolino
et al. (2008). The green, cyan, and magenta regions represents our predictions for ellipticals with
dust surface mass densities in the ranges
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{11756f12.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg125.png) |
Figure 12:
Predicted MZ relations for various elements in spiral galaxies.
Here we have assumed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11756f13.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11756-09/Timg129.png) |
Figure 13:
Predicted [O/Fe] vs. [Fe/H] at z=3.5 ( lower panel) and at z=2.2 ( upper panel)
for elliptical galaxies (blue areas), spirals (cyan areas), and irregulars (magenta areas).
Here we have assumed
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.