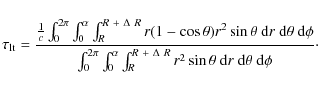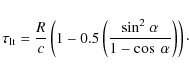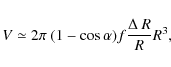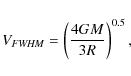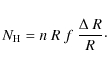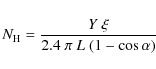| Issue |
A&A
Volume 504, Number 2, September III 2009
|
|
|---|---|---|
| Page(s) | 409 - 414 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200911639 | |
| Published online | 15 July 2009 | |
X-ray narrow line region variability as a geometry probe
The case of NGC 5548
R. G. Detmers1 - J. S. Kaastra1,2 - I. M. McHardy3
1 - SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
2 -
Astronomical Institute, University of Utrecht, Postbus 80000, 3508 TA Utrecht, The Netherlands
3 -
School of Physics and Astronomy, University of Southampton, Southampton SO17 1BJ, UK
Received 9 January 2009 / Accepted 7 July 2009
Abstract
We study the long time scale variability of the gas responsible for the X-ray narrow emission lines in the Seyfert 1 galaxy NGC 5548, in order to constrain the location and geometry of the emitting gas. Using X-ray spectra taken with the Chandra-LETGS and HETGS instruments and with XMM-Newton RGS and combining them with long-term monitoring observations of the Rossi X-ray Timing Explorer (RXTE), we perform a correlation analysis in order to try to constrain the time scale on which the narrow line emitting gas responds to variations of the continuum flux. With the inclusion of the 2007 Chandra-LETGS observation we have an additional observation at an historically low flux level. We conclude that the NLR in NGC 5548 is in the form of an ionization cone, compact in size, and located between 1 and 15 pc from the central source, depending on the exact geometry of the NLR.
Key words: galaxies: active - quasars: emission lines - galaxies: seyfert
1 Introduction
Variability in active galactic nuclei (AGN) is currently one of the best methods to study the properties of the gas surrounding super-massive black holes (SMBH). Whether it is the optical broad-line region (BLR) studied by reverberation methods (see e.g. Peterson et al. 2004) or the warm absorber as studied in the UV (for example Kraemer et al. 2006) and X-ray bands (see e.g. Netzer et al. 2003; Krongold et al. 2007), variability allows us to investigate the physical properties and location of the gas without directly resolving the inner regions of AGN.
The narrow line region (NLR) is the region responsible for the narrow forbidden and coronal lines as observed by optical and UV observations (see e.g. Kraemer et al. 1998). The density of this gas is much lower (
1010-12 m-3) than that of the BLR (1016 m-3) and the width of the lines is also much smaller, less than 1000 km
![]() .
The exact origin of this gas is unknown. The X-ray narrow line region is well known from the observations of various Seyfert 2 galaxies (Bianchi et al. 2006; Kinkhabwala et al. 2002) which show that it consists of photoionized gas in a cone-like geometry of sizes on the order of 100 pc. This gas may be the 'warm absorber' gas seen in emission, although the emission lines show a blueshift in some sources, e.g. NGC 1068 (Kinkhabwala et al. 2002), but not in others, e.g. Mrk 3 (Bianchi et al. 2005).
.
The exact origin of this gas is unknown. The X-ray narrow line region is well known from the observations of various Seyfert 2 galaxies (Bianchi et al. 2006; Kinkhabwala et al. 2002) which show that it consists of photoionized gas in a cone-like geometry of sizes on the order of 100 pc. This gas may be the 'warm absorber' gas seen in emission, although the emission lines show a blueshift in some sources, e.g. NGC 1068 (Kinkhabwala et al. 2002), but not in others, e.g. Mrk 3 (Bianchi et al. 2005).
In Seyfert 1 galaxies it is much harder, with respect to the emission line spectrum observed in Seyfert 2 galaxies, to detect the different narrow emission lines due to the bright continuum which washes out the weaker lines. The strongest line visible in a typical Seyfert 1 high-resolution X-ray spectrum is the O VII forbidden emission line, although other lines are also detected depending on the quality of the spectrum (among others Ne IX f and C V f). No significant blueshift is detected in the emission lines of NGC 5548 (Kaastra et al. 2002), while NGC 3783 shows evidence of redshifted emission lines, which could be an indication of a P-Cygni like wind (Behar et al. 2003; Kaspi et al. 2002).
Recent work on Mrk 335 (Longinotti et al. 2008), done while the source was in a low state, revealed the presence of emission lines, which the authors place at the location of the optical BLR region, which indicates that the emitting region is very compact in size. This a good example of why studying the X-ray NLR in Seyfert 1 galaxies is important. Our understanding of the location and geometry of the X-ray NLR is lacking at the moment, so constraining these is important for determining the origin of the NLR and whether it is connected to the warm absorber. The best method to do this in Type 1 AGN is to take advantage of variability and combine that with high-resolution X-ray spectroscopy.
NGC 5548 is one of the best studied AGN, with optical observations spanning 30 years (Sergeev et al. 2007), seven high-resolution X-ray observations and 11 years of monitoring with the RXTE satellite. This makes it one of the best AGN for studying the intrinsic variability of the X-ray NLR. Detmers et al. (2008) (hereafter D08) previously constrained the location of the narrow emission line region to within 1 pc of the central source (assuming a spherical NLR). This was based on the line flux change between 2002 and 2005, yielding an upper limit to the size of the emitting region of 3 lightyears. With the addition of the new 2007 observation we decided to perform a correlation analysis between the emission line fluxes and the continuum flux in order to see if the upper limit of 1 pc could be further refined and how it depends on the geometry of the NLR. We therefore present results derived from seven high-resolution X-ray observations taken by the XMM-Newton RGS and the Chandra-LETGS and HETGS instruments. These observations give us precise flux measurements for the narrow emission lines. The continuum flux history of NGC 5548 is determined using the RXTE observations, which span the period of 1996 to 2007. NGC 5548 has dropped in flux, on average, by a factor of two in the 2-10 keV band since 2002. This low ``state'' lasts up until the last measurement in September 2007. The LETGS observation of 2007 caught the source at the lowest flux level observed so far, providing us with two observations when NGC 5548 was at a low flux level (2005 being the other observation). The long RXTE lightcurve gives us the opportunity to search for correlations between the strength of the narrow emission lines and the continuum flux. We discuss the observations used and the data reduction briefly in Sect. 2. Section 3 contains the correlation analysis for the continuum and the emission lines. In Sect. 4 we derive the geometry of the NLR. We discuss our results in Sect. 5 and present our conclusions in Sect. 6.
2 Data reduction
We have used data from all 7 observations of NGC 5548 as taken with Chandra-LETGS and HETGS and with XMM-Newton RGS. Table 1 shows the date and the instruments used for each observation. Except for the 2007 LETGS data, all data have been previously published, as indicated in Table 1. The LETGS data were reduced as described in D08 and we have followed the same procedures for fitting the data and error analysis. Briefly, the data were reduced using the standard CXC pipeline up until the level 1.5 event files. After that we follow an independent procedure up to the level 2 event files. For the two RGS observations we have obtained the data using the public archive and used SAS version 8.01 to reduce the data. We use C-statistics for fitting the spectrum. Spectral fitting is done using the SPEX package (Kaastra et al. 1996).
Table 1: High resolution X-ray observations of NGC 5548.
3 Data analysis
For all observations we used the following method to obtain the O VII f line parameters. We model the spectrum with a power-law and blackbody component, absorbed by three photoionized components that are modelled using the xabs model of SPEX. Also the cosmological redshift and Galactic absorption are taken into account. We model the O VII f line with a Gaussian line, which we put outside the range of the warm absorber gas, so it is only affected by the cosmological redshift and the neutral interstellar absorption. This is the same model which was used in D08 to model the spectrum.
The 2007 LETGS observation was taken when the source was at a historically low flux level (
![]() W
W
![]() ), which unfortunately prevented any detailed analysis of the warm absorber due to low statistics. The detected O VII f line is listed in Table 2 along with previous detections in the other observations. The O VII f line flux is different with respect to D08 for the two RGS measures. This is due to the fact that the analysis in D08 was a preliminary one, which was done using the online RGS BIRD
), which unfortunately prevented any detailed analysis of the warm absorber due to low statistics. The detected O VII f line is listed in Table 2 along with previous detections in the other observations. The O VII f line flux is different with respect to D08 for the two RGS measures. This is due to the fact that the analysis in D08 was a preliminary one, which was done using the online RGS BIRD![]() archive. The new fluxes were obtained by using the above method.
archive. The new fluxes were obtained by using the above method.
Table 2:
The unabsorbed flux in ph
![]() for the O VII forbidden emission line for all high resolution spectral observations of NGC 5548.
for the O VII forbidden emission line for all high resolution spectral observations of NGC 5548.
3.1 Method and results
Reverberation mapping methods use the cross-correlation of the continuum light curve with the emission line lightcurve. However due to the sparse sampling of the emission line data we have chosen another method to address this specific problem.
The observed emission line flux does not respond instantaneously to the continuum flux changes, but due to delay effects in the source region the signal will be smeared out over a time
![]() .
Therefore we calculated the average continuum flux before each spectral observation at each of a series of time scales. For example, at the 16 days time scale the average flux between the time of an observation and 16 days before that observation is used. We assume that any variability at
.
Therefore we calculated the average continuum flux before each spectral observation at each of a series of time scales. For example, at the 16 days time scale the average flux between the time of an observation and 16 days before that observation is used. We assume that any variability at
![]() is washed out. So we have seven
is washed out. So we have seven
![]() f snapshots and a corresponding average continuum flux for different timescales.
f snapshots and a corresponding average continuum flux for different timescales.
Then we checked for possible correlations at different time scales, the shortest time scale being 7 days and the longest 1280 days. These timescales were chosen because below 7 days the RXTE lightcurve does not have enough data points in most of the bins. The upper timescale was chosen to correspond to approximately 3 years, which is the upper limit to the variability timescale (the time between the 2002 and 2005 observations). For the longest timescales, the continuum fluxes derived for some observations (basically the first five) are no longer independent of each other, due to overlap. For example, for the 1999(Dec) and 2000(Feb) observations the average continuum flux on a timescale larger than a few months will be the same, because the RXTE data points are the same.
In order to see if there is any correlation between the O VII f fluxes and the average continuum flux on a certain timescale, we perform a Spearman rank coefficient analysis for each timescale. The results are shown in Fig. 1. For all timescales the correlations are not significant. Only at the 1280 day timescale do we find a somewhat significant (95![]() )
correlation, but this method does not include the errors on the average fluxes.
)
correlation, but this method does not include the errors on the average fluxes.
![\begin{figure}
\par\includegraphics[angle= -90,width=9cm,clip]{11639fg1.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg22.png) |
Figure 1:
Spearman's |
| Open with DEXTER | |
3.2 Short term variability
For one of the spectral observations we have a whole week of observing time, namely the 2002 LETGS + HETGS observation (Kaastra et al. 2004; Steenbrugge et al. 2005). As discussed in Kaastra et al. (2004), the source experienced a large flare during the LETGS observation, which allows us to check the short term variability of the O VII f line during that week. During different time segments before, during and after the flare (Kaastra et al. 2004), we fitted a powerlaw between 17 and 24 Å and used a Gaussian line to fit the O VII f emission line. Figure 2 shows the 5 different measurements as well as the fitted average line flux (solid line). All measurements are consistent with the line flux being constant. Despite the factor of 3 variation in continuum flux, the line did not change significantly (less than 25%). This gives us a lower limit of 3 days for the variability time scale of the emission line region, which is consistent with the lower limit derived from the width of the line (D08).
![\begin{figure}
\par\includegraphics[angle= -90,width=9cm,clip]{11639fg2.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg23.png) |
Figure 2: The short time scale variability of the O VII f emission line. Labels indicate the time sequence of the data points. The solid line shows the average line flux of all five observations. |
| Open with DEXTER | |
4 Location and geometry of the NLR
There are four observational quantities based on the O VII f line properties that can be used to constrain the location of the X-ray NLR:
- the variability time
 ;
;
- the velocity width
 ;
;
- the emission measure Y;
- the ratio between the narrow
 f and
f and
 Ly
Ly line flux.
line flux.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11639fg3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg34.png) |
Figure 3:
A sketch of the geometry of the X-ray NLR region in NGC 5548. The ionization cone has a half-opening angle |
| Open with DEXTER | |
4.1 Analysis
There are several basic equations which are needed in order to constrain the location and geometry of the NLR.
First the variability time scale
![]() which is the sum of the recombination time scale and the light travel time:
which is the sum of the recombination time scale and the light travel time:
Secondly, the ionization parameter
Here L is the 1-1000 Rydberg luminosity, for which we use the value of the 2002 observation (see Table 3), R is the distance to the gas and n is the electron density.
Third, the recombination time
![]() scales inversely with the density n of the gas and depends on the recombination rate of the specific ion (Bottorff et al. 2000; Krolik & Kriss 1995):
scales inversely with the density n of the gas and depends on the recombination rate of the specific ion (Bottorff et al. 2000; Krolik & Kriss 1995):
where
The light travel time
![]() depends on the opening angle
depends on the opening angle ![]() in the following way, where we assume that the inclination angle i of the cone with respect to our line of sight is zero, i.e. we are looking straight into the cone:
in the following way, where we assume that the inclination angle i of the cone with respect to our line of sight is zero, i.e. we are looking straight into the cone:
Which results in the following expression for the light travel time in the ionization cone:
The emission measure Y depends on the hydrogen density n and the emitting volume V as
Where the factor of 1.2 is a consequence of
with f the filling factor of the emitting gas.
If we assume that the NLR gas is moving in random Keplerian orbits and has an isotropic velocity distribution, we can determine the minimum distance from the upper limit on the linewidth of the O VII f emission line using the following equation (Netzer 1990):
with M the mass of the supermassive black hole and
We use the observed luminosity of the O VII f line (
![]() W) to determine Y. This is done using an XSTAR run with log
W) to determine Y. This is done using an XSTAR run with log ![]() ,
,
![]() W and a temperature
T = 35 000 K (Steenbrugge et al. 2005). We obtain
W and a temperature
T = 35 000 K (Steenbrugge et al. 2005). We obtain
![]() m-3.
m-3.
Table 3: Important parameters of NGC 5548.
Inserting the observed parameter values as listed in Table 3 into (2)-(1), these equations can be rewritten as functions of R and ![]() only:
only:
-
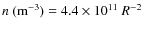 ;
;
-
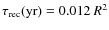 ;
;
-
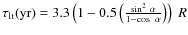 ;
;
-
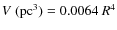 ;
;
-
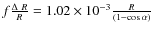 ;
;
-
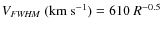 ;
;
-
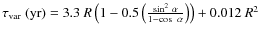 .
.
The limits on the three observational quantities that can be used to constrain the location of the X-ray NLR are:
-
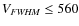 km
km
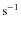 (from Gaussian fit to emission line);
(from Gaussian fit to emission line);
-
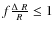 (by definition due to density assumption);
(by definition due to density assumption);
-
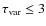 years (see D08).
years (see D08).
We can further constrain the location of the NLR if we assume that the warm absorber and the narrow line emitting gas are one and the same. The average column density can be written as
Using the expression for f
For
If we make the assumption that the gas that produces the
![]() narrow lines also produces the X-ray narrow lines, we get an immediate estimate of the distance from the FWHM of the
narrow lines also produces the X-ray narrow lines, we get an immediate estimate of the distance from the FWHM of the
![]() lines, since they are resolved in the UV. Depending on the assumed model (covered or uncovered NLR, see Brotherton et al. 2002), the FWHM is either 432
lines, since they are resolved in the UV. Depending on the assumed model (covered or uncovered NLR, see Brotherton et al. 2002), the FWHM is either 432 ![]() 12 km
12 km
![]() or 6
or 6![]() km
km
![]() .
These values lead to estimates of R of 2 pc or 0.9 pc, respectively.
.
These values lead to estimates of R of 2 pc or 0.9 pc, respectively.
![\begin{figure}
\includegraphics[angle= -90,width=9cm,clip]{11639fg4.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg76.png) |
Figure 4:
The geometry of the NLR, based on an ionization cone model with half opening angle |
| Open with DEXTER | |
From the minimum value for R of 1.2 pc, it follows that the recombination time scale of the O VII f emitting gas is at least 50 days. However from the lack of response of the O VII f line to the continuum flux on different timescales we can in principle refine the lower limit of response timescale
![]() .
Even though the continuum for the first 5 observations can vary a factor 1.5 between each observation up to a timescale of 600 days, the O VII f line flux is consistent with being constant throughout these five observations. However the line flux for the two RGS observation is a factor of 1.5 higher than the others, if the errors are not considered. This is consistent with the picture that there can be small variations in the line flux on smaller timescales than 3 years, but that a large drop in average continuum flux for a long period is needed for the O VII f line to respond significantly (like in the last two observations in 2005 and 2007). There is also the question of whether the gas is in ionization equilibrium. The continuum of NGC 5548 varies on time scales as fast as
.
Even though the continuum for the first 5 observations can vary a factor 1.5 between each observation up to a timescale of 600 days, the O VII f line flux is consistent with being constant throughout these five observations. However the line flux for the two RGS observation is a factor of 1.5 higher than the others, if the errors are not considered. This is consistent with the picture that there can be small variations in the line flux on smaller timescales than 3 years, but that a large drop in average continuum flux for a long period is needed for the O VII f line to respond significantly (like in the last two observations in 2005 and 2007). There is also the question of whether the gas is in ionization equilibrium. The continuum of NGC 5548 varies on time scales as fast as ![]() 1 day, with a relative amplitude of order unity (see also Sect. 3.2 ). Therefore, strictly speaking, the gas cannot be in ionization equilibrium. However, it can be considered to be in quasi-equilibrium with the average continuum
1 day, with a relative amplitude of order unity (see also Sect. 3.2 ). Therefore, strictly speaking, the gas cannot be in ionization equilibrium. However, it can be considered to be in quasi-equilibrium with the average continuum ![]()
![]() earlier.
earlier.
5 Discussion
From Fig. 4 we can already rule out several options for the geometry of the NLR. A spherical NLR is not possible, since the opening angle ![]() is 180 degrees in that case. The upper limit on
is 180 degrees in that case. The upper limit on
![]() along with the lower limit from
along with the lower limit from
![]() rule out a half opening angle larger than
rule out a half opening angle larger than ![]() 100 degrees, but anything larger than 90 degrees is unlikely, considering that the accretion disk is located at
100 degrees, but anything larger than 90 degrees is unlikely, considering that the accretion disk is located at
![]() degrees and thus blocks the line of sight to the other side. Therefore the most likely geometry for the NLR is an ionization cone, as observed in Seyfert 2 galaxies. The half opening angle of these ionization cones can typically vary between 20 and 45 degrees (Schmitt et al. 2001). Applying this additional constraint to the location of the NLR, we find that R is between 1.2 and 12 pc.
degrees and thus blocks the line of sight to the other side. Therefore the most likely geometry for the NLR is an ionization cone, as observed in Seyfert 2 galaxies. The half opening angle of these ionization cones can typically vary between 20 and 45 degrees (Schmitt et al. 2001). Applying this additional constraint to the location of the NLR, we find that R is between 1.2 and 12 pc.
The above constraints on the location have been obtained with the assumption that
![]() .
This assumption is based on a constant mass outflow rate and on Seyfert 2 ionization cone studies (Bianchi et al. 2006). Since we are not sure if the NLR is really outflowing, the second argument is the strongest indication that this assumption is correct as it is based on photoionization studies by comparing the optical [O III] emitting region to the soft X-ray emitting region. They conclude that constant density models are excluded and that a steep density profile (
.
This assumption is based on a constant mass outflow rate and on Seyfert 2 ionization cone studies (Bianchi et al. 2006). Since we are not sure if the NLR is really outflowing, the second argument is the strongest indication that this assumption is correct as it is based on photoionization studies by comparing the optical [O III] emitting region to the soft X-ray emitting region. They conclude that constant density models are excluded and that a steep density profile (
![]() )
is preferred. Another study of six Seyfert 1 galaxies in the optical show different results however for the density slopes (Bennert et al. 2006). Some Seyfert 1 galaxies show a slope
)
is preferred. Another study of six Seyfert 1 galaxies in the optical show different results however for the density slopes (Bennert et al. 2006). Some Seyfert 1 galaxies show a slope ![]() r-1, others a slope
r-1, others a slope ![]() r-2. When compared to Seyfert 2 galaxies in their sample, the Seyfert 1's on average show a steeper slope, but given the fact that there are only six sources, the scatter for individual sources can be quite large. Also it is not certain that the extended NLR that they probe (scales of
r-2. When compared to Seyfert 2 galaxies in their sample, the Seyfert 1's on average show a steeper slope, but given the fact that there are only six sources, the scatter for individual sources can be quite large. Also it is not certain that the extended NLR that they probe (scales of ![]() 100's pc) is the same gas as the high-ionization X-ray gas we detect in NGC 5548. A better method to investigate the NLR properties would be using a grid of photoionization models for NGC 5548, but given the fact that we only have two lines in the X-ray and two lines in the UV to model, this would be too detailed for the current data we have. A future article where this analysis can be extended to include other Type 1 AGN would be better suited for this level of detail.
100's pc) is the same gas as the high-ionization X-ray gas we detect in NGC 5548. A better method to investigate the NLR properties would be using a grid of photoionization models for NGC 5548, but given the fact that we only have two lines in the X-ray and two lines in the UV to model, this would be too detailed for the current data we have. A future article where this analysis can be extended to include other Type 1 AGN would be better suited for this level of detail.
The constraint on the NLR distance in NGC 5548 places it at a much greater distance than Longinotti et al. (2008) obtained in Mrk 335. However the line ratios of the oxygen triplet are different in Mrk 335 than in NGC 5548. The intercombination line is stronger than the forbidden line in Mrk 335, while in NGC 5548 this clearly is not the case. The line widths they find for the emission lines are also a factor of ![]() 3 greater than those of the O VII f in NGC 5548. These two clues tell us that the emitting gas most likely is not the same in both sources. The gas in Mrk 335, has much more in common with the BLR (high density, large velocity width) than the NLR which we observe in NGC 5548.
3 greater than those of the O VII f in NGC 5548. These two clues tell us that the emitting gas most likely is not the same in both sources. The gas in Mrk 335, has much more in common with the BLR (high density, large velocity width) than the NLR which we observe in NGC 5548.
From the observed warm absorber column density, we conclude that the warm absorber and the NLR gas could be the same given the uncertainties on the column density of the absorber (![]() 30%). However, the connection between absorber and emitter is still uncertain at this moment and will be hard to establish without first independently establish the geometry of both the absorbing and the emitting gas.
30%). However, the connection between absorber and emitter is still uncertain at this moment and will be hard to establish without first independently establish the geometry of both the absorbing and the emitting gas.
The connection between the narrow UV line emitting gas and the X-ray emitting gas is speculative at best at this moment, although the FWHM of both systems is similar and both the UV and X-ray line ratios can be produced by gas with a single ionization parameter (log ![]() ). A more detailed photoionization model, which takes into account the warm absorber and the line emission in both UV and X-ray, with the correct geometry and outflow velocities and time-dependent ionization effects, would be invaluable in comparing the UV and X-ray spectral information from the observations to the model predictions. However such a work is beyond the scope of this paper, since its main purpose is demonstrating the usage of variability as a geometry probe of the X-ray NLR.
Recently, Crenshaw et al. (2009) have studied high-resolution UV spectra of NGC 5548, including one in an extremely low flux state in February 2004. This low flux spectrum reveals for the first time the presence of an intermediate line region (ILR) in NGC 5548. The C IV emission line of this component has a FWHM of 700 km
). A more detailed photoionization model, which takes into account the warm absorber and the line emission in both UV and X-ray, with the correct geometry and outflow velocities and time-dependent ionization effects, would be invaluable in comparing the UV and X-ray spectral information from the observations to the model predictions. However such a work is beyond the scope of this paper, since its main purpose is demonstrating the usage of variability as a geometry probe of the X-ray NLR.
Recently, Crenshaw et al. (2009) have studied high-resolution UV spectra of NGC 5548, including one in an extremely low flux state in February 2004. This low flux spectrum reveals for the first time the presence of an intermediate line region (ILR) in NGC 5548. The C IV emission line of this component has a FWHM of 700 km
![]() and is located at
and is located at ![]() 1 pc from the nucleus. Crenshaw et al. (2009) model this gas with
U= 10-1.5 (log
1 pc from the nucleus. Crenshaw et al. (2009) model this gas with
U= 10-1.5 (log ![]() ),
n = 1013 m-3, a column density of
),
n = 1013 m-3, a column density of
![]() m-2 and a global covering factor of 0.06. The FWHM and location of the O VII f line allow for the possibility that the X-ray emission comes from the same ILR region or only slightly further out. The main difference is that the X-ray emitting region has a
m-2 and a global covering factor of 0.06. The FWHM and location of the O VII f line allow for the possibility that the X-ray emission comes from the same ILR region or only slightly further out. The main difference is that the X-ray emitting region has a ![]() 100 times lower density and a
100 times lower density and a ![]() 10 times higher ionization parameter. This would be consistent with the UV emission coming from dense clumps that are embedded in a low density hotter gas which produces the X-ray emission.
The O VII f line centroid as observed by the LETGS agrees with the surrounding continuum to within 0.217
10 times higher ionization parameter. This would be consistent with the UV emission coming from dense clumps that are embedded in a low density hotter gas which produces the X-ray emission.
The O VII f line centroid as observed by the LETGS agrees with the surrounding continuum to within 0.217
![]() ,
which corresponds to 106 pc at the distance of NGC 5548 (Kaastra et al. 2003), giving a independent upper limit to the size of the NLR.
,
which corresponds to 106 pc at the distance of NGC 5548 (Kaastra et al. 2003), giving a independent upper limit to the size of the NLR.
We therefore conclude that the NLR in NGC 5548 is compact in size, is in the form of clouds with a small covering factor or a narrow stream, has a cone-like geometry and is located between 1 and 15 pc from the central source, which is much smaller than the observed extended emission cones in Seyfert 2 galaxies (Guainazzi et al. 2008; Kinkhabwala et al. 2002). One reason for this compactness could be that in Seyfert 2 galaxies, we can not observe the high density, high emissivity NLR gas that we observe here, since the torus blocks our view. So we are only seeing the lower density, low emissivity gas in Seyfert 2 galaxies, which is visible due to the very low continuum flux. From optical studies it is clear that the high-ionization as well as the high critical density lines tend to be stronger in Seyfert 1's, see e.g. Bennert et al. (2006). This is consistent with the compact size of the NLR we find in NGC 5548.
6 Conclusions
This is the first time that the long-term variability of the X-ray narrow line region has been studied in an AGN. NGC 5548 is the best studied AGN in the X-rays on a long time scale and has the best sampled RXTE lightcurve which last 11 years. With this very rich set of data and the large change in flux after 2002, we are able to put a constraint on the location and geometry of the X-ray NLR. For NGC 5548 we favor a NLR which is located between 1 and 15 pc from the central source, is compact in the form of clouds or a narrow stream and has the geometry of an ionization cone. This is consistent with the picture sketched in Seyfert 2 galaxies, although the distance from the central source is much smaller by almost two orders of magnitude. The geometry and location of the NLR in Seyfert 1 galaxies can be further refined by a long-term monitoring program with regular (every few months) high resolution spectral observations of sufficientlyvariable sources. It will be interesting to study a larger sample of NLR emission lines in Seyfert 1 galaxies, to see if they all are of similar size or if NGC 5548 is unique with its compact NLR.
Acknowledgements
SRON is supported financially by NWO, the Netherlands Organization for Scientific Research. R.G.D. would like to thank Elisa Costantini for discussion of this work.
References
- Behar, E., Rasmussen, A. P., Blustin, A. J. et al. 2003, ApJ, 598, 232 [NASA ADS] [CrossRef]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006, A&A, 459, 55 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bentz, M. C., Denney, K. D., Cackett, E. M. et al. 2007, ApJ, 662, 205 [NASA ADS] [CrossRef]
- Bianchi, S., Miniutti, G., Fabian, A. C., & Iwasawa, K. 2005, MNRAS, 360, 380 [NASA ADS] [CrossRef] (In the text)
- Bianchi, S., Guainazzi, M., & Chiaberge, M. 2006, A&A, 448, 499 [NASA ADS] [CrossRef] [EDP Sciences]
- Bottorff, M. C., Korista, K. T., & Shlosman, I. 2000, ApJ, 537, 134 [NASA ADS] [CrossRef]
- Brotherton, M. S., Green, R. F., Kriss, G. A. et al. 2002, ApJ, 565, 800 [NASA ADS] [CrossRef] (In the text)
- Crenshaw, D. M., Kraemer, S. B., Schmitt, H. R. et al. 2009, ArXiv e-prints (In the text)
- Detmers, R. G., Kaastra, J. S., Costantini, E., McHardy, I. M., & Verbunt, F. 2008, A&A, 488, 67 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Guainazzi, M., Barbarisi, I., Bianchi, S., Osuna, P., & Salgado, J. 2008, AdSpR, 41, 1998 [NASA ADS]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, ed. K. Yamashita & T. Watanabe, 411 (In the text)
- Kaastra, J. S., Steenbrugge, K. C., Raassen, A. J. J. et al. 2002, A&A, 386, 427 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kaastra, J. S., Steenbrugge, K. C., Brinkman, A. C. et al. 2003, in Active Galactic Nuclei: From Central Engine to Host Galaxy, ed. S. Collin, F. Combes, & I. Shlosman, ASPC, 290, 101 (In the text)
- Kaastra, J. S., Steenbrugge, K. C., Crenshaw, D. M. et al. 2004, A&A, 422, 97 [NASA ADS] [CrossRef] [EDP Sciences]
- Kaspi, S., Brandt, W. N., George, I. M. et al. 2002, ApJ, 574, 643 [NASA ADS] [CrossRef]
- Kinkhabwala, A., Sako, M., Behar, E. et al. 2002, ApJ, 575, 732 [NASA ADS] [CrossRef]
- Kraemer, S. B., Crenshaw, D. M., Filippenko, A. V., & Peterson, B. M. 1998, ApJ, 499, 719 [NASA ADS] [CrossRef] (In the text)
- Kraemer, S. B., Crenshaw, D. M., Gabel, J. R., Kriss, G. A. et al. 2006, ApJS, 167, 161 [NASA ADS] [CrossRef] (In the text)
- Krolik, J. H., & Kriss, G. A. 1995, ApJ, 447, 512 [NASA ADS] [CrossRef]
- Krongold, Y., Nicastro, F., Elvis, M. et al. 2007, ApJ, 659, 1022 [NASA ADS] [CrossRef]
- Longinotti, A. L., Nucita, A., Santos-Lleo, M., & Guainazzi, M. 2008, A&A, 484, 311 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Netzer, H. 1990, in 20. Saas-Fee Advanced Course of the Swiss Society for Astrophysics and Astronomy: Active galactic nuclei, ed. R. D. Blandford, H. Netzer, L. Woltjer, T. J.-L. Courvoisier, & M. Mayor, 57 (In the text)
- Netzer, H., Kaspi, S., Behar, E. et al. 2003, ApJ, 599, 933 [NASA ADS] [CrossRef]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., Kaspi, S. et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] (In the text)
- Schmitt, H. R., Antonucci, R. R. J., Ulvestad, J. S. et al. 2001, ApJ, 555, 663 [NASA ADS] [CrossRef] (In the text)
- Sergeev, S. G., Doroshenko, V. T., Dzyuba, S. A. et al. 2007, ApJ, 668, 708 [NASA ADS] [CrossRef] (In the text)
- Steenbrugge, K. C., Kaastra, J. S., de Vries, C. P., & Edelson, R. 2003, A&A, 402, 477 [NASA ADS] [CrossRef] [EDP Sciences]
- Steenbrugge, K. C., Kaastra, J. S., Crenshaw, D. M. et al. 2007, ApJ, 668, 708 2005, A&A, 434, 569 [NASA ADS] [CrossRef] [EDP Sciences]
- Tarter, C. B., Tucker, W. H., & Salpeter, E. E. 1969, ApJ, 156, 943 [NASA ADS] [CrossRef] (In the text)
- Yaqoob, T., George, I. M., Nandra, K. et al. 2001, ApJ, 546, 759 [NASA ADS] [CrossRef]
Footnotes
All Tables
Table 1: High resolution X-ray observations of NGC 5548.
Table 2:
The unabsorbed flux in ph
![]() for the O VII forbidden emission line for all high resolution spectral observations of NGC 5548.
for the O VII forbidden emission line for all high resolution spectral observations of NGC 5548.
Table 3: Important parameters of NGC 5548.
All Figures
![\begin{figure}
\par\includegraphics[angle= -90,width=9cm,clip]{11639fg1.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg22.png) |
Figure 1:
Spearman's |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle= -90,width=9cm,clip]{11639fg2.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg23.png) |
Figure 2: The short time scale variability of the O VII f emission line. Labels indicate the time sequence of the data points. The solid line shows the average line flux of all five observations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11639fg3.eps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg34.png) |
Figure 3:
A sketch of the geometry of the X-ray NLR region in NGC 5548. The ionization cone has a half-opening angle |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[angle= -90,width=9cm,clip]{11639fg4.ps}
\end{figure}](/articles/aa/full_html/2009/35/aa11639-09/Timg76.png) |
Figure 4:
The geometry of the NLR, based on an ionization cone model with half opening angle |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



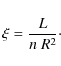
![\begin{displaymath}
\tau_{{\rm rec}} = \left({\alpha_{{\rm r}}(X_{i})~n~(X_{i}) ...
..._{{\rm r}}(X_{i})}\right]}\right)^{-1} \equiv a~(T,\xi)~n^{-1}
\end{displaymath}](/articles/aa/full_html/2009/35/aa11639-09/img38.png)