Thermal modeling of the active Centaur P/2004 A1 (LONEOS)

M. T. Capria; A. Coradini; M. C. De Sanctis; E. Mazzotta Epifani; P. Palumbo

doi:10.1051/0004-6361/20078106

Home

All issues

Volume 504 / No 1 (September II 2009)

A&A, 504 1 (2009) 249-258

Full HTML

Free Access

Issue		A&A Volume 504, Number 1, September II 2009


Page(s)		249 - 258
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/20078106
Published online		15 July 2009

Thermal modeling of the active Centaur P/2004 A1 (LONEOS)

M. T. Capria¹ - A. Coradini² - M. C. De Sanctis¹ - E. Mazzotta Epifani³ - P. Palumbo⁴

1 - INAF - Istituto di Astrofisica Spaziale (IASF), via del Fosso del Cavaliere, 00133 Rome, Italy
2 - INAF - Istituto per la Fisica del Plasma nello Spazio (IFSI), via del Fosso del Cavaliere, 00133 Rome, Italy
3 - INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
4 - Universitá Parthenope, Dip. Scienze applicate, Centro Direzionale Isola C4, 80143 Napoli, Italy

Received 18 June 2007 / Accepted 18 May 2009

Abstract
Context. The Centaurs are a dynamical class of minor bodies in the Solar System, moving on chaotic orbits with perihelion lying between Jupiter and Neptune orbits. P/2004 A1 (LONEOS) is a recently discovered object belonging to this class, observed at the TNG telescope in La Palma (Canary Islands) when it was at the heliocentric distance $R_{\rm h}$ of 5.54 AU, but it already displayed a well-developed coma and a long, sharp tail-like structure.
Aims. We want to investigate whether it is possible to explain the strong activity of this body in terms of the usual sublimation mechanisms.
Methods. We simulated the thermal evolution of LONEOS using a nucleus thermal evolution and differentiation model and took into account that it is being injected for the first time on an inner orbit as a consequence of a close encounter with Saturn experienced in 1992.
Results. We show that, considering its peculiar dynamical history, it is possible to explain the activity of this Centaur with the sublimation of very volatile ices.

Key words: comets: individual: P/2004 A1 (LONEOS) - comets: general - Kuiper Belt

1 Introduction: the unusual activity of P/2004 A1 (LONEOS)

The Centaurs are a dynamical class of minor bodies in the Solar System, moving on highly chaotic orbits with perihelion lying between Jupiter's and Neptune's orbits. They are brief residents of the region between the gas giant planets, with calculated orbital lifetimes of less than 10⁷ years (Holman & Wisdom 1993), and are considered on the way to becoming part of the Jupiter family comets (Levison & Duncan 1997). They can therefore provide easier access to the far regions of our Solar System, and analysis of their dynamical and physical properties can give information about the primordial processes that dominated the early solar nebula.

As of January 2009, more than 100 objects have been classified as pertaining to the Centaur family. Their numbers keep growing, thanks to the dedicated surveys of the ecliptic programmed and executed with the aim of discovering and characterizing new outer Solar System objects (for the most recent survey analyses, see Bernstein et al. 2004; Elliot et al. 2005; Petit et al. 2006).

Centaurs reside in a region of the Solar System where many volatile species begin to have significant sublimation rates (Crovisier 1999; Meech & Svoren 2005): the majority of Centaurs have an asteroidal aspect, without evidence of coma, but several examples of cometary activity have been observed among the group, as summarized in Table 1.

Table 1: Active Centaurs (as of January 2009).

The first important case is that of (2060) Chiron, whose resolved coma was reported after its discovery (Meech & Belton 1989; Hartmann et al. 1990) and fully analyzed (Luu & Jewitt 1990; Capria et al. 2000b) in order to investigate the cause of its cometary activity. Its dust environment was characterized (Fulle 1994) by applying a numerical inverse model of comet dust tails that also takes the fast nucleus rotation into account. This model has been also used to characterize the dust environment of the giant comet (now considered pertaining to the Centaur family) 29P/S-W 1 (Fulle 1992), which has a persistent coma, but with a morphology changing on a short time scale (weeks). Other interesting cases of cometary activity in the Centaur family are summarized in Mazzotta Epifani et al. (2006, 2007, 2008).

One of the more recently discovered active Centaurs is the object P/2004 A1 (LONEOS). It was discovered on January 13, 2004 (Green 2004; Skiff et al. 2004; Descour et al. 2004) on CCD images taken in the course of the LONEOS (Lowell Observatory Near-Earth Object Search) program with the 0.59 m Schmidt telescope. The discovery was confirmed on 1.8-m telescope frames, where the object showed a 3" well-condensed coma and a 12" tail. The object was identified as a comet. Several subsequent observations (Ticha et al. 2004; Naves et al. 2004; Tesi et al. 2004; Buzzi et al. 2004; Cremaschini et al. 2004) allowed the orbital characteristics of the object to be defined as pertaining to the family of Centaurs. The orbital elements of P/2004 A1 (LONEOS) are reported in Table 2.

Table 2: Orbital parameters of the active Centaur P/2004 A1 (LONEOS).

The coma of P/2004 A1 (LONEOS) has been deeply analyzed just after its first perihelion passage on the new orbit (Mazzotta Epifani et al. 2006). It was observed at the Italian Telescopio Nazionale Galileo (TNG) in La Palma (Canary Islands) on April 3rd, 2005, when it was at heliocentric distance $R_{\rm h}$ of 5.54 AU and at geocentric distance $\Delta$ of 4.69 AU. The Centaur displayed a well-developed coma and a long, sharp, tail-like structure elongated almost in the solar direction (perspective anti-tail). This thin spike extends at least up to $1.5 \times 10^5$ km, and it has been identified as a neck-line (Kimura & Liu 1977). With its value of $R_{\rm mag} = 18.56 \pm 0.05$ (in an aperture diameter of 5"), P/2004 A1 (LONEOS) is the darkest active Centaur in the R band among the observed sample. The Af $\rho$ values (cm) (A'Hearn et al. 1984) (where A is the average grain albedo, f the filling factor in the aperture field of view, and $\rho$ the linear radius of the aperture at the comet, i.e. the sky-plane radius) range from 288 to 334 cm. These results indicate a significant dust production rate: values found at a heliocentric distance of 5.5 AU are nearly the same as those found for several active comets at much lower heliocentric distances: 19P/Borrelly, 400-500 cm at 1.4 AU (Schleicher et al. 2003); 81P/Wild 2, $\sim$ 350 cm at 2.1 AU (Schulz et al. 2003); 21P/Giacobini-Zinner, 300-400 cm at 1 AU (Lara et al. 2003); 67P/Churyumov-Gerasimenko, $\sim$ 400 cm at 1.2 AU (Weiler et al. 2004).

The unusually high (as compared to other minor bodies at the same heliocentric distance) level of activity for the Centaur P/2004 A1 (LONEOS) is also confirmed by the results of the application of the same inverse dust tail model applied to other active Centaurs and several short-period comets. The model is extensively described in Fulle (1989) and Epifani et al. (2001). Here we recall only that the approach of the model consists of two main steps: (i) computing the model dust tail and (ii) fitting it to the observed tail and deriving the dust parameters. The solution of the fit gives sampled values of the dust loss rate, $\dot{M}(t)$ , of the size distribution n(d,t), and of the Af $\rho$ . The results of the application of the model to the active Centaur P/2004 A1 (LONEOS) (Mazzotta Epifani et al. 2006) describe the dust environment of the target and the time evolution of its coma and tail in the past years:

1.: well-established orbit computations allow us to derive that the dust tail observed on April 2005 should be composed of large grains ( 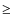$\geq$ 1 cm);
2.: the dust mass-loss rate remained almost constant in the past ten years, with values between 100 and 200 kg s^-1.

Table 3: Changes in the P/2004 A1 (LONEOS) orbital parameters due to Saturn's close encounter.

The analysis of the dynamical history of P/2004 A1 (LONEOS) by means of the JPL Horizons Ephemeris System shows that the orbit that it had followed for hundreds of years changed almost abruptly in 1992, when it experienced a close encounter (0.03 AU) with Saturn (see also Hahn et al. 2006). Table 3 summarizes the orbital change. The perihelion distance dropped from 9.8 to 5.46 AU, and the aphelion distance dropped from 14.6 to 10.4 AU. The inclination raised in few months from 11.4 to 18 degrees, then stabilized to 8 degrees. Figure 1 shows the variation in some of the Centaur orbital parameters from 1954 to the present day. Figure 2 shows the evolution of the heliocentric distance of P/2004 A1 (LONEOS) from 1900 to 2006. The body has now entered, for the first time, the inner part of the Solar System along the new orbit and reached the perihelion on August 2004.

It would almost be straightforward to attribute the unusually high activity of this comet to this change in the orbital parameters. An onset of or an increase in the activity of comets at $R_{\rm h} > 3{-}4$ AU in similar cases has been already observed (Meech & Svoren 2005; Licandro et al. 2000). On the other hand, observations of a large sample of short period comets at large heliocentric distances show that the hypothesis of distant activity induced by changes in perihelion distance cannot be univocally invoked to explain the formation of coma and even dust tail at $R_{\rm h} > 3{-}4$ AU (Mazzotta Epifani et al. 2008).

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg1.eps} \end{figure}$	Figure 1: Variation in the orbital parameters of P/2004 A1 (LONEOS). a) perihelion distance (long-dashed line), aphelion distance (dashed line), and inclination (continuous line) from 1954 to 1995; b) expanded version of top left plot around the close encounter time for perihelion distance; c) same as b) for aphelion distance; d) same as b) for inclination.
Open with DEXTER

2 Answers through nucleus thermal modeling

Looking at the activation temperatures for the onset of some physical processes relevant to comet activity, shown in Table 4, and comparing them to Figs. 2 and 3 (showing the variation of surface temperature at the equator from 1972 to 2006), it is clear that the activity of the Centaur LONEOS cannot be driven, at least not mainly driven, by water ice sublimation, but it must be driven by the sublimation of much more volatile ices. The ideal candidate is CO, one of the more abundant species in comets and sometimes even second in order of abundance with respect to water (Bockelée-Morvan et al. 2005). Its abundance varies widely across the comet population and has no obvious correlation with other known properties. It is difficult to quantify because CO is not only released from the nucleus but is also a photolytic daughter or granddaughter product of several other species, including CO₂, H₂CO, and CH₃OH. The same considerations about CO as a possible explanation apply to the other cases of stable far activity above cited.

Table 4: Temperature regimes for the onset of some physical processes relevant to comets, from Meech & Svoren (2005).

Considering the results of the observation of P/2004 A1 (LONEOS) and its possible explanations, we must answer three main questions:

1.: Is it possible to explain this activity with the known sublimation mechanisms; that is, may we assume that the observed dust is entrained by ice sublimation even at such a heliocentric distance?
2.: What has been the effect of the strong orbit perturbation on the activity of the body?
3.: How can we explain the emission of dust particles with the large sizes derived by orbit computations?

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg2.eps} \end{figure}$	Figure 2: The effect of Saturn's close encounter on the orbit of P/2004 A1 LONEOS: evolution of heliocentric distance from 1900 to 2006.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg3.eps} \end{figure}$	Figure 3: Surface temperature with respect to heliocentric distance of a body on the orbit of P/2004 A1 LONEOS from 1972 to 2006. There is no dust mantle. The cometocentric latitude is the equator. The surface temperature is similar for both Cases described in Sect. 3.
Open with DEXTER

It is impossible to answer these questions through further observations, at least from the ground; this forces us to seek an explanation through theoretical nucleus modeling. One of the main uses of such models is to verify the influence of hypotheses such as the one exposed above, particular phenomena, or composition properties on the evolution of the body. Another possible use is to foresee the behavior along the whole orbit, while observations usually cover a limited time extension. We can say that, if it is possible to explain the activity of this body (and answer to the other questions) by the use of one of these models, there is nothing actually strange in the activity of this Centaur and it is unnecessary to call for ``ad hoc'' phenomena, such as a micrometeorite impact.

Numerical models of comet nuclei thermal evolution and chemical differentiation have been developed during the past two decades, starting from relatively simple ones (Fanale & Salvail 1984; Herman & Podolak 1985; Espinasse et al. 1991) to the present, more complex models (Capria et al. 2001; Cohen et al. 2003; Sarid et al. 2005; De Sanctis et al. 2007; Rosenberg & Prialnik 2007). In Huebner et al. (2006) a complete review of the argument can be found.

In the following, we describe the application of our standard nucleus thermal model to solving the problems posed above.

2.1 Description of the model

The model we applied to simulate LONEOS activity is described well elsewhere (see for example Capria et al. 2000a,b, 2001; De Sanctis et al. 2003, 2005). Capria et al. (2000b) is, in particular, an application of this model to the simulation of the Centaur Chiron, another case of far activity. Hereafter a short description of our model will be given. We explain carefully in the next subsection only the simulation of dust component, dust flux, and mantle structure, because these features have recently been improved in this continuously evolving code.

The model is one-dimensional. The spherical nucleus is porous and composed of ices (water and up to two different species, typically CO and CO₂) and a refractory component. Water ice can initially be amorphous, and in this case a fraction of gases such as CO can be trapped in the amorphous matrix and released during the transition to the crystalline phase. Energy and mass conservation is expressed by the following system of coupled differential equations, solved for the whole nucleus:

$\begin{displaymath}% \rho c \frac{\partial T}{\partial t} = \nabla [K \cdot \nabla T] + \sum_{i=1}^{n} Q_{i} + Q_{\rm am-cr} \end{displaymath}$

(1)

$\begin{displaymath}\frac{1}{RT} \frac{\partial P_i}{\partial t} = \nabla [G_i \cdot \nabla P_i] + Q^\prime_{i} ~~~~i = 1,n \end{displaymath}$

where $\rho$ , c, and K are the bulk density, specific heat and thermal conductivity, Q_i the energy exchanged by the solid matrix in the sublimation and recondensation of the $i_{\rm th}$ ice, $Q_{\rm am-cr}$ the heat released during the transition of water ice from amorphous to crystalline form, R the gas constant, P_i the partial pressure of component i, $G_{\rm i}$ its diffusion coefficient, and $Q^\prime_{i}$ the gas source term caused by sublimation-recondensation processes. If some CO is trapped in the amorphous ice, the gas source term from the release of the trapped gas, $Q_{\rm CO_{\rm tr}}$ , must be added to the CO diffusion equation. The term $Q_{\rm am-cr}$ is computed as

$\begin{displaymath}% Q_{\rm am-cr} = \frac{1620 \cdot N({\rm H_{2}O})_{\rm am}}{t_{\rm cr}} ~~~[{\rm J~ m^{-3}s^{-1}}] \end{displaymath}$

(2)

where 1620 J/mol is the heat released during the transformation (Ghormley 1968). The crystallization time $t_{\rm cr}$ was experimentally found by Schmitt et al. (1989):

$\begin{displaymath}% t_{\rm cr} = 9.54 \times 10^{-14} \cdot {\rm e}^{5370/T} ~~~~[{\rm s}]. \end{displaymath}$

(3)

Gas diffusion coefficients are computed on the basis of the mean free path of the molecules in the pore system. The model accounts for three different diffusion regimes: Knudsen, viscous, and a transition one. In the usual conditions, the diffusion regime is Knudsen, so we can assume that each gas flows independently of the others.

The temperature on the surface is obtained by a balance between the solar input and the energy re-emitted in the infrared, conducted in the interior, and used to sublimate ices present on the surface. When the model is run in a fixed latitude approximation, the following expression is used:

$\displaystyle \frac{S(1-A_{\rm s})}{R_{\rm h}^{2}} \frac{\cos \theta }{\pi} = \... ...cdot H(T_{\rm s})_{\rm H_{2}O} \cdot \dot{\varepsilon} (T_{\rm s})_{\rm H_{2}O}$

(4)

where S is the solar constant, $R_{\rm h}$ the heliocentric distance of the comet, $A_{\rm s}$ the Bond bolometric albedo of the surface, $\epsilon$ the infrared emissivity of surface, $\sigma$ the Stefan-Boltzmann constant, K the thermal conductivity, and $\theta$ the cometary latitude.

The spin axis inclination (seasonal effects) can be taken into account. In the last term of right member of Eq. (4), $f_{\rm H_{2}O}^{\rm s}$ represents the surface fraction covered by water ice, H is the latent heat of sublimation, and $\dot{\varepsilon}$ is the sublimation rate. If ices different than water are present on the surface, similar terms are added to both expressions.

The surface boundary condition used to solve the diffusion equation when ice is present on the surface is

$\begin{displaymath}% P_x = P_{\rm x}^{\rm sat} (T). \end{displaymath}$

(5)

When no ice is present, the surface boundary condition is obtained assuming free sublimation at the comet nucleus surface:

P_x = 0.

(6)

When the temperature rises, ices start to sublimate, beginning from the more volatile ones. Even if the nucleus is initially homogeneous, a differentiated, layered structure is always obtained, in which the boundary between different layers is a sublimation front. Surface erosion due to ice sublimation and particles ejection is taken into account.

2.2 The simulation of the dust component and of the mantle

The dust component is represented as size distributions of spherical grains characterized by a density, a specific heat, and a thermal conductivity. In the code, we can consider up to two distributions, with a maximum of ten size classes each. Density can vary from size class to size class in the same distribution. In this way there is a great flexibility and the possibility to simulate, for example, both silicatic and organic particles with their different physical properties. This version of the code has been applied, for example, to the simulation of the physical properties of the comet 46P/Wirtanen (Capria et al. 2001).

At the beginning of computations, the dust particles are embedded in the porous ice. When the ice sublimates the embedded particles become free, in a number proportional to the amount of sublimated ice, and can undergo the drag exerted by the gas flux. Free particles that are found close to the surface can move toward the surface and be blown off or else accumulate to form a dust mantle. Free particles move under the opposite effects of gravity and gas flux, and only grains smaller than the pore's average size can move toward the surface in the pore system. Average pore size increases because of the ice sublimation: a ``pore widening factor'' proportional to the amount of sublimated ice is locally applied to the pore average size. In this work, a value of 10 has been attributed to this factor. In this way we consider that a sublimating ice produces holes and cavities. As a consequence, free particles can move towards the surface. (Particles can move and be blown off only if they are smaller than the local average pore size.) When the ice is condensing, a proportional amount of free particles become embedded and the average pores size becomes smaller (porosity decreases).

To determine how many particles can be blown off to contribute to dust flux and how many can be accumulated on the surface, the different forces acting on the single grain are compared, obtaining for each distribution a critical radius, depending on grain density. The critical radius represents the radius of the largest particle that can leave the surface of the comet:

$\begin{displaymath}% a^* = \frac{3}{4} \frac{\Phi_{\rm H_{2}O} \cdot V_{\rm H_{2... ...{R_n^2} - R_n \omega^2 \cos^2\:\theta]} \hspace{1cm} [{\rm m}] \end{displaymath}$

(7)

where G is the gravitational constant, M_n the mass of the comet, R_n its radius, $\omega$ its angular rotation velocity, $\rho_{\rm dust}$ the dust grain density, $\Phi_{\rm H_{2}O}$ , $\Phi_{\rm CO_2}$ and $\Phi_{\rm CO}$ are the gas fluxes, and $V_{\rm H_{2}O}$ , $V_{\rm CO_{2}}$ , and $V_{\rm CO}$ the velocities of the gas fluxes. In Eq. (7) the numerator represents the lifting force exerted by the outflowing gases, and the denominator represents the gravitational attraction corrected by the centrifugal force. At each time step, the number of free dust particles for each size class and the value of the critical radius are computed. All the free particles with radius a<a^* are considered ejected (blown off) and contribute to the dust flux, while those with $a\geq a^*$ accumulate on the surface. This refractory surface layer (dust mantle) is not necessarily stable, and can later on be blown off if the gas flux is strong enough. It could also increase in thickness if more and more particles are not able to leave the surface, substantially reducing and then quenching the gas flux. Dust mantle compaction due to a volume reduction when ice is sublimated is taken into account. If the dust mantle is thin enough, the gas flux from the interior is able to entrain a dust flux, so it is possible to have a weaker dust flux even when there is no ice left on the surface.

In this way, even an originally homogeneous body quickly becomes highly inhomogeneous: composition, density, and porosity are changing with depth.

3 Thermal evolution modeling of P/2004 A1 (LONEOS)

3.1 Input parameters

To apply the model to a real case, we need to define the characteristics of the body that we want to simulate, assuming an initial structure and composition and giving a value to the many parameters on which this model depends. These parameters describe the orbit, the initial state and composition of the body and the properties of comet matter. They are defined or derived, when possible, from observation and laboratory experiments. By changing a few parameters giving the initial conditions and keeping all the rest fixed, we can build the so-called ``cases'' that are the subject of the simulation.

Some of the values given to the initial parameters of the model are listed in Table 5. By varying only the parameters describing the composition we have built two cases, that are discussed in a later section. Hereafter, only the parameters common to both cases are discussed.

Table 5: Initial value of the parameters defining the two cases.

The values attributed to the parameters listed in Table 5 can be considered typical of comets and are largely used in comet modeling (Huebner et al. 2006). The dust-to-ice ratio, CO₂/H₂O, and CO/H₂O refer to the initial nucleus composition, not to what could be measured in the coma, which does not necessarily match the nucleus composition and proportions. With these parameters, bulk thermal conductivity has an average value of 0.03 K kg^-1 m^-3 along the whole evolution for both cases, and average density values for the nucleus matter are about 410 kg m^-3. The initial temperature has been assumed to be very low, because the evolution of the body begins in the Kuiper Belt (see following subsection) and this is a typical formation temperature for that region (Weidenschilling 2005). We are making the assumption that the interior temperature of most of comet nuclei is very low, because of both the formation temperature and the extremely low thermal conductivity of comet matter. Only in this way is it possible to keep supervolatile ices in the interiors of comets and consequently explain the detection of supervolatiles emissions in many comets.

The dust component is described with one distribution of 6 classes with different radii and similar density and thermal conductivity. The initial dust size distribution at the beginning of computations, shown in Fig. 4, has a Gaussian shape. The distribution of grains in the nucleus does not necessarily match the one sampled in the coma, which, besides biases due to the observing instrumentation, is probably subjected to fragmentation processes (Kolokolova et al. 2005). Because of the low temperature at which the nucleus is found at the beginning of computation, the initial status of water ice is assumed to be amorphous.

The model has been run in the fixed-latitude approximation; that is, Eq. (4) is used to derive the temperature on the surface. The reasons for this choice are that the rotation period is not known and that the variations in gas and dust production with respect to the daily hour are irrelevant for the present analysis. In this way, the gas and dust production rates only depend on the latitude, which for both cases has been fixed at the equator, and should be considered as an upper limit for the real activity of the comet.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg4.eps}\end{figure}$	Figure 4: Dust-grain size distribution in the nucleus at the beginning of computation. Vertical axis represents the fraction of particles with a given size. Most of the particles (40 percent) have a radius of 10^-4 m.
Open with DEXTER

3.2 Simulating the dynamical history

The dynamical history of a comet has a strong influence on its evolution, so it is important to simulate its effect; moreover, the dynamical history of this body is quite peculiar. For both cases, the computation begins when the Centaur is in the Kuiper Belt, then it is followed until the present orbit. The body is kept revolving on an orbit until its conditions are more or less stabilized, and then it is moved to another orbit without changing its status. The orbital parameters that were used can be found in Table 6.

Table 6: Dynamical parameters of the orbits successively followed by P/2004 A1 LONEOS during its evolution.

The first orbit, where the body is found with its initial parameters, is the beginning of the evolution history. It is a typical Kuiper Belt orbit, in which the body revolves until the first layers are stabilized. The second orbit is a typical transfer orbit for a body entering the inner part of the Solar System. In Figs. 5 and 6, the density profile at the end of the revolutions on the second orbit at two different latitudes, equator and $85 \hbox {$^\circ $ }$ , are shown. The figures refer to case 1 (see the following subsection), in which the body is made by dust and ices of H₂O, CO₂ and CO. At the beginning of the computations, the nucleus is homogeneous, but after a while the layers closer to the surface are depleted in more volatile elements.The third set of orbital parameters, derived from JPL Horizons Ephemeris System, is meant to simulate the orbit the Centaur was following until the close encounter. It is followed for some revolutions, and then stopped at the moment of the close encounter, when the evolution continues with the fourth set of orbital parameters. The fourth orbit is the present one.

The effect of this close encounter, as already discussed above, is an almost abrupt change in orbital parameters, bringing the body closer to the Sun. An equally abrupt increase in surface temperature follows the close encounter (see Fig. 3). Due to the low thermal conductivity value, the effects of this increase are felt almost exclusively by the layers close to the surface.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg5.ps} \end{figure}$	Figure 5: Case 1 - Density profile at the end of the orbit 2 (see Table 6), at the latitude of the equator. CO (continuous line) and CO₂ (dashed line) are shown. The surface is at 10 km of the radius. The first meters close to surface are depleted in CO.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg6.ps} \end{figure}$	Figure 6: Case 1 - Density profile at the end of the orbit 2 (see Table 6), at the latitude of $85 \hbox {$^\circ $ }$ . CO (continuous line) and CO₂ (dashed line) are shown. The surface is at 10 km of the radius. CO ice can be found very close to the surface.
Open with DEXTER

3.3 Case 1: CO-rich model

The first hypothesis (and case) that we want to analyze is a body very rich in CO and volatiles in general. The reason for this hypothesis is clear when looking at the activation temperatures of some physical processes, shown in Table 4, and comparing them to Fig. 3. It is clear that a body rich in CO and entering the inner Solar System for its first time could be active very far from the Sun. How rich? Because we are testing a hypothesis, we can assume that the initial ratio CO/H₂O in the nucleus body was very high, and the value assumed for the case 1 is $20 \%$ with respect to water (see Table 5). While high, this value is realistic, and is in the range of what has been observed and can be found in the literature on active comets (Bockelée-Morvan et al. 2005).

The physical properties of amorphous ice and its thermal behavior are known only from laboratory experiments (Bar-Nun & Owen 1998; Bar-Nun et al. 1985; Bar-Nun et al. 1988; Hudson & Donn 1991; Jenniskens & Blake 1994; Jenniskens et al. 1998). In the experiments, a mixture of water vapor and other gases such as CO are frozen at low temperatures, obtaining amorphous ice. Once the gas is trapped (the more it is, the lower the deposition temperature), its release only depends on changes in the ice structure related to temperature changes. Guest molecules, such as CO and Ar, can be trapped up to temperatures higher than the sublimation temperature of the species in pure ice form. The amount of trapped molecules depends in a complicated way on the initial ice composition, thus it is impossible to uniquely determine the trapped amount of guest molecules. In the experiments, trapped gases are emitted during the transition from the amorphous to the crystalline phase of water ice.

It is a matter of debate if, in a real comet nucleus, CO can be found as an ice or as a trapped gas, or in both states at once. We have assumed, for case 1, that CO is present in both states: as an ice together with CO₂, and as a gas trapped in the amorphous water ice. The trapped CO gas will be released only during the amorphous-crystalline transition. Because of the low thermal conductivity that is thought to be characteristic of the comet matter, amorphous ice buried under the surface can survive for a very long time.

The computation begins, as described in a preceding section, when the Centaur is revolving in the Kuiper Belt zone (orbits 1 and 2 in Table 6). Even that far from the Sun, the body shoes some activity, because some CO gas is slowly sublimating from the interior. In Fig. 5 the density profile at the equator after these first sets of orbits is shown; the first layers are depleted in CO until a depth of nearly 5 m. Figure 6 shows the same density profile at a latitude of $85 \hbox {$^\circ $ }$ . Here the situation is different, with only the first 2 m depleted in CO. In both cases, CO₂ ice can be found on the surface. A more or less strong enrichment in CO, depending on latitude, is located at the sublimation level.

When the body is revolving on the orbit 3, where it remained until the close encounter of 1992, the activity is much stronger (see Figs. 7 and 8): the CO flux is around 10²⁷ molecules/s, and is able to sustain a low dust flux. The close encounter creates a peak in the gas (and dust) emission, because the thermal wave is reaching layers that are still rich in volatile ice. These layers are quickly depleted, and gas and dust production rates settle to a level higher than the one experienced before 1992, close to 10²⁸ molecules/s. The CO₂ production rate reaches 10²⁷ molecules/s and becomes visible in the plot. It must be noted that the production peak of CO is slightly shifted with respect to the corresponding peak of CO₂, because CO is coming from a deeper layer. Even at perihelion the surface temperature remains under 125 K, so there is no contribution from the gas trapped in the amorphous ice.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg7.ps} \end{figure}$	Figure 7: Case 1- CO (continuous line) and $\rm CO_2$ (dashed line) gas fluxes from 1972 to 2006. The peak due to the close encounter in 1992 is clearly visible.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg8.ps} \end{figure}$	Figure 8: Case 1 - Dust flux from 1972 to 2006. The peak due to the close encounter in 1992 is clearly visible.
Open with DEXTER

The dust production enhancement visible in Fig. 8 as an effect of the close encounter with Saturn in 1992 corresponds to a temporary increase in the dust flux and in the emission of larger dust particles. The size distribution of emitted particles is different from the Gaussian distribution initially present in the nucleus (Fig. 4),and only the small particles of the first 3 classes are able to leave the nucleus. Larger particles are only emitted during peaks in the activity.

On the current orbit, the dust flux is quite high at hundreds of kg/s and is able to sustain the coma and tail that have been observed (Mazzotta-Epifani et al. 2006). A certain level of dust activity started even before the close encounter, so matching the observation results with the hypothesis of a long-lasting activity is quite reasonable.

3.4 Case 2: an alternative model

The hypothesis of case 1 is not the only one that explains the activity of P/2004 A1 LONEOS. It is a matter of discussion if extremely volatile molecules such as CO can be present in the nucleus of a comet as an ice, mixed with water and other ices, or if they can only be present in the amorphous water-ice matrix, trapped as gases and released only during the transition phase. It is also unclear, in this case, how much of a gas, and how many different gas species, can be trapped. Modeling and observation are not sufficient, at the moment, for an answer. The possibility exists that the driver of distant activity is a less volatile ice such as CO₂, a species that was found to be abundant in recent observations (Meech & Svoren 2005; Feaga et al. 2006).

For these reasons, and as an alternative hypothesis for case 2, it has been assumed that the nucleus of the Centaur is rich in CO₂ and that no CO (both ice and gas) is present. The assumptions made for case 2 can be seen in the second column of the Table 5. With respect to case 1, there is a higher percentage of CO₂ with respect to water, so the two cases only differ in the initial ice composition and have been run with the same sets of orbital parameters.

The results for this case can be seen in Fig. 9, showing the gas flux along the orbit from 1972 to the present. This figure should be compared with Fig. 7. This time there is no activity when the body is revolving on orbits 1 and 2 (see Table 4 and compare with Fig. 3). The activity begins on orbit 3, with some CO₂ (10²⁷ molecules/s) peaking at perihelion. Also in case 2, the enhancement in the gas production due to the close encounter is seen clearly. CO₂ flux rises immediately, with CO₂ ice very close to the surface, and on the present orbit at perihelion it reaches a value close to 10²⁸ molecules/s. Dust flux is driven by gas flux, so there is a dust emission similar to the one of Case 1 only after the close encounter.

If we consider the present orbit, the total gas production is very similar to the one obtained from case 1. The situation is different for the orbit before the close encounter, where there is almost no gas production, and obviously as a consequence no dust production. With these assumptions the presence of a dust flux since before the close encounter of 1992 is very difficult to explain.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg9.ps} \end{figure}$	Figure 9: Case 2 - CO₂ flux from 1972 to 2006.
Open with DEXTER

3.5 The release of large particles

From orbit computations (Mazzotta-Epifani et al. 2006) the dust tail of LONEOS could be composed of grains larger than 1 cm. If confirmed, this would not be surprising, because different observation techniques (Harmon et al. 2005; Kolokolova et al. 2005) and also the Giotto findings (McDonnell et al. 1991) support the possibility that even larger particles can be released by comets.

The dust release mechanism described above simulates the release of spherical grains from the surface or from layers close to the surface, if the pore diameter allows it. A pore widening factor proportional to the amount of sublimated ice has been implemented in this version of the code. In this way, the release of particles larger than the initial average pore size from layers very close to the surface can be explained. It must be remembered that the dust mantle, when present, is porous, so the gas sublimating underneath can flow into the coma. Anyway, even using this improved version of our model, it is very difficult to obtain the release of particles larger than 1 cm. A very strong flux is needed to lift off from the surface a decimeter or more particle, even if the particle is extremely fluffy and light. We can conclude that the described model cannot account for this kind of phenomenon, at least with the input parameters and assumptions described above, and the majority of emitted particles have sizes well under 1 cm.

Alternative mechanisms, not yet implemented in our code, to the emission of single spherical dust grains entrained by gas flux are possible. In our opinion, the detection of large particles coming from comets could be explained with the fragmentation of the surface, which means the release of more or less large surface fragments, compacted and devolatilized, probably followed in most cases by further fragmentation in the coma. This almost ``explosive'' fragmentation could be the result of a formation of a gas pocket close to a mantled surface. A real nucleus cannot be homogeneous, so it is not difficult to speculate that locally there could be a higher (or lower) ice concentration with respect to the refractary component. Once completely sublimated, this higher local gas concentration could exert strong stress on the dust mantle, ending up with a small ``explosion'' able to release large surface fragments in the coma. To obtain fragments from isolated dust grains we should also assume these grains are sticky enough to form larger aggregates. The release of surface fragments is quite common in the comet's lifetime (Boehnhardt 2005). We can imagine that during the close encounter period the enhanced gas flux could have contributed to the release of such large fragments.

4 Foreseeing the future activity of P/2004 A1 LONEOS

This Centaur is quite peculiar in its activity and dynamical history, because it was discovered when it was entering the inner Solar System for the first time, just after having experienced the close encounter with Saturn. Monitoring its activity along the new orbit will be extremely interesting. Analysis of the dynamical history of P/2004 A1 (LONEOS) by means of the JPL Horizons Ephemeris System shows that its orbit will be quite stable, at least for the next hundred years.

It would be interesting to know for how many revolutions the present activity level will last, and whether it would be possible to distinguish between the two cases discussed before on the basis of the future thermal evolution, hence of observation.

We ran the two cases discussed above for 5 more orbits in the future: the resulting gas fluxes, computed at the equator, can be seen in Figs. 10 and 11. The decreasing level of activity is evident in both cases, but, while in case 1 a strong gas flux, due to the presence of a CO source, is present along the whole orbit, a gas flux is present only around the perihelion in case 2. This leads the dust flux, hence coma and tail, being much more visible and consistent in the hypothesis of case 1. This is not surprising, because it simply means that with the assumptions made for case 2 (no CO ice), we do have no source of activity able to work at the aphelion distance. To help differentiate between the different assumptions made for cases 1 and 2 it would be important to observe LONEOS when it is found close to the aphelion.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106f10.ps} \end{figure}$	Figure 10: Case 1 - CO (continuous line) and CO₂ (dashed line) fluxes for the next 5 orbits in the future.
Open with DEXTER

5 Discussion: possible answers

We now discuss the possible answers to three earlier questions.

Is it possible to explain this activity with the known sublimation mechanisms, that is may we assume that the observed dust is entrained by ice sublimation?

It is clear that by assuming a volatile ice source it is possible to explain the activity on the current days orbit. We have assumed in case 1 the presence of some CO ice not too far from the surface, and with this hypothesis it is possible to obtain an even farther activity. In our opinion this hypothesis (coupled with the hypothesis of a very low thermal conductivity value) could explain the cases of far activity in general.

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106f11.ps} \end{figure}$	Figure 11: Case 2 - CO₂ flux for the next 5 orbits in the future.
Open with DEXTER

This puts interesting constraints on nucleus modeling. Very volatile ices cannot be found on the surface(if not, maybe, as small patches in particular locations), so in cases such as the one described above the dust is entrained by gases flowing from under the surface. This situation could be common on comets, and it could also apply to H₂O ice: dust flux on 9P/Tempel 1 was probably entrained by gases (mostly water in this case) flowing from under a devolatilized surface (Sunshine et al. 2006). Moreover, in a body rich in very volatile ices, we could have dust emission from the night side and all along the orbit, and dust and gas emissions would have a more ``smooth'' profile.

What was the effect of the strong orbit perturbation on the activity of the body?

The orbit perturbation corresponded to a strong and relatively quick increase in the temperature of the layers close to the surface. This gave rise to an improved activity, probably because the heat wave reached fresher layers, still rich in very volatile ices.

How can we explain the emission of big (larger than 1 cm) dust particles?

With the presently implemented version of the the model, it is impossible to explain the release of very large particles. This release could be explained with different mechanisms from the steady mass loss from ice sublimation. The whole mechanism that originates the dust coma and tail is not yet completely understood. It has been pointed out, for example, that cometary mass loss at the measured rates cannot supply the mass estimated in the comet trails even if continuous over the age of the trail (Jewitt 2008). This clearly points to a different way to eject the dust from the nucleus, probably linked to fragmentation and splitting phenomena.

6 Conclusion: why some of the Centaurs are active

We answered the question of why LONEOS was found to be active, but we did not explain why this particular Centaur should be rich in volatile ices or why other bodies with similar orbits (and maybe similar dynamical histories?) are instead inactive. Why can bodies observed at the same distance can display such different levels of activity?

These differences cannot be explained only by dynamical history, because not all the bodies with similar orbits and similar dynamical histories are active, even at a low level. Probably, coupled with the effect of dynamical history, a major role is played by composition differences, because of different birthplaces in the Solar System and evolutionary histories.

The bodies orbiting in the Kuiper Belt zone are subject to the coupled effects of collisional and thermal evolution (Capria & Coradini 2006; Capria et al. 2000b, De Sanctis et al. 2001). Larger bodies could have even been differentiated thanks to the effect of short-lived radiogenic elements ( ²⁶Al, ⁶⁰Fe); these bodies could be devolatilized in the interior, while closer to the surface CO-rich layers could still survive, probably with a complex structure of CO-rich and CO-poor interlaced layers. We can speculate that an impact could then create smaller bodies rich in volatiles.

To conclude, the activity of the Centaur 2004 A1/LONEOS can be explained in terms of the usual sublimation mechanisms, taking its peculiar dynamical history into account and assuming a volatile ice-rich body. This, in turn, would not be impossible following what we know about the evolution of the bodies in the Kuiper Belt.

References

A'Hearn, M. F., Schleicher, D. G., Feldman, P. D., Millis, R. L., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] (In the text)
Bar-Nun, A., & Owen, T. 1998, in Solar System Ices (Dordrecht: Kluwer Academic Publishers), 353 (In the text)
Bar-Nun, A., Herman, G., Laufer, D., & Rappaport, M. L. 1985, Icarus, 63, 317 [NASA ADS] [CrossRef] (In the text)
Bar-Nun, A., Kleinfeld, I., & Kochavi, E. 1988, Phys. Rev. B (Condensed Matter), 38(11), 7749 (In the text)
Bauer, J. M., Fernandez, Y. R., & Meech, K. J. 2003, PASP, 115, 981 [NASA ADS] [CrossRef]
Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ, 128, 1390 [CrossRef] (In the text)
Bockelée-Morvan, D., Crovisier, J., Mumma, M. J., & Weaver, H. A. 2005, The composition of cometary volatiles, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 391 (In the text)
Boehnhardt, H. 2005, Split comets, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 301 (In the text)
Buzzi, L., Naves, R., Campas, M., et al. 2004, MPEC 2004-D23 (In the text)
Capria, M. T., & Coradini, A. 2006, The interior of outer Solar System bodies, in Asteroids, Comets, Meteors, Proceedings of the 229th Symposium of the IAU, ed. D. Lazzaro, S. Ferraz-Mello, & F. Angel, Cambridge Univ., Cambridge, 395 (In the text)
Capria, M. T., Coradini, A., De Sanctis, M. C., & Orosei, R. 2000a, A&A, 357, 359 [NASA ADS] (In the text)
Capria, M. T., Coradini, A., De Sanctis, M. C., & Orosei, R. 2000b, AJ, 119, 3112 [NASA ADS] [CrossRef] (In the text)
Capria, M. T., Coradini, A., De Sanctis, M. C., & Blecka, M. I. 2001, PSS, 49, 907 (In the text)
Cochran, A., Barker, E. S., & Cochran, W. 1980, AJ 85, 474
Cohen, M., Prialnik, D., & Podolak, M. 2003, New Astron., 8, 179 [NASA ADS] [CrossRef] (In the text)
Cremaschini, C., Foglia, S., Marinello, W., et al. 2004, MPEC 2004-E06 (In the text)
Crifo, J. F., & Rodionov, A. V. 1999, Icarus 138, 1, 85 [NASA ADS] [CrossRef]
Crovisier, J. 1999, in Formation and Evolution of Solid in Space, ed. J. M. Greenberg, & A. Li (Kluwer Academic Publisher), 39 (In the text)
De Sanctis, M. C., Capria, M. T., & Coradini, A. 2001, AJ, 121, 2792 [NASA ADS] [CrossRef] (In the text)
De Sanctis, M. C., Capria, M. T., & Coradini, A. 2003, AdSpR, 31, 2519 [NASA ADS] (In the text)
De Sanctis, M. C., Capria, M. T., & Coradini, A. 2005, A&A, 444, 605 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
De Sanctis, M. C., Capria, M. T., Coradini, A., & Ammannito, E. 2007, AJ, 133, 1836 [NASA ADS] [CrossRef] (In the text)
Descour, A. S., Skiff, B. A., Larson, S., et al. 2004, MPEC, 2004-A51 (In the text)
Elliot, J. L., Kern, S. D., Clancy, K. B., et al. 2005, AJ, 129, 1117 [NASA ADS] [CrossRef] (In the text)
Epifani, E., Colangeli, L., Fulle, M., et al. 2001, Icarus, 149, 339 [NASA ADS] [CrossRef] (In the text)
Espinasse, S., Klinger, J., Ritz, C., & Schmitt, B. 1991, Icarus, 92, 350 [NASA ADS] [CrossRef] (In the text)
Fanale, F. P., & Salvail, J. R. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] (In the text)
Feaga, L. M., A'Hearn, M. F., Sunshine, J. M., et al. 2006, in 37th Annual Lunar and Planetary Science Conference, abstract No. 2149 (In the text)
Festou, M. C., Gunnarsson, M., Rickman, H., Winnberg, A., & Tancredi, G. 2001, Icarus, 150, 140 [NASA ADS] [CrossRef]
Fulle, M. 1989, A&A, 217, 283 [NASA ADS] (In the text)
Fulle, M. 1992, Nature, 359, 6390 [CrossRef], 42 (In the text)
Fulle, M. 1994, A&A, 282, 980 [NASA ADS] (In the text)
Ghormley, J. A. 1968, J. Chem. Phys., 48, 503 [NASA ADS] [CrossRef] (In the text)
Green, D. W. E. 2004, IAU Circ., 8430 (In the text)
Hahn, G., Lagerkvist, C.-I., Karksson, O., Oja, T., & Stoss, R. M. 2006, Astron. Nachr., 327, 17 [NASA ADS] [CrossRef] (In the text)
Harmon, J. K., Nolan, M. C., Ostro, S. J., & Campbell, D. B. 2005, Radar Studies of Comet Nuclei and Grain Comae in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 265 (In the text)
Hartmann, W. K., Tholen, D. J., Meech, K. J., & Cruikshank, D. P. 1990, Icarus, 83, 1 [NASA ADS] [CrossRef] (In the text)
Herman, G., & Podolak, M. 1985, Icarus, 61, 252 [NASA ADS] [CrossRef] (In the text)
Holman, M. J., & Wisdom, J. 1993, AJ, 105, 5 [CrossRef], 1987 (In the text)
Hudson, R. L., & Donn, R. 1991, Icarus, 94, 326 [NASA ADS] [CrossRef] (In the text)
Huebner, W. F., Benkhoff, J., Capria, M. T., et al. 2006, Heat and gas diffusion in comet nuclei, International Space Science Institute SR-004, Bern (In the text)
Jenniskens, P., & Blake, D. F. 1994, Science, 265, 753 [NASA ADS] [CrossRef] (In the text)
Jenniskens, P., Blake, D. F., & Kouchi, A. 1998, in Solar System Ices (Dordrecht: Kluwer Academic Publishers), Astrophysics and space science library series, 227, 139 (In the text)
Jewitt, D. C. 2008, Lect. Notes Phys., 758 (In the text)
Kimura, H., & Liu, C.P. 1977, Chin. Astron., 1, 235 [NASA ADS] [CrossRef] (In the text)
Kolokolova L., Hanner M. S., Levasseur-Regourd A.-Ch., & Gustafson B. Å. S. 2005, Physical Properties of ometary Dust from Light Scattering and Thermal Emission, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 577 (In the text)
Lara, L.-M., Licandro, J., Oscoz, A., & Motta, V. 2003, A&A, 399, 763 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Levison, H. F., & Duncan, M. J. 1997, Icarus, 127, 13 [NASA ADS] [CrossRef] (In the text)
Licandro, J., Tancredi, G., Lindgren, M., Rickman, H., & Gil Hutton, R. 2000, Icarus, 147, 161 [NASA ADS] [CrossRef] (In the text)
Luu, J. X., & Jewitt, D. C. 1990, AJ, 100, 913 [NASA ADS] [CrossRef] (In the text)
Mazzotta Epifani, E., Palumbo, P., Capria, M. T., et al. 2006, A&A, 460, 935 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Mazzotta Epifani, E., Palumbo, P., Capria, M. T., et al. 2007, MNRAS, 381, 713 [NASA ADS] [CrossRef] (In the text)
Mazzotta Epifani, E., Palumbo, P., Capria, M. T., et al. 2008, MNRAS, 390, 265 [NASA ADS] [CrossRef] (In the text)
McDonnell, J. A. M., Lamy, P. L., & Pankiewicz, G. S. 1991, Physical properties of cometary dust, in Comets in the Post- Halley Era, ed. R. L. Newburn Jr. et al. (Dordrecht: Kluwer), 1, 1043 (In the text)
Meech, K., & Belton, M. 1989, IAU Circ., 4770 (In the text)
Meech, K., & Svoren, J. 2005, Using cometary activity to trace the physical and chemical evolution of cometary nuclei, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver, University of Arizona (In the text)
Naves, R., Campas, M., Kadota, K., et al. 2004, MPEC, 2004-C07 (In the text)
Petit, J.-M., Holman, M. J., Gladman, B., et al. 2006, MNRAS, 365, 429 [NASA ADS] [CrossRef] (In the text)
Rosenberg, E. D., & Prialnik, D. 2007, New Astron., 12, 523 [NASA ADS] [CrossRef] (In the text)
Sarid, G., Prialnik, D., Meech, K. J., Pittichova, J., & Farnham, T. L. 2005, Publ. Astron. Soc. Pacific, 117, 796 [NASA ADS] [CrossRef] (In the text)
Schleicher, D. G., Woodney, L. M., & Millis, R. L. 2003, Icarus, 162, 2 [CrossRef], 415 (In the text)
Schmitt, B., Espinasse, S., Grim, R. A. J., Greenberg, J. M., & Klinger, J. 1989, Laboratory studies of cometary ice analogues, in Physics and mechanics of cometary material, ESA-SP, 302 (In the text)
Schulz, R., Stüwe, J. A., Boehnhardt, H., Gaessler, W., & Tozzi, G. P. 2003, A&A, 398, 345 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Senay, M. C., & Jewitt, D. C. 1994, Nature, 371, 229 [NASA ADS] [CrossRef]
Skiff, B. A., Miller, H. R., & Young, J. 2004, IAU Circ., 8267 (In the text)
Sunshine, J., A'Hearn, M. F., Groussin, O., et al. 2006, Science, 311, 1453 [NASA ADS] [CrossRef] (In the text)
Tesi, L., Boattini, A., Tombelli, M., et al. 2004, MPEC, 2004-C46 (In the text)
Ticha, J., Tichy, M., Kadota, K., et al. 2004, MPEC, 2004-B54 (In the text)
Weidenschilling, S. J. 2005, From icy grains to comets, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 97 (In the text)
Weiler, M., Rauer, H., & Helbert, J. 2004, A&A, 414, 749 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

All Tables

Table 1: Active Centaurs (as of January 2009).

Table 2: Orbital parameters of the active Centaur P/2004 A1 (LONEOS).

Table 3: Changes in the P/2004 A1 (LONEOS) orbital parameters due to Saturn's close encounter.

Table 4: Temperature regimes for the onset of some physical processes relevant to comets, from Meech & Svoren (2005).

Table 5: Initial value of the parameters defining the two cases.

Table 6: Dynamical parameters of the orbits successively followed by P/2004 A1 LONEOS during its evolution.

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg1.eps} \end{figure}$	Figure 1: Variation in the orbital parameters of P/2004 A1 (LONEOS). a) perihelion distance (long-dashed line), aphelion distance (dashed line), and inclination (continuous line) from 1954 to 1995; b) expanded version of top left plot around the close encounter time for perihelion distance; c) same as b) for aphelion distance; d) same as b) for inclination.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg2.eps} \end{figure}$	Figure 2: The effect of Saturn's close encounter on the orbit of P/2004 A1 LONEOS: evolution of heliocentric distance from 1900 to 2006.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg3.eps} \end{figure}$	Figure 3: Surface temperature with respect to heliocentric distance of a body on the orbit of P/2004 A1 LONEOS from 1972 to 2006. There is no dust mantle. The cometocentric latitude is the equator. The surface temperature is similar for both Cases described in Sect. 3.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg4.eps}\end{figure}$	Figure 4: Dust-grain size distribution in the nucleus at the beginning of computation. Vertical axis represents the fraction of particles with a given size. Most of the particles (40 percent) have a radius of 10^-4 m.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg5.ps} \end{figure}$	Figure 5: Case 1 - Density profile at the end of the orbit 2 (see Table 6), at the latitude of the equator. CO (continuous line) and CO₂ (dashed line) are shown. The surface is at 10 km of the radius. The first meters close to surface are depleted in CO.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg6.ps} \end{figure}$	Figure 6: Case 1 - Density profile at the end of the orbit 2 (see Table 6), at the latitude of $85 \hbox {$^\circ $ }$ . CO (continuous line) and CO₂ (dashed line) are shown. The surface is at 10 km of the radius. CO ice can be found very close to the surface.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg7.ps} \end{figure}$	Figure 7: Case 1- CO (continuous line) and $\rm CO_2$ (dashed line) gas fluxes from 1972 to 2006. The peak due to the close encounter in 1992 is clearly visible.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg8.ps} \end{figure}$	Figure 8: Case 1 - Dust flux from 1972 to 2006. The peak due to the close encounter in 1992 is clearly visible.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106fg9.ps} \end{figure}$	Figure 9: Case 2 - CO₂ flux from 1972 to 2006.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106f10.ps} \end{figure}$	Figure 10: Case 1 - CO (continuous line) and CO₂ (dashed line) fluxes for the next 5 orbits in the future.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{8106f11.ps} \end{figure}$	Figure 11: Case 2 - CO₂ flux for the next 5 orbits in the future.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.