Effects of galactic fountains and delayed mixing in the chemical evolution of the Milky Way

E. Spitoni; F. Matteucci; S. Recchi; G. Cescutti; A. Pipino

doi:10.1051/0004-6361/200911768

Free Access

Issue		A&A Volume 504, Number 1, September II 2009


Page(s)		87 - 96
Section		Galactic structure, stellar clusters, and populations
DOI		https://doi.org/10.1051/0004-6361/200911768
Published online		09 July 2009

Effects of galactic fountains and delayed mixing in the chemical evolution of the Milky Way

E. Spitoni¹ - F. Matteucci^1,2 - S. Recchi^3,2 - G. Cescutti¹ - A. Pipino⁴

1 - Dipartimento di Astronomia, Università di Trieste, via G.B. Tiepolo 11, 34131, Trieste, Italy
2 - INAF Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131, Trieste, Italy
3 - Institute of Astronomy, Vienna University, Türkenschanzstrasse 17, 1180, Vienna, Austria
4 - Department of Physics and Astronomy, University of Southern California, Los Angeles, CA 90089-0484, USA

Received 2 February 2009 / Accepted 10 June 2009

Abstract
Context. The majority of galactic chemical evolution models assumes the instantaneous mixing approximation (IMA). This assumption is probably not realistic, as indicated by the existence of chemical inhomogeneities, although current chemical evolution models of the Milky Way can reproduce the majority of the observational constraints under the IMA.
Aims. The aim of this paper is to test whether relaxing this approximation in a detailed chemical evolution model can improve or worsen the agreement with observations. To do that, we investigated two possible causes for relaxing of the instantaneous mixing: i) the ``galactic fountain time delay effect'' and ii) the ``metal cooling time delay effect''.
Methods. We considered various galactic fountain time delays for the chemical enrichment from massive stars. We then tested a time delay in the enrichment from stars of all masses due to gas cooling in the range 0.5-1 Gyr.
Results. We found that the effect of galactic fountains is negligible if an average time delay of 0.1 Gyr, as suggested in a previous paper, is assumed. Longer time delays produce differences in the results but they are not realistic. We also found that the O abundance gradient in the disk is not affected by galactic fountains. The metal cooling time delays produce strong effects on the evolution of the chemical abundances only if we adopt stellar yields depending on metallicity. If, instead, the yields computed for the solar chemical composition are adopted, negligible effects are produced, as in the case of the galactic fountain delay.
Conclusions. The relaxation of the IMA by means of the galactic fountain model, where the delay is considered only for massive stars and only in the disk, does not affect the chemical evolution results. The combination of metal dependent yields and time delay in the chemical enrichment from all stars starting from the halo phase, instead, produces results at variance with observations.

Key words: Galaxy: abundances - Galaxy: evolution - Galaxy: disk - Galaxy: open clusters and associations: general - stars: supernovae: general

1 Introduction

The first attempts to follow the chemical evolution of galaxies (Schmidt 1963; Searle & Sargent 1963; Tinsley 1974) were based on the Simple Model assumptions: 1) the system is one-zone and closed, i.e., there are no inflows or outflows; 2) the initial gas is primordial (no metals); 3) the initial mass function (IMF) is constant in time; 4) the gas is well mixed at any time ( instantaneous mixing approximation or IMA); 5) stars more massive than 1 $M_{\odot }$ die instantaneously, while stars smaller than 1 $M_{\odot }$ continue forever ( instantaneous recycling approximation or IRA). While the IRA has been relaxed in most of the recent chemical evolution models, there have been only a few attempts to relax the IMA mainly because of difficulties in estimating the dispersal and mixing time of the chemical elements (Roy & Kunth 1995) and because models that retain the IMA provide nevertheless an excellent fit to the data in the Milky Way (e.g. François et al. 2004, hereafter F04). Although there is no doubt that IMA is not realistic (Schmidt 1963; Tinsley 1975), the validity of this assumption depends on the time-scale of the mixing processes. Malinie et al. (1993) claimed that due to chemical inhomogeneities in the disk, mixing and star formation might be delayed by 10^8-9 yr.

One of the very few studies in which IMA has been relaxed is the one of Thomas et al. (1998). They proposed a model in which relaxing IMA was included by splitting the gas components into two different phases: the inactive and active gas phases. The first one consists of a hot and not homogeneously distributed component; stars cannot form out of this phase. The active phase is instead assumed to be cool and well mixed. They discussed various time-scales for the mixing of the stellar ejecta, and they found that a delay of the order of 10⁸ years leads to a better fit of the observational data in the [Mg/Fe]-[Fe/H] diagram than in the IMA hypothesis.

In this paper we test the relaxation of the IMA in the detailed chemical evolution model of F04, considering two physically motivated time delays: i) the ``galactic fountain time delay'' effect and ii) the delay produced by the cooling of the metals (``metal cooling delay model'').

Type II SNe usually occur in OB associations containing several dozen massive stars. Sequential supernova explosions create supershells, which can break out of a stratified medium, producing bipolar outflows. The gas of the supershells can fragment into clouds which eventually fall toward the disk producing the so-called galactic fountains. Spitoni et al. (2008, hereafter Paper I) followed the clouds ejected by SN explosions in the Galaxy both in the purely ballistic model (the cloud is subject only to the gravitational potential of the Galaxy) and in the hybrid one where viscous interactions between the extra-planar halo gas and the cloud are taken into account. They found that the range of the cloud orbits is quite small. The clouds are generally directed outwards but the average landing coordinates differ from the throwing coordinates by at most $\sim$ 1 kpc. Only for a throwing coordinate of 12 kpc and an OB association made of 500 SNe does the ballistic model predict a landing coordinate $\sim$ 2 kpc larger than the throwing one. This result is consistent with the works of Bregman (1980), Fraternali & Binney (2008) and Melioli et al. (2008). Melioli et al. (2009) presented results for a multiple fountain model produced by randomly clustered explosions of SNe originating in stellar associations spread over a disk area of 8 kpc². As in the case of a single fountain, the spreading of the SN ejecta back into the disk is not very large. Most of the gas lifted up by fountains falls back within a distance $\Delta R=\pm$ 0.5 kpc. Therefore it is unlikely that galactic fountains can affect abundance gradients on large scales.

However, as shown in Paper I, the fountains take a finite and non-negligible time to orbit around and fall back into the Galaxy. This implies a delay in the mixing of metals in the interstellar medium (ISM), which conflicts with the IMA assumption. Referring to the results of Paper I, in this paper we test the effect on the chemical evolution of different values of the delay generated by sequential SN explosions at different galactocentric distances.

In this work we also investigate another possible cause of delayed mixing of the ISM such as the delay due to the fact that stars form only in cold gas and that hot gas takes a finite time to cool. However, there is still some debate in the literature on the cooling time-scale. Recchi et al. (2001) studied the effect of a single, instantaneous star-burst on the dynamical and chemical evolution of a gas-rich dwarf galaxy. They found that most of the metals already reside in the cold gas phase after a few tens of Myr. This result is mainly due to the assumed low SNII heating efficiency, and justifies the generally adopted homogeneous and instantaneous mixing of gas in chemical evolution models. On the other hand, Rieschick & Hensler (2000) presented a chemodynamical model of the evolution of a dwarf galaxy in which most of the metals undergo a cycle lasting almost 1 Gyr before being incorporated into the ISM. A similar result has been obtained by Tenorio-Tagle (1996). More recently, in the work of Harfst et al. (2006), a multi-phase description of the ISM was implemented: the ISM was treated as two dynamically independent gas phases: a cloudy and a diffuse one. The two gas phases are linked by the processes of condensation/evaporation and a drag force. In this model, it is assumed that stars form in clouds and that clouds are destroyed by stellar feedback, thereby self-regulating the star formation. Each cloud is assumed to form stars only after a time of inactivity, because not all the gas in clouds is dense or unstable enough for immediate star formation. In this work the time of inactivity considered is a few hundred Myr.

Here, we simply implemented our ``metal cooling delay model'' in the detailed chemical evolution model of F04 by means of a delay in the chemical enrichment.

The paper is organized as follows: in Sect. 2 we describe the reference model of F04, in Sects. 3 and 4 we report the nucleosynthesis prescriptions and the observational data, respectively. In Sect. 5 we present our galactic fountains delay model, and in Sect. 6 the ``metal cooling delay model''. In Sect. 7 we report and discuss our results. Finally, we draw the main conclusions in Sect. 8.

2 The chemical evolution model for the Milky Way

In the model of F04, the Galaxy is assumed to have formed by means of two main infall episodes: the first formed the halo and the thick disk, the second the thin disk. The time-scale for the formation of the halo-thick disk is 0.8 Gyr and the entire formation period does not last more than 2 Gyr. The time-scale for the thin disk is much longer, 7 Gyr in the solar vicinity, implying that the infalling gas forming the thin disk comes mainly from the intergalactic medium and not only from the halo (Chiappini et al. 1997). Moreover, the formation timescale of the thin disk is assumed to be a function of the galactocentric distance, leading to an inside out scenario for the Galaxy disk build-up (Matteucci & François 1989). The galactic thin disk is approximated by several independent rings, 2 kpc wide, without exchange of matter between them.

The main characteristic of the two-infall model is an almost independent evolution between the halo and the thin disk (see also Pagel & Tautvaisienne 1995). A threshold gas density of $7~M_{\odot}~{\rm pc}^{-2}$ in the star formation process (Kennicutt 1989, 1998; Martin & Kennicutt 2001) is also adopted for the disk.

The model already well reproduces an extended set of observational constraints. Some of the most important observational constraints are represented by the various relations between the abundances of metals (C, N, O, $\alpha$ -elements, iron peak elements) as functions of the [Fe/H] abundance (see Chiappini et al. 2003a,b; F04) and by the G-dwarf metallicity distribution. Although this model is probably not unique, in this respect it reproduces the majority of the observed features of the Milky Way. Many of the assumptions of the model are shared by other authors (e.g. Prantzos & Boissier 2000; Alibés et al. 2001; Chang et al. 1999).

The equation below describes the time evolution of G_i, namely the mass fraction of the element i in the gas:

$\begin{displaymath}\dot{G_{i}}(r,t)=-\psi(r,t)X_{i}(r,t) \end{displaymath}$

$\begin{displaymath}\quad+\ \int\limits^{M_{\rm Bm}}_{M_{\rm L}}\psi(r,t-\tau_{\rm m})Q_{mi}(t-\tau_{m})\phi(m){\rm d}m \end{displaymath}$

$\begin{displaymath}\quad+\ A_{\rm Ia}\int\limits^{M_{\rm BM}}_{M_{\rm Bm}}\phi(M... ...^{\rm SNIa}_{mi}(t-\tau_{m2}){\rm d}\mu\right]{\rm d}M_{\rm B} \end{displaymath}$

$\begin{displaymath}\quad+\ (1-A_{\rm Ia})\int\limits^{M_{\rm BM}}_{M_{\rm Bm}}\psi(r,t-\tau_{m})Q_{mi}(t-\tau_{m})\phi(m){\rm d}m \end{displaymath}$

$\begin{displaymath}\quad+\ \int\limits^{M_{\rm U}}_{M_{\rm BM}}\psi(r,t-\tau_{m})Q_{mi}(t-\tau_{m})\phi(m){\rm d}m \end{displaymath}$

$\begin{displaymath}\quad+\ X_{A_{i}}A(r,t) \end{displaymath}$

(1)

where X_i(r,t) is the abundance by mass of the element i and Q_mi indicates the fraction of mass restored by a star of mass min form of the element i, the so-called ``production matrix'' as originally defined by Talbot & Arnett (1973). We indicate with $M_{\rm L}$ the lightest mass which contributes to the chemical enrichment and it is set at $0.8~M_{\odot}$ ; the upper mass limit, $M_{\rm U}$ , is set at $100~M_{\odot}$ .

The star formation rate (SFR) $\psi(r,t)$ is defined as:

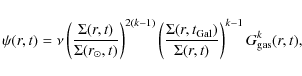$\begin{displaymath}\psi(r,t)=\nu\left(\frac{\Sigma(r,t)}{\Sigma(r_{\odot},t)}\ri... ...r,t_{\rm Gal})}{\Sigma(r,t)}\right)^{k-1}G^{k}_{\rm gas}(r,t), \end{displaymath}$

(2)

where $\nu$ is the efficiency of the star formation process and is set to be 2 Gyr^-1 for the Galactic halo and 1 Gyr^-1 for the disk. $\Sigma(r,t)$ is the total surface mass density, $\Sigma(r_{\odot},t)$ the total surface mass density at the solar position, $G_{\rm gas}(r,t)$ the surface density normalized to the present time total surface mass density in the disk $\Sigma_{D}(r,t_{\rm Gal})$ , where $t_{\rm Gal}=14$ Gyr is the age assumed for the Milky Way and $r_{\odot}=8$ kpc is the solar galactocentric distance (Reid 1993). The gas surface exponent, k, is set equal to 1.5. With these values of the parameters, the observational constraints, in particular in the solar vicinity, are well fitted. Below a critical threshold of the gas surface density ( $7~M_{\odot}~{\rm pc}^{-2}$ ), we assume no star formation. This naturally produces a hiatus in the SFR between the halo-thick disk and the thin disk phases.

For the IMF, we use that of Scalo (1986), constant in time and space. $\tau_{m}$ is the evolutionary lifetime of stars as a function of their mass m (Maeder & Maynet 1989).

The type Ia SN rate has been computed following Greggio & Renzini (1983) and Matteucci & Greggio (1986) and it is expressed as:

$\begin{displaymath}R_{\rm SNeIa}=A_{\rm Ia}\int\limits^{M_{\rm BM}}_{M_{\rm Bm}}... ...}f(\mu)\psi(t-\tau_{M_{2}}){\rm d}\mu \right] {\rm d}M_{\rm B} \end{displaymath}$

(3)

where M₂ is the mass of the secondary, $M_{\rm B}$ is the total mass of the binary system, $\mu=M_{2}/M_{\rm B}$ , $\mu_{\rm m}={\rm max}\left[M_{2}(t)/M_{\rm B},(M_{\rm B}-0.5M_{\rm BM})/M_{\rm B}\right]$ , $M_{\rm Bm}= 3~M_{\odot}$ , $M_{\rm BM}= 16~ M_{\odot}$ . The IMF is represented by $\phi(M_{\rm B})$ and refers to the total mass of the binary system for the computation of the type Ia SN rate, $f(\mu)$ is the distribution function for the mass fraction of the secondary:

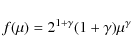$\begin{displaymath}f(\mu)=2^{1+\gamma}(1+\gamma)\mu^{\gamma} \end{displaymath}$

(4)

with $\gamma=2$ ; $A_{\rm Ia}$ is the fraction of systems in the appropriate mass range, which can give rise to type Ia SN events. This quantity is fixed to 0.05 by reproducing the observed type Ia SN rate at the present time (Mannucci et al. 2005). Note that in the case of the type Ia SNe the``production matrix'' is indicated with $Q^{\rm SNIa}_{mi}$ because of its different nucleosynthesis contribution (for details see Matteucci & Greggio 1986; and Matteucci 2001).

The term A(r,t) represents the accretion term and is defined as:

$\begin{displaymath}A(r,t)= a(r) {\rm e}^{-t/ \tau_{H}(r)}+ b(r) {\rm e}^{-(t-t_{\rm max})/ \tau_{D}(r)}. \end{displaymath}$

(5)

X_{A_i} are the abundances in the infalling material, which is assumed to be primordial, while $t_{\rm max}=1$ Gyr is the time for the maximum infall on the thin disk, $\tau_{\rm H}= 0.8$ Gyr is the time scale for the formation of the halo thick-disk and $\tau_{\rm D} (r)$ is the timescale for the formation of the thin disk and is a function of the galactocentric distance (inside-out formation, Matteucci & François 1989; Chiappini et al. 2001).

In particular, we assume that:

$\begin{displaymath}\tau_{\rm D}=1.033 r (\mbox{kpc}) - 1.267~\mbox{Gyr}. \end{displaymath}$

(6)

Finally, the coefficients a(r) and b(r) are obtained by imposing a fit to the observed current total surface mass density in the thin disk as a function of galactocentric distance given by:

$\begin{displaymath}\sigma(r)=\sigma_{\rm D}{\rm e}^{-r/r_{\rm D}}, \end{displaymath}$

(7)

where $\sigma_{\rm D}=531$ $M_{\odot}~$ pc^-2 is the central total surface mass density and $r_{\rm D}= 3.5$ kpc is the scale length.

3 Nucleosynthesis prescriptions

For the nucleosynthesis prescriptions of the Fe and the other elements (namely O, S, Si, Ca, Mg, Sc, Ti, V, Cr, Zn, Cu, Ni, Co and Mn ), we adopted those suggested in F04. They compared theoretical predictions for the [el/Fe] vs. [Fe/H] trends in the solar neighborhood for the above mentioned elements and they selected the best sets of yields required to best fit the data. In particular, for the yields of SNe II they found that the Woosley & Weaver (1995, hereafter WW95) ones provide the best fit to the data. No modifications are required for the yields of Ca, Fe, Zn and Ni as computed for solar chemical composition. For oxygen, the best results are given by the WW95 yields computed as functions of the metallicity. For the other elements, variations in the predicted yields are required to best fit the data (see F04 for details).

In particular, the Mg yields require some adjustments since Mg yields from massive stars are generally too low and predict a a too low Mg solar abundance. However, this fact does not affect the [Mg/Fe] vs. [Fe/H] diagram if the predicted ratios are normalized to the predicted solar abundances. What matters in these diagrams are the proportions of a given element produced in different mass ranges: Mg is mainly produced in massive stars and therefore, irrespective of the predicted Mg abundance, one always obtains an overabundance of Mg relative to Fe in metal poor stars followed by a decrease of the Mg/Fe ratio at the onset of type Ia SNe which produce the bulk of Fe. F04 artificially increased the yields of Mg from WW95 to obtain also a good solar Mg abundance and to give an indication to nucleosynthesis modelers about what might be necessary to fit the absolute Mg abundance. For the Fe-peak elements, the situation is more complex and still very uncertain and we do not show results for these elements in this paper. Concerning O, the best agreement with the [O/Fe] vs. [Fe/H] and the solar O abundance, as measured by Asplund et al. (2005), is obtained by adopting the original WW95 yields from massive stars as functions of metallicity. The same is not true for Fe: it was already known from the paper of Timmes et al. (1995) that the Fe yields as functions of metallicity overestimate the solar Fe and many people use those yields divided by a factor of 2. Alternatively, one can use the yields for solar chemical composition for the whole galactic lifetime and the result is the same. This is due to the still existing uncertainties in the Fe yields.

Concerning the yields from type SNeIa, revisions in the theoretical yields by Iwamoto et al. (1999) are required for Mg, Ti, Sc, K, Co, Ni and Zn to best fit the data. The prescription for single low-intermediate mass stars is by van den Hoek & Groenewegen (1997), for the case of the mass loss parameter, which varies with metallicity (see Chiappini et al. 2003a, model5).

4 Observational data

We used the collection of data elaborated in the work of F04, who adopted a data sample for stars in the solar neighborhood spanning a metallicity range from -4 dex to solar. In particular, for the very metal poor stars ([Fe/H] between -4 and -3 dex), the results from the UVES large program `` First Stars'' (Cayrel et al. 2003) were adopted.

For the abundances in the remaining range of [Fe/H], they adopted already published data in the literature from various sources: for all the elements studied in this paper (O, Mg, Si), F04 used the data of Carney et al. (1997), Nissen & Schuster (1997), Ryan et al. (1991), Edvardsson et al. (1993), Matteucci et al. (1993, and references therein). Moreover, concerning the Mg and Si, but not O, the collection of F04 includes the data of Stephens (1999), Carretta et al. (2002), McWilliam et al. (1995), Fulbright (2000), Gratton & Sneden (1988). For the O, F04 also used the data of Nissen et al. (2002). Here, for O, we also took into account the data of Bensby et al. (2004).

All of these data are normalized to the solar abundances of Grevesse & Sauval (1998) with the exception of oxygen for which we adopted the value of Asplund et al. (2005).

For the galactic abundance gradient for the oxygen, we used the set of data given by Andreievsky et al. (2002a,b) and Luck et al. (2003) by analyzing Galactic Cepheids (see Cescutti et al. 2007).

5 The galactic fountain delay model

In Paper I we used the Kompaneets (1960) approximation for the evolution of the superbubble driven by sequential supernova explosions. We assumed that supershells are fragmented by Rayleigh-Taylor instabilities, and considered each fragment as a cloud with an initial velocity given by the supershell velocity at the moment of fragmentation. Then, we followed the orbit of the clouds either ballistically (the cloud is subject only to the gravitational potential of the Galaxy) or taking into account viscous interaction between the extra-planar gas halo and the cloud.

In Tables 2-4 reported in Paper I, the results are summarized for fragmentation times ( $t_{\rm final}$ ) and the velocities (v_n) of the supershells in the direction perpendicular to the galactic plane at those times for initial throwing coordinates fixed at 4 kpc, 8 kpc and 12 kpc. In our Table 1 we report the average time $\left\langle t_{\rm total}\right\rangle$ necessary to create a cloud from a supershell plus the time necessary for the cloud to fall back onto the Galactic disk:

$\begin{displaymath}\left\langle t_{\rm total}\right\rangle =t_{\rm final}+\left\langle t_{\rm orbit}\right\rangle\! , \end{displaymath}$

(8)

where $\left\langle t_{\rm orbit}\right\rangle$ is the average time required for a cloud to return to the galactic disk once it leaves the supershell. These average values are calculated in the case of OB associations with 10, 50, 100, 500 SNe at 3 galactocentric distances: 4 kpc, 8 kpc, 12 kpc. In Table 2 we show the maximum delay time $t_{\rm total}$ , at a fixed initial galactocentric distance of ejection.

Table 1: The average time $\left\langle t_{\rm total}\right\rangle$ [Myr].

Table 2: The maximum $t_{\rm total}$ as a function of the galactocentric distance.

As mentioned in Sect. 1, a Galactic fountain can affect the chemical evolution of the Galaxy only by means of a time-delay due to the non-negligible time taken by fountains to orbit around and fall back into the Galaxy. We implemented this delay in the chemical evolution model of F04 only during the thin disk phase. In fact, the dynamical effect of a galactic fountain requires the presence of a stratified ISM, which arises only after the end of the halo phase. In the past, several authors (i.e. Mac Low et al. 1989; Tenorio-Tagle 1996) studied the supershell evolution produced by a sequential explosion of type II SNe. They emphasized that a break-out event, necessary for a galactic fountain, requires that the OB associations must sit on a plane stratified disk where the density decreases along the z direction. In the work of Mac Low et al. (1989) a scale height of 100 pc for the ISM was considered. This is the reason why OB associations existed at early times during the formation of the halo but did not produce galactic fountains. Galactic fountains could have formed perhaps during the thick disk phase. However, by computing a fountain with a scale height of 1 kpc (typical of the thick disk), the fountains start at $\simeq$ 3 kpc, i.e. well within the halo. At this height, the stratification is much weaker and the ISM temperature is high, therefore the sound speed is high and the shock can be easily dissipated through sound waves. Moreover the thick disk phase lasts for a very short time (see Fig. 1). We can then conclude that (hypothetical) thick disk fountains would have a negligible impact on the chemical evolution of the Galaxy.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{11768fg1.eps} \end{figure}$	Figure 1: The star formation rate expressed in $M_{\odot }$ pc^-2 Gyr^-1 as a function of the galactic time (in Gyr), as predicted by the two infall model of François et al. (2004) at 4 (dotted line), 8 (dashed line) and 12 kpc (solid line).
Open with DEXTER

Table 3: Beginning of the star formation in the disk after the halo-thick disk transition ( $t_{\rm SFR}$ ).

Table 4: Mass fractions of several elements yielded by the François et al. (2004) model and the delay model at the galactic age of 9.5 Gyr compared to the solar values of Asplund et al. (2005).

Therefore, we consider the galactic fountain delay only for ejecta from massive stars (with mass >8 $M_{\odot }$ ) born after the halo-thick disk transition. In Fig. 1 we show the predicted star formation rate (SFR) expressed in $M_{\odot }$ pc^-2 Gyr^-1 as a function of the galactic time (Gyr) using the model of F04. We note that the SFR is the same for all galactocentric distances during the halo phase. The effect of the two infall model in presence of the threshold in the star formation is clearly shown: the star formation halts during the halo-thin disk transition and the duration of the gap varies as a function of galactocentric distance. At the solar neighborhood the gap is $\simeq$ 0.3 Gyr. This gap seems to be observed in the abundance ratio distribution as shown in Gratton et al. (2000) and Fuhrmann (1999). In Table 3 we report the times at different galactocentric distances at which the SFR in the thin disk begins ( $t_{\rm SFR}$ ) in the F04 model. Ejecta of intermediate-mass stars and type Ia SNe (which are most probably not clumped in OB associations) are not subject to the galactic fountain delay.

As shown in Table 2, a single superbubble can produce a delay in the mixing up to $\sim$ 250 Myr, but the average values are smaller, spanning the range between 40-140 Myr (Table 1). In the simulation, we considered different values up to 1 Gyr. It is possible that the Milky Way formed super-star clusters during more intense phases of star formation, as observed in M 82 (Melo et al. 2005). A delay of 1 Gyr can then be obtained if the number of massive stars in a cluster is $\sim$ 10⁴, which is consistent with the mass of the largest super-star clusters observed in M 82. We considered this long delay as an extreme case.

6 The metal cooling delay model

Roy & Kunth (1995) studied the dispersal and mixing of oxygen in the ISM of gas-rich galaxies. Due to a variety of hydrodynamical processes operating at scales ranging from 1 pc to greater than 10 kpc in the ISM, there are difficulties in estimating the dispersal and mixing timescale: (i) on large galactic scales ( $1 \geq\ l\ \geq 10$ kpc), turbulent diffusion of interstellar clouds in the shear flow of galactic differential rotation is able to remove azimuthal O/H fluctuations in less than 10⁹ yrs; (ii) at the intermediate scale ( $100 \geq\ l\ \geq 1000$ pc), cloud collisions and expanding supershells driven by evolving associations of massive stars, differential rotation and triggered star formation will re-distribute and mix gas efficiently in about 10⁸ yrs; (iii) at small scales ( $1 \geq\ l\ \geq 100$ pc), turbulent diffusion may be the dominant mechanism in cold clouds, while Rayleigh-Taylor and Kelvin-Helmhotz instabilities quickly develop in regions of gas ionized by massive stars, leading to full mixing in $\leq$ $2\times 10^6$ yrs. Malinie et al. (1993) claimed that due to chemical inhomogeneities observed for example in the age-metallicity relation in the solar neighborhood, re-mixing and star formation may be delayed by 10^8-9 yr.

Following the work of Thomas et al. (1998), we relaxed the IMA in the chemical evolution model by splitting the gas component into two different phases (cold and warm). The gas in the interstellar medium is heated by SN events and the stars cannot form in this ``warm gas phase''; only after the gas cools can stars form and then pollute the ISM. We implemented the two gas phases simply by means of a delay in the chemical enrichment. In this case: i) all stellar masses (both type II and type Ia SNe) and ii) both halo and disk stars, are affected by this delay.

7 Results

In this section we discuss our results. First we show how a galactic fountain delay can affect the chemical evolution model, then we present the results for the metal cooling delay model.

We show the model predictions for O, Mg, Si and Fe obtained in particular for the relations [el/Fe] versus [Fe/H] compared with the observational data and try to place constraints on the maximum possible delay.

7.1 Results for the galactic fountain delay model

We have taken into account different values for the delay generated by galactic fountain events from sequential SN explosions: 0.1 Gyr, 0.2 Gyr, 0.5 Gyr, 1 Gyr. We tested the effect at different galactocentric distances: 4, 8, 12 kpc.

Concerning the solar neighborhood, in Table 4 we report the solar abundances by mass as predicted by the F04 model and the delay models compared to the solar values of Asplund et al. (2005). In Fig. 2 we show the results for [O/Fe] versus [Fe/H] in the solar neighborhood compared to the observational data described in Sect 4. Our results are normalized to the ``best model'' of F04 values at 9.5 Gyr (the age of the formation of the solar system). As we can see from this figure and from Table 4, the solar abundances predicted by our models are substantially in agreement with those derived by Asplund et al. (2005). The standard model with no delay shows a discontinuity at $\sim$ -0.8 dex, and this is due to the gap in the SFR discussed before. In fact, during the gap, O stops being produced whereas Fe keeps being produced by type Ia SNe. The effect of the delay due to the fountains is therefore to increase this effect by increasing the duration of the gap.

$\begin{figure} \par\includegraphics[width=9cm]{11768fg2.eps} \end{figure}$

Figure 2:

The abundance ratio [O/Fe] as a function of [Fe/H] in the solar neighborhood. We compared the François et al. (2004) model (solid line) with our galactic fountain delay models: dotted line (0.1 Gyr), short dashed line (0.2 Gyr), long dashed line (0.5 Gyr), dashed dotted line (1 Gyr). The data are taken from the collection used in François et al. (2004) (filled green triangles) and from Bensby et al. (2005) (filled blue circles).

Open with DEXTER

In the description of the delay model, we emphasized that galactic fountains can be seen only in disk stars. The typical delay, due to the fact that massive stars are clumped in OB associations, is 0.1 Gyr. Referring to Fig. 2 we present a first strong result: a delay of 0.1 Gyr produces a negligible effect on the chemical evolution of the Galaxy in the solar neighborhood. We note that the data show a spread in the halo-thick disk transition phase ([Fe/H $]\simeq-0.77$ ). This spread can be explained in terms of a combination of: i) a threshold in the star formation, ii) a delay in the chemical enrichment from the massive stars due a to galactic fountain effect. Moreover, we note that the maximum possible delay, in order not to break the agreement with data, must be lower than 1 Gyr.

The same effect is shown in Figs. 3 and 4 where we analyzed the behavior of such a delay in a chemical evolution model for other two $\alpha$ elements: Mg and Si.

$\begin{figure} \par\includegraphics[width=9cm]{11768fg3.eps} \end{figure}$	Figure 3: The abundance ratio [Mg/Fe] as a function of [Fe/H] in the solar neighborhood. Notation as in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768fg4.eps} \end{figure}$	Figure 4: The abundance ratio [Si/Fe] as a function of [Fe/H] in the solar neighborhood. Notation as in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768fg5.eps} \end{figure}$	Figure 5: The abundance ratio [O/Fe] as a function of [Fe/H] at 4 and 12 kpc. Notation as in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768fg6.eps} \end{figure}$	Figure 6: The abundance ratio [Mg/Fe] as a function of [Fe/H] at 4 and 12 kpc. Notation as in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768fg7.eps} \end{figure}$	Figure 7: The abundance ratio [Si/Fe] as a function of [Fe/H] at 4 and 12 kpc Notation as in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768fg8.eps} \end{figure}$	Figure 8: The type Ia SN rate expressed in pc^-2 Gyr^-1 as a function of the galactic time (Gyr), as predicted by the two infall model of François et al. (2004) at 4, 8 and 12 kpc.
Open with DEXTER

$\begin{figure} \includegraphics[width=9cm]{11768fg9.eps} \end{figure}$	Figure 9: The abundance ratio [O/Fe] as a function of [Fe/H] at 4, 8 and 12 kpc for relative maximum delays as reported in Table 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f10.eps} \end{figure}$	Figure 10: Predicted and observed O abundance gradients in the galactocentric distance range 4-14 kpc. The data points are from Cepheids. The large squares with error bars represent average of the points with their errors. The black solid line is the François et al. (2004) model normalized to the mean value of the bin centered at 8 kpc (see Cescutti et al. 2007).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f11.eps} \end{figure}$	Figure 11: The abundance ratio [O/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our metal cooling delay model. For the O we considered the metallicity dependent yields of WW95. Solid line: model without delay; dotted line and dashed dotted line: 0.5 and 1 Gyr delays, respectively. Symbols as in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f12.eps} \end{figure}$	Figure 12: The abundance ratio [Mg/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our metal cooling delay model. Notation as in Fig. 11.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f13.eps} \end{figure}$	Figure 13: The abundance ratio [Si/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our the metal cooling delay model. Notation as in Fig. 11.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f14.eps} \end{figure}$	Figure 14: The abundance ratio [O/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our metal cooling delay model. For the O we considered the solar yields of WW95. Notation as in Fig. 11.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f15.eps} \end{figure}$	Figure 15: The abundance ratio [el/Fe] as a function of [Fe/H] for the Si and Mg in the solar neighborhood predicted by our metal cooling delay model. For the Si and Mg we considered the metal dependent yields of WW95. Notation as in Fig. 11.
Open with DEXTER

It is also interesting to test the fountain delay at different galactocentric distances. In Figs. 5-7 we report our results for O, Mg and Si, respectively. In each figure we plot the [el/Fe] vs. [Fe/H] at 4 and 12 kpc galactocentric distances. We note that the results are strongly dependent on the galactocentric distance. In fact, as explained before, the drop of the [el/Fe] quantity in the [el/Fe] vs. [Fe/H] plot is due to the iron ejected by the type Ia SNe. The discontinuity predicted at 4 kpc is greater than that predicted at larger galactocentric distances. This effect is due to the higher specific type Ia SN rate at 4 kpc than at larger distances. The specific type Ia SN rate is the SNIa rate per unit mass of gas and it increases toward the Galactic center, the reason being that while the type Ia SN rate is a factor of 8 higher than that in the solar vicinity, because of the higher SFR, the mass of gas is higher by only a factor of 2 relative to the solar region. Therefore, the effect of the pollution by type Ia SNe during the gap is enhanced.

Again in Figs. 5-7 we note that, at a fixed galactocentric distance, the effect of the galactic fountain delay depends also on the considered element: the Si which is also produced by type Ia SNe in a non negligible amount shows a smaller drop of the [Si/Fe] quantity compared to O and Mg.

Even if the galactic fountain effect in the [el/Fe] values is larger at 4 kpc because of the higher rate of type Ia SNe, the delays expected at 4 kpc are smaller with respect to outward galactocentric distances (as shown Tables 1 and 2), as a consequence of the higher gravitational pull. In Fig. 9 we show the [O/Fe] vs. [Fe/H] at 4, 8 and 12 kpc considering the maximum delays in each radius. In the case of a delay produced by a single OB association, the effect of galactic fountains is negligible.

Finally, we explored the effects of galactic fountains on the abundance gradient for oxygen. In Fig. 10 we plot the [O/H] as a function of the galactocentric distance. We note that the average delay due to galactic fountains is longer than 0.1 Gyr only for an OB association composed of 500 SNe at 12 kpc (Table 1); this event is very unlikely, thus the delay of 0.1 Gyr can be considered as an average upper limit for a delay produced by a single OB association at a galactocentric distance in the range 4-12 kpc. Referring to Fig. 10 we can conclude that the time delay produced by a Galactic fountain generated by an OB association has a negligible effect on the abundance gradient in the Galaxy disk.

7.2 Results for the metal cooling delay model

In this section we present the results for the metal cooling delay model. Referring to Malinie et al. (1993), we considered mixing delays of 0.5 Gyr and 1 Gyr. In Figs. 11-13 we show the effect of the metal cooling predicted by our model using the [el/Fe] vs. [Fe/H] plots. Thomas et al. (1998) already discussed the effect of a two- phase gas model relative to Mg. Referring to Fig. 12 we obtain a similar result, but the effect of our delay in the mixing is smaller. For the Si we have a similar behavior as can be seen in Fig. 13. The differences between ours and Thomas et al.'s results are probably due to the different adopted yields for massive stars and IMF. In fact, Thomas et al. adopted Thielemann et al. (1996) yields and the Salpeter (1955) IMF.

A different result is obtained for the [O/Fe] vs. [Fe/H] reported in Fig. 11. In this case, we find that the delay in the mixing leads to large differences in terms of chemical evolution models. We see that in the halo-thick disk phase, the predicted [O/Fe] values are much smaller than for the model with the IMA. The reason for this resides in the fact that in the model of F04, the yields used for O are the WW95 metallicity-dependent ones and in this case the delay induces a situation where the yields for Z=0, lower than those computed for the other metallicities, act for a longer time, thus producing the large depression in the [O/Fe] ratio. To demonstrate that this result is solely due to the choice of nucleosynthetic yields, we plot in Fig. 14 the metal cooling delay model results using, for the oxygen, the yields at solar metallicity given by WW95. As we can see from this figure, in this case the models with delay do not differ considerably compared to the reference model and the oxygen behaves similarly to the other $\alpha$ -elements. In Fig. 15 we report the [el/Fe] vs. [Fe/H] relations for the Mg and Si using for these two elements the metallicity dependent yields of WW95. As expected, the [el/Fe] ratios show a large depression in the halo-thick disk phase as in Fig. 11 due to the choice of metallicity-dependent yields. Therefore we can conclude that the metallicity-dependent yields of WW95 are not compatible with a delayed enrichment of the halo.

$\begin{figure} \par\includegraphics[width=9cm]{11768f16.eps} \end{figure}$	Figure 16: The abundance ratio [Fe/H] as a function of the galactic time [Gyr] in the solar neighborhood predicted by our metal cooling delay model. The data are taken from Ramirez et al. (2007) (filled red triangles). Notation as in Fig. 11.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{11768f17.eps} \end{figure}$	Figure 17: The abundance ratio [Mg/H] as a function of the galactic time [Gyr] in the solar neighborhood predicted by our metal cooling delay model. Notation as in Fig. 11.
Open with DEXTER

Finally, in Figs. 16 and 17 we report age-metallicity relations in the solar neighborhood for [Fe/H] and [Mg/H] respectively, predicted by our metal cooling delay model using the stellar yields adopted in F04. Concerning the evolution of the [Fe/H], we compare our results with the observational data of Ramirez et al. (2007). As one can see, the effects of the delays are more visible in the age-metallicity relations than in the abundance ratios versus [Fe/H], and the reason is that in the abundance ratios these differences are partly erased. We conclude that all delays considered are compatible with the observations due to the very large data spread for the age metallicity relation, but also gives that the age-metallicity relation is not a good constraint for chemical models.

8 Conclusions

In this paper we have studied the relaxation of IMA in chemical evolution models by means of the effects of a delay in the chemical enrichment produced by galactic fountain events and by means of a delay in the mixing due to chemical inhomogeneities in the disk (our metal cooling delay model). The main purpose of this work was to test the results of Paper I in a chemical evolution model. In the present paper, we tested the ``delay'' effect due to the finite and not negligible time for a cloud spend to fall back onto the disk.

Our main conclusions can be summarized as follows:

In the solar neighborhood, we showed that the average delay produced by the galactic fountains has a negligible effect on the chemical evolution for all the 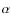$\alpha$ elements, we studied.
In the [el/Fe] versus [Fe/H] relations, the main feature of the galactic fountain is an enhancement of the drop in the [el/Fe] ratios occurring because of the two infall scenario. In fact, the drop in the standard model of F04 is due to the halt of the SFR which produces a halt in the production of the 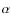$\alpha$ -elements while the Fe from type Ia SNe continues to be produced. The galactic fountain delay has the effect of increasing the period during which there is no pollution from type II SNe.
Results produced by the model with a galactic fountain delay of 1 Gyr are not compatible with observational data. On the other hand, any delay <1 Gyr could be acceptable, given the observed spread in the data.
The time delay produced by a Galactic fountain generated by an OB association has a negligible effect on the abundance gradients in the Galaxy disk.
The metal cooling delay model with the assumed delays (which are those suggested in the literature) has a very small effect on the chemical evolution in the solar neighborhood if yields not depending on metallicity are used.
On the other hand, in the case of the metal dependent yields of WW95, the results differ substantially from the reference model of F04 and do not fit the observations.

Acknowledgements

We thank the referee for the enlightening suggestions. We also thank F. Calura, G. Cupani and A. Saro for many useful discussions. We also thank I. J. Danziger for reading the manuscript. We acknowledge financial support from the PRIN 2007 MUR Prot. No. 2007JJC53X_001.

References

Alibés, A., Labay, J., & Canal, R. 2001, A&A, 370, 1103 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Andrievsky, S. M., Bersier, D., Kovtyukh, V. V., et al. 2002a, A&A, 384, 140 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Andrievsky, S. M., Kovtyukh, V. V., Luck R. E., et al. 2002b, A&A, 381, 32 [NASA ADS] [CrossRef] [EDP Sciences]
Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes III, F. N., Bash, ASP Conf. Ser., 336, 25 (In the text)
Bensby, T., Feltzing, S., & Lundstrom, I. 2004, A&A, 415, 155 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Bregman, J. N. 1980, ApJ, 365, 544 (In the text)
Carney, B. W., Wright, J. S., Sneden, C., et al. 1997, AJ, 114, 363 [NASA ADS] [CrossRef] (In the text)
Carretta, E., Gratton, R. G., Cohen, J. G., et al. 2002, AJ, 124, 481 [NASA ADS] [CrossRef] (In the text)
Cayrel, R., Depagne, E., Spite, M., et al. 2003, A&A, 416, 1117 [NASA ADS] [CrossRef] (In the text)
Cescutti, G., Matteucci, F., Francois, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Chang R. X., Hou J. L., Shu C. G., & Fu C. Q. 1999, A&AS, 141, 491 [NASA ADS] (In the text)
Chiappini, C., Matteucci, F., & Gratton, R., 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] (In the text)
Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] (In the text)
Chiappini, C., Matteucci, F., & Meynet, G. 2003a, A&A, 410, 257 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Chiappini C., Romano D., & Matteucci F. 2003b, MNRAS, 339, 63 [NASA ADS] [CrossRef]
Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] (In the text)
François, P., & Matteucci, F. 1993, A&A, 280, 136 [NASA ADS]
François P., Matteucci F., Cayrel R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Fraternali, F., & Binney, J. 2008, MNRAS, 386, 935 [NASA ADS] [CrossRef] (In the text)
Fuhrmann, K. 1999, Ap&SS, 338,161 (In the text)
Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] (In the text)
Gratton, R. G., & Sneden, C. 1988, A&A, 204, 193 [NASA ADS] (In the text)
Gratton, R., Carretta, E., Matteucci, F., & Sneden, C. 2000, A&A, 358, 671 [NASA ADS] (In the text)
Greggio, L., & Renzini, A. 1983, A&A, 118, 217 [NASA ADS] (In the text)
Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
Harfst, S., Theis, Ch., & Hensler, G. 2006, A&A, 449, 509 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJ Suppl. Ser., 125, 439 [NASA ADS] [CrossRef] (In the text)
Kompaneets, A. S. 1960, Soviet Phys. Dokl., 5, 46 [NASA ADS] (In the text)
Kennicutt, R. C., Jr. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] (In the text)
Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] (In the text)
Luck, R. E., Gieren, W. P., & Andrievsky, S. M., et al. 2003, A&A, 401, 939 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Maeder, A., & Maynet, G. 1989, A&A, 210, 155 [NASA ADS] (In the text)
Malinie, G., Hartmann, D. H., Clayton, D. D., & Mathews G. J. 1993, ApJ, 413, 633 [NASA ADS] [CrossRef] (In the text)
Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Martin, C. L., & Kennicutt, R. C., Jr. 2001, ApJ, 555, 301 [NASA ADS] [CrossRef] (In the text)
Matteucci, F. 2001, The Chemical Evolution Of The Galaxy (Kluwer Academic Publishers) (In the text)
Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] (In the text)
Matteucci, M. F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] (In the text)
Matteucci, F., Raiteri, C. M., Busson, M., Gallino, R., & Gratton, R. 1993, A&A, 272, 421 [NASA ADS] (In the text)
Mc Low, M. M., McCray, R., & Norman, M. L. 1989, ApJ, 1989, 337, 141 (In the text)
McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] (In the text)
Melioli, C., Brighenti, F., D'Ercole, A., & de Gouveia Dal Pino, E.M. 2008, MNRAS, 388, 573 [NASA ADS] [CrossRef] (In the text)
Melioli, C., Brighenti, F., D'Ercole, A., & de Gouveia Dal Pino, E. M. 2009, MNRAS, accepted, [arXiv:0903.0720] (In the text)
Melo, V. L., Munoz-Tunon, C., Maiz-Apellaniz, J., & Tenorio-Tagle, G. 2005, ApJ, 619, 700 [CrossRef] (In the text)
Nissen, P. E., & Schuster, W. J. 1997, A&A, 326, 751 [NASA ADS] (In the text)
Nissen, P. E., Primas, F., Asplund, M., & Lambert, D. L. 2002, A&A, 390, 235 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Pagel, B. E. J., & Tautvaisiene, G. 1995, MNRAS, 276, 505 [NASA ADS] (In the text)
Prantzos, N., & Boisser, S. 2000, MNRAS, 313, 338 [NASA ADS] [CrossRef] (In the text)
Ramirez, I., Prieto, C. A., & Lambert, D. L. 2007, A&A, 465, 271 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Recchi, S., Matteucci, F., & D'Ercole, A. 2001, MNRAS, 322, 800 [NASA ADS] [CrossRef] (In the text)
Reid, M. J. 1993, ARA&A, 31, 345 [NASA ADS] [CrossRef] (In the text)
Rieschick, A., & Hensler, G. 2000, in Cosmic Evolution and Galaxy Formation: Structure, Interactions and Feedback, ASP Conferences Series, ed. J. Franco, E. Terlevich, O. Lòpez Cruz & I. Aretxaga (In the text)
Roy, J., & Kunth, D. 1995, A&A, 294, 432 [NASA ADS] (In the text)
Ryan, S., Norris, J. E., & Bessell, M. S. 1991, AJ, 102, 303 [NASA ADS] [CrossRef] (In the text)
Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
Scalo, J. M. 1986, FCPh, 11, 1 [NASA ADS] (In the text)
Schmidt, M. 1963, ApJ, 137, 758 [NASA ADS] [CrossRef] (In the text)
Searle, L., & Sargent, W. L. W. 1972, ApJ, 173, 25 [NASA ADS] [CrossRef]
Spitoni, E., Recchi, S., & Matteucci, F. 2008, A&A, 484, 743 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Stephens, A. 1999, AJ, 117, 1771 [NASA ADS] [CrossRef] (In the text)
Talbot, R. J., Jr., & Arnett, W. D. 1973, 186, 51 (In the text)
Tenorio-Tagle, G. 1996, AJ, 111, 1641 [NASA ADS] [CrossRef] (In the text)
Thielemann, F.-K., Nomoto, K., & Hashimoto, M. 1996, ApJ, 460, 408 [NASA ADS] [CrossRef] (In the text)
Thomas, D., Greggio, L., & Bender, R. 1998, MNRAS, 296, 119 [NASA ADS] [CrossRef] (In the text)
Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] (In the text)
Tinsley, B. M. 1974, ApJ, 192, 629 [NASA ADS] [CrossRef] (In the text)
Tinsley, B. M. 1975, ApJ, 197, 159 [NASA ADS] [CrossRef] (In the text)
van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS., 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Woosley, S. E., & Weaver, T. A. 1995, ApJ, 101, 181 [NASA ADS] [CrossRef] (In the text)

All Tables

Table 1: The average time $\left\langle t_{\rm total}\right\rangle$ [Myr].

Table 2: The maximum $t_{\rm total}$ as a function of the galactocentric distance.

Table 3: Beginning of the star formation in the disk after the halo-thick disk transition ( $t_{\rm SFR}$ ).

Table 4: Mass fractions of several elements yielded by the François et al. (2004) model and the delay model at the galactic age of 9.5 Gyr compared to the solar values of Asplund et al. (2005).

All Figures

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{11768fg1.eps} \end{figure}$	Figure 1: The star formation rate expressed in $M_{\odot }$ pc^-2 Gyr^-1 as a function of the galactic time (in Gyr), as predicted by the two infall model of François et al. (2004) at 4 (dotted line), 8 (dashed line) and 12 kpc (solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg2.eps} \end{figure}$	Figure 2: The abundance ratio [O/Fe] as a function of [Fe/H] in the solar neighborhood. We compared the François et al. (2004) model (solid line) with our galactic fountain delay models: dotted line (0.1 Gyr), short dashed line (0.2 Gyr), long dashed line (0.5 Gyr), dashed dotted line (1 Gyr). The data are taken from the collection used in François et al. (2004) (filled green triangles) and from Bensby et al. (2005) (filled blue circles).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg3.eps} \end{figure}$	Figure 3: The abundance ratio [Mg/Fe] as a function of [Fe/H] in the solar neighborhood. Notation as in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg4.eps} \end{figure}$	Figure 4: The abundance ratio [Si/Fe] as a function of [Fe/H] in the solar neighborhood. Notation as in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg5.eps} \end{figure}$	Figure 5: The abundance ratio [O/Fe] as a function of [Fe/H] at 4 and 12 kpc. Notation as in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg6.eps} \end{figure}$	Figure 6: The abundance ratio [Mg/Fe] as a function of [Fe/H] at 4 and 12 kpc. Notation as in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg7.eps} \end{figure}$	Figure 7: The abundance ratio [Si/Fe] as a function of [Fe/H] at 4 and 12 kpc Notation as in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768fg8.eps} \end{figure}$	Figure 8: The type Ia SN rate expressed in pc^-2 Gyr^-1 as a function of the galactic time (Gyr), as predicted by the two infall model of François et al. (2004) at 4, 8 and 12 kpc.
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=9cm]{11768fg9.eps} \end{figure}$	Figure 9: The abundance ratio [O/Fe] as a function of [Fe/H] at 4, 8 and 12 kpc for relative maximum delays as reported in Table 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f10.eps} \end{figure}$	Figure 10: Predicted and observed O abundance gradients in the galactocentric distance range 4-14 kpc. The data points are from Cepheids. The large squares with error bars represent average of the points with their errors. The black solid line is the François et al. (2004) model normalized to the mean value of the bin centered at 8 kpc (see Cescutti et al. 2007).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f11.eps} \end{figure}$	Figure 11: The abundance ratio [O/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our metal cooling delay model. For the O we considered the metallicity dependent yields of WW95. Solid line: model without delay; dotted line and dashed dotted line: 0.5 and 1 Gyr delays, respectively. Symbols as in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f12.eps} \end{figure}$	Figure 12: The abundance ratio [Mg/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our metal cooling delay model. Notation as in Fig. 11.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f13.eps} \end{figure}$	Figure 13: The abundance ratio [Si/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our the metal cooling delay model. Notation as in Fig. 11.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f14.eps} \end{figure}$	Figure 14: The abundance ratio [O/Fe] as a function of [Fe/H] in the solar neighborhood predicted by our metal cooling delay model. For the O we considered the solar yields of WW95. Notation as in Fig. 11.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f15.eps} \end{figure}$	Figure 15: The abundance ratio [el/Fe] as a function of [Fe/H] for the Si and Mg in the solar neighborhood predicted by our metal cooling delay model. For the Si and Mg we considered the metal dependent yields of WW95. Notation as in Fig. 11.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f16.eps} \end{figure}$	Figure 16: The abundance ratio [Fe/H] as a function of the galactic time [Gyr] in the solar neighborhood predicted by our metal cooling delay model. The data are taken from Ramirez et al. (2007) (filled red triangles). Notation as in Fig. 11.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{11768f17.eps} \end{figure}$	Figure 17: The abundance ratio [Mg/H] as a function of the galactic time [Gyr] in the solar neighborhood predicted by our metal cooling delay model. Notation as in Fig. 11.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.