| Issue |
A&A
Volume 504, Number 1, September II 2009
|
|
|---|---|---|
| Page(s) | 67 - 71 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200809802 | |
| Published online | 02 July 2009 | |
A comparison of the gamma-ray bursts detected by BATSE and Swift![[*]](/icons/foot_motif.png)
D. Huja1 - A. Mészáros1 - J. Rípa1
Charles University, Faculty of Mathematics and Physics, Astronomical Institute, V Holesovickách 2, 180 00 Prague 8, Czech Republic
Received 18 March 2008 / Accepted 22 May 2009
Abstract
Aims. The durations of 388 gamma-ray bursts detected by the Swift satellite, are analyzed statistically to search for subgroups. The results are then compared with results obtained earlier for data from the BATSE database.
Methods. We apply the standard ![]() test.
test.
Results. As for data in the BATSE database, short and long subgroups are also reliably identified in the Swift data. An intermediate subgroup is also seen in the Swift database.
Conclusions. The analysis of the entire sample of 388 GRBs provides a support for the existence of three subgroups.
Key words: gamma rays: bursts
1 Introduction
During the years 1991-2000, 2704 gamma-ray bursts (GRBs) were detected by the BATSE instrument onboard the Compton Gamma-Ray Observatory (Meegan et al. 2001). After the launch of the Swift satellite (in November 2004), the frequency of GRBs detected by this instrument has been cca 100/year (Gehrels et al. 2005). Any comparison of different databases is highly useful. For example, in the BATSE database, three subgroups (short, intermediate, and long GRBs) have been robustly identified (Horváth et al. 2006; Chattopadhyay et al. 2007, and references therein). The short and long subgroups are physically different phenomena (Balázs et al. 2003). However, in contrast to this, it remains possible that the intermediate subgroup is not a true physically independent subgroup and it is present in the BATSE database because of e.g. some observational biases caused by the BATSE triggering procedure (Horváth et al. 2006). The most reliably way, to resolve the debate concerning whether subgroups or bias are present is to analyze an independent database acquired by another instrument. Hence, it is natural to ask whether these subgroups are also seen in the Swift data-set?
The purpose of this article is the statistical analysis of the Swift
database, which may answer this question.
We proceed in an identical way to the successful statistical analysis
completed for the BATSE catalog (Horváth 1998) leading to the discovery of the
third subgroup
(Balázs et al. 2003; Hakkila et al. 2000; Mukherjee et al. 1998; Horvath 1999; Bagoly et al. 1998; Chattopadhyay et al. 2007; Rajaniemi & Mähönen 2002; Horváth 2003; Horváth et al. 2006; Horváth 2002).
A statistical study of the Swift database - using the
maximum likelihood method - has already shown evidence of a third
subgroup
(Horváth et al. 2008). The ![]() fitting was not used because of the smallness of the
population. However, historically, the first evidence of the third
subgroup in the BATSE database came from the simple
fitting was not used because of the smallness of the
population. However, historically, the first evidence of the third
subgroup in the BATSE database came from the simple ![]() method
(Horváth 1998), and the number of 388 data points not should be too small for this
testing. In all cases, one has to probe this fitting also for the
Swift data sample. Since approximately
one third of the Swift's bursts have already well determined redshifts
(in contrast to the BATSE's GRBs, for which only a few objects have measured
redshifts, Ramirez-Ruiz & Fenimore 2000; Bagoly et al. 2003; Norris 2002),
some additional tests can also be done on samples with and
without redshifts.
method
(Horváth 1998), and the number of 388 data points not should be too small for this
testing. In all cases, one has to probe this fitting also for the
Swift data sample. Since approximately
one third of the Swift's bursts have already well determined redshifts
(in contrast to the BATSE's GRBs, for which only a few objects have measured
redshifts, Ramirez-Ruiz & Fenimore 2000; Bagoly et al. 2003; Norris 2002),
some additional tests can also be done on samples with and
without redshifts.
The paper is organized as follows. The samples are defined in Sect. 2
and also listed in detail at the end of the article.
Section 3 presents the ![]() fitting of these samples.
Section 4 discusses the results of this paper, and Sect. 5 summarizes them.
fitting of these samples.
Section 4 discusses the results of this paper, and Sect. 5 summarizes them.
2 The samples
We define two samples from the Swift data-set (Gehrels et al. 2005): the sample of GRBs without measured redshifts (z) and the sample with measured redshifts. These two samples are collected in Tables 4 and 5. We compiled these tables for convenience; each table contains the name of the GRB, its BAT duration T90, and BAT fluence at range 15-150 keV, BAT 1-sec peak photon flux at range 15-150 keV, and Table 5 also provides its redshift. Only these bursts were taken into account, of which the GRB duration was measured. The combined data sets cover the period from November 2004 to the end of February 2009; the first (last) object is GRB041217 (GRB090205). Table 4 (5) contain 258 (130) GRBs, and hence the total number of GRBs, which are studied in this paper, is 388.
In this paper, we study both samples separately and also together as one single set (the complete sample).
Table 1:
Results of the ![]() fitting of the complete sample of
388 GRBs.
fitting of the complete sample of
388 GRBs.
3 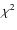 fitting of the GRB durations
fitting of the GRB durations
3.1 The entire sample
Since the ![]() fitting of the GRB duration distribution and the F-test
were successfully used in the work Horváth (1998)
(presenting the first evidence of three GRB subgroups), we proceed in a identical way,
but with the Swift's data.
fitting of the GRB duration distribution and the F-test
were successfully used in the work Horváth (1998)
(presenting the first evidence of three GRB subgroups), we proceed in a identical way,
but with the Swift's data.
The complete sample consists of 388 events with measured
T90.
We fitted the histogram of their decimal
![]() values
seven
times (fits I.-VII.). The results are collected in Table 1,
and the fit No.VI. is seen in Fig. 1. We chose different
binnings for independent fittings of various numbers of bins, with
different bin edges. The bin widths also differ.
In each bin, we applied the sole restriction that the theoretically expected number of GRBs
should be higher than 5.
values
seven
times (fits I.-VII.). The results are collected in Table 1,
and the fit No.VI. is seen in Fig. 1. We chose different
binnings for independent fittings of various numbers of bins, with
different bin edges. The bin widths also differ.
In each bin, we applied the sole restriction that the theoretically expected number of GRBs
should be higher than 5.
The histogram was first fitted with one single theoretical Gaussian
curve of two free parameters (mean ![]() and standard deviation
and standard deviation
![]() ). The best-fit model parameters corresponding to the minimal
). The best-fit model parameters corresponding to the minimal ![]() fit are, e.g.,
for fit No.VI the following:
fit are, e.g.,
for fit No.VI the following:
![]() ,
,
![]() with
with
![]() .
The
goodness-of-fit for
15 - 2 - 1 = 12 degrees of freedom
(dof) provides a
rejection at the level of
.
The
goodness-of-fit for
15 - 2 - 1 = 12 degrees of freedom
(dof) provides a
rejection at the level of ![]() (Kendall & Stuart 1973; Trumpler & Weaver 1953).
This represents a rejection of the null-hypothesis
(i.e. one Gaussian curve is sufficient)
that it is correct, because the probability
of the mistake for this rejection is not higher than
(Kendall & Stuart 1973; Trumpler & Weaver 1953).
This represents a rejection of the null-hypothesis
(i.e. one Gaussian curve is sufficient)
that it is correct, because the probability
of the mistake for this rejection is not higher than ![]() .
The complete sample cannot be described by one single Gaussian curve.
The same situation is also true for the remaining six fittings.
.
The complete sample cannot be described by one single Gaussian curve.
The same situation is also true for the remaining six fittings.
The fitting with the sum of two Gaussian curves (five free parameters:
two means, two standard deviations, and one weight w2(since the first weight is equal to 1-w2)) gave for the
fit No.VI
![]() .
(Note that the value of w2 requires
that 17% (83%) of GRBs should belong to the short (long) subgroup.)
Here d.o.f. =
15 - 5 - 1 = 9 and we
obtained an excellent fit with the significance level 58.6% (i.e.,
if we suppose that the fit is incorrect, then the probability that
this assumption is wrong is higher than 58.6%). The assumption
that the duration distribution is represented by the sum of two
Gaussian curves cannot be - from the statistical point of view - rejected.
The best-fit curve is also presented in Fig. 1, showing a good
correspondence with measured data. The remaining six fits again provide
similar results.
.
(Note that the value of w2 requires
that 17% (83%) of GRBs should belong to the short (long) subgroup.)
Here d.o.f. =
15 - 5 - 1 = 9 and we
obtained an excellent fit with the significance level 58.6% (i.e.,
if we suppose that the fit is incorrect, then the probability that
this assumption is wrong is higher than 58.6%). The assumption
that the duration distribution is represented by the sum of two
Gaussian curves cannot be - from the statistical point of view - rejected.
The best-fit curve is also presented in Fig. 1, showing a good
correspondence with measured data. The remaining six fits again provide
similar results.
![\begin{figure}
\par\includegraphics[width=9.5cm,clip]{18134who.eps}
\end{figure}](/articles/aa/full_html/2009/34/aa09802-08/Timg25.png) |
Figure 1:
Fitting of the
|
| Open with DEXTER | |
We also performed the fitting with the sum of three Gaussian
curves (eight parameters: three means, three standard deviations, and two
independent weights), and obtained an excellent fit with
![]() for fit no.VI, because the goodness-of-fit implies that
for d.o.f. =
15 - 8 - 1 = 6, the significance level is 88.2%.
The best-fit curve is also seen in Fig. 1, which indicate closer
correspondence with the measured data. The same excellent fits are also
obtained for the remaining six binnings.
for fit no.VI, because the goodness-of-fit implies that
for d.o.f. =
15 - 8 - 1 = 6, the significance level is 88.2%.
The best-fit curve is also seen in Fig. 1, which indicate closer
correspondence with the measured data. The same excellent fits are also
obtained for the remaining six binnings.
The key question is whether the decreasing
![]() statistically significant? To answer this question, we proceed similarly to Horváth (1998) and used the test
proposed by Band et al. (1997) in Appendix A. The significance level from the F-test is 3.63%. This implies that the rejection of the null-hypothesis (i.e. that the sum of the two Gaussian curves is enough) is adequate, because the probability of the mistake at this rejection level is not higher than 3.63%. We arrive at the conclusion that the strengthening of
statistically significant? To answer this question, we proceed similarly to Horváth (1998) and used the test
proposed by Band et al. (1997) in Appendix A. The significance level from the F-test is 3.63%. This implies that the rejection of the null-hypothesis (i.e. that the sum of the two Gaussian curves is enough) is adequate, because the probability of the mistake at this rejection level is not higher than 3.63%. We arrive at the conclusion that the strengthening of ![]() need not be a fluctuation. Similar results were obtained for the remaining six fits - only for fit No.VII was the significance just above the usual 5% limit. (The significances lower than 5% are denoted by boldface.) In other words, the introduction of the third subgroup - purely from the statistical point of view - is significant for six of the seven fits completed. We note that the same F-test can also be applied to the difference
need not be a fluctuation. Similar results were obtained for the remaining six fits - only for fit No.VII was the significance just above the usual 5% limit. (The significances lower than 5% are denoted by boldface.) In other words, the introduction of the third subgroup - purely from the statistical point of view - is significant for six of the seven fits completed. We note that the same F-test can also be applied to the difference
![]() ,
and we always obtain the conclusion that the introduction of the second subgroup - instead of the one single group - is strongly supported.
,
and we always obtain the conclusion that the introduction of the second subgroup - instead of the one single group - is strongly supported.
3.2 The sample with z
Table 2:
Results of the ![]() fitting of the sample of 130 GRBs with
the known redshifts.
fitting of the sample of 130 GRBs with
the known redshifts.
The sample contains 130 events with duration information. We also performed seven fits, but the number of bins had to be reduced because of the lower number of objects in the sample. We again in a different way binned data - fits VI. and VII. had 17 bins, but the structure was different. In each bin again the number of GRBs was higher than 5. The results are collected in Table 2, and fit No.II. is shown in Fig. 2.
Here the results, compared with the entire sample, differ for two reasons. First, the fits with one single Gaussian curve are also acceptable, and only for two fits does the F-test show that the introduction of the second subgroup is adequate. Second, the introduction of the third subgroup is not needed from the F-test. All this indicates that this sample can be defined by one single group, and even the separation between short and long GRBs is not needed.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{18134wiz.eps}
\end{figure}](/articles/aa/full_html/2009/34/aa09802-08/Timg29.png) |
Figure 2:
Fitting of
|
| Open with DEXTER | |
3.3 The sample without z
Table 3:
Results of the ![]() fitting of the sample without the known redshift with
258 GRBs.
fitting of the sample without the known redshift with
258 GRBs.
This sample contains 258 events with duration information. We also completed seven fits with different binnings. In each bin, the number of GRBs was again higher than 5. The results are presented in Table 3, and fit No.I. is shown in Fig. 3.
Compared with the entire sample, the results are similar - except that, the introduction of the third subgroup is not needed according to the F-test. All of this shows that this sample can be described well by the sum of two and only two subgroups.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{18134woz.eps}
\end{figure}](/articles/aa/full_html/2009/34/aa09802-08/Timg30.png) |
Figure 3:
Fitting of
|
| Open with DEXTER | |
4 Discussion of the results
We first highlight that we have proven that short and long subgroups
also exist in the Swift data-set. Both the complete sample and the sample with
no redshifts have been found to contain these two subgroups, because
fits attempted with one single Gaussian curve are clearly wrong.
It is also remarkable that the weight of the short
subgroup agrees with this expectation. As follows from
Horváth et al. (2006), in the BATSE catalog the populations of the short,
intermediate, and long bursts are have in terms of number the ratio 20:10:70.
Nevertheless, because the short bursts are harder and Swift is more sensitive to
softer GRBs, one may expect that in the Swift database the population
of short GRBs should be comparable to or lower than 20% because of
instrumental reasons. The weights derived for the entire sample (being between
10 and 26%) agree with this expectation. Entire the other values of the best-fit model parameters - i.e. two means and two standard deviations - are also roughly in the ranges expected on the basis of the BATSE values. The differences can be given by the different instrumentations. For example, the mean values of the
![]() should be slightly longer in the Swift database than for the BATSE data (Band 2006; Barthelmy et al. 2005). In Horváth (1998), the BATSE's means are -0.35 (short) and 1.52 (long), respectively. We obtained for the complete sample values from -0.01 to
0.91 (short) and from 1.60 to 1.94 (long), respectively. In terms of short and long GRBs,
all this implies that the situation is almost identical to that of the BATSE data-set.
should be slightly longer in the Swift database than for the BATSE data (Band 2006; Barthelmy et al. 2005). In Horváth (1998), the BATSE's means are -0.35 (short) and 1.52 (long), respectively. We obtained for the complete sample values from -0.01 to
0.91 (short) and from 1.60 to 1.94 (long), respectively. In terms of short and long GRBs,
all this implies that the situation is almost identical to that of the BATSE data-set.
For the sample with known redshifts, the situation is different, because the fits still allow one single Gaussian curve. This result can be easily explained by selection effects. It is well-known that the observational determination of the redshifts in the Swift data sample is easier for long than short bursts because of observational strategies, i.e., it is more complicated to detect and follow the afterglows of short GRBs (Gehrels et al. 2005).
Concerning the third intermediate subgroup,
the complete sample also supports its existence six out of
seven tests inferred significances of below ![]() .
Hence, strictly speaking, the third subclass does exist and the
probability of the mistake in this claim is not higher than x%,
where
2.52 < x < 5.41. This result agrees with
expectations, once a comparison with the BATSE database is provided.
As stated in the Introduction, for the BATSE database the first evidence
of a third subgroup was provided by this
.
Hence, strictly speaking, the third subclass does exist and the
probability of the mistake in this claim is not higher than x%,
where
2.52 < x < 5.41. This result agrees with
expectations, once a comparison with the BATSE database is provided.
As stated in the Introduction, for the BATSE database the first evidence
of a third subgroup was provided by this ![]() method, and hence for the
Swift database this test should also provide positive support for this subgroup,
if the two datasets are comparable. It is the key result of this article
that this expectation is fulfilled. Our study has shown that the
classical
method, and hence for the
Swift database this test should also provide positive support for this subgroup,
if the two datasets are comparable. It is the key result of this article
that this expectation is fulfilled. Our study has shown that the
classical ![]() fitting - in combination with F-test - may
well also work in the Swift database as for the BATSE database
(Horváth 1998).
fitting - in combination with F-test - may
well also work in the Swift database as for the BATSE database
(Horváth 1998).
Horváth et al. (2008) confirmed the existence of a third subgroup in the Swift dataset by applying the
maximum likelihood (ML) method. Our significance of between 2.52% and
5.41% is weaker than the 0.46% significance obtained by Horváth et al. (2008),
as expected, because the ML method is a more robust
statistical test. This is seen from new two studies, too: the ML test
applied to the databases of RHESSI (Rípa et al. 2009) and BeppoSAX (Horváth 2009)
satellites, respectively,
confirmed the existence of the third intermediate subclass; on the other
hand, the ![]() test was either not of high enough significance
for RHESSI data (Rípa et al. 2009) or was not used at all for BeppoSAX data
(Horváth 2009).
test was either not of high enough significance
for RHESSI data (Rípa et al. 2009) or was not used at all for BeppoSAX data
(Horváth 2009).
It is also expected that the mean
![]() for the intermediate group should be much higher in the
Swift database because of the different redshift distributions
(Band 2006; Bagoly et al. 2006; Jakobsson et al. 2006). The mean value of the BATSE's
intermediate subgroup is 0.64 (Horváth 1998), but here the value is
between
1.02 and 1.64. Horváth et al. (2008) also obtained a similar value of
(1.107). Hence, the typical durations also agree with expectations.
for the intermediate group should be much higher in the
Swift database because of the different redshift distributions
(Band 2006; Bagoly et al. 2006; Jakobsson et al. 2006). The mean value of the BATSE's
intermediate subgroup is 0.64 (Horváth 1998), but here the value is
between
1.02 and 1.64. Horváth et al. (2008) also obtained a similar value of
(1.107). Hence, the typical durations also agree with expectations.
The sample with no redshifts exhibited to sign of a third subgroup, which may be due to the lower number of objects in the sample. The sample with known redshifts is strongly biased by selection effects, and even here the existence of the short subgroup was unclear. Hence, we conclude that the existence of a third subgroup is unclear.
5 Conclusions
Since the ![]() fitting of the GRB duration distribution and the F-test
were successfully used in the work Horváth (1998), which presented the
first evidence of three GRB subgroups, we have proceeded identically,
but with the Swift's data.
fitting of the GRB duration distribution and the F-test
were successfully used in the work Horváth (1998), which presented the
first evidence of three GRB subgroups, we have proceeded identically,
but with the Swift's data.
The results may be summarized in the following four points:
- 1.
- For the short and long subgroups, all of our findings agree with
expectations: they are also detected in the Swift
database and weight of the
short subgroup is lower, which may be because of the Swift's
higher effective sensitivity to softer bursts.
- 2.
- The complete sample of 388 objects appears to contain three
subgroups,
because from seven fits the complete sample, six have
confirmed the existence of the intermediate subgroup on a lower than 5%
significance level. Hence, for the Swift database, the
situation is similar to that of the BATSE dataset, although our signficances
are lower than the measurement of >0.02% of Horváth (1998).
- 3.
- The samples with and without known redshifts are separately either not
enough populated, or strongly biased. Hence, no far reaching
conclusions can be drawn about them.
- 4.
- As for the BATSE database, it is shown again that the classical
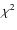 test - in
combination with the F-test - is also effective for the Swift GRB sample.
test - in
combination with the F-test - is also effective for the Swift GRB sample.
Acknowledgements
Thanks are due to valuable discussions with Z. Bagoly, L.G. Balázs, I. Horváth, and P. Veres. This study was supported by the GAUK grant No. 46307, by the OTKA grants No. T48870 and K77795, by the Grant Agency of the Czech Republic grant No. 205/08/H005, and by the Research Program MSM0021620860 of the Ministry of Education of the Czech Republic. The useful remarks of the referee, C. Guidorzi, are kindly acknowledged.
References
- Bagoly, Z., Csabai, I., Mészáros, A., et al. 2003, A&A, 398, 919 [NASA ADS] [CrossRef] [EDP Sciences]
- Bagoly, Z., Mészáros, A., Balázs, L. G., et al. 2006, A&A, 453, 797 [NASA ADS] [CrossRef] [EDP Sciences]
- Bagoly, Z., Meszaros, A., Horvath, I., Balazs, L. G., & Meszaros, P. 1998, ApJ, 498, 342 [NASA ADS] [CrossRef]
- Balázs, L. G., Bagoly, Z., Horváth, I., Mészáros, A., & Mészáros, P. 2003, A&A, 401, 129 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Band, D. L. 2006, ApJ, 644, 378 [NASA ADS] [CrossRef]
- Band, D. L., Ford, L. A., Matteson, J. L., et al. 1997, ApJ, 485, 747 [NASA ADS] [CrossRef] (In the text)
- Barthelmy, S. D., Chincarini, G., Burrows, D. N., et al. 2005, Nature, 438, 994 [NASA ADS] [CrossRef]
- Chattopadhyay, T., Misra, R., Chattopadhyay, A. K., & Naskar, M. 2007, ApJ, 667, 1017 [NASA ADS] [CrossRef]
- Gehrels et al. 2005, (Swift team), http://heasarc.gsfc.nasa.gov/docs/swift/archive/grb_table/ (In the text)
- Hakkila, J., Haglin, D. J., Pendleton, G. N., et al. 2000, ApJ, 538, 165 [NASA ADS] [CrossRef]
- Horváth, I. 1998, ApJ, 508, 757 [NASA ADS] [CrossRef] (In the text)
- Horvath, I. 1999, J. Korean Phys. Soc., 35, 629
- Horváth, I. 2002, A&A, 392, 791 [NASA ADS] [CrossRef] [EDP Sciences]
- Horváth, I. 2003, Statistical Challenges in Modern Astronomy III., ed. E. D. Feigelson & G. J. Babu (Berlin: Springer), 439
- Horváth, I. 2009, ASS, in press, [arXiv:0905.0860] (In the text)
- Horváth, I., Balázs, L. G., Bagoly, Z., Ryde, F., & Mészáros, A. 2006, A&A, 447, 23 [NASA ADS] [CrossRef] [EDP Sciences]
- Horváth, I., Balázs, L. G., Bagoly, Z., & Veres, P. 2008, A&A, 489, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jakobsson, P., Levan, A., Fynbo, J. P. U., et al. 2006, A&A, 447, 897 [NASA ADS] [CrossRef] [EDP Sciences]
- Kendall, M. G. & Stuart, A. 1973, The Advanced Theory of Statistics (London: Griffin)
- Meegan, C. A., et al. 2001, Current BATSE Gamma-Ray Burst Catalog, http://gammaray.msfc.nasa.gov/batse/grb/catalog (In the text)
- Mukherjee, S., Feigelson, E. D., Jogesh Babu, G., et al. 1998, ApJ, 508, 314 [NASA ADS] [CrossRef]
- Norris, J. P. 2002, ApJ, 579, 386 [NASA ADS] [CrossRef]
- Rajaniemi, H. J. & Mähönen, P. 2002, ApJ, 566, 202 [NASA ADS] [CrossRef]
- Ramirez-Ruiz, E. & Fenimore, E. E. 2000, ApJ, 539, 712 [NASA ADS] [CrossRef]
- Trumpler, R. J. & Weaver, H. F. 1953, Statistical Astronomy (Berkeley: University of California Press)
- Rípa, J., Mészáros, A., Wigger, C., et al. 2009, A&A, 498, 399 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Online Material
Table 4: Swift GRBs with no measured redshifts; Part I.
Table 4: Swift GRBs with no measured redshifts; Part II.
Table 4: Swift GRBs with no measured redshifts; Part III.
Table 4: Swift GRBs with no measured redshifts; Part IV.
Table 4: Swift GRBs with no measured redshifts; Part V.
Table 5: Swift GRBs with known redshifts; Part I.
Table 5: Swift GRBs with known redshifts; Part II.
Table 5: Swift GRBs with known redshifts; Part III.
Footnotes
- ... Swift
![[*]](/icons/foot_motif.png)
- Tables 4 and 5 are only available in electronic form at http://www.aanda.org
All Tables
Table 1:
Results of the ![]() fitting of the complete sample of
388 GRBs.
fitting of the complete sample of
388 GRBs.
Table 2:
Results of the ![]() fitting of the sample of 130 GRBs with
the known redshifts.
fitting of the sample of 130 GRBs with
the known redshifts.
Table 3:
Results of the ![]() fitting of the sample without the known redshift with
258 GRBs.
fitting of the sample without the known redshift with
258 GRBs.
Table 4: Swift GRBs with no measured redshifts; Part I.
Table 4: Swift GRBs with no measured redshifts; Part II.
Table 4: Swift GRBs with no measured redshifts; Part III.
Table 4: Swift GRBs with no measured redshifts; Part IV.
Table 4: Swift GRBs with no measured redshifts; Part V.
Table 5: Swift GRBs with known redshifts; Part I.
Table 5: Swift GRBs with known redshifts; Part II.
Table 5: Swift GRBs with known redshifts; Part III.
All Figures
![\begin{figure}
\par\includegraphics[width=9.5cm,clip]{18134who.eps}
\end{figure}](/articles/aa/full_html/2009/34/aa09802-08/Timg25.png) |
Figure 1:
Fitting of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{18134wiz.eps}
\end{figure}](/articles/aa/full_html/2009/34/aa09802-08/Timg29.png) |
Figure 2:
Fitting of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{18134woz.eps}
\end{figure}](/articles/aa/full_html/2009/34/aa09802-08/Timg30.png) |
Figure 3:
Fitting of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


