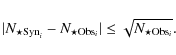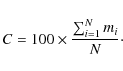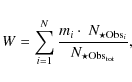| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | 801 - 816 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/20079145 | |
| Published online | 15 June 2009 | |
Properties of stellar clusters around high-mass young
stars![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
F. Faustini1 - S. Molinari1 - L. Testi2,3 - J. Brand4
1 - Istituto di Fisica dello Spazio Interplanetario -
INAF, via Fosso del Cavaliere 100, 00133 Rome, Italy
2 -
European Southern Observatory, Karl Schwarzschild str. 2, Garching bei Muenchen, Germany
3 -
Osservatorio Astronomico di Arcetri - INAF, via Enrico Fermi 5, 50125 Firenze, Italy
4 -
Istituto di Radioastronomia - INAF, via Gobetti 101, Bologna, Italy
Received 26 November 2007 / Accepted 1 April 2009
Abstract
Context. Twenty-six high-luminosity IRAS sources believed to be collection of stars in the early phases of high-mass star formation have been observed in the near-IR (J, H, ![]() )
to characterize the clustering properties of their young stellar population and compare them with those of more evolved objects (e.g., Herbig Ae/Be stars) of comparable mass. All the observed sources possess strong continuum and/or line emission in the millimeter, being therefore associated with gas and dust envelopes. Nine sources have far-IR colors characteristic of UCHII regions, while the other 17 are probably experiencing an evolutionary phase that precedes the hot-cores, as suggested by a variety of evidence collected in the past decade.
)
to characterize the clustering properties of their young stellar population and compare them with those of more evolved objects (e.g., Herbig Ae/Be stars) of comparable mass. All the observed sources possess strong continuum and/or line emission in the millimeter, being therefore associated with gas and dust envelopes. Nine sources have far-IR colors characteristic of UCHII regions, while the other 17 are probably experiencing an evolutionary phase that precedes the hot-cores, as suggested by a variety of evidence collected in the past decade.
Aims. We attempt to gain insight into the initial conditions of star formation in these clusters (initial mass function [IMF], star formation history [SFH]), and to determine mean cluster ages.
Methods. For each cluster, we complete aperture photometry. We derive stellar density profiles, color-color and color-magnitude diagrams, and color (HKCF) and luminosity (KLF) functions. These two functions are compared with simulated KLFs and HKCFs from a model that generates populations of synthetic clusters starting from assumptions about the IMF, SFH, and Pre-MS evolution, and using the average properties of the observed clusters as boundary conditions (bolometric luminosity, dust distribution, infrared excess, extinction).
Results. Twenty-two sources show evidence of clustering with a stellar richness indicator that varies from a few up to several tens of objects, and a median cluster radius of 0.7 pc. A considerable number of cluster members present an infrared excess characteristic of young pre-main-sequence objects. For a subset of 9 detected clusters, we could perform a statistically significant comparison of the observed KLFs with those resulting from synthetic cluster models; for these clusters, we find that the median stellar age ranges between
![]() and
and
![]() years, with evidence of an age spread of the same entity within each cluster. We also find evidence that older clusters tend to be smaller in size, in agreement with our clusters being on average larger than those around relatively older Herbig Ae/Be stars. Our models allow us to explore the relationship between the mass of the most massive star in the cluster and both the cluster richness and the total stellar mass. Although these relationships are predicted by several classes of cluster formation models, their detailed analysis suggests that the properties of our modeled clusters may not be consistent with them resulting from random sampling of the IMF.
years, with evidence of an age spread of the same entity within each cluster. We also find evidence that older clusters tend to be smaller in size, in agreement with our clusters being on average larger than those around relatively older Herbig Ae/Be stars. Our models allow us to explore the relationship between the mass of the most massive star in the cluster and both the cluster richness and the total stellar mass. Although these relationships are predicted by several classes of cluster formation models, their detailed analysis suggests that the properties of our modeled clusters may not be consistent with them resulting from random sampling of the IMF.
Conclusions. Our results are consistent with star formation having occurred continuously over a period of time longer than the typical crossing time.
Key words: stars: formation - stars: imaging - stars: luminosity function, mass function - stars: pre-main sequence - infrared: stars
1 Introduction
There have been considerable efforts to understand how stars form from both a theoretical and an observational point of view. We have reached a good understanding of how isolated low-mass stars form (Klein et al. 2006). The widely accepted scenario is that low-mass stars form by the gravitational collapse of a prestellar core followed at later stages by disk accretion.
Extending this theory to high-mass stars is not trivial.
High-mass (proto-)stars reach the zero age main sequence while still accreting.
When the central protostar reaches a mass of about 10 ![]() hydrogen
fusion ignites in the core and the star's radiation pressure and wind should
prevent further accretion. This is obviously a paradox given that yet more
massive stars do form.
Several theories have been put forward to solve this
dilemma (Zinnecker & Yorke 2007), such as accretion rates of up to
three orders of magnitude higher than in the case of low-mass stars
(Cesaroni 2005), and non-spherical accretion geometries
(Nakano 1989; Yorke 2002; Keto 2003), or
coalescence in dense (proto-)stellar clusters (Bonnell et al. 1998).
hydrogen
fusion ignites in the core and the star's radiation pressure and wind should
prevent further accretion. This is obviously a paradox given that yet more
massive stars do form.
Several theories have been put forward to solve this
dilemma (Zinnecker & Yorke 2007), such as accretion rates of up to
three orders of magnitude higher than in the case of low-mass stars
(Cesaroni 2005), and non-spherical accretion geometries
(Nakano 1989; Yorke 2002; Keto 2003), or
coalescence in dense (proto-)stellar clusters (Bonnell et al. 1998).
All of these theories have predictions that can, in principle, be tested observationally. Significant effort has been made to detect massive accretion disks (Cesaroni et al. 2006), powerful outflows (Beuther et al. 2002; Cesaroni et al. 2005), and dense protostellar clusters (Testi et al. 1999; de Wit et al. 2005), all of which are predicted by one or other formation theory. None of these efforts have provided conclusive arguments in favour or against any of the theories.
In this paper we explore the properties of embedded clusters associated with high-mass protostellar candidates. Our sample was selected from a larger sample of candidate high-mass protostars selected and analyzed by Molinari et al. (1996,1998,2000,2002) and Brand et al. (2001). In Sect. 2, we present the observations and data analysis (source extraction, photometry), and in Sect. 3, we discuss data elaboration and interpretation. In Sect. 4, we present our Synthetic Cluster Generation model and the method of comparison between synthetic and observed clusters and the results of using this technique. Finally, in Sect. 5 we compare our objects with more evolved ones and present our conclusions.
2 Observations and data analysis
Program fields are listed in Table 1 and were imaged in
J, H, and ![]() bands. A total of 15 fields were observed in three nights in
November 1998 at the Palomar 60-inch telescope equipped with a
bands. A total of 15 fields were observed in three nights in
November 1998 at the Palomar 60-inch telescope equipped with a
![]() NICMOS-3 array of pixel scale 0
NICMOS-3 array of pixel scale 0
![]() 62/pix and
total FOV
62/pix and
total FOV
![]() .
The remaining 11 fields were
observed in 3 nights in August 2000 at the ESO-NTT using the
.
The remaining 11 fields were
observed in 3 nights in August 2000 at the ESO-NTT using the
![]() SOFI camera with a pixel scale of 0
SOFI camera with a pixel scale of 0
![]() 29/pix and a
total FOV of
29/pix and a
total FOV of
![]() .
Standard dithering techniques were
used to minimize the impact of bad pixels and optimize flat-fielding,
allowing us to achieve for each field a total of 5min integration time per
band (in the central portion of the observed field) within an area
of
.
Standard dithering techniques were
used to minimize the impact of bad pixels and optimize flat-fielding,
allowing us to achieve for each field a total of 5min integration time per
band (in the central portion of the observed field) within an area
of
![]() of Palomar observations, and 20 min (10 min for
the band
of Palomar observations, and 20 min (10 min for
the band ![]() at NTT of a total covered area of
at NTT of a total covered area of
![]() .
Suitable calibration sources from the list of Hunt
et al. (1988) were observed regularly during the
observations to track atmospheric variations for different
airmasses. Standard stars and target fields were observed at airmasses no
greater than 1.7 at NTT, and 1.3 at Palomar; we determined average zero-point
magnitudes for each night and used them to calibrate our photometry. For each
field, the images in the three bands were registered and astrometric solutions
were determined using a few bright optically visible sources.
.
Suitable calibration sources from the list of Hunt
et al. (1988) were observed regularly during the
observations to track atmospheric variations for different
airmasses. Standard stars and target fields were observed at airmasses no
greater than 1.7 at NTT, and 1.3 at Palomar; we determined average zero-point
magnitudes for each night and used them to calibrate our photometry. For each
field, the images in the three bands were registered and astrometric solutions
were determined using a few bright optically visible sources.
Table 1: Description of observations.
The ![]() images for all observed fields, with superimposed submillimeter continuum emission distribution when available (Molinari et al. 2008a) are presented in Appendix A, and are also available online
images for all observed fields, with superimposed submillimeter continuum emission distribution when available (Molinari et al. 2008a) are presented in Appendix A, and are also available online![]() .
.
2.1 Point source extraction and photometry
The extraction and photometry of point sources for all images were completed using the IRAF package. The rms of the background signal
and the FWHM of point sources were measured throughout the images to
characterize the image noise and PSF properties; these parameters
were fed to the DAOFIND task for source extraction, where a
detection threshold of 3![]() was used for all images.
Sources with saturated pixels were excluded from the analysis; the linearity
of the system response was checked a posteriori comparing, both for the
Palomar and the NTT data, the magnitudes obtained to those from 2MASS using a
few stars with magnitudes reaching up to the maximum values found in our
photometry files; the relations between the 2MASS magnitudes and ours in
the three bands were found to be linear over the entire magnitude range of the
detected sources. There were clearly brighter objects in the various fields,
but their peaks were already flagged as saturated and excluded from the
detection process.
was used for all images.
Sources with saturated pixels were excluded from the analysis; the linearity
of the system response was checked a posteriori comparing, both for the
Palomar and the NTT data, the magnitudes obtained to those from 2MASS using a
few stars with magnitudes reaching up to the maximum values found in our
photometry files; the relations between the 2MASS magnitudes and ours in
the three bands were found to be linear over the entire magnitude range of the
detected sources. There were clearly brighter objects in the various fields,
but their peaks were already flagged as saturated and excluded from the
detection process.
The photometry of sources is difficult to determine in very dense stellar fields such as the inner Galactic plane, where all our target fields are located and the crowding is such that more than one source can enter either any plausible aperture chosen or any annulus used for background estimation. This problem is of course more extreme in the clustered environments close to detected sites of massive star formation (see Sect. 3.1 below).
The first alternative approach that we tried to follow was PSF-fitting photometry that should be less affected by these problems. We chose a subsample of test fields with different levels of stellar crowding. In this procedure, an important aspect was the modeling of the PSF. To test this, we completed several trials selecting a variable number of point-like sources (from 3 to 30) of different brightness levels and different positions in the field. We found that the resulting PSF model was not particularly sensitive to the choice of numbers and/or brightnesses of the stars. However the results, were quite dependent on the mean stellar density of the field. The photometry was carried out using the ALLSTAR task, which was particularly suited to crowded fields. However, we also tested the other two tasks (PEAK and NSTAR) and obtained comparable results for most of the sources. We note, however, that in the most crowded areas in particular, the subtraction of the PSF-fitted sources from the image introduced two spurious effects: an unacceptably high level of residuals with brightness levels well above the detection threshold used and a significant number of negative holes, indicating that the PSF-fit included some background in the source flux estimation and therefore overestimated its value. Both effects are caused by both the limited accuracy of the PSF model that can be obtained for very crowded fields, where faint neighboring stars can enter the area where the PSF model is estimated, and the presence of a significant and variable background, which is quite common and expected for the Galactic plane. A similar conclusion was reached by Hillenbrand & Carpenter (2000) in their study of the inner Orion Nebula Cluster.
The second approach that we followed was standard aperture photometry. The
choice of radii for both the aperture and the background annuli
was of course extremely important. The optimum aperture should be neither too
large to include nearby sources nor too small to truncate significantly
the PSF and underestimate the flux significantly. We completed
several attempts for one of the most crowded fields (Mol30, observed at
NTT) with three different aperture radii equal to the PSF FWHM (typically
0
![]() 7 at NTT and 1
7 at NTT and 1
![]() 4 at Palomar in
4 at Palomar in ![]() ), and
twice and thrice this value. For each photometry run, we analyzed the
source flux distribution and, as expected, the median flux was found
to increase with increasing aperture radius. Increasing the aperture
from one to two PSF FWHMs increased the median source flux by an amount
compatible with the inclusion of the first ring of an Airy
diffraction pattern. In contrast, when the aperture radius was increased to a factor of three higher than the PSF FWHM, the flux increase was far higher than could be attributed to the additional fraction of the Airy profile entering the aperture, and must therefore have been caused by the inclusion of nearby sources. We adopted
an aperture radius equal to the PSF FWHM to
minimize neighbor contamination, and then applied an aperture
correction factor to the fraction of the PSF removed by the
aperture; this was estimated by multi-aperture photometry (starting from a size of
1 FWHM) on relatively isolated stars in the target fields.
), and
twice and thrice this value. For each photometry run, we analyzed the
source flux distribution and, as expected, the median flux was found
to increase with increasing aperture radius. Increasing the aperture
from one to two PSF FWHMs increased the median source flux by an amount
compatible with the inclusion of the first ring of an Airy
diffraction pattern. In contrast, when the aperture radius was increased to a factor of three higher than the PSF FWHM, the flux increase was far higher than could be attributed to the additional fraction of the Airy profile entering the aperture, and must therefore have been caused by the inclusion of nearby sources. We adopted
an aperture radius equal to the PSF FWHM to
minimize neighbor contamination, and then applied an aperture
correction factor to the fraction of the PSF removed by the
aperture; this was estimated by multi-aperture photometry (starting from a size of
1 FWHM) on relatively isolated stars in the target fields.
Given the crowding of our fields, a further effect to be corrected for is the possible contamination by the tails of the brightness profiles of neighbouring stars. To quantify this contamination, we created a grid of simulations with two symmetric Gaussians with a wide variety of peak contrasts and different reciprocal distances. We computed the fraction of the Gaussian profile of the neighbouring source within the photometry aperture centered on the main source, and hence generated a matrix of photometry corrections for different source distances and peak contrasts. We then processed the magnitude file produced by the aperture photometry task and for each source we applied a magnitude correction depending on the presence, distance, and contrast ratios with respect to other neighbouring stars.
In spite of the various issues discussed above, the photometric data obtained with the two methods were in good agreement with each other, apart from at faint magnitudes. For these faint objects, we consistently found that the PSF photometry tends to produce brighter magnitudes (and hence stronger sources) than the aperture photometry; this effect can be easily understood from our finding (see above) that the subtraction of PSF-fitted sources always leaves negative holes in the residual image, and this effect is far more important for faint stars. We thus decided to adopt the magnitudes determined from aperture photometry.
For each target field, we estimated the limiting magnitude (LM) using
artificial star experiments. The fields were populated using the IRAF task
ADDSTAR with 400 fake stars with magnitudes distributed in bins of 0.25 mag
between values of 15 and 21; the percentage of recovered stars as a function
of magnitude provides an estimate of the completeness level of our photometry.
The star recovery percentage was not found to decrease monotonically with increasing
magnitude because fake stars can also be placed very close to bright real
stars and then go undetected by the finding algorithm. However, we find that
the limit of 85-90% recovery fraction is reached on average at around J=18.7,
H=17.7, and
![]() for NTT images, and J=18.0, H=17.3, and
for NTT images, and J=18.0, H=17.3, and
![]() for
Palomar images. We found that the typical photometric uncertainty is below 0.1 mag
close to the limiting magnitude.
for
Palomar images. We found that the typical photometric uncertainty is below 0.1 mag
close to the limiting magnitude.
To verify the integrity of our photometry, we compared our magnitudes with
those extracted from 2MASS point source catalog for all the fields in our
sample. Considering the differences in spatial resolutions between 2MASS and the
telescopes used for our observations, this comparison was limited to
2MASS point-like sources associated with a single source in
the Palomar or NTT images. The median differences with respect to 2MASS for
the various fields are of the order of -0.1, -0.2 and -0.3 mag for J, H,
and ![]() bands, respectively. Within each field, the scatter around these
median values is
bands, respectively. Within each field, the scatter around these
median values is ![]() 0.1 mag in all three bands, confirming the
internal
consistency of our photometry. Noticeable departures (
0.1 mag in all three bands, confirming the
internal
consistency of our photometry. Noticeable departures (![]() 0.5 mag) of the
median difference with 2MASS from the above values are observed for the field
of source Mol11 (Palomar), and for sources Mol103, Mol109 and Mol110 (NTT).
However, the latter sources were observed on the same night, observations for which our log
registered as not good due to sky variations that were not tracked by
night-averaged zero points. We emphasize again, however, that these are
systematic differences with respect to 2MASS in this limited number of cases;
the rms scatter about these median differences are
0.5 mag) of the
median difference with 2MASS from the above values are observed for the field
of source Mol11 (Palomar), and for sources Mol103, Mol109 and Mol110 (NTT).
However, the latter sources were observed on the same night, observations for which our log
registered as not good due to sky variations that were not tracked by
night-averaged zero points. We emphasize again, however, that these are
systematic differences with respect to 2MASS in this limited number of cases;
the rms scatter about these median differences are ![]() 0.1 mag in all
bands and this should provide confidence that the internal consistency of the
photometry in each field is preserved. We then decided to rescale our
photometry to the 2MASS photometric system to remove these systematic effects.
The (J-H) and (H-K) color differences between 2MASS and our photometry are
not correlated with the magnitude, so that no magnitude-dependent color effect
is introduced in this rescaling.
0.1 mag in all
bands and this should provide confidence that the internal consistency of the
photometry in each field is preserved. We then decided to rescale our
photometry to the 2MASS photometric system to remove these systematic effects.
The (J-H) and (H-K) color differences between 2MASS and our photometry are
not correlated with the magnitude, so that no magnitude-dependent color effect
is introduced in this rescaling.
3 Results
3.1 Cluster Identification
Table 2: Results for cluster detection.
The identification of a cluster results from the analysis of stellar
density in the field. Since our target fields are sites of massive
star formation associated with local peaks of dust column densities
and hence of visual extinction, the ![]() images are clearly more
suited for this type of analysis.
images are clearly more
suited for this type of analysis.
Stellar density maps were compiled for each field by counting stars in a running
boxcar of size equal to 20
![]() .
The box size was determined empirically to enhance
the statistical significance of local stellar density peaks and to maximize the
ability to detect the clusters. Larger boxes tend to smear the cluster into the
background stellar density field decreasing the statistical significance of the
peak, which may lead to non-detection of a clearly evident cluster, particularly
in the rich inner Galaxy fields (this happens, e.g., for source Mol103, see
Fig. A.18 in the Appendix). Smaller boxes produce noisy density
maps where the number of sources in each bin starts to be comparable to the
fluctuations in the background density field caused either by intrinsic variations
in the field star density or to variable extinction from diffuse foreground ISM
in the Galactic Plane (where all of our sources are located). For most of our
objects in the outer Galaxy, this analysis is used to locate the position
of the peak stellar density, since the clusters are obvious already from
visual inspection (Mol3 to Mol28, and Mol143 to Mol151, see Appendix). For
the remaining fields, the density maps are used to ascertain the presence
of a cluster; toward the inner Galaxy in particular, the density maps tend to
show more than one peak at comparable levels. It is important to remember,
however, that this is a search for stellar clusters toward regions where
indications of active star formation are already available, and this
information can be used. In particular, the coincidence of these peaks
with cold dust clumps traced by intense submillimeter and millimeter
emission (Beltrán et al. 2006; Molinari et al. 2008a)
is critical before we can consider the density peak to be a true feature associated with
the star formation region. Casual association is excluded by the high number
of positive associations (see Table 2).
.
The box size was determined empirically to enhance
the statistical significance of local stellar density peaks and to maximize the
ability to detect the clusters. Larger boxes tend to smear the cluster into the
background stellar density field decreasing the statistical significance of the
peak, which may lead to non-detection of a clearly evident cluster, particularly
in the rich inner Galaxy fields (this happens, e.g., for source Mol103, see
Fig. A.18 in the Appendix). Smaller boxes produce noisy density
maps where the number of sources in each bin starts to be comparable to the
fluctuations in the background density field caused either by intrinsic variations
in the field star density or to variable extinction from diffuse foreground ISM
in the Galactic Plane (where all of our sources are located). For most of our
objects in the outer Galaxy, this analysis is used to locate the position
of the peak stellar density, since the clusters are obvious already from
visual inspection (Mol3 to Mol28, and Mol143 to Mol151, see Appendix). For
the remaining fields, the density maps are used to ascertain the presence
of a cluster; toward the inner Galaxy in particular, the density maps tend to
show more than one peak at comparable levels. It is important to remember,
however, that this is a search for stellar clusters toward regions where
indications of active star formation are already available, and this
information can be used. In particular, the coincidence of these peaks
with cold dust clumps traced by intense submillimeter and millimeter
emission (Beltrán et al. 2006; Molinari et al. 2008a)
is critical before we can consider the density peak to be a true feature associated with
the star formation region. Casual association is excluded by the high number
of positive associations (see Table 2).
As further confirmation of the positive detection of a cluster
we compiled radial stellar density profiles where stars were counted inside annuli of increasing internal radius and constant width and then divided by the area of
the annuli (Testi et al. 1998); uncertainties were assigned
assuming Poisson statistics for the number of stars in each annulus. We then
assigned a positive cluster identification if the radial profile exhibited at
least two annuli that had values above the background. To refine the
location of the density peak, we repeated the radial density profile analysis
starting from several locations within 10
![]() of the peak derived from the
density maps; the location that maximizes the overall statistical significance
of the annuli was then assigned to the cluster center. Figure 1 shows
the typical footprint of a cluster, where
the stellar density is plotted as a function of distance r
from the start location; the density has a maximum at r=0and decreases until it reaches a constant value, which is the average
background/foreground stellar density.
of the peak derived from the
density maps; the location that maximizes the overall statistical significance
of the annuli was then assigned to the cluster center. Figure 1 shows
the typical footprint of a cluster, where
the stellar density is plotted as a function of distance r
from the start location; the density has a maximum at r=0and decreases until it reaches a constant value, which is the average
background/foreground stellar density.
There were two exceptions in this analysis. The first was for source
Mol160. The ![]() -band image shows clear stellar density enhancement in a
semi-circular annulus surrounding the northern side of the dense millimeter
core (see Fig. A.26 in the Appendix), which appears devoid of stars.
This stellar density enhancement is coincident with the emission patterns visible
in the mid-IR (Molinari et al. 2008b), so is clearly a stellar
population associated with the star-forming region. Since the millimeter peak
is at the center of symmetry of the semi-circular stellar distribution, we
consider this tobe the center of the cluster. This is only for completeness, since we cannot say whether the low density of stars at the millimeter
peak is an effect of extreme visual extinction or reflects an intrinsic paucity
of NIR-visible forming stars, as the proposed extreme youth of the massive YSO
accreting in its depth would seem to suggest (Molinari et al. 2008b).
-band image shows clear stellar density enhancement in a
semi-circular annulus surrounding the northern side of the dense millimeter
core (see Fig. A.26 in the Appendix), which appears devoid of stars.
This stellar density enhancement is coincident with the emission patterns visible
in the mid-IR (Molinari et al. 2008b), so is clearly a stellar
population associated with the star-forming region. Since the millimeter peak
is at the center of symmetry of the semi-circular stellar distribution, we
consider this tobe the center of the cluster. This is only for completeness, since we cannot say whether the low density of stars at the millimeter
peak is an effect of extreme visual extinction or reflects an intrinsic paucity
of NIR-visible forming stars, as the proposed extreme youth of the massive YSO
accreting in its depth would seem to suggest (Molinari et al. 2008b).
The second exception was for source Mol8. The stellar density analysis shows two peaks that are coincident with two distinct dust cores (see Fig. A.2); we therefore assumed the presence of two distinct clusters, rather than a subclustering feature within the same cluster. The radial density profile analysis could not be used here, so we fit elliptical Gaussians to the peaks in the density maps, allowing for an underlying constant level representing the background stellar density. The resulting cluster richness was obtained by integrating the fitted Gaussian, and the cluster radius was taken to be equal to the fitted FWHM (the fitted Gaussians were nearly circular).
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{dens.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg36.png) |
Figure 1: Stellar density (in stars/pc2), for Mol28, as a function of the radial distance (in parsecs) from cluster center. Error-bars are computed as the Poissonian fluctuations of source counts in each bin. |
| Open with DEXTER | |
Always following Testi et al. (1998), we
determined the richness indicator of the cluster ![]() by integrating the
background-subtracted density profile; the cluster radius was taken to be the
radial distance from the start location where the density profile reaches a constant
value. This richness indicator is a very convenient figure to use when no detailed information is available for each single star in the region
and the membership of the cluster cannot be established for each single star.
These values are reported in Col. 3 of Table 2 for all fields
where a cluster has been clearly revealed. Column 1 gives the target name (cf.
Table 1); its kinematic distance is listed in Col. 2. The parameter
by integrating the
background-subtracted density profile; the cluster radius was taken to be the
radial distance from the start location where the density profile reaches a constant
value. This richness indicator is a very convenient figure to use when no detailed information is available for each single star in the region
and the membership of the cluster cannot be established for each single star.
These values are reported in Col. 3 of Table 2 for all fields
where a cluster has been clearly revealed. Column 1 gives the target name (cf.
Table 1); its kinematic distance is listed in Col. 2. The parameter
![]() (Col. 4) is the number of cluster members derived (see
Sect. 4.1 below) from the integration of the
background-subtracted
(Col. 4) is the number of cluster members derived (see
Sect. 4.1 below) from the integration of the
background-subtracted ![]() luminosity function (hereafter KLF, see Sect. 4.1).
Also reported in Col. 8 is the
mass of the hosting molecular clump; this was derived from the cold dust emission
as reported in Molinari et al. (2008a, 2000), integrated over
the entire spatial extent of the cluster; conversion into masses was achieved based on the optically thin assumption and by
assuming T=30 K,
luminosity function (hereafter KLF, see Sect. 4.1).
Also reported in Col. 8 is the
mass of the hosting molecular clump; this was derived from the cold dust emission
as reported in Molinari et al. (2008a, 2000), integrated over
the entire spatial extent of the cluster; conversion into masses was achieved based on the optically thin assumption and by
assuming T=30 K, ![]() (Molinari et al. 2008a), and a mass opacity
(Molinari et al. 2008a), and a mass opacity
![]() which corresponds to a gas/dust weight ratio of 100 (Preibisch et al. 1993). The IRAS source
bolometric luminosity, Col. 9, is taken from Molinari et al.
(1996, 2000, 2002, 2008a); in Col. 10
we list the AV at the peak cluster position estimated from submm
observations (Molinari et al. 2008a, 2000). In
Cols. 11 and 12 the coordinates of the centers of the identified clusters
are reported. Columns 6 and 7 contain parameters that are described later
in the text (see Sect. 3.2).
which corresponds to a gas/dust weight ratio of 100 (Preibisch et al. 1993). The IRAS source
bolometric luminosity, Col. 9, is taken from Molinari et al.
(1996, 2000, 2002, 2008a); in Col. 10
we list the AV at the peak cluster position estimated from submm
observations (Molinari et al. 2008a, 2000). In
Cols. 11 and 12 the coordinates of the centers of the identified clusters
are reported. Columns 6 and 7 contain parameters that are described later
in the text (see Sect. 3.2).
Following the procedure described, a cluster was detected within 1![]() of the IRAS position for 22
out of the 26 observed fields (85% detection rate). In two
cases (Mol38 and Mol59), the stellar density map does not show a clear peak above the fluctuations of
the field stellar density. For Mol98, the radial density profile only shows one annulus above the
background, and therefore fails the criterion that the stellar density enhancement should be resolved
significantly above the background in two annuli. In one case (Mol30), several stellar density
peaks were found in proximity to the IRAS source, but the lack of information about the
submillimeter/millimeter continuum prevents us from drawing any firm conclusion.
of the IRAS position for 22
out of the 26 observed fields (85% detection rate). In two
cases (Mol38 and Mol59), the stellar density map does not show a clear peak above the fluctuations of
the field stellar density. For Mol98, the radial density profile only shows one annulus above the
background, and therefore fails the criterion that the stellar density enhancement should be resolved
significantly above the background in two annuli. In one case (Mol30), several stellar density
peaks were found in proximity to the IRAS source, but the lack of information about the
submillimeter/millimeter continuum prevents us from drawing any firm conclusion.
Figure 2 shows ![]() as a function of the peak AV and suggests that with higher
dust extinction, we may find it more difficult, or it becomes less likely, to detect a cluster at 2.2
as a function of the peak AV and suggests that with higher
dust extinction, we may find it more difficult, or it becomes less likely, to detect a cluster at 2.2 ![]() m.
m.
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{ic_av.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg40.png) |
Figure 2:
Cluster richness indicator |
| Open with DEXTER | |
Our detection rate is quite high and this implies that young stellar clusters in sites of intermediate and massive star formation are ubiquitous. While this was established for relatively old Pre-MS systems such as Herbig Ae/Be stars (Testi et al. 1999), we hereby verify that this is also true in much younger systems, where the most massive stars may even be in a pre-Hot Core stage (Molinari et al. 2008a).
Our detection rate is higher compared to other similar searches of
stellar clusters toward high-mass YSOs. For example Kumar et al.
(2006) used the 2MASS archive and reported a rate of
25% (rising to 60% when neglecting the inner Galaxy regions) toward a larger sample,
which also includes the sources of this work; in particular, we detect all
clusters also detected by Kumar et al. and in addition we reveal clusters
toward 13 objects for which Kumar et al. report no detection. The
reason for this discrepancy may be because we obtained dedicated
observations, while Kumar et al. used data from the 2MASS archive; the
diffraction-limited spatial resolution of our data is between a factor of 4
and a factor of 10 better with respect to 2MASS, and this certainly
facilitates cluster detection especially in particularly crowded areas such as
the inner Galactic plane. To test this hypothesis, we degraded the NTT ![]() image of Mol103, also considered in Kumar et al., to the 2MASS resolution;
extraction and photometry were performed as outlined above but the search
for a cluster based on the stellar radial density profiles revealed no cluster.
The estimated number of members (corrected for the contribution of
fore/background stars) for 7 out of the 10 clusters detected both by us and by
Kumar et al. was at least a factor of two less in the latter study.
image of Mol103, also considered in Kumar et al., to the 2MASS resolution;
extraction and photometry were performed as outlined above but the search
for a cluster based on the stellar radial density profiles revealed no cluster.
The estimated number of members (corrected for the contribution of
fore/background stars) for 7 out of the 10 clusters detected both by us and by
Kumar et al. was at least a factor of two less in the latter study.
Kumar & Grave (2008) conducted a similar study on a large
sample of high-mass YSOs, that included some of our sources, using
data from the GLIMPSE survey (Benjamin et al. 2003).
They detect no significant cluster around any targets in a sample
of 509 objects. As the authors say in their paper, however, GLIMPSE data are
sensitive to 2-4 ![]() pre-main sequence stars at the distance of 3 kpc.
Based on color-magnitude analysis (see later below), our mass sensitivity
is of the order of 1
pre-main sequence stars at the distance of 3 kpc.
Based on color-magnitude analysis (see later below), our mass sensitivity
is of the order of 1 ![]() at a distance of 3.6 kpc and
at a distance of 3.6 kpc and ![]() 0.6
0.6 ![]() at a distance of 2.1 Kpc. Probing longer wavelengths, GLIMPSE is likely to
be more sensitive to younger sources compared to the classical J, H, K range, which also samples relatively older pre-MS objects. The combination
of sampling higher-mass (and hence rarer stars because of the shape of the
IMF) and relatively younger stars (which, as indeed our analysis finds,
may not be the majority in a young cluster) may plausibly be the reason
for the negative cluster detection results of Kumar & Grave.
at a distance of 2.1 Kpc. Probing longer wavelengths, GLIMPSE is likely to
be more sensitive to younger sources compared to the classical J, H, K range, which also samples relatively older pre-MS objects. The combination
of sampling higher-mass (and hence rarer stars because of the shape of the
IMF) and relatively younger stars (which, as indeed our analysis finds,
may not be the majority in a young cluster) may plausibly be the reason
for the negative cluster detection results of Kumar & Grave.
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{ic_rclu.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg41.png) |
Figure 3:
Distribution of the cluster radii in parsecs (full line) and
the cluster richness indicator |
| Open with DEXTER | |
The distribution of the radii of the detected clusters indicated by a full
line in Fig. 3; the median value is 0.7 pc.
The dashed histogram (which refers to the
upper X-axis) shows the distribution of the cluster richness indicator ![]() ,
with a median number of stars of 27. We note that the value of
,
with a median number of stars of 27. We note that the value of ![]() for many of our clusters is less than the limit of 35 suggested by Lada & Lada
(2003) to be a bona fide cluster. This definition stems from the
argument that a less rich agglomerate may not survive the formation process as an
entity. Our interest, however, is to investigate the spatial properties of the
young stellar population in a star-forming region at the time of active formation,
without worrying about its possible persistence as a cluster at the end of the
formation phase. However, we prefer not to introduce a new term to identify
the structures that we see and still use the term cluster, although
in a milder way than Lada & Lada.
for many of our clusters is less than the limit of 35 suggested by Lada & Lada
(2003) to be a bona fide cluster. This definition stems from the
argument that a less rich agglomerate may not survive the formation process as an
entity. Our interest, however, is to investigate the spatial properties of the
young stellar population in a star-forming region at the time of active formation,
without worrying about its possible persistence as a cluster at the end of the
formation phase. However, we prefer not to introduce a new term to identify
the structures that we see and still use the term cluster, although
in a milder way than Lada & Lada.
3.2 Properties of identified clusters
We first derive qualitative measurements related to the nature of the identified clusters using simple diagnostic tools such as color-color and color-magnitude diagrams. These diagrams have been drawn for all detected clusters and are available in electronic form; we illustrate here the particular case for Mol28.
3.2.1 Color-color analysis
Figure 4 shows the [J-H] versus [
![]() ]
diagram for all sources
detected within a distance equal to
]
diagram for all sources
detected within a distance equal to
![]() centered on the stellar density
peak. The full circles represent all sources detected in all three bands,
the arrows representing sources with lower limits (to their magnitude) in the J band.
The plot shows more stars than the
centered on the stellar density
peak. The full circles represent all sources detected in all three bands,
the arrows representing sources with lower limits (to their magnitude) in the J band.
The plot shows more stars than the ![]() value reported in
Table 2 because we also include the fore/background stars that
cannot be individually distinguished from the true cluster members. A
significant fraction of the sources have colors compatible with main-sequence
stars that have a variable amount of extinction reddening (computed by adopting the
Rieke & Lebofsky (1985) extinction curve), but many sources have
colors that are typical of young pre-MS objects with an intrinsic IR excess produced by warm circumstellar dust distributed in disks (Lada & Adams 1992).
The set of dotted curves represents the locus
of two-component black bodies with temperatures as indicated at the start
and end of each dotted line; along each curve, the relative contribution of the the two
black bodies is varied. These curves mimic the effect of a temperature stratification in
the dusty circumstellar envelopes, and the presence of sources in the area
covered by these curves is an indication of the presence of warm
circumstellar dust.
value reported in
Table 2 because we also include the fore/background stars that
cannot be individually distinguished from the true cluster members. A
significant fraction of the sources have colors compatible with main-sequence
stars that have a variable amount of extinction reddening (computed by adopting the
Rieke & Lebofsky (1985) extinction curve), but many sources have
colors that are typical of young pre-MS objects with an intrinsic IR excess produced by warm circumstellar dust distributed in disks (Lada & Adams 1992).
The set of dotted curves represents the locus
of two-component black bodies with temperatures as indicated at the start
and end of each dotted line; along each curve, the relative contribution of the the two
black bodies is varied. These curves mimic the effect of a temperature stratification in
the dusty circumstellar envelopes, and the presence of sources in the area
covered by these curves is an indication of the presence of warm
circumstellar dust.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{colcol.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg44.png) |
Figure 4:
[J-H] vs. [H- |
| Open with DEXTER | |
A straightforward indication of the youth of the cluster may be
provided by the fraction of sources that are not compatible with being
reddened MS stars, i.e., those with IR excess. The number of stars
with an IR excess is normalized to the total number of stars
detected in the cluster area, corrected for the expected number of
fore/background stars estimated from the areas surrounding the cluster (but
still in the same imaged field).
To be conservative we extend the region of the MS by 0.2 mag to the
right corresponding to about a 2![]() uncertainty in measured
magnitudes. This ratio is reported as a percentage value in Col. 6 of
Table 2.
uncertainty in measured
magnitudes. This ratio is reported as a percentage value in Col. 6 of
Table 2.
3.2.2 Color-magnitude analysis
Additional evolutionary indications of the detected clusters may be
derived from the ![]() -[H -
-[H - ![]() ]
diagram, reported for Mol28 in Fig. 5.
Compared to the main sequence (the leftmost almost
vertical curve in the figure) a significant fraction of the
sources are on its right, where the evolutionary tracks for Pre-MS
sources (Palla & Stahler 1999) can also be found, and
could therefore be interpreted as very young pre-MS objects. The
distribution of sources in the diagram spans a much larger region
than that covered by the Pre-MS isochrones, because of
the combined effect of extinction reddening and IR excess.
The extinction effects can be seen from the dotted lines
originating in the main sequence and extending toward the
bottom-right for increasing values of AV. On the other hand,
the presence of a warm dusty circumstellar envelope implies an
increase in both absolute emission and SED steepness, which would
shift a pure photosphere toward the top-right of the diagram (as
shown by the arrow labeled ``IREX'' in Fig. 5). In a similar way
to the color-color analysis, it is impossible to estimate
the age of individual stellar sources based on their location on
the pre-MS isochrones, because we do not know the amount of
]
diagram, reported for Mol28 in Fig. 5.
Compared to the main sequence (the leftmost almost
vertical curve in the figure) a significant fraction of the
sources are on its right, where the evolutionary tracks for Pre-MS
sources (Palla & Stahler 1999) can also be found, and
could therefore be interpreted as very young pre-MS objects. The
distribution of sources in the diagram spans a much larger region
than that covered by the Pre-MS isochrones, because of
the combined effect of extinction reddening and IR excess.
The extinction effects can be seen from the dotted lines
originating in the main sequence and extending toward the
bottom-right for increasing values of AV. On the other hand,
the presence of a warm dusty circumstellar envelope implies an
increase in both absolute emission and SED steepness, which would
shift a pure photosphere toward the top-right of the diagram (as
shown by the arrow labeled ``IREX'' in Fig. 5). In a similar way
to the color-color analysis, it is impossible to estimate
the age of individual stellar sources based on their location on
the pre-MS isochrones, because we do not know the amount of ![]() by which we should de redden each object. We follow a
conservative approach by dereddening each object using half of the
exctinction estimated for each location from millimeter maps; this
corresponds to placing each object midway through the clump.
by which we should de redden each object. We follow a
conservative approach by dereddening each object using half of the
exctinction estimated for each location from millimeter maps; this
corresponds to placing each object midway through the clump.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{colmag.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg46.png) |
Figure 5:
|
| Open with DEXTER | |
A further correction is to remove the IR excess for those sources, which is apparent in the color-color diagram (of Fig. 4), estimated using the formulation suggested by Hillenbrand & Carpenter (2000), and used later in this work (see Sect. 4.2). The ratio of pre-MS stars to the total in each cluster area will remain contaminated by fore/background stars; to estimate this contamination, we choose an off-cluster area in the same imaged field and simply compute the ratio of sources with pre-MS colors to the total (in these off-cluster regions in which there is no significant reddening to correct for). for each cluster, Col. 7 of Table 2 reports the fraction of stars (detected in the cluster area in all three bands) situated more than 0.2 mag to the right of the MS after the various corrections have been applied.
4 Initial mass functions and star formation histories
As is apparent from the qualitative analysis presented in the
previous paragraphs, the diagnostic power of our observations is
limited because we do not know which objects in the cluster area are
true cluster members nor the precise amount of dust
extinction (originating within the hosting clump) and IR excess
(originating in the immediate circumstellar environment) pertaining to
each source. Without this detailed knowledge of individual stars
in the clusters, fundamental quantities such as the initial mass
function (IMF) and the star formation history (SFH) cannot be
derived directly from, e.g., the ![]() luminosity function (KLF). We are
compelled to obtain these using statistical simulations of
clusters based on different input parameters and performing a
statistical comparison between synthetic and observed KLFs and HKCFs.
luminosity function (KLF). We are
compelled to obtain these using statistical simulations of
clusters based on different input parameters and performing a
statistical comparison between synthetic and observed KLFs and HKCFs.
We first derive the observed KLFs from the observations. We then illustrate in detail the model used for the cluster simulations, exploring the sensitivity of the results to a wide range of input parameters finally, modeled and observed KLFs are compared to infer statistically the IMF and SFH for our clusters.
4.1 Observed
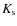 luminosity functions
luminosity functions
The KLF of each cluster is obtained by simply counting all detected
sources within the cluster area as identified from the cluster
density profile (see Sect. 3.1). In a similar way to the other diagnistic
tools (Sects. 3.2.1 and 3.2.2), the KLF is
contaminated by field stars that cannot be individually identified.
To account for the field star contamination in a statistical
way we subtract from the KLF that was compiled for the cluster area, the KLF for a
region outside the cluster area but still in the same imaged field, after
normalising the different areas. The regions in which the field star KLF is
compiled have a lower extinction with respect to the cluster KLF, so the background
contribution to the cluster KLF is likely to be overestimated. Field-subtracted KLFs
for all clusters are presented in Appendix B, and are also available online![]() .
.
The integral of the KLF provides an independent estimate of the number
of cluster members, and these values are reported as
![]() in Table 2. Their agreement with the richness indicator
in Table 2. Their agreement with the richness indicator ![]() confirms
the consistency of our analysis. All KLFs show a dominant peak that is
always close to the completeness limit, showing that our
observations are insufficiently sensitive to the low-mass stellar
component of our clusters. Many of the KLFs present a separate small
peak at low magnitudes (one or two sources at most, on
average). Could this be caused by confusion because of source crowding and insufficient spatial resolution? For each cluster, we studied the distribution of distances of each star
from its nearest neighbour and found that there are
two types of distributions, reported in Fig. 6.
In the first type (full line in figure), the distribution has a peak
corresponding to an inter-star distance significantly higher than the value
corresponding to half the PSF FWHM (the full vertical line); in this
case, the suggestion is that all cluster members have been resolved
from their neighbour. In the second type (dashed line in the figure),
the distribution has its peak very close to half the PSF's FWHM (the
dashed vertical line), indicating that source blending should
certainly be considered possible. We verified that all clusters
with a distance distribution of the second type do exhibit a
second faint peak at high brightness in their KLFs, therefore
confirming that this feature is an artifact of the relatively low
spatial resolution, which in some cases is insufficient to resolve
all cluster members.
confirms
the consistency of our analysis. All KLFs show a dominant peak that is
always close to the completeness limit, showing that our
observations are insufficiently sensitive to the low-mass stellar
component of our clusters. Many of the KLFs present a separate small
peak at low magnitudes (one or two sources at most, on
average). Could this be caused by confusion because of source crowding and insufficient spatial resolution? For each cluster, we studied the distribution of distances of each star
from its nearest neighbour and found that there are
two types of distributions, reported in Fig. 6.
In the first type (full line in figure), the distribution has a peak
corresponding to an inter-star distance significantly higher than the value
corresponding to half the PSF FWHM (the full vertical line); in this
case, the suggestion is that all cluster members have been resolved
from their neighbour. In the second type (dashed line in the figure),
the distribution has its peak very close to half the PSF's FWHM (the
dashed vertical line), indicating that source blending should
certainly be considered possible. We verified that all clusters
with a distance distribution of the second type do exhibit a
second faint peak at high brightness in their KLFs, therefore
confirming that this feature is an artifact of the relatively low
spatial resolution, which in some cases is insufficient to resolve
all cluster members.
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{distr-distance.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg47.png) |
Figure 6: Distribution of identified sources as a function of nearest-neighbor distance (D) for two of our examined fields (Mol28 dashed line and Mol103 full line). |
| Open with DEXTER | |
4.2 Synthetic KLF. Synthetic cluster generator: a near-IR cluster simulator
As already mentioned, we cannot derive masses and ages from our data alone. We thus developed a model to create statistically significant cluster simulations obtained for different assumptions of IMF and SFH (source ages and their distribution), and compare the synthetic KLFs with the observed field-subtracted KLFs. This model we called the synthetic cluster generator (SCG).
4.2.1 SCG: model description
A cluster is created by adding stars whose masses and ages are assigned via a Monte-Carlo extraction
according to the chosen IMF and SFH; the pre-MS evolutionary tracks of Palla & Stahler (1999) are then
used to convert them into J, H, and ![]() magnitudes. The 3D distribution of stars is obtained by randomly
choosing for
each star a set of x,y,z coordinates using the observed stellar density profile
(see Sect. 3.1), approximated to be a radially symmetric Gaussian, as weight-function; using submm continuum images, this is
needed to assign the proper column of cold dust ``required'' to extinguish the near-IR
radiation. Other analytical functions could have been used, e.g., a King profile, but the statistics
of our clusters are insufficiently high to explore the effect of different radial profile assumptions.
magnitudes. The 3D distribution of stars is obtained by randomly
choosing for
each star a set of x,y,z coordinates using the observed stellar density profile
(see Sect. 3.1), approximated to be a radially symmetric Gaussian, as weight-function; using submm continuum images, this is
needed to assign the proper column of cold dust ``required'' to extinguish the near-IR
radiation. Other analytical functions could have been used, e.g., a King profile, but the statistics
of our clusters are insufficiently high to explore the effect of different radial profile assumptions.
To convert the submm flux into dust
column density, we used the dust temperature and emissivity exponent ![]() determined in Molinari et al. (2000); mean values from the latter work were adopted for those fields not covered by our work.
determined in Molinari et al. (2000); mean values from the latter work were adopted for those fields not covered by our work.
To properly simulate the
pre-MS stars, we also need to include the effect of an IR excess
caused by warm dust in the circumstellar envelopes and disks. We used
the distribution (modeled as a Gaussian) of [H - ![]() ]
]![]() color excesses as measured for a sample of Pre-MS stars in
Taurus, as used by Hillenbrand & Carpenter (2000), as a weight-function to randomly assign a
[H -
color excesses as measured for a sample of Pre-MS stars in
Taurus, as used by Hillenbrand & Carpenter (2000), as a weight-function to randomly assign a
[H - ![]() ]
]![]() to each simulated star in our model; the
to each simulated star in our model; the ![]() vs. [H -
vs. [H - ![]() ]
]![]() relationship adopted in the above mentioned work was then used to derive the H and
relationship adopted in the above mentioned work was then used to derive the H and ![]() excess-corrected magnitudes. The
excess-corrected magnitudes. The ![]() magnitude of the synthetic star was then compared with the limiting magnitude typical of the cluster being simulated to determine whether the star could have been detected in our observations. This procedure is repeated until the number of synthetic detectable stars equals the value of
magnitude of the synthetic star was then compared with the limiting magnitude typical of the cluster being simulated to determine whether the star could have been detected in our observations. This procedure is repeated until the number of synthetic detectable stars equals the value of ![]() determined for our observations; at this point, the cluster generation process is complete.
determined for our observations; at this point, the cluster generation process is complete.
Since the simulation is based on Monte Carlo extraction of stellar mass, age, and position in the cluster, each independent run for a fixed set of input parameters can in principle result in very different outputs in terms of cluster luminosity, total stellar mass, maximum stellar mass, and synthetic KLF. To determine the statistical significance, the model is run 200 times for any given set of input parameters, and the median KLF is later adopted for comparison with the observed one. Clearly, the predictive power of this simulation model resides in its capability to characterize the cluster properties of any given parameter set. In other words, the distribution of the resulting quantities should not be uniform but peaked around characteristic values. We return to this point in Sect. 4.2.3
4.2.2 SCG: input assumptions
We tested three different assumptions about the star formation histories
in our cluster simulations. The first was to assume that stars
in the cluster formed in a single burst-like event (hereafter SB)
some t1 years ago. The explored range in the
simulations is
![]() yrs. The second
was that the formation of stars proceeds at a constant rate
(hereafter CR) from a time t1 years ago to a time t2 years
ago. The ranges explored in the simulations are
yrs. The second
was that the formation of stars proceeds at a constant rate
(hereafter CR) from a time t1 years ago to a time t2 years
ago. The ranges explored in the simulations are
![]() yrs and
yrs and
![]() yrs, where we always assume that
t1 > t2. The
third possibility that we explored was a variation in the previous assumption,
where the star formation rate is not constant but varies with time
as a Gaussian function (hereafter GR). Within the boundaries of the
start and end of the star formation process, t1 and t2 that were varied
as above, we also varied both the time
yrs, where we always assume that
t1 > t2. The
third possibility that we explored was a variation in the previous assumption,
where the star formation rate is not constant but varies with time
as a Gaussian function (hereafter GR). Within the boundaries of the
start and end of the star formation process, t1 and t2 that were varied
as above, we also varied both the time ![]() of the
Gaussian peak in the range
of the
Gaussian peak in the range
![]() and Log10(
and Log10(![]() )
of the Gaussian-like SFH, which was allowed to
have one of two values 0.1 and 0.5.
)
of the Gaussian-like SFH, which was allowed to
have one of two values 0.1 and 0.5.
We allowed three different choices of IMFs, i.e., Kroupa
et al. (1993), Scalo (1998), and Salpeter
(1955), with the latter modified by introducing a different slope
for M<1 ![]() coinciding with that of the Scalo (1998) IMF; the
three IMFs were labeled IMF1, IMF2, and IMF3,
respectively. The IMF from Kroupa et al. provides a more accurate description of the low-mass end of the
distribution, while the classical Salpeter IMF is flatter at low
mass but heavier at intermediate and high masses (above 1
coinciding with that of the Scalo (1998) IMF; the
three IMFs were labeled IMF1, IMF2, and IMF3,
respectively. The IMF from Kroupa et al. provides a more accurate description of the low-mass end of the
distribution, while the classical Salpeter IMF is flatter at low
mass but heavier at intermediate and high masses (above 1 ![]() ).
The properties of the Scalo IMF is in-between the other two,
resembling Salpeter's one below 1
).
The properties of the Scalo IMF is in-between the other two,
resembling Salpeter's one below 1 ![]() and above 10
and above 10 ![]() ,
and
Kroupa's for 1
,
and
Kroupa's for 1 ![]() <M<10
<M<10 ![]() .
.
4.2.3 SCG: predictive power
To verify our model's predictive power, we completed 200 simulations for a cluster with a Salpeter IMF and a constant star formation rate with t1=106 yrs and t2=104 yrs. Figure 7 shows the distribution of the predicted number of stars and the total luminosity for the 200 simulations. The number of cluster members shows very little variation, as expected since the number of detectable stars is the parameter that we use to stop the simulation; on the other hand, the distribution of the total luminosity is not particularly peaked, as the central 3 bins containing about 60% of the simulations span almost two decades in luminosity.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{lumnum.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg55.png) |
Figure 7: Distribution of the predicted number of cluster members (full line) and total luminosity (dashed line) for 200 SCG runs for Mol160 with a Salpeter IMF and a constant star formation rate with t1=106 yrs and t2=104 yrs. |
| Open with DEXTER | |
On the other hand, the distributions for the total cluster stellar mass, and for the mass of the most massive member (see Fig. 8) are rather peaked and highlight a relatively higher predictive power of the model for these two quantities. It is to be noted that the distributions are rather skewed, suggesting that neither the mean nor the median are particularly suited to characterize the peak of the distribution. We indeed found that these quantities assume at their distributions peak a more representative value of mass and use them in the following discussion.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{mstars.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg56.png) |
Figure 8: Distribution of the predicted total stellar mass (full line) and mass for the most massive star (dashed line) in a cluster for 200 SCG runs for Mol160 (same inputs as in Fig. 7). |
| Open with DEXTER | |
Concerning the reproducibility of the KLF, for each of the 200 runs the resulting KLF was
fitted with a Gaussian function and the center, peak and ![]() were determined. Figure 9 reports the distribution of
these three parameters for the 200 runs and shows that all of
them are remarkably peaked and symmetric. The formal rms spread
for the three quantities, estimated via a Gaussian fit to the
distributions in the figure, is
were determined. Figure 9 reports the distribution of
these three parameters for the 200 runs and shows that all of
them are remarkably peaked and symmetric. The formal rms spread
for the three quantities, estimated via a Gaussian fit to the
distributions in the figure, is ![]() 0.3 mag for the KLF center,
0.3 mag for the KLF center,
![]() 12% for the KLF peak (about 1.2 sources out of a mean KLF
peak of 10), and
12% for the KLF peak (about 1.2 sources out of a mean KLF
peak of 10), and ![]() 0.25 mag for the KLF FWHM.
0.25 mag for the KLF FWHM.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{dist_klf.ps} \end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg58.png) |
Figure 9: Distribution of the predicted center magnitude (full line - bottom X-axis scale), width (dotted line - bottom X-axis scale) and peak value (dashed line - top X-axis scale) of the predicted Gaussian-fitted KLFs for 200 SCG runs for Mol160 (same inputs as in Fig. 7). |
| Open with DEXTER | |
We completed a similar analysis for HKCF (H-![]() color function; see
Sect. 3.2.2). Figure 10 shows the distribution of Gaussian function centers,
peaks and
color function; see
Sect. 3.2.2). Figure 10 shows the distribution of Gaussian function centers,
peaks and ![]() 's for HKCFs obtained for the same 200 runs used
previously for the KLFs. Gaussian fits to the three distributions in the
figure infer an rms that is
's for HKCFs obtained for the same 200 runs used
previously for the KLFs. Gaussian fits to the three distributions in the
figure infer an rms that is ![]() 0.15 mag for the HKCF center and
0.15 mag for the HKCF center and
![]() 0.14 mag for the HKCF FWHM, while the ``peak'' distribution is
flatter and has an rms value of
0.14 mag for the HKCF FWHM, while the ``peak'' distribution is
flatter and has an rms value of ![]() 21%
for the HKCF peak (about 3.2 sources out of a mean HKCF peak of 15). It is worthwhile to stress that since the position that is assigned to each simulated star in the cluster is different in each of the 200 runs of the model (for any given set of input parameters), the scatter in the properties of the synthetic KLFs and HKCFs also statistically tends to account for the effects of extinction variations in the cluster's hosting clump, which may in principle be relevant in such heavily embedded systems (see Table 2).
21%
for the HKCF peak (about 3.2 sources out of a mean HKCF peak of 15). It is worthwhile to stress that since the position that is assigned to each simulated star in the cluster is different in each of the 200 runs of the model (for any given set of input parameters), the scatter in the properties of the synthetic KLFs and HKCFs also statistically tends to account for the effects of extinction variations in the cluster's hosting clump, which may in principle be relevant in such heavily embedded systems (see Table 2).
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{hkcwp.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg59.png) |
Figure 10: Distribution of the predicted center color (full line - bottom X-axis scale), width (dotted line - bottom X-axis scale) and peak value (dashed line - top X-axis scale) of the predicted Gaussian-fitted HKCFs for 200 SCG runs for Mol160. |
| Open with DEXTER | |
For a given set of input parameters, we conclude that the model results, have a good reproducibility, except concerning the total luminosity. The model therefore has a strong predictive power concerning the median properties of a synthetic cluster. The spread in KLF center magnitudes is indeed, less than the bin amplitude used in compiling the KLFs for the simulations (and is used in the remainder of the work); the median synthetic KLF therefore provides a good representation of the cluster luminosity distribution.
In conclusion, 200 simulation runs for each combination of input parameters (IMF and SFH) can provide a robust assessment of the statistical significance of the synthetic observable properties (KLFs and HKCFs). Although the distributions for the KLFs' (HKCFs') parameters seem rather symmetrical, we adopt the median KLF (HKCF) of the 200 runs as a more reliable characterization for that particular parameters' set. The use of the mean KLF (HKCF) for the comparison does not significantly alter the results.
4.2.4 Exploring the SCG parameter space: cluster parameters
After verifying the robustness of model results in independent runs for the same input parameters, we now measure the sensitivity of the model results to changes in these parameters. We first concentrate on simulated cluster physical parameters (number of cluster members, total luminosity, stellar mass distribution), and in the next paragraph we examine how the KLFs and the appearance of the color-magnitude diagrams, which are the main observables used in our analysis, behave in this respect.
Number of stars
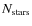 -
-
As a general rule, the older the
cluster is allowed to be, irrespective of the detailed SFH adopted,
the higher is the number of produced stars. This is easily understood
since the SCG cluster formation is stops when the number of the
Stellar masses -
Likewise, the total stellar mass and the mass of the most massive star will be higher the older the cluster is allowed to be. If an IMF1 cluster is a very old SB or a CR with t1=108 yrs and t2=107 yrs for example,
Going from IMF1 to IMF3, both
![]() and
and
![]() significantly increase, as expected. The trend of
significantly increase, as expected. The trend of
![]() with cluster age is less pronounced because with IMF2 and IMF3
it is statistically more likely to produce relatively more massive
(and hence more easily detectable in
with cluster age is less pronounced because with IMF2 and IMF3
it is statistically more likely to produce relatively more massive
(and hence more easily detectable in ![]() )
stars requiring a lower
number of star extractions and hence a lower relative total mass at the end
of the simulation. The age-trend of
)
stars requiring a lower
number of star extractions and hence a lower relative total mass at the end
of the simulation. The age-trend of
![]() is instead the
same (only shifted toward higher masses) because the probability of
extracting a massive star is the same for all ages and is only a
function of the chosen IMF.
is instead the
same (only shifted toward higher masses) because the probability of
extracting a massive star is the same for all ages and is only a
function of the chosen IMF.
Total stellar luminosities and massive object luminosities -
The total stellar luminosity, like the luminosity of the most massive star (
4.2.5 Exploring the SCG parameter space: KLF variations
We now briefly analyze the diagnostic power of the KLF and the HKCF against changes in IMF and SFH choices. Figure 11 shows the KLFs predicted for source Mol3 adopting the same SFH parameters (as indicated in the figure) and using the three different IMF choices.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{gmdgcomp_imf.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg66.png) |
Figure 11:
KLF (using the absolute |
| Open with DEXTER | |
The shape of the resulting KLF changes throughout the MK range; going from Kroupa et al.'s IMF1 to Salpeter's IMF3, the distribution becoming more skewed toward lower magnitudes; this was expected since IMF1 produces more lower mass stars than IMF3. One can certainly argue that the change is not dramatic, but on the other hand the modification does not affect one or two bins but the entire KLF consistently. The change is more apparent in the region between the peak and the completeness limit than at the bright end of the KLF, and for this reason the ability of the model to discriminate between different IMFs is higher for those sources, as Mol3 in the figure, where the KLF's peak is clearly detected above the completeness limit.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{gmdgcomp_ages.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg67.png) |
Figure 12:
KLF (using the absolute |
| Open with DEXTER | |
The difference in predicted KLFs is much more dramatic if different age ranges
are assumed, while keeping fixed the shape of the SFH and the IMF, as it is apparent in
Fig. 12. The peak of the KLF shifts considerably toward higher
magnitudes as the median stellar ages (![]() )
increase. A similar trend is observed by comparing SB models with different
ages, although SB models always produce KLFs that are considerably narrower
than CR or GR models. Older cluster ages would shift the peak of the KLF beyond the completeness limit; in other words, our analysis is insensitive to ages for the majority of stars in excess of
)
increase. A similar trend is observed by comparing SB models with different
ages, although SB models always produce KLFs that are considerably narrower
than CR or GR models. Older cluster ages would shift the peak of the KLF beyond the completeness limit; in other words, our analysis is insensitive to ages for the majority of stars in excess of ![]()
![]() yrs; these old cluster ages would be hard to justify given that they are still heavily embedded in dense clumps.
yrs; these old cluster ages would be hard to justify given that they are still heavily embedded in dense clumps.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{gmdgcomp_sfhs.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg69.png) |
Figure 13:
KLF (using the absolute |
| Open with DEXTER | |
Finally, we briefly show how the KLFs change for different choices of the
SFHs. Figure 13 shows the KLFs obtained for a SB with
t1=106 yrs, compared with a CR with t1=107 yrs and
t2=104 yrs and a GR with the same start and end star formation period,
and with a peak times for star formation rate of
![]() yrs. The KLFs
are clearly different, with a peak magnitude which is quite sensitive to the
formation rate typology and the peak time for star production.
yrs. The KLFs
are clearly different, with a peak magnitude which is quite sensitive to the
formation rate typology and the peak time for star production.
The [
![]() ]
color functions are found to be insensitive to the choice of IMF. As for the KLFs, the main differences between synthetic HKCFs are
more evident for different age ranges especially in the number of detectable stars.
]
color functions are found to be insensitive to the choice of IMF. As for the KLFs, the main differences between synthetic HKCFs are
more evident for different age ranges especially in the number of detectable stars.
4.3 Comparing observed and synthetic KLFs and HKCFs
The detailed comparison of the model KLFs and HKCFs functions to those observed was
carried out only for those sources where the number of detected
stars was sufficient (
![]() )
to allow a statistically significant comparison
(see Col. 3 of Table 2), and where submm information was available to
allow meaningful estimates of extinction (this excludes Mol15 and Mol99).
The number of clusters fulfilling these criteria were 16 out of 23 detected clusters.
The comparison of the observed KLFs and HKCFs (KLF
)
to allow a statistically significant comparison
(see Col. 3 of Table 2), and where submm information was available to
allow meaningful estimates of extinction (this excludes Mol15 and Mol99).
The number of clusters fulfilling these criteria were 16 out of 23 detected clusters.
The comparison of the observed KLFs and HKCFs (KLF
![]() ,
HKCF
,
HKCF
![]() ), with the
synthetic ones produced by SCG (KLF
), with the
synthetic ones produced by SCG (KLF
![]() HKCF
HKCF
![]() ), for the full set
of input parameters (IMF, SFH and age parameters) was carried out
automatically; to ease the process, the observed and
synthetic functions were computed on the same MK and H-K grid.
), for the full set
of input parameters (IMF, SFH and age parameters) was carried out
automatically; to ease the process, the observed and
synthetic functions were computed on the same MK and H-K grid.
The comparison procedure between synthetic and observed KLFs is described below,
but it is the same for HKCFs. The KLFs are first compared bin by bin (the
comparison being limited to those bins brighter than the completeness limit)
identifying with i each bin of the observed KLF, starting
from i=1 for the lower-MK non-zero bin to N for the bin where the
completeness limit for that source is reached (the number N differs clearly for each cluster).
In the case of HKCFs, we exclude objects with H and K magnitudes brighter than the
observed limiting magnitudes for these bands.
A matching flag mi is set to be 1 for those bins where the number of
sources coincide within the 1![]() Poissonian error bar of the observed
KLF, i.e.,
Poissonian error bar of the observed
KLF, i.e.,
The total number of bins where a match is found is divided by the total number of bins useful to the comparison to obtain a KLF compatibility figure (in %) of
The higher is C, the closer is the overall match between KLF
However, the same value of C may result from bins concentrated
at the low-MK end of the KLF, where there are few sources, or in the region
around the peak and in the proximity of the completeness limit, where instead
there are more sources and hence higher statistical significance. A further
figure of merit is then introduced,
where
In this automatic procedure, we select models for which the parameters C and W (at the same time for KLFs and HKCFs) are maximum. For Mol8B, Mol45, and Mol84, the observed KLF has a very irregular and multiple-peaked shape that cannot be matched by any model, and are therefore discarded from further considerations. We are then left with 14 clusters for which a series of models can be found with at least 75% of the bins matching the observations. We find that the best values of C and W are never found for one single set of parameters, but rather we identify ranges of parameter values that produce the best match; in other words, there is a level of degeneracy that the models cannot remove, and this varies from source to source. In 4 clusters (Mol109, 110, 136 and 151), this degeneracy is essentially complete and the model is unable to make any prediction; in one case (Mol148), the comparison selects models with very old stellar ages but with total stellar luminosities by far in excess of the measured bolometric luminosity obtained by integrating the observed luminosities for this region from the mid-IR to the millimeter (see Table 2). In the 9 remaining cases, some degeneracy persists especially in the IMF, confirming (Sect. 4.2.5) that our models are weakly sensitive to the IMFs, but there are clear indications concerning the SFH and ages.
Table 3: Results for SCG runs on detected clusters.
Table 3 reports a summary of the results.The IMF of matching
classes of synthetic cluster models is shown in Col. 2.
Columns. 3-5 contain
the times for the formation of 10%, 50% and 90% of the total number of cluster
members; these values are the median of the values that these times have in all models that match the observations. Column 6 is
the number of cluster members ![]() ,
Col. 7 shows the mass of the most massive
object
,
Col. 7 shows the mass of the most massive
object
![]() ,
and Col. 8 reports the total stellar mass of the cluster
,
and Col. 8 reports the total stellar mass of the cluster
![]() .
We emphasize again that
the analysis selects classes of models other than single models; the values reported in Table 3 are the median value of the parameters for each class of matching models. The table shows
that for some fields multiple IMFs are compatible with the data and, in general,
SFHs with constant (CR) or Gaussian (GR) star-formation rates provide acceptable
solutions for certain age ranges (as reported in the table). Simulations of SFHs
with a single burst are, in general, not accepted. Our modeling is insensitive to bulk stellar ages in a cluster in excess of
.
We emphasize again that
the analysis selects classes of models other than single models; the values reported in Table 3 are the median value of the parameters for each class of matching models. The table shows
that for some fields multiple IMFs are compatible with the data and, in general,
SFHs with constant (CR) or Gaussian (GR) star-formation rates provide acceptable
solutions for certain age ranges (as reported in the table). Simulations of SFHs
with a single burst are, in general, not accepted. Our modeling is insensitive to bulk stellar ages in a cluster in excess of
![]() years (Sect. 4.2.5).
years (Sect. 4.2.5).
5 Discussion
5.1 Cluster ages and star formation histories
Perhaps the most important result of this work is that in all clusters where the comparison of observed KLFs with the ones predicted by the SCG model is possible (see previous paragraph), the observations are consistent with a star formation that continues
over time intervals that in most cases have a duration of between about few 105 and
few 106 yrs, and with a median cluster age of a few 106 yrs. In most cases, we cannot discriminate clearly between a
constant or variable SFR but we are confident that we can exclude the possibility that on average the stars in our clusters
are coeval and originate in a single burst of formation. Detailed studies
toward the Orion Nebula Cluster indicate that stars have been forming for at least 10
![]() ,
or 20
,
or 20
![]() (Palla & Stahler 1999; Hoogerwerf et al.
2001; Hillenbrand 1997), and our results would seem to generalize this on a larger sample
of intermediate and high-mass star-forming regions.
(Palla & Stahler 1999; Hoogerwerf et al.
2001; Hillenbrand 1997), and our results would seem to generalize this on a larger sample
of intermediate and high-mass star-forming regions.
In principle it can be argued that our analysis is incomplete since we did not consider longer wavelength data, which could identify heavily extincted objects that are barely visible, or not visible at all, in the near infrared. However, this does not modify appreciably our conclusions about the age spread within the clusters. Vig et al. (2007) indeed, applied a different analysis to the specific region Mol075, a field not included in our final analysis (Table 3) because the background-subtracted KLF is populated by too few objects for a statistically significant model comparison. Vig et al. also considered Spitzer IRAC and MIPS data, looking for the brighter and redder objects in the area covered by submillimeter emission. In this way, they could identify the younger and more massive objects in the field with an estimated age of the order of 106 years or less. This approach, however, is insensitive to low mass and relatively older pre-MS objects, for which our method is ideally designed. While for this particular field, for the reasons explained above, we cannot perform a direct comparison to our approach, it is clear that the inclusion of longer wavelength data in the analysis might have identified a different, younger, population of objects, rather than increasing the observed age spread deduced for the clusters.
Models of cluster formation by competitive accretion appear to produce an IMF close to those observed because of thanks to the spread in the
accretion rates of the competitive accretion mechanism. However, the
prediction that all stars are formed in about
![]() yrs (Bonnel et al. 2004) for typical conditions in young clusters, corresponding
to a dynamical time or so, seems to disagree with our results. We
instead favour scenarios (Tan & McKee 2002) in which stars continue to forming
over several free-fall times thus providing the required age spread. The finding that the most massive object in the fields considered in this work
are still being formed or have just finished a phase of intense
accretion (Molinari et al. 2008a) is a further indication that star
formation seems to be a long-duration process in the life of a
molecular clump.
yrs (Bonnel et al. 2004) for typical conditions in young clusters, corresponding
to a dynamical time or so, seems to disagree with our results. We
instead favour scenarios (Tan & McKee 2002) in which stars continue to forming
over several free-fall times thus providing the required age spread. The finding that the most massive object in the fields considered in this work
are still being formed or have just finished a phase of intense
accretion (Molinari et al. 2008a) is a further indication that star
formation seems to be a long-duration process in the life of a
molecular clump.
![\begin{figure}
\par\includegraphics[angle=90,width=16.4cm,clip]{llnstar_mmaxnew.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg85.png) |
Figure 14:
Number of cluster members as a function of mass of the highest mass
star. Asterisks are for Testi et al.'s (1997, 1998) Herbig
Ae/Be sample. Other points are for our source sample, where the full diamonds are the
|
| Open with DEXTER | |
How do our clusters compare to more evolved systems, such as the sample of Herbig
Ae/Be stars observed by Testi et al. (1997, 1998)? Figure 14 shows the relationship between the mass of the most massive
source and the total number of cluster stars as provided by the SCG simulations
for our modeled clusters. The filled symbols represent the clusters that we could model (Table 3); the empty symbols instead represent the clusters that could not be modeled for a variety of reasons (see Sect. 4.3), while Testi et al.'s clusters are reported as
asterisks (see figure caption for detailed explanation of the symbols). The figure suggests that the clusters presented in this study are richer than those
surrounding Herbig Ae/Be stars for any given value of the most massive
star in each cluster. The trend persists if we use similar indicators
(e.g,. ![]() ,
the full triangles in the figure).
Furthermore, we note that while
the limiting magnitudes of our observations and those of Testi et al. (1998) are similar, higher AV values toward our sources and the
typically greater distance from the Sun would justify the non-detection of
the fainter cluster members predicted by the SCG models.
It is thus likely that the values of
,
the full triangles in the figure).
Furthermore, we note that while
the limiting magnitudes of our observations and those of Testi et al. (1998) are similar, higher AV values toward our sources and the
typically greater distance from the Sun would justify the non-detection of
the fainter cluster members predicted by the SCG models.
It is thus likely that the values of ![]() derived from our observations
tend to underestimate the cluster memberships.
derived from our observations
tend to underestimate the cluster memberships.
This evidence is clear for values of the most massive star in the cluster below ![]() 10
10 ![]() ,
where the 9 clusters for which we could compare observations with SCG predictions lie (the diamonds). In the clusters for which we haven't simulation results (the empty triangles), the mass for the highest-mass star was estimated by assuming that a fraction of between 30 and 100% of the bolometric luminosity originates in a single ZAMS star. In this case the trend toward richer clusters than Herbig stars (i.e., the asterisks) would become marginal. These estimates, however, place the latter clusters systematically to the right in the plot, compared to the 9 modeled clusters; indeed, if we were to estimate in the same way a maximum stellar mass also for the 9 modeled clusters, we would obtain values in excess (between a factor two and three) of those provided by the detailed SCG modeling. In other words, the evidence that our clusters are richer than those around Herbig stars is marginal at worst (i.e., using the most conservative approach of estimating the mass of the highest-mass star).
,
where the 9 clusters for which we could compare observations with SCG predictions lie (the diamonds). In the clusters for which we haven't simulation results (the empty triangles), the mass for the highest-mass star was estimated by assuming that a fraction of between 30 and 100% of the bolometric luminosity originates in a single ZAMS star. In this case the trend toward richer clusters than Herbig stars (i.e., the asterisks) would become marginal. These estimates, however, place the latter clusters systematically to the right in the plot, compared to the 9 modeled clusters; indeed, if we were to estimate in the same way a maximum stellar mass also for the 9 modeled clusters, we would obtain values in excess (between a factor two and three) of those provided by the detailed SCG modeling. In other words, the evidence that our clusters are richer than those around Herbig stars is marginal at worst (i.e., using the most conservative approach of estimating the mass of the highest-mass star).
The plausibility of this interpretation is strengthened by the results of Baumgardt & Kroupa (2007) who completed extensive numerical simulations of the evolution of stellar clusters as a function of, among other parameters, the cluster gas content. They show that for a wide range of initial conditions and star formation efficiencies, the dispersal of the gas with age causes the cluster to expand overall and disperse a fraction of the stars originally belonging to the cluster. As the cluster expands, its decreasing stellar density ensures that the low-density outer regions of the cluster become ever more difficult to detect against the field stars (especially in the Galactic plane, where all these objects lie), mimicking a smaller cluster from an observational viewpoint. Figure 15 shows the distribution of radii for our clusters (full line) and for those surrounding Ae/Be stars; the radii were derived by the same analysis in the two samples and the histogram clearly shows that our clusters are indeed larger in size, confirming the prediction of Baumgardt & Kroupa (2007).
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{rclu2.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg86.png) |
Figure 15: Distribution of radii for our clusters (full line) and those associated with Herbig Ae/Be stars (from Testi et al. 2001, dashed line). |
| Open with DEXTER | |
This age effect on cluster size is also revealed within our clusters sample. Figure 16 presents the relationship between the cluster radii derived from the
observations and their ages derived from the modeling. The reported correlation has a Spearman rank correlation coefficient of ![]() -0.6, indicating a good correlation with a significance of 92% (between 2 and 3
-0.6, indicating a good correlation with a significance of 92% (between 2 and 3![]() ). Ongoing gas dispersal is certainly plausible in our clusters, given the common detection in these systems of molecular outflows (Zhang et al. 2001, 2005), which are highly effective in
transferring material away from the forming objects and possibly out of the
star-forming region; parsec-scale flows are also commonly observed from low-mass
YSOs.
). Ongoing gas dispersal is certainly plausible in our clusters, given the common detection in these systems of molecular outflows (Zhang et al. 2001, 2005), which are highly effective in
transferring material away from the forming objects and possibly out of the
star-forming region; parsec-scale flows are also commonly observed from low-mass
YSOs.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{rclu-age.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg87.png) |
Figure 16:
Cluster radii (from
Table 2) as a function of the cluster median ages (from
Table 3). Dashed lines
represent the linear fits obtained fitting in turn one plotted variable as a function
of the other; the full line is the bisector of the two dashed lines and represents
the fit which minimizes the quadratic geometric (i.e. not along the X or Y axis
alone) distance of the data from the fit. Following Isobe et al. (1990),
this is the adequate approach when the nature of the data scatter around the
linear fit is not known (and it is not due to classical measurement uncertainties); the slope of the full line is
|
| Open with DEXTER | |
The final stage of gas dispersal, eventually leading to optically revealed clusters such as those around Ae/Be stars, might be triggered by the powerful winds and radiation fields from newborn O and B stars. The indications are (Molinari et al. 2008a,b) that the most massive objects forming in the densest regions of the clumps hosting our clusters may not yet have reached the ZAMS, or are just starting to develop their H II regions. It is quite likely that this event will mark the moment of maximum efficiency of gas dispersal and further evolution of our clusters toward the Ae/Be's ones.
5.2 Physical vs. statistical models for cluster formation
Figure 14 can also be used as a diagnostic to discriminate between different classes of models for the origin of clusters. Testi et al. (2001) called physical the class of models that implies a physical relationship between the most massive star that forms and other environmental properties such as the cluster richness or the mass of the gaseous clump where the stars originate from; examples are the ``turbulent core'' (McKee & Tan 2003), the ``coalescence'' (Bonnell et al., 1998), or the competitive accretion models (Bonnell & Bate 2006). In a second class of models, called statistical, the relationship between the most massive star in a cluster and its richness originates in the higher probability of finding the rare massive stars in rich clusters rather than in isolation (Bonnell & Clarke 1999). If clusters are populated by randomly picking stars from the field stars' initial mass function, and considering a cluster membership-size distribution in the form of an appropriate power law, then the observations of Testi et al. (1999) can be naturally explained. Nevertheless, this model predicts that a significant fraction of high-mass stars are still associated with relatively poorly populated clusters, in other words that massive stars can be found both in high-N clusters and, to a lesser extent, in low-N clusters.
The dashed line in Fig. 14 is the upper boundary of the region that should contain 25% of the cluster realizations obtained by randomly extracting stars from the IMF (Testi et al. 2001).
If we consider our measurements of ![]() for our entire sample
(i.e., the full and empty triangles), a fraction of about 15% of the clusters is found marginally below the dashed line. However, we note that our modeling was possible only for
clusters above a membership threshold derived with
for our entire sample
(i.e., the full and empty triangles), a fraction of about 15% of the clusters is found marginally below the dashed line. However, we note that our modeling was possible only for
clusters above a membership threshold derived with ![]() ,
which is thus a
biased subsample toward rich clusters. Based the extreme assumption that the fields with no detected cluster are cases of systems consisting of a single heavily extincted star, and thus would fall below the dashed line in Fig. 14, this fraction would approach the 25% level. This, however, is an extreme case because, as we have already discussed, the high value of the extinction derived from submillimeter maps may be the
reason for not detecting clusters in at least a number of observed fields.
,
which is thus a
biased subsample toward rich clusters. Based the extreme assumption that the fields with no detected cluster are cases of systems consisting of a single heavily extincted star, and thus would fall below the dashed line in Fig. 14, this fraction would approach the 25% level. This, however, is an extreme case because, as we have already discussed, the high value of the extinction derived from submillimeter maps may be the
reason for not detecting clusters in at least a number of observed fields.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{mmax-mstars.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg88.png) |
Figure 17: Mass for the highest mass star as a function of the total stellar mass for the 9 modeled clusters (see Table 3); the bars associated to each cluster (the diamond symbols) represent the total span of the parameter values for the classes of models selected by our analysis (the diamond marks the median values). The dash-dotted, and dashed lines represents the relationship obtained for numerical simulations of clusters drawn from pure random sampling of the IMF, and using a so-called sorted sampling, following Weidner & Kroupa (2006). The full line is a semi-analytical approximation of this relationship obtained by Weidner & Kroupa (2004). The dotted line is the limit where a cluster is made of just one star. |
| Open with DEXTER | |
As an additional means of differentiating between physical and statistical cluster
models, Weidner & Kroupa (2006) argued that a non-trivial
correlation exists between the highest-mass star in a cluster,
![]() ,
and the total stellar mass of the cluster itself,
,
and the total stellar mass of the cluster itself,
![]() (Fig. 17).
Numerical simulations show that the relationship obtained by pure random
sampling of the IMF with an imposed physical limit of 150
(Fig. 17).
Numerical simulations show that the relationship obtained by pure random
sampling of the IMF with an imposed physical limit of 150 ![]() for
the maximum stellar mass (the dashed-dot line
in Fig. 17) clearly does not represent our data.
for
the maximum stellar mass (the dashed-dot line
in Fig. 17) clearly does not represent our data.
A substantially different result (the dashed line) is obtained if
cluster members are selected in ascending order and constrained to total
cluster masses distributed according to a cluster total mass function
(Weidner & Kroupa 2006). Basically, this second option infers that drawing 10 clusters of 100 stars will not deliver the same
![]() )
as drawing 1 cluster of 1000 stars. This
trend closely resembles a semi-analytical approximation of
)
as drawing 1 cluster of 1000 stars. This
trend closely resembles a semi-analytical approximation of
![]() )
obtained by Weidner & Kroupa (2004),
again assuming that total cluster stellar masses are distributed according to a power-law
mass function. Weidner & Kroupa (2006) suggested that this
sorted sampling way of populating a cluster can be physically
understood in terms of a pre-stellar clump where initial low-amplitude
perturbations start low-mass star formation; as further perturbations
with larger amplitude grow, higher mass stars will start to form until
the feedback from the latter will begin to disrupting the cloud. This scenario
of organised star formation where low-mass stars are the first to
form, is the same as we favor (see Sect. 5.1) considering the age
spread that we find in our clusters in which, based on independent considerations
(Molinari et al. 2008a), the most massive star may not have
formed. By the way, this latter possibility does not change the substance of
the agreement between our data and the physical cluster models
in Fig. 17, since the late addition of the highest mass star
currently not yet visible in the near-IR would shift the points toward the
top-right of the plot.
)
obtained by Weidner & Kroupa (2004),
again assuming that total cluster stellar masses are distributed according to a power-law
mass function. Weidner & Kroupa (2006) suggested that this
sorted sampling way of populating a cluster can be physically
understood in terms of a pre-stellar clump where initial low-amplitude
perturbations start low-mass star formation; as further perturbations
with larger amplitude grow, higher mass stars will start to form until
the feedback from the latter will begin to disrupting the cloud. This scenario
of organised star formation where low-mass stars are the first to
form, is the same as we favor (see Sect. 5.1) considering the age
spread that we find in our clusters in which, based on independent considerations
(Molinari et al. 2008a), the most massive star may not have
formed. By the way, this latter possibility does not change the substance of
the agreement between our data and the physical cluster models
in Fig. 17, since the late addition of the highest mass star
currently not yet visible in the near-IR would shift the points toward the
top-right of the plot.
We verified a posteriori that the range of
![]() and
and
![]() parameters values explored by our simulations is much wider than the area spanned by the bars attached to the single points, and also includes regions compatible with the random sampling cluster model. We then conclude that the result of Fig. 17 is not likely to be produced by
a biased sampling of the clusters' physical parameters explored in our models.
parameters values explored by our simulations is much wider than the area spanned by the bars attached to the single points, and also includes regions compatible with the random sampling cluster model. We then conclude that the result of Fig. 17 is not likely to be produced by
a biased sampling of the clusters' physical parameters explored in our models.
The predictions of the sorted sampling descibed above, with which our data points best agree, are also in good agreement with the results from simulations of clusters forming in a competitive accretion scenario (Bonnell et al. 2004). This model, however, seems to be excluded by the observed ages and age spreads in our clusters which are in clear disagreement with the predicted cluster formation timescales of 2-3 free-fall times.
5.3 Influence of binarity on the interpretation of age spread
Weidner et al. (2008) carried out extensive
numerical simulations to determine how the presence of unresolved binary/multiple
stars can affect the observational properties of a young cluster in a massive
star-forming region. Assuming 100% binarity in a cluster of coeval sources,
they find that unresolved binaries may lead an observer to conclude that
a significant age spread is instead present in the cluster; the full line in
Fig. 18 shows the a posteriori age determination assuming
that all binaries are unresolved. We see that the measured age spread for the
large majority of stars simulated in Weidner et al.'s simulation is comparable
to a log(age) Gaussian distribution with
![]() ,
which is one of the
possible choices of star formation histories in our cluster models. However,
the comparison of our observed KLFs with the SCG models (Table 3)
suggests age spreads much larger than this, and more comparable to a log(age)
distribution with
,
which is one of the
possible choices of star formation histories in our cluster models. However,
the comparison of our observed KLFs with the SCG models (Table 3)
suggests age spreads much larger than this, and more comparable to a log(age)
distribution with
![]() (the dotted line in Fig. 18).
We then conclude that unresolved binaries in our clusters cannot account
for the observed age spread.
(the dotted line in Fig. 18).
We then conclude that unresolved binaries in our clusters cannot account
for the observed age spread.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{age_spread.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg90.png) |
Figure 18:
Full line represents the age spread resulting from the simulations of Weidner et al.
(2008) for a cluster with an input age of
|
| Open with DEXTER | |
6 Conclusions
The main results of this work are the following:
- In the J, H, and
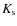 NIR bands, we have imaged 26 intermediate and
high-mass star-forming regions selected from a larger sample of sources
spanning a range in luminosities and presumed youth. We have identified
the presence of 23 young stellar clusters in 22 fields.
NIR bands, we have imaged 26 intermediate and
high-mass star-forming regions selected from a larger sample of sources
spanning a range in luminosities and presumed youth. We have identified
the presence of 23 young stellar clusters in 22 fields.
- The detected clusters have richness indicator values of
between ten and several tens of objects and have median radii of 0.7 pc.
Compared to clusters around Herbig Ae/Be stars, our clusters seem
richer and larger for any given mass for the most massive star in each
cluster. Color-color diagrams show that these clusters are young: many sources
exhibit colors typical of young pre-MS objects with an intrinsic IR excess originating in warm circumstellar dust. This is confirmed by the analysis of
color-magnitude diagrams, where a significant fraction of stars in each cluster
are found to be related to the Pre-MS evolutionary tracks, even after conservative
de-reddening is applied.
- We have been unable to perform a direct inversion of stellar luminosities (and
colors) into masses
and ages; we use a synthetic cluster generator (SCG) model to create statistically-significant
cluster simulations for different initial parameters (IMF,
SFH, source ages, and their distribution), and compare the synthetic KLFs and
HKCFs with the observed (field star-subtracted) ones. For the fraction of clusters for which this comparison selects a clearly defined region of the parameter space, we conclude that
star formation in these regions cannot be represented by a single burst,
but is a process that is spread out in time. Clusters have mean ages of
a few 106 yrs; the ages of most of the clusters members are spread,
within each cluster, between a few 105 yrs and a few
106 yrs. Together with the independent evidence that the most
massive stars in these systems are very young, or not even yet on the ZAMS,
this result is difficult to reconcile with any model predicting cluster
formation in a crossing time.
- The cluster radii seem to be inversely proportional to their age,
as also confirmed by the comparison of cluster parameters with those typical
of Ae/Be systems, which are smaller and less rich. As suggested by numerical
simulations in the literature, dispersal of intra-cluster gas (by, e.g.,
molecular outflows or radiation fields from massive stars) may lead to the
loss of a fraction of cluster stellar population, thus indeed leading to smaller and less rich clusters.
Our results seem in line with this prediction.
- The relation between the mass of the most massive
star in a cluster and the cluster's richness indicator
suggests that a
physical rather than statistical nature of the cluster
origin is more likely.
Acknowledgements
We thank the anonymous referee whose comments greatly helped improving the quality of the data presentation and the overall readability of the paper. We also thank P. Kroupa for his comments and suggestions.
References
- Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] (In the text)
- Behrend, R., & Meader, A. 2001, A&A, 373, 190 [NASA ADS] [CrossRef] [EDP Sciences]
- Beltrán, M. T., Cesaroni, R., Neri, R., et al. 2004, ApJ, 601, L187 [NASA ADS] [CrossRef]
- Beltrán, M. T., Brand, J., Cesaroni, R., et al. 2006, A&A, 447, 221 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Benjamin, R. A., Churchwell, E. B., Babler, B., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] (In the text)
- Bertoldi, F., & McKee, C. F. 1992, ApJ 395, 140
- Bessel, M. S. 1979, PASP, 91, 377 [CrossRef]
- Bessel, M. S. 1991, AJ, 102, 303 [NASA ADS] [CrossRef]
- Bessel, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef]
- Beuther, H., Schilke, P., Sridharan, T. K., et al. 2002, A&A, 383, 892 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Binney, S. J., & Tremaine, S. 1987, Galactic Dynamics (Princeton NJ: Princeton Univ. Press)
- Bonnell, I. A., & Bate, M. R. 2002, MNRAS, 336, 659 [NASA ADS] [CrossRef]
- Bonnell, I. A., & Bate, M. R. 2006, MNRAS, 370, 488 [NASA ADS] (In the text)
- Bonnell, I. A., & Clarke, C. 1999, MNRAS, 309, 461 [NASA ADS] [CrossRef] (In the text)
- Bonnell, I. A., & Davies, M. B. 1998, MNRAS, 295, 691 [NASA ADS] [CrossRef]
- Bonnell, I. A., Bate, M. R., & Zinnecher, H. 1998, MNRAS, 298, 93 [NASA ADS] [CrossRef] (In the text)
- Bonnell, I. A., Bate, M. R., Clarke, C., & Pringle, J. E. 2001, MNRAS, 323, 785 [NASA ADS] [CrossRef]
- Bonnell, I. A., Bate, M. R., & Vine, S. G. 2003, MNRAS, 343, 413 [NASA ADS] [CrossRef]
- Bonnell, I. A., Vine, S. G., & Bate, M. R. 2004, MNRAS, 349, 735 [NASA ADS] [CrossRef] (In the text)
- Brand, J., & Blitz, L. 1993, A&A, 275, 67 [NASA ADS]
- Brand, J., Cesaroni, R., Palla, F., & Molinari, S. 2001, A&A, 370, 230 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cesaroni, R. 2005, Ap&SS, 295, 5 [NASA ADS] [CrossRef] (In the text)
- Cesaroni, R., Neri, R., Olmi, L., et al. 2005, A&A, 434, 1039 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cesaroni, R., Galli, D., Lodato, G., Walmsley, C. M., & Zhang, Q. 2006, Protostars & Planet V, Disks Around Young O-B (Proto)Stars: Observation and Theory (In the text)
- Chini, R., Hoffmeister, V., Kimeswenger, S., et al. 2004, Nature, 429, 155 [NASA ADS] [CrossRef]
- Clarke, C., & Delgrado-Donate, E. 2003, Galactic Star Formation Across the Stellar Mass Spectrum, ASP Conf. Ser., 287
- de Wit, W.-J., Testi, L., Palla, F., & Zinnecker, H. 2005, A&A, 437, 247 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hartmann, L. W., Jones, B. F., Stauffer, J. R., & Kenion, S. J. 1991, AJ, 101, 1050 [NASA ADS] [CrossRef]
- Hillenbrand, L. A., & Carpenter, J. M. 2000, ApJ, 540, 236 [NASA ADS] [CrossRef] (In the text)
- Hoogerwerf, R., de Bruijne, J. H. J., & de Zeeuw, P. T. 2001, A&A, 365, 49 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] (In the text)
- Hunt, L. K., Mannucci, F., Testi, L., et al. 1998, AJ, 115, 259 [NASA ADS] [CrossRef] (In the text)
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] (In the text)
- Klein, R. I., Inutsuka, S., Padoan, P., & Tomisaka, K. 2006, Protostars & Planet V, Current Advances in the Methodology and Computational Simulation of the Formation of Low-Mass Stars (In the text)
- Kenyon, S., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef]
- Keto, E. 2003, ApJ, 599, 1196 [NASA ADS] [CrossRef] (In the text)
- Koornneef, J. 1983, A&A, 128, 84 [NASA ADS]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] (In the text)
- Kumar, M. S. N., Keto, E., & Clerkin, E. 2006, A&A, 449, 1033 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kumar, M. S. N., & Grave, J. M. C. 2008, ASPC, 387, 323 [NASA ADS] (In the text)
- Lada, C., & Adams, F. 1992, ApJ, 393, 278 [NASA ADS] [CrossRef] (In the text)
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] (In the text)
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] (In the text)
- Molinari, S., Brand, J., Cesaroni, R., & Palla, F. 1996, A&A, 308, 573 [NASA ADS] (In the text)
- Molinari, S., Brand, J., Cesaroni, R., Palla, F., & Palumbo, G. G. C. 1998, A&A, 336, 339 [NASA ADS] (In the text)
- Molinari, S., Brand, J., Cesaroni, R., & Palla, F. 2000, A&A, 355, 617 [NASA ADS] (In the text)
- Molinari, S., Testi, L., Rodrguez, L. F., & Zhang, Q. 2002, ApJ, 570, 758 [NASA ADS] [CrossRef]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008a, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Molinari, S., Faustini, F., Testi, L., et al. 2008b, A&A, 487, 1119 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moraux, E., Lawson, W. A., & Clarke, C. 2007, A&A, 473, 163 [NASA ADS] [CrossRef] [EDP Sciences]
- Nakano, T. 1989, ApJ, 345, 464 [NASA ADS] [CrossRef] (In the text)
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 722 [NASA ADS] [CrossRef] (In the text)
- Preibisch, Th., Ossenkopf, V., Yorke, H. W., & Henning, Th. 1993, A&A, 279, 577 [NASA ADS] (In the text)
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] (In the text)
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
- Scalo, J. 1998, The Stellar Initial Mass Function, ed. G. Gilmore, & D. Howell, 142, 201 (In the text)
- Strom, K. M., Strom, S. E., Edwards, S., Cabrit, S., & Skrutskie, M. F. 1989, AJ, 97, 111 [CrossRef]
- Tan, J. C. 2005, Cores to Clusters: Star Formation with Next Generation Telescopes, Astrophys. Space Sci. Lib., 324, 87
- Tan, J. C., & McKee, C. F. 2002, Hot Star Workshop III: The earliest Stages of Massive Star Birth, ASP Conf. Proc., 267, 267 (In the text)
- Tan, J. C., Krumholz, M. R., & McKee, C. F. 2006, ApJ
- Testi, L., Palla, F., & Natta, A. 1998, A&AS, 133, 81 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Testi, L., Palla, F., & Natta, A. 1999, A&A, 342, 515 [NASA ADS] (In the text)
- Testi, L., Palla, F., & Natta, A. 2001, From Darkness to Light, ed. T. Montmerle, & Ph. André, ASP Conf. Ser., 243, 377 (In the text)
- Testi, L., Palla, F., Prusti, T., Natta, A., & Maltagliati, S. 1997, A&A, 320, 159 [NASA ADS] (In the text)
- Vig, S., Testi, L., Walmsley, M., et al. 2007, A&A, 470, 977 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef] (In the text)
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS] (In the text)
- Weidner, C., Kroupa, P., & Maschberger, T. 2008 [arXiv:0811.3730W] (In the text)
- Yorke, H. W. 2002, Hot Star Workshop III: The earliest Stages of Massive Star Birth, ASP Conf. Proc., 267, 165 (In the text)
- Zhang, Q., Hunter, T. R., Brand, J., et al. 2001, ApJ, 552, L167 [NASA ADS] [CrossRef] (In the text)
- Zhang, Q., Hunter, T. R., Brand, J., et al. 2005, ApJ, 625, 864 [NASA ADS] [CrossRef] (In the text)
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] (In the text)
Online Material
Appendix A: K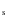 images for all observed fields
images for all observed fields
This appendix contains the ![]() images for all observed fields; these are also available at http://galatea.ifsi-roma.inaf.it/faustini/K-images/
images for all observed fields; these are also available at http://galatea.ifsi-roma.inaf.it/faustini/K-images/
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m003.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg92.png) |
Figure A.1:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m008.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg93.png) |
Figure A.2:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m009.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg94.png) |
Figure A.3:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m011.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg95.png) |
Figure A.4:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m012.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg96.png) |
Figure A.5:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m015.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg97.png) |
Figure A.6:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m028.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg98.png) |
Figure A.7:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m030.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg99.png) |
Figure A.8:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m038.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg100.png) |
Figure A.9:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m045.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg101.png) |
Figure A.10:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m050.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg102.png) |
Figure A.11:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m059.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg103.png) |
Figure A.12:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m075.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg104.png) |
Figure A.13:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m082.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg105.png) |
Figure A.14:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m084.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg106.png) |
Figure A.15:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m098.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg107.png) |
Figure A.16:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m099.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg108.png) |
Figure A.17:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m103.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg109.png) |
Figure A.18:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m109.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg110.png) |
Figure A.19:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m110.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg111.png) |
Figure A.20:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m136.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg112.png) |
Figure A.21:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m139.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg113.png) |
Figure A.22:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m143.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg114.png) |
Figure A.23:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m148.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg115.png) |
Figure A.24:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m151.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg116.png) |
Figure A.25:
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m160.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg117.png) |
Figure A.26:
|
| Open with DEXTER | |
Appendix B: 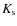 luminosity functions
luminosity functions
This appendix presents the set of background-subtracted
| Figure B.1: Mol003 ( left), Mol008A ( center), Mol008B ( right). |
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{18cm}{!}
{\includegraphics[angle=-0,origin=c,width...
....ps}
\includegraphics[angle=-0,origin=c,width=6cm]{KLF_mol012.ps}}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg119.png) |
Figure B.2: Mol009 ( left), Mol011 ( center), Mol012 ( right). |
| Open with DEXTER | |
| Figure B.3: Mol015 ( left), Mol028 ( center), Mol045 ( right). |
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{18cm}{!}
{\includegraphics[angle=-0,origin=c,width...
....ps}
\includegraphics[angle=-0,origin=c,width=6cm]{KLF_mol082.ps}}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg121.png) |
Figure B.4: Mol050 ( left), Mol075 ( center), Mol082 ( right). |
| Open with DEXTER | |
| Figure B.5: Mol084 ( left), Mol099 ( center), Mol103 ( right). |
|
| Open with DEXTER | |
| Figure B.6: Mol136 ( left), Mol110 ( center), Mol136 ( right). |
|
| Open with DEXTER | |
| Figure B.7: Mol139 ( left), Mol143 ( center), Mol148 ( right). |
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{18cm}{!}
{\includegraphics[angle=-0,origin=c,width...
....ps}
\includegraphics[angle=-0,origin=c,width=6cm]{KLF_mol160.ps}}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg125.png) |
Figure B.8: Mol151 ( left), Mol160 ( right). |
| Open with DEXTER | |
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Appendices are only available in electronic form at http://www.aanda.org
- ...
![[*]](/icons/foot_motif.png)
- Based on observations obtained at the Palomar Observatory and at the ESO La Silla Observatory (Chile), programme 65.I-0310(A).
- ... online
![[*]](/icons/foot_motif.png)
- At http://galatea.ifsi-roma.inaf.it/faustini/K-images/.
- ... online
![[*]](/icons/foot_motif.png)
- At http://galatea.ifsi-roma.inaf.it/faustini/KLF/.
All Tables
Table 1: Description of observations.
Table 2: Results for cluster detection.
Table 3: Results for SCG runs on detected clusters.
All Figures
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{dens.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg36.png) |
Figure 1: Stellar density (in stars/pc2), for Mol28, as a function of the radial distance (in parsecs) from cluster center. Error-bars are computed as the Poissonian fluctuations of source counts in each bin. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{ic_av.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg40.png) |
Figure 2:
Cluster richness indicator |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{ic_rclu.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg41.png) |
Figure 3:
Distribution of the cluster radii in parsecs (full line) and
the cluster richness indicator |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{colcol.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg44.png) |
Figure 4:
[J-H] vs. [H- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{colmag.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg46.png) |
Figure 5:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{distr-distance.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg47.png) |
Figure 6: Distribution of identified sources as a function of nearest-neighbor distance (D) for two of our examined fields (Mol28 dashed line and Mol103 full line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{lumnum.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg55.png) |
Figure 7: Distribution of the predicted number of cluster members (full line) and total luminosity (dashed line) for 200 SCG runs for Mol160 with a Salpeter IMF and a constant star formation rate with t1=106 yrs and t2=104 yrs. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{mstars.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg56.png) |
Figure 8: Distribution of the predicted total stellar mass (full line) and mass for the most massive star (dashed line) in a cluster for 200 SCG runs for Mol160 (same inputs as in Fig. 7). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{dist_klf.ps} \end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg58.png) |
Figure 9: Distribution of the predicted center magnitude (full line - bottom X-axis scale), width (dotted line - bottom X-axis scale) and peak value (dashed line - top X-axis scale) of the predicted Gaussian-fitted KLFs for 200 SCG runs for Mol160 (same inputs as in Fig. 7). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{hkcwp.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg59.png) |
Figure 10: Distribution of the predicted center color (full line - bottom X-axis scale), width (dotted line - bottom X-axis scale) and peak value (dashed line - top X-axis scale) of the predicted Gaussian-fitted HKCFs for 200 SCG runs for Mol160. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{gmdgcomp_imf.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg66.png) |
Figure 11:
KLF (using the absolute |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{gmdgcomp_ages.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg67.png) |
Figure 12:
KLF (using the absolute |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{gmdgcomp_sfhs.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg69.png) |
Figure 13:
KLF (using the absolute |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=16.4cm,clip]{llnstar_mmaxnew.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg85.png) |
Figure 14:
Number of cluster members as a function of mass of the highest mass
star. Asterisks are for Testi et al.'s (1997, 1998) Herbig
Ae/Be sample. Other points are for our source sample, where the full diamonds are the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{rclu2.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg86.png) |
Figure 15: Distribution of radii for our clusters (full line) and those associated with Herbig Ae/Be stars (from Testi et al. 2001, dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{rclu-age.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg87.png) |
Figure 16:
Cluster radii (from
Table 2) as a function of the cluster median ages (from
Table 3). Dashed lines
represent the linear fits obtained fitting in turn one plotted variable as a function
of the other; the full line is the bisector of the two dashed lines and represents
the fit which minimizes the quadratic geometric (i.e. not along the X or Y axis
alone) distance of the data from the fit. Following Isobe et al. (1990),
this is the adequate approach when the nature of the data scatter around the
linear fit is not known (and it is not due to classical measurement uncertainties); the slope of the full line is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{mmax-mstars.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg88.png) |
Figure 17: Mass for the highest mass star as a function of the total stellar mass for the 9 modeled clusters (see Table 3); the bars associated to each cluster (the diamond symbols) represent the total span of the parameter values for the classes of models selected by our analysis (the diamond marks the median values). The dash-dotted, and dashed lines represents the relationship obtained for numerical simulations of clusters drawn from pure random sampling of the IMF, and using a so-called sorted sampling, following Weidner & Kroupa (2006). The full line is a semi-analytical approximation of this relationship obtained by Weidner & Kroupa (2004). The dotted line is the limit where a cluster is made of just one star. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{age_spread.ps}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg90.png) |
Figure 18:
Full line represents the age spread resulting from the simulations of Weidner et al.
(2008) for a cluster with an input age of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m003.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg92.png) |
Figure A.1:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m008.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg93.png) |
Figure A.2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m009.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg94.png) |
Figure A.3:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m011.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg95.png) |
Figure A.4:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m012.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg96.png) |
Figure A.5:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m015.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg97.png) |
Figure A.6:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m028.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg98.png) |
Figure A.7:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m030.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg99.png) |
Figure A.8:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m038.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg100.png) |
Figure A.9:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m045.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg101.png) |
Figure A.10:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m050.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg102.png) |
Figure A.11:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m059.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg103.png) |
Figure A.12:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m075.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg104.png) |
Figure A.13:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m082.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg105.png) |
Figure A.14:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m084.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg106.png) |
Figure A.15:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m098.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg107.png) |
Figure A.16:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m099.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg108.png) |
Figure A.17:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m103.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg109.png) |
Figure A.18:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m109.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg110.png) |
Figure A.19:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m110.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg111.png) |
Figure A.20:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m136.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg112.png) |
Figure A.21:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m139.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg113.png) |
Figure A.22:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m143.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg114.png) |
Figure A.23:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m148.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg115.png) |
Figure A.24:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m151.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg116.png) |
Figure A.25:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[angle=-90,width=13cm,clip]{map_m160.ps} }
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg117.png) |
Figure A.26:
|
| Open with DEXTER | |
| In the text | |
| |
Figure B.1: Mol003 ( left), Mol008A ( center), Mol008B ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{18cm}{!}
{\includegraphics[angle=-0,origin=c,width...
....ps}
\includegraphics[angle=-0,origin=c,width=6cm]{KLF_mol012.ps}}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg119.png) |
Figure B.2: Mol009 ( left), Mol011 ( center), Mol012 ( right). |
| Open with DEXTER | |
| In the text | |
| |
Figure B.3: Mol015 ( left), Mol028 ( center), Mol045 ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{18cm}{!}
{\includegraphics[angle=-0,origin=c,width...
....ps}
\includegraphics[angle=-0,origin=c,width=6cm]{KLF_mol082.ps}}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg121.png) |
Figure B.4: Mol050 ( left), Mol075 ( center), Mol082 ( right). |
| Open with DEXTER | |
| In the text | |
| |
Figure B.5: Mol084 ( left), Mol099 ( center), Mol103 ( right). |
| Open with DEXTER | |
| In the text | |
| |
Figure B.6: Mol136 ( left), Mol110 ( center), Mol136 ( right). |
| Open with DEXTER | |
| In the text | |
| |
Figure B.7: Mol139 ( left), Mol143 ( center), Mol148 ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{18cm}{!}
{\includegraphics[angle=-0,origin=c,width...
....ps}
\includegraphics[angle=-0,origin=c,width=6cm]{KLF_mol160.ps}}
\end{figure}](/articles/aa/full_html/2009/33/aa9145-07/Timg125.png) |
Figure B.8: Mol151 ( left), Mol160 ( right). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.