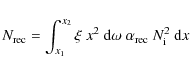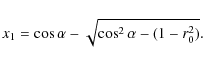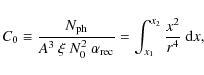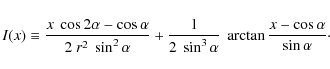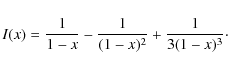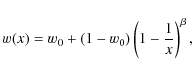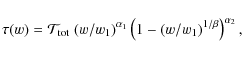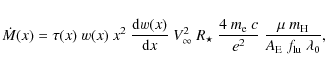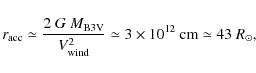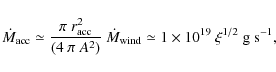EDP Sciences
Home All issues Volume 503 / No 3 (September I 2009) A&A, 503 3 (2009) 899-907 Full HTML
Free Access
Issue
A&A
Volume 503, Number 3, September I 2009
Page(s) 899 - 907
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200912312
Published online 09 July 2009

An analysis of a spectrum of V838 Monocerotis in October 2005

R. Tylenda - T. Kaminski - M. Schmidt

Department for Astrophysics, N. Copernicus Astronomical Center, Rabianska 8, 87-100 Torun, Poland

Received 9 April 2009 / Accepted 30 May 2009

Abstract
Context. V838 Mon erupted at the beginning of 2002 becoming an extremely luminous star with $L=10^6~L_{\hbox{$\odot$ }}$. Among various scenarios proposed to explain the nature of the outburst, the most promising is a stellar merger event.
Aims. We attempt to obtain information about the structure and evolution of the object in the decline from the 2002 eruption.
Methods. The results of spectroscopic observations of the object obtained in October 2005 with the Keck/HIRES instrument, presented in detail in Paper I, are analysed and discussed. Modelling of the observed line profiles has been used to constrain the physical parameters of the system.
Results. The kinematics of the atmosphere of V838 Mon is very complex. Our analysis of the molecular bands and the P-Cyg profiles of atomic lines shows that the object loses matter with a velocity of up to 215 km s-1 and a rate of 10-6,-10-5  $M_{\hbox{$\odot$ }}$ yr-1. In the profiles of some atomic lines, we have, however, found evidence of matter infall. Moreover, a narrow absorption component, which is particularly strong in some P-Cyg profiles, may indicate that a jet-like outflow has also been formed.

We show that the observed emission in the [Fe II] lines and an eclipse-like event observed in November/December 2006 was probably caused by interactions of the expanding matter, ejected by V838 Mon in 2002, with radiation from the B3V companion. In particular, the observed profiles of the [Fe II] lines can be easily modelled in this scenario and allow us to estimate parameters of the system, such as the position of the B3V companion relative to V838 Mon and the line of sight, density in the outflowing matter, and mass lost in the 2002 eruption. The observed appearance of strong H$\alpha$ emission, just before and during the eclipse-like event, can be interpreted as a result of the accretion of the outflowing matter onto the B3V companion: the accreted matter, shocked above the stellar surface, can be a source of extreme-UV and soft X-ray radiation capable of ionizing and exciting H in the outflow.

Key words: stars: individual: V838 Monocerotis - stars: late-type - stars: early-type - stars: peculiar - stars: winds, outflows - line: profiles

  1 Introduction

The eruption of V838 Monocerotis was discovered at the beginning of January 2002. As observed in the optical, the eruption lasted about three months (Munari et al. 2002a; Crause et al. 2003; Kimeswenger et al. 2002). During the event, the object reached a luminosity of $\sim$ $10^6~L_\odot$. After developing an A-F supergiant spectrum at the maximum in the beginning of February 2002, the object evolved to lower effective temperatures and in April 2002 was practically unable to be detected in the optical, remaining very bright however in the infrared. Optical spectroscopy acquired at that time discovered a B3V companion of the erupted object (Munari et al. 2002b). Tylenda (2005) analysed the evolution of V838 Mon during outburst and early decline.

Different outburst mechanisms, including an unusual nova, a He-shell flash, and a stellar merger, were proposed to explain the eruption of V838 Mon. These mechanisms were critically discussed by Tylenda & Soker (2006), the authors conclude that the only mechanism that could satisfactorily account for the observational data was a collision and merger of a low-mass pre-main-sequence star with an $\sim$$8~M_\odot$main-sequence star.

In Kaminski et al. (2009, hereinafter referred to as Paper I), a high resolution spectrum of V838 Mon acquired with the Keck I telescope in October 2005 was presented. In the present paper, we analyse and discuss the results obtained from this spectrum.

2 Evolution of V838 Mon during the decline after the 2002 eruption

A few months after the eruption, discovered at the beginning of January 2002, V838 Mon entered a relatively calm decline phase. V838 Mon then resembled a very cool oxygen-rich (C/O <1) supergiant slowly declining in luminosity (Evans et al. 2003; Tylenda 2005; Munari et al. 2007b). It dominated the observed spectrum at green, red and infrared wavelengths. The blue part of the spectrum was dominated by the light of the B3V companion.

Late in 2004, narrow emission lines, belonging mostly to [Fe II], appeared mainly in the blue part of the spectrum (Barsukova et al. 2006), and strengthened in time (Munari et al. 2007a). During November-December 2006, an eclipse-like event of the B3V companion was observed (Bond 2006; Munari et al. 2007a). At the epoch of the event, the [Fe II] emission lines reached their maximum strength and strong emission in Balmer lines appeared (Munari et al. 2007a).

In October 2005, we obtained an optical spectrum of V838 Mon using the Keck/HIRES instrument. Results of these observations were presented in Paper I. The star V838 Mon itself is seen as a very cool supergiant that dominates the green and red parts of the spectrum. Numerous, often very deep and complex, molecular absorption bands are the main spectral characteristics of this component. All the bands are from oxides and include TiO, VO, AlO, ScO, and YO. The excitation temperature derived from the bands ranges from $\sim$2500 K, identified also as the photospheric temperature of V838 Mon, down to $\sim$500 K, which presumably corresponds to outflowing matter at a few stellar radii. The most positive (heliocentric) radial velocity derived from the bands is $\sim$58 km s-1, which we propose to be the radial velocity of V838 Mon itself. Several atomic lines, mostly resonance, display P-Cyg profiles. They provide evidence of an intense mass outflow with a typical velocity of $\sim$150 km s-1. The blue part of the spectrum is dominated by the spectrum of the B3V companion. The values of $T_{\rm eff}$ and log gderived from the spectrum agree well with those implied by the spectral type. The star is a rapid rotator (V sin  $i \simeq 250$ km s-1) and its (heliocentric) radial velocity is $\sim$40 km s-1. Numerous emission lines were identified, mainly in the blue part of the spectrum. They correspond predominantly to [Fe II] and exhibit the same profile, which can be fitted well with a Lorentzian profile. The lines are centred on a heliocentric radial velocity of $\sim$13 km s-1 and have a FWHM of $\sim$80 km s-1.

Munari et al. (2007a) propose that the appearance of the [Fe II] emission lines and the eclipse-like event observed in November/December 2006 were unrelated, and that the eclipse-like event was caused by an eclipse in a binary system. We argue that both events were strongly related and produced by matter ejected from V838 Mon during the 2002 outburst and reaching the vicinity of the B3V companion (see also Bond 2006; Barsukova et al. 2006).

In principle, one can consider that because of a certain mechanism (e.g., dissipation of mechanical energy), the outer parts of the present V838 Mon wind become excited, producing the observed [Fe II] emission lines. In this case, however, the radial velocity of the lines would be close to that of V838 Mon. This is certainlly not the case. The [Fe II] lines have a radial velocity of $13.3 \pm 0.7$ km s-1 (Sect. 4.1.1 in Paper I), while the radial velocity of V838 Mon is at least 53 km s-1 (see Sect. 3). In this case, it would also be difficult to explain the observed [Fe II] profiles.

All the observed characteristics of the [Fe II] emission lines can, however, be easily explained, if they are assumed to be produced by the matter ejected during the 2002 eruption that approaches the B3V companion. As shown in Sect. 4, the observed line profiles as well as their radial velocities can then be well accounted for. The continuous strengthening of the lines in 2005-2006 is also easy to understand: larger and larger amounts of matter become excited as it approaches the source of excitation. Excitation by radiation from the B3V companion then explains why the emission line spectrum is dominated by Fe II. In the spectrum of a B3V star, there are enough photons capable of ionizing species with an ionization potential of $\sim$7 eV, e.g., Fe, Ni, while there are very few photons capable of ionizing the most abundant elements such as H, He or CNO. Finally, the idea easy explains the $\sim$70 day eclipse-like event observed in November/December 2006 as an occultation by a dense cloud of the matter ejected in 2002 and now crossing the line of sight of the B3V companion. If this is the case, one can expect that the 2006 eclipse should be followed by similar events when other fragments of the 2002 ejecta cross the line of sight. Indeed, a few months later V838 Mon entered another eclipse-like event.[*] We note that the latter would be, at least, difficult to explain as a phenomenon typical of an eclipsing binary system.

3 The radial velocity of V838 Mon

Several molecules observed in the spectrum of V838 Mon reveal bands formed from high excitation-energy levels (see Sect. 5 in Paper I). They are usually indicative of a radial heliocentric velocity of $58\pm5$ km s-1 (see also Sect. 5.1). It is reasonable to assume that they arise very close to the photosphere and have a velocity close to the stellar one. Earlier determinations of the stellar velocity in Kolev et al. (2002) and Kipper et al. (2004) implied a value of 59-62 km s-1, i.e., close to our result.

However, the SiO maser emission observed in V838 Mon (Deguchi et al. 2005; Claussen et al. 2007; Deguchi et al. 2009) is at a heliocentric velocity of 71 km s-1. In the case of late-type stars, the SiO masers usually have a reliable measure of their stellar radial velocity.

There are two possible explanations of this discrepancy. If the SiO maser emission really originates at the stellar velocity then the estimate made in Paper I may indicate that we do not measure molecular bands deep enough that are to reach hydrostatic levels of the V838 Mon atmosphere, i.e., even the highest excitation bands are formed in already expanding layers. The other possibility is that the optical spectroscopic studies provide a correct estimate of the stellar velocity but that the SiO maser is not at the stellar velocity. We note that the radial velocity and width of the main component of the SiO maser are very close to those of the CO rotational lines observed in diffuse matter in the close vicinity of V838 Mon (Kaminski 2008). This point certainly deserves further investigation.

In the present paper, we usually adopt the radial velocity derived from the SiO maser, i.e., 71 km s-1, as the radial velocity of V838 Mon. One has, however, to keep in mind that the results from optical spectroscopy infer a value 10-15 km s-1 lower.

  4 An analysis of the [Fe II] line profile

As discussed in Sect. 2, we assume that the [Fe II] emission lines are formed in the matter ejected by V838 Mon during its 2002 outburst, which is now approaching the B3V companion and ionized by the UV radiation of the companion. In this section, using simplified modelling, we show that the observed profiles of the [Fe II] lines can be easily explained by this scenario.

  4.1 The model

 \begin{figure} \par\includegraphics[angle=-90,scale=0.4]{sketch.eps} \end{figure} Figure 1:

A sketch of the scenario considered in modelling the [Fe II] line profile in Sect. 4.
Open with DEXTER

We consider a system of two stars, S1 and S2, with a separation A (see Fig. 1). We assume that the star S1 is a source of a steady, spherically symmetric wind, that forms an expanding envelope with a r-2 density distribution. We allow for the possibility that matter in the form of clumps or filaments fills a $\xi$ part of the envelope volume, i.e., $\xi \le 1$. The wind started a certain time ago, so the envelope has an outer boundary, r0. The wind has not yet reached star S2, so r0 < A. Star S2 is a source of ionizing radiation and emits $N_{\rm ph}$ ionizing photons isotropically per unit time and unit solid angle. The radiation produces an ionized region in the wind whose boundaries can be determined assuming ionization equillibrium.

We consider ionization along a given direction from star S2 forming an angle $\alpha$ with the axis between the stars. A distance x2 from star S2, to which the wind matter is ionized, can be found from

\begin{displaymath} N_{\rm rec} = N_{\rm ph}~{\rm d}\omega, \end{displaymath} (1)

where

\begin{displaymath} N_{\rm rec} = \int_{x_1}^{x_2} \xi~x^2~{\rm d}\omega~\alpha_{\rm rec}~ N_{\rm i}^2~{\rm d}x \end{displaymath} (2)

is a number of recombinations in a cone of solid angle d$\omega$ along the considered direction, $\alpha_{\rm rec}$ is a recombination coefficient, while $N_{\rm i} = N_0~(A/r)^2$ is an ion number density (electron density is assumed to be equal to ion density). In the following, we assume that A is a unit length, so all the r and x are expressed in terms of A, and x is then related to r and $\alpha$ via

\begin{displaymath} r^2 = 1 + x^2 - 2~x~\cos\alpha. \end{displaymath} (3)

In Eq. (2), x1 is a distance from star S2 to the wind outer boundary along the considered direction, given by

\begin{displaymath} x_1 = \cos \alpha - \sqrt{\cos^2\alpha - (1-r_0^2)}. \end{displaymath} (4)

Equation (1) can be rewritten as

\begin{displaymath} C_0 \equiv \frac{N_{\rm ph}}{A^3~\xi~N_0^2~\alpha_{\rm rec}} = \int_{x_1}^{x_2} \frac{x^2}{r^4}~{\rm d}x, \end{displaymath} (5)

which, using Eq. (3), can be evaluated to give

C0 = I(x2) - I(x1), (6)

where

\begin{displaymath} I(x) \equiv \frac{x~\cos 2\alpha - \cos\alpha}{2~r^2~\sin^2\... ...1}{2~\sin^3\alpha}~\arctan\frac{x-\cos\alpha}{\sin\alpha}\cdot \end{displaymath} (7)

Equation (6) can be solved numerically to obtain x2. Along the separation axis, i.e., when $\alpha = 0$, x1 = 1 - r0, while Eq. (7) reduces to

\begin{displaymath} I(x) = \frac{1}{1-x} - \frac{1}{(1-x)^2} + \frac{1}{3(1-x)^3}\cdot \end{displaymath} (8)

Solving Eq. (6) for a grid of $\alpha$ values in the range $0 \le \alpha \le \arcsin r_0$, allows us to obtain the shape and position of the ionization front in the wind. Matter is ionized between the wind outer boundary and the ionization front. We note that the star separation axis is a symmetry axis of the ionized region. There are two free parameters in the above problem, i.e., r0 and C0.

We assume that the ionized region is isothermal, so that the emission line coefficient varies as Ni2, and that the intrinsic line profile is Gaussian characterized by a thermal and/or turbulent velocity, $V_{\rm t}$. Integrating the intrinsic line profile over the ionized region and taking into account the kinematic properties of the ionized wind, a final emission-line profile can be obtained. Apart from the above-mentioned parameters determining the ionization front, the resultant line profile depends on kinematic parameters of the wind and the stellar system, which are: the wind expansion velocity, $V_{\rm wind}$; the velocity of star S1 (source of the wind) relative to the observer, $V_{\rm s}$; and the angle between the stars separation axis and the line of sight, $\alpha_{\rm s}$.

  4.2 Fitting the model to the observations

Some of the parameters in the above problem can be estimated from observations. As discussed in Sect. 2, we assume that close to the time of the November/December 2006 eclipse, matter ejected during the 2002 eruption of V838 Mon reached the vicinity of the B3V companion. Our observations were completed in October 2005, so we can estimate that $r_0 \simeq 0.75$. During the 2002 outburst of V838 Mon, expansion velocities observed reached $\sim$600 km s-1, although most of mass loss occurred at 150-400 km s-1(Munari et al. 2002a; Tylenda 2005; Crause et al. 2003; Kipper et al. 2004). As discussed in Tylenda (2005), the most intense mass loss occurred in March 2002, which was observed as an expanding photosphere of velocity $\sim$270 km s-1. We therefore assume $V_{\rm wind} \simeq 250~{\rm km~s}^{-1}$ in the present calculations. We also assume that the heliocentric radial velocity of V838 Mon is $V_{\rm s} = 71~{\rm km~s}^{-1}$ (see Sect. 3). Thus, there remain 3 free parameters, i.e., C0, $\alpha_{\rm s}$, and $V_{\rm t}$, which can be obtained by fitting the model profile to the observed profile of the [Fe II] emission lines.

 \begin{figure} \par\includegraphics[scale=0.45]{profil.eps} \end{figure} Figure 2:

A model profile (full curve) compared to the observed profile of [Fe II] 4287 Å (points). The model parameters are discussed in the text.
Open with DEXTER

A fit of this kind is presented in Fig. 2. Points show the observed profile of the [Fe II] 4287 Å line. This is one of the strongest emission lines of [Fe II] in our spectrum. Its profile is free of blending with other lines and affected little by noise. The local continuum was subtracted and the flux was normalized to the peak value. (Note that the profile of [Fe II] 4287 Å  shown in Fig. 2 is practically the same as the mean profile derived from 7 [Fe II] lines displayed in Fig. 4 of Paper I.) The model profile was obtained with the following values of the free parameters: C0 = 0.35, $\alpha_{\rm s} = 77\hbox{$^\circ$ }$, and $V_{\rm t} = 11.5~{\rm km~s}^{-1}$. If $V_{\rm s} = 58~{\rm km~s}^{-1}$ is assumed (as discussed in Sect. 3), the results of the profile fitting remain unchanged, except $\alpha_{\rm s}$, which increases to $80\hbox{$^\circ$ }$.

We note that there is little ambiguity in determining the values of the above free parameters, because each of them affects different characteristics of the model line profile. The value of C0 determines the size of the ionized region, so, for a fixed $V_{\rm wind}$, it affects the wings of the line profile (the higher the value of C0, the more extended and stronger the wings). If $V_{\rm wind}$ and $V_{\rm s}$ are fixed, $\alpha_{\rm s}$ defines the position of the line peak. Finally, $V_{\rm t}$ determines the width of the line core.

  4.3 Discussion

The results of the above modelling of the [Fe II] profile allows us to estimate the parameters of the matter approaching the B3V companion. From the profile fitting, we have C0 = 0.35. Assuming that the matter, expanding with velocity $V_{\rm wind} \simeq 250~{\rm km~s}^{-1}$, reached the B3V companion in November or December of 2006, we derive a distance between V838 Mon and the B3V companion of $A \simeq 3.7 \times 10^{15}$ cm ($\sim$250 AU). Integrating the spectrum of a standard B3V star above the ionization potential of iron, one obtains $N_{\rm ph} = 2.4~ \times~ 10^{46}~{\rm s}^{-1}$. The recombination coefficient of Fe I is $\alpha_{\rm rec} \simeq 2.5 \times 10^{-12}~{\rm cm}^3~{\rm s}^{-1}$(at an electron temperature of 103-104 K; see Nahar et al. 1997). From Eq. (5), one then finds that $N_0 \simeq 7 \times 10^5~\xi^{-1/2}~{\rm cm}^{-3}$, or $N_i \simeq 1.3 \times 10^6~\xi^{-1/2}~{\rm cm}^{-3}$ at the outer edge of the wind envelope, i.e., at r0. We note that at an electron density $\ga$ $10^7~{\rm cm}^{-3}$, the [Fe II] lines become collisionally de-excited. Assuming spherical symmetry, a mass-loss rate during the 2002 outburst can be estimated to be

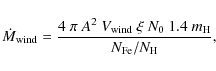\begin{displaymath}\dot{M}_{\rm wind} = \frac{4~\pi~A^2~V_{\rm wind}~\xi~N_0~1.4~m_{\rm H}} {N_{\rm Fe}/N_{\rm H}}, \end{displaymath} (9)

where $N_{\rm Fe}/N_{\rm H}$is the relative-to-H number density of elements with an ionization potential similar to or lower than that of Fe (i.e., Na, Mg, Al, Si, Ca, Ni), while $m_{\rm H}$ is the H atom mass. Assuming solar abundances, $N_{\rm Fe}/N_{\rm H} \simeq 10^{-4}$ and $\dot{M}_{\rm wind} \simeq 7 \times 10^{25}~\xi^{1/2}~{\rm g~s}^{-1} \simeq 1~\xi^{1/2}~{M}_{\odot}~{\rm yr}^{-1}$. The most intense period of mass loss lasted a month (March) in 2002 (Tylenda 2005), so, according to the above estimate, it produced a $\sim$ $0.1~\xi^{1/2}~{M}_{\odot}$ shell. This agrees with the total mass lost in the 2002 outburst, which was estimated to have a mass between $0.001{-}0.6~{M}_{\odot}$ in Tylenda (2005).

  5 Mass outflow in V838 Mon

Munari et al. (2007b) noted presence of continuous mass loss since the outburst. They reported that the outflow observed in K I 7698 Å has not much changed since 2002. The nature of its mass loss is however unclear. In this section, we analyse and discuss results from the profiles of molecular bands and atomic lines observed in October 2005 and presented in Paper I.

  5.1 Outflow as seen in molecular bands

As discussed in Paper I, the spectrum of V838 Mon is dominated by numerous, complex, and often very deep absorption lines related to molecular bands. A simple model of a stellar photosphere plus an outflowing homogeneous layer was used to identify and fit the observed structures of individual bands. In this procedure, it was necessary to adopt various velocities for the outflowing layer to reproduce different band structures. In general, we found that bands originating in more excited levels correspond to higher (more positive) radial velocities than low excitation bands. This effect is shown, in a more quantitative way, in Fig. 3, which plots the heliocentric radial velocity of a particular band versus the excitation energy, $\chi$, of the level from which the band arises. Only results for the TiO molecule, for which we identified the largest number of bands, are shown. As the excitation potential plotted in Fig. 3, we have taken the energy of the lower level of the most blueshifted line in the bandhead. Vertical error bars illustrate uncertainties in the velocity. Uncertainties in the energy have been taken as a range of energies of lower levels of lines lying within $\pm35$ km s-1 of the bandhead (this is the typical velocity broadening adopted in modelling the bands in Paper I).

 \begin{figure} \par\includegraphics[scale=0.45]{figtio.eps} \end{figure} Figure 3:

The heliocentric radial velocity of individual TiO bands plotted against the excitation potential of the lower level of the band. See text for more details.
Open with DEXTER

As can be seen from Fig. 3, there is a clear correlation between the radial velocity of a particular band and the excitation potential of the lower level of the band. This we interpret as evidence of an outward accelerated mass outflow, in which the observed bands are formed. The highest excitation bands can be formed in hotter regions, i.e., close to the photosphere, where the outflow velocity is low. Hence, we postulated in Paper I that the highest radial velocity observed in the high excitation bands, i.e., $\sim$+58 km s-1, corresponds to the radial velocity of V838 Mon. The bands originating in levels close to the ground state can be easily formed in cold outermost layers outflowing with a large velocity.

Figure 4 shows the same data as in Fig. 3 but in a different, more astrophysical, way. Here, instead of the excitation potential, we plot a parameter, log $(gf\lambda )-5040\chi /T_{\rm exc}$, where gf and $\lambda $ are the oscillator strength and wavelength of the band, respectively. Within a constant factor, this parameter is equivalent to the logarithm of the absorption coefficient in a given band. As an excitation temperature, $T_{\rm exc}$, we adopted 500 K, which is a typical value in the outflow, as inferred in Paper I (Sect. 5). The horizontal error bars show uncertainties related to the spread in the excitation energy and oscillator strength for the lines present within 35 km s-1 of the bandhead.

 \begin{figure} \par\includegraphics[scale=0.45]{figtio5.eps} \end{figure} Figure 4:

The heliocentric radial velocity of individual TiO bands plotted against log $(gf\lambda )-5040\chi /T_{\rm exc}$. See text for more details.
Open with DEXTER

As Fig. 3, Fig. 4 can be interpreted as evidence of an increasing outflow velocity with the distance from the photosphere. Bands with a small absorption coefficient require large column densities to be visible in the observed spectrum. Thus, they must be formed deep in the outflow. More opaque bands are effectively formed in more distant layers and their profiles provide information about the kinematics well above the photosphere.

From the span of the radial velocities observed in the TiO bands, shown in Figs. 3 and 4, we can conclude that the wind in V838 Mon is accelerated at least to a velocity of $\sim$180 km s-1.

  5.2 An analysis of the P-Cyg profiles

The presence of lines showing P-Cyg profiles in the spectrum of an observed object is usually considered as strong evidence of an ongoing mass outflow from the object. In our spectrum of V838 Mon, we found about ten atomic lines exhibiting these characteristics (see Sect. 4.2 in Paper I). All of them but one originate from resonant transitions. Below we analyse the profiles of these lines in an attempt to investigate the physics and nature of the outflow.

The terminal velocity of the outflow from V838 Mon can be obtained from the observed K I $\lambda $7698 absorption profile (see Fig. 6 in Paper I). If we take $V_{\rm s} = 71$ km s-1 to be the stellar radial velocity (see discussion in Sect. 3), then the terminal velocity of the outflow is $V_{\infty} = 215 \pm 5$ km s-1. The observed absorption components in other P-Cyg profiles do not reach this velocity, most probably because of the low column density of the atoms in the outer parts of the outflow. Because of the high oscillator strength and the high atomic abundance, the opacity in the K I $\lambda $7698 line is at least two orders of magnitude higher than for any other resonant line observed. Consequently, this line can be observed even with relatively low column densities expected at high velocities. The value of terminal velocity derived from the K I absorption is consistent with, although slightly higher than, the outflow velocity estimated form the molecular bands of TiO analysed in Sect. 5.1. It also agrees with the maximum expansion velocity derived by Geballe et al. (2007) from the CO bands observed half a year after our observations.

To obtain a deeper insight into the nature of the outflow in V838 Mon, we performed a radiative transfer modelling of the P-Cyg profiles. We assume that the profiles are formed in a spherically symmetric expanding envelope. Our modelling procedure is based on the SEI method developed by Lamers et al. (1987), and all details concerning the solution of radiative transfer can be found therein[*]. As the velocity field of the outflow, we adopt the standard $\beta$-law, i.e.,

\begin{displaymath} w(x)=w_0+(1-w_0)\left(1-\frac{1}{x}\right)^{\beta}, \end{displaymath} (10)

where $w=V/V_{\infty}$ is an outflow velocity normalized to the terminal velocity, $x=r/{R_{\star}}$ is a dimensionless radial distance from the star with a photospheric radius $R_{\star}$, while w0 is the normalized initial velocity at the stellar photosphere (taken to be w0=0.01 in our calculations).

As already pointed out in Paper I (Sect. 4.2), the observed P-Cyg absorption components have velocity structure. A majority of the absorption profiles have narrow absorption components (NACs) that appear at different velocities. The most striking example of NAC is seen in the Rb I line at Vh=-82 km s-1(see Fig. 6 in Paper I). Some lines, e.g., those of Cr I and Ba I, seem to exhibit many NACs at once, which dominate the appearance of the profiles. On the other hand, there are also absorption profiles, e.g., those of Ca I $\lambda $6572 and K I $\lambda $7698, which are very smooth and do not seem to be affected by discrete components. The question is whether the narrow components seen in our profiles are superimposed on a broad P-Cyg absorption profile formed in a bulk flow, or whether the entire absorption profile consists of several discrete and strong absorption components that are blended and together form a more or less continuous profile.

As a first attempt, we assumed a distribution of optical thickness in the form

\begin{displaymath} \tau(w)={\mathcal T}_{\rm tot}~(w/w_1)^{\alpha_1} \left(1- (w/w_1)^{1/\beta}\right)^{\alpha_2}, \end{displaymath} (11)

where ${\mathcal T}_{\rm tot}=\int_{w_0}^{w_1}\tau(w)~{\rm d}w$ is the integrated optical thickness and w1 is the normalized velocity at which opacity vanishes (usually taken to be 1). The values of ${\mathcal T}_{\rm tot}$, w1, $\alpha_1$, and $\alpha_2$ were treated as free parameters in our modelling procedure. The radial distribution given by Eq. (11) is known to reproduce ultraviolet (UV) resonant lines formed in winds of hot stars (Castor & Lamers 1979). Our attempts to reproduce the smooth profiles of Ca I, K I, and the overall profile of Rb I (neglecting the NAC), showed that it was impossible to reproduce satisfactorily any of these lines with the opacity distribution in the form of Eq. (11). The best set of the parameters found within this approach resulted in profiles that were too narrow with respect to the observed ones.

We, therefore, modified the optical depth distribution by adding multiple Gaussian components, $\tau_i(w)$, to Eq. (11) parameterized by central velocities, widths, and weights according to which they are added. We note that, for the sake of convenience, the Gaussian components are parameterized in the velocity domain, so the corresponding distributions as functions of radial distance, $\tau_i(x)$, are in general not Gaussian (the profile is modified by the adopted velocity field).

In this multi-component approach, we were able to successfully reproduce the observed profiles. Results for the Rb I $\lambda $7800 line are shown in Fig. 5. At least three discrete components (``shells'') of different widths are needed to obtain a profile that reproduces the observations well. These components, which are clearly present in all the profiles, are located at outflow velocities of about 50, 110, and 150 km s-1 (with respect to $V_{\rm s} = 71$ km s-1).

We attempted to model all the prominent P-Cyg lines independently and, while the central velocities and widths of different components were found to be consistently determined for different lines, the relative contributions of the components differ considerably from line to line. This implies that the relative ion opacities differ considerably between consecutive ``shells''. This can be understand either as changes in excitation conditions or different atomic abundances (chemical composition) in the discrete outflow components. Although the latter seems to be less likely, the changing atomic fractions due to interchanges of atoms with molecules and/or dust grains may play an important role. An extreme case of this effect is observed in the resonant absorption lines of Ti I. Apart from the main component seen close to the stellar velocity (but see Sect. 5.3), these lines appear only in one of the outflowing ``shells'' (see Fig. 6 in Paper I).

 \begin{figure} \par\includegraphics[angle=-90,scale=0.7]{figRb.ps} \end{figure} Figure 5:

Top: the P-Cygni profile of Rb I $\lambda $7800. The observed profile is drawn with a filled grey curve while the result of the SEI modelling is shown with a black line. Bottom: the mass loss rate corresponding to the fitted profile. The modelling was performed with $\beta =0.4$ and $V_{\infty }=215$ km s-1.
Open with DEXTER

Our modelling allows us to place general constraints on the velocity field in the outflow. The adopted value of $\beta$ has a strong influence on the relative strengths of absorption and emission components in a P-Cyg profile (for a given radial distribution of optical thickness). We found that the outflow in V838 Mon can be characterized well by $\beta=0.35\pm0.05$. This result was obtained assuming that collisional deexcitation and photospheric contamination to the P-Cyg profile can be neglected. An influence of collisional de-excitation on the emission component cannot be properly recognized because of unknown electron densities in the outflow. We believe that it is small, at least for lines with high transition probabilities (e.g., the lines of Rb I, K I, and Ba I with an Einstein coefficient $A_{\rm ul}$ of the order of 107-108 s-1). We did not find any signs of photospheric contamination in the observed spectrum and we therefore neglected this effect in our modelling.

The value of $\beta$ derived above implies that the acceleration of material is very rapid and at the distance of 4$R_{\star}$, the wind has a velocity of 0.99  $V_{\infty}$. This steep velocity gradient requires very high densities of material to be able to reproduce strong absorption features at low velocities. Therefore, to reproduce the absorption component at the outflow velocity of 50 km s-1 (which corresponds to $r=1.03~R_{\star}$ for $\beta =0.4$), it was necessary to include an inner narrow shell with a very high optical thickness. For several lines, e.g., the K I line, it was even impossible to reproduce the central parts of the P-Cyg profile without incorporating unreasonably high values of optical thickness. This made us conclude that in the velocity field, generally well described by the $\beta$-law, a sort of a plateau (or plateaus) may exist, i.e., a region of nearly constant velocity extended in the radial direction. These velocity plateaus, or non-monotonicities, were proposed to explain the winds of hot stars (Puls et al. 1993; Prinja & Howarth 1986). The possible existence of similar features in the outflow of V838 Mon is a tentative conclusion, which should be examined by time-dependent observations of the P-Cyg profiles in the spectrum of V838 Mon. The derived radial distributions of optical thickness for different ions can be used to provide a rough estimate of the mass-loss rate in V838 Mon. For a given stellar radius, $R_{\star}$, the mass-loss rate can be estimated from (Groenewegen & Lamers 1989)

\begin{displaymath} \dot{M}(x)=\tau(x)~w(x)~x^2~\frac{{\rm d}w(x)}{{\rm d}x}~V_{... ...~c}{e^2}~\frac{\mu~m_{\rm H}}{A_{\rm E}~f_{\rm lu}~\lambda_0}, \end{displaymath} (12)

where $\mu$ is the mean molecular weight, $m_{\rm H}$ is the hydrogen mass, $A_{\rm E}$ is the abundance of an element with respect to hydrogen, $f_{\rm lu}$ is the oscillator strength, $\lambda_0$ is the laboratory wavelength of the line, and the symbols $m_{\rm e}$, e, and c have their usual meanings. In Eq. (12), it is assumed that all the atoms of a given element are in the ground state and that there is no ionization nor any other form of ion depletion. Taking as the stellar radius $R_{\star}=10^3~R_{\hbox{$\odot$ }}$(see Sect. 5 in Paper I), adopting $\beta =0.4$, and assuming solar abundances, the mass-loss rate derived from the lines of Rb I $\lambda $7800 is on average of $10^{-6} - 10^{-5}~M_{\hbox{$\odot$ }}$ yr-1, with individual mass-loss events reaching $10^{-3}~M_{\hbox{$\odot$ }}$ yr-1 (see Fig. 5).

5.3 Signatures of an infall

The redward broad absorption components seen in the Ti I lines (see Sect. 4.3 in Paper I) can be interpreted as a signature of an infall in V838 Mon. Similar absorption components also contaminate the profiles of the 5060 and 5110 Å lines of Fe I.

These absorption features in the Ti I lines have wings extending out to about $V_{\rm h}=120$ km s-1. Thus, regardless of the velocity of the star in the range 58-71 km s-1 (see Sect. 3), the red wings of these features are evidently redshifted with respect to the photosphere. The maximum infall velocity inferred from these wings is 50-60 km s-1, which agrees very well with the free fall velocity of an $8~M_\odot$ star (Tylenda et al. 2005) at a photospheric radius of $\sim$ $900~R_\odot$ (Sect. 5 in Paper I).

Signatures of an infall were previously observed in V838 Mon. Rushton et al. (2005) observed inverse P-Cyg profiles of Ti I lines in their spectra obtained in the near infrared in December 2003. From the separation of the absorption and emission components, an infall velocity of $\sim$20 km s-1 can be deduced. These authors also argue that the infalling matter, compressed, and heated when colliding with the atmospheric material, provide conditions necessary to excite the SiO lines that they observe. Observations of the ro-vibrational bands of CO by Geballe et al. (2007) in April 2006 revealed a photospheric component redshifted by 15 km s-1 with respect to the velocity of the SiO maser. This suggests, according to the authors, the presence of gas infalling onto the star or contraction of the stellar photosphere.

  5.4 Discussion

As mentioned above, the mass outflow in V838 Mon has been observed continously since the 2002 eruption. Our analysis confirms this statement and provides new results. The question that arises is what drives this outflow. It consists of cold neutral matter that is rich in molecules, and possibly also dust, which is similar to the composition of the winds of cool stars, e.g., objects in the asymptotic giant branch. Velocity fields of these cool winds are usually well described by the $\beta$-law with $\beta\simeq0.5$, which is close to the value derived above for V838 Mon. These cool winds are believed to be dust-driven. They usually do not reach the high terminal velocities found for V838 Mon. A possible reason is that dust is destroyed in collisions, when the outflow is faster than about 30 km s-1 (Olofsson 2004). From this reason, it seems that the outflow in V838 Mon cannot be driven by dust only, since we observe material being accelerated at much higher velocities than 30 km s-1. This driving mechanism can, however, play a role at the base of the outflow, where velocities are low enough.

One can consider a mechanism similar to that driving winds in hot stars, i.e., by radiation pressure absorbed in atomic resonant lines. However, the small number and relative weakness of lines of this type in our spectrum (they are typically 10 times narrower than those in the OB stars) does not support the idea that these lines could be effective in driving mass loss from V838 Mon. More promising is the possibility that the outflow is driven by radiation pressure absorbed in molecular bands in the optical and infrared. The object is very bright in these wavelength ranges and the observed number and strength of molecular bands, as seen in our spectrum (some of them absorb practically all the radiation available in their wavelength ranges - see Paper I), clearly shows that a significant part of the momentum carried out in radiation is indeed absorbed in the outflowing matter. A process of driving winds by radiation pressure absorbed in molecular bands was proposed as a mechanism accelerating cold circumstellar envelopes (see Jørgensen & Johnson 1992, and references therein).

The analysis of the P-Cyg profiles reported in Sect. 5.2 was completed assuming spherical symmetry and a monotonicly increasing outflow velocity described by Eq. (10). Within this approach, the general shape of the observed profiles can be satisfactorily reproduced. This shows that the general pattern of the outflow is more or less spherically symmetric. The profiles however show, at least some of them, narrow structures, which we called NACs. The structure at $V_{\rm h} = -82$ km s-1 is particularly striking. In the spherically symmetric, approach the only way to explain the NACs is to assume that the mass-loss rate varies with time and produces dense shells expanding with a thinner wind. As can be seen in Fig. 5, to explain the strong NAC at $V_{\rm h} = -82$ km s-1 it is necessary to postulate a short lived enhancement in the mass loss rate by two orders of magnitude. However, if the above assumptions are relaxed, the NACs can be explained in other ways. One possibility is that the NACs are produced by mass loss being more intense in certain, more or less discrete, directions. For instance, the NAC at $V_{\rm h} = -82$ km s-1 would then be understood as a stream-like or jet-like outflow with a projected velocity of $\sim$153 km s-1 (adopting the radial velocity of V838 Mon of 71 km s-1; see Sect. 3). Jets usually have counter-jets. The observed lack of any counter-jet in our spectrum as well as the position of the NAC close to the terminal velocity of the P-Cyg profiles suggests that the jet, if responsible for producing the NAC at -82 km s-1, is not far from the line of sight.

Another possibility is that the NAC at $V_{\rm h} = -82$ km s-1 has nothing to do with the presently ongoing mass outflow, but is produced in the matter lost during the 2002 eruption that is now in front of the object. This interpretation would imply the existence of a dense shell at a distance of $\sim$ $1.7~\times~10^{15}$ cm ($\sim$ $2.5~\times~10^4~{R}_\odot$) from the object expanding with a velocity of $\sim$153 km s-1. However, during the 2002 eruption the matter was ejected with velocities ranging from $\sim$100 to $\sim$600 km s-1 (Munari et al. 2002a; Kipper et al. 2004; Crause et al. 2003). Thus, the matter, or at least part of it, would have to have been condensed into a shell at later epochs. This can occur if matter ejected later catches up with slower matter ejected earlier. In the case of V838 Mon, this mechanism does not seem to have worked, since the outflow velocity observed during the 2002 eruption tended to decrease with time (Munari et al. 2002a; Crause et al. 2003). A NAC at $V_{\rm h} = -90$ km s-1 is seen in our spectrum in the Ti I 5147 and 5152 Å lines, which do not display P-Cyg profiles (see panel c in Fig. 6 in Paper I). The close radial velocity and line width suggest that this component is produced in the same enviroment as the NAC in the P-Cyg profiles. If this is the case, our interpretation presented above would have to be excluded. The Ti I lines arise from the levels lying 2.3-2.4 eV above the ground state. Thus, they must arise in a rather warm matter (of temperature comparable to that in the photosphere), while the matter lost in 2002 and now at a distance of $\sim$30 photospheric radii is expected to be cold ($\sim$500 K, if estimated from pure geometric dilution of the radiative energy density). In conclusion, we consider that the interpretation that the NAC at $V_{\rm h} = -82$ km s-1 is related to matter lost in 2002 is less probable than the other two, i.e., varying mass-loss rate in the present wind or jet-like ouflow.

Spectroscopic data allowing analyses of the time-dependent behaviour of the P-Cyg profiles would help to discriminate between interpretations involving varying mass-loss rate, jet-like outflow, or distant matter lost in 2002. In the first case, the NACs are expected to migrate in the profile with time, while in the two other cases the NACs should be rather stable features. It is worth noting that Geballe et al. (2007) in their high-resolution spectra obtained in the K band in April 2006, i.e., half a year after our spectroscopy, indentified several velocity components in the CO absorption line profiles. Apart from the photospheric component (mentioned in Sect. 5.3) the authors found components at expansion velocities of 15, 85, and 150 km s-1. The last feature is practically at the same velocity as our NAC at $V_{\rm h} = -82$ km s-1 suggesting that this is a persistent component. However, the feature in the CO lines is much wider than the NAC, so the conclusion is unclear. The two other components in the CO lines do not match other NACs in our P-Cyg profiles, which are seen at the expansion velocities of 50 and 110 km s-1 (see Sect. 5.2). This suggests that these NACs are transient and produced by varying mass-loss rates.

  6 Summary and discussion

Our analysis of both the positions of the molecular bands (Sect. 5.1) and the P-Cyg profiles (Sect. 5.2) have shown that V838 Mon loses matter with a terminal velocity of $\sim$215 km s-1 at a rate of $10^{-6} - 10^{-5}~M_{\hbox{$\odot$ }}$ yr-1. Thus, the object loses of the order of 10 $L_\odot$ in the form of the kinetic energy of the wind. This is small compared to the radiation luminosity of the object, which is $\sim$ $2.4 \times 10^4~L_\odot$ (see Sect. 5 in Paper I). However, the momentum carried out in the wind is comparable to that in the radiation. Thus, the wind in V838 Mon is likely to be radiation driven, probably due to absorption in the molecular bands, as discussed in Sect. 5.4.

The kinematic pattern of the matter in the atmosphere of V838 Mon is very complex. Both expansion and wind outflow dominate. Most of the outflow is more or less spherically symmetric as suggested by our modelling of the observed P-Cyg profiles (Sect. 5.2). However, as discussed in Sect. 5.4, it is quite possible that we also observe a jet-like outflow. As shown in Sect. 5.3, certain regions, perhaps initially accelerated but not sufficiently to allow them to leave the object, also fall back to the photosphere. We note that simultaneous signatures of infall and outflow have been observed in the winds of hot stars (e.g., Howk et al. 2000) and often in protostars. A possible scenario for creating coexisting mass outflow and infall in asymptotic giant branch stars was discussed in Soker (2008) and may also work in the remnant of the V838 Mon outburst.

As discussed in Tylenda (2005), the evolution of V838 Mon in the post-outburst state is probably dominated by gravitational contraction, i.e., is closely related to that of protostars. If, as argued in Tylenda & Soker (2006), the 2002 outburst of V838 Mon was produced by a stellar merger, then a significant amount of angular momentum should have been stored in the remnant of the event (see also Soker & Tylenda 2007). Gravitational contraction may then result in the flattening of the envelope, eventually leading to the formation of an accretion disc (as in protostellar objects). The possibility discussed in Sect. 5.4, namely that we observe a jet in the spectrum, if confirmed, may imply that a disc has already formed in V838 Mon.

As shown in Sect. 4, the observed profile of the [Fe II] lines can be easily understood as having been produced by matter lost by V838 Mon in the 2002 eruption and now excited by the radiation of the B3V companion. As the matter approaches the companion, a larger and larger proportion of the flux from the star can interact with the matter causing an increase in the [Fe II] emission, as observed. Indeed, the flux in the 20 strongest [Fe II] lines in our spectrum obtained in October 2005 increased by a factor of $\sim$3.5 in the measurements completed by Munari et al. (2007a) in December 2006. At the moment of our observations, the outer boundary of the expanding envelope was presumably at a distance of $\sim$0.75 times the separation between V838 Mon and its B3V companion. Thus, only $\sim$17% of the radiation flux of the B3V companion should then interact with the matter. At the moment of the eclipse-like event in November/December 2006, the matter presumably reached the closest vicinity of the companion and the portion of the stellar radiation capable of exciting the matter increased to 50-100%.

Apart from the [Fe II] emission lines, Munari et al. (2007a) also observed strong Balmer lines in emission. In particular, they discussed in detail the profile of H$\alpha$ observed in December 2006 - April 2007. No H$\alpha$was seen in our spectrum in October 2005. However, in the absorption cores of higher members of the Balmer series (in the spectrum of the B3V companion), we have detected weak emission components (see Sect. 4.1.2 in Paper I). In particular, the emission component in the H$\beta$ line was estimated to have an observed flux of $\sim$ $3 \times 10^{-16}$ erg cm-2 s-1. We note that the profile of the H$\beta$ emission component (see Fig. 5 in Paper I) was remarkably similar to that of the H$\alpha$ line observed by Munari et al. (2007a) in December 2006. Moreover, the parameters of the emission component in H$\beta$ in our spectrum and of the H$\alpha$ emission component in Munari et al. (2007a) (radial velocity and FWHM) are close to those of the [Fe II] lines derived in Paper I. This implies that all these lines probably originate in the same region, i.e., in the part of the V838 Mon envelope (ejected in 2002) approaching the B3V companion. The point is, however, that while in the spectrum of a B3V star there are enough photons capable of ionizing iron and exciting the [Fe II] lines, there are very few photons, capable of ionizing hydrogen. Between October 2005 and December 2006, the flux in the H$\beta$ emission also increased by a factor of $\sim$7, while that in H$\alpha$ increased by at least two orders of magnitude. This large increase cannot be explained by a purely geometric effect, as discussed above in the case of the [Fe II] lines. Therefore, an additional source of excitation of the Balmer lines is necessary, a source, whose intensity significantly increased between October 2006 and December 2007. We suggest that this is provided by matter accretion from the outflowing V838 Mon envelope on the B3V companion. We now complete simplified estimates for this scenario.

We assume that matter flows with a velocity, $V_{\rm wind}$, in the vicinity of a star of mass, $M_{\rm B3V}$. An accretion radius, $r_{\rm acc}$, can be estimated from the standard formula (see e.g., Frank et al. 2002)

\begin{displaymath} r_{\rm acc} \simeq \frac{2~G~M_{\rm B3V}}{V_{\rm wind}^2} \simeq 3 \times 10^{12}~{\rm cm} \simeq 43~R_\odot, \end{displaymath} (13)

where we adopted $M_{\rm B3V} = 7~M_\odot$ and $V_{\rm wind} = 250$ km s-1. An accretion rate can then be estimated from

\begin{displaymath} \dot{M}_{\rm acc} \simeq \frac{\pi~r_{\rm acc}^2}{(4~\pi~A... ...{\rm wind} \simeq 1 \times 10^{19}~\xi^{1/2}~{\rm g~s}^{-1}, \end{displaymath} (14)

where we used the values of $\dot{M}_{\rm wind}$ and A estimated in Sect. 4.3. This implies an accretion luminosity,

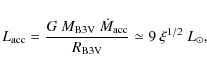\begin{displaymath}L_{\rm acc} = \frac{G~M_{\rm B3V}~\dot{M}_{\rm acc}}{R_{\rm B3V}} \simeq 9~\xi^{1/2}~L_\odot, \end{displaymath} (15)

where $R_{\rm B3V} = 4.5~R_\odot$ has been assumed. This luminosity is small compared to the intrinsic luminosity of a standard B3V star ($\sim$ $1.9~ \times~ 10^3~L_\odot$, Schmidt-Kaler 1982). Thus, no significant effect is expected to be observed in the global energetics of the B3V companion, e.g., in the visual brightness. However, after being dissipated via an accretion shock[*] and thus producing a hot layer above the star surface, the accretion luminosity is expected to be emitted mainly in the far-UV and/or soft X-rays. This can affect the ionization of the expanding envelope of V838 Mon, i.e., produce significant ionization of hydrogen. The accretion from the expanding matter is expected to become effective just before and during the November/December 2006 eclipse. We suggest that this is the reason for the rapid increase in emission of the Balmer lines, particularly in H$\alpha$, observed in the second half of 2006. We note that the luminosity in the Balmer emission lines, dominated by H$\alpha$, as observed by Munari et al. (2007a) during the eclipse, was $\sim$ $3.5~L_\odot$ (assuming EB-V = 0.9 and a 8 kpc distance to V838 Mon). Thus, the accretion, as estimated above, can provide enough energy to explain the observed luminosity in the Balmer lines.

Acknowledgements
The research reported on in this paper has been supported by the Polish Ministry of Science and Higher Education under grant No. N203 004 32/0448, for which the authors are grateful.

References

Footnotes

... event.[*]
See e.g., the website of V. Goranskij (http://jet.sao.ru/goray/v838mon.htm).
... therein[*]
Aware of limitations of the SEI method we have also performed modelling in the more accurate comoving frame formalism (Mihalas et al. 1975). It confirms the results obtained with the former method.
... shock[*]
The specific angular momentum accreted with the matter is negligible in this case and there is no chance to create an accretion disc arround the B3V companion, contrary to the suggestion of Goranskij et al. (2008).

All Figures

  \begin{figure} \par\includegraphics[angle=-90,scale=0.4]{sketch.eps} \end{figure} Figure 1:

A sketch of the scenario considered in modelling the [Fe II] line profile in Sect. 4.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[scale=0.45]{profil.eps} \end{figure} Figure 2:

A model profile (full curve) compared to the observed profile of [Fe II] 4287 Å (points). The model parameters are discussed in the text.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[scale=0.45]{figtio.eps} \end{figure} Figure 3:

The heliocentric radial velocity of individual TiO bands plotted against the excitation potential of the lower level of the band. See text for more details.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[scale=0.45]{figtio5.eps} \end{figure} Figure 4:

The heliocentric radial velocity of individual TiO bands plotted against log $(gf\lambda )-5040\chi /T_{\rm exc}$. See text for more details.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,scale=0.7]{figRb.ps} \end{figure} Figure 5:

Top: the P-Cygni profile of Rb I $\lambda $7800. The observed profile is drawn with a filled grey curve while the result of the SEI modelling is shown with a black line. Bottom: the mass loss rate corresponding to the fitted profile. The modelling was performed with $\beta =0.4$ and $V_{\infty }=215$ km s-1.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.