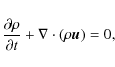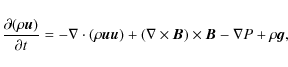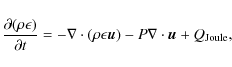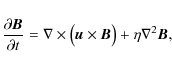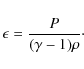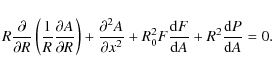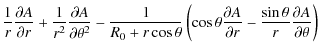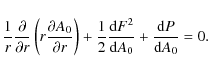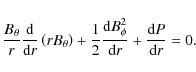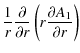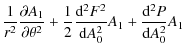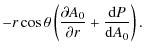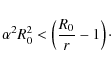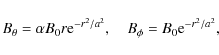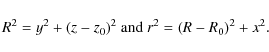| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | 999 - 1011 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912189 | |
| Published online | 22 June 2009 | |
The emergence of toroidal flux tubes from beneath the solar photosphere
A. W. Hood1 - V. Archontis1 - K. Galsgaard2 - F. Moreno-Insertis3
1 - School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife, KY16 9SS, UK
2 - Niels Bohr Institute, 2100 Copenhagen, Denmark
3 - Instituto de Astrofisica de Canarias (IAC), 38200 La Laguna (Tenerife), Spain; also at Department of Astrophysics, Faculty of Physics, Universidad de La Laguna, 38200 La Laguna (Tenerife), Spain
Received 26 March 2009 / Accepted 10 June 2009
Abstract
Context. Models of flux emergence frequently use a twisted cylindrical loop as the initial starting configuration and ignore the coupling between the radiation field and plasma. In these models, the axis of the original tube never emerges through the photosphere. Without the axis emerging, it is very difficult to form a realistic sunspot.
Aims. The aim is to use a toroidal flux loop, placed beneath the solar photosphere and study whether the axis of the system emerges fully into the atmosphere. The toroidal curvature means that the plasma can drain more effectively than in a straight cylindrical tube.
Methods. Three-dimensional magnetohydrodynamic numerical simulations of an emerging magnetic flux tube are presented for an initial toroidal loop model. The simulations use a Lagrangian-Remap code that is particularly suited to dealing with shocks and strong current sheets.
Results. The evolution of the toroidal loop is followed and the characteristics of the emergence process are compared with the traditional cylindrical loops. The flux sources seen at the photosphere are more circular, and there are less shearing motions in the upper photosphere. When the initial magnetic field strength is relatively weak the evolution of the system is similar to the cylindrical loop case, with the formation of a new flux rope above the photosphere. A striking result is that for large values of field strength the axial field of the toroidal loop emerges fully into the corona. This is reported for the first time in experiments of flux emergence in a highly stratified atmosphere that do not solve self-consistently the radiation transfer problem. In addition, the new flux rope forms below the original axis of the toroidal tube when the field strength is sufficiently strong.
Key words: Sun: magnetic fields - magnetohydrodynamics (MHD) - plasmas
1 Introduction
The emergence of magnetic field from the solar interior into the solar atmosphere is a fundamental process that occurs on several different scales, from the large sunspots and active regions down to the small ephemeral sources and the magnetic carpet.
Numerical experiments to simulate the emergence process started with the pioneering 2D work of Shibata et al. (1989), Shibata et al. (1992) who studied the emergence in a highly stratified atmosphere of a horizontal flux sheet through the development of a buoyancy instability and found a self-similar behaviour in the nonlinear phase of the evolution. Further developments of this work were reported by Matsumoto & Shibata (1992) and Nozawa et al. (1992).
The emergence of twisted flux tubes or sheets, in a 2D or 2.5D manner, in a highly stratified atmosphere was the subject of another batch of models (Magara 2001; Isobe et al. 2007; Leake & Arber 2006). These simulations yielded a number of important features such as the expansion of the magnetic field into the corona, the resistive emergence of serpentine-like flux systems, the formation of long arch-like magnetic fields in the high solar atmosphere and the role of partial ionization in the process of flux emergence.
Three-dimensional experiments of flux emergence into a non-magnetized corona have been performed during the last few years by various authors (Fan 2001; Magara & Longcope 2001; Abbett & Fisher 2003; Manchester et al. 2004; Archontis et al. 2004; Murray et al. 2006). In these simulations many interesting results were reported: photospheric distributions of the magnetic field similar to small or ephemeral active regions, X-ray sigmoid-like shapes of current sheets, shear flows along the neutral lines of the active regions, downflows at the periphery of the expanding, rising magnetic field and the 3D fan-like expansion of the field in the solar corona. In most of the above simulations the background atmosphere consisted of a sub-photospheric layer, an isothermal photosphere, a transition region and an isothermal corona. However, these experiments did not include radiative transfer, cooling or explicit heating. Thus, the simulations were performed to study mainly the dynamical aspects of the flux emergence process. A more detailed history on the various numerical models used for studies of flux emergence is given by Archontis (2008).
The majority of the above mentioned three-dimensional experiments have focussed on the emergence of a twisted cylindrical tube. In most of the studies a constant twist profile has been assumed for the initial cylindrical tube. Recently, Murray & Hood (2008) investigated a variety of different twist profiles and found that, irrespective of the profile, if the tube initially has a low tension force it will fail to undergo a magnetic buoyancy instability and rise into the atmosphere. Tubes with stronger tension forces that hold the tube together are able to rise through the photosphere and expand into the corona.
Yet, an open problem is to understand how a flux rope can travel from the tachocline to the surface without
breaking up, due to the dynamically dominant convection flows. Simple models indicate that any flux rope that can remain
intact during this rise phase through the convection zone must be twisted (Moreno-Insertis & Emonet 1996).
Also, Cheung et al. (2007) included granular convection in their simulations and showed that an emerging flux tube must be strong enough
to resist being passively advected and deformed by the convective flow. When the tube is sufficiently weak the magnetic flux reaches the photosphere in a very fragmented state.
Moreover, Brun & Jouve (2008) performed large-scale dynamo simulations and have shown how a twisted flux rope can remain
intact during the rise from the tachocline
through a fully convecting convection zone and up to the photosphere if the magnetic field is sufficiently strong.
Twist is also important when the flux tube reaches the stably stratified photosphere.
Cheung et al. (2007) and Martínez-Sykora et al. (2008) found that with large twist and/or large field strength a large amount of flux crosses
the photosphere into the chromosphere.
Without twist, the flux tube will simply expand sideways, generating a weak horizontal field. To emerge through the
photosphere, the flux tube must remain intact, strengthening as more flux rises, until its field strength reaches a
critical value to trigger a magnetic buoyancy instability.
The onset criterion was given by Newcomb (1961), Thomas & Nye (1975) and
Acheson (1979). The key quantity is the product
![]() ,
with
,
with
![]() the superadiabatic excess of the logarithmic temperature gradient
used in the theory of stellar interiors, which is negative in convectively stable regions, and
the superadiabatic excess of the logarithmic temperature gradient
used in the theory of stellar interiors, which is negative in convectively stable regions, and ![]() the ratio of gas to magnetic pressure. When
the ratio of gas to magnetic pressure. When
![]() is too negative, the stable stratification prevents the development of the magnetic buoyancy instability. This is the case in the photosphere when the magnetic tube first reaches that level. Moreno-Insertis (2006) showed quantitatively, on the basis of the experiments of Archontis et al. (2004), how the subsequent flux pile-up at the photosphere pushes the magnetized plasma to slightly higher levels and increases its field strength. Both effects cause
is too negative, the stable stratification prevents the development of the magnetic buoyancy instability. This is the case in the photosphere when the magnetic tube first reaches that level. Moreno-Insertis (2006) showed quantitatively, on the basis of the experiments of Archontis et al. (2004), how the subsequent flux pile-up at the photosphere pushes the magnetized plasma to slightly higher levels and increases its field strength. Both effects cause ![]() to become smaller, so that
to become smaller, so that
![]() becomes less negative and eventually the magnetic buoyancy instability can develop.
becomes less negative and eventually the magnetic buoyancy instability can develop.
The simple cartoon model is that the complete flux tube emerges, with the approximately round sunspot corresponding to a cross section of the now vertical flux rope and the axis of the tube being the centre of the sunspot. However, in simulations of flux emergence using an initially horizontal, cylindrical magnetic flux tube and not including convection flows, the original axis of the tubes does not fully emerge: it is trapped at low atmospheric heights. The resulting synthetic magnetograms never show a truly round sunspot. Part of the problem is that just beneath the axis there are magnetic field lines that have a dip and this dip can collect any dense plasma, preventing the axis from emerging. What does happen is that a new flux rope forms towards the middle of the photosphere in response to a shearing and converging motion created by the rapid rise of the outer portion of magnetic field during the emergence process (Manchester et al. 2004). The rapid rise causes a reduction in the magnetic pressure in the middle of the photosphere and an in-flow results, causing reconnection and the formation of a new flux rope. This new flux rope contains a fraction of the total magnetic flux but now has less dense plasma attached to the field and, hence, it can rise. We distinguish between the new axis of the flux rope formed by internal reconnection and the original axis of the initial, in this paper, toroidal loop.
On the other hand, models that include convection flows (Martínez-Sykora et al. 2008; Cheung et al. 2008; Tortosa Andreu & Moreno-Insertis 2009; Cheung et al. 2007) show that the whole magnetic tube or sheet rises across the photosphere, possibly helped by the extra push provided by the upflow field of the convection cells. So, is it necessary to solve the full problem, including the coupling between plasma and radiation field and convection flows, for the axis of the original flux tube to emerge? The idea of using a horizontal cylindrical flux tube, buoyant in the central portion, is one of computational convenience. If the actual flux rope has its roots in the deeper layer of the convection zone, it may be more appropriate to consider a curved loop with footpoints anchored in the base of the computational domain. Hence, this paper investigates how a buoyant toroidal flux tube will evolve and emerge.
The evolution of a coronal flux tube with the shape of a toroidal loop or an arch has been investigated by various authors. Fan & Gibson (2003) studied the kink motion of the tube and its interaction with an ambient coronal field. Titov & Démoulin (1999) constructed a force-free model of an anchored twisted flux tube with an arch-like shape embedded in an external potential magnetic field. They reported on the quasi-static rise of the tube when an initial velocity field was imposed and the evolving topological structure (with an S-like shape) configuration of the system. Using the same code, Török & Kliem (2005) studied the ideal helical kink instability of the coronal flux rope, which was anchored in the photosphere and considered whether this instability can be the mechanism of the initiation of solar eruptions. Finally, the formation of a toroidal loop by photospheric motions has been investigated by Gerrard et al. (2004). They applied twisting motions on two photospheric flux patches and found that a twisted loop was formed, surrounded by untwisted fieldlines. When resistivity was included in the simulation, reconnection occured and substantial amount of free magnetic energy was released.
In our paper the toroidal flux tube is placed in the solar interior and emerges in a self-consistent way through the photosphere and the outer atmospheric layers. Our main aim is to study the dynamical properties of the emergence process during the rising motion of the toroidal loop. The structure of the paper is as follows: Sect. 2 contains an introduction to the equations and the numerical methods used to perform the numerical experiments. In Sect. 3 we describe in detail the initial equilibrium of the toroidal loop (3.1) and the initial magnetic topology (3.2), the Cartesion description of the initial magnetic field configuration (3.3) and the initial development of the magnetic field (3.4). Section 4 is devoted to the photospheric properties of the rising magnetic field: the evolution of magnetograms (4.1) and the velocities obtained at the photosphere (4.2). Section 5 explains the dynamical properties of the emergence process: first the rising motion of the toroidal loop and the formation of a flux rope inside the rising magnetic field (5.1), then the converging flows that lead to internal reconnection and flux rope formation (5.2) and finally the topology of fieldlines within the expanding magnetic flux system (5.3). In Sect. 6 we present the results from an experiment where the initial magnetic field strength of the toroidal loop is relatively strong, as compared to the relatively weaker field discussed in the previous sections. We study whether the axis of the toroidal loop emerges fully into the corona and compare the evolution with a weak field case (6.1). In Sect. (6.2) we calculate the amount of flux that is transported to the outer atmosphere due to flux emergence. Section (6.3) illustrates the topology around a flux rope, which is formed within the emerging magnetic field. Conclusions follow at the end of the paper (Sect. 7).
2 Numerical methods
The numerical setup for this experiment is similar to the work of
Archontis et al. (2004). The code used to
simulate the evolution of the model is a 3D version of the Lagrangian
remap scheme
detailed in Arber et al. (2001). We used the above code to perform
experiments with uniform resistivity and with locally enhanced
resistivity, so that the resistivity is switched on only when the
current has exceeded some critical value. The general evolution of the system is similar in the two sets of experiments. Hereafter, we show the evolution in the experiments where resistivity is uniform, with a value of
![]() .
The code also includes small shock viscosity and the resulting viscous heating that is implemented if shocks form (see Arber et al. 2001, for details).
.
The code also includes small shock viscosity and the resulting viscous heating that is implemented if shocks form (see Arber et al. 2001, for details).
For the experimemts described in the paper, we solve the
time-dependent, resistive, MHD equations in three dimensions. They
are written in the dimensionless form
with specific energy density
The basic quantities used in the above equations are the density
The equations are solved in a uniform grid of (160,160,320) in the (x,y,z) directions and the physical size of the box is 17 Mm x 17 Mm x 17 Mm. The background stratification includes a constant-entropy region of 4.25 Mm thickness that simulates the uppermost layers of the solar interior just below the surface; an isothermal layer (T=6500 K) with thickness 1.7 Mm that represents the photosphere and the chromosphere and an isothermal corona at T=106 K with thickness 9.35 Mm. The photosphere and chromosphere are joined to the corona through a transition region with a steep temperature gradient.
Figure 1 shows the logarithm of the initial gas pressure, temperature, magnetic
pressure and density of the stratified environment as a function of
height. All the profiles are normalized according to the photospheric
values:
![]() erg cm-3;
erg cm-3;
![]() g cm-3;
g cm-3;
![]() K and
K and
![]() km. The units of the other variables used in the simulations are: velocity,
km. The units of the other variables used in the simulations are: velocity,
![]() km s-1; time,
km s-1; time,
![]() sec and magnetic field,
sec and magnetic field,
![]() Gauss.
Gauss.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12189fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg25.png) |
Figure 1: Distribution of temperature (dot-dashed), pressure (solid), density (triple dot-dashed) and magnetic pressure (dashed) along height (x=0, y=0) at t=0. |
| Open with DEXTER | |
3 Toroidal flux tube
3.1 Equilibrium
To form an initial toroidal magnetic field, we express our original cartesian coordinates (x,y,z), where the axis of the tube was in the y direction and z is vertical, in terms of cylindrical coordinates
![]() .
Here
.
Here
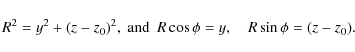
z0 is the value of the base of the computational domain (taken as 0 in our simulations). The magnetic field is expressed in terms of a flux function A=A(R,x) as
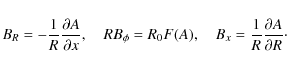
Now assume that the major radius of the torus is R0 and that the minor radius of the flux tube is a. The Grad-Shafranov equation is of the form
Here we have
Changing coordinates, we find that (6) can be expressed as
Now, if we assume that
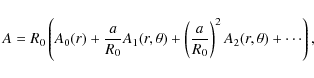
to leading order, we simply get a cylindrically symmetric solution satisfying
Multiplying by
This is the standard cylindrical equation and so we can pick the solutions to be exactly the same as the cylindrical flux tube used by Archontis et al. (2004), namely,
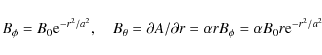
and the excess pressure is
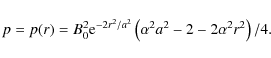
From this, we can calculate the necessary functions of A in the Grad-Shafranov equation. Hence, integrating
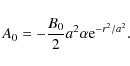
Thus,
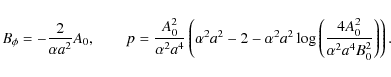
It is possible to calculate the correction to this equilibrium if it is needed. Replace A0 by A and use these forms for P(A) and F(A) in (8). Taking the expansion to the next order gives
Everything on the right hand side is known and so the form of the solution is
with the boundary conditions
3.2 Fieldlines and dips
The equation of the field lines are given near the top of the loop, in the local toroidal system, by constant values of r and
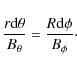
Thus, we have
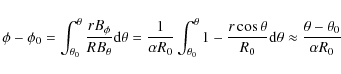
The height of the field line is, therefore, given in terms of the cylindrical coordinates as
| z | = | ||
| = | 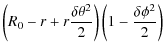 |
or, simplifying
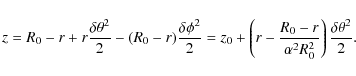
Hence, there is no dip in the field lines at the top of the toroidal loop if
A similar analysis was used by Priest, Hood and Anzer (1989) to identify the formation of dips in their twisted flux tube model of prominences.
So if we make this field buoyant, any over-dense plasma near the tube axis lifted up by the buoyant magnetic field should be able to drain down the field all the way to the computational base if it wants to.
3.3 Cartesian description
The initial toroidal field is given by
Finally, we need to express these back in terms of cartesians coordinates. Thus, we first express
Now we express BR and
where
So
| Bx | = | (20) | |
| By | = | (21) | |
| Bz | = | (22) |
3.4 Initial development
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg80.png) |
Figure 2: Magnetograms of Bz at z = 25, the base of the photosphere, at times t=40, 60, 80 and 100. Contours correspond to values of Bz given by -0.1 (blue), -0.05 (mauve), 0.05 (yellow) and 0.1 (red). |
| Open with DEXTER | |
The toroidal flux tube is made buoyant in a similar way to the cylindrical case. The temperature is set equal to the external temperature and the resulting density is then deduced by maintaining the pressure distribution. The tube becomes buoyant and rises towards the photosphere. Normally, the density deficit is controlled so that the maximum buoyancy effect is near the centre of the tube and is reduced towards the edges. For the cylindrical case the tube is at the same depth beneath the photosphere. Hence, the field has the same distance to travel to the surface but is less buoyant towards the edges. The toroidal case has a curvature that means the field near the base of the box has further to travel to the surface than the field near the top. In addition, the background density and pressure increase towards the base of the box, so that the plasma beta increases and the effect of buoyancy is less important further down. Together these issues make it very difficult to compare the cylindrical and toroidal tubes directly even though they have the same initial parameters of field strength, twist and radius. The main differences between cylindrical and toroidal tubes are, therefore, qualitative rather than quantitative.
In this paper we consider two experiments. Both experiments consider a toroidal loop with a major radius of R0 = 15 and minor radius of a = 2.5.
In the first experiment the loop has axial field strength
of B0=5 and twist
![]() (the weaker field case) and in the second experiment, B0=9 and
(the weaker field case) and in the second experiment, B0=9 and
![]() (the stronger field case).
The initial rise takes the field towards the photosphere where, in keeping with the cylindrical case, it starts to spread out horizontally once it enters the stably stratified isothermal photosphere. This spreading of the field and the continued rise of field from beneath to this layer means that large currents are generated just beneath the photosphere. It is the build up of current and magnetic field strength that eventually trigger the magnetic buoyancy instability. Once it is triggered, the field rises through the photosphere and up towards the corona. The detailed properties are discussed below.
(the stronger field case).
The initial rise takes the field towards the photosphere where, in keeping with the cylindrical case, it starts to spread out horizontally once it enters the stably stratified isothermal photosphere. This spreading of the field and the continued rise of field from beneath to this layer means that large currents are generated just beneath the photosphere. It is the build up of current and magnetic field strength that eventually trigger the magnetic buoyancy instability. Once it is triggered, the field rises through the photosphere and up towards the corona. The detailed properties are discussed below.
4 Photospheric properties
4.1 Magnetograms and their evolution
Two synthetic magnetograms are investigated at the base of the photosphere, z=25 and towards the middle of the photosphere, z=27. Figure 2 shows a horizontal plane at z=25. The vertical magnetic field, Bz, first appears with its neutral line at a slight angle to the east-west (top-bottom) direction. Very quickly the field sources separate and become fully oriented in the east-west direction. The strong field is confined to approximately circular sources of positive and negative polarity and these drift apart. However, since the footpoints of the toroidal loop are anchored at the base of the computational domain, the furthest they can move apart is the initial footpoint separation. It is clear that by time t=100 the sources are no longer moving apart. This is discussed further below. The arrows represent the horizontal velocity components, vx and vy. The velocity is radially outwards from the emergence site, weakening as the sources move to their maximum distance apart. There is no evidence of any shearing motion at this level. This is clear in Fig. 3, where the horizontal velocity components are shown as function of x at y=0 and z=25. The solid curve is at time t=40, the dotted curve at t=60, the dashed curve at t=70, the dot-dashed curve at t=80 and the triple dot-dashed curve at t=100. The y component is almost zero and, since this is at the initial plane of symmetry, this means that there is no obvious shearing motion. The x component shows a diverging flow away from x=0, as would be expected from the emerging field.
After the appearance of the bipolar region at the photosphere, the footpoint separation at the base of the photosphere increases with time. Later on, the separation slows down (and eventually stops) once the distance becomes twice the major radius of the initial tube. Thus, it is likely that the final separation between sunspots in a newly emerging active region may indicate the separation distance of the source of the magnetic field at large depths inside the convection zone. This is different from the cylindrical case in which the footpoints continue spreading until they interact with the sides of the computational box. In fact, this behaviour (sideways separation without limit) was also observed in the early models of the dynamical evolution of thin magnetic tubes rising across the whole convection zone (Moreno-Insertis 1986; D'Silva & Choudhuri 1993; Caligari et al. 1995; Fan et al. 1994).
![\begin{figure}
\par\includegraphics[width=8.8cm]{12189fg6.eps}\par\includegraphics[width=8.8cm]{12189fg7.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg83.png) |
Figure 3: Horizontal velocity components at z=25, the base of the photosphere, at times t=40 (solid), 60 (dotted), 70 (dashed), 80 (dot-dashed) and 100 (triple dot-dashed). |
| Open with DEXTER | |
Figure 4 shows a magnetogram at the height z=27, near the middle of the photosphere. Again the flow is initially radial when the field first reaches this level. However, at t=60, there is evidence of a weak shearing motion as the sources move apart. This shearing becomes stronger by t=70. By the time t=80, the shearing motion appears to have a converging motion as well that strengthens by t=90 and remains strong at t=100. This converging motion brings magnetic field together, creating a current sheet and the subsequent formation of a flux rope. The converging flow is discussed in more detail in Sect. 5.2. The shearing across the neutral line of the vertical field component in the photosphere was obtained in 3D flux emergence experiments by Fan (2001) and explained by the author as resulting from the action of the Lorentz force; similar flow patterns were observed by Strous et al. (1996) in actual emerging flux regions.
Flux rope formation during magnetic flux emergence has been mentioned by Manchester et al. (2004) and noted by Archontis & Hood (2008), Archontis & Török (2008) and Archontis et al. (2009). The typical initial state in these experiments consists of a highly stratified background atmosphere and a horizontal magnetic flux tube with uniform twist placed below the photosphere. During the evolution, the fieldlines that are close to the polarity inversion line of the emerging field become sheared and approach each other building a strong current layer. Later on, the fieldlines reconnect leading to the formation of a new flux rope inside the expanding magnetized field of the original, twisted flux tube. Eventually, the new flux rope rises to the outer atmosphere lifting up some of the dense plasma, which is trapped at the dips of the fieldlines of the magnetic system. This flux rope formation occurs above the original axis of the toroidal tube.
4.2 Photospheric velocities
The shearing motion is more obvious in Fig. 5 at z=27, where the horizontal velocity
components
vy(x,0,25) and
vx(x,0,25) are shown as functions of x in (a) and (b) respectively.
The curves showing different times are labelled in the same manner as Fig. 3. Note that vy now shows a clear shearing motion that increases in time until t=80, before
decreasing towards the end of the simulation at t=100. vx shows an initially diverging motion that weakens with time and becomes a converging flow by t=80. The y component of the
Lorentz force is shown in Fig. 6 as a function of x at y=0 and z=27.
The force has the same shape as the vy profile, indicating that it is the
Lorentz force that is responsible for the shearing motion. Within the Lorentz force, it is the term
involving jx that is dominant and this is mainly given by
![]() .
It arises from the rapid expansion of the emerging field that is initially in the radial direction.
Because there is a slight shear in the emerging field, there is a difference in the resulting Lorentz force.
It is this imbalance in the y component that creates the horizontal shear flow in vy at this height.
.
It arises from the rapid expansion of the emerging field that is initially in the radial direction.
Because there is a slight shear in the emerging field, there is a difference in the resulting Lorentz force.
It is this imbalance in the y component that creates the horizontal shear flow in vy at this height.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg85.png) |
Figure 4: Magnetograms at z=27, the middle of the photosphere, at times t=40, 60, 70, 80, 90 and 100. Contours correspond to values of Bz given by -0.1 (blue), -0.05 (mauve), 0.05 (yellow and 0.1 (red). |
| Open with DEXTER | |
The shearing pattern of the plasma moving on the two sides of the polarity inversion line was first mentioned by Manchester (2001) and also noted by Fan (2001). These authors used a twisted flux tube for the original sub-photospheric magnetic field configuration. Manchester (2001) reported that the shearing flow is a shear Alfven wave and Fan (2001) studied the Lorentz force and found that it is the tension term that drives the shear flow in the two halves of the tube cross section at the photosphere. What is interesting is that the emerging field is sufficiently strong so that it can move the photospheric plasma.
5 Dynamical properties of emergence
5.1 Rise of the loop and flux rope formation
The rising motion of the toroidal loop in the weaker field case is comparable to the case of a straight, twisted flux tube with the same strength and twist. To follow the emergence of the field, we track the axis of the toroidal loop in time. We use a simple method that is reasonable if the flux tube passes through the mid-plane in a near perpendicular manner. The axis is identified by plotting the zero contour for Bx and Bz in the mid-plane and identifying the axis with the intersection of these two zero contours. For this case, Bz is zero along the vertical line at x=0 and y=0. Hence, any zero of Bx, along x=0 and y=0 indicates a possible flux tube axis. The height variation of Bx is shown in the top panel in Fig. 7.
As previously mention in Sect. 4, a new flux rope is formed within the emerging and expanding field of a buoyant and twisted flux tube. It forms when the converging flows result in current sheet formation and reconnection either above or below the axis of the original magnetic flux system, with the location depending on the magnetic field strength.
The initial formation of the new flux rope occurs when the height variation of
Bx(0,0,z) exhibits two new zeros corresponding to the new flux rope axis (denoted by + symbol) and an X-type point (denoted by x symbol) above the original axis. This is shown in the top panel in Fig. 7. At t=70 (black line) there is one O-point at
![]() ,
which
corresponds to the original axis of the toroidal loop. At t=86 (blue line), there are three points where Bx is zero. The first corresponds to the
original axis, the second to an X-type point and the third to the O-point of the new flux rope. The green line shows the evolution of Bx at t=100. The X-type point and the new O-point have moved higher into the atmosphere. The middle figure shows a blow-up of the region illustrating the formation of the new axis and X-type point in more detail.
,
which
corresponds to the original axis of the toroidal loop. At t=86 (blue line), there are three points where Bx is zero. The first corresponds to the
original axis, the second to an X-type point and the third to the O-point of the new flux rope. The green line shows the evolution of Bx at t=100. The X-type point and the new O-point have moved higher into the atmosphere. The middle figure shows a blow-up of the region illustrating the formation of the new axis and X-type point in more detail.
The height of the original axis of the tube (solid line), the leading front edge (dashed), the new O-point (denoted by + symbol) and the X-type point (denoted by x symbol) are shown in the bottom panel in Fig. 7. In this plot, the leading edge is calculated as the height at which the magnetic field strength first increases above a background value of 10-7. Around t=80, a flux rope is formed above the original axis of the tube, which stays at the low photosphere. In general, the rising motion of the firstly expanding field (dashed line) and the flux rope show similar behaviour to the results presented by Archontis & Török (2008). At the beginning, they rise almost linearly with time but as time goes on they slown down as the magnetic pressure falls to the level of the surrounding background gas pressure.
As described in Sect. 6, this method does not work for the strong field case.
5.2 Converging flow and pressure variations
The formation of a new flux rope requires reconnection of magnetic field lines beneath the new axis (at the ``X-type'' point) and this can only occur if there is an inflow. As indicated in Fig. 5, the converging flow starts before t=80. The top panel in Fig. 8 shows the total pressure, magnetic plus gas pressures, as functions of x at y=0 and z=27. As the field starts to emerge, it is clear that the total pressure starts to rise above the surrounding value. However, once the rapid phase of emergence occurs, the total pressure drops below the surrounding region. This pressure deficit will cause an inflow of plasma, enhance the current and start the reconnection process necessary for the flux rope formation.
The difference in total pressure, defined as pT(x=0,0,z) - pT(x=43.75,0,z) is shown as a function of height in the bottom panel in Fig. 8 at times t=40, 60, 70, 80 and 100. The total pressure difference is only negative over a restricted range of heights, towards the middle of the photosphere and above the maximum height of the original toroidal tube axis. The resulting converging flows and the flux rope formation can only occur over these heights.
5.3 Topology of fieldlines
Figure 9 shows the topology of fieldlines after the formation of the flux rope. All the fieldlines have been traced from the vertical mid-plane. In the top panel (t=86), the white fieldlines go through the center of the cross section of the toroidal loop. The axis of the toroidal loop lies among these fieldlines. The blue fieldlines pass through the center of the new flux rope. Orange and green fieldlines reconnect around the X-type point, which is located in between the O-points. The coloured contours show the magnitude of the vertical component of the magnetic field, close to the lower boundary of the numerical domain. Notice, that the vertical segments of the blue fieldlines are rooted away from the center of the two flux sources where Bz through the new flux rope has its maximum value. They are also more twisted than the white fieldlines. This shows that indeed the blue fieldlines are the result of reconnection, possibly between the orange and green fieldlines. The middle panel shows the topology of fieldlines at t=100. The flux rope has reached coronal heights, while the original axis of the toroidal loop remains in the photosphere. Cyan and yellow fieldlines show the general expansion of the field. They have been traced from underneath and above the blue fieldlines of the new flux rope respectively. The bottom panel in Fig. 9 is a top view of the fieldlines visualized at t=100. The yellow fieldlines are the outermost fieldlines and show an azimuthal nature due to the original twist. The cyan fieldlines lie underneath the flux rope and are oriented oppositely to the yellow fieldlines. The white and blue fieldlines are, to a very good approximation, perpendicular to the vertical mid-plane as they go through the O-points connecting the two flux sources.
![\begin{figure}
\par\includegraphics[scale=0.4]{12189f14.eps}\par\includegraphics[scale=0.4]{12189f15.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg87.png) |
Figure 5: Horizontal velocity compoments at z=27, near the middle of the photosphere, at times t=40 (solid), 60 (dotted), 70 (dashed), 80 (dot-dashed) and 100 (triple dot-dashed). |
| Open with DEXTER | |
| |
Figure 6: The y component of the Lorentz force at z=27, near the middle of the photosphere, at times t=40 (solid), 60 (dotted), 70 (dashed), 80 (dot-dashed) and 100 (triple dot-dashed). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{12189f17.eps}\par\includegraphi...
...8.5cm]{12189f18.eps}\par\includegraphics[width=8.5cm]{12189f19.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg89.png) |
Figure 7:
Top: plots of
Bx(0,0,z) as function of height for the times t=70 (black), t=86 (blue) and t=100 (green).
Middle: expanded view of the above figure to show where Bx passes through zero. Bottom: height-time plots, along x=0 and y=0, of the axis of the original toroidal loop (solid), the leading edge (dashed) and the new flux tube axis (+ symbol) and the ``X-point'' ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[scale=0.5]{12189f20.eps}\par\includegraphics[scale=0.5]{12189f21.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg90.png) |
Figure 8: Top: the total pressure in a horizontal cut at y=0 and z=27. The solid curve is time t=40, dotted t=60, dashed t=70, dot-dashed t=80 and triple dot-dashed t=100. Bottom: total pressure difference for the same times as in the top panel. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{12189f22.eps}\\ [2.5mm]
\includ...
...2189f23.eps}\\ [2.5mm]
\includegraphics[width=8.6cm]{12189f24.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg91.png) |
Figure 9: 3D visualization of fieldlines during the expansion of the magnetic field in the weaker field experiment. Two times are shown: t=86 ( top panel) and t =100 ( middle and bottom panel). The bottom panel is a top-view of the same fieldlines visualized at t=100. |
| Open with DEXTER | |
What is clear from the field line shapes is that there are no dips in the field close to the axis of the loop, as predicted in Sect. 3. Due to small twist, the fieldlines initially do not have any concave parts to collect dense plasma and as the loop rises the fieldlines remain free of dips. This remains true as the field lines rise and expand further into the outer atmosphere. Also the curvature of the loop in this model allows the plasma to drain down the field in an efficient way. Thus, one would have thought that due to the lack of dips and the effective draining the axial magnetic field will fully emerge into the higher levels of the atmosphere. However, we find that the majority of the field is trapped just above the photosphere and only a small percentage of the flux actually emerges. So, we asumme that the lack of complete emergence could be due to the relatively weak initial magnetic field strength. The results from experiments with stronger initial field are shown in next section.
6 Strong field case
6.1 Full emergence of the field
In previous experiments, Murray et al. (2006) studied the effects of varying the twist and field strength of an emerging flux tube. They found that for high magnetic field strength (B0 = 9) the tube's axis did not fully emerge into the outer atmosphere. Also, no dramatic change on the emergence of the original axis above the photosphere was evident when the twist of the tube was changed.
In this Section, we investigate the effect of increasing the magnetic field strength on the evolution of the toroidal loop. We use B0 = 9, which is stronger than the field strength used in the weaker field experiment. Also the initial twist is 0.4, twice the twist in the weaker case. The rising motion and the expansion of the magnetic field occurs with a faster rate compared to the case with weaker initial field strength. This is in agreement with the results by Murray et al. (2006). The height of the original axis of the loop is not easily determined using the same method as in Sect. 5.1. While this approach works until the axis reaches the photosphere and before the secondary expansion (t < 47), the method fails subsequently because the original axis and the fieldlines very close to the axis (axial fieldlines) no longer pass through the mid-plane in a strictly orthogonal manner. This is due to the higher initial twist that means the fieldlines are slightly kinked and tilted from the y=0 plane. However, when the new flux rope forms, it does pass through the mid-plane in an almost perpendicular manner and its axis can be tracked by this method. The evolution of this new axis is discussed below.
What happens to the original axis is that the cross section of the toroidal loop becomes highly squashed and a horizontal current layer forms, as the rising plasma slows at the photosphere. This horizontal expansion and narrow vertical extent of the current layer makes it very difficult to continually identify the axis. Instead, to track the original axis beyond t=47, we trace fieldlines from the center of both of the two flux sources where Bz is maximum, at the lower computational domain in the interior and also a group of fieldlines that surround these axial fieldlines. Due to the boundary conditions of the experiment on the lower boundary, the two flux sources at the lower boundary do not move during the simulation and, thus, the evolution of these fieldlines will give an indication as to whether the axis of the original loop rises into the higher atmosphere or stays close to the photosphere.
Figure 10 shows this for the strong field experiment (left panels). The evolution in the weaker field case, is shown in the right panels in the same figure. The horizontal cut reveals the location of the two flux sources on the lower boundary. Coloured contours indicate the magnitude of Bz. Blue fieldlines have been traced from the central region of the two flux sources and, thus, the axis of the loop is located within this set of fieldlines. White and yellow fieldlines are traced from positions surrounding the axial fieldlines.
At t=25 (top left) the fieldlines outline the toroidal-like shape of the initial magnetic flux system. The blue fieldlines lie along the central region of the system, while the other fieldlines are twisted around them. At t=55 (middle left), the flux system has started to expand above the photosphere but has not yet reached coronal heights. Now, the striking result is that at t=80 (bottom left) the axial fieldlines continue their rising motion reaching coronal heights. The original axis of the toroidal loop has fully emerged.
The comparison with the weak field case shows a remarkable difference. In the latter case, the original axis of the toroidal loop remains at low heights and does not emerge into the corona, as has also been described in Sect. 5.1. Notice also, that in the weaker field experiment some of the yellow and white fieldlines become flattened and remain at photospheric heights, while others manage to rise and expand into the higher atmosphere. At all times, the axial fieldlines do not manage to rise above photosphere.
6.2 Amount of emerging flux
Due to the remarkable difference in the rising motion of the axis of the toroidal loop in the weaker and strong field experiments, we expect that the amount of flux which is transported in the high atmosphere will be also different in the two experiments. Thus, we calculate the total amount of vertical unsigned magnetic flux that emerges above the photosphere and into the transition region and corona. Figure 11 shows the vertical unsigned magnetic flux across a horizontal plane at z=35, the base of the transition region, normalized by the total vertical flux of the toroidal loop at the beginning of the simulation.
Not suprisingly, the transported flux fraction to the outer atmosphere is ![]()
![]() for the strong field experiment, while it is only
for the strong field experiment, while it is only ![]()
![]() for the weak field case. In the latter case, the transport of flux starts towards the end of the simulation (
for the weak field case. In the latter case, the transport of flux starts towards the end of the simulation (
![]() )
but there is no further
strong indication that the amount of flux fraction will increase at later times. On the contrary, in the strong field case the majority of the vertical
flux has risen through the photosphere and reached the upper levels of the atmosphere. This is consistent with the fact that the axis of the toroidal loop
in this case has fully emerged into the corona.
)
but there is no further
strong indication that the amount of flux fraction will increase at later times. On the contrary, in the strong field case the majority of the vertical
flux has risen through the photosphere and reached the upper levels of the atmosphere. This is consistent with the fact that the axis of the toroidal loop
in this case has fully emerged into the corona.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig10.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg96.png) |
Figure 10: The emergence of the toroidal loop in the strong field ( left panels) and weaker field ( right panels) experiments. When the initial magnetic field is strong, the axial fieldlines (blue lines) break through the photopshere and emerge fully into the corona. This is not possible in the weaker field experiment, where the axis of the tube stays at low heights. From top to bottom, times are: t=25, t=55 and t=80 for the strong field and t=40, t=80 and t=100 for the weaker field. |
| Open with DEXTER | |
6.3 Flux rope formation
Similar to the weaker field case, a flux rope is formed within the expanding and rising magnetic field due to internal reconnection of neighbouring fieldlines. The expansion of the field and the time evolution of the height of the new axis of the rope are shown in Fig. 12 (top panel). To track the new axis we apply the same method as in Sect. 5.1 because the fieldlines that pass through the center of the rope pierce the x=0, y=0 plane in an orthogonal manner.
The leading edge of the field reaches the photosphere at t=15, moving with a relatively small velocity. Later on, it experiences a runaway expansion due to the
fact that the magnetic pressure inside the rising magnetized volume overwhelms the outside gas pressure and, thus, it reaches the top boundary very quickly (t=80).
The new flux rope is formed at
![]() ,
at heights between the base of the photosphere and the transition region (around z=29). The axis new axis is shown by ``diamonds''. The height-time profile shows that at the beginning
the new rope rises in a linear manner with time but, after the envelope field has reached the upper boundary, the rope slows down approaching coronal heights around
z=60 at the final time t=98. The original axis of the toroidal tube has reached the heights of z=41 at t=45, z=53 at t=60 and z=85 at t=98.
,
at heights between the base of the photosphere and the transition region (around z=29). The axis new axis is shown by ``diamonds''. The height-time profile shows that at the beginning
the new rope rises in a linear manner with time but, after the envelope field has reached the upper boundary, the rope slows down approaching coronal heights around
z=60 at the final time t=98. The original axis of the toroidal tube has reached the heights of z=41 at t=45, z=53 at t=60 and z=85 at t=98.
Now, the fact that the fieldlines through the rope's center are orthogonal to the vertical midplane, is also revealed in Fig. 12 (bottom panel), where we plot a number of fieldlines from certain points along the central vertical (x=0, y=0) line. More precisely, white fieldlines are traced from the center of the new flux rope, yellow fieldlines from heights above the rope, orange fieldlines underneath the rope and blue fieldlines from photospheric heights. As shown in the bottom panel (top view) in Fig. 12 the lower fieldlines adopt a reversed sigmoidal shape while the upper fieldlines are oriented in opposite directions to the blue and orange fieldlines. This is indicative of the strong initial twist of the field and also shows that they are twisted around the white fieldlines. All these fieldlines together form the new rising flux rope. Notice, that the white fieldlines that go along the center of the new rope lie almost in parallel to the y-direction and, thus, are perpendicular to the vertical mid-plane at y=0.
Another indication that the original axis of the toroidal loop has now emerged is revealed by looking at the topology of the orange fieldlines. The orange fieldlines possess dips. These dips actually develop during the evolution of the system and are due to dense plasma, which was previously trapped there. However, they have now been raised into the corona. Initially, these twisted fieldlines were located underneath the original axis of the loop. However, the original axis of the loop is now fully emerged and, thus, they are also able to rise higher into the atmosphere.
Perhaps the key point to note in this section is that a new flux rope forms as before but this time it forms beneath the original axis.
7 Conclusions
We have presented a 3D MHD numerical experiment of the emergence of a toroidal tube with an arch-like shape from the solar interior
into the higher atmosphere and the solar corona. Compared with a considerable number of previous simulations, the initial magnetic field
in the solar interior is sufficiently bent such that the plasma can drain along the fieldlines more efficiently. Two experiments
were performed: where the magnetic field strength and twist are relatively weak (B0=5 and twist
![]() )
and
where both have larger values (B0=9 and twist
)
and
where both have larger values (B0=9 and twist
![]() ).
).
![\begin{figure}
\par\includegraphics[width=9cm]{12189f31.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg98.png) |
Figure 11: The amount of normalized vertical flux, which is transported above photosphere and towards the outer atmosphere in the weaker field (red) and strong field (black) experiments. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{12189f32.eps}\par\includegraphics...
...8.5cm]{12189f33.eps}\par\includegraphics[width=8.5cm]{12189f34.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg99.png) |
Figure 12: Top: height-time plots, along x=0 and y=0, of the axis of the rope (calculated from the zeros of Bx as described in the text and shown by diamonds) and the leading edge of the toroidal flux system (dashed curve) Middle: fieldlines showing the topology of the magnetic field around the rising flux rope (white fieldlines). Time is t=100. Bottom: Top view of the same bunch of fieldlines, showing the relative orientation of the rising field. |
| Open with DEXTER | |
In these simulations we find that the evolution of the axial fieldlines is different in the two experiments. In the weaker field experiment, and similar to what has been found in previous experiments that used a twisted cylindrical flux tube as the initial magnetic field configuration, the axial fieldlines do not emerge fully above photospheric heights. Thus, the toroidal loop cannot emerge bodily into the corona. In this experiment, the initial twist of the fieldlines is weak and the emerging fieldlines that first rise to the photosphere contain less than one full turn of twist. Thus, there are no pronounced dips along the segments of these fieldlines, which could confine dense material close to the original axis and halt the full emergence of the toroidal loop. However, the evolution of the rising field shows that the original axis of the toroidal loop is unable to rise above the photosphere by the end of the experiment. The general emergence process and the dynamics of the buoyant magnetic field are similar to experiments with a cylindrical flux tube.
In strong field experiment, the evolution of the magnetic flux system is different. The axial fieldlines rise to the photopshere where they slow down but
their emergence is not stopped. After a short period of time, they rise into the higher levels of the atmosphere and, finally, emerge into the corona.
As a result of this emergence, almost ![]() of the initial vertical flux is transported into the corona. The corresponding amount of flux
in the weaker field case is not more than
of the initial vertical flux is transported into the corona. The corresponding amount of flux
in the weaker field case is not more than ![]() .
During their emergence, the axial fieldlines are slightly kinked due to the strong initial twist
of the toroidal loop's fieldlines. Because of the strong initial twist, there are more dips along the helical fieldlines around the axis of the
loop and, thus, the deposition of dense material at low heights is efficient.
One could expect that, due to this density enhancement close to the axis of the loop, the full emergence of the field is difficult to achieve.
Also, previous experiments, using a twisted cylindrical flux tube with the same initial values for B0 and
.
During their emergence, the axial fieldlines are slightly kinked due to the strong initial twist
of the toroidal loop's fieldlines. Because of the strong initial twist, there are more dips along the helical fieldlines around the axis of the
loop and, thus, the deposition of dense material at low heights is efficient.
One could expect that, due to this density enhancement close to the axis of the loop, the full emergence of the field is difficult to achieve.
Also, previous experiments, using a twisted cylindrical flux tube with the same initial values for B0 and ![]() ,
have shown that the axis of the tube
does not emerge into the corona. However, as we mentioned above, in the strong field experiment the axis of the tube does rise to coronal heights. Actually, due to the fact that the original axis of the toroidal loop is fully emerged into the corona, the U-shaped dips of the twisted fieldlines do not
remain at photospheric heights but they also rise, following the general emergence of the magnetic flux system. This brings dense plasma into the corona, plasma that is almost two orders of magnitude denser than the background.
,
have shown that the axis of the tube
does not emerge into the corona. However, as we mentioned above, in the strong field experiment the axis of the tube does rise to coronal heights. Actually, due to the fact that the original axis of the toroidal loop is fully emerged into the corona, the U-shaped dips of the twisted fieldlines do not
remain at photospheric heights but they also rise, following the general emergence of the magnetic flux system. This brings dense plasma into the corona, plasma that is almost two orders of magnitude denser than the background.
From the results of the two experiments, we conclude that the initial field strength of the toroidal loop plays an important role for the emergence of the original axis of the system. Moreover, it is the combination of the arch-like shape of the toroidal loop and the high field strength that leads to full emergence, unlike the experiments of twisted cylindrical flux tubes. Experiments that include self-consistently the coupling with the radiation field and convection flows allow the original axis of the system to rise through the photosphere, possibly thanks to the extra push of the convective upflows. Here we have shown that a sufficiently arched shape and a large enough field strength can achieve that result as well.
In both experiments, a new flux rope is formed within the expanding magnetized and rising volume of the original magnetic flux system. The formation of the new rope is the result of reconnection at low atmospheric heights, of neighbouring fieldlines which have been stretched and pressed towards each other by converging motions. The converging flows have a strongly azimuthal nature and bring the magnetic field from the two sides of the polarity inversion line together. As a result, a current sheet is built up and reconnection occurs that leads to the formation of a new flux rope. What is surprising is that the new flux rope forms above the original axis in the weaker field case and the original axis remains low down in the atmosphere. However, for the strong field case, the new axis forms below the original axis and both rise into the corona. As the new rope rises, dense plasma is lifted up and more dense plasma is transported to the corona in the strong field experiment when the strength and the twist of the fieldline are larger.
The main aim of this paper was to show how a toroidal magnetic flux system can rise from the solar interior and emerge fully (including the original axis of the system) into the solar corona. Provided the field strength is large enough this can be achieved. A more detailed investigation to understand the effect of varying the twist and initial field strength of the tube on the emergence process will be considered in a future investigation (MacTaggart & Hood 2009).
Acknowledgements
The simulations were run on the UKMHD Consortium parallel computer, funded jointly by STFC and University of St Andrews (SRIF funding). We acknowledge the financial support by STFC and the EuropeanCommission through the SOLAIRE Network (MTRN-CT-2006-035484). F.M.I. is grateful to the Spanish Ministry of Education for their financial support through projects AYA2007-66502 and CSD2007-00050.
References
- Abbett, W. P., & Fisher, G. H. 2003, ApJ, 582, 475 [NASA ADS] [CrossRef] (In the text)
- Acheson, D. J. 1979, Sol. Phys., 62, 23 [NASA ADS] [CrossRef] (In the text)
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., et al. 2001, J. Comp. Phys., 171, 151 [NASA ADS] [CrossRef] (In the text)
- Archontis, V. 2008, J. Geophys. Res. (Space Physics), 113, 3 (In the text)
- Archontis, V., & Hood, A. W. 2008, ApJ, 674, L113 [NASA ADS] [CrossRef] (In the text)
- Archontis, V., & Török, T. 2008, A&A, 492, L35 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Archontis, V., Moreno-Insertis, F., Galsgaard, K., et al. 2004, A&A, 426, 1047 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Archontis, V., Hood, A. W., Savcheva, A., Golub, L., & Deluca, E. 2009, ApJ, 691, 1276 [NASA ADS] [CrossRef] (In the text)
- Brun, A. S., & Jouve, L. 2008, in IAU Symp., 247, 33 (In the text)
- Caligari, P., Moreno-Insertis, F., & Schüssler, M. 1995, ApJ, 441, 886 [NASA ADS] [CrossRef]
- Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007, A&A, 467, 703 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cheung, M. C. M., Schüssler, M., Tarbell, T. D., et al. 2008, ApJ, 687, 1373 [NASA ADS] [CrossRef]
- D'Silva, S., & Choudhuri, A. R. 1993, A&A, 272, 621 [NASA ADS]
- Fan, Y. 2001, ApJ, 554, L111 [NASA ADS] [CrossRef] (In the text)
- Fan, Y., & Gibson, S. E. 2003, ApJ, 589, L105 [NASA ADS] [CrossRef] (In the text)
- Fan, Y., Fisher, G. H., & McClymont, A. N. 1994, ApJ, 436, 907 [NASA ADS] [CrossRef]
- Gerrard, C. L., Hood, A. W., & Brown, D. S. 2004, Sol. Phys., 222, 79 [NASA ADS] [CrossRef] (In the text)
- Isobe, H., Tripathi, D., & Archontis, V. 2007, ApJ, 657, L53 [NASA ADS] [CrossRef] (In the text)
- Leake, J. E., & Arber, T. D. 2006, A&A, 450, 805 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- MacTaggart, D., & Hood, A. W. 2009, A&A, in preparation (In the text)
- Magara, T. 2001, ApJ, 549, 608 [NASA ADS] [CrossRef] (In the text)
- Magara, T., & Longcope, D. W. 2001, ApJ, 559, L55 [NASA ADS] [CrossRef] (In the text)
- Manchester, W. I. 2001, ApJ, 547, 503 [NASA ADS] [CrossRef] (In the text)
- Manchester, IV, W., Gombosi, T., DeZeeuw, D., et al. 2004, ApJ, 610, 588 [NASA ADS] [CrossRef] (In the text)
- Martínez-Sykora, J., Hansteen, V., & Carlsson, M. 2008, ApJ, 679, 871 [NASA ADS] [CrossRef] (In the text)
- Matsumoto, R., & Shibata, K. 1992, PASJ, 44, 167 [NASA ADS] (In the text)
- Moreno-Insertis, F. 1986, A&A, 166, 291 [NASA ADS]
- Moreno-Insertis, F. 2006, in Solar MHD: Theory and Observations - a High Spatial Resolution Perspective, ed. J. Leibacher, H. Uitenbroek, & R. Stein, Astron Soc Pacific Conf. Ser. (In the text)
- Moreno-Insertis, F., & Emonet, T. 1996, ApJ, 472, L53 [NASA ADS] [CrossRef] (In the text)
- Murray, M. J., & Hood, A. W. 2008, A&A, 479, 567 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Murray, M. J., Hood, A. W., Moreno-Insertis, F., Galsgaard, K., & Archontis, V. 2006, A&A, 460, 909 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Newcomb, W. A. 1961, Phys. Fluids, 4, 391 [NASA ADS] [CrossRef] (In the text)
- Nozawa, S., Shibata, K., Matsumoto, R., et al. 1992, ApJS, 78, 267 [NASA ADS] [CrossRef] (In the text)
- Shibata, K., Tajima, T., Steinolfson, R. S., & Matsumoto, R. 1989, ApJ, 345, 584 [NASA ADS] [CrossRef] (In the text)
- Shibata, K., Nozawa, S., & Matsumoto, R. 1992, PASJ, 44, 265 [NASA ADS] (In the text)
- Strous, L. H., Scharmer, G., Tarbell, T. D., Title, A. M., & Zwaan, C. 1996, A&A, 306, 947 [NASA ADS] (In the text)
- Thomas, J. H., & Nye, A. H. 1975, Phys. Fluids, 18, 490 [NASA ADS] [CrossRef] (In the text)
- Titov, V. S., & Démoulin, P. 1999, A&A, 351, 707 [NASA ADS] (In the text)
- Török, T., & Kliem, B. 2005, ApJ, 630, L97 [NASA ADS] [CrossRef] (In the text)
- Tortosa Andreu, A., & Moreno-Insertis, F. 2009, A&A, submitted
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12189fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg25.png) |
Figure 1: Distribution of temperature (dot-dashed), pressure (solid), density (triple dot-dashed) and magnetic pressure (dashed) along height (x=0, y=0) at t=0. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg80.png) |
Figure 2: Magnetograms of Bz at z = 25, the base of the photosphere, at times t=40, 60, 80 and 100. Contours correspond to values of Bz given by -0.1 (blue), -0.05 (mauve), 0.05 (yellow) and 0.1 (red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{12189fg6.eps}\par\includegraphics[width=8.8cm]{12189fg7.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg83.png) |
Figure 3: Horizontal velocity components at z=25, the base of the photosphere, at times t=40 (solid), 60 (dotted), 70 (dashed), 80 (dot-dashed) and 100 (triple dot-dashed). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg85.png) |
Figure 4: Magnetograms at z=27, the middle of the photosphere, at times t=40, 60, 70, 80, 90 and 100. Contours correspond to values of Bz given by -0.1 (blue), -0.05 (mauve), 0.05 (yellow and 0.1 (red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.4]{12189f14.eps}\par\includegraphics[scale=0.4]{12189f15.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg87.png) |
Figure 5: Horizontal velocity compoments at z=27, near the middle of the photosphere, at times t=40 (solid), 60 (dotted), 70 (dashed), 80 (dot-dashed) and 100 (triple dot-dashed). |
| Open with DEXTER | |
| In the text | |
| |
Figure 6: The y component of the Lorentz force at z=27, near the middle of the photosphere, at times t=40 (solid), 60 (dotted), 70 (dashed), 80 (dot-dashed) and 100 (triple dot-dashed). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{12189f17.eps}\par\includegraphi...
...8.5cm]{12189f18.eps}\par\includegraphics[width=8.5cm]{12189f19.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg89.png) |
Figure 7:
Top: plots of
Bx(0,0,z) as function of height for the times t=70 (black), t=86 (blue) and t=100 (green).
Middle: expanded view of the above figure to show where Bx passes through zero. Bottom: height-time plots, along x=0 and y=0, of the axis of the original toroidal loop (solid), the leading edge (dashed) and the new flux tube axis (+ symbol) and the ``X-point'' ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.5]{12189f20.eps}\par\includegraphics[scale=0.5]{12189f21.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg90.png) |
Figure 8: Top: the total pressure in a horizontal cut at y=0 and z=27. The solid curve is time t=40, dotted t=60, dashed t=70, dot-dashed t=80 and triple dot-dashed t=100. Bottom: total pressure difference for the same times as in the top panel. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{12189f22.eps}\\ [2.5mm]
\includ...
...2189f23.eps}\\ [2.5mm]
\includegraphics[width=8.6cm]{12189f24.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg91.png) |
Figure 9: 3D visualization of fieldlines during the expansion of the magnetic field in the weaker field experiment. Two times are shown: t=86 ( top panel) and t =100 ( middle and bottom panel). The bottom panel is a top-view of the same fieldlines visualized at t=100. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig10.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg96.png) |
Figure 10: The emergence of the toroidal loop in the strong field ( left panels) and weaker field ( right panels) experiments. When the initial magnetic field is strong, the axial fieldlines (blue lines) break through the photopshere and emerge fully into the corona. This is not possible in the weaker field experiment, where the axis of the tube stays at low heights. From top to bottom, times are: t=25, t=55 and t=80 for the strong field and t=40, t=80 and t=100 for the weaker field. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12189f31.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg98.png) |
Figure 11: The amount of normalized vertical flux, which is transported above photosphere and towards the outer atmosphere in the weaker field (red) and strong field (black) experiments. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12189f32.eps}\par\includegraphics...
...8.5cm]{12189f33.eps}\par\includegraphics[width=8.5cm]{12189f34.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12189-09/Timg99.png) |
Figure 12: Top: height-time plots, along x=0 and y=0, of the axis of the rope (calculated from the zeros of Bx as described in the text and shown by diamonds) and the leading edge of the toroidal flux system (dashed curve) Middle: fieldlines showing the topology of the magnetic field around the rising flux rope (white fieldlines). Time is t=100. Bottom: Top view of the same bunch of fieldlines, showing the relative orientation of the rising field. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.