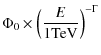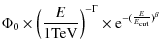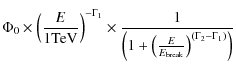| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | 817 - 825 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200811569 | |
| Published online | 02 July 2009 | |
Spectrum and variability of the Galactic center VHE 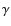 -ray source HESS J1745-290
-ray source HESS J1745-290
F. Aharonian1,13 - A. G. Akhperjanian2 - G. Anton16 - U. Barres de Almeida8,![]() - A. R. Bazer-Bachi3 - Y. Becherini12 - B. Behera14 - K. Bernlöhr1,5 - C. Boisson6 - A. Bochow1 - V. Borrel3 - I. Braun1 - E. Brion7 - J. Brucker16 - P. Brun7 - R. Bühler1 - T. Bulik24 - I. Büsching9 - T. Boutelier17 - P. M. Chadwick8 - A. Charbonnier19 - R. C. G. Chaves1 - A. Cheesebrough8 - L.-M. Chounet10 - A. C. Clapson1 - G. Coignet11 - M. Dalton5 - M. K. Daniel8 - I. D. Davids22,9 - B. Degrange10 - C. Deil1 - H. J. Dickinson8 - A. Djannati-Ataï12 - W. Domainko1 - L. O'C. Drury13 - F. Dubois11 - G. Dubus17 - J. Dyks24 - M. Dyrda28 - K. Egberts1 - D. Emmanoulopoulos14 - P. Espigat12 - C. Farnier15 - F. Feinstein15 - A. Fiasson15 - A. Förster1 - G. Fontaine10 - M. Füßling5 - S. Gabici13 - Y. A. Gallant15 - L. Gérard12 - B. Giebels10 - J. F. Glicenstein7 - B. Glück16 - P. Goret7 - D. Hauser14 - M. Hauser14 - S. Heinz16 - G. Heinzelmann4 - G. Henri17 - G. Hermann1 - J. A. Hinton25 - A. Hoffmann18 - W. Hofmann1 - M. Holleran9 - S. Hoppe1 - D. Horns4 - A. Jacholkowska19 - O. C. de Jager9 - I. Jung16 - K. Katarzynski27 - U. Katz16 - S. Kaufmann14 - E. Kendziorra18 - M. Kerschhaggl5 - D. Khangulyan1 - B. Khélifi10 - D. Keogh8 - Nu. Komin7 - K. Kosack1 - G. Lamanna11 - J.-P. Lenain6 - T. Lohse5 - V. Marandon12 - J. M. Martin6 - O. Martineau-Huynh19 - A. Marcowith15 - D. Maurin19 - T. J. L. McComb8 - M. C. Medina6 - R. Moderski24 - E. Moulin7 - M. Naumann-Godo10 - M. de Naurois19 - D. Nedbal20 - D. Nekrassov1 - J. Niemiec28 - S. J. Nolan8 - S. Ohm1 - J.-F. Olive3 - E. de Oña Wilhelmi12,29 - K.J. Orford8 - M. Ostrowski23 - M. Panter1 - M. Paz Arribas5 - G. Pedaletti14 - G. Pelletier17 - P.-O. Petrucci17 - S. Pita12 - G. Pühlhofer14 - M. Punch12 - A. Quirrenbach14 - B. C. Raubenheimer9 - M. Raue1,29 - S. M. Rayner8 - M. Renaud12,1 - F. Rieger1,29 - J. Ripken4 - L. Rob20 - L. Rolland11 - S. Rosier-Lees11 - G. Rowell26 - B. Rudak24 - C. B. Rulten8 - J. Ruppel21 - V. Sahakian2 - A. Santangelo18 - R. Schlickeiser21 - F. M. Schöck16 - R. Schröder21 - U. Schwanke5 - S. Schwarzburg18 - S. Schwemmer14 - A. Shalchi21 - J. L. Skilton25 - H. Sol6 - D. Spangler8 -
- A. R. Bazer-Bachi3 - Y. Becherini12 - B. Behera14 - K. Bernlöhr1,5 - C. Boisson6 - A. Bochow1 - V. Borrel3 - I. Braun1 - E. Brion7 - J. Brucker16 - P. Brun7 - R. Bühler1 - T. Bulik24 - I. Büsching9 - T. Boutelier17 - P. M. Chadwick8 - A. Charbonnier19 - R. C. G. Chaves1 - A. Cheesebrough8 - L.-M. Chounet10 - A. C. Clapson1 - G. Coignet11 - M. Dalton5 - M. K. Daniel8 - I. D. Davids22,9 - B. Degrange10 - C. Deil1 - H. J. Dickinson8 - A. Djannati-Ataï12 - W. Domainko1 - L. O'C. Drury13 - F. Dubois11 - G. Dubus17 - J. Dyks24 - M. Dyrda28 - K. Egberts1 - D. Emmanoulopoulos14 - P. Espigat12 - C. Farnier15 - F. Feinstein15 - A. Fiasson15 - A. Förster1 - G. Fontaine10 - M. Füßling5 - S. Gabici13 - Y. A. Gallant15 - L. Gérard12 - B. Giebels10 - J. F. Glicenstein7 - B. Glück16 - P. Goret7 - D. Hauser14 - M. Hauser14 - S. Heinz16 - G. Heinzelmann4 - G. Henri17 - G. Hermann1 - J. A. Hinton25 - A. Hoffmann18 - W. Hofmann1 - M. Holleran9 - S. Hoppe1 - D. Horns4 - A. Jacholkowska19 - O. C. de Jager9 - I. Jung16 - K. Katarzynski27 - U. Katz16 - S. Kaufmann14 - E. Kendziorra18 - M. Kerschhaggl5 - D. Khangulyan1 - B. Khélifi10 - D. Keogh8 - Nu. Komin7 - K. Kosack1 - G. Lamanna11 - J.-P. Lenain6 - T. Lohse5 - V. Marandon12 - J. M. Martin6 - O. Martineau-Huynh19 - A. Marcowith15 - D. Maurin19 - T. J. L. McComb8 - M. C. Medina6 - R. Moderski24 - E. Moulin7 - M. Naumann-Godo10 - M. de Naurois19 - D. Nedbal20 - D. Nekrassov1 - J. Niemiec28 - S. J. Nolan8 - S. Ohm1 - J.-F. Olive3 - E. de Oña Wilhelmi12,29 - K.J. Orford8 - M. Ostrowski23 - M. Panter1 - M. Paz Arribas5 - G. Pedaletti14 - G. Pelletier17 - P.-O. Petrucci17 - S. Pita12 - G. Pühlhofer14 - M. Punch12 - A. Quirrenbach14 - B. C. Raubenheimer9 - M. Raue1,29 - S. M. Rayner8 - M. Renaud12,1 - F. Rieger1,29 - J. Ripken4 - L. Rob20 - L. Rolland11 - S. Rosier-Lees11 - G. Rowell26 - B. Rudak24 - C. B. Rulten8 - J. Ruppel21 - V. Sahakian2 - A. Santangelo18 - R. Schlickeiser21 - F. M. Schöck16 - R. Schröder21 - U. Schwanke5 - S. Schwarzburg18 - S. Schwemmer14 - A. Shalchi21 - J. L. Skilton25 - H. Sol6 - D. Spangler8 - ![]() .
Stawarz23 - R. Steenkamp22 - C. Stegmann16 - G. Superina10 - A. Szostek1 - P. H. Tam14 - J.-P. Tavernet19 - R. Terrier12 - O. Tibolla1,14 - C. van Eldik1 - G. Vasileiadis15 - C. Venter9 - L. Venter6 - J. P. Vialle11 - P. Vincent19 - M. Vivier7 - H. J. Völk1 - F. Volpe
1,10,29 - S. J. Wagner14 - M. Ward8 - A. A. Zdziarski24 - A. Zech6
.
Stawarz23 - R. Steenkamp22 - C. Stegmann16 - G. Superina10 - A. Szostek1 - P. H. Tam14 - J.-P. Tavernet19 - R. Terrier12 - O. Tibolla1,14 - C. van Eldik1 - G. Vasileiadis15 - C. Venter9 - L. Venter6 - J. P. Vialle11 - P. Vincent19 - M. Vivier7 - H. J. Völk1 - F. Volpe
1,10,29 - S. J. Wagner14 - M. Ward8 - A. A. Zdziarski24 - A. Zech6
1 - Max-Planck-Institut für Kernphysik, P.O. Box 103980, 69029
Heidelberg, Germany
2 -
Yerevan Physics Institute, 2 Alikhanian Brothers St., 375036 Yerevan,
Armenia
3 -
Centre d'Etude Spatiale des Rayonnements, CNRS/UPS, 9 av. du Colonel Roche, BP
4346, 31029 Toulouse Cedex 4, France
4 -
Universität Hamburg, Institut für Experimentalphysik, Luruper Chaussee
149, 22761 Hamburg, Germany
5 -
Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15,
12489 Berlin, Germany
6 -
LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 Place Jules Janssen, 92190 Meudon,
France
Obserwatorium Astronomiczne, Uniwersytet Ja
7 -
IRFU/DSM/CEA, CE Saclay, 91191 Gif-sur-Yvette, Cedex, France
8 -
University of Durham, Department of Physics, South Road, Durham DH1 3LE, UK
9 -
Unit for Space Physics, North-West University, Potchefstroom 2520,
South Africa
10 -
Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS/IN2P3,
91128 Palaiseau, France
11 -
Laboratoire d'Annecy-le-Vieux de Physique des Particules, CNRS/IN2P3,
9 Chemin de Bellevue, BP 110, 74941 Annecy-le-Vieux Cedex, France
12 -
Astroparticule et Cosmologie (APC), CNRS, Universite Paris 7 Denis Diderot,
10, rue Alice Domon et Leonie Duquet, 75205 Paris Cedex 13, UMR 7164 (CNRS, Université Paris VII, CEA, Observatoire de Paris) France
13 -
Dublin Institute for Advanced Studies, 5 Merrion Square, Dublin 2,
Ireland
14 -
Landessternwarte, Universität Heidelberg, Königstuhl, 69117 Heidelberg, Germany
15 -
Laboratoire de Physique Théorique et Astroparticules, CNRS/IN2P3,
Université Montpellier II, CC 70, Place Eugène Bataillon, 34095
Montpellier Cedex 5, France
16 -
Universität Erlangen-Nürnberg, Physikalisches Institut, Erwin-Rommel-Str. 1,
91058 Erlangen, Germany
17 -
Laboratoire d'Astrophysique de Grenoble, INSU/CNRS, Université Joseph Fourier, BP
53, 38041 Grenoble Cedex 9, France
18 -
Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1, 72076 Tübingen, Germany
19 -
LPNHE, Université Pierre et Marie Curie Paris 6, Université Denis Diderot
Paris 7, CNRS/IN2P3, 4 Place Jussieu, 75252, Paris Cedex 5, France
20 -
Institute of Particle and Nuclear Physics, Charles University,
V Holesovickach 2, 180 00 Prague 8, Czech Republic
21 -
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und
Astrophysik,
Ruhr-Universität Bochum, 44780 Bochum, Germany
22 -
University of Namibia, Private Bag 13301, Windhoek, Namibia
23 -
Obserwatorium Astronomiczne, Uniwersytet Jagiellonski, ul. Orla 171,
30-244 Kraków, Poland
24 -
Nicolaus Copernicus Astronomical Center, ul. Bartycka 18, 00-716 Warsaw,
Poland
25 -
School of Physics & Astronomy, University of Leeds, Leeds LS2 9JT, UK
26 -
School of Chemistry & Physics,
University of Adelaide, Adelaide 5005, Australia
27 -
Torun Centre for Astronomy, Nicolaus Copernicus University, ul.
Gagarina 11, 87-100 Torun, Poland
28 -
Instytut Fizyki Jadrowej PAN, ul. Radzikowskiego 152, 31-342 Kraków,
Poland
29 -
European Associated Laboratory for Gamma-Ray Astronomy, jointly
supported by CNRS and MPG
Received 22 December 2008 / Accepted 1 May 2009
Abstract
Aims. A detailed study of the spectrum and variability of the source HESS J1745-290 in the Galactic Center (GC) region using new data from the H.E.S.S. array of Cherenkov telescopes is presented. Flaring activity and quasi periodic oscillations (QPO) of HESS J1745-290 are investigated.
Methods. The image analysis is performed with a combination of a semi-analytical shower model and the statistical moment-based Hillas technique. The spectrum and lightcurves of HESS J1745-290 are derived with a likelihood method based on a spectral shape hypothesis. Rayleigh tests and Fourier analysis of the H.E.S.S. GC signal are used to study the periodicity of the source.
Results. With a three-fold increase in statistics compared to previous work, a deviation from a simple power law spectrum is detected for the first time. The measured energy spectrum over the three years 2004, 2005 and 2006 of data taking is compatible with both a power law spectrum with an exponential cut-off and a broken power law spectrum. The curvature of the energy spectrum is likely to be intrinsic to the photon source, as opposed to effects of interstellar absorption. The power law spectrum with an exponential cut-off is characterized by a photon index of 2.10 ![]() 0.04
0.04
![]()
![]() 0.10
0.10
![]() and a cut-off energy at 15.7
and a cut-off energy at 15.7 ![]() 3.4
3.4
![]()
![]() 2.5
2.5
![]() TeV. The broken power law spectrum exhibits spectral indices of 2.02
TeV. The broken power law spectrum exhibits spectral indices of 2.02 ![]() 0.08
0.08
![]()
![]() 0.10
0.10
![]() and 2.63
and 2.63 ![]() 0.14
0.14
![]()
![]() 0.10
0.10
![]() with a break energy at 2.57
with a break energy at 2.57 ![]() 0.19
0.19
![]()
![]() 0.44
0.44
![]() TeV. No significant flux variation is found. Increases in the
TeV. No significant flux variation is found. Increases in the ![]() -ray flux of HESS J1745-290 by at least a factor of two would be required for a 3
-ray flux of HESS J1745-290 by at least a factor of two would be required for a 3![]() detection of a flare with time scales of an hour. Investigation of possible QPO activity at periods claimed to be detected in X-rays does not show any periodicities in the H.E.S.S. signal.
detection of a flare with time scales of an hour. Investigation of possible QPO activity at periods claimed to be detected in X-rays does not show any periodicities in the H.E.S.S. signal.
Key words: Galaxy: center - gamma rays: observations - methods: data analysis
1 Introduction
The discovery of very high energy (VHE) ![]() -rays from the Galactic Center (GC) has been reported by CANGAROO (Tsuchiya et al 2004), VERITAS (Kosack et al. 2004), H.E.S.S. (HESS J1745-290, Aharonian et al. 2004b) and MAGIC (Albert et al. 2006). Possible associations of the source with the Sgr A East supernova remnant (Crocker et al. 2005) and more recently with the newly detected plerion G359.95-0.04 (Wang et al. 2006) have been widely discussed in the literature. However, with the reduced systematic pointing error obtained using H.E.S.S. data up to 2006 (van Eldik et al. 2007), Sgr A East is now ruled out as being associated with the VHE emission of HESS J1745-290. The interpretation of the GC TeV signal as annihilation products of dark matter (DM) particles has been discussed in Aharonian et al. (2006c). It is unlikely that the bulk of the signal comes from DM annihilations. One possibility is that the supermassive black hole Sgr A* located at the center of the Milky Way is responsible for the VHE emission of the detected HESS J1745-290 source. In this case, a cut-off in the high energy part of the spectrum might be expected (Ballantyne et al. 2007; Aharonian & Neronov 2005a). Time variability as seen in X-rays and IR might also appear, along with flares, and QPO frequencies such as those found in Aschenbach et al. (2004). QPO periods of
-rays from the Galactic Center (GC) has been reported by CANGAROO (Tsuchiya et al 2004), VERITAS (Kosack et al. 2004), H.E.S.S. (HESS J1745-290, Aharonian et al. 2004b) and MAGIC (Albert et al. 2006). Possible associations of the source with the Sgr A East supernova remnant (Crocker et al. 2005) and more recently with the newly detected plerion G359.95-0.04 (Wang et al. 2006) have been widely discussed in the literature. However, with the reduced systematic pointing error obtained using H.E.S.S. data up to 2006 (van Eldik et al. 2007), Sgr A East is now ruled out as being associated with the VHE emission of HESS J1745-290. The interpretation of the GC TeV signal as annihilation products of dark matter (DM) particles has been discussed in Aharonian et al. (2006c). It is unlikely that the bulk of the signal comes from DM annihilations. One possibility is that the supermassive black hole Sgr A* located at the center of the Milky Way is responsible for the VHE emission of the detected HESS J1745-290 source. In this case, a cut-off in the high energy part of the spectrum might be expected (Ballantyne et al. 2007; Aharonian & Neronov 2005a). Time variability as seen in X-rays and IR might also appear, along with flares, and QPO frequencies such as those found in Aschenbach et al. (2004). QPO periods of ![]() 100 s, 219 s, 700 s, 1150 s and 2250 s have been observed simultaneously in two different datasets collected with the Chandra (Baganoff et al. 2002) and the XMM-Newton (Porquet et al. 2003) observatories in 2000 and 2002, respectively. The power density spectra of the 2003 infrared flare also shows three distinct peaks at
100 s, 219 s, 700 s, 1150 s and 2250 s have been observed simultaneously in two different datasets collected with the Chandra (Baganoff et al. 2002) and the XMM-Newton (Porquet et al. 2003) observatories in 2000 and 2002, respectively. The power density spectra of the 2003 infrared flare also shows three distinct peaks at ![]() 214 s, 733 s and 1026 s (Genzel et al. 2003), fully consistent with three of the five X-ray detected periods. Recently however, the validity of the detection of these periods has been disputed by infrared observations on the Keck II telescope (see Meyer et al. 2008, for references).
214 s, 733 s and 1026 s (Genzel et al. 2003), fully consistent with three of the five X-ray detected periods. Recently however, the validity of the detection of these periods has been disputed by infrared observations on the Keck II telescope (see Meyer et al. 2008, for references).
The search for a curvature in the TeV energy spectrum and time variability in the TeV signal is strongly motivated by GC wideband emission models and multi-wavelength data, respectively. In this paper, updated results on the energy spectrum and variability of HESS J1745-290 are presented, based on a dataset collected in 2004, 2005 and 2006. Preliminary results on the source position and morphology were published in van Eldik et al. (2007).
2 H.E.S.S. observations and analysis
2.1 The H.E.S.S. instrument
The H.E.S.S. (High Energy Stereoscopic System) instrument (Hofmann et al. 2003) consists of four Imaging Atmospheric Cherenkov Telescopes (IACTs) located in the Khomas Highland of Namibia at an altitude of 1800 m above sea level. H.E.S.S. is dedicated to very high energy ![]() -ray astronomy (defined as
-ray astronomy (defined as
![]() GeV), beyond the energy range accessible to satellite-based detectors. The IACTs have a large mirror area of 107 m2, reflecting the Cherenkov light emitted by
GeV), beyond the energy range accessible to satellite-based detectors. The IACTs have a large mirror area of 107 m2, reflecting the Cherenkov light emitted by ![]() -induced air showers onto a camera of 960 photomultiplier tubes (PMTs). Each PMT covers a field of view of 0.16
-induced air showers onto a camera of 960 photomultiplier tubes (PMTs). Each PMT covers a field of view of 0.16![]() .
The total field of view of the camera is 5
.
The total field of view of the camera is 5![]() in diameter. The telescopes are positioned at the corners of a square, of side 120 m, which allows for an accurate reconstruction of the direction and energy of the
in diameter. The telescopes are positioned at the corners of a square, of side 120 m, which allows for an accurate reconstruction of the direction and energy of the ![]() -rays using the stereoscopic technique. The energy threshold of H.E.S.S. is approximately 100 GeV at zenith. More details on the H.E.S.S. instrument can be found in Aharonian et al. (2006d).
-rays using the stereoscopic technique. The energy threshold of H.E.S.S. is approximately 100 GeV at zenith. More details on the H.E.S.S. instrument can be found in Aharonian et al. (2006d).
2.2 Dataset and analysis
Table 1: Details of the observation of the GC region with H.E.S.S. for the 2004, 2005 and 2006 observation campaigns.
The previously published H.E.S.S. observations on the GC (Aharonian et al. 2006c) was on a 48.7 h (live time) data sample collected in 2004. In this paper new results on the spectral analysis of the GC are derived, using data from subsequent observation campaigns carried out in 2005 and 2006, with zenith angles ranging up to 70![]() .
The runs taken at high zenith angles are sensitive to higher
.
The runs taken at high zenith angles are sensitive to higher ![]() -ray energies and allow us to probe the high energy part of the HESS J1745-290 spectrum. The datasets are described in Table 1.
Most of the data were taken in ``wobble mode'' where the telescope pointing is typically shifted by
-ray energies and allow us to probe the high energy part of the HESS J1745-290 spectrum. The datasets are described in Table 1.
Most of the data were taken in ``wobble mode'' where the telescope pointing is typically shifted by ![]() 0.7
0.7![]() from the nominal target position. The dataset used for the analysis was selected using the standard quality criteria, excluding runs taken under bad and variable weather conditions, which would lead to large systematic errors. An additional quality selection was applied using the cosmic ray rate during data collection. Runs with rates deviating by more than 3
from the nominal target position. The dataset used for the analysis was selected using the standard quality criteria, excluding runs taken under bad and variable weather conditions, which would lead to large systematic errors. An additional quality selection was applied using the cosmic ray rate during data collection. Runs with rates deviating by more than 3![]() from the cosmic ray rate averaged over the three years of observation were removed in the subsequent analysis. After the run selection procedure, the dataset amounts to 93 h of live time.
from the cosmic ray rate averaged over the three years of observation were removed in the subsequent analysis. After the run selection procedure, the dataset amounts to 93 h of live time.
Two independent techniques are commonly used to select ![]() -ray events and derive energy spectra and lightcurves. The first technique computes the ``Hillas geometrical moments'' of the shower image (Aharonian et al. 2005) and the second one is based on a semi-analytical model of showers, which predicts the expected intensity in each pixel of the camera (de Naurois et al. 2003). The shower direction, the impact point and the primary particle energy are then derived with a likelihood fit of the model to match the data. Both analysis techniques provide an energy resolution of 15-20
-ray events and derive energy spectra and lightcurves. The first technique computes the ``Hillas geometrical moments'' of the shower image (Aharonian et al. 2005) and the second one is based on a semi-analytical model of showers, which predicts the expected intensity in each pixel of the camera (de Naurois et al. 2003). The shower direction, the impact point and the primary particle energy are then derived with a likelihood fit of the model to match the data. Both analysis techniques provide an energy resolution of 15-20![]() with an angular resolution better than 0.1
with an angular resolution better than 0.1![]() above the analysis energy threshold. Results described in this paper are obtained with a combination of these two analysis techniques, the so-called combined Hillas/Model analysis (de Naurois et al. 2003), which yields an improved background rejection, and were cross-checked against either technique alone. The background is calculated at each position in the field of view using the acceptance corrected background rate from an annulus around that position (the OFF-source region). More details on this so-called ring background method are given in Berge et al. (2004). The OFF-source regions do not overlap with known TeV sources in the GC field of view (Aharonian et al. 2006b) and areas of diffuse emission (Aharonian et al. 2006a).
above the analysis energy threshold. Results described in this paper are obtained with a combination of these two analysis techniques, the so-called combined Hillas/Model analysis (de Naurois et al. 2003), which yields an improved background rejection, and were cross-checked against either technique alone. The background is calculated at each position in the field of view using the acceptance corrected background rate from an annulus around that position (the OFF-source region). More details on this so-called ring background method are given in Berge et al. (2004). The OFF-source regions do not overlap with known TeV sources in the GC field of view (Aharonian et al. 2006b) and areas of diffuse emission (Aharonian et al. 2006a).
The analysis of the whole 2004-2006 dataset shows an excess above the background of 4185 ![]() -events in a 0.11
-events in a 0.11![]() radius region centered on the GC (Table 1). The total significance, calculated according to the method of Li and Ma (1983), is 60.7
radius region centered on the GC (Table 1). The total significance, calculated according to the method of Li and Ma (1983), is 60.7![]() .
Diffuse
.
Diffuse ![]() -ray emission along the galactic plane is visible as shown by the distribution in
-ray emission along the galactic plane is visible as shown by the distribution in ![]() ,
,
![]() being the angle of a reconstructed
being the angle of a reconstructed ![]() -ray relative to Sgr A* (Fig. 1, excess above the background level outside the ON source region). A discussion in Aharonian et al. (2006a) gives a possible interpretation of the emission as cosmic ray interactions in the central molecular zone (CMZ). A point-source + linear background fit to the
-ray relative to Sgr A* (Fig. 1, excess above the background level outside the ON source region). A discussion in Aharonian et al. (2006a) gives a possible interpretation of the emission as cosmic ray interactions in the central molecular zone (CMZ). A point-source + linear background fit to the ![]() distribution has been performed to estimate the diffuse emission contribution to the signal. Extrapolating the linear component inside the ON-source region gives a diffuse emission contribution of 13
distribution has been performed to estimate the diffuse emission contribution to the signal. Extrapolating the linear component inside the ON-source region gives a diffuse emission contribution of 13![]()
![]() 1
1![]() within 0.11
within 0.11![]() .
Diffuse
.
Diffuse ![]() -ray emission located in the ON-source region was not subtracted in the following analysis, since its spectral feature (a simple power law with the same spectral index as the central source) would not influence the result (Aharonian et al. 2006a). Any deviation from a power law spectrum or variability in the lightcurve would be solely due to the point source.
-ray emission located in the ON-source region was not subtracted in the following analysis, since its spectral feature (a simple power law with the same spectral index as the central source) would not influence the result (Aharonian et al. 2006a). Any deviation from a power law spectrum or variability in the lightcurve would be solely due to the point source.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11569fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg23.png) |
Figure 1:
Distribution of the number of |
| Open with DEXTER | |
3 Energy spectrum of HESS J1745-290
3.1 Spectral reconstruction
The energy spectrum of HESS J1745-290 has been derived following the forward folding method. The forward folding method is based on a spectral shape hypothesis for the source spectrum (Piron et al. 2001; Djannati-Atai et al. 1999). Spectral points are then calculated using the adjusted spectral shape and the 1![]() error bars are computed using the error matrix of the fit procedure. Relative systematic errors on the reconstructed spectral indices coming from the presence of broken pixels in the camera are less than 5
error bars are computed using the error matrix of the fit procedure. Relative systematic errors on the reconstructed spectral indices coming from the presence of broken pixels in the camera are less than 5![]() ,
whereas those coming from variations of the atmospheric conditions are negligible. Thus, systematic errors on the spectral indices derived in the following analysis are taken to be 5
,
whereas those coming from variations of the atmospheric conditions are negligible. Thus, systematic errors on the spectral indices derived in the following analysis are taken to be 5![]() .
Systematic errors on the integrated fluxes mainly come from the variations of the atmospheric conditions and the absolute calibration of the response of the telescopes. They amount to 10 to 20
.
Systematic errors on the integrated fluxes mainly come from the variations of the atmospheric conditions and the absolute calibration of the response of the telescopes. They amount to 10 to 20![]() (Aharonian et al. 2006d). The systematic errors on the integrated fluxes above 1 TeV are taken to be 20
(Aharonian et al. 2006d). The systematic errors on the integrated fluxes above 1 TeV are taken to be 20![]() .
A Monte-Carlo study of the reconstruction of the cut-off energy revealed a systematic bias linearly increasing with the cut-off energy:
.
A Monte-Carlo study of the reconstruction of the cut-off energy revealed a systematic bias linearly increasing with the cut-off energy:
| (1) |
The systematic errors on the reconstruction of the cut-off energy amount to 17
3.2 Results
The data taken in 2004, 2005 and 2006 were compared to the folding of three distributions with the detector response: a power law (Eq. (2)), a power law with a high energy exponential cut-off (Eq. (3)) and a smoothed broken power law (Eq. (4)):
where
The measured spectrum for the whole three-year dataset ranges from 160 GeV, the energy threshold of the analysis, to 70 TeV (Fig. 2). For the first time, with additional statistics, a deviation from a pure power law starts to be visible. The spectrum is well described by either Eq. (3) (equivalent ![]() of 23/26 d.o.f.) or Eq. (4) (equivalent
of 23/26 d.o.f.) or Eq. (4) (equivalent ![]() of 20/19 d.o.f.). Figure 2 shows the HESS J1745-290 spectra with fits to Eq. (3) and Eq. (4). The power law with an exponential cut-off fit yields
of 20/19 d.o.f.). Figure 2 shows the HESS J1745-290 spectra with fits to Eq. (3) and Eq. (4). The power law with an exponential cut-off fit yields
![]() TeV-1 cm-2 s-1,
TeV-1 cm-2 s-1,
![]() ,
a cut-off energy
,
a cut-off energy
![]() TeV and an integrated flux above 1 TeV of (
TeV and an integrated flux above 1 TeV of (
![]() )
)
![]() 10-12 cm-2 s-1. The broken power law fit yields
10-12 cm-2 s-1. The broken power law fit yields
![]() TeV-1 cm-2 s-1,
TeV-1 cm-2 s-1,
![]() ,
,
![]() ,
a break energy
,
a break energy
![]() TeV and an integrated flux above 1 TeV of (
TeV and an integrated flux above 1 TeV of (
![]() )
)
![]() 10-12cm-2 s-1. The values of the cut-off energy
10-12cm-2 s-1. The values of the cut-off energy
![]() and break energy
and break energy
![]() are those corrected for the systematic bias mentioned in the previous section. By comparison, a power law spectrum gives a worse equivalent
are those corrected for the systematic bias mentioned in the previous section. By comparison, a power law spectrum gives a worse equivalent ![]() of 64/27 d.o.f. and yields a flux normalisation of (
of 64/27 d.o.f. and yields a flux normalisation of (
![]() )
)
![]() 10-12 TeV-1 cm-2 s-1, a spectral index of
10-12 TeV-1 cm-2 s-1, a spectral index of
![]() with an integrated flux above 1 TeV of (
with an integrated flux above 1 TeV of (
![]() )
)
![]() 10-12cm-2 s-1. The effect of introducing a high cut-off energy in the power law spectrum does not change the integrated flux by more than 10
10-12cm-2 s-1. The effect of introducing a high cut-off energy in the power law spectrum does not change the integrated flux by more than 10![]() ,
less than systematic errors. Integrated fluxes found either with a power law with an exponential cut-off shape or a smoothed broken power law one are consistent with the values given in the previously published H.E.S.S. analysis (Aharonian et al. 2006c). The spectral parameters for the two curved spectral shapes, for year-wise data, are given in the next two subsections.
,
less than systematic errors. Integrated fluxes found either with a power law with an exponential cut-off shape or a smoothed broken power law one are consistent with the values given in the previously published H.E.S.S. analysis (Aharonian et al. 2006c). The spectral parameters for the two curved spectral shapes, for year-wise data, are given in the next two subsections.
![\begin{figure}
\par\includegraphics[height=10cm,clip]{11569fg2a.eps}\hspace*{3mm}
\includegraphics[height=10cm,clip]{11569fg2b.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg47.png) |
Figure 2:
HESS J1745-290 spectra derived with the combined Hillas/Model analysis for the whole H.E.S.S. GC dataset covering the three years 2004, 2005 and 2006. The shaded areas are the 1 |
| Open with DEXTER | |
Table 2:
Spectral parameters values with their respective statistical errors for a power law shape with an exponential cut-off, with ![]() .
The fits are performed in the [160 GeV-70 TeV] energy range.
.
The fits are performed in the [160 GeV-70 TeV] energy range.
Table 3: Spectral parameters values with their respective statistical errors for a smoothed broken power law shape. The fits are performed in the [160 GeV-70 TeV] energy range.
3.2.1 Power law with an exponential cut-off
Spectral parameters for the different years (differential flux normalisation ![]() ,
spectral index
,
spectral index ![]() ,
cut-off energy and integrated flux above 1 TeV, I(
,
cut-off energy and integrated flux above 1 TeV, I(![]() 1 TeV)) are summarized in Table 2. The cut-off energy corrected for the systematic bias mentioned in Sect. 3.1 is also shown. The energy ranges of the 2004 and 2006 spectra do not allow the determination of a significant cut-off. The 2004 and 2006 datasets contain fewer runs collected at high zenith angles than the 2005 one. High zenith angle observations provide an increased effective area at high energies and contribute to the high energy part of the spectrum. The 2005 spectral index value is smaller than the values for 2004 and 2006, because of the correlation between the reconstructed spectral index
1 TeV)) are summarized in Table 2. The cut-off energy corrected for the systematic bias mentioned in Sect. 3.1 is also shown. The energy ranges of the 2004 and 2006 spectra do not allow the determination of a significant cut-off. The 2004 and 2006 datasets contain fewer runs collected at high zenith angles than the 2005 one. High zenith angle observations provide an increased effective area at high energies and contribute to the high energy part of the spectrum. The 2005 spectral index value is smaller than the values for 2004 and 2006, because of the correlation between the reconstructed spectral index ![]() and the cut-off energy induced by the fit procedure. Figure 3 shows a 2-D plot of the fitted photon index
and the cut-off energy induced by the fit procedure. Figure 3 shows a 2-D plot of the fitted photon index ![]() against the cut-off energy for each year's dataset. It can be seen that the spectral parameter values are compatible. Moreover, when fixing the cut-off energy to the uncorrected cut-off energy of 14.7 TeV (see Table 2), the spectral fits give
against the cut-off energy for each year's dataset. It can be seen that the spectral parameter values are compatible. Moreover, when fixing the cut-off energy to the uncorrected cut-off energy of 14.7 TeV (see Table 2), the spectral fits give
![]() ,
,
![]() and
and
![]() for the 2004, 2005 and 2006 datasets, respectively. Spectral indices are thus compatible with each other.
The spectral shape given by Eq. (3) with
for the 2004, 2005 and 2006 datasets, respectively. Spectral indices are thus compatible with each other.
The spectral shape given by Eq. (3) with ![]() = 0.5 is motivated by some shock acceleration scenarios (see discussion in Sect. 5.). A fit over the whole three years with
= 0.5 is motivated by some shock acceleration scenarios (see discussion in Sect. 5.). A fit over the whole three years with ![]() = 0.5 has been performed. It gives a reasonable
= 0.5 has been performed. It gives a reasonable ![]() /d.o.f. of 30/23,
/d.o.f. of 30/23,
![]() TeV-1 cm-2 s-1,
TeV-1 cm-2 s-1,
![]() ,
a low value for the cut-off energy (corrected from the systematic bias) of
,
a low value for the cut-off energy (corrected from the systematic bias) of
![]() )
TeV and an integrated flux above 1 TeV of (1.98
)
TeV and an integrated flux above 1 TeV of (1.98 ![]() 0.04
0.04
![]()
![]() 0.40
0.40
![]() )
)
![]() 10-12cm-2 s-1.
10-12cm-2 s-1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11569fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg65.png) |
Figure 3:
Contours of constant likelihood of the power law with an exponential cut-off fit, as a function of the spectral index |
| Open with DEXTER | |
3.2.2 Smoothed broken power law
Spectral parameters (differential flux normalisation ![]() ,
spectral indices
,
spectral indices ![]() and
and ![]() ,
break energy and integrated flux above 1 TeV, I(
,
break energy and integrated flux above 1 TeV, I(![]() 1 TeV)) are summarized in Table 3. The break energy corrected for the systematic bias mentioned in Sect 3.1 is also given. Parameters show a large dispersion (at most at the 3
1 TeV)) are summarized in Table 3. The break energy corrected for the systematic bias mentioned in Sect 3.1 is also given. Parameters show a large dispersion (at most at the 3![]() level) but remain compatible with each other. The larger value of
level) but remain compatible with each other. The larger value of ![]() for the 2005 data may reflect a possible steepening of the spectrum in the very high energy part.
for the 2005 data may reflect a possible steepening of the spectrum in the very high energy part.
3.2.3 Spectral variability
A refined study of the variations of the spectral index with time over the whole three years has been carried out using time intervals of roughly 5 h, comprising ten consecutive runs. Each data subset has been fitted independently with a power law shape. The spectral index light curve has 25 points. A fit to a constant gives a ![]() of 29/24 d.o.f. confirming that the spectral index did not change significantly over the three years.
of 29/24 d.o.f. confirming that the spectral index did not change significantly over the three years.
3.3 Correction for absorption of very high energy 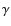 -rays
-rays
A recent calculation of the Galactic interstellar radiation field (Porter & Strong 2006) has shown that the infra-red radiation field near the GC is considerably enhanced compared to what was previously thought. Thus, some attenuation of very high energy ![]() -rays might occur at TeV energies. The attenuation coefficient accounting for very high energy
-rays might occur at TeV energies. The attenuation coefficient accounting for very high energy ![]() -ray absorption by e+e- pair production on the interstellar radiation field (ISRF) toward the GC was derived in Zhang et al. (2006) and can be used to correct the measured spectrum:
-ray absorption by e+e- pair production on the interstellar radiation field (ISRF) toward the GC was derived in Zhang et al. (2006) and can be used to correct the measured spectrum:
| (5) |
where F(E) represents the observed spectrum after attenuation, F0(E) the intrinsic spectrum and
Typically, 1![]() and 10
and 10![]() of
of ![]() -rays are absorbed at 10 TeV and 50 TeV, respectively, with an increase of the attenuation factor at higher energies. As expected, the spectral parameters do not change significantly after applying the correction. Thus, the curvature of the spectrum does not seem to be caused by
-rays are absorbed at 10 TeV and 50 TeV, respectively, with an increase of the attenuation factor at higher energies. As expected, the spectral parameters do not change significantly after applying the correction. Thus, the curvature of the spectrum does not seem to be caused by ![]() -ray absorption and the cut-off (Eq. (3)) or the spectral break (Eq. (4)) is intrinsic to the source spectrum.
-ray absorption and the cut-off (Eq. (3)) or the spectral break (Eq. (4)) is intrinsic to the source spectrum.
![\begin{figure}
\par\includegraphics[height=5.4cm,clip]{11569fg4a.eps}\vspace*{3....
...}\vspace*{3.5mm}
\includegraphics[height=5.4cm,clip]{11569fg4d.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg70.png) |
Figure 4: Run by run light curves of HESS J1745-290. From top to bottom: (1) Data covering the whole 2004-2006 time period. (2), (3) and (4) represent data covering the 2004, 2005 and 2006 time periods, respectively. The dotted lines show the fit to a constant integrated flux of the 2004-2006 lightcurve. |
| Open with DEXTER | |
4 Search for time variability
As mentioned in the introduction, flaring of Sgr A* and QPOs were detected in various bands such as X-rays and IR. In this section, the ``run by run'' and ``night by night'' light curves are used to search for any variablility in the GC source activity.
The run by run light curves are obtained by dividing the data into 28 min intervals and by computing the integrated fluxes above 1 TeV for each of these time intervals. The integrated flux is computed from the results of a power law fit with exponential cut-off whose normalization was varied in the likelihood minimization while the spectral index and cut-off energy were fixed to the values obtained for the 2004-2006 dataset. The flux normalisation is adjusted for each 28 min time slice. The integrated fluxes above a fixed energy of 1 TeV are then calculated. The night by night light curves are derived in the same way as for the 28 min light curves except that the time intervals comprise runs that were recorded in the same night.
4.1 Light curves and flare sensitivity
The run by run integrated flux light curves of the GC covering the 2004, 2005 and 2006 observation seasons are displayed in Fig. 4. The fit of a constant to the data taken over the whole three years gives a ![]() of 233/216 d.o.f. and does not reveal any variability on time scales longer than 28 min.
of 233/216 d.o.f. and does not reveal any variability on time scales longer than 28 min.
Because of the large error bars of the light curve points implied by the low statistics, the H.E.S.S. signal is only sensitive to relatively large amplitude flares. The flare sensitivity was estimated by adding an artificial Gaussian with variable duration ![]() ,
a time of maximum amplification t0 and an amplification at maximum A to the H.E.S.S. light curve (LC):
,
a time of maximum amplification t0 and an amplification at maximum A to the H.E.S.S. light curve (LC):
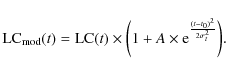 |
(6) |
When varying the time of maximum amplification t0 along the LC, a distribution of the A values compatible with a flare detection at a given significance is obtained. A fit to this distribution by a Landau function gives the most probable value of A and its corresponding 1
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11569fg5.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg73.png) |
Figure 5:
Maximum amplification factor A for a 3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11569fg6.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg74.png) |
Figure 6: Rayleigh power plotted as a function of the frequency. Rayleigh power is normalized such that a pure noise spectrum results in unit power. The dotted line shows the fit to a constant of the Rayleigh spectrum. The arrows denote the 100 s, 219 s, 700 s and 1150 s periods observed in X-rays. |
| Open with DEXTER | |
4.2 Search for QPOs
Four oscillation frequencies ranging from 100 s to 2250 s have been observed in the X-ray light curve of Sgr A* (Aschenbach et al. 2004). These frequencies, if confirmed, are likely to correspond to gravitational cyclic modes associated with the accretion disk of Sgr A*. The occurence of these frequencies was searched for in the data. First, the coherence time of the disk precession is assumed to be less than 28 min. A Rayleigh test (de Jager et al. 1989) is then performed on photon arrival time distributions for continuous observations of 28 min. Each 28 min observation gives a Rayleigh power spectrum. The Rayleigh power averaged over 2004-2006 data is shown in Fig. 6 as a function of the frequency. Error bars are estimated by calculating the variance of the Rayleigh power distribution plotted at the corresponding frequency. The probed frequencies range from 1/28 min-1 to the inverse of the average time spacing between two consecutive events of 1.2 min-1. No Rayleigh power is significantly higher than expected for noise at any probed frequencies. No significant peaks are seen at the 100 s, 219 s, 700 s and 1150 s periods observed in X-rays.
In a second analysis, the coherence time of oscillations is assumed to be of the order of a few hours. The Fourier power distribution using Lomb-Scargle periodograms (Scargle 1982) for each night of the dataset is then constructed. Data are binned into 5 min intervals. The Fourier power averaged over the 2004-2006 data is displayed in Fig. 7 as a function of the frequency. Frequencies tested range from 10-2 min-1 to 0.1 min-1. No significant oscillation frequencies are detected.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11569fg7a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{fig7b.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg75.png) |
Figure 7:
Top panel: [10-2 min-1-0.1 min-1] Lomb-Scargle periodogram of the H.E.S.S. Sgr A* light curve averaged over the 2004-2006 nights of observation. Bottom panel: Fourier power distribution derived from the averaged Lomb-Scargle periodogram. No significant peak is visible from the Lomb-Scargle periodogram and the |
| Open with DEXTER | |
5 Discussion and conclusions
A strong signal has been detected from the GC region with the H.E.S.S. instrument. An energy spectrum has been measured with a differential spectrum well described either by a power law with slope
![]() with an exponential cut-off at
with an exponential cut-off at
![]() TeV, or a smoothed broken power law with photon indices
TeV, or a smoothed broken power law with photon indices
![]() ,
,
![]() and a break energy at
and a break energy at
![]() TeV. An integrated flux above 1 TeV of (
TeV. An integrated flux above 1 TeV of (
![]() )
)
![]() 10-12 cm-2 s-1 is derived using the power law spectrum with an exponential cut-off fit. No indication for variability, flaring or QPOs has been found in the H.E.S.S. data, suggesting a non-variable emission of the GC region in the VHE regime.
10-12 cm-2 s-1 is derived using the power law spectrum with an exponential cut-off fit. No indication for variability, flaring or QPOs has been found in the H.E.S.S. data, suggesting a non-variable emission of the GC region in the VHE regime.
Different mechanisms have been suggested to explain the broadband spectrum of the GC (Fig. 8). Firstly, the stochastic acceleration of electrons interacting with the turbulent magnetic field in the vicinity of Sgr A*, as discussed by Liu et al. (2006), has been advocated to explain the millimeter and sub-millimeter emission. This model would also reproduce the IR and X-ray flaring (Atoyan & Dermer 2004). In addition, it assumes that charged particles are accreted onto the black hole, and predicts the escape of protons from the accretion disk and their acceleration (Liu et al. 2006). These protons produce ![]() mesons by inelastic collisions with the interstellar medium in the central star cluster of the Galaxy.
mesons by inelastic collisions with the interstellar medium in the central star cluster of the Galaxy.
The cut-off energy found in the ![]() -ray spectrum could reflect a cut-off
-ray spectrum could reflect a cut-off
![]() in the primary proton spectrum. In that case, one would expect a cut-off in the
in the primary proton spectrum. In that case, one would expect a cut-off in the ![]() -ray spectral shape at
-ray spectral shape at
![]() /30. The measured value given in Sect. 3.2.1., with the parameter
/30. The measured value given in Sect. 3.2.1., with the parameter ![]() equal to 0.5, would correspond in this scenario to a low cut-off energy in the primary proton spectrum of roughly 100 TeV. It would correspond to a larger value of
equal to 0.5, would correspond in this scenario to a low cut-off energy in the primary proton spectrum of roughly 100 TeV. It would correspond to a larger value of
![]() of
of ![]() 400 TeV if
400 TeV if ![]() .
.
Energy-dependent diffusion models of protons to the outside of the central few parsecs of the Milky Way (Aharonian & Neronov 2005b) are alternative plausible mechanisms to explain the TeV emission observed with the H.E.S.S. instrument. They would lead to a spectral break as in the measured spectrum due to competition between injection and escape of protons outside the vicinity of the GC. A similar mechanism would explain the diffuse emission detected by H.E.S.S. along the galactic plane (Aharonian et al. 2006a).
The recent discovery of the G359.95-0.04 pulsar wind nebulae (PWN) located at 8'' from Sgr A* also provides interesting models as discussed by Wang et al. (2006) and Hinton & Aharonian (2007) to explain the steepening of the measured spectrum of HESS J1745-290. Inverse Compton emission due to a population of electrons whose energies extend up to 100 TeV might be responsible for at least a fraction of the TeV emission. The PWN model of Wang et al. and Hinton and Aharonian would imply a constant flux with time since the time scale for global PWN changes is typically much longer than a few years (more like centuries to millennia).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11569fg8.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg82.png) |
Figure 8: A composite spectral energy distribution of the GC source. The radio data are from Zylka et al. (1995) and Falcke et al. (1998). The IR data are from Hornstein et al. (2002) and Ghez et al. (2004). Chandra data points come from Baganoff et al. (2002, 2003), IGR J1745-2901 ones from Belanger et al. (2006). The HESS J1745-290 spectral points are shown by filled triangles. |
| Open with DEXTER | |
The absence of variability in the TeV data suggests that the emission mechanisms and emission regions differ from those invoked for the variable IR and X-ray emission. Moreover, the above-mentioned models can both accomodate a cut-off in the ![]() -ray energy spectrum and predict the absence of variability in the TeV emission. They are thus viable scenarios to explain the strong TeV signal detected by H.E.S.S. in the GC region.
-ray energy spectrum and predict the absence of variability in the TeV emission. They are thus viable scenarios to explain the strong TeV signal detected by H.E.S.S. in the GC region.
Acknowledgements
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Particle Physics and Astronomy Research Council (PPARC), the IPNP of the Charles University, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment.
References
- Aharonian, F., & Neronov, A. 2005a, ApJ, 619, 306 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F., & Neronov, A. 2005b, Ap&SS, 300, 255 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F., Fortin, X., Garaude, F., Meyer, C., Philippe, F. et al. 2004a, Astropart.Phys., 22, 109 [NASA ADS] [CrossRef]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2004b, A&A, 425, L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005, A&A430, 865 (In the text)
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, Nature, 439, 695 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, ApJ, 636, 777 [NASA ADS] [CrossRef] (In the text)
- Aharonian F., et al. 2006c, , 97, 221102 (In the text)
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al., 2006d, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, A&A, 492, L25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Albert, J., Aliu, E., Anderhub, H., et al. 2006, ApJ, 638, L101 [NASA ADS] [CrossRef] (In the text)
- Aschenbach, B., Grosso, N., Porquet, D., Predehl, P. et al. 2004, A&A, 417, 71 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Atoyan, A., & Dermer, C. 2004, ApJ, 617, L123 [NASA ADS] [CrossRef] (In the text)
- Baganoff, F., Bautz, M., Brandt, W., et al. 2001, Nature, 413, 45 [NASA ADS] [CrossRef] (In the text)
- Baganoff, F., Maeda, Y., Morris, M., et al. 2003, ApJ, 591, 891 [NASA ADS] [CrossRef] (In the text)
- Ballantyne, D., Melia, F., Liu, S., & Crocker, R. 2007, ApJ, 657, L13 [NASA ADS] [CrossRef] (In the text)
- Belanger, G., Goldwurm, A., Renaud, M., et al. 2006, ApJ, 636, L275 [NASA ADS] [CrossRef] (In the text)
- Berge, D., Funk, S., & Hinton, J. 2004, A&A, 466, 1219 [NASA ADS] [CrossRef] (In the text)
- Crocker, R., M., Fatuzzo, M., Jokipii, J. R., et al. 2005, ApJ, 622, 892 [NASA ADS] [CrossRef] (In the text)
- de Jager, O., Swanepoel, J., & Raubenheimer, B. 1989, A&A, 221, 180 [NASA ADS] (In the text)
- de Naurois, M., et al. 2003, Proc. of 28th ICRC (Tsubaka), 5, 2907 (In the text)
- Djannati-Atai, A., Piron, F., Barrau, A., et al. 1999, A&A, 350, 17 [NASA ADS] (In the text)
- Falcke, H., Goss, W. M., Matsuo, H., et al. 1998, ApJ, 499, 731 [NASA ADS] [CrossRef] (In the text)
- Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 934 [NASA ADS] [CrossRef] (In the text)
- Ghez, A., Wright, S. A., Matthews, K., et al. 2004, ApJ, 601, L159 [NASA ADS] [CrossRef] (In the text)
- Hinton, J., & Aharonian, F. 2007, ApJ, 657, 302 [NASA ADS] [CrossRef] (In the text)
- Hofmann, W., et al. 2003, Proc. of the 28th ICRC (Tsubuka), 1, 2811 (In the text)
- Hornstein, S., Ghez, A. M., Tanner, A., et al. 2002, ApJ, 577, L9 [NASA ADS] [CrossRef] (In the text)
- Kosack, K., Badran, H. M., Bond, I. H., et al. 2004, ApJ, 608, L97 [NASA ADS] [CrossRef] (In the text)
- Li, T., & Ma, Y. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] (In the text)
- Liu, S., Melia, F., Petrosian, V., & Fatuzzo, M. 2006, ApJ, 647, 1099 [NASA ADS] [CrossRef] (In the text)
- Meyer, L., Do, T., Ghez, A., & Morris, M. 2008, ApJ, 688, L17 [NASA ADS] [CrossRef] (In the text)
- Porquet, D., Predehl, P., Aschenbach, B., et al. 2003, A&A, 407, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Porter, T., & Strong, A. 2006, A&A, 449, 641 [CrossRef] [EDP Sciences] (In the text)
- Piron, F., Djannati-Atai, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Scargle, J. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] (In the text)
- Tsuchiya, K., Enomoto, R., Ksenofontov, L. T., et al. 2004, ApJ, 606, L115 [NASA ADS] [CrossRef] (In the text)
- van Eldik, C., Bolz, O., Braun, I., et al. 2007, Proc. of the 30th ICRC (Merida) (In the text)
- Wang, Q., Lu, F., & Gotthelf, E. 2006, MNRAS, 367, 937 [NASA ADS] [CrossRef] (In the text)
- Zhang, J.-L, Bi, X.-J., Hu, H.-B. et al. 2006, A&A, 449, 641 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Zylka, R., Mezger, P. G., Ward-Thompson, D., et al. 1995, A&A, 297, 83 [NASA ADS] (In the text)
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Supported by CAPES Foundation, Ministry of Education of Brazil.
All Tables
Table 1: Details of the observation of the GC region with H.E.S.S. for the 2004, 2005 and 2006 observation campaigns.
Table 2:
Spectral parameters values with their respective statistical errors for a power law shape with an exponential cut-off, with ![]() .
The fits are performed in the [160 GeV-70 TeV] energy range.
.
The fits are performed in the [160 GeV-70 TeV] energy range.
Table 3: Spectral parameters values with their respective statistical errors for a smoothed broken power law shape. The fits are performed in the [160 GeV-70 TeV] energy range.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11569fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg23.png) |
Figure 1:
Distribution of the number of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=10cm,clip]{11569fg2a.eps}\hspace*{3mm}
\includegraphics[height=10cm,clip]{11569fg2b.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg47.png) |
Figure 2:
HESS J1745-290 spectra derived with the combined Hillas/Model analysis for the whole H.E.S.S. GC dataset covering the three years 2004, 2005 and 2006. The shaded areas are the 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11569fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg65.png) |
Figure 3:
Contours of constant likelihood of the power law with an exponential cut-off fit, as a function of the spectral index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=5.4cm,clip]{11569fg4a.eps}\vspace*{3....
...}\vspace*{3.5mm}
\includegraphics[height=5.4cm,clip]{11569fg4d.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg70.png) |
Figure 4: Run by run light curves of HESS J1745-290. From top to bottom: (1) Data covering the whole 2004-2006 time period. (2), (3) and (4) represent data covering the 2004, 2005 and 2006 time periods, respectively. The dotted lines show the fit to a constant integrated flux of the 2004-2006 lightcurve. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11569fg5.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg73.png) |
Figure 5:
Maximum amplification factor A for a 3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11569fg6.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg74.png) |
Figure 6: Rayleigh power plotted as a function of the frequency. Rayleigh power is normalized such that a pure noise spectrum results in unit power. The dotted line shows the fit to a constant of the Rayleigh spectrum. The arrows denote the 100 s, 219 s, 700 s and 1150 s periods observed in X-rays. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11569fg7a.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{fig7b.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg75.png) |
Figure 7:
Top panel: [10-2 min-1-0.1 min-1] Lomb-Scargle periodogram of the H.E.S.S. Sgr A* light curve averaged over the 2004-2006 nights of observation. Bottom panel: Fourier power distribution derived from the averaged Lomb-Scargle periodogram. No significant peak is visible from the Lomb-Scargle periodogram and the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11569fg8.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11569-08/Timg82.png) |
Figure 8: A composite spectral energy distribution of the GC source. The radio data are from Zylka et al. (1995) and Falcke et al. (1998). The IR data are from Hornstein et al. (2002) and Ghez et al. (2004). Chandra data points come from Baganoff et al. (2002, 2003), IGR J1745-2901 ones from Belanger et al. (2006). The HESS J1745-290 spectral points are shown by filled triangles. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.