| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | 663 - 671 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200811483 | |
| Published online | 02 July 2009 | |
Radiative transfer in cylindrical threads with incident radiation
VI. A hydrogen plus helium system
P. Gouttebroze1 - N. Labrosse2
1 - Institut d'Astrophysique Spatiale, Univ. Paris XI/CNRS,
Bât. 121, 91405 Orsay cedex, France
2 -
Department of Physics and Astronomy,
University of Glasgow, Glasgow G12 8QQ, Scotland
Received 8 December 2008 / Accepted 19 May 2009
Abstract
Context. Spectral lines of helium are commonly observed on the Sun. These observations contain important information about physical conditions and He/H abundance variations within solar outer structures.
Aims. The modeling of chromospheric and coronal loop-like structures visible in hydrogen and helium lines requires the use of appropriate diagnostic tools based on NLTE radiative tranfer in cylindrical geometry.
Methods. We use iterative numerical methods to solve the equations of NLTE radiative transfer and statistical equilibrium of atomic level populations. These equations are solved alternatively for hydrogen and helium atoms, using cylindrical coordinates and prescribed solar incident radiation. Electron density is determined by the ionization equilibria of both atoms. Two-dimensional effects are included.
Results. The mechanisms of formation of the principal helium lines are analyzed and the sources of emission inside the cylinder are located. The variations of spectral line intensities with temperature, pressure, and helium abundance, are studied.
Conclusions. The simultaneous computation of hydrogen and helium lines, performed by the new numerical code, allows the construction of loop models including an extended range of temperatures.
Key words: methods: numerical - radiative transfer - line: formation - line: profiles - Sun: chromosphere - Sun: corona
1 Introduction
Observation of the upper solar atmosphere with high angular resolution reveals a wealth of filamentary structures produced by magnetic fields. To model these objects, we developed a series of NLTE radiative transfer codes that are described in the present series of papers. Among the filamentary objects relevant to this kind of modeling, we can mention: cool coronal loops, chromospheric fine structure (cf. Patsourakos et al. 2007), prominence (or filament) threads (cf. Heinzel 2007), and spicules. Paper I (Gouttebroze 2004) dealt with 1D (i.e. radius dependent) cylindrical models, a case applicable to cylindrical structures with a vertical axis exposed to an incident radiation field independent of azimuth. Papers II and III (Gouttebroze 2005, 2006, respectively) treated the case of 2D (radius and azimuth dependent) cylinders. Paper II was restricted to a 2-level atom, while Paper III used a multilevel hydrogen atom. Papers IV and V (Gouttebroze 2007, 2008) were dedicated to radiative equilibrium and velocity fields, respectively. All these papers dealt with the hydrogen atom. A certain amount of helium was included in the state equation, but it was assumed to be neutral and without any influence on the radiation field, as well as on the electron density.In the present paper, we assume that the cylinders are filled with a mixture of hydrogen and helium, and treat NLTE radiative transfer and statistical equilibrium of level populations for both atoms in two dimensions. The helium model atom includes the three stages of ionization, and the electron density is recomputed at each iteration in order to satisfy the equation of electric neutrality. In Sect. 2, we describe the computational methods used in the new numerical code. The results concerning hydrogen and helium ionization are detailed in Sect. 3. In Sect. 4, we study the formation of helium lines using a reference model defined in Sect. 2. Finally, in Sect. 5, we show how the helium line intensities react to changes in temperature, pressure and helium abundance.
2 Numerical methods
2.1 Formulation
The computation includes the numerical solution of the equations of NLTE radiative transfer for hydrogen and helium atoms, statistical equilibrium of level populations (for both atoms), pressure equilibrium, and electric neutrality. As in Papers II and III, the object under consideration is a cylinder of diameter D, whose axis makes an angle| (1) |
where
| (2) |
and
| (3) |
The gas pressure is
| (4) |
where k is the Boltzmann constant and T the temperature. The parameter to check the convergence of iterations is the electron-to-hydrogen ratio
| (5) |
The model atom for hydrogen includes 5 discrete levels plus 1 continuum. The equations of radiative transfer for the 10 discrete transitions and the 5 bound-free transitions are treated in detail, except in the case where the optical thicknesses are very low, which generally happens for continua from subordinate levels. The model atom for helium is the same as in Labrosse & Gouttebroze (2001, 2004). It contains 34 levels: 29 for He I, 4 for He II, and 1 for He III. The main part of this model comes from the neutral helium model of Benjamin et al. (1999). It is complemented with parameters of various origins, as described in Labrosse and Gouttebroze (2001). The number of permitted radiative transitions is 76, but most of them are optically thin under the usual conditions. All discrete transitions, for hydrogen as for helium, are treated under the assumption of complete frequency redistribution.
Table 1: Summary of cylindrical thread models.
2.2 Computational scheme
The computation is organized along two parallel series of routines,
one for hydrogen, the other for helium.
In each series of routines,
the variables dependent on the atomic structures as atomic parameters,
populations, intensities in different transitions are gathered into
a specific Fortran ``common'', which is ignored by the main program.
This main program only contains geometric (D, r, ![]() ,
etc.) and
physical (
,
etc.) and
physical (![]() ,
T, vT, etc.) variables and the populations
(
,
T, vT, etc.) variables and the populations
(
![]() ,
,
![]() ,
etc.) necessary to determine the
ionization. The main phases of computations are:
,
etc.) necessary to determine the
ionization. The main phases of computations are:
- initialization: determination of geometrical, physical and atomic parameters. The incident intensities are also computed for each position at the surface of the cylinder and each direction, according to the method explained in Paper II;
-
first evaluation of level populations, in the optically thin
approximation. By averaging the incident intensities, we obtain mean
intensities in the different transitions of hydrogen and helium.
From these intensities and physical parameters, we compute the
radiative and collisional transition rates. Then, we solve
statistical equilibrium equations to obtain atomic level populations
at each point of the (
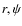 )
mesh. Since the transition rates depend
on electron density, it is necessary to iterate.
We start from an arbitrary value of
)
mesh. Since the transition rates depend
on electron density, it is necessary to iterate.
We start from an arbitrary value of 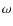 (e.g.
(e.g.
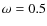 )
and,
using Eqs. (3) and (5), successively deduce:
)
and,
using Eqs. (3) and (5), successively deduce:
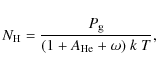
(6)
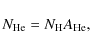
(7)
and
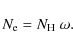
(8)
After computation of transition rates and solution of statistical equilibrium equations, we compute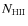 ,
,
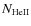 ,
and
,
and
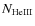 by adding the populations of individual levels
together, and deduce a new value of
by adding the populations of individual levels
together, and deduce a new value of 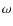 by
by
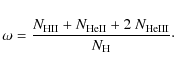
(9)
These operations are repeated until convergence. -
full iterations with radiative transfer.
This is the main part of the computation.
The external scheme is similar to that of the preceding step,
with a variable
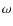 controlling
the convergence of iterations but, in the meantime, the internal
intensities for all transitions of hydrogen and helium are recomputed
according to the principles of NLTE radiative transfer: absorption
coefficients are derived from atomic level populations (determined
in the preceding iteration). Then, intensities are computed by
solving the transfer equation along each ray and integrating with
respect to direction and frequency. At the same time, the diagonal
terms of the
controlling
the convergence of iterations but, in the meantime, the internal
intensities for all transitions of hydrogen and helium are recomputed
according to the principles of NLTE radiative transfer: absorption
coefficients are derived from atomic level populations (determined
in the preceding iteration). Then, intensities are computed by
solving the transfer equation along each ray and integrating with
respect to direction and frequency. At the same time, the diagonal
terms of the 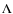 operator are calculated by the method of
Rybicki & Hummer (1991).
The formulae appropriate to the cylindrical geometry are given in
Paper II. The new intensities and the diagonal
operator are calculated by the method of
Rybicki & Hummer (1991).
The formulae appropriate to the cylindrical geometry are given in
Paper II. The new intensities and the diagonal 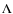 coefficients
are used to form preconditioned statistical equilibrium equations,
similar to those of Werner & Husfeld (1985).
These equations are solved to obtain new level populations.
Generally, one radiative transfer iteration for hydrogen and one
for helium, between two iterations on
coefficients
are used to form preconditioned statistical equilibrium equations,
similar to those of Werner & Husfeld (1985).
These equations are solved to obtain new level populations.
Generally, one radiative transfer iteration for hydrogen and one
for helium, between two iterations on 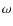 ,
are sufficient to obtain
a good convergence. In a few cases, it was necessary to perform
two radiative transfer iterations for one
,
are sufficient to obtain
a good convergence. In a few cases, it was necessary to perform
two radiative transfer iterations for one 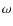 iteration.
These cases are indicated by an asterisk in the last column of Table 1.
iteration.
These cases are indicated by an asterisk in the last column of Table 1.
2.3 Models
The model cylinders are defined by a series of geometric and physical parameters. The geometrical ones, diameter D, altitude Hand inclination3 Ionization
The introduction of helium ionization in models allows the electron density to be greater than the hydrogen density. Let| (10) |
The ionization ratios
3.1 Model with temperature gradient
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg38.png) |
Figure 1:
Variations of temperature T and population ratios
with the distance to the axis (r),
for the model ``p4'' at the foot of the loop ( |
| Open with DEXTER | |
3.2 Isothermal models
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg40.png) |
Figure 2:
Variations of the ionization ratios |
| Open with DEXTER | |
4 Formation of helium lines
The computations described in Sect. 2 provide us with absorption coefficients and source functions in the different lines of hydrogen and helium, which may be subsequently used to calculate the intensities emerging from the cylinder. The introduction of helium ionization has little influence on hydrogen lines, which are formed in regions where helium is essentially neutral. Since hydrogen lines have been treated in preceding papers, we concentrate here on helium lines, and use the standard model ``p4'' to study their formation. ![\begin{figure}
\par\includegraphics[width=17cm]{11483fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg49.png) |
Figure 3: Emission of the loop model ``p4'' in several lines of helium: He I 10 830 Å ( top, left); He I 584 Å ( top, right); He I 5876 Å ( bottom, left); He II 304 Å ( bottom, right). Frequency-integrated intensities are normalized to the maximum value of each image. Horizontal and vertical coordinates indicate distances in megameters. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg51.png) |
Figure 4: Ray path through the cylinder. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg5.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg52.png) |
Figure 5: Total emergent intensities computed from model ``p4'', for different helium lines vs. position across the cylinder. Abscissae are in megameters and grow as the distance from the Sun. Ordinates are intensities in erg cm-2 s-1 sr-1. Dashed line: He I 10 830 Å; dotted line: He I 5876 Å; dot-dashed line: He I 584 Å; continuous line: He II 304 Å. |
| Open with DEXTER | |
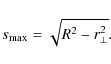 |
(11) |
Let
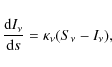 |
(12) |
and the boundary condition
| (13) |
we deduce the emergent intensity
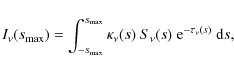 |
(14) |
with the optical thickness between the running point M (abscissa s) and B
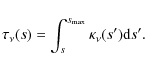 |
(15) |
The total emergent intensity for the line under consideration is then
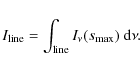 |
(16) |
These frequency-integrated intensities have been computed as functions of r and
To locate the origin of emission inside the cylinder, we rewrite
Eq. (14) as
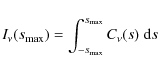 |
(17) |
with
| (18) |
Thus, Eq. (16) becomes
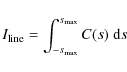 |
(19) |
with
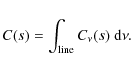 |
(20) |
C(s) is the contribution function appropriate for the frequency-integrated emergent intensity. This function is plotted as shades of gray in Fig. 6 for the three lines at 10 830, 584 and 304 Å. The figure for the 5876 Å line is very similar to that of the 10 830 Å line. The existence of three maxima of emission for the intensity at 10 830 Å is due to the existence of two zones in the contribution function: a central patch and a ring. The patch corresponds to radiative processes of emission by low temperature matter, while the ring corresponds to a range of temperature where the maximum excitation of He I is occuring. The radiative processes of emission that occur in the central patch include direct scattering of incident radiation and the photoionization-recombination process (Hirayama 1971; Zirin 1975). Since these two processes are dependent on incident radiation, the contribution functions in the central zone decrease with height. In contrast, the ring is produced by collisional excitation, so that it is practically independent of
![\begin{figure}
\par\includegraphics[width=6.7cm]{11483fg6.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg69.png) |
Figure 6: Contribution functions corresponding to the standard model with a horizontal axis, for three lines of helium. Top: He I 10 830 Å; Middle: He I 584 Å; Bottom: He II 304 Å. Bright zones correspond to the maximum of the function. Directions are the same as in Fig. 4 (observer at right, Sun below). |
| Open with DEXTER | |
5 Influence of physical parameters
5.1 Temperature
![\begin{figure}
\par\includegraphics[width=8.5cm]{11483fg7.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg70.png) |
Figure 7: Frequency-integrated intensities, averaged over position, emitted by isothermal models ``t1'' to ``t11''. Intensities (erg cm-2 s-1 sr-1) are plotted as functions of the temperature (K) of the model, in 4 transitions: He I 10 830 Å (open circles); He I 584 Å (full circles); He I 5876 Å (open squares); He II 304 Å (full squares). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{11483fg8.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg72.png) |
Figure 8: Helium line half-profiles emitted by five isothermal models: continuous line: ``t1'' (6000 K); dashed line: ``t4'' (15 000 K); dotted line: ``t6'' (30 000 K); dot-dashed line: ``t8'' (50 000 K); long-dashed line: ``t11'' (100 000 K). Each frame corresponds to a specific line, as indicated. |
| Open with DEXTER | |
5.2 Pressure
The effects of gas pressure on emitted intensities are studied by means of a series of models ``p1'' to ``p7''. These models have the same variation of temperature as the standard model, but differ from each other by pressures ranging from 0.02 to 0.5 dyn cm-2. Frequency-integrated intensities for the principal helium lines emitted by these models are displayed in Fig. 9. It appears that all intensities increase with pressure, but the slopes of the curves differ from one line to another. For neutral helium lines, the variation may be understood by considering the two main processes of emission: scattering of incident radiation and collisional excitation. In the optically thin case, the first process yields intensities proportional to atom populations. The second emission process, collisional excitation, which is proportional not only to the emitting atom density, but also to the electron density, tends to produce a quadratic variation of emission as a function of pressure. These considerations apply to the two He I lines at 10 830 and 5876 Å. It is visible in Fig. 9 that the emitted intensities for these two lines are proportional to pressure from 0.02 to about 0.2 dyn cm-2, and that the slope slightly increases at higher pressures, when collisions cease to be negligible. The same considerations apply to the 584 Å line, but the change of slope begins at lower pressures, around 0.1 dyn cm-2. The case of the He II 304 Å line is more complicated, since the slope of I(P) is less than linear below 0.1 dyn cm-2 and greater than linear at higher pressures. It is visible on profiles (Fig. 8) that this line is optically thick and formed in the outermost part of the cylinder (Fig. 6). Whatever the pressure, the incident ultraviolet radiation from the Sun ionizes helium near the surface of the cylinder and creates a zone which scatters the 304 Å radiation. This part of emission due to scattering is nearly constant and constitutes the main contribution at low pressures (0.02 to 0.05 dyn cm-2). In contrast, at high pressures (0.2 to 0.5 dyn cm-2), collisional excitation becomes dominant and results in a quasi-quadratic variation of I(P).
![\begin{figure}
\par\includegraphics[width=8.8cm]{11483fg9.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg75.png) |
Figure 9: Frequency-integrated intensities, averaged over position, emitted by models ``p1'' to ``p7''. Abscissae: gas pressure inside the cylinder (dyn cm-2). Ordinates: intensities in erg cm-2 s-1 sr-1. Spectral lines: He I 10 830 Å (open circles); He I 584 Å (full circles); He I 5876 Å (open squares); He II 304 Å (full squares). |
| Open with DEXTER | |
5.3 Helium abundance
The abundance of helium is one of the most important parameters when
analysing helium lines (see for instance Andretta et al. 2008,
and references therein).
Some observations, like that of filaments by Gilbert
et al. (2007) suggest that very important changes of helium
abundance may occur between the top, and the base of these objects.
To evaluate the importance of this parameter to the emission
of cylinder threads, we use a series of models (``a1'' to ``a7''), with
the same pressure and temperature variation as the standard model,
but helium to hydrogen ratios
![]() varying from 0.01 to 0.3.
The variations of intensities as functions of
varying from 0.01 to 0.3.
The variations of intensities as functions of
![]() are
displayed in Fig. 10.
The interpretation of these curves is relatively easy.
As long as the cylinder is optically thin in the considered transition,
the intensity is proportional to
are
displayed in Fig. 10.
The interpretation of these curves is relatively easy.
As long as the cylinder is optically thin in the considered transition,
the intensity is proportional to
![]() .
This is the case for the 10 830 and 5876 lines until
.
This is the case for the 10 830 and 5876 lines until
![]() .
For higher abundances, the slopes of the curves slightly decrease as
the line centers begin to saturate.
For optically thick lines at 584 and 304 Å, the intensity is still
a growing function of abundance, but the slope is significantly lower
than that corresponding to proportionality.
.
For higher abundances, the slopes of the curves slightly decrease as
the line centers begin to saturate.
For optically thick lines at 584 and 304 Å, the intensity is still
a growing function of abundance, but the slope is significantly lower
than that corresponding to proportionality.
![\begin{figure}
\par\includegraphics[width=9cm]{11483f10.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg77.png) |
Figure 10:
Frequency-integrated intensities, averaged over position,
emitted by models ``a1'' to ``a7''.
Abscissae: log (abundance ratio
|
| Open with DEXTER | |
6 Conclusion
At this stage of our project, it is possible to perform a modeling of solar coronal loops including the following ingredients:- NLTE radiative transfer in cylindrical geometry;
- 2 dimensions (radius and azimuth);
- statistical equilibrium of atomic level populations;
- self-consistent treatment of the two principal chemical elements: hydrogen and helium, including ionization;
- pressure equilibrium.
Acknowledgements
We wish to thank Petr Heinzel for useful suggestions concerning this manuscript.
References
- Andretta, V., & Jones, H. P. 1997, ApJ, 489, 375 [NASA ADS] [CrossRef] (In the text)
- Andretta, V., Mauas, P. J. D., Falchi, A., & Teriaca, L. 2008, ApJ, 681, 650 [NASA ADS] [CrossRef] (In the text)
- Benjamin, R. A., Skillman, E. D., & Smits, D. P. 1999, ApJ, 514, 307 [NASA ADS] [CrossRef] (In the text)
- Gilbert, H. R., Kilper, G., & Alexander, D. 2007, ApJ, 671, 978 [NASA ADS] [CrossRef] (In the text)
- Gouttebroze, P. 2004, A&A, 413, 733 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
- Gouttebroze, P. 2005, A&A, 434, 1165 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II) (In the text)
- Gouttebroze, P. 2006, A&A, 448, 367 [NASA ADS] [CrossRef] [EDP Sciences] (Paper III) (In the text)
- Gouttebroze, P. 2007, A&A, 465, 1041 [NASA ADS] [CrossRef] [EDP Sciences] (Paper IV) (In the text)
- Gouttebroze, P. 2008, A&A, 487, 805 [NASA ADS] [CrossRef] [EDP Sciences] (Paper V) (In the text)
- Heinzel, P. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten, ASP Conf. Ser., 368, 271 (In the text)
- Hirayama, T. 1971, Sol. Phys., 17, 50 [NASA ADS] [CrossRef] (In the text)
- Labrosse, N., & Gouttebroze, P. 2001, A&A, 380, 323 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Labrosse, N., & Gouttebroze, P. 2004, ApJ, 617, 614 [NASA ADS] [CrossRef] (In the text)
- Laming, J. M., & Feldman, U. 1993, ApJ, 403, 434 [NASA ADS] [CrossRef] (In the text)
- Patsourakos, S., Gouttebroze, P., & Vourlidas, A. 2007, ApJ, 664, 1214 [NASA ADS] [CrossRef] (In the text)
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] (In the text)
- Werner, K., & Husfeld, D. 1985, A&A, 148, 417 [NASA ADS] (In the text)
- Zirin, H. 1975, ApJ, 199, L63 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Summary of cylindrical thread models.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg38.png) |
Figure 1:
Variations of temperature T and population ratios
with the distance to the axis (r),
for the model ``p4'' at the foot of the loop ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg40.png) |
Figure 2:
Variations of the ionization ratios |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{11483fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg49.png) |
Figure 3: Emission of the loop model ``p4'' in several lines of helium: He I 10 830 Å ( top, left); He I 584 Å ( top, right); He I 5876 Å ( bottom, left); He II 304 Å ( bottom, right). Frequency-integrated intensities are normalized to the maximum value of each image. Horizontal and vertical coordinates indicate distances in megameters. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg51.png) |
Figure 4: Ray path through the cylinder. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11483fg5.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg52.png) |
Figure 5: Total emergent intensities computed from model ``p4'', for different helium lines vs. position across the cylinder. Abscissae are in megameters and grow as the distance from the Sun. Ordinates are intensities in erg cm-2 s-1 sr-1. Dashed line: He I 10 830 Å; dotted line: He I 5876 Å; dot-dashed line: He I 584 Å; continuous line: He II 304 Å. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.7cm]{11483fg6.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg69.png) |
Figure 6: Contribution functions corresponding to the standard model with a horizontal axis, for three lines of helium. Top: He I 10 830 Å; Middle: He I 584 Å; Bottom: He II 304 Å. Bright zones correspond to the maximum of the function. Directions are the same as in Fig. 4 (observer at right, Sun below). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{11483fg7.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg70.png) |
Figure 7: Frequency-integrated intensities, averaged over position, emitted by isothermal models ``t1'' to ``t11''. Intensities (erg cm-2 s-1 sr-1) are plotted as functions of the temperature (K) of the model, in 4 transitions: He I 10 830 Å (open circles); He I 584 Å (full circles); He I 5876 Å (open squares); He II 304 Å (full squares). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{11483fg8.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg72.png) |
Figure 8: Helium line half-profiles emitted by five isothermal models: continuous line: ``t1'' (6000 K); dashed line: ``t4'' (15 000 K); dotted line: ``t6'' (30 000 K); dot-dashed line: ``t8'' (50 000 K); long-dashed line: ``t11'' (100 000 K). Each frame corresponds to a specific line, as indicated. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{11483fg9.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg75.png) |
Figure 9: Frequency-integrated intensities, averaged over position, emitted by models ``p1'' to ``p7''. Abscissae: gas pressure inside the cylinder (dyn cm-2). Ordinates: intensities in erg cm-2 s-1 sr-1. Spectral lines: He I 10 830 Å (open circles); He I 584 Å (full circles); He I 5876 Å (open squares); He II 304 Å (full squares). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{11483f10.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa11483-08/Timg77.png) |
Figure 10:
Frequency-integrated intensities, averaged over position,
emitted by models ``a1'' to ``a7''.
Abscissae: log (abundance ratio
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


