Chemical evolution of high-redshift radio galaxies

K. Matsuoka; T. Nagao; R. Maiolino; A. Marconi; Y. Taniguchi

doi:10.1051/0004-6361/200811478

Free Access

Issue		A&A Volume 503, Number 3, September I 2009


Page(s)		721 - 730
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/200811478
Published online		15 June 2009

Chemical evolution of high-redshift radio galaxies

K. Matsuoka¹ - T. Nagao^1,2 - R. Maiolino³ - A. Marconi⁴ - Y. Taniguchi²

1 - Graduate School of Science and Engineering, Ehime University, 2-5 Bunkyo-cho, Matsuyama 790-8577, Japan
2 - Research Center for Space and Cosmic Evolution, Ehime University, 2-5 Bunkyo-cho, Matsuyama 790-8577, Japan
3 - INAF - Osservatorio Astrofisico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
4 - Dipartimento di Astronomia e Scienza dello Spazio, Universita degli Studi di Firenze, Largo E. Fermi 2, 50125 Firenze, Italy

Received 5 December 2008 / Accepted 23 April 2009

Abstract
We present new deep optical spectra of 9 high-z radio galaxies (HzRGs) at z > 2.7 obtained with FORS2 on VLT. These rest-frame ultraviolet spectra are used to infer the metallicity of the narrow-line regions (NLRs) in order to investigate the chemical evolution of galaxies in the high-z universe. We focus mainly on the C IV/He II and C III]/C IV flux ratios that are sensitive to both the gas metallicity and ionization parameter. Although the N V emission has been widely used to infer the gas metallicity, it is often too weak to be measured accurately for NLRs. In combining our new spectra with data from the literature, we examine the possible redshift evolution of the NLR metallicity for 57 HzRGs at $1 \la z \la 4$ . Based on the comparison between the observed emission-line flux ratios and the results of our photoionization model calculations, we find no significant metallicity evolution in NLRs of HzRGs, up to $z \sim 4$ . Our results imply that massive galaxies had almost completed their chemical evolution at much higher redshift (z > 5). Finally, although we detect strong N V emission lines in 5 HzRGs at z > 2.7, we point out that high N V/He II ratios are not indicative of high metallicities but correspond to high ionization parameters of gas clouds in NLRs.

Key words: galaxies: active - galaxies: evolution - galaxies: nuclei - quasars: emission lines - quasars: general

1 Introduction

Chemical evolution of galaxies is one of the most important aspects in understanding the formation and evolution of galaxies, since it is closely related to the past star formation history of galaxies. The most straightforward way to investigate the chemical evolution of galaxies is by measuring the metallicity of galaxies at various redshifts and exploring the systematic trends in the metallicity as a function of redshift (see Maiolino et al. 2008 and references therein). The gas-phase metallicity of star-forming galaxies in the local universe can be measured rather easily by analyzing optical emission-line spectra (e.g., [O II] $\lambda$ 3727, H $\beta$ , [O III] $\lambda$ 5007, H $\alpha$ , [N II] $\lambda$ 6584; see Nagao et al. 2006b and references therein). However, this is difficult at z > 1, since these emission lines are generally very faint and shifted into near-infrared wavelengths where sensitive spectroscopic observations are more difficult than in the optical.

An alternative approach is to focus on active galactic nuclei (AGNs) instead of star-forming galaxies. AGNs generally show various emission lines in rest-frame ultraviolet to infrared wavelengths, that arise in gas clouds photoionized by the radiation from their central engines. Here we focus on the rest-frame ultraviolet lines (e.g., N V $\lambda$ 1240, C IV $\lambda$ 1549, He II $\lambda$ 1640, C III] $\lambda$ 1909), since we can easily measure the emission-line fluxes of high-z AGNs by means of optical spectroscopic observations. These UV emission lines in AGN spectra are generally brighter than optical emission lines in star-forming galaxies at similar redshifts.

Table 1: Journal of observations.

The metallicity of AGNs has been studied extensively, especially by focusing on the broad-line regions (BLRs). It has been reported that the BLR metallicity ( $Z_{\rm BLR}$ ) is typically higher than the solar value (e.g., Hamann & Ferland 1992; Dietrich et al. 2003; Nagao et al. 2006c), reaching as much as $Z_{\rm BLR} \sim 15~Z_{\rm\odot}$ in extreme cases (Baldwin et al. 2003b; Bentz et al. 2004). However, it is unclear how the gas metallicity inferred from the broad lines is related to the chemical properties of the host galaxies, since broad lines of AGNs sample only very small regions in galactic nuclei ( $R_{\rm BLR} < 1~{\rm pc}$ ; e.g., Suganuma et al. 2006), which may have evolved more rapidly than their host galaxies. For this reason, we focus on narrow-line regions (NLRs), instead of BLRs.

In contrast to BLRs, the size of NLRs is comparable to the size of their host galaxies ( $R_{\rm NLR} \sim 10^{2-4}~{\rm pc}$ ; e.g., Bennert et al. 2006b). The mass of the NLR is about $M_{\rm NLR} \sim 10^{5-7}~M_{\odot}$ , which is much higher than that of the BLR ( $M_{{\rm BLR}} \sim 10^2{-}10^4$ $M_{\odot}$ ; see, e.g., Baldwin et al. 2003a) and the velocity dispersion of the NLR emission lines is a reliable tracer of the kinematics of their host galaxies (e.g., Greene & Ho 2005; Bennert et al. 2006b). The NLR is therefore a good tracer of chemical properties on galactic scales.

To study NLR metallicities, it is necessary to focus on type-2 AGNs, where BLR and strong continuum emission are obscured and do not affect the accuracy of narrow-line emission measurements. However, very few optically-selected high-z type-2 QSOs have been discovered. We focus on NLRs of high-z radio galaxies (HzRGs), since several of them have been identified even at high-z.

Some studies of the NLR metallicity of HzRGs have already been completed. By studying the emission-line flux ratios of N V $\lambda$ 1240/C IV $\lambda$ 1549 and N V $\lambda$ 1240/He II $\lambda$ 1640, generally used to measure the metallicity of BLRs in AGNs, De Breuck et al. (2000) found that the typical metallicity of HzRGs is roughly $0.4~Z_{\rm\odot} < Z_{\rm NLR} < 3.0~Z_{\rm\odot}$ . They also reported a possible metallicity evolution in their sample: radio galaxies at z > 3 have lower metallicity than those at z < 3. However, the emission-line flux of N V in narrow-line radio galaxies is generally too faint, especially for metal-poor gas. Therefore, only upper-limits to N V are available for the majority of the radio galaxies investigated by De Breuck et al. (2000). Iwamuro et al. (2003) measured lower metallicities in the NLRs in HzRGs at 2.0 < z < 2.6 than De Breuck et al. (2000), based on their analysis of rest-frame optical emission lines from their sensitive near-infrared observations. In contrast, Humphrey et al. (2008) reported that there is no significant difference in NLR metallicities between their sample of HzRGs at $z \sim 2.5$ and the lower-z radio galaxies investigated by Robinson et al. (1987). To explain these apparent contradictions, it is mandatory to carry out further spectroscopic observations of HzRGs.

Nagao et al. (2006a) proposed a new metallicity diagnostic diagram that consists of the C IV $\lambda$ 1549, He II $\lambda$ 1640, and C III] $\lambda$ 1909 emission lines, all of which are moderately strong in the rest-frame ultraviolet spectra of HzRGs, even at low metallicities. They studied the metallicity of NLRs of HzRGs and reported that the observational data do not show any evidence of significant evolution in the gas metallicity of NLRs within the redshift range 1.2 < z < 3.8, and they instead found a clear trend for more luminous AGNs to have more metal-rich gas clouds. We note, however, that their sample included only 5 objects at z > 2.7 (or only 2 objects at z > 3.0). Thus, observing more HzRGs is crucial to assessing the possible metallicity evolution.

In this paper, we present new spectroscopic observations of 9 HzRGs at 2.7 < z <3.5. By combining the new data with the Nagao et al. (2006a) database, we discuss the chemical evolution and the metallicity-luminosity relation of HzRGs in the $z \sim 1{-}4$ redshift range. We adopt a concordance cosmology with $(\Omega_{\rm M}, \Omega_{\rm\Lambda}) = (0.3, 0.7)$ and $H_{\rm0} = 70~{\rm km}~{\rm s}^{-1}~{\rm Mpc}^{-1}$ .

2 Observations

We observed 9 HzRGs at z > 2.7 with FORS2 (FOcal Reducer and low dispersion Spectrograph 2) at the VLT (Very Large Telescope). These targets were selected from the catalog of De Breuck et al. (2000), excluding HzRGs whose C IV, He II and C III] had already been measured. All the observations were executed in service mode. The list of target objects and an observation log is given in Table 1.

Observations were performed with the 300 V dispersion element and the G435 order-sorting filter to cover the $4450~\AA < \lambda_{\rm obs} < 8700~\AA$ range, which, at the redshift of our targets, corresponds to the rest-frame ultraviolet and thus includes the UV emission lines needed for abundance determination. We adopted an on-chip binning mode of $2 \times 2$ with a spectral dispersion of $\approx$ 3.2 Å $\ {\rm pixel}^{-1}$ and a spatial scale along the slit of $\approx$ 0 $.\!\!^{\prime\prime}$ 25 $\ {\rm pixel}^{-1}$ . The slit width was 1 $.\!\!^{\prime\prime}$ 0, narrower than the typical seeing ( $FWHM \sim 1\hbox{$.\!\!^{\prime\prime}$ }4$ ). The individual exposure times were 900 s, and the total integration time for each target is given in Table 1.

Standard data reduction procedures were performed using available IRAF tasks. A bias signal was subtracted by using an averaged bias image, and flat-fielding was performed using dome-flat images. Cosmic-ray events were then removed. The wavelength calibration was completed by using sky lines. After sky subtraction, we extracted spectra using apertures of 2 $.\!\!^{\prime\prime}$ 25 along the slit. The spectra were then flux-calibrated by using the following spectrophotometric standard stars. We note that the weather conditions were good for most of our observations. Examination of the ESO sky monitor database indicates that most (>90%) of our exposures were taken under photometric conditions. Small variations in the absolute calibration because of the varying seeing and transparency are unimportant given that we bin our data into three broad luminosity bins.

$\begin{figure} \par\includegraphics[width=7.5cm]{figure1a.ps}\includegraphics[wi... ...h=7.5cm]{figure1i.ps}\includegraphics[width=7.5cm]{figure1j.ps}\\\end{figure}$	Figure 1: Spectra for 9 objects observed with FORS2 and the composite spectrum of the HzRGs ( lower right), improving by binning by 2 in wavelength direction. Each spectrum is shown on two different flux scales, the first to show strong emission lines and the second to show continuum emission and weak emission lines.
Open with DEXTER

Table 2: Emission-line measurements.

3 Observational results

The final reduced spectra of the observed HzRGs are shown in Fig. 1. In all spectra, continuum emission is very faint; typically $S/N \sim 3$ and ranging $1 \la {S/N} \la 10$ at $\lambda_{\rm rest} \sim 1700$ Å. However the equivalent widths of emission lines are very high and their S/N is accordingly very large. The composite spectrum of HzRGs, which is shown in the lower right panel of Fig. 1, was obtained by stacking the 9 spectra of HzRGs, after converting all spectra to their rest frame, normalizing their He II flux, and performing a 3 sigma-clipping rejection.

Fluxes of observed emission lines are given in Table 2, where the measurements were performed by fitting a Gaussian profile with the IRAF task splot. The flux error was estimated based on the rms of the pixels around each emission line. The detected emission lines were well resolved spectrally and instrumental broadening was negligible in most cases. Observed emission-line widths without correction for instrumental broadening are also presented in Table 2. For each HzRG, we also provide the redshift calculated from the C IV line. For the composite spectrum, the flux ratios of C IV/He II, C III]/C IV, and N V/C IV are 1.618, 0.628, and 0.584, respectively.

All the emission lines of C IV, He II and C III] (required for the metallicity diagnostic method proposed by Nagao et al. 2006a) are detected in the spectra of all 9 HzRGs observed. In addition, a significant N V emission is also detected in 5 out of 9 objects. We provide a 3 $\sigma$ upper limit to the N V emission for objects without significant detection, by assuming an emission-line width of $\sim$ 10 $\AA$ in the rest frame. As shown in Fig. 1, various fainter emission lines are also detected including Si II $\lambda$ 1265, O I+Si II $\lambda$ 1305, C II $\lambda$ 1335, O IV] $\lambda$ 1402, O III] $\lambda$ 1663, Si II $\lambda$ 1808, and [Ne IV] $\lambda2422$ . We will discuss the properties of these faint emission lines in a forthcoming paper (Matsuoka et al. in prep.).

4 Photoionization model

To infer the metallicity from the observed emission-line spectra, we carried out model calculations by using the photoionization code Cloudy version 07.02 (Ferland et al. 1998). We assumed that the clouds in the NLR of HzRGs are mainly photoionized and not significantly affected by shocks. Although Nagao et al. (2006a) demonstrated that this assumption is appropriate when focusing on C IV, He II and C III], we examine how this assumption is valid in Sect. 5.1. The input parameters for the calculations were: (1) the spectral energy distribution (SED) of the photoionizing continuum radiation; (2) the hydrogen density of a cloud ( $n_{\rm H}$ ); (3) the ionization parameter (U), i.e., the ratio of the ionizing photon density to the hydrogen density at the irradiated surface of a cloud; (4) the column density of a cloud ( $N_{\rm H}$ ); and (5) the elemental composition of the gas.

$\begin{figure} \par\includegraphics[width=7.6cm]{figure2.ps} \end{figure}$

Figure 2:

Predicted emission-line luminosity normalized by the number of H-ionizing photons, as functions of the NLR metallicity. The results for N V, C IV, He II, and C III] are shown, from top to bottom. Red and green lines denote the models with hydrogen density of $n_{\rm H} = 10^2~{\rm cm}^{-3}$ and $10^4~{\rm cm}^{-3}$ , respectively. Solid and dashed lines denote the models with ionization parameter of U = 10^-1.6 and 10^-2.0, respectively.

Open with DEXTER

For the SED of the ionizing photons, we used the ``table AGN'' command, which roughly reproduces the typical SED of ionizing photons in AGNs (Mathews & Ferland 1987). We did not examine the dependence of the calculations on the SED but adopted only this particular SED, because Nagao et al. (2006a) concluded that the SED does not affect the NLR metallicity evolution in HzRGs. We adopted gas clouds with the hydrogen density $n_{{\rm H}} = 10^2$ and $10^4~{\rm cm}^{-3}$ and the ionization parameters U = 10^-2.4-10^-1.2. We assumed dust-free gas clouds, since dusty models are inconsistent with observations when high-ionization emission lines of HzRGs are considered (Nagao et al. 2006a). We note that this is also suggested by rest-frame optical or near-infrared emission lines (e.g., Marconi et al. 1994; Ferguson et al. 1997b; Nagao et al. 2003). For the chemical composition of gas, we assumed that all metals scale by keeping solar ratios except for He and N. For helium, we assumed a primary nucleosynthesis component in addition to the primordial value. Nitrogen scales as the square power of other metal abundances because it is a secondary element. We adopted the analytical expressions for the helium and nitrogen relative abundances as functions of the metallicity given in Dopita et al. (2000). Another free parameter in our calculation is the cloud column density. Since we now focus on relatively high-ionization emission lines (N V, C IV, He II, and C III]), we stop our calculations when the hydrogen ionization fraction drops below 15%. This requirements ensures that the line fluxes of interest do not depend on the choice of a particular column density.

In Fig. 2, we show the dependence of the emission-line luminosity on the NLR metallicity, for models with $n_{\rm H} = 10^2~{\rm cm}^{-3}$ and $10^4~{\rm cm}^{-3}$ , and U = 10^-1.6 and 10^-2.0. The line luminosity is normalized by the number of H-ionizing photons in the input continuum emission. The model behavior is completely different between He II and the other emission lines: the He II is a recombination line and its luminosity is proportional to the rate of ${\rm He}^+$ -ionizing photons, while the other emission lines are collisionally excited and their emissivity strongly depends on the gas temperature. The equilibrium temperature of ionized gas clouds is sensitive to metallicity because of the radiative cooling by metal emission lines. Therefore, the luminosity of collisionally excited emission lines decreases at high metallicity. We note that the N V luminosity decreases at much higher metallicity than the C IV and C III] luminosity. This is because the nitrogen abundance increases at high metallicity, i.e., N/H $\propto$ ${\rm (O/H)}^2$ . All of the above results are insensitive to the adopted gas density and ionization parameter.

Figure 2 suggests that the C IV/He II flux ratio is possibly a good metallicity diagnostic. However, this flux ratio also depends on other parameters such as the ionization parameter. This degeneracy can be solved by combining it with the C III]/C IV ratio, which is primarily sensitive to the ionization parameter. Therefore, a diagram involving both the C IV/He II and C III]/C IV ratios is expected to be a powerful metallicity diagnostic, as originally proposed by Nagao et al. (2006a). In Fig. 3, the results of our photoionization model calculations are plotted on this diagnostic diagram. The model grids indicate that this diagram is quite useful for investigating the NLR metallicity. We note that, as shown in Fig. 3, the C IV/He II flux ratio also depends on the gas density and thus the gas metallicity is not uniquely determined by this diagram. However, it can be useful to investigate relative differences in metallicity and assess the possible redshift evolution in the NLR metallicity. In the rest of the paper, we consider only models with $n_{\rm H} = 10^4~{\rm cm}^{-3}$ (a typical NLR density; see, e.g., Nagao et al. 2001a, 2002a).

$\begin{figure} \par\includegraphics[width=7.8cm]{figure3a.ps}\includegraphics[width=7.8cm]{figure3b.ps} \end{figure}$	Figure 3: Calculated model grids plotted on a diagram of C IV/He II versus C III]/C IV. Models for gas clouds with $n_{{\rm H}} = 10^2$ and $10^4~{\rm cm}^{-3}$ are presented in the left and right panels, respectively. Constant metallicity and constant ionization parameter sequences are denoted by solid and dashed lines, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{figure4.ps} \end{figure}$

Figure 4:

The flux ratios of HzRGs plotted on the diagnostic diagram on C IV/He II versus C III]/C IV. Our new data are shown with red-filled circles, while the data compiled by Nagao et al. (2006a) are shown with blue-open circles and arrows. The green-filled star symbol shows the line ratios measured in the composite spectrum of the 9 HzRGs observed by us. The shock models by Allen et al. (2008) are also plotted for comparison. Gray-solid lines denote the predictions of pure shock models with magnetic parameters of B/n^1/2=0, 1, 2, and 4 $\mu$ G ${\rm cm}^{3/2}$ , solar abundance, and shock velocities in the range 200 km ${\rm s}^{-1} < v_{\rm s} < 900$ km ${\rm s}^{-1}$ (constant velocities sequences of 200 km ${\rm s}^{-1}$ and 900 km ${\rm s}^{-1}$ are denoted by gray-dashed lines). The gray-dotted line denote the prediction of shock plus precursor models with B/n^1/2=2 $\mu$ G ${\rm cm}^{3/2}$ , solar abundance, and 200 km ${\rm s}^{-1} < v_{\rm s} < 400$ km ${\rm s}^{-1}$ . Black-solid and black-dashed lines are the same as those in Fig. 3.

Open with DEXTER

5 Discussion

5.1 The metallicity-redshift and metallicity-luminosity relations in HzRGs

By comparing the observed flux ratios of HzRGs with the prediction of the photoionization models, we investigate the gas metallicity. In Fig. 4, we plot the flux ratios of HzRGs on the diagnostic diagram with the calculated model grids. We also plot the flux ratios of the composite spectrum of HzRGs in this diagram. Although 9 new data are at higher redshift than the data in Nagao et al. (2006a) on average, there is no systematic difference in the data distribution between our new observations and the data of Nagao et al. (2006a). This result naively suggests that there is no significant chemical evolution in NLRs of HzRGs, even up to $z \sim 4$ .

We now investigate whether shock models can explain the observed flux ratios of HzRGs. In Fig. 4, we overplot the shock models and shock plus precursor models presented by Allen et al. (2008). Specifically, we plot shock models with shock velocities of 200 km ${\rm s}^{-1} < v_{\rm s} < 900$ km ${\rm s}^{-1}$ , magnetic parameters of B/n^1/2=0, 1, 2, and 4 $\mu$ G ${\rm cm}^{3/2}$ , and solar abundance, and shock plus precursor models with shock velocities of 200 km ${\rm s}^{-1} < v_{\rm s} < 400$ km ${\rm s}^{-1}$ , a magnetic parameter of B/n^1/2=2 $\mu$ G ${\rm cm}^{3/2}$ , solar abundance. As shown in Fig. 4, both pure shock models and shock plus precursor models cannot explain the observed distribution of line ratios, at variance with pure photoionization models. We therefore conclude that the dominant ionization mechanism of gas clouds emitting C IV, He II, and C III] is photoionization.

To investigate the relationship between metallicity and redshift or luminosity, we divided our sample into the following three redshift bins: 1.2 < z < 2.0, 2.0 < z < 2.5, and 2.5 < z < 3.8. As for the luminosity, since the non-thermal AGN continuum is obscured in HzRGs, we used the He II line luminosity as a proxy for the AGN's bolometric luminosity. This directly traces the rate of ${\rm He}^+$ -ionizing photons, which is proportional to the bolometric luminosity. Luminosity bins are as follows: $41.5 < \log L$ (He II) <42.5, $42.5 < \log L$ (He II) <43.0, and $43.0 < \log L$ (He II) <45.0 (see Table 3). In Figs. 5 and 6, we investigate the averaged flux ratios of C IV/He II and C III]/C IV for each luminosity and redshift bin to examine the possible dependence of metallicity on luminosity and redshift. There is no clear dependence between the flux ratios and redshift as shown in Fig. 5, suggesting that the NLRs metallicity of HzRGs does not show significant redshift evolution in the range of $1 \la z \la 4$ . On the other hand, in Fig. 6 we illustrate that the flux ratios are correlated with luminosity, suggesting that more luminous HzRGs have more metal-rich gas clouds. Figure 7 shows the redshift evolution of average metallicity as derived from our sample. Here we use only the HzRG samples with $\log L$ (He II) =42.5-43.0 to minimize possible Malmquist bias. We note that the metallicity shown here is derived by assuming $n_{\rm H}=10^4$ cm^-3 (see Table 3). Figure 7 clearly shows that there is no significant decline in the NLR metallicity at high redshift. In the same way, Fig. 8 shows the luminosity dependence of the averaged NLR metallicity in our sample. Figure 8 clearly shows the correlation between the AGN luminosity and the NLR metallicity. These results are completely consistent with the results of Nagao et al. (2006a) but more reliable since our new sample includes a larger number of HzRGs at high redshift (z > 2.7). We note that the positive correlation between the AGN luminosity and the gas metallicity of ionized clouds is also evident for the BLR, which does not show any redshift evolution (e.g., Hamann & Ferland 1993; Nagao et al. 2006c; see also Jiang et al. 2007; Juarez et al. 2009).

$\begin{figure} \par\includegraphics[width=7.8cm]{figure5.ps} \end{figure}$	Figure 5: Flux ratios averaged logarithmically for each redshift bin, compared with the model predictions on the C IV/He II versus C III]/C IV diagram. The dotted bars denote the rms of the data distribution, and the solid bars denote the estimated errors in the averaged values.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.8cm]{figure6.ps} \end{figure}$	Figure 6: Flux ratios averaged logarithmically for each luminosity bin, compared with the model predictions for the C IV/He II versus C III]/C IV diagram. The error bars are the same as in Fig. 5.
Open with DEXTER

Table 3: Averaged diagnostic flux ratios of HzRGs.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{figure7.ps} \end{figure}$	Figure 7: The NLR metallicity versus redshift diagram, for metallicities of three subsamples with $\log L$ (He II) = 42.5-43.0 at redshift ranges of 1.2 < z < 2.0, 2.0 < z < 2.5, and 2.5 < z < 3.8 (see also Table 3). These metallicities and their errors are estimated from the C IV/He II versus C III]/C IV diagram. Transverse bars show redshift ranges.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.8cm]{figure8.ps} \end{figure}$	Figure 8: The NLR metallicity versus luminosity diagram, for metallicities of three subsamples at luminosity ranges of $41.5 < \log L$ (He II) <42.5, $42.5 < \log L$ (He II) < 43.0 and, $43.0 < \log L$ (He II) < 45.0. These metallicities and their errors are estimated from the C IV/He II versus C III]/C IV diagram. Transverse bars show luminosity ranges.
Open with DEXTER

5.2 Interpretation

In Sect. 5.1, we have reported a significant positive correlation between the NLR metallicity and the AGN luminosity. We discuss two possible origins for this correlation:

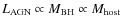the galaxy mass-metallicity relation (assuming $L_{\rm AGN} \propto M_{\rm BH} \propto M_{\rm host}$ );
a dependence of NLR metallicity on the Eddington ratio.

We discuss each of these scenarios below.

One possible explanation of the positive correlation between NLR metallicity and AGN luminosity is that it reflects the relation between galaxy mass and metallicity (e.g., Lequeux et al. 1979; Tremonti et al. 2004; Lee et al. 2006). Since the metal content of NLRs is the result of the past star-formation history in the host galaxies, the metallicity of galaxies and that of NLRs should be closely related. Galaxies are characterized by a clearly defined mass-metallicity relation even at high redshift (Maiolino et al. 2008). On the other hand, AGN luminosities and host galaxy masses should also be closely related, if the Eddington ratio is roughly the same within this class of objects and the correlation between the mass of supermassive black holes (SMBHs) and that of galaxy spheroidal components also holds at high redshift. Therefore, by assuming a narrow range of the Eddington ratios and the $M_{\rm BH}$ -galaxy mass relation, the positive correlation between NLR metallicity and AGN luminosity is naturally expected. Some observational studies indeed report that the Eddington ratio of high-z quasars is limited in a narrow range (e.g., Kollmeier et al. 2006; Trump et al. 2009).

However, this scenario has a serious problem. We have found that the NLR metallicity shows no significant redshift evolution, up to $z \sim 4$ . In contrast, the mass-metallicity relation in galaxies shows significant redshift evolution, at least in the 0 < z < 3 range (e.g., Savaglio et al. 2005; Erb et al. 2006; Liu et al. 2008; Maiolino et al. 2008). If the relation between NLR metallicity and AGN luminosity is caused simply by the galaxy mass-metallicity relation, the NLR metallicity is also expected to show significant redshift evolution, in contrast to our observational results. We discuss below possible reasons for this apparent contradiction and the implications of the relation between NLR metallicity and AGN luminosity.

A possible way of reconciling this problem is that the apparent lack of evolution is the extreme consequence of galaxy downsizing on metal enrichment. We know that low mass galaxies evolve slowly, even from the chemical point of view, on a prolonged timescale extending to the current epoch. In contrast, massive galaxies reach their chemical maturity on short timescales and at high redshift (Maiolino et al. 2008 and references therein). Since the host galaxies of HzRGs are very massive (e.g., De Breuck et al. 2002), their chemical evolution may be completed at much earlier epochs than observed in the current sample, i.e., at z > 3. This scenario predicts that the NLR metallicities in lower-luminosity HzRGs (which are probably hosted in less massive hosts) may show evolution even at z < 3. This prediction can be tested by sensitive spectroscopic observations of faint HzRGs.

Alternatively, the relation between NLR metallicity and AGN luminosity may be independent of the mass-metallicity relation of galaxies, since the Eddington ratio is probably not universal. The BLR metallicity in quasars is understood to be correlated with the Eddington ratio (e.g., Shemmer et al. 2004; see also Nagao et al. 2002b; Shemmer & Netzer 2002). This suggests that the NLR metallicity may also be correlated with the Eddington ratio, although the physical origin is unclear. In this case, the correlation between the AGN luminosity and the NLR metallicity is independent of the galaxy mass-metallcity relation.

Whatever the scenario, our study strongly suggests that HzRGs completed the major part of their chemical enrichment in the very high-z universe, i.e., z > 4. If the minimum timescale for a significant enrichment of carbon ( $\sim$ 0.5 Gyr; e.g., Matteucci 2008) is taken into account, the major epoch of the star formation in HzRGs may have occurred at z > 5.

We note that our conclusions are in contrast to some earlier studies mentioned in Sect. 1. The most significant difference between previous works and our own is in the adopted diagnostics, i.e., we do not use N V emission to investigate the NLR metallicity. While the N V emission is too weak in most HzRGs to be measured accurately, all of the lines used by us (C IV, He II, and C III]) are so strong that we can measure their fluxes rather easily. Therefore, we have been able to investigate the chemical evolution of HzRGs without relying on upper-limit data. Another serious problem with using the N V emission in metallicity studies is that the flux ratios including N V are sensitive not only to the NLR metallicity but also to the ionization parameter as discussed in the following section.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{figure9a.ps}\\ \includegraphics[width=7.8cm,clip]{figure9b.ps} \end{figure}$	Figure 9: The flux ratios of a new sample plotted on a diagram of N V/He II ( upper) and N V/C IV (lower). Our new data are shown with the red-filled circles, and the previous data compiled by Nagao et al. (2006a) are shown with the blue-open circles and arrows.
Open with DEXTER

5.3 The N V emission in HzRGs

Given the high S/N of our spectra, the N V emission line is securely detected in 5 out of 9 objects. Nitrogen is a secondary element and thus its abundance is expected to be proportional to the square of the metallicity [i.e., N/O $\propto$ O/H, or equivalently, N/H $\propto$ ${\rm (O/H)}^2$ ]. Therefore, the N V line is widely regarded as a good metallicity indicator, at least for BLRs (e.g., Hamann & Ferland 1992, 1993; Hamann et al. 2002; Dietrich et al. 2002, 2003; Nagao et al. 2006c). Accordingly, the N V line is sometimes also regarded as a metallicity indicator for NLRs (e.g., van Ojik et al. 1994; De Breuck et al. 2000; Vernet et al. 2001; Overzier et al. 2001; Humphrey et al. 2008). We thus examine the N V/C IV and N V/He II flux ratios as a function of redshift, to measure possible redshift evolution in the NLR metallicity independently of the diagnostic diagram of C IV/He II versus C III]/C IV. These two flux ratios are plotted as a function of redshift in Fig. 9. Our new data at z > 2.7 clearly show the existence of HzRGs with high N V/C IV and N V/He II flux ratios even at z > 2.7, which seems consistent with the idea that there is no significant evolution in the NLR metallicity of HzRGs, as suggested by the C IV/He II and C III]/C IV flux ratios.

Figure 9, however, shows the presence of a large number of HzRGs with very weak N V emission. In particular, some HzRGs exhibit N V/He II <0.1 and N V/C IV <0.1, while others exhibit N V/He II $\sim 1$ and N V/C IV $\sim 1$ . For the models presented by Vernet et al. (2001), these flux ratios would correspond to $Z_{\rm NLR} < 0.4~Z_{\rm\odot}$ for N V-weak HzRGs and $Z_{\rm NLR} \sim 4~Z_{\rm\odot}$ for N V-strong HzRGs. This would suggest that the NLR metallicity of HzRGs varies from object to object across a very wide range (>1 dex). This seems inconsistent with the results obtained by the analysis of the C IV/He II and C III]/C IV emission-line ratios (Fig. 3). To investigate the origin of this apparent contradiction, in Fig. 10 we plot the observational data in the N V/He II versus N V/C IV diagram and compare them with our model calculations. The distribution of the observational data on this diagram seems consistent with the area spanned by model grids. The near horizontal lines of constant-U in Fig. 10 suggest that the N V/He II flux ratio is sensitive to the ionization parameter but insensitive to the NLR metallicity. The N V/C IV ratio appears to depend on both U and $Z_{\rm NLR}$ . In other words, the increase in the ionization parameter for a given metallicity results in high N V/He II and N V/C IV flux ratios, while the increase in the metallicity for a given ionization parameter results in high N V/C IV but nearly constant N V/He II flux ratios. This suggests that the N V/He II flux ratio is sensitive to the ionization parameter rather than the NLR metallicity. This is demonstrated more clearly in Fig. 11, where we show the N V/He II versus C III]/C IV diagram. The narrow coverage of the model grids in this diagram suggests that both N V/He II and C III]/C IV flux ratios depend mainly on the ionization parameter but are nearly independent of the NLR metallicity. We note that the observational data appears to be distributed across a wider range than predicted by the models. Only the models with $n_{\rm H} = 10^4~{\rm cm}^{-3}$ are plotted in the diagram and most of the observational data are upper limits.

$\begin{figure} \par\includegraphics[width=8cm]{figure10.ps} \end{figure}$	Figure 10: The flux ratios of HzRGs plotted on the diagnostic diagram on N V/He II versus N V/C IV. Red-filled circles, blue-open circles, arrows and green-filled star symbols are the same as those in Fig. 3. Solid and dashed lines are the same as those in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.8cm]{figure11.ps} \end{figure}$	Figure 11: The flux ratios of HzRGs plotted on the diagnostic diagram on N V/He II versus C III]/C IV. Red-filled circles, blue-open circles, arrows and green-filled star symbols are the same as those in Fig. 3. Solid and dashed lines are the same as those in Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{figure12.ps} \end{figure}$	Figure 12: The flux ratios of HzRGs plotted on the diagnostic diagram of N V/C IV versus C IV/He II. Red-filled circles, blue-open circles, arrows, and green-filled star symbols represent the same quantities as those in Fig. 3. Solid and dashed lines are the same as those in Fig. 2.
Open with DEXTER

The physical reason why the N V/He II flux ratio is less sensitive to metallicity than the N V/C IV flux ratio is shown in Fig. 2 and described in Sect. 4. Both N V and C IV are collisionally excited emission lines and thus become weak at high metallicity where the equilibrium temperature is low. However, N V emission decreases far more slowly with metallicity than C IV, because nitrogen is a secondary element. This is the main reason for the metallicity dependence of the N V/C IV flux ratio. However, especially at U > 10^-2.0, the metallicity dependence of the N V emission is low (see the top panel of Fig. 2). As already mentioned in Sect. 4, the He II emission is also insensitive to the metallicity because it is a recombination line. This is demonstrated in Fig. 12, where we plot the N V/C IV versus C IV/He II diagram. Here $Z_{\rm NLR}$ -sequences are mostly perpendicular to U-sequences, and $Z_{\rm NLR}$ -sequences go towards the upper-left direction with increasing NLR metallicity. This diagram is, however, less useful than the C IV/He II versus C III]/C IV diagram in inferring the NLR metallicity, because N V/C IV flux ratios of HzRGs are difficult to be measured accurately; indeed most of the observational data in Fig. 12 are upper-limit values.

In Figs. 9-12, the inferred ionization parameter for the N V-detected HzRGs is much higher than suggested by the diagram in Fig. 4. This is because of the higher ionization potential of the ${\rm N}^{4+}$ ion (77.4 eV) compared to the ${\rm C}^{3+}$ (47.9 eV) and ${\rm He}^{2+}$ (54.4 eV) ions; i.e., the N V emission tends to originate in regions characterized by higher ionization parameters than C IV and He II. Although multi-zone photoionization models for NLRs (e.g., Ferguson et al. 1997a; Nagao et al. 2001b) can solve this discrepancy in ionization parameter, this is beyond the scope of this paper and thus they are not discussed further.

6 Conclusion

To investigate the metallicity evolution of galaxies in the high-z universe, we have performed new spectroscopic observations of 9 HzRGs at z > 2.7, which complement data available at lower redshifts. By comparing the total set of data of 57 HzRGs at $1 \la z \la 4$ with photoionization models, we found the following results:

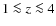1.: Our analysis of the emission-line flux ratios of C IV, He II, and C III] suggests that there is no significant chemical evolution in the redshift range of $1 \la z \la 4$ .
2.: We found a positive correlation between the NLR metallicity and the AGN luminosity. There are two possible origins for this correlation: the galaxy mass-metallicity relation and a dependence of the NLR metallicity on the Eddington ratio.
3.: The non-evolution in the gas metallicity of the NLRs implies that the major epoch of star formation in the host galaxies is at z > 5;
4.: we detected the N V emission in the spectra of 5 HzRGs at 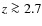$z \ga 2.7$ , and found that there are some HzRGs with high N V/C IV and N V/He II flux ratios even at such high redshift.
5.: However, high N V/He II ratios do not always imply high NLR metallicities, but correspond mainly to high ionization parameters.

Acknowledgements

We would like to thank the VLT staff for their invaluable help during the observations and G. Ferland for providing the excellent photoionization code Cloudy to the public. We also thank the anonymous referee for useful comments and suggestions. This work was financially supported in part by the Japan Society for the Promotion of Science (Nos. 15340059, 17253001, and 19340046). K.M. acknowledges financial support from the Circle for the Promotion of Science and Engineering of Japan. TN is financially supported through the Research Promotion Award of Ehime University. R.M. and A.M. acknowledge partial support by the Italian Space Agency (ASI) through contract ASI-INAF I/016/07/0.

References

Allen, M. G., Groves, B. A., Dopita, M. A., et al. 2008, ApJS, 178, 20 [NASA ADS] [CrossRef] (In the text)
Baldwin, J. A., Ferland, G. J., Korista, K. T., et al. 2003a, ApJ, 582, 590 [NASA ADS] [CrossRef] (In the text)
Baldwin, J. A., Hamann, F., Korista, K. T., et al. 2003b, ApJ, 583, 649 [NASA ADS] [CrossRef]
Bennert, N., Jungwiert, B., Komossa, S., et al. 2006a, A&A, 456, 953 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Bennert, N., Jungwiert, B., Komossa, S., et al. 2006b, A&A, 459, 55 [NASA ADS] [CrossRef] [EDP Sciences]
Bentz, M. C., Hall, P. B., & Osmer, P. S. 2004, AJ, 128, 561 [NASA ADS] [CrossRef] (In the text)
De Breuck, C., Röttgering, H., Miley, G., et al. 2000, A&A, 362, 519 [NASA ADS] (In the text)
De Breuck, C., van Breugel, W., Stanford, S. A., et al. 2002, AJ, 123, 637 [NASA ADS] [CrossRef] (In the text)
Dietrich, M., Hamann, F., Shields, J. C., et al. 2002, ApJ, 581, 912 [NASA ADS] [CrossRef] (In the text)
Dietrich, M., Hamann, F., Shields, J. C., et al. 2003, ApJ, 589, 722 [NASA ADS] [CrossRef] (In the text)
Dopita, M. A., Kewley, L. J., Heisler, C. A., et al. 2000, ApJ, 542, 224 [NASA ADS] [CrossRef] (In the text)
Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] (In the text)
Ferguson, J. W., Korista, K. T., Baldwin, J. A., et al. 1997a, ApJ, 487, 122 [NASA ADS] [CrossRef] (In the text)
Ferguson, J. W., Korista, K. T., & Ferland, G. J. 1997b, ApJS, 110, 287 [NASA ADS] [CrossRef]
Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [NASA ADS] [CrossRef] (In the text)
Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef]
Gebhardt, K., Bender, R., Bower, G., et al. 2000a, ApJ, 539, L13 [NASA ADS] [CrossRef]
Gebhardt, K., Richstone, D., Kormendy, J., et al. 2000b, AJ, 119, 1157 [NASA ADS] [CrossRef]
Greene, J. E., & Ho, L. C. 2005, ApJ, 627, 721 [NASA ADS] [CrossRef] (In the text)
Hamann, F., & Ferland, G. J. 1992, ApJ, 391, L53 [NASA ADS] [CrossRef] (In the text)
Hamann, F., & Ferland, G. J. 1993, ApJ, 418, 11 [NASA ADS] [CrossRef] (In the text)
Hamann, F., Korista, K. T., Ferland, G. J., et al. 2002, ApJ, 564, 592 [NASA ADS] [CrossRef] (In the text)
Humphrey, A., Villar-Martín, M., Vernet, J., et al. 2008, MNRAS, 383, 11 [NASA ADS] (In the text)
Iwamuro, F., Motohara, K., Maihara, T., et al. 2003, ApJ, 598, 178 [NASA ADS] [CrossRef] (In the text)
Jiang, L., Fan, X., Vestergaard, M., et al. 2007, AJ 134, 1150
Juarez, Y., Maiolino, R., Mujica, R., et al. 2009, A&A 494, L25 (In the text)
Kollmeier, J. A., Onken, C. A., Kochanek, C. S., et al. 2006, ApJ, 648, 128 [NASA ADS] [CrossRef] (In the text)
Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [NASA ADS]
Lee, H., Skillman, E. D., Cannon, J. M. et al. 2006, ApJ, 647, 970 [NASA ADS] [CrossRef] (In the text)
Lequeux, J., Peimbert, M., Rayo, J. F., et al. 1979, A&A, 80, 155 [NASA ADS] (In the text)
Liu, X., Shapley, A. E., Coil, A. L., et al. 2008, ApJ, 678, 758 [NASA ADS] [CrossRef] (In the text)
Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef]
Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef]
Marconi, A., Moorwood, A. F. M., Salvati, M., et al. 1994, A&A, 291, 18 [NASA ADS] (In the text)
Mathews, W. G., & Ferland, G. J. 1987, ApJ, 323, 456 [NASA ADS] [CrossRef] (In the text)
Matteucci, F. 2008 [arXiv:0804.1492] (In the text)
Nagao, T., Murayama, T., Taniguchi, Y. 2001a, ApJ, 546, 744 [NASA ADS] [CrossRef] (In the text)
Nagao, T., Murayama, T., Taniguchi, Y. 2001b, ApJ, 549, 155 [NASA ADS] [CrossRef]
Nagao, T., Murayama, T., Shioya, Y., et al. 2002a, ApJ, 567, 73 [NASA ADS] [CrossRef] (In the text)
Nagao, T., Murayama, T., Shioya, Y., et al. 2002b, ApJ, 575, 721 [NASA ADS] [CrossRef]
Nagao, T., Murayama, T., Shioya, Y., et al. 2003, AJ, 125, 1729 [NASA ADS] [CrossRef] (In the text)
Nagao, T., Maiolino, R., & Marconi, A. 2006a, A&A, 447, 863 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Nagao, T., Maiolino, R., & Marconi, A. 2006b, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences]
Nagao, T., Marconi, A., & Maiolino, R. 2006c, A&A, 447, 157 [NASA ADS] [CrossRef] [EDP Sciences]
Overzier, R. A., Röttgering, H. J. A., Kurk, J. D., et al. 2001, 370, L39 (In the text)
Robinson, A., Binette, L., Fosbury, R. A. E., et al. 1987, MNRAS, 227, 97 [NASA ADS] (In the text)
Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] (In the text)
Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef]
Shemmer, O., & Netzer, H. 2002, ApJ, 567, L19 [NASA ADS] [CrossRef] (In the text)
Shemmer, O., Netzer, H., Maiolino, R., et al. 2004, ApJ, 614, 547 [NASA ADS] [CrossRef] (In the text)
Suganuma, M., Yoshii, Y., Kobayashi, Y., et al. 2006, ApJ, 639, 46 [NASA ADS] [CrossRef] (In the text)
Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] (In the text)
Trump, J. R., Impey, C. D., Kelly, B. C., et al. 2009, ApJ, submitted (In the text)
van Ojik, R., Röttgering, H. J. A., Miley, G. K., et al. 1994, A&A, 289, 54 [NASA ADS] (In the text)
Vernet, J., Fosbury, R. A. E., Villar-Martín, M., et al. 2001, A&A, 366, 7 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

Footnotes

... galaxies: Based on data obtained at the VLT through the ESO programs 076.A-0664 and 077.B-0051.
... 07.02: We proved for some models that the results of the calculations do not change significantly with the use of Cloudy version 08.00 instead of version 07.02; the difference is $\sim$ 10% at most.

All Tables

Table 1: Journal of observations.

Table 2: Emission-line measurements.

Table 3: Averaged diagnostic flux ratios of HzRGs.

All Figures

$\begin{figure} \par\includegraphics[width=7.5cm]{figure1a.ps}\includegraphics[wi... ...h=7.5cm]{figure1i.ps}\includegraphics[width=7.5cm]{figure1j.ps}\\\end{figure}$	Figure 1: Spectra for 9 objects observed with FORS2 and the composite spectrum of the HzRGs ( lower right), improving by binning by 2 in wavelength direction. Each spectrum is shown on two different flux scales, the first to show strong emission lines and the second to show continuum emission and weak emission lines.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.6cm]{figure2.ps} \end{figure}$	Figure 2: Predicted emission-line luminosity normalized by the number of H-ionizing photons, as functions of the NLR metallicity. The results for N V, C IV, He II, and C III] are shown, from top to bottom. Red and green lines denote the models with hydrogen density of $n_{\rm H} = 10^2~{\rm cm}^{-3}$ and $10^4~{\rm cm}^{-3}$ , respectively. Solid and dashed lines denote the models with ionization parameter of U = 10^-1.6 and 10^-2.0, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm]{figure3a.ps}\includegraphics[width=7.8cm]{figure3b.ps} \end{figure}$	Figure 3: Calculated model grids plotted on a diagram of C IV/He II versus C III]/C IV. Models for gas clouds with $n_{{\rm H}} = 10^2$ and $10^4~{\rm cm}^{-3}$ are presented in the left and right panels, respectively. Constant metallicity and constant ionization parameter sequences are denoted by solid and dashed lines, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{figure4.ps} \end{figure}$	Figure 4: The flux ratios of HzRGs plotted on the diagnostic diagram on C IV/He II versus C III]/C IV. Our new data are shown with red-filled circles, while the data compiled by Nagao et al. (2006a) are shown with blue-open circles and arrows. The green-filled star symbol shows the line ratios measured in the composite spectrum of the 9 HzRGs observed by us. The shock models by Allen et al. (2008) are also plotted for comparison. Gray-solid lines denote the predictions of pure shock models with magnetic parameters of B/n^1/2=0, 1, 2, and 4 $\mu$ G ${\rm cm}^{3/2}$ , solar abundance, and shock velocities in the range 200 km ${\rm s}^{-1} < v_{\rm s} < 900$ km ${\rm s}^{-1}$ (constant velocities sequences of 200 km ${\rm s}^{-1}$ and 900 km ${\rm s}^{-1}$ are denoted by gray-dashed lines). The gray-dotted line denote the prediction of shock plus precursor models with B/n^1/2=2 $\mu$ G ${\rm cm}^{3/2}$ , solar abundance, and 200 km ${\rm s}^{-1} < v_{\rm s} < 400$ km ${\rm s}^{-1}$ . Black-solid and black-dashed lines are the same as those in Fig. 3.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm]{figure5.ps} \end{figure}$	Figure 5: Flux ratios averaged logarithmically for each redshift bin, compared with the model predictions on the C IV/He II versus C III]/C IV diagram. The dotted bars denote the rms of the data distribution, and the solid bars denote the estimated errors in the averaged values.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm]{figure6.ps} \end{figure}$	Figure 6: Flux ratios averaged logarithmically for each luminosity bin, compared with the model predictions for the C IV/He II versus C III]/C IV diagram. The error bars are the same as in Fig. 5.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{figure7.ps} \end{figure}$	Figure 7: The NLR metallicity versus redshift diagram, for metallicities of three subsamples with $\log L$ (He II) = 42.5-43.0 at redshift ranges of 1.2 < z < 2.0, 2.0 < z < 2.5, and 2.5 < z < 3.8 (see also Table 3). These metallicities and their errors are estimated from the C IV/He II versus C III]/C IV diagram. Transverse bars show redshift ranges.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm]{figure8.ps} \end{figure}$	Figure 8: The NLR metallicity versus luminosity diagram, for metallicities of three subsamples at luminosity ranges of $41.5 < \log L$ (He II) <42.5, $42.5 < \log L$ (He II) < 43.0 and, $43.0 < \log L$ (He II) < 45.0. These metallicities and their errors are estimated from the C IV/He II versus C III]/C IV diagram. Transverse bars show luminosity ranges.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{figure9a.ps}\\ \includegraphics[width=7.8cm,clip]{figure9b.ps} \end{figure}$	Figure 9: The flux ratios of a new sample plotted on a diagram of N V/He II ( upper) and N V/C IV (lower). Our new data are shown with the red-filled circles, and the previous data compiled by Nagao et al. (2006a) are shown with the blue-open circles and arrows.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm]{figure10.ps} \end{figure}$	Figure 10: The flux ratios of HzRGs plotted on the diagnostic diagram on N V/He II versus N V/C IV. Red-filled circles, blue-open circles, arrows and green-filled star symbols are the same as those in Fig. 3. Solid and dashed lines are the same as those in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm]{figure11.ps} \end{figure}$	Figure 11: The flux ratios of HzRGs plotted on the diagnostic diagram on N V/He II versus C III]/C IV. Red-filled circles, blue-open circles, arrows and green-filled star symbols are the same as those in Fig. 3. Solid and dashed lines are the same as those in Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{figure12.ps} \end{figure}$	Figure 12: The flux ratios of HzRGs plotted on the diagnostic diagram of N V/C IV versus C IV/He II. Red-filled circles, blue-open circles, arrows, and green-filled star symbols represent the same quantities as those in Fig. 3. Solid and dashed lines are the same as those in Fig. 2.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.