| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | 883 - 888 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200810909 | |
| Published online | 23 June 2009 | |
Plausible explanations for the variations of orbital period in the old nova DQ Herculis![[*]](/icons/foot_motif.png)
Z. B. Dai1,2,3 - S. B. Qian1,2
1 - National Astronomical Observatories/Yunnan Observatory,
Chinese Academy of Sciences, PO Box 110, 650011 Kunming, PR China
2 -
United Laboratory of Optical Astronomy, Chinese
Academy of Science (ULOAC), 100012 Beijing, PR China
3 -
Graduate School of the CAS, Beijing, PR China
Received 4 September 2008 / Accepted 28 April 2009
Abstract
Aims. Several mechanisms are presented to explain the observed small variation in the orbital period of the old nova DQ Herculis.
Methods. We have combined two new CCD times of light minimum of DQ Herculis with all 226 available times of light minimum, including 79 visual observations, for the new orbital period analysis.
Results. Based on this analysis, the best-fit of the O-C diagram for DQ Herculis is a quadratic-plus-sinusoidal fit. A secular orbital period increase with a rate of
![]() is confirmed, which corresponds to a lower limit of the mass transfer rate of
is confirmed, which corresponds to a lower limit of the mass transfer rate of
![]() .
We investigate three plausible mechanisms (direct change of the red dwarf's radius, Applegate's mechanism and the light travel-time effect) to explain the quasi-periodic variation shown in the O-C diagram. Although previous works have suggested that solar-type magnetic cycles in the red dwarf can explain the quasi-periodic variation in the orbital period, we were not able to reproduce this finding. Accordingly, a light trave-time effect is proposed, with a brown dwarf as a tertiary component with a significance level of
.
We investigate three plausible mechanisms (direct change of the red dwarf's radius, Applegate's mechanism and the light travel-time effect) to explain the quasi-periodic variation shown in the O-C diagram. Although previous works have suggested that solar-type magnetic cycles in the red dwarf can explain the quasi-periodic variation in the orbital period, we were not able to reproduce this finding. Accordingly, a light trave-time effect is proposed, with a brown dwarf as a tertiary component with a significance level of
![]() orbiting around nova DQ Herculis. In order to interpret the small departure from the best-fit near 60 000 cycles, we assume an eccentric orbit of the third body with a small eccentricity. However, a satisfying result was obtained because the eccentricity e=0.12 is close to zero. The parameters of this elliptical orbit are similar to that of a circular orbit.
orbiting around nova DQ Herculis. In order to interpret the small departure from the best-fit near 60 000 cycles, we assume an eccentric orbit of the third body with a small eccentricity. However, a satisfying result was obtained because the eccentricity e=0.12 is close to zero. The parameters of this elliptical orbit are similar to that of a circular orbit.
Key words: stars: novae, cataclysmic variables - stars: binaries: eclipsing - stars: individual: DQ Herculis
1 Introduction
The remnant of the nova Herculis 1934, named DQ Herculis,
was first detected at a magnitude of
![]() (Campbell 1935). It is not
only a well-observed prototype of intermediate Polar stars, but also
a moderately slow galactic nova. This means that the binary system
not only contains a white dwarf with a strong magnetic field, which
can partially control the accreting stream from the red dwarf along
the magnetic field lines to fall onto one or both magnetic poles of
the white dwarf (Patterson 1994), but also has thermonuclear runaway
on the surface of the white dwarf (Starrfield 1989). The discovery
of eclipses in DQ Herculis (Walker 1956) was pivotal in
establishing the standard picture of cataclysmic variables. At the
same time, Walker (1956) reported a coherent 71 s photometric
oscillation. The spectral type of the red dwarf is estimated to be
M3 due to the detection of faint TiO bands (Young & Schneider 1981). Since
DQ Herculis is an eclipsing binary with an orbital period
of
(Campbell 1935). It is not
only a well-observed prototype of intermediate Polar stars, but also
a moderately slow galactic nova. This means that the binary system
not only contains a white dwarf with a strong magnetic field, which
can partially control the accreting stream from the red dwarf along
the magnetic field lines to fall onto one or both magnetic poles of
the white dwarf (Patterson 1994), but also has thermonuclear runaway
on the surface of the white dwarf (Starrfield 1989). The discovery
of eclipses in DQ Herculis (Walker 1956) was pivotal in
establishing the standard picture of cataclysmic variables. At the
same time, Walker (1956) reported a coherent 71 s photometric
oscillation. The spectral type of the red dwarf is estimated to be
M3 due to the detection of faint TiO bands (Young & Schneider 1981). Since
DQ Herculis is an eclipsing binary with an orbital period
of
![]() and has been extensively observed, its properties
are well known. For example, recent estimations of
and has been extensively observed, its properties
are well known. For example, recent estimations of
![]() and
and
![]() (Horne et al. 1993) correct the
previous results from earlier works (e.g. Smak 1980; Robinson 1976).
(Horne et al. 1993) correct the
previous results from earlier works (e.g. Smak 1980; Robinson 1976).
Since the mass transfer in DQ Herculis detected by
Kraft (1959), a variation in the orbital period is expected. Mumford (1969)
and Nather & Warner (1969) suggested that the orbital period is increasing, and
later works (Africano & Olson 1981; Zhang et al. 1995; Wood et al. 2005; Patterson et al. 1978) indicated that a sinusoidal
modulation with a period of
![]() is likely. However, an
updated O-C analysis (Wood et al. 2005) concluded that there is not strong
evidence for a secular orbital period increase. They did not produce
an explanation for the cyclical variation in the O-C diagram of
DQ Herculis. According to Patterson et al. (1978), light travel-time
effects cannot be applied to explain the O-C cyclic variation
because a similar variation is not present in the 71 s oscillation
timings. Therefore, there is no convincing explanation for the
orbital period variation of DQ Herculis so far.
is likely. However, an
updated O-C analysis (Wood et al. 2005) concluded that there is not strong
evidence for a secular orbital period increase. They did not produce
an explanation for the cyclical variation in the O-C diagram of
DQ Herculis. According to Patterson et al. (1978), light travel-time
effects cannot be applied to explain the O-C cyclic variation
because a similar variation is not present in the 71 s oscillation
timings. Therefore, there is no convincing explanation for the
orbital period variation of DQ Herculis so far.
226 available times of light minimum from 1954 to 2008 are presented in Sect. 2, including two new data points from our observations and 79 visual data points. Section 3 gives the O-C analysis for DQ Herculis. A discussion of the possible mechanisms for orbital period change is given in Sect. 4.
2 Observation of times of light minimum
Two new times of light minimum are obtained from our CCD photometric observations with the PI1024 TKB CCD photometric system attached to the 1.0-m reflecting telescope at the Yunnan Observatory in China. The first CCD photometric observation of DQ Herculis was carried out on February 10, 2008 in white light, and the second observation on March 28, 2008 was through the R-filter, which is close to the Johnson standard photometric system. Two nearby stars that have a similar brightness in the same viewing field of the telescope were chosen as the comparison star and the check star. All images were reduced by using PHOT (measured magnitudes for a list of stars) in the aperture photometry package of IRAF. Two CCD times of light minimum were derived by using a parabolic fitting method. Both light curves of eclipsing parts and their parabolic fits are displayed in upper planes of Figs. 1 and 2, respectively. The residuals of differential photometries shown in the lower planes of Figs. 1 and 2 suggest that the times of light minimum in our observations can be derived by a parabolic fit with high precision.
As the two new eclipsing times obtained from CCD observations are to
4 significant figures, we infer that the previous times of light
minimum obtained by using photographic or visual methods without
given error, should have lower accuracy. Therefore, we assume that
the CCD or photoelectric data and the photographic or visual data
without given errors have default errors of
![]() and
and
![]() ,
respectively. The collected times of light minimum were
checked again because some data were obtained from many years ago,
and some identical times of light minimum may have small
differences, as they were observed at different observatories or in
different filters. In this case, the average value should be
reliable and may be applied. In addition, Zhang et al. (1995) and Wood et al. (2005)
reported their 44 eclipse times in Heliocentric Julian Ephemeris
Dates (HJED), which correspond to ephemeris time (ET). Thus, we
converted them to Heliocentric Julian Dates (HJD), which correspond
to coordinated Universal time (UTC). All 226 available times of
light minimum covering half a century listed in Table 1 have been
checked carefully, and those obviously inaccurate were corrected or
abandoned. For example, the 7 photographic data points before 1954
are not used in this paper because of the very large scatter.
,
respectively. The collected times of light minimum were
checked again because some data were obtained from many years ago,
and some identical times of light minimum may have small
differences, as they were observed at different observatories or in
different filters. In this case, the average value should be
reliable and may be applied. In addition, Zhang et al. (1995) and Wood et al. (2005)
reported their 44 eclipse times in Heliocentric Julian Ephemeris
Dates (HJED), which correspond to ephemeris time (ET). Thus, we
converted them to Heliocentric Julian Dates (HJD), which correspond
to coordinated Universal time (UTC). All 226 available times of
light minimum covering half a century listed in Table 1 have been
checked carefully, and those obviously inaccurate were corrected or
abandoned. For example, the 7 photographic data points before 1954
are not used in this paper because of the very large scatter.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg13.png) |
Figure 1: The light curve of the eclipsing part of DQ Herculis shown in the upper figure, obtained on Feb. 10, 2008 in white light. The solid line represents the best parabolic fit. The lower figure shows the residuals of differential photometry. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg14.png) |
Figure 2: Upper panel is the R-band light curve of the eclipsing part of DQ Herculis obtained on Mar. 28, 2008. The solid line represents the best parabolic fit. The lower figure shows the residuals of differential photometry. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg15.png) |
Figure 3: The O-C values calculated with Eq. (1) versus the cycles. The 79 visual data points and the photoelectric or CCD data are plotted as open circles and solid circles, respectively. |
| Open with DEXTER | |
3 Analysis of orbital period changes
The ephemeris derived by Africano & Olson (1981) is used to calculate the O-C
values of DQ Herculis and, after linear revision, the new
epochs and average orbital period of DQ Herculis were
derived as
| (1) |
with variance
| |
= | ||
| (2) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg21.png) |
Figure 4: The O-C values of DQ Herculis fitted with the formulas displayed in Eqs. (2) and (3). The fitting curves are plotted in the top and middle figure, respectively. The residuals and their linear fitted solid line are presented in the bottom plane. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg5.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg22.png) |
Figure 5: The O-C values of DQ Herculis obtained from the elements in Eq. (4). The fitting curves are plotted in the top figure. The residuals are presented in the bottom plane. |
| Open with DEXTER | |
| |
= | ||
| (3) |
with variance
| |
= | ||
| (4) |
with variance
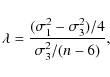 |
(5) |
where n is the number of data points. Thus, a calculation gives F(4,220)=26.0, which indicates that it is significant well above the
Although Pringle (1975), Africano & Olson (1981) and Wood et al. (2005) suggested that the
orbital period of DQ Herculis is constant, the residuals of
this quadratic-plus-sinusoidal fit shown in the bottom panel of Fig. 5
never show a detectable variation, which implies the existence of
quadratic variation in O-C diagram. Moreover, the standard model of
cataclysmic variables (Smak 1971; Warner & Nather 1971) indicates that mass transfer is
a common phenomena. According to the coefficient of the quadratic
term in Eq. (4), the orbital period change rate of DQ
Herculis, ![]() ,
can be calculated to be
,
can be calculated to be
![]() .
.
4 Discussion
4.1 Secular orbital period increase
Considering that the secular orbital period change for DQ
Herculis remains a matter of debate, the mass transfer between both
components may be low or non-existent, a situation that corresponds
to the presence of a faint hot spot in many eclipse light curves of
DQ Herculis (Bianchini et al. 2004). Although the accurate masses of both
components are still not available, it is definite that the mass
ratio,
q=M2/M1, is less than unity. Therefore, mass transfer
from the red dwarf to the white dwarf is a very reasonable
explanation for the orbital period increase shown in Figs. 4 and 5.
According to Kepler's third law, the orbital period change with
conservation can be given by
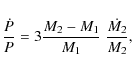 |
(6) |
where
4.2 Quasi-periodic variation
4.2.1 Variations of the red dwarf's radius
A
![]() quasi-period variations is seen in the O-C
diagram of DQ Herculis. Warner (1988) applied a technique
sensitive to mass overflow, which means that the mass transfer from
the red dwarf can be changed by a slight variation of its radius.
This can explain the cyclical change in the O-C diagram. He proposed
that a change in radius of the tidally distorted secondary star is
the result of solar-type magnetic cycles. The variation of radius of
the red dwarf,
quasi-period variations is seen in the O-C
diagram of DQ Herculis. Warner (1988) applied a technique
sensitive to mass overflow, which means that the mass transfer from
the red dwarf can be changed by a slight variation of its radius.
This can explain the cyclical change in the O-C diagram. He proposed
that a change in radius of the tidally distorted secondary star is
the result of solar-type magnetic cycles. The variation of radius of
the red dwarf, ![]() ,
can be described as,
,
can be described as,
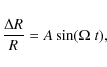 |
(7) |
where A is the amplitude of radius variations. The modulation of mass transfer rate
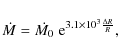 |
(8) |
where
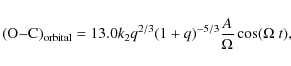 |
(9) |
where t is in days, k2 and q are the apsidal coefficient and the mass ratio, respectively. Compared to Eq. (4),
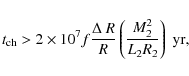 |
(10) |
where f, M2 and L2 are outer mass fraction, the mass and the luminosity of the red dwarf, respectively. Schneider & Greenstein (1979) estimated the spectral type of the secondary star of DQ Herculis to be M4 or later, and Young & Schneider (1981) pointed out that its spectral type should be M3+V due to the TiO band ratio found. This means that the luminosity of the red dwarf can be estimated to be
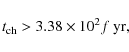 |
(11) |
with
4.2.2 Applegate's mechanism
Since Marsh & Pringle (1990) pointed out the required energy problem, Applegate (1992)
proposed an alterative mechanism, which is magnetic activity-driven
change in the quadrupole momentum of the red dwarf. According to
this mechanism, the relationship between the orbital period P and
the variation of the quadrupole momentum ![]() is given by
is given by
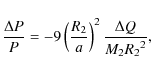 |
(12) |
where R2 and a are the radius of the secondary star and the binary separation, respectively. Using
![\begin{figure}
\par\includegraphics[width=7cm,clip]{10909fg6.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg77.png) |
Figure 6: The correlation between the energy required to produce the orbital period oscillation of DQ Herculis by using the Applegate (1992) mechanism and the assumed different shell masses of the fully convective red dwarf (solid line). The star denotes the minimum required energy, and the dotted line is the total radiant energy of the red dwarf over the whole oscillation period. |
| Open with DEXTER | |
In order to discuss the internal angular momentum transport, which
can produce the orbital period variation in a fully convective star,
the whole star is split into an inner core and an outer shell. The
energy ![]() required to cause the angular momentum transfer
required to cause the angular momentum transfer
![]() between the shell and core, is estimated by the
formula (Applegate 1992)
between the shell and core, is estimated by the
formula (Applegate 1992)
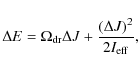 |
(13) |
where
4.2.3 Light travel-time effect
Another plausible mechanism to explain the sinusoidal variation in the O-C diagram is the light travel-time effect, which is caused by a perturbations from a tertiary component (Borkovits & Hegedues 1996; Irwin 1952). Patterson et al. (1978) suggested that the light travel-time effect is not a good explanation for the periodic oscillation in the O-C diagram of DQ Herculis because no evidence for a similar sinusoidal variation is found in the O-C diagram of 71 s. However, the detection of 71 s has a large error because of the very short time scale and the large oscillation phase shifts, which may affect the continuity of the times of maximum and the precision of the ephemeris. Moreover, there is no clear evidence that the O-C diagrams of 71 s well reflect the motion of the mass-center of DQ Herculis. Therefore, we investigated the possible light travel-time effect.
Table 2: The best-fit coefficients.
The strictly sinusoidal fit presented in Fig. 5 is a special case
that corresponds to the assumption of a circular orbit. We assumed
that the small departure near 60 000 cycles shown in the top panel of
Fig. 5 is caused by a small orbital eccentricity of the third body,
which can be described by (Irwin 1952);
![\begin{displaymath}{\rm O{-}C}=\frac{a~\sin i}{c}\left[\frac{1-{e}^{2}}{1+{e}\cos \nu}~\sin(\nu+\omega)+{e}~\sin\omega\right],
\end{displaymath}](/articles/aa/full_html/2009/33/aa10909-08/img98.png) |
(14) |
where a, c, i, e,
| |
= | ||
| (15) |
where
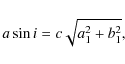 |
(16) |
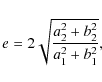 |
(17) |
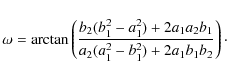 |
(18) |
Based on the above O-C analysis, a quadratic term should be added to Eq. (15), which leads to:
| |
= | ||
| (19) |
where
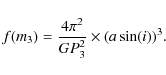 |
(20) |
Since the eccentricity e=0.12 is near zero, the elliptic orbit should be close to the circular orbit. Accordingly, the parameters of the third body derived from an eccentric fit are similar to that derived from a strictly sinusoidal fit (see Table 3). In addition, the
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg7.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg118.png) |
Figure 7:
The relationship between the mass of the third body and its
orbital inclination in the left panel, and the distances between the
third body and mass center corresponding to different inclinations
are in the right panel. The dashed line in the left and right panels
denotes the upper limit of the masses of the brown dwarf
(
|
| Open with DEXTER | |
Table 3: The parameters of the elliptic and circular orbit
5 Conclusion
All 226 available times of light minimum covering 54 years are
compiled and a new O-C diagram of DQ Herculis is obtained.
The fit shown in Fig. 5 implies that the best-fit of the O-C diagram
is a sinusoidal variation with an
![]() period
superimposed on the secular orbital period increase. This resolves
the long-term debate of whether the orbital period of DQ
Herculis is increasing or not. The increased orbital period is
calculated to be
period
superimposed on the secular orbital period increase. This resolves
the long-term debate of whether the orbital period of DQ
Herculis is increasing or not. The increased orbital period is
calculated to be
![]() .
Using the
absolute parameters of DQ Herculis derived by Horne et al. (1993), we
estimated the lower limit of the mass transfer rate to be
.
Using the
absolute parameters of DQ Herculis derived by Horne et al. (1993), we
estimated the lower limit of the mass transfer rate to be
![]() .
In order to check the
results of the orbital period increase presented in this paper,
photometric observations with a longer base line are needed.
.
In order to check the
results of the orbital period increase presented in this paper,
photometric observations with a longer base line are needed.
Although there is a small departure near 60 000 cycles, the overall
trend in the O-C diagram can be well described by a
quadric-plus-sinusoidal formula. Since there is no detailed analysis
for the episodes of quasi-period oscillation, we investigated three
plausible mechanisms, which are a red dwarf radius variation,
Applegate's mechanism and the light travel-time effect, to explain
the observed orbital period variation. According to the first
mechanism, we concluded that the red dwarf's radius variation with
an amplitude
![]() is sufficient to
account for the small quasi-sinusoidal oscillation seen in Fig. 5.
But this requires too much energy, and the time scale
is sufficient to
account for the small quasi-sinusoidal oscillation seen in Fig. 5.
But this requires too much energy, and the time scale
![]() is
far longer than the oscillation period. Thus a direct change in
radius of the tidally distorted secondary star cannot explain the
observed quasi-periodic variation. Then Applegate's mechanism was
used to probe whether the solar-type magnetic activity is
responsible for the observed modulations in the O-C diagram.
However, this still gives a negative result. In order to show that
the magnetic activity cycle of the red dwarf star in DQ
Herculis is strong enough to cause the observed modulation in the
O-C diagram, A detailed analysis of variation in its brightness is
necessary. Finally, an eccentric orbit of the tertiary component
with a small eccentricity was attempted to explain the small
departure displayed in the top panel of Fig. 5. The derived orbital
eccentricity, e=0.12, is small enough, which means that the
parameters of the third body derived from an elliptic orbit are
similar to that derived from the circular orbit (see Table 3). This
suggests that further studies are needed to explain the departure
occurring in
is
far longer than the oscillation period. Thus a direct change in
radius of the tidally distorted secondary star cannot explain the
observed quasi-periodic variation. Then Applegate's mechanism was
used to probe whether the solar-type magnetic activity is
responsible for the observed modulations in the O-C diagram.
However, this still gives a negative result. In order to show that
the magnetic activity cycle of the red dwarf star in DQ
Herculis is strong enough to cause the observed modulation in the
O-C diagram, A detailed analysis of variation in its brightness is
necessary. Finally, an eccentric orbit of the tertiary component
with a small eccentricity was attempted to explain the small
departure displayed in the top panel of Fig. 5. The derived orbital
eccentricity, e=0.12, is small enough, which means that the
parameters of the third body derived from an elliptic orbit are
similar to that derived from the circular orbit (see Table 3). This
suggests that further studies are needed to explain the departure
occurring in
![]() .
Based on the analysis of the light
travel-time effect, a brown dwarf as a third component of the system
is possible, with a significance level of
.
Based on the analysis of the light
travel-time effect, a brown dwarf as a third component of the system
is possible, with a significance level of
![]() .
Alternatively, the third body may be a massive extrasolar planet, as
long as the orbital inclination of the third body is high enough.
However, more convincing evidence, for example, further studies on
the behavior of the 71 s oscillation in DQ Herculis, are
needed to confirm the results in this paper.
.
Alternatively, the third body may be a massive extrasolar planet, as
long as the orbital inclination of the third body is high enough.
However, more convincing evidence, for example, further studies on
the behavior of the 71 s oscillation in DQ Herculis, are
needed to confirm the results in this paper.
Acknowledgements
This work was partly Supported by Special Foundation of the President of the Chinese Academy of Sciences and West Light Foundation of The Chinese Academy of Sciences, Yunnan Natural Science Foundation (2008CD157), the Yunnan Natural Science Foundation (No. 2005A0059M) and Chinese Natural Science Foundation (No.10573032, No. 10573013 and No.10433030). CCD photometric observations of DQ Herculis were obtained with the 1.0-m telescope at Yunnan Observatory.We thank the referee very much for the helpful comments and suggestions that helped to improve this paper greatly.
References
- Africano, J., & Olson, E. 1981, PASP, 93, 130 [NASA ADS] [CrossRef]
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] (In the text)
- Bianchini, A., Mastrantonio, E., Canterna, R., Stute, J., & Cantrell, K. 2004, A&A, 426, 669 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Borkovits, T., & Hegedues, T. 1996, A&AS, 120, 63 [NASA ADS] [CrossRef] [EDP Sciences]
- Campbell, L. 1935, Harvard College Observatory Bulletin, 898, 20 [NASA ADS] (In the text)
- Dibai, É. A., & Shakhovskoi, N. M. 1966, SvA, 10, 1059 [NASA ADS]
- Diethelm, R. 2003, IBVS, 5438
- Diethelm, R. 2004, IBVS, 5543
- Hall, D. S. 1991, ApJ, 380, L85 [NASA ADS] [CrossRef] (In the text)
- Horne, K., Welsh, W. F., & Wade, R. A. 1993, ApJ, 410, 357 [NASA ADS] [CrossRef] (In the text)
- Irwin, J. B. 1952, ApJ, 116, 211 [NASA ADS] [CrossRef]
- Kopal, Z. 1959, Close Binary Systems (London: Chapman & Hall).
- Kopal, Z. 1978, Dynamics of Close Binary Systems, D. Reidel. Co.
- Kraft, R. P. 1959, ApJ, 130, 110 [NASA ADS] [CrossRef] (In the text)
- Livio, M. 1992, in Interacting Binaries, 22nd SF Advanced Course, ed. H. Nussbaumer
- Locher, K. 1978, BBSAG Bull., 39, 4
- Locher, K. 1979, BBSAG Bull., 42, 2
- Locher, K. 1979, BBSAG Bull., 43, 2
- Locher, K. 1979, BBSAG Bull., 44, 3
- Locher, K. 1979, BBSAG Bull., 45, 4
- Locher, K. 1980, BBSAG Bull., 46, 3
- Locher, K. 1980, BBSAG Bull., 47, 3
- Locher, K. 1980, BBSAG Bull., 48, 2
- Locher, K. 1980, BBSAG Bull., 49, 4
- Locher, K. 1980, BBSAG Bull., 50, 3
- Locher, K. 1981, BBSAG Bull., 54, 2
- Locher, K. 1981, BBSAG Bull., 55, 2
- Locher, K. 1981, BBSAG Bull., 56, 5
- Locher, K. 1981, BBSAG Bull., 57, 4
- Locher, K. 1982, BBSAG Bull., 58, 3
- Locher, K. 1982, BBSAG Bull., 59, 2
- Locher, K. 1982, BBSAG Bull., 60, 3
- Locher, K. 1982, BBSAG Bull., 61, 3
- Locher, K. 1982, BBSAG Bull., 63, 2
- Locher, K. 1983, BBSAG Bull., 64, 4
- Locher, K. 1983, BBSAG Bull., 65, 3
- Locher, K. 1983, BBSAG Bull., 66, 3
- Locher, K. 1983, BBSAG Bull., 67, 3
- Locher, K. 1983, BBSAG Bull., 68, 4
- Locher, K. 1983, BBSAG Bull., 69, 4
- Locher, K. 1984, BBSAG Bull., 71, 2
- Locher, K. 1984, BBSAG Bull., 72, 2
- Locher, K. 1984, BBSAG Bull., 73, 4
- Locher, K. 1984, BBSAG Bull., 84, 3
- Locher, K. 1985, BBSAG Bull., 77, 4
- Locher, K. 1986, BBSAG Bull., 80, 3
- Locher, K. 1986, BBSAG Bull., 81, 3
- Locher, K. 1986, BBSAG Bull., 82, 4
- Locher, K. 1987, BBSAG Bull., 83, 3
- Locher, K. 1987, BBSAG Bull., 84, 3
- Locher, K. 1987, BBSAG Bull., 85, 3
- Locher, K. 1988, BBSAG Bull., 88, 4
- Locher, K. 1988, BBSAG Bull., 89, 7
- Locher, K. 1989, BBSAG Bull., 92, 3
- Locher, K. 1990, BBSAG Bull., 94, 3
- Locher, K. 1990, BBSAG Bull., 95, 3
- Locher, K. 1990, BBSAG Bull., 96, 5
- Locher, K. 1991, BBSAG Bull., 97, 6
- Locher, K. 1991, BBSAG Bull., 98, 7
- Locher, K. 1993, BBSAG Bull., 104, 5
- Locher, K. 1994, BBSAG Bull., 106, 5
- Locher, K. 1994, BBSAG Bull., 107, 8
- Locher, K. 1995, BBSAG Bull., 108, 7
- Locher, K. 1995, BBSAG Bull., 109, 9
- Locher, K. 1996, BBSAG Bull., 112, 7
- Locher, K. 1997, BBSAG Bull., 114, 8
- Locher, K. 1998, BBSAG Bull., 117, 8
- Locher, K. 1998, BBSAG Bull., 118, 6
- Locher, K. 2000, BBSAG Bull., 121, 6
- Locher, K. 2001, BBSAG Bull., 126, 5
- Locher, K. 2002, BBSAG Bull., 127, 5
- Marsh, T. R., & Pringle, J. E. 1990, ApJ, 365, 677 [NASA ADS] [CrossRef] (In the text)
- Martin, P. G. 1989, in Classical Novae, ed. M. F. Bode, & A. Evans (Chichester: Wiley), Chap. 6
- Mumford, G. S. 1969, in Mass Loss from Stars, ed. M. Hack (Dordrecht: Reidel Publishing Co.), 204 (In the text)
- Nagai, K. 2006, Var. Star. Bull. Japan, 44
- Nather, R. E., & Warner, B. 1969, MNRAS, 143, 145 [NASA ADS] (In the text)
- Nelson, M. R., & Olson, E. C. 1976, ApJ, 207, 195 [NASA ADS] [CrossRef]
- Patterson, J. 1994, PASP, 106, 209 [NASA ADS] [CrossRef]
- Patterson, J., Robinson, E. L., & Nather, R. E. 1978, ApJ, 224, 570 [NASA ADS] [CrossRef]
- Pringle, J. E. 1975, MNRAS, 170, 633 [NASA ADS] (In the text)
- Robinson, E. L. 1976, ApJ, 203, 485 [NASA ADS] [CrossRef]
- Schneider, D. P., & Greenstein, J. L. 1979, ApJ, 233, 935 [NASA ADS] [CrossRef] (In the text)
- Schoembs, R., & Rebhan, H. 1989, A&A, 224, 42 [NASA ADS]
- Smak, J. 1971, , 21, 15
- Smak, J. 1980, , 30, 267
- Smak, J. 2004, , 54, 433
- Starrfield, S, 1989, in Classical Novae, ed. M. F. Bode, & A. Evans (Chichester: Wiley), Chap. 3
- Swedlund, J. B., Kemp, J. C., & Wolstencroft, R. D. 1974, ApJ, 193, 11 [NASA ADS] [CrossRef]
- Vaytet, N. M. H., O'Brien, T. J., & Rushton, A. P. 2007, MNRAS, 380, 175 [NASA ADS] [CrossRef]
- Walker, M. F. 1956, ApJ, 123, 68 [NASA ADS] [CrossRef] (In the text)
- Walker, M. F. 1958, ApJ, 127, 319 [NASA ADS] [CrossRef]
- Warner, B. 1988, Nature 336, 10 (In the text)
- Warner, B., & Nather, R. E. 1971, MNRAS, 152, 219 [NASA ADS]
- Warner, B., Peters, W. L., Hubbard, W. B, & Nather, R. E. 1972, MNRAS, 159, 321 [NASA ADS]
- Wood, M. A., Robertson, J. R., & Simpson, J. C., et al. 2005, ApJ, 634, 570 [NASA ADS] [CrossRef]
- Young, P. J., Schneider, D. P. 1981, ApJ, 247, 960 [NASA ADS] [CrossRef] (In the text)
- Zhang, E., Robinson, E. L., Stiening, R. F., & Horne, K. 1995, ApJ, 454, 447 [NASA ADS] [CrossRef]
Online Material
Table 1: The times of light minimum for the old nova DQ Herculis.
Footnotes
- ... Herculis
![[*]](/icons/foot_motif.png)
- Table 1 is only available in electronic form at http://www.aanda.org
All Tables
Table 2: The best-fit coefficients.
Table 3: The parameters of the elliptic and circular orbit
Table 1: The times of light minimum for the old nova DQ Herculis.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg13.png) |
Figure 1: The light curve of the eclipsing part of DQ Herculis shown in the upper figure, obtained on Feb. 10, 2008 in white light. The solid line represents the best parabolic fit. The lower figure shows the residuals of differential photometry. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg14.png) |
Figure 2: Upper panel is the R-band light curve of the eclipsing part of DQ Herculis obtained on Mar. 28, 2008. The solid line represents the best parabolic fit. The lower figure shows the residuals of differential photometry. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg15.png) |
Figure 3: The O-C values calculated with Eq. (1) versus the cycles. The 79 visual data points and the photoelectric or CCD data are plotted as open circles and solid circles, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg21.png) |
Figure 4: The O-C values of DQ Herculis fitted with the formulas displayed in Eqs. (2) and (3). The fitting curves are plotted in the top and middle figure, respectively. The residuals and their linear fitted solid line are presented in the bottom plane. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg5.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg22.png) |
Figure 5: The O-C values of DQ Herculis obtained from the elements in Eq. (4). The fitting curves are plotted in the top figure. The residuals are presented in the bottom plane. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{10909fg6.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg77.png) |
Figure 6: The correlation between the energy required to produce the orbital period oscillation of DQ Herculis by using the Applegate (1992) mechanism and the assumed different shell masses of the fully convective red dwarf (solid line). The star denotes the minimum required energy, and the dotted line is the total radiant energy of the red dwarf over the whole oscillation period. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{10909fg7.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa10909-08/Timg118.png) |
Figure 7:
The relationship between the mass of the third body and its
orbital inclination in the left panel, and the distances between the
third body and mass center corresponding to different inclinations
are in the right panel. The dashed line in the left and right panels
denotes the upper limit of the masses of the brown dwarf
(
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


