EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 503 / No 3 (September I 2009) A&A, 503 3 (2009) 1023-1036 Full HTML
Free Access
Issue
A&A
Volume 503, Number 3, September I 2009
Page(s) 1023 - 1036
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/200810798
Published online 09 July 2009

A variability sample catalogue selected from the Sydney Observatory Galactic Survey[*]

A. Fresneau1 - W. H. Osborn2

1 - Observatoire astronomique, UMR 7550, 11 rue de l'Université, 67000 Strasbourg, France
2 - Department of Physics, Central Michigan University, Mt. Pleasant, MI 48859, USA

Received 13 August 2008 / Accepted 1 July 2009

Abstract
Context. A set of $55\times 10^3$ stars brighter than about B-magnitude 14 and having at least three observations are identified in the Sydney Observatory Galactic Survey, carried out over the years 1892-1932 along the galactic equator section $l\in[275^\circ,335^\circ]$ with galactic latitude $b\in[-7^\circ,7^\circ]$. Short-term (30 min) and long-term (decades) magnitude variations in the data set are analyzed.
Aims. Evidence is sought for a correlation between short-term and long-term variabilities which would identify stars in a non-quiescent phase.
Methods. We use a reduced proper motion diagram to classify the stars in our sample into probable dwarfs, giants and other types. The validity of the kinematical classification is checked using objective-prism spectroscopic classification for $10\times 10^3$ early-type stars. A search is made for statistical correlations between our variability indicators and physical and kinematical stellar properties.
Results. We find that suspected photospheric activity for giant and dwarf stellar candidates is correlated with the time to cross the galactic thin disk. We estimate a significant apparent B-magnitude variation of $\pm$0.25 over the 40 years of photographic observations, and candidates for monitoring for possible photospheric activity at the present time are selected employing a statistical colour-diagram which uses the total proper motion component as a distance indicator.
Conclusions. Follow up studies of our tentative findings are suggested. Toward this aim the derived data for the set of $55\times 10^3$ stars with variability information is archived as the variability Sample Catalogue. The data for a set of $2.4\times 10^5$ stars along the section of the galactic equator $l\in[275^\circ,335^\circ]$, $\mid\!\! b\!\! \mid ~\leq 7^\circ$, and a set of of $1.7\times 10^5$ stars along the section of the galactic meridian $330^\circ \pm5^\circ$, $b\in[-64^\circ,-7^\circ]$ is also archived as a quick-look facility for seeking long-term magnitude changes since the century-old photographic observations were obtained.

Key words: surveys - stars: variables: general

1 General characteristics of the Sydney Observatory Galactic Survey

The Sydney Observatory Galactic Survey (SOGS) is a catalogue of half a million stars down to about about B-magnitude $14\pm 0.5$ in two bands, one along the galactic equator ( $272^\circ \leq l\leq 341^\circ$, $\vert b\vert\leq7^\circ$) and the other along a galactic meridian ( $l=330^\circ ~\pm~5^\circ$, $b\in[-64^\circ,-7^\circ]$). The catalogue has been created using the Sydney Observatory Astrographic Program (SOAP) photographic plates, which were taken in the years 1892-1932 with a 33-cm aperture,   ${\it f}/10$ astrographic refractor of ${\it f}=3.41$ m focal length, to survey the declination zone from $-52^\circ$ to $-64^\circ$ (an area of 2285 square degrees, or about five percent of the sky). The original sample of $2\times 10^6$ stars with J2000 equatorial coordinates and photographic (blue) magnitudes mb at epoch $1915\pm 20$ was compared to modern-epoch observations in the V-band (the GSC 1.2) to produce the $5\times 10^5$ stars in SOGS. The catalog is available on line through the VizieR system[*] with catalogue identifications J/AJ/130/2701 for the section along the galactic equator and J/A+A/469/1221 for the section along the galactic meridian. Additional details about the SOGS are given in Fresneau et al. (2005, 2007).

The SOAP observing program consisted of 1400 overlapping fields of $2^\circ \times 2^\circ $ field-of-view centered on even and odd degrees of declination (at B1900.0) and spaced proportionally in RA by a quantity $\Delta\alpha$. The nominal B1900 coordinates of the plate centers $\delta_0$, ( $\alpha_0)_j$ are given in Table 1 along with the numbers of regions (n), the RA spacing ( $\Delta\alpha$) of plate j, where $j\in[1,n]$. The mean epoch (and dispersion) of the observations for each zone is indicated. The numbers (k,m) of fields sampled along the galactic meridian ($k\ll n$) and along the equator ($m\ll n$) in each declination zone using the deeper plates in constructing the SOGS are indicated. Blue-sensitive plates were employed (which have roughly a 1400 Å-wide bandwith around the Fraunhofer G-line at 4308 Å) and no filter was used in the observations. The photometric wide band system of the survey is noted b, close to the B Johnson system (centered on $4350\pm 970$ Å). The stellar magnitudes mb are derived from the image diameters and a calibration curve (between image diameters and B-magnitude) computed for the Tycho 2 stars (Hog et al. 2000) detected on each plate.

Table 1:   Distribution of the B1900.0 centers of the 1400 $2^\circ \times 2^\circ $ fields of the Sydney Observatory Astrographic Program.

Exposures of 8 min were obtained of all 1400 fields, and the measures of the stars brigher than b-mag. 12 on these plates were used in the construction of the astrographic catalog (Urban et al. 1998). Less well known is that there were also systematic sets of longer exposure plates:

a.
the 740 fields centered on even-degree declinations were covered by plates having three consecutive exposures of 30 min. The 30-min plates have mean epochs 1915 or later and a limiting b-magnitude of 14.5 and were were intended to permit star images to be separated from plate defects;

b.
the 660 fields centered on odd-degree declinations were photographed with a single exposure of 80 min. These plates have epochs earlier than 1915 and the increased exposure time gave a limiting b-magnitude of about 16;

c.
some very long exposure plates (3-6 h) were taken by the SOAP observers to be used to make prints of objects of special interest (Russell 1891); these have a b-magnitude limit down to 18 as determined from a set of ten plates of the LMC (Fresneau et al. 2005).

The SOAP plates are now archived at the Macquarie University Library in Sydney and 628 of the 30- and 80-min SOAP astrographic plates have, so far, been been measured. This was done in 2000 using the automated plate measuring (APM) machine at Cambridge (England), which was built in the 1970's for handling large Schmidt telescope plates (Kibblewhite et al. 1984). The plates chosen for measurement were selected to cover the 4th quadrant of the galactic equator and a section of the 330$^\circ$ galactic meridian. The APM measures produced data for about $2\times 10^6$ objects, compiled into the SOGS. The SOGS can be considered an extension of the Tycho 2 survey (Hog et al. 2000) to fainter magnitudes along sections of the galactic equator and the 330$^\circ$ galactic meridian.

In the present study we examine the SOGS photometric data. Because of the overlapping-field approach, taken together the deeper SOAP plates contain three to four separate exposures for each $1^\circ\times 1^\circ$ quarter of a standard field, except of course along the 1$^\circ$ border of the survey zone. Thus, SOGS data contain two distinct potential indicators of variability. First, one can look at the differences in the mb magnitudes derived from each of the three 30-min exposures on the same plate. The rms scatter $\sigma _1$ generally can be taken as the internal photometric error for the plate, which we will show is about $0.45\pm 0.10$ mag identical to the internal error of similar photographic observations (Ortiz-Gil et al. 1998; Lamareille et al. 2003). Larger scatter may indicate rapid blue-light variability, which we will call flickering. Similarly, there is the rms scatter $\sigma _2$ of the measured mb magnitude for a given star on different plates, both the 80-min and 30-min ones, during the 1892-1932 period of observation. Large $\sigma _2$ values may indicate long-term variability. The data should therefore allow us to identify suspected short-term variables (objects showing variations over the three 30-min consecutive exposures) as well as possible long-term variables (those exhibiting changes over the 40 years needed to complete the SOAP) as long as the variations are sufficiently large.

We must emphasize that the main use of the SOGS data is for statistical studies. While the lists of suspected variables can be expected to contain some physically interesting objects, they will also no doubt contain some spurious cases of variability. Individual objects should mainly be considered targets for follow-up studies, which could easily be done using the numerous wide-field multi-colour surveys now available on-line (Sesar et al. 2007) in order to gather additional information on the targets we selected with rudimentary data. Our main goal will be to investigate if there is any statistical correlation in our star sample between flickering and/or long-term variability and distance above the galactic plane. Such an effect is suggested by the observed changes in frequency of magnetically active stars with height above the galactic plane (West et al. 2006, 2008). We would like to connect, in the SOGS data, the stellar chromospheric activity in the optical with the orientation of the velocity ellipse of stellar systems that we determined as a function of the altitude over the galactic plane (Fresneau et al. 2007). Such a correlation might indicate a star's passage through the dense ISM of the thin disk has an effect on stellar chromospheric activity (seen in the optical), but other causes of chromospheric activity are perhaps more likely (e.g. magnetic effects) and no definitive conclusion about the source of such a correlation would be possible in view of the low accuracy of our data. Without a theory that could explain the observed variability with the dust scale height (Marshall el al. 2006), we suggest a linkage between the dust density distribution and the stellar distribution. We try to classify the SOGS sources into two physical categories of H-burning and He-burning candidates as a first step and to select, from the fully automated classification, a manageable list of targets suitable to learn more about the causes for variability. The chromospheric activity has been studied (West et al. 2008) and significant dispersion in the chromospheric activity-age relation is found even among coeval stars (Pace & Pasquini 2004). Our goal is to disentangle a category of stars linked to the thin disk crossing time.

2 Photometric performance in the SOGS

Our original sample contained $2\times 10^6$ measurements on a set of 628 photographic plates taken in the years 1892-1932. The photometric measurements were reduced to mb magnitudes using Tycho-2 reference stars (Hog et al. 2000). The internal error of magnitudes determined from a given plate has been estimated from $\sigma _1$, the scatters of the measures for the various stars around the mean values mb of the multiple exposures on the plate.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f1.ps} \end{figure} Figure 1:

The mean error in measured magnitude as a function of apparent magnitude mb.
Open with DEXTER

The plate-to-plate uncertainties, which we call the external error, has been determined from the magnitudes measured for the same star on different plates, either the pre-1915 80-min plates or the post-1915 30-min triple exposure plates. Figure 1 shows the internal error and the external errors for the 80-min and 30-min plates as a function of apparent magnitude mb. The internal errors were derived from the full set of $2\times 10^6$ measurements. Two sets of the external (plate-to-plate) errors are shown in Fig. 1, one based on comparisons of magnitudes from the single 80-min exposure plates (taken before 1915) and the second from comparisons of magnitudes from the triple 30-min exposure plates (taken later than 1915). The data from the triple-exposure plates have been put in 0.1 mag bins and then averaged. Based on the graph, we adopt ( $0.45\pm 0.10$) mag as the typical error for a magnitude determined from these century-old plates for stars fainter than apparent magnitude mb=10 (which are about 95% from the sample of $2\times 10^6$ stars). We note that the external error for the triple-exposure plates becomes larger for stars with $m_b\leq 11$, as was found previously for similar plates (Dick et al. 1993; Geffert et al. 1996). For all plates both the internal and external errors increase for the brighter stars, reaching 0.6 for mb=8. Our tentative explanation is that such large errors result from the stellar images used in the brighter magnitude determinations being overexposed.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f2.ps} \end{figure} Figure 2:

The cumulative frequency of the magnitude errors is plotted for observations performed after and before 1915.
Open with DEXTER

In order to identify genuine stellar outbursts in the set of $2\times 10^6$ observations over the period 1892-1932, we plot in Fig. 2 the cumulative distribution of the apparent magnitude mb internal error (derived from multiple exposure plates taken before and after 1915) and the external error (derived from plate-to-plate). The curves indicate the probability (between 0 and 1 along the Y-axis) for a star to be observed with a scatter larger than the value $\sigma_{mb}$ along the X-axis. The mean magnitude internal error is estimated to 0.25 after 1915 and 0.35 before 1915, suggesting an improvement in the photographic plate emulsion over the years. A difference in plate quality is duly observed over the 40 years needed to complete the survey. We also observe in Fig. 2 that the mean external error is larger than the internal errors, on the order of 0.4, suggesting that a level of systematic effect around 0.3 mag has crept into the external calibration of the magnitude mb. The main result of these photometric accuracies is to suspect that a short-term variability observed at the level of 1 mag concerns less than 10% of the stellar sample and can be a signature of a particular photospheric activity.

In order to add more information to the set of $2\times 10^6$ measurements of equatorial coordinates and apparent magnitude mb, the plates taken in period 1892-1932 have been compared to the GSC version 1.2. The GSC is derived from the Quick V survey (Lasker et al. 1990) V-bandpass plates made around 1980. We obtain in this procedure proper motions (p.m.) and colour indices (mb-V). The derived values are sufficient for our purposes so we have not made comparisons between the SOAP and other catalogs, such as the GSC II (Lasker et al. 2008) or 2MASS (Kleinmann 1992; Skrutskie et al. 2006). The proper motions $\mu$ are used to segregate the nearer stars from distant ones, which we will refer to as foreground and background stars, respectively. We adopted $\mu=0.02''$ yr-1 as our threshold based on our estimate that the error in our proper motions is about 0.003'' yr-1, which follows from the $\approx$90-yr epoch difference between the SOAP and the Quick V survey and equatorial coordinates accurate at a 0.3'' level. We investigated the p.m. errors as function of the apparent magnitude mb and we observed that the level of 0.003'' yr-1 is similar to the result obtained in other studies dealing with the same type of 100-yr old observations (Ducourant et al. 2006).

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f3.ps} \end{figure} Figure 3:

The numbers N of foreground and background stars as function of the apparent magnitude $m_b\geq 10$.
Open with DEXTER

We plot in Fig. 3 the numbers N of foreground and background stars as a function of apparent magnitude $m_b\geq 10$. With the trends of $\log{N_1}\approx 3+\frac{1}{2}(m_b-10)$ for the foreground star numbers and $\log{N_2}\approx 3.5+\frac{1}{2}({\it m_b}-10)$ for the background star numbers, we derive that the original sample of $2\times 10^6$ stars is complete to magnitude $ m_l\approx 14.5\pm0.5$. This follows from computing the integral ${\int_{10}}^{m_l}(N_1(m_b)+N_2(m_b))$dmb that should be equal to the total observed number of $2\times 10^6$ stars.

3 Calibration of a basic 2-D relation valid for stellar groups

The reduced proper motion (RPM) is defined as $H_b= m_b+5\log\mu+5$, where $\mu$ is the observed total p.m. component (Luyten 1922; Hertzsprung 1929). In our case, we only consider our derived p.m. significant, and hence suitable for calculation of RPM, when $\mu \geq 0.02''$ yr-1. Using that $\mu=\frac{T} {4.74~d}$ and $m_b=M_b+5\log d-5$ (where T is the transverse velocity in km s-1, d is the distance in pc and Mb is the absolute b-magnitude), then the RPM is $H_b=M_b+5\log{T}-3.378$ (we ignore the total interstellar absorption Ab).

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f4.ps} \end{figure} Figure 4:

Number N of stars with $m_b\geq 10$ as a function of the quantity Hb.
Open with DEXTER

Figure 4 shows the numbers N of SOGS stars with $m_b\geq 10$ as a function of the quantity Hb. The trend shows a linear component $\log N \propto H_b$, i.e. a power law relation, suggesting that to Hb =14 we have a distance-limited sample with a constant transverse velocity. This indicates a distance-limited sample (i.e., an absolute limiting magnitude $M_l\simeq 10$) for a stellar system with a constant transverse velocity $T\simeq 45$ km s-1 and an apparent magnitude $m_l\simeq 14.5$, that we associate with the Main Sequence stars in the solar neighborhoud, and two bumps in the trend around $H_b=6.5~ \pm~0.5$ and $H_b =9.5~\pm~1.5$ that we attribute to contamination of the Main Sequence star system by other types of stellar systems (probably giants). This stellar sample can be associated with the system of main sequence stars with apparent magnitudes $8.0\leq m_b\leq 13.5$ that are predominant in the solar neighborhood (Herbst & Sawyer 1981). The deviations from linearity at $H_b=6.5\pm0.5$, equivalent to $M_b\simeq 9.4-5\log T$, and at $H_b=9\pm 1$, equivalent to $M_b\simeq14.3-5\log T$, suggests contamination of the Main Sequence sample at these values by stars of different kinematical properties, likely giants. The figure illustrates the usefulness of computing RPM since it is equivalent to an absolute magnitude Mb with an offset of $5\log T-3.378$.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f5.ps} \end{figure} Figure 5:

The relation between absolute magnitudes from objective prism spectra (MB) and the RPM quantity Hb for a set of 104 stars in SOGS.
Open with DEXTER

We want to derive from our observations of mb and $\mu$ some physical characteristic related to absolute magnitude in order to derive a distance. We use a set of about 104 mostly OB stars for which MK and HD spectral types have been determined by objective-prism observations (Andersen 1977). Figure 5 compares the computed Hb with the absolute magnitude MB derived from the spectral type and corresponding tables (Strand 1963). We note that objective-prism spectral classification for hot stars is not very efficient in discriminating luminosity effects for hot stars (Johnson & Morgan 1953). We find a linear trend MB =0.86 H b-3.6 that has a correlation coefficient of 0.93. We also show in Fig. 5 the lines corresponding to $M_b=H_b-5\log T+3.378$ when T=50 km s-1 (upper line) and T=20 km s-1 (lower line), which indicates the relationship is for reasonable values of T. We adopt Mb =0.86 Hb-3.6, assuming the deviation from a 1:1 relation is an artifact of interstellar absorption Ab or uncalibrated effects in the relationship between Hb and MB.

The scatter of about 1 mag in the upper part of the diagram ($M_B\leq 2$) suggests this is the level of uncertainty for absolute magnitudes, determined in this way, at least for O-A stars. We observe that the absolute magnitudes derived from our kinematical classification (by converting Hb into MB) have similar precision to those from automated classification of medium dispersion objective-prism observations (von Hippel et al. 1994). We therefore conclude that, with a 1 mag uncertainty, a star's absolute magnitude Mb can be derived from the observed quantity $H_b= m_b+5\log\mu+5$.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f6.ps} \end{figure} Figure 6:

The absolute magnitude Mb derived from the calibration of Fig. 5, is plotted as function of the colour index (b-V).
Open with DEXTER

We present in Fig. 6 the RPMD for the set of stars plotted in Fig. 5 and with absolute magnitudes determined from Mb=0.86 Hb-3.6 and with the colour index (b-V). Also shown are the ridge-lines corresponding to main sequence stars, red giants of Pop. I (RG I) and Pop. II (RGII) and blue horizontal branch stars (Chiu 1980). The RPMD shows that once we have estimated Mb from Hb, we can then estimate (B-V)0 from (mb-V) and the appropriate ridge-line. For example, for the Main Sequence the adjustment of Mb to the ( MB,(B-V)0) of the ridge-line yields a linear relation (B-V)0 = 0.26+ 0.82(mb-V) for converting our (mb - V) color index into a dereddened (B-V)0 color. We have not derived relationships between (B-V)0 and (mb-V) for non-main sequence stars, but we suggest that even with our dereddened colors we can segregate giants from dwarfs based on number counting, as shown in Fig. 4.

In summary, the advantage of a RPMD with calibrated colour-magnitude relationships (Jones 1972) is that we can obtain from our observed quantities ( $m_b, V, \mu$) for a large number of stars some basic physical information, such as luminosity and radius, that can be investigated for a correlation with variability. The traditional HR diagram (HRD) in the ( $\log{T_{\rm e}},\log{L}$)-plane for a magnitude-limited sample (see, for example, Sowell et al. 2007) would obviously permit a more accurate separation of H-burning and He-burning stars; such will be available for our sample once the GAIA space-borne mission is completed around 2020 (Perrymann et al. 2000).

4 Validity of the RPMD for stellar group classification in SOGS

We consider that the relationship derived in the previous section is valid for the sample of stars in SOGS. We plot in Fig. 7 the numbers of foreground stars (those with $\mu \geq 0.02''$ yr-1) and background stars ( $\mu \leq 0.02''$ yr-1) as a function of the (B-V)0 colour derived using our calibration (B-V)0=0.26+0.82(mb-V). We note that Fresneau et al. (2007) found no colour effect when deriving p.m. at the level of 0.002'' yr-1 by comparing century-old astrographic observations and second-epoch Schmidt telescope ones used in the GSC 1.2 construction. While that result was based on Tycho-2 stars (Hog et al. 2000) brighter than mb=12 (Fresneau et al. 2005), we presume it is valid for even fainter stars, and hence no severe systematic effect has been introduced into the data by our proper motion determinations.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f7.ps} \end{figure} Figure 7:

Numbers N of foreground ( $\mu \geq 0.02''$ yr-1) and background ( $\mu \leq 0.02''$ yr-1) stars with $m_b\geq 10$ according to the color derived from the adjustment of Hb to a ( MB,(B-V)0) ZAMS.
Open with DEXTER

We see in Fig. 7 that the numbers of foreground and background stellar candidates are similar when the derived color (B-V)0 is redder than 0.8 mag. We also notice that the maximum number of foreground stars occurs a little redder than the Parenago's discontinuity at $(B-V)_0\simeq 0.62$. The linear trends for stars bluer than (B-V)0=0.4 in the two systems suggest that most of the background stars (those with unsignificant p.m.) are hotter than the foreground stars and hence are visible at distances larger than those that produce a noticeable p.m. We suggest therefore that our kinematical selection criterion of $\mu \geq 0.02''$ yr-1 yields a stellar sample of mostly F-G stars, with distances out to d=500 pc and a mixture of varying metallicities (Roman 1950; Ivezic et al. 2008). Thus, the SOGS data provide a good source for extending analyses of the local system of stars (Nordström et al. 2004). It is known (Binney et al. 2000) that stars redwards to the Parenago's discontinuity typically have a transverse velocity in the galactic plane $T\geq45$ km s-1 and stars bluewards a transverse velocity $T\leq25$ km s-1.

We can use the relation Mb=-3.6+0.86 Hb to estimate a distance modulus $m_b-M_b=5\log d-5$, and can use the derived distance d to compute the star's altitude z above the galactic plane $z=d\sin{b}$ in the galactic latitude direction b. We then use the Parenago's discontinuity to check if we are really separating distinct stellar groups. Figure 8 plots the numbers N of stars ( $m_b\geq 10$) bluer and redder than (B-V)0=0.62, the Parenago discontinuity value, as function of computed altitude over the galactic plane z in pc. We expect stars bluer than (B-V)0=0.62 to have lifetimes smaller than the age of the Galaxy and to more likely be members of the thin disk and those redder to have a higher probability of belonging to the thick disk, the two populations having significantly different scale heights of about 300 and 900 pc respectively (Bahcall & Soneira 1980; Gilmore & Reid 1983; Juric et al. 2008; Siegel et al. 2002; Bensby et al. 2004). The thin disk stellar candidates belong to a much flatter system, with a scale height on the order of 250-300 pc. The results show the bluer stars are indeed more concentrated to the galactic plane than the redder ones. With our low accuracy data, we cannot claim to segregate the stellar populations as well as can be done with the extensive data from modern surveys (Munn et al. 2004).

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f8.ps} \end{figure} Figure 8:

Numbers N of stars ( $m_b\geq 10$) as function of the altitude z above the galactic plane.
Open with DEXTER

We point out that we assumed $m_B\simeq m_b$, but given the low accuracy of our magnitudes ( $\simeq0.45\pm 0.10$ mag) a more accurate approach is not warranted. Similarly, we felt it was sufficient to merely apply the basic trigonometric relations between distance and galactic coordinates (l,b) and neglect such corrections as the effect of the sun's galactic altitude ${\it z}_\odot=15$ pc on the calculations (Bash 1986; Larsen & Humphreys 2003).

To this point, we have mainly been counting numbers related to the observational data in SOGS (equatorial coordinates, p.m. components, mb and V magnitudes). This was done in an attempt to show how the data can be used to identify stellar groups with different scale heights that can be linked to an age effect using that the blue stars are younger. In the following sections of this paper, we investigate the information added by stellar variability data.

5 Construction of the variability sample catalog (VSC)

From the approximately $5\times 10^5$ stars in the SOGS having p.m. sufficiently large that we can estimate a distance, we extracted about $55\times 10^3$ stars for which there are at least one triple image plate and at least three separate plates (which may include triple image plates) taken on diferent dates over the 1892-1932 SOGS observation period. This comprises a stellar sample suitable for investigating possible variability. We call this stellar set the variability sample catalog (VSC).

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f9.ps} \end{figure} Figure 9:

The reduced proper motion diagram (RPMD) [Hb,(b-V)] of the VSC stars that results by converting to a Mb, (B-V)0 diagram by applying the relations Mb=0.86 Hb-3.6 and (B-V)0=0.82(b-V)+0.26 as determined from Figs. 5 and 6.
Open with DEXTER

The reduced proper motion diagram (RPMD) for the stars in the VSC, i.e. their positions in the (Hb, mb-V)-plane is shown in Fig. 9. Adopting the same ridge lines in the ( MB,[B-V]0)-plane as defined in Table 9 of Chiu (1980), we estimated absolute magnitudes - $M_B=(0.772\pm0.005)~H_b- (3.12\pm0.02)$ - and dereddened colour - $(B-V)_0 =(0.84~\pm~0.05)(b-V) +(0.38\pm0.02)$ (Fresneau 1994). These relations follow from the assumption that the mean dispersion of the transverse velocity of foreground stars observed along the direction of each $2^\circ \times 2^\circ $ field of view is on the order of 45 km s-1 (Fresneau et al. 2003). These relations between Hb and Mb are based on a different stellar sample (Fresneau et al. 2005) than the one used in Sect. 4. The ridge-lines allow the derivation of an interstellar extinction Ab that we estimate as approximately 1 mag kpc-1. A MB,(B-V)0 Main Sequence (MS I) is fitted in the [Hb,(b-V)] plane of the Pop. I suggested stellar system (without applying any bolometric corrections) to convert the b-magnitude into the Johnson B photometric system.

One then finds a correlation between the statistically derived parallax $\pi$ in 10-3 arcsec and the p.m. total component $\mu$ in 10-3 arcsec yr-1 - $\pi=(0.072\pm 0.001)\mu +(0.284 \pm0.005)$ - which is similar to the relation that was found using stars with measured trigonometric parallax $\pi \geq 10^{-3}$ arcsec and p.m. $\mu \geq 10^{-2}$ arcsec yr-1 in the space-based Hipparcos survey of stars brighter than apparent magnitude 11 (Fresneau et al. 2005). We have not checked to see if this result is changed by the recent improvements in the Hipparcos catalog (van Leeuwen 2007; Perryman 2009).

In our study, we will call the the 2-D diagram derived from the RPMD, plotted as [Mb,(b-V)], as the statistical HRD and call the parallax $\pi =\frac{1}{d}$, derived from the d (in pc) given by the distance modulus $m_b-M_B=5\log{d}-5$, as the statistical parallax.

Using $(B-V)_0=\alpha(b-V)+\beta$ and $M_b=\gamma H_b+\delta$, we consider the [ (B-V)0,MB] ridge-line that is closest to the star's position in the [(b-V),Hb] RPMD to estimate MB. The set of coefficients ( $\alpha,\beta,\gamma,\delta$) is derived from the fit of the MS stars. Because we use p.m. as our distance indicator, the error in p.m. can be converted to a standard deviation in the statistical parallax that allows us to assess the uncertainty of the absolute magnitude determinations. We estimate this error from the variation in p.m. derived from different plate pairs. The absolute magnitude is $M\propto 5\log\frac {1} {\mu}$, so the the error $\Delta M$ resulting from a p.m. error $\Delta\mu$ is $\Delta M\propto 5\log{\it e}\frac {\Delta\mu} {\mu}$. Using $\log {\it e}=0.434$, we adopt $\Delta M=2.17\frac {\Delta\mu} {\mu}$ as the reliability in M resulting from the error in p.m.

The data for the stars in the variability sample catalog (VSC) is available on-line under anonymous ftp[*]. The catalog gives for each star the mean equatorial coordinates (Equinox 2000), V-magnitude (taken from the GSC 1.2), mean mb (from SOAP), mean dereddened colour index (B-V)0 (obtained by comparing the star's location in the (Hb, b-V) RPMD with the ( MB, [B-V]0) ridge-lines defined by Table 9 of Chiu 1980), short-term apparent magnitude scatter $\sigma _1$, long-term apparent magnitude scatter $\sigma _2$, error in absolute magnitude determination due to the p.m. component error $\sigma_3=2.17\frac {\Delta\mu} {\mu}$, annual p.m. in arcsec in galactic longitude $\mu_1$ and in galactic latitude $\mu_2$, derived parallax $\pi$ in milliarcsec, and a correlation coefficient c, which has values from 0 to 1.0 and will be explained later in our study. We also give our adopted classification of the star as a Pop. I main sequence (MS I), red giant (RG I), or white dwarf (WD I) or a Pop. II subdwarf (SD II), red giant (RG II) or horizontal branch (HB II) star based on the statistical HRD that results from the observed blue ($\approx$mb) and V magnitudes and p.m. components as explained in our previous studies (Fresneau 1990).

The kinematical information permits us to separate the star sample into H-burning or He-burning stellar candidates. We emphasize that, as for our variability criteria, this technique of stellar classification primarily allows one to identify a set of objects to be further investigated. Cuisinier et al. (1994) found they could identify halo dwarfs with a success rate of 10%. Smart et al. (2007) used a RPMD to identify extreme sub-dwarf candidates in the LHS Hipparcos-sample. These results show that a [Hb,b-V] RPMD cannot only be a substitute for the traditional HRD [ MB,(B-V)0] when parallax (hence absolute magnitude) is not available (Hertzsprung 1929), but also suggest that this is a straightforward way to explore a magnitude-limited stellar sample having only p.m. and apparent magnitudes in two passbands (Finch et al. 2007). This then makes it very attractive for extracting information from the extensive photographic surveys of the past (Luyten 1977; Gliese & Jahreiss 1980), even when work with century-old astrographic plate material generally relegated to history (Chinnici 2008) has an archaeological tinge. We recognize that modern CCD observations have significantly higher precision than photographic images from the past. However, our interest is in the possibility of using this largely neglected observational material on the most densely star-studded regions in the sky to harvest astrophysically interesting targets (for which there would be some baseline temporal information) for follow up by present day surveys (Munn et al. 2004; Kilic et al. 2006; Finch et al. 2007; Becker et al. 2004).

Figure 10 shows the statistical HRD for the VSC sample of $55\times 10^3$ stars using the values of (B-V)0 and absolute magnitude Mb obtained from the RPMD. Pop. I and Pop. II sequences (MS = main sequence, RG = red giants, HB = horizontal branch) are easily visible and are labeled. The plot parameters are Mb=0.772 Hb-3.12 and (B-V)0=0.84(mb-V)+0.38. This figure illustrates how a statistical HRD allows one to classify a star on the probability, from its kinematical properties, that it is a MS I, RG I, WD I, SD II, RG II or HB II star. We emphasize, however, that our classification technique based on ridge-lines forces stars to belong either the Pop. I or Pop. II sequence, without the possibility to fill any other locations in the diagram. We also label in the figure what we tentatively suggest to be an instability strip (I.S.) based on an excess of stars along the vertical line of approximately constant color $(B-V)_0\approx-0.1$ from Mb=1 to Mb=3 and down to the WD region. In the case of variability candidates, the identification of an instability strip (I.S.) location is probably a way to identify some potentially interesting targets among misclassified stars. A well-developed Red Giant Branch (RG I) at $M_b\simeq 2$ and $(B-V)_0\geq 0.6$ is identified redwards to the Hertzsprung gap. Little else can be said without additional observations on these targets other than there appears to be some kind of feature in the diagram (reflecting the I.S.) that extends from the HBII through the MS I and down to the hot WD regime.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f10.ps} \end{figure} Figure 10:

The statistical HRD for the Variable Sample Catalogue (VSC) set of $55\times 10^3$ targets.
Open with DEXTER

We again emphasize that Fig. 10 is just a convenient way to roughly classify stars in a survey with rudimentary information on colour and an RPM quantity. Our classification is not exact and does not yield pure Pop. I and Pop. II groups. For example, in the $55\times 10^3$ stars of Fig. 10, our classification gives $13\times 10^3$ Pop. II candidates and $42\times 10^3$ Pop. I candidates, which suggests poor classification efficiency since Pop. I stars should outnumber the Pop. II stars by a factor of about 500 (Bahcall & Casertano 1986). A set of 80% of all observed stars in a magnitude $(m_l\leq 14.5$) and distance ( $M_l\leq 10$) limited sample should lie on the main sequence MS I, not just a set of 60% as we observe (Allen 1973; Sowell et al. 2007). Nevertheless, the data are adequate statistically to investigate how stellar properties are correlated; this was demonstrated in a previous study where stars classified as Pop. I candidates were used to trace the thin disk kinematics in the solar neighborhood up to a distance of 500 pc (Fresneau et al. 2005).

6 Stellar variability information in the VSC

We use the VSC sample of $55\times 10^3$ stars from SOAP that have magnitudes determined from at least three separate plates and at least one set of three measures on the same plate to look for statistical stellar variability effects. We have, of course, to keep in mind the uncertainties of $0.45\pm 0.10$ for our apparent magnitudes and 1.0 for the estimated absolute magnitudes.

The two fundamental indicators of variability are the rms magnitude scatter indices $\sigma _1$ (called flickering) and $\sigma _2$ (the long-term apparent magnitude scatter). Because we want to associate the variability indicators with particular types of stars, as classified in Fig. 10, we also are interested in absolute magnitudes. Our derived absolute magnitudes have uncertainties arising from two sources: plate-to-plate differences in the measured apparent magnitudes and errors in the distance determinations. We therefore compute an additional scatter index $\sigma _3$ that results from the scatter in the p.m. $\Delta\mu$. The scatter $\sigma _3$can be used to estimate the errors in the absolute magnitude determinations that result from errors in the distance calculations. Therefore, we adopt as our measure for the uncertainty of a given absolute magnitude Mb in the VSC $\Delta M=\sqrt { {\sigma _2}^2 +{\sigma _3}^2}$. A particularly large value of $\Delta M$ may reflect either long-term variability $\sigma _2$ or an inaccurate distance determination.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f11.ps} \end{figure} Figure 11:

Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for the set of $55\times 10^3$ VSC stars plotted as a function of the apparent blue magnitude mb.
Open with DEXTER

Figure 11 shows how the three variability measures $\sigma _1$, $\sigma _2$, $\sigma _3$ depend on apparent magnitude mb. The $55\times 10^3$ points have been divided into 400 equally-spaced bins and each plotted point represents the rms of the value in a bin. We rediscover (as from Fig. 1) that stars brighter than mb=10 show the largest scatter, as is expected since these stellar images will tend to be overexposed. This indicates that the VSC sample should be considered a survey of moderately faint stars, in the apparent magnitude range $10\leq m_b\leq15$, for which $\sigma_1\simeq 0.5$ and $\sigma_2\simeq0.8$. We restrict the rest of our analysis to stars fainter than mb=10 (97% of the VSC).

Figures 12 and 13 show how the three variability indicators $\sigma _1$, $\sigma _2$, $\sigma _3$ depend on colour (B-V)0 and on computed absolute magnitude MB for stars with $m_b\geq 10$. We see that:

a.
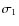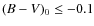$\sigma _1$, our measure of internal magnitude scatter on one plate, ranges from about 0.8 for $(B-V)_0\leq -0.1$ to 0.5 for 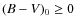$(B-V)_0\geq 0$;

b.
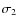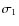$\sigma _2$, the scatter in long-term variability in apparent magnitude, which is our indicator of the random plate-to-plate error, is systematically larger than $\sigma _1$ and fluctuates between 0.7 and 0.9;

c.
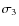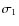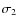$\sigma _3$, the p.m. contribution to the absolute magnitude uncertainty, averages 0.3 or less, significantly smaller than both $\sigma _1$ and $\sigma _2$, i.e. the photometric measurement errors.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f12.ps} \end{figure} Figure 12:

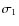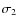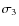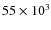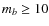Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for the set of $55\times 10^3$ VSC stars plotted as a function of the colour (B-V)0 for stars of $m_b\geq 10$.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f13.ps} \end{figure} Figure 13:

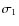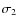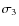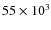Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for the set of $55\times 10^3$ VSC stars with 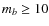$m_b\geq 10$ plotted as a function of absolute magnitude Mb (as estimated from the statistical HRD of Fig. 10).
Open with DEXTER

We adopt $0.45\pm 0.10$ as the typical error for measurement of a magnitude on a given plate and 0.8 as the typical scatter from measures on different plates. The small values of $\sigma _3$ show errors in the distance determinations have a small effect on the uncertainties in the absolute magnitudes. Since we observed $\Delta\mu\approx0.003''$ yr-1 and $\mu \geq 0.02''$ yr-1, we duly observe $\sigma_3\approx 0.2$.

Figure 12 shows that $\sigma _1$ and $\sigma _2$ are significantly larger than the typical values of 0.5 and 0.8, respectively, for the bluest $(B-V)_0\leq -0.1$and reddest $(B-V)_0 \geq 0.9$ stars. Figure 13 shows similar anomalously large variations for the intrinsically brightest ($M_B\leq 2$) and faintest ( $M_B \geq 5$) objects. Taken together, the two diagrams indicate that, statistically, there is greater stellar variability for our probable OB stars and hot white dwarfs, supergiants and red giants and faint red stars. This is consistent with observations (Gautschy & Saio 1995, 1996). We note that we rediscover that stellar flaring candidates should be searched for in the region $(B-V)_0\geq1.2$ and $M_B \geq 5$ (Fresneau et al. 2001). We must keep in mind that these are statistical results and merely suggest the types of stars in our sample that appear to be the best candidates for follow up studies.

In an attempt to quantify the success rate of our simplified classification, we give in Table 2 the numbers of stars in the statistical HRD of Fig. 10 found when separated according to $\sigma_1=0.4$ (considered as the lowest level to consider flickering activity as significant) and $\sigma_2=1.2=3\sigma_1$, which we adopted as our criteria for possible long-term variability. We find that neither the flickering nor long-term variability candidates fall into well-defined classes. For instance, in all groups the percentage of candidates classified as MS I is on the order of 60%, when the real percentage is 80% for stars of absolute magnitude brighter than 10 in the solar neighborhood (Allen 1973). We conclude that $\sigma _1$ and $\sigma _2$ by themselves are not useful for improving the classification of the VSC stars. We will show in the next section, however, that a correlation between $\sigma _1$ and $\Delta M=\sqrt { {\sigma _2}^2 +{\sigma _3}^2}$ can be used to improve the segregation of the stellar system into dwarfs and giants.

Table 2:   Distribution of the numbers of stars fainter than mb=10 in the statistical HRD of Fig. 10 separated into groups according to $\sigma _1$ and $\sigma _2$ levels.

7 Construction of a power-law for a scattering process with a dynamical time

In Fig. 8 we showed we could distinguish two distinct components of our stellar system, those with $(B-V)_0\leq 0.62$ and a galactic scale-height of 50 pc and those with $(B-V)_0 \geq 0.62$ and a scale-height of 100 pc. At this point we want to explore how our variability statistics depend on the time to cross the thin disk of the Milky Way, since we distinguished in Fig. 8 two components of the stellar system with $(B-V)_0\leq 0.62$ (and a scale-height of 50 pc) and with $(B-V)_0 \geq 0.62$ (and a scale-height of 100 pc).

We consider the dynamical time t (in Myr) for the crossing of a star as t =  $\mid\!\! \!\frac {z} {w}\!\! \!\mid$ where z (in pc) is the star's altitude above the galactic plane and w (in km s-1) is its velocity perpendicular to the plane. The w-velocity can be computed from the p.m. component in galactic latitude $\mu_2$, the distance d (in pc) and the galactic latitude b: w=4.73  $d\mu_2\cos~b$. We ignore the line-of-sight (los) velocity and we again restrict the sample to stars with total p.m. $\mu \geq 0.02''$ yr-1, which converts to a maximum distance of 500 pc if the mean velocity is $\approx$50 km s-1. The effect of the los-velocity on w depends on $\sin~b$, and our stellar sample along the galactic meridian verifies $\mid\!\! b\!\!\mid$ $\leq$ $64^\circ$, indicating that the los-velocity needs to be on the order of 75 km s-1 to have an effect on w of 50 km s-1. We also restrict the analysis to stars with $z\leq 100$ pc (a sample of $29\times 10^3$ VSC stars), where a thin disk crossing effect has previously been detected (Fresneau et al. 2007). Figure 14 shows the trends of $\sigma _1$, $\sigma _2$, and $\sigma _3$ as a function of dynamical time t. We observe that, while the $\sigma _3$ relation is relatively flat, $\sigma _1$ and $\sigma _2$ show the same upturn for $t\leq 1$ Myr. This suggests that stellar variability may be correlated with the dynamical crossing time t for $t~\leq ~1$ Myr. A strong correlated increase in $\sigma _1$ ($\geq$0.5) and $\sigma _2$ ($\geq$0.8) is seen when $t\leq 1$ Myr.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f14.ps} \end{figure} Figure 14:

Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for stars with $m_b\geq 10$ plotted as a function of computed thin disk crossing time t.
Open with DEXTER

We now use this dynamical time t =  $\mid\!\! \!\frac {z} {w}\!\! \!\mid$ as a convenient time-scale (in error on the order of 20%) to look for kinematical evolutionary effects[*]. We investigate how the $\frac {\sigma_w} {\sigma_v}$-ratio depends on t when $t\leq 6$ Myr, where w and v are respectively the velocity components perpendicular to the galactic plane (w positive in the direction of the north galactic pole and v in the direction of the galactic rotation) $v=4.74\mu_2d~\sin~b\sin~l+4.74\mu_1d\cos~b~\cos l$. Again, we ignore the los-velocity since along the galactic equator $\mid\!\!\! b\!\!\!\mid$ $\leq$ $7^\circ$ and $l\approx 330^\circ$ along the galactic meridian. The nuclear age-velocity relations (AVR) for old stars (age $\geq$ 4 Gyr) are flat while for young stars the total velocity dispersion increases as the square root of the stellar age (Binney & Merrifield 1998; Bernkopf & Fuhrmann 2006; Holmberg et al. 2007; Fuhrmann 2008). The time-scale that we consider ($t\leq 6$ Myr) is short compared to the Gyr-length of the AVR relations. Therefore, our observed variability effect when $t\leq 1$ Myr must be due to some other factor (we will assume it is photospheric activity) and we search for some kinematical signature in $\frac {\sigma_w} {\sigma_v}$ over the same time scale. The increase of $\frac {\sigma_w} {\sigma_v}$ with time has been investigated on a theoretical basis (Spitzer & Schwarzshild 1953; Lacey 1984) and suggested to be the consequence of a rotation mechanism due to collisions.

One can assume a stellar system with its own intrinsic relaxation mechanism (Gilmore et al. 1989) and can hypothesize that the $\frac {\sigma_w} {\sigma_v}$-trend is due to spatial diffusion of stellar groups caused by viscous stress in the relative rotation of the gaseous and stellar disks. This suggests that the scattering of stars by spiral features in the thin disk (Toomre 1964; Goldreich & Lynden Bell 1965; Jenkins & Binney 1990) can be explored by measuring $\frac {\sigma_w} {\sigma_v}$.

As in our previous study (Fresneau et al. 2007), we use a stepwise regression method to minimize the relation between the computed v and w stellar velocity components according to a Schwarschild ellipsoidal velocity distribution in the solar neighborhood (Binney & Merrifield 1998):

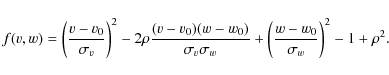
\begin{displaymath}f(v,w)= \left(\frac {v-v_0} {\sigma_v}\right)^2 -2\rho\frac {... ..._v\sigma_w} +\left(\frac {w-w_0} {\sigma_w}\right)^2-1+\rho^2. \end{displaymath}

The velocity ellipse of a stellar sample is described by its center (v0, w0), the length of the major and minor axes $\sigma_v,\sigma_w$ and the inclination $\theta=\frac {1} {2}\arctan\frac {\rho\sigma_w\sigma_v} {{\sigma_v}^2-{\sigma_w}^2}$ of the major axis to the (v, w)-plane. While this formulation is mainly descriptive (old stars have larger velocity dispersions $\sigma_v$, $\sigma_w$ than the young ones), it is a key tool in the study of the kinematics and the structure of various galactic components in the solar neighborhood. In particular, the alignment of the velocity ellipsoid major axis with the direction to the galactic center (Famaey et al. 2008) is a way to investigate the galactic potential. Here we consider the ratio $\frac {\sigma_w} {\sigma_v}$ to be a signature of some physical process at work during the 6 Myr time-scale we detected in our stellar sample.

From our observations, we compute the velocities $ v=4.74 \mu_2d~\sin{l}~\sin{b}+4.74\mu_1d~\cos{b}\cos{l}$, $w=4.74\mu_2d~\sin{b}$, for each star at distance d (in pc) and galactic coordinates (l,b), assuming one more time that the lack of information on the los-velocity does not introduce any error larger than 20 km s-1.

The use of a velocity ellipse is just a convenient way to describe a stellar system. We want to explore the evolution of $\frac {\sigma_w} {\sigma_v}$ over a time-scale of a few Myr connected to a crossing time of the galactic thin disk. We consider $32\times 10^3$ stars out of the set of $55\times 10^3$ VSC stars that have a height above the galactic plane $z\leq 100$ pc. The $32\times 10^3$ stars were grouped into sets of 105 objects in order to get a weight $\propto\!\!\sqrt{100}$ in our mean estimate for the 5 unknowns v0, u0, $\sigma_v$, $\sigma_w$, $\rho$ of each 105 star group ordered by increasing mean dynamical time t. This weight of $\sqrt{100}$ suggests expected mean errors in the estimates of (V0, W0, $\sigma_V$, $\sigma_W$) of 5 km s-1, since the transverse velocity is $T\approx 50$ km s-1. Figure 15 plots the $\frac {\sigma_w} {\sigma_v}$ velocity-dispersion ratio, derived from a weighted least squares fit to f( v,w)=0, for the various 105-star groups as a function of mean crossing time t for those groups with $t\leq 6$ Myr. The ratio $\frac {\sigma_w} {\sigma_v}$ measures the anisotropy of the velocity ellipse. We observe a weak, but definite correlation between $\log\frac {\sigma_w} {\sigma_v}$ and $\log{(t)}$. A simple linear fit produces the power law: $\frac {\sigma_w} {\sigma_v} =(0.45\pm0.01)~t^{0.26\pm0.03}$ (t in Myr). The derived power law suggests the existence of some relaxation mechanism, lasting on the order of an equipartition time of t0=6 Myr, in order that the velocity ellipse be stabilized at its known value of $\frac {\sigma_w} {\sigma_v}\approx 0.7 (0.7=0.45{t_0}^{0.26})$for stars in the solar neighborhood (Dehnen & Binney 1998; Binney et al. 2000). The derived power law exponent of the order of $\frac {1} {4}$, suggests that the relaxation for the selected stellar system is faster than the increase of total velocity dispersion with age, which is about a power law with an exponent $\frac {1} {2}$.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f15.ps} \end{figure} Figure 15:

The ratio $\frac {\sigma_w} {\sigma_v}$ is fitted to a power-law with the mean dynamical crossing time t as argument.
Open with DEXTER

We cannot explore further the evolution of the stellar velocity ellipse given the rudimentary nature of our data. We will only use the observed correlation of $\frac {\sigma_w} {\sigma_v}$ with dynamical time $\leq$6 Myr to justify a way for selecting candidates for stars with photospheric activity suspected to have lasted over that 6 Myr time-scale.

8 Stellar flickering for giant and dwarf stellar candidates

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f16.ps} \end{figure} Figure 16:

The short-term $\sigma _1$ and long-term $\Delta M=\sqrt { {\sigma _2}^2 +{\sigma _3}^2}$ magnitude scatters are correlated differently for probable giant and dwarf stars.
Open with DEXTER

In order to be able to compare stars of similar physical type, we use for our measure of long-term variability our absolute magnitude parameter $\Delta M=\sqrt { {\sigma _2}^2 +{\sigma _3}^2}$ rather than $\sigma _2$ variation in apparent magnitude. We recall that $\sigma_3 \ll \sigma_2$, so the error resulting from the uncertainty in the distance determination has a small effect on $\Delta M$. It follows that particularly large $\Delta M$ values are indicators of possible long-term variability.

We can now investigate two indicators that are related to possible changes in stellar luminosity: $\sigma _1$, which measures short-term absolute (as well as apparent) magnitude scatter, and $\Delta M$, which largely measures the long-term absolute magnitude scatter. We present in Fig. 16 the relationship between the observed short-term ($\sigma _1$) and long-term ($\Delta M$) scatter for the 105-star groups of Fig. 15 whose individual velocity ellipses f(v,w)=0 fit reasonably well (at a $\chi^2$ of 15% level) the derived power law $\frac {\sigma_w} {\sigma_v} = At^\alpha$ adopted in the previous section ( $A=0.45\pm0.01$, $\alpha=0.26\pm0.03$, t =  $\mid\!\!\frac {z} {w}\!\!\mid$). Our requirement of a reasonable power law fit led to the rejection of about 50% of the VSC stars. The resulting set of $23\times 10^3$ objects are plotted with different symbols for the H-burning and He-burning stars, as determined by our kinematical classification. We notice conspicuous correlations between the short-term $\sigma _1$and long-term $\Delta M$ scatters that are different for the two types of stars. The differing relations suggests a variability mechanism related to stellar radius, probably pulsation (Cox 1980).

Table 3:   Distribution of the numbers of probable giants and dwarfs in the VSC according to the correlation level c and at an altitude z above the galactic plane.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f17.ps} \end{figure} Figure 17:

The statistical HRD for the giant and dwarf candidates that fit the trends shown in Fig. 16 with a probability of 75%.
Open with DEXTER

We observe that $\Delta M \approx 0.8$ could be a simple criterion to help segregate dwarfs and giants. We improve upon this by using the trends found in Fig. 16 of $\sigma_1\propto(0.89\pm0.03)\Delta M$ for dwarfs and $\sigma_1 \propto (1.13\pm0.04)\Delta M $for giants to improve our classification of the VSC stars into H-burning or He-burning candidates. We compute a correlation coefficient c that reflects the probability for a star being part of a Gaussian distribution around one or the other of the two trend lines, i.e. either for H-burning or for He-burning candidates, marked in Fig. 16. This coefficient, which ranges from 0 to 1, reflects how well correlated are the short-term and long-term magnitude scatters for a star. Table 3 gives the numbers of stars at different levels of c for the various stellar types as determined from the statistical HRD (WD I = white dwarfs, MS I = main sequence stars, RG I = red giants of Pop. I, SD II = subdwarfs, RG II = red giants of Pop. II, HB II = blue horizontal branch stars) and at an altitude z above the galactic plane. We suggest that the Pop. I stellar system with $c\geq\frac {3} {4}$ and $\mid\! \!z \!\!\mid $ $\leq$ 100 pc is the most appropriate distance-limited sample in view of the numbers of MS I and RG I candidates.

 \begin{figure} \par\includegraphics[width=9cm,clip]{10798f18.ps} \end{figure} Figure 18:

The statistical HRD for the possible optical counterparts of X-ray sources.
Open with DEXTER

It must be remembered that the stars in Fig. 16 are only suspected variables, i.e. there are both stars that are indeed varying and ones for which the variability is an artifact of errors in the data. The (Mb,[B-V]0)-diagram for those objects most likely to be true variables, i.e. those with $c\geq\frac {3} {4}$, is shown Fig. 17. We immediately see that this statistical HRD shows mostly dwarfs - both Pop. I and Pop. II - along with some Pop. I red giants; there are few evolved Pop. II stars (RG II and HB II stars). The tentative instability strip is marked. We feel that it is the blue objects in this region, that is those stars with $(B-V)_0\leq 0$, that have the most probability of being actual variables. We suggest that these probable O, B, and A0 stars are the most interesting objects for follow up studies. This shows the improvement in the classification of stars compared to Fig. 10 by adding the fitting criterion of Fig. 16. The suggested instability strip (I.S.) extending from the Blue Horizontal Branch through the ZAMS and down to the hot WD I candidates is shown.

Table 4:   List of VSC stellar candidates as possible optical counterparts of known X-ray sources.

The poor time coverage and our restriction that all stars in the VSC catalog appear on at least three plates (see Sect. 5) makes identifying long-period variables such as Mira's more difficult because of the probability that their large amplitudes caused them to be too faint to appear on one or more of the three plates of a field. Therefore, we have focused the test of our selection procedure on our suspected short-period variables. We have matched the list of the VSC stars plotted in Fig. 17 with the Rosat All Sky Survey (ROSAT) in order to see if larger than normal short-term photometric scatter indeed identifies some known and suspected variables, in this case known X-ray emitters suspected to be pre-main sequence stars (PMS). The typical positional uncertainty of ROSAT is around 15 arcsec, but for some sources it is as large as 40 arcsec. We used a conservative search radius of 15 arcsec which resulted in 67 possible coincidences that are presented in Table 4. It is obvious that some of these are simply chance since the VSC stars are extracted from a deep survey down to $m_b \approx 14.5$ and in some cases the star density makes a coincidence with a low-accuracy ROSAT position likely. Nevertheless, we were pleased to find that larger than normal photometric scatter identifies some known and probable variables, which we classified as Pop. I candidates with $c\geq\frac {3} {4}$. In 13 cases, our star had previously been identified as the X-ray source: 7 PMSs, 2 CanVen stars, 2 Algol-type stars, one emission-line star and one BY Dra variable (Caillault 1982). The only information that supports any of the other candidates being the X-ray source is the positional agreement with the VSC arcsecond precise coordinates. We plot in Fig. 18 the set of 67 candidates, which seems to show that a larger than expected number of stars are bluewards to the Parenago's discontinuity. We also show in Fig. 18 the lines that border our suspected instability region (the line on the left is from the VSC analysis and shown in Fig. 17). The statistical HRD for the possible optical counterparts of X-ray sources with crossing time of the thin disk $t\leq 6$ Myr suggests a lower level for the instability strip suggested in Fig. 17. In order to say more, our list of stars with suspected photospheric activity needs follow-up observations, particularly for the bluer candidates in order to check our prediction these stars in a non-quiescent state and to explore our tentatively-identified instability strip. The stars in Table 4 with no specific type archived in Simbad could be good targets of opportunity to establish if they are active stars and intrinsic X-ray emitters. For stars on the main sequence, two mechanisms are known to be responsible for the possible X-ray emission. In O and early B-type stars, the X-rays are produced by instabilities arising in stellar winds (Lucy & White 1980; Owocki & Cohen 1999) and in late-type stars a solar-like magnetic dynamo is thought to heat and confine hot coronal plasma which is a tracer of stellar activity (Parker 1955). Fairly low-mass dwarfs are known to show anomalous strong activity when they are rapidly rotating (with periods in the 5-10 day range). We suggest therefore the observation of v$\sin{i}$ among these targets to confirm the observed correlation between the blue bright stellar outbursts and the dynamical crossing time t.

9 Does the VSC reveal any true interesting behavior?

We have stressed that we are dealing with only variability indicators - short-term and long-term magnitude dispersions - for stars tentatively classified as giants, dwarfs or other types using kinematical properties. Our results are only statistical in nature in view of the very rudimentary way we segregate giants from dwarfs in the RPMD. We used a relation derived from the RPMD between total p.m. $\mu$ and parallax $\pi$ that follows from the known values in the solar neighborhood of $T\leq 20$ km s-1 if $(B-V)_0 \leq 0.45$ and $T\geq45$ km s-1 if $(B-V)_0 \geq 0.85$ (Dehnen & Binney 1998). Then we classify the VSC stars into different groups based how close a star lies to one or another of the well-calibrated Pop. I and II ridge-lines. While this appoach is judged adequate for a quick-look investigation of a physical mechanism linked to a stellar radius, such an automated classification procedure will obviously be misleading in many cases.

We propose $\sigma _1$ and $\Delta M=\sqrt { {\sigma _2}^2 +{\sigma _3}^2}$as possible indicators of variability that can also serve to improve our classification into H-burning and He-burning stars for those candidates at an altitude over the galactic plane $\vert z\vert\leq 100$ pc. Thus, this work is essentially just an exploratory analysis to see what might be extracted from data obtained from a photographic survey that was intended exclusively for charting purposes. Confirmation and understanding of our tentative findings will need follow-up observations (Fresneau et al. 2001).

Obviously, our low-accuracy data cannot be used for thorough analyses. Rather, we have used the data to come up with a manageable list of targets for further study (Jenkins et al. 2006; Waelkens et al. 1998). For example, by restricting the interesting candidates to those VSC stars that meet the criteria $c\geq\frac {3} {4}$ and $\vert z\vert\leq 100$ pc, one has a target list suitable for checking our observed correlations between short-term and long-term magnitude variations. Such a target list would be very appropriate for follow up using current all-sky monitoring programs such as ROTSE (Akerlof 2000; Akerlof et al. 2003) and ASAS (Pojmanski 2004; Wozniak 2004).

10 Selected areas for monitoring the VSC behavior

The positions in the SOAP, SOGS and VSC catalogs are sufficiently accurate that the stars are readily identified and hence the reality of the short-term magnitude variations for given stars could be readily confirmed using modern epoch surveys (Barron et al. 2008; Pojmanski & Maciejewski 2004). In order to identify targets for detailed study, such as photometric or spectroscopic monitoring (Jenkins et al. 2006), we have prepared two files suitable for investigating our tentative findings, first a correlation between flickering and long-term variability and second a correlation between long-term variability and galactic plane crossing time $t=\vert\frac {z} {w} \vert$ when $t\leq 6$ Myr.

The first list has 236797 stars along the galactic equator section $l\in[275^\circ,335^\circ]$ and $b\in[-7^\circ,7^\circ]$ suitable for monitoring flickering and long-term magnitude scatter[*]. The second list has 164691 stars along the galactic meridian segment $l=(330\pm 5)^\circ$, $b\in[-64^\circ,-7^\circ]$[*] that is suitable for exploring long-term magnitude scatter as a function of crossing time. We suggest that crossings of the Sagittarius Spiral Arm could be investigated by adding los-velocity information on the targets, such as could be provided by current observing programs (Minchev & Quillen 2008). The objects in both lists contain data on galactic thin disk kinematics (derived from the stars' p.m. components and the statistical parallaxes), and we suggest these as potential tracers of the interface between the thin and thick disks in the solar neighborhood (Fresneau et al. 2007). Each target file has for each star the J2000 equatorial coordinates, p.m. in galactic components (in ''yr-1), our estimated statistical parallax and its error (in 10 $^{-3\prime\prime}$), apparent V-magnitude (from GSC1.2), mean mb and its scatter and mean epoch. The files are accessible at ftp://cdsarc.u-strasbg.fr/incoming/fresneau/havs.

11 Conclusion

The Sydney Observatory Astrographic Program (SOAP) was part of an extensive photographic survey of the southern sky (Pickering 1903) that took over 40 years (1892-1932) to complete (White 1988). Unfortunately, the program lasted too long (Hearnshaw 1996) and this rich set of data from four decades of observations has never been fully analyzed. The only results were positions and rough magnitudes ($\pm$0.4) for stars brighter than 12th mag that were used in the Sydney Observatory's contributions to the astrographic catalog (Urban et al. 1998) and a list of double stars noted on the plates (Barton 1937).

New measurements of previously unstudied plates has produced a catalog of $5\times 10^5$ stars (the SOGS), the data for which is available on-line thanks to the VizieR data mining system. Present day surveys (such as SDSS, OGLE, DENIS, 2MASS, and UKIDSS) are plainly superior and photographic surveys are now obsolete. One might therefore question the value of the SOGS data, given the low accuracy ($\pm$0.3 arcsec in equatorial coordinates, $\pm$0.4 in derived magnitudes), but the early epoch permits such things as improving p.m. (Frankowski et al. 2007), separating physical visual binaries from optical pairs (Lopez 2003; Ficher 1975), and detecting stellar changes with time scales of centuries (Lopez 2004). We have applied to one early survey an automated procedure to identify in a RPMD stellar candidates of special interest - in this case ones with interesting photospheric activity.

Previous exploratory work has shown that these data can be used to study stellar kinematics in the Galaxy. Results were the detection of a density wave linked to the Sagittarius spiral arm (Fresneau et al. 2005, 2007) and evidence of the deflection of galactic orbits by the Southern Coalsack (Fresneau et al. 2003). Our present study suggests evolution of the stability of the stellar system with time, given that the $\frac {\sigma_w} {\sigma_v}$ ratio of the velocity ellipse apparently increases from 0.45 up to 0.75 over about 6 Myr. Further, for this time scale we found a tentative correlation between photometric flickering and long-term variability that differs for giants and dwarfs, and can therefore be used to help segregate stars into these classes.

We produced a statistical HRD of suspected variables, and showed that it can be improved through the observed scatter of the photometric measures of different observations of the same star. The result is a set of $55\times 10^3$ potential variable stars that we call the Variable Sample Catalog (VSC). The catalog contains objects brighter than about mb=14, suspected of rapid variations (approximately 30 min time scale) as well as on longer scales in the years 1892-1932. The stars with $(B-V)_0\leq 0$are considered the most interesting objects for follow up studies. The catalog is accessible through anonymous ftp[*]. The VSC archival material leads to a target list for monitoring by modern ground-based surveys, especially automated wide-field programs that observe the sky on a time scale of hours (Eyer & Blake 2005). Our tentative identification of flickering effects on moderately faint stars shows that the systematic study of the archival material can be valuable (van Genderen et al. 1997), especially along the Galaxy equator.

Acknowledgements
We thank Christian Motch from Strasbourg astronomical observatory for his advice in the matching process by stellar coordinates of our results with the Rosat All Sky Survey. We thank the referee for his (or her) constructively critical reviews that improved the clarity of our paper.

References

Footnotes

... Survey[*]
Data files are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/503/1023
... system[*]
http://vizier.u-strasbg.fr/viz-bin/VizieR
... ftp[*]
ftp://cdsarc.u-strasbg.fr/incoming/fresneau/havs/vsc.dat
... effects[*]
We note that the Sun, with an altitude of 15 pc (Binney et al. 1998a; Hammersley et al. 1995; Drimmel & Spergel 2001) above the galactic plane and an upwards velocity of 9 km s-1 (Stothers 1998; Torbett 1986) crossed the galactic equator about 1.5 Myr ago.
... scatter[*]
ftp://cdsarc.u-strasbg.fr/incoming/fresneau/havs/equator.dat
...$b\in[-64^\circ,-7^\circ]$[*]
ftp://cdsarc.u-strasbg.fr/incoming/fresneau/havs/meridian.dat
... ftp[*]
ftp://cdsarc.u-strasbg.fr/incoming/fresneau/havs/vsc.dat

All Tables

Table 1:   Distribution of the B1900.0 centers of the 1400 $2^\circ \times 2^\circ $ fields of the Sydney Observatory Astrographic Program.

Table 2:   Distribution of the numbers of stars fainter than mb=10 in the statistical HRD of Fig. 10 separated into groups according to $\sigma _1$ and $\sigma _2$ levels.

Table 3:   Distribution of the numbers of probable giants and dwarfs in the VSC according to the correlation level c and at an altitude z above the galactic plane.

Table 4:   List of VSC stellar candidates as possible optical counterparts of known X-ray sources.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f1.ps} \end{figure} Figure 1:

The mean error in measured magnitude as a function of apparent magnitude mb.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f2.ps} \end{figure} Figure 2:

The cumulative frequency of the magnitude errors is plotted for observations performed after and before 1915.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f3.ps} \end{figure} Figure 3:

The numbers N of foreground and background stars as function of the apparent magnitude $m_b\geq 10$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f4.ps} \end{figure} Figure 4:

Number N of stars with $m_b\geq 10$ as a function of the quantity Hb.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f5.ps} \end{figure} Figure 5:

The relation between absolute magnitudes from objective prism spectra (MB) and the RPM quantity Hb for a set of 104 stars in SOGS.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f6.ps} \end{figure} Figure 6:

The absolute magnitude Mb derived from the calibration of Fig. 5, is plotted as function of the colour index (b-V).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f7.ps} \end{figure} Figure 7:

Numbers N of foreground ( $\mu \geq 0.02''$ yr-1) and background ( $\mu \leq 0.02''$ yr-1) stars with $m_b\geq 10$ according to the color derived from the adjustment of Hb to a ( MB,(B-V)0) ZAMS.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f8.ps} \end{figure} Figure 8:

Numbers N of stars ( $m_b\geq 10$) as function of the altitude z above the galactic plane.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f9.ps} \end{figure} Figure 9:

The reduced proper motion diagram (RPMD) [Hb,(b-V)] of the VSC stars that results by converting to a Mb, (B-V)0 diagram by applying the relations Mb=0.86 Hb-3.6 and (B-V)0=0.82(b-V)+0.26 as determined from Figs. 5 and 6.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f10.ps} \end{figure} Figure 10:

The statistical HRD for the Variable Sample Catalogue (VSC) set of $55\times 10^3$ targets.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f11.ps} \end{figure} Figure 11:

Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for the set of $55\times 10^3$ VSC stars plotted as a function of the apparent blue magnitude mb.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f12.ps} \end{figure} Figure 12:

Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for the set of $55\times 10^3$ VSC stars plotted as a function of the colour (B-V)0 for stars of $m_b\geq 10$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f13.ps} \end{figure} Figure 13:

Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for the set of $55\times 10^3$ VSC stars with $m_b\geq 10$ plotted as a function of absolute magnitude Mb (as estimated from the statistical HRD of Fig. 10).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f14.ps} \end{figure} Figure 14:

Short-term $\sigma _1$ and long-term $\sigma _2$ apparent magnitude scatters and the absolute magnitude uncertainty $\sigma _3$ due to p.m. error for stars with $m_b\geq 10$ plotted as a function of computed thin disk crossing time t.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f15.ps} \end{figure} Figure 15:

The ratio $\frac {\sigma_w} {\sigma_v}$ is fitted to a power-law with the mean dynamical crossing time t as argument.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f16.ps} \end{figure} Figure 16:

The short-term $\sigma _1$ and long-term $\Delta M=\sqrt { {\sigma _2}^2 +{\sigma _3}^2}$ magnitude scatters are correlated differently for probable giant and dwarf stars.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f17.ps} \end{figure} Figure 17:

The statistical HRD for the giant and dwarf candidates that fit the trends shown in Fig. 16 with a probability of 75%.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{10798f18.ps} \end{figure} Figure 18:

The statistical HRD for the possible optical counterparts of X-ray sources.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.