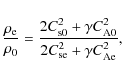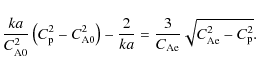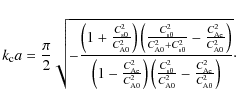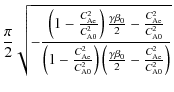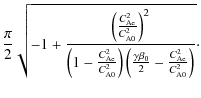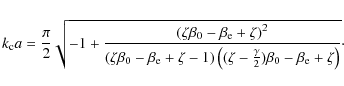| Issue |
A&A
Volume 503, Number 2, August IV 2009
|
|
|---|---|---|
| Page(s) | 569 - 575 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912088 | |
| Published online | 02 July 2009 | |
Characteristics of magnetoacoustic sausage modes
A. R. Inglis - T. Van Doorsselaere - C. S. Brady - V. M. Nakariakov
Centre for Fusion, Space and Astrophysics, Physics Department, University of Warwick, Coventry, CV4 7AL, UK
Received 17 March 2009 / Accepted 4 June 2009
Abstract
Aims. We perform an advanced study of the fast magnetoacoustic sausage oscillations of coronal loops in the context of MHD coronal seismology to establish the dependence of the sausage mode period and cut-off wavenumber on the plasma-![]() of the loop-filling plasma. A parametric study of the ratios for different harmonics of the mode is also carried out.
of the loop-filling plasma. A parametric study of the ratios for different harmonics of the mode is also carried out.
Methods. Full magnetohydrodynamic numerical simulations were performed using Lare2d, simulating hot, dense loops in a magnetic slab environment. The symmetric Epstein profile and a simple step-function profile were both used to model the density structure of the simulated loops. Analytical expressions for the cut-off wavenumber and the harmonic ratio between the second longitudinal harmonic and the fundamental were also examined.
Results. It was established that the period of the global sausage mode is only very weakly dependent on the value of the plasma-![]() inside a coronal loop, which justifies the application of this model to hot flaring loops. The cut-off wavenumber
inside a coronal loop, which justifies the application of this model to hot flaring loops. The cut-off wavenumber ![]() for the global mode was found to be dependent on both internal and external values of the plasma-
for the global mode was found to be dependent on both internal and external values of the plasma-![]() ,
again only weakly. By far the most important factor in this case was the value of the density contrast ratio between the loop and the surroundings. Finally, the deviation of the harmonic ratio P1/2P2 from the ideal non-dispersive case was shown to be considerable at low k, again strongly dependent on plasma density. Quantifying the behaviour of the cut-off wavenumber and the harmonic ratio has significant applications to the field of coronal seismology.
,
again only weakly. By far the most important factor in this case was the value of the density contrast ratio between the loop and the surroundings. Finally, the deviation of the harmonic ratio P1/2P2 from the ideal non-dispersive case was shown to be considerable at low k, again strongly dependent on plasma density. Quantifying the behaviour of the cut-off wavenumber and the harmonic ratio has significant applications to the field of coronal seismology.
Key words: magnetohydrodynamics (MHD) - Sun: corona - Sun: oscillations - Sun: flares
1 Introduction
In recent years, improvements in instrumentation, data analysis techniques, and theory have led to confirmed observations of magnetoacoustic waves in the solar corona, particularly the longitudinal, kink, and sausage modes (e.g. Nakariakov & Verwichte 2005). These waves attract attention mainly because of the possible role they play in coronal heating and as natural probes of coronal plasma. The latter concept gave rise to MHD coronal seismology, the novel approach to coronal plasma diagnostics by means of MHD waves.
The sausage mode (also known as peristaltic or m=0 mode) is a symmetric perturbation of the loop minor radius, in the form of periodic broadening and narrowing of a plasma tube (see Fig. 1). This mode, with typical periods in the range 5-30 s, is believed to be detected in the microwave and hard X-ray emission associated with flaring solar loops (e.g. Nakariakov et al. 2003; Inglis et al. 2008; Melnikov et al. 2005), and also in H![]() emission from cool, post-flare loops (Srivastava et al. 2008). The sausage mode is essentially compressible, with the density perturbations in phase with the perturbations of the magnetic field and in anti-phase with the perturbations of the loop minor radius. This mode is a robust collective disturbance of a plasma structure, which is practically insensitive to small scale irregularities of the plasma (Pascoe et al. 2007a). The sausage mode can be manifest in both standing and travelling form. It is highly dispersive, with a pronounced dependence of the phase and group speeds upon the wave number. In the standing regime, this makes the spectrum of the resonant frequencies of different spatial harmonics non-equidistant. Long wavelength (in comparison with the minor radius of the oscillating loop) sausage modes are subject to a cut-off, in contrast with all other (kink and various fluting or ballooning) magnetoacoustic modes. Modes with wavelengths longer than the cut-off
are leaky, and their phase speed is slightly higher than the external Alfvén speed (Pascoe et al. 2007b). For shorter wavelengths, sausage modes are trapped in the guiding structure, and have phase speeds in the range between the internal and external Alfvén speeds. This cut-off wavelength is dependent on the density contrast between the loop and its surroundings. As flaring loops are usually dense, thick and short, both trapped and leaky regimes can occur. The main properties of the sausage mode are derived from the straight cylinder or slab model. Clearly, the slab and the cylindrical cases are not identical, as has been discussed in Kopylova et al. (2007). In particular, Terradas et al. (2006) demonstrated the important difference in the wave leaking between these geometries. However, the difference in geometry should not be the principal difference in the resonant periods of sausage modes, as the behaviour of this mode is known to be almost identical in the slab and cylinder geometries in the trapped regime. Future study of the sausage mode of a plasma cylinder will provide a final answer, but is out of the scope of this paper.
emission from cool, post-flare loops (Srivastava et al. 2008). The sausage mode is essentially compressible, with the density perturbations in phase with the perturbations of the magnetic field and in anti-phase with the perturbations of the loop minor radius. This mode is a robust collective disturbance of a plasma structure, which is practically insensitive to small scale irregularities of the plasma (Pascoe et al. 2007a). The sausage mode can be manifest in both standing and travelling form. It is highly dispersive, with a pronounced dependence of the phase and group speeds upon the wave number. In the standing regime, this makes the spectrum of the resonant frequencies of different spatial harmonics non-equidistant. Long wavelength (in comparison with the minor radius of the oscillating loop) sausage modes are subject to a cut-off, in contrast with all other (kink and various fluting or ballooning) magnetoacoustic modes. Modes with wavelengths longer than the cut-off
are leaky, and their phase speed is slightly higher than the external Alfvén speed (Pascoe et al. 2007b). For shorter wavelengths, sausage modes are trapped in the guiding structure, and have phase speeds in the range between the internal and external Alfvén speeds. This cut-off wavelength is dependent on the density contrast between the loop and its surroundings. As flaring loops are usually dense, thick and short, both trapped and leaky regimes can occur. The main properties of the sausage mode are derived from the straight cylinder or slab model. Clearly, the slab and the cylindrical cases are not identical, as has been discussed in Kopylova et al. (2007). In particular, Terradas et al. (2006) demonstrated the important difference in the wave leaking between these geometries. However, the difference in geometry should not be the principal difference in the resonant periods of sausage modes, as the behaviour of this mode is known to be almost identical in the slab and cylinder geometries in the trapped regime. Future study of the sausage mode of a plasma cylinder will provide a final answer, but is out of the scope of this paper.
Because of its compressibility, the sausage mode can be readily seen in microwave, EUV and soft X-ray bands, provided sufficient time resolution is available. Also, this mode is capable of modulating the population of nonthermal electrons via changes in the magnetic mirror ratio in the flaring loop, leading to periodic precipitation of electrons to the loop footpoint. This causes modulation of the emission in hard X-ray and white light because of bremsstrahlung (Zaitsev & Stepanov 1982).
The seismological potential of the sausage mode is connected with estimating the magnetic field outside the oscillating plasma structure (Pascoe et al. 2007b), and with determining the transverse profile of the plasma density in the flaring loop (Nakariakov et al. 2004). Also, in the case when the microwave spectrum is generated by the gyrosynchrotron mechanism and is spatially resolved, this mode provides a promising basis for combined MHD-microwave diagnostics of flaring plasmas. As the sausage mode often causes pronounced modulation of the emission light curve, it also opens up possibilities for the diagnostics of stellar coronae (Nakariakov 2008).
One popular topic of MHD coronal seismology is the use of the ratios of global (or fundamental) modes and their second harmonics (variously referred to as the P1/2P2 ratio or the P2/P1 ratio) for determining the longitudinal profile of the plasma parameters in the oscillating loop. Andries et al. (2005) noticed that for the kink mode the discrepancy between the observed P1/2P2 ratio and that theoretically calculated with the use of the straight cylinder model could be attributed to the variation of the plasma density along the loop, e.g. because of gravitational stratification. There have been several attempts to account for this stratification in the theoretical model (see Verth & Erdélyi 2008; Donnelly et al. 2006; Dymova & Ruderman 2006; McEwan et al. 2008), and also to extend this study to longitudinal modes (e.g. Díaz & Roberts 2006). One of the difficulties with the full scale implementation of the P1/2P2-based technique in MHD coronal seismology is that the higher harmonics of the kink mode are rarely detected because of insufficient temporal resolution of solar EUV imagers.
As the sausage mode is usually observed with the instruments which have very high time resolution (e.g. 0.1 or 1 s in the case of the Nobeyama Radioheliograph), it is possible to detect several harmonics of this mode (Nakariakov et al. 2003; Melnikov et al. 2005). However, as in contrast with the kink mode the sausage mode is highly dispersive, the identification of the sausage mode harmonic number is a non-trivial task. This is partly due to a significant departure of the P1/2P2-ratio from unity because of the dispersive modification of the phase speed even in the absence of longitudinal stratification. It becomes especially difficult when spatial resolution is not available. Hence there is need for detailed theoretical modelling of various regimes of the sausage mode dynamics.
It is not likely that in flaring loops the sausage mode is affected by gravitational stratification, as in such loops the density scale height is large because of the high temperature. The effect of the variable cross-section of the flaring loop on the resonant periods of the standing
sausage mode was recently considered by Pascoe et al. (2009). It was established that the sausage mode continued to be supported despite variations in the loop cross-section. It was also shown that the characteristic periods of the global mode and higher harmonics were effected, but weakly so. A similarly small variation in parameters was found when investigating the effects of twist in loops (Erdélyi & Fedun 2006).
However, the high temperatures and densities of flaring loops also lead to the increase in the plasma-![]() inside the loops (Shibasaki 2001). This can cause a significant deviation of the resonant periods and cut-offs from the results obtained in the zero-
inside the loops (Shibasaki 2001). This can cause a significant deviation of the resonant periods and cut-offs from the results obtained in the zero-![]() approximation studied in Pascoe et al. (2007b); Cooper et al. (2003).
approximation studied in Pascoe et al. (2007b); Cooper et al. (2003).
| |
Figure 1: Illustrations of a) the global sausage mode and b) the second (longitudinal) harmonic of the sausage mode, shown as filled density contours. In both cases the perturbation is symmetric about the loop axis, which remains unperturbed. |
| Open with DEXTER | |
The purpose of this study is to establish the effect of finite plasma-![]() on the resonant periods of the sausage mode by full numerical MHD modelling, and also to investigate the behaviour of the harmonic ratio for the sausage mode. The paper is organised as follows: in Sect. 2 we describe the standard theoretical approach to modelling wave modes in a magnetic slab geometry. Section 3 details the numerical methods used for the modelling in this paper. In Sect. 4 we present our results, which are then discussed in more detail in Sect. 5.
on the resonant periods of the sausage mode by full numerical MHD modelling, and also to investigate the behaviour of the harmonic ratio for the sausage mode. The paper is organised as follows: in Sect. 2 we describe the standard theoretical approach to modelling wave modes in a magnetic slab geometry. Section 3 details the numerical methods used for the modelling in this paper. In Sect. 4 we present our results, which are then discussed in more detail in Sect. 5.
2 Sausage modes in a magnetic slab
Following the standard approach, we model magnetoacoustic oscillations in a coronal loop as perturbations of a field aligned enhancement in plasma density. The magnetic field is taken to be in the y-direction. The density profile is uniform in the y-direction. In the transverse direction the density is given by the profile (Nakariakov & Roberts 1995b)
where
The equilibrium condition is the total pressure balance between the internal and external plasmas. This may be written as (Edwin & Roberts 1982)
where
For a symmetric Epstein profile, the solutions describing the perturbation of the transverse velocity component in the sausage mode are given by
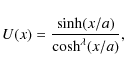 |
(3) |
where
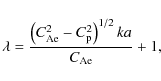 |
(4) |
where k is the wavenumber and the phase speed
Since ![]() is typically a large fraction of
is typically a large fraction of
![]() (for trapped modes)
(for trapped modes) ![]() is usually of order 1. The phase speed
is usually of order 1. The phase speed ![]() can be worked out analytically from the dispersion relation
can be worked out analytically from the dispersion relation
This equation allows for the exact analytical solution for the phase speed
For a realistic flaring loop the situation is likely to be more complex. A perfect pressure balance, for example, may not hold. Nor are the background plasma parameters likely to be uniform, or the amplitudes of oscillation sufficiently small to be considered linear. However, the global sausage mode is a very robust perturbation, and it remains desirable to examine its properties in a more idealised case before considering higher order effects. It is also likely that the choice of geometry is relatively unimportant for the MHD sausage mode. Part of the reason for this is its simplicity; a symmetric density perturbation about the loop axis independent of the azimuthal angle. This is in contrast to other MHD modes. In the following analysis, we simulate sausage modes using both a step-function density profile and a classical Epstein profile, noting the rationale in each case.
3 Numerical model
The numerical simulations of MHD sausage modes presented here were performed in slab geometry using Lare2d (Arber et al. 2001). The code solves the MHD equations in normalised form. The defined normalisation constants used in this paper are:

This leads to the additional quantities:
The normalised MHD equations may then be written as
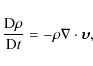 |
(6) |
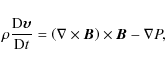 |
(7) |
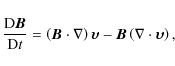 |
(8) |
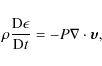 |
(9) |
where
An initial structure in equilibrium was set up as described in Sect. 2. In order to control the value of ![]() ,
the magnetic field was reduced inside the loop as shown in Fig. 2. All of the values in Fig. 2 are normalised. The internal density of the loop,
,
the magnetic field was reduced inside the loop as shown in Fig. 2. All of the values in Fig. 2 are normalised. The internal density of the loop, ![]() ,
is also fixed. The internal gas pressure is left as a free parameter in order to maintain total pressure balance. As a result the plasma temperature varies with the internal gas pressure. Consequently, the simulated plasma structures are both hotter and denser than the surroundings, consistent with the known properties of physical coronal loops.
,
is also fixed. The internal gas pressure is left as a free parameter in order to maintain total pressure balance. As a result the plasma temperature varies with the internal gas pressure. Consequently, the simulated plasma structures are both hotter and denser than the surroundings, consistent with the known properties of physical coronal loops.
![\begin{figure}
\par\hspace*{7mm} \includegraphics[width=7.2cm]{12088f2a.ps}\vspace*{4mm}
\includegraphics[width=8cm]{12088f2b.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg44.png) |
Figure 2:
Top panel: plot of the normalised initial parameters as a function of the transverse coordinate. The solid line is the density, the dashed line is the magnetic field By, and the dot-dashed line is the temperature. The temperature has been multiplied by a factor of 5 for clarity. Bottom panel: the |
| Open with DEXTER | |
A convenient way to modify the equilibrium is to adjust the profile of the magnetic field, keeping all other parameters the same. This is the approach that will be used throughout this paper. This would allow us to consider the important case of flaring loops filled in with a hot and dense, high-![]() plasma.
plasma.
In the following, the values of plasma-![]() in the centre of the loop and at infinity are referred to as
in the centre of the loop and at infinity are referred to as ![]() and
and
![]() ,
respectively. To simulate a sausage mode we set up an initial transverse velocity perturbation of the form
,
respectively. To simulate a sausage mode we set up an initial transverse velocity perturbation of the form
where A is an amplitude and x and y are the coordinates across and along the slab respectively. This velocity distribution disturbs the loop at its centre and ensures that a global standing mode is developed. To avoid nonlinear effects the amplitude of the perturbation must be small compared to the equilibrium parameters. We choose A = 0.002 in all cases, resulting in perturbations which are very small fractions of the equilibrium magnetic field and density (typically
Theoretically, any excitation of a mode in this way would lead to the excitation of higher harmonics (Terradas et al. 2005). However, the excitation we choose is always sufficiently close to the eigenmode that the amplitude of these harmonics is very small with respect to the fundamental oscillation, and they are quickly damped. Thus, by running the simulation for sufficient time, the dominance of the desired mode is ensured (Pascoe et al. 2007b).
To measure the periods of oscillation, the perturbation of the plasma parameters at the relevant anti-node are studied. For the global sausage mode this is at the loop centre. The period is determined by applying a Fourier transform to the time series data from this point, thus the uncertainty in the measurement is connected with the half-width of the peak in the Fourier spectrum.
4 Results
4.1 The period of the sausage mode
According to Nakariakov et al. (2003), the period of the global sausage mode near the wavenumber cut-off in the trapped regime is given by
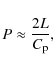 |
(11) |
where L is the loop length and
![\begin{figure}
\par\includegraphics[width=8cm]{12088f3.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg48.png) |
Figure 3:
Period of the global sausage mode as a function of loop length L, for a number of |
| Open with DEXTER | |
The results shown in Fig. 3 are in excellent agreement with those presented in Pascoe et al. (2007b). Above approximately 20 Mm the mode becomes leaky and the phase speed is slightly higher than the external Alfven speed. Furthermore, the near-independence of the oscillation period on ![]() is clear. As a further illustration, we investigate the period dependence on
is clear. As a further illustration, we investigate the period dependence on ![]() at a fixed length L. The length of the loop was set at L=15 Mm - corresponding to trapped modes - and the value of
at a fixed length L. The length of the loop was set at L=15 Mm - corresponding to trapped modes - and the value of ![]() was varied as described in Sect. 3.
was varied as described in Sect. 3.
![]() was kept constant and small throughout. The result is displayed in Fig. 4.
was kept constant and small throughout. The result is displayed in Fig. 4.
![\begin{figure}
\par\includegraphics[width=8cm]{12088f4.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg49.png) |
Figure 4:
The sausage mode period dependence on |
| Open with DEXTER | |
The period of the sausage mode should also depend on the loop width a. This is due to dispersion, since a change in a essentially corresponds to movement along the dispersion curve derived from Eq. (5) and hence a change in phase speed ![]() .
To illustrate this, we performed numerical simulations of a sausage mode in a loop of fixed length L=15 Mm while varying the width of the Epstein profile. The results are illustrated in Fig. 5. As expected, the period increases as a function of a within the trapped regime, whereas for leaky modes - corresponding to a < 2.2 Mm - the period tends to a constant value. This is a consequence of the phase speed remaining close to the external Alfven speed in this regime.
.
To illustrate this, we performed numerical simulations of a sausage mode in a loop of fixed length L=15 Mm while varying the width of the Epstein profile. The results are illustrated in Fig. 5. As expected, the period increases as a function of a within the trapped regime, whereas for leaky modes - corresponding to a < 2.2 Mm - the period tends to a constant value. This is a consequence of the phase speed remaining close to the external Alfven speed in this regime.
![\begin{figure}
\par\includegraphics[width=8cm]{12088f5.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg50.png) |
Figure 5: The sausage mode period dependence on width a for a loop of fixed length L=15 Mm, where the density contrast ratio is 10. The solid line corresponds to the solution of the dispersion relation for an Epstein profile. |
| Open with DEXTER | |
It is clear from these results that, although there is a slight increase in the period with respect to ![]() ,
the variation is very small (less than 5%) compared to the effect of other parameters such as loop length. Thus we may say that the period of the sausage mode is very stable with respect to the value of
,
the variation is very small (less than 5%) compared to the effect of other parameters such as loop length. Thus we may say that the period of the sausage mode is very stable with respect to the value of ![]() .
.
4.2 The second longitudinal harmonic
An often-neglected aspect of sausage mode behaviour is the relationship between the periods of separate harmonics. For dispersionless standing modes in a resonator, the frequency of the Nth harmonic is simply N times that of the fundamental. Being strongly dispersive, the sausage mode harmonics deviate significantly from this pattern.
The true behaviour of the harmonic ratio is explored for the fundamental and second harmonic modes. For a given value of k1 (the wavenumber corresponding to the fundamental mode), the period ratio P1/2P2 is measured from numerical simulations. By varying the loop length L, we control the wavenumber k1 and subsequently measure the period ratio as a function of k1. Figure 6 displays the results.
![\begin{figure}
\par\includegraphics[width=8cm]{12088f6a.ps}\par\includegraphics[width=8cm]{12088f6b.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg51.png) |
Figure 6:
Top panel: the ratio P1/2P2 observed via full numerical simulation for the sausage mode as a function of the longitudinal wave number k1 for both the step-function (stars) and Epstein profile (diamonds) geometries. The density contrast ratio is 20 and
|
| Open with DEXTER | |
For non-dispersive waves, the expected ratio of P1/2P2 is 1. It is clear that the sausage mode harmonics do not follow this pattern. For large values of k1 corresponding to the uniform plasma (and hence dispersionless) limit, the ratio does indeed tend towards the ideal value. However, for smaller k1, the period of the second harmonic becomes a much greater fraction of the fundamental period, as illustrated in both panels of Fig. 6. The top panel shows the quantitative difference between simulations of an Epstein profile (diamonds) and a step-function profile (stars). Although this deviation is noticeable at low k1 values, the overall behaviour remains the same, as expected. The solid line shows the theoretical curve for an Epstein profile derived from the dispersion relation given in Eq. (5), corresponding to the zero-![]() case. The agreement between the theoretical and numerical results is impressive.
The bottom panel of Fig. 6 shows the same theoretical curve for a range of density contrast ratios. Clearly there is a strong effect on the behaviour of the period ratio; the denser the loop, the greater the deviation from the ideal, non-dispersive case. However, the range for the period ratio in all cases lies between 0.5 and 1. The turnover of the period ratio curve seen at low k1 is a product of being very close to the cut-off wavenumber
case. The agreement between the theoretical and numerical results is impressive.
The bottom panel of Fig. 6 shows the same theoretical curve for a range of density contrast ratios. Clearly there is a strong effect on the behaviour of the period ratio; the denser the loop, the greater the deviation from the ideal, non-dispersive case. However, the range for the period ratio in all cases lies between 0.5 and 1. The turnover of the period ratio curve seen at low k1 is a product of being very close to the cut-off wavenumber ![]() .
.
In coronal seismology, the ratios of observed oscillatory periods - say, in a coronal loop or solar flare - are often used to make judgements about the underlying MHD modes. Figure 6 provides a powerful illustration of the dispersive nature of sausage mode harmonics, and that for entirely realistic values of k it is not expected that the harmonic ratio be close to 1 regardless of any non-uniformity in the longitudinal direction.
4.3 The cut-off wavenumber
According to Nakariakov & Roberts (1995a), the cutoff wavenumber for a sausage mode in a magnetic slab with a step function profile of finite-![]() plasma is given by
plasma is given by
An analytical expression for the wavenumber cut-off is not readily obtainable in the finite-
In order to investigate the dependence of this cut-off wavelength on the plasma-![]() ,
we write the sound speed as
,
we write the sound speed as
![]() .
Equation (12) then becomes
.
Equation (12) then becomes
Using the equation for magnetostatic pressure balance (Eq. (2)), we can eliminate

Inserting this expression into Eq. (14), we obtain
This dependence is shown in Fig. 7. For any value of
![\begin{figure}
\par\includegraphics[width=8cm]{12088f7.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg62.png) |
Figure 7:
Surface showing the dependence of the cut-off wavenumber on |
| Open with DEXTER | |
By comparison, we numerically evaluate Eq. (12) for increasing values of ![]() ,
while maintaining a fixed and low
,
while maintaining a fixed and low
![]() .
We maintain fixed external values of
.
We maintain fixed external values of ![]() and B. Inside the loop, the value of B is decreased, increasing the value of
and B. Inside the loop, the value of B is decreased, increasing the value of ![]() .
For the structure to remain stable, the internal gas pressure must be left a free parameter to maintain total pressure balance. As before, the temperature is allowed to vary with the gas pressure, ensuring that the simulated loops are hot and dense. The results are shown in Fig. 8, where the solid line corresponds to a density contrast ratio of 10.
.
For the structure to remain stable, the internal gas pressure must be left a free parameter to maintain total pressure balance. As before, the temperature is allowed to vary with the gas pressure, ensuring that the simulated loops are hot and dense. The results are shown in Fig. 8, where the solid line corresponds to a density contrast ratio of 10.
In both cases, the value of the cut-off wavenumber clearly decreases while ![]() is increased from zero to one. Figure 8 shows the same result for a number of different density contrast ratios, illustrating that the density has a strong impact on the confinement of the sausage mode. Again though for any starting - and fixed - value of the density contrast, the cut-off wavenumber will decrease as a function of
is increased from zero to one. Figure 8 shows the same result for a number of different density contrast ratios, illustrating that the density has a strong impact on the confinement of the sausage mode. Again though for any starting - and fixed - value of the density contrast, the cut-off wavenumber will decrease as a function of ![]() .
.
To further corroborate these results, we perform full numerical simulations of the global sausage mode for varying values of ![]() .
This is achieved by controlling the internal magnetic field as explained in Sect. 2.
.
This is achieved by controlling the internal magnetic field as explained in Sect. 2.
To measure the cut-off wavenumber itself, we simulate the global mode for varying L (and hence k) and examine the time series of the loop anti-node as described in Sect. 3. Here the criterion for a mode to be leaky is that the amplitude of the oscillation inside the loop is damped. When far into the leaky regime, the damping effect is strong and evident (see for example Pascoe et al. 2007b). However, closer to the trapped regime it can be difficult to ascertain whether significant damping is taking place. This effect is mitigated by running the simulations for a sufficiently long time. However an exact determination of the cut-off wavenumber ![]() remains difficult.
remains difficult.
![\begin{figure}
\par\includegraphics[width=8cm]{12088f8.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg63.png) |
Figure 8:
Plot showing the dependence of
|
| Open with DEXTER | |
The results of these MHD simulations are overlayed in Fig. 8. The simulations show the same general trend as the analytical and numerical solutions of Eq. (12), although the agreement is not exact. The curve of the simulated result is noticeably shallower than the theoretical predictions. In part this is likely due to the difficulty in determining exactly the transition between the trapped and leaky regimes, a problem that is reflected in the size of the error bars shown for the numerical results.
5 Conclusions
Using numerical simulation and analytical study, we have carried out detailed analysis encompassing various aspects of MHD sausage mode behaviour. The key findings may be summarised as follows:
- 1.
- In the finite-
 regime, the period of the global sausage mode was found to be determined by the length of the loop L, which confirmed previous findings of Nakariakov et al. (2003), Aschwanden et al. (2004) and Pascoe et al. (2007b).
regime, the period of the global sausage mode was found to be determined by the length of the loop L, which confirmed previous findings of Nakariakov et al. (2003), Aschwanden et al. (2004) and Pascoe et al. (2007b).
- 2.
- In the trapped regime the period is also dependent on the loop width a due to dispersion, but becomes weakly dependent in the leaky regime.
- 3.
- The period of the global sausage mode is not significantly affected by finite values of
 ,
with the variation remaining less than 5% for
,
with the variation remaining less than 5% for
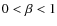 .
.
- 4.
- The ratio between the second longitudinal harmonic and the fundamental, P1/2P2, varies between approximately 0.5 and 1 for ``reasonable'' values of k1 and
 ,
and is strongly dependent on both k1 and
,
and is strongly dependent on both k1 and  .
.
- 5.
- The cut-off wavenumber for the global mode is a function of
 ,
,
 and the density contrast ratio
and the density contrast ratio  .
For a given density and
.
For a given density and
 ,
the
,
the
 is a decreasing function with respect to
is a decreasing function with respect to  .
.
These results also have immediate practical applications in the context of MHD coronal seismology. For multi-periodic oscillations, an understanding of the relationship between sausage mode harmonics enables informed judgements about the nature of the observed mode.
For example, in Srivastava et al. (2008) a period ratio of
![]() was reported, with the favoured interpretation being the fundamental and second harmonic of the sausage mode. From their estimates of the loop length (
was reported, with the favoured interpretation being the fundamental and second harmonic of the sausage mode. From their estimates of the loop length (
![]() Mm) and our independent estimate of the loop width (
Mm) and our independent estimate of the loop width (
![]() Mm), it is possible to examine this conclusion. Given the values of L and a, we estimate that
Mm), it is possible to examine this conclusion. Given the values of L and a, we estimate that
![]() .
It is clear from Fig. 6 that, for the period ratio reported this is very much in the leaky regime for the sausage mode. However, the data presented in Srivastava et al. (2008) does not show significant evidence of damping. Therefore, although it must be pointed out that the uncertainty in k1 a is considerable, it seems that the observed P1/2P2 ratio is an indication that another mode may be responsible.
.
It is clear from Fig. 6 that, for the period ratio reported this is very much in the leaky regime for the sausage mode. However, the data presented in Srivastava et al. (2008) does not show significant evidence of damping. Therefore, although it must be pointed out that the uncertainty in k1 a is considerable, it seems that the observed P1/2P2 ratio is an indication that another mode may be responsible.
We apply the same analysis to the event analysed in Nakariakov et al. (2003), where a fundamental and possible second harmonic was reported. In this case the observed period ratio is
![]() .
Given the published estimates of the loop length (
.
Given the published estimates of the loop length (
![]() Mm) and width (
Mm) and width (
![]() Mm) we find that in this case
Mm) we find that in this case
![]() .
Again, we can compare this with the results shown in Fig. 6. In this case, the observed period ratio and wavenumber are broadly consistent with a trapped fundamental and second harmonic of the sausage mode, provided the density contrast ratio is not too large, say 5 or perhaps even 10. Although this is not particularly large for a hot flaring loop, it is certainly possible and consistent with a trapped mode regime. Another possibility to consider is that the observed oscillations are actually triggered by a nearby non-flaring loop, which might have a lower density contrast than the flaring loop itself (Nakariakov et al. 2006). These two examples show how the results obtained here can be readily applied to observational examples of multi-period QPP.
.
Again, we can compare this with the results shown in Fig. 6. In this case, the observed period ratio and wavenumber are broadly consistent with a trapped fundamental and second harmonic of the sausage mode, provided the density contrast ratio is not too large, say 5 or perhaps even 10. Although this is not particularly large for a hot flaring loop, it is certainly possible and consistent with a trapped mode regime. Another possibility to consider is that the observed oscillations are actually triggered by a nearby non-flaring loop, which might have a lower density contrast than the flaring loop itself (Nakariakov et al. 2006). These two examples show how the results obtained here can be readily applied to observational examples of multi-period QPP.
Nevertheless, significant scope for improvement remains, both in observational and theoretical terms. In general, the uncertainties in both P1/2P2 and k1 a are substantial in observational studies of QPP. Additionally, as has been shown in Fig. 6, the geometry of the theoretical model has a bearing on the quantitative values of the period ratio. Potentially important effects such as loop curvature and gravity have also been neglected in this study. Understanding the impact of these effects may prove an important next step in quantifying the characteristics of sausage modes.
Acknowledgements
A.R.I. would like to acknowledge the support of a STFC Ph.D. studentship. T.V.D. was supported by a Marie Curie Intra-European Fellowship within the 7th European Community Framework Programme.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] (In the text)
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] (In the text)
- Aschwanden, M. J., Nakariakov, V. M., & Melnikov, V. F. 2004, ApJ, 600, 458 [NASA ADS] [CrossRef] (In the text)
- Cooper, F. C., Nakariakov, V. M., & Williams, D. R. 2003, A&A, 409, 325 [NASA ADS] [CrossRef] [EDP Sciences]
- Díaz, A. J., & Roberts, B. 2006, A&A, 458, 975 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Donnelly, G. R., Díaz, A. J., & Roberts, B. 2006, A&A, 457, 707 [NASA ADS] [CrossRef] [EDP Sciences]
- Dymova, M. V., & Ruderman, M. S. 2006, A&A, 457, 1059 [NASA ADS] [CrossRef] [EDP Sciences]
- Edwin, P. M., & Roberts, B. 1982, Sol. Phys., 76, 239 [NASA ADS] [CrossRef] (In the text)
- Erdélyi, R., & Fedun, V. 2006, Sol. Phys., 238, 41 [NASA ADS] [CrossRef] (In the text)
- Inglis, A. R., Nakariakov, V. M., & Melnikov, V. F. 2008, A&A, 487, 1147 [NASA ADS] [CrossRef] [EDP Sciences]
- Kopylova, Y. G., Melnikov, A. V., Stepanov, A. V., Tsap, Y. T., & Goldvarg, T. B. 2007, Astron. Lett., 33, 706 [NASA ADS] [CrossRef] (In the text)
- McEwan, M. P., Díaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences]
- Melnikov, V. F., Reznikova, V. E., Shibasaki, K., & Nakariakov, V. M. 2005, A&A, 439, 727 [NASA ADS] [CrossRef] [EDP Sciences]
- Nakariakov, V. M. 2008, J. Phys. Conf. Ser., 118, 012038 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., & Roberts, B. 1995a, Sol. Phys., 159, 213 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., & Roberts, B. 1995b, Sol. Phys., 159, 399 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., & Verwichte, E. 2005, Living Rev. Sol. Phys., 2, 3 [NASA ADS] (In the text)
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences]
- Nakariakov, V. M., Arber, T. D., Ault, C. E., et al. 2004, MNRAS, 349, 705 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., Foullon, C., Verwichte, E., & Young, N. P. 2006, A&A, 452, 343 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007a, Sol. Phys., 246, 165 [NASA ADS] [CrossRef] (In the text)
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007b, A&A, 461, 1149 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pascoe, D. J., Nakariakov, V. M., Arber, T. D., & Murawski, K. 2009, A&A, 494, 1119 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shibasaki, K. 2001, ApJ, 557, 326 [NASA ADS] [CrossRef] (In the text)
- Srivastava, A. K., Zaqarashvili, T. V., Uddin, W., Dwivedi, B. N., & Kumar, P. 2008, MNRAS, 388, 1899 [NASA ADS] [CrossRef] (In the text)
- Terradas, J., Oliver, R., & Ballester, J. L. 2005, A&A, 441, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Terradas, J., Oliver, R., & Ballester, J. L. 2006, ApJ, 650, L91 [NASA ADS] [CrossRef] (In the text)
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences]
- Zaitsev, V. V., & Stepanov, A. V. 1982, SVA Lett., 8, 132 [NASA ADS] (In the text)
All Figures
| |
Figure 1: Illustrations of a) the global sausage mode and b) the second (longitudinal) harmonic of the sausage mode, shown as filled density contours. In both cases the perturbation is symmetric about the loop axis, which remains unperturbed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{7mm} \includegraphics[width=7.2cm]{12088f2a.ps}\vspace*{4mm}
\includegraphics[width=8cm]{12088f2b.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg44.png) |
Figure 2:
Top panel: plot of the normalised initial parameters as a function of the transverse coordinate. The solid line is the density, the dashed line is the magnetic field By, and the dot-dashed line is the temperature. The temperature has been multiplied by a factor of 5 for clarity. Bottom panel: the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12088f3.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg48.png) |
Figure 3:
Period of the global sausage mode as a function of loop length L, for a number of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12088f4.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg49.png) |
Figure 4:
The sausage mode period dependence on |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12088f5.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg50.png) |
Figure 5: The sausage mode period dependence on width a for a loop of fixed length L=15 Mm, where the density contrast ratio is 10. The solid line corresponds to the solution of the dispersion relation for an Epstein profile. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12088f6a.ps}\par\includegraphics[width=8cm]{12088f6b.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg51.png) |
Figure 6:
Top panel: the ratio P1/2P2 observed via full numerical simulation for the sausage mode as a function of the longitudinal wave number k1 for both the step-function (stars) and Epstein profile (diamonds) geometries. The density contrast ratio is 20 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12088f7.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg62.png) |
Figure 7:
Surface showing the dependence of the cut-off wavenumber on |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12088f8.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12088-09/Timg63.png) |
Figure 8:
Plot showing the dependence of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\rho(x) = \left( \rho_0 - \rho_{\rm e} \right) {\rm sech}^{2} \left[ \left( \frac{x}{a} \right)^n \right] + \rho_{\rm e}
\end{displaymath}](/articles/aa/full_html/2009/32/aa12088-09/img13.png)