| Issue |
A&A
Volume 503, Number 2, August IV 2009
|
|
|---|---|---|
| Page(s) | 533 - 540 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200912073 | |
| Published online | 02 July 2009 | |
Statistical equilibrium of silicon in the atmospheres of metal-poor stars![[*]](/icons/foot_motif.png)
J. R. Shi1,2 - T. Gehren2 - L. Mashonkina2,3 - G. Zhao1
1 - National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China
2 - Universitäts-Sternwarte München, Scheinerstrasse 1, 81679 München, Germany
3 - Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya Str. 48, 109017 Moscow, Russia
Received 16 March 2009 / Accepted 6 May 2009
Abstract
Aims. The statistical equilibrium of neutral and ionized silicon in the atmospheres of metal-poor stars is discussed. Non-local thermodynamic equilibrium effects (NLTE) are investigated and the silicon abundances in metal-poor stars determined.
Methods. We have used high resolution, high signal to noise ratio spectra from the UVES spectragraph at the ESO VLT telescope. Line formation calculations of Si I and Si II in the atmospheres of metal-poor stars are presented for atomic models of silicon including 174 terms and 1132 line transitions. Recent improved calculations of Si I and Si II photoionization cross-sections are taken into account, and the influence of the free-free quasi-molecular absorption in the Ly![]() wing is investigated by comparing theoretical and observed fluxes of metal-poor stars. All abundance results are derived from LTE and NLTE statistical equilibrium calculations and spectrum synthesis methods.
wing is investigated by comparing theoretical and observed fluxes of metal-poor stars. All abundance results are derived from LTE and NLTE statistical equilibrium calculations and spectrum synthesis methods.
Results. It is found that the extreme ultraviolet radiation is very important for metal-poor stars, especially for the high temperature, very metal-poor stars. The radiative bound-free cross-sections also play a very important role for these stars.
Conclusions. NLTE effects for Si are found to be important for metal-poor stars, in particular for warm metal-poor stars. It is found that these effects depend on the temperature. For warm metal-poor stars, the NLTE abundance correction reaches ![]() 0.2 dex relative to standard LTE calculations. Our results indicate that Si is overabundant for metal-poor stars.
0.2 dex relative to standard LTE calculations. Our results indicate that Si is overabundant for metal-poor stars.
Key words: line: formation - line: profiles - stars: abundances - stars: late-type - Galaxy: evolution
1 Introduction
Silicon is not only an important reference element for comparision of various types of cosmic matter with the Sun, but also one of the main electron contributors and opacity sources in the near UV in the atmospheres of cool stars. With few exceptions, silicon also represents the only ![]() -element measurement for a given damped Ly
-element measurement for a given damped Ly![]() system (DLA, Prochaska & Wolfe 2002). Although silicon is a refractory element, its depletion is mild in lightly
depleted regions of the ISM, and therefore the observed column densities for the DLA system should nearly reflect the total Si column density.
system (DLA, Prochaska & Wolfe 2002). Although silicon is a refractory element, its depletion is mild in lightly
depleted regions of the ISM, and therefore the observed column densities for the DLA system should nearly reflect the total Si column density.
The current paradigm is that silicon is made during oxygen and neon burning in massive stars, and it would therefore be ejected by type II supernove (Woosley & Weaver 1995; Umeda et al. 2000; Ohkubo et al. 2006). Type Ia supernove also produce some silicon (Tsujimoto et al. 1995; Iwamoto et al. 1999).
Previous abundance determinations of Si have been carried out under the assumption of local thermodynamic equilibrium (LTE). They show pronounced star-to-star scatter at all metallicities, and
particularly for extremely metal-poor stars, where the observed Si abundance is represented by only two lines and affected by the contamination of CH and H![]() lines. This is seen in Fig. 1. Preston et al. (2006) and Lai et al. (2008) found that the derived Si abundance depends only on
lines. This is seen in Fig. 1. Preston et al. (2006) and Lai et al. (2008) found that the derived Si abundance depends only on
![]() and not on log g, and Preston et al. (2006)
suggested that the Si abundances for stars with
and not on log g, and Preston et al. (2006)
suggested that the Si abundances for stars with
![]() > 5800 K probably do not represent the true values. Cohen et al. (2004) noted that the observational picture for Si shows a
puzzle - the abundance ratio [Si/Fe] of giants is about 0.4 dex larger than that obtained for dwarfs (also see Ryan et al. 1996), and they discussed in detail the possibility of this
difference:
> 5800 K probably do not represent the true values. Cohen et al. (2004) noted that the observational picture for Si shows a
puzzle - the abundance ratio [Si/Fe] of giants is about 0.4 dex larger than that obtained for dwarfs (also see Ryan et al. 1996), and they discussed in detail the possibility of this
difference:
- There is a problem for the transition probabilities of the two very strong Si I lines. Cohen et al. (2004) studied high temperature extremely metal-poor dwarfs, but they
used only the 3905 Å Si I line. This line overlaps a CH feature; however, it is very weak in such stars. Cayrel et al. (2004) relied instead on a single line of Si I at
4102.9 Å, which is close to H
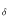 .
In cooler giants the 3905 Å line is too blended with CH even in normal carbon abundance stars. Both Cohen et al. (2004) and Cayrel et al. (2004) adopted the log gf value from the laboratory work of Garz (1973). However, NIST gives -2.92 dex for the 4102 Å line, which is 0.22 dex higher than the laboratory
value. Thus, the Si abundance derived by Cayrel et al. (2004) would be 0.22 dex lower if the NIST gf value were adopted.
.
In cooler giants the 3905 Å line is too blended with CH even in normal carbon abundance stars. Both Cohen et al. (2004) and Cayrel et al. (2004) adopted the log gf value from the laboratory work of Garz (1973). However, NIST gives -2.92 dex for the 4102 Å line, which is 0.22 dex higher than the laboratory
value. Thus, the Si abundance derived by Cayrel et al. (2004) would be 0.22 dex lower if the NIST gf value were adopted.
- Only one non-local thermodynamic equilibrium (NLTE) analysis has been published to date, in which Wedemeyer (2001) reported the influence of deviations from LTE upon the Si abundances in the Sun and Vega, with no reference to line formation in metal-poor stars; he demonstrated that NLTE for Si in the Sun is negligibly small. However, he did not consider line formation for the two strong lines.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12073fg1.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg18.png) |
Figure 1:
Silicon abundances of metal-poor stars determined from LTE analyses of Fulbright (2000, Filled circles |
| Open with DEXTER | |
The present work is based on a sample of metal-poor stars and aims at exploring their [Si/Fe] abundance ratios applying a full spectrum synthesis based on level populations calculated from the statistical equilibrium equations. In Sect. 2 we present the observational technique and the atmospheric models and stellar parameters are discussed in Sect. 3. NLTE line formation is discussed in Sect. 4. The results and comparison with other works are shown in Sect. 5. The discussion is presented in Sect. 6, and the conclusions are given in Sect. 7.
2 Observations
Our approach to obtain a representative silicon abundance investigation involves analyzing a sample of metal-poor stars with high resolution and high signal to noise ratio spectra. The spectra
of 13 metal-poor dwarf stars were observed in March 2001 with the UVES échelle spectrograph mounted at the ESO VLT2. UVES observations cover a spectral range between 3300 and 6650 Å with
gaps of ![]() 100 Å around 4570 Å due to the beam splitter and near 5580 Å at the edge of the butted CCD. The spectral resolution is around R = 60 000. These observations were originally
intended to show a high signal in the blue (see Mashonkina et al. 2003). Consequently, the green/red spectra have a S/N near 300 in most of the single exposures. We also use high-quality observed spectra from the ESO UVESPOP survey (Bagnulo et al. 2005) for HD 122563. For G 64-12 we use the spectrum from the High Dispersion Spectrograph at the Nasmyth focus of the Subaru 8.2 m telescope (Noguchi et al. 2002).
100 Å around 4570 Å due to the beam splitter and near 5580 Å at the edge of the butted CCD. The spectral resolution is around R = 60 000. These observations were originally
intended to show a high signal in the blue (see Mashonkina et al. 2003). Consequently, the green/red spectra have a S/N near 300 in most of the single exposures. We also use high-quality observed spectra from the ESO UVESPOP survey (Bagnulo et al. 2005) for HD 122563. For G 64-12 we use the spectrum from the High Dispersion Spectrograph at the Nasmyth focus of the Subaru 8.2 m telescope (Noguchi et al. 2002).
Data extraction followed the standard automatic IDL program environment designed for the FOCES spectrograph (Pfeiffer et al. 1998), but with slight modifications also applicable to the UVES data. All échelle images including flat field and ThAr were corrected for bias and scattered light background. Objects and ThAr exposures were extracted and corrected for flat field response. Bad pixels were detected and as far as possible removed by comparison of the 3 single exposures (see Gehren et al. 2004, for detail).
3 Method of calculation
3.1 Model atmospheres
Our analyses are all based on the same type of atmospheric model, irrespective of temperature, gravity or metal abundance. We use line-blanketed LTE model atmospheres, generated as discussed by
Fuhrmann et al. (1997). The main characteristics are: the iron opacity was calculated with the improved meteorite value log
![]() (Anders & Grevesse 1989); opacities
for metal-poor stars with [Fe/H] < -0.6 were calculated using
(Anders & Grevesse 1989); opacities
for metal-poor stars with [Fe/H] < -0.6 were calculated using ![]() -element (O, Mg, Si and Ca) abundances enhanced by 0.4 dex, and the mixing-length parameter l/H
-element (O, Mg, Si and Ca) abundances enhanced by 0.4 dex, and the mixing-length parameter l/H![]() was adopted to be 0.5, in order to determine consistent temperatures for H
was adopted to be 0.5, in order to determine consistent temperatures for H![]() and the higher Balmer lines (see Fuhrmann et al. 1993).
and the higher Balmer lines (see Fuhrmann et al. 1993).
3.2 Stellar parameters
For most of our program stars, we adopted the stellar parameters determined by Gehren et al. (2004, 2006), where the effective temperatures are derived from the wings of the Balmer lines; surface gravities are based on the HIPPARCOS parallaxes. Iron abundances are obtained from Fe II lines, and the microturbulence velocities are estimated by requiring that the iron
abundance derived from Fe II lines should not depend on equivalent width. For HD 84937 and HD 122563 the parameters were taken from Mashonkina et al. (2008), where the stellar
effective temperatures were determined from the hydrogen H![]() and H
and H![]() line wing fitting based on NLTE line formation; surface gravities are based on the HIPPARCOS parallaxes, and iron
abundances are derived from Fe II lines and the microturbulence velocity was derived from the strongest Fe II, Ca I, and Mg I lines. For consistency with the whole series of our earlier NLTE studies (from Baumüller & Gehren 1997 to the most recent paper of Shi et al. 2008), we adopt effective temperatures based on the hydrogen resonance broadening calculated with Ali & Griem (1966) theory. We note that two papers of Barklem et al. (2000) and Allard et al. (2008) obtain larger values of the hydrogen self-broadening cross-sections. An impact of using the self-broadening formalism of Barklem et al. (2000) on
effective temperature determinations for metal-poor stars is discussed by Mashonkina et al. (2008). The uncertainties for the temperature, surface gravity, metal abundance and
microturbulence velocities are generally assumed to be
line wing fitting based on NLTE line formation; surface gravities are based on the HIPPARCOS parallaxes, and iron
abundances are derived from Fe II lines and the microturbulence velocity was derived from the strongest Fe II, Ca I, and Mg I lines. For consistency with the whole series of our earlier NLTE studies (from Baumüller & Gehren 1997 to the most recent paper of Shi et al. 2008), we adopt effective temperatures based on the hydrogen resonance broadening calculated with Ali & Griem (1966) theory. We note that two papers of Barklem et al. (2000) and Allard et al. (2008) obtain larger values of the hydrogen self-broadening cross-sections. An impact of using the self-broadening formalism of Barklem et al. (2000) on
effective temperature determinations for metal-poor stars is discussed by Mashonkina et al. (2008). The uncertainties for the temperature, surface gravity, metal abundance and
microturbulence velocities are generally assumed to be ![]() 50 K, 0.05 dex, 0.05 dex and 0.1 km s-1 respectively.
50 K, 0.05 dex, 0.05 dex and 0.1 km s-1 respectively.
3.3 Atomic line data
Table 1 lists the relevant line data with their final solar fit values (Shi et al. 2008, hereafter Paper I). Collisional broadening through van der Waals interaction with hydrogen atoms is important for strong Si lines. As already pointed out by Gehren et al. (2001, 2004), the resulting values of the van der Waals damping constants are mostly near those calculated according to Anstee & O'Mara's (1991, 1995) tables. In our analysis, the absolute value of the oscillator strengths is unimportant because the abundances are evaluated in a fully differential way with respect to the sun.
Table 1: Atomic data of silicon lines*.
4 NLTE calculations
4.1 Atomic model
The silicon model atom includes the most important levels of Si I and Si II and comprises 132 terms of Si I, 41 terms of Si II, plus the Si III ground state. The atomic properties are documented in Shi et al. (Paper I). Oscillator strengths and photoionization cross-sections were calculated by Nahar & Pradhan (1993). The full analysis of the solar spectrum (Kurucz et al. 1984) allows a reasonable choice of the hydrogen collision enhancement factor resulting in
![]() = 0.1 for Si (see Paper I).
= 0.1 for Si (see Paper I).
All calculations are carried out with a revised version of the DETAIL program (Butler & Giddings 1985) using accelerated lambda iteration (see Gehren et al. 2001, 2004, for details).
![\begin{figure}
\par\resizebox{9cm}{6.6cm}{\includegraphics[width=9.3cm]{12073f2a...
...r\resizebox{9cm}{6.6cm}{\includegraphics[width=9.3cm]{12073f2c.ps}}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg46.png) |
Figure 2: Difference of [Si/Fe] abundance ratios calculated under NLTE and LTE assumptions for the two strong Si I 3905 and 4102 Å lines as a function of metal abundance a), temperature b), and surface gravity c). |
| Open with DEXTER | |
4.2 NLTE effects
The abundance analyses of silicon clearly show the NLTE effect. There is a tendency that the NLTE effect is large for warm metal-poor stars, as would be expected. Our results confirm that LTE abundances can be significantly different from their NLTE counterparts, with differences reaching more than 0.20 dex in extreme cases. It is evident that the NLTE effects are systematically stronger for hotter models, which is in agreement with the statistical equilibrium of sodium, magnesium and aluminium (Shi et al. 2004; Zhao & Gehren 2000; Baumüller et al. 1997). As expected, the strongest departures from LTE are found for models with high temperature and low metallicity. For our program stars, the differences of abundance between LTE and NLTE analyses for the strong 3905 and 4102 Å lines are plotted in Fig. 2 as a function of metal abundance, temperature and surface gravity, respectively.
Table 2: Stellar silicon LTE and NLTE (for each star, the first and the second row, respectively) abundances given relative to the iron LTE abundances derived from the Fe II lines*.
It should be noted that the NLTE effects differ from line to line, reflecting their individual properties. For example, the strong 3905 and 4102 Å lines show large NLTE effects compared to the other weak lines. From Table 2, we can see the importance of the NLTE effects on different lines in the silicon abundance determination:
- the weak lines show the smallest NLTE abundance effects (<0.02 dex) for the stars studied here, so they are the best abundance indicators for LTE analyses of moderately metal-poor stars;
- in the 3905 Å line, which is very important for determining the silicon abundances of extremely metal-poor stars, the NLTE correction is relatively small (
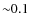 dex) for moderately
metal-poor dwarfs; it increases for extremely metal-poor warm stars (>0.15 dex). Therefore, this line should no longer be analyzed with LTE;
dex) for moderately
metal-poor dwarfs; it increases for extremely metal-poor warm stars (>0.15 dex). Therefore, this line should no longer be analyzed with LTE;
- the 4102 Å line is also important in determining the silicon abundances of metal-poor stars; it is necessary to take account of the NLTE effects, except for very cool and metal-rich stars. For warm metal-poor stars, the NLTE correction can reach more than 0.25 dex;
- for the two Si II lines, NLTE abundance corrections are negative. A similar behaviour is found for Ca II lines (Mashonkina et al. 2007).
4.3 The influence of the quasi-molecular absorption in Ly
Recent calculations using the R-matrix code provide detailed photoionisation cross-sections with autoionization resonances for the most important energy levels of Si I and Si II.
For Si I, the cross-sections of the lowest three terms,
![]() ,
,
![]() and
and
![]() are an order of magnitude greater than those of the next terms. It tends
to efficiently decouple the metastable terms from the excited ones. The thresholds of the three terms are 1500, 1700 and 2000 Å (Paper I). In this wavelength region, the most important
continuous absorption is the free-free quasi-molecular absorption and satellites in Ly
are an order of magnitude greater than those of the next terms. It tends
to efficiently decouple the metastable terms from the excited ones. The thresholds of the three terms are 1500, 1700 and 2000 Å (Paper I). In this wavelength region, the most important
continuous absorption is the free-free quasi-molecular absorption and satellites in Ly![]() due to collosions with H and H+ (Allard et al. 1998), especially for warm metal-poor
stars. In Fig. 3, we compare the synthetic ultraviolet (UV) fluxes for HD 84937 without and with this process considered. When this effect is included, the flux near 1700 Å decreases by more than an order of magnitude, and it allows us to reproduce the most characteristic UV features of warm metal-poor stars, as illustrated by a comparison with IUE data (Cacciari 1985) for the hot metal-poor star HD 84937 (Fig. 4).
due to collosions with H and H+ (Allard et al. 1998), especially for warm metal-poor
stars. In Fig. 3, we compare the synthetic ultraviolet (UV) fluxes for HD 84937 without and with this process considered. When this effect is included, the flux near 1700 Å decreases by more than an order of magnitude, and it allows us to reproduce the most characteristic UV features of warm metal-poor stars, as illustrated by a comparison with IUE data (Cacciari 1985) for the hot metal-poor star HD 84937 (Fig. 4).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12073fg3.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg55.png) |
Figure 3:
The UV flux emerging from MAFAGS-ODF model for HD 84937 without (dashed line) and with (solid line) the Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12073fg4.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg56.png) |
Figure 4: The comparision of the UV flux from MAFAGS-ODF model (solid line) with the IUE observations (dashed line) for HD 84937. |
| Open with DEXTER | |
As already discussed in Paper I, there is an unusually large energy gap between the ground state,
![]() ,
the two metastable terms
,
the two metastable terms
![]() and
and
![]() ,
and the
first excited levels of neutral silicon. These gaps are
,
and the
first excited levels of neutral silicon. These gaps are ![]() 5, 4, and 3 eV, respectively, and they shift all lines emerging from those levels into the UV, most of them below 2000 Å, Therefore,
the interaction of the three most populated Si I levels with the Si II ion is completely based on bound-free processes, where photoionisation and ionisation by electron
collisions compete in strength. Due to the large photoinisation cross-sections for the three lowest levels, the departure coefficients of Si I are very sensitive to the UV radiation field. When the Ly
5, 4, and 3 eV, respectively, and they shift all lines emerging from those levels into the UV, most of them below 2000 Å, Therefore,
the interaction of the three most populated Si I levels with the Si II ion is completely based on bound-free processes, where photoionisation and ionisation by electron
collisions compete in strength. Due to the large photoinisation cross-sections for the three lowest levels, the departure coefficients of Si I are very sensitive to the UV radiation field. When the Ly![]() continuum absorption is not included, the extreme underpopulation of Si I levels in the atmospheres of warm metal-poor stars is clearly seen. The depopulation with respect to the LTE case already starts in very deep photospheric layers, with a very large net pumping to the Si II ground state due to the strong UV radiation. For
continuum absorption is not included, the extreme underpopulation of Si I levels in the atmospheres of warm metal-poor stars is clearly seen. The depopulation with respect to the LTE case already starts in very deep photospheric layers, with a very large net pumping to the Si II ground state due to the strong UV radiation. For
![]() the departure coefficients bi drop near to 0 at log
the departure coefficients bi drop near to 0 at log ![]() = 0.5 (Fig. 5, top). As expected, the
= 0.5 (Fig. 5, top). As expected, the
![]() and
and
![]() terms follow
terms follow
![]() tightly. This would not affect neutral Si line formation very much, except that the strong 4102 Å line turns into emission for warm metal-poor stars, such as HD 84937, as shown in Fig. 6. Also, the NLTE correction would be very large (
tightly. This would not affect neutral Si line formation very much, except that the strong 4102 Å line turns into emission for warm metal-poor stars, such as HD 84937, as shown in Fig. 6. Also, the NLTE correction would be very large (![]() 1.0 dex) for the 3905 Å line.
1.0 dex) for the 3905 Å line.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073f5a.ps}\vspace*{5mm}
\includegraphics[width=8.5cm,clip]{12073f5b.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg58.png) |
Figure 5:
Departure coefficients as a function of log |
| Open with DEXTER | |
Models with Ly![]() continuum absorption included produce much smaller departures (Fig. 5, bottom), as radiative processes (photoionisation) are compensated by hydrogen and
electron collisions. Since all the excited terms are only loosely coupled to each other and to other high-excitation terms, their departure coefficients tend to diverge at
continuum absorption included produce much smaller departures (Fig. 5, bottom), as radiative processes (photoionisation) are compensated by hydrogen and
electron collisions. Since all the excited terms are only loosely coupled to each other and to other high-excitation terms, their departure coefficients tend to diverge at
![]() .
More importantly, similar abundances can be obtained from both the 3905 and 4102 Å lines.
.
More importantly, similar abundances can be obtained from both the 3905 and 4102 Å lines.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg6.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg60.png) |
Figure 6:
Theoretical NLTE flux profiles (
|
| Open with DEXTER | |
5 Results
5.1 Stellar silicon abundances
The abundance determinations for our program stars are made using spectral synthesis. The synthetic spectra are convolved with macroturbulence, rotational and instrumental broadening profiles, in order to match the observed spectral lines. Considering the NLTE abundances, our results do not show a large abundance discrepancy between different lines; the final abundance scatter of single lines is between 0.01 and 0.14. The derived abundances are presented in Table 2.
5.2 Comparison with other work
Silicon abundances for metal-poor stars have been determined by several groups based on LTE analyses. In Fig. 7, we compare the [Si/Fe] values (NLTE) determined in this paper with those from the literature. Some systematic differences can be seen from this figure. In the remaining part of this section we will briefly discuss some possible reasons for these differences.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg7.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg61.png) |
Figure 7:
Comparison of derived [Si/Fe] (NLTE) for stars in common with other studies. Triangle ( |
| Open with DEXTER | |
Decauwer et al. (2005).
Decauwer et al. (2005) performed a LTE line formation analysis for a sample of moderately metal-poor stars, and they used weak Si I lines when determining the Si abundances. We have one star in common with theirs. Our [Si/Fe] is about 0.1 dex higher than theirs. The gf values adopted in their study are nearly the same as those used here. We note that the optical Si I lines are very weak in metal-poor stars, so the determination of the continuum is difficult, while the NLTE effects for these lines can be negligible. The difference is mostly due to the determination of the continuum.
Fulbright (2000, 2002).
This analysis deals with a large number of metal-poor stars, of which three stars are in common with our sample. For the three stars in common with our list we obtain
Gratton et al. (2003).
The authors determined the silicon abundances for 150 field subdwarfs and subgiants. Our results are mostly in agreement with theirs. For the six stars in common, the average difference is 0.003
Honda et al. (2004).
Using high resolution, high signal to noise ratio spectra of 22 very metal-poor stars from Subaru/HDS, the authors confirmed the overabundance ratio [Si/Fe] of metal-poor giants found previously by Cayrel et al. (2004). Their results were determined from the 4102 Å line; the gf value adopted in this study is also from the laboratory work of Garz (1973). It is 0.15 dex lower than ours. We have two stars in common with this work; the giant star HD 122563 and the subgiant star HD 140283. For the giant, the silicon abundance determined by this study is 0.22 dex higher than ours; most of the difference comes from the different gf value adopted. For the subgiant, their result is -0.04 dex lower than ours; this is due to the large NLTE effects (+0.19 dex) in this star. Thus, the difference in gf value is compensated for by the large NLTE effect.
Ryan et al. (1996).
This work analysed 19 metal-poor stars using the 3905 Å line. The gf value adopted in this study was also from the laboratory work of Garz (1973), and it is nearly same as the value we adopted. The results of Ryan et al. (1996) are in agreement with ours. For the two common stars from Ryan et al. (1996), the average difference between theirs and ours is 0.025
6 Discussion
6.1 Si I/Si II ionization equilibrium in metal-poor stars
There are nine stars in our sample with Si abundances determined from both Si I and Si II lines, and excellent agreement between the two ionization stages is achieved. The average difference of ![]() [Si I/Fe]-[Si II/Fe] is 0.001
[Si I/Fe]-[Si II/Fe] is 0.001 ![]() 0.04. The largest difference between Si I and Si II abundances is found to be 0.09 for CD -51
0.04. The largest difference between Si I and Si II abundances is found to be 0.09 for CD -51![]() 4628. It may due to the large uncertainty in the HIPPARCOS parallax
for this star (
4628. It may due to the large uncertainty in the HIPPARCOS parallax
for this star (![]() 20%). We conclude that, within the modelling uncertainties, NLTE leads to
consistent Si abundances derived from the two ionization stages, while LTE fails to give consistent results.
20%). We conclude that, within the modelling uncertainties, NLTE leads to
consistent Si abundances derived from the two ionization stages, while LTE fails to give consistent results.
6.2 Silicon abundance and nucleosynthesis in the early Galaxy
The variation of [Si/Fe] with the stellar metallicity [Fe/H] contains information about the chemical evolution of the Galaxy. Figure 8 displays the behaviour of the [Si/Fe] ratio (calculated in LTE and NLTE) with the metal abundance for all stars considered in this paper. One important feature that can be seen from Fig. 8 is that there is a large scatter in the LTE results, while when the NLTE effects are included, the bulk of [Si/Fe] ratio is ![]() 0.3 for our program stars. The higher [Si/Fe] ratio at lower metallicity found in some studies of metal-poor stars (e.g. Fulbright 2002; Stephens & Boesgaard 2002) is not confirmed by this work. The obvious
exceptions are the two moderately metal-poor stars (CD -51
0.3 for our program stars. The higher [Si/Fe] ratio at lower metallicity found in some studies of metal-poor stars (e.g. Fulbright 2002; Stephens & Boesgaard 2002) is not confirmed by this work. The obvious
exceptions are the two moderately metal-poor stars (CD -51![]() 4628 and HD 122196), which exhibit relatively low [Si/Fe] values. We note that these two stars also show lower values of magnesium. Such stars were also found by Nissen & Schuster (1997) and Cohen et al. (2007, 2008).
4628 and HD 122196), which exhibit relatively low [Si/Fe] values. We note that these two stars also show lower values of magnesium. Such stars were also found by Nissen & Schuster (1997) and Cohen et al. (2007, 2008).
Detailed modelling of Galactic chemical evolution has been attempted by many authors (e.g. Timmes et al. 1995; Goswami & Prantzos 2000; Kobayashi et al. 2006). Based on
Woosley & Weaver's (1995) metallicity-dependent yields, Timmes et al. (1995) calculate the behaviour of [Si/Fe] as a function of metallicity. Their result predicts that [Si/Fe]
increases from [Fe/H] ![]() -0.5 to
-0.5 to
![]() ,
while it decreases from [Fe/H]
,
while it decreases from [Fe/H] ![]() -2 to
-2 to ![]() (see their Fig. 21). The decrease of [Si/Fe] with decreasing metallicity is due to
(unspecified) uncertainties in the low-metallicity massive star models. However, using the same yields but with an iron yield reduced by a factor of 2, Goswami & Prantzos (2000) show
that the [Si/Fe] increases from [Fe/H]
(see their Fig. 21). The decrease of [Si/Fe] with decreasing metallicity is due to
(unspecified) uncertainties in the low-metallicity massive star models. However, using the same yields but with an iron yield reduced by a factor of 2, Goswami & Prantzos (2000) show
that the [Si/Fe] increases from [Fe/H] ![]() 0 to [Fe/H]
0 to [Fe/H] ![]() -4. They predict that the [Si/Fe] ratio is about 0.5 dex at [Fe/H] = -3. Their result suggests an increasing [Si/Fe] towards the lower metallicity regime. They used a different initial mass function and a different halo model. A similar result was found by Kobayashi et al. (2006, see their Fig. 10). The Si yields of this work are larger for more massive metal-free stars.
-4. They predict that the [Si/Fe] ratio is about 0.5 dex at [Fe/H] = -3. Their result suggests an increasing [Si/Fe] towards the lower metallicity regime. They used a different initial mass function and a different halo model. A similar result was found by Kobayashi et al. (2006, see their Fig. 10). The Si yields of this work are larger for more massive metal-free stars.
Using magnesium instead of iron as the reference can remove type Ia SNe from consideration, because most of the silicon and nearly all the magnesium are produced in massive stars (Timmes et al. 1995). Calculations of nucleosynthesis for SNe Ia show that they should produce some silicon (Nomoto et al. 1997). The overall behaviour of the [Si/Mg] ratios versus [Fe/H] is shown in Fig. 9, where magnesium abundances are taken from Gehren et al. (2004, 2006) and Mashonkina et al. (2008). Although there is a scatter, our result shows that the [Si/Mg] ratio is around -0.1.
Our observational results provide some implications for the nucleosynthesis of silicon. Theoretically, it is expected that silicon is synthesized predominantly in moderate mass (![]() 20
20 ![]() )
type II SNe, while magnesium is produced primarily in the higher mass (
)
type II SNe, while magnesium is produced primarily in the higher mass (![]() 35
35 ![]() )
type II SNe (Woosley & Weaver 1995). The overabundance of silicon and the ratio of [Si/Mg] is about -0.1 in metal-poor stars, suggests that, similar to magnesium, silicon is produced by massive type II SNe. The slightly lower [Si/Fe] values for extremely metal-poor stars may indicate that silicon is produced more by moderately massive type II SNe.
This result agrees with nucleosynthesis calculations of massive stars by Woosley & Weaver (1995), but it is at variance with the calculations by Nomoto et al. (2006). It should be noted that there is only one extremely metal-poor star in our sample; it is necessary to investigate more extreme metal-poor stars to confirm this suggestion. From a theoretical point of view, since silicon is produced in a deeper region than magnesium, the ratio of Mg/Si is
sensitive to the explosion energy and the outer border of the mixed region. The higher explosion energy yields a smaller Mg/Si ratio, while the Mg/Si ratio decreases with the increasing outer boundary of the mixed region (Umeda & Nomoto 2005).
)
type II SNe (Woosley & Weaver 1995). The overabundance of silicon and the ratio of [Si/Mg] is about -0.1 in metal-poor stars, suggests that, similar to magnesium, silicon is produced by massive type II SNe. The slightly lower [Si/Fe] values for extremely metal-poor stars may indicate that silicon is produced more by moderately massive type II SNe.
This result agrees with nucleosynthesis calculations of massive stars by Woosley & Weaver (1995), but it is at variance with the calculations by Nomoto et al. (2006). It should be noted that there is only one extremely metal-poor star in our sample; it is necessary to investigate more extreme metal-poor stars to confirm this suggestion. From a theoretical point of view, since silicon is produced in a deeper region than magnesium, the ratio of Mg/Si is
sensitive to the explosion energy and the outer border of the mixed region. The higher explosion energy yields a smaller Mg/Si ratio, while the Mg/Si ratio decreases with the increasing outer boundary of the mixed region (Umeda & Nomoto 2005).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg8.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg67.png) |
Figure 8:
Abundance ratios [Si/Fe] as a function of [Fe/H]. Filled circles ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg9.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg68.png) |
Figure 9: Abundance ratios [Si/Mg] for NLTE analysis as a function of [Fe/H]. |
| Open with DEXTER | |
6.3 Comparison with DLA abundances
The chemistry of high-redshift DLA systems should represent at least crudely the state of the ISM gas at an early stage in the formation of the halo of the Galaxy. It is expected that the abundance ratios of elements determined from DLA would be consistent with those deduced from spectra of extremely metal-poor stars in our Galacy, although the metallicities of DLA systems do not reach values as low as those of individual Galactic halo stars. The Si/Fe ratio is of crucial importance in understanding the chemical nature of DLAs (Henry & Prochaska 2007).
As DLA systems are generally in young evolutionary stages, it is expected that supersolar [Si/Fe] values will be observed. Prochaska & Wolfe (2002) found that [Si/Fe] values exhibt a plateau
![]() dex at [Si/H] < -1.5, and Dessauges-Zavadsky et al. (2006) found an average [Si/Fe]
dex at [Si/H] < -1.5, and Dessauges-Zavadsky et al. (2006) found an average [Si/Fe] ![]() 0.43 dex for their sample, which indicates significant
0.43 dex for their sample, which indicates significant ![]() -enrichment in the DLA systems at low metallicity. Based on a large number of high
precision measurements obtained with échelle spectrometers on 8- to 10-m-class telescopes, Henry & Prochaska (2007) also found that [Si/Fe] for all their objects is +0.44. However, the
mean [Si/Fe] predicted by their model for their sample is +0.31 dex, and the ratio is roughly constant. This is very similar to our observational results, but is slightly lower than the value obtained from DLA systems. The most likely explanation is Fe depletion onto dust (Savage & Sembach 1996) in DLA systems.
-enrichment in the DLA systems at low metallicity. Based on a large number of high
precision measurements obtained with échelle spectrometers on 8- to 10-m-class telescopes, Henry & Prochaska (2007) also found that [Si/Fe] for all their objects is +0.44. However, the
mean [Si/Fe] predicted by their model for their sample is +0.31 dex, and the ratio is roughly constant. This is very similar to our observational results, but is slightly lower than the value obtained from DLA systems. The most likely explanation is Fe depletion onto dust (Savage & Sembach 1996) in DLA systems.
7 Conclusions
We have determined silicon abundances for 14 metal-poor stars, spanning the range -3.5 < [Fe/H] < -1.4. All abundances are derived from NLTE statistical equilibrium calculations. Based on our results we come to the following conclusions:
- 1.
- The [Si/Fe] ratios are overabundant for metal-poor stars, and there is an indication that [Si/Fe] slightly decreases with decreasing metallicity.
- 2.
- The NLTE effects are different from line to line. The weak lines are insensitive to NLTE effects, while the strong 3905 and 4102 Å lines show large NLTE effects. Large departures from LTE appear in warm metal-poor stars. The NLTE effects increase with increasing temperature, which can partly explain the observed results of an anomalous
 dependence of [Si/Fe] (Preston et al. 2006; Lai et al. 2008).
dependence of [Si/Fe] (Preston et al. 2006; Lai et al. 2008).
- 3.
- A different situation is found for Si II. For the two Si II lines, NLTE leads to enhanced absorption in the line cores and negative abundance corrections over the range of stellar parameters studied here.
- 4.
- The Ly
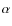 continuum absorption and the radiative bound-free cross-sections are very important for Si line formation, especially for warm metal-poor stars.
continuum absorption and the radiative bound-free cross-sections are very important for Si line formation, especially for warm metal-poor stars.
- 5.
- Taking advantage of our statistical equilibrium approach and accurate atomic data for the investigated lines, we obtain good agreement between the Si I and Si II abundances. We show that NLTE largely removes obvious discrepancies between Si I and Si II obtained under an LTE assumption.
- 6.
- Our results suggest that, similar to magnesium, silicon is produced by massive type II SNe.
Acknowledgements
J.R. acknowledges Dr. Aoki for providing the Subaru spectrum for G64-12. This research was supported by the National Natural Science Foundation of China under grant Nos. 10821061, 10778626, 10811130393 and the National Basic Research Program of China (973 Program) under grant No. 2007CB815103, by the Deutsche Forschungsgemeinschaft with grant 446 CHV 112/1,2 and the Russian Foundation for Basic Research with grant 08-02-92203-NNSF.
References
- Ali, A. W., & Griem, H. R. 1966, Phys. Rev., 144, 366 [NASA ADS] [CrossRef] (In the text)
- Allard, N. F., Drira, I., Gerbaldi, M., Koester, D., & Spielfiedel, A. 1998, A&A, 335, 1124 [NASA ADS] (In the text)
- Allard, N. F., Kielkopf, J. F., Cayre, R., & van't Veer-Menneret, C. 2008, A&A, 480, 581 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Anstee, S. D., & O'Mara, B. J. 1991, MNRAS, 253, 549 [NASA ADS] (In the text)
- Anstee, S. D., & O'Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] (In the text)
- Aoki, W., Honda, S., Beers, T. C., et al. 2005, ApJ, 632, 611 [NASA ADS] [CrossRef] (In the text)
- Bagbulo, S., Jehin, E., Ledoux, C., et al. 2005, ESO messenger, 114, 10 [NASA ADS] (In the text)
- Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&A, 355, L5 [NASA ADS] (In the text)
- Baumüller, D., & Gehren, T. 1996, A&A, 307, 961 [NASA ADS] (In the text)
- Baumüller, D., & Gehren, T. 1997, A&A, 325, 1088 [NASA ADS] (In the text)
- Butler, K., Giddings, J. R. 1985, Newsletter on the analysis os astronomical spectra No. 9, University of London (In the text)
- Butler, K., Mendoza, C., & Zeippen, C. J. 1993, J. Phys. B, 26, 4409 [NASA ADS] [CrossRef]
- Cacciari, C. 1985, A&AS, 61, 407 [NASA ADS] (In the text)
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cohen, J. G., Christlieb, N., & McWilliam, A. 2004, ApJ, 612, 1107 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G., McWilliam, A., Christlieb, N., et al. 2007, ApJ, 659, L161 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G., Christlieb, N., McWilliam A., et al. 2008, ApJ, 672, 230 [NASA ADS] [CrossRef] (In the text)
- Decauwer, H., Jehin, E., Parmentier, G., & Magain, P. 2005, A&A, 433, 285 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dessauges-Zavadsky, M., Prochaska, J. X., D'Odorico, S., Calura, F., & Matteucci, F. 2006, A&A, 445, 93 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] (In the text)
- Fuhrmann, K., Pfeiffer, M., Frank, C., et al. 1997, A&A, 323, 909 [NASA ADS] (In the text)
- Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] (In the text)
- Fulbright, J. P. 2002, AJ, 123, 404 [NASA ADS] [CrossRef] (In the text)
- Garz, T. 1973, A&A, 26, 471 [NASA ADS] (In the text)
- Gehren, T., Butler, K., Mashonkina, L., et al. 2001, A&A, 366, 981 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gehren, T., Liang, Y. C., Shi, J. R., et al. 2004, A&A, 413, 1045 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gehren, T., Shi, J. R., Zhang, H. W., Zhao, G., & Korn, A. J. 2006, A&A, 451, 1065 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Goswami, A., & Prantzos, N. 2000, A&A, 359, 191 [NASA ADS] (In the text)
- Gratton, R. G., Carretta, E., Claudi, R., et al. 2003, A&A, 404, 187 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Henry, R. B. C., & Prochaska, J. X. 2007, PASP, 119, 962 [NASA ADS] [CrossRef] (In the text)
- Honda, S., Aoki, W., Kajino, T., et al. 2004, ApJ, 607, 474 [NASA ADS] [CrossRef] (In the text)
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] (In the text)
- Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653, 1145 [NASA ADS] [CrossRef] (In the text)
- Korn, A., Shi, J., & Gehren, T. 2003, A&A, 407, 691 [NASA ADS] [CrossRef] [EDP Sciences]
- Kurucz, R. L., Furenlid, I., Brault, J., et al. 1984, Solar Flux Atlas from 296 to 1300 nm, Nat. Solar Obs., Sunspot, New Mexico (In the text)
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] (In the text)
- Mashonkina, L., Gehren, T., Travaglio, C., et al. 2003, A&A, 397, 275 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mashonkina, L., Korn, A., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mashonkina, L., Gehren, T., Shi, J. R., Korn, A., & Grupp, F. 2009, in preparation
- McWilliam, A., Preston, G. W., Sneden, C., et al. 1995, AJ, 109, 2736 [NASA ADS] [CrossRef] (In the text)
- Nahar, S. N., & Pradhan, A. K. 1993, J. Phys. B, 26, 1109 [NASA ADS] [CrossRef] (In the text)
- Nissen, P. E., & Schuster, W. J. 1997, A&A, 326, 751 [NASA ADS] (In the text)
- Noguchi, K., Aoki, W., & Kawanomoto, S. 2002, PASJ, 54, 855 [NASA ADS] (In the text)
- Nomoto, K., Iwamoto, K., Nakasato, N., et al. 1997, Nucl. Phys. A, 621, 467c [NASA ADS] [CrossRef] (In the text)
- Nomoto, K., Tominaga, N., Umeda, H., Kobsysdhi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] (In the text)
- Ohkubo, T., Umeda, H., Maeda, K., et al. 2006, ApJ, 645, 1352 [NASA ADS] [CrossRef] (In the text)
- Pfeiffer, M. J., Frank, C., Baumüller, D., et al. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Preston, G. W., Sneden, C., Thompson, I. B., Shectman, S. A., & Burley, G. S. 2006, AJ, 132, 85 [NASA ADS] [CrossRef] (In the text)
- Prochaska, J. X., & Wolfe, A. M. 2002, ApJ, 566, 68 [NASA ADS] [CrossRef] (In the text)
- Prochaska, J. X., Naumov, S. O., Carney, B. W., et al. 2000, AJ, 120, 2513 [NASA ADS] [CrossRef]
- Ryan, S. G., Norris, J. E., & Beers, T. C. 1996, ApJ, 471, 254 [NASA ADS] [CrossRef] (In the text)
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] (In the text)
- Shi, J. R., Gehren, T., & Zhao, G. 2004, A&A, 423, 683 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shi, J. R., Gehren, T., Butler, K., Mashonkina, L., & Zhao, G. 2008, A&A, 486, 303 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stephens, A., & Merchant Boesgaard, A. M. 2002, AJ, 123, 1647 [NASA ADS] [CrossRef] (In the text)
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] (In the text)
- Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] (In the text)
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] (In the text)
- Umeda, H., Nomoto, K., & Nakamura, T. 2000, in The first Stars, ed. A. Weiss, T. Abel, & V. Hill (Heidelberg: Springer), 150 (In the text)
- Wedemeyer, S. 2001, A&A, 373, 998 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] (In the text)
- Zhao, G., & Gehren, T. 2000, A&A, 362, 1077 [NASA ADS] (In the text)
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Based on observations obtained in the frame of the ESO programme ID 165.N-0276(A).
All Tables
Table 1: Atomic data of silicon lines*.
Table 2: Stellar silicon LTE and NLTE (for each star, the first and the second row, respectively) abundances given relative to the iron LTE abundances derived from the Fe II lines*.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12073fg1.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg18.png) |
Figure 1:
Silicon abundances of metal-poor stars determined from LTE analyses of Fulbright (2000, Filled circles |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{6.6cm}{\includegraphics[width=9.3cm]{12073f2a...
...r\resizebox{9cm}{6.6cm}{\includegraphics[width=9.3cm]{12073f2c.ps}}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg46.png) |
Figure 2: Difference of [Si/Fe] abundance ratios calculated under NLTE and LTE assumptions for the two strong Si I 3905 and 4102 Å lines as a function of metal abundance a), temperature b), and surface gravity c). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12073fg3.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg55.png) |
Figure 3:
The UV flux emerging from MAFAGS-ODF model for HD 84937 without (dashed line) and with (solid line) the Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12073fg4.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg56.png) |
Figure 4: The comparision of the UV flux from MAFAGS-ODF model (solid line) with the IUE observations (dashed line) for HD 84937. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073f5a.ps}\vspace*{5mm}
\includegraphics[width=8.5cm,clip]{12073f5b.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg58.png) |
Figure 5:
Departure coefficients as a function of log |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg6.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg60.png) |
Figure 6:
Theoretical NLTE flux profiles (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg7.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg61.png) |
Figure 7:
Comparison of derived [Si/Fe] (NLTE) for stars in common with other studies. Triangle ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg8.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg67.png) |
Figure 8:
Abundance ratios [Si/Fe] as a function of [Fe/H]. Filled circles ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12073fg9.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa12073-09/Timg68.png) |
Figure 9: Abundance ratios [Si/Mg] for NLTE analysis as a function of [Fe/H]. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


