| Issue |
A&A
Volume 503, Number 1, August III 2009
|
|
|---|---|---|
| Page(s) | 73 - 86 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912181 | |
| Published online | 23 June 2009 | |
Molecular gas in NUclei of GAlaxies (NUGA)![[*]](/icons/foot_motif.png)
XII. The head-on collision in NGC 1961
F. Combes1 - A. J. Baker2 - E. Schinnerer3 - S. García-Burillo4 - L. K. Hunt5 - F. Boone1 - A. Eckart6 - R. Neri7 - L. J. Tacconi8
1 - Observatoire de Paris, LERMA, 61 Av. de
l'Observatoire, 75014 Paris, France
2 -
Rutgers, The State University of NJ, 136 Frelinghuysen Road,
Piscataway, NJ 08854-8019, USA
3 -
Max-Planck-Institut für Astronomie,
Königstuhl 17, 69917 Heidelberg, Germany
4 -
Observatorio Astronómico Nacional (OAN), Observatorio
de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
5 -
INAF-Osservatorio Astrofisico di Arcetri, Largo E.
Fermi 5, 50125 Firenze, Italy
6 -
Universität zu Köln, I. Physikalisches Institut,
Zülpicher Strasse 77, 50937 Köln, Germany
7 -
Institut de Radio-Astronomie Millimétrique,
300 rue de la Piscine, 38406 St. Martin-d'Hères, France
8 -
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, 85741 Garching, Germany
Received 25 March 2009 / Accepted 9 June 2009
Abstract
We present high-resolution maps of the CO(1-0) and CO(2-1)
emission from the LINER 2 galaxy NGC 1961. This galaxy is unusual among
late-type (Sc) disk galaxies in having a very large radial extent and
inferred dynamical mass. We propose a head-on collision scenario to
explain the perturbed morphology of this galaxy - both the off-centered
rings and the inflated radius. This scenario is supported by the detection
of a steep velocity gradient in the CO(1-0) map at the position of a southwest
peak in radio continuum and near-infrared emission. This peak would represent the remnant
of the disrupting companion. We use
numerical models to demonstrate the plausibility of the scenario.
While ram pressure stripping could in principle be important for shocking
the atomic gas and produce the striking head-tail morphology,
the non detection of this small galaxy group in X-ray emission
suggests that any hot intragroup medium has too low a density.
A prediction of the collision model is the propagation of
ring waves from the center to the outer parts, superposed on
a probable pre-existing m=2 barred spiral feature, accounting for
the observed complex structure of rings and spokes. This lopsided wave accounts
for the sharp boundary observed in the atomic gas on the southern side. Through
dynamical friction, the collision finishes quickly in a minor merger, the
best fit being for a companion with a mass ratio 1:4.
We argue that NGC 1961 has a strongly warped disk, which
gives the false impression of a nearly face-on system; the main
disk is actually more edge-on, and this error in the true inclination has
led to the surprisingly high dynamical mass for a morphologically
late-type galaxy. In addition, the outwardly propagating ring artificially
enlarges the disk. The collision de-stabilizes the inner disk
and can provide gas inflow to the active nucleus.
Key words: galaxies: individual: NGC 1961 - galaxies: interactions - galaxies: ISM - galaxies: kinematics and dynamics - galaxies: nuclei - radio lines: galaxies
1 Introduction
The tight correlation between black hole mass and central velocity dispersion
(
![]() relation,
Merritt & Ferrarese 2001; Tremaine et al. 2002) offers
strong evidence that galaxies' stellar spheroids and central black holes
are built up by mechanisms that are closely linked, if not identical. In disk
galaxies, black holes of increasing mass can scatter more disk stars into a
bulge (Norman et al. 1996) and drive secular evolution along the
Hubble sequence. A more generally applicable scenario (holding for both early
and late-type galaxies), however, centers on the balance of nuclear
fuelling and feedback. If the relative fractions of inflowing gas consumed by nuclear star
formation and accretion onto a black hole are roughly constant, then the
relation,
Merritt & Ferrarese 2001; Tremaine et al. 2002) offers
strong evidence that galaxies' stellar spheroids and central black holes
are built up by mechanisms that are closely linked, if not identical. In disk
galaxies, black holes of increasing mass can scatter more disk stars into a
bulge (Norman et al. 1996) and drive secular evolution along the
Hubble sequence. A more generally applicable scenario (holding for both early
and late-type galaxies), however, centers on the balance of nuclear
fuelling and feedback. If the relative fractions of inflowing gas consumed by nuclear star
formation and accretion onto a black hole are roughly constant, then the
![]() relation is naturally explained.
relation is naturally explained.
Since nearly half of all nearby systems host low-luminosity active galactic nuclei (AGN: Ho et al. 1997a), the supply of fuel to the Schwarzschild radius (not to mention circumnuclear star-forming regions) is still very much an ongoing process. Because black holes appear to occupy the centers of nearly all galaxies with massive bulges, high-resolution studies of the gas dynamics in virtually any system with a massive spheroid should therefore shed light on the role of fuelling in driving the coevolution of black holes and host galaxies. This prospect is the motivation for our observations of the Nuclei of Galaxies (NUGA) sample at the IRAM Plateau de Bure Interferometer (PdBI: Guilloteau et al. 1992). The NUGA survey is designed to explore the molecular gas content and mechanisms for nuclear fuelling at high angular resolution; initial observations of a sample of twelve nearby AGN (García-Burillo et al. 2003) will ultimately be combined with a larger sample of both active and quiescent nuclei for the purpose of statistical comparisons. In this paper, the twelfth in an initial series focused on individual objects, we present the PdBI data for the NUGA target NGC 1961.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f1.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg27.png) |
Figure 1:
Blue DSS image of NGC 1961. Note the sharp linear feature to the
southeast (oriented at 45 |
| Open with DEXTER | |
Judging by its nuclear properties, NGC 1961 is a relatively unremarkable
low-luminosity AGN. Its optical spectrum is classified as a Low-Ionization
Nuclear Emission-line Region (LINER) by Ho et al. (1997b); it shows no
broad-line emission, although its narrow-line profiles do show asymmetric blue
wings (Ho et al. 1997c). NGC 1961 has attracted significantly more
attention for being one of the most massive known disk galaxies (Rubin et al.
1979), one that is unusually massive for its late (Sc) Hubble type.
This peculiarity cannot be attributed to a distance error, since NGC 1961 is
associated with a group of ten galaxies that all lie within
![]() of each other at small separations on the sky (Gottesman et al.
2002). NGC 1961 appears to be impinging on this group from the
northwest: its large-scale optical morphology shows a pronounced linear
feature to the southeast which connects to an anomalous asymmetric arm winding
from south to west (Fig. 1).
of each other at small separations on the sky (Gottesman et al.
2002). NGC 1961 appears to be impinging on this group from the
northwest: its large-scale optical morphology shows a pronounced linear
feature to the southeast which connects to an anomalous asymmetric arm winding
from south to west (Fig. 1).
Some CO emission has already been detected in NGC 1961 (Young et al.
1995; Komugi et al. 2008), corresponding to a molecular
gas mass of
![]() .
The H I content of
NGC 1961 is substantial (nearly
.
The H I content of
NGC 1961 is substantial (nearly
![]() of atomic
hydrogen: Haan et al. 2008), which suggests a very late type galaxy.
However, the galaxy has a large radial extent, both optically and in H I,
apparently much larger than expected for its morphological type. The H I
morphology revealed by
recent VLA observations (Haan et al. 2008) is striking because of its
head-tail shape, with a very sharp boundary in the south. This feature suggests
a ram-pressure shock, although no diffuse X-ray emission has
been detected by ROSAT
in this galaxy group (Mulchaey et al. 2003).
Shostak et al. (1982) first noted the sharp H I cut-off displaced
with respect to the stellar boundary and suggested a ram pressure shock
was responsible.
This linear feature of higher H I column density coincides with a higher
radio continuum surface brightness at frequencies from 1.5 to 15.4 GHz
(Lisenfeld et al. 1998).
of atomic
hydrogen: Haan et al. 2008), which suggests a very late type galaxy.
However, the galaxy has a large radial extent, both optically and in H I,
apparently much larger than expected for its morphological type. The H I
morphology revealed by
recent VLA observations (Haan et al. 2008) is striking because of its
head-tail shape, with a very sharp boundary in the south. This feature suggests
a ram-pressure shock, although no diffuse X-ray emission has
been detected by ROSAT
in this galaxy group (Mulchaey et al. 2003).
Shostak et al. (1982) first noted the sharp H I cut-off displaced
with respect to the stellar boundary and suggested a ram pressure shock
was responsible.
This linear feature of higher H I column density coincides with a higher
radio continuum surface brightness at frequencies from 1.5 to 15.4 GHz
(Lisenfeld et al. 1998).
The galaxy as a whole has an unusually high radio continuum luminosity
relative to its optical (blue) and far-infrared (40-120 ![]() m)
luminosities. Lisenfeld et al. (1998) suggest
that a second nucleus in their radio continuum map may be the remnant of an
infalling dwarf galaxy, and attribute the high radio luminosity to
cosmic rays that have been produced in the putative minor merger. The
observed morphology can constrain its orbit type:
the lack of extended tidal tail features in the H I map
suggests that any recent merger at the
very least cannot have had a prograde encounter geometry with respect to
NGC 1961's sense of rotation. We use the molecular line observations
and the numerical simulations reported in this paper
to help identify which of these two mechanisms is more
plausibly responsible for the large-scale asymmetries in NGC 1961.
m)
luminosities. Lisenfeld et al. (1998) suggest
that a second nucleus in their radio continuum map may be the remnant of an
infalling dwarf galaxy, and attribute the high radio luminosity to
cosmic rays that have been produced in the putative minor merger. The
observed morphology can constrain its orbit type:
the lack of extended tidal tail features in the H I map
suggests that any recent merger at the
very least cannot have had a prograde encounter geometry with respect to
NGC 1961's sense of rotation. We use the molecular line observations
and the numerical simulations reported in this paper
to help identify which of these two mechanisms is more
plausibly responsible for the large-scale asymmetries in NGC 1961.
We describe our observations in Sect. 2 and their results in Sect. 3, focusing on the m = 1 asymmetry
and off-centered ring morphology evident in the CO maps.
A dynamical model is proposed and arguments developed in
Sect. 4 to explain the perturbed morphology and asymmetries
observed on large scales as the result of a recent head-on collision.
Section 5 describes in detail the adopted model,
the technique of the simulations, and their results.
Our discussion of the collision scenario and its
implications for AGN fuelling are presented in Sect. 6, and our
conclusions in Sect. 7. Throughout this paper, we will use the
distance
![]() specified by Tully (1988), and a
CO-to-
specified by Tully (1988), and a
CO-to-![]() conversion factor
conversion factor
![]() as recommended by Solomon & Barrett (1991).
as recommended by Solomon & Barrett (1991).
2 Observations
2.1 CO interferometry
We observed the CO(1-0) and CO(2-1) lines in NGC 1961 with the
IRAM PdBI between December 2000 and January 2002. During this period, the
array included from four to six 15 m diameter antennas; deployment in the B,
C, and D configurations yielded a total of 35 distinct baselines ranging from
24 m to 280 m in length. In March 2003, the A configuration
added longer baselines, up to 420 m for the CO(2-1) line, and provided
sub-arcsecond resolution
(see documentation on configurations at http://www.iram.fr).
Each antenna was equipped with both
single-sideband 3 mm and double-sideband 1 mm SIS receivers that were used
simultaneously; receiver temperatures were 60-80 K, and corrected outside
the atmosphere yielded typical system temperatures of ![]()
![]() and
and
![]()
![]() at 3 mm and 1 mm, respectively. We deployed four
correlator modules - giving a total of 580 MHz of continuous bandwidth at
2.5 MHz resolution - across each of the two lines. The CO(1-0) and CO(2-1)
lines were observed in the upper and lower sidebands relative to the 3 mm
and 1 mm reference frequencies. As the phase (pointing) center for the
observations, we adopted a galaxy's optical position, slightly
different from that listed in NED -
at 3 mm and 1 mm, respectively. We deployed four
correlator modules - giving a total of 580 MHz of continuous bandwidth at
2.5 MHz resolution - across each of the two lines. The CO(1-0) and CO(2-1)
lines were observed in the upper and lower sidebands relative to the 3 mm
and 1 mm reference frequencies. As the phase (pointing) center for the
observations, we adopted a galaxy's optical position, slightly
different from that listed in NED -
![]() 05:42:04.8 and
05:42:04.8 and
![]() +69:22:43.3
+69:22:43.3![]() .
.
We calibrated our data using the CLIC routines in the IRAM GILDAS software
package (Guilloteau & Lucas 2000). For passband calibration, we
used the bright quasars 3C111, 3C279, and 3C454.3. Observations of the blazar
0716+714 interleaved with our source data every ![]() 30 min were used to
remove phase drifts and amplitude gain variations. The flux density of
0716+714 was in turn determined at each epoch by comparisons with the
calibration sources CRL618 and MWC349; we estimate the uncertainties in the flux scales to
be
30 min were used to
remove phase drifts and amplitude gain variations. The flux density of
0716+714 was in turn determined at each epoch by comparisons with the
calibration sources CRL618 and MWC349; we estimate the uncertainties in the flux scales to
be ![]()
![]() .
Table 1 lists the details of our observations and
calibrations, including the flux densities adopted for 0716+714 at both 3 mm
and 1 mm. The fact that 0716+714 is a blazar explains its strong variability.
.
Table 1 lists the details of our observations and
calibrations, including the flux densities adopted for 0716+714 at both 3 mm
and 1 mm. The fact that 0716+714 is a blazar explains its strong variability.
Table 1: Log of PdBI observations of NGC 1961.
Before constructing uv tables from our calibrated data, we smoothed them to
a frequency resolution of 5 MHz (velocity resolutions
![]() for the CO(1-0) line and
for the CO(1-0) line and
![]() for the
CO(2-1) line).
The primary beam sizes at the two frequencies are 43 and 21.5
for the
CO(2-1) line).
The primary beam sizes at the two frequencies are 43 and 21.5
![]() respectively.
The full datasets include the (on-source, six-telescope)
equivalents of 16.8 h of 3 mm data and 13.9 h of 1 mm data. In
the 3 mm data cube, CO(1-0) line emission is detected out to
respectively.
The full datasets include the (on-source, six-telescope)
equivalents of 16.8 h of 3 mm data and 13.9 h of 1 mm data. In
the 3 mm data cube, CO(1-0) line emission is detected out to
![]() blueward and
blueward and
![]() redward of the systemic
redward of the systemic
![]() LSR (see Sect. 3.2). We constructed a 3 mm continuum channel from the
upper-sideband channels outside this velocity range, and upon mapping (with
natural weighting) discovered the presence of a
LSR (see Sect. 3.2). We constructed a 3 mm continuum channel from the
upper-sideband channels outside this velocity range, and upon mapping (with
natural weighting) discovered the presence of a
![]() continuum source offset
continuum source offset ![]()
![]() to the northwest of the nucleus (see
Sect. 3.4). In order to avoid contamination of the CO(1-0) line
maps, we used the GILDAS task UV_SUBTRACT to remove a uv model for this
continuum source from all of the 3 mm uv data. Our maps of the
continuum-subtracted line cube used natural weighting, which (as for the 3 mm
continuum data) yielded a synthesized beam of
to the northwest of the nucleus (see
Sect. 3.4). In order to avoid contamination of the CO(1-0) line
maps, we used the GILDAS task UV_SUBTRACT to remove a uv model for this
continuum source from all of the 3 mm uv data. Our maps of the
continuum-subtracted line cube used natural weighting, which (as for the 3 mm
continuum data) yielded a synthesized beam of
![]() at position angle
at position angle ![]() .
The rms per
.
The rms per
![]() channel is
channel is
![]() .
.
At 1 mm, no continuum emission was evident (with an rms of 0.4 mJy)
in a map made from the upper
(line-free) sideband visibility data, leading us to conclude that no
subtraction of continuum from our 1 mm line data would be necessary.
CO(2-1) emission is seen over a velocity range of
![]() relative to
relative to
![]() ,
smaller than the full CO(1-0) range because gas
moving at the highest velocities in the CO(1-0) data cube lies outside the
smaller CO(2-1) primary beam. We used uniform weighting to reach an angular
resolution of
,
smaller than the full CO(1-0) range because gas
moving at the highest velocities in the CO(1-0) data cube lies outside the
smaller CO(2-1) primary beam. We used uniform weighting to reach an angular
resolution of
![]() (
(![]()
![]() in projection) at position angle
in projection) at position angle ![]() .
The rms per
.
The rms per
![]() channel is
channel is
![]() .
.
We measured the integrated intensity ratio
![]() as a function of position using maps made from uv datasets
truncated at an identical radius of
as a function of position using maps made from uv datasets
truncated at an identical radius of
![]() for
both lines (i.e., slightly larger than the minimum uv radius reached for the
CO(2-1) data on the shortest projected baselines). The loss of
short-spacing information means that a map made from the truncated CO(1-0)
data has a smaller synthesized beam
than the original version made from the full data; the
new CO(2-1) map, in contrast, is hardly changed at all. We then applied
corrections for the primary beam response to both maps, convolved the CO(2-1)
map to the resolution of the (uv-truncated) CO(1-0) map, and divided them.
for
both lines (i.e., slightly larger than the minimum uv radius reached for the
CO(2-1) data on the shortest projected baselines). The loss of
short-spacing information means that a map made from the truncated CO(1-0)
data has a smaller synthesized beam
than the original version made from the full data; the
new CO(2-1) map, in contrast, is hardly changed at all. We then applied
corrections for the primary beam response to both maps, convolved the CO(2-1)
map to the resolution of the (uv-truncated) CO(1-0) map, and divided them.
2.2 Optical and infrared imaging
We have extracted optical and near-infrared images of NGC 1961 from the
Hubble Space Telescope (HST) archive. Images were acquired using
WFPC2 through the F547M and F606W (![]() V) filters, and using NICMOS through
the F160W (
V) filters, and using NICMOS through
the F160W (![]() H) filter (see Martini et al. 2003; Hunt & Malkan 2004).
To show the large-scale optical morphology of the galaxy, we have taken red and blue optical images
from the Digitized Palomar Sky Survey (DSS); the blue image is shown in Fig. 1.
H) filter (see Martini et al. 2003; Hunt & Malkan 2004).
To show the large-scale optical morphology of the galaxy, we have taken red and blue optical images
from the Digitized Palomar Sky Survey (DSS); the blue image is shown in Fig. 1.
For wide-field near-IR information, we have turned to the Two Micron All Sky
Survey (2MASS: Skrutskie et al. 1997). Jarrett et al.
(2003) have included NGC 1961 in their 2MASS ``Large Galaxy Atlas'';
we have downloaded their reduced images from the IPAC website. A ![]() image is shown in Sect. 4.
image is shown in Sect. 4.
IRAC images at 3.6 ![]() m, 4.5
m, 4.5 ![]() m and 8.0
m and 8.0 ![]() m
were retrieved from the Spitzer archive.
We started with the Basic Calibrated Data images,
and aligned and combined them with MOPEX
(Makovoz & Marleau 2005) which accounts
for distortion and rotates to a fiducial coordinate system.
1
m
were retrieved from the Spitzer archive.
We started with the Basic Calibrated Data images,
and aligned and combined them with MOPEX
(Makovoz & Marleau 2005) which accounts
for distortion and rotates to a fiducial coordinate system.
1
![]() 20 pixels were imposed for the final images,
roughly the same as the original IRAC detector.
Significant banding was present
and this was corrected for by
interpolation over the affected rows before combination with MOPEX.
The 8.0
20 pixels were imposed for the final images,
roughly the same as the original IRAC detector.
Significant banding was present
and this was corrected for by
interpolation over the affected rows before combination with MOPEX.
The 8.0 ![]() m IRAC filter tends to be dominated by aromatic features of
polycyclic aromatic hydrocarbons (PAHs), but also contains a contribution
from stellar photospheres. The IRAC images at shorter wavelengths (3.6,
4.5
m IRAC filter tends to be dominated by aromatic features of
polycyclic aromatic hydrocarbons (PAHs), but also contains a contribution
from stellar photospheres. The IRAC images at shorter wavelengths (3.6,
4.5 ![]() m) can be suitably combined and scaled to estimate the stellar
emission. Following Helou et al. (2004), we obtained a non-stellar (dust)
image by subtracting
from the 8.0
m) can be suitably combined and scaled to estimate the stellar
emission. Following Helou et al. (2004), we obtained a non-stellar (dust)
image by subtracting
from the 8.0 ![]() m image a scaled linear combination of the 3.6
and 4.5
m image a scaled linear combination of the 3.6
and 4.5 ![]() m images. The IRAC images were originally
published by Pahre et al. (2004).
m images. The IRAC images were originally
published by Pahre et al. (2004).
3 Results
3.1 CO line morphologies
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f2.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg59.png) |
Figure 2:
CO(1-0) zeroth moment map, with coordinates defined relative to the
PdBI phase center. The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f3.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg60.png) |
Figure 3:
CO(1-0) zeroth moment map contours (as in Fig. 2)
overlaid on the 8.4 GHz radio continuum map from Lisenfeld et al.
(1998) in greyscale. Coordinates are defined relative to the VLA
phase center adopted for the 8.4 GHz observations, whose |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f4.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg61.png) |
Figure 4: PdBI CO(1-0) zeroth moment map contours (as in Fig. 2) overlaid on the blue DSS image in greyscale. Coordinates are defined relative to the PdBI phase center. |
| Open with DEXTER | |
We derived zeroth moment maps from our CO data cubes using the Groningen Image
Processing SYstem (GIPSY: van der Hulst et al. 1992); emission was
integrated over the observed line widths after clipping all ![]()
![]() pixels in the individual channels. Figure 2 shows the result for
the CO(1-0) line. The global molecular gas distribution is dominated by a
strong central concentration of dimensions
pixels in the individual channels. Figure 2 shows the result for
the CO(1-0) line. The global molecular gas distribution is dominated by a
strong central concentration of dimensions ![]()
![]() .
This structure is encircled to the north and east by a winding gaseous arc
containing a number of knots, the strongest of which lie
.
This structure is encircled to the north and east by a winding gaseous arc
containing a number of knots, the strongest of which lie ![]()
![]() east
and
east
and ![]()
![]() northwest of the nucleus. To the southwest, there is an
isolated concentration of gas whose relationship to the rest of the disk is
not immediately apparent. An important clue to its nature comes from Fig. 3, which shows CO(1-0) contours overlaid on a greyscale image
of 8.4 GHz continuum emission from Lisenfeld et al. (1998).
Although the CO(1-0) primary beam does not extend over the entire 8.4 GHz
map, a comparison in the inner
northwest of the nucleus. To the southwest, there is an
isolated concentration of gas whose relationship to the rest of the disk is
not immediately apparent. An important clue to its nature comes from Fig. 3, which shows CO(1-0) contours overlaid on a greyscale image
of 8.4 GHz continuum emission from Lisenfeld et al. (1998).
Although the CO(1-0) primary beam does not extend over the entire 8.4 GHz
map, a comparison in the inner ![]()
![]() is already instructive. The
anomalous CO(1-0) emission southwest of the nucleus coincides almost exactly
with the off-center 8.4 GHz feature that Lisenfeld et al. (1998)
identify as a ``second nucleus.'' This agreement adds some weight to the
authors' suggestion that the off-nuclear peak represents the remnant of a
smaller galaxy that has merged with NGC 1961 (see also Sect. 4 below).
There is a slight offset between the two positions, which is certainly
expected, since the small companion is likely to be strongly perturbed and the
CO emission itself is lopsided.
is already instructive. The
anomalous CO(1-0) emission southwest of the nucleus coincides almost exactly
with the off-center 8.4 GHz feature that Lisenfeld et al. (1998)
identify as a ``second nucleus.'' This agreement adds some weight to the
authors' suggestion that the off-nuclear peak represents the remnant of a
smaller galaxy that has merged with NGC 1961 (see also Sect. 4 below).
There is a slight offset between the two positions, which is certainly
expected, since the small companion is likely to be strongly perturbed and the
CO emission itself is lopsided.
In Fig. 4, we show an overlay of the CO(1-0) contours of Fig. 2 on the (inner region of the) blue DSS image of Fig. 1 in greyscale. The anomalous CO(1-0) feature to the southwest of the nucleus coincides with a region of high extinction in the optical image, suggesting that the molecular gas structure may lie on the near side of the galactic disk. This region also corresponds to the possible second nucleus. The eastern section of the winding arc also aligns very nicely with a region of high extinction, very likely a dust lane, although the northern section does not. This contrast offers the first of several hints that the CO(1-0) arc does not trace a single spiral arm. Instead, as will be clear in the CO(2-1) map, the CO emission suggests a distorted ring-like structure.
The reliability of the CO(1-0) line luminosity as an extragalactic mass
tracer (e.g., Dickman et al. 1986; Solomon & Barrett 1991)
allows us to convert the line fluxes of various structures in the CO(1-0) map
into molecular gas masses. Including a factor of 1.36 to account for helium,
the gas mass bound into molecular clouds can be calculated as
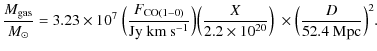 |
(1) |
After correcting Fig. 2 for primary beam response, we estimate the masses of the central disk, and of the CO ring including the anomalous southwestern emission, to be
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f5.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg74.png) |
Figure 5:
CO(2-1) zeroth moment map, with coordinates defined relative to the
PdBI phase center. The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f6.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg75.png) |
Figure 6: Top: CO(2-1) zeroth moment contours (as in Fig. 5) overlaid on HST F160W colourscale. Bottom: same contours superposed on the Unsharp Mask version of the NICMOS image. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f7.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg76.png) |
Figure 7: CO(2-1) zeroth moment contours (as in Fig. 2) overlaid on CO(1-0) zeroth moment greyscale. |
| Open with DEXTER | |
Figure 5 shows the zeroth moment of the CO(2-1) line. Due to
primary beam attenuation, only the strongest (![]()
![]() northwest) knot
in the northern portion of the CO(1-0) arc is detected in CO(2-1). However,
the central concentration in the CO(1-0) map is clearly resolved into a more
compact structure encircled to the south by a clearly continuous but
strongly asymmetric spiral arm or arc. This southern arm coincides with an optical
dust lane, which is better seen on the CO(2-1)/unsharp mask NICMOS image overlay shown in Fig. 6. The southern arc winds up toward the north in a ring,
and lacks the constant-sign pitch angle that an arm would have.
This overlay has been done by making the dynamical
CO(2-1) map coincide with the peak in the NICMOS image
(corresponding also to the peak in the CO(2-1) image).
The NICMOS image in Fig. 6 (top) shows some evidence of a nuclear
stellar bar of diameter roughly 1 kpc (
northwest) knot
in the northern portion of the CO(1-0) arc is detected in CO(2-1). However,
the central concentration in the CO(1-0) map is clearly resolved into a more
compact structure encircled to the south by a clearly continuous but
strongly asymmetric spiral arm or arc. This southern arm coincides with an optical
dust lane, which is better seen on the CO(2-1)/unsharp mask NICMOS image overlay shown in Fig. 6. The southern arc winds up toward the north in a ring,
and lacks the constant-sign pitch angle that an arm would have.
This overlay has been done by making the dynamical
CO(2-1) map coincide with the peak in the NICMOS image
(corresponding also to the peak in the CO(2-1) image).
The NICMOS image in Fig. 6 (top) shows some evidence of a nuclear
stellar bar of diameter roughly 1 kpc (![]() 4 arcsec), oriented along PA =
4 arcsec), oriented along PA =
![]() .
The signature of the nuclear bar is clearly seen in the F160W radial
brightness profile (not shown) as an ellipticy peak over a constant
PA
.
The signature of the nuclear bar is clearly seen in the F160W radial
brightness profile (not shown) as an ellipticy peak over a constant
PA ![]()
![]() .
This is clearly a nuclear bar, since its elongation and position angle is
different from the rest of the disk.
.
This is clearly a nuclear bar, since its elongation and position angle is
different from the rest of the disk.
In Fig. 7, which shows CO(2-1) contours overlaid on CO(1-0) greyscale, it appears that the tip of the southern arm in the CO(2-1) map is more or less continuous with the northern section of the CO(1-0) arc. It is obvious, however, that the complex structure of arcs does not correspond to a simple and classical m=2 spiral structure. Instead, the pitch angle of the arcs is very low, and they wind up over almost a turn, more closely resembling a ring morphology. The CO is distributed in 2 or 3 embedded, offset rings, suggesting an m=1 asymmetry. This ringed CO(2-1) + CO(1-0) structure would then continue to be embedded in another ring structure seen on large scales in the optical. The external ring is much more asymmetrical and off-centered. These features provide strong clues as to the nature of the event that produced the large-scale asymmetries summarized in Sect. 1. Although it is possible to explain the small-scale lopsideness by internal mechanisms only (e.g., Jog & Combes 2009), the external ring's off-centering suggests a galaxy collision.
The innermost CO(2-1) contours reveal a double-lobed structure of dimensions
![]()
![]() that is not aligned with the near-infrared nuclear bar
in the HST-NICMOS image of Fig. 6.
This structure could correspond to the gas response to the nuclear bar,
although this is not the only possible explanation in all
cases (Schinnerer et al. 2000; Baker & Scoville 1998).
The peak in the CO(2-1) emission occurs in the southern lobe at an offset of (-1
that is not aligned with the near-infrared nuclear bar
in the HST-NICMOS image of Fig. 6.
This structure could correspond to the gas response to the nuclear bar,
although this is not the only possible explanation in all
cases (Schinnerer et al. 2000; Baker & Scoville 1998).
The peak in the CO(2-1) emission occurs in the southern lobe at an offset of (-1
![]() ,
-1
,
-1
![]() )
with respect to the PdBI pointing position
(Fig. 5), and coincides with the NED optical center
(see Table 2).
)
with respect to the PdBI pointing position
(Fig. 5), and coincides with the NED optical center
(see Table 2).
Table 2: Parameters for NGC 1961.
3.2 CO line kinematics
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f8.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg89.png) |
Figure 8:
CO(1-0) first moment map, with coordinates defined relative to the
PdBI phase center. The synthesized beam at lower left is as in Fig. 2; contours are in steps of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f9.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg90.png) |
Figure 9: CO(2-1) first moment map, with coordinates defined relative to the PdBI phase center. The synthesized beam at lower left is as in Fig. 5; contours are as in Fig. 8. |
| Open with DEXTER | |
We have also used GIPSY to analyze the CO velocity fields in NGC 1961.
Figures 8 and 9 show the first moments of the
CO(1-0) and CO(2-1) lines, constructed with clipping of (respectively) ![]()
![]() and
and ![]()
![]() pixels in the original velocity channels. As
expected given the orientation of the galaxy's isophotal major axis on the
sky, the predominant velocity gradient in both first moment maps runs in the
same east-west direction; the ascending node has a position angle
pixels in the original velocity channels. As
expected given the orientation of the galaxy's isophotal major axis on the
sky, the predominant velocity gradient in both first moment maps runs in the
same east-west direction; the ascending node has a position angle ![]()
![]() .
The larger amount of dust seen towards the southern part of the disk,
both in the DSS image on large scales and in the HST image on small scales,
establishes that the near side is south and the far side is north.
The receding velocities in the western half of NGC 1961 then imply
that most arcs are trailing, but some are also leading.
As noticed in the previous section, many arcs are part of large-scale rings, with almost
zero pitch angle. When spokes are seen between two rings,
these are unambiguously trailing.
.
The larger amount of dust seen towards the southern part of the disk,
both in the DSS image on large scales and in the HST image on small scales,
establishes that the near side is south and the far side is north.
The receding velocities in the western half of NGC 1961 then imply
that most arcs are trailing, but some are also leading.
As noticed in the previous section, many arcs are part of large-scale rings, with almost
zero pitch angle. When spokes are seen between two rings,
these are unambiguously trailing.
In contrast to the fairly regular velocity field in the main
disk, however, Fig. 8 shows
an obvious discontinuity to the southwest of the
nucleus at the location of the putative second
nucleus. If considered as a distinct structure, the velocity gradient of
![]()
![]() along a kinematic major axis of
along a kinematic major axis of ![]()
![]() would imply an enclosed dynamical mass of
would imply an enclosed dynamical mass of ![]()
![]() within a radius of
within a radius of
![]() ,
assuming an edge-on system. This is 3 times smaller
than the central molecular gas mass estimated in Sect. 3.1 above.
However, the dynamical mass could be higher, if a more
face-on inclination is assumed.
Because the range of velocities seen in the southwestern peak is reasonably
continuous with those seen in the adjoining region of the disk, we cannot
completely rule out the possibility that it is in the disk plane, but
experiencing rather strong and irregular streaming motions.
In Fig. 8, two other kinematically perturbed regions can be seen at
,
assuming an edge-on system. This is 3 times smaller
than the central molecular gas mass estimated in Sect. 3.1 above.
However, the dynamical mass could be higher, if a more
face-on inclination is assumed.
Because the range of velocities seen in the southwestern peak is reasonably
continuous with those seen in the adjoining region of the disk, we cannot
completely rule out the possibility that it is in the disk plane, but
experiencing rather strong and irregular streaming motions.
In Fig. 8, two other kinematically perturbed regions can be seen at
![]() and
and
![]() ,
with a 100 km s-1 gradient over 3
,
with a 100 km s-1 gradient over 3
![]() .
Both correspond to large molecular condensations,
that provide their own self-gravity,
in addition to the large-scale velocity gradient. These do not
require extra mass.
.
Both correspond to large molecular condensations,
that provide their own self-gravity,
in addition to the large-scale velocity gradient. These do not
require extra mass.
At the higher resolution afforded by Fig. 9, it is clear that
the true dynamical center of NGC 1961 lies between the two lobes seen in
Fig. 5, rather than coincident with either of them, with the
optical peak, or with the coordinates we adopted as the phase center for the
PdBI observations. A fit to the CO(2-1) velocity field locates the dynamical
center ![]()
![]() south and
south and ![]()
![]() west of the phase center,
i.e., at a position
west of the phase center,
i.e., at a position
![]() 05:42:04.7 and
05:42:04.7 and
![]() +69:22:42.3. With respect to this center, we have derived circular
velocity curves for NGC 1961 in both CO lines. Using the GIPSY task ROTCUR
in automated mode, we have derived fits to the CO(1-0) and CO(2-1) velocity
fields depicted in Figs. 8 and 9; the results are
presented as dashed lines in Fig. 10. The effects of beam
smearing in reducing the dv/dr slope of the CO(1-0) rotation curve relative
to the higher-resolution CO(2-1) data are immediately apparent. As an
alternative, we have also used the interactive GIPSY task INSPECTOR to derive
rotation curves from the full data cubes. These results are shown as solid
lines in Fig. 10. Because the fits to the full data cubes are
less strongly affected by beam smearing, they yield higher peak velocities at
small radii, and thus convey a more accurate impression of the high mass
densities in the galaxy's inner arcseconds.
+69:22:42.3. With respect to this center, we have derived circular
velocity curves for NGC 1961 in both CO lines. Using the GIPSY task ROTCUR
in automated mode, we have derived fits to the CO(1-0) and CO(2-1) velocity
fields depicted in Figs. 8 and 9; the results are
presented as dashed lines in Fig. 10. The effects of beam
smearing in reducing the dv/dr slope of the CO(1-0) rotation curve relative
to the higher-resolution CO(2-1) data are immediately apparent. As an
alternative, we have also used the interactive GIPSY task INSPECTOR to derive
rotation curves from the full data cubes. These results are shown as solid
lines in Fig. 10. Because the fits to the full data cubes are
less strongly affected by beam smearing, they yield higher peak velocities at
small radii, and thus convey a more accurate impression of the high mass
densities in the galaxy's inner arcseconds.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f10.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg101.png) |
Figure 10: CO-derived rotation curves for NGC 1961. CO(1-0) and CO(2-1) curves are plotted in black and gray, respectively; fits to the two-dimensional velocity fields with ROTCUR and to the three-dimensional data cubes with INSPECTOR are plotted as dashed and solid lines, respectively. None of the curves are corrected for inclination. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f11.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg102.png) |
Figure 11:
Position-velocity cuts along the kinematic major (PA
|
| Open with DEXTER | |
The full complexity of the velocity field in NGC 1961 can perhaps best be
appreciated from inspection of the four panels of Fig. 11. Here
we have extracted position-velocity cuts along the kinematic major (position
angle ![]() )
and minor (position angle
)
and minor (position angle ![]() )
axes. The spatial
widths of the cuts are
)
axes. The spatial
widths of the cuts are
![]() for the CO(1-0) cube and
for the CO(1-0) cube and
![]() for the
CO(2-1) cube. Along the minor axis, we see substantial central velocity
dispersions and indications of streaming motions within the inner
for the
CO(2-1) cube. Along the minor axis, we see substantial central velocity
dispersions and indications of streaming motions within the inner
![]()
![]()
![]() .
Along the major axis, the CO(1-0) cut reveals that
both the western section of the arc (at the most positive X-offsets)
and - especially - the eastern concentration (at the most negative offsets)
are moving at velocities faster than would be expected if motions
at smaller radii were straightforwardly extrapolated. The CO(2-1) major-axis
cut is markedly asymmetric and turns over towards the east. This pattern
can be explained either by strong streaming motions in the central
.
Along the major axis, the CO(1-0) cut reveals that
both the western section of the arc (at the most positive X-offsets)
and - especially - the eastern concentration (at the most negative offsets)
are moving at velocities faster than would be expected if motions
at smaller radii were straightforwardly extrapolated. The CO(2-1) major-axis
cut is markedly asymmetric and turns over towards the east. This pattern
can be explained either by strong streaming motions in the central ![]()
![]() ,
or by a scenario in which the eastern CO(1-0) concentration
has its own sense of motion and is not following circular rotation in the
disk plane.
,
or by a scenario in which the eastern CO(1-0) concentration
has its own sense of motion and is not following circular rotation in the
disk plane.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{12181-f12.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg109.png) |
Figure 12: Map of the CO(2-1)/CO(1-0) ratio obtained after smoothing the CO(2-1) map to the resolution of the CO(1-0) map. The contours are from 0.8 to 2.0 in steps of 0.2. The ratio increases from 0.7 in the center to 1.5 in the ring. |
| Open with DEXTER | |
3.3 CO(2-1)/CO(1-0) intensity ratio
Figure 12 shows our measurement of the intensity ratio
![]() for
regions where both CO(1-0) and CO(2-1) maps have surface brightnesses
for
regions where both CO(1-0) and CO(2-1) maps have surface brightnesses
![]()
![]() .
Over most of the disk of NGC 1961, we measure
.
Over most of the disk of NGC 1961, we measure
![]() to be 0.7-1.0, close to the mean ratio
to be 0.7-1.0, close to the mean ratio
![]() measured for
local galaxies (Braine & Combes 1992) and consistent with optically
thick emission from thermally excited lines. However, contrary to most galaxies,
where the ratio decreases from the center outwards, here the ratio increases
from 0.7 in the very center to 1.5 in the CO(2-1) ring of radius 5
measured for
local galaxies (Braine & Combes 1992) and consistent with optically
thick emission from thermally excited lines. However, contrary to most galaxies,
where the ratio decreases from the center outwards, here the ratio increases
from 0.7 in the very center to 1.5 in the CO(2-1) ring of radius 5
![]() = 1.3 kpc.
The high excitation in the ring could be due to more intense star formation.
= 1.3 kpc.
The high excitation in the ring could be due to more intense star formation.
3.4 Millimeter continuum emission
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f13.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg116.png) |
Figure 13:
3 mm continumm contours overlaid on the CO(2-1) zeroth moment map in greyscale. The resolution of the 3 mm continuum map is
|
| Open with DEXTER | |
NGC 1961 is one of a growing number of nearby AGN which reveal continuum
emission at millimeter wavelengths (other examples include NGC 1068,
NGC 3031, NGC 3147, NGC 3718 and NGC 4579: Helfer et al. 2003, Krips et al.
2005, 2006). Our non-detection of 1 mm continuum emission
(with rms of 0.4 mJy) excludes dust as a possible explanation, except in
the unlikely event that the
![]() beam at 1 mm has
resolved out a structure that was unresolved at the
beam at 1 mm has
resolved out a structure that was unresolved at the
![]() resolution of our 3 mm map.
If the 1.3 mJy source detected at 3mm was coming from dust emission,
given typical dust temperatures,
a 1mm intensity of at least 5 mJy would be expected,
which would have been detected at 12
resolution of our 3 mm map.
If the 1.3 mJy source detected at 3mm was coming from dust emission,
given typical dust temperatures,
a 1mm intensity of at least 5 mJy would be expected,
which would have been detected at 12![]() .
A flat spectrum can also be ruled out at 3
.
A flat spectrum can also be ruled out at 3![]() .
We conclude that the continuum
emission must be nonthermal in origin, implying that the source of ionizing
photons responsible for the galaxy's optical LINER spectrum is more likely to
be accretion than star formation. Figure 13 illustrates
the
.
We conclude that the continuum
emission must be nonthermal in origin, implying that the source of ionizing
photons responsible for the galaxy's optical LINER spectrum is more likely to
be accretion than star formation. Figure 13 illustrates
the ![]()
![]() offset of the continuum peak to the northeast of the
dynamical center estimated from our fit to the CO(2-1) velocity field in Sect. 3.2. Although the
offset of the continuum peak to the northeast of the
dynamical center estimated from our fit to the CO(2-1) velocity field in Sect. 3.2. Although the ![]()
![]() resolution of the Lisenfeld et al. (1998) radio continuum data are not sufficient to permit a
detailed comparison, we believe this discrepancy is real; however, we do not
view it as evidence for the migration of a supermassive black hole away from
the center of the galaxy's potential. Instead, as is also the case for much
of the 3 mm continuum emission in NGC 1068 (Schinnerer et al.
2000), we might be seeing offset jet emission.
The implied emergence of the jet from the
nucleus at an angle
resolution of the Lisenfeld et al. (1998) radio continuum data are not sufficient to permit a
detailed comparison, we believe this discrepancy is real; however, we do not
view it as evidence for the migration of a supermassive black hole away from
the center of the galaxy's potential. Instead, as is also the case for much
of the 3 mm continuum emission in NGC 1068 (Schinnerer et al.
2000), we might be seeing offset jet emission.
The implied emergence of the jet from the
nucleus at an angle
![]() with respect to the disk plane would
not be exceptional, given the skewed configurations inferred for many other
nearby low-luminosity AGN (Kinney et al. 2000).
At very small scales,
centimeter VLBI observations provide evidence of extended
emission, which could be the base of the jet (Krips et al. 2007).
with respect to the disk plane would
not be exceptional, given the skewed configurations inferred for many other
nearby low-luminosity AGN (Kinney et al. 2000).
At very small scales,
centimeter VLBI observations provide evidence of extended
emission, which could be the base of the jet (Krips et al. 2007).
4 A possible minor merger
NGC 1961 is the largest galaxy in a small group that contains only spirals,
with a velocity dispersion of
![]() too low for the group
to contain hot and diffuse X-ray emitting gas
(Pence & Rots 1997). The absence of an intragroup medium (IGM)
does not favor a scenario in which ram pressure has a large effect on the
perturbed morphology. On the other hand,
there are no close companions presently near NGC 1961, although
there are several group galaxies at distance larger than 100 kpc, mainly
to the south-east (Shostak et al. 1982).
The only plausible scenario involving a galaxy interaction
is thus a minor merger, and there are indeed signs of a possible satellite
remnant within the confines of NGC 1961.
too low for the group
to contain hot and diffuse X-ray emitting gas
(Pence & Rots 1997). The absence of an intragroup medium (IGM)
does not favor a scenario in which ram pressure has a large effect on the
perturbed morphology. On the other hand,
there are no close companions presently near NGC 1961, although
there are several group galaxies at distance larger than 100 kpc, mainly
to the south-east (Shostak et al. 1982).
The only plausible scenario involving a galaxy interaction
is thus a minor merger, and there are indeed signs of a possible satellite
remnant within the confines of NGC 1961.
The morphological and kinematic information we have gleaned from our CO(1-0) and CO(2-1) observations of NGC 1961 has provided a set of important clues which we can use, in conjunction with data at other wavelengths, to try to understand the galaxy's recent dynamical history:
- 1.
- Most of the molecular gas within a radius of
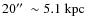 is distributed in a disk whose velocity field is reasonably regular.
At a radius of
is distributed in a disk whose velocity field is reasonably regular.
At a radius of
 ,
however, we see an isolated
structure with
,
however, we see an isolated
structure with
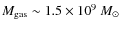 and (if self-gravitating)
and (if self-gravitating)
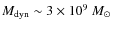 at least, or higher according to its inclination,
roughly coincident with the location of a peak in 8.4 GHz continuum.
at least, or higher according to its inclination,
roughly coincident with the location of a peak in 8.4 GHz continuum.
- 2.
- The morphologies of the molecular gas structures are quite asymmetric,
with a one-armed spiral winding through roughly
 in
azimuth, or more likely (since the pitch angle is close to zero)
a molecular ring.
The CO(1-0) reveals a ring of diameter 35
in
azimuth, or more likely (since the pitch angle is close to zero)
a molecular ring.
The CO(1-0) reveals a ring of diameter 35
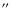 = 8.9 kpc, and the
CO(2-1) reveals an asymmetrically embedded ring of
diameter 9
= 8.9 kpc, and the
CO(2-1) reveals an asymmetrically embedded ring of
diameter 9
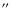 = 2.3 kpc. A hint of a nuclear gas
bar is visible in the high-resolution CO(2-1) map, with a diameter of
0.7 kpc, and a PA of 15
= 2.3 kpc. A hint of a nuclear gas
bar is visible in the high-resolution CO(2-1) map, with a diameter of
0.7 kpc, and a PA of 15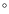 .
There is a nuclear stellar bar of roughly 1 kpc in diameter,
revealed by HST in the near-infrared, with a
PA of
.
There is a nuclear stellar bar of roughly 1 kpc in diameter,
revealed by HST in the near-infrared, with a
PA of 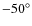 .
We note that the two CO rings at
radii of roughly 1 kpc and 4 kpc could correspond
to the ILR and OLR of this bar, if it had a
pattern speed of
.
We note that the two CO rings at
radii of roughly 1 kpc and 4 kpc could correspond
to the ILR and OLR of this bar, if it had a
pattern speed of 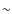
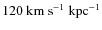 (from Fig. 17) .
(from Fig. 17) .
- 3.
- The southwestern CO(1-0) emission coincides with a peak in
the near infrared map, at about 5 kpc from the center of NGC 1961.
This NIR secondary peak is split in three smaller components,
suggesting the disruption of a stellar system. This splitting
could also be partially due to dust, although not likeky, given
the moderate average gas column density in the region.
In the absence of IGM, we arrive therefore at the conclusion that a tidal encounter or minor merger is the most likely explanation for NGC 1961's current state of disruption. The galaxy interaction cannot be a prograde grazing passage, as in this case extended tidal H I tails will form, which are not observed. The interaction must be either retrograde, or nearly head-on. The rings we have detected in the CO maps favor a head-on encounter, with a small impact parameter.
Since there is no obvious interaction partner remaining on the scene, it is also reasonable to conclude that the smaller galaxy has already merged with NGC 1961; this hypothesis has the advantage of naturally accounting for the distinct kinematic axis of the southwestern peak in CO(1-0). We can expect a priori that the merger mass ratio should be of order 1:5, to account for the substantial (but not total) disruption of the original disk of the smaller galaxy. These considerations together provide us with starting conditions to develop a detailed minor merger model.
The Spitzer IRAC images bring new insight on the true morphology of NGC 1961. As can be seen in Fig. 14, the dust emission clearly reveals two off-centered rings, in a morphology similar to that of the Cartwheel galaxy (e.g. Appleton & Struck-Marcell 1996). In particular, the ring morphology is closely related to spokes in the disk: multiple spokes link the inner ring to the outer off-centered ring, starting nearly tangential to the inner ring and ending perpendicular to the outer ring. These specific details are not so apparent in the optical image, which is confused by star-formation spots and extinction, although the spokes still can be seen. The spokes bridging the gap between off-centered rings are typical of a head-on collision in a spiral galaxy: either the latter possesses a spiral structure with a large pitch angle before the collision, and this structure is superposed on rings that propagate outwards from the center during the collision (e.g., Block et al. 2006), or the spiral structure forms through gas instabilities during the collision (e.g., Hernquist & Weil 1993).
The ring and spokes morphology of even the central stellar and ISM components
in NGC 1961 suggests a nearly head-on encounter. Of course, this could also be superposed
on some ram-pressure phenomenon. However, the superposition of the H I
and IRAC PAH-dust images in Fig. 15 shows a rather good correspondence,
suggesting a dominant gravitational phenomenon, which will similarly drag the different
ISM components, diffuse or clumpy. The stellar component, traced by the IRAC 3.6 ![]() m
image, also follows the sharp southern arc (Pahre et al. 2004).
m
image, also follows the sharp southern arc (Pahre et al. 2004).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f14.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg126.png) |
Figure 14: Short-wavelength dust (non-stellar) emission from the Spitzer IRAC images (see Sect. 2.2). North is up, East to the left; the field-of-view is 4.2 arcmin on a side. |
| Open with DEXTER | |
The possible existence of the satellite remnant, suggested already by
Lisenfeld et al. (1998) from the radio map, is also supported
by the near-infrared images that trace the stellar density. In the 2MASS
images (see Fig. 16), there is clearly a second nucleus,
which appears split into 3 clumps. Its average distance from the
center of NGC 1961 is 24
![]() or 6.1 kpc.
This feature cannot be seen in the HST NICMOS images, since
it falls outside of the field of view.
or 6.1 kpc.
This feature cannot be seen in the HST NICMOS images, since
it falls outside of the field of view.
The NOT image of NGC 1961![]() constructed by J. Näränen and K. Torstensson in 2004 by combining B, V,
and R exposures shows that the satellite nucleus is partially hidden
by a dust lane, and is split into 2-3 clumps. It is clear in this image
that star formation is strongly enhanced in the rings,
which are delineated by multiple blue hot spots.
constructed by J. Näränen and K. Torstensson in 2004 by combining B, V,
and R exposures shows that the satellite nucleus is partially hidden
by a dust lane, and is split into 2-3 clumps. It is clear in this image
that star formation is strongly enhanced in the rings,
which are delineated by multiple blue hot spots.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f15.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg127.png) |
Figure 15:
The Spitzer 8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f16.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg128.png) |
Figure 16:
2MASS K-band image of the central 76.6
|
| Open with DEXTER | |
Summarizing, the evidence that NGC 1961 has experienced a head-on collision followed by a minor merger includes:
- 1.
- the off-centered ring-like morphology (recalling that the main arcs/arms
have no obvious sense of winding), observed in many components and
wavelengths, including in CO and in dust emission (e.g., Fig. 14);
- 2.
- the very sharp southern edge of the disk observed in the gas and dust component,
in particular in the H I 21 cm map (see Fig. 15), which could
be the tracer of an expanding ring wave;
- 3.
- the existence of ``spokes'' linking the ring features, with a large
pitch angle, particularly visible
in the Spitzer dust image (Fig. 14); and
- 4.
- the presence of a perturbation in the CO
velocity field 5 kpc from the center, coinciding with a secondary stellar
peak and a radio continuum peak.
5 Simulation of the head-on collision
To test the plausibility of a head-on encounter leading to a minor merger in NGC 1961, we performed a self-consistent simulation of the collision.
5.1 Galaxy model and numerical techniques
The simulations are 3D N-body with stars and gas but
not including star formation.
They are fully self-consistent, with a live dark halo, and
use a Particle-Mesh code based on FFT with a useful grid of
1283 (the algorithm of James 1977 allows us to suppress
the Fourier images).
The grid size is (72 kpc)3, and the model galaxy is truncated
at an initial radius of 22 kpc.
The softening is equal to the size of a cell, i.e., 560 pc.
The time step is 1 Myr.
The gas is represented by sticky particles,
and a total of
![]() particles are used.
The non-dissipative components, stars and dark matter,
are represented by 2 million particles, and the gas component by
particles are used.
The non-dissipative components, stars and dark matter,
are represented by 2 million particles, and the gas component by
![]() .
First tests for the simulations were done with 10 times fewer particles,
and the total number were used only when a reasonable fit was found.
The comparison between simulations with different particle numbers
reveal that the main features (propagating ring waves, off-centering) are a fundamental
and persisting result, while secondary ones such as the exact positions of spokes
or the contrast of the arms/rings, are changing.
.
First tests for the simulations were done with 10 times fewer particles,
and the total number were used only when a reasonable fit was found.
The comparison between simulations with different particle numbers
reveal that the main features (propagating ring waves, off-centering) are a fundamental
and persisting result, while secondary ones such as the exact positions of spokes
or the contrast of the arms/rings, are changing.
The stellar component is composed of a bulge and a disk.
The bulge is initially distributed as a Plummer sphere, with a potential:
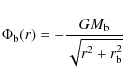 |
(2) |
where
The stellar disk is initially a Kuzmin-Toomre disk of surface density
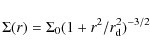 |
(3) |
with a mass
Table 3: Initial conditions.
The gas is treated as a self-gravitating component in the N-body
simulation, and its dissipation is represented by a sticky particle code,
following Combes & Gerin (1985). We varied the initial gas-to-total mass ratio
between 4 and 8% to control the stability of the disk prior
to the collision.
The mass of one gas particle therefore varied between
![]() and
and
![]() .
This is meant to represent mainly the molecular gas.
The initial gas distribution is also a Kuzmin-Toomre disk,
but truncated at 34 kpc, and with a characteristic radial scale of 8 kpc.
Initially, its velocity dispersion corresponds to a Toomre Q parameter
of 1. The gas clouds are subject to inelastic collisions, with a collision
cell size of 560 pc (the volume within which particles are selected
to possibly collide). This corresponds to a lower limit for the average mean
free path of clouds between two collisions. The collisions are considered
every 10 Myr. In a collision, the sign of the relative
cloud velocities is reversed and the absolute values are reduced:
relative velocities after the collision are only
.
This is meant to represent mainly the molecular gas.
The initial gas distribution is also a Kuzmin-Toomre disk,
but truncated at 34 kpc, and with a characteristic radial scale of 8 kpc.
Initially, its velocity dispersion corresponds to a Toomre Q parameter
of 1. The gas clouds are subject to inelastic collisions, with a collision
cell size of 560 pc (the volume within which particles are selected
to possibly collide). This corresponds to a lower limit for the average mean
free path of clouds between two collisions. The collisions are considered
every 10 Myr. In a collision, the sign of the relative
cloud velocities is reversed and the absolute values are reduced:
relative velocities after the collision are only
![]() times their
original value, with the elasticity factor
times their
original value, with the elasticity factor
![]() in the radial direction
controlling the dissipation rate. The
in the radial direction
controlling the dissipation rate. The
![]() parameter must be adapted to the particle number, so that a given
gas particle experiences a reasonable loss of energy in a rotation.
This is calibrated in simulations of the isolated galaxy, where there
is an equilibrium between the dissipative cooling,
and the dynamical heating due to spiral arm formation.
The
parameter must be adapted to the particle number, so that a given
gas particle experiences a reasonable loss of energy in a rotation.
This is calibrated in simulations of the isolated galaxy, where there
is an equilibrium between the dissipative cooling,
and the dynamical heating due to spiral arm formation.
The
![]() parameter
has been fixed to 0.65 for low particle numbers, and 0.85 for high particle
numbers (10 times more particles).
The analogous coefficient in the tangential
direction is fixed to 1, to conserve angular momentum in each
individual cloud collision.
All gas particles have the same mass (
parameter
has been fixed to 0.65 for low particle numbers, and 0.85 for high particle
numbers (10 times more particles).
The analogous coefficient in the tangential
direction is fixed to 1, to conserve angular momentum in each
individual cloud collision.
All gas particles have the same mass (
![]() in the
standard model). The particle mass for the dissipationless
components, stars and dark matter, is identically
in the
standard model). The particle mass for the dissipationless
components, stars and dark matter, is identically
![]() .
.
The rotation curve corresponding to the standard run is plotted in comparison to the data points in Fig. 17. All other runs have similar rotation curves. The parameters varied were essentially the geometry of the interaction, the mass of the companion, and the stability of the disk before the interaction.
One of the most surprising characteristics of NGC 1961 is its high dynamical
mass relative to its late type. This problem is alleviated by the choice
of a higher inclination of the main disk with respect to the plane of the sky.
It will be shown in the next section that the outer disk is warped, making
the galaxy artificially appear more face-on. Here we adopt a high inclination
of 65-70![]() for the initial disk orientation, and hence for the
calculated rotation curve.
for the initial disk orientation, and hence for the
calculated rotation curve.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{12181-f17.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg146.png) |
Figure 17:
Rotation curve and derived frequencies |
| Open with DEXTER | |
The companion is represented by a Plummer potential, where radius and mass are given in Table 3. The collision corresponds to a minor merger with a mass ratio around 1:4. Since we want to explain the morphology of NGC 1961, and have no constraint on its satellite, the companion is simulated as a rigid body. Its orbit is computed from the forces exerted on the satellite by all the particles in the main galaxy, so that most of the dynamical friction is taken into account. The contribution to dynamical friction from the companion disruption is not considered, and could decrease the merging time (see Prugniel & Combes 1992). Given the many free parameters, we do not aim to reproduce exactly the whole collision or the exact position of the companion now, but just to demonstrate that this type of collision is able to provide the right order of magnitude for the perturbation, and morphologies similar to those observed.
5.2 Simulation results
About a dozen runs have been carried out, to test the various geometrical parameters of the encounter and also to select the initial morphology of the galaxy. Indeed, a bar and a spiral wave develop in the disk during the first period when the galaxy simulation is run in isolation, and the starting time of the collision plays an important role in determining the final morphology. Similar experiments were carried out to simulate the head-on collision of the Andromeda galaxy: a small satellite (possibly M32) could have triggered the propagation of two ring waves in the disk, which superposed on the pre-existing spiral structure give the complex and perturbed morphology of M31 (cf. Block et al. 2006).
The orbit of the companion is defined by its energy and its impact
parameter.
The energy is computed from the equivalent two-body problem,
assuming that all the mass of NGC 1961 is concentrated in a point
(of mass M).
The energy per unit mass of the reduced particle is then:
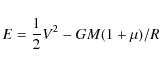 |
(4) |
where
The initial distance of the companion is 70 kpc, with a dominant
component perpendicular to the plane of the main galaxy.
The kinetic energy and relative velocity are then obtained, assuming
either a ``hyperbolic'' type of orbit with positive energy,
or an ``elliptic'' type with negative energy. The dynamical friction
then reduces the relative energy from its initial value, and all orbits
end up as bound. The best run (presented
here) has initially a negative energy, of
![]() .
.
The various experiments revealed that the impact parameter must lie between 4 and 10 kpc; it can be no larger than 10 kpc if the ring waves characteristic of a head-on collision are to appear, but no smaller than 4 kpc if the collision is to generate sufficient asymmetry and off-centering of the rings.
During the head-on collision, part of the outer disk is raised outside the plane in a huge warp. This global motion should be even more visible in the outer gas disk, and we suggest that the conspicuous northwestern features seen in the H I map, forming a fan with low-projected radial velocity along the line of sight, is a consequence of this warp. The deformation of the plane to a more face-on orientation has thus deceived us as to the true inclination of the main plane and the inferred dynamical mass.
In the run presented in a few snapshots in Figs. 18 and 19, the initial galaxy model was run in isolation for 280 Myr, and formed a barred spiral. Then the companion was introduced at 70 kpc, and the collision was followed during the subsequent 440 Myr. At this epoch, estimated to give the best fit to the observations, the ring waves have already begun to propagate outwards, and it is easily seen how the apparent radius of the galaxy inflates in the figures. After 1.5 Gyr of evolution, the galaxy could then become a giant LSB galaxy, as proposed by Mapelli et al. (2008).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{12181-f18.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg149.png) |
Figure 18:
Particle plots from the simulation of the collision,
projected to be similar to the observations (inclination 70 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{12181-f19.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg150.png) |
Figure 19: Same as Fig. 18, but now the snapshots correspond to 400 and 440 Myr ( top and bottom respectively). Note how the radius of the galaxy inflates while the ring wave propagates outward. |
| Open with DEXTER | |
A density map of the stellar and gas component is plotted in Fig. 20 and the corresponding velocity fields in Fig. 21. It is possible to see a small accumulation of particles accreted by the companion on its way back to merge with the main galaxy. Since the companion's position is not fit to what is observed, the velocity gradient observed around it is located too far north; however, the physics of the satellite were not actually addressed in these simulations. It is not even known whether the molecular gas observed in this region is coming from the main galaxy or from the merging satellite.
| |
Figure 20: Projected density of the model, at a time of 440 Myr after the beginning of the collision: the stars ( left), and the gas ( right). The scale is in kpc. The black line is the trajectory of the companion starting from the southeast. |
| Open with DEXTER | |
The velocity fields do show the gross features of what is observed, to order of magnitude. In particular, they show reasonably regular rotation in spite of a quite perturbed galaxy ``plane''.
| |
Figure 21:
Same as Fig. 20, for radial velocities.
The color bar indicated at the right side goes from -210 to
|
| Open with DEXTER | |
A feature that is well reproduced by the collisional model is the sharp boundary in the southern edge of the gas disk (Fig. 20). This sharp edge was one piece of evidence that had seemed to favor the ram pressure shock scenario. An additional point of agreement is that the gas boundary appears in projection to be shifted to the north with respect to the stellar component boundary. This is because the gas disk is much thinner than the stellar disk, which is heated in the collision. The fact that the gas front was pushed ``inside'' the stellar disk was advanced as one of the main arguments to suggest a ram-pressure scenario by Shostak et al. (1982). In the present collisional model, it is only a projection effect, arising from two components of different geometrical thickness.
Another feature reproduced by the simulations is the ``spoke'' morphology connecting the two off-centered rings (see Sect. 4). This kind of feature is typical for head-on collisions, as is shown in the Cartwheel simulations (e.g. Hernquist & Weil 1993; Horellou & Combes 2001). These are visible in the models in the gas component only, similar to the 8-micron dust-only image where they are clearly visible. Although the spokes in NGC 1961 are not at the same locations as those in our simulations, the similarity suggests that a head-on collision is capable of reproducing, at least qualitatively, the main morphological features observed.
6 Discussion
The head-on collision model reproduces quite well the ring morphology and the sharp gas edge, which were difficult to account for with ram pressure, given that hot IGM is almost absent in this small group of spiral galaxies. The minor merger scenario can also hold in the absence of a nearby interacting galaxy.
One interesting outcome of the simulation is that it also gives a possible solution to the surprisingly large radius of the galaxy with respect to its late (Sc) Hubble type. The outward propagating ring waves of the collision can increase the disk size to what appears to be abnormal proportions.
One question that can still be asked is how such a galaxy in a relatively rich environment can retain such a late type, without a significant bulge. It may be that the galaxy is entering the group for the first time. Alternatively, even if it has already interacted and merged with some members of the group, they are all gas rich (Shostak et al. 1982) and could have replenished the disk. The in-plane accretion of a large number of satellite galaxies and intergalactic H I clouds with much lower masses can quietly build up the disk mass without dynamically heating a spheroid (see Bournaud & Combes 2002), thereby depressing NGC 1961's bulge-to-disk ratio and driving its evolution towards later Hubble type. The most recent encounter has been sufficiently disruptive, however, that we would predict a reversion to an earlier type as the result of dynamical heating. The fact that we do not see more galaxies which are too massive for their Hubble types, suggests that this merger of moderate mass ratios must correspond to a quick transient phase in poor groups.
NGC 1961 is a low-luminosity AGN. From the central velocity dispersion,
the mass of the central black hole can be estimated to be
![]() (Krips et al. 2007). From the X-ray
luminosity of the nucleus and its deduced bolometric luminosity, its
Eddington ratio is estimated to be
(Krips et al. 2007). From the X-ray
luminosity of the nucleus and its deduced bolometric luminosity, its
Eddington ratio is estimated to be
![]() .
This means that the fuelling is not intense at this moment, and must be
intermittent. The very different time-scales between dynamical phenomena
at the extreme large and small scales is indeed an issue.
.
This means that the fuelling is not intense at this moment, and must be
intermittent. The very different time-scales between dynamical phenomena
at the extreme large and small scales is indeed an issue.
NGC 1961 is however a good candidate for minor-merger induced fuelling of a low luminosity AGN; at least the minor merger made more potential fuel available in the inner kpc. This was proposed by several authors (see e.g., Taniguchi 1999), and debated by others (e.g., Corbin 2000). Hopkins & Hernquist (2009) recently proposed to separate the fuelling of high-luminosity AGN (quasars), which would be fuelled by major mergers, from the low-luminosity ones, where secular evolution or minor merging is sufficient. NGC 1961 could be just an example of the transition between the two regimes.
7 Conclusions
Based on our observational and theoretical investigation of the asymmetries evident in NGC 1961 on both large and small scales, we have reached the following conclusions:
- 1.
- The galaxy's large-scale optical asymmetries can be explained as the
result of a head-on collision followed by a minor merger with mass ratio
of
 1:4. Models that rely
exclusively on ram pressure stripping cannot account for the
level of disturbance observed in the galaxy's stellar light.
1:4. Models that rely
exclusively on ram pressure stripping cannot account for the
level of disturbance observed in the galaxy's stellar light.
- 2.
- Our preferred minor merger model can naturally account for the
excitation of m = 1 asymmetries in the galaxy's inner disk, and also
for embedded off-centered rings in the CO maps. It can also explain the
very sharp gas boundary in the southern part. Due to the geometrically thin gas
plane, this sharp edge appears in projection shifted inside the stellar disk, a
feature that had previously been thought to favor only a ram-pressure scenario.
- 3.
- The head-on collision explains the ring wave propagating outwards,
but also the spokes with large pitch angle that connect the two rings.
On the smallest scales, the relaxation time is sufficiently small compared to
the merging timescale that the inner molecular disk has been able to become
bar-unstable, as reflected in the m = 2 or nuclear bar morphology seen in
the CO(2-1) map.
The galaxy could have been barred before the merger, but the latter could
have enhanced the bar strength, or create a new one,
helping the gas inflow to fuel the AGN.
- 4.
- Our collision scenario explains the exceptionally large
size of NGC 1961 for its late type. The large disk warp accounts
for an under-estimation of its true inclination in the plane of the sky,
and thus an over-estimation of its dynamical mass. NGC 1961
may have built up a significant fraction of its current
disk mass by the relatively quiescent accretion of intracluster gas. This
scenario can account for the low bulge-to-disk ratio of this spiral galaxy in a
relatively rich environment. The most recent and traumatic
merger event, however, is likely to force NGC 1961 to revert to an earlier
Hubble type.
Acknowledgements
We are grateful to IRAM staff members at the PdBI and in Grenoble for making these observations possible. We thank Ute Lisenfeld for providing electronic versions of her radio continuum maps. This work made use of the HyperLEDA and NED databases.
References
- Appleton, P. N., & Struck-Marcell, C. 1996, Fund. Cosm. Phys., 16, 111 [NASA ADS] (In the text)
- Baker, A. J., & Scoville, N. Z. 1998, in The Central Regions of the Galaxy and Galaxies, ed. Y. Sofue (Dordrecht: Kluwer), 221 (In the text)
- Block, D. L., Bournaud, F., Combes, F., et al. 2006, Nature, 443, 832 [NASA ADS] [CrossRef] (In the text)
- Bournaud, F., & Combes, F. 2002, A&A, 392, 83 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Braine, J., & Combes, F. 1992, A&A, 264, 433 [NASA ADS] (In the text)
- Combes, F., & Gerin, M. 1985, A&A, 150, 327 [NASA ADS]
- Corbin, M. R. 2000, ApJ, 536, L73 [NASA ADS] [CrossRef] (In the text)
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer Verlag)
- Dickman, R. L., Snell, R. L., & Schloerb, F. P. 1986, ApJ, 309, 326 [NASA ADS] [CrossRef] (In the text)
- García-Burillo, S., Combes, F., Eckart, A., et al. 2003, in Active Galactic Nuclei: From Central Engine to Host Galaxy, ed. S. Collin, F. Combes, & I. Shlosman (San Francisco: ASP), 423 (In the text)
- Gottesman, S. T., Hunter, J. H., Jr., & Boonyasait, V. 2002, MNRAS, 337, 34 [NASA ADS] [CrossRef] (In the text)
- Guilloteau, S., & Lucas, R. 2000, in Imaging at Radio through Submillimeter Wavelengths, ed. J. G. Mangum, & S. J. E. Radford (San Francisco: ASP), 299 (In the text)
- Guilloteau, S., Delannoy, J., Downes, D., et al. 1992, A&A, 262, 624 [NASA ADS] (In the text)
- Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] (In the text)
- Haan, S., Schinnerer, E., Mundell, C. G., García-Burillo, S., & Combes, F. 2008, AJ, 135, 232 [NASA ADS] [CrossRef] (In the text)
- Helfer, T. T., Thornley, M. D., Regan, M. W., et al. 2003, ApJS, 145, 259 [NASA ADS] [CrossRef] (In the text)
- Helou, G., Roussel, H., Appeleton, P., et al. 2004, ApJS, 154, 253 [NASA ADS] [CrossRef]
- Hernquist, L., & Weil, M. L. 1993, MNRAS, 261, 804 [NASA ADS] (In the text)
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997a, ApJ, 487, 568 [NASA ADS] [CrossRef] (In the text)
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997b, ApJS, 112, 315 [NASA ADS] [CrossRef] (In the text)
- Ho, L. C., Filippenko, A. V., Sargent, W. L. W., & Peng, C. Y. 1997c, ApJS, 112, 391 [NASA ADS] [CrossRef] (In the text)
- Hopkins, P., & Hernquist, L. 2009, ApJ, 694, 599 [NASA ADS] [CrossRef] (In the text)
- Horellou, C., & Combes, F. 2001, Ap&SS, 276, 1141 [NASA ADS] [CrossRef]
- Hunt, L. K., & Malkan, M. A. 2004, ApJ, 616, 707 [NASA ADS] [CrossRef] (In the text)
- Jachym, P., Palous, J., Köppen, J., & Combes, F. 2007, A&A, 472, 5 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jachym, P., Köppen, J., Palous, J., & Combes, F. 2009, A&A, 500, 693 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- James, R. A. 1977, J. Comput. Phys., 25, 71 [NASA ADS] [CrossRef] (In the text)
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] (In the text)
- Jog, C., & Combes, F. 2009, Phys. Rep., 471, 75 [NASA ADS] [CrossRef] (In the text)
- Kinney, A. L., Schmitt, H. R., Clarke, C. J., et al. 2000, ApJ, 537, 152 [NASA ADS] [CrossRef] (In the text)
- Komugi, S., Sofue, Y., Kohno, K., et al. 2008, ApJS, 178, 225 [NASA ADS] [CrossRef] (In the text)
- Krips, M., Eckart, A., Neri, R., et al. 2005, A&A, 442, 479 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Krips, M., Eckart, A., Neri, R., et al. 2006, A&A, 446, 113 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Krips, M., Eckart, A., Krichbaum, T. P., et al. 2007, A&A, 464, 553 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lisenfeld, U., Alexander, P., Pooley, G. G., & Wilding, T. 1998, MNRAS, 300, 30 [NASA ADS] [CrossRef] (In the text)
- Makovoz, D., & Marleau, F. R. 2005, PASP, 117, 1113 [NASA ADS] [CrossRef] (In the text)
- Mapelli, M., Moore, B., Ripamonti, E., et al. 2008, MNRAS, 383, 1223 [NASA ADS] [CrossRef] (In the text)
- Martini, P., Regan, M. W., Mulchaey, J. S., Pogge, R. W. 2003, ApJS, 146, 353 [NASA ADS] [CrossRef] (In the text)
- Merritt, D., & Ferrarese, L. 2001, ApJ, 547, 140 [NASA ADS] [CrossRef] (In the text)
- Mulchaey, J. S., Davis, D. S., Mushotzky, R. F., & Burstein, D. 2003, ApJS, 145, 39 [NASA ADS] [CrossRef] (In the text)
- Norman, C. A., Sellwood, J. A., & Hasan, H. 1996, ApJ, 462, 114 [NASA ADS] [CrossRef] (In the text)
- Pahre, M., Ashby, M. L. N., Fazio G. G., & Willner S. P. 2004, ApJS, 154, 235 [NASA ADS] [CrossRef] (In the text)
- Pence, W. D., & Rots, A. H. 1997, ApJ, 478, 111 [NASA ADS] [CrossRef] (In the text)
- Prugniel, Ph., & Combes, F. 1992, A&A, 259, 25 [NASA ADS] (In the text)
- Roediger, E., & Brüggen, M. 2006, MNRAS, 369, 567 [NASA ADS] [CrossRef] (In the text)
- Rubin, V. C., Ford, W. K., Jr., & Roberts, M. S. 1979, ApJ, 230, 35 [NASA ADS] [CrossRef] (In the text)
- Schinnerer, E., Eckart, A., Tacconi, L. J., Genzel, R., & Downes, D. 2000, ApJ, 533, 850 [NASA ADS] [CrossRef] (In the text)
- Shostak, G. S., Hummel, E., Shaver, P. A., van der Hulst, J. M., & van der Kruit, P. C. 1982, A&A, 115, 293 [NASA ADS] (In the text)
- Skrutskie, M. F., Schneider, S. E., Stiening, R., et al. 1997, in The Impact of Large Scale Near-IR Sky Surveys, ed. F. Garzón, N. Epchtein, A. Omont, W. B. Burton, & P. Persi (Dordrecht: Kluwer), 25 (In the text)
- Solomon, P. M., & Barrett, J. W. 1991, in Dynamics of Galaxies and Their Molecular Cloud Distributions, ed. F. Combes, & F. Casoli (Dordrecht: Kluwer), 235 (In the text)
- Taniguchi, Y. 1999, ApJ, 524, 65 [NASA ADS] [CrossRef] (In the text)
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] (In the text)
- Tully, R. B. 1988, Nearby Galaxies Catalog (Cambridge: Cambridge University Press) (In the text)
- van der Hulst, J. M., Terlouw, J. P., Begeman, K. G., Zwitser, W., & Roelfsema, P. R. 1992, in Astronomical Data Analysis Software and Systems I, ed. D. M. Worrall, C. Biemesderfer, & J. Barnes (San Francisco: Astronomical Society of the Pacific), 131 (In the text)
- Vollmer, B. 2003, A&A, 398, 525 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vollmer, B., Braine, J., Balkowski, C., Cayatte, V., & Duschl, W. J. 2001, A&A, 374, 824 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Young, J. S., Xie, S., Tacconi, L., et al. 1995, ApJS, 98, 219 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... (NUGA)
![[*]](/icons/foot_motif.png)
- Based on observations conducted at the IRAM Plateau de Bure Interferometer. IRAM is supported by the INSU/CNRS (France), the MPG (Germany), and the IGN (Spain).
- ...
 +69:22:43.3
+69:22:43.3![[*]](/icons/foot_motif.png)
- These coordinates were originally derived relative to the position of SN 1998eb.
- ... NGC 1961
![[*]](/icons/foot_motif.png)
- see the web site http://www.not.iac.es/general/photos/astronomical/extragalactic/
All Tables
Table 1: Log of PdBI observations of NGC 1961.
Table 2: Parameters for NGC 1961.
Table 3: Initial conditions.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f1.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg27.png) |
Figure 1:
Blue DSS image of NGC 1961. Note the sharp linear feature to the
southeast (oriented at 45 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f2.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg59.png) |
Figure 2:
CO(1-0) zeroth moment map, with coordinates defined relative to the
PdBI phase center. The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f3.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg60.png) |
Figure 3:
CO(1-0) zeroth moment map contours (as in Fig. 2)
overlaid on the 8.4 GHz radio continuum map from Lisenfeld et al.
(1998) in greyscale. Coordinates are defined relative to the VLA
phase center adopted for the 8.4 GHz observations, whose |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f4.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg61.png) |
Figure 4: PdBI CO(1-0) zeroth moment map contours (as in Fig. 2) overlaid on the blue DSS image in greyscale. Coordinates are defined relative to the PdBI phase center. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f5.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg74.png) |
Figure 5:
CO(2-1) zeroth moment map, with coordinates defined relative to the
PdBI phase center. The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f6.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg75.png) |
Figure 6: Top: CO(2-1) zeroth moment contours (as in Fig. 5) overlaid on HST F160W colourscale. Bottom: same contours superposed on the Unsharp Mask version of the NICMOS image. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f7.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg76.png) |
Figure 7: CO(2-1) zeroth moment contours (as in Fig. 2) overlaid on CO(1-0) zeroth moment greyscale. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f8.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg89.png) |
Figure 8:
CO(1-0) first moment map, with coordinates defined relative to the
PdBI phase center. The synthesized beam at lower left is as in Fig. 2; contours are in steps of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f9.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg90.png) |
Figure 9: CO(2-1) first moment map, with coordinates defined relative to the PdBI phase center. The synthesized beam at lower left is as in Fig. 5; contours are as in Fig. 8. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f10.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg101.png) |
Figure 10: CO-derived rotation curves for NGC 1961. CO(1-0) and CO(2-1) curves are plotted in black and gray, respectively; fits to the two-dimensional velocity fields with ROTCUR and to the three-dimensional data cubes with INSPECTOR are plotted as dashed and solid lines, respectively. None of the curves are corrected for inclination. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f11.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg102.png) |
Figure 11:
Position-velocity cuts along the kinematic major (PA
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{12181-f12.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg109.png) |
Figure 12: Map of the CO(2-1)/CO(1-0) ratio obtained after smoothing the CO(2-1) map to the resolution of the CO(1-0) map. The contours are from 0.8 to 2.0 in steps of 0.2. The ratio increases from 0.7 in the center to 1.5 in the ring. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f13.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg116.png) |
Figure 13:
3 mm continumm contours overlaid on the CO(2-1) zeroth moment map in greyscale. The resolution of the 3 mm continuum map is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f14.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg126.png) |
Figure 14: Short-wavelength dust (non-stellar) emission from the Spitzer IRAC images (see Sect. 2.2). North is up, East to the left; the field-of-view is 4.2 arcmin on a side. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f15.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg127.png) |
Figure 15:
The Spitzer 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12181-f16.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg128.png) |
Figure 16:
2MASS K-band image of the central 76.6
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{12181-f17.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg146.png) |
Figure 17:
Rotation curve and derived frequencies |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{12181-f18.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg149.png) |
Figure 18:
Particle plots from the simulation of the collision,
projected to be similar to the observations (inclination 70 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{12181-f19.ps}
\end{figure}](/articles/aa/full_html/2009/31/aa12181-09/Timg150.png) |
Figure 19: Same as Fig. 18, but now the snapshots correspond to 400 and 440 Myr ( top and bottom respectively). Note how the radius of the galaxy inflates while the ring wave propagates outward. |
| Open with DEXTER | |
| In the text | |
| |
Figure 20: Projected density of the model, at a time of 440 Myr after the beginning of the collision: the stars ( left), and the gas ( right). The scale is in kpc. The black line is the trajectory of the companion starting from the southeast. |
| Open with DEXTER | |
| In the text | |
| |
Figure 21:
Same as Fig. 20, for radial velocities.
The color bar indicated at the right side goes from -210 to
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


