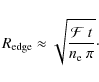| Issue |
A&A
Volume 503, Number 1, August III 2009
|
|
|---|---|---|
| Page(s) | 1 - 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200911778 | |
| Published online | 22 June 2009 | |
Non-linear evolution of the diocotron instability in a pulsar electrosphere: two-dimensional particle-in-cell simulations
J. Pétri1
Observatoire Astronomique de Strasbourg, 11 rue de l'Université, 67000 Strasbourg, France
Received 3 February 2009 / Accepted 27 April 2009
Abstract
Context. The physics of the pulsar magnetosphere near the neutron star surface remains poorly constrained by observations. Indeed, little is known about its emission mechanism, from radio to high-energy X-ray and gamma-rays. Nevertheless, it is believed that large vacuum gaps exist in this magnetosphere, and a non-neutral plasma partially fills the neutron star surroundings to form an electrosphere in differential rotation.
Aims. According to several of our previous works, the equatorial disk in this electrosphere is diocotron and magnetron unstable, at least in the linear regime. To better assess the long term evolution of these instabilities, we study the behavior of the non-neutral plasma using particle simulations.
Methods. We designed a two-dimensional electrostatic particle-in-cell (PIC) code in cylindrical coordinates, solving Poisson equation for the electric potential. In the diocotron regime, the equation of motion for particles obeys the electric drift approximation. As in the linear study, the plasma is confined between two conducting walls. Moreover, in order to simulate a pair cascade in the gaps, we add a source term feeding the plasma with charged particles having the same sign as those already present in the electrosphere.
Results. First we checked our code by looking for the linear development of the diocotron instability in the same regime as the one used in our previous work, for a plasma annulus and for a typical electrosphere with differential rotation. To very good accuracy, we retrieve the same growth rates, supporting the correctness of our PIC code. Next, we consider the long term non-linear evolution of the diocotron instability. We found that particles tend to cluster together to form a small vortex of high charge density rotating around the axis of the cylinder with only little radial excursion of the particles. This grouping of particles generates new low density or even vacuum gaps in the plasma column. Finally, in more general initial configurations, we show that particle injection into the plasma can drastically increase the diffusion of particles across the magnetic field lines. The newly formed vacuum gaps cannot be replenished by simply invoking diocotron instability.
Conclusions. Diocotron instability offers a new possibility to solve the current closure problem in a pulsar magnetosphere. It is a promising mechanism leading to highly unstable flows in the pulsar inner magnetosphere. When flowing towards the light cylinder, some relativistic and particle inertia effects (not included in this study) appear. Nevertheless, the system should remain unstable because of the relativistic diocotron or the magnetron instability. Therefore, we expect an electric current to circulate in the closed magnetosphere and to feed the base of the wind with charged particles.
Key words: instabilities - plasmas - methods: numerical - pulsars: general
1 Introduction
The detailed structure of charge distribution and electric-current circulation in the closed magnetosphere of a pulsar remains puzzling. Although it is often assumed that the plasma fills the space entirely and corotates with the neutron star, it is on the contrary very likely that it only partly fills it, leaving large vacuum gaps between plasma-filled regions. The existence of such gaps in aligned rotators has been very clearly established by Krause-Polstorff & Michel (1985b,a). Since then, a number of different numerical approaches to the problem have confirmed their conclusions, including some work by Rylov (1989), Shibata (1989), Zachariades (1993), Neukirch (1993), Thielheim & Wolfsteller (1994), Spitkovsky & Arons (2002), and ourselves (Pétri et al. 2002b). This conclusion about the existence of vacuum gaps has been reached from a self-consistent solution of the Maxwell equations in the case of the aligned rotator. Moreover, Smith et al. (2001) have shown by numerical modelling that an initially filled magnetosphere like the Goldreich-Julian model evolves by opening up large gaps and stabilizes at the partially filled and partially void solution found by Krause-Polstorff & Michel (1985a) and also by Pétri et al. (2002b). The status of models of the pulsar magnetospheres, or electrospheres, has been critically reviewed by Michel (2005). A solution with vacuum gaps has the peculiar property that those parts of the magnetosphere that are separated from the star's surface by a vacuum region are not corotating and so undergo differential rotation, an essential ingredient that will lead to non-neutral plasma instabilities in the closed magnetosphere.
This kind of non-neutral plasma instability is well known to plasma physicists (O'Neil & Smith 1992; Oneil 1980; Davidson 1990). Their good confinement properties makes them a valuable tool for studying plasmas in the laboratory, by using for instance Penning traps. In the magnetosphere of a pulsar, far from the light cylinder and close to the neutron star surface, the instability reduces to its non-relativistic and electrostatic form, the diocotron instability. The linear development of this instability for a differentially rotating charged disk was studied by Pétri et al. (2002a), in the thin disk limit, and by Pétri (2008,2007a,b) in the thick disk limit. It both cases, the instability proceeds at a growth rate comparable to the star's rotation rate. The non-linear development of this instability was studied by Pétri et al. (2003), in the framework of an infinitely thin disk model. They have shown that the instability causes a cross-field transport of these charges in the equatorial disk, evolving into a net out-flowing flux of charges. Spitkovsky & Arons (2002) have numerically studied the problem and concluded that this charge transport tends to fill the gaps with plasma. The appearance of a cross-field electric current as a result of the diocotron instability has been observed by Pasquini & Fajans (2002) in laboratory experiments in which charged particles were continuously injected in the plasma column trapped in a Malmberg-Penning configuration.
Numerical simulations of the non-linear development of the diocotron instability have been investigated by different authors. For instance, Pétri et al. (2003) used a numerical scheme similar to those used for MHD codes. This has the drawback of poorly treating vacuum gaps which eventually are created in the electrosphere. To better deal with these gaps, we decided to design a particle simulation code that does not suffer from the presence of vacuum. Particle-in-cell (PIC) methods have already been successful in investigating the diocotron instability (Yatsuyanagi et al. 2003; Neu & Morales 1995). Problems with injection have also been considered see for instance Bettega et al. (2007).
In this paper, we extend the work initiated by Pétri (2007b) and look for the non-linear evolution of the diocotron instability by performing 2D electrostatic PIC simulations. The question of the influence of pair creation will also be addressed by permitting injection of charged particles into the system. The paper is organized as follows. In Sect. 2, we briefly recall the initial setup of the plasma column as done in Pétri (2007b). In Sect. 3, we show the results of our 2D PIC simulations. First we checked the code by computing some linear growth rates for special cases like a constant density plasma column for which we know exact analytical solutions, see for instance Pétri (2007a). Second, we check that we retrieve the same linear growth rates for the electrosphere as those found in Pétri (2007b). Third, we let the system evolve on long time scales and look for significant particle diffusion. Finally, in a last set of runs, we injected some charged particles into the system to study the behavior of the instability in the presence of a source of charges, Sect. 4. The extreme case starting with vacuum will also be presented. The conclusions and the possible generalizations are presented in Sect. 5.
2 The model
We first review the plasma configuration as described in
Pétri (2007b). We study the motion of a non-neutral
plasma column of infinite axial extend along the z-axis. We adopt
cylindrical coordinates denoted by
![]() and define the
corresponding orthonormal basis vectors by
and define the
corresponding orthonormal basis vectors by
![]() .
In the initial state
corresponding to an equilibrium, the plasma is only rotating in the
azimuthal direction, with no motion in the radial direction along ror the vertical direction along z.
.
In the initial state
corresponding to an equilibrium, the plasma is only rotating in the
azimuthal direction, with no motion in the radial direction along ror the vertical direction along z.
2.1 Plasma and field setup
Unlike other magnetospheric models, our pulsar electrospheric plasma
is assumed to be completely charge-separated. So we consider a
single-species non-neutral fluid consisting of particles with
mass ![]() and charge q trapped between two cylindrically
conducting walls located at the radii W1 and W2 > W1. The
plasma column itself is confined between the radii
and charge q trapped between two cylindrically
conducting walls located at the radii W1 and W2 > W1. The
plasma column itself is confined between the radii
![]() and
and
![]() ,
with R1<R2. This allows us to take into account
vacuum regions between the plasma and the conducting walls. Such
geometric configurations will also be useful to investigate particle
diffusion across magnetic field lines into this vacuum and will
clearly demonstrate the efficiency of the diocotron instability to
fill gaps with plasma, as shown in some examples in the last section.
,
with R1<R2. This allows us to take into account
vacuum regions between the plasma and the conducting walls. Such
geometric configurations will also be useful to investigate particle
diffusion across magnetic field lines into this vacuum and will
clearly demonstrate the efficiency of the diocotron instability to
fill gaps with plasma, as shown in some examples in the last section.
In order to simulate the presence of a charged neutron star generating
a radial electric quadrupole field coming from the rotating magnetic
dipole, the inner wall at W1 can carry a charge Q per unit length
such that its electric field is simply given by the Maxwell-Gauss
theorem, (we use MKSA units)
In the equilibrium configuration, the particle number density is n(r) and the charge density is
The electric field is made of two parts, the first one arising from the plasma column
The total electric field, directed along the radial direction,
In the non-relativistic diocotron regime, we do not solve the full set of Maxwell equations but only the electrostatic part. This means that the magnetic field perturbation induced by the plasma flow is neglected. Thus, the externally imposed magnetic field, Eq. (2), remains constant during the simulations. This assumption is justified when the plasma is confined well inside the light-cylinder and when its rest mass energy density remains negligible compared to the magnetic field energy density, in other words
with c the speed of light in vacuum.
2.2 Equation of motion
The motion of the plasma is governed by the conservation of charge,
which in the non-neutral plasma case is equivalent to conservation of
the number of particles, the Maxwell-Poisson equation, and the
electric drift approximation, respectively
2.3 Code description
We designed an algorithm using standard techniques for particle in cell (PIC) codes (Birdsall & Langdon 2005; Hockney 1988). We use explicit schemes to advance both the particles and the electric field in time. A description of our own code on how to evolve field and particles is briefly discussed in the following subsections.
2.3.1 Integration of the equation of motion
We assume that the inner and outer conductors act mechanically as
solid walls in such a way that particles are reflected at these
boundaries. The equation of motion for particles in the electric drift
approximation takes a very simple form, allowing us to solve
immediately for the velocity vector, see Eq. (8). From a
computational point of view, this equation of motion,
Eq. (8), is integrated with a leapfrog scheme, which is
second order in time. More precisely, denoting
![]() as
the time at the nth iteration, where
as
the time at the nth iteration, where ![]() is the time step,
positions are computed at integer times tn whereas velocities are
computed at half-integer times
is the time step,
positions are computed at integer times tn whereas velocities are
computed at half-integer times
![]() for each
particle labelled with the index i such that
for each
particle labelled with the index i such that
The electromagnetic field at half-integer time is evaluated from the position of the particles at the same time, positions updated according to the speed known only at preceding times tn-1/2:
Then, the electromagnetic field at half-integer time following from these positions at the location of particle number i are
| |
= | (13) | |
| = | (14) |
We use a Lagrangian description, which means that no grid is associated with the position of the particle. Because the initial velocity and position are given for t=0 by
We then evolve positions and velocities according to Eqs. (10), (11). Note that in all the simulations, the electric and magnetic fields do not explicitly depend on time.
2.3.2 Field solver
The Poisson equation is solved on an Eulerian grid by a Fourier
transform in the azimuthal direction ![]() and a finite difference
scheme for the radial dependence. Note that in
Eq. (10), both the electric and the magnetic fields are
evaluated at a half-integer time tn+1/2. Because the electric
field is derived from a potential
and a finite difference
scheme for the radial dependence. Note that in
Eq. (10), both the electric and the magnetic fields are
evaluated at a half-integer time tn+1/2. Because the electric
field is derived from a potential ![]() ,
we need only to consider a
scalar Poisson equation. The potential
,
we need only to consider a
scalar Poisson equation. The potential ![]() as well as the charge
density are developed into a real
as well as the charge
density are developed into a real ![]() /
/![]() Fourier series as
Fourier series as
Because of the linearity of the Poisson equation, the azimuthal modes decouple into a set of independent ordinary differential equations for each natural integer m. Using a classical finite difference discretization in radius, we derive a set of matrices for each pair of unknown functions
Charges are deposited on the Eulerian grid
![]() in order to
deduce the source terms
in order to
deduce the source terms
![]() for the Poisson equation.
The electromagnetic field is evaluated on particle positions by 2D
linear interpolation between points in this Eulerian
grid
for the Poisson equation.
The electromagnetic field is evaluated on particle positions by 2D
linear interpolation between points in this Eulerian
grid
![]() .
.
2.3.3 Particle injection
Finally, we simulate the pair creation mechanism in the magnetosphere
by injecting charged particles somewhere inside the system. The
deposition is uniform in the azimuthal direction and prescribed to be
at a given radius and rate, both fixed by the user. Typically, we
took an injection radius
![]() .
Formally, the
shape function can be thought of a delta-Dirac distribution in the
radial direction, let us say
.
Formally, the
shape function can be thought of a delta-Dirac distribution in the
radial direction, let us say
![]() .
.
![]() is the particle flux.
Nevertheless, this is a user-defined source function and can be taken
to behave very differently, and can also evolve in space and time.
There is no particular restriction on its shape. As a starting point,
we took the most simple dependence, constant in time and
is the particle flux.
Nevertheless, this is a user-defined source function and can be taken
to behave very differently, and can also evolve in space and time.
There is no particular restriction on its shape. As a starting point,
we took the most simple dependence, constant in time and ![]() and
sharply concentrated in radius. To be more realistic, pair creation
should be incorporated by taking into account different processes like
photon-photon disintegration or photon-(strong) magnetic field
interaction (which is formally the same process as the former, as the
magnetic field can be thought of as a photon field from a quantum
mechanical point of view). Monte Carlo simulations would be a valuable
tool for such a study, but this will not be included in this work.
and
sharply concentrated in radius. To be more realistic, pair creation
should be incorporated by taking into account different processes like
photon-photon disintegration or photon-(strong) magnetic field
interaction (which is formally the same process as the former, as the
magnetic field can be thought of as a photon field from a quantum
mechanical point of view). Monte Carlo simulations would be a valuable
tool for such a study, but this will not be included in this work.
3 Results without particle injection
First, we checked our algorithm in different configurations by picking out the linear regime from our runs and compare the growth rates with those predicted by the linear analysis.
In order to keep the particle noise as weak as possible to clearly see the linear stage evolving over a few order of magnitudes, we need to start with an initial state with minimal energy. This is achieved by using a so-called ``quiet start'', such that space is regularly filled with particles, see for instance Birdsall & Langdon (2005).
The resolution of the spatial grid on which the electric potential is
solved and charge is deposited is
![]() ,
if not otherwise specified. On average, at the beginning of the
runs, there are 25 particles per cell, giving a total number of
1 280 000. Time is given in units of
,
if not otherwise specified. On average, at the beginning of the
runs, there are 25 particles per cell, giving a total number of
1 280 000. Time is given in units of
![]() where
where
![]() is the cyclotron frequency. We also tried
different resolutions and find no qualitative discrepancy, we adopted
the aforementioned canonical values.
is the cyclotron frequency. We also tried
different resolutions and find no qualitative discrepancy, we adopted
the aforementioned canonical values.
Note that for all the runs shown below, the charge Q carried by the inner conductor is set to zero, Q=0. The purpose of this work is not to make a parametric study of the diocotron instability behavior but rather to point out its main non-linear characteristics for a closed (without particle injection or loss) and an open (with particle injection or loss) system. Moreover, in this and subsequent sections, the magnetic field is uniform and constant over the whole plasma column. Let us now discuss the main results.
3.1 Plasma annulus
Table 1:
Eigenvalues ![]() for the constant density
plasma annulus, for different modes m and different aspect ratios,
d1 = R1 / W2, and
d2 = R2 / W2, obtained from
the analytical expression found in Davidson (1990).
for the constant density
plasma annulus, for different modes m and different aspect ratios,
d1 = R1 / W2, and
d2 = R2 / W2, obtained from
the analytical expression found in Davidson (1990).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f1a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f1b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg74.png) |
Figure 1:
Evolution of the total electrostatic increase in
energy
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{11778f2a.eps}\hspace*{2mm}
\includegraphics[width=8.9cm,clip]{11778f2b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg75.png) |
Figure 2: Snapshot of the charge density in the plasma column showing the m=3 pattern ( on the left) and the m=7 pattern ( on the right). The chosen time corresponds to the transition between the linear phase and the beginning of the non-linear regime, associated with the total electrostatic energy curves discussed in Fig. 1. |
| Open with DEXTER | |
For completeness, we briefly recall the main characteristics of the
configuration. The magnetic field is constant and uniform outside the
plasma annulus, namely
Bz = B0, for r>R2. We solve the
Maxwell-Poisson equation in the space between the inner and the outer
wall,
R1 < r < R2. The particle number density and charge density
are constant over the whole plasma column such that
To initiate the instability, we disturb the axisymmetric configuration by overlapping a tiny density perturbation with a relative magnitude (i.e. compared to the background density) of the order h=10-6. To pick out a given mode, the perturbation is modulated with the appropriate azimuthal pattern m. To be more precise, the initial axisymmetric equilibrium position of each particle
In this cylindrical geometry, an exact analytical solution of the dispersion relation has been found for the diocotron instability, see Davidson (1990). We use these results to check our code, as was already done in Pétri (2007a). Some exact analytical eigenvalues are listed in Table 1 for different radial plasma extensions and azimuthal modes. In order to quantify the growth rate of the diocotron instability in our simulations, we estimate the total electrostatic energy in the system by computing the integral
To determine the linear growth phase, we calculate the increase in electrostatic energy by determining the difference between the actual and the initial electrostatic energy as
Note that because
Two examples of a run are now discussed. The simulation domain is located between W1=1 and W2=10. For the first run, the plasma annulus is located between R1=4 and R2=5 with a perturbation m=3, called A1, while for the second run we took R1=6, R2=7with a perturbation m=7, called A2. We examine the evolution of the electrostatic energy given by Eq. (23) and depicted in Fig. 1 on a logarithmic scale.
For the first run, at small times, t<100, the linear regime sets in and the measured growth rate is close to the one predicted by linear analysis (red straight line); the perturbed pattern grows at a speed predicted by the linear theory. The plasma column stays roughly confined between R1 and R2 and no strong density rearrangement is perceptible. Note also that no other mode is excited and no cascade due to non-linear effects is observed because they are to weak.
In some runs, such as the first mentioned above, it can happen that
the initial electrostatic fluctuations decrease slightly before a
significant increase of many orders of magnitude, after a while,
inducing a
![]() at the beginning and thus making the
logarithm not defined at this early stage. In
Fig. 1, it is unreliable to give a physical
interpretation to this initial behaviour because it corresponds to
numerical round off error, close to the machine precision (we work
with double precision numbers, i.e. 16 significant digits). Moreover,
the gaps are probably due to the particle noise inherent in the PIC
method, proportional to the inverse of the square root of the number
of particles N, (i.e.
at the beginning and thus making the
logarithm not defined at this early stage. In
Fig. 1, it is unreliable to give a physical
interpretation to this initial behaviour because it corresponds to
numerical round off error, close to the machine precision (we work
with double precision numbers, i.e. 16 significant digits). Moreover,
the gaps are probably due to the particle noise inherent in the PIC
method, proportional to the inverse of the square root of the number
of particles N, (i.e. ![]() N-1/2). Tiny fluctuations in
positions, especially particles receding to the inner wall, tend to
decrease the total electrostatic energy, at least at the beginning of
the simulations.
N-1/2). Tiny fluctuations in
positions, especially particles receding to the inner wall, tend to
decrease the total electrostatic energy, at least at the beginning of
the simulations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11778f3a.eps}\hspace*{2mm}
\includegraphics[width=8.5cm,clip]{11778f3b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg84.png) |
Figure 3:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
In a second step, non-linear effects come into play and the initial
plasma distribution is destroyed. The azimuthal pattern with the
typical m=3 mode becomes clearly visible in left part of
Fig. 2. Particles ``merge'' to form large
vortices and leave behind them vacuum gaps which will not be
replenished. For some time, these vortices rotate around the axis of
the cylinder, keeping their m=3 structure. In a last step, almost
all particles hit the inner wall W1; this happens when t>400. The
total electrostatic energy saturates, reaching a plateau at the end.
When the non-linear effects set in, we are interested in the diffusion
of particles across magnetic field lines and on its consequences on a
longer timescale. To get a better idea of this diffusion process, we
quantify it by computing the azimuthally integrated charge density as
It can be interpreted as an equivalent radial charge density. Indeed
gives the total charge contained in the plasma column at time t. Some examples related to the simulations shown in Fig. 1 are given in Fig. 3. We immediately see that for t<100 (linear stage), the boundary of the plasma column remains unchanged, as discussed before. In a second stage, non-linear effects become important and strongly disturb the boundaries of the plasma annulus. Some very coherent patterns emerge while continuing to rotate. During this period, roughly 100<t<400, the barycenter of the charges moved closer to the inner wall as seen in the left part of Fig. 3. The structure implodes and radial forces shift particles closer to the inner wall. In a final stage, only a few particles have moved outwards, while the main fraction drift close to the inner boundary. Therefore we do not observe any significant diffusion radially outwards.
The situation is very similar for the second run, A2. Here also, the
linear regime exists until
![]() and the observed growth rate
is in close agreement with the linear analysis (red straight line in
the right part of Fig. 1). The plasma column
stays roughly confined between R1 and R2, right part of
Fig. 3, no strong density rearrangement
is perceptible during this linear phase. During the transition from
the linear to the non-linear state, the m=7 structure emerges in the
density map as shown in the right part of
Fig. 2. Vacuum gaps are formed and seven
vortices rotate around the cylinder axis until some of them merge,
destabilizing the whole system and shrinking down to the inner wall.
and the observed growth rate
is in close agreement with the linear analysis (red straight line in
the right part of Fig. 1). The plasma column
stays roughly confined between R1 and R2, right part of
Fig. 3, no strong density rearrangement
is perceptible during this linear phase. During the transition from
the linear to the non-linear state, the m=7 structure emerges in the
density map as shown in the right part of
Fig. 2. Vacuum gaps are formed and seven
vortices rotate around the cylinder axis until some of them merge,
destabilizing the whole system and shrinking down to the inner wall.
These conclusions apply to all of our runs starting with an initial equilibrium as a plasma annulus. Such behavior is expected because of the confinement theorem which states that on average, the radial excursion of particles is limited due to angular momentum conservation of the system (particles + electromagnetic field), see Davidson (1990).
3.2 Electrosphere
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f4a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f4b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg88.png) |
Figure 4:
Evolution of the total electrostatic increase in energy for
the differentially rotating plasma column obtained from our 2D PIC
simulations (black dots) and compared with the linear growth rate
obtained from Table 3 (red line), on
the left for the case
|
| Open with DEXTER | |
Next, we switch to the results obtained for the electrosphere. As in
our previous works, the rotation profile is chosen to mimic the
rotation curve existing in the 3D electrosphere. We recall that
different analytical expressions for the radial dependence of ![]() are chosen mainly by varying the gradient in differential shear as
follows
are chosen mainly by varying the gradient in differential shear as
follows
Table 2: Parameters for the three rotation profiles used to mimic the azimuthal velocity of the plasma in the electrospheric disk.
To summarize these simulations, we demonstrated that our 2D PIC code is able to accurately reproduce the growth rates of the diocotron instability in the linear stage of its development, in accordance with our previous analytical study.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f5a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f5b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg97.png) |
Figure 5: Snapshot of the charge density corresponding to the runs shown in Fig. 4 at the transition phase between linear and non-linear regimes. The m=3 patterns are clearly identified for sufficiently small times. |
| Open with DEXTER | |
The long period of time in the non-linear stage showed no significant particle diffusion across magnetic field lines. Current flow in the system is not efficient.
Nevertheless, the pulsar magnetosphere is believed to be subject to copious pair creation feeding the electrosphere with highly relativistic, freshly born electrons and positrons. This external source of charge can drastically change the long term behavior of the diocotron instability. That is why in the next and last paragraph, we add a particle injection mechanism into the plasma column (or electrosphere) in order to represent the pair cascade phenomenon in a simple manner.
Table 3:
Eigenvalues ![]() for the electrospheric model
for the electrospheric model ![]() ,
,
![]() and
and ![]() for some azimuthal modes m.
for some azimuthal modes m.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f6a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f6b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg98.png) |
Figure 6:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f7a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f7b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg99.png) |
Figure 7:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
4 Results with particle injection
The most interesting case is the one assuming that the non-neutral plasma is not isolated but is an open system from which particles can freely enter or exit. Our main focus is on the electrospheric plasma around a neutron star. Close to its surface, due to the high magnetic field intensity, some quantum electrodynamical processes can convert photons into electron-positron pairs. Therefore, in a crude way, we can think of it as a (time-dependent) source feeding the electrosphere with charged particles. Moreover, these charges are responsible for synchrotron and curvature radiation. All these phenomena can drastically affect the behavior of the diocotron instability.
Our goal in this last section is to study in detail the first effect, namely an external source of charges feeding the plasma with a flux of particles. In the most general picture, the spatial and time behavior can be quite complicated. To simplify it, we will assume that the source is located at an arbitrary fixed radius and that the particle flux is constant in time.
In order to investigate the consequences of particle injection into the system, we run the same configurations as above but add a source of particle injected at a radius chosen to be r=2 W1. Some simulation results are described in the following subsections.
4.1 Plasma column
First, we consider again the plasma annulus with constant charge density trapped between the two conducting walls. In all these runs, we adopt the same conditions as before except that we remove the initial density perturbation. Indeed, we are no longer interested in the linear growth rate. In this way, the exact pattern of the perturbation is not relevant.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f8a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f8b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg100.png) |
Figure 8: Snapshot of the charge density in the plasma column having the same initial conditions as in Fig. 2. Due to particle injection, a second inner ring appears, with size slowly growing over time. The weak initial particle noise is sufficient to ignite the unstable modes which interact with the inner annulus. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f9a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f9b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg101.png) |
Figure 9:
Snapshot of the charge density for the differentially
rotating electrosphere, on the left for the case |
| Open with DEXTER | |
The integrated density is shown in
Fig. 7 and should be compared with
Fig. 3. Note that the color scales are
different in both situations. At the beginning of the runs, the plasma
annulus rotates around its axis without any significant perturbation.
However, around
![]() and
and
![]() for the first and
second run respectively, the equilibrium configuration has been
destroyed and particles shrink to the inner wall. As the simulations
start, the location of the source is easily determined on these maps.
Particles are injected at a radius r=2 W1, depicted in the plots
by a thin strip.
Typical perturbations of the density within the annulus are shown in
Fig. 8. In both cases, it seems that the
fastest growing mode corresponds to a pattern m=6. The source of
particles corresponds to the inner annulus. In the first simulation,
in the left figure, there exists a strong interaction between both
rings because they show the same azimuthal pattern, at least at the
beginning of the non-linear stage. However, this effect is much less
pronounced in the second run, on the right, due to the larger
separation between the rings.
From a careful comparison between the cases with and without
injection, we conclude that the radial extension at the end of the
simulation is significantly larger (on average) when a source is
present. For instance, for the annulus A1, the integrated density
does not extend farther than r=2 W1 when the source is switched
off whereas its extension reaches r=5 W1 when charges are
injected. The diffusion process would have been even more extensive
if the time span would have been longer. We will make this statement
more clear in the discussion of last two sets of runs. The annulus
configuration was just a starting point to relate our numerical
results to analytically known solutions for the growth rates.
for the first and
second run respectively, the equilibrium configuration has been
destroyed and particles shrink to the inner wall. As the simulations
start, the location of the source is easily determined on these maps.
Particles are injected at a radius r=2 W1, depicted in the plots
by a thin strip.
Typical perturbations of the density within the annulus are shown in
Fig. 8. In both cases, it seems that the
fastest growing mode corresponds to a pattern m=6. The source of
particles corresponds to the inner annulus. In the first simulation,
in the left figure, there exists a strong interaction between both
rings because they show the same azimuthal pattern, at least at the
beginning of the non-linear stage. However, this effect is much less
pronounced in the second run, on the right, due to the larger
separation between the rings.
From a careful comparison between the cases with and without
injection, we conclude that the radial extension at the end of the
simulation is significantly larger (on average) when a source is
present. For instance, for the annulus A1, the integrated density
does not extend farther than r=2 W1 when the source is switched
off whereas its extension reaches r=5 W1 when charges are
injected. The diffusion process would have been even more extensive
if the time span would have been longer. We will make this statement
more clear in the discussion of last two sets of runs. The annulus
configuration was just a starting point to relate our numerical
results to analytically known solutions for the growth rates.
4.2 Electrosphere
Next, we study the behavior of the electrosphere. We take the same configurations as in the previous section and add the source located at r=2 W1. However, in order to look for particle diffusion farther away than the outer wall located at r=20 W1, we used an initial box larger with size W1=1 and W2=100. This allows us to investigate the large radial excursion of the particle and is a strong indication that charges effectively diffuse across the magnetic field lines.
We investigate the charge density at the end of the runs. A snapshot
is given in Fig. 9 for ![]() on the
left, and
on the
left, and ![]() on the right. We recall that in the first place,
the electrospheric plasma was only filled between r=W1 and
r=20 W1. In the above pictures, we clearly see a non negligible
charge density up to radii larger than
(40-50) W1 or so. This is
unambiguous evidence of the efficiency of the diocotron instability to
generate a current across the field lines.
This fact is supported by inspecting
Fig. 10. The integrated density
shows a monotonic and regular expansion. During a first rearrangement
state, the plasma shrinks and approaches the neutron star surface.
This is the meaning of the thin horizontal strip in green-yellow
between r=W1 and r=20 W1 for time less than roughly t<20.
Thus a gap is forming, but after sufficient particles have been
injected into the system, these vacuum regions will be replenished and
expand even farther radially outwards.
on the right. We recall that in the first place,
the electrospheric plasma was only filled between r=W1 and
r=20 W1. In the above pictures, we clearly see a non negligible
charge density up to radii larger than
(40-50) W1 or so. This is
unambiguous evidence of the efficiency of the diocotron instability to
generate a current across the field lines.
This fact is supported by inspecting
Fig. 10. The integrated density
shows a monotonic and regular expansion. During a first rearrangement
state, the plasma shrinks and approaches the neutron star surface.
This is the meaning of the thin horizontal strip in green-yellow
between r=W1 and r=20 W1 for time less than roughly t<20.
Thus a gap is forming, but after sufficient particles have been
injected into the system, these vacuum regions will be replenished and
expand even farther radially outwards.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f10a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f10b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg103.png) |
Figure 10:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{11778f11a.eps}\hspace*{2mm}
\includegraphics[width=8.9cm,clip]{11778f11b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg104.png) |
Figure 11: Snapshot of the charge density at the final time of the simulation, starting with vacuum. |
| Open with DEXTER | |
4.3 Vacuum
It is also possible to start with the extreme situation containing no particle, i.e. vacuum. This is the most relevant case to show the efficiency of particle transport across magnetic field lines.
As in the previous cases, we inject particles at r=2 W1 and let the system evolve in a self-consistent manner according to the electric drift approximation. In the first run, the two conducting walls are relatively close to each other, with W1=1 and W2=20 W1. In this way, we are able to see what is happening in the region close to the injection radius. Depending on the particle injection flux, the plasma column grows radially outwards more or less quickly. As seen in the density snapshot shown in the left part of Fig. 11, during the simulation, particles tend to fill all the space between the two walls. Charge transport across magnetic field lines seems to be very efficient. This is confirmed by inspecting the left part of Fig. 12 in which we see a monotonic increase in outer edge of the integrated charge density. Starting with r around 2 W1, the plasma annulus has non negligible density at r=13 W1 at the end of the run.
Finally, in order to clearly view the long term behavior of this
diocotron instability, we performed a run with higher resolution
![]() as well as larger distance between
the conducting walls, W1=1 and W2=100. The most relevant
results are given in the right part of Figs. 11 and 12, for the density and the
integrated density respectively. Here again, for a sufficiently long
time, plasma fills the entire vacuum and spreads out over the whole
space. The barycenter of the charges drifts to larger and larger
radii. This last run is an unambiguous proof demonstrating the crucial
role of this non-neutral plasma instability in the modeling of pulsar
magnetosphere. Plasma injection in the electrosphere will unavoidably
push particles farther away from the neutron star.
as well as larger distance between
the conducting walls, W1=1 and W2=100. The most relevant
results are given in the right part of Figs. 11 and 12, for the density and the
integrated density respectively. Here again, for a sufficiently long
time, plasma fills the entire vacuum and spreads out over the whole
space. The barycenter of the charges drifts to larger and larger
radii. This last run is an unambiguous proof demonstrating the crucial
role of this non-neutral plasma instability in the modeling of pulsar
magnetosphere. Plasma injection in the electrosphere will unavoidably
push particles farther away from the neutron star.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f12a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f12b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg106.png) |
Figure 12:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
4.4 Discussion
We showed that the non-neutral plasma behaves very differently when
isolated compared to the situation in which a source of particles is
added. In the former case, charges tend to migrate radially inwards,
whereas in the latter case, the total charge of the system is not
conserved and they are allowed to move radially outwards. This
migration to larger distances is induced by the increasing electric
repulsion between particles. In the initial (unstable) equilibrium
state, the Lorentz force,
![]() ,
exactly
compensates the centrifugal force. The self-field parameter, defined
by
,
exactly
compensates the centrifugal force. The self-field parameter, defined
by
![]() ,
is such that an equilibrium is permitted. For a
constant density plasma column it corresponds to
,
is such that an equilibrium is permitted. For a
constant density plasma column it corresponds to
![]() .
We
introduced the plasma frequency (squared) by
.
We
introduced the plasma frequency (squared) by
![]() ,
the cyclotron frequency by
,
the cyclotron frequency by
![]() ,
the mass of the particle
,
the mass of the particle ![]() (electron or positron in our case), its charge e and the particle
density number
(electron or positron in our case), its charge e and the particle
density number ![]() .
.
Due to the evident dichotomy between an isolated system for
which migration inwards is observed and a system with injection of
particles and a radially outwards expansion of the plasma as
consequences, we could imagine a situation in between such that no
significant radial motion is induced. However, we do not believe that
such a regime is reachable, because a charge density increase will
inevitably lead to a growing self-field parameter ![]() to values
eventually larger than those expected to find an equilibrium solution
(which is unity for the constant density plasma column). Remember
that the self-field parameter is by definition proportional to the
particle density number for a fixed magnetic field intensity. For a
plasma column, it is well known that the limit
to values
eventually larger than those expected to find an equilibrium solution
(which is unity for the constant density plasma column). Remember
that the self-field parameter is by definition proportional to the
particle density number for a fixed magnetic field intensity. For a
plasma column, it is well known that the limit
![]() corresponds to
the Brillouin zone and forbids radial confinement above this limit,
(Davidson 1990). For this reason, there will be no particle
injection rate at which both effects cancel exactly. The secular
evolution is always particle diffusion across magnetic field lines to
larger distances.
corresponds to
the Brillouin zone and forbids radial confinement above this limit,
(Davidson 1990). For this reason, there will be no particle
injection rate at which both effects cancel exactly. The secular
evolution is always particle diffusion across magnetic field lines to
larger distances.
A qualitative and illustrative picture is as follows. For simplicity
we take the example of the plasma column without inner voids, uniform
density and a constant uniform axial magnetic field. The rotation
profile for this column is therefore constant, in other words, the
plasma column is in solid body rotation. Because the plasma is
confined, the self-field parameter should be less than unity. If some
particles were added to the system, keeping the magnetic field
constant, the particle number density ![]() increases, as does
the self-field parameter by the same proportion. When the Brillouin
limit is reached, confinement is broken and particles diffuse to
larger radii. A new equilibrium state could be reached in principle
whenever
increases, as does
the self-field parameter by the same proportion. When the Brillouin
limit is reached, confinement is broken and particles diffuse to
larger radii. A new equilibrium state could be reached in principle
whenever ![]() becomes less than unity due to particle dilution
in a greater volume. Because the timescale for charge diffusion is
much less than the azimuthal rotation period, we can think about a
slow, almost adiabatic motion. The column always readjusts to a new
``quasi''-equilibrium state. Thus, electrostatic repulsion is at the
heart of the diffusion process.
becomes less than unity due to particle dilution
in a greater volume. Because the timescale for charge diffusion is
much less than the azimuthal rotation period, we can think about a
slow, almost adiabatic motion. The column always readjusts to a new
``quasi''-equilibrium state. Thus, electrostatic repulsion is at the
heart of the diffusion process.
Finally, we give an estimate for the time evolution of the outer
boundary of the system in the following way. In our simulations, at a
fixed injection rate, the radial excursion slows down because
particles have more space to ``dilute'' in (area in 2D (or volume in 3D)
proportional to
![]() )
and therefore decreasing more
efficiently their density number as r grows. This is indeed
observed in our runs. The outer edge of the plasma filled
region
)
and therefore decreasing more
efficiently their density number as r grows. This is indeed
observed in our runs. The outer edge of the plasma filled
region
![]() can roughly be fitted as evolving in time as a
function of
can roughly be fitted as evolving in time as a
function of ![]() .
Indeed, assuming that the number of particles
injected per unit time is
.
Indeed, assuming that the number of particles
injected per unit time is
![]() ,
they should be contained
within the radius
,
they should be contained
within the radius
![]() .
Assuming a uniform density within
the column, starting from r=0 at t=0, we get
.
Assuming a uniform density within
the column, starting from r=0 at t=0, we get
![]() ,
leading to the
expected
,
leading to the
expected ![]() function
function
This curve is shown as a black solid parabola line in Figs. 10 and 12. The constant factor in front of the
5 Conclusion
We designed a 2D electrostatic PIC code to study the long time non-linear evolution of the diocotron instability in a background electromagnetic field with a particular emphasise on the pulsar magnetosphere, where we believe that non-neutral plasmas made of pairs form an electrosphere, known to be diocotron unstable.
We first checked our PIC code by looking for the linear growth stage of the diocotron unstable modes. We found very good agreement between the analytical predictions from the linear analysis and the growth rates derived from our PIC code.
These high growth rates quickly destroy the laminar flow pattern due to differential rotation. Fluid elements merge to form some macroparticles with high density and leaving large vacuum space between them. Moreover, if the system remains isolated, there is no significant particle transport across magnetic field lines. Nevertheless, we found that when adding some external source of charge, there is a net outflow of charge towards the light cylinder. This is believed to come from pair creation in the innermost part of the electrosphere. Non-neutral plasma instabilities like the one presented here are an efficient way to transport particles from regions close to the neutron star to the region where the wind is launched. The connection between the wind and the close magnetosphere still needs to be explained. We think that our work will be a fruitful alternative to existing models.
In this approach, we neglected the magnetic field perturbation induced by the plasma. This assumption is true only for plasma flowing far away from the light cylinder (and inside it). In order to take into account the magnetic field back reaction caused by the plasma, we need to solve the full set of Maxwell equations. This work will be presented in a forthcoming paper and will extend the results already founded in Pétri (2007a) about relativistic stabilization effects on the diocotron instability.
References
- Bettega, G., Cavaliere, F., Cavenago, M., et al. 2007, Phys. Plasmas, 14, 042104 [NASA ADS] [CrossRef] (In the text)
- Birdsall, C., & Langdon, A. 2005, Plasma physics via computer simulation (IOP Publishing)
- Davidson, R. C. 1990, Physics of non neutral plasmas (Addison-Wesley Publishing Company)
- Hockney, R. W., & Eastwood, J. W. 1988, Computer Simulation Using Particles (Institute of Physics Publishing)
- Krause-Polstorff, J., & Michel, F. C. 1985a, MNRAS, 213, 43P [NASA ADS]
- Krause-Polstorff, J., & Michel, F. C. 1985b, A&A, 144, 72 [NASA ADS]
- Michel, F. C. 2005, in Rev. Mex. Astron. Astrofis. Conf. Ser., 27 (In the text)
- Neu, S. C., & Morales, G. J. 1995, in AIP Conf. Ser., 331, 124
- Neukirch, T. 1993, A&A, 274, 319 [NASA ADS] (In the text)
- Oneil, T. M. 1980, Phys. Fluids, 23, 2216 [NASA ADS] [CrossRef]
- O'Neil, T. M., & Smith, R. A. 1992, Phys. Fluids B, 4, 2720 [NASA ADS] [CrossRef]
- Pasquini, T., & Fajans, J. 2002, in Non-Neutral Plasma Physics IV, ed. F. Anderegg, C. F. Driscoll, & L. Schweikhard, AIP Conf. Proc., 606, 453 (In the text)
- Pétri, J. 2007a, A&A, 469, 843 [NASA ADS] [CrossRef] [EDP Sciences]
- Pétri, J. 2007b, A&A, 464, 135 [NASA ADS] [CrossRef] [EDP Sciences]
- Pétri, J. 2008, A&A, 478, 31 [NASA ADS] [CrossRef] [EDP Sciences]
- Pétri, J., Heyvaerts, J., & Bonazzola, S. 2002a, A&A, 387, 520 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pétri, J., Heyvaerts, J., & Bonazzola, S. 2002b, A&A, 384, 414 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pétri, J., Heyvaerts, J., & Bonazzola, S. 2003, A&A, 411, 203 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Press, W., Teukolsky, S., & V. W. F. B. 2002, Numerical Recipes in C++ (Cambridge University Press) (In the text)
- Rylov, I. A. 1989, Ap&SS, 158, 297 [NASA ADS] [CrossRef] (In the text)
- Shibata, S. 1989, Ap&SS, 161, 187 [NASA ADS] [CrossRef] (In the text)
- Smith, I. A., Michel, F. C., & Thacker, P. D. 2001, MNRAS, 322, 209 [NASA ADS] [CrossRef] (In the text)
- Spitkovsky, A., & Arons, J. 2002, in Neutron Stars in Supernova Remnants, ed. P. O. Slane, & B. M. Gaensler, ASP Conf. Ser., 271, 81 (In the text)
- Thielheim, K. O., & Wolfsteller, H. 1994, ApJ, 431, 718 [NASA ADS] [CrossRef] (In the text)
- Yatsuyanagi, Y., Kiwamoto, Y., Ebisuzaki, T., Hatori, T., & Kato, T. 2003, Phys. Plasmas, 10, 3188 [NASA ADS] [CrossRef]
- Zachariades, H. A. 1993, A&A, 268, 705 [NASA ADS] (In the text)
All Tables
Table 1:
Eigenvalues ![]() for the constant density
plasma annulus, for different modes m and different aspect ratios,
d1 = R1 / W2, and
d2 = R2 / W2, obtained from
the analytical expression found in Davidson (1990).
for the constant density
plasma annulus, for different modes m and different aspect ratios,
d1 = R1 / W2, and
d2 = R2 / W2, obtained from
the analytical expression found in Davidson (1990).
Table 2: Parameters for the three rotation profiles used to mimic the azimuthal velocity of the plasma in the electrospheric disk.
Table 3:
Eigenvalues ![]() for the electrospheric model
for the electrospheric model ![]() ,
,
![]() and
and ![]() for some azimuthal modes m.
for some azimuthal modes m.
All Figures
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f1a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f1b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg74.png) |
Figure 1:
Evolution of the total electrostatic increase in
energy
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{11778f2a.eps}\hspace*{2mm}
\includegraphics[width=8.9cm,clip]{11778f2b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg75.png) |
Figure 2: Snapshot of the charge density in the plasma column showing the m=3 pattern ( on the left) and the m=7 pattern ( on the right). The chosen time corresponds to the transition between the linear phase and the beginning of the non-linear regime, associated with the total electrostatic energy curves discussed in Fig. 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11778f3a.eps}\hspace*{2mm}
\includegraphics[width=8.5cm,clip]{11778f3b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg84.png) |
Figure 3:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f4a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f4b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg88.png) |
Figure 4:
Evolution of the total electrostatic increase in energy for
the differentially rotating plasma column obtained from our 2D PIC
simulations (black dots) and compared with the linear growth rate
obtained from Table 3 (red line), on
the left for the case
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f5a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f5b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg97.png) |
Figure 5: Snapshot of the charge density corresponding to the runs shown in Fig. 4 at the transition phase between linear and non-linear regimes. The m=3 patterns are clearly identified for sufficiently small times. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f6a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f6b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg98.png) |
Figure 6:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{11778f7a.eps}\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{11778f7b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg99.png) |
Figure 7:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f8a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f8b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg100.png) |
Figure 8: Snapshot of the charge density in the plasma column having the same initial conditions as in Fig. 2. Due to particle injection, a second inner ring appears, with size slowly growing over time. The weak initial particle noise is sufficient to ignite the unstable modes which interact with the inner annulus. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f9a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f9b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg101.png) |
Figure 9:
Snapshot of the charge density for the differentially
rotating electrosphere, on the left for the case |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f10a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f10b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg103.png) |
Figure 10:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{11778f11a.eps}\hspace*{2mm}
\includegraphics[width=8.9cm,clip]{11778f11b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg104.png) |
Figure 11: Snapshot of the charge density at the final time of the simulation, starting with vacuum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11778f12a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{11778f12b.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11778-09/Timg106.png) |
Figure 12:
Time evolution of the azimuthally integrated charge density
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



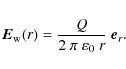
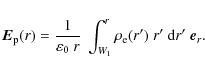
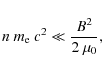
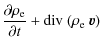
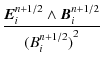
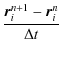
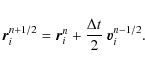
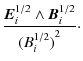
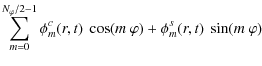
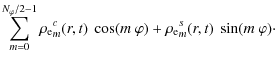

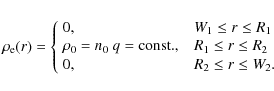
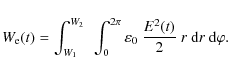
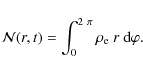
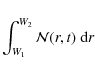
![\begin{displaymath}
\Omega(r) = \Omega_* ~ ( 2 + \tanh[ \alpha ~ ( r - r_0 ) ] ~
{\rm e}^{-\beta~r^4} ) ;
\end{displaymath}](/articles/aa/full_html/2009/31/aa11778-09/img90.png)