Free core nutation resonance parameters from VLBI and superconducting gravimeter data

S. Rosat; S. B. Lambert

doi:10.1051/0004-6361/200811489

Free Access

Issue		A&A Volume 503, Number 1, August III 2009


Page(s)		287 - 291
Section		Celestial mechanics and astrometry
DOI		https://doi.org/10.1051/0004-6361/200811489
Published online		15 June 2009

Free core nutation resonance parameters from VLBI and superconducting gravimeter data

S. Rosat¹ - S. B. Lambert²

1 - Institut de Physique du Globe de Strasbourg, IPGS - UMR 7516, CNRS et Université de Strasbourg (EOST), 67084 Strasbourg, France
2 - Observatoire de Paris, Département Systèmes de Référence Temps Espace (SYRTE), UMR 8630, CNRS, 75014 Paris, France

Received 9 December 2008 / Accepted 20 May 2009

Abstract
Context. Free core nutation (FCN) can be observed by its associated resonance effects on the forced nutations of the Earth's figure axis, as observed by very long baseline interferometry (VLBI), or on the diurnal tidal waves, retrieved from the time-varying surface gravity recorded by superconducting gravimeters (SG).
Aims. In this paper, we study the sensitivity of both techniques to FCN parameters.
Methods. We analyze surface gravity data from 15 SG stations and VLBI delays accumulated over the last 24 years.
Results. We obtain estimates of the FCN period and quality factor that are consistent for both techniques. The inversion leads to a quality factor centered on $\sim$ 16 600 with an uncertainty of $\sim$ 3500 from SG and of $\sim$ 900 from VLBI, and to a resonant period within [-423.3, -430.5] days for SG and [-427.8, -431.4] days for VLBI (3 $\sigma$ interval).

Key words: reference systems - Earth

1 Introduction

Free core nutation (FCN) is a rotational normal mode of the Earth that exists because of the presence of a fluid core inside the visco-elastic mantle. In a space-fixed reference frame, the resonant period of the FCN is close to 430 days retrograde, leading to an amplification of the Earth's nutational and deformational responses to tidal forcing.

The resonance associated with the FCN has been widely studied in time-varying gravity data recorded with relative gravimeters, mainly superconducting gravimeters (SG) of the Global Geodynamics Project (GGP, Crossley et al. 1999). The first analysis of the FCN effects in gravity data was performed by Neuberg et al. (1987); attempting to determine the resonant period, they obtained $T_{\rm FCN}=-431\pm6$ days and a quality factor $Q_{\rm FCN}=2~800\pm500$ , defined so the complex frequency is $(0.99727/T_{\rm FCN}-1)(1-{\rm i}/2Q_{\rm FCN})$ in cycles per sidereal day. This study was followed by many others (e.g., Cummins & Wahr 1993; Sato et al. 1994, 2004; Ducarme et al. 2009). Defraigne et al. (1994, 1995), using a combination of very long baseline interferometry (VLBI) nutation and SG gravity data, obtained a period of $-433\pm3$ days and a quality factor higher than 17 000. More recently, Ducarme et al. (2009) analyzed the European SG data, and found a period of $-430\pm2$ days and a quality factor of $15~000\pm8000$ .

The signature of the FCN in the forced nutations was studied by Herring et al. (1986) and Gwinn et al. (1986) using VLBI observations. The authors interpreted the enhancement of the amplitude of the retrograde annual nutation induced by the resonance in terms of a departure of the core-mantle boundary from its hydrostatic figure. Using an improved theoretical background, Mathews et al. (2002) built a nutation model (referred to as MHB) based on a limited number of parameters describing the Earth's interior and adjusted to VLBI data up to 1999. Comparisons of the VLBI nutation time series with this model reveal differences of the order of 200 microarc seconds ( $\mu$ as) in rms. These residuals are the consequence of various mismodeled or unmodeled influences in the observational strategy as well as in geophysical processes (see e.g., Dehant et al. 2003). The authors found an FCN resonant period of -430.21 days and a quality factor of 20 000. The values of the FCN period and quality factor were confirmed by Vondrák et al. (2005) using a combination of VLBI and GNSS-derived nutation amplitudes and inverting only the resonance parameters (to which the nutation amplitudes are the most sensitive within the diurnal band). However, Lambert & Dehant (2007), who analyzed VLBI data sets produced independently by various VLBI analysis centers, noticed a smaller value for $Q_{ \rm FCN}$ . (Note that in their paper, the values of the quality factor were incorrect due to a sign error in the code: their symmetry with respect to 20 000 must be considered, leading to values around 17 000 instead of 23 000.) The values of other geophysical parameters estimated in MHB were recently confirmed by Koot et al. (2008) using a longer VLBI data set and a different estimation method. Although the FCN period found in the latter work is close to the MHB value, the quality factor appears to be lower by $\sim$ 30%. The reason for the discrepancy has not yet been determined.

Some studies tried to identify a time variation of the frequency of the FCN resonance, either in VLBI nutation or in SG gravity data (Roosbeek et al. 1999; Hinderer et al. 2000). In both papers, the authors concluded that the apparent time-variation is not real but is due to the time-variable excitation of the free mode. Vondrák & Ron (2006) and Lambert & Dehant (2007) have shown that the resonant period is stable around -430 days to within half a day. The former authors argued that the FCN period, being given by the internal structure of the Earth (mainly the flattening of the core), it is highly improbable that it is very variable in time.

In the studies listed above, large discrepancies appear between VLBI- and SG-derived values of $Q_{ \rm FCN}$ . This paper aims at investigating these differences. To that purpose, we check the sensitivity of both gravity and nutation data to the Earth's interior parameters. The functions describing the response in gravity and in nutation to the tidal forcing, and their sensitivity, are addressed in Sect. 2. In Sect. 3, the FCN resonance parameters are retrieved from the gravity and nutation data. Results are discussed in Sect. 4.

2 Response in gravity and nutation to the tidal forcing

2.1 Tidal gravity

The tidal variations observed at the Earth's surface are induced by the direct effect of the tidal potential, the deformation and the mass redistribution in the mantle due to this potential. The (direct, deformation and mass redistribution) effects of the centripetal potential due to the Earth's wobble must also be considered. Also, the inertial pressure at the core-mantle boundary (CMB) due to the differential rotation between the mantle and the core induces a deformation of the CMB as well as mass redistribution in the mantle that also generates time variations of the gravity field. Summing all these effects and dividing by the gravity variations for a non-rotating rigid Earth leads to the tidal gravimetric factor (Neuberg et al. 1987; Hinderer et al. 1991; Legros et al. 1993):

$\displaystyle T^{(g)}(\sigma)=\delta_2(1-e)-\frac{eN_2}{\sigma^{\prime}- s_2} \biggl[\delta_2 \sigma^{\prime}+\overline \delta_1 \frac{A}{A_{\rm f}} \biggr],$

(1)

hereafter referred to as the gravimetric transfer function, where

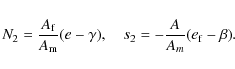$\begin{displaymath}N_2=\frac{A_{\rm f}}{A_{\rm m}}(e-\gamma), \quad s_2=-\frac{A}{A_m}(e_{\rm f}-\beta). \end{displaymath}$

(2)

In the above expressions, s₂ is the complex resonant frequency of the FCN, e and $e_{\rm f}$ the flattenings of the Earth and the fluid outer core, respectively, and A, $A_{\rm m}$ and $A_{\rm f}$ the equatorial moments of inertia of the whole Earth, of the mantle and of the fluid outer core, respectively. The complex parameter N₂ represents the strength of the FCN resonance. The compliances $\gamma$ and $\beta$ characterize the deformability of the CMB under tidal forcing and the centrifugal forcing associated with the wobble of the fluid outer core relative to the mantle. One has $\gamma=q_0h^f/2$ and $\beta = q_0\overline h_1^f/2$ , where $h^f\approx1.14$ is the Love number expressing the deformation of the CMB induced by a volumic potential evaluated at the CMB, and $\overline h_1^f\approx0.35$ is the Love number expressing the deformation of the CMB under an inertial pressure (Dehant et al. 1993). The Love number $\delta_2$ represents the static response of the Earth to the tidal potential of degree two, and $\overline \delta _1$ is the Love number which characterizes the elastic response (effect of mass redistribution + deformation; $\overline\delta_1=\overline h_1-\frac{3}{2} \overline k_1$ ) of the Earth to the inner pressure acting at the CMB. Because the mantle should possess some anelasticity (Hinderer et al. 1991) that would also contribute to the damping of the FCN, the gravimetric factor $\overline \delta _1$ is complex.

An Earth made up of a mantle, a fluid core and a solid inner core admits three additional resonances. Two of them are in the low-frequency band: the Chandler wobble (CW) and the inner core wobble (ICW); the remaining one, the free inner core nutation (FICN), lies in the quasi diurnal band. To the model proposed in Eq. (1), we could add these resonance effects (see for instance Legros et al. 1993; Mathews et al. 1995). However, their effects would be far smaller than the error of the gravity data, so we have decided not to include them.

Equation (1) allows one to compute how much the T^(g) is sensitive to departures of the various parameters from their ``standard'' values. We compute the sensitivity $S(\sigma;p)$ to a parameter pincremented by $\Delta p$ at the frequency $\sigma$ as

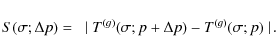$\begin{displaymath}S(\sigma;\Delta p)=~\mid T^{(g)}(\sigma;p+\Delta p)-T^{(g)}(\sigma;p)\mid\!. \end{displaymath}$

(3)

The two-dimensional functions S are drawn in Fig. 1 for parameters $T_{\rm FCN}$ , $Q_{ \rm FCN}$ , N₂ (central values taken in the MHB paper), and $\overline \delta _1$ (central value taken in Rosat et al. 2009). The white, vertical pattern showing up in the plots reflects the FCN resonance. Tidal waves away from the resonance are generally poorly (if at all) affected by departures of the parameters from their central values. Nevertheless, it appears that small effects of a few tenths of a percent are expected for $\overline \delta _1$ and, to a lesser extent, for N₂. Small departures of the FCN parameters $T_{\rm FCN}$ and $Q_{ \rm FCN}$ will mainly affect tidal waves that are very close to the resonance (i.e., within the white, vertical bands crossing the two upper plots). The function T^(g) is therefore primarily sensitive to the gravimetric factor $\overline \delta _1$ and to N₂ for tidal waves away from the FCN resonance, but mainly sensitive to the FCN parameters immediately around the resonance.

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm]{11489fg1.eps}\hspace{1mm... ...g3.eps}\hspace{1mm} \includegraphics[width=4.4cm]{11489fg4.eps} }\end{figure}$	Figure 1: Sensitivity of the gravimetric transfer function T^(g) to the parameters $T_{\rm FCN}$ , $Q_{ \rm FCN}$ , N₂, and $\overline \delta _1$ .
Open with DEXTER

2.2 Nutation

The frequency domain response of the space motion of the Earth's figure axis to the tidal potential can be written with a transfer function that expresses the ratio between rigid and non-rigid nutation amplitudes (resp. $\eta_{R}$ and $\eta$ ; see, e.g., Mathews et al. 2002). One has $\eta(\sigma) = T^{(n)}(\sigma)~\eta_R(\sigma)$ , wherein, neglecting the ICW effects,

$\begin{displaymath} T^{(n)}(\sigma)=\frac{e-\sigma}{e+1}\left[1 -\frac{\sigma^{\... ..._2} +\frac{\sigma^{\prime}N_3}{\sigma^{\prime}- {s}_3}\right], \end{displaymath}$

(4)

where the last three bracketed terms express the CW, FCN, and FICN resonance, respectively, with

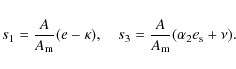$\begin{displaymath}s_1=\frac{A}{A_{\rm m}}(e-\kappa), \quad s_3=\frac{A}{A_{\rm m}}(\alpha_2e_{\rm s}+\nu). \end{displaymath}$

(5)

The flattening $e_{\rm s}$ is relevant to the solid inner core. The compliance $\kappa$ is expressed as $ek/k_{\rm s}$ , where k and $k_{\rm s}$ are the elastic and fluid Love number, respectively. It expresses the deformability at the surface under degree 2 tidal forcing. The full, complicated expression for the strength N₃ can be found in, e.g., Dehant et al. (2005).

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm]{11489fg5.eps}\hspace{1mm... ...g7.eps}\hspace{1mm} \includegraphics[width=4.4cm]{11489fg8.eps} }\end{figure}$	Figure 2: Sensitivity of the nutation transfer function T⁽ⁿ⁾ to the parameters $T_{\rm FCN}$ , $Q_{ \rm FCN}$ , N₂, and $T_{\rm FICN}$ .
Open with DEXTER

The sensitivity analysis of T⁽ⁿ⁾ to parameters N₂, s₁, s₂, and s₃ (Fig. 2) reveals that the nutations are primarily sensitive to the FCN frequency s₂, then to its amplitude N₂, and less sensitive to the Chandler frequency s₁ (not shown in the figure) and to the FICN frequency s₃.

3 Determination of the FCN resonance parameters

3.1 Tidal gravity

Since we are looking for Earth's global interior parameters, we take advantage of worldwide records in order to minimize local effects. Thus, we analyze 15 datasets from the SG located in Boulder (USA), Bad-Homburg (Germany), Cantley (Canada), Canberra (Australia), Esashi (Japan), Matsushiro (Japan), Moxa (Germany), Membach (Belgium), Medicina (Italy), Metsahovi (Finland), Potsdam (Germany), Strasbourg (France), Vienna (Austria), Wettzell (Germany) and Wuhan (China). For all, the record length is more than 5 years.

The SG time-varying gravity records have been corrected for any gaps, spikes, steps and other disturbance so that a tidal analysis with the ETERNA software package (Wenzel 1996) is possible. Before the tidal analysis is done, the minute data are resampled to 1 h (using a filter with a cut-off period of 3 h). ETERNA then performs a least-square fit to tides, local air pressure and instrumental drift to give complex gravimetric factors, residual gravity, an adjusted barometric admittance, and a polynomial drift function. The data to be inverted are the complex gravimetric factors corrected for the ocean tide loading effect according to the FES 2004 ocean model (Lyard et al. 2006). An example of tidal gravimetric factors obtained at Strasbourg and corrected for the ocean loading effect is superimposed on the observed nutation amplitudes in Fig. 3. The errors on the imaginary parts of the tidal waves $\Psi_1$ and $\Phi_1$ , which are the closest to the resonance, are very large, while the corresponding nutation amplitudes (annual and semi-annual retrograde) are well determined.

We use optimized linearized least-squares based on the Levenberg-Marquardt algorithm (Marquardt 1963; Defraigne et al. 1994, 1995). To force the quality factor to be positive, we introduce the variable $x = {\rm log}_{10}(Q_{\rm FCN})$ . The least-squares implicitly suppose that the parameters are Gaussian distributed, which is not the case for $Q_{ \rm FCN}$ (Florsch & Hinderer 2000), but should be the case for x if the data had weak errors (Rosat et al. 2009). Rosat et al. (2009) have demonstrated that there is a good agreement between the linearized Levenberg-Marquardt results and the Bayesian statistic method.

Because of the strong correlation of N₂ with $\overline \delta _1$ (99%), and the small number of tidal gravity data points (only 9 diurnal tidal waves), we will not invert this parameter from gravity tidal factors but rather fix it to the value obtained from the inversion of the nutation data. Indeed, the value of N₂ has been well constrained in MHB or Koot et al. (2008). Thus, the inversion is carried out for x, $T_{\rm FCN}$ , $\delta_1^R$ and $\delta_1^I$ . Finally, we get $\overline \delta_1=(0.03407 - {\rm i}~0.0031) \pm 1.0\times10^{-4}$ . The period of the FCN is $T_{\rm FCN}=-426.9 \pm 1.2$ days and its quality factor is $Q_{\rm FCN}=16~630 \pm 3~562$ . (The errors correspond to $1\sigma$ .)

3.2 Nutation

Nutation time series were obtained by a single inversion of ionosphere-free VLBI delays accumulated during $\sim$ 3800 24-h observing sessions of routine geodetic VLBI observations spanning 1984.0-2008.7. Earth orientation parameters were estimated once per session, while station coordinates and velocities and most of radio source coordinates were estimated as global parameters over the 24 years. The celestial frame was maintained by a no net rotation constraint over the coordinates of 247 sources selected by Feissel-Vernier et al. (2006), ensuring a relative time stability of the frame axes. Doing so, one avoids contaminating the estimated nutation offsets by radio source instabilities. All the calculations used the Calc 10.0/Solve 2008.12.05 geodetic VLBI analysis software package developped and maintained at NASA/Goddard Space Flight Center, and were carried out at the Paris Observatory IVS Analysis Center (Gontier et al. 2008) as part of the International VLBI Service for Geodesy and Astrometry (IVS, Schlüter & Behrend 2007).

Prograde and retrograde amplitudes of the terms listed in Table 1 of the MHB paper, jointly with a linear trend on each component, were obtained by a weighted least-squares fit to the time series. To get realistic errors on data, we inflated the variance of each data point by an additive variance of 0.015 mas², and a scale factor of 1.8 (see Herring et al. 1991, 2002; Lambert et al. 2008). The obtained nutation amplitudes were corrected for effects that are not, or are non linearly, linked to non rigidity, including the geodetic nutation, the S1 atmospheric tide, and the contribution of second order terms in the dynamical equations of the Earth's rotation. The relevant values were taken from Table 6 of the MHB paper for the former two effects, and in Lambert & Mathews (2006, 2008) for the latter. The ratio of the observed (fitted) nutation amplitudes to the rigid ones taken in the REN 2000 theory (Souchay et al. 1999) are plotted in Fig. 3. Note the good agreement between the observations and the MHB transfer function using $T_{\rm FCN}=-430.21$ days and $Q_{\rm FCN}=20~000$ .

$\begin{figure} \par\includegraphics[width=9cm,clip]{11489fg9.eps} \end{figure}$	Figure 3: Observed transfer functions for nutation (dots) and gravity (stars) obtained from VLBI and SG measurements, respectively. The corresponding theoretical ones are plotted in solid line for nutation, and in dashed line for gravity.
Open with DEXTER

From the fitted set of nutation amplitudes, we estimate s₁, N₂, s₂, and s₃. These geophysical parameters are correlated and the highest correlation ( $\sim$ 0.9) shows up between the FCN and the FICN frequencies s₂ and s₃.

In order to check that the inverted parameters are Gaussian distributed, we compute their probability density functions (pdfs) using the full transfer function of the resonance as defined in Eq. (4). As our knowledge of the parameters is imperfect, we consider them as probabilistic rather than deterministic. The resulting joint pdfs are represented in Fig. 4 for the parameters x, $T_{\rm FCN}$ , s₁ and N₂. The $\chi^2$ -test shows that the distribution for xcan be supposed Gaussian with an error of $5\%$ . Note also the tilted shape of the pdfs between the real and imaginary parts of s₁ and N₂ that indicates a correlation between these parameters. The Levenberg-Marquardt least-square fit gives $T_{\rm FCN}=-429.6 \pm 0.6$ days, $Q_{\rm FCN} = 16~683 \pm 884$ , $N_2 = (0.0490 + {\rm i}~0.0015) \pm 2\times10^{-4}$ , $s_1 = (0.00261 - {\rm i}~0.00126) \pm 3\times10^{-5}$ , $T_{\rm FICN}=1~139 \pm 736$ days, $Q_{\rm FICN} = 550 \pm 171$ , with the error corresponding to $1\sigma$ .

$\begin{figure} \par\includegraphics[width=9cm,clip]{11489f10.eps} \end{figure}$	Figure 4: Joint probability density functions of x, $T_{\rm FCN}$ , s₁ and N₂ estimated from the nutation amplitudes.
Open with DEXTER

A joint inversion of VLBI nutation and SG gravity data has also been performed to determine x and $T_{\rm FCN}$ . However, the amplitudes of the tidal waves that best constrain the FCN frequency and damping (mainly $\Psi_1$ and $\Phi_1$ ) are weak while the corresponding nutation amplitudes (mainly the annual and semi-annual retrograde) are substantial. The ocean loading effect is a main source of error on the gravity signal while the effect of the tidal ocean on the Earth's nutation is weak. Therefore x and $T_{\rm FCN}$ are better estimated using VLBI data than using surface gravity data, and a joint inversion does not improve the results obtained using VLBI data alone.

4 Concluding remarks

Estimates of the FCN resonance parameters from nutation or gravity measurements are comparable within the error bars (Table 1). The FCN period is close to -430 days using VLBI and slightly lower by a few days from gravity data. The FCN quality factor estimated either from nutation or from gravity data tends to be around 17 000 with error bars of $\sim$ 1000. Tidal gravity observations bring additional constraints to the Earth's interior by leading to an estimate of the internal pressure Love number. Interpretation of these estimates in terms of dissipative torques at the core boundaries needs more assumptions and internal modeling to separate the respective parts of electromagnetism and viscosity. This problem will not be addressed here.

Table 1: Values of the FCN resonance parameters obtained from nutation and gravity measurements.

Our study has shown that surface gravity is as sensitive as nutation to the FCN resonance frequency and damping factor. The discrepancy between gravity and nutation is due to the large errors arising from the diurnal tidal wave determinations that are the closest to the FCN resonance.

As time elapses, improvements in both techniques are progressively removing systematic effects that produce discrepancies in estimates of the same geophysical quantities. Geophysical parameters estimated from VLBI will improve in accuracy in the next five or ten years, not only because of better quality data or reference frame realization, but also because the longer time span will permit one to decorrelate the 18.6-yr tidal term and the linear trend. For SG data, longer time-series will enable us to better determine $\Psi_1$ and $\Phi_1$ tidal waves but improvements are also necessary in the modeling of the ocean loading effects in the diurnal frequency band.

Acknowledgements

We would like to thank M. Llubes for her computation of the ocean loading corrections at the SG sites. We are also grateful to the GGP members for making the SG datasets available, and to the IVS for their constant effort in scheduling VLBI sessions and correlating them. S. Rosat particularly thanks N. Florsch for his useful explanations about the Bayesian method. We are finally grateful to the anonymous reviewer for comments on this manuscript.

References

Crossley, D., Hinderer, J., Casula, G., et al. 1999, EOS, 80, 121 [NASA ADS] [CrossRef] (In the text)
Cummins, P., & Wahr, J. 1993, J. Geophys. Res., 98, 2091 [NASA ADS] [CrossRef] (In the text)
Defraigne, P., Dehant, V., & Hinderer, J. 1994, J. Geophys. Res., 99, 9203 [NASA ADS] [CrossRef] (In the text)
Defraigne, P., Dehant, V., & Hinderer, J. 1995, J. Geophys. Res., 100 (B2), 2041 (In the text)
Dehant, V., Hinderer, J., Legros, H., & Lefftz, M. 1993, Phys. Earth Planet. Interiors, 76, 259 [NASA ADS] [CrossRef] (In the text)
Dehant, V., Feissel-Vernier, M., de Viron, O., et al. 2003, J. Geophys. Res., 108, 2275 [CrossRef]
Dehant, V., de Viron, O., & Greff-Lefftz, M. 2005, A&A, 438, 1149 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Ducarme, B., Rosat, S., Vandercoilden, L., et al. 2009, in Observing our Changing Earth, ed. M. G. Sideris, Proc. 2007 IAG General Assembly, 523 (In the text)
Dziewonski, A. M., & Anderson, D. L. 1981, PEPI, 25, 297 [NASA ADS]
Florsch, N., & Hinderer, J. 2000, PEPI, 117, 21 [NASA ADS] (In the text)
Feissel-Vernier, M., Ma, C., Gontier, A.-M., & Barache, C. 2006, A&A, 452, 1107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gontier, A.-M., Lambert, S. B., & Barache, C. 2008, in International VLBI Service for Geodesy and Astrometry (IVS) 2007 Annual Report, ed. D. Behrend, K. D. Baver, NASA/TP-2008-214162, 224 (In the text)
Gwinn, C. R., Herring, T. A., & Shapiro, I. I. 1986, J. Geophys. Res., 91, 4755 [NASA ADS] [CrossRef] (In the text)
Herring, T. A., Gwinn, C. R., & Shapiro, I. I. 1986, J. Geophys. Res., 91, 4745 [NASA ADS] [CrossRef] (In the text)
Herring, T. A., Buffet, B. A., Mathews, P. M., & Shapiro, I. I. 1991, J. Geophys. Res., 96 (B5), 8259 (In the text)
Herring, T. A., Mathews, P. M., & Buffet, B. A. 2002, J. Geophys. Res., 107 (B4), 10.1029/2001JB000165 (In the text)
Hinderer, J., Zürn, W., & Legros, H. 1991, in Proc. 11th Int. Symp. Earth Tides, Schweitzerbart, ed. J. Kakkuri (Stuttgart: Verlag), 549 (In the text)
Hinderer, J., Boy, J.-P., Gegout, P., et al. 2000, Phys. Earth Planet. Interiors, 117, 37 [NASA ADS] [CrossRef] (In the text)
Koot, L., Rivoldini, A., de Viron, O., & Dehant, V. 2008, J. Geophys. Res., 113, (B08414), 10.1029/2007JB005409 (In the text)
Lambert, S. B., & Dehant, V. 2007, A&A, 469, 777 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lambert, S. B., & Mathews, P. M. 2006, A&A, 453, 363 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lambert, S. B., & Mathews, P. M. 2008, A&A, 481, 883 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lambert, S. B., Dehant, V., & Gontier, A.-M. 2008, A&A, 481, 535 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Legros, H., Hinderer, J., Lefftz, M., & Dehant, V. 1993, Phys. Earth Planet. Interiors, 76, 283 [NASA ADS] [CrossRef] (In the text)
Lyard, F., Lefèvre, F., Letellier, T., & Francis, O. 2006, Ocean Dynamics, 56, 394 [NASA ADS] [CrossRef] (In the text)
Marquardt, D. 1963, J. Soc. Indust. Appl. Math., 11, 431 [CrossRef] (In the text)
Mathews, P. M., Buffet, B. A., & Shapiro, I. I. 1995, J. Geophys. Res., 100, 9935 [NASA ADS] [CrossRef] (In the text)
Mathews, P. M., Herring, T. A., & Buffet, B. A. 2002, J. Geophys. Res., 107 (B4), 10.1029/2001JB000390 (In the text)
Neuberg, J., Hinderer, J., & Zürn, W. 1987, Geophys. J. R. Astr. Soc., 91, 853 (In the text)
Roosbeek, F., Defraigne, P., Feissel, M., & Dehant, V. 1999, Geophys. Res. Lett., 26, 131 [NASA ADS] [CrossRef] (In the text)
Rosat, S., Florsch, N., Hinderer, J., & Llubes, M. 2009, J. Geodyn., in press (In the text)
Sato, T., Tamura, Y., Higashi, T., et al. 1994, J. Geomag. Geoelectr., 46, 571 (In the text)
Sato, T., Tamura, Y., Matsumoto, K., et al. 2004, J. Geodyn., 38, 375 [CrossRef] (In the text)
Schlüter, W., & Behrend, D. 2007, J. Geod., 81, 479 [CrossRef] (In the text)
Souchay, J., Loysel, B., Kinoshita, H., & Folgueira, M. 1999, A&A, 135, 111 [NASA ADS] [CrossRef] (In the text)
Vondrák, J., & Ron, C. 2006, Acta Geodyn. Geomater., 3, 53 (In the text)
Vondrák, J., Ron, C., & Weber, R. 2005, A&A, 444, 297 [NASA ADS] [CrossRef] [EDP Sciences]
Wenzel, H. G. 1996, Bull. Inf. Marées Terrestres, 124, 9425 (In the text)

Footnotes

... 1984.0-2008.7: The data set and its description file are available via anonymous ftp at ftp://ivsopar.obspm.fr/vlbi/ivsproducts/eops/opa2008d.eops.gz, ftp://ivsopar.obspm.fr/vlbi/ivsproducts/eops/opa2008d.eops.txt.

All Tables

Table 1: Values of the FCN resonance parameters obtained from nutation and gravity measurements.

All Figures

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm]{11489fg1.eps}\hspace{1mm... ...g3.eps}\hspace{1mm} \includegraphics[width=4.4cm]{11489fg4.eps} }\end{figure}$	Figure 1: Sensitivity of the gravimetric transfer function T^(g) to the parameters $T_{\rm FCN}$ , $Q_{ \rm FCN}$ , N₂, and $\overline \delta _1$ .
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=4.4cm]{11489fg5.eps}\hspace{1mm... ...g7.eps}\hspace{1mm} \includegraphics[width=4.4cm]{11489fg8.eps} }\end{figure}$	Figure 2: Sensitivity of the nutation transfer function T⁽ⁿ⁾ to the parameters $T_{\rm FCN}$ , $Q_{ \rm FCN}$ , N₂, and $T_{\rm FICN}$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11489fg9.eps} \end{figure}$	Figure 3: Observed transfer functions for nutation (dots) and gravity (stars) obtained from VLBI and SG measurements, respectively. The corresponding theoretical ones are plotted in solid line for nutation, and in dashed line for gravity.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11489f10.eps} \end{figure}$	Figure 4: Joint probability density functions of x, $T_{\rm FCN}$ , s₁ and N₂ estimated from the nutation amplitudes.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.