| Issue |
A&A
Volume 503, Number 1, August III 2009
|
|
|---|---|---|
| Page(s) | 35 - 46 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200809809 | |
| Published online | 15 June 2009 | |
The radial dependence of temperature and iron abundance
Galaxy clusters from z = 0.14 to z = 0.89
S. Ehlert1,3 - M. P. Ulmer2,3
1 - Max-Planck-Institut für Kernphysik, PO Box 103980, 69029 Heidelberg, Germany
2 - LAM, Pôle de l'Etoile Site de Château-Gombert, 38, rue Frédéric Joliot-Curie,
13388 Marseille Cedex 13, France
3 - Department of Physics and Astronomy, Northwestern University, 2131 Sheridan Road, Evanston, IL 60208-2900, USA
Received 19 March 2008 / Accepted 3 June 2009
Abstract
Context. The origin and evolution of the intracluster medium (ICM) are still not fully understood. A better understanding is not only interesting in its own right, but it is also important for modeling hierarchical structure growth and for using cluster surveys to determine cosmological parameters.
Aims. To determine if there exists any evidence for evolution in the temperature or iron abundance gradients between
![]() and
and
![]() ,
therefore elucidating the origin of energy and metal input to the ICM.
,
therefore elucidating the origin of energy and metal input to the ICM.
Methods. By using a sample of 35 observations of 31 clusters of galaxies found in the archival data of Chandra and XMM-Newtonwith redshifts between 0.14 and 0.89, we derived the temperature and iron abundance radial profiles. To compare clusters with similar properties, the data were divided into comparable subsets.
Results. There is no substantial evidence to suggest that the iron abundance radial profiles in galaxy clusters evolve with redshift in any of the chosen subsets. Temperature radial profiles also do not appear to be changing with redshift once selection effects are taken into account.
Conclusions. The lack of evolution in the iron profiles is consistent with scenarios where the galaxies in clusters are stripped of their gas at higher redshifts. The temperature and iron abundance profiles also suggest that the primary source of heating in high redshift clusters is the gravitational infall of mass. These findings further emphasize the importance of modeling the local environment of clusters in cosmological studies and have important implications for studies that go to larger redshifts.
Key words: X-rays: galaxies: clusters
1 Introduction
Many dynamic processes occur in the high temperature, iron rich intracluster medium (ICM) of rich clusters of galaxies. Radiative cooling, supernova driven winds, and ram pressure stripping are just a few of the processes by which thermal energy and iron may be injected into the ICM. The theory of these processes is discussed in detail elsewhere (e.g., Sarazin 1988; Rosati et al. 2002; Arnaud 2005). In order to help resolve which processes most significantly contribute to the heating and iron enrichment within clusters, the location and evolution with redshift of both iron abundance and thermal energy can be used to provide significant clues.
Both Chandra and XMM-Newtonhave the angular resolution to make two-dimensional maps for nearby clusters such as Coma and Perseus (e.g., Fabian et al. 2006), but the statistical significance of the archival data is not generally sufficient for these types of measurements in distant clusters.
Many have already investigated how overall temperatures or iron abundances might vary with redshift, including Balestra et al. (2007), Bonamente et al. (2006), Tozzi et al. (2003), and Sanderson et al. (2006). So far very little evidence for the evolution of the ICM in galaxy clusters up to
![]() has been discovered (Matsumoto et al. 2000), but even subtle hints of changes with redshift could have a profound impact on the general understanding of the processes involved in the ICM. This current study spatially resolves the temperature and metal (iron) abundance to higher redshifts than
previous works, as well as determines whether there exists evidence for changes in the temperature or iron abundance profile with redshift.
has been discovered (Matsumoto et al. 2000), but even subtle hints of changes with redshift could have a profound impact on the general understanding of the processes involved in the ICM. This current study spatially resolves the temperature and metal (iron) abundance to higher redshifts than
previous works, as well as determines whether there exists evidence for changes in the temperature or iron abundance profile with redshift.
Table 1: Basic information about Chandra data sets used in this study.
For higher redshift clusters, studies of the evolution of the radial temperature and metallicity profiles has been reported out to a redshift ![]() (Leccardi & Molendi 2008b,a), and here the work is extended out to
(Leccardi & Molendi 2008b,a), and here the work is extended out to ![]() .
The goal is to search for evolutionary changes in the radial profiles. The results can be used to determine the relative significance of processes such as ram pressure stripping, Active Galactic Nucleus (AGN) activity, and galactic winds in clusters of galaxies. The end results can then be compared directly to simulations such as Domainko et al. (2006). Throughout this paper the concordance model of cosmology with H0= 71 km s-1 Mpc-1
.
The goal is to search for evolutionary changes in the radial profiles. The results can be used to determine the relative significance of processes such as ram pressure stripping, Active Galactic Nucleus (AGN) activity, and galactic winds in clusters of galaxies. The end results can then be compared directly to simulations such as Domainko et al. (2006). Throughout this paper the concordance model of cosmology with H0= 71 km s-1 Mpc-1
![]() and
and
![]() = 0.27 is assumed. All calculations of cosmic distances and times are based on Wright (2006).
= 0.27 is assumed. All calculations of cosmic distances and times are based on Wright (2006).
2 The data
All data in this study were taken from the Chandra and XMM-Newtonpublic archives, and are listed in Tables 1 and 2. Most of these observations were chosen after being included in Bonamente et al. (2006), Tozzi et al. (2003) or Leccardi & Molendi (2008b). All clusters listed here that are not found in these studies were found by searching the Chandra and XMM-Newtonarchives for galaxy cluster observations. The resulting sample was chosen to cover a large range of redshift with reasonable uniformity. This allowed for the sample to be conveniently divided into subsets which will be compared to one
another, building on previous work at lower redshifts (De Grandi et al. 2004). The redshifts and coordinates of these clusters were provided by the NASA/IPAC Extragalactic Database (NED), and the hydrogen column densities are given by the ![]() calculator provided on the HEASARC website.
Investigations into the element abundances of galaxy clusters suggest that most of the elemental emission is dominated by iron, and that many other elements have abundance levels that do not change much with redshift (Baumgartner et al. 2005). This allowed for the use of iron abundance and metal abundance interchangeably, and although the model used in this work fit the abundance of all
metals, the results of these fits will hereafter be called the iron abundance measurements.
calculator provided on the HEASARC website.
Investigations into the element abundances of galaxy clusters suggest that most of the elemental emission is dominated by iron, and that many other elements have abundance levels that do not change much with redshift (Baumgartner et al. 2005). This allowed for the use of iron abundance and metal abundance interchangeably, and although the model used in this work fit the abundance of all
metals, the results of these fits will hereafter be called the iron abundance measurements.
Table 2: Basic information about XMM-Newtondata sets used in analysis.
2.1 Chandra data processing
All Chandra observations used herein were observed with the ACIS camera. All processing of Chandra data was carried out using CIAO 3.3 and all the contained packages including Sherpa and ChIPS and followed the general procedure found in Tozzi et al. (2003). For each data set the standard issue EVENTS LEVEL 1 file was reset to remove all corrections already implemented on the data set. The
process
![]() was run on the reset file to detect all bad pixels. Next, the standard Level 1 events processing,
was run on the reset file to detect all bad pixels. Next, the standard Level 1 events processing,
![]() ,
was run on the reset file to create a new EVENTS LEVEL 1 file. Detection of very faint pixels was done whenever the data itself was taken in VFAINT mode. The new Level 1 file was then filtered to only include the standard event grades 0, 2, 3, 4, and 6 and also filtered further with the pipeline good time intervals to create a new EVENTS LEVEL 2 file. The new Level 2 file was processed further using the
,
was run on the reset file to create a new EVENTS LEVEL 1 file. Detection of very faint pixels was done whenever the data itself was taken in VFAINT mode. The new Level 1 file was then filtered to only include the standard event grades 0, 2, 3, 4, and 6 and also filtered further with the pipeline good time intervals to create a new EVENTS LEVEL 2 file. The new Level 2 file was processed further using the
![]() routine and then using the
routine and then using the
![]() routine as part of the ChIPS package to determine in greater detail the good time intervals. The bin time used for all data sets was 200 s. The de-streaked file was then filtered again using these good time intervals. As a final step in processing, the image was then filtered only to include the energy range of 0.3-10 keV. Filtering on the energy improves the signal to noise ratio of the image. The resulting event list was then used in all subsequent imaging and spectral analysis. There are 25 clusters observed using 27 Chandra observations, with redshifts ranging from 0.142 to 0.890. All of the cluster data sets, along with their Equatorial coordinates, redshifts,
galactic hydrogen column densities, and net exposure times after all processing are listed in Table 1.
routine as part of the ChIPS package to determine in greater detail the good time intervals. The bin time used for all data sets was 200 s. The de-streaked file was then filtered again using these good time intervals. As a final step in processing, the image was then filtered only to include the energy range of 0.3-10 keV. Filtering on the energy improves the signal to noise ratio of the image. The resulting event list was then used in all subsequent imaging and spectral analysis. There are 25 clusters observed using 27 Chandra observations, with redshifts ranging from 0.142 to 0.890. All of the cluster data sets, along with their Equatorial coordinates, redshifts,
galactic hydrogen column densities, and net exposure times after all processing are listed in Table 1.
2.2 XMM-Newton data processing
All XMM-Newtondata analyzed in this project used all three EPIC cameras: MOS1, MOS2, and the PN camera. The software used was SAS version 7.0, the standard XMM-Newtonprocessing software. All data sets
were processed using the images script available on the XMM-Newtonwebsite. The images script first runs the fundamental SAS algorithms cifbuild, odfingest, epchain, and emchain. It then
processes the standard event list further to improve signal-to-noise. In order to minimize the significance of flare events, the images script allows for the user to input desired
Good-Time-Interval (GTI) for each data set. In this case the GTI intervals were chosen as time windows where the rate was less than 35 counts per 100 s for the MOS cameras, and 40 counts per 100 s for the PN camera. After GTI filtering the images script then cleans for bad pixels based on a separate input script, with default bad pixels provided by the XMM-Newtondata center. The standard
bad pixel table provided by the images script was used here. Although the images script was originally designed to create high quality images from all three cameras, the resulting event
lists are still useful for spectral studies. Unlike the case of the Chandra data sets, the event lists used for XMM-Newtonanalysis have not been subject to any energy filtering before determining radial
profiles. However, all spectra for both instruments are restricted to the energy range from 0.5-8.0 keV. As a final restriction, the PATTERNS on the events were limited to single, double, triple, and quadruple events for the MOS cameras (PATTERN ![]() 12) and limited to single and double events for the PN camera (PATTERN
12) and limited to single and double events for the PN camera (PATTERN ![]() 4). Eight XMM-Newtondata sets were considered in this study. They are listed along with Equatorial coordinates, redshifts, hydrogen column density, and net exposure times after all processing in Table 2.
4). Eight XMM-Newtondata sets were considered in this study. They are listed along with Equatorial coordinates, redshifts, hydrogen column density, and net exposure times after all processing in Table 2.
2.3 Scale lengths: the core and counts radius
In order to average clusters together in a meaningful way, a scale length was needed. Two scale lengths were calculated for each cluster and used to divide the cluster into four annular regions: the first scale length was calculated by fitting the net intensity to a one-dimensional beta fit
and the second by dividing the cluster into four regions with roughly equal numbers of net counts. The outer radii in these regions are labeled r1, r2, r3, and r4 in Table 3. These radial profiles were determined using either the surface brightness (core) or the net counts (counts), and the background region for these calculations was always an annular region at least 5
![]() wide. This annular region was usually sufficiently small to minimize contamination from line-of-sight point sources while also containing enough counts (
wide. This annular region was usually sufficiently small to minimize contamination from line-of-sight point sources while also containing enough counts (![]() 100-1000) to be statistically significant(
100-1000) to be statistically significant(
![]() ). In some cases, the background region needed to be larger to reach this level of significance, but a region with a significant number of counts (
). In some cases, the background region needed to be larger to reach this level of significance, but a region with a significant number of counts (![]() )
was always used. The profiles are not strongly sensitive to the number of counts used in the background regions, which were chosen specifically to be radially symmetric. For each
cluster, both radii have been calculated using annular regions 2
)
was always used. The profiles are not strongly sensitive to the number of counts used in the background regions, which were chosen specifically to be radially symmetric. For each
cluster, both radii have been calculated using annular regions 2
![]() 5 wide to determine the intensity profile across the cluster. Both scale radii were then used to determine regions for extracting spectra and measuring the average temperature and iron abundance profiles. The only profiles and measurements shown in the text will use the counts radius, the reasons for which
will be discussed in Sect. 2.3.3. The measured core radius and counts regions are found in Table 3.
5 wide to determine the intensity profile across the cluster. Both scale radii were then used to determine regions for extracting spectra and measuring the average temperature and iron abundance profiles. The only profiles and measurements shown in the text will use the counts radius, the reasons for which
will be discussed in Sect. 2.3.3. The measured core radius and counts regions are found in Table 3.
2.3.1 The core radius
The basis for using a core radius length scale is that cluster dynamics and the evolution of the ICM could be inter-related (e.g., Rosati et al. 2002), so a one-dimensional beta fit was performed
on each cluster to determine the core radius scale. The centers were chosen by eye, and consistent with all attempts to determine the center of emission analytically. The error for choosing this center was always a factor of 10 smaller than the calculated core radius. The radial profile of surface brightness was calculated using the the CIAO command dmextract, and the net counts annuli described in Sect. 2.3, and it was fit to the Sherpa beta1d model. The beta1d mode fits the data to a function of the form
![\begin{displaymath}%
I(x)=A \times \left[1+\left(\frac{x-x_0}{{r}_{{\rm c}} }\right)^{2}\right]^{-3\beta+1/2}
\end{displaymath}](/articles/aa/full_html/2009/31/aa09809-08/img23.png) |
(1) |
where
Table 3: Radial profile parameters for all clusters. The XMM-Newtonclusters are listed first.
2.3.2 The counts radius
Upon examination of the one-dimensional beta fits and their reduced ![]() statistics, it appeared as though the beta model fits derived from Sherpa were not statistically robust. The
reduced
statistics, it appeared as though the beta model fits derived from Sherpa were not statistically robust. The
reduced ![]() for these fits was often above 2, and although others have used similar results (Sakelliou & Ponman 2004), it was judged necessary to find a second method used to independently verify the profiles. Therefore, a second set of temperature and iron profiles were calculated with the same set of data. The second method used was to divide the cluster into radial regions not by a constant length scale, but instead by giving each region a constant number of counts. The furthest extent of spectral extraction was also determined by the net counts in a 2
for these fits was often above 2, and although others have used similar results (Sakelliou & Ponman 2004), it was judged necessary to find a second method used to independently verify the profiles. Therefore, a second set of temperature and iron profiles were calculated with the same set of data. The second method used was to divide the cluster into radial regions not by a constant length scale, but instead by giving each region a constant number of counts. The furthest extent of spectral extraction was also determined by the net counts in a 2
![]() 5 wide region. If the net counts next the 2
5 wide region. If the net counts next the 2
![]() 5 wide region out ever dropped below 20 for Chandra or 100 for XMM-Newtondata, then this defined the edge of the cluster due to their low signal-to-noise ratio of the regions beyond this point. The four calculated counts regions for each cluster are listed in Table 3. Dividing the cluster in this manner also allows for all of the spectra for one cluster to be comparably significant instead of having a wide disparity in spectral quality. The spectra were extracted in exactly the same manner as the core radius spectra, which will be
described in detail in Sect. 2.5. This process of sub-dividing the cluster will
be called the counts profile or counts radius, hereafter. They will also be listed as
5 wide region out ever dropped below 20 for Chandra or 100 for XMM-Newtondata, then this defined the edge of the cluster due to their low signal-to-noise ratio of the regions beyond this point. The four calculated counts regions for each cluster are listed in Table 3. Dividing the cluster in this manner also allows for all of the spectra for one cluster to be comparably significant instead of having a wide disparity in spectral quality. The spectra were extracted in exactly the same manner as the core radius spectra, which will be
described in detail in Sect. 2.5. This process of sub-dividing the cluster will
be called the counts profile or counts radius, hereafter. They will also be listed as
![]() ,
and
,
and
![]() as an abbreviation in the tables, particularly in Table 3
as an abbreviation in the tables, particularly in Table 3
2.3.3 Differences between the two profiles
The radial profiles in each cluster are compared in two ways in Tables 3 and 4. Table 3 shows the extents of each individual counts region as well as the calculated core radius and virial radius r200 in arcseconds. Table 4 shows the
average core and counts regions in terms of kpc. It was found that there were insignificant differences between the two radii on average, except for the very outer region. The outermost counts regions are usually much wider than 2![]() (see the averages given in Table 4). Therefore, the average temperature and iron abundance measurements should be strongly correlated between the core and counts radius, with differences only being expected in the
outermost regions. Also included in Table 3 is the calculated virial radius in arcseconds. The virial radius is calculated as found in Jones et al. (2003), divided by 1.4 to take into
account the difference between cosmologies (
H0 = 50 km s-1 Mpc-1 in Jones et al. (2003) while
H0 = 71 km s-1 Mpc-1 here). The formula itself is given as
(see the averages given in Table 4). Therefore, the average temperature and iron abundance measurements should be strongly correlated between the core and counts radius, with differences only being expected in the
outermost regions. Also included in Table 3 is the calculated virial radius in arcseconds. The virial radius is calculated as found in Jones et al. (2003), divided by 1.4 to take into
account the difference between cosmologies (
H0 = 50 km s-1 Mpc-1 in Jones et al. (2003) while
H0 = 71 km s-1 Mpc-1 here). The formula itself is given as
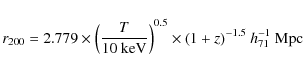 |
(2) |
and the temperature used was the overall temperature measured by the procedure described in Sect. 2.5. This allows for a direct comparison with other work that uses the virial radius. Typically a counts region bin corresponds to about 0.1
Table 4: Average outer extent of the core and counts radius regions in kpc.
2.4 Excluded data
Each cluster had to satisfy two general conditions before included in this study. Each cluster first needed to have a sufficient number of counts to measure a temperature that was significantly (
![]() )
above zero. All of the clusters in this sample have more than an average of 1000 counts per detector (3000 for XMM-Newtonobservations, 1000 for Chandra observations) within two core radii, and the minimum luminosity of all clusters from zero to two core radii is 1
)
above zero. All of the clusters in this sample have more than an average of 1000 counts per detector (3000 for XMM-Newtonobservations, 1000 for Chandra observations) within two core radii, and the minimum luminosity of all clusters from zero to two core radii is 1 ![]() 1044 erg
1044 erg
![]() .
The second condition was morphological in nature, as it was necessary to have a reasonable
.
The second condition was morphological in nature, as it was necessary to have a reasonable ![]() -fit to the data. Any observations that showed obvious visual signs of recent large merger activity were immediately excluded. Beyond that, several sets were excluded based on the values derived from the
-fit to the data. Any observations that showed obvious visual signs of recent large merger activity were immediately excluded. Beyond that, several sets were excluded based on the values derived from the ![]() -fit. In these cases the best fit core radius was larger than the furthest extent of the radial profile. These sets often had
-fit. In these cases the best fit core radius was larger than the furthest extent of the radial profile. These sets often had ![]() values that were unrealistically large as well, usually well above
values that were unrealistically large as well, usually well above ![]() .
Since the fit was
unreliable in both parameters, these clusters were not considered in this sample. Table 6 lists all the observations investigated, but not included, in this study and why they were not considered.
.
Since the fit was
unreliable in both parameters, these clusters were not considered in this sample. Table 6 lists all the observations investigated, but not included, in this study and why they were not considered.
Table 5: Observations investigated and not included in this study, along with the reasons they were excluded.
Table 6: Temperature and iron abundance measurements for all clusters by counts region.
2.4.1 The unusual case of RX J1347.5-1145
The very luminous cluster RX J1347.5-1145 was also investigated using two observations:
Chandra observation #3592 (Allen et al. 2002) and XMM-Newtonobservation #0112960101 (Gitti & Schindler 2005). Although it was sufficiently luminous and symmetric to be included here; the temperatures measured between these two observations did not agree within ![]() .
After this work began, Ota et al. (2008) found a hot bubble in the southeast region of this cluster. Thus, it was judged that this cluster is not relaxed enough to be considered in this study and was also excluded.
.
After this work began, Ota et al. (2008) found a hot bubble in the southeast region of this cluster. Thus, it was judged that this cluster is not relaxed enough to be considered in this study and was also excluded.
2.5 The spectra
Spectra for each data set were extracted with routines in CIAO for Chandra or SAS for XMM-Newton. If the data set was from Chandra then the spectra were extracted using the
![]() routine. If the data set was from XMM-Newton, then the OGIP Spectral Products routine found in the Graphical Interface of SAS after running XMMSelect was used. Spectra were
taken of all four annular regions in both scale lengths. When determining the average cluster temperature and iron abundance a circular region from
routine. If the data set was from XMM-Newton, then the OGIP Spectral Products routine found in the Graphical Interface of SAS after running XMMSelect was used. Spectra were
taken of all four annular regions in both scale lengths. When determining the average cluster temperature and iron abundance a circular region from
![]() region was used. Background regions were always circles with radii comparable or larger than two core radii outside of
the detectable emission and always on the same chip as the cluster image. The background regions remained consistent within each data set. These background regions are specifically chosen to contain as many counts as possible without including sources. Since radial symmetry is not a major concern with the spectral background, while the total number of counts is, this region is not the same background region used to determine the radial profiles. The software used to do the spectral fitting was XSPEC 12.4.0, and the MEKAL model in XSPEC was always used along with the TBABS
galactic absorption model. Since the spectra often had low numbers of counts, the modified Cash statistic was always used to determine the best-fit temperature and iron abundance simultaneously. The modified Cash statistic is ideal for fitting spectra with a low number of counts in each bin (Nousek & Shue 1989) and also allows for the use of a local background spectrum instead of fitting the background to a model. The only remaining free parameter in the fit was the normalization. The other parameters of the model were fixed: the redshifts were frozen at the values given by the NASA/IPAC Extragalactic Database (NED) while the hydrogen column densities were frozen to the values given by the
region was used. Background regions were always circles with radii comparable or larger than two core radii outside of
the detectable emission and always on the same chip as the cluster image. The background regions remained consistent within each data set. These background regions are specifically chosen to contain as many counts as possible without including sources. Since radial symmetry is not a major concern with the spectral background, while the total number of counts is, this region is not the same background region used to determine the radial profiles. The software used to do the spectral fitting was XSPEC 12.4.0, and the MEKAL model in XSPEC was always used along with the TBABS
galactic absorption model. Since the spectra often had low numbers of counts, the modified Cash statistic was always used to determine the best-fit temperature and iron abundance simultaneously. The modified Cash statistic is ideal for fitting spectra with a low number of counts in each bin (Nousek & Shue 1989) and also allows for the use of a local background spectrum instead of fitting the background to a model. The only remaining free parameter in the fit was the normalization. The other parameters of the model were fixed: the redshifts were frozen at the values given by the NASA/IPAC Extragalactic Database (NED) while the hydrogen column densities were frozen to the values given by the ![]() calculator on the HEASARC website. The solar abundance values
used were those from Anders & Grevesse (1989). For the XMM-Newtonspectra, all three instruments were fit simultaneously to the same spectral model to ensure the best use of the available statistics.
The measured temperature and iron abundance profiles for each cluster are found in Table 6. For the four clusters in this study with multiple observations, the temperature and iron abundance were determined by fitting all of the observations simultaneously.
calculator on the HEASARC website. The solar abundance values
used were those from Anders & Grevesse (1989). For the XMM-Newtonspectra, all three instruments were fit simultaneously to the same spectral model to ensure the best use of the available statistics.
The measured temperature and iron abundance profiles for each cluster are found in Table 6. For the four clusters in this study with multiple observations, the temperature and iron abundance were determined by fitting all of the observations simultaneously.
3 Selection effects
In any population study, it is important to take into account selection effects within the sample itself. Two selection effects are important in this study: overall temperature and cooling time. These selection effects combined with the separation by redshift lead to eight different subsets of the sample which were then compared to one another. In Table 7, 8 subsets defined by their temperatures and cooling time are listed along with the number of clusters in each subset.
3.1 Temperature and luminosity
The average temperature of this sample of clusters follows a trend that needs to be taken into
consideration. There is an inherent expectation that clusters at higher redshift should exhibit higher temperatures due to the
![]() relationship (e.g., Pacaud et al. 2007; Ettori et al. 2002; Ota et al. 2006, and references
therein). This is because more distant (higher redshift) clusters need to be more intrinsically luminous to be detected than low luminosity clusters. The
X-ray bolometric luminosity is proportional to temperature as
relationship (e.g., Pacaud et al. 2007; Ettori et al. 2002; Ota et al. 2006, and references
therein). This is because more distant (higher redshift) clusters need to be more intrinsically luminous to be detected than low luminosity clusters. The
X-ray bolometric luminosity is proportional to temperature as
![]() (e.g., Ota et al. 2006). Thus on average, the observed clusters at higher redshift should tend to higher average temperatures. It was necessary to take into account this selection effect when searching for variations with redshift. Based on the available sample, the boundary between high and low temperature clusters was set to 6.8 keV. Setting the boundary to this temperature allows for comparably sized subsets for high and low temperature clusters, even after the two other selection effects (cooling time and redshift) are taken into account. The average radial profiles presented below are not strongly dependent on small changes (
(e.g., Ota et al. 2006). Thus on average, the observed clusters at higher redshift should tend to higher average temperatures. It was necessary to take into account this selection effect when searching for variations with redshift. Based on the available sample, the boundary between high and low temperature clusters was set to 6.8 keV. Setting the boundary to this temperature allows for comparably sized subsets for high and low temperature clusters, even after the two other selection effects (cooling time and redshift) are taken into account. The average radial profiles presented below are not strongly dependent on small changes (![]() 0.2 keV) to this boundary.
0.2 keV) to this boundary.
Table 7: The eight subsets of the sample used to calculate average temperature and iron abundance profiles.
3.2 Central cooling
An important mechanism in galaxy cluster evolution is the process of radiative cooling. The cooling time for a cluster can be well approximated by Sarazin (1988) as
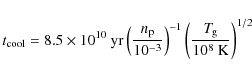 |
(3) |
where
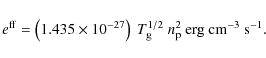 |
(4) |
This assumes that the X-ray emission is all due to thermal bremsstrahlung and also that the density and temperature of the ICM is constant within
The results of these calculations are listed in Table 8. The presence of cooling core clusters leads directly to another important process: central Active Galactic Nucleus (AGN)
activity. For nearby clusters with cooling cores, it has been shown that they do not cool as quickly as the theoretical cooling times suggest (Fabian 1994). AGN activity could influence the temperature as far out as
![]() kpc, which is, on average, approximately
kpc, which is, on average, approximately
![]() or in the first counts profile bin. The majority of cool core clusters exhibit the radio emission or bubbles usually associated with AGN activity (Dunn & Fabian 2006).The findings of Dunn & Fabian (2006) also show that only a small fraction of cool core clusters
show no evidence of AGN activity as either bubbles or radio sources. Therefore, it is expected that central AGN activity is generally (if not always) present in the cooling core clusters in this
sample as well. For completeness, all clusters were searched for possible counterpart radio sources within one arc-minute of the cluster position. The presence of sources was done using the NVSS catalog (Condon et al. 1998), and the sources were confirmed as being associated with the cluster
using NED. The clusters with likely radio counterparts are denoted with a dagger in Table 8. The presence of central AGN activity will be assumed in discussing the results for cool core clusters.
or in the first counts profile bin. The majority of cool core clusters exhibit the radio emission or bubbles usually associated with AGN activity (Dunn & Fabian 2006).The findings of Dunn & Fabian (2006) also show that only a small fraction of cool core clusters
show no evidence of AGN activity as either bubbles or radio sources. Therefore, it is expected that central AGN activity is generally (if not always) present in the cooling core clusters in this
sample as well. For completeness, all clusters were searched for possible counterpart radio sources within one arc-minute of the cluster position. The presence of sources was done using the NVSS catalog (Condon et al. 1998), and the sources were confirmed as being associated with the cluster
using NED. The clusters with likely radio counterparts are denoted with a dagger in Table 8. The presence of central AGN activity will be assumed in discussing the results for cool core clusters.
Table 8:
General information for each cluster: the overall (defined here to be from
![]() )
temperature and iron abundance, the overall luminosity, the total number of counts in the cluster, the calculations relevant to the cooling time, and finally the subset as defined in Table 7.
)
temperature and iron abundance, the overall luminosity, the total number of counts in the cluster, the calculations relevant to the cooling time, and finally the subset as defined in Table 7.
4 Results
After dividing the sample into eight comparable subsets based on temperature, cooling time, and redshift, relevant average profiles were calculated and compared. These divisions had to be made so as to make valid comparisons between profiles derived from low and high redshifts. Since there is currently little evidence for evolution in galaxy clusters even at high redshifts (Matsumoto et al. 2000; Mushotzky & Loewenstein 1997), the null hypothesis for statistical tests will be that cluster abundance and temperature profiles do not change with redshift. See also Leccardi & Molendi (2008b,a) for z = 0.1-0.3 studies. Only if the statistics conclusively suggest rejecting this hypothesis will evolution be considered.
4.1 Zero iron abundances and N/A values
As seen in Table 6, there are several instances where the best fit iron abundance was zero. As a compromise between ignoring these points altogether and producing an un-weighted average, the derived uncertainties to these points were used as statistical weights (one over the error squared). Since these zero values were most likely due to an insufficient number of detected
photons rather than a true lack of iron in the ICM, this averaging was judged to be a valid approach. As a cross check, these points were excluded from the averaging as well, and the results were all within ![]() of each other in both weighted and unweighted averages (see Sect. 4.2). Also, there was one instance where the measurement failed to converge for both the temperature and iron abundance simultaneously, and no measurement errors could be
calculated. This measurement is listed with a ``N/A'' in Table 6.
of each other in both weighted and unweighted averages (see Sect. 4.2). Also, there was one instance where the measurement failed to converge for both the temperature and iron abundance simultaneously, and no measurement errors could be
calculated. This measurement is listed with a ``N/A'' in Table 6.
4.2 Averaging procedures
In order to make the most robust study of the data, two averaging procedures (weighted and unweighted) were done on each subset listed in the following sections. The primary averaging process used was a weighted average that took into account the measurement error on each observation. For a given sample of N clusters, the weighted temperature/iron abundance average ![]() is calculated using the measurements mi and the measurement error
is calculated using the measurements mi and the measurement error
![]() as
as
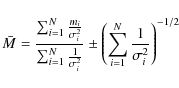 |
(5) |
As a check to ensure that no significant biases arise due to the weighting procedure, a standard (unweighted) mean and standard deviation on that mean were also calculated, both of which only depend on the measurements themselves and not the error on those measurements. The unweighted averages further demonstrate the robustness of these measurements, as the choice of weighted or unweighted averaging does not affect the basic conclusions.
4.3 Average profiles
The average temperature and iron abundance profiles are written out in Tables 9 and 10. They are organized by subset and radial region, and show the unweighted values in parentheses next to the weighted averages. Since the weighted mean emphasizes measurements with the smallest errors and there was substantial variance in the quality of the spectra, the weighted mean was chosen to be the basis for the subsequent figures and discussion. However, both means exhibited the same general trends and results.
Table 9: Average temperature as a function of counts radius, separated by redshift, temperature and cooling times. Unweighted averages are in parentheses.
Table 10: Average iron abundance as a function of counts radius, separated by redshift, temperature and cooling times. Unweighted averages are in parentheses.
4.4 Temperature profiles
The temperature profiles of Table 9 suggest that the overall temperature and cooling time completely define the temperature profiles of clusters. The average temperature profiles for cooling core clusters exhibit a clear increase in temperature with radius, while clusters without cool cores are either isothermal or have temperatures that decrease with radius. Similar temperature profiles for non-cool core clusters has been confirmed by Sanderson et al. (2006) and Leccardi & Molendi (2008b).
There are also no differences between the temperature profiles of high and low temperature clusters of comparable cooling times with the exception of an overall offset due to the higher overall temperatures. Because the temperature profiles do not seem to deviate from expectations based on their overall temperature and cooling times, the discussion in Sect. 5 will focus primarily on the measured iron abundance profiles.
4.5 Iron profiles
The iron abundance radial profiles are now taken into consideration.
4.5.1 Low temperature, cool core clusters
The first subsets to consider are those of low temperature, cool core clusters. These clusters have been shown to have strong iron abundance gradients (De Grandi et al. 2004) at low redshifts and are often associated with central AGN activity. Not only do the two subsets considered here (subsets # 1 and 5) show no evidence for evolution with redshift, the iron abundance profile is almost identical to the profiles of still lower (
![]() )
redshift clusters discussed in De Grandi et al. (2004). The results of De Grandi et al. (2004) have been re-projected to the length scale used here and corrected for the differences in their solar abundance model. All three profiles are shown in Fig. 1. From Fig. 1 there is no evidence for evolution in the iron abundance of cool core clusters
from
)
redshift clusters discussed in De Grandi et al. (2004). The results of De Grandi et al. (2004) have been re-projected to the length scale used here and corrected for the differences in their solar abundance model. All three profiles are shown in Fig. 1. From Fig. 1 there is no evidence for evolution in the iron abundance of cool core clusters
from
![]()
![]() 0.7 to
0.7 to
![]()
![]() 0. It should also be noted in Table 10 that low temperature cool core clusters (subsets 1 and 5) do not have
statistically significant differences in overall iron abundance or in average iron abundance
profiles versus redshift. The same lack of difference is also seen when comparing high temperature
cool core clusters (subsets 2 and 6).
0. It should also be noted in Table 10 that low temperature cool core clusters (subsets 1 and 5) do not have
statistically significant differences in overall iron abundance or in average iron abundance
profiles versus redshift. The same lack of difference is also seen when comparing high temperature
cool core clusters (subsets 2 and 6).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg1.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg482.png) |
Figure 1: Iron abundance as a function of radius for clusters with low temperatures and short cooling times, separated by redshift. The dotted line corresponds to subset #1 (z < 0.4) while the dashed line corresponds to subset #5 (z > 0.4). The solid line is from De Grandi et al. (2004). |
| Open with DEXTER | |
4.5.2 High temperature, cool core clusters
There are only two clusters in the high redshift subset for clusters with high temperatures and cool cores (subset #6) which is too small of a sample to be considered representative of the entire population. However, it should nevertheless be noted that the average iron abundance profile for this small subset is entirely consistent point-for-point with the results of the larger low redshift sample. As can be seen in Fig. 2, the average profile in both cases has a higher central abundance, with evidence for a decreasing gradient outward. Even though the average profile for the high redshift sample may not represent the population, this small sample still shows no evidence for evolution in the iron abundance profile with redshift.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg2.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg483.png) |
Figure 2: Iron abundance as a function of radius for clusters with high temperatures and short cooling times, separated by redshift. The solid line corresponds to subset #2 (z < 0.4). The dashed line corresponds to subset #6 (z > 0.4). |
| Open with DEXTER | |
4.5.3 Low temperature, non-cool core clusters
Subsets #3 and 7 describe the average profiles for low temperature clusters without cool cores. Although both of these samples are small, Fig. 3 shows that the two profiles are very consistent with one another.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg3.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg484.png) |
Figure 3: Iron abundance as a function of radius for clusters with low temperatures and long cooling times, separated by redshift. The solid line corresponds to subset #3 (z < 0.4). The dashed line corresponds to subset #7 (z > 0.4). |
| Open with DEXTER | |
4.5.4 High temperature, non-cool core clusters
Both subsets in this case have a relatively high number of clusters. Again in these two subsets, the two radial profiles are wholly consistent with one another, with no reason to believe that the iron abundance in these subsets is changing with redshift. All of the analysis suggests that the iron abundance is not evolving with redshift independent of the temperature and cooling time.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg4.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg485.png) |
Figure 4: Iron abundance as a function of radius for high temperature clusters with long cooling times, separated by redshift. The solid line corresponds to subset #4 (z < 0.4). The dashed line corresponds to subset #8 (z > 0.4). |
| Open with DEXTER | |
5 Discussion
5.1 The data analysis
Before discussing the radial dependencies of the iron abundance and the temperature, it is worthwhile to review why and how the data from the clusters were averaged together in the manner that was done. As noted in Sects. 2.3 and 2.4, two different radii/scales were chosen. The first was the core radius derived from a single ![]() model. This radius corresponds directly to the dynamical scale of the cluster. This is the natural choice for a scale length here, as it
is based on the dynamics of the cluster.
model. This radius corresponds directly to the dynamical scale of the cluster. This is the natural choice for a scale length here, as it
is based on the dynamics of the cluster.
A second scale length was used to find four radial regions with approximately equal numbers of net counts. Although this scale is independent of the dynamics, it is useful for testing whether the profiles are sensitive to the scale length chosen. This ``equal counts per enclosed area'' process was chosen for its simplicity in calculation, and for its ability to increase the significance of measurements in the outer regions of the clusters. When the counts and core radii were converted into a linear projected length scale such as Mpc, they cover very similar ranges. The main inconsistency occurs in the outermost regions, where the counts radius extends much further outward than the core radius. Therefore, overall consistency between the results derived by the two different methods was expected. Since the counts radius is so strongly correlated with the core radius and offers better statistics across each cluster, the results of the core radius measurements have been omitted from the text even though they are wholly consistent with these results.
Another possible choice of length scale is the virial radius of the cluster, but the easiest way of estimating
![]() (or r200) relates directly to the overall temperature
(e.g., Jones et al. 2003). If the virial radius was used in this case, the temperature would be correlated with the radial regions. Because of the
(or r200) relates directly to the overall temperature
(e.g., Jones et al. 2003). If the virial radius was used in this case, the temperature would be correlated with the radial regions. Because of the
![]() relationship (e.g. Ota et al. 2006) and clusters at higher redshifts must be on average more luminous to be detected with a sufficient statistical significance, the scale radius chosen needs to take into account this selection effect. Because the virial radius is related to the overall temperature, and therefore luminosity, it is difficult to correct for this selection effect. As an example, there
exist nearby clusters such as Perseus (Arnaud et al. 1994) and Coma (e.g., De Grandi et al. 2004; Adami et al. 2006; Watanabe et al. 1999) with comparable X-ray luminosities that exhibit very different temperature and iron
abundance profiles.
relationship (e.g. Ota et al. 2006) and clusters at higher redshifts must be on average more luminous to be detected with a sufficient statistical significance, the scale radius chosen needs to take into account this selection effect. Because the virial radius is related to the overall temperature, and therefore luminosity, it is difficult to correct for this selection effect. As an example, there
exist nearby clusters such as Perseus (Arnaud et al. 1994) and Coma (e.g., De Grandi et al. 2004; Adami et al. 2006; Watanabe et al. 1999) with comparable X-ray luminosities that exhibit very different temperature and iron
abundance profiles.
As a further check of our analysis, our results were compared with other published measurements such as Kotov & Vikhlinin (2005) for CL 0016+16 (MS 0015.9+1609), and the temperature/abundance results published here tend to be higher by
![]() than those of Kotov & Vikhlinin (2005). The work of Balestra et al. (2007) shows how using an updated analysis tool can bring out differences of this scale. Furthermore, the differences may be due to systematics between the Chandra and XMM-Newtonanalysis chains as well as the statistics between the two observations themselves. These differences in the core radius measurements are on the order of about 20% which should not strongly affect the results of the average profiles. The measured profiles of Kotov & Vikhlinin (2005) also measure the radial profile in a different energy band than our measurement (0.5-2 keV in Kotov & Vikhlinin (2005) versus 0.5-10 keV in this work). Three other clusters were studied by Snowden et al. (2008), and these results are consistent within 10-20% and usually within 1 standard deviation. An important caveat is that Snowden et al. (2008) used the MOS cameras of XMM-Newton, whereas Chandra was used in this study for measuring the temperature of
Abell 1413 and Abell 2204. The systematic differences in response and sensitivity may be responsible for the discrepancies between the results of Snowden et al. (2008) and those listed here.
than those of Kotov & Vikhlinin (2005). The work of Balestra et al. (2007) shows how using an updated analysis tool can bring out differences of this scale. Furthermore, the differences may be due to systematics between the Chandra and XMM-Newtonanalysis chains as well as the statistics between the two observations themselves. These differences in the core radius measurements are on the order of about 20% which should not strongly affect the results of the average profiles. The measured profiles of Kotov & Vikhlinin (2005) also measure the radial profile in a different energy band than our measurement (0.5-2 keV in Kotov & Vikhlinin (2005) versus 0.5-10 keV in this work). Three other clusters were studied by Snowden et al. (2008), and these results are consistent within 10-20% and usually within 1 standard deviation. An important caveat is that Snowden et al. (2008) used the MOS cameras of XMM-Newton, whereas Chandra was used in this study for measuring the temperature of
Abell 1413 and Abell 2204. The systematic differences in response and sensitivity may be responsible for the discrepancies between the results of Snowden et al. (2008) and those listed here.
The results of the counts profiles results will now be taken at face value, and the physical interpretation of noticeable variations will be discussed.
5.2 Review and comparison with previous work on the chemical evolution of the ICM
Balestra et al. (2007), Maughan et al. (2008) and Werner et al. (2008) all discuss evidence for the chemical evolution of the ICM. Older works (e.g., Mushotzky & Loewenstein 1997; Rizza et al. 1998) did not report any statistically significant evidence for chemical evolution with redshift. The recent work that found the strongest evidence for evolution is Balestra et al., but this evolution was found only when data based on all the z < 1 clusters in their sample were combined (compare with the smaller previous set in their Fig. 3). Furthermore, the derived chemical evolution required the use of the formal statistical best fit uncertainty instead of the observed dispersions (e.g. their Fig. 14). In contrast, for a similar redshift range (below about 0.9), the results of Maughan et al. are consistent with no evolution.
From the theoretical point of view as described in Kapferer et al. (2007), Sarazin (1988), and references therein, the chemical evolution of the ICM is a complex combination of effects due to cluster merging, infall of enriched material, galactic ram pressure stripping, galactic winds, and other possible causes. For the relaxed clusters considered in this paper Kapferer et al. (2007) predicted no observable chemical evolution from redshift 0.15 to 0.9.
Our paper shows how it is important to compare like clusters and that there is room for further theoretical studies to understand the apparent lack of evolution of the radial dependence of the enriched material of the ICM, and at the same time heating via infall of metal rich gas clouds.
5.3 Scenarios for heating and iron enrichment
The data presented here are consistent with no evolution in radial profiles of iron abundance and temperature. The modeling of this should be consistent with the concept of hierarchical formation of structure in the universe (e.g. Gao et al. 2008, and references therein). Because the iron abundance does not appear to be strongly correlated to the overall temperature, gravitational infall is the most likely scenario for heating clusters beyond ![]() 6.5 keV. This infall must take place in such a manner as not to change the radial profile of iron abundance or temperatures. For non-cooling clusters this means the clusters somehow have no measurable temperature gradients inside about 500 kpc but maintain their abundance gradients while (presumably) increasing in temperature in a hierarchical growth model. In order to demonstrate why infall is the preferred major energy input, the process of heating has to be considered in some detail.
6.5 keV. This infall must take place in such a manner as not to change the radial profile of iron abundance or temperatures. For non-cooling clusters this means the clusters somehow have no measurable temperature gradients inside about 500 kpc but maintain their abundance gradients while (presumably) increasing in temperature in a hierarchical growth model. In order to demonstrate why infall is the preferred major energy input, the process of heating has to be considered in some detail.
An estimate of the amount of near solar abundance material that is added along with the energy to boost the
![]() from 4 keV to 8 keV is made now. We assume typical
from 4 keV to 8 keV is made now. We assume typical
![]() (Stanek et al. 2006; Ota et al. 2006; Ettori et al. 2004b) and
(Stanek et al. 2006; Ota et al. 2006; Ettori et al. 2004b) and
![]() (e.g. Stanek et al. 2006; Rykoff et al. 2008) relations apply to the clusters studied here. Under these assumptions, if the temperature
increases by a factor of 2 then the luminosity increases by at least a factor of 4 and the mass
by a factor of 3, the amount of mass added to the clusters being on the order of 3
(e.g. Stanek et al. 2006; Rykoff et al. 2008) relations apply to the clusters studied here. Under these assumptions, if the temperature
increases by a factor of 2 then the luminosity increases by at least a factor of 4 and the mass
by a factor of 3, the amount of mass added to the clusters being on the order of 3 ![]()
![]() .
Since galaxies are thought to make up only about 1/5 of the baryonic mass in clusters (see Loewenstein 2006, and references there in), it is implausible that this mass and additional gravitational energy is added by normal galaxies. This mass and gravitational energy must come instead from the infall of atypical galaxies that have gas masses that greatly exceed their stellar masses or gas clouds that never formed into galaxies. Damped Lyman
.
Since galaxies are thought to make up only about 1/5 of the baryonic mass in clusters (see Loewenstein 2006, and references there in), it is implausible that this mass and additional gravitational energy is added by normal galaxies. This mass and gravitational energy must come instead from the infall of atypical galaxies that have gas masses that greatly exceed their stellar masses or gas clouds that never formed into galaxies. Damped Lyman ![]() absorbers (DLAs) have metallicities that are near solar at z of 1 or higher (Meiring et al. 2007, and references
therein) which makes the ability to add both mass and metals via infalling clouds plausible. It is beyond the scope of this work, though, to carry out detailed calculations of
this infall scenario. However, an implication of the estimates made here is that sight lines on the outskirts of clusters should show the presence of DLAs at the cluster redshift. Furthermore, if mass is added with energy as implied by the L-T and L-M relationships used here, this rules out processes which might provide energy and metals but not significant amounts of additional mass, such as SN or AGNs.
absorbers (DLAs) have metallicities that are near solar at z of 1 or higher (Meiring et al. 2007, and references
therein) which makes the ability to add both mass and metals via infalling clouds plausible. It is beyond the scope of this work, though, to carry out detailed calculations of
this infall scenario. However, an implication of the estimates made here is that sight lines on the outskirts of clusters should show the presence of DLAs at the cluster redshift. Furthermore, if mass is added with energy as implied by the L-T and L-M relationships used here, this rules out processes which might provide energy and metals but not significant amounts of additional mass, such as SN or AGNs.
Instead, suppose that the L-M relationship used here doesn't apply to these high z clusters. In this case, supernovae would still not be a plausible explanation. This is because the energy input of approximately 1064 erg would require an unreasonably high number of SNe when all the available energy is transferred to the ICM (Conroy & Ostriker 2008). For example, suppose there are 1000 galaxies per cluster. This translates into 1010 SNe per galaxy or 101 SNe/year for 109 years. It is also implausible that a central AGN could provide this much heat (1064 erg), as this heat would require 1055 erg/year deposited for 1 Gy, or 1047 erg s-1 minimum energy generation assuming 100% efficiency in transfering energy to heat. Since the magnitude of heating seems beyond what central AGN activity could provide, an infall scenario is a more likely explanation.
5.4 Scenarios for mixing
Since there is no evidence for evolution in every type of cluster considered in this study (as seen in the figures), it will be assumed for the sake of discussion that clusters are not mixing over this range of redshifts.
Beginning with the cool core clusters in Fig. 1, it is seen that they exhibit almost no signs of evolution in their iron abundance profiles from the 0.4-0.9 redshift bin up to the present day, even though there is a very clear gradient at all redshifts. This suggests two possible scenarios: either enrichment and mixing both exist in such a way that neither is dominant, or neither process occurs. If neither process occurs, the unchanging iron abundance profile can be explained as being due to the average cluster galaxy having lost most of its gas by
![]() .
In this case the galaxies have no gas to stir up and mix the ICM. An absence of gas in cluster galaxies would also manifest itself in a low, non-evolving star formation rate (Homeier et al. 2005). A low star formation rate occurs if ram pressure stripping has removed the majority of the gas from most of the cluster galaxies before redshift z = 0.8 within 500 kpc of the cluster center, well within the regions observed in this study. The suggestion that most gas is stripped from
galaxies by
.
In this case the galaxies have no gas to stir up and mix the ICM. An absence of gas in cluster galaxies would also manifest itself in a low, non-evolving star formation rate (Homeier et al. 2005). A low star formation rate occurs if ram pressure stripping has removed the majority of the gas from most of the cluster galaxies before redshift z = 0.8 within 500 kpc of the cluster center, well within the regions observed in this study. The suggestion that most gas is stripped from
galaxies by
![]() was also seen by Dressler et al. (1997); Butcher & Oemler (1984).
was also seen by Dressler et al. (1997); Butcher & Oemler (1984).
As the gradient in iron abundance has remained constant with redshift, there is also no evidence for growth in the gradient. Substantial changes in the abundance gradient would be expected if there was continuous activity from the central AGN. Therefore, energy input to the ICM beyond gravitational infall (Bode et al. 2007) must not have caused appreciable iron enrichment.
For non-cool core and high temperature clusters, there is less statistical evidence to suggest that the iron abundance decreases with radius in the same manner as low temperature cool-core clusters. However, as noted above, it is assumed there is no evolution in the radial profiles of the ICM with redshift. In this case, galactic motion within the cluster does not result in ram pressure stripping, one of the key processes for iron enrichment (and possibly mixing) in the ICM. Without ram pressure stripping from galaxies to enrich or mix the ICM, the iron abundance (and iron abundance profile) of the ICM remains static over long times.
6 Summary and conclusions
Average radial profiles of the temperature and iron abundance of X-ray bright clusters in the redshift range from about 0.14 to 0.9 were calculated. We find no evidence for evolution within similar sets of clusters. The total element abundance remains constant with decreasing z and the gradients remain approximately the same. These observations suggest that gravitational infall is the dominant mechanism for heating of the ICM, and also that ram pressure stripping does not substantially change the ICM out to large redshifts. If clusters experience a significant (factor of 2 or more) amount of gravitational mass infall, then the iron abundance profile remains constant while the overall temperature increases. This infall needs to simultaneously keep the profile (within error of about 20%) isothermal while also maintaining the same iron abundance profile. Mass and energy considerations suggest infall of metal rich gas, but how the process takes place needs further theoretical study. These same considerations of mass and energy suggest that although central AGN activity is directly related to cooling cores, the central AGN does not produce significant amounts of metal rich gas and energy to the ICM beyond its local environment of about 50-100 kpc.
Other theoretical challenges to consider include how clusters formed in the first place with both abundance gradients and isothermal temperature profiles. Work also needs to be done on how the frequency and scale of merger activity (e.g. Wik et al. 2008) changes the abundance and temperature gradients of clusters. Another potentially important aspect of modeling galaxy clusters theoretically appears to be an accurate modeling of the local environment surrounding the cluster, as the infall of material initially outside of the cluster could play an important role in its evolution.
From an observational point of view it will be interesting to measure temperature and abundance
gradients for clusters at z greater than 0.9 as well as make measurements of DLAs by means of QSOs whose sight lines are at ![]() Mpc distances from the centers of rich clusters.
These measurements may help determine more conclusively whether galaxy clusters are evolving
in the ways described here and what kind of material might be falling in to cause the highest temperature clusters of galaxies.
Mpc distances from the centers of rich clusters.
These measurements may help determine more conclusively whether galaxy clusters are evolving
in the ways described here and what kind of material might be falling in to cause the highest temperature clusters of galaxies.
Acknowledgements
This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We would like to thank the Max PlanckInstitut für Kernphysik in Heidelberg, Germany and Le Laboratoire d'Astrophysique de Marseille in Marseille, France for their hospitality. We would also like to thank A. Kathy Romer and Kivanc Sabirli for providing processed XMM data used in the early stages of this analysis. We would also like to thank Wilifried Domainko for his review and suggestions for improvement. We thank the referee for many insightful comments that greatly improved the manuscript. Finally, we would like to acknowledge support from NASA Illinois Space Grant NGT5-40073.
References
- Adami, C., Picat, J. P., Savine, C., et al. 2006, A&A, 451, 1159 [NASA ADS] [CrossRef] [EDP Sciences]
- Allen, S. W., Schmidt, R. W., & Fabian, A. C. 2002, MNRAS, 335, 256 [NASA ADS] [CrossRef] (In the text)
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [NASA ADS] [CrossRef] (In the text)
- Arnaud, M. 2005, in Background Microwave Radiation and Intracluster Cosmology, ed. F. Melchiorri, & Y. Rephaeli, 77
- Arnaud, K. A., Mushotzky, R. F., Ezawa, H., et al. 1994, ApJ, 436, L67 [NASA ADS] [CrossRef] (In the text)
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baumgartner, W. H., Loewenstein, M., Horner, D. J., & Mushotzky, R. F. 2005, ApJ, 620, 680 [NASA ADS] [CrossRef] (In the text)
- Bode, P., Ostriker, J. P., Weller, J., & Shaw, L. 2007, ApJ, 663, 139 [NASA ADS] [CrossRef] (In the text)
- Bonamente, M., Joy, M. K., LaRoque, S. J., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] (In the text)
- Butcher, H., & Oemler, Jr., A. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] (In the text)
- Conroy, C., & Ostriker, J. P. 2008, ApJ, 681, 151 [NASA ADS] [CrossRef] (In the text)
- De Grandi, S., Ettori, S., Longhetti, M., & Molendi, S. 2004, A&A, 419, 7 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Domainko, W., Mair, M., Kapferer, W., et al. 2006, A&A, 452, 795 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dressler, A., Oemler, A. J., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef]
- Dunn, R. J. H., & Fabian, A. C. 2006, MNRAS, 373, 959 [NASA ADS] [CrossRef] (In the text)
- Ettori, S., De Grandi, S., & Molendi, S. 2002, A&A, 391, 841 [NASA ADS] [CrossRef] [EDP Sciences]
- Ettori, S., Tozzi, P., Borgani, S., & Rosati, P. 2004a, A&A, 417, 13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ettori, S., Tozzi, P., Borgani, S., & Rosati, P. 2004b, A&A, 417, 13 [NASA ADS] [CrossRef] [EDP Sciences]
- Fabian, A. C. 1994, ARA&A, 32, 277 [NASA ADS] [CrossRef] (In the text)
- Fabian, A. C., Sanders, J. S., Taylor, G. B., et al. 2006, MNRAS, 366, 417 [NASA ADS] [CrossRef] (In the text)
- Gao, L., Navarro, J. F., Cole, S., et al. 2008, MNRAS, 387, 536 [NASA ADS] [CrossRef] (In the text)
- Gitti, M., & Schindler, S. 2005, Adv. Space Res., 36, 613 [NASA ADS] [CrossRef] (In the text)
- Homeier, N. L., Demarco, R., Rosati, P., et al. 2005, ApJ, 621, 651 [NASA ADS] [CrossRef] (In the text)
- Jones, L. R., Ponman, T. J., Horton, A., et al. 2003, MNRAS, 343, 627 [NASA ADS] [CrossRef] (In the text)
- Kapferer, W., Kronberger, T., Weratschnig, J., et al. 2007, A&A, 466, 813 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kotov, O., & Vikhlinin, A. 2005, ApJ, 633, 781 [NASA ADS] [CrossRef] (In the text)
- Leccardi, A., & Molendi, S. 2008a, A&A, 487, 461 [NASA ADS] [CrossRef] [EDP Sciences]
- Leccardi, A., & Molendi, S. 2008b, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences]
- Loewenstein, M. 2006, ApJ, 648, 230 [NASA ADS] [CrossRef] (In the text)
- Matsumoto, H., Tsuru, T. G., Fukazawa, Y., Hattori, M., & Davis, D. S. 2000, PASJ, 52, 153 [NASA ADS] (In the text)
- Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2008, ApJS, 174, 117 [NASA ADS] [CrossRef] (In the text)
- Meiring, J. D., Lauroesch, J. T., Kulkarni, V. P., et al. 2007, MNRAS, 376, 557 [NASA ADS] [CrossRef] (In the text)
- Mushotzky, R. F., & Loewenstein, M. 1997, ApJ, 481, L63 [NASA ADS] [CrossRef]
- Nousek, J. A., & Shue, D. R. 1989, ApJ, 342, 1207 [NASA ADS] [CrossRef] (In the text)
- Ota, N., Kitayama, T., Masai, K., & Mitsuda, K. 2006, ApJ, 640, 673 [NASA ADS] [CrossRef]
- Ota, N., Murase, K., Kitayama, T., et al. 2008, A&A, 491, 363 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pacaud, F., Pierre, M., Adami, C., et al. 2007, MNRAS, 382, 1289 [NASA ADS]
- Rizza, E., Burns, J. O., Ledlow, M. J., et al. 1998, MNRAS, 301, 328 [NASA ADS] [CrossRef]
- Rosati, P., Borgani, S., & Norman, C. 2002, ARA&A, 40, 539 [NASA ADS] [CrossRef]
- Rykoff, E. S., Evrard, A. E., McKay, T. A., et al. 2008, MNRAS, 387, L28 [NASA ADS]
- Sakelliou, I., & Ponman, T. J. 2004, MNRAS, 351, 1439 [NASA ADS] [CrossRef] (In the text)
- Sanderson, A. J. R., Ponman, T. J., & O'Sullivan, E. 2006, MNRAS, 372, 1496 [NASA ADS] [CrossRef] (In the text)
- Sarazin, C. L. 1988, X-ray emission from clusters of galaxies, Cambridge Astrophys. Ser. (Cambridge: Cambridge University Press)
- Snowden, S. L., Mushotzky, R. F., Kuntz, K. D., & Davis, D. S. 2008, A&A, 478, 615 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stanek, R., Evrard, A. E., Böhringer, H., Schuecker, P., & Nord, B. 2006, ApJ, 648, 956 [NASA ADS] [CrossRef]
- Tozzi, P., Rosati, P., Ettori, S., et al. 2003, ApJ, 593, 705 [NASA ADS] [CrossRef] (In the text)
- Watanabe, M., Yamashita, K., Furuzawa, A., et al. 1999, ApJ, 527, 80 [NASA ADS] [CrossRef]
- Werner, N., Durret, F., Ohashi, T., Schindler, S., & Wiersma, R. P. C. 2008, Space Sci. Rev., 134, 337 [NASA ADS] [CrossRef] (In the text)
- Wik, D. R., Sarazin, C. L., Ricker, P. M., & Randall, S. W. 2008, ApJ, 680, 17 [NASA ADS] [CrossRef] (In the text)
- Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Basic information about Chandra data sets used in this study.
Table 2: Basic information about XMM-Newtondata sets used in analysis.
Table 3: Radial profile parameters for all clusters. The XMM-Newtonclusters are listed first.
Table 4: Average outer extent of the core and counts radius regions in kpc.
Table 5: Observations investigated and not included in this study, along with the reasons they were excluded.
Table 6: Temperature and iron abundance measurements for all clusters by counts region.
Table 7: The eight subsets of the sample used to calculate average temperature and iron abundance profiles.
Table 8:
General information for each cluster: the overall (defined here to be from
![]() )
temperature and iron abundance, the overall luminosity, the total number of counts in the cluster, the calculations relevant to the cooling time, and finally the subset as defined in Table 7.
)
temperature and iron abundance, the overall luminosity, the total number of counts in the cluster, the calculations relevant to the cooling time, and finally the subset as defined in Table 7.
Table 9: Average temperature as a function of counts radius, separated by redshift, temperature and cooling times. Unweighted averages are in parentheses.
Table 10: Average iron abundance as a function of counts radius, separated by redshift, temperature and cooling times. Unweighted averages are in parentheses.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg1.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg482.png) |
Figure 1: Iron abundance as a function of radius for clusters with low temperatures and short cooling times, separated by redshift. The dotted line corresponds to subset #1 (z < 0.4) while the dashed line corresponds to subset #5 (z > 0.4). The solid line is from De Grandi et al. (2004). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg2.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg483.png) |
Figure 2: Iron abundance as a function of radius for clusters with high temperatures and short cooling times, separated by redshift. The solid line corresponds to subset #2 (z < 0.4). The dashed line corresponds to subset #6 (z > 0.4). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg3.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg484.png) |
Figure 3: Iron abundance as a function of radius for clusters with low temperatures and long cooling times, separated by redshift. The solid line corresponds to subset #3 (z < 0.4). The dashed line corresponds to subset #7 (z > 0.4). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09809fg4.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa09809-08/Timg485.png) |
Figure 4: Iron abundance as a function of radius for high temperature clusters with long cooling times, separated by redshift. The solid line corresponds to subset #4 (z < 0.4). The dashed line corresponds to subset #8 (z > 0.4). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


