| Issue |
A&A
Volume 502, Number 3, August II 2009
|
|
|---|---|---|
| Page(s) | 951 - 956 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200912333 | |
| Published online | 15 June 2009 | |
High-resolution spectroscopy for Cepheids distance determination
V. Impact of the cross-correlation method on the p-factor
and the 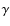 -velocities
-velocities![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
N. Nardetto1 - W. Gieren1 - P. Kervella2 - P. Fouqué3 - J. Storm4 - G. Pietrzynski1,5 - D. Mourard6 - D. Queloz7
1 - Departamento de Astronomía, Universidad de
Concepción, Casilla 160-C, Concepción, Chile
2 - Observatoire de
Paris-Meudon, LESIA, UMR 8109, 5 Place Jules Janssen, 92195 Meudon
Cedex, France
3 - Observatoire Midi-Pyrénées, Laboratoire
d'Astrophysique, UMR 5572, Université Paul Sabatier, Toulouse 3,
14 avenue Edouart Belin, 31400 Toulouse, France
4 -
Astrophysikalisches Institut Postdam, An der Sternwarte 16, 14482
Postdam, Germany
5 - Warsaw University Observatory, AL. Ujazdowskie
4, 00-478 Warsaw, Poland
6 - OCA/CNRS/UNS, Dpt. Fizeau, UMR6525,
Avenue Copernic, 06130 Grasse, France
7 - Observatoire de
Genève, Université de Genève, 51 Ch. des Maillettes, 1290
Sauverny, Switzerland
Received 15 April 2009 / Accepted 14 May 2009
Abstract
Context. The cross correlation method (hereafter CC) is widely used to derive the radial velocity curve of Cepheids when the signal to noise ratio of the spectra is low. However, if it is used with an inaccurate projection factor, it might introduce some biases in the Baade-Wesselink (BW) methods of determining the distance of Cepheids. In addition, it might affect the average value of the radial velocity curve (or ![]() -velocity) important for Galactic structure studies.
-velocity) important for Galactic structure studies.
Aims. We aim to derive a period-projection factor relation (hereafter Pp) appropriate to be used together with the CC method. Moreover, we investigate whether the CC method can explain the previous estimates of the ``K-term'' of Cepheids.
Methods. We observed eight galactic Cepheids with the HARPS![]() spectrograph. For each star, we derive an interpolated CC radial velocity curve using the HARPS pipeline. The amplitudes of these curves are used to determine the correction to be applied to the semi-theoretical projection factor. Their average value (or
spectrograph. For each star, we derive an interpolated CC radial velocity curve using the HARPS pipeline. The amplitudes of these curves are used to determine the correction to be applied to the semi-theoretical projection factor. Their average value (or ![]() -velocity) are also compared to the center-of-mass velocities derived in previous works.
-velocity) are also compared to the center-of-mass velocities derived in previous works.
Results. The correction in amplitudes allows us to derive a new Pp relation:
![]() .
We also find a negligible wavelength dependence (over the optical range) of the Pp relation. We finally show that the
.
We also find a negligible wavelength dependence (over the optical range) of the Pp relation. We finally show that the ![]() -velocity derived from the CC method is systematically blue-shifted by about
-velocity derived from the CC method is systematically blue-shifted by about
![]() km s-1 compared to the center-of-mass velocity of the star. An additional blue-shift of 1.0 km s-1 is thus needed to totally explain the previous calculation of the ``K-term'' of Cepheids (around 2 km s-1).
km s-1 compared to the center-of-mass velocity of the star. An additional blue-shift of 1.0 km s-1 is thus needed to totally explain the previous calculation of the ``K-term'' of Cepheids (around 2 km s-1).
Conclusions. The new Pp relation we derived is a reliable tool for distance scale calibration, and especially to derive the distance of LMC Cepheids with the infrared surface brightness technique. Further studies should be devoted to determining the impact of the signal to noise ratio, the spectral resolution, and the metallicity on the Pp relation.
Key words: techniques: spectroscopic - stars: atmospheres - stars: oscillations - stars: variables: Cepheids - stars: distances
1 Introduction
The Baade-Wesselink (hereafter BW) method of determining the distance of Cepheids was recently used to calibrate the period-luminosity (PL) of Galactic Cepheids (Fouqué et al. 2007). The basic principle of this method is to compare the linear and angular size variation of a pulsating star in order to derive its distance through a simple division. The angular diameter is either derived by interferometry (for e.g. Kervella et al. 2004; Davis et al. 2008) or using the infrared surface brightness (hereafter IRSB) relation (Gieren et al. 1998, 2005a). However, when determining the linear radius variation of the Cepheid by spectroscopy, one has to use a conversion projection factor from radial to pulsation velocity. This quantity has been studied using hydrodynamic calculations by Sabbey et al. (1996), and more recently Nardetto et al. (2004, 2007).
Following the work of Burki et al. (1982), we showed in Nardetto et al. (2006, hereafter Paper I) that the first moment of the spectral
line is the only method which is independent of the spectral line
width (average value and variation) and the rotation velocity of the
star. The centroid radial velocity (
![]() ), or the first
moment of the spectral line profile, is defined as
), or the first
moment of the spectral line profile, is defined as
We thus used this definition of the radial velocity in paper two of this series (Nardetto et al. 2007, hereafter Paper II), to derive a semi-theoretical period-projection factor (hereafter Pp) relation based on spectroscopic measurements with the HARPS high resolution spectrograph. This relation was derived from the specific Fe I 4896.439 Å spectral line which has a relatively low depth for all stars at all pulsation phase (around 8% of the continuum). It was shown that such a low depth value is suitable to reduce the uncertainty on the projection factor due to the velocity gradient between the photosphere (corresponding to angular diameter measurements) and the line-forming region (corresponding to the radius estimation from spectroscopic measurements).
In the cross-correlation method (hereafter CC method), a mask
(composed of hundreds or thousands) of spectral lines is convolved
to the observed spectrum. The resulting average profile is then
fitted by a Gaussian. In such a method, there is first a mix of
different spectral lines forming at different levels (more or less
sensitive to a velocity gradient). Second, the resulting velocity
can be dependent on the abundances or effective temperature (through
the line width), or the rotation of the stars. Third, in Paper III
of this series (Nardetto et al. 2008), we derived calibrated
center-of-mass velocities of the stars of our HARPS sample. By
comparing these so-called ![]() -velocities with the ones found in
the literature (generally based on the CC method) and in particular
in the Galactic Cepheid Database (Fernie et al. 1995), we obtained
an average correction of
-velocities with the ones found in
the literature (generally based on the CC method) and in particular
in the Galactic Cepheid Database (Fernie et al. 1995), we obtained
an average correction of
![]() km s-1. This result shows that
the ``K-term'' of Cepheids stems from an intrinsic property of
Cepheids. But, it shows also that the cross-correlation might
introduce a bias (up to a few kilometers per second) on the average
value of the radial velocity curve.
km s-1. This result shows that
the ``K-term'' of Cepheids stems from an intrinsic property of
Cepheids. But, it shows also that the cross-correlation might
introduce a bias (up to a few kilometers per second) on the average
value of the radial velocity curve.
After a careful definition of the projection factor (Sect. 2), we apply the cross-correlation method to the
Cepheids of our HARPS sample (Sect. 3), in order to
derive a period-projection factor relation appropriate for the CC
method (Sect. 4). As the HARPS pipeline also provides
cross-correlated radial velocities for each spectral order, we take
the opportunity to study the wavelength dependence of the projection
factor law (Sect. 5). Finally, we quantify the impact
of the CC method on the ![]() -velocities (Sect. 6).
-velocities (Sect. 6).
2 Definition of the ``CC projection factor''
In this section, we recall some results obtained in Paper II and we
define the projection factor suitable for the cross-correlation
method. In Paper II, we defined the projection factor as:
where
This relation was then used to quantify the correction (
Table 1: The Cepheids studied listed with increasing period.
The projection factor suitable to the cross-correlation method
(hereafter
![]() )
is then simply:
)
is then simply:
where
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{12333f1.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg39.png) |
Figure 1:
Interpolated radial velocity curves based on the
cross-correlation method are presented for each Cepheid in our
sample. Uncertainties are too small to be seen (around 0.5 km s-1).
The horizontal lines near extrema give an indication of
|
| Open with DEXTER | |
3 The CC method applied to HARPS observations
We consider eight Cepheids which have been observed with the HARPS
spectrometer (R=120 000): R Tra, S Cru,
Y Sgr, ![]() Dor,
Dor, ![]() Gem,
RZ Vel,
Gem,
RZ Vel, ![]() Car, RS Pup. Information
about observations (number of measurements, pulsation phases) can be
found in Paper I.
Car, RS Pup. Information
about observations (number of measurements, pulsation phases) can be
found in Paper I.
We apply the HARPS pipeline to our data in order to calculate the
cross-correlated radial velocities (Baranne et al. 1996; Pepe et al.
2002). The basic principle of the CC method is to build a mask, made
of zero and non-zero value-zones, where the non-zero zones
correspond to the theoretical positions and widths of thousands of
metallic spectral lines at zero velocity, carefully selected from a
synthetic spectrum of a G2 star. A relative weight is considered for
each spectral line according to its depth (derived directly from
observations of a G2 type star). An average spectral line profile is
finally constructed by shifting the mask as a function of the
Doppler velocity. The corresponding radial velocity is derived
applying a classical ![]() minimization algorithm between the
observed line profile and a Gaussian function. The whole profile is
considered in the fitting procedure, not only the line core. The
average value of the fitted Gaussian corresponds to the
cross-correlated radial velocity (hereafter
minimization algorithm between the
observed line profile and a Gaussian function. The whole profile is
considered in the fitting procedure, not only the line core. The
average value of the fitted Gaussian corresponds to the
cross-correlated radial velocity (hereafter
![]() ). The
HARPS instrument has 72 spectral orders. The pipeline provides
). The
HARPS instrument has 72 spectral orders. The pipeline provides
![]() averaged over the 72 spectral orders, or
independently for each order. We first use the averaged values and
the corresponding uncertainties.
averaged over the 72 spectral orders, or
independently for each order. We first use the averaged values and
the corresponding uncertainties.
The
![]() curves are then carefully interpolated using a
periodic cubic spline function. This function is calculated either
directly on the observational points or using arbitrary pivot
points. In the latter case, a classical minimization process between
observations and the interpolated curve is used to optimize the
position of the pivot points (Mérand et al. 2005). For Y Sgr and
RS Pup, pivot points are used due to an inadequate phase coverage.
When the phase coverage is good (which is the case for all other
stars), the two methods are equivalent (Fig. 1). From these
curves we are finally able to calculate
curves are then carefully interpolated using a
periodic cubic spline function. This function is calculated either
directly on the observational points or using arbitrary pivot
points. In the latter case, a classical minimization process between
observations and the interpolated curve is used to optimize the
position of the pivot points (Mérand et al. 2005). For Y Sgr and
RS Pup, pivot points are used due to an inadequate phase coverage.
When the phase coverage is good (which is the case for all other
stars), the two methods are equivalent (Fig. 1). From these
curves we are finally able to calculate
![]() (Table 2). The statistical uncertainty on
(Table 2). The statistical uncertainty on
![]() is set as the average value of the uncertainty
obtained for all measurements over a pulsation cycle of the star.
is set as the average value of the uncertainty
obtained for all measurements over a pulsation cycle of the star.
4 A Pp relation dedicated to the CC method
Table 2:
The projection factor (
![]() )
and the
)
and the
![]() -velocities (
-velocities (
![]() [CC]) derived from the CC
radial velocity curves.
[CC]) derived from the CC
radial velocity curves.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12333f2.ps}\par\includegraphics[width=8.5cm,clip]{12333f3.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg96.png) |
Figure 2:
a) The correction factor
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{12333f5.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg97.png) |
Figure 3:
a) Wavelength dependency of the amplitude of the
cross-correlated radial velocity curves for each star in our sample.
The corresponding linear relation are defined as:
|
| Open with DEXTER | |
From
![]() and
and
![]() obtained for all stars we derive the correction
factor
obtained for all stars we derive the correction
factor
![]() using Eq. (2). The result is
plotted as a function of the period in Fig. 2a. No
particular trend is found. However, the
using Eq. (2). The result is
plotted as a function of the period in Fig. 2a. No
particular trend is found. However, the
![]() correction
factors are clearly statistically dispersed around a mean value of
correction
factors are clearly statistically dispersed around a mean value of
![]() .
.
Following our definition (
![]() ),
the corrected projection factors suitable for the CC method are
given in Table 2. The relation between the period and
),
the corrected projection factors suitable for the CC method are
given in Table 2. The relation between the period and
![]() remains clear according to the statistical
uncertainties:
remains clear according to the statistical
uncertainties:
The corresponding reduced
We have several possible explanations for these results. The cross-correlation induces two biases:
- 1.
- The cross-correlated radial velocities are
derived using a Gaussian fit, making the result sensitive both to
the spectral line width (i.e. the effective temperature and
abundances) and the rotation velocity projected on the line of
sight. These two quantities, independently, and even more the
combination of both, are not expected to vary linearly with the
logarithm of the period. This might explain why no clear linear
relation is found between
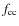 and the period of the
star. However, the mean values of the correction factors (around
and the period of the
star. However, the mean values of the correction factors (around
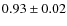 )
have a non negligible impact on the zero-point of
the Pp relation, which decreases from 1.376 to 1.31 (5%).
)
have a non negligible impact on the zero-point of
the Pp relation, which decreases from 1.376 to 1.31 (5%).
- 2.
- The cross-correlation method implies a mix of different
spectral lines forming at different levels. In the Pp relation,
the only quantity sensitive to the line depth is
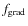 (as defined in Paper II) which compares the amplitude of the
pulsation velocity corresponding to the line-forming region, and the
photosphere. It is thus an estimate of the velocity gradient within
the pulsating atmosphere of the star. The Pp relation was derived
in Paper II for the 4896 spectral line which forms very close
to the photosphere (
(as defined in Paper II) which compares the amplitude of the
pulsation velocity corresponding to the line-forming region, and the
photosphere. It is thus an estimate of the velocity gradient within
the pulsating atmosphere of the star. The Pp relation was derived
in Paper II for the 4896 spectral line which forms very close
to the photosphere (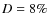 ), while the cross-correlated radial
velocity is a mix of thousands of spectral lines forming at
different levels, with an average depth of around
), while the cross-correlated radial
velocity is a mix of thousands of spectral lines forming at
different levels, with an average depth of around
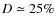 .
The cross-correlation method is thus more sensitive to the velocity
gradient (because the average line depth is large), which may
explain the increase (in absolute value) of the slope from -0.064to -0.08. Moreover, in Paper II we provided a very rough estimate
of the Pp relation associated with the cross-correlation method,
considering only the impact of the velocity gradient (which
means discarding the bias related to the Gaussian fit). We found
.
The cross-correlation method is thus more sensitive to the velocity
gradient (because the average line depth is large), which may
explain the increase (in absolute value) of the slope from -0.064to -0.08. Moreover, in Paper II we provided a very rough estimate
of the Pp relation associated with the cross-correlation method,
considering only the impact of the velocity gradient (which
means discarding the bias related to the Gaussian fit). We found
![$p
= [-0.075 \pm 0.031] \log P + [1.366 \pm 0.036]$](/articles/aa/full_html/2009/30/aa12333-09/img103.png) (see Sect. 7 of
Paper II). The slope we find here (-0.08) is consistent with this
previous rough estimate of -0.075.
(see Sect. 7 of
Paper II). The slope we find here (-0.08) is consistent with this
previous rough estimate of -0.075.
5 Wavelength dependence of the projection factor
With the data at hand, we check for a possible dependence of the
projection factor on the wavelength range used for the
cross-correlation radial velocity measurement. For each order, we
derive the cross-correlated interpolated radial velocity curves, and
then the corresponding amplitudes
![]() .
Orders 59, 68 and 72 are not considered due to
instrumental characteristics and/or unrealistic results. For all
stars,
.
Orders 59, 68 and 72 are not considered due to
instrumental characteristics and/or unrealistic results. For all
stars,
![]() is plotted as a
function of the wavelength, defined as the orders' average values
(Fig. 3a). We find linear relations between these two
quantities:
is plotted as a
function of the wavelength, defined as the orders' average values
(Fig. 3a). We find linear relations between these two
quantities:
where
where
We also find a relation between
![]() and the
logarithm of the period of the star:
and the
logarithm of the period of the star:
From these results we can make two comments. First, the amplitude of the cross-correlated radial velocity curves decreases with wavelength. From hydrodynamical modelling, we know that the spectral lines form over a larger part of the atmosphere in the infrared compared to optical (Sasselov et al. 1990). This effect might help us to understand our result: the more extended the line forming regions are, the lower the amplitude of the radial velocity curves. Second, this effect is greater for long-period Cepheids than short-period Cepheids. A reason might be that the mean radius, the size of the line-forming regions and the velocity gradient increase with the logarithm of the period.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12333f6.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg110.png) |
Figure 4:
Corrections to apply to the
|
| Open with DEXTER | |
Table 3: Coefficients of the linear relations between the amplitude of the radial velocity curve and the wavelength.
In order to quantify the wavelength dependency of the
![]() relation, we define two correction factors
(
relation, we define two correction factors
(
![]() and
and
![]() ). We find the
following correcting relation as a function of the logarithm of the
period:
). We find the
following correcting relation as a function of the logarithm of the
period:
and
The reduced
6 The CC  -velocity and the K-term of Cepheids
-velocity and the K-term of Cepheids
Interestingly, for each Cepheid in our sample, we found in Paper III
a linear relation between the ![]() -velocities (derived using the
first moment method) of the various spectral lines and their
corresponding
-velocities (derived using the
first moment method) of the various spectral lines and their
corresponding ![]() -asymmetries. Using these linear relations, we
provided a physical reference to derive the center-of-mass
-asymmetries. Using these linear relations, we
provided a physical reference to derive the center-of-mass
![]() -velocity of the stars (
-velocity of the stars (
![]() [N08]): it
should be zero when the
[N08]): it
should be zero when the ![]() -asymmetry is zero. These values are
consistent with an axisymmetric rotation model of the Galaxy.
Conversely, previous measurements of the
-asymmetry is zero. These values are
consistent with an axisymmetric rotation model of the Galaxy.
Conversely, previous measurements of the ![]() -velocities found
in the literature (for e.g. Fernie et al. 1995: the Galactic
Cepheid Database, hereafter
-velocities found
in the literature (for e.g. Fernie et al. 1995: the Galactic
Cepheid Database, hereafter
![]() [GCD]) were based on
the cross-correlation method, and by using generally only a few
measurements over the pulsation cycle. These results led to an
apparent ``fall'' of Galactic Cepheids towards the Sun (compared to
an axisymmetric rotation model of the Milky Way) with a mean
velocity of about 2 km s-1. This residual velocity shift has been
dubbed the ``K-term'', and was first estimated by Joy (1939) to be
-3.8 km s-1.
[GCD]) were based on
the cross-correlation method, and by using generally only a few
measurements over the pulsation cycle. These results led to an
apparent ``fall'' of Galactic Cepheids towards the Sun (compared to
an axisymmetric rotation model of the Milky Way) with a mean
velocity of about 2 km s-1. This residual velocity shift has been
dubbed the ``K-term'', and was first estimated by Joy (1939) to be
-3.8 km s-1.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12333f4.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg132.png) |
Figure 5:
|
| Open with DEXTER | |
We aim to understand why such a 2 km s-1 error was obtained before. An
hypothesis is that the cross-correlation method is biased by the
dynamical structure of the atmosphere of Cepheids. To verify this
hypothesis, we have the unique opportunity to compare quantitatively
and in a consistent way
![]() [N08],
[N08],
![]() [GCD] and the
[GCD] and the ![]() -velocities derived from
our HARPS cross-correlated radial velocity curves (hereafter
-velocities derived from
our HARPS cross-correlated radial velocity curves (hereafter
![]() [CC]). The comparison is done by plotting
[CC]). The comparison is done by plotting
![]() [CC] as a function of
[CC] as a function of
![]() [GCD]
and
[GCD]
and
![]() [N08] respectively (Fig. 5). The data
are presented in Table 2 and the resulting linear relations
are respectively:
[N08] respectively (Fig. 5). The data
are presented in Table 2 and the resulting linear relations
are respectively:
and
| (12) |
The reduce
Several conclusions can be drawn. The slope of these relations are
similar and close to one, which means that there is no particular
trend of the ![]() -velocity with the period of the star, or at
least, it remains negligible here. As in Paper III, we find a
systematic difference of
-velocity with the period of the star, or at
least, it remains negligible here. As in Paper III, we find a
systematic difference of
![]() km s-1 between
km s-1 between
![]() [N08] and
[N08] and
![]() [GCD], which is
consistent with the K-term of Cepheids. However, the
[GCD], which is
consistent with the K-term of Cepheids. However, the
![]() -velocities we derive in this Paper using the
cross-correlation method are systematically lower by (
-velocities we derive in this Paper using the
cross-correlation method are systematically lower by (
![]() )
km s-1 than the ones found in the literature (
)
km s-1 than the ones found in the literature (
![]() [GCD]), and they are systematically larger by
[GCD]), and they are systematically larger by
![]() km s-1
than the calibrated center-of-mass velocities (
km s-1
than the calibrated center-of-mass velocities (
![]() [N08]). As a consequence, the cross-correlation method alone cannot
explain alone the K-term. The CC method is sensitive to the
dynamical structure of the Cepheids' atmosphere in such a way that
it is responsible for
[N08]). As a consequence, the cross-correlation method alone cannot
explain alone the K-term. The CC method is sensitive to the
dynamical structure of the Cepheids' atmosphere in such a way that
it is responsible for ![]() 50% of the K-term. An additional term
is required to explain the presence of such offsets in previous
determinations of the gamma-velocity. It could be related, for
instance, to the quality of observations in the past (Joy et al.
1939) or to the different methods used to derive the
50% of the K-term. An additional term
is required to explain the presence of such offsets in previous
determinations of the gamma-velocity. It could be related, for
instance, to the quality of observations in the past (Joy et al.
1939) or to the different methods used to derive the
![]() -velocity (Pont et al. 1994).
-velocity (Pont et al. 1994).
7 Conclusions
By comparing the amplitude of our cross-correlated radial velocity
curves with previous results based on the first moment method (Paper II), we derived a new Pp relation applicable to radial
velocities measured by the cross-correlation method. This relation
is crucial for the distance scale calibration, and in particular to
derive the distances of LMC and SMC Cepheids (Gieren et al. 2005a;
Gieren et al. 2009, in preparation). We also find a slight
dependence of the Pp relation on the wavelength. Considering
our current uncertainties this effect is negligible, but it might
become significant in the near future. The next steps are to test
the impact of the signal to noise ratio, the spectral resolution and
the metallicity on the projection factor. The latter point will
require a large sample of Cepheids with well-measured metallicities.
These studies (including this work) are part of the international
``Araucaria Project'' whose purpose is to provide an improved local
calibration of the extragalactic distance scale out to distances of
a few Megaparsecs (Gieren et al. 2005b). Moreover, the fact that the
cross-correlation method over-estimates the amplitude of the radial
velocity curve and under-estimates the ![]() -velocity (compared
to the calibrated values presented in Paper III) might have some
implications for other kinds of pulsating stars, for e.g. in
asteroseismology.
-velocity (compared
to the calibrated values presented in Paper III) might have some
implications for other kinds of pulsating stars, for e.g. in
asteroseismology.
Moreover, we show in Paper III that the K-term of Cepheids vanishes if one considers carefully the dynamical structure of Cepheid atmosphere. From the results presented in this paper, we can state that the cross-correlation method might not be totally responsible for the K-term found in the previous studies (only 50% seems to be a consequence of the cross-correlation method). There seems to be another contribution whose nature should be investigated.
Acknowledgements
Based on observations collected at La Silla observatory, Chile, in the framework of European Southern Observatory's programs 072.D-0419 and 073.D-0136. This research has made use of the SIMBAD and VIZIER databases at CDS, Strasbourg (France). N.N. and W.G. acknowledge financial support from the FONDAP Center of Astrophysics 15010003, and the BASAL Center of Astrophysics CATA. N.N. acknowledges the Geneva team for support in using the HARPS pipeline.
References
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Burki, G., Mayor, M., & Benz, W. 1982, A&A, 109, 258 [NASA ADS] (In the text)
- Davis, J., Jacob, A. P., Robertson, J. G., et al. 2009, MNRAS, tmp, 244 (In the text)
- Fernie, J. D., Beattie, B., Evans, N.R., & Seager, S. 1995, IBVS No. 4148 (In the text)
- Fouqué, P., Arriagada, P., Storm, J., et al. 2007, A&A, 476, 73 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gieren, W. P., Fouqué, P., & Gómez, M. 1998, ApJ, 496, 17 [NASA ADS] [CrossRef] (In the text)
- Gieren, W. P., Storm, J., Barnes, T. G., et al. 2005a, ApJ, 627, 224 [NASA ADS] [CrossRef] (In the text)
- Gieren, W., Pietrzynski, G., Bresolin, F., et al. 2005b, Msngr, 121, 23 [NASA ADS] (In the text)
- Joy, A. H. 1939, ApJ, 89, 356 [NASA ADS] [CrossRef] (In the text)
- Kervella, P., Nardetto, N., Bersier, D., et al. 2004, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mérand, A., Kervella, P., Coude du Foresto, V., et al. 2005, A&A, 438, L9 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Nardetto, N., Fokin, A., Mourard, D., et al. 2004, A&A, 428, 131 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
- Nardetto, N., Mourard, D., Mathias, Ph., et al. 2007, A&A, 471, 661N [NASA ADS] [CrossRef] (Paper II) (In the text)
- Nardetto, N., Stoekl, A., Bersier, D., et al. 2008, A&A, 489, 1255 [NASA ADS] [CrossRef] [EDP Sciences] (Paper III) (In the text)
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pont, F., Mayor, M., & Burki, G. 1994, A&A, 285, 415 [NASA ADS] (In the text)
- Sabbey, C. N., Sasselov, D. D., Fieldus, M. S., et al. 1995, ApJ, 446, 250 [NASA ADS] [CrossRef]
- Sasselov, D. D., Lester, J. B., & Fieldus, M. S. 1990, ApJ, 362, 333 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
 -velocities
-velocities![[*]](/icons/foot_motif.png)
- Based on observations made with ESO telescopes at the Silla Paranal Observatory under programme IDs 072.D-0419 and 073.D-0136.
- ...
![[*]](/icons/foot_motif.png)
- Tables 4 and 5 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/502/951
- ... HARPS
![[*]](/icons/foot_motif.png)
- High Accuracy Radial velocity Planetary Search project developed by the European Southern Observatory.
All Tables
Table 1: The Cepheids studied listed with increasing period.
Table 2:
The projection factor (
![]() )
and the
)
and the
![]() -velocities (
-velocities (
![]() [CC]) derived from the CC
radial velocity curves.
[CC]) derived from the CC
radial velocity curves.
Table 3: Coefficients of the linear relations between the amplitude of the radial velocity curve and the wavelength.
All Figures
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{12333f1.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg39.png) |
Figure 1:
Interpolated radial velocity curves based on the
cross-correlation method are presented for each Cepheid in our
sample. Uncertainties are too small to be seen (around 0.5 km s-1).
The horizontal lines near extrema give an indication of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12333f2.ps}\par\includegraphics[width=8.5cm,clip]{12333f3.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg96.png) |
Figure 2:
a) The correction factor
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{12333f5.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg97.png) |
Figure 3:
a) Wavelength dependency of the amplitude of the
cross-correlated radial velocity curves for each star in our sample.
The corresponding linear relation are defined as:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12333f6.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg110.png) |
Figure 4:
Corrections to apply to the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12333f4.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa12333-09/Timg132.png) |
Figure 5:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



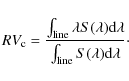
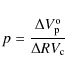
![\begin{displaymath}
p_{\rm cc} = p \frac{\Delta RV_{{\rm c}}[\rm
4896]}{\Delta RV_{\rm cc}} = p f_{{\rm cc}}
\end{displaymath}](/articles/aa/full_html/2009/30/aa12333-09/img37.png)