---

Simultaneous multiwavelength observations of the second exceptional -ray flare of PKS 2155-304 in July 2006

F. Aharonian^1,13 - A. G. Akhperjanian² - G. Anton¹⁶ - U. Barres de Almeida^8, - A. R. Bazer-Bachi³ - Y. Becherini¹² - B. Behera¹⁴ - W. Benbow¹ - K. Bernlöhr^1,5 - C. Boisson⁶ - A. Bochow¹ - V. Borrel³ - E. Brion⁷ - J. Brucker¹⁶ - P. Brun⁷ - R. Bühler¹ - T. Bulik²⁴ - I. Büsching⁹ - T. Boutelier¹⁷ - P. M. Chadwick⁸ - A. Charbonnier¹⁹ - R. C. G. Chaves¹ - A. Cheesebrough⁸ - L.-M. Chounet¹⁰ - A. C. Clapson¹ - G. Coignet¹¹ - L. Costamante ^1,29,31 - M. Dalton⁵ - M. K. Daniel⁸ - I. D. Davids^22,9 - B. Degrange¹⁰ - C. Deil¹ - H. J. Dickinson⁸ - A. Djannati-Ataï¹² - W. Domainko¹ - L. O'C. Drury¹³ - F. Dubois¹¹ - G. Dubus¹⁷ - J. Dyks²⁴ - M. Dyrda²⁸ - K. Egberts¹ - D. Emmanoulopoulos¹⁴ - P. Espigat¹² - C. Farnier¹⁵ - F. Feinstein¹⁵ - A. Fiasson¹⁵ - A. Förster¹ - G. Fontaine¹⁰ - M. Füßling⁵ - S. Gabici¹³ - Y. A. Gallant¹⁵ - L. Gérard¹² - B. Giebels¹⁰ - J. F. Glicenstein⁷ - B. Glück¹⁶ - P. Goret⁷ - D. Göhring¹⁶ - D. Hauser¹⁴ - M. Hauser¹⁴ - S. Heinz¹⁶ - G. Heinzelmann⁴ - G. Henri¹⁷ - G. Hermann¹ - J. A. Hinton²⁵ - A. Hoffmann¹⁸ - W. Hofmann¹ - M. Holleran⁹ - S. Hoppe¹ - D. Horns⁴ - A. Jacholkowska¹⁹ - O. C. de Jager⁹ - C. Jahn¹⁶ - I. Jung¹⁶ - K. Katarzynski²⁷ - U. Katz¹⁶ - S. Kaufmann¹⁴ - E. Kendziorra¹⁸ - M. Kerschhaggl⁵ - D. Khangulyan¹ - B. Khélifi¹⁰ - D. Keogh⁸ - W. Kluzniak²⁴ - T. Kneiske⁴ - Nu. Komin⁷ - K. Kosack¹ - G. Lamanna¹¹ - J.-P. Lenain⁶ - T. Lohse⁵ - V. Marandon¹² - J. M. Martin⁶ - O. Martineau-Huynh¹⁹ - A. Marcowith¹⁵ - D. Maurin¹⁹ - T. J. L. McComb⁸ - M. C. Medina⁶ - R. Moderski²⁴ - L. A. G. Monard³⁰ - E. Moulin⁷ - M. Naumann-Godo¹⁰ - M. de Naurois¹⁹ - D. Nedbal²⁰ - D. Nekrassov¹ - J. Niemiec²⁸ - S. J. Nolan⁸ - S. Ohm¹ - J.-F. Olive³ - E. de Oña Wilhelmi^12,29 - K. J. Orford⁸ - M. Ostrowski²³ - M. Panter¹ - M. Paz Arribas⁵ - G. Pedaletti¹⁴ - G. Pelletier¹⁷ - P.-O. Petrucci¹⁷ - S. Pita¹² - G. Pühlhofer¹⁴ - M. Punch¹² - A. Quirrenbach¹⁴ - B. C. Raubenheimer⁹ - M. Raue^1,29 - S. M. Rayner⁸ - M. Renaud^12,1 - F. Rieger^1,29 - J. Ripken⁴ - L. Rob²⁰ - S. Rosier-Lees¹¹ - G. Rowell²⁶ - B. Rudak²⁴ - C. B. Rulten⁸ - J. Ruppel²¹ - V. Sahakian² - A. Santangelo¹⁸ - R. Schlickeiser²¹ - F. M. Schöck¹⁶ - R. Schröder²¹ - U. Schwanke⁵ - S. Schwarzburg¹⁸ - S. Schwemmer¹⁴ - A. Shalchi²¹ - M. Sikora²⁴ - J. L. Skilton²⁵ - H. Sol⁶ - D. Spangler⁸ - . Stawarz²³ - R. Steenkamp²² - C. Stegmann¹⁶ - G. Superina¹⁰ - A. Szostek^23,17 - P. H. Tam¹⁴ - J.-P. Tavernet¹⁹ - R. Terrier¹² - O. Tibolla^1,14 - M. Tluczykont⁴ - C. van Eldik¹ - G. Vasileiadis¹⁵ - C. Venter⁹ - L. Venter⁶ - J. P. Vialle¹¹ - P. Vincent¹⁹ - M. Vivier⁷ - H. J. Völk¹ - F. Volpe ^1,10,29 - S. J. Wagner¹⁴ - M. Ward⁸ - A. A. Zdziarski²⁴ - A. Zech⁶

1 - Max-Planck-Institut für Kernphysik, PO Box 103980, 69029 Heidelberg, Germany
2 - Yerevan Physics Institute, 2 Alikhanian Brothers St.,375036 Yerevan, Armenia
3 - Centre d'Étude Spatiale des Rayonnements, CNRS/UPS, 9 Av. du Colonel Roche, BP 4346, 31029 Toulouse Cedex 4, France
4 - Universität Hamburg, Institut für Experimentalphysik, Luruper Chaussee 149, 22761 Hamburg, Germany
5 - Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15, 12489 Berlin, Germany
6 - LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 Place Jules Janssen, 92190 Meudon, France
7 - IRFU/DSM/CEA, CE Saclay, 91191 Gif-sur-Yvette, Cedex, France
8 - University of Durham, Department of Physics, South Road, Durham DH1 3LE, UK
9 - Unit for Space Physics, North-West University, Potchefstroom 2520, South Africa
10 - Laboratoire Leprince-Ringuet, École Polytechnique, CNRS/IN2P3, 91128 Palaiseau, France
11 - Laboratoire d'Annecy-le-Vieux de Physique des Particules, CNRS/IN2P3, 9 Chemin de Bellevue, BP 110,74941 Annecy-le-Vieux Cedex, France
12 - Astroparticule et Cosmologie (APC), CNRS, Universite Paris 7 Denis Diderot, 10, rue Alice Domon et Leonie Duquet,75205 Paris Cedex 13; UMR 7164, CNRS, Université Paris VII, CEA, Observatoire de Paris, France
13 - Dublin Institute for Advanced Studies, 5 Merrion Square, Dublin 2, Ireland
14 - Landessternwarte, Universität Heidelberg, Königstuhl, 69117 Heidelberg, Germany
15 - Laboratoire de Physique Théorique et Astroparticules, Université Montpellier 2, CNRS/IN2P3, CC 70, Place Eugène Bataillon,34095 Montpellier Cedex 5, France
16 - Universität Erlangen-Nürnberg, Physikalisches Institut,Erwin-Rommel-Str. 1, 91058 Erlangen, Germany
17 - Laboratoire d'Astrophysique de Grenoble, INSU/CNRS, Université Joseph Fourier, BP 53, 38041 Grenoble Cedex 9, France
18 - Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
19 - LPNHE, Université Pierre et Marie Curie Paris 6, Université Denis Diderot Paris 7, CNRS/IN2P3, 4 Place Jussieu, 75252 Paris Cedex 5, France
20 - Charles University, Faculty of Mathematics and Physics, Institute of Particle and Nuclear Physics, V Holesovickách 2, 180 00
21 - Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
22 - University of Namibia, Private Bag 13301, Windhoek, Namibia
23 - Obserwatorium Astronomiczne, Uniwersytet Jagiellonski, ul. Orla 171, 30-244 Kraków, Poland
24 - Nicolaus Copernicus Astronomical Center, ul. Bartycka 18,00-716 Warsaw, Poland
25 - School of Physics & Astronomy, University of Leeds, Leeds LS2 9JT, UK
26 - School of Chemistry & Physics, University of Adelaide, Adelaide 5005, Australia
27 - Torun Centre for Astronomy, Nicolaus Copernicus University, ul. Gagarina 11, 87-100 Torun, Poland
28 - Instytut Fizyki Jadrowej PAN, ul. Radzikowskiego 152,31-342 Kraków, Poland
29 - European Associated Laboratory for Gamma-Ray Astronomy, jointly supported by CNRS and MPG
30 - Bronberg Observatory, CBA Pretoria, PO Box 11426, Tiegerpoort 0056, South Africa
31 - Stanford University, W.W. Hansen Experimental Physics Laboratory & Kavli Institute for Particle Astrophysics and Cosmology, Stanford, CA 94305-4085, USA

Received 21 March 2009 / Accepted 17 April 2009

Abstract
Aims. The X-ray-TeV connection and the evolution of the emitting particle population is studied in high-energy peaked BL Lac objects, by obtaining spectral information in both bands on sub-hour timescales.
Methods. Simultaneous observations with HESS, and the Bronberg optical observatory were performed on the BL Lac object PKS 2155-304 in the night of July 29-30 2006, when the source underwent a major -ray outburst during its high-activity state of Summer 2006. This event took place about 44 h after the other major outburst of the night of July 27-28, which is known for its ultrafast variability. An unprecedented 6 to 8 h of simultaneous, uninterrupted coverage was achieved, with spectra and light curves measured down to 7 and 2 min timescales, respectively.
Results. The source exhibited one major flare along the night, at high energies. The -ray flux reached a maximum of 11 times the Crab flux (>400 GeV), with rise/decay timescales of 1 h, plus a few smaller-amplitude flares superimposed on the decaying phase. The emission in the X-ray and VHE -ray bands is strongly correlated, with no evidence of lags. The spectra also evolve with similar patterns, and are always soft (photon index ), indicating no strong shift of the peaks in the spectral energy distribution towards higher energies. Only at the flare maximum is there evidence that the -ray peak is inside the observed passband, at 400-600 GeV. The VHE spectrum shows a curvature that is variable with time and stronger at higher fluxes. The huge VHE variations () are only accompanied by small-amplitude X-ray and optical variations (factor 2 and 15% respectively). The source has shown for the first time in a high-energy peaked BL Lac object a large Compton dominance (/ ) - rapidly evolving - and a cubic relation between VHE and X-ray flux variations, during a decaying phase. These results challenge the common scenarios for the TeV-blazar emission.

Key words: galaxies: active - galaxies: BL Lacertae objects: individual: PKS 2155-304 - gamma rays: observations - X-rays: galaxies

1 Introduction

Among blazars, high-energy peaked BL Lac objects (HBL, Giommi & Padovani 1994) are characterized by the highest energy particles and most violent acceleration processes. In the X-ray band, they have shown extreme spectral properties (see e.g., Costamante et al. 2001) and variability (e.g., Mkn 501, Pian et al. 1998). At very high energies (VHE, 100 GeV), doubling timescales as short as a few minutes and flux variations of a factor of 10 in less than one hour have been observed (Aharonian et al. 2007a; Albert et al. 2007). Their spectral energy distribution (SED) is dominated by two broad peaks, located at UV-X-ray frequencies and in the GeV-TeV band. Their overall properties and behaviour have been most successfully - though not exclusively - explained as synchrotron and inverse Compton (IC) emission from a population of relativistic electrons (see e.g., Guetta et al. 2004; Sikora & Madejski 2001; Ghisellini et al. 2002; Spada et al. 2001; Ghisellini et al. 1998, and references therein), which upscatter their own self-produced synchrotron photons (synchrotron self-Compton, SSC; Maraschi et al. 1992; Königl 1981; Bloom & Marscher 1996) or external photons produced by different parts of the jet (Ghisellini et al. 2005; Georganopoulos & Kazanas 2003). Target photons can also be provided by the accretion disk and broad line region (Dermer & Schlickeiser 1993; Ghisellini & Madau 1996; Sikora et al. 1994, BLR,) or by a dusty torus (Sikora et al. 2002; Wagner & Witzel 1995; Sikora 1994). In general, all of these seed photons can contribute significantly to the production of the observed SED, according to their energy density in the comoving frame. In HBL however, the lack of evidence of intense diffuse external fields (both directly from almost featureless optical-UV spectra and from TeV -rays transparency arguments) has favoured the SSC model and external Compton process on photons from different parts of the jet as the most likely channels.

Providing two handles on the one electron distribution responsible for both emissions, simultaneous observations in the X-ray and VHE bands represent both a powerful diagnostic tool and a very stringent testbed for the model itself (Coppi & Aharonian 1999), especially during large flares when the emission from a single region is expected to dominate the SED. Alternatively, hadronic scenarios explain the -ray peak as being produced by ultra high energy protons (  eV; see e.g. Mücke & Protheroe 2001; Aharonian 2000).

Imaging atmospheric Cherenkov telescopes (IACT) provide a unique chance to study rapidly-variable sources at -ray energies, thanks to their large collecting area. Multiwavelength campaigns performed on a few very bright sources (namely Mkn 501, Mkn 421 and 1ES 1959+650) have shown that X-ray and VHE emission are generally highly correlated (e.g., Pian et al. 1998; Djannati-Atai et al. 1999; Sambruna et al. 2000; Giebels et al. 2007; Bazejowski et al. 2005; Krawczynski et al. 2002; Fossati et al. 2008; Aharonian et al. 1999a; Krawczynski et al. 2004; Aharonian et al. 1999b), down to sub-hour timescales with no evidence of significant lags (Fossati et al. 2008; Maraschi et al. 1999; Fossati et al. 2004). Moreover, the correlation seems to tighten when individual flares can be fully sampled (Fossati et al. 2008). These results provide strong support to the idea that both emissions during flares are produced by a single electron population (``one zone'' SSC scenario).

On the other hand, the same campaigns have also unveiled a more complex and puzzling behaviour, which represents a challenge to the SSC scenario. Two main problems have recently emerged:

1)

the X-ray and VHE emissions do not always correlate (e.g., in Mkn 421; Bazejowski et al. 2005). In particular, VHE flares seem to occur also without any visible X-ray counterpart (so-called ``orphan'' flares). The most striking example has been provided by 1ES 1959+650 during the high state of 2002, when a strong (>4 Crab) and rapid TeV flare (7 h of doubling timescale) was not accompanied by detectable variations in the RXTE band (Krawczynski et al. 2004). True orphan events are quite difficult to explain with a standard SSC scenario. However, the generally sparse sampling does not allow the exclusion of lagged counterparts (Bazejowski et al. 2005) or counterparts emerging in a different energy band (Krawczynski et al. 2004).

2)

Mkn 421 exhibited a quadratic relation between VHE and X-ray flux variations during both the rising and decaying phases of a flare (Fossati et al. 2008,2004). This is not expected if the source is in the Klein-Nishina (KN) regime.

A blazar is generally said to be ``in the Klein-Nishina regime'' when the observed -ray emission is produced by TeV electrons which do not upscatter their own self-produced synchrotron photons - since inhibited by the smaller cross-section of the KN regime - but upscatter in the Thomson regime lower-energy photons produced by lower-energy electrons (see e.g., Tavecchio et al. 1998). This condition changes the mapping of the synchrotron and Compton components, so that the two peaks are not produced by electrons of the same energy. In this situation, the VHE emission tends to track the X-ray synchrotron variations only linearly instead of quadratically, although a flare that is achromatically extended over a sufficiently wide energy range can still yield a quadratic increase (Fossati et al. 2008). However, the energy dependence of both synchrotron and IC cooling () prevents this relation during the decaying phase: since higher-energy electrons cool faster than lower-energy electrons, they see a roughly constant seed-photon energy density, resulting in a mostly linear decrease. A quadratic decrease could be achieved by imposing the strict Thomson condition, but that seems to require extremely large beaming factors for Mkn 421 (Fossati et al. 2008; Katarzynski et al. 2005).

To investigate these issues, a multiwavelength study of single flares is essential. Although many efforts have been made to achieve a good sampling, so far the short variability timescales have been difficult to study, because of the lack of sensitivity of the past-generation of IACTs. However, these are extremely interesting timescales: the results of HEGRA on Mkn 421, for example, have already revealed an entire ``zoo'' of intra-night flares with different rise and decay times (Aharonian et al. 2002b), indicative of a complex interplay between acceleration/injection and cooling processes (e.g., Kirk & Mastichiadis 1999)

When the IACT array HESS became operational, a project was therefore developed with specific ToO proposals, to investigate the fast variability timescales with a whole night (6-8 h) of continuous, simultaneous observations during a bright -ray state. To achieve this aim, was chosen because it is the only X-ray satellite capable of a full coverage of the entire HESS visibility window during most of the year, and without the interruptions on sub-hour timescales which are typical of low-orbit satellites. The efforts paid off in July 2006, when the HBL PKS 2155-304 (z=0.116) became highly active at VHE, with a flux level a factor of 10 higher than its typical quiescent flux of 4  10^-11 cm^-2 s^-1 above 200 GeV. PKS 2155-304 is one of the brightest and most studied BL Lacs in the Southern Hemisphere, at every wavelength, and it can be detected by HESS on almost a nightly basis since 2002 (see Aharonian et al. 2005b,a, and references therein).

In the first days of activity, ToO observations were also triggered for other X-ray satellites such as RXTE and Swift, to sample the source behaviour over several days and weeks. Then, in the early hours of July 28 2006, a giant outburst occurred at VHE ( above the quiescent level), with a peak flux of 15 Crab above 200 GeV (corresponding to 9.9 Crab above 400 GeV) and repeated flares with doubling timescales of few minutes (Aharonian et al. 2007a). Unfortunately, this dramatic outburst occurred too early with respect to the already-triggered but not-yet-started X-ray observations (which were acquired from the night after). Therefore, the event of most exceptional variability remained without multiwavelength coverage.

Two days later however, on the night of July 29-30, the source underwent a second major VHE flare, this time in coincidence with our planned Chandra-HESS ToO campaign, and with the further coverage in the optical band provided by the Bronberg Observatory in South Africa. Snapshot observations of few ks were also taken with RXTE and Swift. This second outburst has reached even higher fluxes than the first one (11 Crab above 400 GeV). As a result, in this single night the most dense and sensitive X-ray/TeV campaign to date was obtained, during one of the brightest states ever observed from an HBL at VHE.

This paper focuses on the multiwavelength results of this exceptional night, presenting new optical, X-ray and VHE data. The results of the whole VHE activity of PKS 2155-304 between July and October 2006 will be presented in forthcoming papers, together with the overall multiwavelength coverage.

Since this is a very rich and complex dataset, the data have been divided into several subsets of different time windows, to highlight specific aspects (e.g., different VHE thresholds, integration times, or X-ray coverage). These subsets and their rationale will be introduced in the relevant Sects., but a summary list with corresponding time windows is given in Table 1, for reference. Throughout the paper, the following cosmological parameters are used: H₀ =70 km s^-1 Mpc^-1, , and . Conforming to the convention adopted in all previous HESS publications, unless otherwise indicated, all errors are given at the 1 confidence level for one parameter of interest ( ). For simplicity, in the text the values of MJD are given as MJD MJD-53 900.

2 Observations and data reduction

2.1 HESS

HESS is an array of four Imaging Atmospheric Cherenkov Telescopes located in the Khomas Highlands of Namibia (23S, 15E, 1800 m a.s.l.). Each telescope has a surface area of 107 m² and a total field of view of 5. A camera consisting of 960 photo-multipliers is located at the focal length of 13 m. Each camera images the dim Cherenkov flashes from air-showers of VHE -rays in the atmosphere, collected by its mirrors (for more details about the layout of the telescopes, see Bernlöhr et al. 2003). The camera images are calibrated following the prescriptions in Aharonian et al. (2004). The stereoscopic view of the air showers allows the reconstruction of the direction of the primary -ray with an accuracy of 0.1 following method 1 of Hofmann et al. (1999).

The recorded signal in the field of view is dominated by the constant background from hadronic cosmic rays entering the atmosphere. Most of the hadronic background can be identified from by the shape of the shower images and the arrival direction of the recorded showers. The remaining hadronic background can be statistically removed by estimating it from sky regions with no -ray signal. In the analysis shown here, loose cuts and the reflected background method were applied for background substraction (Aharonian et al. 2006b). Light curve and spectra were derived following the standard HESS analysis also described in this reference.

HESS observed PKS 2155-304 throughout the night of July 29-30. A total of 15 runs (each 28 min long) were taken, all passing the standard quality criteria specified in Aharonian et al. (2006b). The total lifetime after dead-time corrections is 6.58 h. A -ray excess of 32 612 events was detected with a significance of 254 following Eq. (17) in Li & Ma (1983). The excess is point-like, taking into account the point spread function of HESS, with a best fit position of , , consistent with the position of PKS 2155-304 ( ; Ma et al. 1998). Because of the long duration of the observations, the zenith angle of the source varied strongly during the night, going from 53 at the beginning, to 8 at the middle, and back to 50 at the end of the night. Observations at larger zenith angles imply a higher energy threshold of the analysis. For the observations discussed here the energy threshold varies between 200 and 700 GeV for the applied energy reconstruction (Aharonian et al. 2006b). This results in a tradeoff between energy and time coverage for the analysis, as we discuss later.

HESS has a systematic uncertainty in the normalization of its energy scale of 15%. The main source of this systematic error are uncertainties in the atmospheric conditions (for a more detailed discussion see Aharonian et al. 2006b). During the night the atmospheric conditions were stable. This can be verified to timescales shorter than one minute in the overall trigger rate and background rates in regions off the source. The differential energy spectrum of PKS 2155-304 at VHE energies is generally steep, with a photon index of about 3.4 in a power-law model (Aharonian et al. 2007a,2005b,a). The systematic error in the energy scale of the detector therefore transforms into an error of 40% in the overall flux normalization. The systematic error in the slope of differential energy spectra is 0.1 for the photon index (see Aharonian et al. 2006b).

2.2 Chandra

PKS 2155-304 was observed with (Weisskopf et al. 2000) for a total duration of 30 ks with the Low Energy Transmission Grating (LETG) spectrometer coupled with the ACIS-S detector (ObsId 6874; set-up with 1/8 subarray and 6 active chips, for a 0.7 s frametime). Because of difficulties in placing our constrained ToO observation within the schedule, the observation started later than requested, missing the first 1.7 h of the HESS window. Unfortunately, the main flare occurred in the first few hours of the HESS window. As a result, the rising part of the main VHE flare has no X-ray coverage.

Data reduction was performed according to the standard CXC procedures, using the CIAO software version 3.4 with the corresponding Calibration Database CALDB version 3.3.0 and HEASOFT v6.3.2. Event files on timescales as short as 2 min were obtained using dmcopy, which propagates all deadtime corrections correctly. Grating spectra were then extracted with tgextract and their ancillary files were generated with fullgarf for each arm; then added together to obtain the first-order spectrum. The scientific analysis was completed mainly on the first-order spectrum, because of its higher S/N and photon statistics. A check was performed that the centroid of the source obtained from the zero-order image was indeed coincident with the coordinates of the source on the detector. The response matrix was produced using mkgrmf applied to the entire observation, since no difference was found from files created in different epochs during the night. The analysis was optimized and performed only on the continuum properties: the study of the total grating spectrum at its highest resolution is beyond the scope of this paper and is left to future publications. The background and source spectra in each time-bin were then extracted with the tool tg_bkg for use in XSPEC.

The hundreds of spectra (one for each time bin, down to 2-min bins) have been routinely fitted in XSPEC version 11.3.2, using a source model plus photoelectric absorption (wabs), with the equivalent hydrogen column density fixed at Galactic values (  cm^-2; Dickey & Lockman 1990). This is also the value obtained from the best fit to the total exposure with free absorption, to within 1 sigma. The integrated flux and its error were calculated from the spectral fit using the specific error routine in XSPEC. The error in the unabsorbed flux was then obtained from the percentage error of the absorbed fit. The results of this procedure were later checked to be fully consistent with the values from the specific Tcl routine fluxerror.tcl recently provided by HEASARC with XSPEC v12, for calculating the error in the flux from single components of the model. In the following, all X-ray fluxes are quoted as unabsorbed values. The time analysis was also performed using the direct count rate and its error in the energy band of interest, for each time-bin, obtaining fully consistent results. The average count rate observed from PKS 2155-304 in the LETG is 8 cts/s, ranging between 12 and 6 cts/s. These count rates allow the spectra to be extracted down to 2-4 min timescales with typically 1000-2000 counts each. For the observed flux, the grating spectra do not suffer from pile-up problems: the total fraction of piled-up events estimated at the peak of the effective area (1-2 keV) and source peak flux is less than 5%.

One of the calibration issues with the ACIS instrument is the excess absorption seen below 1 keV due to the build-up of contaminants on the optical blocking filter. These contaminants (thought to be carbon compounds) cause a significant absorption in the 0.3-0.4 keV range, which is taken into account by the calibration but which also severely reduces the count rate in that range, yielding very few counts during short exposures. Therefore, for the spectra extracted on 2 and 4 min timescales, the interval 0.3-0.4 keV was excluded from the analysis. At high energies, data were included in the fit up to the energy where positive net source counts were present. As a result, short-timescale spectra were fitted in the range 0.23-0.3 and 0.4-6 keV, while longer-exposure spectra could be fitted from 0.23 to 8-9 keV. The spectra were generally rebinned to have more than 30 counts per bin, using different schemes. A fixed coarse binning was used for all the spectra on short timescales (<7 min). Various checks have shown that, within the uncertainties, the obtained results are independent of the adopted rebinning.

The analysis of the total exposure shows evidence of a slight residual excess absorption in the 0.3-0.4 keV range, not yet fully accounted for by the calibration. The effect is small, and does not affect the fit values significantly. Nevertheless, it was taken into account by simply adding an edge model at the carbon K edge, 0.31 keV, with a fixed value of . These are the best-fit parameters obtained from the fit of the total spectrum (see Sect. 4.2).

2.3 RossiXTE

As part of the ToO campaign for a daily monitoring, RossiXTE (Jahoda et al. 1996) pointed PKS 2155-304 twice during the night of July 29-30, for a total exposure of 2.6 ks (44 min). Figure 2 shows the epochs of the RXTE windows with respect to the overall HESS and light curves, together with the time-windows of the Swift  observation. The latter is analyzed and discussed in Foschini et al. (2007). Since the Swift  passband mainly overlays the  band, we focus only on the RXTE spectrum, to extend the X-ray spectrum in the hard band. The data reduction and analysis were performed using FTOOLS v6.3.2 with the standard procedures and filtering criteria recommended by the RXTE Guest Observer Facility after September 2007. For a more accurate spectral determination, only the PCU2 data were considered. The average net count rate from the source is measured at 6 cts/s/pcu, in the 3-20 keV band.

The RXTE spectrum was then fitted in XSPEC together with the spectrum extracted from the same time window, obtaining a spectral measurement over two decades in energy (0.2-20 keV). Without adjustments, the two spectra have very similar normalizations, indicative of a very good inter-calibration between the two instruments. To obtain the most accurate spectral determination, the RXTE / normalization was fixed at the value measured by fitting the same power-law model in the overlapping energy range (3-7 keV), namely 1.08 (see Sect. 4.2).

2.4 Optical data

Optical observations in the V filter were performed using the 32 cm Schmidt-Cassegrain telescope at Bronberg Observatory, Pretoria, South Africa (see Imada et al. 2008, for details about observations of variable sources with this telescope). After de-biasing and flat fielding, data were analyzed using relative aperture photometry with a K-type star of similar magnitude (12.6). Frames were taken every 30 s and then smoothed over 6 successive data points to calculate the mean value in each bin. Each point of the optical light curve therefore has a time duration of 180 s.

The comparison with the reference star shows that the rise in optical intensity is highly significant. The K-star light curve is constant with an intrinsic scatter in the datapoints - using the same smoothing procedure - of 0.02 mag. The errors were determined from the variance of each 6 successive data points for both the source and reference star. No time variability in the intensity of the reference star is seen. The optical fluxes were corrected for Galactic extinction with  mag.

3 Temporal analysis

3.1 TeV light curves

The measured VHE light curve in two-minute time bins is shown in Fig. 1, divided into five different energy bands. The time coverage increases with threshold energy, due to the aforementioned zenith-angle effect. A full coverage of the observation is thus reached for an energy threshold of 700 GeV, while light curves (and spectra) down to 300 GeV are obtained only for the central five hours of the observing window (see Table 1). The different time windows have therefore been labelled according to the respective energy thresholds (from T200 to T700), for reference.

The source underwent a major flare in the first hours of observation, reaching a peak flux of 9.9  10^-10 cm^-2 s^-1 (>400 GeV) at MJD45.90, corresponding to 11 times the Crab Nebula flux (Aharonian et al. 2006b) above the same threshold. This peak flux is about 20% higher than the peak flux measured during the night of July 27-28, above the same threshold (9 Crab, 8  10^-10 cm^-2 s^-1  > 400 GeV). The fluxes measured in these two nights (July 27-28 and 29-30) are the highest ever observed at VHE from PKS 2155-304. The total amplitude of flux variation during this night was about a factor of 20, above 400 GeV (T400 covers both the highest and lowest flux epochs), similar to the flux variation observed in the night of July 27-28 ().

The main flare seems to occur with similar rise and decay timescales, of the order of 1 h (half-to-maximum amplitudes, measured using a ``generalized Gaussian'' function as in Aharonian et al. 2007a). After the peak, the VHE flux decreased overall during the night reaching its minimum around MJD 46.12, but with two other smaller-amplitude flares superimposed: a short burst around MJD 45.96 of duration 20 min, and a longer flare or plateau between MJD 46.0 and 46.1, with a duration of 2-3 h.

In addition, two further sub-flares are evident in all covered energy bands, around MJD 45.885 and MJD 45.920 (dotted lines in Fig. 1). These structures have a duration of 10 min, similar to the flares of the night of July 27-28. Although there are hints of even shorter variability (few minutes), the significance is limited.

Table 1:   Summary of the subsets of VHE data used in this paper (MJD = MJD-53 900).

3.2 Comparison with X-ray and optical light curves

The combined VHE, X-ray and optical light curves are shown in Figs. 2 and 3. Significant flaring activity is visible in all three bands, but with different amplitudes. To emphasize the specific variability patterns, the vertical scales in Fig. 2 were adjusted differently for each band. Fig. 3 shows instead the light curves on the same flux scale, but with a representation. They correspond to slices of the SED at the three energies of 0.3 TeV, 0.3 keV, and 2.25 eV (i.e. 5500 Å). In this way, it is possible to highlight the overall changes and time evolution SED-wise.

The 0.3 TeV fluxes were calculated from the integrated >300 GeV light curve (T300 window) using the average power-law spectrum measured in the respective epochs (namely, the T300-High spectral index in the high state, and the T300-Low index elsewhere, see Sect. 4.1). The same procedure was used to calculate the 0.3 TeV fluxes from the >500 GeV light curve (T500 window), during the epoch not covered by T300 (empty circles in Fig. 3). A comparison with the results of the >300 GeV light curve in the overlapping window shows that the extrapolation from 500 GeV does not introduce differences of more than 2%. The 0.3 TeV fluxes were then corrected for the absorption effect caused by - interactions with the Extragalactic Background Light (EBL), using the model by Franceschini et al. (2008) (discussed in Sect. 4.1.1). This corresponds to a low density of the EBL, close to the lower limits obtained by galaxy counts. The plotted fluxes therefore can be considered as lower limits to the intrinsic VHE emission of the source. The X-ray fluxes at 0.3 keV were calculated with the same procedure, using the power-law spectrum fitted in each of the individual bins. Anticipating the result that both the VHE and X-ray spectra are steep (; see Sect. 4), the plotted  fluxes - at the low-energy end of the respective passbands - provide an estimate of the emission closer to the respective SED peaks than the fluxes in the hard band.

Several remarkable features can be noted. The first is the huge difference in amplitude between the variations in the three energy bands. In few hours, the VHE flux changed by more than an order of magnitude, whereas the X-ray flux varied by only a factor 2 and the optical flux by less than 15% (the contribution of the host galaxy is negligible, see Sect. 6.3). The source thus shows a dramatic increase in variability with photon energy.

Secondly, the VHE emission dominates the energy output by far in the three bands. In Fig. 3, the comparison between the 0.3 TeV and 0.3 keV fluxes shows the evolution of the Compton dominance of the source, i.e. the ratio of the IC -ray luminosity to the synchrotron power ( ). The -ray luminosity dominates the synchrotron luminosity by a factor 8 close to the flare maximum, evolving rapidly towards comparable levels at the end of the night. This is the first time that such high and rapidly variable Compton dominance is observed in an HBL, irrespective of the choice of EBL density. The swiftness of the changes in the -ray emission and SED properties also underlines the danger in modeling X-ray and VHE data taken even only a few hours apart, during such events. As shown in Fig. 2, both RXTE and Swift  observations occurred when the Compton dominance had already decreased significantly.

Thirdly, despite this difference in amplitude, the X-ray and VHE light curves are strongly correlated, with the X-ray emission following closely the same pattern traced by the VHE light curve (see next section). The optical light curve, instead, does not correlate on short timescales with the other two bands. However, there is a rise of 15% in flux, which appears to begin at the same time as the main VHE flare. A conservative estimate of the chance probability of coincidence - considering only the data of this night - is of the order of a few percent. We discuss in Sect. 8.2 the possible implications if this simultaneity is genuine.

3.3 Inter-band time lags

The degree of correlation and possible time lags between different light curves have been quantified by means of cross-correlation functions. The correlation analysis was performed between X-ray and -ray light curves and between hard and soft energy bands within each passband. As main tool it was used the discrete correlation function (DCF) from Edelson & Krolik (1988). The DCF is especially suited to unevenly spaced data, such as the VHE light curves, which have gaps of a few minutes every 28 min between the stop and start of consecutive runs. The time lags between light curves are determined to be the maximum of a Gaussian plus linear function fitted to the central peak of the DCF. This procedure is robust against spurious peaks at zero time-tag caused by correlated errors (Edelson & Krolik 1988). The error in the measured time lag is determined by simulations. Ten thousand light curves were generated by varying each measured point within its errors. The entire correlation procedure was repeated for each of these simulations, resulting in a cross correlation peak distribution (CCPD). The rms of the CCPD then provides an estimate of the statistical error in the measured time lag (Maoz & Netzer 1989; Peterson et al. 1998). The time binning of the light curves and the DCF introduces an additional systematic error. The latter was estimated to be 30 s by injecting various artificial time shifts into the original VHE photon list, smaller than the duration of the time bins, and by measuring the relative shift of the CCPD.

At VHE, the analysis was performed on the simultaneous light curves between 300-700 GeV and above 700 GeV in two-minute time bins (Fig. 1). This choice yields a good compromise between event statistics, time coverage, and a maximum energy difference between the bands. The resulting time lag between the higher and lower energy band is ( ) s (see Fig. 4). This time lag does not differ significantly from zero, as for the flare of two nights before (Aharonian et al. 2008b), and we derive a 95% confidence upper limit of 129 s. This value was calculated by assuming a Gaussian probability distribution around the measured time lag. The width of the distribution was set to be the linear sum of the statistical and systematic error, to be conservative. Afterwards symmetric intervals around zero were integrated, until a 95% containment was achieved.

In the X-ray band, an analogous procedure was applied. The total light curve was divided into a soft (0.2-1.0 keV) and hard (2.0-6.0 keV) band. Because of the larger errors, in this case 4-min time bins were used. The measured time lag is ( ) s. This value again does not differ significantly from zero, resulting in a 95% upper limit of 482 s.

The cross-correlation analysis between the X-ray and -ray emission was performed on the simultaneous light curves with two-minute time bins shown in Fig. 6 (in the T300-X time window). The resulting cross-correlation is shown in Fig. 5. The two light curves overall are highly correlated, with a maximal correlation of DCF , and no significant lag is found. The time lag of the X-rays with respect to the -ray is ( ) s, yielding a 95% confidence upper limit to a time lag of 208 s. To test whether this result was caused by an averaging of lags with opposite signs, the correlation analysis was also performed on sub-intervals, namely in the interval around the first small flare at MJD 45.96 (MJD45.94-46.0) and after MJD 46.0. The two emissions are again highly correlated (DCF ), with no evidence of time lags. The strong correlation is determined not merely by the overall decaying trend of both light curves, but also by their specific patterns: a DCF max value of 0.7-0.8 is still obtained after whitening the light curves by removal of either a linear or quadratic trend. On the shortest timescales (<4-8 min), however, the VHE light curve shows few small flares apparently not mirrored in the X-ray band (see e.g. MJD45.925 and 46.060 in Fig. 6). Although this might indicate a more complex correlation on the fastest timescales, at present no firm conclusions can be drawn, since the significance of these structures is low.

The correlation analysis was also performed using the task CROSSCOR of the Xronos 5.21 package, which measures the correlation function (CCF) with a direct Fourier algorithm. This algorithm requires a continuous light curve without interruptions, therefore the few gaps were filled with the running mean value calculated over the 8 closest bins (e.g., Ravasio et al. 2004). The results are fully consistent with the DCF analysis, indicating that the small gaps in the VHE light curves - the X-ray light curve is continuous - do not introduce significant distortions for such well sampled data.

The cross-correlation analysis between VHE and X-ray light curves was limited to the strictly simultaneous window, to avoid artifacts in the lag determination due to the different timespans and the light curves characteristics. Because both light curves have each one main flaring feature, the cross-correlation performed on different intervals tends simply to match the maxima of the two emissions in those intervals, irrespective of the smaller amplitude patterns. This would yield an artificial, window-dependent ``lag'' with typically lower correlation values (as is the case here, with a timespan of 3200 s between the maxima of the overall VHE and X-ray light curves and lower DCF/CCF values 0.7).

4 Time-resolved spectral analysis

4.1 VHE spectra

A search for spectral variations in the VHE data was performed by fitting a power-law spectrum to a fixed energy range in fixed time bins. The unprecedented statistics of this dataset allow the sampling in 7 to 14-min bins in the T300 time window (Table 1). On these short integration times, the power-law function gives a statistically good description of the data. The results are shown in Fig. 7. The spectrum generally hardens with increasing flux. The fit to a constant photon index results in a  probability of only 1.6%. These spectra are also used for comparison with the X-ray spectra extracted in exactly the same time bins, and discussed in Sect. 5.

Table 2:   Spectral fit of the measured VHE spectra extracted in different epochs (see Table 1).

Table 3:   Spectral fit of the same VHE spectra given in Table 2, but corrected for EBL absorption (statistical errors only).

A study of the spectral variations was also performed on the T500 dataset, which allows the sampling of a wider time span and in particular of both the rise and decay phases of the main -ray flare. However, the lower number statistics requires longer integration times, yielding a lower time resolution. The result is shown in Fig. 8, where spectra were extracted in 14 and 28 min bins. The spectral variations follow the same pattern as for the T300 spectra, both in time and in the flux-index relation. No significant spectral changes are observed between the rising and decaying part of the flare, with the possible exception of a hardening event that precedes the peak of the -ray emission by 28 min.

The study of the spectral shape in more detail requires higher event statistics. To achieve this, the dataset was divided into similar spectral states, namely a high and a low flux state (T300-High and T300-Low, respectively; see Fig. 7). In addition, spectra were extracted in three other important epochs: a) around the peak of the -ray emission (see Fig. 8), yielding a spectrum with a threshold of 400 GeV (T400-Peak); b) in the central five hours characterized by a threshold as low as 200 GeV (T200 dataset); c) in the epoch simultaneous with the RXTE exposure (T300-RXTE window, 44 min overall, see Table 1), where the combined X-ray spectrum can be measured over 2 decades in energy.

The results of the spectral fits are given in Table 2, with a selection shown in Fig. 9. The spectra present a significant curvature with respect to the pure power-law. The probabilities show that the latter is completely excluded in the high states, and is unlikely in the low state. The spectral curvature is generally well described either by a power-law model with an exponential cutoff around 1 TeV ( ), or a log-parabolic function ( ). Most remarkably, the curvature of the spectrum is strongly variable with time. In particular, the curvature is more pronounced (i.e., the parameter b is larger) in the brightest state and decreases as the source dims. This represents direct proof that the curvature of the VHE spectrum in PKS 2155-304 is also of intrinsic origin, inside the emitting region, and cannot be attributed entirely to - absorption on the EBL or on any local external field that is constant on the observed timescales.

Besides providing the widest energy coverage, the T200 spectrum allows a direct comparison with the spectrum measured during the first exceptional flare on the night of July 27-28. The latter has the same energy threshold (200 GeV) and is well described by a broken power-law ( for and for ) with , , and  GeV. Fitting this function to the T200 spectrum yields almost identical results, of the same break energy, slopes and change in spectral index by (Table 2). This shows that the source was in a similar state, even though the overall average normalization is about 30% lower than two nights before. As for the July 27-28 night, the T200 spectrum is not well fitted by a power-law model with exponential cutoff or a log-parabolic function (F-test >99% compared to the broken power-law). Both functions underestimate significantly the -ray flux at higher energies.

4.1.1 Correction for intergalactic - absorption

The VHE -ray emission from extragalactic sources is expected to be attenuated by photon-photon interactions with the EBL photons in the optical-to-IR waveband. The energy dependence of the optical depth - which is determined by the spectrum of the diffuse background - causes a general steepening of the emitted -ray spectrum, more or less severe according to the energy band considered (see e.g., Aharonian 2001, and references therein). At redshift z=0.116, this effect is substantial and must be taken into account to study the true energy output, spectral properties, and location of the Compton peak in the SED (Aharonian et al. 2005b,2006a). Source diagnostic based on flux or spectral variability, instead, is unaffected, since intergalactic absorption is a constant factor for all purposes related to blazar variability (the diffuse background varies only on cosmological timescales).

The EBL waveband that affects the observed VHE band the most is dominated by the direct starlight emission. To correct for EBL absorption, as reference we adopted the model of the EBL spectral energy distribution by Franceschini et al. (2008), which is based on the emission from galaxies. This model takes into account the most recent results on galaxy properties and evolution and is consistent with both the lower limits from source counts - in the UV-optical (Madau & Pozzetti 2000) as well as near-mid infrared waveband (Dole et al. 2006; Fazio et al. 2004) - and with the upper limits derived from the TeV spectra of high-redshift blazars (Aharonian et al. 2007b,2002a,2007c,2006a). It is similar in shape to both the model by Primack et al. (2005) and the ``low-IR'' calculation by Kneiske et al. (2004). The spectra were corrected by applying the optical depth calculated for the average observed photon energy in each energy bin.

However, it is important to recall that a significant uncertainty in the SED of the EBL still remains, since it could be both lower and higher than assumed: either down to the absolute lower limits given by HST galaxy counts (Madau & Pozzetti 2000) (as in the model by Primack et al. 2005), or up to the upper limits given by TeV blazars (Aharonian et al. 2006a). To estimate this uncertainty in both shape and normalization, we also used the shape of the model by Primack et al. (2005), rescaled to these two levels. In the energy range around the starlight peak (1-3 m), the residual uncertainty in the EBL absolute normalization is of the order of 50% (from 8 to 12 nW m^-2 sr^-1 at 2.2 micron, while our reference model gives 9.4 nW m^-2 sr^-1). This translates into a systematic uncertainty of the order of in the reconstructed -ray spectrum. Namely, the reconstructed spectra (which we call ``intrinsic'') discussed in the following Sects. can actually be up to 0.2 steeper or harder than indicated. When relevant, we take this systematic uncertainty into consideration, but as we show in the following, it does not change the main properties of the -ray spectrum and Compton peak frequency of PKS 2155-304.

4.1.2 Absorption-corrected -ray spectra

For the power-law spectra measured on short timescales (as given in Fig. 7), the intrinsic spectra are again well fitted by a power-law model with a slope that is typically harder by -0.8 (namely, ). The results of the fits to the spectra with higher event statistics are provided in Table 3. Even after correction for the steepening induced by EBL absorption, the -ray spectra show clear evidence of curvature, and the power-law model is excluded with high confidence for all states but the RXTE epoch (which has the lowest exposure). The spectral curvature is well described by either the log-parabolic function or a power-law model with an exponential cutoff around 1-2 TeV, for all spectra, including the T200 dataset.

When a spectrum shows a relatively uniform curvature as in this case, however, the log-parabolic model is generally preferable. It has the advantage of providing a more direct measure of the curvature in the true observed band, whereas the exponential cutoff model tends to match a given curvature in the observed passband by using a specific section of its cutoff region, and pushing the power-law component outside the actual observed range. This often yields artificial values for the slope, which are typically too hard. The log-parabolic fit allows also a straightforward estimate of the location of the SED peak ( , defined by ) from the curvature itself, with a minimum of free parameters. To this aim we used the functional form described in Tramacere et al. (2007), where b and are the independent free parameters instead of b and . The comparison of the curvatures among different states and between the synchrotron and IC components can also provide important clues about the source emission regime (Thomson or KN) and the acceleration mechanisms (Massaro et al. 2006).

By comparing the spectra in the 3 different flux states (T400-Peak, T300-High and T300-Low), one can see that the curvature changes significantly along the night (at a confidence level >99.99%) and so does the Compton peak energy. A clear trend emerges: both the curvature parameter b and increase with the VHE flux. At the maximum of the VHE flare, the spectrum is strongly curved ( ), with the Compton peak estimate at  GeV. As the flux decreases, the curvature flattens (b=0.62 to 0.35), while the IC peak shifts to lower energies (  GeV to  GeV, respectively). A lower/higher EBL level does not change these results substantially: a higher level yields similar curvatures (b=1.4, 0.76, and 0.48, respectively) and slightly higher IC peak energies because of the generally harder spectra ( 0, 370, and 180 GeV, respectively). It is important to recall that the absolute value of the curvature b depends on the particular choice of the EBL spectrum used, but not the trend itself. This trend is opposite to what is generally observed and expected for the synchrotron emission in TeV blazars. For example, in Mkn 421 the curvature b decreases as both and the flux increase (Massaro et al. 2004). We also note that the spectral index  does not correlate (and possibly anti-correlate) with the curvature b, in contrast to what is observed in the X-ray band for this (see next section) and other HBL (Massaro et al. 2004).

4.2 X-ray spectra

The spectra were extracted both by a uniform sampling of the whole exposure, in different time bins (2-4-8-16 min), and strictly coincident with the VHE time bins. The spectra were all fitted using an equivalent hydrogen column density fixed at Galactic values (  cm^-2) with different source models. On short integration times (<1 h), a single power-law model provides statistically good fits for all datasets, while evidence of curvature is found only when larger exposures are considered or a wider energy band is available (for example including the RXTE data).

Table 4:   Fit of the X-ray spectra simultaneous to the VHE data.

The time evolution in the X-ray spectrum during the entire pointing - which extends few hours beyond the end of the HESS observation- is shown in Fig. 10. There is a clear trend of ``harder-when-brighter'' behaviour in the first part of the dataset, corresponding to the decaying phase of the main VHE flare. This behaviour is also followed by the small-amplitude flares, whose paths in the flux-index plane overlap tightly with the overall trend of the decaying phase (Fig. 10 right panel).

However, the relation changes in the last part of the observation (MJD > 46.16): as the X-ray flux starts to increase again, the spectral index continues to soften. This ``softer-when-brighter'' behaviour in the rising phase of a new flare reveals a change in conditions for the emitting region. It is indicative of a slow acceleration/injection process, whose timescale is comparable with the other timescales of the system ( ). The information about the flare then propagates from lower to higher energies as particles are gradually accelerated (Ravasio et al. 2004; Kirk et al. 1998). If the optical variations are indeed associated with the flaring zone, the optical data would support this scenario as well, exhibiting increasing flux just before the X-ray rise at the end of the observation. Together, the two patterns of the X-ray data draw part of a counter-clockwise loop in the flux-index plane (Fig. 10).

Figure 11 shows the spectra of both the total exposure and the RXTE simultaneous window. The results of the fits performed on the HESS -simultaneous datasets are given in Table 4. All datasets correspond to strictly simultaneous windows except for the T300-High spectra, for which the X-ray window does not include the first 10 min of the 1.3-h VHE window above 300 GeV. Since there are no significant spectral changes at VHE in that window, the VHE spectrum can be considered to accurately represent the -ray spectral shape in the X-ray window.

For all spectra in Table 4, there is clear evidence of curvature, and the single power-law model is rejected with high confidence (F-test > 99.99%). The spectra show a continuous steepening towards higher energies up to 20 keV, which is well represented by both a broken power-law and log-parabolic models. A power-law with an exponential cutoff is excluded as well ( ) for the spectra with the highest statistics (T200 and total spectrum). The drop rate in the cutoff region is significantly slower than and also slightly slower than , as indeed expected for the synchrotron emission of a particle distribution with an exponential cutoff (Aharonian 2000).

As is clear from Fig. 10 and Table 4, during all times the X-ray spectrum of PKS 2155-304 remains steep, with a convex shape and no signs of flattening at high energies (as instead found in XMM-Newton observations performed in November 2006; Zhang 2008; Foschini et al. 2008). This means that the peak of the synchrotron emission has not entered the observed energy range at any time, and that there is no sign of the possible emergence of the IC component in the hard X-ray band.

It is interesting to compare the curvature parameters and SED peak location given by the log-parabolic fits. Both the spectral index and the curvature increases (slightly) as the flux decreases. This is also corroborated by the fits of spectra extracted in even shorter intervals at the two extreme of the X-ray flux range (namely T300-Xmax and T400-Xmin). The log-parabolic fit yields and versus and , respectively, for an integrated flux and 1.65   10^-10 erg cm^-2 s^-1. The change in the two spectral parameters, however, is such that the estimate of the location of the SED peak remains basically constant: for all spectra, the synchrotron falls within the range 40-50 eV (with a typical 1- statistical error of 20 eV). In contrast to the behaviour in -rays, in the X-ray band the photon index shows a positive correlation with the curvature b, as typically observed for example in Mkn 421 (Massaro et al. 2004). The absolute values of the curvature are similar to those found for most other HBL (Massaro et al. 2008).

5 X-ray vs. TeV correlations

5.1 Spectral variability

The exceptional -ray brightness observed in this night, coupled with the sensitivity of the HESS array and the continuous coverage provided by , allows the emission in the two bands to be compared with unprecedented time resolution in the spectral domain as well.

Figure 12 shows the simultaneous flux and spectral properties measured in 7 and 14 min time bins, in the T300-X window. Inside this window, the VHE spectral index can be well constrained (0.1) over approximately a decade in energy (0.3-2 TeV). The different binning was chosen to achieve comparable S/N ratio during the night, and as a good compromise between spectral determination at VHE and time resolution (see Sect. 4.1). Both X-ray and VHE spectra have been extracted in exactly the same time bins. The spectra were fitted with a single power-law model, which provides a good fit for each time bin. The integrated energy fluxes were calculated using the specific spectral value measured in each bin.

Two general properties can immediately be noted. The first is that the VHE emission shows a definite correlation with the X-ray emission not only in flux but also spectrally. The spectral evolution follows the same overall pattern in the two bands, although with different amplitudes. The correlation coefficient between the X-ray and -ray spectra is r=0.65, with a probability P<0.1% of a chance correlation.

The second property, as previously illustrated by Fig. 3, is that the source shows amplitude variations much larger in -rays than in X-rays. This is now evident also for the spectra, although not as dramatically as for the flux: the spectral variation at VHE is about 3 times the variations in the X-ray band ( vs. ).

The combination of such large-amplitude variability at VHE with correlated but small-amplitude variations in X-rays yields one of the most striking features of this dataset: the VHE flux varies more than quadratically with respect to the X-ray flux during a decaying phase.

5.2 Cubic relation between X-ray and TeV fluxes

Figure 13 shows the VHE flux as a function of the X-ray flux, in a log-log diagram. The data are divided into three subsets (``A'', ``B'', and ``C'') corresponding to three characteristic epochs: epoch ``A'' covers the first 35 min of the simultaneous window; epoch ``B'' corresponds to the full rise and decay phases of the small-amplitude flare at MJD 45.96; epoch ``C'' covers the remainder of the dataset, corresponding to the broader flare (see Fig. 12).

The data were fitted with a linear relationship in the log-log space ( ), for the total dataset and in each subset separately. The results are reported in Table 5, together with the fits of the same datasets with a finer sampling (4-min bins).

The -ray flux traces the variations in the X-ray flux far more than quadratically, namely approximately as . With the exception of the first few minutes of epoch A, all points lie on a narrow path, also during the small flare on MJD 45.96 (epoch B). In epoch A, instead, the two emissions do not seem to correlate. The lack of correlation is limited to a few points and in a short interval; however, one may speculate whether this is caused by the rapid, low-significance structures in the VHE light curve, which are not evident in X-rays (as discussed in Sect. 3.3).

One of these subflares is indeed present in epoch A around MJD ₀ =45.925 (see Fig. 6), and its exclusion does bring the -ray emission more in line with the X-ray pattern. This type of -ray subflares on top of correlated emissions have been recently envisaged by Ghisellini et al. (2009), but more sensitive instruments are required to draw any conclusions.

In the epochs B and C, the cubic correlation is obtained by considering both the two zones separately and together, for which an even steeper slope of is obtained. This cubic correlation is robust with respect to the inclusion or exclusion of single data points and, in particular, does not depend on the lowest VHE point.

The flux-flux correlation is plotted using the same units for both X-ray and VHE bands, namely the integrated energy fluxes. Compared to previous studies, which used the observed event rates, our approach is more consistent and it is allowed by the good spectral determination in each time bin. However, we remark that the measured relation does not depend significantly on the particular approach used (see discussion in Fossati et al. 2008): a cubic relation is also obtained by using the event rates, both in the VHE band (as photons cm^-2 s^-1) and in the X-ray band (count rate).

The correlation found in the total dataset is less steep than in each subset, while in the B+C epoch it is slightly steeper than for each of B and C separately. This can be caused by a possible shift in the flux-flux paths among different datasets/epochs. While individual paths still obey a specific steep trend, taken together they can produce a flatter (or steeper) envelope. This effect was indeed observed in Mkn 421 (Fossati et al. 2008), when considering data for different days.

During the decaying phase of a flare, a cubic relation between the -ray and X-ray fluxes is not easy to explain even for a source in Thomson condition, if both fluxes sample the emission beyond the respective SED peaks (Katarzynski et al. 2005). It is the first time that such a steep slope has been observed in the history of the X-ray/TeV correlation studies, though indication of a super-quadratic relation was recently reported for Mkn 421 (Fossati et al. 2008), during single flares.

Table 5:   Values of the slope of the correlation . Fluxes integrated over each respective energy band (0.5-5 keV and 0.3-3 TeV) and in strictly simultaneous bins. The parameter is shown for fits performed with two different binnings (4 min and 7-14 min) and over three different intervals, as shown in Fig. 12.

Table 6:   Values of the slope of the correlation , for fluxes integrated over different energy bands, as indicated. The 3-15 keV flux is obtained by extrapolation of the power-law model in the   passband. Fit of the dataset ``B+C'' in the 7-14 min binning.

These correlations have been studied so far mainly with the RXTE -PCA instrument, which samples higher energies than those observed here. If the spectrum changes with the flux, and with a ``harder-when-brighter'' behaviour as in this case, the amplitude of the variations changes with energy, and thus the slope of the correlation can depend on the observed band.

To quantify this effect, we also investigated the flux-flux relation by extrapolating the spectrum in the RXTE band (namely, integrating the best-fit model in the 3-15 keV range), and dividing the VHE range into soft and hard bands (0.3-0.7 and >0.7 TeV, respectively). The result is shown in Table 6. The same cubic correlation observed in and HESS translates into a quadratic relation (in fact quite similar to that observed in Mkn 421) between the hard X-ray and soft VHE bands, while an even steeper slope () is obtained between the soft X-ray band and hard VHE band. We note however that the cubic relation is not simply the effect of a pivoting type of variability seen in different energy bands. The VHE band is closer to the IC peak (i.e. the pivoting point) than the X-ray band to the synchrotron one, thus the X-ray variations should be larger than the VHE ones, in contrast to what is observed. It is the entire IC peak that has actually varied far more than the synchrotron peak, as shown also by the nearly constant and cubic values of the correlation between corresponding bands (i.e., soft-soft and hard-hard, see Table 3).

Comparing these 2006 data (low state) with the X-ray/TeV campaign of 2003 (Aharonian et al. 2005b), the overall brightening in the X-ray (2-10 keV) and VHE (>300 GeV) bands is similar (a factor of 2.7 and 5, respectively), and corresponds to a relation between the two epochs. Thus PKS 2155-304 has varied its overall synchrotron and IC luminosity sub-quadratically on very long timescales, but super-quadratically on intra-night timescales, at least during this major flaring event.

6 Spectral energy distributions

6.1 X-ray/-ray spectra pairs

To highlight the evolution of the SED during the night, a gallery of selected pairings of simultaneous X-ray and VHE spectra is shown in Fig. 14. The scales on both axes are kept the same for both X-ray and -ray energies, to enable visually a correct comparison of the spectral slopes. For reference, a selection of historical observations is also plotted, in particular the data from the first X-ray/TeV multiwavelength campaign performed on PKS 2155-203 in October 2003 (Aharonian et al. 2005b). These data (obtained with RXTE and HESS) correspond to one of the historically lowest states ever observed from this object.

The panels show the SED-snapshots taken in the brightest/hardest state (T300-Xmax), in the faintest/softest state (T400-Xmin), and simultaneously with the RXTE pointing (T300-RXTE). In addition, Fig. 14 also shows the T400-Peak spectrum (i.e., extracted around the maximum of the -ray flare; see Table 3 and Fig. 8). This spectrum unfortunately lacks X-ray coverage (the pointing started a few minutes later), but it corresponds to the brightest -ray emission ever recorded from PKS 2155-304.

Both synchrotron and IC peaks do not shift across the observed passbands, despite the large flux variations. There is no evidence of the dramatic changes displayed by Mkn 501 or 1ES 1959+650. Only at the flare maximum does the Compton peak become visible in the observed passband (between 400 and 600 GeV, depending on the EBL normalization). The X-ray spectrum hardens apparently pivoting around the UV band. This behaviour is typically observed also in Mkn 421, Mkn 501 and 1ES 1959+650, but in these sources the amplitude of the spectral hardening tends to be significantly more pronounced, leading to a shift of the synchrotron peak in the hard X-ray band. In the VHE band instead the behaviour is more complex, since the hardening at higher fluxes is also accompanied by a stronger curvature/cutoff (see Fig. 14, right panel).

The slopes of the X-ray (above 1 keV) and VHE spectra are very similar, going from (0.04) to 2.9 (0.11) between the high and low states. It is also interesting to note that the X-ray spectrum is significantly less curved than the spectrum measured by BeppoSAX during the high state of 1998 (Chiappetti et al. 1999). While the slopes above few keV are quite similar (see Fig. 14), the flare in this night seems characterized by a higher luminosity in the soft X-ray band.

6.2 Compton dominance

The time evolution of the fluxes close to the SED peaks is provided by Fig. 3. As one can see, the / ratio is of the order of 8, but it is rapidly variable - on the same timescales as the flux variations - decreasing to the usual values of 1 in a few hours.

We estimated the Compton dominance using also the more detailed spectral shape obtained for the T300-High dataset, and renormalizing the flux to the 2 and 4-min light curves. Considering the integrated luminosity over a decade in energy, namely 0.3-3 TeV and 0.3-3 keV, the / ratio is 10 in the first minutes of the simultaneous window. Assuming that the cubic trend between -ray and X-ray fluxes is maintained up to the flare maximum (which occurred 25 min before the start of the X-ray observation), one obtains /14 at the flare maximum. The flux at the peak of the SED can instead be estimated from the log-parabolic fit, based on the assumption that the curvature of the spectrum also remains the same outside the observed energy band. Using the aforementioned procedure, one obtains a / 5 in the simultaneous window, increasing to 6 at the flare maximum. The values are lower because the estimate of the synchrotron peak energy (45 eV) locates the X-ray band farther away from the synchrotron peak than the VHE band is from the Compton peak (400-600 GeV).

This is the first time that such high / ratios are observed in an HBL, irrespective of the amount of the intergalactic EBL absorption. While the Compton dominance can be up to 100 in powerful FSRQ, boosted by the IC emission on the intense external photon fields from the disk and the BLR (Ghisellini et al. 1998; Sikora et al. 1994), so far it has been of the order of unity or less in HBL. High Compton dominances in HBL were previously obtained only in the presence of a very high density of the EBL (Aharonian et al. 2002a,2006a), which is now considered very unlikely (Franceschini et al. 2008; Madau & Silk 2005; Aharonian et al. 2006a).

6.3 Overall SED properties

The overall SED of PKS 2155-304 in the highest and lowest states during this night is shown in Fig. 15, together with historical data. To plot the -ray spectral shape in more detail while preserving the amplitude variation, the VHE spectra shown in Fig. 15 are the T300-High and T300-Low average spectra described in Sect. 4.1 (see Figs. 7 and 9), rescaled to match the highest and lowest fluxes in the 4-min light curve. Since within these two subsets, the spectra are compatible with a constant value (see Fig. 7), this procedure should not introduce significant distortions in the VHE spectral shape. For clearer visibility, the SED focuses on data above 10¹¹ Hz, thus excluding the radio frequencies (VLBI range). With the flux and variability timescale (3 h) shown at optical (and higher) frequencies, the synchrotron emission coming from this region becomes self-absorbed already at frequencies below 10¹² Hz, and is thus not expected to contribute significantly in the radio range.

From the results of the log-parabolic fits, it is possible to estimate the peak frequency and luminosity of both the synchrotron and Compton emission. By considering the highest state, the synchrotron and Compton peak luminosities are estimated to be at and  erg/s, respectively, with peak frequencies of 50 eV and 260 GeV. Extrapolating the X-ray data with the observed trends up to the flare maximum, one obtains and  erg/s at 50 eV and 500 GeV, respectively. In the lowest state, instead, the peak luminosities become comparable ( and  erg/s, respectively, at 50 eV and 70 GeV). As discussed in Sect. 4.1, even the lowest possible EBL density does not alter substantially these estimates.

In the optical band, the contribution of the host galaxy is negligible: the host galaxy is resolved in optical (Falomo et al. 1991; Falomo 1996) and NIR (Kotilainen et al. 1998), and found to be a giant elliptical galaxy of M(R)=-24.4. This translates into an apparent using the typical colours for an elliptical galaxy ( V-R=0.61-0.71, Fukugita et al. 1995). The optical flux of PKS 2155-304 is thus always dominated by the jet emission (see e.g., Dolcini et al. 2007): the historical light curves from long-term photometric monitoring in the V band show variations in the range 12.3-13.9 mag (Carini & Miller 1992; Osterman et al. 2007). During this night, the optical flux is very high but still far from the highest fluxes observed from this object.

In the X-ray band, instead, the flux is close to the highest state observed historically, as measured by RXTE -PCA in 1996 ( 1.6  10^-10 erg cm^-2 s^-1, Urry et al. 1999). PKS 2155-304 is observed frequently in the X-ray band, since it is a calibration and monitoring source for XMM-Newton, , and Swift, but was never found at the level observed during this night, in the 2-10 keV band (see e.g. Massaro et al. 2008; Donato et al. 2001). Quite interestingly, the spectrum in the highest state also seems to connect smoothly with the flux and spectrum measured by RXTE -HEXTE in 1996 (Urry et al. 1999, butterfly in Fig. 15). It is also interesting to note that the extrapolation to lower energies of the log-parabolic fit for the average T200 spectrum matches quite well the flux in the optical band.

7 Summary of the main observational findings

Before discussing the implications in the context of blazar physics, it is useful to summarize the main observational findings of this phenomenologically rich dataset.

• Large-amplitude -ray variations are accompanied by small X-ray and optical changes. In a few hours, the -ray flux changes by more than an order of magnitude, reaching a luminosity of 10⁴⁷ erg/s, while the X-ray flux varies by only a factor 2 overall, and the optical V flux by less than 15%.

• The X-ray and -ray emission correlate strongly, overall and on short (sub-hour) timescales. On very short timescales (few minutes), the behaviour might be more complex.

• There is no evidence of time lags between the X-ray and -ray emissions, with a 95% upper limit of 3 minutes for the overall light curve. In addition, no lags are found between the hard and soft energies of each passband.

• The optical light curve shows a 15% rise that appears to start simultaneously with the -ray flare, but develops on much longer timescales, reaching a plateau about 2 h later than the VHE peak. The optical emission does not show any correlation with the other two bands on short timescales.

• When correlated, the -ray flux decreases as the cube of the X-ray flux ( 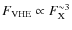). This cubic relation holds both during the overall decaying phase and considering shorter intervals separately.

• The X-ray and -ray (>300 GeV) spectra correlate as well, following similar patterns in their time evolution, but again of different amplitudes. The VHE variations ( 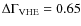) are wider by a factor of 3 than those in the X-ray band ( ).

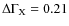• The -ray spectra are significantly curved, and the curvature changes with time, in correlation with the flux state: the higher the flux, the more curved the spectrum (the curvature parameter b goes from 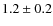at the maximum to 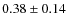in the low state).

• The synchrotron and Compton peaks show no strong shift in frequency across the observed bands, despite the dramatic luminosity changes ( the quiescent state, in this single night), remaining close to their historical values. From the curvature of the spectra, the synchrotron peak can be estimated at 40-50 eV constantly along the night, while the Compton peak shifts from  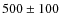GeV at the maximum to 70⁺¹¹⁰_-10 GeV at the end of the night (uncertainties given by the range on the EBL normalization).

• A very large Compton dominance is observed ( 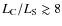). This is the first time that such a high ratio is seen in an HBL, irrespective of the level of intergalactic EBL absorption. However, it also evolves rapidly, decreasing in a few hours to the more usual values of 1.

• X-ray and VHE spectra shows a similar ``harder-when-brighter'' behaviour in the simultaneous window. The X-ray data alone also sample the start of another flare, characterized instead by a ``softer when brighter'' behaviour.

8 Discussion

The results obtained from this campaign seem to both corroborate and challenge the one-zone SSC interpretation at the same time.

On the one hand, the strong correlation between variations in the X-ray and VHE bands - the emission follow the same variability patterns in terms of both flux and spectrum, and without apparent lags - do indicate that the same particle distribution, in the same physical region, is likely responsible for the activity in both energy bands. The simultaneity of the occurrence of the optical and VHE flares also suggests that the emission in all three bands is responding to the same flaring event.

On the other hand, the cubic relation during the decaying phase cannot be easily accounted for within a one-zone SSC scenario. This is shown for example by Katarzynski et al. (2005), who investigated the different X-ray/VHE correlations achievable in a one-zone SSC scenario, for a plausible range of physical parameters and considering all possible combinations of fluxes from both sides of the SED peaks. The relation between X-ray and -ray fluxes when both bands sample the emission above their respective SED peaks is typically less than quadratic. Even imposing the Thomson condition for the IC scattering of X-ray photons, which in this case would require the extreme values of and  mG (see next par.), at most a quadratic relationship can be obtained, but not in the decaying phase if the latter is due to radiative cooling. In general, correlations steeper than quadratic (cubic or even more) are indeed possible, but only when the X-ray band corresponds to frequencies below or close to the synchrotron peak, as in the case of the 1997 flare of Mkn 501 (see e.g., Tavecchio et al. 2001).

A further ingredient is therefore needed to obtain a cubic relation, in a one-zone SSC scenario. It is important to remind here that ``one-zone'' does not mean the request that the entire SED is produced by a single zone. It is generally understood that the SED is always formed by the superposition of radiation from different zones along the jet, both in space (e.g., the radio emission has to come from a much larger region than for the rapidly variable X-ray or optical emission, to avoid synchrotron self-absorption) and in time (multiple injections). What is generally tested with a ``one-zone scenario'' is the hypothesis that at any given time - but during large flares in particular - it is one single region or population that dominates the entire radiative output, determining both peaks of the SED. This scenario has been very successful in explaining so far the spectral and temporal properties of blazars, both among different objects and in single sources during large flares (e.g., Mkn 501, 1ES 1959+650). We now consider if this can also be the case for this flare of PKS 2155-304.

8.1 One-zone SSC analysis

8.1.1 Thomson condition and beaming factor

In a single-zone, homogeneous SSC model, the knowledge of the frequencies of the synchrotron and Compton SED peaks ( and , respectively), their luminosities ( and ), and the requirement of Thomson condition for X-ray photons () form a closed system of three equations in the unknown variables (beaming factor), B (magnetic field), and R (size) of the emitting region (see e.g., Katarzynski et al. 2005, Appendix A). These values can then be compared with the size of the emitting region obtained from variability timescales ( ), and with the condition that the cooling times of the electrons emitting at the peak ( ) is equal to or shorter than the variability timescales (namely, ; see e.g., Tavecchio et al. 1998).

With the parameters measured for this flare (  eV,  TeV,  erg/s,  erg/s), the Thomson limit for photons in the middle of the passband ( keV) requires that ,  mG and  cm. This solution seems unrealistic: besides the quite extreme values of the beaming factor and severe efficiency problems, it is not consistent with the VHE spectra. The Thomson -ray spectrum should extend to 10 TeV with the same slope shown by the X-ray spectrum up to 1 keV, in contrast to observations.

For electrons emitting at the SED peaks, instead, PKS 2155-304 is almost certainly in the Thomson regime. The Thomson regime is already satisfied for , but the condition of transparency for 1-TeV photons (see e.g., Begelman et al. 2008; Dondi & Ghisellini 1995) requires , adopting for reference the variability timescale of the main -ray flare (  h). The Thomson regime for the SED peaks is also indicated by the absence of a significant change of (<) in the presence of an inferred shift of . Since in the KN regime the ratio , the change in should have been accompanied by an increase in by (vs. in Thomson), bringing it well within the band.

Therefore, the SED peaks of PKS 2155-304 are in the Thomson regime, but a part of the passband is most likely affected by KN effects. With , consistency between the size of the emitting region estimated from both the observed Compton dominance and the variability timescale is obtained, yielding  cm,  mG and a Thomson condition at  keV. This is also the result obtained by an analysis on the  plane following the analytical approach described in Tavecchio et al. (1998).

However, this solution is not consistent with the cooling times of the peak electrons being equal to or shorter than the escape timescales. Because of the low values of the magnetic field and high beaming factors, in all the above cases the energy of the electrons cooling within the variability timescale ( ), either by synchrotron or IC, is extremely high, namely . This value is well above , meaning that the whole electron distribution up to the energies sampled by our observations did not have time to cool.

In the one-zone frameset, therefore, the peaks of the SED cannot be explained by radiative cooling. This result is quite different from all previous estimates for the SSC parameters in PKS 2155-304, and is mainly due to the increase by a factor 10 in the separation between the synchrotron and Compton peak frequencies.

8.1.2 Expanding blob

An intriguing possibility is to explain the observed decrease of both synchrotron and IC emission as adiabatic cooling due to a rapid expansion of the emitting region from an initially very compact size (``explosion''), with the total number of particles N roughly constant. This hypothesis has two immediate advantages: 1) it accounts for the initial high value of the Compton dominance as well as its rapid decrease (since in the Thomson limit , where is the average over the electron distribution, see e.g. Ghisellini & Tavecchio 2008b); 2) it can explain in a natural way the change of curvature of the VHE spectra through a change of internal transparency to - interactions.

The initial region cannot be too compact, or otherwise it would not be transparent to -ray photons. However, in the case of PKS 2155-304, the steep and curved VHE spectra can allow for a moderate amount of possible internal absorption to be considered ( -2, as obtained for example with -40), without requiring anomalous spectral shapes. The optical depth increases with -ray photon energy as , where is the energy spectral index of the synchrotron target photons ( ; ), and has a radial dependence R^-2, for a constant N. Therefore, internal absorption can explain the stronger curvature in the brightest state and a rapid expansion would decrease the optical depth making the -ray spectrum less curved at lower fluxes, as observed. In fact, the observed change of curvature is opposite to that expected from radiative cooling (e.g., Massaro et al. 2008), though it could also be due to a change of the maximum electron energy.

To obtain the cubic correlation, however, one must assume correlated variations of a second parameter, in order to shift the radiative output from the IC to the synchrotron channel. This can be achieved by varying the magnetic field B (see e.g. Coppi & Aharonian 1999): for a given particle injection, an increase of the magnetic field can lead to a reduction (B^-2) of the flux of the inverse Compton -rays while increasing the synchrotron emission.

Using the same formalism as in Katarzynski et al. (2005), it is possible to find the relation that yields . The evolution of the radius R and magnetic field Bcan be parameterized as R=R₀ (t/t₀)^r and B=B₀ (t/t₀)^-m (see also Atoyan & Aharonian 1999). The adiabatic losses sustained by the particles during the expansion are taken into account. With the values for the spectral indices before and after the synchrotron peak of (assumed for the optical spectrum) and (as measured in the X-ray band), respectively, a cubic correlation is obtained with (0.1 considering between 0.5 to 0.9). Namely, the magnetic field must increase as the blob expands at a rate , and on the same timescales as the flux variations. This implies that the total energy of the magnetic field in the region must increase substantially, as . Thus it should be created either locally (presumably by turbulent dynamo effects) or supplied from outside (see e.g., discussion in Atoyan & Aharonian 1999).

However, such strong and rapid amplification of the magnetic field seems not consistent with the optical data. Rapid variations of B within the emitting region are also bound to affect the synchrotron emission before the peak, produced by particles not yet cooled. With the previous parameters, the observed decay of a factor 2 in the X-ray band would cause a decrease of the optical flux by 15% (compare vs. in Katarzynski et al. 2005), and on the same timescales as the X-ray and VHE variations. This disagrees with the optical light curve, which is still slightly rising (by 5%) and then remains basically constant during the overall X-ray/VHE decay (see Fig. 2). While it might be possible to further trim this scenario to cancel out any variation in the optical band, this would require an extreme fine-tuning.

For all of these reasons, it is very unlikely that both of the peaks in the PKS 2155-304 SED during this night are produced by the synchrotron and SSC emission of one single zone.

8.2 Two-SED scenario

A simpler and possibly more realistic explanation is provided by the superposition of two SEDs, produced by two different emitting zones. The first is responsible for the usual ``persistent'' SED of PKS 2155-304, which, presumably, peaks in the UV and at a few tens GeV, but with rather low VHE fluxes. It is typically variable on longer timescales (0.2-1 days), as shown for example by the long ASCA, BeppoSAX , and XMM-Newton observations (Zhang et al. 2006,2002; Tanihata et al. 2001). The second zone is responsible for the dramatic flaring activity of this night, and most likely of all the active period of July-August 2006. It needs to be much more compact and have higher bulk motion to account for the much faster variability timescales (0.05-1 hrs). The true variations of the X-ray emission from this second zone can therefore be as large as the -ray ones, but they are simply seen diluted in the ``persistent'' component, which have comparable or higher synchrotron fluxes. These variations are instead fully visible in the VHE band because there the contribution of the standard SED is at much lower fluxes.

A two-zone scenario is rather common for explaining major flares in blazars. The main novelty of this event with respect to all previous HBL flares is that the bulk of the luminosity of the new component is now emitted in the Compton channel instead of the synchrotron channel. The synchrotron emission of this flare is not bright enough to ``break through'' the persistent emission and thus dominate both peaks of the SED.

Within this scenario, one can try to estimate the SED of this new component at its brightest state during the simultaneous observations, assuming that the flux of the persistent component is roughly constant. This is shown in Fig. 16. In the -ray domain, the flux of the persistent component is supposed to be negligible with respect to the observed flare. The spectrum of the flaring region is therefore given, to a first order, by the highest VHE state directly observed (the same as in Fig. 15). In the optical band, at the maximum of the flare the detected variation is 15%, so the flux in the flaring zone should be 0.15 of the observed flux. In the X-ray band, we have used the lowest-state spectrum observed at the end of the night as background file for the highest-state spectrum. As a result, a spectrum with flux F_0.5-5=1.98   10^-10 erg cm^-2 s^-1 is obtained, which is well fitted by a log-parabolic model with and curvature . This gives the estimate for the synchrotron peak position around 0.4 keV, which is also consistent with the optical flux being much lower than the X-ray flux (see Fig. 16).

This underlying SED yields comfortable values for the synchrotron-Compton modeling, and becomes consistent with the peak being due to radiative cooling. Such scenario also agrees with the spectral variations being larger in the VHE band than in the X-ray band (for the same diluting effect), and would naturally account for the behaviour of the optical data as well, if the optical rise is indeed associated with the VHE flare. The optical band would be reacting to the electron injection in the rising phase but not in the decaying phase, due to the much longer cooling times. The variations at VHE can then be allowed to scale linearly or quadratically with the X-ray variations, as required by the specific modeling.

8.3 Diagnostic of the flaring region

Although the amplitude of the synchrotron variations of the new component is unknown, important constraints can still be derived on its properties in both cases of a quadratic or linear relationship between X-ray and -ray fluxes.

With the new parameters, a quadratic decay obtained through radiative cooling is readily possible with a pure SSC scenario because the peak of the synchrotron emission falls now directly within the passband. Indeed a solution in the Thomson regime can be obtained with the comfortable values of ,  Gauss, and . However, the high Compton dominance requires the emitting region to be very compact, with  cm. The flare therefore would originate in a region whose size is of the same order as the Schwarzschild radius of the putative central black hole, which is estimated to be (see discussion in Aharonian et al. 2007a).

If instead the X-ray flux scaled linearly with the VHE flux, it implies that the new component has a high Compton dominance (20) constant in time, during all flux variations. This behaviour points towards an origin of the -ray peak from external Compton emission rather than a pure SSC mechanism.

This is indeed expected in scenarios with a strong radiative interplay between different parts of the jet, such as the ``Needle/Jet'' model proposed by Ghisellini & Tavecchio (2008a): a compact and fast region moving throughout a larger jet sees the dense target field produced by the latter (which is thought to be responsible for the persistent SED), boosting significantly its Compton emission. Unlike the way it is envisaged by the authors, however, the SED of such needle should also contribute significantly in the X-ray band, in order to explain the small-amplitude but correlated variability. Alternatively, the dominant seed photons could come from regions further down inside the jet, where the flow has already strongly decelerated (i.e., at the VLBI scale, Piner & Edwards 2004; Georganopoulos & Kazanas 2003), or by circumnuclear radiation fields if the flaring region is close to the central engine. In the latter case, - interactions with these photon fields could leave a distinct absorption feature imprinted onto the broad-band -ray spectrum (Aharonian et al. 2008a), which the combined observations with Fermi-LAT  and IACT might be able to reveal (Costamante et al. 2007). More complex models with several interacting zones or jet stratification have also been developed, and recently applied to the variability of PKS 2155-304 in 2006 (see e.g. Katarzynski et al. 2008; Boutelier et al. 2008). They seems capable of reproducing some features of the present observations (e.g., Boutelier et al. 2008).

8.4 New mode of flaring in HBL

On a more general basis, it is interesting to compare this flare of PKS 2155-304 with the other major flaring events observed in both X-ray and VHE bands, namely from Mkn 421 in 2000 (Fossati et al. 2008), Mkn 501 in 1997 (Krawczynski et al. 2002; Tavecchio et al. 2001) and 1ES 1959+650 in 2002 (Krawczynski et al. 2004).

There are many common traits: they all display a pre-flare, ``persistent'' SED with the synchrotron emission peaking in the UV/soft-X-ray band, a steep X-ray spectrum that hardens during the flare pivoting around the UV/soft-X-ray band, and a flare luminosity approximately one order of magnitude higher than the typical source luminosity. The mechanisms and properties of the flare injection thus seem common. It is the radiative output that now differs significantly.

In the previous events, such a high luminosity was emitted mostly through the synchrotron process, leading to a dramatic shift of the peak position in the SED according to the new peak frequency of the emerging component. The typical Compton luminosity, even at the flare maximum, has always been equal to or less than the synchrotron power (using the same EBL model for all sources). In this event, instead, the bulk of the flare luminosity is emitted through the Compton channel, yielding only minor modifications of the overall synchrotron emission.

A bimodality therefore seems to emerge in the mode of flaring for HBL: either synchrotron dominated or Compton dominated, with the most extreme example possibly being provided by the ``orphan flare'' event of 1ES 1959+650, which likewise occurred during one single night (June 4, 2002).

It is intriguing to note that this difference might simply depend on the environment, namely on the location of the flaring zone with respect to the region responsible for the persistent SED: if the new injection/flare is taking place far away, there is little radiative interplay between the two zones, leading to a typical SSC-type flare. When the flare occurs close to it, or close to the black hole where external fields are more intense, the outcome is external Compton-dominated flares. More campaigns targeted on the intra-night variability are needed to address this issue, but the diagnostic potential on the jet structure and the location of the ``-ray zone'' is very promising.

9 Summary and conclusions

A full night of simultaneous, uninterrupted observations in the optical, X-ray and VHE bands was performed during an exceptionally bright state of PKS 2155-304 in July 2006. A sampling of both light curves and spectra with unprecedented detail is obtained. For the first time among HBL, a high Compton dominance is observed, with a peak luminosity reaching 10⁴⁷ erg/s. The variations in the X-ray and VHE bands are confirmed to be highly correlated, both in flux and spectrally, but they follow a cubic relationship during the decay phase. Homogeneous one-zone SSC scenarios do not provide a consistent explanation for both the observed SED and the variability behaviour, indicating that a single particle population cannot be responsible for both peaks of the SED during this night.

We have interpreted the data as the emergence of a new component in the SED, strongly Compton-dominated and thus without enough luminosity in the synchrotron channel to overcome the ``persistent'' emission of PKS 2155-304. This new component must be either very compact - of the order of the Schwarzschild radius of the putative central black hole (10⁹ ) - if the emission mechanism is pure SSC, or external-Compton dominated, as would be expected in models with a strong radiative interplay between different parts of the jet.

The richness and quality of the data obtained from this exceptional campaign provide a fundamental testbed for a time-dependent treatment of the emission scenarios, which is needed to fully extract the information on the physical conditions in the source (see e.g., Krawczynski et al. 2002; Boutelier et al. 2008; Coppi & Aharonian 1999). This is beyond the scope of this paper, and therefore left to future studies, but it is a necessary step forward with respect to more common parametric fits, which simply postulate the prompt electron spectrum and treat different states as uncorrelated emissions.

From an observational point of view, the results from this night raise the bar for the requirements of future multiwavelength campaigns on HBL, at least during major flaring events. With flares as rapid as a few minutes (Aharonian et al. 2007a) and flux changes of 1 order of magnitude in less than an hour, sufficiently long, continuous and strictly simultaneous observations are mandatory for a meaningful analysis. Delays, gaps, or mismatches in the simultaneous coverage, even as short as 30 minutes, can be fatal for the diagnostic potential. The multiwavelength coverage should also care to sample the SED on both sides of the emission peaks: as shown in the present case, without the optical light curve some scenarios could not be excluded. In this respect, Fermi-LAT will provide the missing piece of information on the -ray hump for many objects, though typically on longer timescales. The all-sky monitor provided by this observatory will be of great importance to catch the brightest Compton-dominated flares among HBL, triggering X-ray and IACT observations and thus allowing the study of this apparent flare bimodality (synchrotron or Compton-dominated) on a larger sample.

The flaring activity of PKS 2155-304 in July 2006 demonstrates in a compelling way that the fast, intra-night variability is of fundamental importance to gain insights into the acceleration mechanism, emission processes, and location and environment of the emitting regions, which are simply lost or smeared out with a sparser, long-term sampling. The final goal is to achieve full multiwavelength coverage of large-amplitude and ultra-rapid events such as those observed on the night of July 27-28.

Acknowledgements

The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of HESS is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. The authors thank the team for the help and support during the prompt response to our ToO request, as well as the RXTE and Swift  teams. The authors wish to thank P. Coppi, G. Ghisellini and F. Tavecchio for the support during the initial phases of the project. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.

References

• Aharonian, F. 2000, New Astron., 5, 377 [NASA ADS] [CrossRef]
• Aharonian, F. 2001, in International Cosmic Ray Conference, International Cosmic Ray Conference, ed. S. Plueschke, M. Cervino, R. Diehl, K. Kretschmer, D. H. Hartmann, & J. Knoedlseder, 27, I250 (In the text)
• Aharonian, F., Akhperjanian, A. G., Barrio, J. A., et al. (HEGRA Collaboration) 1999a, A&A, 349, 29
• Aharonian, F., Akhperjanian, A. G., Barrio, J. A., et al. (HEGRA Collaboration) 1999b, A&A, 349, 11
• Aharonian, F., Akhperjanian, A., Barrio, J., et al. (HEGRA Collaboration) 2002a, A&A, 384, L23
• Aharonian, F., Akhperjanian, A., Beilicke, M., et al. (HEGRA Collaboration) 2002b, A&A, 393, 89 (In the text)
• Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. (HESS Collaboration) 2004, Astropart. Phys., 22, 109 (In the text)
• Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. (HESS Collaboration) 2005a, A&A, 430, 865
• Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2005b, A&A, 442, 895
• Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2006a, Nature, 440, 1018
• Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2006b, A&A, 457, 899 (In the text)
• Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2007a, ApJ, 664, L71
• Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (HESS Collaboration) 2007b, A&A, 473, L25
• Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (HESS Collaboration) 2007c, A&A, 475, L9
• Aharonian, F., Khangulyan, D., & Costamante, L. 2008a, MNRAS, 387, 1206 [NASA ADS] [CrossRef] (In the text)
• Aharonian, F., et al. (HESS Collaboration) 2008b, Phys. Rev. Lett., 101, 170402 (In the text)
• Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 669, 862 [NASA ADS] [CrossRef]
• Atoyan, A. M., & Aharonian, F. A. 1999, MNRAS, 302, 253 [NASA ADS] [CrossRef] (In the text)
• Begelman, M. C., Fabian, A. C., & Rees, M. J. 2008, MNRAS, 384, L19 [NASA ADS]
• Bernlöhr, K., Carrol, O., Cornils, R., et al. 2003, Astropart. Phys., 20, 111 [NASA ADS] [CrossRef] (In the text)
• Bertone, E., Tagliaferri, G., Ghisellini, G., et al. 2000, A&A, 356, 1 [NASA ADS]
• Bazejowski, M., Blaylock, G., Bond, I. H., et al. 2005, ApJ, 630, 130 [NASA ADS] [CrossRef]
• Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef]
• Boutelier, T., Henri, G., & Petrucci, P.-O. 2008, MNRAS, L102
• Carini, M. T., & Miller, H. R. 1992, ApJ, 385, 146 [NASA ADS] [CrossRef]
• Chiappetti, L., Maraschi, L., Tavecchio, F., et al. 1999, ApJ, 521, 552 [NASA ADS] [CrossRef] (In the text)
• Coppi, P. S., & Aharonian, F. A. 1999, ApJ, 521, L33 [NASA ADS] [CrossRef] (In the text)
• Costamante, L., Ghisellini, G., Giommi, P., et al. 2001, A&A, 371, 512 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Costamante, L., Aharonian, F., & Khangulyan, D. 2007, in The First GLAST Symposium, ed. S. Ritz, P. Michelson, & C. A. Meegan, AIP Conf. Ser., 921, 157 (In the text)
• Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef]
• Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] (In the text)
• Djannati-Atai , A., Piron, F., Barrau, A., et al. 1999, A&A, 350, 17 [NASA ADS]
• Dolcini, A., Farfanelli, F., Ciprini, S., et al. 2007, A&A, 476, 1219 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Dole, H., Lagache, G., Puget, J.-L., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences]
• Donato, D., Ghisellini, G., Tagliaferri, G., & Fossati, G. 2001, A&A, 375, 739 [NASA ADS] [CrossRef] [EDP Sciences]
• Dondi, L., & Ghisellini, G. 1995, MNRAS, 273, 583 [NASA ADS]
• Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] (In the text)
• Falomo, R. 1996, MNRAS, 283, 241 [NASA ADS]
• Falomo, R., Giraud, E., Melnick, J., et al. 1991, ApJ, 380, L67 [NASA ADS] [CrossRef]
• Fazio, G. G., Ashby, M. L. N., Barmby, P., et al. 2004, ApJS, 154, 39 [NASA ADS] [CrossRef]
• Foschini, L., Ghisellini, G., Tavecchio, F., et al. 2007, ApJ, 657, L81 [NASA ADS] [CrossRef] (In the text)
• Foschini, L., Treves, A., Tavecchio, F., et al. 2008, A&A, 484, L35 [NASA ADS] [CrossRef] [EDP Sciences]
• Fossati, G., Buckley, J., Edelson, R. A., Horns, D., & Jordan, M. 2004, New Astron. Rev., 48, 419 [NASA ADS] [CrossRef]
• Fossati, G., Buckley, J. H., Bond, I. H., et al. 2008, ApJ, 677, 906 [NASA ADS] [CrossRef]
• Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] (In the text)
• Georganopoulos, M., & Kazanas, D. 2003, ApJ, 594, L27 [NASA ADS] [CrossRef]
• Ghisellini, G., & Madau, P. 1996, MNRAS, 280, 67 [NASA ADS]
• Ghisellini, G., & Tavecchio, F. 2008a, MNRAS, 386, L28 [NASA ADS] (In the text)
• Ghisellini, G., & Tavecchio, F. 2008b, MNRAS, 387, 1669 [NASA ADS] [CrossRef] (In the text)
• Ghisellini, G., Celotti, A., Fossati, G., Maraschi, L., & Comastri, A. 1998, MNRAS, 301, 451 [NASA ADS] [CrossRef]
• Ghisellini, G., Celotti, A., & Costamante, L. 2002, A&A, 386, 833 [NASA ADS] [CrossRef] [EDP Sciences]
• Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [NASA ADS] [CrossRef] [EDP Sciences]
• Ghisellini, G., Tavecchio, F., Bodo, G., & Celotti, A. 2009, MNRAS, 393, L16 [NASA ADS] [CrossRef] (In the text)
• Giebels, B., Dubus, G., & Khélifi, B. 2007, A&A, 462, 29 [NASA ADS] [CrossRef] [EDP Sciences]
• Giommi, P., & Padovani, P. 1994, MNRAS, 268, L51 [NASA ADS] (In the text)
• Guetta, D., Ghisellini, G., Lazzati, D., & Celotti, A. 2004, A&A, 421, 877 [NASA ADS] [CrossRef] [EDP Sciences]
• Hofmann, W., Jung, I., Konopelko, A., et al. 1999, Astropart. Phys., 12, 135 [NASA ADS] [CrossRef] (In the text)
• Imada, A., Kato, T., Monard, L. A. G. B., et al. 2008, PASJ, 60, 267 [NASA ADS] (In the text)
• Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conf. Ser., 2808 ed. O. H. Siegmund & M. A. Gummin, 59 (In the text)
• Katarzynski, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences]
• Katarzynski, K., Lenain, J.-P., Zech, A., Boisson, C., & Sol, H. 2008, MNRAS, 390, 371 [NASA ADS] [CrossRef]
• Kirk, J. G. & Mastichiadis, A. 1999, Astropart. Phys., 11, 45 [NASA ADS] [CrossRef] (In the text)
• Kirk, J. G., Rieger, F. M., & Mastichiadis, A. 1998, A&A, 333, 452 [NASA ADS]
• Kneiske, T. M., Bretz, T., Mannheim, K., & Hartmann, D. H. 2004, A&A, 413, 807 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Königl, A. 1981, ApJ, 243, 700 [NASA ADS] [CrossRef]
• Kotilainen, J. K., Falomo, R., & Scarpa, R. 1998, A&A, 336, 479 [NASA ADS] (In the text)
• Krawczynski, H., Coppi, P. S., & Aharonian, F. 2002, MNRAS, 336, 721 [NASA ADS] [CrossRef]
• Krawczynski, H., Hughes, S. B., Horan, D., et al. 2004, ApJ, 601, 151 [NASA ADS] [CrossRef]
• Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] (In the text)
• Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] (In the text)
• Madau, P., & Pozzetti, L. 2000, MNRAS, 312, L9 [NASA ADS] [CrossRef] (In the text)
• Madau, P., & Silk, J. 2005, MNRAS, 359, L37 [NASA ADS]
• Maoz, D., & Netzer, H. 1989, MNRAS, 236, 21 [NASA ADS]
• Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef]
• Maraschi, L., Fossati, G., Tavecchio, F., et al. 1999, ApJ, 526, L81 [NASA ADS] [CrossRef]
• Massaro, E., Perri, M., Giommi, P., & Nesci, R. 2004, A&A, 413, 489 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Massaro, E., Tramacere, A., Perri, M., Giommi, P., & Tosti, G. 2006, A&A, 448, 861 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Massaro, F., Tramacere, A., Cavaliere, A., Perri, M., & Giommi, P. 2008, A&A, 478, 395 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Moderski, R., Sikora, M., Coppi, P. S., & Aharonian, F. 2005, MNRAS, 363, 954 [NASA ADS] [CrossRef]
• Mücke, A., & Protheroe, R. J. 2001, Astropart. Phys., 15, 121 [NASA ADS] [CrossRef]
• Osterman, M. A., Miller, H. R., Marshall, K., et al. 2007, ApJ, 671, 97 [NASA ADS] [CrossRef]
• Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [NASA ADS] [CrossRef]
• Pian, E., Vacanti, G., Tagliaferri, G., et al. 1998, ApJ, 492, L17 [NASA ADS] [CrossRef] (In the text)
• Piner, B. G., & Edwards, P. G. 2004, ApJ, 600, 115 [NASA ADS] [CrossRef]
• Primack, J. R., Bullock, J. S., & Somerville, R. S. 2005, in American Institute of Physics Conference Series, Vol. 745, High Energy Gamma-Ray Astronomy, ed. F. A. Aharonian, H. J. Völk, & D. Horns, p23 (In the text)
• Ravasio, M., Tagliaferri, G., Ghisellini, G., & Tavecchio, F. 2004, A&A, 424, 841 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Sambruna, R. M., Aharonian, F. A., Krawczynski, H., et al. 2000, ApJ, 538, 127 [NASA ADS] [CrossRef]
• Sikora, M. 1994, ApJS, 90, 923 [NASA ADS] [CrossRef]
• Sikora, M., & Madejski, G. 2001, in ed. F. A. Aharonian & H. J. Völk, AIP Conf. Ser., 558, 275
• Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef]
• Sikora, M., Bazejowski, M., Moderski, R., & Madejski, G. M. 2002, ApJ, 577, 78 [NASA ADS] [CrossRef]
• Spada, M., Ghisellini, G., Lazzati, D., & Celotti, A. 2001, MNRAS, 325, 1559 [NASA ADS] [CrossRef]
• Tanihata, C., Urry, C. M., Takahashi, T., et al. 2001, ApJ, 563, 569 [NASA ADS] [CrossRef]
• Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [NASA ADS] [CrossRef] (In the text)
• Tavecchio, F., Maraschi, L., Pian, E., et al. 2001, ApJ, 554, 725 [NASA ADS] [CrossRef] (In the text)
• Tramacere, A., Giommi, P., Massaro, E., et al. 2007, A&A, 467, 501 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Urry, C. M., Sambruna, R. M., Brinkmann, W. P., & Marshall, H. 1999, Nucl. Phys. B Proc. Suppl., 69, 419 [NASA ADS] [CrossRef] (In the text)
• Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS]
• Weisskopf, M. C., Tananbaum, H. D., Van Speybroeck, L. P., & O'Dell, S. L. 2000, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 4012, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, ed. J. E. Truemper, & B. Aschenbach, 2 (In the text)
• Zhang, Y. H. 2008, ApJ, 682, 789 [NASA ADS] [CrossRef]
• Zhang, Y. H., Treves, A., Celotti, A., et al. 2002, ApJ, 572, 762 [NASA ADS] [CrossRef]
• Zhang, Y. H., Treves, A., Maraschi, L., Bai, J. M., & Liu, F. K. 2006, ApJ, 637, 699 [NASA ADS] [CrossRef]

 

Footnotes

...

Supported by CAPES Foundation, Ministry of Education of Brazil.

... electrons

Note that this case is different from the condition where the observed -rays are indeed produced by IC-scatterings occurring in the Klein-Nishina regime, or when the cooling itself is determined by Klein-Nishina losses, see e.g., Moderski et al. (2005).

... model

See http://xspec.gsfc.nasa.gov/docs/xanadu/xspec/fluxerror.html

... 2007

See http://www.universe.nasa.gov/xrays/programs/rxte/pca/doc/bkg/bkg-2007-saa/

All Tables

Table 1:   Summary of the subsets of VHE data used in this paper (MJD = MJD-53 900).

Table 2:   Spectral fit of the measured VHE spectra extracted in different epochs (see Table 1).

Table 3:   Spectral fit of the same VHE spectra given in Table 2, but corrected for EBL absorption (statistical errors only).

Table 4:   Fit of the X-ray spectra simultaneous to the VHE data.

Table 5:   Values of the slope of the correlation . Fluxes integrated over each respective energy band (0.5-5 keV and 0.3-3 TeV) and in strictly simultaneous bins. The parameter is shown for fits performed with two different binnings (4 min and 7-14 min) and over three different intervals, as shown in Fig. 12.

Table 6:   Values of the slope of the correlation , for fluxes integrated over different energy bands, as indicated. The 3-15 keV flux is obtained by extrapolation of the power-law model in the   passband. Fit of the dataset ``B+C'' in the 7-14 min binning.

All Figures

---

Copyright ESO 2009