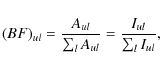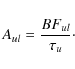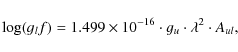Experimental Ca I oscillator strengths for the 4p–5s triplet

M. Aldenius; H. Lundberg; R. Blackwell-Whitehead

doi:10.1051/0004-6361/200911844

Free Access

Issue		A&A Volume 502, Number 3, August II 2009


Page(s)		989 - 994
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/200911844
Published online		15 June 2009

Experimental Ca I oscillator strengths for the 4p-5s triplet

M. Aldenius¹ - H. Lundberg² - R. Blackwell-Whitehead¹

1 - Atomic Astrophysics, Lund Observatory, Lund University, Box 43, 221 00 Lund, Sweden
2 - Atomic Physics, Department of Physics, Lund Institute of Technology, Box 118, 221 00 Lund, Sweden

Received 13 February 2009 / Accepted 7 May 2009

Abstract
Context. Transition lines of neutral calcium are observed in the spectra of stellar and substellar objects. In particular, the abundance of $\alpha$ -elements in metal-poor stars can place important constraints on the galactic chemical evolution. Such stellar abundance analyses rely heavily on accurate values for the oscillator strength of the observable transitions. Theoretical oscillator strengths are available for most neutral calcium lines visible in stellar spectra, but there are a limited number of experimental values in the literature.
Aims. We present new and improved experimental oscillator strengths for the optical Ca I 4p-5s triplet (6102.7, 6122.2, 6162.2 Å). In addition, we present experimental radiative lifetimes for seven energy levels in the triplet system of Ca I.
Methods. The oscillator strengths were determined by combining radiative lifetimes with branching fractions. The radiative lifetimes were measured using laser-induced fluorescence, and the branching fractions were determined using intensity calibrated spectra measured with Fourier transform spectrometry. In addition, the spectra were used to determine accurate ( ${\rm d}\lambda = 0.001$ Å, ${\rm d}\sigma = 0.002~{\rm cm}^{-1}$ ) laboratory wavelengths for the 4p-5s transitions.
Results. Oscillator strengths for the Ca I 4p-5s lines were determined with an absolute uncertainty of 9%, an uncertainty of $\pm 0.04$ dex in the log(gf) values. The branching fractions were determined with a higher accuracy, resulting in relative uncertainties of 2-3%.

Key words: atomic data - line: profiles - methods: laboratory - techniques: spectroscopic - stars: abundances

1 Introduction

Calcium belongs to the $\alpha$ -element group, which are light elements ( $Z \leq 2$ 2) synthesized through $\alpha$ capture. The abundance of $\alpha$ -elements in stellar or substellar objects is an indicator of the object's enrichment history, and can thus place strong constraints on the galactic chemical evolution. In addition, calcium is the only element in extremely metal-poor stars ( ${\rm [Fe/H]} < -5$ ), which is observable in two ionization stages, Mashonkina et al. (2007).

The most prominent calcium lines in the optical spectral region are the Ca II H and K lines at 3968.5 and 3933.7 Å respectively and the Ca I 4p-5s lines (6102.7, 6122.2, 6162.2 Å), the latter of which can be seen as prominent features in the solar spectrum, see Fig. 1. The 4p-5s triplet lines are often used for abundance determinations of calcium in metal-poor stars, Aoki et al. (2007), Barbury et al. (2006), and for stars with more solar-like metallicities, Chen et al. (2000). These Ca I lines are in the relatively uncrowded low energy range of the optical spectrum and are suitable for abundances from solar-type values down to ${\rm [Ca/H]} = -4$ , Cayrel et al. (2004).

The most recent experimental oscillator strengths (f-value, gf, or log(gf)) for the Ca I 4p-5s triplet lines are the furnace absorption measurements by Smith & O'Neill (1975), who used radiative lifetimes from Gornik et al. (1973) to put their measurements on an absolute scale. The commonly used work by Smith & Raggett (1981) and Smith (1988) for Ca I transitions with energies between 2.5 and 3.0 eV do not include the 4p-5s triplet lines. Oscillator strengths for the 4p-5s triplet lines have also been reported by Olsen et al. (1959) using furnace absorption, Ostrovskii $\&$ Penkin (1961) using the ``hook'' method and Köstlin (1964) using an axial-symmetric electric arc. The National Institute of Standards and Technology (NIST) Atomic Spectra Database, Ralchenko et al. (2008), includes the oscillator strengths of Smith & O'Neill (1975). However, the frequently used online atomic line database of semi-empirical calculations by Kurucz, Kurucz CD-ROM No. 23, Kurucz & Bell (1995), cites the earlier work in the NBS (National Bureau of Standards, now NIST) compilation of Weise et al. (1969). The oscillator strengths in the NBS compilation of Weise et al. (1969) are an average of the measurements of Ostrovskii $\&$ Penkin (1961) and Köstlin (1964) and the values for the 4p-5s triplet lines include a correction that assumes LS coupling. The most recent theoretical work that includes transition probabilities for the 4p-5s triplet lines are the MCHF (Multiconfiguration Hartree-Fock) calculations by Froese Fischer & Tachiev (2003). In addition, Cowan code calculations of oscillator strengths for Ca I have been determined by Kurucz (2008).

Radiative lifetimes for Ca I including the 4s5s ³S and 4s4d ³D terms have been measured by Brinkmann et al. (1969) using the zero-field level crossing technique (Hanle effect), Gornik et al. (1973) using the laser-induced fluorescence technique (LIF), Emmoth et al. (1975) using the beam-foil technique, Osherovich & Pul'kin (1977) using the delayed coincidence technique and Havey et al. (1977) using LIF. Further measurements were carried out on the singlet terms in Ca I by Chenevier et al. (1967), Hunter et al. (1985) and Hunter & Peck (1986).

In this paper we present experimental oscillator strengths for the 4p-5s triplet in Ca I measured by combining branching fractions with radiative lifetimes. Branching fractions were determined from intensity calibrated spectra measured with Fourier transform spectroscopy. In addition, radiative lifetimes were measured for the 4s5s ³S, 4s4d ³D and 4s5d ³D LS terms of Ca I. It has been possible to determine the branching fractions to a relatively high accuracy because of the high signal-to-noise ratios ( ${\it S/N}$ ) of the observed spectral lines, and their closeness in wavelength. The relative uncertainties of the log(gf) values were determined to be 2-3% and the absolute uncertainties were estimated to be 9%.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11844fg1.eps} \end{figure}$	Figure 1: Spectrum of the Sun in the region of the 4p-5s Ca I triplet. The Ca I lines are marked with air wavelengths in Å. From the solar flux atlas by Kurucz et al. (1984).
Open with DEXTER

2 Radiative lifetimes

The radiative lifetimes were measured using laser-induced-fluorescence and a partial energy level diagram of the levels investigated is displayed in Fig. 2. The levels were selectively excited by wavelength-tuned pulsed laser radiation and the time for the subsequent decay was detected. Free calcium atoms were produced by focusing a pulsed Nd:YAG laser beam (Nd:YAG laser 1) onto a rotating calcium target. The laser pulse creates a small plasma that expands from the target and contains electrons, atoms and ions of various ionization stages. The laser pulse had a duration of 10 ns and typical energy of 10 mJ. This atom and ion source has the advantage of high particle density and the possibility of using populated metastable levels as a starting point for laser excitation. The measurements were performed on atoms in the later, slower part of the plasma by adjusting the time delay of the excitation pulse.

The triplet levels 4s5s ³S₁, 4s4d ³D_J and 4s5d ³D_J have very weak transitions to the singlet ground state, 4s² ¹S₀. However, these triplet levels have relatively strong transitions to the metastable 4s4p ³P_J levels and these metastable levels were used as a starting point for the selective excitation. These levels were found to be sufficiently well populated in the afterglow of the plasma to provide pump electrons to populate the 4s5s ³S₁, 4s4d ³D_J and 4s5d ³D_J levels. The 4s4p ³P_J levels were selectively excited using a pulsed, tuneable laser signal produced by a second Nd:YAG laser system (Nd:YAG laser 2). The injection-seeded frequency-doubled Nd:YAG laser produced 10 ns long pulses which were compressed to 1 ns using stimulated Brillouin scattering in a water cell. The compressed pulse was then used to pump a dye laser and the output was frequency-doubled in a non-linear crystal and Raman wavelength-shifted in a hydrogen cell to produce the appropriate excitation energy. This excitation beam interacted with the calcium atoms at approximately 1 cm above the target. The fluorescent decay was observed with a 0.25 m vacuum monochromator and a multichannel-plate photo-multiplier with a rise time of 0.2 ns. The photo-multiplier was connected to a digital transient recorder with an analog bandwidth of 1 GHz and real-time sampling rate of 2 GSamples/s. The lifetimes were evaluated by fitting an exponential to the fluorescence signal and the final lifetime values given in Table 1 are averages from a series of recordings. The uncertainty in the lifetime is two standard deviations in the measured values. A more detailed description of the experimental setup can be found in Li et al. (1999).

$\begin{figure} \par\includegraphics[width=9cm,clip]{11844fg2.eps} \end{figure}$	Figure 2: Partial energy level diagram of Ca I displaying the ground state, the 4s4p ³P levels and the levels for which the lifetimes were measured in the present work. The 4p-5s lines are marked with air wavelengths in Å.
Open with DEXTER

3 Branching fractions and wavelengths

3.1 Experimental method

A water cooled hollow cathode discharge lamp (HCL) was used to produce the Ca I spectrum. The cylindrical cathode was made of pure iron and a small piece of calcium was inserted into the centre of the discharge area. The inner diameter of the cathode was 7.0 mm and had a length of 50 mm. Argon was used as the carrier gas in the HCL, since it has fewer strong lines in the measured wavenumber region and provides Ar II lines for wavenumber calibration.

Calcium easily forms a white coating of nitride when exposed to air and the initial HCL discharge was unstable due to this external coating and out-gassing from the calcium sample. However, it was found that the HCL became stable after several hours of low current operation and continual evacuation had removed the nitride. The optimal operating conditions were found to be a pressure of 0.4-0.5 torr and a discharge current of 0.03-0.20 A. Even at low currents (0.05 A) the signal-to-noise ratios for the Ca I 4p-5s triplet lines were high ( ${\it S/N} > 100$ ) and measurements at multiple currents and pressures were recorded. An example of the observed FT spectrum of the Ca I lines is displayed in Fig. 3.

An external continuous tungsten ribbon lamp with a relative spectral radiance calibration from the Swedish National Testing and Research Institute (2 $\sigma$ uncertainty = 3%, in the spectral range 4000-8000 Å) was used to correct the line intensities for the instrumental response of the spectrometer and optics. The HCL and the calibration lamp were placed on the same optical path using a T-setup and a folding mirror equidistant from the two lamps was used to direct the light to the input aperture of the FT spectrometer. This made it possible to switch between the two light sources without moving them. Calibration spectra were recorded before and after the calcium spectrum measurement to determine if the instrument response had changed during the calcium measurement. The spectra were acquired with the Lund FT500 UV Fourier Transform (FT) spectrometer, which is optimized in the wavelength range of 2000-7000 Å. In addition, a hot-mirror filter and a colored glass GG475 cut-off filter were used to minimize the noise contribution from lines outside of the wavelength region of interest.

The three Ca I 4p-5s spectral lines are relatively close in wavenumber, within $\sim$ 160 cm^-1. Therefore only one spectral region was required to measure the lines, 11 000-22 000 cm^-1 (9100-4500 Å) at a resolution of 0.03 cm^-1. This was sufficient to resolve the doppler broadened lines. Approximately ten scans were co-added for each spectral acquisition to achieve a good signal-to-noise ratio ( ${\it S/N} > 100$ ).

Table 1: Experimental radiative lifetimes of Ca I.

3.2 Analysis

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{11844fg3.eps} \end{figure}$	Figure 3: FT spectrum of the HCL showing the 4p-5s Ca I triplet. The intensities in the figure are uncalibrated. The weaker lines belong to Ca I and Ar II.
Open with DEXTER

The intensities of all lines from an upper level are required to determine the branching fraction of a transition. The branching fraction is defined as the transition probability, A_ul, of a single line divided by the sum of all transition probabilities from the same upper level, u

$\begin{displaymath}\left( BF \right)_{ul} = \frac{A_{ul}}{\sum_{l}A_{ul}} = \frac{I_{ul}}{\sum_{l}I_{ul}}, \end{displaymath}$

(1)

where I_ul is the line intensity.

The Ca I line intensities were determined from the intensity calibrated calcium spectra using the FT spectrometry analysis computer program XGREMLIN, Nave et al. (1997), which is based on the GREMLIN code of Brault & Abrams (1989). The spectral lines were fitted with Voigt profiles using a least-squares fit procedure. The fitted lines were found to be close to pure Gaussians, due to the dominance of Doppler broadening in the HCL. The integrated area of the fitted profile was used as a measurement of the intensity of the spectral line.

Spectra observed by FT spectrometry have a linear wavenumber scale which can be calibrated by applying a multiplicative correction factor, $k_{{\rm eff}}$ , Learner & Thorne (1988)

$\begin{displaymath}\sigma_{{\rm corr}}=(1+k_{{\rm eff}})\sigma_{{\rm obs}}, \end{displaymath}$

(2)

where $\sigma_{{\rm corr}}$ is the corrected wavenumber and $\sigma_{{\rm obs}}$ is the observed, uncorrected, wavenumber. The factor $k_{{\rm eff}}$ can be determined to an accuracy of 1 part in 10⁷ by measuring the wavenumbers of internal wavenumber standard lines. In principle, it is possible to use only one calibration line, but to reduce the uncertainty of the calibration, several calibration lines are used for each recorded spectrum. The Ca I spectra were calibrated using Ar II 4s-4p transition lines from the carrier gas in the HCL. The wavenumbers of 24 Ar II calibration lines were taken from Whaling et al. (1995) in the wavenumber range 12469.2 to 21149.7 cm^-1 (8017.5 to 4726.9 Å). A further discussion of wavenumber calibration and uncertainties can be found in Aldenius et al. (2006).

3.3 Self-absorption

The 4s4p ³P_J levels have different decay channels; the 4s4p ³P₁ level has a decay channel with a spin-forbidden transition to the ground state and a lifetime of $\tau \sim 0.3$ ms, Drozdowski et al. (1997). The other two levels are metastable and thus have longer lifetimes, $\tau\sim 130$ min for 3p ³P₂ and $\tau\sim 5$ min (⁴³Ca) for ³P₀, Santra et al. (2004). These two levels can be highly populated and the emitted photons may be reabsorbed in the HCL plasma. This reabsorption will distort the line profile, reduce the observed intensity and give a transition probability that is lower than the correct value.

The population of the lower level depends on the plasma density and temperature. Different discharge currents in the HCL produce different plasma densities and thus different amounts of self-absorption. By measuring the line intensities at six different HCL currents, 0.03, 0.05, 0.10, 0.15, 0.20 and 0.25 A, a curve of growth for each line was determined and the amount of self-absorption of the lines was investigated. At zero current the lines are assumed to be free of self-absorption. For lines unaffected by self-absorption the observed BF values should not change with discharge current. For our measurements the BFs were determined from relatively low current recordings where the curves of growth and line fit residuals indicated there was no self-absorption.

4 Oscillator strengths

Table 2: Experimental oscillator strengths of the Ca I 4p-5s triplet

The transition probabilities, A_ul, in Table 2 were determined by combining the experimental lifetimes, $\tau_{u}$ , with the BF_ul

$\begin{displaymath}A_{ul} = \frac{BF_{ul}}{\tau_{u}}\cdot \end{displaymath}$

(3)

The oscillator strengths, f, are determined from the transition probability using the following equation

$\begin{displaymath}\log (g_{l}f) = 1.499 \times 10^{-16} \cdot g_{u} \cdot \lambda^{2} \cdot A_{ul}, \end{displaymath}$

(4)

where g_u and g_l are the statistical weights for the upper and lower level respectively, $\lambda$ is the wavelength in Å, A_ul is in s^-1, and log(g_lf) has been abbreviated to log(gf) for the general usage in this paper, see Thorne et al. (1999), Huber & Sandeman (1986).

4.1 Uncertainties

The branching fraction uncertainty depends on the uncertainty of the intensity measurement for the transition and the uncertainty of the intensity measurements for all other transitions from the same upper level. The intensity measurement uncertainty includes the intensity calibration uncertainty and the uncertainty in the line fitting procedure. The radiative lifetime uncertainty for the laser-induced fluorescence technique is dominated by the signal to noise of the exponential decay curve. The oscillator strength uncertainty includes contributions from the branching fraction uncertainty and the radiative lifetime uncertainty and is determined in the same manner as described by Sikström et al. (2002).

5 Results

Table 3: A comparison of the branching fractions presented in this paper with laboratory, theoretical and semi-empirical branching fractions in the literature.

5.1 Radiative lifetimes

In Table 1 we present new and remeasured radiative lifetimes for 7 energy levels in the triplet series of Ca I including the 4s5s ³S₁ level required for the oscillator strength measurements in this paper. In addition, the 4snd ³D_J levels were measured to provide a consistency check with other results in the literature and to extend the laboratory database for Ca I lifetimes. Our lifetime for the 4s5s ³S₁ level is longer than other values in the literature, but our new value agrees with the work of Gornik et al. (1973) to within the uncertainties of both measurements. In addition, the lifetime for the 4s4d ³D₁ level agrees to within the experimental uncertainties with the values of Gornik et al. (1973) and Osherovich & Pul'kin (1977). Our results indicate that the 4s4d ³D₁ and 4s5s ³S₁ levels have lifetimes that are approximately the same value and this is in agreement with the MCHF calculations of Froese Fischer & Tachiev (2003). Furthermore, the Cowan code calculations of Kurucz (2008) indicate that the lifetimes for the 4s5d ³D_J levels should be longer than the lifetimes for the 4s4d ³D_J levels and this is confirmed by our measurements.

5.2 Wavelengths, BFs and oscillator strengths

The results for the wavelengths, branching fractions, transition probabilities and log(gf) values of the three 4p-5s transitions are presented in Table 2 together with comparisons to log(gf) values in the literature. The wavenumbers in Table 2 have an uncertainty of ${\rm d}\sigma = 0.002~{\rm cm}^{-1}$ ( ${\rm d}\lambda = 0.001$ Å) which corresponds to two standard deviations in the Ar II wavenumbers, Whaling et al. (1995). The uncertainty in our log(gf) values is 9% which is approximately 0.04 dex. The semi-empirical log(gf) values of Kurucz & Bell (1995) refer to the compilation of Weise et al. (1969) and references therein. Weise et al. (1969) suggest an uncertainty of 25% (0.1 dex) for these values. The experimental log(gf) values of Smith & O'Neill (1975) quote an uncertainty of 15% (0.07 dex). However, Smith & O'Neill (1975) use the lifetimes of Gornik et al. to place their relative gf values on an absolute scale, but the lifetime values of Gornik et al. have an uncertainty of 15%. Therefore it is possible that the log(gf) values of Smith & O'Neill (1975) have an uncertainty that is larger than 15%.

It can be seen that our log(gf) values agree to within the uncertainties with Smith & O'Neill (1975) and Froese Fischer & Tachiev (2003). However, our values are weaker than the values given by Smith & O'Neill (1975) and Froese Fischer & Tachiev (2003). This difference is an artifact of the longer lifetime used in our oscillator strength measurement which provides an absolute scaling factor to the BFs. If we only consider the BFs in the literature it is possible to compare values without the variation due to the lifetime scaling factor, see Table 3. In Table 3 we have also included the Cowan code calculations of Kurucz (2008) which do not include experimental data. To obtain the BF values we have used the sum of the transition probabilities, see Eq. (1). It can be seen that there is a very weak (log(gf) = -4.84, Kurucz 2008) IR transition at 12 675.3 Å that has not been included in our measurements or the measurements of Smith & O'Neill (1975). However, this IR transition contributes less than 0.001% to the sum of the BFs as discussed by Froese Fischer & Tachiev (2003).

There is a relatively small difference in the branching fraction distribution of our work compared to the previous measurements of Smith & O'Neill (1975). However, the difference between our values and Smith & O'Neill (1975) is less than the uncertainty in the measurements. Furthermore, our measurements agree to within our uncertainty with the MCHF calculations of Froese Fischer & Tachiev (2003) and the Cowan calculations of Kurucz (2008), but uncertainties for these calculations are not given. The only significant difference is observed between our BFs and the semi-empirical calculated BFs of Kurucz & Bell (1995). The online database of Kurucz & Bell (1995) refers to log(gf) values from Weise et al. (1969) which use an average of the log(gf) values of Ostrovskii $\&$ Penkin (1961) and Köstlin (1964) with a scaling ratio that assumes LS coupling. It is possible that a chromatic shift is present in the values of Weise et al. (1969) as discussed by Smith & O'Neill (1975).

6 Conclusion

We present a self consistent set of oscillator strengths for the Ca I 4p-5s triplet lines (6102.7, 6122.2, 6162.2 Å), which are of particular interest to the analysis of metal poor stars. Accurate wavenumbers and wavelengths were determined for the three transitions to an uncertainty of ${\rm d}\sigma = 0.002~{\rm cm}^{-1}$ , ${\rm d}\lambda = 0.001$ Å. In addition, experimental BFs and radiative lifetimes were measured to determine absolute oscillator strengths for the Ca I lines. Our new absolute oscillator strength values have an uncertainty of 9% which is lower than the published values of Smith & O'Neill (1975), but there is a good agreement, to within the uncertainty, with our new values, Smith & O'Neill (1975) and the MCHF calculations of Froese Fischer & Tachiev (2003).

Acknowledgements

We thank Dr H. Xu for his assistance in the laboratory during the lifetime measurements and Dr H. Nilsson for discussions regarding the branching fraction measurements. In addition, we would like to thank Dr J. Fuhr at NIST, USA for his help in finding the original references for the N.B.S. publication NSRDS-NBS 22 (1969). This work was supported by the Swedish Research Council through the Linneus grant. R.B.W. would like to gratefully acknowledge the support received from the European Community for a Marie Curie Intra-European Fellowship.

References

Aldenius, M., Johansson, S., & Murphy, M. T. 2006, MNRAS, 370, 444 [NASA ADS] (In the text)
Aldenius, M., Tanner, J. D., Johansson, S., Lundberg, H., & Ryan, S.G. 2007, A&A, 461, 767 [NASA ADS] [CrossRef] [EDP Sciences]
Aoki, W., Beers, T. C., & Christlieb, N. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] (In the text)
Barbuy, B., Zoccali, M., & Ortolani, S. 2006, A&A, 449, 349 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Brault, J. W., & Abrams, M. C. 1989, High Resolution Fourier Transform Spectroscopy, OSA Technical Digest Series (Washington: Optical Society of America), 6, 110 (In the text)
Brinkmann, U., Goschler, J., Streudel, A., & Walther, H. 1969, Z. Phys., 228, 427 [NASA ADS] [CrossRef] (In the text)
Cayrel, R., Depagne, E., & Spite, M. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Chenevier, M., Dufayard, J., & Pebay-Peyrovla, J. C. 1967, Phys. Lett. A, 25, 283 [NASA ADS] [CrossRef] (In the text)
Drozdowski, R., Ignaciuk, M., Kwela, J., & Heldt, J. 1997, Zeitschrift fur Physik D, 41, 125 [CrossRef] (In the text)
Emmoth, B., Braun, M., Bromander, J., & Martinson, I. 1975, Phys. Scr., 12, 75 [NASA ADS] [CrossRef] (In the text)
Froese Fischer, C., & Tachiev, G. 2003, Phys. Rev. A, 68, 012507 [NASA ADS] [CrossRef] (In the text)
Gornik, W., Kaiser, D., & Lange, W. 1973, Phys. Lett. A, 45, 219 [NASA ADS] [CrossRef] (In the text)
Havey, M. D., Balling, L. C., & Wright, J. J. 1977, J. Opt. Soc. Am., 67, 488 [NASA ADS] [CrossRef] (In the text)
Huber, M. C. E., & Sandeman, R.J. 1986, Rep. Prog. Phys., 49, 397 [NASA ADS] [CrossRef] (In the text)
Hunter, L. R., & Peck, S.K. 1986, Phys. Rev. A, 33, 4452 [NASA ADS] [CrossRef] (In the text)
Hunter, L. R., Watson, G. M., Weiss, D. S., & Zajonc, A. G. 1985, Phys. Rev. A, 31, 2268 [NASA ADS] [CrossRef] (In the text)
Köstlin, H. Z. 1964, Z. Phys., 178, 200 [NASA ADS] [CrossRef] (In the text)
Kurucz, R. L. 2008, http://kurucz.harvard.edu/ (In the text)
Kurucz, R. L., & Bell, B. 1995, Atomic Line Data Kurucz CD-ROM No. 23, Cambridge, Mass.: Smithsonian Astrophysical Observatory, 23 (In the text)
Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 to 1300 nm, National Solar Observatory Atlas No. 1 (In the text)
Learner, R. C. M., & Thorne, A. P. 1988, J. Opt. Soc. Am. B, 5, 2045 [NASA ADS] [CrossRef] (In the text)
Li, Z. S., Lundberg, H., Sikström, C. M., & Johansson, S. 1999, Eur. Phys. J. D, 6, 9 [NASA ADS] [EDP Sciences] (In the text)
Mashonkina, L., Korn, A.J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Nave, G., Sansonetti, C.J., & Griesmann, U. 1997, in Fourier Transform Spectroscopy, OSA Technical Digest Series (Washington DC: Optical Society of America), 3, 38 (In the text)
Olsen, K. H., Routly, P. M., & King, R. B. 1959, ApJ, 130, 688 [NASA ADS] [CrossRef] (In the text)
Osherovich, A.L., & Pul'kin, S.A. 1977, Vestn. Leningr. Univ. Fiz. Khim., 16, 58 (In the text)
Ostrovskii, Yu.I., & Penkin, N.P. 1961, Opt. Spectros., 10, 219 [NASA ADS] (In the text)
Ralchenko, Yu., Kramida, A.E., Reader, J., & NIST ASD Team (2008), NIST Atomic Spectra Database, version 3.1.5, available: http://physics.nist.gov/asd3 (2009), National Institute of Standards and Technology, Gaithersburg, MD (In the text)
Risberg, G. 1968, Ark. Fys., 37, 231
Santra, R., Christ, K.V., & Greene, C.H. 2004, Phys. Rev. A, 69, 042510 [NASA ADS] [CrossRef] (In the text)
Sikström, C.M., Nilsson, H., Litzén, U., Blom, A., & Lundberg, H. 2002, J. Quant. Spectr. Radiat. Transf., 74, 355 [NASA ADS] [CrossRef] (In the text)
Smith, G. 1988, J. Phys. B: At. Mol. Opt. Phys., 21, 2827 [NASA ADS] [CrossRef] (In the text)
Smith, G., & O'Neill, J.A. 1975, A&A, 38, 1 [NASA ADS] (In the text)
Smith, G., & Raggett, D.S.J. 1981, J. Phys. B, 14, 4015 [NASA ADS] [CrossRef] (In the text)
Thorne, A.P., Litzén, U., & Johansson, S. 1999, Spectrophysics: principles and applications (Berlin Heidelberg: Springer-Verlag) (In the text)
Whaling, W., Anderson, W.H.C., Carle, M.T., Brault, J.W., & Zarem, H.A. 1995, J. Quant. Spectrosc. Radiat. Transf., 53, 1 [NASA ADS] [CrossRef] (In the text)
Wiese, W.L., Smith, M.W., & Miles, B.M. 1969, Atomic transition probabilities. 2, Sodium through Calcium, A critical data compilation (NSRDS-NBS, Washington, D.C.: US Department of Commerce, National Bureau of Standards) (In the text)

All Tables

Table 1: Experimental radiative lifetimes of Ca I.

Table 2: Experimental oscillator strengths of the Ca I 4p-5s triplet

Table 3: A comparison of the branching fractions presented in this paper with laboratory, theoretical and semi-empirical branching fractions in the literature.

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{11844fg1.eps} \end{figure}$	Figure 1: Spectrum of the Sun in the region of the 4p-5s Ca I triplet. The Ca I lines are marked with air wavelengths in Å. From the solar flux atlas by Kurucz et al. (1984).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11844fg2.eps} \end{figure}$	Figure 2: Partial energy level diagram of Ca I displaying the ground state, the 4s4p ³P levels and the levels for which the lifetimes were measured in the present work. The 4p-5s lines are marked with air wavelengths in Å.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{11844fg3.eps} \end{figure}$	Figure 3: FT spectrum of the HCL showing the 4p-5s Ca I triplet. The intensities in the figure are uncalibrated. The weaker lines belong to Ca I and Ar II.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.