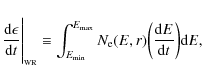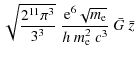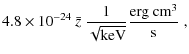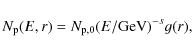| Issue |
A&A
Volume 502, Number 3, August II 2009
|
|
|---|---|---|
| Page(s) | 711 - 719 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200911843 | |
| Published online | 15 June 2009 | |
On the inverse Compton scattering interpretation of the hard X-ray excesses in galaxy clusters: the case of Ophiuchus
S. Colafrancesco1,2 - P. Marchegiani2,3
1 - ASI-ASDC c/o ESRIN, via G. Galilei snc, 00040 Frascati, Italy
2 - INAF - Osservatorio Astronomico di Roma via Frascati 33, 00040 Monteporzio, Italy
3 - Dipartimento di Fisica, Università di Roma La Sapienza, P.le A. Moro 2, Roma, Italy
Received 13 February 2009 / Accepted 14 April 2009
Abstract
Context. Populations of high energy electrons can produce hard X-ray (HXR) emission in galaxy clusters by up-scattering CMB photons via the inverse Compton scattering (ICS) mechanism. However, this scenario has various astrophysical consequences.
Aims. We discuss here the consequences of the presence of a population of high energy particles for the multi-frequency emissivity of the same clusters and the structure of their atmospheres.
Methods. We derive predictions for the ICS HXR emission in the specific case of the Ophiuchus cluster (for which an interesting combination of observational limits and theoretical scenarios have been presented) for three main scenarios producing high-E electrons: primary cosmic ray model, secondary cosmic rays model and neutralino DM annihilation scenario. We further discuss the predictions of the Warming Ray model for the cluster atmosphere. Under the assumption to fit the HXR emission observed in Ophiuchus, we explore the consequences that these electron populations induce on the cluster atmosphere.
Results. We find that: i) primary electrons can be marginally consistent with the available data provided that the electron spectrum is cutoff at
![]() and
and
![]() MeV for electron spectral index values of 3.5 and 4.4, respectively; ii) secondary electron models from pp collisions are strongly inconsistent with the viable gamma-ray limits, cosmic ray protons produce too much heating of the intracluster (IC) gas and their pressure at the cluster center largely exceeds the thermal one; iii) secondary electron models from DM annihilation are also strongly inconsistent with the viable gamma-ray and radio limits, and electrons produce too much heating of the IC gas at the cluster center, unless the neutralino annihilation cross-section is much lower than the proposed value. In that case, however, these models no longer reproduce the HXR excess in Ophiuchus.
MeV for electron spectral index values of 3.5 and 4.4, respectively; ii) secondary electron models from pp collisions are strongly inconsistent with the viable gamma-ray limits, cosmic ray protons produce too much heating of the intracluster (IC) gas and their pressure at the cluster center largely exceeds the thermal one; iii) secondary electron models from DM annihilation are also strongly inconsistent with the viable gamma-ray and radio limits, and electrons produce too much heating of the IC gas at the cluster center, unless the neutralino annihilation cross-section is much lower than the proposed value. In that case, however, these models no longer reproduce the HXR excess in Ophiuchus.
Conclusions. We conclude that ICS by secondary electrons from both neutralino DM annihilation and pp collisions cannot be the mechanism responsible for the HXR excess emission; primary electrons are still a marginally viable solution provided that their spectrum has a low-energy cutoff at
![]() MeV. We also find that diffuse radio emission localized at the cluster center is expected in all these models and requires quite low values of the average magnetic field (
MeV. We also find that diffuse radio emission localized at the cluster center is expected in all these models and requires quite low values of the average magnetic field (
![]()
![]() G in primary and secondary-pp models;
G in primary and secondary-pp models;
![]()
![]() G in secondary-DM models) to agree with the available observations. Finally, the WR model (with
G in secondary-DM models) to agree with the available observations. Finally, the WR model (with
![]()
![]() G) offers, so far, the most accurate description of the cluster in terms of the temperature distribution, heating and pressure and multi-frequency spectral energy distribution. Fermi observations of Ophiuchus will provide further constraints to this model.
G) offers, so far, the most accurate description of the cluster in terms of the temperature distribution, heating and pressure and multi-frequency spectral energy distribution. Fermi observations of Ophiuchus will provide further constraints to this model.
Key words: cosmology: theory - galaxies: clusters: general - galaxies: clusters: individual: Ophiuchus - radiation mechanisms: non-thermal
1 Introduction
Hard X-ray (HXR) excess emission in galaxy clusters has been observed in the direction of several nearby systems (see Nevalainen et al. 2004) but its origin remains disputed. It has been proposed that this HXR emission is produced by inverse Compton scattering (ICS) of relativistic electrons with the cosmic microwave background (CMB) (Blasi & Colafrancesco 1999; Atoyan & Volk 2000; Ensslin & Biermann 1998; Sarazin 1999; Brunetti 2004; Profumo 2008, see Petrosian et al. 2008 for a recent review), bremsstrahlung emission from a supra-thermal electron population (Dogiel et al. 2007, see Petrosian et al. 2008 for a recent review), or a population of PeV electrons that radiates in hard X-rays by synchrotron emission (Timokhin et al. 2004; Inoue et al. 2005). None of these models has been definitely proven or rejected, so far, because of the lack of instrumental sensitivity (spatial and spectral) of the available experiments operating in this HXR band.
In this context, the Ophiuchus cluster (z=0.028, Johnston et al.
1981) has been at the center of an interesting dispute about the combination of new observational evidence of HXR emission and various theoretical considerations about its origin.
The Ophiuchus cluster appears to have a high plasma temperature
![]() keV (Johnston et al. 1981).
Measurements of the IC gas temperature vary from
keV (Johnston et al. 1981).
Measurements of the IC gas temperature vary from
![]() keV
(INTEGRAL; Eckert et al. 2008) to
9.5+1.4 -1.1 keV (Swift/BAT; Ajello et al. 2009). Watanabe et al. (2004) also found a large (
keV
(INTEGRAL; Eckert et al. 2008) to
9.5+1.4 -1.1 keV (Swift/BAT; Ajello et al. 2009). Watanabe et al. (2004) also found a large (
![]() ), hot (kT > 13 keV) region, 20 arcmin
west of the cluster center, which led them to conclude that the
cluster is not dynamically relaxed, and suggested that it
experienced a major merging event in the recent past (
), hot (kT > 13 keV) region, 20 arcmin
west of the cluster center, which led them to conclude that the
cluster is not dynamically relaxed, and suggested that it
experienced a major merging event in the recent past (
![]() Gyr).
Gyr).
Eckert et al. (2008) reported a tentatively resolved (![]() 5') X-ray source at the cluster center, and the presence of a non-thermal emission tail with a flux of
5') X-ray source at the cluster center, and the presence of a non-thermal emission tail with a flux of
![]() erg cm-2 s-1 in the 20-60 keV energy band. These authors interpreted the non-thermal hard X-ray emission as
ICS emission from relativistic electrons scattered off the CMB in
the intracluster (IC) medium.
Suzaku observations of the Ophiuchus cluster by Fujita et al.
(2008) have, however, failed to detect the non-thermal component detected by Eckert et al. (2008), although their quoted upper
limit of
erg cm-2 s-1 in the 20-60 keV energy band. These authors interpreted the non-thermal hard X-ray emission as
ICS emission from relativistic electrons scattered off the CMB in
the intracluster (IC) medium.
Suzaku observations of the Ophiuchus cluster by Fujita et al.
(2008) have, however, failed to detect the non-thermal component detected by Eckert et al. (2008), although their quoted upper
limit of
![]() erg cm-2 s-1 in the
20-60 keV energy band is still compatible with the INTEGRAL
detection. Ajello et al. (2009) have found, using Swift/BAT spectra (with a IC gas temperature of kT = 9.5 keV), an upper limit on the Ophiuchus non-thermal X-ray emission in the 20-60 keV band, of
erg cm-2 s-1 in the
20-60 keV energy band is still compatible with the INTEGRAL
detection. Ajello et al. (2009) have found, using Swift/BAT spectra (with a IC gas temperature of kT = 9.5 keV), an upper limit on the Ophiuchus non-thermal X-ray emission in the 20-60 keV band, of
![]() erg cm-2 s-1 (90% c.l.).
We note that the INTEGRAL detection and the Swift-BAT upper limit
are consistent, at the same 90% confidence level, in the flux
range
erg cm-2 s-1 (90% c.l.).
We note that the INTEGRAL detection and the Swift-BAT upper limit
are consistent, at the same 90% confidence level, in the flux
range
![]() erg cm-2 s-1. This is
the flux range in which the HXR excess detected from Ophiuchus is
consistent with both Swift-BAT and INTEGRAL observations. In our
study of the origin of this HXR excess, we refer to the value
erg cm-2 s-1. This is
the flux range in which the HXR excess detected from Ophiuchus is
consistent with both Swift-BAT and INTEGRAL observations. In our
study of the origin of this HXR excess, we refer to the value
![]() erg cm-2 s-1as the maximum value of its flux and we discuss how our results
change by also considering the minimum flux of the HXR,
erg cm-2 s-1as the maximum value of its flux and we discuss how our results
change by also considering the minimum flux of the HXR,
![]() erg cm-2 s-1, which is
erg cm-2 s-1, which is
![]()
![]() less than the previous maximum value.
less than the previous maximum value.
The possible presence of an ICS tail of HXR emission in Ophiuchus
was previously related to a steep-spectrum radio source MSH 17-203
(also dubbed Cul 1709-231) as a radio mini halo (Johnston et al.
1981), which would thus imply the presence of relativistic electrons, and hence the relative ICS emission emerging from the thermal bremsstrahlung emission in the X-ray band at
![]() keV.
keV.
However, the high resolution study of Perez-Torres et al. (2008)
performed with 240 and 607 MHz GMRT radio observations of the
Ophiuchus cluster of galaxies, along with archival 74 and 1400 MHz
VLA data, indicates that there is no significant diffuse radio
emission in the core of the Ophiuchus, and that the previous
measurements of radio flux from the MSH 17-203 source (Slee &
Higgins 1975; Slee 1977) do not refer to the radio halo of the
cluster: these authors present new upper limits to the integrated,
diffuse non-thermal radio emission from the cluster core.
Govoni et al. (2009) pointed out that there is a diffuse radio
mini-halo located at the center of the Ophiuchus cluster, with
angular size of ![]()
![]() arcmin2; the flux of the
mini halo is
arcmin2; the flux of the
mini halo is ![]() 8 times lower than the old measurement of
Johnston et al. (1981), which had a resolution of 80 arcmin (see details in Perez-Torres et al. 2008).
8 times lower than the old measurement of
Johnston et al. (1981), which had a resolution of 80 arcmin (see details in Perez-Torres et al. 2008).
There is no other information on non-thermal emission from
Ophiuchus: gamma-ray emission from this cluster has not been
detected and therefore the only information that we have directly
about the high-E particle population of Ophiuchus is an upper
limit obtained by EGRET
![]() cm-2 s-1 (Reimer et al. 2003).
cm-2 s-1 (Reimer et al. 2003).
In this obervational scenario (similar to that of other clusters
where an HXR emission detection was claimed) the HXR emission
excess from Ophiuchus was interpreted as ICS emission from either
a population of primary cosmic ray electrons (Eckert et al. 2008) or secondary electrons produced in neutralino DM annihilation (Profumo 2008). In particular, Profumo (2008) proposed that a
combination of three different neutralino DM models [
![]() )
and
)
and
![]() GeV] is
consistent with all non-thermal emission data for Ophiuchus, from
radio to HXR and gamma-rays.
The available data on diffuse radio emission in the core of
Ophiuchus and the overall analysis of its multi-frequency SED
further led Perez-Torres et al. (2008) to conclude that: i) a
synchrotron+ICS model from primary cosmic ray electrons is in
marginal agreement with the the available data, for a range of
magnetic field values
GeV] is
consistent with all non-thermal emission data for Ophiuchus, from
radio to HXR and gamma-rays.
The available data on diffuse radio emission in the core of
Ophiuchus and the overall analysis of its multi-frequency SED
further led Perez-Torres et al. (2008) to conclude that: i) a
synchrotron+ICS model from primary cosmic ray electrons is in
marginal agreement with the the available data, for a range of
magnetic field values
![]()
![]() G; ii) that a pure
neutralino annihilation scenario cannot reproduce both radio and
HXR emission, unless extremely low magnetic field values
(10-2 to 10-3
G; ii) that a pure
neutralino annihilation scenario cannot reproduce both radio and
HXR emission, unless extremely low magnetic field values
(10-2 to 10-3 ![]() G) are assumed; iii) a scenario in
which synchrotron and ICS arise from PeV electron-positron pairs
(via interactions with the CMB), can also be excluded, since it
predicts a non-thermal soft X-ray emission that largely exceeds the thermal bremsstrahlung emission measured by INTEGRAL.
G) are assumed; iii) a scenario in
which synchrotron and ICS arise from PeV electron-positron pairs
(via interactions with the CMB), can also be excluded, since it
predicts a non-thermal soft X-ray emission that largely exceeds the thermal bremsstrahlung emission measured by INTEGRAL.
In this paper, we take a more radical approach to the problem of the HXR emission of Ophiuchus and consider not only the SED properties of synchrotron plus ICS scenarios (from both primary and secondary electrons) but also the physical consequences of the ICS origin of the HXR emission in all models so far viable: primary electron model (Sect. 2.1), secondary electron models from pp collisions (Sect. 2.2) and from DM annihilation (Sect. 2.3) and finally a Warming Ray model (Sect. 3). We discuss our conclusions in Sect. 4.
Throughout the paper, we use a flat, vacuum-dominated cosmological model with
![]() ,
,
![]() and h = 0.7.
and h = 0.7.
2 Modeling the electron populations in Ophiuchus
The spatial distribution of the IC thermal plasma in the Ophiuchus
cluster can be represented by
where
Non-thermal electrons capable of producing the cluster HXR
emission by ICS on CMB photons must have energies
![]() in the range
in the range ![]() 1.6-2.7 GeV, in the case of HXR emission observed in the 20-60 keV range (see, e.g., Colafrancesco et al. 2005).
1.6-2.7 GeV, in the case of HXR emission observed in the 20-60 keV range (see, e.g., Colafrancesco et al. 2005).
We discuss, in the following, the predictions of various models for the origin of the high-E electrons: i) primary electron model (PEM) (see, e.g., Colafrancesco et al. 2005 and references therein); ii) secondary electron model produced by proton-proton (pp) collisions in the cluster atmosphere (SEM-pp) (see, e.g., Colafrancesco & Blasi 1998; Blasi & Colafrancesco 1999; Marchegiani et al. 2007); iii) secondary electron models produced by neutralino Dark Matter annihilation (SEM-DM) (see e.g., Colafrancesco et al. 2006; Profumo 2008).
The electron spectra expected in the previous models are normalized by assuming that the produced ICS HXR emission equals the Swift-BAT/INTEGRAL data.
In addition to the previous models, we also consider a self-consistent warming-ray (WR) electron model (see e.g. Colafrancesco & Marchegiani 2008; Colafrancesco et al. 2004) in which the cluster atmosphere is heated - in a quasi stationary equilibrium condition between heating and cooling - by the interactions of non-thermal cosmic-ray protons with the IC gas. We note that this WR model reproduces the X-ray properties of the thermal IC gas (namely its temperature and density profiles) and, therefore, we use this constraint to predict the cluster ICS HXR emission.
2.1 Primary electron model (PEM)
The high-E electron spectrum is usually constrained by using the
radio halo synchrotron spectrum that provides direct information
about the electron spectral shape (see e.g., Colafrancesco et al.
2005 for a discussion).
However, the upper limits to the Ophiuchus radio halo (see
Perez-Torres et al. 2008) and the measurement at 1.4 GHz made by Govoni et al. (2009) are insufficient to determine precisely the electron spectrum. Therefore, we choose to adopt here a simple power-law model
with p=3.5, which corresponds to a radio spectral index of
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0,clip]{AA118...
...udegraphics[height=8.cm,width=8.cm,angle=0.0,clip]{AA11843Fig1b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg45.png) |
Figure 1:
The diffuse radio-emission spectrum produced by primary electrons with p=3.5 ( upper panel) and p=4.4 ( lower panel) is shown for different values of the uniform magnetic field (in units of |
| Open with DEXTER | |
The value of the normalization of the electron spectrum
![]() can be derived by reproducing the value of the HXR flux set by the
Swift-BAT and INTEGRAL experiments: for the previous spectral
index, we obtain the value
can be derived by reproducing the value of the HXR flux set by the
Swift-BAT and INTEGRAL experiments: for the previous spectral
index, we obtain the value
![]() GeV-1 cm-3 for p=3.5, and
GeV-1 cm-3 for p=3.5, and
![]() GeV-1 cm-3 for p=4.4.
GeV-1 cm-3 for p=4.4.
All the previous information can be derived, strictly speaking, for only the range of the electron energies that produce the HXR emission by means of ICS. To obtain information about other energy ranges of the electron spectrum, one must consider other constraints.
The only other constraint that can be placed on the electron
spectrum comes from the requirement that the heating rate of the
IC gas produced by non-thermal electron Coulomb collisions does
not exceed the bremsstrahlung cooling rate of the IC gas.
The heating rate produced by an electron with Lorentz
factor ![]() and velocity
and velocity ![]() is given by
is given by
where Z2 is the (suitably averaged) squared charge of the plasma's nuclei,
As a consequence, the heating rate induced by the electrons with
the spectrum assumed in Eq. (2) is given by:
while the cooling rate is given by
where
The two expressions in Eqs. (4) and (5)
equal (to the value
![]() erg cm-3 s-1) for the energy
erg cm-3 s-1) for the energy
![]() MeV for p=3.5, and for
MeV for p=3.5, and for
![]() MeV for p=4.4; we therefore,
assume that these energy values represent the minimum energy of
the primary electron spectra. As for the maximum electron energy,
we can safely choose
MeV for p=4.4; we therefore,
assume that these energy values represent the minimum energy of
the primary electron spectra. As for the maximum electron energy,
we can safely choose
![]() since its
specific value is irrelevant for the assumed spectral index.
since its
specific value is irrelevant for the assumed spectral index.
Based on these assumptions, it is possible to calculate the overall radiation emission by the various emission mechanisms in different frequency ranges.
The synchrotron emission spectrum produced at radio frequencies by
primary electrons is shown in Fig. 1 for
different values of the magnetic field (the B-field has been
assumed to be constant in the emission region, and this
corresponds, approximately, to consider a volume averaged value of
the magnetic field). From the radio emission, we can derive a
value of the average magnetic field of ![]() 0.1
0.1 ![]() G for
p=3.5 and
G for
p=3.5 and ![]() 0.2
0.2 ![]() G for p=4.4, which is in agreement
with that derived by Ajello et al. (2009) and Perez-Torres et al. (2008).
G for p=4.4, which is in agreement
with that derived by Ajello et al. (2009) and Perez-Torres et al. (2008).
In the gamma-ray frequency range, these primary electrons emit via non-thermal bremsstrahlung and ICS against CMB radiation field if their energy spectrum, as we assume in this case, extends up to high energies (at least up to
![]() GeV in order to produce ICS emission in the energy range 0.1-10 GeV).
Figure 2 shows that the EGRET upper limit on
Ophiuchus,
GeV in order to produce ICS emission in the energy range 0.1-10 GeV).
Figure 2 shows that the EGRET upper limit on
Ophiuchus,
![]() cm-2 s-1 (Reimer et al. 2003), is not exceeded in the p=3.5case, while it is marginally exceeded in the p=4.4 case.
In the first case, we can conclude that the HXR observation of the
Ophiuchus cluster sets a constraint on the ICS emission from
relativistic electrons that is stronger than the analogous limit
set by EGRET; in the second case, the EGRET limit is stronger than
the HXR limit. The signals we derive here for the gamma-ray
emission of Ophiuchus in the PEM, and in particular the one
derived from non-thermal bremsstrahlung emission, are sensibly
larger than the Fermi sensitivity at
cm-2 s-1 (Reimer et al. 2003), is not exceeded in the p=3.5case, while it is marginally exceeded in the p=4.4 case.
In the first case, we can conclude that the HXR observation of the
Ophiuchus cluster sets a constraint on the ICS emission from
relativistic electrons that is stronger than the analogous limit
set by EGRET; in the second case, the EGRET limit is stronger than
the HXR limit. The signals we derive here for the gamma-ray
emission of Ophiuchus in the PEM, and in particular the one
derived from non-thermal bremsstrahlung emission, are sensibly
larger than the Fermi sensitivity at
![]() MeV;
therefore, this experiment could be able either to detect the
bremsstrahlung gamma-ray emission from Ophiuchus or set even
stronger limits on the non-thermal electron density.
MeV;
therefore, this experiment could be able either to detect the
bremsstrahlung gamma-ray emission from Ophiuchus or set even
stronger limits on the non-thermal electron density.
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig2b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg71.png) |
Figure 2:
The gamma-ray spectrum produced by primary electrons with p=3.5 ( upper panel) and p=4.4 ( lower panel) via ICS (dashed) and bremsstrahlung (dot-dashed) are compared to the sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
We emphasize that the HXR data also sets indirectly a lower
cut-off of
![]() and 90 MeV for the two electron
spectrum models considered in order to ensure that the heating
rate does not exceeds the cooling rate.
and 90 MeV for the two electron
spectrum models considered in order to ensure that the heating
rate does not exceeds the cooling rate.
2.2 Secondary electron model from pp collisions (SEM-pp)
To calculate the overall radiation emission from secondary
electrons produced by collisions of cosmic ray (CR) non-thermal
protons and the thermal protons of the IC gas (see Marchegiani et al. 2007 for details), we assume that the non-thermal protons have the following spectrum
and we further assume, also in this case, that their spatial distribution is the same as that of the thermal IC gas out to the virial radius.
In a way similar to the PEM model, we assume proton spectral
indices of s=2.5 and s=3.4, which again provide radio
spectral indices of
![]() and 1.7, respectively.
and 1.7, respectively.
The HXR data explained in terms of the ICS emission of the
secondary electrons, provides values of
![]() GeV-1 cm-3 (for s=2.5) and
GeV-1 cm-3 (for s=2.5) and
![]() GeV-1 cm-3 (for s=3.4) for the
normalization of the spectrum in Eq. (6).
GeV-1 cm-3 (for s=3.4) for the
normalization of the spectrum in Eq. (6).
These values of the proton density normalization imply serious problems for Ophiuchus:
- i)
- first, the proton pressure at the center of the cluster is more than 5 times higher than the thermal gas pressure for s=2.5 and 367 times higher for s=3.4, which causes serious problems for the cluster stability;
- ii)
- secondly, the heating rate (Coulomb losses and hadronic
collisions) induced by non-thermal protons in the cluster center
is
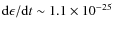 erg cm-3 s-1for s=2.5, and
erg cm-3 s-1for s=2.5, and
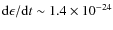 erg cm-3 s-1 for s=3.4; these values are about 23 and 298 times higher than the cooling rate. This implies that there is a quite rapid heating of the cluster,
erg cm-3 s-1 for s=3.4; these values are about 23 and 298 times higher than the cooling rate. This implies that there is a quite rapid heating of the cluster,
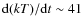 keV Gyr-1 and
keV Gyr-1 and
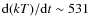 keV Gyr-1, that will bring in a short time the whole IC gas to a temperature sensitively different (larger) from the observed one;
keV Gyr-1, that will bring in a short time the whole IC gas to a temperature sensitively different (larger) from the observed one;
- iii)
- finally, the gamma-ray emission produced by both secondary electrons and neutral pion decay (see Fig. 3) exceeds the EGRET upper limit for Ophiuchus by a factor
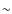 18
and 170, for s=2.5 and 3.4, respectively.
18
and 170, for s=2.5 and 3.4, respectively.
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig3b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg80.png) |
Figure 3:
The gamma-ray spectrum of Ophiuchus
with s=2.5 ( upper panel) and s = 3.4 ( lower panel) produced by ICS (dashes) and bremsstrahlung (dot dashes) of secondary electrons and by neutral pion decay (long dashes).
We compare the predictions of the SEM-pp model with the sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
2.3 Secondary electron model from DM annihilation (SEM-DM)
We consider here three neutralino DM models (similar to the
analysis of Profumo 2008) with neutralino masses
![]() ,
and
,
and
![]() GeV.
GeV.
For each neutralino model, we consider a radial DM density profile
given by
(Navarro et al. 2004), where
To derive the equilibrium spectrum of these secondary electrons in
Ophiuchus, we consider the role of the dominant energy-loss
mechanisms. These are ICS losses against CMB photons and
synchrotron losses for electrons of energy higher than a few
hundred MeV (note that synchrotron losses for magnetic fields <3 ![]() G, are negligible compared to the ICS losses), while at low energies (
G, are negligible compared to the ICS losses), while at low energies (![]() 150 MeV) the dominant energy loss mechanisms
are Coulombian interactions with the IC gas particles.
For this reason, the final spatial distribution of secondary
electrons is proportional to
150 MeV) the dominant energy loss mechanisms
are Coulombian interactions with the IC gas particles.
For this reason, the final spatial distribution of secondary
electrons is proportional to
![]() at high energies (>150 MeV) and proportional to
at high energies (>150 MeV) and proportional to
![]() at low energies (<150 MeV).
at low energies (<150 MeV).
The DM-produced secondary electron density is fixed, also in this
case, by requiring that their ICS emission fits the observed HXR
emission; this constraint corresponds to fixing the value of the
neutralino annihilation cross-section,
![]() ,
because both the neutralino mass and its composition have been
fixed by the chosen model.
,
because both the neutralino mass and its composition have been
fixed by the chosen model.
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig4.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg90.png) |
Figure 4:
The heating rate induced by secondary electrons produced by DM annihilation is shown at different radii for different neutralino models:
|
| Open with DEXTER | |
This SEM-DM model also has serious implications for the Ophiuchus cluster:
- i)
- the heating rate at the cluster center produced by the
secondary SEM-DM electrons is very high; Fig. 4
shows the secondary electrons heating rate at different radii
compared to the cooling rate of the thermal IC gas. In fact, the
heating rate largely exceeds the cooling rate in the cluster core
at r<30 kpc. This result implies a rapid over-heating of the
Ophiuchus core, even though the volume integral of the heating
rate is always lower than the volume integral of the cooling rate
(this last quantity is
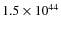 erg s-1, while the
integrated heating rate is
erg s-1, while the
integrated heating rate is
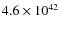 erg s-1,
erg s-1,
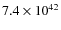 erg s-1, and
erg s-1, and
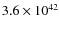 erg s-1 for
erg s-1 for
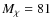 ,
40, and 10 GeV, respectively);
,
40, and 10 GeV, respectively);
- ii)
- we show in Fig. 5 the gamma-ray emission
spectra produced by the DM composite model worked out here via the
three main mechanisms of gamma-ray emission: ICS and
bremsstrahlung from secondary electrons, and neutral pion decay.
All the three DM models considered in this composite DM model for
Ophiuchus produce a gamma-ray flux that exceeds the EGRET limit,
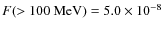 cm-2 s-1 (the
low-mass neutralino model with
cm-2 s-1 (the
low-mass neutralino model with
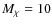 GeV is marginally
consistent with the EGRET limit). The gamma-ray flux of Ophiuchus
at E > 100 MeV produced under the assumption that the same DM model reproduces the HXR data, are
GeV is marginally
consistent with the EGRET limit). The gamma-ray flux of Ophiuchus
at E > 100 MeV produced under the assumption that the same DM model reproduces the HXR data, are
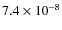 ,
,
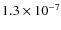 ,
and
,
and
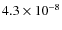 cm-2 s-1 for neutralino masses of 81, 40, and 10 GeV.
A direct prediction of this DM model is that the gamma-ray flux
produced by the three neutralino models considered here should be
easily detectable by the Fermi experiment, whose results will be
able, therefore, to validate or exclude this model for the origin
of the HXR emission of Ophiuchus;
cm-2 s-1 for neutralino masses of 81, 40, and 10 GeV.
A direct prediction of this DM model is that the gamma-ray flux
produced by the three neutralino models considered here should be
easily detectable by the Fermi experiment, whose results will be
able, therefore, to validate or exclude this model for the origin
of the HXR emission of Ophiuchus;
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig5.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg100.png)
Figure 5: The overall gamma-ray spectrum produced by the composition of the contributions of the secondary SEM-DM electrons (ICS and bremsstrahlung) and of the neutral pion decay for the three neutralino models here considered. The sensitivity curves of EGRET and Fermi (5
 ,
1 year observation) are shown
for comparison.
,
1 year observation) are shown
for comparison. Open with DEXTER - iii)
- Figure 6 shows the diffuse synchrotron radio spectra produced by the same secondary SEM-DM electrons by
assuming a reference value of the average intracluster magnetic
field in Ophiuchus of 0.1
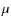 G. This figure shows that, for this
value of magnetic field, a model with neutralino mass between 40
and 80 GeV can reproduce the radio data.
G. This figure shows that, for this
value of magnetic field, a model with neutralino mass between 40
and 80 GeV can reproduce the radio data.
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig6.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg103.png) |
Figure 6:
The radio halo spectrum produced from secondary SEM-DM electrons via synchrotron emission in a constant magnetic field of 0.1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig7.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg104.png) |
Figure 7:
The radio halo spectrum produced from secondary SEM-DM electrons via synchrotron emission in a constant magnetic field of 0.055, 0.18, and 0.39 |
| Open with DEXTER | |
3 Warming ray model
We abandon now the strategy of fitting the ICS emission produced
by high-E electrons to the HXR data of Swift and INTEGRAL because
we evaluate - in the framework of the warming ray (WR) model (see
Colafrancesco & Marchegiani 2008; Colafrancesco et al. 2004) -
the spectral and spatial characteristics of the WR proton
population producing through their heating action the temperature
structure of the Ophiuchus cluster, namely a constant temperature
radial profile at the observed value of
![]() keV.
keV.
The proton spectrum is written as in Eq. (6),
with the values s=2.5 and s=3.4, and assuming a radial
distribution given by
![]() ,
where the
value of
,
where the
value of ![]() is found by fitting the radial temperature
profile of the cluster (see Colafrancesco & Marchegiani 2008, for technical details). The best fit analysis of the temperature profile of Ophiuchus provides the value
is found by fitting the radial temperature
profile of the cluster (see Colafrancesco & Marchegiani 2008, for technical details). The best fit analysis of the temperature profile of Ophiuchus provides the value
![]() ,
in analogy to what is found for other isothermal clusters (see discussion in Colafrancesco & Marchegiani 2008), while the central WR density
is
,
in analogy to what is found for other isothermal clusters (see discussion in Colafrancesco & Marchegiani 2008), while the central WR density
is
![]() cm-3 GeV-1 and
cm-3 GeV-1 and
![]() cm-3 GeV-1 for s=2.5 and
s=3.4 respectively, i.e., a factor
cm-3 GeV-1 for s=2.5 and
s=3.4 respectively, i.e., a factor ![]() 31 and 362 lower
than that required to reproduce, in this model, the Swift
BAT/INTEGRAL HXR data.
Consequently, the pressure ratio of the WR to the thermal gas at
the cluster center is
31 and 362 lower
than that required to reproduce, in this model, the Swift
BAT/INTEGRAL HXR data.
Consequently, the pressure ratio of the WR to the thermal gas at
the cluster center is
![]() for s=2.5 and
for s=2.5 and
![]() for s=3.4: the first value does not affect the overall stability of the cluster in any way, while the second one is a problematic situation.
for s=3.4: the first value does not affect the overall stability of the cluster in any way, while the second one is a problematic situation.
The diffuse radio emission produced by the secondary electron in
this WR model is shown in Fig. 8 for various
values of the uniform magnetic field; our results indicate that a
uniform B-field of the order of ![]() 0.4
0.4 ![]() G is required to
fit the available data for s=2.5, and
G is required to
fit the available data for s=2.5, and
![]()
![]() G for
s=3.4.
G for
s=3.4.
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig8b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg114.png) |
Figure 8:
The radio halo spectrum produced by secondary electrons with s=2.5 ( upper panel) and s=3.4 ( lower panel) in the WR model is shown for different values of a constant IC magnetic field (as labeled) in units of |
| Open with DEXTER | |
Figure 9 shows the diffuse gamma-ray emission
from Ophiuchus as expected in the WR model: this emission consists
of the combination of the neutral pion decay spectrum and ICS and
bremsstrahlung emission from secondary electrons. The overall
gamma-ray emission of Ophiuchus in the WR model,
![]() cm-2 s-1 and
cm-2 s-1 and
![]() cm-2 s-1 for s=2.5 and s=3.4, respectively, is below the EGRET limit. However, the neutral pion decay gamma-ray emission predicted in this WR model should be detectable by Fermi with a 1 yr observation (5
cm-2 s-1 for s=2.5 and s=3.4, respectively, is below the EGRET limit. However, the neutral pion decay gamma-ray emission predicted in this WR model should be detectable by Fermi with a 1 yr observation (5![]() c.l.).
c.l.).
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig9b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg117.png) |
Figure 9:
The gamma-ray spectrum produced by secondary electrons with s=2.5 ( upper panel) and s=3.4 ( lower panel) via ICS (dashes) and bremsstrahlung (dot-dashes) and neutral pion decay (solid) in the WR model constrained to reproduce the observed temperature structures of the IC gas in Ophiuchus. The sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
4 Discussion and conclusions
We have demonstrated that various and serious problems exist with the ICS interpretation of the HXR excess emission from the Ophiuchus cluster and, in general, of galaxy clusters for which an HXR emission excess has been detected. These problems are:
- i)
- The true level of the HXR emission flux. The derivation of an HXR emission excess in clusters seems to depend strongly on the precise determination of the background thermal bremsstrahlung
emission. Using INTEGRAL data, Eckert et al. (2008) derived an HXR flux in the 20-60 keV band of
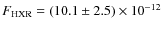 erg cm-2 s-1, for an IC gas temperature of
erg cm-2 s-1, for an IC gas temperature of
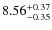 keV. Using Swift BAT data, Ajello et al. (2009) derived an upper limit
(90% c.l.) of
keV. Using Swift BAT data, Ajello et al. (2009) derived an upper limit
(90% c.l.) of
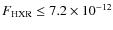 erg cm-2 s-1, for a different IC gas temperature of
9.5+1.4-1.1 keV; we note that the same authors (Ajello et al. 2009) derived an upper limit to the HXR flux of
erg cm-2 s-1, for a different IC gas temperature of
9.5+1.4-1.1 keV; we note that the same authors (Ajello et al. 2009) derived an upper limit to the HXR flux of
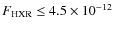 erg cm-2 s-1 by using a higher value of temperature
erg cm-2 s-1 by using a higher value of temperature
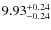 keV, obtained by using a combination of Chandra and Swift-BAT data.
keV, obtained by using a combination of Chandra and Swift-BAT data.
In conclusion, it is clear that a crucial input quantity in determining the value of the HXR excess flux is the detailed modeling of the thermal emission of the IC gas, because different values assumed for the IC gas temperature lead to different conclusions about the amount of HXR excess flux (see, e.g., the long standing discussion about evidence and counter evidence of the HXR excess in Coma, Fusco-Femiano et al. 1999, 2004, 2007, 2008; Rossetti & Molendi 2004, 2007; see also Petrosian et al. 2008 for a review). For this reason, it would be extremely important to estimate the temperature of the IC gas with measurements that are independent of those obtained in the X-ray band. In this context, we note that a reliable method of measuring IC gas temperatures can be found by using Sunyaev-Zel'dovich observations over a wide spectral band (from 100 to
100 to  400 GHz) reaching high frequencies
where the sensitivity of the SZE to the cluster temperature is
maximal (discussion of this issue in detail is found in a
dedicated paper, Colafrancesco & Marchegiani 2009; see also
Colafrancesco et al. 2003; Colafrancesco 2007 for a review).
400 GHz) reaching high frequencies
where the sensitivity of the SZE to the cluster temperature is
maximal (discussion of this issue in detail is found in a
dedicated paper, Colafrancesco & Marchegiani 2009; see also
Colafrancesco et al. 2003; Colafrancesco 2007 for a review).
- ii)
- The ICS HXR scenario. The hypothesis that high-E electrons are responsible for an ICS HXR emission at the level found by the combination of Swift-BAT and INTEGRAL observations leads to some important consequences.
First, to reconcile the HXR excess value with the relative diffuse synchrotron radio emission (from the same electron population) at the level observed in the same cluster, the value of the average magnetic field must be quite low and of the order of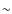 0.1
0.1 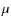 G for p = 3.5 and
G for p = 3.5 and 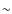 0.2
0.2 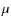 G for p = 4.4 (see Fig. 1). The result found for Ophiuchus is analogous to that derived for other clusters (see also our previous results discussed in Colafrancesco et al. 2005,
Marchegiani et al. 2007). Specifically, we found
that the data are consistent with an IC magnetic field of order
G for p = 4.4 (see Fig. 1). The result found for Ophiuchus is analogous to that derived for other clusters (see also our previous results discussed in Colafrancesco et al. 2005,
Marchegiani et al. 2007). Specifically, we found
that the data are consistent with an IC magnetic field of order
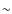 0.7 and 1.2
0.7 and 1.2 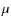 G at the cluster center with a decreasing
radial profile similar to that of the IC gas, for p = 3.5 and 4.4,
respectively.
G at the cluster center with a decreasing
radial profile similar to that of the IC gas, for p = 3.5 and 4.4,
respectively.
Secondly, there is a strong relation between the ICS HXR emission level and the relative gamma-ray emission and the consequences on the physics of the cluster, i.e., the heating of the IC gas and the ratio of non-thermal to thermal pressures:
- if the electrons producing the HXR emission are primaries, their gamma-ray emission (dominated at E < 1 GeV by non-thermal bremsstrahlung) is slightly lower than the EGRET upper limit in the p = 3.5 model, and slightly higher than this limit in the p = 4.4 model, but certainly detectable by Fermi (see Fig. 2). If Fermi does not detect this gamma-ray emission, one should conclude that the ICS HXR emission is much lower than the Swift-INTEGRAL HXR detection and that the relativistic electron content of Ophiuchus is consequently much lower. The HXR data imply, in addition, a lower cut-off of and 93 MeV (for p = 3.5 and 4.4) on the electron spectrum in order to maintain a heating rate not higher than the cooling rate;
and 93 MeV (for p = 3.5 and 4.4) on the electron spectrum in order to maintain a heating rate not higher than the cooling rate;
- if the electrons responsible for the ICS HXR emission are secondary particles produced in the decay of charged pions generated by cosmic-ray proton collisions with the IC gas protons (SEM-pp), then an ICS flux set at the HXR observations has unacceptable consequences. Specifically, we find that: in the s = 2.5 case, the pressure exerted by relativistic protons at the cluster center is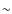 5 times higher than the thermal gas one; the heating rate induced by the same relativistic protons at the cluster center is
5 times higher than the thermal gas one; the heating rate induced by the same relativistic protons at the cluster center is 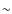 23 times higher than the IC gas cooling rate; and the gamma-ray emission produced by neutral pion decay exceeds the EGRET limit by a factor
23 times higher than the IC gas cooling rate; and the gamma-ray emission produced by neutral pion decay exceeds the EGRET limit by a factor  18; in the s = 3.4 case, these quantities increase to
18; in the s = 3.4 case, these quantities increase to  367, 298, and 170, respectively (see Fig. 3). For all these reasons, we conclude that if
electrons produce an ICS HXR emission in the observed range, they
cannot be secondary (in the SEM-pp). This conclusion is analogous
to that found for other clusters like Coma, A2199, A2163, and
Perseus (see Colafrancesco & Marchegiani 2008);
367, 298, and 170, respectively (see Fig. 3). For all these reasons, we conclude that if
electrons produce an ICS HXR emission in the observed range, they
cannot be secondary (in the SEM-pp). This conclusion is analogous
to that found for other clusters like Coma, A2199, A2163, and
Perseus (see Colafrancesco & Marchegiani 2008);
- if electrons are produced by neutralino DM annihilation, we have found that: the heating rate they induce at the cluster center is quite high (see Fig. 4); the relative gamma-ray emission exceeds the EGRET limit for the two high-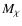 models considered here (
models considered here (
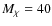 and 81 GeV) (see Fig. 5), with a marginal consistency for the low-mass model with
and 81 GeV) (see Fig. 5), with a marginal consistency for the low-mass model with 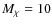 GeV; the radio flux produced by electrons is consistent with the available data for
GeV; the radio flux produced by electrons is consistent with the available data for
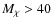 GeV, and for B < 0.18
GeV, and for B < 0.18 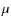 G. Therefore, the information inferred by gamma and
radio data are not compatible, and we conclude that it is not
possible to conceive that the ICS HXR emission of secondary SEM-DM
electrons has a flux close to that of the available observations
(i.e., the maximum allowed flux set by Swift and INTEGRAL, see
Sect. 1), and thus their annihilation cross-section must be much
lower than the values used by Profumo (2008).
Even normalizing these models to the lower allowed flux value of
the HXR excess of Ophiuchus (see our discussion in Sect. 1), all
the previous results vary (decrease) by
G. Therefore, the information inferred by gamma and
radio data are not compatible, and we conclude that it is not
possible to conceive that the ICS HXR emission of secondary SEM-DM
electrons has a flux close to that of the available observations
(i.e., the maximum allowed flux set by Swift and INTEGRAL, see
Sect. 1), and thus their annihilation cross-section must be much
lower than the values used by Profumo (2008).
Even normalizing these models to the lower allowed flux value of
the HXR excess of Ophiuchus (see our discussion in Sect. 1), all
the previous results vary (decrease) by 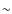 15%, leaving our
basic conclusions unchanged.
15%, leaving our
basic conclusions unchanged.
- iii)
- Relaxing the assumption of recovering the observed HXR excess and assuming that non-thermal protons act as warming rays (see Colafrancesco & Marchegiani 2008), it is possible to paint a much more acceptable scenario in which the unacceptable pressure ratios derived in SEM models do not hold since the ratio
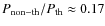 and 1.0 for s=2.5 and 3.4, respectively, and is constant throughout the cluster (this is because non-thermal protons must have the same spatial distribution as the thermal IC gas to recover the spatial
temperature distribution of the cluster).
and 1.0 for s=2.5 and 3.4, respectively, and is constant throughout the cluster (this is because non-thermal protons must have the same spatial distribution as the thermal IC gas to recover the spatial
temperature distribution of the cluster).
- i)
- it does not induce excess heating effects, since a quasi-stationary balance between heating and cooling is the working assumption of the WR model;
- ii)
- we found that the diffuse
radio emission produced in this case requires, for s=2.5 and
s=3.4 respectively, a value of the average magnetic field of
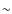 0.4 and 2
0.4 and 2 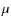 G (see Fig. 8) and a
central value of
G (see Fig. 8) and a
central value of 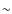 1.1 and 6
1.1 and 6 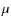 G with a radial profile
similar to that of the IC gas, which is consistent with the
general findings for clusters with Faraday Rotation measurements
(see, e.g., Carilli & Taylor 2002; Govoni & Feretti 2004);
G with a radial profile
similar to that of the IC gas, which is consistent with the
general findings for clusters with Faraday Rotation measurements
(see, e.g., Carilli & Taylor 2002; Govoni & Feretti 2004);
- iii)
- the gamma-ray emission produced in this model is considerably lower than the EGRET limit but definitely detectable by Fermi (see Fig. 9). The Fermi detection of this gamma-ray emission from Ophiuchus will have a crucial impact in proving or disproving this model.
To conclude, models of high-E electrons in clusters that can be adjusted to reproduce their ICS HXR emission at the level indicated by the available observations fail to work because they would imply unacceptable levels of heating and gamma-ray emission. In contrast, models of high-energy particles that are able to reproduce the IC gas temperature structure (i.e., the WR model) predict a level of non-thermal HXR ICS emission that is far below the current limits obtained with INTEGRAL and Swift-BAT, and provide an overall Spectral Energy Distribution that is consistent with all the available data - from radio to gamma-rays - for Ophiuchus as well as for other clusters.
Acknowledgements
We thank P. Ullio for providing detailed source spectra of the neutralino annihilation models considered in this paper. We also thank the referee, M. A. Perez-Torres, for his comments and suggestions that allowed us to improve the presentation of our results.
References
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2009, ApJ, 690, 367 [NASA ADS] [CrossRef] (In the text)
- Atoyan, A., & Volk, H. 2000, ApJ, 535, 45 [NASA ADS] [CrossRef] (In the text)
- Blasi, P., & Colafrancesco, S. 1999, Astropart. Phys., 12, 169 [NASA ADS] [CrossRef] (In the text)
- Brunetti, G. 2004, JKAS, 37, 493 [NASA ADS] (In the text)
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] (In the text)
- Colafrancesco, S. 2007, New Astron. Rev., 51, 394 [NASA ADS] [CrossRef] (In the text)
- Colafrancesco, S., & Blasi, P. 1998, Astropart. Phys., 9, 227 [NASA ADS] [CrossRef] (In the text)
- Colafrancesco, S., & Marchegiani, P. 2008, A&A, 484, 51 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Colafrancesco, S., & Marchegiani, P. 2009, preprint (In the text)
- Colafrancesco, S., Marchegiani, P., & Palladino, E. 2003, A&A, 397, 27 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Colafrancesco, S., Dar, A., & De Rújula, A. 2004, A&A, 413, 441 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Colafrancesco, S., Marchegiani, P., & Perola, G. C. 2005, A&A, 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Colafrancesco, S., profumo, S., & Ullio, P. 2006, A&A, 455, 21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dogiel, V. A., Colafrancesco, S., Ko, C. M., et al. 2007, A&A, 461, 433 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Eckert, D., Produit, N., Paltani, S., Neronov, A., & Courvoisier, T. J.-L. 2008, A&A, 479, 27 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ensslin, T., & Biermann, P. 1998, A&A, 330, 90 [NASA ADS] (In the text)
- Fujita, Y., Hayashida, K., Nagai, M., et al. 2008, PASJ, 60, 1133 [NASA ADS] (In the text)
- Fusco-Femiano, R., dal Fiume, D., Feretti, L., et al. 1999, ApJ, 513, L21 [NASA ADS] [CrossRef] (In the text)
- Fusco-Femiano, R., Orlandini, M., Brunetti, G., et al. 2004, ApJ, 602, L73 [NASA ADS] [CrossRef] (In the text)
- Fusco-Femiano, R., Landi, R., & Orlandini, M. 2007 [arXiv:astro-ph/0702576] (In the text)
- Fusco-Femiano, R., & Orlandini M. 2008 [arXiv:0802.1817] (In the text)
- Govoni, F., & Feretti, L. 2004, Inter. J. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef] (In the text)
- Govoni, F., Murgia, M., Markevitch, M., et al. 2009, A&A, 499, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Inoue, S., Aharonian, F. A., & Sugiyama, N. 2005, ApJ, 628, L9 [NASA ADS] [CrossRef] (In the text)
- Johnston, M. D., Bradt, H. V., Doxsey, R. E., et al. 1981, ApJ, 245, 799 [NASA ADS] [CrossRef] (In the text)
- Marchegiani, P., Perola, G. C., & Colafrancesco, S. 2007, A&A, 465, 41 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mohr, J. J., Mathiesen, B., & Evrard, A. E. 1999, ApJ, 517, 627 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., Hayashi, E., & Power, C. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] (In the text)
- Nevalainen, J., Oosterbroek, T., Bonamente, M., & Colafrancesco, S. 2004, ApJ, 608, 166 [NASA ADS] [CrossRef] (In the text)
- Perez-Torres, M. A., Alberdi, A., Romero-Canizales, C., et al. 2008 [arXiv:0812.3598] (In the text)
- Petrosian, V., Bykov, A., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 191 [NASA ADS] [CrossRef] (In the text)
- Profumo, S. 2008, AIP Conf. Proc., 1078, 551 [NASA ADS] (In the text)
- Reimer, O., Pohl, M., Sreekumar, P., & Mattox, J. R. 2003, ApJ, 588, 155 [NASA ADS] [CrossRef] (In the text)
- Rossetti, M., & Molendi, S. 2004, A&A, 414, L41 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rossetti, M., & Molendi, S. 2007 [arXiv:astro-ph/0702417] (In the text)
- Sarazin, C. 1999, ApJ, 520, 529 [NASA ADS] [CrossRef] (In the text)
- Slee, O. B. 1977, AuJPA, 43, 1 [NASA ADS] [CrossRef] (In the text)
- Slee, O. B., & Higgins, C. S. 1975, AuJPA, 36, 1 [NASA ADS] (In the text)
- Takahashi, T., Makishima, K., Fukazawa, Y., et al. 2004, New AR, 48, 269 [NASA ADS] [CrossRef] (In the text)
- Timokhin, A. N., Aharonian, F. A., & Neronov, A. Yu. 2004, A&A, 417, 391 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Watanabe, M., Yamashita, K., Furuzawa, A., Kunieda, H., & Tawara, Y. 2001, PASJ, 53 605 (In the text)
All Figures
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0,clip]{AA118...
...udegraphics[height=8.cm,width=8.cm,angle=0.0,clip]{AA11843Fig1b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg45.png) |
Figure 1:
The diffuse radio-emission spectrum produced by primary electrons with p=3.5 ( upper panel) and p=4.4 ( lower panel) is shown for different values of the uniform magnetic field (in units of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig2b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg71.png) |
Figure 2:
The gamma-ray spectrum produced by primary electrons with p=3.5 ( upper panel) and p=4.4 ( lower panel) via ICS (dashed) and bremsstrahlung (dot-dashed) are compared to the sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig3b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg80.png) |
Figure 3:
The gamma-ray spectrum of Ophiuchus
with s=2.5 ( upper panel) and s = 3.4 ( lower panel) produced by ICS (dashes) and bremsstrahlung (dot dashes) of secondary electrons and by neutral pion decay (long dashes).
We compare the predictions of the SEM-pp model with the sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig4.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg90.png) |
Figure 4:
The heating rate induced by secondary electrons produced by DM annihilation is shown at different radii for different neutralino models:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig5.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg100.png) |
Figure 5:
The overall gamma-ray spectrum produced by the composition of the contributions of the secondary SEM-DM electrons (ICS and bremsstrahlung) and of the neutral pion decay for the three neutralino models here considered. The sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig6.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg103.png) |
Figure 6:
The radio halo spectrum produced from secondary SEM-DM electrons via synchrotron emission in a constant magnetic field of 0.1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig7.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg104.png) |
Figure 7:
The radio halo spectrum produced from secondary SEM-DM electrons via synchrotron emission in a constant magnetic field of 0.055, 0.18, and 0.39 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig8b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg114.png) |
Figure 8:
The radio halo spectrum produced by secondary electrons with s=2.5 ( upper panel) and s=3.4 ( lower panel) in the WR model is shown for different values of a constant IC magnetic field (as labeled) in units of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig...
...\includegraphics[height=8.cm,width=8.cm,angle=0.0]{AA11843Fig9b.ps}
\end{figure}](/articles/aa/full_html/2009/30/aa11843-09/Timg117.png) |
Figure 9:
The gamma-ray spectrum produced by secondary electrons with s=2.5 ( upper panel) and s=3.4 ( lower panel) via ICS (dashes) and bremsstrahlung (dot-dashes) and neutral pion decay (solid) in the WR model constrained to reproduce the observed temperature structures of the IC gas in Ophiuchus. The sensitivity curves of EGRET and Fermi (5 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}n_{\rm th}(r)=n_{{\rm th},0} \left[ 1+\left( \frac{r}{r_{\rm c}} \right)^2 \right]^{-q_{\rm th}}
\end{displaymath}](/articles/aa/full_html/2009/30/aa11843-09/img34.png)
![$\displaystyle -{{\rm d}E\over {\rm d}t}\approx K ~ z^2~ Z^2~{1\over \beta}~
\left [\ln {2~ m_{\rm e}~ c^2~ \beta^2 \gamma^2\over I_{\rm p}} -\beta^2\right],$](/articles/aa/full_html/2009/30/aa11843-09/img51.png)