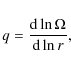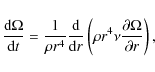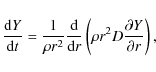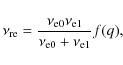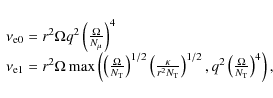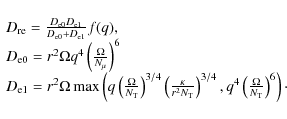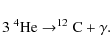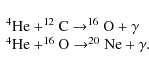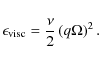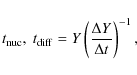EDP Sciences
Home All issues Volume 502 / No 3 (August II 2009) A&A, 502 3 (2009) 871-881 Full HTML
Free Access
Issue
A&A
Volume 502, Number 3, August II 2009
Page(s) 871 - 881
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200911619
Published online 15 June 2009

The effect of rotation on the stability of nuclear burning in accreting neutron stars

L. Keek1,2,[*] - N. Langer1 - J. J. M. in 't Zand2

1 - Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
2 - SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands

Received 5 January 2009 / Accepted 3 May 2009

Abstract
Hydrogen and/or helium accreted by a neutron star from a binary companion may undergo thermonuclear fusion. Different burning regimes are discerned at different mass accretion rates. Theoretical models predict helium fusion to proceed as a thermonuclear runaway for accretion rates below the Eddington limit and as stable burning above this limit. Observations, however, place the boundary close to 10% of the Eddington limit. We study the effect of rotationally induced transport processes on the stability of helium burning. For the first time, detailed calculations of thin-shell helium burning on neutron stars are performed using a hydrodynamic stellar evolution code including rotation and rotationally induced magnetic fields. We find that in most cases the instabilities from the magnetic field provide the dominant contribution to the chemical mixing, while Eddington-Sweet circulations become important at high rotation rates. As helium is diffused to greater depths, the stability of the burning is increased, such that the critical accretion rate for stable helium burning is found to be lower. Combined with a higher heat flux from the crust, as suggested by recent studies, turbulent mixing could explain the observed critical accretion rate. Furthermore, close to this boundary we find oscillatory burning, which previous studies have linked to mHz QPOs. In models where we continuously lower the heat flux from the crust, the period of the oscillations increases by up to several tens of percents, similar to the observed frequency drift, suggesting that this drift could be caused by the cooling of deeper layers.

Key words: accretion, accretion disks - stars: neutron - stars: rotation - stars: magnetic fields - X-rays: binaries

1 Introduction

Neutron stars in low-mass X-ray binaries (LMXBs) accrete matter from a companion star through Roche-lobe overflow. Because of conservation of angular momentum, the matter forms a disk around the neutron star, where it radiates away a large fraction of the potential energy before reaching the neutron star surface. The companion is typically a main sequence star, donating matter with a large hydrogen abundance. For a number of systems likely to have a white dwarf companion, hydrogen may be deficient but helium is not (Nelson et al. 1986; in 't Zand et al. 2005; Webbink et al. 1983).

The accreted matter is thought to quickly spread over the neutron star surface, forming a thin layer. When this layer is a few meters thick, the temperature and density at the base reach the ignition conditions for hydrogen and helium fusion. The thermonuclear burning can proceed in a stable or an unstable manner, depending on the temperature dependence of the burning and cooling rates, which in turn depend on the conditions in the thin burning shell. These conditions are largely set by the mass accretion rate (Fujimoto et al. 1981; see also Bildsten 1998). Models predict that hydrogen burning via the CNO cycle is stable for $\dot{M}\gtrsim10^{-2}~\dot{M}_{{\rm Edd}}$(assuming spherical symmetry), while it is unstable for lower accretion rates (assuming a neutron star mass of $1.4~{M_{\odot}}$with a $10~{\rm km}$ radius, a hydrogen mass fraction X=0.7and a CNO mass fraction $Z_{{\rm CNO}}=0.01$; $\dot{M}_{{\rm Edd}}$is the critical accretion rate where the accretion luminosity equals the Eddington luminosity). For helium burning via the triple-alpha process, theory places the critical accretion rate at the Eddington limit $\dot{M}\simeq~\dot{M}_{{\rm Edd}}$ (Ayasli & Joss 1982; Fujimoto et al. 1981), which suggests that stable helium burning does not take place in practice. If the accreted matter is hydrogen-deficient, the transition is expected to take place at an even higher accretion rate because of the lack of heating by stable hydrogen burning: $\dot{M}\simeq10~\dot{M}_{{\rm Edd}}$(Bildsten 1998).

Nevertheless, there are observational indications that stable helium burning takes place at lower accretion rates. Van Paradijs et al. (1988) observed from ten sources, most of which are thought to accrete hydrogen-rich material, that the fraction of hydrogen and helium that is burned in a stable manner increases strongly with the mass accretion rate, while no bursts are observed at accretion rates of $\dot{M}\gtrsim0.3~\dot{M}_{{\rm Edd}}$. Cornelisse et al. (2003) found for 4U 1820-30, which likely has a hydrogen-deficient mass donor, that the burst rate is lower by a factor of 5 for $\dot{M}\gtrsim0.07~\dot{M}_{{\rm Edd}}$than for lower mass accretion rates, while no bursts are observed at $\dot{M}\gtrsim0.14~\dot{M}_{{\rm Edd}}$. Therefore, the transition of unstable to stable burning probably takes place within several tens of percents of $0.1~\dot{M}_{{\rm Edd}}$.

A possible solution for this discrepancy is to include mixing processes. If hydrogen and/or helium are mixed to greater depths, where temperature and density are higher, the conditions under which the fuel is burned are different. An efficient source of mixing is formed by rotationally induced hydrodynamic instabilities (Fujimoto 1993). Yoon et al. (2004a) studied the effect of rotational mixing processes on thin shell burning in accreting white dwarfs and find that burning proceeds more stably. Piro & Bildsten (2007) calculated the effect of turbulent mixing in neutron stars, including mixing due to rotationally induced magnetic fields (Spruit 2002). They find that the magnetic fields are the main driver of the mixing. Their analysis of helium accretion onto an iron layer shows that, in the case of unstable burning, rotationally induced mixing allows for lower recurrence times for helium flashes. Furthermore, their models including mixing allow for steady-state burning at accretion rates below $\dot{M}_{{\rm Edd}}$. Analytically, the dependence of $\dot{M}_{{\rm st}}$, the accretion rate at the transition between stable and unstable burning, on the rotation rate of the neutron star, $\Omega $, is derived as $\dot{M}_{{\rm st}}\propto\Omega^{0.62}$. For neutron stars that rotate slower than 10% of the Keplerian velocity at the surface, Piro & Bildsten (2007) find $0.25~\dot{M}_{{\rm Edd}}\lesssim~\dot{M}_{{\rm st}}\lesssim~\dot{M}_{{\rm Edd}}$.

Piro & Bildsten (2007) created one-dimensional numerical models of the neutron star envelope using analytical approximations of chemical mixing and of helium burning. In this paper we study the effect of mixing due to rotation and a rotationally induced magnetic field on the stability of helium burning in the neutron star envelope in more detail. We present the results of detailed numerical simulations, where we use a one-dimensional multi-zone model of the outer layers of the neutron star. We introduce both rotation and magnetic fields in the model. Using a stellar-evolution code, we investigate the stability of the burning as a function of the mass accretion rate, the rotation rate of the neutron star core and the heat flux emanating from the crust.

2 Method

To model the outer layers of the neutron star we employ a stellar evolution code that is a modified version of the code used by Yoon et al. (2004a) to model the nuclear burning of helium shells in white dwarfs. It implicitly solves the stellar structure equations on a one-dimensional grid consisting of a series of mass shells. The effect of the centrifugal force on the stellar structure is taken into account. Consequently, the mass shells are isobars rather than spherical shells (cf. Heger et al. 2000). The chemical evolution is modeled by an extensive nuclear network. The effects of rotation on the chemical mixing and the transport of angular momentum are calculated. The effects of a rotationally induced magnetic field on the mixing of angular momentum and chemical species are calculated as well (Spruit 2002). Convection is taken into account using the Ledoux criterion. Neutrino losses are calculated using the results of Itoh et al. (1996). We make use of the OPAL tables (Iglesias & Rogers 1996) for determining opacities. Heating due to viscous energy dissipation is not taken into account because it will prove to be negligible with respect to the assumed flux from the crust or the energy release from nuclear burning.

We consider the accretion of matter that is hydrogen-deficient, but has a large (99%) helium content. This allows us to study the stability of helium shell burning without the complication of the nuclear processes involving hydrogen. We discuss the potential effect of including hydrogen on our results.

Relativistic effects are not considered during the simulation, since they are small in the thin helium-burning shell. The effect of general relativity on observables, such as the luminosity and mass accretion rate, can be taken into account with appropriate gravitational redshift factors (e.g. Woosley et al. 2004), reducing the values for the observables typically by several tens of percent. We do not apply these corrections to our results, as we are primarily interested in the relative effect of rotationally induced mixing on the stability of shell burning.

As our models are one-dimensional, any asymmetries in the longitudinal and latitudinal directions are not resolved. For example, burning likely starts at one location in the envelope, after which it spreads to other regions (Bildsten 1995; Spitkovsky et al. 2002; Cooper & Narayan 2007). This idea is supported by the observation of so-called burst oscillations (Strohmayer et al. 1996; Strohmayer & Bildsten 2006), which are periodic variations in the light curve at the spin frequency of the neutron star that are observed during some type-I bursts. Also, Bildsten (1995) proposes a regime where the burning spreads relatively slowly across the surface on a similar timescale to the accretion of matter. We restrict ourselves to the case of stable helium burning, where flame spreading is not an issue.

2.1 Grid

The one-dimensional grid divides the star in shells with a certain mass and is separated into two parts to facilitate matter accretion, while limiting numerical noise in the nuclear burning region. In the inner Lagrangian part, each shell is assigned an absolute amount of mass, while in the outer so-called pseudo-Lagrangian part, a shell is assigned an amount of mass relative to the total mass in the model. To minimize numerical diffusion, we choose these regions such that the nuclear burning takes place in the Lagrangian part. After each time step, the grid is adjusted to ensure that any gradients in, for instance, temperature, energy generation rate or chemical composition are well resolved.

Apart from the different grid points our model has the notion of a ``core'', which represents the inner part of the star, which is not modeled in detail and which sets the inner boundary conditions of our grid. The core has a mass, radius, rotation rate and a luminosity. These quantities are kept at fixed values. During consecutive time steps, angular momentum is exchanged between the grid and the core, after which we return the angular momentum and velocity of the core to the initial values, effectively preventing the core to spin up or down. We can safely make this approximation, since the amount of angular momentum that is accreted on the timescale of nuclear burning is negligible with respect to the angular momentum of the core.

2.2 Accretion

Mass accretion is implemented by increasing the total amount of mass and scaling the mass of the grid points in the pseudo-Lagrangian region. The mass fractions of the isotopes at each of these grid points are set to the weighted mean of the original composition of the grid point and the assumed composition of the accreted matter, where we weigh by, respectively, the original mass of the grid point and the accreted mass that is added to the grid point.

The accreted matter originally carries angular momentum corresponding to orbital motion at the Keplerian angular velocity at the surface of $\Omega_{{\rm K}}=\sqrt{{\rm G}MR^{-3}}$, where M and R are the mass and radius of the star, respectively. We assume, however, that the angular momentum of the accreted material is quickly shared with a number of the outermost grid points. This region coincides with or is slightly smaller than the pseudo-Lagrangian region where the mass is added. The distribution of the angular momentum is done such that the specific angular momentum is constant in the outer region. After the accreted angular momentum is added to the model, the mixing of angular momentum resulting from the different viscous processes is applied to the model. As in the treatment of the accretion of mass, we make sure that the region where angular momentum is accreted lies outside the region of interest, i.e. well above the helium-burning shell.

2.3 Diffusivity and viscosity

Due to the accretion of angular momentum, the outer layers of the star spin faster than the core. Therefore a non-zero shear q is present:

\begin{displaymath}q=\frac{{\rm d}\ln\Omega}{{\rm d}\ln r}, \end{displaymath} (1)

where r is the radial coordinate. The shear can give rise to hydrodynamical instabilities. We consider the dynamical shear instability, the secular shear and the Solberg-Høiland instability as well as Eddington-Sweet circulation (see, e.g., Heger et al. 2000 for details of the implementation). Furthermore, we consider the presence of a rotationally induced magnetic field.

A magnetic field is employed following the prescription of the ``Tayler-Spruit dynamo'' presented by Spruit (2002). A small initial radial magnetic field Br winds up due to the shear to create a much stronger toroidal field $B_{\phi}$. The field growth is limited by magnetohydrodynamic (MHD) instabilities. In this process Bris increased as well, such that once an equilibrium situation is reached, the initial field strength Br is unimportant. Equilibrium is reached on much shorter timescales than the mixing processes induced by the magnetic field. Therefore, in our model we employ the equilibrium values for Br and $B_{\phi}$.

Both the magnetic and non-magnetic hydrodynamic instabilities cause turbulence, which allows for chemical mixing and the transport of angular momentum. Furthermore, angular momentum is also transported because of magnetic torques. We treat the chemical and angular momentum mixing as diffusion processes. Transfer of angular momentum is governed by the one-dimensional diffusion equation

\begin{displaymath}\frac{{\rm d}\Omega}{{\rm d}t}=\frac{1}{\rho r^{4}}\frac{{\rm... ...r}\left(\rho r^{4}\nu\frac{\partial\Omega}{\partial r}\right), \end{displaymath} (2)

with $\nu $ the viscosity and $\rho$ the density. Diffusion of the mass fraction Y of a given isotope, e.g. 4He, is calculated via

\begin{displaymath}\frac{{\rm d}Y}{{\rm d}t}=\frac{1}{\rho r^{2}}\frac{{\rm d}}{{\rm d}r}\left(\rho r^{2}D\frac{\partial Y}{\partial r}\right), \end{displaymath} (3)

where D is the diffusivity. D and $\nu $ are measures for the efficiency of the respective diffusion processes. The value of Dis generally less than $\nu $, since it requires more work to exchange material than to exchange angular momentum. For the non-magnetic instabilities we use $\nu=30D$ (Chaboyer & Zahn 1992). This is not the case for the D and $\nu $ that follow from the Tayler-Spruit mechanism, where angular momentum is transported due to magnetic torques, such that D and $\nu $ differ in their dependencies on q and $\Omega $.

The Tayler-Spruit formalism accounts for both compositional and a temperature gradients, which provide a stabilizing stratification against the magnetohydrodynamic instabilities that limit the growth of the magnetic field. The effective radial viscosity $\nu_{{\rm re}}$is described as a function of $\nu_{{\rm e0}}$ and $\nu_{{\rm e}1}$, the viscosities when thermal diffusion either can be ignored or dominates, respectively:

\begin{displaymath}\nu_{{\rm re}}=\frac{\nu_{{\rm e0}}\nu_{{\rm e1}}}{\nu_{{\rm e0}}+\nu_{{\rm e1}}}f(q), \end{displaymath} (4)

where the factor 0<f(q)<1 is introduced to ensure $\nu_{{\rm re}}$vanishes smoothly below a certain minimum shear (Spruit 2002).

\begin{displaymath}\begin{array}{l} \nu_{{\rm e0}}=r^{2}\Omega q^{2}\left(\frac{... ...}\left(\frac{\Omega}{N_{{\rm T}}}\right)^{4}\right),\end{array}\end{displaymath} (5)

with $N_{\mu}$ and $N_{{\rm T}}$ the ``compositional'' and thermal part of the buoyancy frequency, respectively, and $\kappa$the opacity (see Spruit 2002 for more details). Analogously, Spruit (2002) derive the following expression for the effective radial diffusivity $D_{{\rm re}}$:

\begin{displaymath}\begin{array}{l} D_{{\rm re}}=\frac{D_{{\rm e0}}D_{{\rm e1}}}... ...t(\frac{\Omega}{N_{{\rm T}}}\right)^{6}\right)\cdot \end{array}\end{displaymath} (6)

Analytic studies often use as approximation only $\nu_{{\rm e0}}$, $D_{{\rm e0}}$ or $\nu_{{\rm e}1}$, $D_{{\rm e1}}$. Since we study thermonuclear burning in a thin shell, both thermal and compositional gradients are expected to be important in the shell. In our models we, therefore, use Eqs. (4) and (6) including both parts.

While the Tayler-Spruit dynamo is often applied in the spherical approximation, we use it here for a thin shell (see also Piro & Bildsten 2007). For the dynamo to work, the presence of a non-zero shear locally is sufficient. Since the resulting magnetic field is predominantly toroidal, the angular momentum transport and the chemical mixing induced by the dynamo are limited to the radial region where the shear is present.

In Sect. 4.1 we discuss some potential problems with the Tayler-Spruit mechanism.

2.4 Nuclear network

An extensive nuclear network consisting of 35 isotopes and 65 nuclear reactions is employed to model the chemical evolution. The most important reaction sequence for our models is the triple alpha process, for which the net reaction is

\begin{displaymath}3~^{4}{\rm He\rightarrow^{12}C}+\gamma. \end{displaymath} (7)

Furthermore, alpha capture reactions onto carbon and oxygen are considered:

\begin{displaymath}\begin{array}{l} ^{4}{\rm He}+^{12}{\rm C}\rightarrow^{16}{\r... ...\rm He}+^{16}{\rm O}\rightarrow^{20}{\rm Ne}+\gamma.\end{array}\end{displaymath} (8)

We disable the energy output of the ${\rm ^{12}C+{}^{12}C}$ and ${\rm ^{12}C+{}^{16}O}$ reactions to prevent the occurrence of unstable carbon burning at greater depths in our models. Any heating that stable carbon may have provided can be modeled as an extra contribution to the heat flux from the crust (see Sect. 2.7).

2.5 Viscous and compressional heating

Viscous energy release due to the presence of shear heats the neutron star envelope. The energy generation rate per unit mass by viscous heating, $\epsilon_{{\rm visc}}$, can be calculated as

\begin{displaymath}\epsilon_{{\rm visc}}=\frac{\nu}{2}\left(q\Omega\right)^{2}. \end{displaymath} (9)

We find that the relatively small shear present in our models, in the range of rotation rates and mass accretion rates we consider, leads to a negligible amount of viscous heating, as the total energy generated per unit time is several orders of magnitude smaller than the assumed flux from the crust or the energy generated by stable helium burning (see also Piro & Bildsten 2007). Therefore, we do not take viscous heating into account in our calculations.

The continuous accretion of matter onto the neutron star compresses the matter in the envelope. This gives rise to compressional heating, which is calculated in our models.

2.6 Initial model

We start with a grid of approximately 600 grid points that represent the outer layers of the neutron star from a column depth of $y\simeq1~{\rm g~cm^{-2}}$ down to $y\simeq10^{11}~{\rm g~ cm^{-2}}$, with a total mass of $\simeq10^{24}~{\rm g}$. As initial composition we take 50% ${\rm ^{12}C}$ and 50% ${\rm ^{16}O}$. This acts as a buffer that is inert with respect to the triple-alpha reactions of helium burning. On this grid matter is accreted with a composition of 99% ${\rm ^{4}He}$ and 1% other isotopes, based on the equilibrium mass fractions of the CNO cycle.

We use a core with a mass of $M=1.4~M_{\odot}$ and a radius $R=10~{\rm km}$ for a canonical neutron star. The angular velocity of the core, $\Omega $, is expressed in units of the Keplerian angular velocity at the surface: $\Omega_{{\rm K}}=1.4\times10^{4}~{\rm radians~ s^{-1}}$. We create models with different values for $\Omega $. The heat flux from the neutron star crust is modeled by setting the luminosity at the inner boundary of our grid to a fixed value $L_{{\rm crust}}$.

2.7 Flux from the crust

As the ignition of the accreted helium depends strongly on the temperature and we do not consider heating by stable hydrogen burning, it is influenced by $L_{{\rm crust}}$. The crust is a deeper layer of the neutron star starting at $y \simeq10^{12}~{\rm g~ cm^{-2}}$ and extending down to the core where densities exceed the nuclear density. When matter is accreted onto the neutron star, the crust is compressed. This gives rise to pycnonuclear burning and electron-capture reactions that heat both the neutron star core and the outer layers. Therefore, this heat flux is generally assumed to scale with the accretion rate and a fixed energy generated per accreted nucleon is applied. Previous studies often use a value close to 0.1 MeV/nucleon (Haensel & Zdunik 2003). Cumming et al. (2006) use values in the range of 0.1-0.3 MeV/nucleon when studying the ignition conditions of long duration type I X-ray bursts. The analysis of the superburst from 4U 1608-52 (Keek et al. 2008) indicates that the temperature of the crust was likely much higher than predicted by current models. Recently Gupta et al. (2007) have calculated the thermal structure of the crust, for the first time including electron captures into excited states, finding a heat flux from the crust up to ten times higher than obtained in previous studies (see also Gupta et al. 2008). It is clear that the value of the heat flux from the crust is still not well determined. Therefore, we choose to vary it independently from the mass accretion rate.

Heat from helium burning in the envelope may be conducted into the core. From here it is either dissipated by neutrino emission or conducted outwards, back to the envelope on a thermal timescale on the order of $10^{4}~{\rm yr}$. This gives an extra contribution to $L_{{\rm crust}}$, the size of which depends on the amount of heat from the envelope conducted inwards and on the efficiency of neutrino cooling of the core. The latter is determined from the equation of state of the core (see discussion in Cumming et al. 2006), which is not well-constrained at this moment (see, e.g., Lattimer & Prakash 2007). Therefore, a certain value for $L_{{\rm crust}}$ can physically be obtained by different combinations of an outward flux from the core and the crust as well as an inward heat flux from the envelope. In our calculations we do not go into these details, but treat $L_{{\rm crust}}$ as a free parameter. When we make a comparison to the physical situation, we will assume that crustal heating gives the dominant contribution to $L_{{\rm crust}}$.

By choosing a certain value for $L_{{\rm crust}}$, we fix the total heat flow into and out of the envelope to a net flux into the envelope. For studying unstable burning, a flash would give rise to a large heat flow out of the envelope and our boundary condition would not be valid for the duration of the flash. However, we only consider stable burning, which leads to a relatively lower heat flux that is constant in time and is compatible with our boundary condition.

3 Results

3.1 Turbulent mixing

The accretion of angular momentum gives rise to shear, which causes turbulence and induces a magnetic field. These drive the transport of angular momentum and the mixing of the chemical composition. In turn, the chemical and angular velocity profiles influence the diffusivity and viscosity, until an equilibrium is reached. We present the properties of equilibrium models with different rotation rates of the core and different mass accretion rates. The heat flux from the crust is set to a value such that steady-state burning is achieved.

Figure 1 shows the rotational velocity profile for several values of the mass accretion rate. The viscous processes transport angular momentum efficiently through the outer layers of the neutron star into the core, resulting in a small difference in $\Omega $ between the outer and inner part of our model of $\Delta\Omega/\Omega \sim10^{-4}$. The largest change in $\Omega $ is at $y\simeq10^{8}~{\rm g~ cm^{-2}}$. We will see that at this depth helium burning generates heat and changes the chemical composition. In the figure we indicate the region of the model where the accreted angular momentum is added as described in the previous section. Since the accreted angular momentum is quickly shared with this region, the angular momentum transport is not calculated in a physically correct way in that part of the model. Furthermore, at $y \lesssim 10^{7}~{\rm g~ cm^{-2}}$ lies the pseudo-Lagrangian region where the accreted matter is added. Therefore, we limit most plots to show the Lagrangian part, $y\gtrsim10^{7}~{\rm g~ cm^{-2}}$.

 \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg1} \end{figure} Figure 1:

Rotational velocity $\Omega $ as a function of column depth y for three values of the mass accretion rate and an angular velocity of the core of $0.1~\Omega_{{\rm K}}$. Accreted angular momentum is shared with the region to the left of the vertical line.
Open with DEXTER

For higher accretion rates, angular momentum is added faster to the star, resulting in a higher shear (Fig. 2 top), although the difference is less than an order of magnitude in the range of accretion rates we consider. Since the accreted material originally rotates with the Keplerian velocity, models with a more slowly rotating core experience an up to 103 times larger shear (Fig. 2 bottom). The shear profiles show two broad ``bumps'': one in the region $10^{7}\lesssim y\lesssim10^{9}~{\rm g~ cm^{-2}}$and another at $y\gtrsim10^{10}~{\rm g~ cm^{-2}}$. We will see below that nuclear burning and diffusion lead to a gradient in the chemical composition in these regions. This gradient has a stabilizing effect that reduces the angular momentum transport, causing a somewhat larger shear.

 \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg2}\par\includegraphics[clip,width=9cm]{11619fg3} \end{figure} Figure 2:

Comparison of shear q with column depth y. Top: models with different mass accretion rates and their rotation rate of the core fixed to $\Omega=0.1~\Omega_{{\rm K}}$. The model with $\dot{M}=0.6~\dot{M}_{{\rm Edd}}$ accreted for a longer time and, therefore, reaches greater depths. Bottom: models with different rotation rates of the core and a fixed accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. The model with $\Omega=0.9~\Omega_{{\rm K}}$ suffers from numerical noise.
Open with DEXTER

The presence of shear causes turbulence and induces a magnetic field, which both drive diffusion and viscous processes. We obtain a magnetic field with a radial component $B_{r}\simeq10^{5}~{\rm G}$ and a toroidal component $B_{\phi}\simeq10^{10}~{\rm G}$. We calculate D and $\nu $ both due to the hydrodynamic instabilities and due to the (generation of) the magnetic field (Figs. 3-5). We find the latter to have the largest contribution to the diffusivity and viscosity. Of the non-magnetic instabilities, Eddington-Sweet circulation is the dominant process. At $y\simeq10^{8}~{\rm g~ cm^{-2}}$D and $\nu $ due to this process peak, since at this depth the luminosity gradient is largest due to helium burning. Note that convective mixing plays no role in our models of steady-state burning, because heat transport is radiative throughout our models, except at the onset of a flash, similar to what is found by Woosley et al. (2004).

We investigate how D and $\nu $ depend on the rotation rate $\Omega $. The contribution from the non-magnetic instabilities increases with increasing $\Omega $ (Fig. 3). For the Eddington-Sweet circulation the diffusivity and viscosity are proportional to $\Omega^{2}$ (Heger et al. 2000; Kippenhahn 1974).

 \begin{figure} \par\includegraphics[bb=170bp 302bp 450bp 463bp,clip,width=9cm]{11619fg4} \end{figure} Figure 3:

Non-magnetic diffusivity D and viscosity $\nu $ due to Eddington-Sweet circulation as a function of column depth y for different values of the angular velocity of the core $\Omega $ and an accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. Note that $\nu $ is larger than D by a fixed factor of 30. Especially the model with $\Omega=0.9~\Omega_{{\rm K}}$ suffers from numerical noise.
Open with DEXTER
The diffusivity due to the magnetic field generation increases towards lower rotation rates as, approximately, $D\propto\Omega^{-3/4}$ (Fig. 4).
 \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg5} \end{figure} Figure 4:

Magnetic diffusivity D as a function of column depth y for different values of the angular velocity of the core and an accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. A minimum in D is apparent at $\Omega\simeq0.1~\Omega_{{\rm K}}$. The model with $\Omega=0.9~\Omega_{{\rm K}}$ suffers from numerical noise.
Open with DEXTER
The precise dependence is influenced by buoyancy effects from temperature and compositional gradients (Sect. 2.3; Spruit 2002). The magnetic viscosity, which is induced by the magnetic torques instead of MHD instabilities, increases towards higher $\Omega $, since it mostly depends on the rotation rate: $D\propto\Omega^{3/2}$(Fig. 5). Interestingly, while the magnetic diffusivity dominates at most depths, for models with $\Omega\gtrsim0.1~\Omega_{{\rm K}}$Eddington-Sweet circulation gives a contribution to the diffusivity which is equal or larger at the depth of $y\simeq10^{8}~{\rm g~ cm^{-2}}$where helium is burned.
 \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg6} \end{figure} Figure 5:

Magnetic viscosity $\nu $ as a function of column depth y for different values of the angular velocity of the core $\Omega $. The model with $\Omega=0.9~\Omega_{{\rm K}}$suffers from numerical noise.
Open with DEXTER

During our calculations we assume angular momentum is accreted with an efficiency of 100%. Due to viscous processes in the disk, the actual efficiency may be lower. We investigate the dependency of the shear, diffusivity and viscosity on the accretion efficiency by comparing a model with 100% to a model with 0% efficiency. In the helium-burning region, the difference is at most several tens of percent. For more realistic efficiencies, the deviation from the 100% efficient model is likely even less. Therefore, we neglect this effect in our calculations.

 \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg7} \end{figure} Figure 6:

Nuclear energy generation rate $\epsilon _{{\rm nuc}}$ and isotope mass fractions as a function of column depth y for two models with $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$ and $\Omega=0.1~\Omega_{{\rm K}}$. One model is calculated including chemical diffusion, while the other is not.
Open with DEXTER

The viscosity allows for the transport of angular momentum, leading in the envelope to the angular velocity profile we presented in Fig. 1. Similarly, diffusion mixes the chemical composition of our model. Without diffusion, the chemical profile consists on the outside of the star (Fig. 6 middle, left-hand side) of accreted helium, which burns at $y\simeq10^{8}~{\rm g~ cm^{-2}}$, forming a layer of mostly carbon. On the inside (right-hand side) the composition is that of the initial model: 50% 12C and 50% 16O. When we include diffusion, 4He is mixed down to higher column depths, while some 12C is mixed all the way to the surface (Fig. 6 bottom). Due to the increased helium abundance at $y\gtrsim10^{8}~{\rm g~ cm^{-2}}$, the energy generation rate is higher there compared to the models without diffusion (Fig. 6 top). For models with different rotation rates of the core, we see that those with higher diffusivity (see Fig. 4) mix helium deeper inwards and consequently release more energy due to thermonuclear burning at larger column depths (Fig. 7).

 \begin{figure} \par\includegraphics[width=9cm,clip]{11619fg8} \end{figure} Figure 7:

Nuclear energy generation rate $\epsilon _{{\rm nuc}}$ as a function of column depth y for different values of the angular velocity of the core $\Omega $. Models with higher diffusivity (see Fig. 4) have more He burning at higher column depths. The model with $\Omega=0.9~\Omega_{{\rm K}}$suffers from numerical noise.
Open with DEXTER
 \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg9} \end{figure} Figure 8:

Timescales for helium burning, chemical diffusion and accretion as a function of column depth y for $\Omega=0.1~\Omega_{{\rm K}}$and $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$.
Open with DEXTER

In the steady state helium is burned typically at the depth where the accretion timescale equals the burning timescale. In the case of diffusive mixing of the chemical composition, fuel can be transported to deeper layers than the accretion column. In this case, helium is burned down to the depth where the burning timescale equals the diffusion timescale. We determine as a function of column depth the burning and chemical diffusion timescales $t_{{\rm nuc}}$ and $t_{{\rm diff}}$for 4He by calculating

\begin{displaymath}t_{{\rm nuc}},~ t_{{\rm diff}}=Y\left(\frac{\Delta Y}{\Delta t}\right)^{-1}, \end{displaymath} (10)

with Y the 4He mass fraction and $\Delta Y$ the change in Y due to nuclear burning or chemical diffusion during one time step $\Delta t$ of our calculations (Fig. 8). In the inner part of the burning zone, where helium is mixed in, the chemical diffusion and burning timescales differ by at most a few tens of percent, ensuring that steady-state burning can take place down to greater depths than without diffusion.

 \begin{figure} \par\includegraphics[bb=164bp 300bp 418bp 490bp,clip,width=9cm]{1... ...ncludegraphics[bb=164bp 300bp 418bp 490bp,clip,width=9cm]{11619f11} \end{figure} Figure 9:

Nuclear luminosity $L_{{\rm nuc}}$ due to helium burning as a function of time, while lowering $L_{{\rm crust}}$ at a constant rate. Shown are the last $10^{5}~{\rm s}$ before the onset of unstable burning. The insets zoom in on the last $10^{4}~{\rm s}$. Top: model without diffusion for $\Omega=0.1~\Omega_{{\rm K}}$, $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. While burning is initially stable, we see an increase in the amplitude of the oscillations, until finally burning becomes unstable. Bottom: similar model including diffusion. The amplitude of oscillatory burning is much larger and less regular than for the model without diffusion.
Open with DEXTER

3.2 Effect of mixing on stability

The temperature in the burning shell has an important influence on the stability of the nuclear burning. Typically, burning is stable for higher temperatures of the neutron-star envelope, which depends strongly on the heat flux from the crust. We express this heat flux as a luminosity $L_{{\rm crust}}$ and investigate for which values burning is stable by starting at a high value of $L_{{\rm crust}}$and subsequently lowering it at a rate that is slow with respect to the thermal timescale of the inner part of our model. For a certain value of $L_{{\rm crust}}$ nuclear burning no longer proceeds stably and a flash occurs. We refer to this as the critical luminosity $L_{{\rm crit}}$. At that point we stop the calculation.

We perform this procedure for two models with $\Omega=0.1~\Omega_{{\rm K}}$and $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. Both models take viscous processes into account, such that the angular velocity profiles are similar. However, we enable chemical diffusion only for one model, while the other is calculated without chemical diffusion. For the model excluding chemical mixing, we start with stable burning (Fig. 9 top). Lowering $L_{{\rm crust}}$, helium shell burning exhibits oscillations with increasing amplitude. These oscillations are well resolved in time by our calculations. For $L_{{\rm crust}}=2.448\times10^{35}~{\rm erg~ s^{-1}}$the oscillation amplitude increases rapidly, until a flash occurs. We regard this as the onset of unstable burning. It is possible that what we regard as the onset of instability is actually just an oscillation with a large amplitude, which could be followed by a series of oscillations before the unstable situation is reached. Nevertheless, observing how fast the amplitude of the oscillations increases in a small interval of $L_{{\rm crust}}$, we expect that our measure of $L_{{\rm crit}}$is accurate within 0.2%. The period of the pulses increases, from approximately $6 \times 10^{2}~{\rm s}$ at $L_{{\rm crust}}=2.448\times10^{35}~{\rm erg~ s^{-1}}$to $9\times10^{2}~{\rm s}$ at $L_{{\rm crust}}=2.444\times10^{35}~{\rm erg~ s^{-1}}$, just before the final two oscillations.

 \begin{figure} \par\includegraphics[bb=175bp 302bp 450bp 464bp,clip,width=9cm]{11619f12} \end{figure} Figure 10:

The heat flux from the crust at the transition of stable to unstable burning $L_{{\rm crit}}$ as a function of the angular velocity $\Omega $ of the core in units of the Keplerian velocity at the surface for models with $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. Each dot represents one model. Two series of models are calculated: without ( upper) and with chemical diffusion ( lower). One model is calculated without the effect of magnetic fields ( middle). Here the secular shear instability drives the chemical mixing. The right-hand vertical axis indicates the heat generated in the crust per accreted nucleon, $Q_{{\rm crust}}$, for the given accretion rate. The dotted line indicates $Q_{{\rm crust}}=0.1~{\rm MeV~ nucleon^{-1}}$, which is used in many studies.
Open with DEXTER

For the model including diffusion, the behavior is similar (Fig. 9 bottom). The amplitude of the oscillations, however, is large for a broader range of $L_{{\rm crust}}$ and the behavior is less regular. During intervals of $10^{4}{-}10^{5}~{\rm s}$, the amplitude slowly increases and subsequently decreases either slowly or fast. The cause of the irregularities is likely the increased complexity of our model when turbulent mixing is included, giving rise to more ``noise''. Despite the irregular behavior, we can still discern a general trend towards oscillations with larger amplitudes while we lower $L_{{\rm crust}}$. The period of the oscillations is $\sim$ $1.2\times10^{3}~{\rm s}$ and does not change significantly. The value of $L_{{\rm crit}}$ we obtain for this model is over a factor two lower than for the model without diffusion: $L_{{\rm crit}}=1.180\times10^{35}~{\rm erg~ s^{-1}}$. This shows the substantial stabilizing effect of turbulent mixing. The uncertainty in $L_{{\rm crit}}$ is likely larger than for the model without diffusion because of the increased noise. Note that for the chosen angular velocity of the core, $\Omega=0.1~\Omega_{{\rm K}}$, the diffusivity is at its minimum value. For another choice of $\Omega $, the effect is likely to be even stronger.

We investigate the dependence of $L_{{\rm crit}}$ on $\Omega $by calculating two series of models, one including and one excluding chemical diffusion. Due to the increased noise, the models that include diffusion are computationally more expensive. Therefore, we limit ourselves to two models with relatively low rotation rates, $\Omega=0.05\Omega_{{\rm K}},~0.1\Omega_{{\rm K}}$, and two models with high rotation rates: $\Omega=0.8\Omega_{{\rm K}},~0.9\Omega_{{\rm K}}$. We find that $L_{{\rm crit}}$ is lower by more than a factor of 2 for all values of $\Omega $ we consider (Fig. 10). Furthermore, even for the models without diffusion we see a decrease in $L_{{\rm crit}}$ of up to 12% when going to higher rotation rates. This stabilizing effect stems from the centrifugal force $F_{{\rm cf}}\propto\Omega^{2}$, which lowers the effective gravity, increasing the efficiency of stabilizing effects. Note that because of the one-dimensional approximation we use, this is likely an underestimation (see Sect. 4.2).

We noted earlier that diffusivity due to Eddington-Sweet circulation can be comparable to or even exceed the diffusivity due to magnetic fields. To investigate the effect of nonmagnetic instabilities alone, we created a model with $\Omega=0.05\Omega_{{\rm K}}$ and $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$including only angular momentum transport and chemical diffusion due to nonmagnetic instabilities. Angular momentum transport is much less efficient, leading to a large shear. The secular shear instability drives the diffusivity and viscosity. For this model we find $L_{{\rm crit}}=1.948\times 10^{35}~{\rm erg~s^{-1}}$, which is $23\%$ lower than what we find without diffusion (Fig. 10).

When we change $L_{{\rm crust}}$, it takes a thermal timescale for our model to adjust. Since we lower $L_{{\rm crust}}$ continuously, this introduces a systematic error in the value of $L_{{\rm crit}}$we obtain, as the model is not fully adjusted to that value of $L_{{\rm crust}}$when we stop the calculation. To estimate the systematical error, we take one model and lower $L_{{\rm crust}}$ at different rates, all slow with respect to the thermal timescale of the model, and find that the difference in $L_{{\rm crit}}$ and, ergo, the systematic error is about 4%.

3.3 Mass accretion rate dependence

The dependence of $L_{{\rm crit}}$ on the mass accretion rate is investigated by calculating two series of models with and without chemical diffusion, in a similar way to how we studied the dependence on $\Omega $. The angular velocity of the core is set to $0.1\Omega_{{\rm K}}$. We find that $L_{{\rm crit}}$ increases towards higher mass accretion rates (Fig. 11). For the models without chemical diffusion, the accretion rate above which the luminosity of the crust exceeds $L_{{\rm crit}}$ as expected from a crustal energy release of $Q_{{\rm crust}}=0.1~{\rm MeV~ nucleon^{-1}}$, which is used in many studies (see Sect. 2.7), lies at $\dot{M}_{{\rm Edd}}$. This is lower than found in previous studies (e.g., Bildsten 1998). Including chemical diffusion, the transition takes place at lower rate: approximately $0.4~\dot{M}_{{\rm Edd}}$.

 \begin{figure} \par\includegraphics[clip]{11619f13} \end{figure} Figure 11:

The heat flux from the crust at the transition of stable to unstable burning $L_{{\rm crit}}$ as a function of the accretion rate $\dot{M}$ for models with $\Omega=0.1~\Omega_{{\rm K}}$. Each dot represents one model. Two series of models are calculated: without ( upper) and with chemical diffusion ( lower). The dotted line indicates the luminosity from the crust as a function of $\dot{M}$for an energy release of $Q_{{\rm crust}}=0.1~{\rm MeV~ nucleon^{-1}}$, which is used in many studies.
Open with DEXTER

To understand the behavior of increasing $L_{{\rm crit}}$ for higher values of $\dot{M}$, we follow the stability analysis of thermonuclear burning in a thin shell by Giannone & Weigert (1967) (see also Yoon et al. 2004b). These authors derive an expression for the inverse of the growth timescale of temperature perturbations, $\tau_{{\rm pert}}^{-1}$, by considering both thermonuclear burning and radiative cooling (Eq. (16) in Giannone & Weigert 1967). In this expression the luminosity from below the thin shell is ignored. We can include $L_{{\rm crust}}$ by adding it to the luminosity of the shell, which results in an extra term in the numerator of the right-hand side of Eq. (16) in Giannone & Weigert (1967): $\tau_{{\rm pert}}^{-1}\propto-L_{{\rm crust}}/\Delta M$. Here, $\Delta M$ is the mass of the shell, which for steady-state burning is proportional to the mass accretion rate. Increasing $\dot{M}$leads to a lower perturbation growth timescale. Therefore, to keep the same perturbation growth timescale, a larger value of $L_{{\rm crust}}$ is required at higher $\dot{M}$. This simple picture suggests that $L_{{\rm crit}}$ depends linearly on $\dot{M}$, while Fig. 11 suggests for the series of models without chemical diffusion that the relation deviates from a linear dependence. In fact, for higher $\dot{M}$ also the temperature and density in the shell are higher, which influences the perturbation growth timescale as well.

4 Discussion

We performed detailed calculations of thin shell burning of accreted helium on a neutron star. Similar to what was found by Yoon et al. (2004a) for white dwarfs, also for neutron stars rotational mixing leads to more stable burning. As was demonstrated by Piro & Bildsten (2007), rotationally induced magnetic fields provide in most cases the dominant contribution to the diffusivity and viscosity. Yoon et al. (2004a) considered only nonmagnetic hydrodynamic instabilities. In those models the transport of angular momentum is less efficient, resulting in a much larger shear. The secular shear instability is in that case the driver of turbulent mixing. We take magnetic fields into account through the Tayler-Spruit dynamo (Spruit 2002), which causes efficient angular momentum transport and turbulent mixing. Eddington-Sweet circulation also plays an important role, especially in the burning zone, at the peak of the energy generation rate, where there is a steep gradient in the luminosity.

In our models with diffusion the geometrical thickness of the burning shell is greater (Fig. 6). For instance, for a model with $\Omega=0.1~\Omega_{{\rm K}}$ and $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$ the thickness of the burning shell is $6.7~{\rm m}$ excluding and $8.7~{\rm m}$ including chemical diffusion, where we define the shell such that at the boundary the energy generation rate is 10-3 times the peak value. This results in an increased stability of thermonuclear burning.

Due to the increased stability, the critical value of the heat flux for the crust $L_{{\rm crit}}$ at the transition of stable and unstable burning is lower for models that include chemical diffusion. Even for the rotation rate which gives the minimum diffusivity, nuclear burning proceeds stably down to values of $L_{{\rm crit}}$ that are a factor of two lower than for the non-diffusion case. In these calculations we vary the flux from the crust independent of the mass accretion rate. For several values of $\dot{M}$ and $\Omega $ we determine $L_{{\rm crit}}$. Observationally, this boundary is placed at $\dot{M}\simeq0.1~\dot{M}_{{\rm Edd}}$. At this accretion rate, we find $L_{{\rm crit}}=0.508\times10^{35}~{\rm erg~ s^{-1}}$for a model with $\Omega=0.1\Omega_{{\rm K}}$. Assuming the heat flux from the crust is the main source of this luminosity, this corresponds to an emergent heat from the crust of $0.27~{\rm MeV~ nucleon^{-1}}$. This is almost three times the value of $0.1~{\rm MeV~ nucleon^{-1}}$used in many previous studies. Nevertheless, it is in agreement with the increased heat deposition in the crust from calculations by Gupta et al. (2007).

It is especially interesting to note that we already obtain this result at the value for $\Omega $ for which the diffusivity is minimal. Piro & Bildsten (2007) find this behavior only at low rotation rates: $\Omega\lesssim0.1\Omega_{{\rm K}}$. The Taylor-Spruit mechanism considers stabilizing effects due to temperature and compositional stratification. Piro & Bildsten (2007) simplify their models by taking into account only the former when determining the recurrence time of bursts and the condition for stable burning. This allows for a simple dependence of D on $\Omega $ of $D\propto\Omega^{-3/4}$. However, by including both stabilizing effects, the dependence of D on $\Omega $ and q is more complex. In our calculations we find that the spread in the diffusivity in the considered range of rotation rates is at most one order of magnitude. Furthermore, we find that at high angular velocities Eddington-Sweet circulations drive mixing just as efficiently as the magnetic instabilities at low rotation rates. This means that, for all rotation rates, the stability of shell burning is increased by chemical mixing due to rotation and rotationally induced magnetic fields.

4.1 Mixing efficiencies

In our models we find that the magnetic instabilities and torques provide the most efficient mixing of the chemical composition and angular momentum. The only exception is found at higher rotation rates, where the Eddington-Sweet circulations provide an important contribution to the diffusivity in the helium burning shell. Note that we employ a one-dimensional approximation of the diffusivity due to Eddington-Sweet circulations (Kippenhahn 1974). At higher rotation rates two-dimensional effects may be important that cannot be tested with our model, but that may influence the efficiency of mixing due to these circulations.

Several studies need the Tayler-Spruit dynamo to reproduce observed quantities. Heger et al. (2005) model the pre-supernova evolution of massive stars and use the angular momentum transport due to rotationally induced magnetic fields to explain observed pulsar frequencies. Suijs et al. (2008) performed similar calculations for white dwarf progenitors and find that angular momentum transport by magnetic torques is needed to explain the observed range of white dwarf rotation rates.

However, the mechanism of the Tayler-Spruit dynamo is uncertain. Zahn et al. (2007) performed calculations with three-dimensional models which do not reproduce the dynamo effect. Therefore, it is possible that this mechanism has a lower efficiency or is absent (see, e.g., the discussion in Maeder et al. 2008). In that case, non-magnetic instabilities drive chemical mixing and angular momentum transport. These are less efficient by many orders of magnitude. This leads to a large shear, causing the secular shear instability to provide the dominant contribution to D and $\nu $, similarly to what Yoon et al. (2004a) found in white dwarf models which did not include a rotationally induced magnetic field. We performed calculations on one model without a rotationally induced magnetic field and we find a value of $L_{{\rm crit}}$that is 23% lower than for similar models that do not take chemical diffusion into account (Fig. 10). This model has a rotation rate of $0.05\Omega_{{\rm K}}$. Models with a slower rotating core will have a higher shear, which may result in a lower value of $L_{{\rm crit}}$. Therefore, even without magnetic fields, the effect of rotational mixing on the stability of helium shell burning is considerable.

4.2 Centrifugal force

Another stabilizing effect of rotation is provided by the centrifugal force. Yoon et al. (2004a) found that for shell burning in white dwarfs, the centrifugal force lowers the density and degeneracy in the shell, which leads to increased stability. We created a series of models without chemical mixing and found that for increasing $\Omega $, $L_{{\rm crit}}$is lower by up to 12%. However, this is probably an underestimation. Our implementation of the centrifugal force is a one-dimensional approximation. The centrifugal force depends on latitude, being strongest at the equator and vanishing at the poles. Our calculations use a value that is averaged over latitude (e.g. Heger et al. 2000). In the case of rigidly rotating polytropes, this approximation has been found accurate for rotation rates up to $0.6\Omega_{{\rm K}}$ (Yoon et al. 2004a and references therein). Therefore, we limit the effect of the centrifugal force above 60% of the critical velocity. In actuality, the centrifugal force may reduce $L_{{\rm crit}}$ even further for fast-spinning neutron stars.

4.3 Marginally stable burning

Revnivtsev et al. (2001) observe from the LMXBs 4U 1636-53, 4U 1608-52 and Aql X-1 millihertz quasi-periodic oscillations (mHz QPOs) and speculate that this phenomenon may be related to a special mode of nuclear burning. This behavior is thought to occur at the boundary of stable and unstable burning, since it is observed in a narrow range of accretion rates, where type I X-ray bursts were observed at lower accretion rates, while they were absent at higher accretion rates. The oscillatory burning mode at this boundary was expected from one-zone models by Paczynski (1983) as ``marginally stable burning''. Heger et al. (2007) reproduce this behavior in multi-zone numerical models of the neutron star envelope and derive the period of the oscillations $P_{{\rm osc}}$ to be the geometric mean of the accretion and thermal timescales: $P_{{\rm osc}}=\sqrt{t_{{\rm acc}}t_{{\rm therm}}}$.

Altamirano et al. (2008) observe frequency drifts in mHz QPOs from 4U 1636-53. The mHz QPOs are observable for approximately $10^{4}~{\rm s}$. During this time the frequency drops by several tens of percent. At a certain point, a type I X-ray burst is observed, after which no oscillations are detected for some time. The change in period is not found to be directly related to variations in the X-ray flux on short timescales. Therefore, the frequency of the oscillations does not appear to be sensitive to variations in the accretion rate. Furthermore, Molkov et al. (2005) observed a long type I X-ray burst from SLX 1735-269 that exhibits $\sim$ $10~{\rm mHz}$ oscillations during the burst decay. Also in this case, a drift to lower frequencies takes place during the part of the X-ray light curve where the black body temperature is observed to decrease.

In our models we also observe oscillations at the boundary of stable and unstable burning. This is most pronounced in the models without chemical diffusion. When we lower $L_{{\rm crust}}$, effectively cooling our burning layer, the frequency of the oscillations decreases by several tens of percents until a flash occurs. The frequency drift takes place over a narrow range of $L_{{\rm crust}}$, just before the onset of a flash. The amplitude of the oscillations is greater in this range, making the oscillations more easily detectable. This supports the suggestion by Altamirano et al. (2008) that the frequency drifts are due to cooling of deeper layers and could explain why it is not sensitive to short-term variations in the accretion rate. The cooling could, for instance, be caused by the slow release of energy from a deeper layer that was heated up during an X-ray burst.

The models that include diffusion display oscillations as well, but the behavior is much more irregular, as the amplitude of the oscillations changes in a seemingly erratic way. This makes it difficult to draw conclusions from the oscillatory behavior. We suspect that numerical noise is the source of this behavior. A different implementation of the mixing processes in the model may be required to improve this.

4.4 Further consequences of mixing

Apart from the increased stability of helium burning, chemical mixing can give rise to other effects. Superbursts, which are energetic type I X-ray bursts that last up to a day, are thought to be the result of a carbon flash (Strohmayer & Brown 2002; Cumming & Bildsten 2001). Fifteen superbursts have been observed from ten sources, most of which have accretion rates $\dot{M}\gtrsim0.1~\dot{M}_{{\rm Edd}}$ (in 't Zand et al. 2004; Kuulkers 2004; Remillard et al. 2005; Kuulkers 2005). As noted by Piro & Bildsten (2007), turbulent mixing could allow for stable burning of helium at these accretion rates, building up a thick carbon layer. However, all superbursters exhibit normal type I bursts as well. In the presence of hydrogen, the rp-process creates heavy isotopes, while lowering the carbon abundance. It has proven difficult to explain how carbon can survive many normal bursts to fuel a superburst (e.g., Keek et al. 2008).

While helium is mixed down, we find that carbon is mixed up to smaller column depths (Fig. 6). For our helium-accreting model this is of little consequence, but many neutron stars in LMXBs accrete hydrogen-rich material. Hydrogen burns via the hot-CNO cycle. The energy generation rate of this process depends on the mass fractions of the CNO seed nuclei, which are increased if carbon is mixed into the hydrogen/helium layer. This may lower the hydrogen mass fraction in the burning shell. If subsequently a hydrogen/helium flash occurs, there is less hydrogen present for the rp-process to destroy the carbon created by helium fusion. This could allow for the creation of a thick carbon layer to fuel a superburst. Further calculations are needed to assess the magnitude of this effect.

Our models show that carbon is mixed all the way to the neutron star photosphere at $y={\rm 1~g~cm^{-2}}$. In case hydrogen-rich material is accreted, the ashes of hydrogen and helium burning can contain heavy isotopes, e.g. iron. If mixing increases the mass fractions of these isotopes near the surface, this would allow for the detection of absorption lines from the neutron star. Measuring the gravitational redshift of the absorption line provides constraints on the neutron-star equation of state, such as has been shown with the tentative result of Cottam et al. (2002) (Özel 2006). This is analogous to the calculations of Weinberg et al. (2006), who predict that convection during particularly luminous X-ray bursts can mix heavy elements to the photosphere.

5 Conclusion

A longstanding problem for the theory of thermonuclear burning in the envelope of accreting neutron stars is the accretion rate at which the burning changes from unstable to stable. While observations point to $\dot{M}\simeq0.1~\dot{M}_{{\rm Edd}}$, the models find $\dot{M}\simeq~\dot{M}_{{\rm Edd}}$when hydrogen-rich material is accreted and $\dot{M}\simeq10~\dot{M}_{{\rm Edd}}$when it is hydrogen-deficient. Recent analytical and numerical models (Piro & Bildsten 2007) suggest that turbulent mixing due to rotationally induced magnetic fields leads to an increased stability of the thin shell burning on neutron stars, similar to the effect of mixing due to hydrodynamic instabilities in the white dwarf case (Yoon et al. 2004a).

We perform for the first time detailed calculations of nuclear burning of accreted helium in the neutron star envelope using an extensive numerical model including both magnetic and non-magnetic hydrodynamic instabilities. In most cases the magnetic instabilities and torques provide the largest contribution to the diffusivity and the viscosity, respectively, while Eddington-Sweet circulations become important at high rotation rates. We create models with an accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$ and different rotation rates of the core. We do not couple the heat flux from the crust to the mass accretion rate, but leave it as a free parameter, finding the threshold value between stable and unstable burning. This value is lower by at least a factor of two for models including diffusion, in comparison with models without chemical mixing. If we ignore the rotationally induced magnetic fields, mixing due to the secular shear instability can lower the critical heat flux by several tens of percent. For higher rotation rates, the centrifugal force allows for stable burning at crustal heat fluxes that are up to 12% smaller in our models. Note, however, that this is likely an underestimation, because of the employed approximation of the centrifugal force in our one-dimensional model.

These effects show that the stability of helium shell burning is increased due to rotation, such that stable burning can take place at sub-Eddington accretion rates. Magnetic field generation through the Tayler-Spruit dynamo yields the strongest effect. However, even without magnetic fields, hydrodynamic instabilities and the centrifugal force increase stability substantially. We calculate models including chemical diffusion for several values of the accretion rate and find that, at approximately 40% of the Eddington-limited rate, the critical heat flux from the crust equals the value inferred from an energy release of $Q_{{\rm crust}}=0.1~{\rm MeV~ nucleon^{-1}}$, which is used in many previous studies. Therefore, to explain the observed transition at $0.1~\dot{M}_{{\rm Edd}}$, an increased energy release is required, as found recently by Gupta et al. (2007). Combined with this larger energy release, rotational mixing and rotationally induced magnetic fields may explain the transition from unstable to stable burning at the observed accretion rate. A better understanding of the mixing efficiencies is required to further constrain the importance of these mixing processes.

Our models exhibit oscillations close to the transition of stable to unstable burning, which have been related to the observed mHz QPOs (Heger et al. 2007). When we lower the heat flux from the crust at a constant rate, we find that the frequency of the oscillations is reduced by up to several tens of percent. This supports the suggestion by Altamirano et al. (2008) that the frequency drifts observed in mHz QPOs are due to cooling.

Acknowledgements
L.K. acknowledges support from the Netherlands Organization for Scientific Research (NWO). We thank D. Altamirano, P. G. Jonker and A. Heger for interesting discussions and we are grateful for helpful comments from the referee.

References

Footnotes

...[*]
Present address: School of Physics and Astronomy, University of Minnesota, 116 Church Street S.E., Minneapolis, MN 55455, USA.

All Figures

  \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg1} \end{figure} Figure 1:

Rotational velocity $\Omega $ as a function of column depth y for three values of the mass accretion rate and an angular velocity of the core of $0.1~\Omega_{{\rm K}}$. Accreted angular momentum is shared with the region to the left of the vertical line.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg2}\par\includegraphics[clip,width=9cm]{11619fg3} \end{figure} Figure 2:

Comparison of shear q with column depth y. Top: models with different mass accretion rates and their rotation rate of the core fixed to $\Omega=0.1~\Omega_{{\rm K}}$. The model with $\dot{M}=0.6~\dot{M}_{{\rm Edd}}$ accreted for a longer time and, therefore, reaches greater depths. Bottom: models with different rotation rates of the core and a fixed accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. The model with $\Omega=0.9~\Omega_{{\rm K}}$ suffers from numerical noise.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=170bp 302bp 450bp 463bp,clip,width=9cm]{11619fg4} \end{figure} Figure 3:

Non-magnetic diffusivity D and viscosity $\nu $ due to Eddington-Sweet circulation as a function of column depth y for different values of the angular velocity of the core $\Omega $ and an accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. Note that $\nu $ is larger than D by a fixed factor of 30. Especially the model with $\Omega=0.9~\Omega_{{\rm K}}$ suffers from numerical noise.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg5} \end{figure} Figure 4:

Magnetic diffusivity D as a function of column depth y for different values of the angular velocity of the core and an accretion rate of $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. A minimum in D is apparent at $\Omega\simeq0.1~\Omega_{{\rm K}}$. The model with $\Omega=0.9~\Omega_{{\rm K}}$ suffers from numerical noise.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg6} \end{figure} Figure 5:

Magnetic viscosity $\nu $ as a function of column depth y for different values of the angular velocity of the core $\Omega $. The model with $\Omega=0.9~\Omega_{{\rm K}}$suffers from numerical noise.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg7} \end{figure} Figure 6:

Nuclear energy generation rate $\epsilon _{{\rm nuc}}$ and isotope mass fractions as a function of column depth y for two models with $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$ and $\Omega=0.1~\Omega_{{\rm K}}$. One model is calculated including chemical diffusion, while the other is not.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11619fg8} \end{figure} Figure 7:

Nuclear energy generation rate $\epsilon _{{\rm nuc}}$ as a function of column depth y for different values of the angular velocity of the core $\Omega $. Models with higher diffusivity (see Fig. 4) have more He burning at higher column depths. The model with $\Omega=0.9~\Omega_{{\rm K}}$suffers from numerical noise.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[clip,width=9cm]{11619fg9} \end{figure} Figure 8:

Timescales for helium burning, chemical diffusion and accretion as a function of column depth y for $\Omega=0.1~\Omega_{{\rm K}}$and $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=164bp 300bp 418bp 490bp,clip,width=9cm]{1... ...ncludegraphics[bb=164bp 300bp 418bp 490bp,clip,width=9cm]{11619f11} \end{figure} Figure 9:

Nuclear luminosity $L_{{\rm nuc}}$ due to helium burning as a function of time, while lowering $L_{{\rm crust}}$ at a constant rate. Shown are the last $10^{5}~{\rm s}$ before the onset of unstable burning. The insets zoom in on the last $10^{4}~{\rm s}$. Top: model without diffusion for $\Omega=0.1~\Omega_{{\rm K}}$, $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. While burning is initially stable, we see an increase in the amplitude of the oscillations, until finally burning becomes unstable. Bottom: similar model including diffusion. The amplitude of oscillatory burning is much larger and less regular than for the model without diffusion.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=175bp 302bp 450bp 464bp,clip,width=9cm]{11619f12} \end{figure} Figure 10:

The heat flux from the crust at the transition of stable to unstable burning $L_{{\rm crit}}$ as a function of the angular velocity $\Omega $ of the core in units of the Keplerian velocity at the surface for models with $\dot{M}=0.3~\dot{M}_{{\rm Edd}}$. Each dot represents one model. Two series of models are calculated: without ( upper) and with chemical diffusion ( lower). One model is calculated without the effect of magnetic fields ( middle). Here the secular shear instability drives the chemical mixing. The right-hand vertical axis indicates the heat generated in the crust per accreted nucleon, $Q_{{\rm crust}}$, for the given accretion rate. The dotted line indicates $Q_{{\rm crust}}=0.1~{\rm MeV~ nucleon^{-1}}$, which is used in many studies.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[clip]{11619f13} \end{figure} Figure 11:

The heat flux from the crust at the transition of stable to unstable burning $L_{{\rm crit}}$ as a function of the accretion rate $\dot{M}$ for models with $\Omega=0.1~\Omega_{{\rm K}}$. Each dot represents one model. Two series of models are calculated: without ( upper) and with chemical diffusion ( lower). The dotted line indicates the luminosity from the crust as a function of $\dot{M}$for an energy release of $Q_{{\rm crust}}=0.1~{\rm MeV~ nucleon^{-1}}$, which is used in many studies.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.