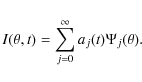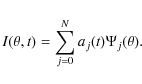Spatio-temporal analysis of solar activity: main periodicities and period length variations

A. Vecchio; V. Carbone

doi:10.1051/0004-6361/200811024

Free Access

Issue		A&A Volume 502, Number 3, August II 2009


Page(s)		981 - 987
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361/200811024
Published online		15 June 2009

Spatio-temporal analysis of solar activity: main periodicities and period length variations

A. Vecchio¹ - V. Carbone^1,2

1 - Dipartimento di Fisica, Universitá della Calabria, Ponte P. Bucci cubo 31C, 87036 Rende (CS), Italy
2 - Liquid Crystal Laboratory, INFM/CNR, Ponte P. Bucci cubo 33B, 87036 Rende (CS), Italy

Received 23 September 2008 / Accepted 8 May 2009

Abstract
Aims. The spatio-temporal dynamics of solar activity has been investigated by studying the main oscillations and the time evolution of the basic periods.
Methods. The spatio-temporal behavior of the green coronal emission line at 530.3 nm, recorded from 1939 to 2005, has been analyzed by using proper orthogonal decomposition, to extract the main components of the system, and the wavelet analysis to further investigate their time behaviour.
Results. In addition to the main 11-year periodicity, a high-frequency component has been recorded mainly on the polar regions of the Sun, thus indicating a different origin from the emergence of active regions. Evidence for variations in the period lengths of this component has been found for the first time. The calculated period length varies between 1.5 years and 4 years, in good agreement with frequencies attributed to the quasi-biennial cycle extracted by different solar activity indicators. Our analysis shows that, unlike the main periodicity, the high-frequency component does not show the typical properties of a true mode of oscillation but seems to originate, in a narrow band of frequencies, from a stochastic superposition of different oscillators.
Conclusions. The observed solar cycle frequencies in the range 1.5-4 years, commonly considered as independent modes of oscillation, could be the manifestation of the temporal modulation of a unique quasi-biennial periodicity. Our findings can provide more constraints on dynamo models introduced to describe the different components of the solar cycle. The calculated period length variations could also be helpful to improve our knowledge of the relationship between solar activity, neutrino flux variations and cosmic ray modulation.

Key words: Sun: activity - methods: data analysis - Sun: corona

1 Introduction

It is well known that solar magnetic activity is characterized by a periodic behavior of about 11 years (cf. e.g. Stix 2002), usually related to the emergence of magnetic field at active regions within the photosphere. Although the most evident signature of the solar activity is the cyclic time variation of the sunspot number, the 11-year periodicity can be also recognized by looking at different indicators (e.g. flares occurrence, 10-cm flux, Ca K index). The length of this main cycle is not constant (Friis-Christensen & Lassen 1991; Fligge et al. 1999; Eddy 1976), rather, an apparently stochastic time modulation generates a kind of ``solar melody'' (Beer et al. 1994). This relates the solar activity to effects on the Earth's climate. In fact, even if the topic is under debate (see e.g. Scafetta & West 2008), it has been pointed out that a high correlation exists between the solar cycle length and the northern hemisphere Earth temperature records (Friis-Christensen & Lassen 1991).

$\begin{figure} \par\includegraphics[width=16cm,clip]{1024fg0.eps} \end{figure}$	Figure 1: The daily intensity emission of the solar corona in the period 1939-2005 as observed in the time-angle plane. The latitude $\theta =0$ corresponds to solar equator. The color scale is linear.
Open with DEXTER

Short-term periodicities in the solar activity range from few days to years (e.g. Vecchio et al. 2005; Rusin & Zverko 1990; Penza et al. 2006; Kane 2005; Gnevyshev 1977; Bay 2003). Among the yearly periodicities, the most noticeable periods are 1.3 years and 3.6 years, along with some periods in the range between 2.6 years and 2.8 years (for a complete classification of the high-frequency periodicities observed in many solar indices see e.g. Kane 2005). Many authors (Cadavid et al. 2005; Knaack et al. 2004; Krivova & Solanki 2002; Knaack et al. 2005; Li et al. 2006), using different techniques of analysis and different activity indicators, have shown that the observed high frequency periodicities are not recognized as a typical feature of every solar cycle but seem to appear only from time to time. A corresponding quasi-biennial periodicity has also been found in contexts related to solar variability. The first evidence of this is the quasi-biennial oscillation of solar neutrino fluxes first observed by Sakurai (1979) with the Homestake experiment and followed by different detections from the GALLEX (GNO) and the Super-Kamiokande experiments (e.g. Shirai 2004; Sakurai et al. 2008; Haubold 1998). In another context, a quasi-biennial variation has been detected in the proton fluxes recorded by the CPME instrument, onboard IMP 8, in the interplanetary space in the energy bands $0.50 \div 0.96$ MeV and $190 \div 440$ MeV (Laurenza et al. 2009).

The study of short-term periods in the Sun and defining their properties can be very interesting since:

they can provide useful information on the global properties of the Sun (Benevolenskaya 1998; Vecchio & Carbone 2008a,b), for example on the solar dynamo theory;
the short-term periodicities can be related to the time variation of neutrino solar flux and proton fluxes in interplanetary space;
in the case of non-constant period lengths they could enrich the ``solar melody'' with further components, perhaps influencing the climate on Earth (Friis-Christensen & Lassen 1991).

The present paper addresses these points by analyzing the spatio-temporal properties of solar activity and by searching for variations in the period length of the components of the solar cycle. We will show the results of a spatio-temporal analysis on the green coronal emission line at 530.3 nm by using proper orthogonal decomposition (POD) (Holmes 1996) together with the well known wavelet analysis. In particular, the first technique is able to identify and separate the contribution of the short-term components from the main solar cycle, while wavelets are useful to characterize the time behavior of the various POD modes. The period length variations can be calculated from the wavelet spectra by using a method developed by Fligge et al. (1999). By using the POD as a filter, we are able to identify the short-term signal more clearly than in the raw data. The POD analysis allows us to recognize that the main cycle and the quasi-biennial periodicity are generated by different phenomena in the framework of the dynamo effect. In particular, the short-term component is likely to be generated by a stochastic phenomenon, since the observed quasi-biennial cycle results from a superposition of different oscillators with random phases rather than a pure oscillating phenomenon.

2 Data analysis

The data set consists of a scalar field $I(\theta ,t)$ representing monthly observations (in the period 1939-2005) of the green coronal emission line Fe XIV at 530.3 nm. Each month, 72 values of intensities, in millionths of intensity of the solar disk, from $0 \leq \theta \leq 355$ degrees of latitude (in increments of 5 degrees) are given. The green coronal emission dynamics has been investigated in the past (Vecchio et al. 2005; Mininni 2002; Vecchio & Carbone 2008b) to characterize the solar activity. Here we analyze the revised data set of green coronal emission (Rybanský et al. 2005). This new data set has been corrected for an anomalous monotonic increase of the maximum of coronal emission from cycle 18 to cycle 20. With respect to the uncorrected coronal emission, the chosen set shows some advantages, namely:

the amplitudes of the found solar cycle periodicities can be correctly quantified;
these values of the coronal emission enable the exact time localization of the different short-term periodicities;
the calculated period length variations are not affected by spurious contributions due to an artificial activity increase.

Figure 1 shows the spatio-temporal plot of the dataset. All features characterizing the solar cycle, namely the temporal 11-year period and the migration of activity toward the solar equator giving rise to the butterfly diagram, are visible.

In a first step, the spatio-temporal field $I(\theta ,t)$ has been analyzed through POD. In this framework the coronal emission can be described by a superposition of N modes (Holmes 1996), characterized by temporal modal coefficients a_j(t) and spatial basis functions $\Psi_j(\theta)$ not fixed a priori:

$\begin{displaymath}% I(\theta,t) = \sum_{j=0}^{\infty} a_j(t) \Psi_j(\theta). \end{displaymath}$

(1)

The basis functions in (1) are calculated by maximizing the averaged projection of $I(\theta ,t)$ onto $\Psi_j(\theta)$ constrained to unitary norm, which leads to a Fredholm integral equation

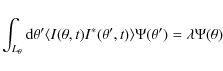$\begin{displaymath}% \int_{L_{\theta}}{\rm d}\theta' \langle I(\theta,t) I^*(\theta',t) \rangle \Psi(\theta') = \lambda \Psi(\theta) \end{displaymath}$

(2)

in which $L_{\theta}$ represents the lengths of spatial integration domain and brackets are time averages. The solution provides both eigenfunctions $\Psi_j$ and eigenvalues $\lambda_j$ , ordered such that $\lambda_j \geq \lambda_{j+1}$ . $\lambda_j$ s are a countable set and represent the energy associated with each mode, quantifying the relative contribution of each mode to the signal reconstruction. The POD temporal coefficients are then calculated by projecting the original field onto the corresponding basis functions. A reconstruction of the field by selectively choosing a finite number N of the most energetic modes is possible. In this way, we form a subspace spanned by the first N eigenfunctions

$\begin{displaymath}% I(\theta,t) = \sum_{j=0}^{N} a_j(t) \Psi_j(\theta). \end{displaymath}$

(3)

The POD procedure yields a complete set of modes that are optimal in energy (Holmes 1996), thus a truncated POD expansion such as (3) describes typical members of the ensemble better than any other decomposition of the same truncation order. This analysis has been used in solar physics to investigate some different properties of the solar cycle (Vecchio et al. 2005; Mininni 2002; Vecchio & Carbone 2008b), photospheric turbulence (Vecchio et al. 2008) and magnetic field evolution (Lawrence 2004; Rees 2000).

$\begin{figure} \par\includegraphics[width=6.3cm,clip]{1024fg1.eps} \end{figure}$	Figure 2: Cumulated energy of the first nine POD modes as a function of the index j ( $j = 0,\dots , 8$ ). Panel b) refers to the equatorial sample, panels a), c) correspond to polar data sets.
Open with DEXTER

3 Results

Excluding the number and area of sunspot, the coronal emission represents the longest solar activity indicator providing spatial information. However, while sunspot properties are related to the emergence of magnetic field in the active regions, $I(\theta ,t)$ also contains information about the global solar magnetic field. The contribution of the active regions and large scale magnetic fields to the coronal emission can be coarsely separated by dividing the whole dataset into three main regions according to their latitudes: i) an equatorial region, in the latitude range $-45^\circ \leq \theta \leq 45^\circ$ , associated with the active region emergence; ii) two polar areas, a northern and a southern region in the range of latitudes $50^\circ \leq \theta \leq 90^\circ$ and $-90^\circ \leq \theta \leq -50^\circ$ (from the equatorial plane) respectively.

3.1 Spatio-temporal characteristics of solar activity

The POD has been applied to each region separately, thus obtaining a set of coefficients a_j(t) and eigenfunctions $\Psi_j(\theta)$ ( $j = 0,\dots, 18$ for equatorial region, and $j = 0,\dots , 8$ for poles) which furnish information about the spatio-temporal dynamics of the solar cycle.

$\begin{figure} \par\includegraphics[width=7.3cm,clip]{1024fg2.eps} \end{figure}$	Figure 3: Equatorial data set: time evolution of the first three POD coefficients a_j(t) for $0\leq j\leq 2$ .
Open with DEXTER

In Fig. 2 we report, for all samples, the cumulated energies of the first nine ( $j = 0,\dots , 8$ ) POD modes. About $99\%$ of the total energy is shared among the first three modes $j=0\div2$ for the equatorial sample (Fig. 2, panel b), and between the first two modes $j=0\div1$ for the polar samples (Fig. 2, panels a, c). This means that the first few POD modes, together containing $99\%$ of the energy, suffice to describe the main features of the solar cycle at both high and equatorial latitudes.

$\begin{figure} \par\includegraphics[width=12cm,clip]{1024fg3.eps} \end{figure}$	Figure 4: Reconstructed intensity $I(\theta ,t)$ for the equatorial area, represented in the $(t,\theta )$ plane, using different N in Eq. (3). N=0 (panel a)), N=1 (panel b)). N=2 (panel c)) contains the $99\%$ of the total energy. The color scale is linear.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{1024fg4.eps} \end{figure}$	Figure 5: Polar data sets: time evolution of the first two POD coefficients a_j(t) for j=0,1 for the northern (panels a), c)) and southern regions (panels b), d)).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{1024fg5.eps} \end{figure}$	Figure 6: Reconstructed intensity $I(\theta ,t)$ , using the first two modes containing $99\%$ of the total energy, represented in the $(t,\theta )$ plane. Panel a) refers to the northern region and panel b) to the southern region.
Open with DEXTER

The POD analysis is a very efficient tool to recognize and to select individual contributions to the solar cycle, according to their spatial pattern, and their time behavior is directly described by the coefficients a_j(t). The POD coefficients corresponding to the high energy modes for the equatorial and polar samples are shown in Figs. 3 and 5. In Fig. 3 (panels a,b) it can be seen that the first two most energetic modes (j=0,1) describe the main 11-year cycle. However, a₀(t) and a₁(t), although characterized by the same periodicity, can be associated with different feature of the global pattern since they are out of phase and are characterized by non-correlated amplitude fluctuation. This is clear by looking at the spatio-temporal intensities (Fig. 4, panels a,b), reconstructed according to Eq. (3). While the mode j=0 is associated with the basic 11-year spatial periodicity, the mode j=1 describes the north-south occurrence of the active region contributing to the butterfly wings in the usual time-latitude diagrams. The lower energy j=2 mode, which seems to contain many spatial scales (see Fig. 3, panel c), describes small scale fluctuations of the main solar cycle. The effect of this mode on the spatio-temporal intensity pattern (Fig. 4, panel c) is to enhance the fluctuations of the signal and to form the north-south asymmetries in the wings of the butterfly diagram (see e.g. Badalyan et al. 2008; Pontieri et al. 2003; Knaack et al. 2004).

Conversely, only the j=0 mode is associated with the main 11-year solar cycle in both polar regions (Fig. 5, panels a,b). At these latitudes, the main cycle does not show a complex spatial structure, thus one POD mode suffices to describe it. At first sight, a₁(t) coefficients, from both north and south regions, show high frequency fluctuations but no evident oscillating behavior can be seen. These modes could thus represent a stochastic short-term component of the cycle. Reconstructions of the coronal emission at high latitude using only the first j=0,1 modes are shown in Fig. 6

The main spatio-temporal peculiarities of solar activity are explained within the context of dynamo theory. In this framework, the magnetic field of the Sun is generated through a turbulent $\alpha-\omega$ process. Our results provide observational constraints for theoretical modeling of the solar dynamo effect. Firstly, the nature of the 11-year and the high frequency contributions are quite different. This can be inferred by simply studying the time behaviour of the main polar and equatorial coefficients a_j(t) by building up a kind of phase space. This is defined by plotting two coefficients, one versus the other. Since the equatorial a₀(t), a₁(t) and the polar a₀(t) describe the main solar cycle while both polar a₁(t) are associated with the high-frequency components, we will study how the phase space is modified when the coefficients on the plot axis are changed. Figure 7 shows the phase space of the equatorial $a^{\rm eq}_1(t)$ versus the equatorial $a^{\rm eq}_0(t)$ (panel a), the polar j=0 coefficients versus the equatorial $a^{\rm eq}_0(t)$ (panel b,c) and both polar j=0 coefficients, namely a^s₀(t) versus aⁿ₀(t) (panel d). These coefficients are associated with the main solar periodicity, thus the phase space plots appear quite regular, excluding small local fluctuations of phase and frequency, and indicate that two orthogonal oscillators, with the same frequency, are present. More precisely, while panel a, characterized by more or less concentric and rotating ellipses, describes two out of phase oscillations with non-correlated amplitude variations, phase spaces b-d, in which the points are sorted approximately along a straight line, can be associated with oscillations with zero phase difference and correlated amplitude variations. The behaviour illustrated in panel a can be explained by remembering that equatorial j=0,1 modes describe different aspects of the solar activity, namely the basic spatial periodicity and the north-south occurrence of the active regions. Both phenomena show the same periodicity in time, but the amplitudes and phase difference change in a different way.

$\begin{figure} \par\includegraphics[width=18cm,clip]{1024fg6.eps} \end{figure}$	Figure 7: Phase space of two POD coefficients. a): $a^{\rm eq}_0(t)$ versus $a^{\rm eq}_1(t)$ for the equatorial data set. b), c): equatorial $a^{\rm eq}_0(t)$ versus northern and southern a₀(t). d): northern aⁿ₀(t) versus southern $a^{\rm s}_0(t)$ . e): northern aⁿ₁(t) versus southern $a^{\rm s}_1(t)$ .
Open with DEXTER

This is a clear indication that the main solar cycle represents a true oscillation mode and thus it can be described by a simple nonlinear oscillator (Pontieri et al. 2003; Mininni et al. 2000) within a narrow band of frequencies and with a well defined phase.

The phase space of the j=1 polar coefficients (panel e), associated with the short-term component of the solar activity, shows a stochastic behavior. This kind of plot is very different from the phase space generated by two coherent oscillations. These simple considerations indicate that the short term component of the solar activity is probably generated by a turbulence-like phenomenon in a narrow band of frequencies. Dynamo models describing the source of solar periodicities must take into account these properties.

3.2 Time evolution of POD coefficients: Wavelet analysis and period length variation

Wavelets have been chosen to study the temporal behaviour of the POD modes and to characterize the high frequency modulation of coefficients a_j(t). To this purpose, the well known Mexican Hat Wavelet analysis (Torrence & Compo 1998) has been applied to each a_j(t) thus obtaining a set of wavelet coefficients W_j(T,t) (T is the period). The choosen form for the wavelet mother function ensures a good compromise between spatial and temporal resolution (Torrence & Compo 1998).

Figures 8 and 9 show the local wavelet power spectrum |W_j(T,t)|² in the time-period domain (left figure of each panel) and the global wavelet spectrum $P_j(T) = \int \vert W_j(T,t)\vert^2 {\rm d}t$ (right figure of each panel) respectively for the equatorial and polar data sets. The local spectrum contains information on the time localization of the detected frequencies. The global spectra, being integrated over time, are analogous to the Fourier spectra and are helpful to detect the dominant frequencies at work in the system. When the frequencies are strongly modulated in time, global and local spectra could give different results. In fact the time integration, performed in the P_j(T) calculation, produces strong peaks when the frequency is almost constant in time. In Figs. 8 and 9, cross-hatched regions represent the cone of influence (COI), namely the area of the local wavelet spectrum in which edge effects become important (Torrence & Compo 1998), thus influencing the result. The color scale, chosen to draw spectra, associates blue with low power and yellow with high power areas, passing through green and red. The significance levels for the spectra are established through statistical significance tests developed by deriving theoretical wavelet spectra for white noise processes (Torrence & Compo 1998).

$\begin{figure} \par\hspace*{-2.6mm}\includegraphics[width=6cm,clip]{1024fg7a.eps... ...clip]{1024fg7e.eps}\includegraphics[width=2.5cm,clip]{1024fg7f.eps} \end{figure}$

Figure 8:

The most energetic POD modes for the equatorial region. Each panel shows the local wavelet power spectrum |W_j(T,t)|² of the POD coefficient a_j(t) in the period-time plane (left figure) and the corresponding global wavelet spectrum P_j(T) (right panel). Panels a), b), c) refer respectively to j=0,1,2. Solid lines in the local and dotted lines in the global spectrum mark the power significance at $95\%$ . Color scale is in arbitrary units.

Open with DEXTER

$\begin{figure} \par\includegraphics[height=3.1cm,width=6cm,clip]{1024fg8a.eps}\i... ...g.eps}\includegraphics[height=3.3cm,width=2.5cm,clip]{1024fg8h.eps} \end{figure}$

Figure 9:

The most energetic POD modes for the polar regions. Each panel shows the local wavelet power spectrum |W_j(T,t)|² of the POD coefficient a_j(t) in the period-time plane ( left figure) and the corresponding global wavelet spectrum P_j(T) ( right figure). Panels a), c) refer respectively to j=0,1 coefficients of the northern region. Panels b), d) refer to j=0,1 coefficients of the southern region. Solid lines in the local and dotted lines in the global spectrum mark the power significance at $95\%$ . Color scale is in arbitrary units.

Open with DEXTER

Let us consider in detail Figs. 8 and 9. The local wavelet power is distributed along ridges around 11 years both for equatorial j=0,1 (Fig. 8, panels a, b) and polar j=0 coefficients (Fig. 9, panels a, b). This is confirmed by a look at the global power spectrum, dominated by a peak at a period of about 11 years. The global wavelet spectra also reveal a power excess at a period close to 25 years. This low-frequency peak, pronounced in equatorial j=1 and polar j=0 spectra, is reminiscent of the so-called Hale's law (see e.g. Stix 2002), the 22-year cycle related to the inversion of the magnetic field, that could also influence the coronal emissions (Tritakis et al. 1988). The length of our data set, lasting about 45 years, is probably insufficient to precisely detect this period. Although at first sight the coefficient a₂(t) of the equatorial sample does not show any evident periodicity (see Fig. 3, panel c), a peak in the global power spectrum, at about 11 years, can be identified (Fig. 8, panel c). The local wavelet spectrum for the coefficient j=2, although dominated by the 11 year contribution, shows significant power in the low period range typical of the quasi-biennial oscillations. For the polar j=1 coefficients, the signal associated with the quasi-biennial component is the dominant one. This is clearly indicated by the corresponding local spectra where the highest values of power are distributed at periods shorter than the main 11 years cycle (Fig. 9, panels c, d). The quasi-biennial component of the solar cycle, although weaker than the main one, is very robust since it has been recorded by many indicators (see e.g. Cadavid et al. 2005; Penza et al. 2006; Li et al. 2006; Kane 2005). The peak in P_j(T) corresponding to the short-term contribution, although significant, is underestimated compared to the main cycle peak. This effect is due to the strong modulation or the quasi-biennial frequencies varying from a period to another.

POD, discriminating the different phenomena according to their spatial pattern, is able to separate the main cycle, associated with the classical butterfly pattern, from other components. Moreover the POD modes are orthonormal, so that this analysis in general is able to separate independent phenomena within a complex behaviour. Being captured by the low energy POD modes, the occurrence of the high frequency cycles is a phenomenon energetically less relevant than the main 11-year cycle. The quasi-biennial components, isolated in a single mode by POD, are characterized by similar spatial scales. The quasi-biennial signal is detected, with similar amplitudes, in the analyzed latitude bands: the polar areas, where the contribution to the solar cycle is only due to the large-scale global magnetic field, and the equatorial region, where the cycle is dominated by the emergence of active regions. Our results show that the quasi-biennial periodicity is related to the global large scale magnetic field and its origin must be a phenomenon, within the dynamo process, different from the emergence of active regions (Benevolenskaya 1998; Vecchio & Carbone 2008b) and with turbulent properties, as indicated by the phase-space considerations. In fact it is better detected in the polar regions, while it is masked by the strong and spatially structured 11 year contribution in the equatorial band. However, the strengths of the two mechanisms could be related. As shown by the local wavelet power |W_j(T,t)|² that furnishes useful information about the time localization of the high-frequency periodicities, the amplitudes of the short-term component are more pronounced during the maxima of the solar main activity.

The joint analysis of POD and wavelet underlines that the period of the detected quasi-biennial high-frequency component is not constant. For the POD coefficients associated with this component, the maximum of the local wavelet power is not fixed but oscillates in time (see Fig. 9, panels c, d). A modulation of the period length, as for the main solar cycle, seems to occur for the quasi-biennial contribution. We can add more harmonics to the ``solar melody'' generated by the time variation of the period of the main 11-year cycle. The period length variations can be calculated following the approach proposed by Fligge et al. (1999). The method has been applied to measure the period length variations for the quasi-biennial contribution and to recalculate the modulation of the main solar cycle using our dataset rather than the usual sunspot series. The period length at a given time is found by identifying the periods corresponding to local maxima of |W_j(T,t)|² in a narrow band around P₀ = 11 years, for the main component, and P₁ = 2.5 years for the quasi-biennial component, and by following them in time. Only the maxima corresponding to a wavelet significance level greater than $95\%$ and outside the COI are taken into account. The error bars assigned to each length represent the wavelet period resolution at the calculated values. The results are presented in Fig. 10 where the time evolution of both periods, of the main and quasi-biennial solar cycle, extracted from the first two POD modes of equatorial, north and south high-latitude samples (panels a-c respectively) is shown. The main 11-year cycle, described by the coefficients j=0,1 (panel a) of the equatorial and j=0 (panels b, c) of the polar samples, shows the well know modulation with period, oscillating between about 11 and 9.5 years (Friis-Christensen & Lassen 1991; Fligge et al. 1999). The characteristic period of the quasi-biennial component, extracted from coefficients j=0 of the equatorial and j=1 of the polar data sets, varies between 1.5 and 4 years in the range of values in which low-term components of the solar cycle are commonly detected.

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{1024fg9a.eps}\par\includeg... ...]{1024fg9b.eps}\par\includegraphics[width=6.5cm,clip]{1024fg9c.eps} \end{figure}$	Figure 10: Time variations of 11 year and quasi-biennial period lengths obtained from the wavelet analysis of the significant POD coefficients for the equatorial region ( upper panel), the northern region ( middle panel) and the southern region ( lower panel).
Open with DEXTER

4 Discussion and conclusions

The main purpose of this paper is the investigation of the spatio-temporal dynamics of solar activity using time series of the spatial green coronal emission line at 530.3 nm, in the period of time from 1939 to 2005. Besides the main 11-year cycle we found a well defined high-frequency quasi-biennial period of activity. The contribution of the 11-year component of the solar activity, being related to the emergence of active regions, is dominant in the equatorial sample, even if it is also present in the polar bands at lower amplitudes. Conversely, the quasi-biennial periodicity is better detected in the polar data, where the contribution to the solar cycle is mainly due to the large scale magnetic field. The energy contents of the two phenomena are noticeably different. This represents a further indication that the high frequency component must be described with a dynamo mechanism different from the process generating the emergence of active regions. This can also be seen by making simple considerations about the phase space, built using two POD coefficients. The phase-space of the modes dominated by 11-year oscillations shows a regular behaviour, explicable as the result of wave-like phenomena. On the other hand, the modes associated with the 2-year component of the solar cycle generate a stochastic pattern. This indicates that the short term component of the solar activity is probably generated by a turbulence-like phenomenon in a narrow band of frequency.

Other properties of the solar cycle can be inferred from our analysis. First of all the high-frequency component shows a variation of the period length over time. Its period changes between 4 years and 1.5 years. We found a good agreement between the frequencies of a quasi-biennial cycle detected by different indicators, observed only in some solar cycles (see e.g. Cadavid et al. 2005; Li et al. 2006; Knaack et al. 2004,2005), and the calculated lengths in the short-term periods investigated here. All these considerations indicate that this component of the solar activity, commonly considered as a sequence of multiple oscillations with different frequencies, could be simply the manifestation of the temporal modulation of a unique quasi-biennial activity cycle. All the found properties of the cycle represent constraints that should be taken into account in the dynamo models built to describe the source of solar periodicities.

Our analysis of the quasi-biennial solar cycle can be directly related to other astrophysical fields. In particular, the quasi-biennial solar cycle could be correlated to the quasi-biennial variation of solar neutrino fluxes (e.g. Sakurai 1979) and modulate the cosmic ray flux in interplanetary space (Laurenza et al. 2009).

Acknowledgements

We thank the referee for useful comments and help in improving the presentation of results. This work was partially supported by the Italian Space Agency ASI/INAF grant I/015/07/0 ``Studi di Esplorazione del Sistema Solare'', and by INAF (PRIN-INAF 2007) ``Scientific exploitation of the Interferometric Bidimensional Spectrometer (IBIS). Magnetic structuring of the lower solar atmosphere''.

References

Badalyan, O. G., Obridko, V. N., & Sýkora, J. 2008, Sol. Phys., 247, 379 [NASA ADS] [CrossRef]
Bay, T. 2003, ApJ, 591, 406 [NASA ADS] [CrossRef]
Beer, J., Baumgartner, S. T., Dittrich-Hannen, B., et al. 1994, in The Sun as a Variable Star: Solar and Stellar Irradiance Variations (Cambridge: Cambridge Univ. Press), IAU Coll., 143, 291 (In the text)
Benevolenskaya, E. E. 1998, ApJ, 509, L49 [NASA ADS] [CrossRef]
Cadavid, A. C., Lawrence, J. K., McDonald, D. P., & Ruzmaikin, A. 2005, Sol. Phys., 226, 359 [NASA ADS] [CrossRef]
Eddy, J. A. 1976, Science, 192, 1189 [NASA ADS] [CrossRef]
Fligge, M., Solanki, S. K., & Beer, J. 1999, A&A, 346, 313 [NASA ADS]
Friis-Christensen, E., & Lassen, K. 1991, Science, 254, 698 [NASA ADS] [CrossRef]
Gnevyshev, M. N. 1977, Sol. Phys., 51, 175 [NASA ADS] [CrossRef]
Haubold, H. J. 1998, Astrophys. Space Sci., 258, 201 [NASA ADS] [CrossRef]
Holmes, P., Lumley, J. L., & Berkooz, G. 1996, Turbulence, Coherent Structures, Dynamical Systems and Symmetry (Cambridge University Press) (In the text)
Kane, R. P. 2005, Sol. Phys., 227, 155 [NASA ADS] [CrossRef]
Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2004, A&A, 418, L17 [NASA ADS] [CrossRef] [EDP Sciences]
Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2005, A&A, 438, 1067 [NASA ADS] [CrossRef] [EDP Sciences]
Krivova, N. A., & Solanki, S. M. 2002, A&A, 394, 701 [NASA ADS] [CrossRef] [EDP Sciences]
Laurenza, M., Storini, M., Giangravé, S., & Moreno, G. 2009, J. Geophys. Res., 114, A01103 [CrossRef] (In the text)
Lawrence, J. K., Cadavid, A., & Ruzmaikin, A. 2004, Sol. Phys., 225, 1 [NASA ADS] [CrossRef]
Li, K. J., Li, Q. X., Su, T. W., & Gao, P. X. 2006, Sol. Phys., 239, 493 [NASA ADS] [CrossRef] (In the text)
Mininni, P. D., Gómez, D. O., & Mindlin, G. B. 2000, , 85, 5476
Mininni, P. D., Gómez, D. O., & Mindlin, G. B. 2002, , 89, 061101
Penza, V., Pietropaolo, E., & Livingston, W. 2006, A&A, 454, 349 [NASA ADS] [CrossRef] [EDP Sciences]
Pontieri, A., Lepreti, F., Sorriso-Valvo, L., Vecchio, A., & Carbone, V. 2003, Sol. Phys., 213, 195 [NASA ADS] [CrossRef]
Rees, D. E., López Ariste, A., Thatcher, J., & Semel, M. 2000, A&A, 355, 759 [NASA ADS]
Rybanský, M., Rusin, V., Minarovjech, M., & Gaspar, P. 1994, Sol. Phys., 152, 153 [NASA ADS] [CrossRef]
Rybanský, M., Rusin, V., Minarovjech, M., Klocok, L., & Cliver, E. W. 2005, J. Geophys. Res., 110, A08106 [CrossRef] (In the text)
Rusin, V., & Zverko, J. 1990, Sol. Phys., 128, 261 [NASA ADS] [CrossRef]
Sakurai, K. 1979, Nature, 278, 146 [NASA ADS] [CrossRef] (In the text)
Sakurai, K., Haubold, H. J., & Shirai, T. 2008, Space Rad., 5, 207
Scafetta, N., & West, B. J. 2008, Physics Today, 61, 50 [CrossRef] (In the text)
Shirai, T. 2004, Sol. Phys., 222, 199 [NASA ADS] [CrossRef]
Stix, M. 2002, The Sun, an introduction (Berlin: Springer-Verlag) (In the text)
Torrence, C., & Compo, G. 1998, Bull. Am. Meterol., 79, 61 [CrossRef] (In the text)
Tritakis, V. P., Mavromichalaki, H., & Petropoulos, B. 1988, Sol. Phys., 115, 367 [NASA ADS] [CrossRef] (In the text)
Vecchio, A., & Carbone, V. 2008a, Sol. Phys., 249, 11 [NASA ADS] [CrossRef]
Vecchio, A., & Carbone, V. 2008b, ApJ, 683, 536 [NASA ADS] [CrossRef]
Vecchio, A., Primavera, L., Carbone, V., & Sorriso-Valvo, L. 2005, Sol. Phys., 229, 359 [NASA ADS] [CrossRef]
Vecchio, A., Carbone, V., Lepreti, F., et al. 2008, Sol. Phys., 251, 163 [NASA ADS] [CrossRef] (In the text)

Footnotes

... set: The full data set is available at ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SOLAR_CORONA/LOMNICKY/5-degree-data/. The coronal intensities are given in millionths of intensity of the solar disk (coronal units) and converted to the photometrical scale of Lomnický Stít Station at a height of 40'' above the solar limb (cf. Rybanský et al. 2005; Rybanský 1994). Several stations were used in this database, namely: Lomnický Stít, Sacramento Peak, Norikura, Kislovodsk, Pic Du Midi, Wendelstein, Arosa, and Kanzelhöhe. Lomnický Stít is the primary station since 1965.

All Figures

$\begin{figure} \par\includegraphics[width=16cm,clip]{1024fg0.eps} \end{figure}$	Figure 1: The daily intensity emission of the solar corona in the period 1939-2005 as observed in the time-angle plane. The latitude $\theta =0$ corresponds to solar equator. The color scale is linear.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.3cm,clip]{1024fg1.eps} \end{figure}$	Figure 2: Cumulated energy of the first nine POD modes as a function of the index j ( $j = 0,\dots , 8$ ). Panel b) refers to the equatorial sample, panels a), c) correspond to polar data sets.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.3cm,clip]{1024fg2.eps} \end{figure}$	Figure 3: Equatorial data set: time evolution of the first three POD coefficients a_j(t) for $0\leq j\leq 2$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{1024fg3.eps} \end{figure}$	Figure 4: Reconstructed intensity $I(\theta ,t)$ for the equatorial area, represented in the $(t,\theta )$ plane, using different N in Eq. (3). N=0 (panel a)), N=1 (panel b)). N=2 (panel c)) contains the $99\%$ of the total energy. The color scale is linear.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{1024fg4.eps} \end{figure}$	Figure 5: Polar data sets: time evolution of the first two POD coefficients a_j(t) for j=0,1 for the northern (panels a), c)) and southern regions (panels b), d)).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{1024fg5.eps} \end{figure}$	Figure 6: Reconstructed intensity $I(\theta ,t)$ , using the first two modes containing $99\%$ of the total energy, represented in the $(t,\theta )$ plane. Panel a) refers to the northern region and panel b) to the southern region.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=18cm,clip]{1024fg6.eps} \end{figure}$	Figure 7: Phase space of two POD coefficients. a): $a^{\rm eq}_0(t)$ versus $a^{\rm eq}_1(t)$ for the equatorial data set. b), c): equatorial $a^{\rm eq}_0(t)$ versus northern and southern a₀(t). d): northern aⁿ₀(t) versus southern $a^{\rm s}_0(t)$ . e): northern aⁿ₁(t) versus southern $a^{\rm s}_1(t)$ .
Open with DEXTER
In the text

$\begin{figure} \par\hspace*{-2.6mm}\includegraphics[width=6cm,clip]{1024fg7a.eps... ...clip]{1024fg7e.eps}\includegraphics[width=2.5cm,clip]{1024fg7f.eps} \end{figure}$	Figure 8: The most energetic POD modes for the equatorial region. Each panel shows the local wavelet power spectrum \|W_j(T,t)\|² of the POD coefficient a_j(t) in the period-time plane (left figure) and the corresponding global wavelet spectrum P_j(T) (right panel). Panels a), b), c) refer respectively to j=0,1,2. Solid lines in the local and dotted lines in the global spectrum mark the power significance at $95\%$ . Color scale is in arbitrary units.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[height=3.1cm,width=6cm,clip]{1024fg8a.eps}\i... ...g.eps}\includegraphics[height=3.3cm,width=2.5cm,clip]{1024fg8h.eps} \end{figure}$	Figure 9: The most energetic POD modes for the polar regions. Each panel shows the local wavelet power spectrum \|W_j(T,t)\|² of the POD coefficient a_j(t) in the period-time plane ( left figure) and the corresponding global wavelet spectrum P_j(T) ( right figure). Panels a), c) refer respectively to j=0,1 coefficients of the northern region. Panels b), d) refer to j=0,1 coefficients of the southern region. Solid lines in the local and dotted lines in the global spectrum mark the power significance at $95\%$ . Color scale is in arbitrary units.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{1024fg9a.eps}\par\includeg... ...]{1024fg9b.eps}\par\includegraphics[width=6.5cm,clip]{1024fg9c.eps} \end{figure}$	Figure 10: Time variations of 11 year and quasi-biennial period lengths obtained from the wavelet analysis of the significant POD coefficients for the equatorial region ( upper panel), the northern region ( middle panel) and the southern region ( lower panel).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.