Is the energy generation rate of nuclear reactions in hot accretion flows important?

H. Zhang; Y. Wang; F. Yuan; F. Ding; X. Luo; Q. H. Peng

doi:10.1051/0004-6361/200912005

Home

All issues

Volume 502 / No 2 (August I 2009)

A&A, 502 2 (2009) 419-422

Full HTML

Free Access

Issue		A&A Volume 502, Number 2, August I 2009


Page(s)		419 - 422
Section		Astrophysical processes
DOI		https://doi.org/10.1051/0004-6361/200912005
Published online		15 June 2009

Is the energy generation rate of nuclear reactions in hot accretion flows important?
(Research Note)

H. Zhang^1,2 - Y. Wang³ - F. Yuan¹ - F. Ding³ - X. Luo⁴ - Q. H. Peng^4,5

1 - Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatories, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, China
2 - Graduate School of the Chinese Academy of Sciences, Beijing 100039, PR China
3 - University of Science and Technology of China, Hefei, Anhui 230026, PR China
4 - Department of Astronomy, Nanjing University, Nanjing 210093, PR China
5 - The Open Laboratory of Cosmic Ray and High Energy Astrophysics, Chinese Academy of Sciences, Beijing 100049, PR China

Received 8 March 2009 / Accepted 13 May 2009

Abstract
The temperature of hot accretion flows around black holes is sufficiently high for the ignition of nuclear reactions. This is potentially an important nucleosynthesis mechanism in the universe. As the first step in studying this problem, we need to measure physical quantities such as density and temperature of the accretion flow. In usual studies of the hot accretion flow, viscous dissipation is considered to be the only heating mechanism, while the heating caused by nuclear reactions is not considered. In this paper, we investigate whether the energy generation rate of nuclear reaction is important compared to the viscous heating. Our calculation indicates that the former is at most one percent of the latter and thus is not important. The dynamics of accretion flow can be therefore calculated in the usual way, without the need to consider heating due to nuclear reactions.

Key words: accretion, accretion disks - black hole physics - nuclear reactions, nucleosynthesis, abundances

1 Introduction

Observations imply that there maybe a supermassive black hole at the center of almost every galaxies. There is a large fraction for which the accretion flow can be described by a hot accretion flow, such as advection-dominated accretion flow (ADAF, Narayan & Yi 1994, 1995; Abramowicz et al. 1995; for a review of ADAF, see Narayan et al. 1998; for a review of the applications of ADAF, see Yuan 2007) and luminous hot accretion flow (LHAF, Yuan 2001). Hot accretion flow also exists in some states of black hole X-ray binaries. The temperature of the hot flow is very high, $T_{i}\sim10^{12}$ K/r, r being the radius in unit of Schwarzschild radius $r_{\rm s}$ . This temperature is high enough to ignite significant nuclear reactions in the hot flow. This process is potentially interesting because it is a promising means of producing new elements. The analysis of observations by Juarez et al. (2009; see also Hamann & Ferland 1999) found that the metallicity of the BLR of redshift quasars is very high. One explanation is that the massive stars had formed before the quasars were created, and these stars then enriched the metallicities of quasars. It is also possible that BLR gas originates in accretion flows. Although accretion flows in quasars are generally assumed to be in the regime of higher accretion rates than that of a hot accretion flow, i.e., the standard thin disk, the detailed structure of the accretion flow is still largely unknown because the thin disk can not explain the origin of the X-ray emission widely observed in quasars. The presence of X-ray emission implies that ADAF or LHAF-like hot accretion flow is also likely to exist in quasars, not only in some low-luminosity AGNs. One possible reason for the high metallicity in quasars is therefore that nucleosynthesis occurs in the accretion flow (see the review paper of Hamann & Ferland 1999).

Some people have already studied the nuclear reactions and nucleosynthesis in accretion flows around black holes (e.g., Jin et al. 1989; Arai & Hashimoto 1992; Chakrabarti & Mukhopadhyay 1999; Mukhopadhyay & Chakrabarti 2000; Mukhopadhyay & Chakrabarti 2001; Hu & Peng 2008). In these works, however, the accretion flow models adopted are quite different from ADAFs. The works of Jin et al. and Arai & Hashimoto are based on a ``thick disk'', while the two works by Mukhopadhyay & Chakrabarti are based on a simplified inviscid accretion flow, which differs again from ADAFs. These particular accretion models have received little attention these years. Hu & Peng (2008) studied nucleosynthesis in ADAFs, but their work was based on the self-similar solution of ADAF. This solution is affected by significant error in the inner region of the accretion flow, where most nuclear reactions occur.

We therefore revisit the study of nucleosynthesis in hot accretion flows. We first constrain the dynamics of accretion flows. Although the global solution of ADAF has been known for many years, since nuclear reactions have not previously been taken into account, we need to investigate whether they are important compared to the viscous heating. If they are then, the self-consistent global solution of ADAF needs to be recalculated. We neglect the photodisintegration because the optical depth in ADAFs is very small and most of the photos can escape from the hot accretion flow without being scattered.

The structure of the paper is as follows. We briefly introduce ADAFs in Sect. 2.1 and the calculation method of energy generation rate in Sect. 2.2. The calculation results will be shown in Sect. 2.3. In Sect. 3 we summarize our results.

2 Energy generation rate in hot accretion flow

2.1 Advection dominated accretion flow

The dynamics of the ADAF is described by the continuity equation, the radial and azimuthal components of momentum equation, and the energy equations of electrons and ions (Narayan et al. 1998)

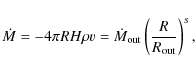$\begin{displaymath}\dot{M}=-4\pi R H \rho v = \dot{M}_{\rm out}\left(\frac{R}{R_{\rm out}} \right)^s, \end{displaymath}$

(1)

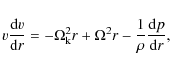$\begin{displaymath}v \frac{{\rm d}v}{{\rm d}r}= -\Omega_{\rm k}^2 r+\Omega^2 r-\frac{1}{\rho}\frac {{\rm d}p}{{\rm d}r}, \end{displaymath}$

(2)

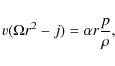$\begin{displaymath}v(\Omega r^2-j)= \alpha r \frac{p}{\rho}, \end{displaymath}$

(3)

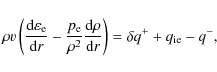$\begin{displaymath}\rho v \left(\frac{{\rm d}\varepsilon_{\rm e}}{{\rm d}r}- {p_... ...rac{{\rm d} \rho}{{\rm d}r}\right) =\delta q^++q_{\rm ie}-q^-, \end{displaymath}$

(4)

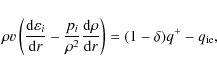$\begin{displaymath}\rho v \left(\frac{{\rm d}\varepsilon_i}{{\rm d}r}- {p_i \ove... ...c{{\rm d} \rho}{{\rm d}r} \right) =(1-\delta)q^+-q_{\rm ie}, \end{displaymath}$

(5)

where $\dot{M}_{\rm out}$ is the mass-flow rate at the outer boundary ( $R_{\rm out}$ ) of the flow, the exponent s describes the strength of the outflow, $\delta$ is the fraction of turbulent viscous energy that directly heats the electrons, q⁺ is the viscosity heating rate, $q_{\rm ie}$ is the Coulomb energy exchange rate between electrons and ions, and q^- is the radiative cooling rate per unit volume. The main radiative processes are synchrotron emission, bremsstrahlung, and their respective Comptonizations. The eigenvalue j corresponds to the specific angular momentum loss at the inner boundary, $\varepsilon_{\rm i}$ ( $\varepsilon_{\rm e}$ ) is the internal energy of ions (electrons), and $P_{\rm i}$ ( $P_{\rm e}$ ) is the pressure due to ions (electrons).

The global solution of these equations needs to satisfy three conditions. The first one is the no-torque condition at the horizon. This condition can be automatically satisfied if we adopt the viscous description of $\tau_{r \phi}=\alpha (P_{\rm gas} + P_{\rm mag})$ , where $\tau_{r \phi}$ is the viscous stress tensor, and $P_{\rm gas}$ and $P_{\rm mag}$ are the gas pressure and magnetic pressure, respectively. The second condition is the transonic condition. When the matter enters into the horizon of the black hole, its speed should be equal to the light speed. A sonic point must therefore exist where the radial speed of flow equals the local sonic speed. The solution should finally satisfy the boundary condition at $R_{\rm out}$ . Here we chose the temperature of ions and electrons $T_{\rm i,e}$ , and the ratio of the radial velocity of the flows to the local speed of sound $v/c_{\rm s}$ at $R_{\rm out}$ . We adopt the Paczynski & Wiita (1980) potential to mimic the geometry of a Schwarzschild black hole. We adjust the eigenvalue j and use the shooting method to derive the global solution that satisfies the conditions above. For the parameters of the hot accretion flow, we choose their typical values constrained by modeling black hole X-ray binaries (e.g., Yuan et al. 2005) and the supermassive black hole in our Galactic center, Sgr A*, which is the most well studied supermassive black hole system observationally (Yuan et al. 2003). They are the viscous parameter $\alpha=0.3$ (but see discussions below), $\beta=0.9$ , s=0.3, and $\delta=0.5$ , where $\beta$ is the ratio of the gas pressure to the total pressure, sdescribes the strength of the outflow, and $\delta$ is the fraction of viscous dissipation that directly heats the electrons. The detailed numerical approach can be found in Yuan (2001) or Yuan et al. (2003).

As is well known, when the accretion rate is very low, almost all of the viscously dissipated energy is stored in the accretion flow and advected into the horizon of the black hole, rather than radiated away. This is because the radiative timescale is far longer than the accretion timescale. However, when the accretion rate increases, the radiative timescale becomes shorter, and less energy is advected into the black hole. In the regime of LHAF, the energy advection even becomes negative. In this case, the radiative efficiency of the hot accretion flow increases, even reaching that of the standard thin disk (Shakura & Sunyaev 1973). Unlike the standard thin disk, ADAF is of course, still hot and geometrically thick. The temperature of the ions is almost always virial, and is a power-law function of radius.

2.2 Calculation of nuclear reaction heating

We make the following assumptions. The first is that the element abundance in the accretion flow is the same as that in the solar atmosphere (Grevesse & Sauval 2000). The companion of the stellar mass black hole could be a main-sequence star, and the accretion matter of a supermassive black hole at the galactic center is presumably supplied by a number of nearby stars. Second, we assume that the element abundance due to nuclear reaction does not differ significantly from the initial abundance. This is obviously not a robust assumption if significant nucleosynthesis does occur in the accretion flow. Before we know the final result, we must however make this assumption. We could complete some ``iteration'' if we knew how the abundance changes. Third, in the large-scale universe, the relative abundance of an isotope compared to other isotopes of the same element is quite constant. You can find the relative abundance of isotopes from the table at the website. In our calculation here, we accept the assume isotope abundances given in this table.

The nuclear reactions in the star and in the hot accretion flow are different. In the star, different sets of burnings are well separated by appreciable temperature differences in the star. However, in the hot accretion flow, these nuclear reactions can be ignited almost simultaneously because the temperature is sufficiently high to ignite different nuclear burning at the same time. In principle, nuclear reaction can proceed for many kinds of elements if the temperature is high enough. We considered only H, He, and C burning after finding that other nuclear reactions were not important contributors to the energy generation rate. Our second assumption is therefore justified.

The temperature of the accretion flow increases when it is closer to the central black hole, when an increasing number of elements are burned. Different nuclear reactions are ignited at different temperatures. Hydrogen is burned when the temperature is higher than $7 \times 10^6$ K. Helium can be burned when the temperature reaches $1{-}2 \times 10^8$ K, and for carbon, this temperature is about $7 \times 10^8$ K. The total energy generation rates in different temperature ranges are as follows:

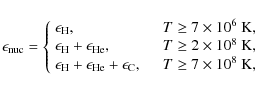$\begin{displaymath}\epsilon_{\rm nuc}=\left\{ \begin{array}{ll} \epsilon_{\rm H}... ...& \quad T \geq 7 \times 10^8~{\rm K}, \end{array} \right. \\ \end{displaymath}$

(6)

$\epsilon_{\rm H}$ , $\epsilon_{\rm He}$ , and $\epsilon_{\rm C}$ is the total energy generation rate of hydrogen, helium, and carbon, respectively, and $\epsilon_{\rm nuc}$ represents their sum. They are defined to be the energy produced per unit mass and time

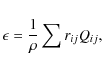$\begin{displaymath}\epsilon=\frac{1}{\rho}\sum r_{ij}Q_{ij}, \end{displaymath}$

(7)

where r_ij is the reaction rate per unit i.e., volume and time between the nuclei i and j, and Q_ij is the energy released per reaction,

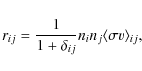$\begin{displaymath}r_{ij}=\frac{1}{1+\delta_{ij}}n_in_j \langle \sigma v \rangle _{ij}, \end{displaymath}$

(8)

where,

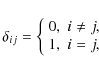$\begin{displaymath}\delta_{ij}=\left\{ \begin{array}{ll} 0, &i \neq j, \\ 1, &i = j,\end{array}\right. \end{displaymath}$

(9)

$\langle \sigma v \rangle _{ij}$ is the average cross-section, and n_i and n_j is the number density of particles i and j, which can also be written as

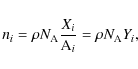$\begin{displaymath}n_{i}=\rho N_{\rm A} \frac{X_i}{{\rm A}_i}=\rho N_{\rm A}Y_i, \end{displaymath}$

(10)

where X_i, Y_i, and A_i are the mass abundance, number abundance, and atomic weight of element i, respectively, and $N_{\rm A}$ is Avogadro number. According to Eqs. (7)-(10), the energy generation rate of nuclear reactions can be written as

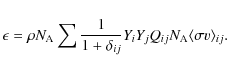$\begin{displaymath}\epsilon=\rho N_{\rm A} \sum \frac{1}{1+\delta_{ij}} Y_iY_jQ_{ij}N_{\rm A} \langle \sigma v \rangle _{ij}. \end{displaymath}$

(11)

The detailed calculations can be found in Huang (1998), Fowler et al. (1975), Harris et al. (1983), and Georgeanne & Fowler (1988).

We study the energy generation rates of nuclear reactions for accretion flows of various parameters. For the mass of the black hole, we consider a stellar mass black hole ( $10~M_{\odot}$ ), an intermediate-mass black hole ( $10^3~M_{\odot}$ ), and a supermassive black hole ( $10^8~M_{\odot}$ ). These values are typical of black hole X-ray binaries, some possible ultraluminous X-ray sources, and AGNs, respectively. For the case of supermassive black holes, we consider various mass accretion rates, namely $10^{-4}~\dot M_{\rm E}$ ( $\dot M_{\rm E}$ is the Eddington accretion rate, $\dot M_E=10 L_{\rm Edd}/c^2$ ), $10^{-3}~\dot M_{\rm E}$ , 0.01 $\dot M_{\rm E}$ , and 0.1 $\dot M_{\rm E}$ .

After deriving the global solutions of the hot accretion flow by solving Eqs. (1)-(5), we measure the physical quantities of the hot accretion flow as a function of radius in each case, including temperature $T_{\rm i}$ and $T_{\rm e}$ and mass density $\rho$ , and calculate the viscosity heating rate q⁺ (defined as the viscosity heating rate per unit volume). We then calculate the energy generation rate $\epsilon_{\rm nuc}$ of the nuclear reactions at different radii based on temperatures and densities obtained above from Eq. (11). We note that $\epsilon_{\rm nuc}$ is the energy generation rate per unit mass, but q⁺ is usually defined as the viscosity heating rate per unit volume. We therefore define $\varepsilon_{\rm nuc} = \rho \epsilon_{\rm nuc}$ for consistency, and also denote q⁺ by $\varepsilon_{\rm vis}$ . Finally, we derive the ratio of energy generation rate of nuclear reaction to viscosity heating rate, i.e., $\varepsilon_{\rm nuc}/\varepsilon_{\rm vis}$ . If this ratio is high, the ADAF model must obviously be revised by including the heating caused by nuclear reactions.

$\begin{figure} \par\includegraphics[width=9cm,clip]{12005fg1.eps} \end{figure}$

Figure 1:

The ratio of nuclear-reaction energy generation rate to viscous heating rate as a function of radius for different black hole masses. The solid, dashed, and dotted lines represent the cases of $M=10~M_{\odot}$ , $10^3~M_{\odot}$ , and $10^8~M_{\odot}$ . The mass accretion rate $\dot{M}= 0.1~\dot M_{\rm E}$ in all three cases.

$\begin{figure} \par\includegraphics[width=9cm,clip]{12005fg2.eps} \end{figure}$

Figure 2:

The ratio of energy generation rate of nuclear reaction to the viscous heating rate as a function of radius for different mass accretion rates. The solid, dotted, dashed, and dot-dashed lines represent the cases of $\dot{M}= 0.1~\dot M_{\rm E}$ , $10^{-2}~\dot M_{\rm E}$ , $10^{-3}~\dot M_{\rm E}$ , and $10^{-4}~\dot M_{\rm E}$ . The mass of the black hole is $10^8M_{\odot }$ .

2.3 Calculation results

The calculation results are shown in Figs. 1 and 2 . Figure 1 shows the ratio of the heating rate for nuclear reactions to that for viscous dissipation for $\dot{M}= 0.1~\dot M_{\rm E}$ but different black hole masses. We find from this figure that the ratio is roughly proportional to $(r/r_{\rm s})^{-3}$ . This is because in our case $\varepsilon_{\rm nuc}$ is roughly proportional to $\rho^2 T^5$ , while $\varepsilon_{\rm vis}\propto \rho r^{-5/2-s}$ . So $\varepsilon_{\rm nuc}/\varepsilon_{\rm vis} \propto \rho r^{5/2+s} T^5$ . Since $\rho\propto (r/r_{\rm s})^{-3/2+s}$ while $T\propto r^{-1}$ , we have $\varepsilon_{\rm nuc}/\varepsilon_{\rm vis}\propto r^{2s-4}\propto r^{-3.4}$ . The ratio does not depend on the mass of the black hole.

Figure 2 shows this ratio as a function of radius for different $\dot{M}$ but the same black hole mass. The ratio is roughly proportional to $\dot{M}$ (or density), because the nuclear reaction heating rate is proportional to $\dot{M}^2$ while the viscous heating is proportional to $\dot{M}$ , and the ions temperature is always virial, independent of $\dot{M}$ . However, even at $\dot{M}= 0.1~\dot M_{\rm E}$ , almost the highest accretion rate a hot accretion flow can have, this ratio is less than $1\%$ , i.e., the heating rate of nuclear reactions in the hot accretion flow is not important. We therefore do not need to include the nuclear reaction in calculating the dynamics of ADAF.

In our calculation, the value of the viscosity parameter $\alpha$ is adopted to be 0.3, which is ``typical'' of ADAFs. We should emphasize that this value has some uncertainties. The value of $\alpha$ is perhaps constrained most reliably by observations of dwarf nova outbursts, where $\alpha \sim 0.1{-}0.2$ (Smak 1984). Three dimensional magnetohydrodynamic (MHD) numerical simulation suggest that $\alpha \sim 10^{-2}{-}10^{-1}$ (Hawley & Krolik 2001). King et al. (2007) argued that according to the highest quality observational evidence, $\alpha \sim 0.1{-}0.4$ in thin and fully ionized discs. For a given accretion rate, the density of the flow is proportional to $\alpha^{-1}$ . The ratio of the heating rate between nuclear reaction and viscous dissipation is therefore proportional to $\alpha^{-1}$ .

3 Summary and discussion

The temperature of the hot accretion flow such as ADAFs is very high, so nuclear reaction should occur. To study the nucleosynthesis, the first step is to determine the dynamics of the accretion flow. For this purpose, we have investigated the ratio of the heating rate for the nuclear reactions to that for the viscous dissipation. We have found that the ratio increases with accretion rates. However, even for the highest accretion rate for which the hot accretion flow solution exists, the ratio is $\la$ 1%. Therefore, the heating caused by nuclear reaction can be neglected. This result indicates that the previously obtained global solution of hot accretion flow is self-consistent and can be used directly in future studies of nucleosynthesis.

As we mentioned in introduction, some authors have previously studied nuclear reactions and nucleosynthesis in accretion flows around black holes (e.g., Jin et al. 1989; Arai & Hashimoto 1992; Chakrabarti & Mukhopadhyay 1999; Mukhopadhyay & Chakrabarti 2000; Mukhopadhyay & Chakrabarti 2001). They found that significant nuclear reactions can occur and many heavy elements can be synthesized, which is quite different from our results. There are three reasons for this discrepancy. The first is that, as we mentioned in the introduction, the works by Jin et al. and Arai & Hashimoto are based on a ``thick disk'' model in which the radial velocity is several orders of magnitude lower than that in ADAFs if the accretion rate is the same. Secondly, the accretion rates in most of the above-mentioned works are super-Eddington, while the accretion rate in ADAFs is lower than the Eddington rate. The third reason is that the value of the viscous parameter adopted in previous work is muchsmaller than that we adopt, $\alpha=10^{-7}$ (Jin et al. 1989), 10^-10 (Arai & Hashimoto 1992), and 0(Chakrabarti & Mukhopadhyay 1999; Mukhopadhyay & Chakrabarti 2000; Mukhopadhyay & Chakrabarti 2001), respectively. So the density of the accretion flow will be much higher than that in ADAFs. Since the efficiency of nuclear synthesis will increase in proportion to density, this explains why they found that the nuclear reaction is so significant.

Acknowledgements

We thank Lei Zhao for useful discussions on nuclear reaction. This work was supported in part by the Natural Science Foundation of China (grants 10773024, 10833002, 10821302, and 10825314), Bairen Program of Chinese Academy of Sciences, and the National Basic Research Program of China (973 Program 2009CB824800).

References

Arai, K., & Hashimoto, M. 1992, A&A, 254, 191 [NASA ADS] (In the text)
Abramowicz, M., et al. 1995, ApJ, 438, L37 [NASA ADS] [CrossRef] (In the text)
Chakrabarti, S. K., & Mukhopadhyay, B. 1999, A&A, 344, 105 [NASA ADS] (In the text)
Fowler, W. A., Caughlan, G. R., & Zimmerman, B. A. 1975, ARA&A, 13, 69 [NASA ADS] [CrossRef] (In the text)
Georgeanne, R. C., & Fowler, W. A. 1988, Atomic Date and Nuclear Date Tables, 40, 283 [CrossRef] (In the text)
Grevesse, N., & Sauval, A. J. 2000, in Origin of Elements in the Solar System, Implications of Post-1957 Observations, ed. O. Manuel (Dordrecht: Kluwer), 261 (In the text)
Hamann, F., & Ferland, G. 1999, ARA&A, 37, 487 [NASA ADS] [CrossRef] (In the text)
Harris, M. J., et al. 1983, ARA&A, 21, 165 [NASA ADS] [CrossRef] (In the text)
Hawley, J. F., & Krolik, J. H. 2001, ApJ, 548, 348 [NASA ADS] [CrossRef] (In the text)
Hu, T., & Peng, Q. H. 2008, ApJ, 681, 96 [NASA ADS] [CrossRef] (In the text)
Huang, R. Q. 1998, in Stellar Physics (Science Press) (In the text)
Jin, L. P., Arnett, W. D., & Chakrabarti, S. K. 1989, ApJ, 336, 572 [NASA ADS] [CrossRef] (In the text)
Juarez, Y. et al. 2009, [arXiv:0901.0974] (In the text)
King, A. R., Pringle, J. E., & Livio, M. 2007, MNRAS, 376, 1740 [NASA ADS] [CrossRef] (In the text)
Mukhopadhyay, B., & Chakrabarti, S. K. 2000, A&A, 353, 1029 [NASA ADS] (In the text)
Mukhopadhyay, B., & Chakrabarti, S. K. 2001, ApJ, 555, 816 [NASA ADS] [CrossRef] (In the text)
Narayan, R. 2005, Ap&SS, 300, 177 [NASA ADS] [CrossRef]
Narayan, R., & Yi, I. 1994, ApJ, 428, 13 [NASA ADS] [CrossRef] (In the text)
Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] (In the text)
Narayan, R., Mahadevan, R., & Quataert, E. (2009) [arXiv:astro-ph/9803141]
Paczynski, B., & Witta, P. J. 1980, A&A, 88, 23 [NASA ADS] (In the text)
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
Smak, J. 1984, Acta Astron., 34, 161 [NASA ADS] (In the text)
Yuan, F. 2001, MNRAS, 324, 119 [NASA ADS] [CrossRef] (In the text)
Yuan, F. 2007, in The Central Engine of Active Galactic Nuclei, ed. L. C. Ho, & J. M. Wang (San Francisco: ASP), 95 (In the text)
Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [NASA ADS] [CrossRef] (In the text)
Yuan, F., Cui, W., & Narayan, R. 2005, ApJ, 620, 905 [NASA ADS] [CrossRef] (In the text)
Yuan, F., Zdziarski, A. A., Xue, Y. Q., & Wu, X. B. 2007, ApJ, 659, 541 [NASA ADS] [CrossRef]

Footnotes

... website: http://www.chem.queensu.ca/FACILITIES/NMR/nmr/mass-spec/mstable3.htm

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{12005fg1.eps} \end{figure}$	Figure 1: The ratio of nuclear-reaction energy generation rate to viscous heating rate as a function of radius for different black hole masses. The solid, dashed, and dotted lines represent the cases of $M=10~M_{\odot}$ , $10^3~M_{\odot}$ , and $10^8~M_{\odot}$ . The mass accretion rate $\dot{M}= 0.1~\dot M_{\rm E}$ in all three cases.
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{12005fg2.eps} \end{figure}$	Figure 2: The ratio of energy generation rate of nuclear reaction to the viscous heating rate as a function of radius for different mass accretion rates. The solid, dotted, dashed, and dot-dashed lines represent the cases of $\dot{M}= 0.1~\dot M_{\rm E}$ , $10^{-2}~\dot M_{\rm E}$ , $10^{-3}~\dot M_{\rm E}$ , and $10^{-4}~\dot M_{\rm E}$ . The mass of the black hole is $10^8M_{\odot }$ .
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Is the energy generation rate of nuclear reactions in hot accretion flows important? (Research Note)