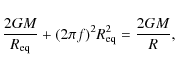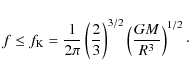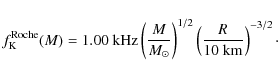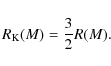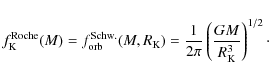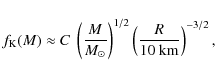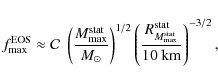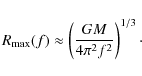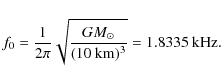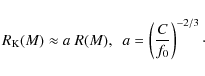| Issue |
A&A
Volume 502, Number 2, August I 2009
|
|
|---|---|---|
| Page(s) | 605 - 610 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811605 | |
| Published online | 22 June 2009 | |
Keplerian frequency of uniformly rotating neutron stars and strange stars
P. Haensel1 - J. L. Zdunik1 - M. Bejger1 - J. M. Lattimer2
1 - N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
2 - Department of Physics and Astronomy, State University of New York at Stony Brook, Stony Brook, NY 11794-3800, USA
Received 30 December 2008 / Accepted 30 April 2009
Abstract
Aims. We calculate Keplerian (mass shedding) configurations of rigidly rotating neutron stars and strange stars with crusts. We check the validity of the empirical formula for Keplerian frequency, ![]() ,
proposed by Lattimer & Prakash,
,
proposed by Lattimer & Prakash,
![]() ,
where M is the (gravitational) mass of the Keplerian configuration, R is the (circumferential) radius of the non-rotating configuration of the same gravitational mass, and C=1.04 kHz.
,
where M is the (gravitational) mass of the Keplerian configuration, R is the (circumferential) radius of the non-rotating configuration of the same gravitational mass, and C=1.04 kHz.
Methods. Numerical calculations are performed using precise 2D codes based on the multi-domain spectral methods. We use a representative set of equations of state (EOSs) of neutron stars and quark stars.
Results. We show that the empirical formula for
![]() holds within a few percent for neutron stars with realistic EOSs, provided
holds within a few percent for neutron stars with realistic EOSs, provided
![]() ,
where
,
where
![]() is the maximum allowable mass of non-rotating neutron stars for an EOS, and
is the maximum allowable mass of non-rotating neutron stars for an EOS, and
![]() kHz. Similar precision is obtained for strange stars with
kHz. Similar precision is obtained for strange stars with
![]() .
For maximal crust masses we obtain
.
For maximal crust masses we obtain
![]() kHz, and the value of
kHz, and the value of
![]() is not very sensitive to the crust mass. All our Cs are significantly larger than the analytic value from the relativistic Roche model,
is not very sensitive to the crust mass. All our Cs are significantly larger than the analytic value from the relativistic Roche model,
![]() kHz. For
kHz. For
![]() ,
the equatorial radius of the Keplerian configuration of mass M,
,
the equatorial radius of the Keplerian configuration of mass M,
![]() ,
is, to a very good approximation, proportional to the radius of the non-rotating star of the same mass,
,
is, to a very good approximation, proportional to the radius of the non-rotating star of the same mass,
![]() ,
with
,
with
![]() .
The value of
.
The value of
![]() is very weakly dependent on the mass of the crust of the strange star. Both a values are smaller than the analytic value
is very weakly dependent on the mass of the crust of the strange star. Both a values are smaller than the analytic value
![]() from the relativistic Roche model.
from the relativistic Roche model.
Key words: dense matter - equation of state - stars: neutron - stars: rotation
1 Introduction
Because of their strong gravity, neutron stars can be very rapid rotators. In view of the high stability of pulsar frequency (even the giant glitches produce relatively small fractional
changes of rotation frequency,
![]() ), one can treat pulsar rotation as rigid. The frequency f of stable rotation of a star of gravitational mass M and baryon mass lower than the maximum allowable for non-rotating stars is limited by the (Keplerian) frequency
), one can treat pulsar rotation as rigid. The frequency f of stable rotation of a star of gravitational mass M and baryon mass lower than the maximum allowable for non-rotating stars is limited by the (Keplerian) frequency ![]() of a test particle co-rotating on an orbit at the stellar equator. The relation between
of a test particle co-rotating on an orbit at the stellar equator. The relation between ![]() and stellar gravitational mass M,
and stellar gravitational mass M,
![]() ,
depends on the (unknown) equation of state (EOS) at supranuclear densities. Both quantities, M and f, are measurable, and the condition implied by a measured frequency
,
depends on the (unknown) equation of state (EOS) at supranuclear densities. Both quantities, M and f, are measurable, and the condition implied by a measured frequency
![]() of a pulsar of mass M,
of a pulsar of mass M,
![]() ,
could be used to constrain theoretical models of dense matter (for a recent review of the theory of dense matter see Lattimer & Prakash 2006; Haensel et al. 2007). Reliable determination of
,
could be used to constrain theoretical models of dense matter (for a recent review of the theory of dense matter see Lattimer & Prakash 2006; Haensel et al. 2007). Reliable determination of
![]() requires precise 2D calculations of stationary, extremely rapid rotating configurations in general relativity. Therefore, the search for a sufficiently precise, approximate but universal formula for
requires precise 2D calculations of stationary, extremely rapid rotating configurations in general relativity. Therefore, the search for a sufficiently precise, approximate but universal formula for
![]() is of great interest. Lattimer & Prakash (2004) proposed an approximate empirical formula
is of great interest. Lattimer & Prakash (2004) proposed an approximate empirical formula
![]() ,
where R=R(M) is the circumferential radius of static star of mass M, and C=1.04 kHz does not depend on the EOS. In the present paper we calculate precise 2D models of rapidly rotating neutron stars and quark stars with different EOSs. We use the relativistic Roche model (Shapiro et al. 1983) to motivate the empirical
formula for
,
where R=R(M) is the circumferential radius of static star of mass M, and C=1.04 kHz does not depend on the EOS. In the present paper we calculate precise 2D models of rapidly rotating neutron stars and quark stars with different EOSs. We use the relativistic Roche model (Shapiro et al. 1983) to motivate the empirical
formula for
![]() proposed by Lattimer & Prakash (2004). We calculate the optimal value of prefactor C and we establish limits for the validity of the empirical formula.
proposed by Lattimer & Prakash (2004). We calculate the optimal value of prefactor C and we establish limits for the validity of the empirical formula.
As of this writing, the maximum rotation frequency of a pulsar is 716 Hz (PSR J1748-2446ad, Hessels et al. 2006). Kaaret et al. (2007) reported the discovery of an oscillation frequency of 1122 Hz in an X-ray burst from the X-ray transient, XTE J1739-285, and concluded that ``this oscillation frequency suggests that XTE J1739-285 contains the fastest rotating neutron star yet found'', but this observation has not been confirmed or reproduced.
The problem of the constraint
![]() was considered by Shapiro et al. (1983) after the discovery of the first millisecond pulsar, PSR 1937+214, with
was considered by Shapiro et al. (1983) after the discovery of the first millisecond pulsar, PSR 1937+214, with
![]() (Backer et al. 1982). Shapiro et al. (1983) used a formula for
(Backer et al. 1982). Shapiro et al. (1983) used a formula for
![]() based on the relativistic Roche model. After the announcement of the discovery of a 2 kHz pulsar, this formula was used to show that nearly all EOSs of dense matter existing at that time were ruled out by this observation (Shapiro et al. 1989).
based on the relativistic Roche model. After the announcement of the discovery of a 2 kHz pulsar, this formula was used to show that nearly all EOSs of dense matter existing at that time were ruled out by this observation (Shapiro et al. 1989).
In Sect. 2, we summarize results obtained with the relativistic Roche model. Section 3 contains description of realistic EOSs of nuclear matter, Sect. 4 provides the assumptions and methods used to calculate rotating stellar models. In Sect. 5 we check the validity of the empirical formula against results of precise 2D calculations for nine realistic EOS for neutron stars. Hypothetical self-bound quark stars with normal crusts are considered in Sect. 6. Section 7 presents the static and rotating configurations in the mass-radius plane. In Sect. 8 we derive approximate relations between the circumferential radius of a static configuration and that of a Keplerian configuration of the same gravitational mass, for neutron stars and quark stars. A discussion of our results is presented in Sect. 9.
2 Relativistic Roche model
There is a useful model of neutron stars for which an analytic formula for
![]() can be obtained (Shapiro et al. 1989,1983). It is a relativistic Roche model, in which the mass of the star is assumed to be strongly centrally condensed. Consider a continuous sequence of stationary configurations of constant gravitational mass M, and rotation frequencies ranging from zero to
can be obtained (Shapiro et al. 1989,1983). It is a relativistic Roche model, in which the mass of the star is assumed to be strongly centrally condensed. Consider a continuous sequence of stationary configurations of constant gravitational mass M, and rotation frequencies ranging from zero to ![]() .
Let the circumferential radius of the non-rotating configuration be R. Under the
assumption of an extreme central mass condensation, Shapiro et al. (1989,1983) found an equation satisfied by the coordinates of the stellar surface (Eq. (2) of Shapiro et al. 1989). In the special
case of the stellar equator, this equation implies that for normal equilibrium configurations rotating uniformly at f, the equatorial circumferential radius
.
Let the circumferential radius of the non-rotating configuration be R. Under the
assumption of an extreme central mass condensation, Shapiro et al. (1989,1983) found an equation satisfied by the coordinates of the stellar surface (Eq. (2) of Shapiro et al. 1989). In the special
case of the stellar equator, this equation implies that for normal equilibrium configurations rotating uniformly at f, the equatorial circumferential radius
![]() satisfies
satisfies
where the extreme central concentration of matter implies that gravitational mass can be treated as constant and equal to the static value M. The left-hand-side of Eq. (1) reaches a minimum at
Therefore, the Keplerian frequency is
As stated in Shapiro et al. (1989), ``the Relativistic Roche model provides a surprisingly accurate estimate of the maximum rotation rate along constant-rest mass sequences'' for many realistic EOSs.
It is easy to show that an additional relation between the Keplerian and static configurations
can be obtained. Using Eq. (1), one obtains a formula expressing
![]() for the Keplerian configuration,
for the Keplerian configuration, ![]() ,
in terms of R for a static configuration of the same mass M,
,
in terms of R for a static configuration of the same mass M,
The formula for
3 Realistic EOSs of hadronic matter
In view of our high degree of ignorance concerning the EOS of dense hadronic matter at supranuclear densities (![]()
![]()
![]() ), it is common to consider a set of EOSs based on different dense matter theories (for reviews, see Haensel et al. 2007; Lattimer & Prakash 2006). We used nine theoretical EOSs. These EOSs are listed in Table 1, where the basic information (label of the EOS, theory of dense matter, reference to the original paper) is also presented.
), it is common to consider a set of EOSs based on different dense matter theories (for reviews, see Haensel et al. 2007; Lattimer & Prakash 2006). We used nine theoretical EOSs. These EOSs are listed in Table 1, where the basic information (label of the EOS, theory of dense matter, reference to the original paper) is also presented.
Five EOSs are based on realistic models involving only nucleons (FPS, BBB, DH, APR, GN3). The remaining EOSs are softened at high density either by the appearance of hyperons (GNH3, BGN1H1), or a phase transition to a kaon-condensed state (GMGS-Km, GMGS-Kp).
For GMGS-Km and GMGS-Kp models, the hadronic Lagrangian is the same. However, to obtain GMGS-Kp, one assumes that the phase transition takes place between two pure phases and is accompanied by a density jump, calculated using the Maxwell construction. The GMGS-Km EOS is obtained assuming that the transition occurs via a mixed state of two phases (Gibbs construction). A mixed state is energetically preferred when the surface tension between the two phases is below a certain critical value. As the value of the surface tension is very uncertain, we considered both cases.
In all EOSs models (except FPS), the core EOS was joined with the DH EOS of the crust (Douchin & Haensel 2001). For the FPS model, the FPS EOS of the core was supplemented with the FPS crust EOS of Lorenz et al. (1993).
Our set of EOSs includes very different types of models. This is reflected by a large scatter of the maximum allowable masses of non-rotating stars,
![]() ,
and a range of circumferential radii of non-rotating stars with
,
and a range of circumferential radii of non-rotating stars with
![]() ,
,
![]() (Table 1).
(Table 1).
Table 1: Equations of state of the neutron star core.
4 Calculating stationary rotating configurations
The stationary configurations of rigidly rotating neutron stars have been computed in full general relativity by solving the Einstein equations for stationary axisymmetric spacetime (see Bonazzola et al. 1993; Gourgoulhon et al. 1999, for the complete set of partial differential equations to be integrated). The numerical computations were performed using the
![]() code from the LORENE library (http://www.lorene.obspm.fr). The code implements a multi-domain spectral method introduced in Bonazzola et al. (1998). A description of the code can be found in Gourgoulhon et al. (1999). The accuracy of the calculations has been checked by evaluation of the GRV2 and GRV3 virial error indicators (Gourgoulhon & Bonazzola 1994; Bonazzola & Gourgoulhon 1994), which showed values lower than
code from the LORENE library (http://www.lorene.obspm.fr). The code implements a multi-domain spectral method introduced in Bonazzola et al. (1998). A description of the code can be found in Gourgoulhon et al. (1999). The accuracy of the calculations has been checked by evaluation of the GRV2 and GRV3 virial error indicators (Gourgoulhon & Bonazzola 1994; Bonazzola & Gourgoulhon 1994), which showed values lower than
![]() .
.
5 Maximum frequencies for realistic EOSs of neutron stars
Our aim is to approximately reproduce precisely calculated Keplerian frequencies using
an empirical formula
where M is the gravitational mass of rotating star and R is the radius of the non-rotating star of mass M, R=R(M).
Let us first consider each EOS separately and find a parameter
![]() for an empirical formula suitable for that EOS. We found that the parameter
for an empirical formula suitable for that EOS. We found that the parameter
![]() can be very well defined using the approximately linear segment of each
can be very well defined using the approximately linear segment of each
![]() curve (Figs. 1-2) in the mass range
curve (Figs. 1-2) in the mass range
![]() .
The values of
.
The values of
![]() were determined by least square fits and range from 1.07 kHz (GN3) up to 1.09 kHz (APR), with an rms deviation of the order of 0.5%. These values of
were determined by least square fits and range from 1.07 kHz (GN3) up to 1.09 kHz (APR), with an rms deviation of the order of 0.5%. These values of
![]() are systematically larger than the value 1.04 kHz proposed in Lattimer & Prakash (2004), and significantly larger the value 1.00 kHz from the Relativistic Roche model (Eq. (3). We defined the EOS-independent
are systematically larger than the value 1.04 kHz proposed in Lattimer & Prakash (2004), and significantly larger the value 1.00 kHz from the Relativistic Roche model (Eq. (3). We defined the EOS-independent
![]() kHz to be used in Eq. (6) as the mean value of the 9
kHz to be used in Eq. (6) as the mean value of the 9
![]() coefficients for the EOSs of Table 1.
coefficients for the EOSs of Table 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f1.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg71.png) |
Figure 1:
(Color online) Precise values of Keplerian frequency |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f2.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg73.png) |
Figure 2:
(Color online) Same as Fig. 1 but for BGN1H1, GNH3, GMGS-Km and GMGS-Kp EOSs. Notice that due to a very strong softening by the kaon condensate and the simultaneous constraint
|
We recommend the use of this value over a somewhat broader range of masses,
![]() .
In Figs. 1-2 we compare precisely calculated Keplerian frequencies with those given by the empirical formula, assuming
.
In Figs. 1-2 we compare precisely calculated Keplerian frequencies with those given by the empirical formula, assuming
![]() kHz. The precision of the empirical formula for
kHz. The precision of the empirical formula for ![]() stays remarkably high for
stays remarkably high for
![]() .
Relative deviations are typically within 2%, with a largest deviation of at most
.
Relative deviations are typically within 2%, with a largest deviation of at most ![]() at the highest mass end for the GNH3 EOS.
at the highest mass end for the GNH3 EOS.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f3.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg77.png) |
Figure 3:
(Color online) Same as Fig. 1 but for three EOSs of strange stars. Strange stars possess maximal crust, with bottom density
|
Table 2: Parameters of the bag models for strange stars.
6 Strange stars
The case of strange stars, built from self-bound quark matter, is different from that of ordinary neutron stars. Matter distribution within quark stars has a very low density contrast between the quark core edge and its center. We considered three EOSs of self-bound quark matter, based on the MIT Bag Model (Zdunik 2000; Farhi & Jaffe 1984). Model parameters are given in Table 2. Strange stars are likely to have a thin normal matter crust, with bottom density,
![]() ,
not exceeding the neutron drip density
,
not exceeding the neutron drip density
![]()
![]()
![]() .
The maximum mass of normal crusts is reached for
.
The maximum mass of normal crusts is reached for
![]() .
.
First we consider strange stars with a maximum crust. We computed the coefficient
![]() kHz using an identical procedure to that for neutron stars described in the previous
section. As we see in Fig. 3, the precision of an empirical formula within the mass range
kHz using an identical procedure to that for neutron stars described in the previous
section. As we see in Fig. 3, the precision of an empirical formula within the mass range
![]() is as high as for neutron stars (typical relative deviation within 2%, largest deviation of about 4% at highest masses). However, the value of C is higher than for neutron stars.
is as high as for neutron stars (typical relative deviation within 2%, largest deviation of about 4% at highest masses). However, the value of C is higher than for neutron stars.
Let us consider now quark star models with less massive crusts. These models were constructed assuming
![]() .
The effect on the optimum value
.
The effect on the optimum value
![]() turned out to be very small. At a fixed M, a decrease of
turned out to be very small. At a fixed M, a decrease of
![]() leads to an increase of
leads to an increase of ![]() (a more compact star).
Simultaneously, however, the static value of R(M) decreases, and therefore both effects cancel out to a large extent. Consequently,
(a more compact star).
Simultaneously, however, the static value of R(M) decreases, and therefore both effects cancel out to a large extent. Consequently,
![]() depends rather weakly on the crust mass,
and one may use
depends rather weakly on the crust mass,
and one may use
![]() kHz for any crust size.
kHz for any crust size.
If strange quark matter is not the ground state of the matter at zero pressure, strange stars bound by the strong interactions cannot exist. However, one can still consider hybrid stars bound by
gravitation, with quark matter cores inside a baryon envelope. Rapid rotation of hybrid stars with quark cores was studied by Ippolito et al. (2008). The transition to quark matter usually strongly softens the EOS, and decreases the values of
![]() and
and
![]() .
However, a quark core does not appear below
.
However, a quark core does not appear below
![]() and therefore does not appreciably influence the value of C, which is essentially identical to
and therefore does not appreciably influence the value of C, which is essentially identical to
![]() .
This situation is qualitatively similar to the case of kaon condensation, appearing in the GMGS-Km and GMGS-Kp EOSs.
.
This situation is qualitatively similar to the case of kaon condensation, appearing in the GMGS-Km and GMGS-Kp EOSs.
7 Static and rotating configurations in the mass-radius plane
The formulae for
![]() are based on a one-to-one correspondence between a static configuration S, belonging to static boundary
are based on a one-to-one correspondence between a static configuration S, belonging to static boundary ![]() of the region of rotating configurations, and the rotation frequency of a Keplerian configuration K on the
of the region of rotating configurations, and the rotation frequency of a Keplerian configuration K on the ![]() boundary. This
correspondence is visualized in Fig. 4, based on the numerical results obtained for the DH EOS. The frequency of rotation of a Keplerian configuration K is obtained via the mass and radius of a static configuration S with same M. Both configurations are connected by a horizontal line in the
boundary. This
correspondence is visualized in Fig. 4, based on the numerical results obtained for the DH EOS. The frequency of rotation of a Keplerian configuration K is obtained via the mass and radius of a static configuration S with same M. Both configurations are connected by a horizontal line in the
![]() plane.
plane.
The empirical formula for the absolute upper bound on f of stably rotating configurations for a given EOS,
![]() (Haensel et al. 1995; Shapiro et al. 1989; Lattimer et al. 1990; Friedman et al. 1989; Haensel & Zdunik 1989),
is of a different character. It results from an (approximate but precise) one-to-one correspondence between the parameters of two extremal configurations, static
(Haensel et al. 1995; Shapiro et al. 1989; Lattimer et al. 1990; Friedman et al. 1989; Haensel & Zdunik 1989),
is of a different character. It results from an (approximate but precise) one-to-one correspondence between the parameters of two extremal configurations, static
![]() and Keplerian
and Keplerian
![]() (filled circles), and reads
(filled circles), and reads
where
The functional form of Eq. (7) is, in fact, exact in general relativity for uniform rotation of stars with the so-called minimum period EOS of Koranda et al. (1997). This EOS contains the single parameter
![]() ,
which is the transition energy density
between the low-density EOS with P=0 and the high-density EOS with
,
which is the transition energy density
between the low-density EOS with P=0 and the high-density EOS with
![]() .
The value of
.
The value of ![]() for the maximum mass case is 1.35 kHz.
for the maximum mass case is 1.35 kHz.
In Fig. 4 we give the correspondence between the stellar configurations of the same baryon number. The line
![]() separates ``supramassive''
configurations from the ``normal'' ones, which can be reached by spinning up a non-rotating star. The maximum rotational frequency for the ``normal'' sequences (reached at point
separates ``supramassive''
configurations from the ``normal'' ones, which can be reached by spinning up a non-rotating star. The maximum rotational frequency for the ``normal'' sequences (reached at point
![]() )
has been discussed by Cook et al. (1994b,a) for polytropic and realistic EOSs (their Tables 3 and 7 respectively). It should be noted that this value cannot be estimated using our formula for
)
has been discussed by Cook et al. (1994b,a) for polytropic and realistic EOSs (their Tables 3 and 7 respectively). It should be noted that this value cannot be estimated using our formula for
![]() ,
Eq. (6), because our formula is valid within a restricted mass range
,
Eq. (6), because our formula is valid within a restricted mass range
![]() .
.
Formula (6) connects configurations of the same gravitational mass M. For example, it connects a
![]() non-rotating star (filled circle -
non-rotating star (filled circle -
![]() )
with a Keplerian configuration
(filled square -
)
with a Keplerian configuration
(filled square -
![]() ), in Fig. 5. They are joined by a solid horizontal line. At a fixed baryon mass,
), in Fig. 5. They are joined by a solid horizontal line. At a fixed baryon mass, ![]() ,
M increases with increasing rotation frequency. The dotted line connecting the filled circle (
,
M increases with increasing rotation frequency. The dotted line connecting the filled circle (
![]() )
and the open square near
)
and the open square near
![]() contains configurations with fixed
contains configurations with fixed ![]() ,
equal to that of a non-rotating star with
,
equal to that of a non-rotating star with
![]() .
Deviation of the solid line from the dotted one shows the rotational increase of M at a fixed
.
Deviation of the solid line from the dotted one shows the rotational increase of M at a fixed ![]() .
For a
.
For a
![]() star, the fractional increase is equal to 1.7%, and for the maximum static mass (dotted line
star, the fractional increase is equal to 1.7%, and for the maximum static mass (dotted line
![]() )
it reaches 3.8%.
)
it reaches 3.8%.
8 Relation between R(M) and R
 (M)
(M)
Let us consider a family (sequence) of stationary configurations rotating stably at a frequency f. They form a curve in the
![]() plane (see examples in Fig. 4). The curve is bound at
plane (see examples in Fig. 4). The curve is bound at
![]() by the axisymmetric instability, implying star collapse into
a Kerr black hole. The largest circumferential radius is reached for the Keplerian configuration,
by the axisymmetric instability, implying star collapse into
a Kerr black hole. The largest circumferential radius is reached for the Keplerian configuration,
![]() .
Bejger et al. (2007) have shown that
.
Bejger et al. (2007) have shown that
![]() is (within 2%) equal to the radius of an orbit of a point particle moving in the Schwarzschild space-time around a
point (or a spherical) mass M. This implies
is (within 2%) equal to the radius of an orbit of a point particle moving in the Schwarzschild space-time around a
point (or a spherical) mass M. This implies
For convenience, we introduce a frequency f0,
The validity of the empirical formula, Eq. (6), then suggests an approximate proportionality
For the extreme relativistic Roche model,
The dependence of
![]() on the crust mass,
on the crust mass,
![]() ,
is very weak. This can be explained via the effects of
,
is very weak. This can be explained via the effects of
![]() on R(M) and
on R(M) and
![]() .
These effects are opposite: at fixed
M, R(M) increases, and
.
These effects are opposite: at fixed
M, R(M) increases, and
![]() decreases, with increasing
decreases, with increasing
![]() .
The cancellation of both effects results in an only slight decrease of
.
The cancellation of both effects results in an only slight decrease of
![]() with increasing
with increasing
![]() (see Fig. 5).
(see Fig. 5).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f5.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg119.png) |
Figure 5:
(Color online) Equatorial circumferential radius of the Keplerian configuration,
|
Lasota et al. (1996) derived an approximate relation between equatorial radius of a maximally rotating configuration,
![]() and the radius of non-rotating neutron star with maximum allowable mass,
and the radius of non-rotating neutron star with maximum allowable mass,
![]() .
The maximally rotating configuration, stable both with respect to mass shedding and axisymmetric perturbations, is actually very close to that with the highest mass,
.
The maximally rotating configuration, stable both with respect to mass shedding and axisymmetric perturbations, is actually very close to that with the highest mass,
![]() (in Fig. 4 they are indistinguishable). The approximate proportionality found by Lasota et al. (1996) for neutron stars is
(in Fig. 4 they are indistinguishable). The approximate proportionality found by Lasota et al. (1996) for neutron stars is
![]() .
This relation connects two extremal configurations. They have different masses, related by
.
This relation connects two extremal configurations. They have different masses, related by
![]() (Lasota et al. 1996). In contrast, Eq. (10) connects normal configurations of neutron stars and strange stars with the same gravitational mass and holds for
(Lasota et al. 1996). In contrast, Eq. (10) connects normal configurations of neutron stars and strange stars with the same gravitational mass and holds for
![]() .
.
9 Discussion and conclusions
We have tested empirical formulae for the Keplerian (mass shedding) frequency of neutron stars of mass M, proposed by Lattimer & Prakash (2004). Using numerical results of precise 2D calculations, performed for ten representative realistic EOSs of dense matter based on different dense matter models, we find the prefactor
![]() kHz, slightly higher than 1.04 kHz proposed by Lattimer & Prakash (2004). With our prefactor, the formula is precise for
kHz, slightly higher than 1.04 kHz proposed by Lattimer & Prakash (2004). With our prefactor, the formula is precise for
![]() (typically within 2%, maximum deviation occurring for highest M not exceeding 5%). Strange stars can reach larger
(typically within 2%, maximum deviation occurring for highest M not exceeding 5%). Strange stars can reach larger
![]() than neutron stars. With a maximum crust on strange stars, we get
than neutron stars. With a maximum crust on strange stars, we get
![]() kHz. The value of
kHz. The value of
![]() does not depend significantly on the crust mass, and also can be used for bare strange stars. We notice that both
does not depend significantly on the crust mass, and also can be used for bare strange stars. We notice that both
![]() and
and
![]() are significantly larger than for the relativistic Roche model,
are significantly larger than for the relativistic Roche model,
![]() kHz (Shapiro et al. 1983).
kHz (Shapiro et al. 1983).
Using an approximate but quite precise Schwarzschild-like formula, relating M, ![]() ,
and
,
and ![]() (Bejger et al. 2007), we show that to a very good approximation the mass-shedding radius at a given M is proportional to the static radius R(M), provided
(Bejger et al. 2007), we show that to a very good approximation the mass-shedding radius at a given M is proportional to the static radius R(M), provided
![]() .
For neutron stars and strange stars we obtain the best-fit proportionality factor
.
For neutron stars and strange stars we obtain the best-fit proportionality factor
![]() .
These proportionality factors are smaller than the exact factor 1.5 obtained for the relativistic Roche model.
.
These proportionality factors are smaller than the exact factor 1.5 obtained for the relativistic Roche model.
We derived a set of empirical formulae, expressing Keplerian frequency and equatorial radius of the Keplerian configuration in terms of the mass and radius of the normal configuration of the same mass. These formulae can be used for masses
![]() .
The formulae are approximate but quite precise, and therefore might be useful constraining the EOS of dense matter by the observations of pulsars.
.
The formulae are approximate but quite precise, and therefore might be useful constraining the EOS of dense matter by the observations of pulsars.
Acknowledgements
This work was partially supported by the Polish MNiSW grant No. N20300632/0450 and by the US DOE grant DE-AC02-87ER40317. M.B. was partially supported by Marie Curie Fellowship No. ERG-2007-224793 within the 7th European Community Framework Programme.
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef]
- Backer, D. C., Kulkarni, S. R., Heiles, C., et al. 1982, Nature, 300, 61 [CrossRef] (In the text)
- Balberg, S., & Gal, A. 1997, Nucl. Phys. A., 625, 435 [NASA ADS] [CrossRef]
- Balberg, S., Lichtenstadt, I., & Cook, G. B. 1999, ApJ, 121, 515 [NASA ADS] [CrossRef]
- Baldo, M., Bombaci, I., & Burgio, G. F. 1997, A&A, 328, 274 [NASA ADS]
- Bejger, M., Haensel, P., & Zdunik, J. L. 2007, A&A, 464, L49 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bonazzola, S., & Gourgoulhon, E. 1994, Class. Quantum Grav., 11, 1775 [NASA ADS] [CrossRef]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J.-A. 1993, A&A, 278, 421 [NASA ADS]
- Bonazzola, S., Gourgoulhon, E., & Marck, J.-A. 1998, Phys. Rev. D, 58, 104020 [NASA ADS] [CrossRef] (In the text)
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1994a, ApJ, 422, 227 [NASA ADS] [CrossRef]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1999, ApJ, 424, 823 [NASA ADS] [CrossRef]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Farhi, E., & Jaffe, R. L. 1984, Phys. Rev. D, 30, 2379 [NASA ADS] [CrossRef]
- Friedman, J. L., Ipser, J. R., & Parker, L. 1989, Phys. Rev. Lett., 62, 3015 [NASA ADS] [CrossRef]
- Glendenning, N. K. 1985, ApJ, 293, 470 [NASA ADS] [CrossRef]
- Gourgoulhon, E., & Bonazzola, S. 1994, Class. Quantum Grav., 11, 443 [NASA ADS] [CrossRef]
- Gourgoulhon, E., Haensel, P., Livine, R., et al. 1999, A&A, 349, 851 [NASA ADS]
- Haensel, P., & Zdunik, J. L. 1989, Nature, 340, 313 [CrossRef]
- Haensel, P., Salgado, M., & Bonazzola, S. 1995, A&A, 296, 745 [NASA ADS]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1, Equation of State and Structure (New York: Springer) (In the text)
- Hessels, J. W. T., Ransom, S. M., Stairs I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] (In the text)
- Ippolito, N. D., Ruggieri, M., Rischke, D. H., Sedrakian, A., & Weber, F. 2008, Phys. Rev. D, 77, 023004 [NASA ADS] [CrossRef] (In the text)
- Kaaret, P., Prieskorn, Z., In't Zand, J. J. M., et al. 2007, ApJ, 657, L97 [NASA ADS] [CrossRef] (In the text)
- Koranda, S., Stergioulas, N., & Friedman, J. L. 1997, ApJ, 488, 799 [NASA ADS] [CrossRef] (In the text)
- Lasota, J.-P., Haensel, P., & Abramowicz, M. A. 1996, ApJ, 456, 426 [CrossRef] (In the text)
- Lattimer, J. M., & Prakash, M. 2004, Science, 304, 536 [NASA ADS] [CrossRef] (In the text)
- Lattimer, J. M., & Prakash, M. 2006, Nucl. Phys. A, 777, 479 [NASA ADS] [CrossRef] (In the text)
- Lattimer, J. M., Prakash, M., Masak, D., & Yahil, A. 1990, ApJ, 355, L241 [NASA ADS] [CrossRef]
- Lorenz, C. P., Ravenhall, D. G., & Pethick, C. J. 1993, Phys. Rev. Lett., 70, 379 [NASA ADS] [CrossRef] (In the text)
- Pandharipande, V. R., & Ravenhall, D. G. 1989, in Proc. NATO Advanced Research Workshop on nuclear matter and heavy ion collisions, Les Houches, ed. M. Soyeur et al. (New York: Plenum), 103
- Pons, J. A., Reddy, S., Ellis, P. J., Prakash, M., & Lattimer, J. M. 2000, Phys. Rev. C, 62, 035803 [NASA ADS] [CrossRef]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars (New York: Wiley)
- Shapiro, S. L., Teukolsky, S. A., & Wasserman, I. 1983, ApJ, 272, 702 [NASA ADS] [CrossRef] (In the text)
- Shapiro, S. L., Teukolsky, S. A., & Wasserman, I. 1989, Nature, 340, 451 [NASA ADS] [CrossRef] (In the text)
- Zdunik, J. L. 2000, A&A, 359, 311 [NASA ADS]
All Tables
Table 1: Equations of state of the neutron star core.
Table 2: Parameters of the bag models for strange stars.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f1.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg71.png) |
Figure 1:
(Color online) Precise values of Keplerian frequency |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f2.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg73.png) |
Figure 2:
(Color online) Same as Fig. 1 but for BGN1H1, GNH3, GMGS-Km and GMGS-Kp EOSs. Notice that due to a very strong softening by the kaon condensate and the simultaneous constraint
|
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f3.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg77.png) |
Figure 3:
(Color online) Same as Fig. 1 but for three EOSs of strange stars. Strange stars possess maximal crust, with bottom density
|
| In the text | |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{11605f4.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg89.png) |
Figure 4:
(Color online) Gravitational mass, M, versus equatorial radius,
|
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11605f5.eps}
\end{figure}](/articles/aa/full_html/2009/29/aa11605-08/Timg119.png) |
Figure 5:
(Color online) Equatorial circumferential radius of the Keplerian configuration,
|
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.