Absolute dimensions of solar-type eclipsing binaries

J. V. Clausen; H. Bruntt; A. Claret; A. Larsen; J. Andersen; B. Nordström; A. Giménez

doi:10.1051/0004-6361/200912362

Free Access

Issue		A&A Volume 502, Number 1, July IV 2009


Page(s)		253 - 265
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/200912362
Published online		27 May 2009

II. V636 Centauri: A 1.05 M $_{{\odot}}$ primary with an active, cool, oversize 0.85 M $_{{\odot}}$ secondary

J. V. Clausen¹ - H. Bruntt^1,2 - A. Claret³ - A. Larsen¹ - J. Andersen^1,4 - B. Nordström¹ - A. Giménez⁵

1 - Niels Bohr Institute, Copenhagen University, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
2 - Sydney Institute for Astronomy, School of Physics, University of Sydney, NSW 2006, Australia
3 - Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
4 - Nordic Optical Telescope Scientific Association, Apartado 474, 38 700 Santa Cruz de La Palma, Spain
5 - Centro de Astrobiologia (CSIC/INTA), 28 850 Torrejon de Ardoz, Madrid, Spain

Received 21 April 2009 / Accepted 9 May 2009

Abstract
Context. The influence of stellar activity on the fundamental properties of stars around and below 1 $M_{\odot }$ is not well understood. Accurate mass, radius, and abundance determinations from solar-type binaries exhibiting various levels of activity are needed for a better insight into the structure and evolution of these stars.
Aims. We aim to determine absolute dimensions and abundances for the solar-type detached eclipsing binary V636 Cen, and to perform a detailed comparison with results from recent stellar evolutionary models.
Methods. ${\it uvby}$ light curves and ${\it uvby}\beta$ standard photometry were obtained with the Strömgren Automatic Telescope, radial velocity observations with the CORAVEL spectrometer, and high-resolution spectra with the FEROS spectrograph, all at ESO, La Silla. State-of-the-art methods were applied for the photometric and spectroscopic analyses.
Results. Masses and radii that are precise to 0.5% have been established for the components of V636 Cen. The 0.85 $M_{\odot }$ secondary component is moderately active with starspots and Ca II H and K emission, and the 1.05 $M_{\odot }$ primary shows signs of activity as well, but at a much lower level. We derive a $[{\rm Fe/H}]$ abundance of $-0.20 \pm 0.08$ and similar abundances for Si, Ca, Ti, V, Cr, Co, and Ni. Corresponding solar-scaled stellar models are unable to reproduce V636 Cen, especially its secondary component, which is $\sim$ 10% larger and $\sim$ 400 K cooler than predicted. Models adopting significantly lower mixing-length parameters $l/H_{\rm p}$ remove these discrepancies, seen also for other solar-type binary components. For the observed $[{\rm Fe/H}]$ , Claret models for $l/H_{\rm p} = 1.4$ (primary) and 1.0 (secondary) reproduce the components of V636 Cen at a common age of 1.35 Gyr. The orbit is eccentric ( $e = 0.135 \pm 0.001$ ), and apsidal motion with a 40% relativistic contribution has been detected. The period is $U = 5~270 \pm 335$ yr, and the inferred mean central density concentration coefficient, log(k₂) = $-1.61 \pm 0.05$ , agrees marginally with model predictions. The measured rotational velocities, $13.0 \pm 0.2$ (primary) and $11.2 \pm 0.5$ (secondary) kms^-1, are in remarkable agreement with the theoretically predicted pseudo-synchronous velocities, but are about 15% lower than the periastron values.
Conclusions. V636 Cen and 10 other well-studied inactive and active solar-type binaries suggest that chromospheric activity, and its effect on envelope convection, is likely to cause radius and temperature discrepancies, which can be removed by adjusting the model mixing length parameters downwards. Noting this, the sample may also lend support to theoretical 2D radiation hydrodynamics studies, which predict a slight decrease of the mixing length parameter with increasing temperature/mass for $\it inactive$ main sequence stars. More binaries are, however, needed for a description/calibration in terms of physical parameters and level of activity.

Key words: stars: evolution - stars: fundamental parameters - Stars: abundances - stars: activity - stars: binaries: eclipsing - techniques: spectroscopic

1 Introduction

As pointed out by e.g. Hoxie (1973), Popper (1997), Clausen et al. (1999), Torres & Ribas (2002), Ribas (2003), Dawson & De Robertis (2004), and López-Morales & Ribas (2005), current stellar models, scaled to the Sun, are unable to reproduce the measured temperatures and radii for many binary components less massive the Sun. Such models tend to predict too high temperatures, and radii, which are up to 10% too small, compared to a measured accuracy of about 1% for several systems. The model luminosities seem, however, to agree fairly well with observations. Chromospheric activity has been suggested as a likely cause, and e.g. Gabriel (1969), Cox et al. (1981), Clausen et al. (1999), and Torres et al.(2006) have demonstrated that the model fits can be improved by using a reduced mixing-length parameter when calculating envelope convection. The latter authors also show that there is a link between activity and increased radii. Morales et al. (2008) find strong radius and temperature dependencies on stellar activity for both single and binary low-mass stars, and López-Morales (2007) finds correlation between activity level (X-ray emission level) and radius for faster rotating binary components, but not for slowly rotating single stars. On the theoretical side, Chabrier et al. (2007) have, via a phenomenological approach, examined the consequences on the evolution of low-mass stars and brown dwarf eclipsing binaries of a) inhibiting convection due to rotation and/or internal magnetic field, and b) the presence of surface magnetic spots.

The current situation is summarized by Ribas et al. (2008). Clearly, accurate data for additional binaries are needed, as well as more models, which include first of all dynamo magnetic fields and the evolution of stellar rotation and activity (e.g. D'Antona et al. 2000). We are presently studying several new systems with solar-type components, either constant or exhibiting various levels of chromospheric activity (e.g. Clausen et al. 2001), and in this paper, we present results from a complete analysis of the F8/G0 V system V636 Cen = HD 124 784 = HIP 69 781.

2 V636 Cen

V636 Cen was discovered by Hoffmeister (1958) to be a $4\hbox{$.\!\!^{\rm d}$ }3$ period eclipsing binary, and Popper (1966) reported sharp but single lines. Today V636 Cen is known to be double-lined, but the lines of the secondary component are much fainter than those of the primary. V636 Cen is well detached with two quite different components in an eccentric orbit (e = 0.135). Apsidal motion with a period of $U = 5~270 \pm 335$ yr has been detected (Clausen et al. 2008a, hereafter CVG08). Signs of chromospheric activity (spots) are clearly present in the light curves, but the level of the light variations is modest (CVG08). Furthermore, we see emission from both components in the Ca II H and K lines, whereas ${\rm H_{\alpha}}$ emission is not noticed; see Sect. 3. Chromospheric emission in the Ca II H and K lines was also observed by Henry et al. (1996), and X-ray emission was detected in the ${\it ROSAT}$ All-Sky Survey (Voges et al. 1999).

Our study is based on the first modern light curves and spectroscopic observations for V636 Cen; preliminary dimensions based on part of the data were derived by Larsen (1998). For the spectroscopic and photometric analyses of V636 Cen presented below, we have adopted the linear ephemeris by CVG08 (Eq. (4)). Throughout the paper, the component eclipsed at the deeper eclipse at phase 0.0 is referred to as the primary (p), and the other as the secondary (s) component.

3 Photometric elements

The uvby light curves of V636 Cen (CVG08) contain 853 observations in each band and were observed on 76 nights during six periods between March 1985 and April 1991. The number of observations per season are 8 (1985), 165 (1987), 261 (1988), 233 (1989), 17 (1990), and 169 (1991). Further eclipse observations, but none outside eclipses, were done on ten nights between January 2002 and July 2007, primarily to determine the apsidal motion period of the eccentric orbit. Primary eclipse is much deeper than secondary eclipse, which is total and occurs near phase 0.52.

The average observational accuracy per data point is about 5 mmag ( ${\it vby}$ ) and 7 mmag (u), and the magnitude differences between the two comparison stars were found to be constant at that level. Additional scatter due to chromospheric activity (spots) is, however, clearly seen in the light curves, with total amplitudes increasing from about 0.02 mag in y to about 0.04 mag in u, and changing somewhat from year to year. We refer to Fig. 6 and Table 9 in CVG08 for further details.

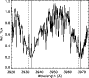$\begin{figure} \epsfxsize=90mm \epsfbox{12362f1.ps} \end{figure}$	Figure 1: Ca II H and K emission in V636 Cen. The vertical lines show the positions for the primary (full) and secondary (dashed) components. The FEROS spectrum of V636 Cen was observed at JD2451211.85 (orbital phase 0.63).
Open with DEXTER

As mentioned in Sect. 1, Ca II H and K emission is present from both components. This is seen in two orders of two FEROS spectra from February 1999 (Table 6), and (dark) spots may therefore be present at the surface of both stars. Figure 1 illustrates that the emission features of the two components appear to have about the same strength, but since the primary dominates the total light of V636 Cen, the real emission from the secondary is by far the strongest.

Between 1987 and 1991, the depths of the total secondary eclipses were nearly identical, whereas those of the primary eclipses differed significantly. During this period, the activity must therefore have been dominated by contributions from the secondary component. As mentioned below, this is supported by frequency analyses of the out-of-eclipse data. On the other hand, the depths of both eclipses varied from 2002 to 2006. This is not due to the slow apsidal motion detected for V636 Cen, and must be caused by spots at both stars during at least some of those years. The Rossby numbers for the primary and secondary components are approximately 0.44 and 0.10, respectively. This places the secondary in the range where other stars tend to show spot activity and the primary close to onset of spottedness (Hall 1994).

Table 1: Photometric solutions for V636 Cen from JKTEBOP analyses of the 1987 and 1988 light curve observations (426 points per band).

Out-of-eclipse phases were covered on several nights during 1987, 1988, 1989, and 1991. Frequency analyses of the corresponding data, done separately for each year and band, reveal the existence of one significant period per year. The results from the four bands agree well, and the average periods and estimated uncertainties are $4\hbox{$.\!\!^{\rm d}$ }05 \pm 0\hbox{$.\!\!^{\rm d}$ }06$ (1987), $4\hbox{$.\!\!^{\rm d}$ }16 \pm 0\hbox{$.\!\!^{\rm d}$ }01$ (1988), $4\hbox{$.\!\!^{\rm d}$ }13 \pm 0\hbox{$.\!\!^{\rm d}$ }01$ (1989), and $4\hbox{$.\!\!^{\rm d}$ }06 \pm 0\hbox{$.\!\!^{\rm d}$ }12$ (1991). They are all shorter than the orbital period $4\hbox{$.\!\!^{\rm d}$ }28$ , but transformed to equatorial surface velocities they agree quite well with the observed rotational velocities of both components (Sect. 4).

Based on this information on eclipse depths and periodicity of the out-of-eclipse variability, we conclude that the 1987-1991 surface activities can be modeled adequately by including a few dominating spots (or spot groups) on the surface of the secondary component.

We have used the Wilson-Devinney (WD) model and code for the analyses. As described below, some initial analyses, which ignore surface activity, were based on the JKTEBOP program. We refer to Clausen et al. (2008b, hereafter CTB08) for references and details on the binary models and codes, and on the general approach applied. In tables and text, we use the following symbols: i orbital inclination; r relative radius; $k = r_{\rm s}/r_{\rm p}$ ; $\Omega$ surface potential; u linear limb darkening coefficient; y gravity darkening coefficient; J central surface brightness; L luminosity; $T_{\rm eff}$ effective temperature.

A linear limb darkening law has been assumed throughout with coefficients adopted from Van Hamme (1993) and/or Claret (2000). They differ by 0.02-0.10 only, leading to identical photometric elements within errors. Gravity darkening coefficients/exponents corresponding to convective atmospheres were applied, and bolometric reflection albedo coefficients of 0.5 were chosen in the WD analyses, again due to convection. For JKTEBOP, the simple bolometric reflection model was used. The mass ratio between the components was kept at the spectroscopic value ( $M_{\rm s}/M_{\rm p}=0.812\pm0.002$ ). In order to model the spots properly, the (very nearly spherical) components were assumed to rotate at the periods determined from the frequency analyses mentioned above. As initial analyses showed that the orbital eccentricity is not as well constrained from the light curve analyses as from the spectroscopic orbit, we have adopted the spectroscopic result throughout; see Table 5. The longitude of periastron $\omega$ is then defined through $e \cos \omega$ from the well determined phase of central secondary eclipse, which did not change significantly relative to primary eclipse during the light curve observations from 1987 to 1991.

Table 2: WD solutions from the 1987 light curve observations (165 per band).

As the activity level of V636 Cen is modest, it is appropriate to first analyse the light curves without taking spots into account, and to adopt a simple but adequate binary model/code like JKTEBOP, which allows easy determination of realistic errors of the photometric elements from Monte Carlo simulations. Since the average out-of-eclipse level of the 1991 observations is significantly off, and since there are very few 1985 and 1990 observations, these data sets were not included in the analyses. Results from the combined 1987 and 1988 observations, which both cover all phases well, are given in Table 1. Including also the 1989 observations increases the scatter significantly but leads to identical solutions within errors. As seen, the results from the four bands agree remarkably well, and relative radii with a realistic precision of about 1% are obtained. Changing the adopted orbital eccentricity by +0.005, i.e. four times the error of the spectroscopic result, decreases the relative radii of both components by only 0.5%. Adjusting e and $\omega$ leads to spurious results, due to asymmetries in the observed light curves caused by spots. As expected, photometric elements from similar WD analyses, not accounting for spots, agree very well with those from JKTEBOP.

Results from WD analyses of the 1987 and 1988 observations are presented in Tables 2 and 3, and out-of-eclipse comparisons in the y band are shown in Figs. 2 and 3. The activity is modeled by including two rather big spots at the surface of the secondary component. Most probably, this simplified approach does not represent the real surface structure in detail, but it reproduces the light variations quite closely, and somewhat better than if only one spot is included. Based on extensive tests, the spots were placed at the equator of the secondary component, and a ratio of 0.9 between the temperatures of spotted and unspotted areas was selected. Longitudes (LO) and angular radii (AR) of the spots were adjusted together with orbital and stellar parameters.

As seen, the eight independent WD solutions yield nearly identical relative radii of the components, which are systematically about 1.5% smaller than the JKTEBOP results (Table 1). The orbital inclinations of the 1987 solutions are on average about $0\hbox{$.\!\!^\circ$ }25$ higher than those from the 1988 solutions, but tests show that the realistic error of i is at least 3-4 times larger than the formal errors listed. The luminosity ratios given in Tables 2 and 3, which for the sake of comparison do not include the spots, agree well within realistic errors; we will return to this point below. For each year, the spot parameters from the four bands differ slightly, but not more than can be expected from the simple approach we have adopted and the limited number of observations available. The two spots applied cover about 10% of the surface of the secondary component. Finally, the rms errors ( $\sigma$ ) of the fits to the observations are close to the observational errors per data point.

Similar WD analyses of the 1989 observations were not successful. The ascending branch of secondary eclipse is not covered, and the level of activity seems to have changed during the last half of the observing period. Secondary eclipse was not covered in 1991, and very few 1985 and 1990 observations exist, so these data sets were not analysed.

Table 3: WD solutions from the 1988 light curve observations (261 per band). See Table 2.

$\begin{figure} \epsfxsize=180mm \epsfbox{12362f2.ps} \end{figure}$	Figure 2: Fit of the theoretical light curve of the WD solution from Table 2 to the 1987 y observations.
Open with DEXTER

$\begin{figure} \epsfxsize=180mm \epsfbox{12362f3.ps} \end{figure}$	Figure 3: Fit of the theoretical light curve of the WD solution from Table 3 to the 1988 y observations.
Open with DEXTER

As a further test of the simple spot model adopted, it is of interest to compare the 1987 and 1988 light curves cleaned for spot effects. This is easily done by calculating, year by year and band per band, theoretical light curves with and without spots and then subtract the difference between them from the observations. First, the cleaned 1987 and 1988 light curves agree well, and second, JKTEBOP analyses of the combined cleaned data yield stellar radii, which are now in perfect agreement with those from the WD solutions. The orbital inclination is close to the mean of the 1987 and 1988 WD results.

The adopted photometric elements are presented in Table 4. The main result of the photometric analyses is that we have, in spite of the surface activity, been able to determine very accurate relative radii for the components of V636 Cen. The system is well detached and the stars are quite different, especially with respect to temperature and luminosity. As seen, the orbital inclination is high, and consequently secondary eclipse is total. The luminosity ratios listed in Table 4 are based on the mean stellar and orbital parameters and include the average spot level seen in the 1987 and 1988 observations; errors reflect the difference between the two years. This approach was adopted in order to allow calculation of realistic ${\it uvby}$ indices for the components; see Table 8. Due to the spots on the surface of the secondary component, the ratio of the light contributions outside eclipses of course change significantly through the orbit. However, the b-y, m₁, and c₁ indices of the components remain nearly unaffected.

4 Spectroscopic orbit

Table 4: Adopted photometric elements for V636 Cen.

The radial velocity measurements of V636 Cen were obtained with the photoelectric cross-correlation spectrometer CORAVEL (Baranne et al. 1979; Mayor 1985) operated at the Danish 1.5-m telescope at ESO, La Silla. In total, 38 and 39 measurement were obtained for the primary and secondary components, respectively, on 30 nights between March 1986 and June 1989. The internal velocity errors range between 0.39 and 0.65 kms^-1 (median 0.44 kms^-1) for the primary component and between 0.71 and 1.81 kms^-1 (median 0.88 kms^-1) for the fainter secondary component. The observations, which cover the out-of-eclipse phases well, are listed in Table A.1.

The spectroscopic orbits were calculated using the method of Lehman-Filhés implemented in the SBOP program (Etzel 2004), which is a modified and expanded version of an earlier code by Wolfe, Horak & Storer (1967). Following several tests, we have decided to weight the individual radial velocities according to the inverse square of their internal errors. The SB1 and SB2 solutions for V636 Cen are given in Table 5, and the observations and computed orbit are shown in Fig. 4. As seen, the SB2 solution, which we adopt, agrees well with the individual SB1 solutions. The semiamplitudes yield minimum masses accurate to about 0.4% for both components, and the eccentricity and periastron longitude of the orbit are well constrained. Also, the standard deviations of a single velocity agree well with the internal median velocity errors.

The measured $v \sin i$ values are $13.0 \pm 0.2$ kms^-1 and $11.2 \pm 0.5$ kms^-1, respectively, with the velocity of the secondary being more uncertain due to its much weaker lines. These rotational velocities are supported by the frequency analyses of the out-of-eclipse photometry described in Sect.3. As discussed in Sect. 6, the rotation of the components corresponds closely to pseudo-synchronization.

5 Abundances

For abundance determinations, we have obtained two high-resolution spectra of V636 Cen with the FEROS fiber echelle spectrograph at ESO, La Silla in February 1999; see Table 6. Details on the spectrograph and the reduction of the spectra are given by CTB08. The late-type components of V636 Cen have rich absorption line spectra, and unlike many known solar-type systems (Table 10), the components of V636 Cen are relatively slow rotators. This is a clear advantage for the abundances studies. The ideal case would be to have enough spectra for disentangling, since mutual blending is avoided and the reconstructed component spectra get a higher signal-to-noise ratio than each of the observed spectra. However, as will be demonstrated below, the wide spectral coverage of FEROS provides a large number of unblended lines from both components which are usable for the analyses of the combined spectra. Furthermore, the two spectra have been observed at different phases giving opposite line shifts. Since the primary component is 3-5 times more luminous than the secondary, depending on wavelength, its lines are only diluted by a factor of about 1.3, meaning that an accuracy close to that for a similar single star with spectra of comparable quality can be reached. For the secondary, the situation is on the other hand worse; its dilution factor is about 4.7. A lower accuracy must therefore be expected for the secondary due to higher errors of the intrinsic equivalent widths. In general, also intrinsically stronger lines, for which the equivalent widths are less sensitive to abundance and more sensitive to e.g. microturbulence and pressure broadening, have to be used for the secondary. This is in principle avoided in disentangling, but the signal-to-noise ratio of the reconstructed spectrum for the secondary would on the other hand still be much lower than for the primary.

The basic approach followed in the abundance analyses is described by CTB08. The versatile VWA tool, now extended to analyses of double-lined spectra, was used; we refer to Bruntt et al. (2004, 2008) for an updated description of VWA. It uses the SYNTH software (Valenti & Piskunov 1996) to generate the synthetic spectra. Atmosphere models were interpolated from the grid of modified ATLAS9 models by Heiter et al. (2002). Line information was taken from the Vienna Atomic Line Database (VALD; Kupka et al. 1999), but in order to derive abundances relative to the Sun, log (gf) values have been adjusted in such a way that each measured line in the Wallace et al. (1998) solar atlas reproduces the atmospheric abundances by Grevesse & Sauval (1998). Analyses of a FEROS sky spectrum reproduce these adjustments closely.

Table 5: Spectroscopic orbital elements of V636 Cen.

Table 6: Log of the FEROS observations of V636 Cen.

The abundance results derived from all useful lines in both spectra are presented in Table 7. Except for a few ions, we have only included lines with measured equivalent widths above 10 mÅ and below 80 mÅ (primary) and 50 mÅ (secondary). Comparing the results from the individual spectra, we find no significant differences. The effective temperatures, surface gravities and rotational velocities listed in Table 8 were adopted. Microturbulence velocities were tuned until Fe I abundances were independent of line equivalent widths, and the resulting values are 1.15 (primary) and 1.35 (secondary) kms^-1. The calibration by Edvardsson et al. (1993) predicts $1.25 \pm 0.31$ kms^-1 for the primary component, whereas the secondary lies outside its effective temperature range. For the adopted effective temperatures we see no dependency of the abundance on excitation potential, which, however, occurs if they are changed by more than $\pm$ 100-150 K.

$\begin{figure} \epsfxsize=095mm \epsfbox{12362f4.ps} \end{figure}$	Figure 4: Spectroscopic orbital solution for V636 Cen (solid line: primary; dashed line: secondary) and radial velocities (filled circles: primary; open circles: secondary). The dotted line ( upper panel) represents the center-of-mass velocity of the system. Phase 0.0 corresponds to central primary eclipse.
Open with DEXTER

As seen, a robust $[{\rm Fe/H}]$ is obtained for the primary, with identical results from Fe I and Fe II lines. Within errors, the less precise result for the secondary from Fe I lines agrees; unfortunately no suitable, unblended Fe II lines are available. Changing the primary model temperatures by $\pm$ 100 K modifies $[{\rm Fe/H}]$ from the Fe I lines by ${\pm} 0.05$ dex, and a similar but opposite effect is seen for Fe II lines. If 0.3 kms^-1 higher microturbulence velocities are adopted, $[{\rm Fe/H}]$ decreases by about 0.05 dex for both neutral and ionized lines. Finally, changing the adopted luminosity ratio between the components (Table 4) by +1 $\sigma$ changes $[{\rm Fe/H}]$ by +0.015 dex for the primary and -0.04 dex for the secondary. Taking these contributions to the uncertainties into account, and giving higher weight to the primary, we adopt $[{\rm Fe/H}]$ = $-0.20 \pm 0.08$ for V636 Cen. Except for Cr II we also find relative abundances close to -0.20 dex for the other ions listed in Table 7, including the $\alpha$ -elements. The reason for the Cr II discrepancy is not clear, but a similar result was recently found for the G0 V system WZ Oph (CTB08).

Table 7: Abundances ( [El./H]) for the primary and secondary components of V636 Cen determined from the two FEROS spectra.

We have also done abundance analyses based on the recent grid of MARCS model atmospheres (Gustafsson et al. 2008), which adopt the solar composition by Grevesse et al. (2007). Adjusting the log (gf) accordingly, as described above, we obtain abundances for V636 Cen which agree with those listed in Table 7 within about ${\pm} 0.05$ dex.

As a supplement to the spectroscopic abundance analyses, we have derived metal abundances from the de-reddened ${\it uvby}$ indices for the individual components (see Table 8) and the calibration by Holmberg et al. (2007). For the primary component, the result, $[{\rm Fe/H}]$ = $-0.23\pm0.11$ , agrees perfectly well with the spectroscopic determination, whereas an unrealistically low value, $[{\rm Fe/H}]$ = $-0.77\pm0.17$ , is obtained for the secondary. Their previous calibration for late type stars (Nordström et al. 2004) gives $[{\rm Fe/H}]$ = $-0.86\pm0.20$ . The quoted $[{\rm Fe/H}]$ errors include the uncertainties of the photometric indices and the published spread of the calibrations, and the reason for the discrepancy between the primary and secondary results is not clear. It may, however, very likely be due to m₁ deficiency for the secondary related to activity, as in fact seen for active binaries (Giménez et al. 1991), rather than a strong metal underabundance. Adopting the definitions by Giménez et al., we find $\delta m_1 \sim 0.11$ and $\delta c_1 \sim 0.00$ for the secondary. If we modify m₁ accordingly and assume that b-y is unaffected, the two calibrations mentioned above lead to $[{\rm Fe/H}]$ $=-0.34\pm0.18$ and $[{\rm Fe/H}]$ = $-0.36\pm0.21$ , respectively, i.e. reasonable agreement with the result for the primary is reached.

6 Absolute dimensions

Table 8: Astrophysical data for V636 Cen.

Absolute dimensions for the components of V636 Cen are calculated from the elements given in Tables 4 and 5. As seen in Table 8, both masses and radii have been obtained to an accuracy of about 0.5%.

Individual standard ${\it uvby}$ indices are included in Table 8, as calculated from the combined indices of V636 Cen outside eclipses (CVG08) and the luminosity ratios (Table 4). The calibration by Olsen 1988, the ${\it uvby}$ indices of the primary component and $\beta$ observations obtained during the total secondary eclipse ( $\beta = 2.601 \pm 0.008$ ) then yield a very small interstellar reddening of $E(b-y) = 0.005 \pm 0.008$ .

The adopted effective temperatures (5900 K, 5000 K) were calculated from the calibration by Holmberg et al. (2007), assuming $[{\rm Fe/H}]$ = -0.20(Sect. 5). The uncertainties include those of the ${\it uvby}$ indices, E(b-y), $[{\rm Fe/H}]$ and the calibration itself. Temperatures based on the calibrations by Alonso et al. (1996) and Ramírez & Meléndez (2005) agree within errors, but are, however, systematically about 100 K lower for the primary component.

From the orbital and stellar parameters, the observed rotational velocities, and the apsidal motion period determined by CVG08, we derive a mean central density coefficient of log(k₂) = $-1.61 \pm 0.05$ . The observed rate of change of the longitude of periastron $\dot\omega = 0.00080 \pm 0.00005$ $^\circ$ /c was corrected for a 40% relativistic contribution of $\dot\omega = 0.00032$ $^\circ$ /c, as calculated from general relativity (Giménez 1985). The higher order k₃ and k₄ terms are negligible. From theoretical coefficients, calculated for the models described in Sect. 7.2 along the lines described by Claret (1995,1997), we derive a theoretical log (k₂) of -1.74.

As seen in Table 8, the measured rotational velocities are in remarkable agreement with the theoretically predicted pseudo-synchronous velocities (Hut 1981, Eq. (42)), but are about 15% lower than the periastron values. The turbulent dissipation and radiative damping formalism of Zahn (1977,1989) predicts synchronization time scales of 0.1 Gyr for both components and a time scale for circularization of 7.5 Gyr, whereas the hydrodynamical mechanism by Tassoul & Tassoul (1997, and references therein) yields much lower values of 0.3 Myr (primary synchronization), 0.4 Myr (secondary synchronization), and 0.04 Gyr (circularization). We refer to Claret & Cunha (1997) and Claret et al. (1995) for details on the calculations. From model comparisons (Sect. 7.2), we derive an age for V636 Cen of about 1.35 Gyr, meaning that both theories are in agreement with the observed pseudo-synchronization. On the other hand, the mechanism by Tassoul & Tassoul predicts a circular orbit, which is certainly not the case.

The distance to V636 Cen was calculated from the ``classical'' relation (see e.g. CTB08), adopting the solar values and bolometric corrections given in Table 8 and A_V/E(b-y) = 4.27, and accounting for all error sources. As seen, nearly identical results are obtained from the two components. The mean distance, 71.8 pc, which has been established to about 4%, is in perfect agreement with the result of the new Hipparcos reduction by van Leeuwen (2007), $72.2 \pm 4.7$ pc, but is marginally larger than the original Hipparcos result $65.1 \pm 4.7$ pc (ESA 1997). We note that V636 Cen belongs to the group of eclipsing binaries within 125 pc, discussed by Popper (1998), which could be useful for improving the radiative flux scale.

7 Discussion

In the following, we first compare the absolute dimensions obtained for V636 Cen with properties of recent theoretical stellar evolutionary models. We then compare V636 Cen to other well-studied eclipsing binaries with at least one component in the 0.8-1.1 $M_{\odot }$ mass interval.

7.1 Comparison with solar-scaled models

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f5.ps} \end{figure}$

Figure 5:

V636 Cen compared to Y² models calculated for the measured abundance $[{\rm Fe/H}]$ =-0.20. Tracks for the component masses (full drawn, thick) and isochrones for 0.5, 2.0, 4.0, and 6.0 Gyr (dashed) are shown. The uncertainty in the location of the tracks coming from the mass errors are indicated (dotted lines). To illustrate the effect of the abundance uncertainty, tracks for $[{\rm Fe/H}]$ =-0.12 are included (full drawn, thin).

Open with DEXTER

Figures 5, 6, and 7 illustrate the results from comparisons with the Yonsei-Yale (Y²) evolutionary tracks and isochrones by Demarque et al. (2004). The mixing-length parameter in convective envelopes is calibrated using the Sun, and is held fixed at $l/H_{\rm p} = 1.7432$ . The enrichment law Y = 0.23 + 2Z is adopted, together with the solar mixture by Grevesse et al. (1996), leading to (X, Y, Z) $_{{\odot}}$ = (0.71564, 0.26624, 0.01812). Only models for $[{\rm\alpha/Fe}]$ = 0.0 have been considered. We refer to CTB08 for a brief description of other aspects of their up-to-date input physics.

As seen from Fig. 5, models for the observed masses and abundance, $[{\rm Fe/H}]$ = -0.20, equivalent to (X, Y, Z) = (0.73475, 0.25350, 0.01175), are significantly hotter than observed, especially for the secondary component. The uncertainty of $[{\rm Fe/H}]$ is ${\pm} 0.08$ dex, and models for $[{\rm Fe/H}]$ = -0.12, equivalent to (X, Y, Z) = (0.72809, 0.25790, 0.01397), marginally fit the primary but not the secondary component. In order to fit the primary perfectly, Y² models with a heavy element content close to solar, or a higher He abundance, are required. Such models would, however, still be unable to reproduce the secondary. The same picture is seen for e.g. Victoria-Regina (VandenBerg et al. 2006) and BaSTI (Pietrinferni et al. 2004) models, which differ slightly from Y², e.g. with respect to input physics and He enrichment law. We refer to CTB08 for a brief comparison of the three model grids.

The most direct comparison, based on the scale independent masses and radii of V636 Cen, is shown in Fig. 6. For the primary component, the models predict an age of 2.6-3.2 Gyr, depending on the assumed $[{\rm Fe/H}]$ , whereas the secondary is predicted to be more than two times older. At the predicted age of the primary, the observed radius of the secondary, which has been determined to an accuracy of 0.5%, is about 10% larger than that of the corresponding model. Mass-luminosity comparisons are shown in Fig. 7. Within the errors of the observed luminosities, the models predict identical - but lower - ages for the two components.

In conclusion, the secondary component of V636 Cen is significantly larger and $\sim$ 400 K cooler than predicted by models which adopt a mixing-length parameter matching the Sun. For the observed $[{\rm Fe/H}]$ , such models are $\sim$ 200 K hotter than the primary component, indicating a discrepancy as well.

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f6.ps} \end{figure}$	Figure 6: V636 Cen compared to Y² models calculated for $[{\rm Fe/H}]$ = -0.20. Isochrones for 0.5, 2.0, 4.0, and 6.0 Gyr are shown. For comparison, 2 Gyr isochrones for $[{\rm Fe/H}]$ = -0.12 (dashed) and $[{\rm Fe/H}]$ = 0.00 (dotted) are included.
Open with DEXTER

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f7.ps} \end{figure}$	Figure 7: V636 Cen compared to Y² models calculated for $[{\rm Fe/H}]$ = -0.20. Isochrones for 0.5, 2.0, 4.0, and 6.0 Gyr are shown. For comparison, 2 Gyr isochrones for $[{\rm Fe/H}]$ = -0.12 (dashed) and $[{\rm Fe/H}]$ = 0.00 (dotted) are included.
Open with DEXTER

7.2 Comparison with mixing-length ``tuned'' models

As mentioned in Sect. 1, several authors have demonstrated that models which adopt a reduced envelope convection mixing-length parameter fit active late-type binary components better. Since V636 Cen exhibits intrinsic variation and Ca II H and K emission (Fig. 1), and has relatively high rotational velocities (Table 8), compared to single field G-type stars, we have investigated such models.

Models with reduced mixing-length parameters, including non-gray atmospheres and an improved equation of state, have been published by Baraffe et al. (1998), but only for solar metallicity (up to 1.4 $M_{\odot }$ ) and $[{\rm Fe/H}]$ = -0.5 (up to 1.0 $M_{\odot }$ ).

Guided by a comparison between V636 Cen and these models, we have calculated dedicated models for the observed masses and $[{\rm Fe/H}]$ , tuning the mixing length parameter individually for the components. We have adopted the code by Claret (2004, 2005, 2006, 2007), which assumes an enrichment law of Y = 0.24 + 2.3Z together with the solar mixture by Grevesse & Sauval (1998), leading to (X, Y, Z) $_{{\odot}}$ = (0.704, 0.279, 0.017). The observed $[{\rm Fe/H}]$ = -0.20 then corresponds to (X, Y, Z) = (0.724, 0.264, 0.012). We note that the envelope mixing length parameter needed to reproduce the Sun is $l/H_{\rm p} = 1.68$ .

Table 9: Ages (Gyr) for the primary (p) and secondary (s) components of V636 Cen determined from comparison between their masses and radii and Claret models for different mixing length parameters and abundances.

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f8.ps} \end{figure}$	Figure 8: V636 Cen compared to Claret models for the observed masses, calculated with different mixing length parameters. The four cases listed in Table 9 are shown. The circles on the evolutionary tracks mark model ages of 1.0, 2.0, and 3.0 Gyr. Case 1 = full drawn, thick; Case 2 = dashed; Case 3 = full drawn, thin, open circles; Case 4 = dotted.
Open with DEXTER

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f9.ps} \end{figure}$

Figure 9:

V636 Cen compared to Claret models. The four cases listed in Table 9 are shown. The curves illustrate model radii as function of age for the component masses (upper: primary; lower: secondary). Case 1 = full drawn, thick; Case 2 = dashed; Case 3 = full drawn, thin; Case 4 = dotted. The horizontal full drawn lines mark the observed radii of the components with errors (dotted lines). The vertical line marks the common age (1.35 Gyr) predicted by the case 1 models.

Open with DEXTER

Four different cases, listed in Table 9, will be discussed here. Figure 8 shows temperature-radius comparisons between V636 Cen and models with different mixing length parameters, calculated for the component masses. For the observed $[{\rm Fe/H}]$ , the temperature of the primary component is fitted well by the $l/H_{\rm p} = 1.4$ model, whereas 1.0 is adequate for the secondary (case 1). As seen from the age-radius diagram in Fig. 9, these models also predict practically identical ages for the components. Changing the mixing length parameters by just +0.1 (case 2), i.e. considering models which still fit the observed masses and temperatures within errors (Fig. 8), lead to significantly higher ages, which are, however, no longer identical for the components. To illustrate the effect of the abundance uncertainty ${\pm} 0.08$ dex, models for $[{\rm Fe/H}]$ = -0.12 have been included in the two figures (case 3). For this abundance, mixing length parameters of about 1.6 (primary) and 1.1 (secondary) are needed to fit the observed masses and temperatures. Ages determined from the masses and radii become even higher, and they differ for the components. Finally, Claret models adopting a solar $l/H_{\rm p}$ are, like the Y² models, unable to fit V636 Cen (case 4).

Table 10: Properties of well-studied main sequence binaries (e.g. footnote 9) with at least one component in the 0.80-1.10 $M_{\odot }$ mass interval.

Table 9 summarizes the ages derived from the different model cases. Effects from the mass uncertainties are negligible and have not been included; see Fig. 5. In conclusion, only the case 1 models reproduce all observed properties of the components of V636 Cen well at a common age (1.35 Gyr). This implies that $l/H_{\rm p}$ can be tuned fairly precisely, provided accurate dimensions and abundances are available. We finally note, that according to the Claret models both components have pronounced convective envelopes, starting at $0.78~ R_{\rm p}$ and $0.73~ R_{\rm s}$ .

7.3 Comparison with other binaries

$\begin{figure} \epsfxsize=100mm \epsfbox{12362f10.ps} \end{figure}$	Figure 10: Main-sequence binaries with one or both components in the 0.80-1.10 $M_{\odot }$ interval having well-established masses and radii (2% or better); see Table 10. The components of V636 Cen are connected by a solid line. The dotted lines are Y² isochrones (0.5 Gyr and 1-10 Gyr, step 1 Gyr) for Z=0.0181, i.e. solar composition (Demarque et al. 2004).
Open with DEXTER

Currently, nine other main sequence eclipsing binaries with at least one component in the 0.80-1.10 $M_{\odot }$ mass interval have well-established ( ${\approx}2\%$ or better) masses and radii . Furthermore, the A and B components of $\alpha$ Cen can be added, since their masses, radii, temperatures, and abundances are known to high accuracy (e.g. Eggenberger et al. 2004).

These 11 binaries are listed in Table 10 and shown in Fig. 10 together with Y² solar composition isochrones. We note, that V636 Cen and $\alpha$ Cen are the only systems in this sample with $[{\rm Fe/H}]$ measured spectroscopically. With one exception, VZ Cep, the systems fall in two groups:

1.: For CG Cyg, CV Boo, ZZ UMa, FL Lyr, and V1061 Cyg, like for V636 Cen, the Y² models predict higher ages for the secondary components than for the primary components, resulting from larger radii than predicted. Also, the effective temperatures of the secondary components are lower than predicted. Their orbital periods are short ( 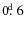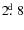$0\hbox{$.\!\!^{\rm d}$ }6$ - $2\hbox{$.\!\!^{\rm d}$ }8$ ), and the rotational velocities of their components are high (20-73 kms^-1). Intrinsic variations are present, and some of the binaries are known, strong X-ray sources. Information on Ca II emission is unfortunately scarce. A few further systems with similar characteristics, but less accurate dimensions (RT And, BH Vir, UV Leo, and UV Psc), could be added to this group (Clausen et al. 1999).
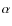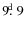2.: For HS Aur, RW Lac, $\alpha$ Cen, and V568 Lyr (V20 in NGC 6791), the observed masses, radii, and temperatures agree much better with those predicted by the solar-scaled Y² models. They have fairly long orbital periods ( $9\hbox{$.\!\!^{\rm d}$ }9$ -79.9 yr), and the rotational velocities of the components are below 6 kms^-1. Popper et al. (1986) saw no Ca II emission but found evidence for intrinsic variability of HS Aur and/or the K0 comparison star used (HD 49 987). The other three binaries are reported to be stable; no information on Ca II emission is available. None of the four is a known strong X-ray source. According to models, RW Lac is somewhat metal deficient, and its age is about 11 Gyr (Lacy et al. 2005). V568 Lyr has an age of about 8 Gyr and its metal content is about 2.5 times solar (Grundahl et al. 2008).

For the exception, VZ Cep, the observed masses and radii are well reproduced by the Y² models, but the observed temperature of the secondary component is about 250 K lower than predicted (Torres et al. 2009). Therefore, it is also less luminous than predicted, which is in general not the case for the rest of the sample. VZ Cep is a strong X-ray source, and as for the binaries in group 1, the orbital period is short and the components rotate fast. On the other hand, no intrinsic variations are reported.

From a comparison of V1061 Cyg and FL Lyr (group 1) against RW Lac and HS Aur (group 2), Torres et al. (2006) identified chromospheric activity as the likely cause of the radius and temperature discrepancies. Our sample strengthens this suggestion, not at least through a comparison between V636 Cen and V568 Lyr, whose components have nearly identical masses.

7.4 Mixing-length calibrations

It is worth linking our sample to the ongoing discussion on the mixing-length parameter for stars in the 0.7-1.1 $M_{\odot }$ range, where stars have convective envelopes but are not fully convective. From 2D radiation hydrodynamics (RHD) calculations, Ludwig et al. (1999) calibrated the mixing-length parameter for solar-type stars ( $T_{\rm eff}$ 4300-7100 K; $\log g~ 2.54$ -4.74) and found a moderate but significant variation of $l/H_{\rm p}$ . On the main sequence, a decrease with increasing temperature, and thereby mass, from about 1.8 to about 1.3 was obtained. On the other hand, Yildiz et al. (2006) and Yildiz (2008) found a significant increase with mass from model fits to four Hyades binaries, FL Lyr, and V442 Cyg. As an illustration, $l/H_{\rm P}$ values calculated from the fitting functions by these authors are listed in Table 11; no scaling, e.g. to the Sun, has been done. Finally, including seismic constraints, several studies of $\alpha$ Cen, most recently by Eggenberger et al. (2004) and Yildiz (2007), find that $l/H_{\rm p}$ is higher for the less massive B component than for the A component. Eggenberger et al., who use the seismological data by Carrier & Bourban (2003), obtain 1.83 (A) and 1.97 (B), and Yildiz, who include the data by Kjeldsen et al. (2005), get 1.64 (A) and 2.10 (B).

Table 11: Mixing-length parameters ( $l/H_{\rm p}$ ) for the binary components (Table 10) calculated from the temperature-gravity fitting function by Ludwig et al. (1999) and the mass fitting formula by Yildiz et al. (2006).

The fact that our sample can be divided in two different groups seems to suggest that the behaviour of the mixing length parameter may be governed by two different effects:

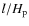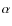a slight decrease of $l/H_{\rm p}$ with increasing temperature/mass for inactive main sequence stars, as predicted by Ludwig et al. (1999) and found for $\alpha$ Cen and possibly also V568 Lyr (Grundahl et al. 2008), and
a decrease of 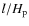$l/H_{\rm p}$ for active stars compared to inactive ones of similar mass, as seen for group 2.

If this is the case, the result by Yildiz et al. (2006) and Yildiz (2008) might then be questioned, since at least two of the binaries in their samples, the Hyades binary V818 Tau and FL Lyr, have active component(s).

It would be of interest to extend the systematic study of the evolution of low-mass stars and brown dwarf eclipsing binaries by Chabrier et al. (2007) to higher masses. For masses up to 0.8 $M_{\odot }$ , they found that the effects of decreasing $l/H_{\rm p}$ , i.e. reducing the convective efficiency, increases with mass, leading to lower effective temperatures, luminosities, central temperatures, and nuclear energy production. In parallel, magnetic spots covering a significant fraction of the stellar surfaces cause similar changes. They adopted a phenomenological approach, and more complete models, which directly couple rotation, convection, and dynamo magnetic fields are also desirable; see e.g. D'Antona et al. (2000) for pre-main-sequence models.

8 Summary and conclusions

From state-of-the-art observations and analyses, precise (0.5%) absolute dimensions have been obtained for the totally eclipsing solar-type system V636 Cen. A detailed spectroscopic analysis yields a Fe abundance relative to the Sun of $[{\rm Fe/H}]$ = $-0.20 \pm 0.08$ and similar relative abundances for Si, Ca, Ti, V, Cr, Co, and Ni.

The 0.85 $M_{\odot }$ secondary component is found to be moderately active with starspots and Ca II H and K emission, and the 1.05 $M_{\odot }$ primary shows signs of activity as well, but at a much lower level. Apsidal motion ( $U = 5~270 \pm 335$ yr) with a 40% relativistic contribution has been detected for the eccentric orbit ( $e = 0.135 \pm 0.001$ ), and the inferred mean central density concentration coefficient, log (k₂) = $-1.61 \pm 0.05$ , agrees marginally with model predictions. The measured rotational velocities, $13.0 \pm 0.2$ (primary) and $11.2 \pm 0.5$ (secondary) kms^-1, are in remarkable agreement with the theoretically predicted pseudo-synchronous velocities, but are about 15% lower than the periastron values.

We have shown that stellar models with solar-scaled mixing length parameters are unable to match the components of V636 Cen at identical ages. At the age of the primary, the secondary component is $\sim$ $10\%$ larger than predicted. Also, the components are $\sim$ 200 K (primary) and $\sim$ 400 K (secondary) cooler than predicted.

However, models adopting significantly lower mixing-length parameters can remove these discrepancies. For the observed $[{\rm Fe/H}]$ , Claret models for $l/H_{\rm p} = 1.4$ (primary) and 1.0 (secondary) reproduce the properties of the components of V636 Cen well for a common age of 1.35 Gyr.

Currently, 10 other solar-type binaries have well-established dimensions, although spectroscopic abundance results are lacking for most of them; see Fig. 10 and Table 10. With one exception, VZ Cep, they fall in two groups: Four long period, slowly rotating inactive systems, which seem to be fitted reasonably well by solar-scaled models. And five systems, which exhibit intrinsic variation, and have short orbital periods and high rotational velocities. Like V636 Cen, they can not be reproduced by solar-scaled models. Therefore, the sample strengthens the suggestion by Torres et al. (2006), based on fewer systems, that chromospheric activity, and the associated changes of the convective envelope, is the likely cause of the radius and temperature discrepancies. The strongest case is perhaps a comparison between V636 Cen (active) and the newly studied V568 Lyr in NGC 6791 (inactive), whose components have nearly identical masses.

Finally, the clear division of our sample in two groups might suggest that two different effects influence the mixing length parameter for 0.7-1.1 $M_{\odot }$ main sequence stars: a) a slight decrease of $l/H_{\rm p}$ with increasing temperature/mass for inactive main sequence stars, as found by e.g. Ludwig et al. (1999) and seen for $\alpha$ Cen and possibly also V568 Lyr; and b) a decrease of $l/H_{\rm p}$ for active stars compared to inactive ones of similar mass.

More well-studied eclipsing binaries, as well as more complete stellar models, are needed to fully understand and describe envelope convection in terms of effective temperature, gravity, mass, age, rotation, dynamo magnetic field, activity level etc. We are presently studying several systems with main sequence components in the 0.5-1.2 $M_{\odot }$ range, including V1123 Tau, V963 Cen, AL Dor, QR Hya, KY Hya, AL Ari, UW LMi, EW Ori, and NY Hya; see also Clausen et al. (2001). They exhibit various levels of activity, from none to modest, and should therefore provide valuable new insight into this matter. Spectroscopic abundance determinations will be part of the analyses.

Acknowledgements

We thank M. Imbert and L. Prévot for the use of their CORAVEL observations, and P. Figueira for extracting the radial velocity data from the CORAVEL database. We are grateful to the referee, G. Torres, for a prompt and very helpful report. The projects ``Stellar structure and evolution - new challenges from ground and space observations'' and ``Stars: Central engines of the evolution of the Universe'', carried out at Copenhagen University and Aarhus University, are supported by the Danish National Science Research Council. Furthermore, this investigation was supported by the Spanish Science Research Council. J.A. and B.N. acknowledge support from the Carlsberg Foundation. H.B. was supported by the Australian Research Council. The following internet-based resources were used in research for this paper: the NASA Astrophysics Data System; the SIMBAD database and the VizieR service operated by CDS, Strasbourg, France; the VALD database made available through the Institute of Astronomy, Vienna, Austria.

References

Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] (In the text)
Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. 1998, A&A, 337, 403 [NASA ADS] (In the text)
Baranne, A., Mayor, M., & Poncet, J.-L. 1979, Vistas in Astron., 23, 279 [NASA ADS] [CrossRef] (In the text)
Bruntt, H., Bikmaev, I. F., Catala, C., et al. 2004, A&A, 425, 683 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Bruntt, H., De Cat, P., & Aerts, C. 2008, A&A, 478, 487 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Carrier, F. & Bouran, G. 2003, A&A, 406, L23 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Chabrier, G., Gallardo, J., & Baraffe, I. 2007, A&A, 472, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Claret, A. 1995, A&AS, 109, 441 [NASA ADS] (In the text)
Claret, A. 1997, A&AS, 125, 439 [NASA ADS] [CrossRef] [EDP Sciences]
Claret, A. 2000, A&A, 363, 1081 [NASA ADS] (In the text)
Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Claret, A. 2005, A&A, 440, 647 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Claret, A. 2006, A&A, 453, 769 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Claret, A. 2007, A&A, 467, 1389 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Claret, A., & Cunha, N. C. S. 1997, A&A, 318, 187 [NASA ADS] (In the text)
Claret, A., Giménez, A., & Cunha, N. C. S. 1995, A&A, 299, 724 [NASA ADS] (In the text)
Clausen, J. V., Baraffe, I., Claret, A., & VandenBerg, D. B. 1999, in Theory and Tests of Convection in Stellar Structure, ed. A. Giménez, E. F. Guinan, & B. Montesinos, ASP Conf. Ser., 173, 265 (In the text)
Clausen, J. V., Helt, B. E., & Olsen, E. H. 2001, A&A, 374, 980 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Clausen, J. V., Vaz, L. P. R., García, J. M., et al. 2008a, A&A, 487, 1081 [NASA ADS] [CrossRef] [EDP Sciences] (CVG08) (In the text)
Clausen, J. V., Torres, G., Bruntt, H., et al. 2008b, A&A, 487, 1095 [NASA ADS] [CrossRef] [EDP Sciences] (CTB08) (In the text)
Cox, A. N., Shaviv, G., & Hodson, S. W. 1981, ApJ, 245, L37 [NASA ADS] [CrossRef] (In the text)
D'Antona, F., Ventura, P., & Mazzitelli, I. 2000, ApJ, 543, L77 [NASA ADS] [CrossRef] (In the text)
Dawson, P. C., & De Robertis, M. M. 2004, AJ, 127, 2909 [NASA ADS] [CrossRef] (In the text)
Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] (In the text)
Eggenberger, P., Charbonnel, C., Talon, S., et al. 2004, A&A, 417, 235 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 (In the text)
Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] (In the text)
Etzel, P. B. 2004, SBOP: Spectroscopic Binary Orbit Program San Diego State University) (In the text)
Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef]
Gabriel, M. 1969, in Low-Luminosity Stars, ed. S. S. Kumar (New York: Gordon & Breach), 267 (In the text)
Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] (In the text)
Giménez, A., Reglero, V., de Castro, E., & Fernández-Figueroa, M. J. 1991, A&A, 248, 563 [NASA ADS] (In the text)
Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
Grevesse, N., Noels, A., & Sauval, A. J. 1996, in Cosmic Abundances, ed. S. S. Holt, & G. Sonneborn (San Francisco: ASP), 117 (In the text)
Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef] (In the text)
Grundahl, F., Clausen, J. V., Hardis, S., & Frandsen, S. 2008, A&A, 492, 171 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hall, D. S. 1994, Mem. Soc. Astron. Italiana, 65, 73 [NASA ADS] (In the text)
Heiter, U., Kupka, F., van't Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Henry, T. J., Soderblom, D. R., Donahue, R. A., & Baliunas, S. L. 1996, AJ, 111, 439 [NASA ADS] [CrossRef] (In the text)
Hoffmeister, C. 1958, Veröffentlichungen der Sternwarte in Sonneberg, 3, 439 [NASA ADS] (In the text)
Holmberg, J., Nordström, B., & Andersen, J. 2007 A&A, 475, 519 (In the text)
Houk, N. 1978, Michigan Catalogue of two-dimensional spectraltypes for HD stars, 2, Dep. Astron., Univ. Michigan, Ann Arbor, Michigan, USA
Hoxie, D. T. 1973, A&A, 26, 437 [NASA ADS] (In the text)
Hut, P. 1981, A&A, 99, 126 [NASA ADS] (In the text)
Kjeldsen, H., Bedding, T. R., Butler, R. P., et al. 2005, ApJ, 635, 1281 [NASA ADS] [CrossRef] (In the text)
Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lacy, C. H. S., Torres, G., Claret, A., & Vaz, L. P. V. 2005, AJ, 130, 2838 [NASA ADS] [CrossRef] (In the text)
Larsen, A. 1998, Master Thesis, Copenhagen University (In the text)
López-Morales, M. 2007, ApJ, 660, 732 [NASA ADS] [CrossRef] (In the text)
López-Morales, M., & Ribas, I. 2005, ApJ, 631, 1120 [NASA ADS] [CrossRef] (In the text)
Ludwig, H:-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] (In the text)
Mayor, M. 1985, in Stellar Radial Velocities, ed. A. G. D. Philip, & D. W. Latham (Schenectady, New York: L. Davis Press), IAU Coll., 88, 35 (In the text)
Morales, J. C., Ribas, I., & Jordi, C. 2008, A&A, 478, 507 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Motch, C., Guillout, P., Haberl, F., et al. 1997, A&AS, 122, 201 [NASA ADS] [CrossRef] [EDP Sciences]
Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Olsen, E. H. 1988, A&A, 189, 173 [NASA ADS] (In the text)
Pietrinferni, A., Cassisi, S., & Salaris, M. 2004, Mem. Soc. Astron. Italiana, 75, 170 [NASA ADS] (In the text)
Popper, D. M. 1966, AJ, 71, 175 [NASA ADS] [CrossRef] (In the text)
Popper, D. M. 1997, AJ, 114, 1195 [NASA ADS] [CrossRef] (In the text)
Popper, D. M. 1998, PASP, 110, 919 [NASA ADS] [CrossRef] (In the text)
Popper, D. M., Lacy, C. H., Frueh, M. I., & Turner, A. E. 1986, AJ, 91, 383 [NASA ADS] [CrossRef] (In the text)
Ramírez, I., & Meléndez, J. 2005, AJ, 626, 465 [NASA ADS] [CrossRef] (In the text)
Ribas, I. 2003, A&A, 398, 239 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Ribas, I., Morales, J. C., Jordi, C. et al. 2008, Mem. Soc. Astron. Italiana, 79, 562 [NASA ADS] (In the text)
Stassun, K. G., Mathieu, R. D., Vaz, L. P. R., et al. 2004, ApJS, 151, 357 [NASA ADS] [CrossRef]
Siviero, A., Munari, U., Sordo, R., et al. 2004, A&A, 417, 1083 [NASA ADS] [CrossRef] [EDP Sciences]
Tassoul, M. & Tassoul, J.-L. 1997, ApJ, 481, 363 [NASA ADS] [CrossRef] (In the text)
Torres, G., & Ribas, I. 2002, ApJ, 567, 1140 [NASA ADS] [CrossRef] (In the text)
Torres, G., & Lacy, C. H. S. 2009, AJ, 137, 507 [NASA ADS] [CrossRef] (In the text)
Torres, G., Lacy, C.H., Marschall, L. A., Sheets, H. A., & Mader, J. A. 2006, AJ, 640, 1018 [NASA ADS] [CrossRef] (In the text)
Valenti, J., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006 ApJS, 162, 375 (In the text)
Van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] (In the text)
van Leeuwen, F. 2007, Hipparcos, the new reduction of the raw data (Dordrecht: Springer) (In the text)
Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] (In the text)
Voges, W., Aschenbach, B., Boller, T., et al. 2000, IAU Circ., 7432, 1 [NASA ADS]
Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] (In the text)
Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS]
Wallace, L., Hinkle, K., & Livingston, W. 1998, An atlas of the spectrum of the solar photosphere from 13 500 to 28 000 cm^-1 (3570 to 7405 A), Tucon, AZ: NOAO (In the text)
Wolfe, R. H., Horak, H. G., & Storer, N. W. 1967, in Modern Astrophysics: a Memorial to Otto Struve, ed. M. Hack, 251 (In the text)
Yildiz, M. 2007, MNRAS, 374, 1264 [NASA ADS] [CrossRef] (In the text)
Yildiz, M. 2008, in The Art of Modelling Stars in the 21th Century, ed. L. Deng, & K. L. Chan, IAU Symp., 252, 183 (In the text)
Yildiz, M., Yakut, K., Bakis, H., & Noels, A. 2006, MNRAS, 368, 1941 [NASA ADS] [CrossRef] (In the text)

Footnotes

... binaries: Based on observations carried out at the Strömgren Automatic Telescope (SAT), the Danish 1.54 m telescope, and the 1.5 m telescope (62.L-0284) at ESO, La Silla, Chile.
... secondary: Table A.1 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/502/253
... F8/G0 V: Houk (1978); spectral type of primary component.
... Rossby: Defined as the ratio of the rotation period to the convective turnover time.
... SBOP: Spectroscopic Binary Orbit Program, http://mintaka.sdsu.edu/faculty/etzel/
... disentangling: About 10 spectra with 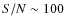$S/N \sim 100$ , well distributed in phase, would be required.
...2004): http://www.astro.yale.edu/demarque/yystar.html
...2006): http://www1.cadc-ccda.hia-iha.nrc-cnrc.gc.ca/cvo/community/VictoriaReginaModels/
...2004): http://www.te.astro.it/BASTI/index.php
...1998): ftp.ens-lyon.fr
... radii: see e.g. http://www.astro.keele.ac.uk/~jkt/
...: Two additional binaries in this mass interval, the pre-main-sequence system V1174 Ori (Stassun et al. 2004), and V432 Aur, which has an evolved component (Siviero et al. 2004), have not been been included in the comparison.

All Tables

Table 1: Photometric solutions for V636 Cen from JKTEBOP analyses of the 1987 and 1988 light curve observations (426 points per band).

Table 2: WD solutions from the 1987 light curve observations (165 per band).

Table 3: WD solutions from the 1988 light curve observations (261 per band). See Table 2.

Table 4: Adopted photometric elements for V636 Cen.

Table 5: Spectroscopic orbital elements of V636 Cen.

Table 6: Log of the FEROS observations of V636 Cen.

Table 7: Abundances ( [El./H]) for the primary and secondary components of V636 Cen determined from the two FEROS spectra.

Table 8: Astrophysical data for V636 Cen.

Table 10: Properties of well-studied main sequence binaries (e.g. footnote 9) with at least one component in the 0.80-1.10 $M_{\odot }$ mass interval.

All Figures

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f1.ps} \end{figure}$	Figure 1: Ca II H and K emission in V636 Cen. The vertical lines show the positions for the primary (full) and secondary (dashed) components. The FEROS spectrum of V636 Cen was observed at JD2451211.85 (orbital phase 0.63).
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=180mm \epsfbox{12362f2.ps} \end{figure}$	Figure 2: Fit of the theoretical light curve of the WD solution from Table 2 to the 1987 y observations.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=180mm \epsfbox{12362f3.ps} \end{figure}$	Figure 3: Fit of the theoretical light curve of the WD solution from Table 3 to the 1988 y observations.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=095mm \epsfbox{12362f4.ps} \end{figure}$	Figure 4: Spectroscopic orbital solution for V636 Cen (solid line: primary; dashed line: secondary) and radial velocities (filled circles: primary; open circles: secondary). The dotted line ( upper panel) represents the center-of-mass velocity of the system. Phase 0.0 corresponds to central primary eclipse.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f5.ps} \end{figure}$	Figure 5: V636 Cen compared to Y² models calculated for the measured abundance $[{\rm Fe/H}]$ =-0.20. Tracks for the component masses (full drawn, thick) and isochrones for 0.5, 2.0, 4.0, and 6.0 Gyr (dashed) are shown. The uncertainty in the location of the tracks coming from the mass errors are indicated (dotted lines). To illustrate the effect of the abundance uncertainty, tracks for $[{\rm Fe/H}]$ =-0.12 are included (full drawn, thin).
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f6.ps} \end{figure}$	Figure 6: V636 Cen compared to Y² models calculated for $[{\rm Fe/H}]$ = -0.20. Isochrones for 0.5, 2.0, 4.0, and 6.0 Gyr are shown. For comparison, 2 Gyr isochrones for $[{\rm Fe/H}]$ = -0.12 (dashed) and $[{\rm Fe/H}]$ = 0.00 (dotted) are included.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f7.ps} \end{figure}$	Figure 7: V636 Cen compared to Y² models calculated for $[{\rm Fe/H}]$ = -0.20. Isochrones for 0.5, 2.0, 4.0, and 6.0 Gyr are shown. For comparison, 2 Gyr isochrones for $[{\rm Fe/H}]$ = -0.12 (dashed) and $[{\rm Fe/H}]$ = 0.00 (dotted) are included.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f8.ps} \end{figure}$	Figure 8: V636 Cen compared to Claret models for the observed masses, calculated with different mixing length parameters. The four cases listed in Table 9 are shown. The circles on the evolutionary tracks mark model ages of 1.0, 2.0, and 3.0 Gyr. Case 1 = full drawn, thick; Case 2 = dashed; Case 3 = full drawn, thin, open circles; Case 4 = dotted.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=90mm \epsfbox{12362f9.ps} \end{figure}$	Figure 9: V636 Cen compared to Claret models. The four cases listed in Table 9 are shown. The curves illustrate model radii as function of age for the component masses (upper: primary; lower: secondary). Case 1 = full drawn, thick; Case 2 = dashed; Case 3 = full drawn, thin; Case 4 = dotted. The horizontal full drawn lines mark the observed radii of the components with errors (dotted lines). The vertical line marks the common age (1.35 Gyr) predicted by the case 1 models.
Open with DEXTER
In the text

$\begin{figure} \epsfxsize=100mm \epsfbox{12362f10.ps} \end{figure}$	Figure 10: Main-sequence binaries with one or both components in the 0.80-1.10 $M_{\odot }$ interval having well-established masses and radii (2% or better); see Table 10. The components of V636 Cen are connected by a solid line. The dotted lines are Y² isochrones (0.5 Gyr and 1-10 Gyr, step 1 Gyr) for Z=0.0181, i.e. solar composition (Demarque et al. 2004).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.