Robust correlators

P. Fridman

doi:10.1051/0004-6361/200912006

Home

All issues

Volume 502 / No 1 (July IV 2009)

A&A, 502 1 (2009) 401-408

Full HTML

Free Access

Issue		A&A Volume 502, Number 1, July IV 2009


Page(s)		401 - 408
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/200912006
Published online		27 May 2009

Robust correlators

P. Fridman

ASTRON, Oudehoogeveensedijk 4, Dwingeloo, 7991PD, The Netherlands

Received 8 March 2009 / Accepted 19 April 2009

Abstract
Context. Radio frequency interference (RFI) already limits the sensitivity of existing radio telescopes in several frequency bands and may prove to be an even greater obstacle for future generation instruments to overcome.
Aims. I aim to create a structure of radio astronomy correlators which will be statistically stable (robust) in the presence of interference.
Methods. A statistical analysis of the mixture of system noise + signal noise + RFI is proposed here which could be incorporated into the block diagram of a correlator. Order and rank statistics are especially useful when calculated in both temporal and frequency domains.
Results. Several new algorithms of robust correlators are proposed and investigated here. Computer simulations and processing of real data demonstrate the efficacy of the proposed algorithms.

Key words: instrumentation: interferometers - methods: data analysis - methods: statistical

1 Introduction

Correlators are central to the signal processing system of radio interferometer, (Thompson et al. 2001). Signals received from radio sources mixed with system noise (sky noise + receiver noise) can be represented as stochastic processes with a Gaussian (normal) distribution. Each pair of random numbers at the input of the correlator is described as a bivariate random value (X,Y) with the distribution ${\cal N}(\mu _{X},\mu _{Y}, \sigma _{X}^{2},\sigma _{Y}^{2},\rho_{0} )$ where $\mu _{X}=\mu _{Y} = 0$ are the mean values, $\sigma _{X}^{2}$ and $\sigma _{Y}^{2}$ are variances proportional to the intensity of the input noise and $\rho$ is the correlation coefficient (normalized visibility for a particular baseline). From the sequences x₁,...,x_N and y₁,...,y_N the correlator calculates the so-called Pearson's correlation coefficient

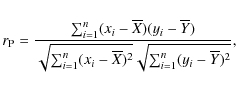$\begin{displaymath}r_{\rm P}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{X})(y_{i}-\ove... ...erline{X})^{2}}\sqrt{\sum_{i=1}^{n}(y_{i}-\overline{Y})^{2}}}, \end{displaymath}$

(1)

where $\overline{X}$ and $\overline{Y}$ are the arithmetic averages of x and y, respectively. The value $\lim_{n \rightarrow \infty}r_{\rm P} =\rho_{0}$ . This is valid both for XF and FX correlators (the correlation of complex numbers is reduced to separate correlations of the real and imaginary components).

The sample correlation coefficient $r_{\rm P}$ is very sensitive to outliers (samples which are not consistent with the normal distribution ${\cal N}(\mu _{X},\mu _{Y}, \sigma _{X}^{2},\sigma _{Y}^{2},\rho_{0} )$ , .i.e., the estimate (1) is not statistically robust (Gnanadesikan 1997; Huber 1981). Radio frequency interference (RFI) can produce considerable outliers, yielding a bias of $r_{\rm P}$ and increasing the standard deviation (rms) of $r_{\rm P}$ . In this paper the terms ``RFI'' and ``outliers'' are interchangeable.

Methods of robust statistics allow stable estimates to be obtained in the presence of outliers in several radio-astronomical applications (Fridman 2008). Here these methods are applied to correlation measurements of radio interferometers.

There are different types of RFI (Fridman & Baan 2001) and they differ significantly over the radio astronomy frequency band. Strong and impulse-like RFI on the time-frequency plane are visible in practically all frequency bands of LOFAR, and these types of RFI are considered here because data from the LOFAR Core Station (CS1) are used as examples later in this paper. Figure 1 gives an impression of the types of interferences in one sub-band: the auto-spectrum of the system noise + RFI from the LOFAR CS1 is represented in this figure with high spectral and time resolution.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg1.eps} \end{figure}$	Figure 1: Autospectrum of system noise + RFI from LOFAR CS1 at the central frequency f₀=217.1875 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f\approx 38$ Hz, integration time $t \approx 1$ s.
Open with DEXTER

The following approximate classification is proposed for the strong RFI visible at LOFAR:

a): narrow-band and persistent RFI;
b): narrow impulses (<1 s, <100 Hz) on the time-frequency plane;
c): impulse-like RFI in the time domain (several seconds) which are also wide-band (5-10 MHz);
d): random-form bursts on the time-frequency plane.

There are several types of RFI which cannot be treated as outliers: they may be persistent and wide-band, weak or strong, fully or partly correlated at the sites of a radio interferometer. Methods using the spatial separation of the source of RFI and the radio source can effectively address this issue, see (Ellingson & Hampson 2003; Jeff et al. 2005; Kesteven 2007; Cornwell et al. 2004).

Several types of robust correlators that are able to mitigate the impulse-like, strong RFI in both temporal and frequency domains have been studied in this paper. They are used in applications where input data are contaminated with outliers, and these correlators are statistically more stable than correlator (1). Some of them could be used in radio astronomy, especially in radio interferometric systems with software correlators where the calculation of visibilities is carried out on general-purpose computers, as in LOFAR (2009) and JIVE (Kruithof2009). Software correlators are, by definition, much more flexible than traditional hardware correlators: any algorithm adapted or modified for a particular observation can be optionally downloaded as a subroutine.

There are two operations in the numerator of (1): multiplication of the input samples of X and Y and summation (averaging). Here it is proposed that they be modified to make the correlator more robust.

The new features can be introduced in the first operation to analyze the statistics of X and Y and to introduce a type of editing in order to eliminate outliers.

The second operation, summation, which is considered as post-correlation averaging, can be divided into three steps: primary averaging over a time interval which is not too long to smooth RFI bursts appearing at this stage above the noise level, RFI mitigation and secondary averaging to the required time interval depending on the observational specifications (wavelength, baseline, radio source properties), see end of Sect. 3 and Figs. 13-15.

Different types of correlators described in the following section are compared with Pearson's correlator (1) using two criteria:

1.: the bias of the estimate 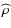$\widehat {\rho }$ produced by RFI compared to the input correlation coefficient $\rho_{0}$ ;
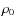2.: the effectiveness of an estimator is judged by the rms at the output of the correlator in both the presence and in the absence of outliers.

Computer simulations were performed to estimate these values, of the bias and rms. Also some results of the processing of CS1 data will be shown.

2 Estimators of the correlation coefficient

There are two classic estimators of correlation coefficients using ranks of samples instead of the samples themselves, (Kendall 1970).

Let two input sample sequences x₁,...x_n and y₁,...y_n be sorted in ascending order: $x_{(1)}\leq x_{(2)}\leq ...\leq x_{(n)}$ and $y_{(1)}\leq y_{(2)}\leq ...\leq y_{(n)}$ . The ith value x_(i) is called ith-order statistic. Each sample x_j has its kth position in the sorted series x₍₁₎,...x_(n). This number k is the rank of the sample x_j and is denoted by p_j(=k). Similarly, the rank of y_j is denoted by q_j. Let (x_i,y_i) and (x_j,y_j) with i=1,...n and j=i+1,...n be two data pairs from the original data sequences. If p_j-p_i and q_j-q_i have the same sign, these two data pairs are said to be concordant, otherwise, they are discordant. Let $n_{\rm c}$ be the number of concordant pairs and $n_{\rm d}$ the number of discordant pairs. It is clear that $n_{\rm c}+n_{\rm d} = n(n-1)/2$ .

2.1 Spearman's correlator

The Spearman's correlation coefficient is calculated by

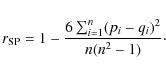$\begin{displaymath}r_{\rm SP}=1-\frac{6\sum_{i=1}^{n}(p_{i}-q_{i})^2}{n(n^{2}-1)}\cdot \end{displaymath}$

(2)

The bivariate correlation coefficient corresponding to Pearson's $r_{\rm P}$ can be restored using the relationship:

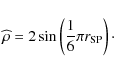$\begin{displaymath}\widehat{\rho} = 2 \sin \left(\frac{1}{6}\pi r_{\rm SP}\right)\cdot \end{displaymath}$

(3)

2.2 Kendall's correlator

Kendall's correlation coefficient is calculated by

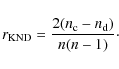$\begin{displaymath}r_{\rm KND}=\frac{2(n_{\rm c}-n_{\rm d})}{n(n-1)}\cdot \end{displaymath}$

(4)

The bivariate correlation coefficient corresponding to Pearson's $r_{\rm P}$ can be restored using the relationship:

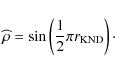$\begin{displaymath}\widehat{\rho}=\sin \left(\frac{1}{2}\pi r_{\rm KND}\right)\cdot \end{displaymath}$

(5)

2.3 Correlator using sums and differences

One of the first constructions of a robust correlator is based on the quarter square identity (Gnanadesikan & Kettenring 1972; Huber 1981):

$\begin{displaymath}{\rm cov}(X,Y)=1/4[{\rm var} (X+Y) - {\rm var} (X-Y)], \end{displaymath}$

(6)

where cov denotes covariance and var denotes variance. The correlation coefficient can be obtained with

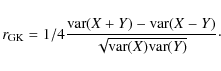$\begin{displaymath}r_{\rm GK}=1/4\frac{{\rm var} (X+Y)-{\rm var} (X-Y)}{\sqrt{{\rm var} (X){\rm var} (Y)}}\cdot \end{displaymath}$

(7)

Therefore, any robust estimators of variance can be used for this correlator (Fridman 2008). Several of them are applied here to (7).

2.3.1 Trimming

Samples Z₁ = X + Y and Z₂ = X - Y are sorted in ascending order: z₍₁₎,...z_(n). Let $\gamma$ denote the chosen amount of trimming, $0 \le \gamma\le 0.5$ and $k = [\gamma n]$ . Sample-trimmed variance is computed by removing k of the largest and k of the smallest data and using the values that remain:

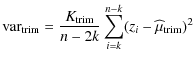$\displaystyle {\rm var}_{\rm trim}=\frac{K_{\rm trim}}{n-2k}\sum_{i=k}^{n-k}(z_{i}-\widehat{\mu }_{\rm trim})^{2}$			(8)
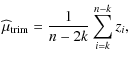$\displaystyle \widehat{\mu}_{\rm trim}=\frac{1}{n-2k}\sum_{i=k}^{n-k}z_{i},$

where $\mu_{\rm trim}$ is the sample mean of the trimmed data. Trimming lessens the variance of data and the coefficient $K_{\rm trim}$ makes ${\rm var}_{\rm trim}$ a consistent estimator for data with a normal distribution. The value of $K_{\rm trim}$ depends on $\gamma$ , (Fridman 2008), but in the context of Eq. (7), this is not important, because $K_{\rm trim}$ appears symmetrically in the numerator and denominator of (7).

2.3.2 Winsorization

A sample Z is sorted in ascending order. For the chosen $0 \leq \gamma \leq 0.5$ and $k = [\gamma n]$ , Winsorization of the sorted data consists of setting

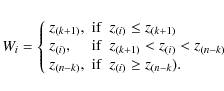$\begin{displaymath}W_{i}=\left\{ \begin{array}{lcl} z_{(k+1)}, & {\rm if} & z_{(... ...}, & {\rm if} & z_{(i)} \geq z_{(n-k}).\\ \end{array} \right. \end{displaymath}$

(9)

The Winsorized sample mean is $\widehat{\mu_{\rm w}}=\frac{1}{n}\sum_{i=1}^{n}W_{i}$ and the Winsorized sample variance is

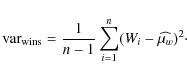$\begin{displaymath}{\rm var}_{\rm wins}=\frac{1}{n-1}\sum_{i = 1}^{n}(W_{i}-\widehat{\mu _{w}})^{2}\cdot \end{displaymath}$

(10)

The essence of Winsorization is to replace the k of the lowest and k of the highest samples of the sorted data z by the values of their nearest neighbors z_(k+1) and z_(n-k), respectively.

2.3.3 Median absolute deviation (MAD)

This estimate of the variance of sorted data $z_{(1)} \leq z_{(2)} \leq...\leq z_{(n)}$ is defined by

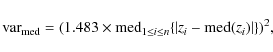$\begin{displaymath}{\rm var}_{\rm med} = (1.483 \times {\rm med}_{1\leq i\leq n}\{\left\vert z_{i}-{\rm med}(z_{i})\right\vert \})^2, \end{displaymath}$

(11)

where

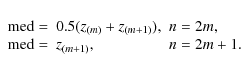
$\begin{displaymath}\left. \begin{array}{lll} {\rm med} = & 0.5(z_{(m)}+z_{(m+1)}... ...,\\ {\rm med} = & z_{(m+1)}, & n=2m+1.\\ \end{array} \right. \end{displaymath}$

Using ${\rm med} (z_{i})$ in the place of sample mean and $({\rm med} \left\vert z_{i}-{\rm med} (z_{i})\right\vert)^2$ in the place of sample variance provides a more robust estimate of variance: only central samples of sorted data (central order statistics) are used, according to the definition of the median, and outliers are excluded. This procedure works well with data contaminated by up to $\approx$ 50% outliers , but the rms of the estimator (11) is larger than that of the classic variance estimate (see Sect. 3, Table 4).

2.3.4 Qn estimate

This estimate is proposed in Rousseuw & Croux (1993) and is moderately effective. It combines the ideas of the Hodges-Lehmann estimate and the Gini estimate, (Kendal & Stuart 1967):

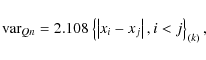$\begin{displaymath}{\rm var}_{Qn}=2.108\left\{\left\vert x_{i}-x_{j}\right\vert, i < j\right\}_{(k)}, \end{displaymath}$

(12)

where $k={h \choose 2}$ and h=[n/2]+1, that is $k \approx {n \choose 2}/4$ . This estimator works as follows: the interpoint (pairwise) distances $\left\vert x_{i}-x_{j}\right\vert, i<j,$ are sorted in ascending order. The kth value of this sorted sequence (the kth order statistics) multipled by consistency factor 2.108 is then taken as the estimate of variance. The value of the consistency factor is also not critical, as for trimming (Sect. 2.3.1).

Other robust algorithms can also be applied for example, the M-estimator, (Huber 1981) but here I was not attempting to make a comprehensive study of all types of robust correlators. Rather I wished to direct attention to the options hitherto unused in designing correlators.

3 Testing the algorithms

3.1 Mitigation of outliers in the temporal domain

The two input signals X and Y are modeled by bivariate random numbers with normal distribution, zero mean, standard deviation $\sigma = 1.0$ and correlation coefficient $\rho = 0.0;0.05;0.1;0.2$ . Such $\rho$ are typical of many radio interferometric observations when weak signals are processed. The number of samples in each data sequence is n and the number of repetitions of the correlation is m. Outliers rfi_i added to the inputs x_i and y_i are modeled by the following expression:

$\begin{displaymath}rfi_{i}=s_{i} \times {\rm sign} (z_{i}) \times (A_{\rm rfi}+\sigma _{\rm rfi} \times u_{i}), \end{displaymath}$

(13)

where s_i is the Poisson random value with the parameter $\lambda = 0.01$ , $A_{\rm rfi} = 20.0$ is the amplitude of outliers randomized by adding the normal random numbers u_i with the standard deviation $\sigma _{\rm rfi}=0.3~A_{\rm rfi}$ . The random polarities of the outliers are provided by the ${\rm sign}(z_{i}), z_{i}$ is the other auxiliary random normal number. Figure 2 gives the example of a sequence of input samples.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg2.eps} \end{figure}$	Figure 2: Input signals representing Gaussian noise + impulse-like outliers, the number of samples n=10 000.
Open with DEXTER

Table 1: Bias and rms of $\widehat {\rho }$ for the Spearman and Kendall correlators, n=1000, m=1000, 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00205$ , for rms: $\delta _{\rm rms} = \pm 0.0014$ .

Table 2: Bias and rms of $\widehat {\rho }$ for trimming, $\gamma = 0.1, n = 1000, m = 10~000$ , 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00062$ , for rms: $\delta _{\rm rms}=\pm 0.00044$ .

Table 3: Bias and rms of $\protect\widehat{\rho}$ for Winsorization, $\gamma = 0.1, n = 1000, m = 10~000$ , $95\%$ -confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00062$ , for rms: $\delta _{\rm rms}=\pm 0.00044$ .

Table 4: Bias and rms of $\widehat {\rho }$ for median absolute deviation (MAD), n = 1000, m = 10 000, 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00097$ , for rms: $\delta _{\rm rms} = \pm 0.00069$ .

Table 5: Bias and rms of $\widehat {\rho }$ for Q2-estimator, n = 1000, m = 1000, 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00205$ , for rms: $\delta _{\rm rms} = \pm 0.0014$ .

The results of computer simulations, bias and rms of the estimate of $\widehat {\rho }$ are presented in Tables 1-5. The bias of the estimate $\widehat {\rho }$ is: ${\rm bias} = \widehat{\rho}-\rho$ . The confidence intervals are calculated for the 95%-confidence level and for ${\rm rms}_{\widehat{\rho}}=1/\sqrt{mn}$ for $\widehat {\rho }$ and ${\rm rms}_{\widehat{\rm rms}}=1/\sqrt{2~{ mn}}$ for rms (the approximations that are valid for small $\rho$ and large mn).

Looking at Tables 1-5 several remarks can be made:

1.: in the absence of outliers, robust correlators reproduce practically the same values of 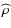$\widehat {\rho }$ as the Pearson's correlator (not showing a significant bias) and keeping the effectiveness close to 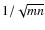$1/\sqrt {mn}$ (except MAD). Figure 3 shows this for correlator (7) with Winsorization;
2.: the output of the Pearson's correlator is dramaticaly decorrelated with the growth of the outlier's amplitudes whereas robust correlators analyze local statistics (n samples) and eliminate outliers regardless of their amplitudes, see Fig. 4;
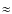
3.: in the presence of outliers, robust correlators show a small positive bias which is equal to 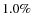$\approx$ $1.0\%$ of $\rho$ ;
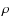4.: Spearman's and Kendall's correlators (Table 1) provide a considerable reduction of bias in the presence of RFI compared to the reduction of bias in Pearson's correlator and keep the rms, i.e., there is no loss in effectiveness within the limits of error. These correlators require more operating capacity per lag, due to the sorting and ranking of samples (this is also valid for the following algorithms);
5.: trimming and Winsorization (Tables 2 and 3) show good results with regard to bias and effectiveness. The rms for trimming is increased 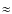$\approx$ 10% than for Winsorization. The choice of 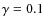$\gamma = 0.1$ presumes a percentage of outliers of less than 10%. So there is a considerable safety margin here but the growth of rms for 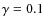$\gamma = 0.1$ is insignificant. In practice, an adaptive choice of 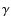$\gamma$ is possible in each sub-band when the value of 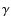$\gamma$ is chosen after taking into account a real RFI environment situation, i.e., the presence or absence of RFI and its duty cycle;
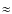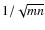6.: median absolute deviation (MAD) (Table 4) gives the best results for the bias, but as predicted theoretically, it has the largest rms: $\approx$ 1.65 greater than $1/\sqrt {mn}$ ;
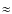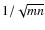7.: the Qn estimate (Table 5) requires more operating capacity than the others. The bias is as little as for the other algorithms, the rms is slightly larger ( $\approx$ 10%) than $1/\sqrt {mn}$ ;
8.: the proposed methods are effective in the presence of strong impulse-like outliers. When not intercepted, they decorrelate the correlator's output and it is practically impossible to improve this situation with subsequent processing. Low-amplitude outliers are more difficult to detect because they are similar to the rare Gaussian noise spikes, but their decorrelation impact is also much weaker. 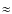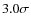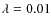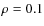For example, with an RFI amplitude $\approx$ $3.0\sigma$ , $\lambda = 0.01$ and $\rho = 0.1$ (signal-of-interest), the output of Pearson's correlator is 0.092 and the output of Spearman's correlator 0.098;
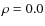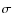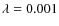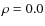9.: the situation is different when outliers are correlated at the inputs of the correlator. In this case outliers produce an excessive, false correlation even in the absence of a signal-of-interest, $\rho =0.0$ . For example, for strong 100%-correlated RFI with an amplitude equal to 30.0 $\sigma$ , $\lambda = 0.001$ and $\rho =0.0$ , the output of Pearson's correlator is 0.349 and the output of the MAD-correlator is 0.001.
For correlated RFI, other methods exploiting this correlation property can be more effective, see (Ellingson & Hampson 2003; Jeff et al. 2005; Kesteven 2007; Cornwell et al. 2004).

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg3.eps} \end{figure}$	Figure 3: Correlation coefficients in the absence of outliers for Pearson's correlator (1), ( upper panel), and Winsorized correlator (7), ( lower panel), each of the m=100 correlation coefficients are calculated for n=1000 data samples, $\rho =0.05$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg4.eps} \end{figure}$	Figure 4: Correlation coefficients in the presence of outliers for Pearson's correlator (1), ( upper panel), and Winsorized correlator (7), ( lower panel), $A_{\rm rfi} = 20.0, \rho =0.05$ . The solid line in the upper panel shows the total loss of correlation, the dashed line corresponds to the absence of outliers, while the solid and dashed lines in the lower panel practically coincide.
Open with DEXTER

3.2 Mitigation of outliers in the frequency domain

Narrow-band RFI can be detected as an impulse-like outlier in the frequency domain. The following example illustrates the application of trimming (8) in this case. RFI is generated as a phase-modulated sinusoidal carrier, see Fig. 5. The power spectrum of the unmodulated carrier is shown in the upper panel and in the lower panel, the power spectrum of the randomly phase-modulated signal is represented:

$\begin{displaymath}s=A_{\rm rfi}{\rm sin} (2 \pi Fi + (\pi/2){\rm rect} (i)), i = 1 ... n \end{displaymath}$

(14)

where rect(i) is a rectangular wave with Poisson's law distributed random jumps from -1 to +1, and the parameter of Poisson distribution $\lambda = 0.01$ .

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg5.eps} \end{figure}$	Figure 5: Power spectra of the unmodulated sinusoidal carrier ( upper panel) and the randomly-phased modulated carrier with the phase jumps $\pm \pi /2$ .
Open with DEXTER

The mixture of two input signals and their power spectra are represented in Fig. 6. The amplitudes $A1_{\rm rfi} = A2_{\rm rfi} = 0.5$ and frequencies F1 = 0.3 and F2 = 0.4. Therefore, RFI is not visible in the temporal domain but is easily visible in the spectral domain after FFT with n = 2048 as two bursts.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg6.eps} \end{figure}$	Figure 6: Input signal x noise +RFI ( upper panel) and its power spectra ( upper middle panel), input signal y ( lower middle panel) and its power spectra ( lower panel).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg7.eps} \end{figure}$	Figure 7: Pearson's correlator output ( upper panel) and the ``sum-difference'' correlator ouput ( lower panel), $\rho =0.0$ .
Open with DEXTER

The statistics of the power spectra are analyzed following (8) and the indexes of outliers exceeding the level equal to the 1.5%-percentile are used to reject the samples of the complex spectra of signals $\protect\widetilde{x}$ and $\protect\widetilde{y}$ , where $\widetilde{(.)}$ denotes the Fourier transform. These indexes are tagged with the indicator function ind(i) taking the numbers 0 or 1, i = 1...n and assigned to the sequence of n samples of the complex spectra $\protect\widetilde{x}$ and $\protect\widetilde{y}$ . The ``sum-difference'' correlator (7) is used in the spectral domain (FX-correlator):

$\displaystyle {\rm var} ({\rm sum})= {\rm var} (\Re ({\rm sum}))+{\rm var}(\Im ({\rm sum})), {\rm sum} = \widetilde{x} + \widetilde{y},$
$\displaystyle {\rm var}({\rm dif}) = {\rm var}(\Re({\rm dif})) + {\rm var} (\Im(dif)), {\rm dif} = \widetilde{x}-\widetilde{y}.$			(15)

Robust variance using the trimming algorithm (8) is applied while calculating (15): outliers are marked by the indicator function ${\rm ind}(i)$ . The results of computer simulation for n=2048 and m=100 are shown in Figs. 7-9. Figure 7 shows the m outputs of the Pearson's correlator, upper panel, and the robust correlator (15), lower panel, for the correlation coefficient of the input signals $\rho = 0$ , i.e., for the uncorrelated inputs, except RFI, which are 100% correlated. The upper panel shows considerable bias, while the fluctuations of correlator output in the lower panel vary around zero. Figure 8 gives the same situation but for $\rho = 0.1$ and Fig. 9 - for $\rho = 0.2$ . In all these examples a considerable bias is visible for the Pearson's correlator and there is an absence of bias for the ``sum-difference'' correlator.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg8.eps} \end{figure}$	Figure 8: Pearson's correlator output ( upper panel) and the ``sum-difference'' correlator ouput ( lower panel), $\rho = 0.1$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg9.eps} \end{figure}$	Figure 9: Pearson's correlator output ( upper panel) and the ``sum-difference'' correlator ouput ( lower panel), $\rho = 0.2$ .
Open with DEXTER

Of course, other post-correlation methods can be used in the case of narrow-band persistent RFI with a stable spatial orientation, for example, (Cornwell et al. 2004). But in the case of sporadic burst-like RFI, the proposed pre-correlation statistical analysis is more appropriate: only $n \approx 2000$ samples were used for each correlator input, which corresponds to a microsecond time scale for typical bandwidths.

3.2.1 Processing of observational data

Several examples of applications of the aforementioned algorithms are presented here.

The auto-spectrum in Fig. 10 is calculated using the ``raw'' data recorded at LOFAR CS1 for three hours. Data consisting of complex eight-bit numbers and having a sample time interval equal to 6.4 $\mu$ s were recorded on the subband with central frequency f₀ = 205.781 MHz, bandwidth $\Delta f=156.25$ KHz. This time-frequency presentation corresponds to 32 frequency channels, i.e., the frequency resolution is $\delta f \approx 4.88$ KHz, and the integration time $t \approx 1.7$ s.

Figure 11 demonstrates the auto-spectrum calculated from the same data for 1024 frequency channels. The high spectral resolution, $\delta f\approx 153$ Hz, permits the separation of RFI spikes, i.e., not smoothing them, as would have been in the case of 32 channels, see Fig. 10. Only half of the 3-h duration auto-spectrum is shown in Fig. 11 (due to the constraints of computer memory). The auto-spectrum in Fig. 11 is calculated without any censoring of outliers.

Figure 12 shows the ``cleaned'' auto-spectrum where Winsorization was applied. The Winsorized spectrum in Fig. 12 is smoothed so as to get a final frequency resolution $\delta f \approx 4.88$ KHz as in Fig. 10.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f10.eps} \end{figure}$	Figure 10: Auto-spectrum of system noise +RFI from LOFAR CS1 at the central frequency f₀ = 205.781 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f \approx 4.88$ KHz, integration time $t \approx 1.7$ s.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f11.eps} \end{figure}$	Figure 11: Auto-spectrum of system noise +RFI from LOFAR CS1 at the central frequency f₀=205.781 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f\approx 153$ Hz, integration time $t \approx 1.7$ s.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f12.eps} \end{figure}$	Figure 12: Auto-spectrum of the same data as in Fig. 11 calculated with Winsorization.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f13.eps} \end{figure}$	Figure 13: Post-correlation cross-spectrum, central frequency f₀ = 131.4453 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f=610$ Hz, time resolution $\delta t=1$ s.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f14.eps} \end{figure}$	Figure 14: Post-correlation cross-spectrum from Fig. 13 with outliers removed.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f15.eps} \end{figure}$	Figure 15: Averaged cross-spectra corresponding to Fig. 13 ( upper and middle (zoomed) panels) and to Fig. 14 ( lower panel).
Open with DEXTER

This example shows the importance of a sufficiently high frequency resolution. All RFI visible in Fig. 11 are invisible in the temporal domain; they are too weak and they are ``below'' the system noise. The low level of RFI also made it necessary to average the instantaneous power spectra obtained after each FFT. The number of averaged spectra is 256 and thus the time resolution in the Fig. 11 is $6.4 \times 10^{-6} \times 1024 \times 256 = 1.677$ s. The ripple structure clearly visible in the auto-spectra is produced by the transfer functions of LOFAR digital filters separating the whole input bandwidth into dozens of sub-bands with the partial bandwidths $\Delta f=156.25$ KHz (or 200 KHz).

The censoring of outliers may also be useful in the case of post-correlation data produced by the LOFAR correlator. The filter bank of the LOFAR backend divides each of the 156 KHz-bandwidth sub-bands into 256 narrow ``sub-sub-bands'' with a bandwidth equal to 610.3516 Hz. The sample time interval after preliminary averaging is 1 s. This good time-frequency resolution allows the fine-grain structure of RFI to be seen.

The following example in Fig. 13 shows the post-correlation cross-spectrum on frequency f₀ = 131.4453 MHz.

Figure 14 shows the corresponding Winsorized cross-spectrum and Fig. 15 shows the averaged cross-spectra along the whole time interval $4 \times 10^{4}$ s - without Winsorization (upper and middle panels) and with Winsorization (lower panel). The weak correlated component (the signal-of-interest) is produced by some cross-polarization effects and bears a ripple structure similar to the auto-spectra.

4 Conclusions

1.: Estimates of the correlation coefficient are an important part of both classical and of robust statistics. Statistical analysis of raw data with the finest available time and frequency resolution can help during observations in an RFI contaminated environment. Growing concern about RFI pollution should persuade the radio astronomy community to pay more attention to the variety of algorithms developed in the realm of robust statistics. This framework of robust estimates puts the successfully tested blanking of RFI on a more stable foundation.
2.: Statistically faithful, robust estimates of the correlation coefficient are especially appropriate for application in an impulse-like strong RFI environment. RFI is effectively suppressed and the accompanying bias and effectiveness are tolerable. The aforementioned robust algorithms can be usefully applied in these particular situations.
3.: The choice of a particular algorithm depends upon the type and intensity of the RFI. The proportion of RFI presence in data is also important. The type of implementation may determine the choice: off-line or real-time. It is difficult to equip existing conventional hardware correlators with these tools. Future generations of radio telescopes (LOFAR, ATA, SKA) will generate such huge amounts of data that real-time processing is vital: DSP, FPGA or supercomputers are possible solutions. Software correlators are especially suited to the implementation of robust schemes as optional subroutines.

Acknowledgements

My discussions with Ger de Bruyn and Jan Noordam have been very helpful and I am grateful for their continued support.

References

Cornwell, T. J., Perley, R. A., Golap, K., & Bhatnagar, S. 2004, EVLA Memo 86 (In the text)
Devlin, S. J., Gnanadesikan, R., & Kettenring, J. R. 1975, Biometrica, 62, 531 [CrossRef]
Ellingson, S. W., & Hampson, G. A. 2003, ApJS, 147, 167 [NASA ADS] [CrossRef] (In the text)
Fridman, P. A. 2008 AJ, 135, 1810 (In the text)
Fridman, P. A., & Baan, W. 2001, A&A, 378, 327 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gnanadesikan, R., & Kettenring, J. R. 1972, Biometrics, 28, 81 [CrossRef] (In the text)
Gnanadesikan, R. 1997, Methods for Statistical Data Analysis of Multivariate Observations (John Wiley & Sons, Inc.), Chap. 5.2.3 (In the text)
Jeff, B. D., Li, L., & Warnick, K. 2005, IEEE Trans. Signal Process., 53, 439 [NASA ADS] [CrossRef] (In the text)
Huber, P. J. 1981, Robust Statistics (John Wiley & Sons, Inc.), Chap. 8 (In the text)
Kendall, M. G. 1970, Rank Correlation Methods, 4th edn (London: Griffin) (In the text)
Kendall, M. G., & Stuart, A. 1967, The advanced theory of statistics (London: Griffin), 1, Chap. 3 (In the text)
Kesteven, M. 2007, URSI Radio Sci. Bull., 322, 9 (In the text)
Kruithof, N. 2009, Signals and Communication Technology (US: Springer), 537 (In the text)
LOFAR, http://www.lofar.org/p/systems_centrprocess.htm (In the text)
Rousseuw, P. J., & Croux, C. 1993, J. Amer. Stat. Assoc., 88, 1273 [CrossRef]
Thompson, A. R., Moran, J. M., & Swenson, G. W. 2001, Interferometry and Synthesis in Radio Astronomy (John Wiley & Sons, Inc.), Chap. 8 (In the text)

All Tables

Table 1: Bias and rms of $\widehat {\rho }$ for the Spearman and Kendall correlators, n=1000, m=1000, 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00205$ , for rms: $\delta _{\rm rms} = \pm 0.0014$ .

Table 2: Bias and rms of $\widehat {\rho }$ for trimming, $\gamma = 0.1, n = 1000, m = 10~000$ , 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00062$ , for rms: $\delta _{\rm rms}=\pm 0.00044$ .

Table 3: Bias and rms of $\protect\widehat{\rho}$ for Winsorization, $\gamma = 0.1, n = 1000, m = 10~000$ , $95\%$ -confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00062$ , for rms: $\delta _{\rm rms}=\pm 0.00044$ .

Table 4: Bias and rms of $\widehat {\rho }$ for median absolute deviation (MAD), n = 1000, m = 10 000, 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00097$ , for rms: $\delta _{\rm rms} = \pm 0.00069$ .

Table 5: Bias and rms of $\widehat {\rho }$ for Q2-estimator, n = 1000, m = 1000, 95%-confidence intervals for bias: $\delta _{\rm bias} = \pm 0.00205$ , for rms: $\delta _{\rm rms} = \pm 0.0014$ .

All Figures

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg1.eps} \end{figure}$	Figure 1: Autospectrum of system noise + RFI from LOFAR CS1 at the central frequency f₀=217.1875 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f\approx 38$ Hz, integration time $t \approx 1$ s.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg2.eps} \end{figure}$	Figure 2: Input signals representing Gaussian noise + impulse-like outliers, the number of samples n=10 000.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg3.eps} \end{figure}$	Figure 3: Correlation coefficients in the absence of outliers for Pearson's correlator (1), ( upper panel), and Winsorized correlator (7), ( lower panel), each of the m=100 correlation coefficients are calculated for n=1000 data samples, $\rho =0.05$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg4.eps} \end{figure}$	Figure 4: Correlation coefficients in the presence of outliers for Pearson's correlator (1), ( upper panel), and Winsorized correlator (7), ( lower panel), $A_{\rm rfi} = 20.0, \rho =0.05$ . The solid line in the upper panel shows the total loss of correlation, the dashed line corresponds to the absence of outliers, while the solid and dashed lines in the lower panel practically coincide.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg5.eps} \end{figure}$	Figure 5: Power spectra of the unmodulated sinusoidal carrier ( upper panel) and the randomly-phased modulated carrier with the phase jumps $\pm \pi /2$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg6.eps} \end{figure}$	Figure 6: Input signal x noise +RFI ( upper panel) and its power spectra ( upper middle panel), input signal y ( lower middle panel) and its power spectra ( lower panel).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg7.eps} \end{figure}$	Figure 7: Pearson's correlator output ( upper panel) and the ``sum-difference'' correlator ouput ( lower panel), $\rho =0.0$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg8.eps} \end{figure}$	Figure 8: Pearson's correlator output ( upper panel) and the ``sum-difference'' correlator ouput ( lower panel), $\rho = 0.1$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12006fg9.eps} \end{figure}$	Figure 9: Pearson's correlator output ( upper panel) and the ``sum-difference'' correlator ouput ( lower panel), $\rho = 0.2$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f10.eps} \end{figure}$	Figure 10: Auto-spectrum of system noise +RFI from LOFAR CS1 at the central frequency f₀ = 205.781 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f \approx 4.88$ KHz, integration time $t \approx 1.7$ s.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f11.eps} \end{figure}$	Figure 11: Auto-spectrum of system noise +RFI from LOFAR CS1 at the central frequency f₀=205.781 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f\approx 153$ Hz, integration time $t \approx 1.7$ s.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f12.eps} \end{figure}$	Figure 12: Auto-spectrum of the same data as in Fig. 11 calculated with Winsorization.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f13.eps} \end{figure}$	Figure 13: Post-correlation cross-spectrum, central frequency f₀ = 131.4453 MHz, bandwidth $\Delta f=156.25$ KHz, frequency resolution $\delta f=610$ Hz, time resolution $\delta t=1$ s.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f14.eps} \end{figure}$	Figure 14: Post-correlation cross-spectrum from Fig. 13 with outliers removed.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{12006f15.eps} \end{figure}$	Figure 15: Averaged cross-spectra corresponding to Fig. 13 ( upper and middle (zoomed) panels) and to Fig. 14 ( lower panel).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.