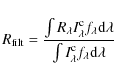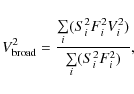| Issue |
A&A
Volume 501, Number 3, July III 2009
|
|
|---|---|---|
| Page(s) | 1073 - 1085 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200911938 | |
| Published online | 27 May 2009 | |
Interferometric properties of pulsating C-rich AGB stars
Intensity profiles and uniform disc diameters of dynamic model atmospheres
C. Paladini1 - B. Aringer1,2 - J. Hron1 - W. Nowotny1 - S. Sacuto1 - S. Höfner3
1 - Department of Astronomy, University of Vienna,
Türkenschanzstrasse 17, 1180 Wien, Austria
2 -
INAF-OAPD, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
3 -
Department of Physics and Astronomy,
Uppsala University, Box 515, 75120 Uppsala, Sweden
Received 24 February 2009 / Accepted 10 April 2009
Abstract
Aims. On the basis of a set of dynamic model atmospheres of C-rich AGB stars, we present the first theoretical study of centre-to-limb variation (CLV) properties and relative radius interpretation on narrow and broad-band filters. We computed visibility profiles and the equivalent uniform disc (UD) radii to investigate the dependence of these quantities on the wavelength and pulsation phase.
Methods. After an accurate morphological analysis of the visibility and intensity profiles determined in narrow and broad-band filters, we fitted our visibility profiles with a UD function simulating the observational approach. The UD-radii were computed using three different fitting-methods to investigate the influence of the visibility sampling profile: single point, two points and a least squares method.
Results. The intensity and visibility profiles of models characterises by mass loss show a behaviour very different from a UD. We found that UD-radii are wavelength dependent and that this dependence is stronger if mass loss is present. Strong opacity contributions from C2H2 affect all radius measurements at 3 ![]() m and in the N-band, resulting in higher values for the UD-radii. In the case of models with mass loss the predicted behaviour of UD-radii versus phase is complicated, while the radial changes are almost sinusoidal for models without mass loss. Compared to the M-type stars, for the C-stars no windows are available for measuring the pure continuum.
m and in the N-band, resulting in higher values for the UD-radii. In the case of models with mass loss the predicted behaviour of UD-radii versus phase is complicated, while the radial changes are almost sinusoidal for models without mass loss. Compared to the M-type stars, for the C-stars no windows are available for measuring the pure continuum.
Key words: techniques: interferometric - stars: AGB and post-AGB - stars: carbon - stars: atmospheres - stars: late-type
1 Introduction
The Asymptotic Giant Branch (AGB) is a late evolutionary stage of stars with masses lower than about
![]() .
The objects on the AGB are characterised by a degenerate C-O core
and He/H-burning shells, a convective envelope, and a very extended atmosphere containing molecules and
in many cases even dust grains. The atmospheres are affected by the pulsation of the interior
creating shocks in the outer layers.
Because of the third dredge-up, the AGB stars may have
C/O > 1 (Iben & Renzini 1983) and therefore their spectra
maybe dominated by features of carbon species such as C2, C2H2, C3,
CN, and HCN (Loidl et al. 2001; Goebel et al. 1981; Yamamura & de Jong 2000; Lançon et al. 2000; Joyce 1998). These are the classical carbon stars.
In these objects, dust is mainly present in the form of amorphous carbon grains.
.
The objects on the AGB are characterised by a degenerate C-O core
and He/H-burning shells, a convective envelope, and a very extended atmosphere containing molecules and
in many cases even dust grains. The atmospheres are affected by the pulsation of the interior
creating shocks in the outer layers.
Because of the third dredge-up, the AGB stars may have
C/O > 1 (Iben & Renzini 1983) and therefore their spectra
maybe dominated by features of carbon species such as C2, C2H2, C3,
CN, and HCN (Loidl et al. 2001; Goebel et al. 1981; Yamamura & de Jong 2000; Lançon et al. 2000; Joyce 1998). These are the classical carbon stars.
In these objects, dust is mainly present in the form of amorphous carbon grains.
Studying stellar atmospheres is essential to a clearer comprehension of this late stage of stellar evolution, the complicated interaction of pulsation and atmospheric structure, and the processes of dust formation and mass loss. The atmospheres of C-rich AGB stars with no pronounced pulsation can be described by hydrostatic models (Loidl et al. 2001; Jørgensen et al. 2000). As the stars evolve, the effective temperatures decrease and the atmospheres become more extended. At the same time, the effects of time-dependent phenomena (dynamic processes) become important and static models are no longer a good approximation. More sophisticated tools are needed to describe these objects i.e., dynamic model atmospheres. The status of modelling atmospheres of cool AGB stars is summarised in different reviews by Willson (2000), Woitke (2003), and Höfner (2007,2009,2005). Comparison of dynamic models with spectroscopy for C-rich stars can be found in Hron et al. (1998), Loidl et al. (2001), Gautschy-Loidl et al. (2004, henceforth GL04), Nowotny et al. (2005a,b), Nowotny (2005), and Nowotny et al. (2009).
Because of their large atmospheric extension and their high brightness in the red and infrared, AGB stars are perfect candidates for interferometric investigations. Moreover, since most observed AGB stars are very far away (at distances larger than 100 pc), only the resolution reached by optical interferometry allows a study of the close circumstellar environment of these objects.
The complex nature of their atmospheres raises the question of how a unique radius can be defined for these stars. Several radius definitions have been used, as summarised in the reviews of Baschek et al. (1991) and Scholz (2003, henceforth S03). This is not an important problem when dealing with objects that have a less extended and almost hydrostatic atmosphere, because in most cases the different definitions of radius converge to a similar final result. However, one can find large differences when the envelope of the star is affected by the phenomena of pulsation and mass loss. Baschek et al. (1991) proposed the use of the intensity radius, which is ``a monochromatic (or filter-integrated) quantity depending on wavelength or on the position and width of a specific filter''. This radius is determined from the centre-to-limb variation (CLV) as the point of inflection of the CLV curve, in other words as the point where the second derivative of the intensity profile equals zero. To determine this value, a very accurate knowledge of the CLV must, however, be available. For AGB stars, this can be difficult because the intensity profile of an evolved object can exhibit a quite complicated behaviour and only a few data points are generally measured. In the case of a poorly measured CLV, the standard procedure is to use analytical functions such as the uniform disc (UD), a fully darkened disc (FDD), or a Gaussian fit to the profile. The result of this fit is the so-called fitting radius (S03).
Various theoretical and observational studies have been completed of the different properties of the CLV and radius interpretations for M-type stars, which are summarised in the review of S03. According to this review paper, the CLV shapes can be classified into four types:
- small to moderate limb-darkening, when the behaviour of the profile is well fitted by a UD;
- the Gaussian-type CLV is typical of extended atmospheres, where there is a large difference in temperature between the cool upper atmosphere layers and the deep layers where the continuum is formed;
- the CLV with tail or protrusion-type extension consists of two components, a central part described by the CLV of a near-continuum layer, and a tail shape given by the CLV of an outer shell;
- the uncommon CLVs, which are profiles exhibiting strange behaviour that is characteristic of complex extended and cool atmospheres.
Following the definition given by Scholz & Takeda (1987), a filter radius
requires a good knowledge of the filter transmission curve, and the filter itself must be chosen carefully to avoid impure-filter-like effects (see Sect. 5 of S03 for more details). A very common definition of radius is the Rosseland radius, which corresponds to the distance between the stellar centre and the layer with Rosseland optical depth
A suitable window at 1.04 ![]() m
for determining the continuum radius of M-type stars was discussed by Scholz & Takeda (1987), Hofmann et al. (1998), Jacob & Scholz (2002), and
Tej et al. (2003b,a).
These authors defined a narrow-bandpass located in this part of the spectrum, mostly free from contamination by molecules
and lines. They indicated that this radius
is the most appropriate for studying the geometric pulsation.
Unfortunately, such a window does not exist
for C-rich AGB stars (cf. Sect. 5), and model assumptions must be
made in defining a continuum radius. On the other hand, available dynamic atmospheric models for carbon-stars (Höfner et al. 2003)
are more advanced than for M-type stars, the main reason being a clearer understanding of the dust formation.
m
for determining the continuum radius of M-type stars was discussed by Scholz & Takeda (1987), Hofmann et al. (1998), Jacob & Scholz (2002), and
Tej et al. (2003b,a).
These authors defined a narrow-bandpass located in this part of the spectrum, mostly free from contamination by molecules
and lines. They indicated that this radius
is the most appropriate for studying the geometric pulsation.
Unfortunately, such a window does not exist
for C-rich AGB stars (cf. Sect. 5), and model assumptions must be
made in defining a continuum radius. On the other hand, available dynamic atmospheric models for carbon-stars (Höfner et al. 2003)
are more advanced than for M-type stars, the main reason being a clearer understanding of the dust formation.
Following the same approach adopted for M-stars by Scholz and collaborators, we started investigating the CLV characteristics of a set of dynamic models of pulsating C-stars (Hron et al. 2008). We summarise the main properties of the intensity and visibility profiles in narrow and broad-band filters for dynamic model atmospheres with and without mass loss (Sect. 2.2). We then use the UD function to determine the UD-radius of the models, and investigate the dependence of the latter upon wavelength and pulsation phase. We also discuss a new definition of a continuum radius for the carbon stars (Sect. 5).
2 Dynamic models and interferometry
The dynamic models used in this work are described in detail in Höfner et al. (2003), GL04, and Nowotny et al. (2005a).
2.1 Overview of the dynamic models
The models are spherically symmetric and characterised
by time-dependent dynamics and frequency-dependent radiative transfer.
Assuming LTE for both gas and dust,
the radiative energy transport in the atmosphere and wind
is computed using opacity sampling in typically
50-60 wavelength points.
For the gas component, an energy equation is solved together
with the dynamics, defining the gas temperature stratification
(and allowing, in principle, for deviations from
radiative equilibrium, e.g., in strong shocks).
For the dust, on the other hand, the corresponding grain
temperature is derived by assuming radiative equilibrium.
Dust formation (in this sample only amorphous carbon dust is considered) is treated by the ``moment method'' (Gail & Sedlmayr 1988; Gauger et al. 1990), while
the stellar pulsation is simulated by a piston at the inner boundary.
Assuming a constant flux there, this leads to a sinusoidal bolometric
light curve, which can be used to assign bolometric phases to each ``snapshot''
of the model with ![]() = 0 corresponding to phases of maximum light.
= 0 corresponding to phases of maximum light.
In Table 1, the main parameters of the models used are summarised (see also GL04).
Luminosity ![]() ,
effective temperature
,
effective temperature ![]() ,
and C/O ratio refer to the initial hydrostatic model
used to start the dynamic computation.
This model can be compared with classical model atmospheres such as MARCS (Gustafsson et al. 2008). The stellar radius
,
and C/O ratio refer to the initial hydrostatic model
used to start the dynamic computation.
This model can be compared with classical model atmospheres such as MARCS (Gustafsson et al. 2008). The stellar radius ![]() of the initial hydrostatic model is derived from
of the initial hydrostatic model is derived from ![]() and
and ![]() and corresponds to the Rosseland radius.
The piston-velocity amplitude
and corresponds to the Rosseland radius.
The piston-velocity amplitude
![]() and the period P are also input parameters that control the pulsation, while
the mass-loss rate
and the period P are also input parameters that control the pulsation, while
the mass-loss rate
![]() and the mean degree of condensation
and the mean degree of condensation
![]() are the result of the dynamic computations.
The free parameter
are the result of the dynamic computations.
The free parameter
![]() is
introduced to adjust the amplitude of the luminosity variation at the inner boundary such that
is
introduced to adjust the amplitude of the luminosity variation at the inner boundary such that
![]() (GL04). All the initial models have
a mass
(GL04). All the initial models have
a mass
![]() and solar metallicity.
and solar metallicity.
Table 1: Parameters of the dynamic model atmospheres used in this work.
The models used in this work were chosen to investigate the effects of the different parameters on radius measurements, mass-loss, primarily, but also effective temperature, C/O and piston amplitude. Keeping this purpose in mind, the sample can be divided into two main groups: models with and without mass-loss (in Table 1, series D and N, respectively).
It was already mentioned that the pulsation of the inner
layers can influence the outer atmosphere of the star. The propagation of the shock waves causes a levitation of the
outer layers and in certain cases formation of dust grains can take place. The radiation pressure on the dust grains
may drive a stellar wind characterised by terminal velocities ![]() and mass-loss rates
and mass-loss rates ![]() .
In Fig. 1, an example of the radial structure of the dynamic model
atmosphere D1 (scaled to
.
In Fig. 1, an example of the radial structure of the dynamic model
atmosphere D1 (scaled to ![]() )
is plotted for different phases.
For comparison, the area covered by the model N1 is also shown grey-shaded.
In particular,
we show the effect of the dust-driven wind that appears on the model structure D1.
The different atmospheric extensions of the two models are clearly evident.
)
is plotted for different phases.
For comparison, the area covered by the model N1 is also shown grey-shaded.
In particular,
we show the effect of the dust-driven wind that appears on the model structure D1.
The different atmospheric extensions of the two models are clearly evident.
In the series D of Table 1, two models, D1 and D2, differ from the others in having a higher luminosity (![]() ).
The only distinction between these two models are different values
of the period P and the parameter
).
The only distinction between these two models are different values
of the period P and the parameter
![]() .
The effect on the structure of the atmosphere is that dust shells observed at a few
.
The effect on the structure of the atmosphere is that dust shells observed at a few ![]() are more pronounced in the case of D2.
The models D4 and D5 have the same luminosity, temperature, and period but different
piston velocities and different resulting degrees of dust condensation.
In the structure of D4, compared with D5, there is a smoother transition between the region
dominated by pulsation and the one dominated by
the dust-driven wind (see Fig. 2 of Nowotny et al. 2005a).
are more pronounced in the case of D2.
The models D4 and D5 have the same luminosity, temperature, and period but different
piston velocities and different resulting degrees of dust condensation.
In the structure of D4, compared with D5, there is a smoother transition between the region
dominated by pulsation and the one dominated by
the dust-driven wind (see Fig. 2 of Nowotny et al. 2005a).
In the N set of models, we can identify N1 on the basis of its higher temperature and lower luminosity. All the other models have the same luminosity but differ in terms of other parameters. Both N3 and N4 are examples of studying the effect of different piston velocities on models without mass-loss. The atmospheric structure of N4 is more extended but the outer layers are not yet cool and dense enough for dust formation. N2 and N3 have different C/O ratios causing differences in their spectral features and in the estimation of the diameter at certain wavelengths (Sect. 5).
We use model D1 as a reference for models with mass-loss.
GL04 compared this model with observed
spectra of the star S Cep and demonstrated that different
phases of D1 can reproduce the S Cep spectra shortward of ![]() 4
4 ![]() m.
The same model is in qualitative agreement with the observed CO and CN line-profile variations of S Cep and other
Miras (Nowotny et al. 2005a,b).
Concerning models without mass-loss, we use model N1 as a reference, which provides
the best-fit solution of spectra and colour measurements for TX Psc in GL04.
Each of these reference models also represents the most extreme case of its sub-group.
m.
The same model is in qualitative agreement with the observed CO and CN line-profile variations of S Cep and other
Miras (Nowotny et al. 2005a,b).
Concerning models without mass-loss, we use model N1 as a reference, which provides
the best-fit solution of spectra and colour measurements for TX Psc in GL04.
Each of these reference models also represents the most extreme case of its sub-group.
![\begin{figure}
\par\includegraphics[width = 8.8cm]{image/11938fg1.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg33.png) |
Figure 1: Radial structure of the dynamic model D1. Gas temperature ( upper panel) and density ( lower panel) are plotted for different phases during the pulsation period. For comparison, the grey-shaded area marks the range where the structure of the model N1 at different phases can be found. More details about the structure of the models can be found in the text and in Nowotny et al. (2005a,b). |
| Open with DEXTER | |
2.2 Synthetic intensity and visibility profiles
To compute the intensity and visibility profiles for each model we proceeded in the following way.
For a given atmospheric structure (where temperature and density
stratifications were both taken directly from the dynamical simulation),
opacities were computed
using the COMA code, originally developed by Aringer (2000):
all important species, i.e., CO, CH, C2, C3, C2H2, HCN, and CN were included.
The data sources used for the continuous opacity
were presented in Lederer & Aringer (2009). Voigt profiles were used for atomic lines,
while Doppler profiles were computed for the molecules. Conditions of LTE and a microturbulence value of
![]() were assumed.
All references to the molecular data are listed in Table 2 of Lederer & Aringer (2009). The source for the
amorphous carbon opacity is Rouleau & Martin (1991).
These input data agree with the
previous works (Nowotny 2005; Aringer et al. 2009; Lederer & Aringer 2009), and with the opacities used in computing the dynamic models.
Information about recent updates to the COMA code
and opacity data can be found in Nowotny (2005), Lederer & Aringer (2009), Aringer et al. (2009), and Nowotny et al. (2009).
The resolution of the opacity sampling adopted in our computations is 18 000.
The resulting opacities were used as input to a spherical radiative
transfer code that computes the spectrum at a selected resolution
for a chosen wavelength range. In addition, the code computes the spatial
intensity profiles for every frequency point of the calculation.
Velocity effects were not taken into account in the radiative transfer.
were assumed.
All references to the molecular data are listed in Table 2 of Lederer & Aringer (2009). The source for the
amorphous carbon opacity is Rouleau & Martin (1991).
These input data agree with the
previous works (Nowotny 2005; Aringer et al. 2009; Lederer & Aringer 2009), and with the opacities used in computing the dynamic models.
Information about recent updates to the COMA code
and opacity data can be found in Nowotny (2005), Lederer & Aringer (2009), Aringer et al. (2009), and Nowotny et al. (2009).
The resolution of the opacity sampling adopted in our computations is 18 000.
The resulting opacities were used as input to a spherical radiative
transfer code that computes the spectrum at a selected resolution
for a chosen wavelength range. In addition, the code computes the spatial
intensity profiles for every frequency point of the calculation.
Velocity effects were not taken into account in the radiative transfer.
The monochromatic spatial intensity profiles were subsequently convolved with different filter curves (narrow and broad-band) in the near- to mid-IR range to obtain averaged intensity profiles. The narrow-band filters were rectangular (transmission 1), while the broad-band filters are the standard filters from Bessel & Brett (1988). The visibility profiles were the two-dimensional Fourier transform of the intensity distribution of the object, but under the condition of spherical symmetry (as for our 1D models), this reduces to the more simple Hankel transform of the intensity profiles (e.g., Bracewell 1965).
The intensity and visibility profiles in the case of the broad-band filters were computed with the following procedure.
Each broad-band filter was divided into a set of 10 narrow-band subfilters![]() and the squared broad-band visibility was computed as
and the squared broad-band visibility was computed as
where the sum was calculated over all the narrow subfilters,
![]() is the transfer function of the broad-band filter
within the corresponding narrow-band subfilter,
Fi is the flux integrated over the corresponding narrow-band subfilter, and Vi is the visibility of the
narrow-band subfilter computed from the average intensity profile of the corresponding filters.
is the transfer function of the broad-band filter
within the corresponding narrow-band subfilter,
Fi is the flux integrated over the corresponding narrow-band subfilter, and Vi is the visibility of the
narrow-band subfilter computed from the average intensity profile of the corresponding filters.
In the following two sections, we discuss the characteristics of the intensity and visibility profiles for different models and the effects of using different filters. In the case of broad-band filter we also discuss the so-called band-width smearing effect (Kervella et al. 2003; Verhoelst 2005).
![\begin{figure}
\par\includegraphics[width = 16.cm]{image/11938fg2.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg37.png) |
Figure 2:
Synthetic spectrum (R = 360) calculated on the basis of the hydrostatic initial atmospheric structure of model D1.
All necessary opacity sources (continuous, atoms, molecules, dust) are included for the spectral synthesis, (see Fig. 4
of Aringer et al. (2009) for the individual contributions of the different molecular species).
The flux is normalised to a calculation for which only the continuous opacities were taken into account.
Overplotted are the narrow-band filters as defined in Table 2, for which the central
wavelengths in |
| Open with DEXTER | |
Table 2: Definitions of the narrow- and broad-band filters.
3 Synthetic profiles for narrow-band filters
Twenty-one narrow-band filters were defined in the near-to mid-IR range
with a ``resolution'' ranging from 50 to 200
to study effects of different molecular features characteristic for C-star spectra,
following the approach described in Bessel et al. (1996,1989).
Figure 2 shows the location of the filters on top of a typical synthetic (continuum-normalised)
spectrum of a C-type star for illustration. Table 2 gives an overview of our complete set
of filters with name of the bands, characteristic features (for narrow-bands), central wavelengths, band widths, and
morphological class.
A few of these filters are labelled ``cont'' meaning that the contamination by molecular features
is comparably low in this spectral region, but this does not necessarily represent the true continuum.
At extremely high spectral resolutions, it may be possible to identify
very narrow windows in the spectrum of a C-star, where no molecular lines are located (e.g., Fig. 6 in Nowotny et al. 2005b).
However, in general and at the resolutions available nowadays, the observed spectra of evolved C-type stars in the visual
and IR are crowded with absorption features. Because of this blending, the continuum level F/
![]() is never reached as in Fig. 2. This effect is more and more pronounced with lower effective
temperatures and decreasing spectral resolutions (cf. Nowotny et al. 2009).
is never reached as in Fig. 2. This effect is more and more pronounced with lower effective
temperatures and decreasing spectral resolutions (cf. Nowotny et al. 2009).
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width = 8.8cm]{image/119...
... \includegraphics[width = 8.8cm]{image/11938fg4.ps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg42.png) |
Figure 3:
Intensity and visibility profiles for the narrow-band filters at the maximum phase of
the mass-loss model D1 on the left side, and the model without mass-loss N1
on the right side. All the opacities are included in the computations.
Profiles for three representative filters are shown together with
the equivalent UD function for the 3.175 |
| Open with DEXTER | |
As a first step, we study the morphology of different intensity and visibility profiles. We then proceed to investigate the main opacity contributors to the features that appear in the profiles. For this purpose, we compute three different sets of intensity and visibility profiles for the two reference models: (i) profiles including all necessary opacity sources, i.e., continuous, atomic, molecular, and dust opacities; (ii) profiles where the opacities of dust were neglected, to analyse only molecular and atomic contributions; and (iii) profiles for which only the continuous gas opacity is considered, to derive theoretical continuum profiles.
For the narrow-band filters, the intensity profiles of models with mass-loss can be divided into three
morphological classes listed in the last column of Table 2. It turns out that this classification
is related mainly
to the wavelength region with the exception of the filter ![]() m, which belongs to the third class (that contains filters
centred around
m, which belongs to the third class (that contains filters
centred around ![]() m) instead of the second (that contains all the other filters in the
m) instead of the second (that contains all the other filters in the ![]() m region, plus the 9 and 11
m region, plus the 9 and 11 ![]() m
filters).
In Fig. 3, the intensity and visibility profiles for the representative filters of each class are illustrated.
Models with mass-loss (left panels)
are more extended than models without mass-loss (right), and their intensity profiles fit
into the category of ``uncommon profiles'' of S03.
m
filters).
In Fig. 3, the intensity and visibility profiles for the representative filters of each class are illustrated.
Models with mass-loss (left panels)
are more extended than models without mass-loss (right), and their intensity profiles fit
into the category of ``uncommon profiles'' of S03.
The first class of profiles contains the filters
in the near IR from ![]() m to
m to
![]() m.
It can be well represented by filter 1.53 (C2H2, HCN, CN).
Its morphology is characterised first by a limb-darkened disc,
followed by a bump caused by molecular contributions, and a peak indicating the inner radius of the dust shell.
At 1.53
m.
It can be well represented by filter 1.53 (C2H2, HCN, CN).
Its morphology is characterised first by a limb-darkened disc,
followed by a bump caused by molecular contributions, and a peak indicating the inner radius of the dust shell.
At 1.53 ![]() m, a feature due to
the molecular species of C2H2 and HCN
is predicted by some of the cool dynamic models with a wind (GL04). This feature
was observed in the spectra of cool C-rich Miras, such as R Lep (Lançon et al. 2000),
V Cyg, cya 41 (faint Cygnus field star), and
some other faint high-Galactic-latitude carbon stars (Joyce 1998).
m, a feature due to
the molecular species of C2H2 and HCN
is predicted by some of the cool dynamic models with a wind (GL04). This feature
was observed in the spectra of cool C-rich Miras, such as R Lep (Lançon et al. 2000),
V Cyg, cya 41 (faint Cygnus field star), and
some other faint high-Galactic-latitude carbon stars (Joyce 1998).
The third class of profiles is represented by filter 3.175 (C2H2, HCN),
which is placed right in the centre of an extremely strong
absorption feature characteristic of C-star spectra (Fig. 2). Observations in this spectral region
are a very powerful tool in understanding the upper photosphere.
Here, the inner central part of the intensity profile can be described by
an extended plateau due to the strong molecular opacity. All the filters defined around 12 ![]() m
- where C2H2 has an enhanced absorption -
also belong to this class.
m
- where C2H2 has an enhanced absorption -
also belong to this class.
The second class of profiles has a behaviour in-between that of the two
illustrated before with an indication of an outer dust shell around 8 AU.
It is represented by filter 9.975 (``cont'') and covers the behaviour of
the filter at
![]() m plus those defined in the 3
m plus those defined in the 3 ![]() m region (except 3.175
m region (except 3.175 ![]() m).
m).
In Fourier space, the three representative visibility profiles also differ markedly (lower left panel of Fig. 3).
The UD function, computed by fitting the point at
visibility![]() V= 0.3 of the 3.175
V= 0.3 of the 3.175 ![]() m
profile (for details, see Sect. 5), is shown for comparison
in Fig. 3. The visibility profiles from the model and the UD differ
at visibility <0.2, and in this region the model
profile is less steep and has a less pronounced second lobe compared with the UD.
m
profile (for details, see Sect. 5), is shown for comparison
in Fig. 3. The visibility profiles from the model and the UD differ
at visibility <0.2, and in this region the model
profile is less steep and has a less pronounced second lobe compared with the UD.
In the right panel of Fig. 3 we present the intensity and visibility profiles for the phase of maximum luminosity
of the reference model without mass-loss. As expected from the model structures, the intensity profiles
are more compact than those for models with mass-loss. In the intensity profile corresponding to the filter 9.975 around
![]() ,
a peak related to the molecular opacity of C3 is visible.
Jørgensen et al. (2000) showed that C3 is particularly sensitive to the
temperature-pressure structure and, hence, tends to be found in narrower regions than other molecules.
The peak visible at 3 AU of the profile of the model D1 is produced mainly by C3 but
also produce other molecular and dust opacity contributions.
These
,
a peak related to the molecular opacity of C3 is visible.
Jørgensen et al. (2000) showed that C3 is particularly sensitive to the
temperature-pressure structure and, hence, tends to be found in narrower regions than other molecules.
The peak visible at 3 AU of the profile of the model D1 is produced mainly by C3 but
also produce other molecular and dust opacity contributions.
These ![]() m peaks in the intensity profiles mean a marginally ``ring''-type appearance of the disc.
The shape of the intensity profiles for the models without mass-loss can be classified
as having small to moderate limb-darkening (S03).
In the Fourier space, the visibility profiles of the three filters for the series N look very similar, apart from tiny
differences especially in the second lobe. In all cases, they can be approximated well
by a UD in the first lobe.
m peaks in the intensity profiles mean a marginally ``ring''-type appearance of the disc.
The shape of the intensity profiles for the models without mass-loss can be classified
as having small to moderate limb-darkening (S03).
In the Fourier space, the visibility profiles of the three filters for the series N look very similar, apart from tiny
differences especially in the second lobe. In all cases, they can be approximated well
by a UD in the first lobe.
Plots of theoretical continuum profiles for both reference models are very similar to UDs. The classification of filters is also valid for all other models in our sample listed in Table 1.
![\begin{figure}
\par\begin{tabular}{c c}
\includegraphics[width = 8.8 cm]{image/...
...\includegraphics[width = 8.8 cm]{image/11938fg6.ps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg51.png) |
Figure 4: Visibility profiles computed in broad-band filters for the maximum phase of the model D1 with mass-loss on the left side, and the model N1 without mass-loss on the right side. The solid line corresponds to the model, while the dashed line is the equivalent UD computed by fitting one point at visibility V = 0.3. |
| Open with DEXTER | |
4 Synthetic profiles for broad-band filters
We also investigated intensity and visibility profiles for
the broad-band filters J, H, K, and ![]() ,
because several
observations of C-stars exist in these filters.
,
because several
observations of C-stars exist in these filters.
In Fig. 4, the resulting broad-band visibility profiles computed for the maximum
phase of the reference models are shown together with the corresponding UD visibility,
which was calculated with the one-point-fit method at V = 0.3.
In the case of model D1 (with mass-loss), the broad-band profiles exhibit a completely different behaviour from that of the UD.
The slopes of the model profiles are always less steep than the corresponding UD at ![]() .
The synthetic visibility profile shows a characteristic tail-shape instead of the clearly pronounced second lobe in the UD.
The broad-band visibilities for the model N1 are represented well by a UD and, as in the case of the narrow-bands,
the major (but small) differences occur in the second lobe of the profiles.
.
The synthetic visibility profile shows a characteristic tail-shape instead of the clearly pronounced second lobe in the UD.
The broad-band visibilities for the model N1 are represented well by a UD and, as in the case of the narrow-bands,
the major (but small) differences occur in the second lobe of the profiles.
When comparing observations with in a broad-band filter, particular attention must be paid to the
smearing effect (also known as bandwidth smearing) affecting the measurements (Verhoelst 2005; Kervella et al. 2003; Davis et al. 2000).
This is the chromatic aberration caused by observations never being monochromatic
but integrated over a certain wavelength range defined by the broad-band filter curve.
Furthermore, each physical baseline, B, corresponds to a different spatial frequency u
with
![]() .
Calculated at a given projected baseline, a broad-band visibility will result in a
superposition of all the monochromatic profiles over the width of the band.
.
Calculated at a given projected baseline, a broad-band visibility will result in a
superposition of all the monochromatic profiles over the width of the band.
According to Kervella et al. (2003) and Wittkowski et al. (2004), the bandwidth smearing is stronger at low visibilities close to the first zero of the visibility profile. We demonstrated that the shape of the profile also plays an important role in the smearing effect.
We investigated this effect with the help of our reference models in the J, H, K, and
![]() filters.
As explained in Sect. 2.2, the broad-band profile was computed by dividing the broad-band interval into ten
narrow-band subfilters
and then averaging the resulting profiles. To take into account the bandwidth smearing, we again divided the broad-band
interval into the same set of 10 narrow-band subfilters.
The spatial frequencies were then converted from AU-1 to baselines
in meters, fixing the distance for an hypothetical object (500 pc)
and using as corresponding ``monochromatic wavelength'' the respective central wavelength of the narrow-band filter.
The resulting broad-band profile was then obtained using the above Eq. (2).
filters.
As explained in Sect. 2.2, the broad-band profile was computed by dividing the broad-band interval into ten
narrow-band subfilters
and then averaging the resulting profiles. To take into account the bandwidth smearing, we again divided the broad-band
interval into the same set of 10 narrow-band subfilters.
The spatial frequencies were then converted from AU-1 to baselines
in meters, fixing the distance for an hypothetical object (500 pc)
and using as corresponding ``monochromatic wavelength'' the respective central wavelength of the narrow-band filter.
The resulting broad-band profile was then obtained using the above Eq. (2).
Figure 5 illustrates the bandwidth-smearing effect in the K band for the
two reference model atmospheres (D1 on the left and N1 on the right).
In the upper panels, it is clearly visible in the upper panels that the profiles of the
narrow-band subfilters reach the first zero at different baselines.
The bandwidth-smearing causes the broad-band profile to never reach zero, as noted in
Kervella et al. (2003). We compared the resulting visibility curve with a corresponding one
obtained without taking into account the bandwidth effect. The result of this experiment can be seen in the
lower panels of Fig. 5, where
we plot the difference (in percentage) between the visibility with and without
taking into account the bandwidth smearing (BW and NBW respectively).
For both types of models - with and without mass-loss -
the smearing accounts for the differences in the profiles, which at certain baselines reaches more than ![]() .
For model N1,
the major difference occurs close to the first and the second zero and is negligible elsewhere
(as already shown in Wittkowski et al. 2004; Kervella et al. 2003), while in the case of the model D1 the behaviour of the relative difference
is less obvious.
This result is also confirmed for the other broad-band profiles.
However, it obviously depends on the shape of the visibility profile and hence on the model.
.
For model N1,
the major difference occurs close to the first and the second zero and is negligible elsewhere
(as already shown in Wittkowski et al. 2004; Kervella et al. 2003), while in the case of the model D1 the behaviour of the relative difference
is less obvious.
This result is also confirmed for the other broad-band profiles.
However, it obviously depends on the shape of the visibility profile and hence on the model.
In all the cases, we conclude it is important to compute accurate profiles by taking into account the bandwidth smearing.
![\begin{figure}
\par\begin{tabular}{c c}
\includegraphics[angle = 90, width = 8...
...s[angle = 90, width = 8.6cm]{image/11938f10.ps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg55.png) |
Figure 5: Representation of the bandwidth smearing effect for the phase maximum of the model D1 ( left panels) and N1 ( right panels) in the K-band. In the upper panels, visibility profiles are shown as a function of baseline for the individual narrow-band subfilters (dotted lines) and for the resulting broad-band filter (solid line), computed by taking into account the bandwidth smearing. In the inset, a zoom of the region around the first zero is represented. The lower panels show the visibility profiles computed with bandwidth smearing (BW, solid line), and profiles computed neglecting the effect (NBW, dotted line). The dashed lines present the difference between the two profiles (scale on the right y-axis). |
| Open with DEXTER | |
5 Uniform disc (UD) diameters
For all models in the sample and all considered filters, we computed the equivalent UD-radii using three different methods: (i) a single-point fit at visibility V= 0.3; (ii) a two-point fit at visibilities V= 0.1 and 0.4; and (iii) finally a non-linear least squares fit using a Levenberg-Marquardt algorithm method, and taking into account all the points with visibility V > 0.1. As emphasised in Sect. 5 of Ireland et al. (2004a), none of these procedures are fully consistent because the UD does not represent the true shape of the profile (especially in the case of models with mass-loss). However, the UD is often chosen to interpret interferometric data with a small sampling of the visibility curve. Thus, the three different methods were used in this work to investigate the influence of the visibility profile sampling, in particular when only a few visibility measurements are available. We used the visibility V = 0.3 for the one-point-fit following Ireland et al. (2004a,b), who identified this point as a good estimator of the object size. While this is true for the M-type models presented in Ireland et al. (2004a,b), it is not obvious for our C-rich models with mass-loss, which are very far from exhibiting a UD behaviour (Sect. 3). However, keeping in mind that a UD is a first approximation, we also used this value for our computations of the one-point fit.
The aim of this section is to study the behaviour of the UD-radius versus both wavelength and phase, as well as the dependence on the different parameters of the models.
As we pointed out previously, while for the M-type stars the continuum
radius can be measured around 1.04 ![]() m (e.g. Jacob & Scholz 2002),
our calculations show that the C-star spectra do not contain any suitable window for this determination.
However, the continuum radius is a relevant quantity to modelling the stellar interior and pulsation.
Therefore, we computed for our sample of dynamic model atmospheres
a set of profiles by taking into account only the continuous gas opacity.
The resulting profiles correspond to the pure theoretical continuum absorption
of the models.
An equivalent UD-continuum radius was computed for
this theoretical ``pure-continuum'' profile. This allows us to study how the
UD-continuum radius depends upon wavelength and phase and
may provide a possibility of converting observed radii into the continuum radius.
m (e.g. Jacob & Scholz 2002),
our calculations show that the C-star spectra do not contain any suitable window for this determination.
However, the continuum radius is a relevant quantity to modelling the stellar interior and pulsation.
Therefore, we computed for our sample of dynamic model atmospheres
a set of profiles by taking into account only the continuous gas opacity.
The resulting profiles correspond to the pure theoretical continuum absorption
of the models.
An equivalent UD-continuum radius was computed for
this theoretical ``pure-continuum'' profile. This allows us to study how the
UD-continuum radius depends upon wavelength and phase and
may provide a possibility of converting observed radii into the continuum radius.
5.1 Uniform disc radii as a function of wavelength
The UD-radii resulting from least square fits at the maximum phase
of all models are plotted versus wavelength in Fig. 6.
They are scaled to ![]() to minimise the effects of the initial stellar parameters and enhance the effects of the dynamics and dust formation.
The UD-continuum radii are represented with the cross symbols
for D1 (upper panel) and N1 (lower panel).
The major difference is found between models with and without mass-loss.
In both cases, the UD-radius generally increases with wavelength, but this
behaviour is more pronounced for mass-loss models.
At 3.175
to minimise the effects of the initial stellar parameters and enhance the effects of the dynamics and dust formation.
The UD-continuum radii are represented with the cross symbols
for D1 (upper panel) and N1 (lower panel).
The major difference is found between models with and without mass-loss.
In both cases, the UD-radius generally increases with wavelength, but this
behaviour is more pronounced for mass-loss models.
At 3.175 ![]() m, there is a notable ``discontinuity''
(value significantly higher than its surroundings) in the UD-radius due to the high C2H2 opacity.
The UD-continuum radius is almost completely independent of wavelength and
can thus be adopted as a good reference radius (although it is not observable for C-stars!).
In fact, a small increase in its size can hardly be noted at longer wavelengths
(see Fig. 6), and at
m, there is a notable ``discontinuity''
(value significantly higher than its surroundings) in the UD-radius due to the high C2H2 opacity.
The UD-continuum radius is almost completely independent of wavelength and
can thus be adopted as a good reference radius (although it is not observable for C-stars!).
In fact, a small increase in its size can hardly be noted at longer wavelengths
(see Fig. 6), and at ![]() m the minimum opacity of H- is visible.
The ratio of the apparent size of the continuum radius at 11
m the minimum opacity of H- is visible.
The ratio of the apparent size of the continuum radius at 11 ![]() m to that
at 2.2
m to that
at 2.2 ![]() m is 1.14 in the case of the model with mass-loss D1
and 1.06 for the model without mass-loss
N1. This change in apparent size
can be explained by the electron-hydrogen continuum, according to Tatebe & Townes (2006).
All the models show a value of UD-continuum radius that is lower than the stellar radius
m is 1.14 in the case of the model with mass-loss D1
and 1.06 for the model without mass-loss
N1. This change in apparent size
can be explained by the electron-hydrogen continuum, according to Tatebe & Townes (2006).
All the models show a value of UD-continuum radius that is lower than the stellar radius ![]() .
This is a consequence of the definition
of
.
This is a consequence of the definition
of ![]() .
.
![\begin{figure}
\par\includegraphics[angle = 90, width = 9cm]{image/11938f11.ps}\\
\includegraphics[angle = 90, width = 9cm]{image/11938f12.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg57.png) |
Figure 6: UD-radii versus wavelength for the maximum phase of different models with ( upper panel) and without ( lower panel) mass-loss. The cross symbol represents the UD-continuum radius computed for the two reference models (D1, N1). The method used for the UD determination is a least squares fit using all the points of the synthetic profile with visibility >0.1. |
| Open with DEXTER | |
On the other hand, in the absence of dusty winds the models with the same parameters except for C/O
(N2 versus N3) have very similar radii.
The difference is barely detectable at 3 ![]() m
and at longer wavelengths.
If, besides different C/O ratios, the temperature of the model also changes (e.g., as between N4 and N5),
the resulting UD-radii show more pronounced differences.
The UD-radii of N1 always overlap with that of N2,
even if the models have different temperatures (higher for N1), luminosity
(higher for N2), and period (longer for N2).
N3 and N4 have all the same parameters except for the piston velocity, and the resulting UD-radii is
larger for the second model, which has a higher value of
m
and at longer wavelengths.
If, besides different C/O ratios, the temperature of the model also changes (e.g., as between N4 and N5),
the resulting UD-radii show more pronounced differences.
The UD-radii of N1 always overlap with that of N2,
even if the models have different temperatures (higher for N1), luminosity
(higher for N2), and period (longer for N2).
N3 and N4 have all the same parameters except for the piston velocity, and the resulting UD-radii is
larger for the second model, which has a higher value of
![]() .
Model N4 is also the most extended among its subgroup.
.
Model N4 is also the most extended among its subgroup.
5.2 Separating models observationally
Compared with classical hydrostatic models, the dynamic model atmospheres provide, a self-consistent treatment of time-dependent phenomena (shock propagation, stellar wind, dust formation). It is thus of course highly interesting if observed UD-radii at different wavelengths can be used to distinguish between the different models and then assign a given model to a given star.
If the model UD-radii are not scaled to their respective ![]() ,
the D models differ between
,
the D models differ between ![]() and
and ![]() .
These
differences should be detectable given the typical distance uncertainties of
.
These
differences should be detectable given the typical distance uncertainties of ![]() .
However, as discussed above, this would mostly
separate the effects of the fundamental stellar parameters (initial radius, luminosity) and allows to differentiate
between N and D models,
but dynamic effects within each series are only of the order of
between
.
However, as discussed above, this would mostly
separate the effects of the fundamental stellar parameters (initial radius, luminosity) and allows to differentiate
between N and D models,
but dynamic effects within each series are only of the order of
between ![]() and
and ![]() .
This can be seen
in Fig. 6 or
if one scales each model to e.g., its UD-radius in the K-band. The latter approach would be the most sensitive since it eliminates
errors in the distance (provided the measurements were completed at the same pulsating phase, better within the same pulsation cycle).
Assuming that individual UD-radii can be determined with an accuracy between
.
This can be seen
in Fig. 6 or
if one scales each model to e.g., its UD-radius in the K-band. The latter approach would be the most sensitive since it eliminates
errors in the distance (provided the measurements were completed at the same pulsating phase, better within the same pulsation cycle).
Assuming that individual UD-radii can be determined with an accuracy between ![]() and
and ![]() ,
the dynamic effects
are (barely) identifiable in the D models. The most sensitive wavelengths in this respect would be
filters in the K- and L-band. The N-band shows a similar sensitivity to dynamic effects, although
at a reduced observational accuracy.
For the N models, these effects are less then 10%, the largest difference again occurring redward of the K-band.
Nevertheless, the optimal strategy for choosing the correct dynamic model is to combine spectroscopic
and interferometric observations.
,
the dynamic effects
are (barely) identifiable in the D models. The most sensitive wavelengths in this respect would be
filters in the K- and L-band. The N-band shows a similar sensitivity to dynamic effects, although
at a reduced observational accuracy.
For the N models, these effects are less then 10%, the largest difference again occurring redward of the K-band.
Nevertheless, the optimal strategy for choosing the correct dynamic model is to combine spectroscopic
and interferometric observations.
Finally, we note, that for a larger grid of models (e.g., Mattsson et al. 2009), a wider separation of models might become evident. This will however be the subject of a future paper.
![\begin{figure}
\par\includegraphics[angle = 90,width = 17cm]{image/11938f13.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg64.png) |
Figure 7: UD-radii versus phase are shown for three different narrow-band filters. The three upper panels represent results for the dynamic model D1 with mass-loss, the three panels at the bottom being for the model N1 without mass-loss. Triangles are for UD-radius computed by taking into account only continuum opacity. For the continuum, the same symbol is used for the different methods because there is no appreciable difference between the results. Crosses, stars, and diamonds represent the different methods (one point, two points, least squares, respectively) used for fitting the visibility profiles of models with UDs. |
| Open with DEXTER | |
5.3 UD-radii as a function of time
The behaviour of the UD-radius as a function of phase predicted by the models is rather complex, especially in the case of mass-losing models. In Fig. 7, the UD-radius at a given wavelength/filter versus phase is plotted for the two reference models. The presence of molecular and dust opacities increases the UD-radius significantly compared to the UD-continuum radius. In both types of models, we can observe the periodic movement in the stellar interior, which is pronounced to a different degree for different models of Table 1. The periodic variation in the UD-radius in all the models without mass-loss reflects how the movement of the complete atmosphere closely follows the pulsation. The time scales introduced by dust formation in the atmosphere of the models with mass-loss may deform the sinusoidal pattern, a behaviour that can be reproduced by outer layers that do not move parallel to the inner ones. This is represented well in Fig. 2 of Höfner et al. (2003), but one should keep in mind that the movement of theoretical mass shells should not be directly compared to the changes in the atmospheric radius-density structure that we observe by interferometric measurements.
From the lower three panels of Fig. 7
(no mass-loss), it is obvious that there is no significant difference between the UD-radius
and UD-continuum radius for the model N1, especially for the 1.53 ![]() m and 9.975
m and 9.975 ![]() m filter
close to minimum luminosity. We find the largest difference for the maximum luminosity (
m filter
close to minimum luminosity. We find the largest difference for the maximum luminosity (![]() ),
where the ratio of the UD-radius to the UD-continuum radius is 1.09 for the filter 3.175
),
where the ratio of the UD-radius to the UD-continuum radius is 1.09 for the filter 3.175 ![]() m
and 1.04 for the other two filters.
For the model D1 (upper panels), the value of the same ratio is
3.03 for the filter 1.53
m
and 1.04 for the other two filters.
For the model D1 (upper panels), the value of the same ratio is
3.03 for the filter 1.53 ![]() m, 4.29 for 3.175
m, 4.29 for 3.175 ![]() m, and
4.12
for 9.975
m, and
4.12
for 9.975 ![]() m, much higher than the values found for the models without mass-loss.
m, much higher than the values found for the models without mass-loss.
The three different fitting methods
provide mostly the same result in the case of the model without mass-loss,
while in the case of models with mass-loss, the UD-radius is smaller for the
first 2 methods (one- and two-points fit) than for the
least squares result.
This last result can be explained by going back to our initial classification of profiles (Sect. 3).
The first and third class of profiles belong to the ``uncommon'' profiles of S03, which cannot be approximated by UD functions.
The third class of profiles (9.975 ![]() m) in particular
deviates the most from a UD (see Fig. 3).
m) in particular
deviates the most from a UD (see Fig. 3).
Even after increasing the number of fitting points, the resulting UD-radius cannot be considered reliable because of the particular shape of the profiles. From Fig. 7, for the narrow-filter it is also clear that it is impossible to define a single, phase-independent scaling factor that enables the UD-radii to be converted to the UD-continuum radii.
![\begin{figure}
\par\includegraphics[angle = 90,width = 16cm]{image/11938f14.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg66.png) |
Figure 8:
UD-radius versus phase for
|
| Open with DEXTER | |
We also computed the equivalent UD-radii and UD-continuum radii for the broad-band filters.
The results are shown in Fig. 8.
The broad-band has the effect of smoothing the visibility profile as
can be inferred in the UD-radii behaviour versus phase from the smaller amplitude of the radius variation.
As for the narrow-band, in the case of broad-band filters
the UD-radius versus phase for the set of models D also shows a behaviour
that is not synchronised with the pulsation.
The ratio of the UD-radius to UD-continuum radius is not constant with phase and/or with wavelength.
For the phase zero, it corresponds to 2.08 in J,
2.83 in H, 2.14 in K, and 2.54
in ![]() band.
In the lower panels of Fig. 8, where the model N1 is represented, the resulting UD-radius
is always closer to the UD-continuum radius. The ratio of the UD-radius to the UD-continuum radius for the phase zero is
almost constant: 1.03 for J and H, 1.04 for K and
band.
In the lower panels of Fig. 8, where the model N1 is represented, the resulting UD-radius
is always closer to the UD-continuum radius. The ratio of the UD-radius to the UD-continuum radius for the phase zero is
almost constant: 1.03 for J and H, 1.04 for K and ![]() .
Again, the amplitudes of variation in the radius for the N models are smaller than for the narrow-band filters, and
the variation follows the near-sinusoidal behaviour of the inner layers.
.
Again, the amplitudes of variation in the radius for the N models are smaller than for the narrow-band filters, and
the variation follows the near-sinusoidal behaviour of the inner layers.
For the broad-band filters, the difference in the fitting methods confirms the trend found for the narrow-band case. For the models with mass-loss, the one-point and two-points fit methods produce smaller UD-radii than those produced by the least squares method. The UD-radii, resulting from different methods, agree closely in the case of models without mass-loss and the same result is also obtained for all the UD-continuum measurements.
The dependence of UD-radius on the pulsation cycle is not covered by this contribution, and it will be topic of a future contribution.
5.4 Comparison with M-type stars
Compared to the M-type stars,
for the C-stars we emphasise the lack of a spectral window for measuring a pure continuum radius.
A model-dependent definition of the continuum radius is thus needed for the cool carbon stars.
In Ireland et al. (2004a), the phase variation in filter radii in units of the parent star radius Rp![]() is represented for different near-continuum narrow and broad-band filters.
They demonstrate how measurements of radii in near-continuum band passes are affected by
molecular contaminations that mask the geometrical pulsation. This contamination is
negligible only close
to the visual maximum. Other suitable band passes for measuring the pulsation of the continuum layers
for M-type stars are the broad-band filters J and H, or the sub-bandpasses of H and K.
is represented for different near-continuum narrow and broad-band filters.
They demonstrate how measurements of radii in near-continuum band passes are affected by
molecular contaminations that mask the geometrical pulsation. This contamination is
negligible only close
to the visual maximum. Other suitable band passes for measuring the pulsation of the continuum layers
for M-type stars are the broad-band filters J and H, or the sub-bandpasses of H and K.
It is difficult to complete a consistent comparison between the UD-radii computed in this work for C-stars
and the resulting UD-radii of Jacob & Scholz (2002)
for M-type stars because of the intrinsic differences between the modelling approaches,
and because of the different stellar
parameters. However as a general statement we can say that the ratios of UD-radii to UD-continuum that we obtain
are systematically larger for our models with mass-loss than those presented for M-type stars in Figs. 4
and 5 of Ireland et al. (2004a).
More comparable are the resulting ratios for models without mass-loss.
The largest difference is caused by the strong molecular (first of all C2H2) and dust opacities
that characterise the C-star spectra.
The UD-radius increases with wavelength and in the case of carbon-rich model atmospheres with mass-loss,
this increase is larger than that found by Jacob & Scholz (2002) for M-type stars.
In particular, the ratio of the UD-radius in J to the UD-radius
in ![]() for our model D1 at phase zero is 2.07, while for the M-type models presented in Fig. 4 and Fig. 5 of Jacob & Scholz (2002), it is 1.4
in the case of largest discrepancy (phase 1.5).
The same ratio for our N1 model is 1.03, meaning that this model
without mass-loss shows an increase in the UD-radius with wavelength
lower than that of the M-type stars.
for our model D1 at phase zero is 2.07, while for the M-type models presented in Fig. 4 and Fig. 5 of Jacob & Scholz (2002), it is 1.4
in the case of largest discrepancy (phase 1.5).
The same ratio for our N1 model is 1.03, meaning that this model
without mass-loss shows an increase in the UD-radius with wavelength
lower than that of the M-type stars.
![\begin{figure}
\par\includegraphics[angle = 90,width = 17.3cm]{image/11938f15.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg67.png) |
Figure 9:
UD-Radius versus phase for
|
| Open with DEXTER | |
6 Conclusions
We have presented, for the first time, a theoretical study of the intensity and visibility profiles computed for a set of dynamic model atmospheres of C-rich AGB stars. The main results of our investigation can be summarised as follows:- The profiles computed in the narrow-band filters for our set of models can be divided into 3 morphological classes
mainly according to wavelength region, with the exception of the filter located at 3.175
 m
in the middle of a strong absorption feature characteristic of C-star spectra.
This filter shows a behaviour
more closely related to one of the narrow-band filters in the region around 12
m
in the middle of a strong absorption feature characteristic of C-star spectra.
This filter shows a behaviour
more closely related to one of the narrow-band filters in the region around 12  m
than to the surrounding wavelength range.
We have chosen three filters to represent the morphology of intensity and visibility profiles: 1.53, 9.975, and
m
than to the surrounding wavelength range.
We have chosen three filters to represent the morphology of intensity and visibility profiles: 1.53, 9.975, and 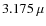 m,
for the first, second, and third class, respectively.
The intensity profile of the first class is characterised by a limb-darkened disc
followed by a tail-shape with a bump and a peak.
The 3.175-like profiles show an extended plateau due to strong molecular opacity.
The second class is intermediate between the other two.
m,
for the first, second, and third class, respectively.
The intensity profile of the first class is characterised by a limb-darkened disc
followed by a tail-shape with a bump and a peak.
The 3.175-like profiles show an extended plateau due to strong molecular opacity.
The second class is intermediate between the other two.
- The morphology of the profiles (narrow and broad-band) of models with mass-loss is very far from the UD shape. Models without mass-loss, and all theoretical continuum profiles can be approximated quite well by a UD.
- Bandwidth smearing affects the resulting broad-band profiles with an error of about 70% for certain baselines. For models with mass-loss, the difference is notable not only close to the first zero but also on the flank of the first lobe of the visibility profile. When comparing models with observations in broad-band, it is important to take this effect properly into account.
- C-star UD-radii are wavelength-dependent.
The dependency is stronger in the case of models with mass-loss, in this case the UD-radii
also exhibit significant large phase dependence.
Around
 m and in the N-band, the star appears more extended because of C2H2 opacity.
The UD-continuum radius is mostly independent
of the wavelength and phase.
m and in the N-band, the star appears more extended because of C2H2 opacity.
The UD-continuum radius is mostly independent
of the wavelength and phase.
- The extensions of the models increase for higher mass-loss rates and lower temperatures.
- Models with mass-loss show a complicated behaviour of the UD-radius versus phase compared to models without mass-loss. This behaviour is not dependent on the pulsation of the interior.
- Using only one or two points of visibility to determine the UD-radii of objects characterised by strong pulsation and mass-loss,it is shown that the radius of the star is smaller than the one measured using more points (least squares method). In the case of models without mass-loss, the different methods of fitting yield the same UD-radii.
- The UD-radius is very close to the UD-continuum radius in the case of models without mass-loss.
- The trend of the UD-radii versus phase in broad-band is smoother than in the case of the narrow-band filters.
- In contrast to O-rich stars, for C-rich stars no spectral windows for observing the continuum radius are available in the case of C-stars, and some assumptions based on models are necessary. A useful replacement for a measured continuum radius is the UD-continuum radius defined in Sect. 5, which is basically independent of wavelength and pulsation phase.
- The difference in the UD-radii between the models should be detectable observationally, in particular in the L-band where MATISSE (Lopez et al. 2006) will provide new observational opportunities.
- The radius computed with the UD function must be considered only as a first guess of the true size of the star.
The intensity and visibility profiles of a C-star, especially in the case of models producing mass-loss,
are very far from being UD-like.
Acknowledgements
This work has been supported by Projects P19503-N16 and P18939-N16 of the Austrian Science Fund (FWF). It is a pleasure to thank T. Verhoelst and T. Driebe for many helpful comments and suggestions. BA acknowledges funding by the contract ASI-INAF I/016/07/0.
References
- Aringer, B. 2000, Ph.D. Thesis, University of Vienna (In the text)
- Aringer, B., Nowotny, W., & Höfner, S. 2008, Perspective in Radiative Transfer and Interferometry, ed. S. Wolf, F. Allard, & Ph. Stee, EAS Publ. Ser., 28, 67 (In the text)
- Aringer, B., Girardi, L., Nowotny, W., et al. 2009, A&A, accepted
- Baschek, B., Scholz, M., & Wehrse, R. 1991, A&A, 246,374 (In the text)
- Bessel, M. S., & Brett, J. M. 1988, PASP100, 1134 (In the text)
- Bessel, M. S., Brett, J. M., Scholz, M., & Wood, P. R. 1989, A&A, 213, 209 [NASA ADS]
- Bessel, M. S., Scholz, M., & Wood, P. R. 1996, A&A, 307, 481 [NASA ADS]
- Bracewell, R. N. 1965, The Fourier Transform and its Applications (New York: McGraw-Hill) (In the text)
- Davis, J., Tango, W. J., & Booth, A. J. 2000, MNRAS, 318, 387 [NASA ADS] [CrossRef]
- Gail, H. P., & Sedlmayr, E. 1988, A&A, 206, 153 [NASA ADS]
- Gauger, A., Gail., H. P., & Sedlmayr, E. 1990, A&A, 235, 245
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] (GL04) (In the text)
- Goebel, J. H., Bregman, J. D., Wittenborn, F. C., & Taylor, B. J. 1981, ApJ, 246, 455 [NASA ADS] [CrossRef]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hofmann, K.-H., Scholz, M., & Wood, P. R. 1998, A&A, 339, 846 [NASA ADS] (In the text)
- Höfner, S., Gautschy-Loidl, R., Aringer, B., & Jørgensen, U. G. 2003, A&A, 399, 589 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Höfner, S. 2005, 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, ed. F. Favata, G. A. J. Hussian, & B. Battrick, ESA SP-560, 335
- Höfner, S. 2007, Why Galaxies Care About AGB Stars, ed. F. Kerschbaum, C. Charbonnel, & R. F. Wing, ASP Conf. Ser., 378, 145
- Höfner, S. 2009, Cosmic Dust - Near and Far, ed. Th. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., in press [arXiv:0903.5280]
- Hron, J., Loidl, R., & Höfner, S., et al. 1998, A&A, 335, L69 [NASA ADS] (In the text)
- Hron, J., Aringer, B., Nowotny, W., & Paladini, C. 2008, Evolution and Nucleosynthesis in AGB stars, ed. Guandalini, R., Palmerini, S., & Busso, M., AIP Conf. Proc., 1001, 185 (In the text)
- Hughes, S. M. G., & Wood, P. R. 1990,A&A, 99, 784
- Jacob, A. P., & Scholz, M. 2002, MNRAS, 336, 1377 [NASA ADS] [CrossRef] (In the text)
- Jørgensen, U. G. 1997, in Molecules in Astrophysics: Probes and Processes, ed. E. F. van Dishoeck, IAU Symp., 178 (Kluwer), 441
- Jørgensen, U. G., Hron, J., & Loidl, R. 2000,A&A, 356, 253
- Joyce, R. R. 1998, AJ, 115, 2059 [NASA ADS] [CrossRef]
- Kervella, P., Thévenin, F., Ségrasan, D., et al. 2003, A&A, 404, 1087 [NASA ADS] [CrossRef] [EDP Sciences]
- Iben, I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] (In the text)
- Ireland, M. J., Scholz, M., & Wood, P. R. 2004a, MNRAS, 352, 318 [NASA ADS] [CrossRef] (In the text)
- Ireland, M. J., Scholz, M., Tuthill, P. G., & Wood, P. R. 2004b, MNRAS, 355, 444 [NASA ADS] [CrossRef]
- Lançon, A., & Wood, P. R. 2000, A&AS, 146, 217 [NASA ADS] [CrossRef] [EDP Sciences]
- Lederer, M. T., & Aringer, B. 2009, A&A, 494, 403 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Loidl, R., Lançon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences]
- Lopez, B., Wolf, S., Lagarde, S., et al. 2006, SPIE, 6268, 31 [NASA ADS] (In the text)
- Mattsson, L., Wahlin, R., & Höfner, S. 2009, A&A, subm. (In the text)
- Nowotny, W. 2005, Ph.D. Thesis, University of Vienna (In the text)
- Nowotny, W., Aringer, B., Höfner, S., et al. 2005a, A&A, 437, 273 [NASA ADS] [CrossRef] [EDP Sciences]
- Nowotny, W., Lebzelter, T., Hron, J., & Höfner, S. 2005b, A&A, 437, 285 [NASA ADS] [CrossRef] [EDP Sciences]
- Nowotny, W., Aringer, B., & Höfner, S. 2009 A&A, submitted (In the text)
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] (In the text)
- Scholz, M. 2003, Proc. SPIE, 4838, 163 [NASA ADS] (S03) (In the text)
- Scholz, M., & Takeda, Y. 1987, A&A, 186, 200 [NASA ADS] (In the text)
- Tatebe, K., & Townes, C. H. 2006, ApJ, 644, 1145 [NASA ADS] [CrossRef] (In the text)
- Tej, A., Lançon, A., & Scholz, M. 2003a, A&A, 401, 347 [NASA ADS] [CrossRef] [EDP Sciences]
- Tej, A., Lançon, A., Scholz, M., & Wood, P. R. 2003b, A&A, 412, 481 [NASA ADS] [CrossRef] [EDP Sciences]
- Verhoelst 2005, Ph.D. Thesis, University of Leuven
- Willson, L. A. 2000, ARA&A, 38, 573 [NASA ADS] [CrossRef] (In the text)
- Wittkowski, M., Aufdenberg, J. P., & Kervella. P. 2004, A&A, 413, 711 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Woitke, P. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, 387 (In the text)
- Yamamura, I., & de Jong, T. 2000, ESA SP, 456, 155 [NASA ADS]
Footnotes
- ... subfilters
![[*]](/icons/foot_motif.png)
- In principle, this should be done monochromatically but for computational reasons the usual number of narrow-band subfilters was limited to 10. However, we compared the resulting broad-band filters computed with a set of 10 narrow-band subfilters with the one computed with a set of 100 and 200 subfilters without finding any significant difference in the resulting broad-band visibility profile. We also emphasise that the maximum resolution for the computation of the broad-band filter is given by the opacity-sampling resolution.
- ... visibility
![[*]](/icons/foot_motif.png)
- All the visibility values V have to be interpreted as normalised visibilities V/V0.
- ... Rp
![[*]](/icons/foot_motif.png)
- Rp is defined as the Rosseland radius that ``the Mira variable would assume if the pulsation stopped and the stratification of the star becomes static'' (Jacob & Scholz 2002).
All Tables
Table 1: Parameters of the dynamic model atmospheres used in this work.
Table 2: Definitions of the narrow- and broad-band filters.
All Figures
![\begin{figure}
\par\includegraphics[width = 8.8cm]{image/11938fg1.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg33.png) |
Figure 1: Radial structure of the dynamic model D1. Gas temperature ( upper panel) and density ( lower panel) are plotted for different phases during the pulsation period. For comparison, the grey-shaded area marks the range where the structure of the model N1 at different phases can be found. More details about the structure of the models can be found in the text and in Nowotny et al. (2005a,b). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width = 16.cm]{image/11938fg2.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg37.png) |
Figure 2:
Synthetic spectrum (R = 360) calculated on the basis of the hydrostatic initial atmospheric structure of model D1.
All necessary opacity sources (continuous, atoms, molecules, dust) are included for the spectral synthesis, (see Fig. 4
of Aringer et al. (2009) for the individual contributions of the different molecular species).
The flux is normalised to a calculation for which only the continuous opacities were taken into account.
Overplotted are the narrow-band filters as defined in Table 2, for which the central
wavelengths in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width = 8.8cm]{image/119...
... \includegraphics[width = 8.8cm]{image/11938fg4.ps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg42.png) |
Figure 3:
Intensity and visibility profiles for the narrow-band filters at the maximum phase of
the mass-loss model D1 on the left side, and the model without mass-loss N1
on the right side. All the opacities are included in the computations.
Profiles for three representative filters are shown together with
the equivalent UD function for the 3.175 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c c}
\includegraphics[width = 8.8 cm]{image/...
...\includegraphics[width = 8.8 cm]{image/11938fg6.ps} \end{tabular}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg51.png) |
Figure 4: Visibility profiles computed in broad-band filters for the maximum phase of the model D1 with mass-loss on the left side, and the model N1 without mass-loss on the right side. The solid line corresponds to the model, while the dashed line is the equivalent UD computed by fitting one point at visibility V = 0.3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\begin{tabular}{c c}
\includegraphics[angle = 90, width = 8...
...s[angle = 90, width = 8.6cm]{image/11938f10.ps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg55.png) |
Figure 5: Representation of the bandwidth smearing effect for the phase maximum of the model D1 ( left panels) and N1 ( right panels) in the K-band. In the upper panels, visibility profiles are shown as a function of baseline for the individual narrow-band subfilters (dotted lines) and for the resulting broad-band filter (solid line), computed by taking into account the bandwidth smearing. In the inset, a zoom of the region around the first zero is represented. The lower panels show the visibility profiles computed with bandwidth smearing (BW, solid line), and profiles computed neglecting the effect (NBW, dotted line). The dashed lines present the difference between the two profiles (scale on the right y-axis). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle = 90, width = 9cm]{image/11938f11.ps}\\
\includegraphics[angle = 90, width = 9cm]{image/11938f12.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg57.png) |
Figure 6: UD-radii versus wavelength for the maximum phase of different models with ( upper panel) and without ( lower panel) mass-loss. The cross symbol represents the UD-continuum radius computed for the two reference models (D1, N1). The method used for the UD determination is a least squares fit using all the points of the synthetic profile with visibility >0.1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle = 90,width = 17cm]{image/11938f13.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg64.png) |
Figure 7: UD-radii versus phase are shown for three different narrow-band filters. The three upper panels represent results for the dynamic model D1 with mass-loss, the three panels at the bottom being for the model N1 without mass-loss. Triangles are for UD-radius computed by taking into account only continuum opacity. For the continuum, the same symbol is used for the different methods because there is no appreciable difference between the results. Crosses, stars, and diamonds represent the different methods (one point, two points, least squares, respectively) used for fitting the visibility profiles of models with UDs. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle = 90,width = 16cm]{image/11938f14.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg66.png) |
Figure 8:
UD-radius versus phase for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle = 90,width = 17.3cm]{image/11938f15.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa11938-09/Timg67.png) |
Figure 9:
UD-Radius versus phase for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.