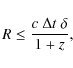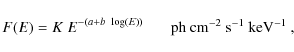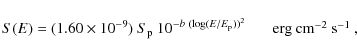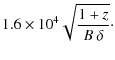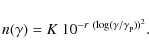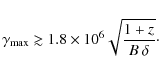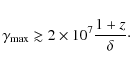| Issue |
A&A
Volume 501, Number 3, July III 2009
|
|
|---|---|---|
| Page(s) | 879 - 898 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810865 | |
| Published online | 29 April 2009 | |
Swift observations of the very intense flaring activity of Mrk 421 during 2006. I. Phenomenological picture of electron acceleration and predictions for MeV/GeV emission
A. Tramacere1,2 - P. Giommi3 - M. Perri3 - F. Verrecchia3 - G. Tosti4,5
1 - CIFS - Torino, Viale Settimio Severo 3, 10133 Torino, Italy
2 - SLAC, 2575 Sand Hill Road, Menlo Park, CA 94025, USA
3 - ASI Science Data Center, c/o ESRIN, via G. Galilei, 00044 Frascati, Italy
4 - Dipartimento di Fisica, via A. Pascoli, 06100 Perugia, Italy
5 - INFN Perugia, via A. Pascoli, 06100 Perugia, Italy
Received 27 August 2008 / Accepted 28 January 2009
Abstract
Aims. We present the results of a deep spectral analysis of all Swift observations of Mrk 421 between April 2006 and July 2006, when it reached its highest X-ray flux recorded until the end of 2006. The peak flux was about 85 milli-Crab in the 2.0-10.0 keV band, and the peak energy (![]() )
of the spectral energy distribution (SED) was often at energies higher than 10 keV. We study trends between the spectral parameters, and the physical insights the parameters provide into the underlying acceleration and emission mechanisms.
)
of the spectral energy distribution (SED) was often at energies higher than 10 keV. We study trends between the spectral parameters, and the physical insights the parameters provide into the underlying acceleration and emission mechanisms.
Methods. We performed a spectral analysis of Swift observations to investigate trends between the spectral parameters. We searched for acceleration and energetic features phenomenologically linked to the SSC model parameters, by predicting their effects in the ![]() -ray band, and in particular, the spectral shape expected in the Fermi Gamma-ray Space Telescope-LAT band.
-ray band, and in particular, the spectral shape expected in the Fermi Gamma-ray Space Telescope-LAT band.
Results. We confirm that the X-ray spectrum is described well by a log-parabolic distribution close to ![]() ,
that the peak flux of the SED (
,
that the peak flux of the SED (![]() )
is correlated with
)
is correlated with ![]() ,
and that
,
and that ![]() is anti-correlated with the curvature parameter (b). The spectral evolution in the Hardness-ratio-flux plane shows both clockwise and counter-clockwise patterns. During the most energetic flares, the UV-to-soft-X-ray spectral shape requires an electron distribution spectral index of
is anti-correlated with the curvature parameter (b). The spectral evolution in the Hardness-ratio-flux plane shows both clockwise and counter-clockwise patterns. During the most energetic flares, the UV-to-soft-X-ray spectral shape requires an electron distribution spectral index of
![]() .
.
Conclusions. We demonstrate that the UV-to-X-ray emission from Mrk 421 is probably generated by a population of electrons that is actually curved, and has a low energy power-law tail. The observed spectral curvature is consistent with both stochastic acceleration or energy-dependent acceleration probability mechanisms, whereas the power-law slope of XRT-UVOT data is close to that inferred from the GRBs X-ray afterglow and in agreement with the universal first-order relativistic shock acceleration models. This scenario implies that magnetic turbulence may play a twofold role: spatial diffusion relevant to the first order process and momentum diffusion relevant to the second order process.
Key words: galaxies: active - galaxies: BL Lacertae objects: individual: Mrk 421- X-rays: individuals: Mrk 421 - radiation mechanisms: non-thermal - acceleration of particles
1 Introduction
BL Lac objects are Active Galactic Nuclei (AGNs) characterized by a polarised and highly variable nonthermal continuum emission extending from radio to
The Spectral Energy Distribution (SED) of these objects has a typical
two-bump shape. According to current models, the lower-frequency bump
is interpreted as synchrotron emission from highly relativistic electrons
with Lorentz factors ![]() in excess of 102. This component peaks at frequencies
ranging from the IR to the X-ray band. The true position of this peak was proposed
by Padovani & Giommi (1995) as an indicator in classifying sources;
they define LBL (Low energy peaked BL Lac) to be objects with the first bump in
the IR-to-optical band, and HBL (High energy peaked BL Lac) as those with SEDs peaking in
the UV-X-ray band. According to the Synchrotron Self Compton (SSC) emission mechanism,
the higher-frequency bump can be attributed to inverse Compton scattering
of synchrotron photons by the same population of relativistic electrons that
produce the synchrotron emission (Jones et al. 1974; Ghisellini & Maraschi 1989).
in excess of 102. This component peaks at frequencies
ranging from the IR to the X-ray band. The true position of this peak was proposed
by Padovani & Giommi (1995) as an indicator in classifying sources;
they define LBL (Low energy peaked BL Lac) to be objects with the first bump in
the IR-to-optical band, and HBL (High energy peaked BL Lac) as those with SEDs peaking in
the UV-X-ray band. According to the Synchrotron Self Compton (SSC) emission mechanism,
the higher-frequency bump can be attributed to inverse Compton scattering
of synchrotron photons by the same population of relativistic electrons that
produce the synchrotron emission (Jones et al. 1974; Ghisellini & Maraschi 1989).
Table 1: Swift observation journal and exposures of Mrk 421.
With its redshift z = 0.031, Mrk 421 is among the closest and most well studied HBL.
It is one of brightest BL Lac objects in the UV and the X-ray bands, and was
observed in ![]() rays by EGRET (Lin et al. 1992); it was also the first extragalactic
source detected at TeV energies in the range 0.5-1.5 TeV by the Whipple
telescopes (Petry et al. 1996; Punch et al. 1992).
rays by EGRET (Lin et al. 1992); it was also the first extragalactic
source detected at TeV energies in the range 0.5-1.5 TeV by the Whipple
telescopes (Petry et al. 1996; Punch et al. 1992).
The source is classified as HBL because its synchrotron emission peak ranges from a fraction of a keV to several keV. Its flux variations go along with significant spectral variations (Massaro et al. 2004; Fossati et al. 2000a) and the spectral shape in general exhibits a curvature that is described well by a log-parabolic model (Massaro et al. 2004; Tramacere et al. 2007b).
In spring/summer 2006, Mrk 421 reached its highest X-ray flux recorded until that time. The peak flux was about 85 milli-Crab in the 2.0-10.0 keV band, and corresponded to a peak energy of the spectral energy distribution (SED) that was often at energies higher than 10 keV.
In this paper (Paper I), we present data collected from Swift observations performed during this intense flaring period. We study the evolution in the spectral parameters as a function of the flaring activity, and the correlations between the spectral parameters. This provides a phenomenological picture of the physical mechanism driving the observed patterns. In Paper II, we will frame this scenario in the theoretical context of stochastic acceleration (Tramacere 2009).
In the phenomenological context of jets in HBLs, the spectral curvature is relevant to the understanding of both the radiative and acceleration mechanisms.
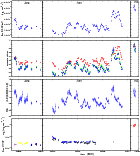 |
Figure 1: From top to bottom: a) light curve of the flux in the band 0.2-10.0 keV. b) light curves for three different bands soft (0.2-3.0 keV, red points) medium (3.0-5.0 keV, green points) and hard ( 5.0-10.0 keV, blue points), normalized to their maximum value. c) the evolution of the hardness ratio (HR) evaluated as the ratio of the 2.0-10.0 keV band to the 0.2-2.0 keV band. d) light curve from the Swift-UVOT instrument, different colors refers to different filters (V = brown, U = black, UVM2 = red, UVW1 = blue, UVW2 = yellow). (See the electronic edition of the Journal for a color version of this figure) |
| Open with DEXTER | |
Many studies have demonstrated that the X-ray spectral shape of Mrk 421 is curved and described by a log-parabolic distribution with a mildly curved and symmetric spectral shape (Tanihata et al. 2004; Massaro et al. 2004; Tramacere et al. 2007a; Fossati et al. 2000b). Massaro et al. (2004) interpreted this feature in the framework of energy-dependent acceleration efficiency that naturally corresponds to log-parabolic spectral distributions with a possible power-law tail at lower energies. Kardashev (1962) showed that a log-parabolic distribution results from a stochastic acceleration scenario with a mono-energetic or quasi-mono energetic particle injection. Katarzynski et al. (2006) and Giebels et al. (2007) used a relativistic Maxwellian electron distribution, produced by a stochastic acceleration process, to describe the X-ray/TeV emission of Mrk 501 and Mrk 421 , respectively. Stawarz & Petrosian (2008) showed that a distribution with similar spectral properties can be obtained as a steady-state energy spectra of particles undergoing momentum diffusion due to resonant interactions with turbulent MHD modes.
Tramacere et al. (2007b) suggested that the connection between the X-ray curvature and
the emitting particles, and its evolution with the source state,
could be investigated in testing the prediction of the scenarios listed above.
In particular, both stochastic (Kardashev 1962) and energy-dependent
acceleration mechanisms predict an anticorrelation between the curvature
and the SED peak energy (![]() ). The pattern traced by the peak height (
). The pattern traced by the peak height (![]() )
of the SED as
)
of the SED as ![]() varies,
can indicate the evolution in the parameters characterizing the energetics
of the synchrotron emission, in particular the average particle energy and the
number density of the emitting particles.
varies,
can indicate the evolution in the parameters characterizing the energetics
of the synchrotron emission, in particular the average particle energy and the
number density of the emitting particles.
During the most violent flares, a crucial issue is to understand whether the shape of the X-ray spectrum can also be described by a single log-parabolic spectral distribution. A typical X-ray detector shows only a slice (usually up to two decades in energy) of the overall emission from the observed object. During strong flares involving significant variation in the SED peak energy, it is possible to understand whether the electron distribution is curved even far from the peak energy. We can also benefit from the unique opportunity provided by Swift to perform simultaneous UV-to-X-ray observations, and extend the spectral window from about 1015 Hz to 1019 Hz. The presence of a power-law tail at low photon energies and its slope can provide information about the low-energy tail of the underlying electron distribution as well as the acceleration mechanism generating such a spectral shape.
By developing the phenomenological results from the present analysis,
we attempt to model the SED of Mrk 421 within the synchrotron-self-Compton (SSC)
scenario, predicting the possible spectral behaviour at
![]() -ray energies. In particular, we are able to relate the typical spectral shape
of the UV-to-soft-X-ray emission to that expected in the MeV/GeV band covered by the
Fermi Gamma-ray Space Telescope-LAT instrument.
-ray energies. In particular, we are able to relate the typical spectral shape
of the UV-to-soft-X-ray emission to that expected in the MeV/GeV band covered by the
Fermi Gamma-ray Space Telescope-LAT instrument.
This paper is organized as follows. In Sect. 2, we present our data set and the procedure used to reduce the Swift data. In Sect. 3, we report the results of an analysis of the rapid variability of the source. In Sect. 4 we present spectral analysis results. In Sect. 5 we analyse the spectral evolution of the source. In Sect. 6 we study the correlations between the spectral parameters and compare these results with those of previous studies directing particular attention to the link between these trends and expectations from different scenarios for the acceleration mechanism. In Sect. 7, we study the connection between the UVOT and the XRT spectra, showing the relevance of the derived spectral shape in the context of the first order acceleration processes. In Sect. 8, we model the SED within the SSC framework, focusing on the phenomenological interpretation of the data. In Sect. 9, we discuss our results, and in Sect. 10, we draw our overall conclusions.
2 Swift observations and data analysis
We present results of temporally-resolved spectral analyses of 15 Swift simultaneous
observations in the UV/X-ray band performed between April and July
2006, when the source was so bright that it was automatically targeted by the
high-energy instrument ![]() three times with the assumption that it was a
Gamma Ray Burst.
The log of UV/X-ray observations is reported in Table 1.
three times with the assumption that it was a
Gamma Ray Burst.
The log of UV/X-ray observations is reported in Table 1.
In Fig. 1, we report the XRT light curves derived from the single-orbit spectra. In the first panel from the top, we show the light curve of the flux obtained by integrating the model from Eq. (2) (see Sect. 4.2) between 0.2 and 10.0 keV, according to the parameters and parameter errors reported in Table 2. Fluxes in Table 2 refer to the 0.3-10.0 keV interval because the XRT response function is calibrated only for that range. We extrapolated the flux to the 0.2-10.0 keV band to ensure more robust comparisons with data from other X-ray telescopes, which are usually given in the 0.2-10.0 keV band.
The second panel from the top shows the light curve for three different bands: soft (0.2-3.0 keV), medium (3.0-5.0 keV), and hard ( 5.0-10.0 keV), normalized by their respective maximum values. In the third panel from the top, we report the evolution of the hardness ratio (HR) evaluated as the ratio of the 2.0-10.0 keV band to the 0.2-2.0 keV band.
The bottom panel of Fig. 1 shows the light curve obtained from the Swift-UVOT observations.
2.1 Swift-XRT data analysis
All the data were reduced using the
The operational mode of XRT is controlled automatically by the onboard software
that uses the appropriate CCD readout mode to reduce or eliminate the effects of
photon pile-up.
When the target count-rate is higher than ![]() 1 cts/s the system is operated
normally in Windowed Timing (WT) mode, whereas the Photon Counting (PC) mode is
used for fainter sources (see Burrows et al. 2005; Hill et al. 2004, for more details on XRT observing modes).
The observations presented here were all performed in WT mode, owing to the
extremely high flux rate of the source (40-80 cts/s).
1 cts/s the system is operated
normally in Windowed Timing (WT) mode, whereas the Photon Counting (PC) mode is
used for fainter sources (see Burrows et al. 2005; Hill et al. 2004, for more details on XRT observing modes).
The observations presented here were all performed in WT mode, owing to the
extremely high flux rate of the source (40-80 cts/s).
For WT mode we selected photons with grades in the range 0-2; we also used default screening parameters to produce level 2 cleaned event files. To take advantage of the statistics offered by these high numbers of events we decided to make a high temporal resolved analysis, extracting spectra for each Swift orbit. We rejected only two out of the 174 obtained spectra, because of a strongly biased exposure due to the dead columns on the CCD. The resulting XRT database presented in this work therefore includes 172 time intervals.
2.2 Swift-UVOT data analysis
The Swift UV and Optical Telescope (UVOT, Roming et al. 2005) observations included
in this paper have exposures in all filters except for the White one.
Photometry of the source was performed using the standard UVOT software developed
and distributed within the HEAsoft 6.4 package. Counts were extracted from an
aperture of 5
![]() radius for all single exposures within an observation and
for all filters, while the background was carefully estimated in a few ways.
In almost all observations, the source was found in the ``ghost wings'' (Li et al. 2006)
of the nearby star 51 UMa, so we estimated the background within a circular aperture
of 15
radius for all single exposures within an observation and
for all filters, while the background was carefully estimated in a few ways.
In almost all observations, the source was found in the ``ghost wings'' (Li et al. 2006)
of the nearby star 51 UMa, so we estimated the background within a circular aperture
of 15
![]() radius away from the source but in the wings, excluding stray light and
support shadows. These background values were compared with those obtained for a
region outside the wings, which highlighted differences in most cases to within the errors.
radius away from the source but in the wings, excluding stray light and
support shadows. These background values were compared with those obtained for a
region outside the wings, which highlighted differences in most cases to within the errors.
We completed astrometry of each exposure, verifying the aperture positioning.
Count rates were then converted to fluxes using the standard zero points. We
discarded some exposures for which the count rate was close to the limit of acceptability
for the ``coincidence loss'' correction factor included in the CALDB
(![]() 90 cts s-1).
90 cts s-1).
 |
Figure 2:
Light curve binned with 50 s intervals,
from the first orbit of the 2006 April 26 pointing. Significant variability ( |
| Open with DEXTER | |
The fluxes were then dereddened using a value of E(B-V) equal to 0.014 mag
(Schlegel et al. 1998) with
![]() ratios calculated for UVOT filters
(for the latest effective wavelengths) using the mean Galactic interstellar
extinction curve from Fitzpatrick (1999).
ratios calculated for UVOT filters
(for the latest effective wavelengths) using the mean Galactic interstellar
extinction curve from Fitzpatrick (1999).
2.3 Swift-UVOT data analysis
We analysed the data that automatically triggered the BAT instrument (labelled with a (*) symbol in Table 1). To reduce the data we followed the instructions reported in the BAT analysis threads
3 Fast source variability
Temporal variability is one of the most interesting features characterizing HBLs.
In the X-ray band, the typical timescales of flux changes decrease to the order
of hour or minutes. The identification of the most rapid significant flux
change allows us to estimate the source size, given by the well-known relation:
where c is the speed of the light,
According to Eq. (1), a 1200 s timescale implies that
![]() cm. Assuming a beaming factor approximately 10, we derive
cm. Assuming a beaming factor approximately 10, we derive
![]() cm, which is indicative of a compact emitting region.
cm, which is indicative of a compact emitting region.
Lichti et al. (2008) analysed the temporal variability of Mrk 421 using observations
performed by the INTEGRAL-ISGRI instrument in the 40-100 keV band, and overlapping
our data set during the June pointings. The most rapid variability observed in
the INTEGRAL-ISGRI light curves, estimated by fitting the data with a rise-time law
of the form
![]() ,
inferred that
,
inferred that
![]() cm.
We performed the same analysis for the 2006 April 26 light curve and we found that
cm.
We performed the same analysis for the 2006 April 26 light curve and we found that
![]() s which implies
s which implies
![]() cm.
We used this timescale to constrain the size of the emission region in the following
analyses (Sect. 8).
cm.
We used this timescale to constrain the size of the emission region in the following
analyses (Sect. 8).
Timescales of similar length of that in the 2006 April 26 pointing were also observed by
Tanihata et al. (2001) in ASCA data, about 5 ks
(
![]() cm), and by Giebels et al. (2007)
(about 2 ks), who analysed TeV data from the CAT telescope
(
cm), and by Giebels et al. (2007)
(about 2 ks), who analysed TeV data from the CAT telescope
(
![]() cm).
cm).
4 Spectral analysis
4.1 XRT spectral analysis
 |
Figure 3:
Spectrum from the first orbit of the ObsID 00030352013 performed
on 2006 June 22. Left Panel: the systematic deviations on both sides of
the residuals from a best fit with a power-law with Galactic |
| Open with DEXTER | |
For most spectra analysed, we detected systematic deviations
(see Fig. 3) in the residuals
obtained when fitting the data by means of a power-law spectrum with
![]() fixed at the Galactic value. This behaviour implies heuristically
that the spectra are intrinsically curved. This was known previously
(Tanihata et al. 2004; Massaro et al. 2004; Tramacere et al. 2007b,a; Fossati et al. 2000b).
All of these authors agreed that when the spectral shape of Mrk 421 is curved,
can be difficult to describe its curvature in terms of absorption alone because this
would require a column density much higher than the Galactic value of
fixed at the Galactic value. This behaviour implies heuristically
that the spectra are intrinsically curved. This was known previously
(Tanihata et al. 2004; Massaro et al. 2004; Tramacere et al. 2007b,a; Fossati et al. 2000b).
All of these authors agreed that when the spectral shape of Mrk 421 is curved,
can be difficult to describe its curvature in terms of absorption alone because this
would require a column density much higher than the Galactic value of
![]() cm-2
(Lockman & Savage 1995), and would also yield unacceptable fits of high
cm-2
(Lockman & Savage 1995), and would also yield unacceptable fits of high ![]() .
Moreover, brightness profile derived from high resolution images of the host early-type
galaxy of Mrk 421 do not exhibit any evidence of large amounts of absorbing material (Urry et al. 2000).
Based on these phenomenological results, we performed the spectral analysis by
fixing the
.
Moreover, brightness profile derived from high resolution images of the host early-type
galaxy of Mrk 421 do not exhibit any evidence of large amounts of absorbing material (Urry et al. 2000).
Based on these phenomenological results, we performed the spectral analysis by
fixing the
![]() absorbing column densities to the Galactic values and using the
following log-parabolic spectral law (LP):
absorbing column densities to the Galactic values and using the
following log-parabolic spectral law (LP):
where a is the photon index at 1 keV and b measures the spectral curvature.
Both the SED peak energy (![]() )
and height (
)
and height (![]() )
can be derived
easily from Eq. (2), but, in this case, they are affected by an intrinsic
analytical correlation. This bias can be removed by using an equivalent functional
relationship that is a log-parabola expressed in terms of
)
can be derived
easily from Eq. (2), but, in this case, they are affected by an intrinsic
analytical correlation. This bias can be removed by using an equivalent functional
relationship that is a log-parabola expressed in terms of ![]() ,
,
![]() ,
and b (LPEP):
,
and b (LPEP):
where
4.2 Orbit-resolved analysis
Because of the bright state of the source, we were able to extract spectra for each orbit, for a total of 172 spectra. A motivation for performing an orbit-resolved analysis is the strong variability of the source during these pointings. Integrating spectra over timescales much longer than the typical variability produces misleading results in estimating of the curvature,
The results of the spectral analysis are reported in Table 2
(which is at the end of the text; rejected spectra are indicated by (*)), where all statistical
errors refer to the ![]() confidence level (equal to one Gaussian standard deviation).
The second, third, and forth columns in Table 2 report the best-fit
parameters estimates for the model in Eq. (2). The fifth column reports the value of
the SED peak estimated analytically from Eq. (2) according to the best-fit model results (
confidence level (equal to one Gaussian standard deviation).
The second, third, and forth columns in Table 2 report the best-fit
parameters estimates for the model in Eq. (2). The fifth column reports the value of
the SED peak estimated analytically from Eq. (2) according to the best-fit model results (
![]() ). The sixth and seventh columns report the
). The sixth and seventh columns report the ![]() and
and ![]() best-fit
model estimates using Eq. (3) as the best-fitting model. In the eighth column,
we report the flux in the 0.3-10.0 keV band, evaluated by integrating the model function
in Eq. (2). In the last column, we report the reduced
best-fit
model estimates using Eq. (3) as the best-fitting model. In the eighth column,
we report the flux in the 0.3-10.0 keV band, evaluated by integrating the model function
in Eq. (2). In the last column, we report the reduced ![]() statistics
for the fit with Eq. (2).
statistics
for the fit with Eq. (2).
The SED peak energy was often difficult to estimate. This was because
during this particularly high brightness state, the spectra were in some cases
hard, with a photon index of
![]() and of low spectral
curvature, implying a peak energy far from the XRT energy band.
and of low spectral
curvature, implying a peak energy far from the XRT energy band.
To test the robustness of the ![]() estimate, we first derived the peak
energy from the spectral parameters of Eq. (2) (
estimate, we first derived the peak
energy from the spectral parameters of Eq. (2) (
![]() ). We then fitted
the spectra using Eq. (3), by setting the initial curvature value to that
returned from the fit with Eq. (2). To test the stability of the
results, we adopted the following criteria:
). We then fitted
the spectra using Eq. (3), by setting the initial curvature value to that
returned from the fit with Eq. (2). To test the stability of the
results, we adopted the following criteria:
- 1.
- The value of
 is statistically significant. Given the asymmetric
uncertainties, we define
is statistically significant. Given the asymmetric
uncertainties, we define
 to be half of the 2 sigma confidence level, and
require that
to be half of the 2 sigma confidence level, and
require that
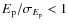 .
.
- 2.
-
 consistent with
consistent with  to a one sigma uncertainty .
to a one sigma uncertainty .
All spectra for which the stability conditions were satisfied returned
values of
![]() keV.
keV.
4.3 Orbit-merged analysis
An orbit-resolved spectral analysis has the ability to follow accurately
the strong variability in the source, even though the ![]() estimates are affected by significant
uncertainties. In any case, based on the spectral/flux pattern traced by the previous
analysis, we can identify all the orbits indicating essentially the same
spectral/flux states.
We can use these intervals to perform an orbit-merged spectral analysis, and achieve
smaller uncertainties in the
estimates are affected by significant
uncertainties. In any case, based on the spectral/flux pattern traced by the previous
analysis, we can identify all the orbits indicating essentially the same
spectral/flux states.
We can use these intervals to perform an orbit-merged spectral analysis, and achieve
smaller uncertainties in the ![]() value, without integrating the
source over periods that exhibits significant changes.
value, without integrating the
source over periods that exhibits significant changes.
The results of this analysis are reported in Table 3 (which is at the end of the text).
In this analysis, when ![]() and
and
![]() can be determined, the typical
uncertainties are smaller. We use the values from this table to perform
can be determined, the typical
uncertainties are smaller. We use the values from this table to perform
![]() and
and
![]() trend analysis in the following sections, selecting only data
with reliable
trend analysis in the following sections, selecting only data
with reliable ![]() estimates. In this case, all spectra with
estimates. In this case, all spectra with ![]() well-constrained have
well-constrained have
![]() keV.
keV.
 |
Figure 4: Joint XRT BAT spectral analysis from the 2006 April 22 pointing. |
| Open with DEXTER | |
4.4 Joint XRT-BAT spectral analysis
For the three observations with simultaneous Swift-XRT and Swift-BAT data
(with the BAT in automatic trigger mode, see Table 1), we performed
a joint XRT-BAT spectral analysis. The results are reported in Table 3 (lines labelled X+B).
The spectral curvature produced by the joint analysis is slightly larger than
for the XRT data alone, but is always consistent
within one sigma. As already discussed, the estimation of ![]() is more difficult.
We use the superscript X+B hereafter to refer to the joint XRT and BAT
analysis.
is more difficult.
We use the superscript X+B hereafter to refer to the joint XRT and BAT
analysis.
For the 2006 15 July pointing, the two curvatures are
![]() and
and
![]() ,
and the two values of
,
and the two values of ![]() which are consistent to within one
confidence interval
are
which are consistent to within one
confidence interval
are
![]() keV and
keV and
![]() keV.
For the case of the 2006 April 22 pointing (Fig. 4),
the peak energies are
keV.
For the case of the 2006 April 22 pointing (Fig. 4),
the peak energies are
![]() keV and
keV and
![]() and the curvatures are
and the curvatures are
![]() and
and
![]() .
.
For the 2006 June 23 pointing, the XRT curvature is estimated to be
![]() which should be compared with the value of
which should be compared with the value of
![]() .
In this case,
the smaller the value of the curvature, as discussed in the previous section, the more difficult the
estimate of the
.
In this case,
the smaller the value of the curvature, as discussed in the previous section, the more difficult the
estimate of the ![]() value becomes. We found that the XRT data alone are unable to identify the true peak
energy, and the estimate from our joint analysis is
value becomes. We found that the XRT data alone are unable to identify the true peak
energy, and the estimate from our joint analysis is
![]() keV.
keV.
The results of our joint XRT-BAT analysis confirm that ![]() values
estimated from XRT data, at energies higher than about 20 keV, are possibly
biased. The selection applied to the present analysis should ensure that the
bias affecting the trends between
values
estimated from XRT data, at energies higher than about 20 keV, are possibly
biased. The selection applied to the present analysis should ensure that the
bias affecting the trends between ![]() ,
b, and
,
b, and ![]() are as small as possible.
are as small as possible.
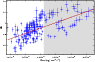 |
Figure 5: Scatter plot of the HR vs. the flux in the 0.2-10 keV band (HR is evaluated as the ratio of the 2.0-10.0 keV band to the 0.2-2.0 keV band). The points in the shaded area are almost all from the period 2006 June 23 to 2006 June 27 and 2006 July 15. |
| Open with DEXTER | |
5 Spectral evolution
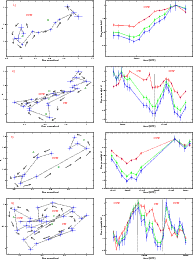 |
Figure 6: Left panels: spectral patterns in the a-flux plane showing clockwise and counterclockwise trends. Right panels: Swift-XRT light curves at three different bands: soft (0.2-3.0 keV, red), medium (3.0-5.0 keV, green), and hard ( 5.0-10.0 keV, red) . Capital letters guide the reader during the comment in the text. In both left and right panels, the fluxes are normalized to the maximum value reached during that particular time-interval. |
| Open with DEXTER | |
We now complete a classical hardness-ratio (HR) analysis, to investigate cooling and/or acceleration features. The HR is evaluated as the ratio of the flux measured in the 2.0-10.0 keV band to that in the 0.2-2.0 keV band.
An analysis of the evolution in the HR indicates that the correlations between variations in the soft and hard bands modulates the HRs, producing spectra that are harder when the source is brighter and softer when it is weaker. This trend is clearly visible in Fig. 5. The significant scatter in the data points implies that the evolutions of the flares are different from each other due to the different underlying physical conditions.
We also note that all but 3 of the data points in the shaded area belong to the period from 2006 June 23 to 2006 June 27 and to the 2006 July 15 pointing, when the source was brighter than in the previous pointings.
A deeper understanding of the spectral evolution can be achieved by analysing the hysteresis patterns of the single flares in the a-flux or HR-flux plane, where a is the photon index at 1 keV (see Table 2).
The timescales relevant to understanding the patterns in the a-flux plane are
those of injection (
![]() ), escape (
), escape (
![]() ), cooling (
), cooling (
![]() ),
acceleration (
),
acceleration (
![]() )
and light crossing (
)
and light crossing (
![]() )
time.
According to Kirk et al. (1998), the loops are
expected to be clockwise (CW) and have soft lag when the flare is observed at
frequencies where the higher energy variability occurs more rapidly than at lower energy
(as in the case of synchrotron cooling).
In contrast, when observed at frequencies for which the acceleration and cooling
timescale are almost equal, the loops are expected to be counter-clockwise (CCW)
with a possible hard lag.
)
time.
According to Kirk et al. (1998), the loops are
expected to be clockwise (CW) and have soft lag when the flare is observed at
frequencies where the higher energy variability occurs more rapidly than at lower energy
(as in the case of synchrotron cooling).
In contrast, when observed at frequencies for which the acceleration and cooling
timescale are almost equal, the loops are expected to be counter-clockwise (CCW)
with a possible hard lag.
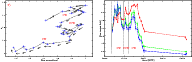 |
Figure 7: Left panels: spectral patterns in the a-flux plane showing clockwise and counterclockwise trends. Right panels: Swift-XRT light curves at three different bands: soft (0.2-3.0 keV, red), medium (3.0-5.0 keV, green), and hard ( 5.0-10.0 keV, red) . Capital letters are referenced in the discussion in the text. In both left and right panels, the fluxes are normalized to the maximum value reached during that particular time interval. |
| Open with DEXTER | |
We investigated carefully all the patterns from our data-set,
and in Figs. 6 and 7 we report the 5 flares
showing a clear CW or CCW loop.
The left panels show the evolution of a as a function of the flux, and the
right panels show the light curves in three different bands. The fluxes are
normalized to the maximum value reached in that particular time interval.
As a general result, we did not find any significant plateau among the light
curves of these flares, which implies that
![]() .
We describe the
behaviour of the flares individually:
.
We describe the
behaviour of the flares individually:
- Flare 1)
- the flare has a CCW pattern; it begins with a softening of the
spectrum with a flux almost steady (A) probably reflecting the cooling from
the previous flaring episode, followed by a flux increase with a spectral
hardening (B);
- Flare 2)
- the flare has two patterns: one CW and one CCW. It starts with
a decreasing flux and a spectral softening (A) (
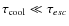 ).
Figure 6 (left panel) shows that the flux in the soft
band is still increasing when the fluxes in the medium and hard bands are
already decreasing.
When the spectrum starts to become harder (B), the flux is still decreasing, which may
imply that we are seeing the propagation of the new injection from the
hard band, as the soft band is still decreasing. The flux then starts to increase
with the spectrum hardening (C). When the flare begins to decay (D) the pattern
switches to CCW and we witness a decrease in the flux and a spectral softening;
).
Figure 6 (left panel) shows that the flux in the soft
band is still increasing when the fluxes in the medium and hard bands are
already decreasing.
When the spectrum starts to become harder (B), the flux is still decreasing, which may
imply that we are seeing the propagation of the new injection from the
hard band, as the soft band is still decreasing. The flux then starts to increase
with the spectrum hardening (C). When the flare begins to decay (D) the pattern
switches to CCW and we witness a decrease in the flux and a spectral softening;
- Flare 3)
- the flare has a CCW pattern, starts with a flux
decrease and a spectral softening (A), then the flux increases and the
spectrum hardens (B). In the last part (C), the flux decreases and the spectrum
still hardens. As in the previous case this may hint the start of a new
hard flaring component;
- Flare 4)
- this flare has three patterns: CCW, CW, and CCW. It starts with
a CCW loop. Initially, there is a spectral change with an almost steady flux (A),
followed by a weak spectral hardening with a flux increase (B). The CW loop
is dominated by the cooling time. The final CCW pattern is characterized
by a flux increase and a rapid spectral hardening.
In this case, the new flaring component also seems to start in the hard band.
The flux decrease (C) is almost achromatic in this case, and the escape time
may dominate over the cooling one (
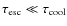 );
);
- Flare 5)
- this flare has three patterns: CW, CCW, and CW. It does not have features that differs from those of other patterns.
6 Spectral parameter trends
We compare the trends between the spectral parameters with those detected in the statistical analysis of Tramacere et al. (2007b). We extend the data set presented in that work with the results from the observations analysed in this paper. We note that this entire data set spans about ten years, sampling the source in different brightness states and making the final result more statistically significant.
6.1 E
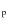 - b trend
- b trend
The evolution in the curvature parameters as a function of the peak energy
highlights the features relevant to the acceleration process.
This analysis indicates that as the peak energy of the emission increases,
the cooling timescale shortens and can compete with the timescales for acceleration,
it is then possible to observe a bias in the
We analysed the data in Table 3, identifying cooling-dominated
observations (lines labelled with (c)), characterized by a strong flux decrease
and strong spectral softening (![]() ). In Fig. 8, we plot with
green empty circles the whole XRT data set from Table 3 and with
black squares the points without the strong cooling contamination
discussed above.
). In Fig. 8, we plot with
green empty circles the whole XRT data set from Table 3 and with
black squares the points without the strong cooling contamination
discussed above.
In the same figure, we also report data from Tramacere et al. (2007b), showing that
the trend in our sample is consistent with that from the historical data.
This agreement confirms that the spectral curvature decreases as ![]() moves
toward higher energies.
moves
toward higher energies.
This phenomenon can be interpreted by two different scenarios.
A first scenario is that of an energy-dependent acceleration probability process
(EDAP). Within this context, Massaro et al. (2004) showed that when the acceleration
efficiency is inversely proportional to the energy itself, the energy distribution
approaches a log-parabolic shape. According to this model, the curvature (r)
is related to the fractional acceleration gain (
![]() )
by
)
by
![]() .
A possible example is given by
particles confined by a magnetic field, whose confinement efficiency (
.
A possible example is given by
particles confined by a magnetic field, whose confinement efficiency (
![]() )
decreases as the gyration radius (RL) increases. From
)
decreases as the gyration radius (RL) increases. From
![]() and
and
![]() ,
the negative trend
between
,
the negative trend
between ![]() and b follows. This trend is in agreement with the observed trend.
and b follows. This trend is in agreement with the observed trend.
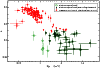 |
Figure 8:
Scatter plot of the curvature (b) vs. |
| Open with DEXTER | |
An alternative explanation is provided by the stochastic acceleration framework (SA)
and the presence of a momentum-diffusion term. In this scenario, the diffusion
term acts on the electron spectral shape broadening the distribution.
In particular, Kardashev (1962) showed that a log-parabolic spectrum results
from a Fokker-Planck equation with a momentum-diffusion term and a monoenergetic
or quasi-monoenergetic particle injection.
The results presented in Tramacere et al. (2007b) rely on the theoretical prediction
from the Kardashev (1962) model, that the curvature term (r) is inversely
proportional to the diffusion term (D):
This relation leads to the following trend between the peak energy of the electron distribution (
In Paper II (Tramacere 2009) we will discuss in detail how the stochastic acceleration can be used to reproduce this trend by developing a physical scenario that fits these phenomenological results. Here, we remark that both the momentum-diffusion term D and, the fractional acceleration gain
6.2 S
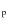 (L
(L
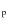 )
- E
)
- E
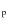 trend
trend
In terms of the synchrotron emission the trend between ![]() and
and ![]() has implications for the driver of the spectral changes in the X-rays.
This trend can be used to understand how the luminosity of the
jet evolves as the particle energy increases.
In the framework of the synchrotron theory (Rybicki & Lightman 1979), the dependence of
has implications for the driver of the spectral changes in the X-rays.
This trend can be used to understand how the luminosity of the
jet evolves as the particle energy increases.
In the framework of the synchrotron theory (Rybicki & Lightman 1979), the dependence of ![]() on
on ![]() can be expressed in the form of a power-law:
can be expressed in the form of a power-law:
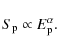 |
(6) |
Starting from the following functional relation, the SED peak height reads:
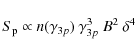 |
(7) |
and the peak energy is given by:
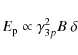 |
(8) |
where
If we take into account a log-parabolic distribution for the electrons emitting
the X-ray photons, then it is easy to show that the total emitters number
![]() ,
with
,
with
![]() the
peak of
the
peak of
![]() .
This in terms of
.
This in terms of ![]() ,
implies that
,
implies that
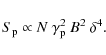 |
(9) |
Thus
To obtain a deeper understanding of the relation to the jet energetics,
we plot on the y axis of Fig. 9,
![]() ,
where
,
where
![]() Mpc is the luminosity distance
Mpc is the luminosity distance![]() . We report the
. We report the ![]() values both in Tables 2
and 3.
The resulting scatter-plot represents the
values both in Tables 2
and 3.
The resulting scatter-plot represents the
![]() trend obtained from merging our
data sample with that from Tramacere et al. (2007b).
We fitted the data by means of
a simple power law (PL)
trend obtained from merging our
data sample with that from Tramacere et al. (2007b).
We fitted the data by means of
a simple power law (PL)
![]() ,
and a broken power-law (BPL)
,
and a broken power-law (BPL)
| |
(10) | ||
The simple power-law fit gives a value of
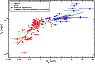 |
Figure 9:
Scatter plot of |
| Open with DEXTER | |
We focus on the results from the BPL fit. Although the break energy is not well
constrained, we note that spectral slopes differ with a
high statistical significance. This break in the trend implies that for
![]() keV and
keV and
![]() erg/s, the driver follows the
relation with
erg/s, the driver follows the
relation with
![]() (we define this state the quiescent sate),
whilst for
(we define this state the quiescent sate),
whilst for
![]() keV and
keV and
![]() erg/s, the driver relates to
erg/s, the driver relates to
![]() (we define this to be the high state).
(we define this to be the high state).
In Paper II (Tramacere 2009), we will discuss in detail how the stochastic acceleration or the energetics of the jet can be used to reproduce this trend.
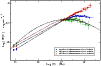 |
Figure 10: Three different spectral shapes from the data presented in this paper. Red boxes represent a power-law spectrum observed during Orbit 3 (ObsID 00030352010) on 2006 June 16. Blue diamonds represent a spectrum that is a log-parabola with a low energy power-law tail, from Orbit 3 (ObsID 00030352005) on 2006 April 25. Green circles represent a log-parabolic spectrum from Orbit 4 (ObsID 00030352008) on 2006 June 14. |
| Open with DEXTER | |
7 The Swift-UVOT Swift-XRT connection: the low-energy power-law tail in the electron distribution
Both the
![]() and
and
![]() trends allowed us to understand
the shape of the electron distribution for particles emitting at energies close
to
trends allowed us to understand
the shape of the electron distribution for particles emitting at energies close
to ![]() .
The particle energy distribution can develop a low energy
shape that differs from the extrapolation of the high energy branch. This
difference is relevant in discriminating between different acceleration
processes.
In this perspective, the connection between the UV and X-ray spectra can provide
useful information about the low energy tail of the electrons emitting
in the X-ray. We analysed carefully all of the spectra with simultaneous X-ray and
UV observations. As a result, we found that joint UVOT-XRT SEDs can be classified
in three categories:
.
The particle energy distribution can develop a low energy
shape that differs from the extrapolation of the high energy branch. This
difference is relevant in discriminating between different acceleration
processes.
In this perspective, the connection between the UV and X-ray spectra can provide
useful information about the low energy tail of the electrons emitting
in the X-ray. We analysed carefully all of the spectra with simultaneous X-ray and
UV observations. As a result, we found that joint UVOT-XRT SEDs can be classified
in three categories:
- a)
- described by a log-parabola (LP)
- b)
- described by a power law (PL)
- c)
- described by a spectral law that is a power law at its low energy tail,
becoming a log-parabola function at its high energy one (LPPL) (Massaro et al. 2006),
whose functional form can be expressed by
where is the spectral index of the SED (
is the spectral index of the SED (
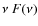 ), and
), and 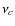 is
the frequency at which the turn-over in the SED occurs (Fig. 10).
is
the frequency at which the turn-over in the SED occurs (Fig. 10).
If the spectral shape is consistent with the same log-parabola extending from the X-ray band down to the UV band (case a), then it means that electrons radiating at UV frequencies belong to the same electron population and according to Eq. (12), we have
The condition
![]() may occur when we observe
a PL (case b) or a LPPL (case c).
If
may occur when we observe
a PL (case b) or a LPPL (case c).
If
![]() ,
then the spectra in the X-ray-to-UV band
will be described by the asymptotic low-energy approximation of the single particle synchrotron emission that is a power law with slope
,
then the spectra in the X-ray-to-UV band
will be described by the asymptotic low-energy approximation of the single particle synchrotron emission that is a power law with slope
![]() (
(
![]() )
(Rybicki & Lightman 1979).
)
(Rybicki & Lightman 1979).
For both cases b) and c) we note that our data infer
![]() ,
a value that differs significantly from the asymptotic synchrotron kernel expectation.
This implies that in both cases the UV photons probably are emitted by
an electron distribution that has a power-law tail in the energetic range
radiating in the UV-to-soft-X-ray band. A phenomenological option to explain the
case c) is an electron distribution that is a power law at low energies with a
log-parabolic high-energy branch (LPPL) (Massaro et al. 2006):
,
a value that differs significantly from the asymptotic synchrotron kernel expectation.
This implies that in both cases the UV photons probably are emitted by
an electron distribution that has a power-law tail in the energetic range
radiating in the UV-to-soft-X-ray band. A phenomenological option to explain the
case c) is an electron distribution that is a power law at low energies with a
log-parabolic high-energy branch (LPPL) (Massaro et al. 2006):
where
In the case b), the electron distribution is assumed to be a pure power-law.
Interestingly for case b) and case c), we can also constrain the typical slope
of the power-law branch of the electron distribution, using the well-known relation
between the spectral index in the particle distribution s and that in the SED
(Rybicki & Lightman 1979):
| (14) |
For the typical values of
The presence of a power-law feature and the range of observed spectral indices are relevant both in the context of Fermi first-order acceleration models and from an observational point of view.
From the observational side, we note that Waxman (1997) and
Mészáros (2002), studying the the afterglow X-ray emission of ![]() ray
bursts (GRB), inferred an electron distribution index of
ray
bursts (GRB), inferred an electron distribution index of
![]() .
This is close to those found in our data, but corresponds to a quite different
class of sources.
.
This is close to those found in our data, but corresponds to a quite different
class of sources.
From a theoretical point of view, several works study relativistic-shock
acceleration models that start from different analytical or numerical
approaches and find values of
![]() (Ellison & Double 2004; Achterberg et al. 2001; Gallant et al. 1999; Blasi & Vietri 2005; Lemoine & Pelletier 2003).
These values are consistent with those from our data set.
(Ellison & Double 2004; Achterberg et al. 2001; Gallant et al. 1999; Blasi & Vietri 2005; Lemoine & Pelletier 2003).
These values are consistent with those from our data set.
The power-law feature is also consistent with a purely stochastic scenario.
The usual limitation of the stochastic model to explain a
universal index relies on the fine tuning required to the ratio of
the acceleration timescale to the loss time (
![]() ),
to reproduce the observed values.
),
to reproduce the observed values.
We stress that a power-law electron distribution
![]() is inconsitent with a Maxwellian-like
distribution (
is inconsitent with a Maxwellian-like
distribution (
![]() )
resulting from the equilibrium
of SA processes without relevant particle escape.
)
resulting from the equilibrium
of SA processes without relevant particle escape.
In conclusion, both cases c) and b) are explained more accurately by a first order process. We will discuss this topic further in Sect. 9.
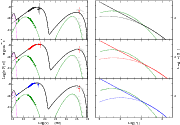 |
Figure 11: SSC fits of three different observations with simultaneous UVOT XRT and BAT data. Left panels show the SSC model, from top to bottom: solid circles represent data from 2006 April 22, 2006 June 23, and 2006 July 15 Swift observations. Green triangles show Swift-XRT data on 2005 March 31 from Tramacere et al. (2007b). Solid grey polygons represent non-simultaneous EBL corrected TeV data. Solid gray squares represent the high state on 2001 observed by Whipple, data from Albert et al. (2007). Solid gray diamonds represent the average 2004-2005 TeV spectrum as observed by MAGIC (Albert et al. 2007). Solid gray right triangles represent the average spectrum from December 2005 to February 2006 as observed by TACTIC (Yadav et al. 2007). The solid red triangle represents a Whipple observation on June 18, 19, 21 from Lichti et al. (2008), that is very close in time to our 2006 June 23 data set. The solid lines represent the best fit by a SSC model to our simultaneous Swift observation, and the dashed line is the best SSC fit to the Swift data on 03/31/2005. The dotted lines represent the modelling of the galaxy contribution by means of black body spectral shape. Right panels show the electron distributions for the SSC models in the left panels. The solid lines in the right panels represent the electron distributions for the best fit models of the three 2006 Swift observations, the dotted lines represent the extrapolation of the LP branch of the LPPL distribution, and the dashed lines represent the electron distribution for the 2005 March 31 data. |
| Open with DEXTER | |
Table 4: SSC best-fit model results for the 2006 Swift observations and using as electron distribution a log-parabola with a power-law low-energy branch (Eq. (13)).
Table 5: SSC best fit results for 2005 March 31 Swift observation and using a log-parabolic electron distribution as defined in Eq. (15).
8 SED modelling and GeV/MeV predictions
We model the SEDs of three observations with simultaneous XRT, BAT , and UVOT data, using a standard one-zone SSC scenario. The only useful TeV data found in the literature are from Whipple observations on June 18, 19, and 21 (Lichti et al. 2008). Almost simultaneous only with the 06/23/2006 Swift pointing, these data provide only the TeV flux, without giving a description of the spectrum. For this reason, they are only used to estimate the TeV flux level during that pointing.
To estimate the spectral and flux range of variability, we also plot Swift-XRT data from 2005 March 31 (Tramacere et al. 2007a), and some TeV SEDs representing the source in different flaring states (Yadav et al. 2007; Albert et al. 2007) (see left panel of Fig. 11).
The 2006 SEDs that we want to model have a power-law spectral dependence between
the UVOT and XRT bands. As described in Sect. 7, the most generic distribution
accounting for this spectral shape is a power-law at low energy with a log-parabolic
high-energy branch (Eq. (13)).
In contrast, the 2005 March 31 SED can be modelled using a log-parabolic electron
distribution that we express in terms of the peak energy as (LPEP):
Since we do not know the true shape and flux at TeV energies (we have only an estimate of the flux at
The first constraint comes from the source variability (see Sect. 3):
| (16) |
A second constraint comes from the analysis of the UVOT connection with the XRT data that provides an upper limit to
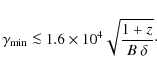 |
(17) |
To constrain the value of the maximum electron energy, we can use the maximum energy of the synchrotron emission, taking as the corresponding energy the most energetic bin of the BAT detector with a significant signal (
A further constraint on
Following Bednarek & Protheroe (1999) and combining Eqs. (19) and (18), we obtain an upper limit to the magnetic field:
The best-fit model was obtained by combining our numerical SSC code (Tramacere 2007) with a numerical minimizer. According to the observationally derived constraints, we fixed the value of the beaming factor to
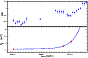 |
Figure 12:
Lower panel: the increase of |
| Open with DEXTER | |
In the left panels of Fig. 11 we show the best-fit model
results for the SSC model for the 2006 data and for the 2005 March 31 pointing.
In the right panels, we show the corresponding electron distributions.
The values of the electron curvature are consistent with those observed in the
X-ray emission according to the relation
![]() .
The typical value of the ratio
.
The typical value of the ratio
![]() corresponds to that
in a particle-dominated jet agreeing with the typical values for TeV HBLs peaking in the
hard X-ray (Kino et al. 2002; Sato et al. 2008).
The low-energy power-law branch of the electron energy distribution
follows
corresponds to that
in a particle-dominated jet agreeing with the typical values for TeV HBLs peaking in the
hard X-ray (Kino et al. 2002; Sato et al. 2008).
The low-energy power-law branch of the electron energy distribution
follows
![]() ,
in agreement with the analysis
presented in Sect. 7.
,
in agreement with the analysis
presented in Sect. 7.
We note that UV data are weakly contaminated by the host-galaxy emission.
In the left panel of Fig. 11, we plot the contribution of the galaxy emission modelled as a black-body spectral shape (dotted-line). This plot clearly shows how the UVOT data considered lie beyond the galaxy emission spectral cut-off. In contrast, during the low states, the possible power-law tail would lay typically at optical and lower frequencies, where the emission is typically dominated by the galaxy. This implies that we are unable to determine whether the electron distribution also has a power-law tail during the lower state. The SED model of data on 2005 March 31 shows that the UVOT points are consistent with the synchrotron emission from a log-parabolic electron population.
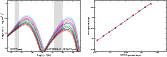 |
Figure 13:
The strong correlation between the UVOT spectral slope and that in the LAT band for a SSC
scenario. In the left panel we show the SSC SEDs and in
the right panel we show the correlation
between the spectral slope in the UVOT band and that in the Fermi- LAT band. Basic parameters
for the SSC model are: particle number density
|
| Open with DEXTER | |
If present in the 2005 SED, a power-law low-energy branch would yield an index harder than those from 2006, but of much lower flux.
Another interesting analysis can be performed by looking at the acceleration timescales
determined by the rate of the variation in EP. In particular, we can use
the e-folding time of ![]() to infer the electron acceleration timescale
to infer the electron acceleration timescale
![]() .
From
.
From
![]() ,
it follows that the rate of
change in
,
it follows that the rate of
change in ![]() can be related to the rate of change in
can be related to the rate of change in ![]() for electrons
radiating in the hard X-ray band. In Fig. 12, we show a
flare with well constrained values of
for electrons
radiating in the hard X-ray band. In Fig. 12, we show a
flare with well constrained values of ![]() for the rising side. In this
figure, we plot the values of
for the rising side. In this
figure, we plot the values of ![]() as a function of time. The e-folding
time for
as a function of time. The e-folding
time for ![]() results in a
results in a ![]() e-folding time of about 0.15 days,
which is the value of the typical acceleration timescale. This is the timescale
that will compete with the cooling one to generate the equilibrium in
the
e-folding time of about 0.15 days,
which is the value of the typical acceleration timescale. This is the timescale
that will compete with the cooling one to generate the equilibrium in
the ![]() distribution. In particular, taking into account the synchrotron cooling:
distribution. In particular, taking into account the synchrotron cooling:
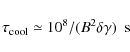 |
(21) |
the equilibrium of the distribution for a log-parabolic or Maxwellian-like distribution is the peak of
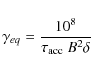 |
(22) |
For
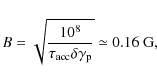 |
(23) |
which is consistent with the upper limit of Eq. (20) and with our best-fit model field strength.
8.1 The connection between the UV slope and that at MeV/GeV energies
An important consequence of the spectral shape in the UV band is due to the connection with the shape expected at MeV/GeV energies, and in particular in the Fermi Gamma-ray Space Telescope-LAT band.
To explore this, we simulated SSC emission by accounting for a typical HBL SED. As the electron distribution, we used a power-law at low energy with a log-parabolic high energy branch (LPPL) (Eq. (13)). The SSC parameter are reported in the caption of Fig. 13. In the left panel of this figure, we show different SEDs obtained by varying the s parameter in the range [2.1:2.5], and in the right panel, we show how the spectral shape in the UVOT band is tightly correlated with that in the Fermi-LAT energy range. This means that a comparison between the two spectral slopes derived from simultaneous observations can help us to determine whether the UV photons from the same component emitting in the X-ray are also responsible for the SSC emission.
9 Discussion
We have analysed the spectral and flux evolution of Mrk 421 during Swift observations between April and July 2006 , with the June pointings monitoring the source almost continuously for 12 days. During this period, the source exhibited both flux levels and SED peak energies each equal to their historic maximums until 2006. This very intense flaring state of Mrk 421 represented a unique opportunity to test the correlations among the spectral parameters presented in previous works (Tramacere et al. 2007b), increasing the temporal extent to about 10 years and enlarging the volume of the parameter space.The spectral evolution of the source and the patterns in the a-flux plane (Sect. 4) suggest that each flare had a different characterization in terms of competition between the relevant timescales. Some flares showed a rise in the hard and medium X-ray band much faster than observed in the soft X-rays. This behaviour is probably due to the flaring component starting in the hard X-ray band and implies that the driver of those flares is the rapid injection of very energetic particles rather than a gradual acceleration.
The
![]() and
and
![]() trends follow those presented in Tramacere et al. (2007b), where
trends follow those presented in Tramacere et al. (2007b), where
![]() and
and ![]() are correlated, and
are correlated, and ![]() ,
b anti-correlated. These trends are
relevant in understanding the physical mechanisms driving the evolution of
the electron distribution under the effect of acceleration processes and may
represent a common scenario for HBLs. Massaro et al. (2008) confirmed that
the
,
b anti-correlated. These trends are
relevant in understanding the physical mechanisms driving the evolution of
the electron distribution under the effect of acceleration processes and may
represent a common scenario for HBLs. Massaro et al. (2008) confirmed that
the
![]() relation holds for five of the TeV HBLs included in their analysis
(PKS 0548-322, 1H 1426+418, Mrk 501, 1ES 1959+650, PKS 2155-304)),
and that, as for
the
relation holds for five of the TeV HBLs included in their analysis
(PKS 0548-322, 1H 1426+418, Mrk 501, 1ES 1959+650, PKS 2155-304)),
and that, as for
the
![]() relation, the only exception to the previous list is PKS 2155-304.
relation, the only exception to the previous list is PKS 2155-304.
The
![]() relation shows a possible signature of acceleration processes that
produce curved electron distributions, where the curvature decreases as
the acceleration becomes more efficient.
A first consistent with these results is an energy-dependent
acceleration probability process (Massaro et al. 2004).
An alternative explanation is provided by the stochastic acceleration framework and
the presence of a momentum-diffusion term (Tramacere et al. 2007b; Kardashev 1962).
Both scenarios predict a negative correlation between
relation shows a possible signature of acceleration processes that
produce curved electron distributions, where the curvature decreases as
the acceleration becomes more efficient.
A first consistent with these results is an energy-dependent
acceleration probability process (Massaro et al. 2004).
An alternative explanation is provided by the stochastic acceleration framework and
the presence of a momentum-diffusion term (Tramacere et al. 2007b; Kardashev 1962).
Both scenarios predict a negative correlation between ![]() and b and
are consistent with the the data plotted in Fig. 8.
We note that the data presented here cover a significant range of the parameter
space, confirming that the relation between the curvature and the
peak energy follows the same trend between the faintest and the strongest flaring
activity, implying that the acceleration process remains the same.
and b and
are consistent with the the data plotted in Fig. 8.
We note that the data presented here cover a significant range of the parameter
space, confirming that the relation between the curvature and the
peak energy follows the same trend between the faintest and the strongest flaring
activity, implying that the acceleration process remains the same.
A future investigation may be focused on understanding which physical parameters control the acceleration process. An interesting investigation may be the connection of the stochastic scenario with the turbulence spectrum of the MHD waves and of the resulting diffusion coefficient (Katarzynski et al. 2006; Park & Petrosian 1995; Stawarz & Petrosian 2008; Becker et al. 2006). Understanding the role of both the turbulence spectrum and, in general, the fluctuation in the particle energy gain is a complex task and requires a more detailed analysis that is beyond the purpose of this paper and will be presented in Paper II (Tramacere 2009).
The
![]() trend demonstrates the connection between the average energy of the particle
distribution and the power output of the source. Compared with the observed values of
trend demonstrates the connection between the average energy of the particle
distribution and the power output of the source. Compared with the observed values of ![]() ,
the expected power-law dependence
,
the expected power-law dependence
![]() excludes
excludes ![]() and N, indicating
and N, indicating
![]() as the main driver of
the
as the main driver of
the
![]() trend, confirming the result from Tramacere et al. (2007b). A more
detailed analysis of the scatter plot reported in Fig. 9
revealed that the trend has a break at about 1 keV, where the typical source luminosity is
about
trend, confirming the result from Tramacere et al. (2007b). A more
detailed analysis of the scatter plot reported in Fig. 9
revealed that the trend has a break at about 1 keV, where the typical source luminosity is
about
![]() erg/s. This break may be interpreted as either an indicator of
the competition between systematic and momentum-diffusion acceleration or in terms
of the energetic content of the jet. We study this scenario in Paper II,
where also take into account the effect of the
erg/s. This break may be interpreted as either an indicator of
the competition between systematic and momentum-diffusion acceleration or in terms
of the energetic content of the jet. We study this scenario in Paper II,
where also take into account the effect of the
![]() trend on
trend on
![]() .
.
Another interesting result from our analyses is the presence a power-law tail connecting the UV data to the soft-X-ray ones. As explained in Sect. 7, we cannot determine whether this tail is a characteristic only of highly energetic flares, or whether it is also present during low states. In the latter case, it would be puzzling to relate a harder index with a lower flux. If this feature were present only during strong flares then a relevant change may have occurred in the acceleration environment. Both the SA and EDAP scenarios require the presence of a significant escape term to develop a power-law tail.
The value of the power-law spectral index in the electron distribution
![]() is close to the prediction of relativistic Fermi first-order acceleration
models (Ellison & Double 2004; Achterberg et al. 2001; Gallant et al. 1999; Blasi & Vietri 2005; Lemoine & Pelletier 2003) and is
similar to that found in the X-ray observations of GRB afterglows (Waxman 1997).
is close to the prediction of relativistic Fermi first-order acceleration
models (Ellison & Double 2004; Achterberg et al. 2001; Gallant et al. 1999; Blasi & Vietri 2005; Lemoine & Pelletier 2003) and is
similar to that found in the X-ray observations of GRB afterglows (Waxman 1997).
This observational feature, which is in close agreement with first-order acceleration
models, may contradict the results from the
![]() trend,
supporting a stochastic scenario. A more careful analysis indicates that such
a contradiction is only apparent. As demonstrated by Spitkovsky (2008),
diffusive shock acceleration models rely on the presence of a magnetic turbulence close to
the shock responsible for the scattering process, although these models do not
clearly determine the possible role of turbulence in the acceleration.
Our observational analysis appears to indicate the simultaneous
roles of the first and second order processes, where the stochastic acceleration
arises from the magnetic turbulence and is indicated by the curvature and more generally
by the
trend,
supporting a stochastic scenario. A more careful analysis indicates that such
a contradiction is only apparent. As demonstrated by Spitkovsky (2008),
diffusive shock acceleration models rely on the presence of a magnetic turbulence close to
the shock responsible for the scattering process, although these models do not
clearly determine the possible role of turbulence in the acceleration.
Our observational analysis appears to indicate the simultaneous
roles of the first and second order processes, where the stochastic acceleration
arises from the magnetic turbulence and is indicated by the curvature and more generally
by the
![]() relation, and the first order is indicated by the slope of the electron
power-law tail.
relation, and the first order is indicated by the slope of the electron
power-law tail.
In these circumstances the study of the curvature may offer an observational constraint for the turbulence properties, and may be used to constraint recursively the scattering process close to the shock in the first order models.
We also note that the model presented by Spitkovsky (2008), in which the shock
acceleration process is studied in a self-consistent fashion, provides results that
are consistent with our phenomenological picture.
The result from this numerical study is a relativistic
Maxwellian, and a high-energy tail with
![]() ,
plus an exponential cut-off
moving to higher energies with time of the simulation.
,
plus an exponential cut-off
moving to higher energies with time of the simulation.
This phenomenological scenario underlines the relevance of the multi-wavelength observations, and highlights the pitfalls of extrapolating the observed spectral shape over too wide a range. In this regard, we emphasize the unique capabilities of Swift to perform simultaneous UV-to-X-ray observations.
Concerning the UV observations, a further point is given by the expected
correlation of this spectral band with MeV/GeV band. Because of the effect of
the Klein-Nishina suppression in the Inverse Compton process, we expect the UV
photons to be upscattered the most efficiently at GeV energies by the electrons
radiating in the X-ray. This implies a strong correlation between the spectral slope in the
UV-to-soft-X-ray band and the slope at both MeV/GeV energies and in particular, in the
Fermi-LAT band. It would be useful to test this correlation to understand
whether the photons upscattered at ![]() -ray energies are cospatial with the
electrons emitting in the X-ray.
-ray energies are cospatial with the
electrons emitting in the X-ray.
10 Conclusions
We have illustrated the complexity of the physical scenario at work in the jets of HBL objects. We have shown that the flaring activity of Mrk 421 not only causes enormous flux variation but also results in complex spectral evolutions and drastic changes in the electron energy distribution. The evolution in the spectral parameters, in particularAs a final emphasize, we stress that as already pointed out in Massaro et al. (2006), the curvature observed in the X-ray spectra of HBLs is reflected in the TeV spectrum. The consequence is that the TeV cut-off observed in the nearby HBLs is almost entirely due to the intrinsic electron curvature rather than to the interaction with EBL photons. This scenario is therefore consistent with a low EBL density that makes the universe more transparent to high-energy radiation than previously assumed, which is consistent with the discovery of HBLs objects at high redshift, such as H 2356-309 (z=0.165), 1ES 1101-232 (z=0.186) (Aharonian et al. 2006), and 1ES 128-304 (z=0.182) (Albert et al. 2006).
Acknowledgements
A. Tramacere acknowledges support by a fellowship of the Italian Space Agency (ASI) and Istituto Nazionale di Astrofisica (INAF) related to the GLAST Space Mission, through the ASI/INAF I/010/06/0 contract. Gino Tosti acknowledges support by the ASI/INAF I/010/06/0 contract. We thank Dr. D. Paneque and Dr. S. Digel for useful comments.
Table 2: Swift-XRT spectral analysis of Mrk 421.
Table 3:
Swift-XRT orbit merged spectral analysis of Mrk 421.
References
Footnotes
- ... threads
![[*]](/icons/foot_motif.png)
- http://swift.gsfc.nasa.gov/docs/swift/analysis/threads/batspectrumthread.html
- ... distance
![[*]](/icons/foot_motif.png)
- We used a flat
cosmology model with H0=0.71 km/(s Mpc)
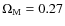 and
and
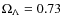 .
.
All Tables
Table 1: Swift observation journal and exposures of Mrk 421.
Table 4: SSC best-fit model results for the 2006 Swift observations and using as electron distribution a log-parabola with a power-law low-energy branch (Eq. (13)).
Table 5: SSC best fit results for 2005 March 31 Swift observation and using a log-parabolic electron distribution as defined in Eq. (15).
Table 2: Swift-XRT spectral analysis of Mrk 421.
Table 3: Swift-XRT orbit merged spectral analysis of Mrk 421.
All Figures
 |
Figure 1: From top to bottom: a) light curve of the flux in the band 0.2-10.0 keV. b) light curves for three different bands soft (0.2-3.0 keV, red points) medium (3.0-5.0 keV, green points) and hard ( 5.0-10.0 keV, blue points), normalized to their maximum value. c) the evolution of the hardness ratio (HR) evaluated as the ratio of the 2.0-10.0 keV band to the 0.2-2.0 keV band. d) light curve from the Swift-UVOT instrument, different colors refers to different filters (V = brown, U = black, UVM2 = red, UVW1 = blue, UVW2 = yellow). (See the electronic edition of the Journal for a color version of this figure) |
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
Light curve binned with 50 s intervals,
from the first orbit of the 2006 April 26 pointing. Significant variability ( |
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
Spectrum from the first orbit of the ObsID 00030352013 performed
on 2006 June 22. Left Panel: the systematic deviations on both sides of
the residuals from a best fit with a power-law with Galactic |
| Open with DEXTER | |
| In the text | |
 |
Figure 4: Joint XRT BAT spectral analysis from the 2006 April 22 pointing. |
| Open with DEXTER | |
| In the text | |
 |
Figure 5: Scatter plot of the HR vs. the flux in the 0.2-10 keV band (HR is evaluated as the ratio of the 2.0-10.0 keV band to the 0.2-2.0 keV band). The points in the shaded area are almost all from the period 2006 June 23 to 2006 June 27 and 2006 July 15. |
| Open with DEXTER | |
| In the text | |
 |
Figure 6: Left panels: spectral patterns in the a-flux plane showing clockwise and counterclockwise trends. Right panels: Swift-XRT light curves at three different bands: soft (0.2-3.0 keV, red), medium (3.0-5.0 keV, green), and hard ( 5.0-10.0 keV, red) . Capital letters guide the reader during the comment in the text. In both left and right panels, the fluxes are normalized to the maximum value reached during that particular time-interval. |
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Left panels: spectral patterns in the a-flux plane showing clockwise and counterclockwise trends. Right panels: Swift-XRT light curves at three different bands: soft (0.2-3.0 keV, red), medium (3.0-5.0 keV, green), and hard ( 5.0-10.0 keV, red) . Capital letters are referenced in the discussion in the text. In both left and right panels, the fluxes are normalized to the maximum value reached during that particular time interval. |
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
Scatter plot of the curvature (b) vs. |
| Open with DEXTER | |
| In the text | |
 |
Figure 9:
Scatter plot of |
| Open with DEXTER | |
| In the text | |
 |
Figure 10: Three different spectral shapes from the data presented in this paper. Red boxes represent a power-law spectrum observed during Orbit 3 (ObsID 00030352010) on 2006 June 16. Blue diamonds represent a spectrum that is a log-parabola with a low energy power-law tail, from Orbit 3 (ObsID 00030352005) on 2006 April 25. Green circles represent a log-parabolic spectrum from Orbit 4 (ObsID 00030352008) on 2006 June 14. |
| Open with DEXTER | |
| In the text | |
 |
Figure 11: SSC fits of three different observations with simultaneous UVOT XRT and BAT data. Left panels show the SSC model, from top to bottom: solid circles represent data from 2006 April 22, 2006 June 23, and 2006 July 15 Swift observations. Green triangles show Swift-XRT data on 2005 March 31 from Tramacere et al. (2007b). Solid grey polygons represent non-simultaneous EBL corrected TeV data. Solid gray squares represent the high state on 2001 observed by Whipple, data from Albert et al. (2007). Solid gray diamonds represent the average 2004-2005 TeV spectrum as observed by MAGIC (Albert et al. 2007). Solid gray right triangles represent the average spectrum from December 2005 to February 2006 as observed by TACTIC (Yadav et al. 2007). The solid red triangle represents a Whipple observation on June 18, 19, 21 from Lichti et al. (2008), that is very close in time to our 2006 June 23 data set. The solid lines represent the best fit by a SSC model to our simultaneous Swift observation, and the dashed line is the best SSC fit to the Swift data on 03/31/2005. The dotted lines represent the modelling of the galaxy contribution by means of black body spectral shape. Right panels show the electron distributions for the SSC models in the left panels. The solid lines in the right panels represent the electron distributions for the best fit models of the three 2006 Swift observations, the dotted lines represent the extrapolation of the LP branch of the LPPL distribution, and the dashed lines represent the electron distribution for the 2005 March 31 data. |
| Open with DEXTER | |
| In the text | |
 |
Figure 12:
Lower panel: the increase of |
| Open with DEXTER | |
| In the text | |
 |
Figure 13:
The strong correlation between the UVOT spectral slope and that in the LAT band for a SSC
scenario. In the left panel we show the SSC SEDs and in
the right panel we show the correlation
between the spectral slope in the UVOT band and that in the Fermi- LAT band. Basic parameters
for the SSC model are: particle number density
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.