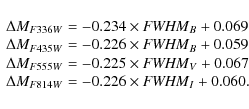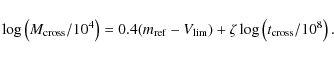| Issue |
A&A
Volume 501, Number 3, July III 2009
|
|
|---|---|---|
| Page(s) | 949 - 964 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200810614 | |
| Published online | 29 April 2009 | |
Imaging of star clusters in unperturbed spiral galaxies with the Advanced Camera for Surveys![[*]](/icons/foot_motif.png)
II. A comparison of star cluster systems in five late type
spirals![[*]](/icons/foot_motif.png)
M. D. Mora1 - S. S. Larsen2 - M. Kissler-Patig3 - J. P. Brodie4 - T. Richtler5
1 -
Departamento de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaíso. Av. Gran Bretaña 1111, Valparaíso, Chile
2 -
Astronomical Institute, University of Utrecht, Princetonplein 5,
3584 CC, Utrecht, The Netherlands
3 -
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
4 -
UCO/Lick Observatory, University of California, Santa Cruz, CA 95064, USA
5 -
Universidad de Concepción, Departamento de Astronomía. Casilla 160-C, Concepción, Chile
Received 15 July 2008 / Accepted 3 February 2009
Abstract
Aims. Our goal is to investigate the formation of star clusters in relatively unperturbed environments. To do this, we studied the five nearby spiral galaxies: NGC 45, NGC 1313, NGC 4395, NGC 5236, and NGC 7793.
Methods. We obtained images of the galaxies and their star cluster systems in
![]() using the Advanced Camera for Surveys (ACS) and the Wide Field Planetary Camera 2 (WFPC2) on board the Hubble Space Telescope. From a comparison of the broad-band colours with simple stellar population (SSP) models, we derived individual properties for each galaxy for the clusters such as masses, ages, and sizes, as well as global star cluster system properties such as the age distribution, luminosity function, and disruption time for clusters.
using the Advanced Camera for Surveys (ACS) and the Wide Field Planetary Camera 2 (WFPC2) on board the Hubble Space Telescope. From a comparison of the broad-band colours with simple stellar population (SSP) models, we derived individual properties for each galaxy for the clusters such as masses, ages, and sizes, as well as global star cluster system properties such as the age distribution, luminosity function, and disruption time for clusters.
Results. We identified about 600 star cluster candidates in the five galaxies, typically spanning ages from 3.9 Myr up to 1 Gyr and masses from 102 ![]() up to 105
up to 105 ![]() .
We used the cluster age distribution to reconstruct the recent star formation history of each galaxy and observed significant variations from galaxy to galaxy. We went on to derive the luminosity function of the young star clusters and found slopes around
.
We used the cluster age distribution to reconstruct the recent star formation history of each galaxy and observed significant variations from galaxy to galaxy. We went on to derive the luminosity function of the young star clusters and found slopes around
![]() (similar to the ones found in previous studies) and the brightest star cluster magnitudes consistent with a random sampling of the luminosity function without involving an upper luminosity cut off. Finally, the sample includes only a handful of old globular clusters in each galaxy from which we derive low globular cluster specific frequencies.
(similar to the ones found in previous studies) and the brightest star cluster magnitudes consistent with a random sampling of the luminosity function without involving an upper luminosity cut off. Finally, the sample includes only a handful of old globular clusters in each galaxy from which we derive low globular cluster specific frequencies.
Key words: galaxies: star clusters - galaxies: photometry
1 Introduction
The formation of star clusters accompanies the formation of stars in the evolution of a galaxy; and yet, the final ratio of stars to clusters is observed to vary considerably (Harris 1991), and it remains unclear which factors influence this ratio. Understanding this aspect is, however, important for progressing in our general understanding of both star formation in a galaxy and the formation mechanisms of star clusters.
One particular aspect is the influence of environment and the extent it affects the star cluster formation. We have evidence that violent star-forming events, such as galaxy mergers and starbursts, stimulate star cluster formation (e.g.Harris et al. 2004; Whitmore & Schweizer 1995; Holtzman et al. 1992; Bastian et al. 2005c). But large-scale mergers are not necessarily needed for the formation of massive clusters. Young globular clusters are also observed in the starbursts of blue compact dwarf galaxies (Conti & Vacca 1994) and their formation efficiency has also been found to positively correlate with the star formation rate in more or less ``normal'' spiral galaxies (e.g. Larsen & Richtler 2000).
But the ratio of stars to clusters is dictated not only by the formation mechanism, but it is also a function of the destruction processes, in particular the ones that affect young star clusters at early stages of their evolution. Disruption times of young star clusters as a function of their properties (e.g. Fall 2004,2006; Boutloukos & Lamers 2003) or as a function of the interactions between them and their surrounding media such as spiral arms and molecular clouds (e.g. Gieles et al. 2006b,2007a), have attracted considerable interest in the past few years. Are destruction processes the main drivers of the varying star-to-cluster ratios observed in galaxies? (See Pellerin et al. (2007) for a star field approach to this question in NGC 1313.)
In this paper, we investigate both the formation and disruption history of star clusters in the relatively unperturbed environments of normal, non-interacting disk galaxies.
We build on our first example NGC 45 (Mora et al. 2007),
and extend the analysis to four more spiral galaxies: NGC 1313, NGC 4395, NGC 5236, and NGC 7793.
Our sample includes late-type galaxies with both grand-design and
flocculent spiral structure, spanning a wide range in area-normalised
star formation rate (Larsen & Richtler 2000) and cluster surface
density as determined from ground-based observations. To minimize
the extinction, all galaxies are close to face-on orientation and
all have a similar distance modulus of
![]() .
.
The five galaxies of our sample have been previously studied from the ground by Larsen & Richtler (2000,1999) and Larsen (1999). Massive star cluster candidates were found, supporting the fact that they can form as an continuos process, as well as in star formation bursts. Also that ratio of stars to clusters correlates with the star formation rate, and the formation of young massive star clusters is favoured in environments with active star formation. The formation of massive young star clusters in starburst or mergers may be the extreme case of a more general phenomenon.
Taking advantage of the excellent spatial resolution of the Advanced Camera for Surveys (ACS) on board of HST, we investigate in this work how the star cluster properties, such as sizes, ages, masses, disruption time-scales, compare between the galaxies of the sample. The work is structured as follows. The observations, data reduction, photometry and completeness analysis are described in Sect. 2. In Sect. 3, we explain our star cluster selection criteria, before showing the colour-colour and colour-magnitude diagrams for the star clusters in Sect. 4. In Sect. 5, we discuss the properties of individual clusters, such as masses, ages, extinctions, and measured sizes. In Sects. 6 and 7, we turn to the global properties of the systems and present the star cluster luminosity functions, and star cluster age distributions, respectively. In Sect. 8 and 9, we briefly get back to extended objects and old globular clusters. Finally, in Sect. 10, we discuss our results and draw some conclusions.
Throughout this work, we frequently followed procedures tested and outlined in our pilot study of NGC 45 (Mora et al. 2007) and refer to this paper for details.
2 Observation and reductions
The galaxies were observed with the HST ACS Wide Field Channel and the WFPC2. The pixel
scales are 0.05
![]() and 0.1
and 0.1
![]() for the ACS and the WFPC2, respectively.
Two different regions were observed for each galaxy , with the exception of NGC 1313 for which three
pointings were obtained. All ACS pointings, together with the WFPC2 footprint are shown in Fig. 1. Exposure times and pointing coordinates are listed in Table 1.
for the ACS and the WFPC2, respectively.
Two different regions were observed for each galaxy , with the exception of NGC 1313 for which three
pointings were obtained. All ACS pointings, together with the WFPC2 footprint are shown in Fig. 1. Exposure times and pointing coordinates are listed in Table 1.
The ACS images, after the standard ``on-the-fly'' pipeline reduction, were drizzled using the MULTIDRIZZLE task (Koekemoer et al. 2002) in the STSDAS / PyRAF package. We used default parameter values but disabled the automatic sky subtraction due to the highly non-uniform background level. The WFPC2 images were combined using the CRREJ task with standard parameter settings.
![\begin{figure}
\par\mbox{\includegraphics[width=5.3cm]{0614fig1.ps} \includegrap...
...5.3cm]{0614fig8.ps} \includegraphics[width=5.3cm]{0614fig9.ps} }
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg16.png) |
Figure 1: ACS colour images for all pointings of our galaxy sample, with over-layed WFPC2 field-of-view. The arrows indicate North. |
| Open with DEXTER | |
Table 1: Pointing coordinates and exposure times for the galaxies in our sample. For NGC 45 see Mora et al. (2007)
Table 2: Summary of galaxy properties.
2.1 Photometry
Sources were detected in the deepest ACS band (
![]() )
using
the SExtractor (Bertin & Arnouts 1996) package and setting the detection threshold to
5 connected pixels 4 sigma over the background.
The coordinates of the detected objects were used as input for the SExtractor
runs in the two other ACS bands.
)
using
the SExtractor (Bertin & Arnouts 1996) package and setting the detection threshold to
5 connected pixels 4 sigma over the background.
The coordinates of the detected objects were used as input for the SExtractor
runs in the two other ACS bands.
The aperture photometry in ![]() was performed with the PHOT task (using the SExtractor coordinates as input) in IRAF
was performed with the PHOT task (using the SExtractor coordinates as input) in IRAF![]() .
At the distance of our galaxies (
.
At the distance of our galaxies (![]() 5 Mpc), the ACS pixel
size corresponds to
5 Mpc), the ACS pixel
size corresponds to ![]() 1 pc, while typical star cluster sizes are a few pc.
As a compromise between the object size and crowding, we used for the photometry an aperture radius of 6 pix (with the sky determined in an annulus 5 pix wide at
8 pix radius).
1 pc, while typical star cluster sizes are a few pc.
As a compromise between the object size and crowding, we used for the photometry an aperture radius of 6 pix (with the sky determined in an annulus 5 pix wide at
8 pix radius).
The
![]() -band photometry was performed on the WFPC2 images.
Here also, we used the ACS object coordinates, transformed (using
-band photometry was performed on the WFPC2 images.
Here also, we used the ACS object coordinates, transformed (using ![]() 20 common objects and the task GEOMAP) into the WFPC2 frames, to identify the objects. The
transformed coordinates were accurate to
20 common objects and the task GEOMAP) into the WFPC2 frames, to identify the objects. The
transformed coordinates were accurate to ![]() 0.5 pix rms and
were used as input for the WFPC2 aperture photometry.
The aperture photometry and sky determination in the WFPC2 images were done using the same physical sizes as used for the ACS images: 3 pix aperture radius (sky annulus at 4 pix, 2.5 pix wide)
for the WFPC2; and 6 pix aperture radius (sky annulus at 8 pix, 5 pix wide) for the Planetary Camera (PC).
0.5 pix rms and
were used as input for the WFPC2 aperture photometry.
The aperture photometry and sky determination in the WFPC2 images were done using the same physical sizes as used for the ACS images: 3 pix aperture radius (sky annulus at 4 pix, 2.5 pix wide)
for the WFPC2; and 6 pix aperture radius (sky annulus at 8 pix, 5 pix wide) for the Planetary Camera (PC).
The counts were converted to the Vega magnitude
system using the HST zero points taken from the HST web
page![]() based
on the spectrophotometric calibration of Vega from Bohlin & Gilliland (2004).
Also charge transfer efficiency corrections were applied to the
based
on the spectrophotometric calibration of Vega from Bohlin & Gilliland (2004).
Also charge transfer efficiency corrections were applied to the
![]() band following the updated version of
Dolphin (2000)
band following the updated version of
Dolphin (2000)![]() .
.
In Fig. 2 we show the photometric error versus magnitude for objects detected on the ACS and the WFPC2 (
![]() )
down to mag = 24. Photometry from the ACS shows errors lower than 0.2 mag down to mag = 24, while the photometry from the WFPC2 shows errors below 0.5 mag, reflecting that
)
down to mag = 24. Photometry from the ACS shows errors lower than 0.2 mag down to mag = 24, while the photometry from the WFPC2 shows errors below 0.5 mag, reflecting that
![]() images are not as deep as the ACS exposures (despite that
images are not as deep as the ACS exposures (despite that
![]() exposures have the longest exposure time).
exposures have the longest exposure time).
The aperture corrections were performed in the same way as in Mora et al. (2007):
we created 6 artificial source types with different FWHMs: 0.2, 0.5, 0.9, 1.2, 1.5, and 1.8 pixels.
On each of them, we performed the aperture correction from 6 pixels up to a nominal
1.
![]() 45 reference aperture for the ACS and the WFPC2, and thus derived an empirical relation between the object sizes and their aperture correction.
In this way, we corrected the photometry of each object according to its size.
Because the object sizes were only measured in the ACS band (and not in the WFPC2 frames), we assumed
that objects have the same size in the U-band as on the F435W images.
The aperture corrections that we derive as a function of FWHM (in pix) are
45 reference aperture for the ACS and the WFPC2, and thus derived an empirical relation between the object sizes and their aperture correction.
In this way, we corrected the photometry of each object according to its size.
Because the object sizes were only measured in the ACS band (and not in the WFPC2 frames), we assumed
that objects have the same size in the U-band as on the F435W images.
The aperture corrections that we derive as a function of FWHM (in pix) are
For an object size
2.2 Size measurements
As a next step, we disentangled extended objects from point-like sources by measuring their intrinsic, PSF-corrected sizes (as opposed to FWHM on the images). This was performed using the ISHAPE task in BAOLAB (Larsen 1999): each source was modelled using a King (1962) profile with a concentration parameter c=30, convolved with the instrument PSF (as derived from images of the globular cluster 47 Tuc, see Mora et al. (2007) for details). For each object the output of ISHAPE included the physical FWHM, chi-square of the fitting, flux, signal to noise, and a residual image. These sizes are discussed below in Sects. 5.4 and 9.1.1.
2.3 Completeness tests
By adding artificial objects to our images, we quantified our detection limits and test the reliability of the derived magnitudes and sizes using a series of completeness tests.
For these tests, we selected the most crowded field for each galaxy (pointing 1 in all cases) and added 300 artificial objects in three different regions: 100 objects were added at random position in each of a low-/intermediate-/high-background region. We followed the process described in more detail in Mora et al. (2007) and finally compared the number of added and recovered stars in each field.
For each galaxy, the estimated completeness fraction versus magnitude for objects of different
sizes, as well as the uncertainty on the size as a function of magnitude, are shown in Fig. 3.
As expected, extended objects are more difficult to detect than less extended ones. For objects with
![]() pix, we computed a 50% completeness limit between
pix, we computed a 50% completeness limit between
![]() and 25.3 mag.
and 25.3 mag.
As for the sizes, we show the average value of the absolute difference between the input and recovered FWHM.
We notice that extended objects in more crowded galaxies (NGC 7793 and NGC 5236) have
greater uncertainties than the same extended objects in less crowded galaxies at the same magnitude.
On average, sizes can be measured with an accuracy of ![]() 0.2 pix down to about one magnitude above the 50% completion limit.
0.2 pix down to about one magnitude above the 50% completion limit.
3 Star cluster selection
3.1 Sample selection by size and brightness limit
We based the selection of star clusters on the object size, as measured both by ISHAPE and by SExtractor. Similar to the procedure in Mora et al. (2007), we excluded all point sources and considered all extended objects as star cluster candidates.
The ISHAPE and SExtractor size distributions display narrow peaks, with the vast majority of objects at
![]() pixels and
pixels and
![]() pixels, respectively (see Fig. 4). These are considered to be point sources, and we define the above thresholds as our cut-on for star cluster candidates. This corresponds to physical sizes of roughly 0.3 pc and greater at the distance of our sample, which should not exclude any star cluster. The largest objects have sizes up to 10 pc, similar to the largest clusters observed in the Milky Way.
pixels, respectively (see Fig. 4). These are considered to be point sources, and we define the above thresholds as our cut-on for star cluster candidates. This corresponds to physical sizes of roughly 0.3 pc and greater at the distance of our sample, which should not exclude any star cluster. The largest objects have sizes up to 10 pc, similar to the largest clusters observed in the Milky Way.
In a second step, we apply an absolute magnitude cut-off to the complete sample. In order to do so, we determined the limiting magnitude (at 60% completeness) for the worst case (extended objects in NGC 7793) to be
![]() .
This corresponds to an absolute magnitude
.
This corresponds to an absolute magnitude
![]() at the distance of our sample
and we apply it to the rest of the galaxies.
at the distance of our sample
and we apply it to the rest of the galaxies.
In summary, we selected objects more extended than ![]() 0.3 pc in size, and brighter than -5 mag in MV as star cluster candidates for our further analysis.
The number of objects detected in the ACS fields and the sub-group included in the WFPC2 fields are listed in Table 3.
0.3 pc in size, and brighter than -5 mag in MV as star cluster candidates for our further analysis.
The number of objects detected in the ACS fields and the sub-group included in the WFPC2 fields are listed in Table 3.
3.2 Selection of old star clusters in the colour-magnitude diagrams
We focussed in this work on young stellar clusters, but will discuss the population of old globular clusters further below. In order to identify the population of old globular clusters in our sample galaxies, we used the colour-magnitude diagrams, shown in Fig. 5. In the case of face-on spiral-galaxies, disentangling the old from the young star cluster population is a challenging task, as young reddened star clusters might exhibit similar colours to old globular clusters. Reddening will, however, make the star clusters appear fainter, so that by imposing both a colour and magnitude cut, we can recover the bright fraction of the old globular cluster population.
To do this, we chose the
![]() colour-magnitude diagrams, most capable of separating the two populations.
The clearest separation in our sample between young and old cluster candidates are seen in NGC 5236,
where the young star cluster population is limited to
colour-magnitude diagrams, most capable of separating the two populations.
The clearest separation in our sample between young and old cluster candidates are seen in NGC 5236,
where the young star cluster population is limited to
![]() and centred
at
and centred
at
![]() .
The globular cluster candidates have
.
The globular cluster candidates have
![]() .
As expected, below
the turn-over magnitude of the globular cluster luminosity function (GCLF in Fig. 5) reddened young
cluster increasingly scatter into the globular cluster colours.
.
As expected, below
the turn-over magnitude of the globular cluster luminosity function (GCLF in Fig. 5) reddened young
cluster increasingly scatter into the globular cluster colours.
For further analysis (see Sect. 9), we use the case of NGC 5236, to adopt the selection criteria for globular
cluster candidates, therefore we will consider objects with colours
![]() and
and
![]() magnitude brighter than 0.2 mag below the globular cluster luminosity function turn over as globular clusters; i.e.
magnitude brighter than 0.2 mag below the globular cluster luminosity function turn over as globular clusters; i.e.
![]() where
where
![]() from Carney (2001). These criteria yield 4 globular cluster candidates in NGC 1313 and NGC 7793,
8 globular cluster candidates in NGC 5236, and none in NGC 4395.
from Carney (2001). These criteria yield 4 globular cluster candidates in NGC 1313 and NGC 7793,
8 globular cluster candidates in NGC 5236, and none in NGC 4395.
![\begin{figure}
\par\includegraphics[width=9.3cm]{0614fi10.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg55.png) |
Figure 2: Photometric error versus magnitude. Each row corresponds to the error as function of magnitude for each galaxy. The corresponding passband is indicated on each panel. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm]{0614fi11.ps} \includegraphics[width=9cm]{0614fi12.ps} }
\par\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg56.png) |
Figure 3: Left: completeness in object finding as a function of magnitude for our four galaxies. Right: average absolute difference between the input and recovered FWHM as a function of object magnitude. |
| Open with DEXTER | |
4 Colour-colour distributions
The determination of ages, masses, and internal extinction towards our candidate clusters relies on colour-colour diagrams that we briefly present in this section.
In Fig. 6 the colour-colour diagrams (corrected for foreground extinction but not for internal extinction)
are shown for all the galaxies. Simple stellar population (SSP) models from GALEV (Anders & Fritze-v. Alvensleben 2003) and Girardi
(private communication)![]() for different metallicities are overplotted.
for different metallicities are overplotted.
Ages increase along the tracks from blue towards redder colours . The feature around
![]() and
and
![]() is strongly
metallicity dependent and corresponds to the appearance of the red supergiant stars at 107 yr.
In general, star clusters have colours which are in agreement with the theoretical tracks. Some prominent features are:
is strongly
metallicity dependent and corresponds to the appearance of the red supergiant stars at 107 yr.
In general, star clusters have colours which are in agreement with the theoretical tracks. Some prominent features are:
- in the case of NGC 4395, star clusters are seen in two groups, one at
 (corresponding to
(corresponding to 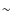 3.9-10 Myr) and the other at
3.9-10 Myr) and the other at
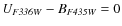 (corresponding to
(corresponding to
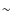
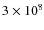 yr). According to the position of
the clusters and the model track, there are no clusters older than 109 yr;
yr). According to the position of
the clusters and the model track, there are no clusters older than 109 yr;
- in the case of NGC 7793, star clusters are seen along the model tracks uniformly
distributed. NGC 7793 does not show clusters redder than
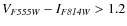 ;
;
- NGC 5236, as well as NGC 1313, show star clusters concentrated at intermediates ages,
mostly around 100 Myr (
 ). Several star clusters are seen
below the model tracks (at
). Several star clusters are seen
below the model tracks (at
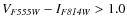 ), consistent with being reddened, very young star clusters;
), consistent with being reddened, very young star clusters;
- NGC 1313 shows a minor concentration of young (
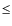 107 yr) star clusters at
107 yr) star clusters at
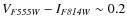 and
and
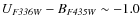 .
.
5 Ages, masses, and sizes
5.1 Fitting ages, masses, and internal extinction simultaneously
In this section, we discuss the ages, masses, the process of deriving them, and the sizes of the star clusters
in more details. One of the main problems in deriving ages and masses is
the uncertainty of the internal extinction toward the individual
star clusters. This makes it impossible to compare directly-observed star cluster colours and magnitudes with
SSP models. This can be solved using a method known as ``3D fitting'' (Bik et al. 2003).
The method relies on simple stellar populations (SSP) models (broad band colours as
a function of age for fixed metallicities) and compares model colours with the observed ones,
searching for the best-fitting extinction and age for each star cluster, using a minimum ![]() criteria. Masses are derived using the mass-to-light ratios predicted by the models in combination
with the reddening-corrected observed magnitudes and an assumed distance modulus.
The extinction toward individual clusters was fitted in steps of
E(B-V)=0.01 (extinction steps smaller than
E(B-V)=0.01 do not change the final output values) introducing some discretisation in the ages and masses.
criteria. Masses are derived using the mass-to-light ratios predicted by the models in combination
with the reddening-corrected observed magnitudes and an assumed distance modulus.
The extinction toward individual clusters was fitted in steps of
E(B-V)=0.01 (extinction steps smaller than
E(B-V)=0.01 do not change the final output values) introducing some discretisation in the ages and masses.
Two different SSP models were used for comparison: the GALEV (Anders & Fritze-v. Alvensleben 2003) and the Girardi
(private communication) models![]() .
The GALEV models are based on the SSP models of Schulz et al. (2002) including gaseous continuum and line emission assuming a Salpeter or Scalo IMF (in this work we used only the Salpeter IMF). The models have an age range from 3.98 Myr up to
15.9 Gyr for all the metallicities ranging from Z=0.0004 to Z=0.05.
The Girardi SSP models are based on a combination of stellar evolutionary tracks from Girardi et al. (2000)
(low and intermediate-mass stars), Bertelli et al. (1994) and Girardi et al. (1996), all including convective
overshooting and assuming radiative opacities from Iglesias et al. (1992).
Girardi models have an age range from 3.98 Myr up to 17.7 Gyr for the metallicities
Z=0.004 and Z=0.019; and an age range from 63 Myr up to 17.7 Gyr for the metallicities Z=0.001 and Z=0.03.
.
The GALEV models are based on the SSP models of Schulz et al. (2002) including gaseous continuum and line emission assuming a Salpeter or Scalo IMF (in this work we used only the Salpeter IMF). The models have an age range from 3.98 Myr up to
15.9 Gyr for all the metallicities ranging from Z=0.0004 to Z=0.05.
The Girardi SSP models are based on a combination of stellar evolutionary tracks from Girardi et al. (2000)
(low and intermediate-mass stars), Bertelli et al. (1994) and Girardi et al. (1996), all including convective
overshooting and assuming radiative opacities from Iglesias et al. (1992).
Girardi models have an age range from 3.98 Myr up to 17.7 Gyr for the metallicities
Z=0.004 and Z=0.019; and an age range from 63 Myr up to 17.7 Gyr for the metallicities Z=0.001 and Z=0.03.
In Fig. 7 we plot the derived cluster masses against cluster ages for our five galaxies, as a function of four different metallicities from the GALEV and the Girardi models, respectively. The discrete extinction and age grids create stripes and gaps at fixed ages (see also Whitmore et al. 2007; Bik et al. 2003; Fall et al. 2005; Gieles et al. 2005; Bastian et al. 2005a).
In the case of the Girardi models with Z=0.001 and Z=0.03 a concentration of clusters in one or two bins around 63 Myr is seen in all galaxies. This artifact stems from most of these piled clusters having ages younger than the ages provided by the model and the method assigned the youngest available age on the model. Star clusters older than 1 Gyr are not seen in any metallicities except for Z=0.019 from Girardi where two clusters are seen at almost 10 Gyr. Excluding Girardi models for Z=0.001 and Z=0.03, we observe in NGC 5236 and NGC 1313 that the star clusters are distributed more uniformly across the ages with respect to the three other galaxies.
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi13.ps} %\par\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg70.png) |
Figure 4: Histogram of the objects sizes in the full sample, as measured using ISHAPE ( bottom) and SExtractor ( top). The dotted line shows our size selection criteria. |
| Open with DEXTER | |
Table 3: Number of selected star clusters in the ACS and WFPC2 field-of-views.
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi14.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg71.png) |
Figure 5:
|
| Open with DEXTER | |
The Girardi and GALEV SSP models have two metallicities in common:
Z=0.004 and
Z=0.02/0.019.
In Fig. 8 we compare the ages derived from the two models as a function of mass. For solar metallicity the
models agree on the measured ages, although some scatter is seen, especially on NGC 5236. For metallicity Z=0.004,
two main concentrations are observed around
![]() and
and
![]() as is the case for NGC 1313 and NGC 5236. It corresponds to the gaps in the age range observed in the GALEV models
in the Fig. 7 (with a length
as is the case for NGC 1313 and NGC 5236. It corresponds to the gaps in the age range observed in the GALEV models
in the Fig. 7 (with a length ![]()
![]() ).
We also explore how ages correlate between the two models as function of age. In Fig. 9 we plot Girardi ages versus GALEV ages. We noted that for Z=0.004 ages do not agree and a triangular shape is seen because many clusters (using GALEV) were assigned ages
).
We also explore how ages correlate between the two models as function of age. In Fig. 9 we plot Girardi ages versus GALEV ages. We noted that for Z=0.004 ages do not agree and a triangular shape is seen because many clusters (using GALEV) were assigned ages
![]() ,
while the same clusters show
Giradi ages more uniformly distributed in the age axis. At old ages the situation is the opposite, because
Girardi models assign to many clusters
,
while the same clusters show
Giradi ages more uniformly distributed in the age axis. At old ages the situation is the opposite, because
Girardi models assign to many clusters
![]() ,
while very few clusters show that age derived with GALEV. In summary,
considering Z=0.004, GALEV ages will be younger than the ages derived with Girardi models and vice versa.
,
while very few clusters show that age derived with GALEV. In summary,
considering Z=0.004, GALEV ages will be younger than the ages derived with Girardi models and vice versa.
Coming back to Fig. 7, we found 6 star clusters with masses greater than
![]() :
4 in NGC 1313 and 2 in NGC 5236 (see also Fig. 13). Among the 4 star clusters in NGC 1313, three are in common with Larsen (1999): ID: n1313-379, n1313-275 and, n1313-780 which correspond in this work to the object
ID = NGC 1313_3_7, NGC 1313_2_50, and NGC 1313_1_4, respectively. The other object is ID = NGC 1313_2_39.
One of the two massive star clusters in NGC 5236, (the object ID = NGC 5236_1_3) is probably contaminated by a neighbour and might not be as massive as derived, nevertheless, and for completeness, this object is listed in Table 11. The other object is ID = NGC 5236_2_82.
:
4 in NGC 1313 and 2 in NGC 5236 (see also Fig. 13). Among the 4 star clusters in NGC 1313, three are in common with Larsen (1999): ID: n1313-379, n1313-275 and, n1313-780 which correspond in this work to the object
ID = NGC 1313_3_7, NGC 1313_2_50, and NGC 1313_1_4, respectively. The other object is ID = NGC 1313_2_39.
One of the two massive star clusters in NGC 5236, (the object ID = NGC 5236_1_3) is probably contaminated by a neighbour and might not be as massive as derived, nevertheless, and for completeness, this object is listed in Table 11. The other object is ID = NGC 5236_2_82.
5.2 Internal extinction
As mentioned above, the 3D-fit code returns the extinction internal to the galaxy toward the individual clusters. In Table 4 we show the median internal extinction for the star clusters for each pointing and the total median extinction in a given galaxy.Table 4: Median internal extinction E(B-V) towards the star clusters.
Clearly, towards the detected clusters, the internal extinction is low with very little variations between pointings in a galaxy: median E(B-V)=0 for NGC 4395 and NGC 7793, and median E(B-V)=0.1-0.15 for NGC 1313 and NGC 5236.
These median extinction values explain why no objects are located below the model tracks in the colour-colour diagrams in NGC 4395 and NGC 7793, while in NGC 1313 and NGC 5236 some objects (see Fig. 6) show extinction values up to 0.7 mag.
We note that far less clusters are detected in NGC 4395 and NGC 7793 than in the two other galaxies. If this was due to extinction, the median extinction would be at least as high as in the two other galaxies. Thus, we rather interpret this as a physical effect instead the pointings partly covering each galaxy and
variations from pointing to pointing may be present). The small number of clusters is a consequence of the area-normalised star formation rate
![]() observed in these two galaxies (see Table N 2 from Larsen & Richtler 2000; and Larsen 2002, for further details), also consistent with the low number of clusters found in NGC 45 and its
observed in these two galaxies (see Table N 2 from Larsen & Richtler 2000; and Larsen 2002, for further details), also consistent with the low number of clusters found in NGC 45 and its
![]() .
.
![\begin{figure}
\par\includegraphics[width=15.6cm]{0614fi15.ps} %
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg79.png) |
Figure 6:
Colour-colour diagrams of the young star cluster candidates in
NGC 1313, NGC 4395, NGC 5236, and NGC 7793.
The arrow in each plot represents the extinction correction of AV=1.0.
The plotted tracks correspond to GALEV and Girardi simple stellar population models for ages from 3.9 Myr up to 15 Gyr.
Objects above the tracks are objects with large error in the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm]{0614fi16.ps} %
\\
\includegraphics[width=11.5cm]{0614fi17.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg80.png) |
Figure 7: Mass as a function of cluster age as derived using four fixed metallicities. Top: GALEV models. Bottom: Girardi models. See text for details. |
| Open with DEXTER | |
5.3 Cumulative age distributions
We compared the star-cluster age distributions in the different galaxies by comparing their cumulative age distributions. We summed the clusters from old to young, the ages for a single case being derived using a fixed metallicity and given model.
First, we examined whether the star-cluster formation history is a local process or can be averaged over an entire galaxy.
In Fig. 10, we show for each galaxy the cumulative distribution for each pointing, and note that the cluster formation history varies more from galaxy to galaxy than spatially inside a given galaxy. Kolmogorov-Smyrnov tests
(K-S tests) between the distributions
(corresponding to the pointing on each galaxy), show D values ![]() 0.2 and
P values
0.2 and
P values ![]() 0.1 for NGC 7793 and NGC 1313,
indicating that the distributions differ significantly. In the case of NGC 5236 and NGC 4395, the K-S test shows D values greater than 0.2 and P values
0.1 for NGC 7793 and NGC 1313,
indicating that the distributions differ significantly. In the case of NGC 5236 and NGC 4395, the K-S test shows D values greater than 0.2 and P values ![]() 0, indicating that distributions do not differ significantly. For NGC 45, the test gives values of
0, indicating that distributions do not differ significantly. For NGC 45, the test gives values of ![]() and
and ![]() hinting that the distributions do not differ.
Keeping in mind that some distributions differ, but to analyse (and compare) the star cluster distributions from each galaxy, we combined the distributions.
hinting that the distributions do not differ.
Keeping in mind that some distributions differ, but to analyse (and compare) the star cluster distributions from each galaxy, we combined the distributions.
Second, we examined the influence of our assumed fixed metallicity on the formation histories as represented by our cumulative age distributions. From the literature (see Table 2), we know the galaxies do not share the same metallicity. In Fig. 11, we assume the same metallicity for each galaxy, derive the ages (using a GALEV model in that case), and compare the cumulative distribution. Clearly, the assumed metallicity influences the shape of the cumulative distribution but does not remove any general trend that might be present (e.g. NGC 4395 shows for all assumed metallicity a sharp rise at young ages, NGC 5236 shows a much steadier increase in all cases).
Finally, we verify that the model used to derive the ages does not significantly affect the shape of the cumulative age distribution (see Fig. 12 top panels) and show the overall comparison between the cumulative age distributions of the five galaxy in Fig. 12, bottom panel. Indeed, the cumulative distributions using ages derived from the Girardi model do not significantly differ from the ones using ages derived by the GALEV models.
For the final comparison (Fig. 12, bottom panel) we assigned the metallicity as found in the literature to each galaxy. The cumulative age distributions clearly differ. We quantified this by running K-S tests between the distributions (testing for single maximal deviations). All K-S tests returned D values over 0.2 and P values near 0, indicating that the distributions significantly differ.
Qualitatively, NGC 1313 and NGC 5326 show a steadier rise of the cumulative distribution, indicating a more continuous cluster formation history. Taken together with the significantly higher number of young star clusters found in these two galaxy when compared to the three others, this indicates that they maintained a steadily high star-cluster formation over the last few hundred Myr. This in turn could explain the higher median extinction (due to the presence of more gas and dust).
The three other galaxies (NGC 45, NGC 4395, and NGC 7793) are characterised by shallower distributions, with a clear rise at very young ages (tens of Myr). Together with the lower number of clusters detected, this leads to the interpretation that the young star-cluster population in these galaxies is dominated by a recent increase in the star-formation activity. However, we note that the age distributions will also be affected by possibly different disruption time-scales in the different galaxies (see Sect. 7).
![\begin{figure}
\par\includegraphics[width=9.3cm]{0614fi18.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg86.png) |
Figure 8:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9.3cm]{0614fi19.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg87.png) |
Figure 9: GALEV ages versus Girardi ages for Z=0.004, and Z=0.02/0.019. Triangles correspond to NGC 1313, open squares to NGC 7793, stars to NGC 4395, and filled circles to NGC 5236. Z is indicated in each panel. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9.0cm]{0614fi20.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg88.png) |
Figure 10: Normalised cumulative star-cluster age distributions for each pointing in each galaxy. Ages were derived here using the GALEV models and a fixed metallicity per galaxy. Variations in the cumulative distribution are greater from galaxy to galaxy than inside a given galaxy. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi21.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg89.png) |
Figure 11: Normalised cumulative cluster distributions according to GALEV. Each panel shows all galaxies with different metallicities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0614fi22.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg90.png) |
Figure 12: Normalised cumulative cluster distributions according to GALEV. The top and the middle panel correspond to the normalised cumulative cluster distribution for Girardi models. In the bottom, the normalised distributions for all the galaxies considering the closest metallicities from the literature. |
| Open with DEXTER | |
5.4 Sizes
The size distributions for the young star cluster candidates were derived in Sect. 2.2 and the median sizes for each galaxy are shown in Table 5. We note that sizes derived in this work are slightly smaller than in Larsen (2004).
The reason for this is probably that in our sample we include star clusters with masses lower than 1000 ![]() ,
while in Larsen (2004) the mean sizes were derived for star clusters with masses greater than 1000
,
while in Larsen (2004) the mean sizes were derived for star clusters with masses greater than 1000 ![]() .
.
Also, the size distribution might be partly influenced by the completeness criteria, as the
most extended objects are not detected and the size distribution gets slightly biased towards smaller sizes.
For example: of the artificial star clusters created in NGC 7793 with a magnitude
![]()
![]()
![]() with
with
![]() pixels were not recovered, while only
pixels were not recovered, while only ![]()
![]() of the objects with
of the objects with
![]() pixels were not detected.
pixels were not detected.
Nonetheless, the slight biases do not prevent investigation of any relation between size and mass.
In similar previous studies (e.g. Bastian et al. 2005b; Larsen 2004), the relation between sizes and masses
for young star clusters had already been investigated, and a slight trend was found toward more massive star clusters being more extended. We considered the masses derived assuming the metallicities from Table 2.
Figure 13 shows the young star cluster candidate sizes plotted against the masses. A function of the form
was applied for each galaxy and the values obtained from the minimum
As in previous studies, we observe in all galaxies a slight tendency for the more massive objects to be more extended in all galaxies. A physical interpretation could be that massive star clusters form in higher pressure environment than the lower mass ones, which also form less bound, therefore the most difuse low-mass clusters are more affected by the disruption than higher mass counterparts.
In Table 5 all galaxies have similar mean effective radii for the star clusters, except NGC 1313 where the mean effective radius is higher (see also
Fig. 13), because above 1000 ![]() the range of sizes at a given mass is significantly broader than in the other galaxies.
the range of sizes at a given mass is significantly broader than in the other galaxies.
Table 5: Young star cluster median effective radii.
Table 6: Size coefficients.
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=9cm,clip]{0614fi23.ps} %
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg115.png) |
Figure 13:
Effective radius versus mass of young star clusters.
The lines correspond to fits of the form
|
| Open with DEXTER | |
We also note that the slopes of the power-law fits are significantly steeper than the values (![]() 0.10)
reported in previous studies. This might partly come from the different mass ranges probed here.
However, we caution that the reliability of the size measurements may be questionable
for the lowest mass clusters, whose luminosity profiles tend to be dominated by a few individual stars.
Therefore, the importance of stochastic effects on the size determinations at low mass needs to be taken into account
and investigated further.
0.10)
reported in previous studies. This might partly come from the different mass ranges probed here.
However, we caution that the reliability of the size measurements may be questionable
for the lowest mass clusters, whose luminosity profiles tend to be dominated by a few individual stars.
Therefore, the importance of stochastic effects on the size determinations at low mass needs to be taken into account
and investigated further.
6 Luminosity functions
The star cluster luminosity functions for four of our five galaxies are shown in Fig. 14. The one for NGC 45 was presented in Mora et al. (2007). Data were corrected with the completeness function calculated for an object of FWHM = 1.2 pixels. Each histogram was fitted by minimumThe slope a was then converted to the slope of the luminosity function, represented as a power law d
Table 7: Luminosity function coefficients.
The luminosity slopes derived for NGC 1313 and NGC 5236 agree with the values derived in Larsen (2002):
![]() and
and
![]() ;
the slightly steeper slope in NGC 5236 seems to be confirmed by our study.
Overall, we find luminosity slopes compatible with
;
the slightly steeper slope in NGC 5236 seems to be confirmed by our study.
Overall, we find luminosity slopes compatible with
![]() ,
in agreement with the values reported in the literature for the young star cluster systems.
,
in agreement with the values reported in the literature for the young star cluster systems.
We went on to compared the expected magnitude of the brightest clusters as predicted from the luminosity functions with the actual observed values. Such a comparison indicates whether a special physical mechanism is required for the formation of the brightest clusters, or whether they can be explained simply by the size of the sample.
We simulated each galaxy luminosity function 1000 times considering the observed number of star clusters with magnitudes randomly selected up to Mv=-5.1, the observational cut-off magnitude of the sample. The results are summarised in
Table 7. There,
(1) and (2) correspond to a and b coefficient from
Eq. (3); (3) to ![]() slope of the luminosity function;
(4) to the expected
slope of the luminosity function;
(4) to the expected
![]() magnitude of the brightest star cluster from the extrapolation of the luminosity function; (5),(6) and (7) to the V mean, V median, and
magnitude of the brightest star cluster from the extrapolation of the luminosity function; (5),(6) and (7) to the V mean, V median, and ![]() of the brightest star cluster from the simulated luminosity functions; (8) to the observed
of the brightest star cluster from the simulated luminosity functions; (8) to the observed
![]() magnitude of the brightest cluster; (9) and (10) to the mass and age of the observed brightest star cluster
in
magnitude of the brightest cluster; (9) and (10) to the mass and age of the observed brightest star cluster
in ![]() and yr respectively; and (11) to the metallicity used for mass and age derivations.
and yr respectively; and (11) to the metallicity used for mass and age derivations.
For all galaxies we found good agreement within the errors between the observed and the expected
brightest cluster. NGC 1313 presents an exception, as the observed value is
![]() 3 mag (
3 mag (![]()
![]() )
brighter than the prediction. The brightest star clusters
in the luminosity function are generally dictated by size-of-sample effects
(Hunter et al. 2003) and correspond to a stochastic sampling of the luminosity function (see Larsen 2002).
However, some galaxies seem to produce brighter star clusters; in that respect, NGC 1313 also showed clusters of larger average sizes. Although a connection is not demonstrated here, it might be an interesting aspect to investigate further.
It should be noted that a physical truncation of the cluster mass function might still exist, even if the luminosity function is limited by size-of-sample effects. One signature of such a physical limit to the MF is a steepening of the LF at the bright end (Gieles et al. 2006a), as hinted at in the case of NGC 5236.
)
brighter than the prediction. The brightest star clusters
in the luminosity function are generally dictated by size-of-sample effects
(Hunter et al. 2003) and correspond to a stochastic sampling of the luminosity function (see Larsen 2002).
However, some galaxies seem to produce brighter star clusters; in that respect, NGC 1313 also showed clusters of larger average sizes. Although a connection is not demonstrated here, it might be an interesting aspect to investigate further.
It should be noted that a physical truncation of the cluster mass function might still exist, even if the luminosity function is limited by size-of-sample effects. One signature of such a physical limit to the MF is a steepening of the LF at the bright end (Gieles et al. 2006a), as hinted at in the case of NGC 5236.
7 Cluster disruption
In following section, we investigate the disruption time scales of the clusters. We adopt the simplified description of cluster disruption developed by Boutloukos & Lamers (2003), and thus assume that the ``disruption time scale''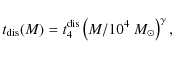 |
(4) |
where
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi24.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg157.png) |
Figure 14:
Luminosity functions for our galaxy sample. Solid histograms are the uncorrected luminosity functions, while the dashed
histograms are the completeness corrected luminosity functions. Straight lines represent the power-law fit of the form
d
|
| Open with DEXTER | |
Boutloukos & Lamers (2003) defined this in an empirical way, assuming that clusters are formed in a constant number per unit time within a certain mass range and with a fixed cluster initial mass function in the form of a power law. Under these assumptions, the number of clusters per age interval, which are detected above a certain fixed magnitude limit, will only depend on the fading due to stellar evolution, as long as there is no cluster disruption. As soon as cluster disruption becomes significant, this behaviour is broken and the number of clusters decreases more rapidly with time.
Considering Eqs. (15) and (16) from Boutloukos & Lamers (2003),
the time scale on which cluster disruption is important can be derived
from either the cluster age or mass distributions:
![\begin{displaymath}\log \left(\frac{t_{\rm cross}}{10^8} \right) =
\frac{1}{1-...
...0^8}\right)
+ 0.4 \gamma (m_{\rm ref} - V_{\rm lim})
\right]
\end{displaymath}](/articles/aa/full_html/2009/27/aa10614-08/img158.png) |
(5) |
![\begin{displaymath}\log \left(\frac{M_{\rm cross}}{10^4} \right) =
\frac{1}{1-...
...is}}{10^8}\right)
+ 0.4 (m_{\rm ref} - V_{\rm lim})
\right].
\end{displaymath}](/articles/aa/full_html/2009/27/aa10614-08/img159.png) |
(6) |
In these equations,
The scenario described above makes no distinction between cluster disruption due to interaction with the interstellar medium, bulge/disk shocks, and internal events such as two-body relaxation, and assumes that a single ``disruption time-scale'' applies. Furthermore, this formulation does not account for the apparently mass-independent loss of very young objects, sometimes dubbed ``infant mortality'' (e.g. Fall et al. 2005). This process is believed to operate mostly within the first few 107 years.
In Fig. 15 we plot the age distributions for the star clusters in our galaxy sample
limited by a magnitude cut of
![]() .
Several bin widths were tried but none revealed any obvious
breaks in the age distributions. Thus, we selected an intermediate bin width
of
.
Several bin widths were tried but none revealed any obvious
breaks in the age distributions. Thus, we selected an intermediate bin width
of
![]() .
We then fitted straight lines of the form
.
We then fitted straight lines of the form
![]() ,
and found slopes in the range -1.22 > a >-1.43.
,
and found slopes in the range -1.22 > a >-1.43.
The derived values are inconsistent with the expected slope value (![]() -0.7) for a cluster age distribution
that assumes no star cluster dissolution and limited by a V-band magnitude (see Gieles et al. 2007b).
For U-band limited magnitude samples, the slopes are expected to be
-0.7) for a cluster age distribution
that assumes no star cluster dissolution and limited by a V-band magnitude (see Gieles et al. 2007b).
For U-band limited magnitude samples, the slopes are expected to be ![]() -1. Also, in this scenario,
and assuming
-1. Also, in this scenario,
and assuming
![]() and
and ![]() ,
the values are somewhat shallower than the disruption
slope for a V-band limited sample, which is expected to be
,
the values are somewhat shallower than the disruption
slope for a V-band limited sample, which is expected to be ![]() -1.6.
-1.6.
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi25.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg169.png) |
Figure 15:
The age distributions for our galaxy sample. Lines correspond to the best fitting of the
form
|
| Open with DEXTER | |
As shown in Lamers et al. (2005a), the process of fading and star cluster disruption is not a process on which the break between this two stages suddenly occurs. It is a continuous process that gradually goes from the fading of the cluster regime up to the cluster disruption regime, and an approximation of straight lines (one for each regime) is valid when these two regimes are well defined. Therefore, it is not surprising that the derived values lie between these two regimes because the disruption regime may be present, but it is impossible to disentangle it from the fading regime, probably as a consequence of using a magnitude-limited sample i.e. older objects (which are more likely to be affected by disruption) end up below our limit detection.
An additional disruption mechanism has been discussed by Whitmore et al. (2007). From observations of young star clusters in the
Antennae galaxy, these authors find evidence of a constant fraction (between 80% and 90%) of the clusters being lost per unit logarithmic age
interval up to at least 108 years. This mass-independent disruption has been named ``infant mortality''. For a mass-limited
sample, this results in an age distribution with a logarithmic slope of
![]() ,
i.e. a = -0.7 and a=-1 for
an ``infant mortality'' rate of 80% and 90%, respectively.
However, for a magnitude-limited sample we would expect a slope of a=-1.35
and a=-1.65 (for IMR = 80% and IMR = 90%, respectively, considering a
V-band limited sample).
Clearly the 90% is significantly steeper than our observed
values and an IMR = 80% shows values consistent with our measured slopes
of -1.22 to -1.44. These values are consistent (within the errors) with infant mortality rates of less than 75%-85% for ages up to 1 Gyr.
,
i.e. a = -0.7 and a=-1 for
an ``infant mortality'' rate of 80% and 90%, respectively.
However, for a magnitude-limited sample we would expect a slope of a=-1.35
and a=-1.65 (for IMR = 80% and IMR = 90%, respectively, considering a
V-band limited sample).
Clearly the 90% is significantly steeper than our observed
values and an IMR = 80% shows values consistent with our measured slopes
of -1.22 to -1.44. These values are consistent (within the errors) with infant mortality rates of less than 75%-85% for ages up to 1 Gyr.
In summary, the slopes of our cluster age distributions are too steep to be explained by fading alone, but our data do not allow us to clearly distinguish between mass-dependent and mass-independent disruption.
8 Radial distributions
In the following section, we discuss the radial distribution of the young star clusters in four galaxies (NGC 45 being presented in Mora et al. 2007). Since our images do cover the galaxies asymmetrically, a spatial completeness correction first needed to be computed.
8.1 Spatial completeness correction
We evaluated the spatial completeness as a function of radius by using concentric circles (centred on the galaxy) with increasing radius in steps of 18
8.2 Radial distribution of the surface density
For the surface density we considered the expected number of clusters corrected by the spatial completeness. Each galaxy was divided into 9 concentric rings and the completeness-corrected radial surface density was calculated by dividing the expected number of clusters by the area of the ring where they lie. In Fig. 16 we plot the completeness-corrected surface density of star clusters as a function of radius, as well as the completeness asa function of the radius.For three galaxies the centre was covered by the ACS images (i.e. a 100% completeness was reached in the centre of the galaxy). For NGC 5236 the pointing did not cover the central part of the galaxy. Further, note that the bumpy shapes of the completeness lines are due to the different ACS orientations for each pointing. For each galaxy, we evaluated the completeness-corrected radial surface densities profile over nine bins. The bins were defined from the centre outwards to the most distant cluster in our sample.
For a qualitative comparison between the galaxies, we fitted to each completeness-corrected radial surface density profile (distance being linear, surface density being logarithmic) a line of the form
The results of the fits are listed in Table 8. We notice that the surface density profiles for young star cluster span a very wide range in our sampled galaxies: from almost no radial dependence in NGC 5236 and NGC 4395 (i.e. homogeneous formation of star clusters with radius) to very concentrated distribution in NGC 7793 and in particular in NGC 1313. In the latter, the surface density increases by two orders of magnitude towards the centre over the inner
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi26.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg172.png) |
Figure 16: Radial surface density profiles of the star clusters, corrected for completeness. Solid lines show the spatial completeness correction (in percent) described in Sect. 8.1. Dashed lines show the power-law fits to the profiles. |
| Open with DEXTER | |
Table 8: Derived values from Eq. (8).
Table 9: Total numbers of globular clusters and specific frequencies in the observed region.
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi27.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg198.png) |
Figure 17: Stamps of all the globular cluster candidates detected in our sample. First row: NGC 1313, second and third row: NGC 5236, and fourth row: NGC 7793. |
| Open with DEXTER | |
9 Globular clusters
After discussing above the more prominent young star clusters, here we briefly describe the old globular clusters found in the sample galaxies. As mentioned in Sect. 3.2, we considered
globular cluster candidates to be objects with
![]() and colours
and colours
![]() .
.
9.1 Total number of globular clusters
To derive the total number of globular clusters in our covered area (inner 6-8 kpc), we considered the detection completeness affecting our sample, as well as the spatial incompleteness. For the detection completeness, we used the values derived in Sect. 2.3. For the spatial completeness correction we used the method described in Sect. 8.1.
We then extrapolated the total number of globular clusters over the full globular cluster
luminosity function.
We assumed that the globular cluster luminosity function in our galaxies follows the ``universal''
Gaussian shape and, following Jordán et al. (2006), that the Gaussian dispersion
is described by the relation
Given the small number of observed objects (0 to 8), the extrapolation is necessarily uncertain. The evaluated approximate uncertainties take into account the errors in the dispersion, the magnitude of faintest globular cluster candidate with respect to the luminosity function turnover (indicating the fraction of the total area of the Gaussian that we observed), as well as the error in the globular cluster luminosity function turnover given the known distance. We maximised and minimised these (1
Table 10: Red star cluster mean effective radii.
Table 11: Derived star cluster properties for all the galaxies (Sample).
9.1.1 Specific frequencies
Harris & van den Bergh (1981) defined the specific frequency as
| (10) |
where
To compare these values with global values as found in the literature (e.g. Harris 1991), we would need to estimate the total number of globular clusters not only in the observed region but over the whole galaxy. In principle, we could use the surface density profiles and extrapolate them to large radii, but have no indication of how far out radii these would hold. Instead, as a rough estimate, we consider the Milky Way, a late-type galaxy in the luminosity range of our sample, which hosts about a third to half of its globular clusters in the inner 6 to 8 kpc. Thus, global specific frequencies for our galaxies might be two to three times higher than derived for the inner regions.
The specific frequencies listed Table 9 lie well below 1, i.e. in the range of low specific frequencies. Even if these were doubled or tripled to reflect global values, they would be in the range 0.5 to 1 as expected for late-type galaxies (see Harris 1991).
For NGC 5236, Chandar et al. (2004) derived in a previous study SN of ![]() ,
about twice our inner value, in good agreement with our estimate for the global value.
,
about twice our inner value, in good agreement with our estimate for the global value.
We conclude that the (low) number of globular clusters observed lies within the expectations for the type of galaxies in our sample.
9.1.2 Globular cluster sizes
From ISHAPE measurements (see Sect. 2.2), we calculated the mean effective radii of the globular cluster candidates. The values are shown in
Table 10. Our values are slighter higher than the average half-light radius found in the ACS Virgo Cluster Survey (Jordán et al. 2005), but in good agreement with the median size (![]() 3.2 pc) of the Milky Way globular clusters.
3.2 pc) of the Milky Way globular clusters.
Note that, within the errors, the globular clusters (as opposed to the young star clusters) in NGC 1313 do not display abnormal sizes.
10 Summary and discussion
We have analysed the star cluster populations in five nearby spiral galaxies. Candidates were selected
applying a size criterion. Ages and masses were derived from broad band colours and compared
with SSP models. Thanks to the excellent ACS resolution we were able to observe compact young star clusters down to masses of the order of 200 ![]() .
.
The properties of the young star clusters show considerable diversity. The star cluster formation history shows galaxies forming young star clusters rather homogeneously over the past Gyr, as well as galaxies with increased cluster formation activity on short periods. The galaxies with a rather continuous star cluster formation show a higher number of young star clusters (by almost an order of magnitude) than the ones forming star clusters in bursts. The specific frequency of old globular clusters
appears to be normal (i.e. low) for these late-type spirals in our sample.
In this respect, the four galaxies studied here contrast with the case of NGC 45 (Mora et al. 2007),
where we found an unusually high
![]() for a late-type galaxy of
1.4-1.9.
for a late-type galaxy of
1.4-1.9.
We have tried to investigate the star cluster disruption. Fading alone is clearly ruled out and distributions seem to be consistent with 80% of IMR, however we were not able to distinguish between mass-dependent and mass-independent disruption, i.e. characterise the exact disruption law. The spatial distribution of star clusters also varies greatly in our galaxies. Some galaxies appear to form star clusters homogeneously over the 6-8 kpc probed in our study, while others show the young star cluster density to be (very) peak towards the galaxy centre.
The star cluster luminosity functions support earlier findings in the literature and are compatible with power-law distributions with a slope of around -2. The brightest clusters are compatible with a random sampling of the luminosity function given the size of the samples. NGC 1313 presents an exception with the brightest star clusters being about three magnitudes brighter than expected. In this regard, it is worth noticing that NGC 1313 also displays slightly large sizes (or a larger scatter in sizes) for its young star clusters and has by far the most concentrated spatial distribution of star clusters. Potentially, another or additional star cluster formation processes are at work in this galaxy.
Finally, we analysed the (small) population of globular cluster candidates in our galaxies and found it to be normal both in terms of number of objects and specific frequencies, as well as in the sizes.
Acknowledgements
We would like to thank H.J.G.L.M. Lamers for providing the 3D code program and for useful feedback and thank Nate Bastian and Mark Gieles for interesting comments about this work during the 12 Questions on Star and Massive Star Cluster Formation workshop, as well as B. Whitmore for his help on the CTE corrections. Also we acknowledge the anonymous referee for his/her comments. M.D.M. was supported by ALMA FUND Grant No. 31060010. T.R. has been supported by the Chilean Center of Astrophysics Conicyt FONDAP No. 125010003.
References
- Anders, P., & Fritze-v. Alvensleben, U. 2003, A&A, 401, 1063 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bastian, N., Gieles, M., Efremov, Y. N., & Lamers, H. J. G. L. M. 2005a, A&A, 443, 79 [NASA ADS] [CrossRef] [EDP Sciences]
- Bastian, N., Gieles, M., Lamers, H. J. G. L. M., Scheepmaker, R. A., & de Grijs, R. 2005b, A&A, 431, 905 [NASA ADS] [CrossRef] [EDP Sciences]
- Bastian, N., Hempel, M., Kissler-Patig, M., Homeier, N. L., & Trancho, G. 2005c, A&A, 435, 65 [NASA ADS] [CrossRef] [EDP Sciences]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] (In the text)
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bik, A., Lamers, H. J. G. L. M., Bastian, N., Panagia, N., & Romaniello, M. 2003, A&A, 397, 473 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bohlin, R. C., & Gilliland, R. L. 2004, AJ, 127, 3508 [NASA ADS] [CrossRef] (In the text)
- Bottinelli, L., Gouguenheim, L., Paturel, G., & de Vaucouleurs, G. 1985, ApJS, 59, 293 [NASA ADS] [CrossRef]
- Boutloukos, S. G., & Lamers, H. J. G. L. M. 2003, MNRAS, 338, 717 [NASA ADS] [CrossRef]
- Bresolin, F., & Kennicutt, Jr., R. C. 2002, ApJ, 572, 838 [NASA ADS] [CrossRef]
- Carignan, C. 1985, ApJS, 58, 107 [NASA ADS] [CrossRef]
- Carney, B. W. 2001, in Saas-Fee Advanced Course 28: Star Clusters, ed. L. Labhardt, & B. Binggeli (In the text)
- Chandar, R., Whitmore, B., & Lee, M. G. 2004, ApJ, 611, 220 [NASA ADS] [CrossRef] (In the text)
- Conti, P. S., & Vacca, W. D. 1994, ApJ, 423, 97 [NASA ADS] [CrossRef] (In the text)
- de Vaucouleurs, G. 1963, ApJ, 137, 720 [NASA ADS] [CrossRef]
- de Vaucouleurs, G. 1979, AJ, 84, 1270 [NASA ADS] [CrossRef]
- Dolphin, A. E. 2000, PASP, 112, 1397 [NASA ADS] [CrossRef] (In the text)
- Fall, S. M. 2004, in The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 399
- Fall, S. M. 2006, ApJ, 652, 1129 [NASA ADS] [CrossRef]
- Fall, S. M., Chandar, R., & Whitmore, B. C. 2005, ApJ, 631, L133 [NASA ADS] [CrossRef]
- Gieles, M., Bastian, N., Lamers, H. J. G. L. M., & Mout, J. N. 2005, A&A, 441, 949 [NASA ADS] [CrossRef] [EDP Sciences]
- Gieles, M., Larsen, S. S., Bastian, N., & Stein, I. T. 2006a, A&A, 450, 129 [NASA ADS] [CrossRef] [EDP Sciences]
- Gieles, M., Portegies Zwart, S. F., Baumgardt, H., et al. 2006b, MNRAS, 371, 793 [NASA ADS] [CrossRef]
- Gieles, M., Athanassoula, E., & Portegies Zwart, S. F. 2007a, MNRAS, 376, 809 [NASA ADS] [CrossRef]
- Gieles, M., Lamers, H. J. G. L. M., & Portegies Zwart, S. F. 2007b, ApJ, 668, 268 [NASA ADS] [CrossRef] (In the text)
- Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Harris, J., Calzetti, D., Gallagher, III, J. S., Smith, D. A., & Conselice, C. J. 2004, ApJ, 603, 503 [NASA ADS] [CrossRef]
- Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E., & van den Bergh, S. 1981, AJ, 86, 1627 [NASA ADS] [CrossRef] (In the text)
- Holtzman, J. A., Faber, S. M., Shaya, E. J., et al. 1992, AJ, 103, 691 [NASA ADS] [CrossRef]
- Hunter, D. A., Elmegreen, B. G., Dupuy, T. J., & Mortonson, M. 2003, AJ, 126, 1836 [NASA ADS] [CrossRef] (In the text)
- Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1992, ApJ, 397, 717 [NASA ADS] [CrossRef] (In the text)
- Jordán, A., Côté, P., Blakeslee, J. P., et al. 2005, ApJ, 634, 1002 [NASA ADS] [CrossRef] (In the text)
- Jordán, A., McLaughlin, D. E., Côté, P., et al. 2006, ApJ, 651, L25 [NASA ADS] [CrossRef] (In the text)
- Karachentsev, I. D., & Drozdovsky, I. O. 1998, A&AS, 131, 1 [NASA ADS] [CrossRef] [EDP Sciences]
- Karachentsev, I. D., Grebel, E. K., Sharina, M. E., et al. 2003, A&A, 404, 93 [NASA ADS] [CrossRef] [EDP Sciences]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] (In the text)
- Koekemoer, A. M., Fruchter, A. S., Hook, R. N., & Hack, W. 2002, in The 2002 HST Calibration Workshop, ed. S. Arribas, A. Koekemoer, & B. Whitmore, 337 (In the text)
- Lamers, H. J. G. L. M., Bastian, N., & Gieles, M. 2004, in The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 409
- Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005a, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences]
- Lamers, H. J. G. L. M., Gieles, M., & Portegies Zwart, S. F. 2005b, A&A, 429, 173 [NASA ADS] [CrossRef] [EDP Sciences]
- Larsen, S. S. 1999, A&AS, 139, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Larsen, S. S. 2002, AJ, 124, 1393 [NASA ADS] [CrossRef] (In the text)
- Larsen, S. S. 2004, A&A, 416, 537 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Larsen, S. S., & Richtler, T. 1999, A&A, 345, 59 [NASA ADS]
- Larsen, S. S., & Richtler, T. 2000, A&A, 354, 836 [NASA ADS] (In the text)
- Larsen, S. S., Mora, M. D., Brodie, J. P., & Richtler, T. 2007 [arXiv:astro-ph/0701697]
- Mora, M. D., Larsen, S. S., & Kissler-Patig, M. 2007, A&A, 464, 495 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences]
- Pellerin, A., Meyer, M., Harris, J., & Calzetti, D. 2007, ApJ, 658, L87 [NASA ADS] [CrossRef] (In the text)
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
- Schulz, J., Fritze-v. Alvensleben, U., Möller, C. S., & Fricke, K. J. 2002, A&A, 392, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- van Zee, L., Salzer, J. J., Haynes, M. P., O'Donoghue, A. A., & Balonek, T. J. 1998, AJ, 116, 2805 [NASA ADS] [CrossRef]
- Whitmore, B. C., & Schweizer, F. 1995, AJ, 109, 960 [NASA ADS] [CrossRef]
- Whitmore, B. C., Chandar, R., & Fall, S. M. 2007, AJ, 133, 1067 [NASA ADS] [CrossRef]
Footnotes
- ... Surveys
![[*]](/icons/foot_motif.png)
- Based on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with programme # 9774.
- ... spirals
![[*]](/icons/foot_motif.png)
- Full Table 11 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/501/949
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the National Optical Astronomical Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc, under cooperative agreement with the National Science Foundation.
- ...
page
![[*]](/icons/foot_motif.png)
- http://www.stsci.ed/hst/acs/analysis/zeropoints/
- ...Dolphin (2000)
![[*]](/icons/foot_motif.png)
- http://www-int.stsci.edu/instruments/wfpc2/Wfpc2_cte/dolphin_cte.html
- ... communication)
![[*]](/icons/foot_motif.png)
- http://pleiadi.pd.astro.it/isoc_photsys.02/isoc_acs_hrc/index.html
- ... models
![[*]](/icons/foot_motif.png)
- http://pleiadi.pd.astro.it/isoc_photsys.02/isoc_acs_hrc/index.html
All Tables
Table 1: Pointing coordinates and exposure times for the galaxies in our sample. For NGC 45 see Mora et al. (2007)
Table 2: Summary of galaxy properties.
Table 3: Number of selected star clusters in the ACS and WFPC2 field-of-views.
Table 4: Median internal extinction E(B-V) towards the star clusters.
Table 5: Young star cluster median effective radii.
Table 6: Size coefficients.
Table 7: Luminosity function coefficients.
Table 8: Derived values from Eq. (8).
Table 9: Total numbers of globular clusters and specific frequencies in the observed region.
Table 10: Red star cluster mean effective radii.
Table 11: Derived star cluster properties for all the galaxies (Sample).
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=5.3cm]{0614fig1.ps} \includegrap...
...5.3cm]{0614fig8.ps} \includegraphics[width=5.3cm]{0614fig9.ps} }
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg16.png) |
Figure 1: ACS colour images for all pointings of our galaxy sample, with over-layed WFPC2 field-of-view. The arrows indicate North. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.3cm]{0614fi10.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg55.png) |
Figure 2: Photometric error versus magnitude. Each row corresponds to the error as function of magnitude for each galaxy. The corresponding passband is indicated on each panel. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm]{0614fi11.ps} \includegraphics[width=9cm]{0614fi12.ps} }
\par\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg56.png) |
Figure 3: Left: completeness in object finding as a function of magnitude for our four galaxies. Right: average absolute difference between the input and recovered FWHM as a function of object magnitude. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi13.ps} %\par\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg70.png) |
Figure 4: Histogram of the objects sizes in the full sample, as measured using ISHAPE ( bottom) and SExtractor ( top). The dotted line shows our size selection criteria. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi14.ps}
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg71.png) |
Figure 5:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.6cm]{0614fi15.ps} %
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg79.png) |
Figure 6:
Colour-colour diagrams of the young star cluster candidates in
NGC 1313, NGC 4395, NGC 5236, and NGC 7793.
The arrow in each plot represents the extinction correction of AV=1.0.
The plotted tracks correspond to GALEV and Girardi simple stellar population models for ages from 3.9 Myr up to 15 Gyr.
Objects above the tracks are objects with large error in the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.5cm]{0614fi16.ps} %
\\
\includegraphics[width=11.5cm]{0614fi17.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg80.png) |
Figure 7: Mass as a function of cluster age as derived using four fixed metallicities. Top: GALEV models. Bottom: Girardi models. See text for details. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.3cm]{0614fi18.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg86.png) |
Figure 8:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.3cm]{0614fi19.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg87.png) |
Figure 9: GALEV ages versus Girardi ages for Z=0.004, and Z=0.02/0.019. Triangles correspond to NGC 1313, open squares to NGC 7793, stars to NGC 4395, and filled circles to NGC 5236. Z is indicated in each panel. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.0cm]{0614fi20.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg88.png) |
Figure 10: Normalised cumulative star-cluster age distributions for each pointing in each galaxy. Ages were derived here using the GALEV models and a fixed metallicity per galaxy. Variations in the cumulative distribution are greater from galaxy to galaxy than inside a given galaxy. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi21.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg89.png) |
Figure 11: Normalised cumulative cluster distributions according to GALEV. Each panel shows all galaxies with different metallicities. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0614fi22.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg90.png) |
Figure 12: Normalised cumulative cluster distributions according to GALEV. The top and the middle panel correspond to the normalised cumulative cluster distribution for Girardi models. In the bottom, the normalised distributions for all the galaxies considering the closest metallicities from the literature. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=9cm,clip]{0614fi23.ps} %
\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg115.png) |
Figure 13:
Effective radius versus mass of young star clusters.
The lines correspond to fits of the form
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi24.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg157.png) |
Figure 14:
Luminosity functions for our galaxy sample. Solid histograms are the uncorrected luminosity functions, while the dashed
histograms are the completeness corrected luminosity functions. Straight lines represent the power-law fit of the form
d
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi25.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg169.png) |
Figure 15:
The age distributions for our galaxy sample. Lines correspond to the best fitting of the
form
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi26.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg172.png) |
Figure 16: Radial surface density profiles of the star clusters, corrected for completeness. Solid lines show the spatial completeness correction (in percent) described in Sect. 8.1. Dashed lines show the power-law fits to the profiles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{0614fi27.ps} %\end{figure}](/articles/aa/full_html/2009/27/aa10614-08/Timg198.png) |
Figure 17: Stamps of all the globular cluster candidates detected in our sample. First row: NGC 1313, second and third row: NGC 5236, and fourth row: NGC 7793. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.