| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 729 - 734 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/20078154 | |
| Published online | 19 May 2009 | |
Variability of the polarization profiles of the Ba II D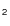 line in the solar atmosphere
line in the solar atmosphere
A. López Ariste1 - A. Asensio Ramos2 - R. Manso Sainz2 - M. Derouich2 - B. Gelly1
1 - THEMIS - CNRS UPS 853, C/ Vía Láctea s/n. 38200, La Laguna, Tenerife, Spain
2 -
Instituto de Astrofísica de Canarias, C/ Vía Láctea s/n. 38200, La Laguna, Tenerife, Spain
Received 25 June 2007 / Accepted 31 March 2009
Abstract
Context. Resonance-scattering polarization and the Hanle effect are powerful but seldom exploited probes into the magnetism of the quiet solar atmosphere. They are also very interesting checks of the quantum theory of atomic polarization. The Ba II D2 line has been known for more than 20 years as presenting a conspicuous signal of resonance scattering polarization thanks to its atomic configuration and the presence of five different isotopes of Ba, two of which present a hyperfine structure.
Aims. A model that considers most of the known ingredients of the atomic polarization of Ba II related to the formation of the D2 line was presented in 2007. We intend to observe all the variability of the Stokes profiles of this line in conditions of resonance scattering to verify the general validity of the model and to ascertain the use of the model for magnetic field diagnostics in the quiet solar chromosphere and in spicules.
Methods. The new CCD cameras at THEMIS and the recently commissioned tip-tilt tracking system gave us the opportunity to perform the required observations with unprecedented precision and reliability, resulting in data ready to confront the present theory.
Results. The Stokes Q profiles, both off-limb and on disk, appear to verify this theory in qualitative terms. The observed departures in terms of overall signal amplitude and relative ratios among the three spectral features point to a refinement of the theory for quantitative purposes, perhaps including radiative-transfer effects. We observed, on the other hand, anomalous Stokes V profiles in the absence of Zeeman effect that remain unexplained.
Conclusions. The qualitative agreement between the theory and the observations encourages an increased effort to also match the observations from a quantitative point of view, including the observed anomalous Stokes V profiles.
Key words: polarization - techniques: polarimetric - Sun: chromosphere
1 Introduction
In the search for increasingly sensitive tools for solar magnetometry, the Hanle effect has long been sought as a powerful tool for the diagnosis of the weaker fields in the solar atmosphere (Trujillo Bueno 2000; Stenflo 1994; Trujillo Bueno et al. 2004). Although its diagnostic potential is widely recognized, the Hanle effect has unfortunately not been used in standardized measuring techniques but for a few notable exceptions (e.g. Bommier et al. 2005; Faurobert-Scholl 1996; Bianda et al. 1999; Schukina & Trujillo Bueno 2003; Bianda et al. 1998b; Faurobert-Scholl et al. 1995; Bianda et al. 1998a), including the case of prominence observations (Bommier et al. 1981; Casini et al. 2003; Bommier et al. 1994; Leroy et al. 1984; López Ariste & Casini 2002). Two reasons can be brought up to explain the failure to incorporate the Hanle effect into routine magnetic measurements. The first one is related to the Hanle effect not generating polarization per se (save the particular case of forward scattering), but rather modifies polarization created by other physical phenomena. In the solar atmosphere, it is the polarization created by resonant scattering that is modified by the Hanle effect. Such a source of polarization and the Hanle effect itself are intimately linked to the subtle quantum behavior of the atomic system being observed. As a result, the outcoming polarization shows a variability that is difficult to tackle except for the few spectral lines combining a simple atomic model and a strong polarization signal. Secondly, the spectral profile seen as the signature of both resonant scattering and the Hanle effect is quite often a simple Gaussian function, minimizing the chances of unambiguously identifying the magnetic field as the source of any change in amplitude and width, rather than another source of change such as temperature, pressure, collisions, etc.
Simultaneous Hanle observations in two or more lines (differential Hanle effect) can reduce the ambiguity and model dependence, as demonstrated in Stenflo et al. (1998), Trujillo Bueno (2003), Manso Sainz et al. (2004), or Berdyugina & Fluri (2004). But the ingredients for a feasible measurement in a single line are exemplified by the successful application of Hanle diagnostics to prominences. The spectral line most widely used for this purpose, He I D3, can be accurately modeled using just five terms of the He I triplet system (Bommier 1980), thus making it very easy to compute line emission in realistic atmospheric models. Six transitions are involved in the observed profile, including one separated 350 mÅ from the five others and giving the line its characteristic two-lobe profile. Since D3 is not a resonant line, the lower level can carry atomic polarization and all six transitions are linearly polarized to several degrees. Furthermore, the transitions are very sensitive to the transfer of atomic alignment into atomic orientation, a phenomenon that produces circular polarization with a symmetric spectral signature in addition to the usual antisymmetric Zeeman profile (Kemp et al. 1984).
If some of the characteristics of the He D3 line were found in other lines formed under different conditions, it is apparent that similar performances would be achieved. That is the main idea driving the present work.
The observed non-magnetic linear polarization pattern of the Ba II D2 line with its distinctive three lobes structure has been successfully modeled accounting for the hyperfine structure splitting and isotope composition by Stenflo (1997) and Stenflo & Keller (1997). More recently, Belluzzi et al. (2007) (see also Belluzzi et al. 2006) have extended the theory to make it more complete and to include the polarization effects of magnetic fields. As its Na I counterpart, the Ba II D2 line shows a prominent profile in linear polarization with amplitudes easily reaching 1% of the continuum level when observing near the solar limb. The presence of five stable barium isotopes, two of them with hyperfine structure, guarantees a spectral profile in linear polarization rich in features that can be easily assigned to the different isotopes and transitions and that show a differential sensitivity to the magnetic topology. Unlike its sodium counterpart, the higher atomic weight of the barium ion and the particular atomic parameters of these transitions result in a narrower formation region and, consequently, in easier modeling of the line formation. All together make the Ba II D2 line a promising spectral feature matching many of the advantages that have made the use of Hanle diagnostics feasible in other lines like the He D3 line for the case of prominences. However, to become a magnetic probe of the weak fields of the higher photosphere, a better understanding of the variability of the polarization signatures of this line is required, as well as an initial assessment of the validity of the theory presented by Belluzzi et al. (2007).
2 Observations
We observed the solar limb on August 9 and 10, 2006 (i.e., during the solar minimum), with the THEMIS telescope in spectrograph mode.
The observations consisted of two time series of exposures with the spectrograph slit placed parallel to the visible limb and close to the
solar North Pole (heliographic angles 357.7 and 357.5, respectively). The data presented here were obtained
thanks to two recent instrumental developments in THEMIS: a tip-tilt system and new, fast, very sensitive CCD cameras.
The tip-tilt system performances are described by Gelly et al. (2008). We just point out that it allowed us to fix the slit position with
respect to the solar limb to better than 0.1 arcsec, thus increasing signal coherence in our observations. The new CCD camera is an
Andor iXon EM-CCD with
![]() pixels. Its potential well (160 000 electrons) is smaller than the old cameras available at THEMIS, a
drawback compensated for by its higher quantum efficiency (the chip is back-illuminated) and its much faster cadence (up to 30 images/second).
It incorporates an electron-multiplying gain that was not used in our observations. The camera was set up at the spectrograph exit with a
scale-reduction factor of 4, resulting in a pixel size of 0.25 arcsec in the spatial dimension and 9.3 m
pixels. Its potential well (160 000 electrons) is smaller than the old cameras available at THEMIS, a
drawback compensated for by its higher quantum efficiency (the chip is back-illuminated) and its much faster cadence (up to 30 images/second).
It incorporates an electron-multiplying gain that was not used in our observations. The camera was set up at the spectrograph exit with a
scale-reduction factor of 4, resulting in a pixel size of 0.25 arcsec in the spatial dimension and 9.3 m![]() in the spectral direction.
The slit, opened to 1 arcsec, degraded both resolutions by roughly a factor 3.
in the spectral direction.
The slit, opened to 1 arcsec, degraded both resolutions by roughly a factor 3.
Each time series consisted of 300 modulation cycles. Each modulation cycle was made of six images with different polarimeter configurations to ensure optimal polarimetric efficiency (Sainz Dalda & López Ariste 2007). Each image was made of the addition of six acquisitions of 220 ms each. With a duty cycle exceeding 75%, it took about 86 min to complete each one of the time series.
The data, flat-field exposures at disk center, and zero bias (the dark current in this CCD has been measured and is at the 0.003 e-/s level, thus having no influence on short exposures) were reduced with a new algorithm for high polarimetric sensitivity available at THEMIS, whose main characteristics are sketched here.
The beam-exchange technique and the demodulation techniques successfully remove temporal and spatially
dependent errors (e.g., seeing-induced crosstalk) to a certain extent. Whenever the polarimetric analysis happens early in the
instrument (as in THEMIS, where it takes place at the F1 focus), one should also be aware of spectrograph seeing arising not just
from air turbulence in the optical path, but also from mechanical drifts and vibrations of the instrument. These effects are negligible for typical
solar polarimetry, but have to be considered when approaching polarimetric sensitivities on the order of 10-5 as in this
work![]() . One solution is to accelerate the modulation cycle to ensure that the modulation takes place before nothing
else can physically change (Keller et al. 1994). As of today, THEMIS works with a slow polarimeter (250 ms to switch positions of the retarders), making it
very sensitive to any source of spectrograph seeing. To allow for highly sensitive polarimetry, we implemented a new data reduction
scheme that takes advantage of the sequence of identical (from the solar point of view) measurements present in the time series.
The core idea goes as follows.
. One solution is to accelerate the modulation cycle to ensure that the modulation takes place before nothing
else can physically change (Keller et al. 1994). As of today, THEMIS works with a slow polarimeter (250 ms to switch positions of the retarders), making it
very sensitive to any source of spectrograph seeing. To allow for highly sensitive polarimetry, we implemented a new data reduction
scheme that takes advantage of the sequence of identical (from the solar point of view) measurements present in the time series.
The core idea goes as follows.
The demodulation process can be split into a spatial and a temporal phase. In the spatial phase, the two beams with orthogonal polarizations simultaneously measured on different places of the detector are combined, and in the temporal phase each individual beam with swapped polarization at two different times is combined with itself. Usually, both phases are simultaneously performed on the data to retrieve the Stokes profiles. With the new approach the spatial phase is done first and the two temporal images are compared row by row before being combined. The continuum of the spectra is supposed to be unpolarized up to an unknown offset identical for all the data. However, after the spatial phase, this is seen not to be the case, and the continuum polarization is both non-zero and spatially varying. This is interpreted as a signature of time-varying crosstalks and uncorrected spurious signals. When comparing the continua of the two images at different times, one should expect an identical value if just space-varying crosstalks are in play. The profiles are combined in that case into the incumbent Stokes parameter. Otherwise, the row under examination is considered at risk of carrying uncorrected spurious signals and so is rejected.
Instead of the strict equality condition, we introduce a threshold as follows. Differences smaller than a given percentage of the continuum value are accepted as valid. This criterion is applied to every row of the CCD along the slit and each Stokes parameter individually. As a result of the threshold, only a small number of lines is accepted for each modulation cycle. As the time series reduction goes on, more and more images are deemed acceptable, and they keep adding and building up the S/N. The more stringent the threshold, the higher quality in the resulting data, but also the more images rejected and the lower S/N. A tradeoff is established between S/N and signal quality that should be resolved case by case.
The resulting algorithm appears highly reliable, and the user quickly finds the right threshold beyond which unacceptable signals start appearing. In THEMIS in the present conditions, about 50 to 70% of the data are typically rejected by the algorithm as susceptible to spurious signals. The new and faster CCD used in this work has taken the efficiencies closer to 50% as compared with the old CCDs, and S/Ns of 104 per pixel are reached. A last summation along the slit can take this value slightly beyond 105 for a single profile.
2.1 Defringing
Fringes are an undesired guest in the process of improving polarimetric sensitivity. High-amplitude intensity fringes and spectral channels are
satisfactorily eliminated during the demodulation process. One is left with polarization-dependent fringes (Semel 2003) and time-dependent fringes.
In THEMIS, polarization dependent fringes appear at the level of
![]() the intensity of the continuum. They show a
period of approximately 2 Å and can be safely attributed to the retardance plates of the polarimeter at the Cassegrain focus of the telescope. The
low frequency makes them easy to eliminate by fitting a sinusoidal or, more generally, a spline to them. Demodulating the flat field data may also
be a good manner of modeling them but, unfortunately, the integration time of flat-field exposures is not long enough to achieve an S/N similar
to the data and there is a risk of introducing spurious signals. We prefer to fit splines to the fringes directly observed in the data carefully
selecting the points along the spectrum considered free of solar polarization signal.
The spline-fitting method is also of great help with other fringe systems of smaller amplitude. Particularly annoying is a system with a period of
approximately 200 mÅ and amplitudes of
the intensity of the continuum. They show a
period of approximately 2 Å and can be safely attributed to the retardance plates of the polarimeter at the Cassegrain focus of the telescope. The
low frequency makes them easy to eliminate by fitting a sinusoidal or, more generally, a spline to them. Demodulating the flat field data may also
be a good manner of modeling them but, unfortunately, the integration time of flat-field exposures is not long enough to achieve an S/N similar
to the data and there is a risk of introducing spurious signals. We prefer to fit splines to the fringes directly observed in the data carefully
selecting the points along the spectrum considered free of solar polarization signal.
The spline-fitting method is also of great help with other fringe systems of smaller amplitude. Particularly annoying is a system with a period of
approximately 200 mÅ and amplitudes of
![]() to
to
![]() times the intensity of the continuum. Its origin is unknown
at this time. This system of fringes drifts in time and therefore, no flat-field modeling can be used.
times the intensity of the continuum. Its origin is unknown
at this time. This system of fringes drifts in time and therefore, no flat-field modeling can be used.
After modeling these two systems of fringes by fitting splines, one is left with the residuals from model errors and a third system of fringes with a
period of about 20-40 mÅ. Both are at levels never greater than
![]() and were left uncorrected in this work.
and were left uncorrected in this work.
3 Observed changes in the amplitude of the Ba II features
3.1 Stokes Q profiles
The conspicuous linear polarization of the Ba II D2 line in resonance scattering was noticed in the very first explorations of the
second solar spectrum (Stenflo et al. 1980; Wiehr 1981). Stenflo & Keller (1997) and Gandorfer (2002) show for this line a Stokes Q profile with three prominent spectral
features. The central feature stems from both the isotopes without hyperfine structure (134Ba, 136Ba, and 138Ba), and those with
non-zero nuclear spin (135Ba and 137Ba, with
![]() ), while the outer shoulders only come from the former ones.
The central peak is always much higher than the lateral ones and, among these ones, the red peak is
), while the outer shoulders only come from the former ones.
The central peak is always much higher than the lateral ones and, among these ones, the red peak is ![]() 10% higher than the blue one.
Stenflo & Keller (1997) and Stenflo (1997) showed that such spectral features were easily recovered when quantum interferences between the hyperfine structure
terms in the atomic model were taken into account. Although their approach used the last scattering approximation, thereby avoiding
radiative transfer and other difficulties, the relative amplitudes were well fit, while the total amplitude was recovered through an empirical
fit of the respective line and continuum contributions.
10% higher than the blue one.
Stenflo & Keller (1997) and Stenflo (1997) showed that such spectral features were easily recovered when quantum interferences between the hyperfine structure
terms in the atomic model were taken into account. Although their approach used the last scattering approximation, thereby avoiding
radiative transfer and other difficulties, the relative amplitudes were well fit, while the total amplitude was recovered through an empirical
fit of the respective line and continuum contributions.
Figure 1 shows the polarization pattern in an off-limb observation. By off-limb we mean a distance of 1 and up to 2 arcsec off the visible limb in G-band images, enough to keep the disk off the spectrograph slit at all times despite limb deformations (since movements are compensated for by the tip-tilt system) induced by seeing. Such a distance off-limb corresponds to the low spicular region, as proven by the broadening of the spectral features in Ba II (when compared to on-disk profiles, as seen in the following figures of this paper, the central peak broadens almost 10%, from a Gaussian fit with FWHM of 110 mÅ on disk to 123 mÅ off disk). This broadening is characteristic of spicules (López Ariste & Casini 2005; Trujillo Bueno et al. 2005; Krat & Krat 1971) and is considered as non-thermal in nature. The polarization pattern in Fig. 1 shows the classical profile behavior as seen in the Atlas of Gandorfer (2002) and in the observations of Stenflo & Keller (1997) and Stenflo (1997).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8154fig1.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg11.png) |
Figure 1: Fractional linear polarization Q/I (solid line) and normalized intensity (dotted line, right scale), around the Ba II D2 line (4554 Å) at 1 arcsec off the solar disk. The positive Q direction is along the slit and parallel to the solar limb. There is an emission Fe I line at 4555.8 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8154fig2.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg12.png) |
Figure 2: As for Fig. 1 but for 0.5 arcsec on the solar disk from the limb, with profiles averaged over 30 arcsec along the slit. |
| Open with DEXTER | |
As soon as we enter the solar disk, the Stokes Q profile changes dramatically (see Fig. 2). First, the full signature amplitude is reduced by an order of magnitude. Second, the three peaks narrow as compared to the off-limb profile. Finally, the central peak falls close to the level of the red one, while the blue peak falls at less than half the amplitude of the red peak. The central peak can diminish even further and fall to amplitudes similar to those of the blue peak (see Fig. 3). Such behavior is correlated with the presence of strong magnetic fields as revealed by the transverse Zeeman signature of the neighboring Fe I lines (notice also the longitudinal Zeeman signatures in the corresponding Stokes V profile of Fig. 5).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8154fig3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg13.png) |
Figure 3: As in Fig. 1 but for 0.5 arcsec on the solar disk from the limb. Profiles averaged over 3 arcsec along the slit. |
| Open with DEXTER | |
Figures 1-3 show the variability of the linear polarization pattern in the Ba II D2 line across the solar limb and between weakly and moderately magnetized regions. The variability across the limb is explained by the change in the scattering and line formation geometry. Above the limb, the line of sight crosses the spicular regions of the upper chromosphere, regions that are known to broaden other emission lines (e.g., He I D3). In contrast, over the disk we see deeper into the chromosphere, where spicules contribute less and the radiation field is more isotropic. These differences explain the observed broadening of the peaks and the larger amplitudes for the off-limb observations.
More interesting are the fluctuations with magnetic field intensity. The presence of relatively strong magnetic fields in the region observed in Fig. 3 is apparent from the clear transverse Zeeman profiles shown by neighboring iron lines (see also lowermost panels in Fig. 5). Comparison of Figs. 2 and 3 show that, for increased magnetic activity, first the central peak is substantially depressed (it halves, dropping even below the red shoulder), and second, the relative difference between red and blue shoulders decreases (though the red shoulder barely changes). This general behavior is described by Belluzzi et al. (2007). The relative polarization of the red and blue shoulders is very sensitive to the presence of a background continuum, which explains why this ratio is not a good magnetic field indicator. It changes more abruptly by crossing the limb than between magnetic and non-magnetic regions. It is the relative variation in the red and blue shoulders to the central peak that gives a good indication of magnetic activity, in agreement with the Belluzzi et al. (2007) theory.
Although the results of Belluzzi et al. (2007) qualitatively reproduce the behavior seen in our observations, quantitative agreement fails. For example, while their modeling shows similar amounts of polarization in both the red and blue shoulders, one can be up to twice the other in our observations (see Fig. 4). Before these type of observations can be used as a reliable diagnostic technique for magnetic fields, these discrepancies must be accounted for by the theory.
Probably, the most important ingredient the theoretical modeling lacks is radiative transfer. Neglecting radiative transfer in the formation of the Ba II D2can only be justified if 1) polarization is formed at the top of the line formation region, where the source function is larger than the Planck function; or 2) partial redistribution effects are important for close-to-the-limb modeling (Rutten & Milkey 1979; Rutten 1978), so that the line wings can be considered to be formed in an optically thin medium.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8154f4a.ps}\includegraphics[width=8.8cm,clip]{8154f4b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg14.png) |
Figure 4: Ratios of the amplitudes of the three spectral features of Stokes Q. The legends in the top left corner of both plots identify what ratio of peak amplitudes is depicted by which symbol. In the left plot, the ratios are measured on profiles from observations off-limb (illustrated by the profile in Fig. 1). In the right plot, the ratios are measured on profiles from observations inside the solar disk illustrated in the profiles of Figs. 2 and 3. The strong field shown in Fig. 3 corresponds to the right region (beyond 30 arcsec) of this right plot. The vertical lines draw the limits of the 3 bars in the observing mask. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18.2cm,clip]{8154fig5.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg15.png) |
Figure 5: As Figs. 1-3 ( uppermost, middle, and lowermost panels, respectively), but for Stokes U ( leftmost panels) and circular polarization Stokes V ( rightmost panels). |
| Open with DEXTER | |
Whatever these changes may be, they are not expected to alter the qualitative behavior of the 3 spectral features with respect to the model of Belluzzi et al. (2006). And a drop in amplitude of the central feature compared to the red feature will always translate into a stronger magnetic field, in the example of Fig. 3 where the disappearance of the central feature coincides with the presence of a strong transverse Zeeman signature in the Fe lines to the red of the Ba II line. The ratio of the central feature to the red one in Fig. 4 can therefore be seen as a direct proxy to changes in the strength of the solar magnetic field. On the other hand, the ratio of amplitudes of the blue and red components appears in the theory of Belluzzi et al. (2006) as an indication of changes in the inclination of the field. It clearly appears that the respective ratios of the 3 features contain all the information needed to correctly infer the magnetic field vector if only we trust that an improvement in the present theory will lead to explaining the on-disk observed changes.
3.2 Stokes U and V profiles
We observed the four Stokes parameters simultaneously. Figure 5 shows U/I (left panels), and V/I (right panels), at the three spatial positions considered above (Figs. 1-3). Stokes U appears as a single lobe at line core with a slight asymmetry towards the red. This behavior is described by Belluzzi et al. (2007) theory. The mere existence of a U signal implies the breaking of the axial symmetry of the magnetic field at the spatio-temporal scale of the observations. Accordingly, the U lobe can take both signs, depending on the large scale orientation of the magnetic field. The important point, nevertheless, is that such Stokes U profiles will contribute positively to any quantitative diagnostic technique based on the Hanle effect of the Ba II D2 line in the terms that we discussed in the introduction.
More interesting is the behavior of the V profiles. In moderately magnetized regions, and well into the solar disk (close to disk center), we observe antisymmetric V profiles characteristic of the longitudinal Zeeman effect. However, as we proceed to close-to-the-limb and off-the-limb regions, anomalous V profiles such as the ones shown in Fig. 5 appear in the Ba II D2 line. That these profiles are an instrumental artifact can be ruled out for various reasons. First of all, as we just mentioned, we observe typical antisymmetric profiles in other regions of the sun. Moreover, even when the Ba II D2 line shows anomalous V signals, neighboring Fe I lines show a classic antisymmetric Zeeman V profile and transverse Zeeman Q and U profiles (see Fig. 3 and lowermost panels in Fig. 5). Furthermore, the lack of a central peak in the V profiles rules out crosstalk from other Stokes parameters. Finally, the V peaks lie at exactly the same wavelengths as the shoulders of the Q pattern, which suggests a link between these features by the physics of line formation.
Not surprisingly, these anomalous V profiles cannot be accounted for by the theory of Belluzzi et al. (2007). Theoretical interpretation of these signals requires more realistic (and complicated) radiative transfer modeling of line formation.
In the advent of a new physical explanation for this circular polarization signature, it should be said that, from an observational point of view, the Stokes V profile of the Ba II D2 line, being sensitive to both the Zeeman effect and the new anomalous phenomena, holds plenty of potential. The mixture of both phenomena results in a huge amount of information buried in their shape and relative amplitudes. Such information concerns not just the magnetic field topology but also the actual physical conditions encountered by the Ba II ion in spicules and, if well understood and modeled, may become a powerful probe of the physical conditions encountered by plasma in those solar features.
4 Conclusions
The theory developed by Belluzzi et al. (2007) appears to agree qualitatively with the observations of the linear polarization of the Ba II D2 line at the limb, both inside and out. In the absence of magnetic fields, the cited theory falls back to the same successful explanation of observed profiles already given by Stenflo (1997) or Stenflo & Keller (1997). But in the presence of magnetic fields this theory is also successful in predicting the general trends and relative behaviors of the three profile peaks, and we observe the ratio of the external to the central peaks drop, while the ratio between the two external peaks becomes close to one, when magnetic fields are present. Furthermore, the theory is also correct in predicting the shape of the Stokes U profile. The agreement between the theory and the observations is therefore remarkable in qualitative terms, but while the general shapes and trends of variation are described well by it, the quantitative predictions for the amplitude of the peaks and their ratios are not correct. The deep reasons for such a departure of the observations from the model of Belluzzi et al. (2007) remain unclear, although the effects of emission of polarization from just the upper layers of the formation regions, or of partial redistribution effects on the line formation, appear as the main candidates to complete the qualitative and quantitative description of the observed linear polarization profiles.
The main departure of the theory by Belluzzi et al. (2007) from the observations comes from the observed Stokes V profiles. They show an anomalous shape with two external peaks, coincident in position to those seen in Stokes Q, while the central peak seen in linear polarization is absent in circular polarization. The Zeeman signature, whenever present, appears inside the two main features. No atomic process can be identified at this time as the origin of this circular polarization signal, and any test seeking an instrumental origin for this profile has resulted in a negative answer, while we can find arguments that justify its solar origin. If such should be the case, the physical phenomena involved is even more enigmatic than the departures observed in linear polarization. Impact polarization by an anisotropic electron distribution for example is unlikely to explain the features, since it would also call for a predominant role of collisions in the formation of the Stokes Q profile as well, leaving no room for atomic polarization induced by the ubiquitous anisotropy of the radiation field. The probable presence of geometry effects into radiative transfer or, perhaps, partial redistribution (an essential physical ingredient according to Rutten 1978, and Rutten & Milkey 1979) may also contain the solution to the anomalous Stokes V signature.
Despite the voids in the model for the resonance scattering polarization of the Ba II D2 line, it is clear that as presented, the theory by Belluzzi et al. (2006) succeeds in explaining, if only qualitatively, the main features of Stokes Q and U and their variations in the presence of a magnetic field, as needed for quantitative modeling. This, in addition to the great variability of its spectral components and the considerable amplitudes of the observed signals, makes this line a powerful probe of the physical conditions encountered in the chromosphere and solar spicules.
Acknowledgements
This research has been partially funded by the Spanish Ministerio de Educación y Ciencia through project AYA2007-63881.
References
- Belluzzi, L., Trujillo Bueno, J., & Landi Degl'Innocenti, E. 2006, in Solar Polarization 4, ed. R. Casini, & B. Lites, ASP Conf. Ser., 358, 459 (In the text)
- Belluzzi, L., Trujillo Bueno, J., & Landi Degl'Innocenti, E. 2007, ApJ, 666, 588 [NASA ADS] [CrossRef] (In the text)
- Berdyugina, S. V., & Fluri, D. M. 2004, A&A, 417, 775 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bianda, M., Solanki, S. K., & Stenflo, J. O. 1998a, A&A, 331, 760 [NASA ADS]
- Bianda, M., Stenflo, J. O., & Solanki, S. K. 1998b, A&A, 337, 565 [NASA ADS]
- Bianda, M., Stenflo, J. O., & Solanki, S. K. 1999, A&A, 350, 1060 [NASA ADS]
- Bommier, V. 1980, A&A, 87, 109 [NASA ADS] (In the text)
- Bommier, V., Sahal-Bréchot, S., & Leroy, J. L. 1981, A&A, 100, 231 [NASA ADS]
- Bommier, V., Landi Degl'Innocenti, E., Leroy, J.-L., & Sahal-Bréchot, S. 1994, Sol. Phys., 154, 231 [NASA ADS] [CrossRef]
- Bommier, V., Derouich, M., Landi degl'Innocenti, E., Molodij, G., & Sahal-Bréchot, S. 2005, A&A, 432, 295 [NASA ADS] [CrossRef] [EDP Sciences]
- Casini, R., López Ariste, A., Tomczyk, S., & Lites, B. W. 2003, ApJ, 598, L67 [NASA ADS] [CrossRef]
- Faurobert-Scholl, M. 1996, Sol. Phys., 164, 79 [NASA ADS] [CrossRef]
- Faurobert-Scholl, M., Feautrier, N., Machefert, F., Petrovay, K., & Spielfiedel, A. 1995, A&A, 298, 289 [NASA ADS]
- Gandorfer, A. 2002, The Second Solar Spectrum: A high spectral resolution polarimetric survey of scattering polarization at the solar limb in graphical representation, Vol. II: 3910 Å to 4630 Å (Zurich: vdf Hochschulverlag) (In the text)
- Gelly, B., Le Men, C., López Ariste, A., Delaigue, C., & Gónzalez Perez, R. 2008, Exp. Astron., 22, 67 [NASA ADS] [CrossRef] (In the text)
- Keller, C. U., Povel, H.-P., & Stenflo, J. O. 1994, in Polarization Analysis and Measurement II, ed. D. H. Goldstein, & D. B. Chenault, Proc. SPIE, 2265, 222 (In the text)
- Kemp, J. C., Macek, J. H., & Nehring, F. W. 1984, APJ, 278, 863 [NASA ADS] [CrossRef] (In the text)
- Krat, V. A., & Krat, T. V. 1971, Sol. Phys., 17, 355 [NASA ADS] [CrossRef]
- Leroy, J. L., Bommier, V., & Sahal-Bréchot, S. 1984, A&A, 131, 33 [NASA ADS]
- López Ariste, A., & Casini, R. 2002, ApJ, 575, 529 [NASA ADS] [CrossRef]
- López Ariste, A., & Casini, R. 2005, A&A, 436, 325 [NASA ADS] [CrossRef] [EDP Sciences]
- Manso Sainz, R., Landi Degl'Innocenti, E., & Trujillo Bueno, J. 2004, ApJ, 614, L89 [NASA ADS] [CrossRef] (In the text)
- Rutten, R. 1978, Sol. Phys., 56, 237 [NASA ADS] [CrossRef]
- Rutten, R., & Milkey, R. 1979, ApJ, 231, 277 [NASA ADS] [CrossRef]
- Sainz Dalda, A., & López Ariste, A. 2007, A&A, 469, 721 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schukina, N., & Trujillo Bueno, J. 2003, in Solar Polarization, ed. J. Trujillo-Bueno, & J. Sanchez Almeida, ASP Conf. Proc., 307, 336
- Semel, M. 2003, A&A, 401, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stenflo, J. 1994, Solar Magnetic Fields (Kluwer)
- Stenflo, J. 1997, A&A, 324, 344 [NASA ADS] (In the text)
- Stenflo, J. O., & Keller, C. U. 1997, A&A, 321, 927 [NASA ADS] (In the text)
- Stenflo, J. O., Baur, T. G., & Elmore, D. F. 1980, A&A, 84, 60 [NASA ADS]
- Stenflo, J. O., Keller, C. U., & Gandorfer, A. 1998, A&A, 329, 319 [NASA ADS] (In the text)
- Trujillo Bueno, J. 2000, in Advanced Solar Polarimetry: Theory, Observations and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 161
- Trujillo Bueno, J. 2003, in ASP Conf. Ser. 307, ed. J. Trujillo-Bueno, & J. Sanchez Almeida, 407 (In the text)
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [NASA ADS] [CrossRef]
- Trujillo Bueno, J., Merenda, L., Centeno, R., Collados, M., & Landi Degl'Innocenti, E. 2005, ApJ, 619, L191 [NASA ADS] [CrossRef]
- Wiehr, E. 1981, A&A, 95, 54 [NASA ADS]
Footnotes
- ... work
![[*]](/icons/foot_motif.png)
- At these spectral resolutions, a shift of 1% of the pixel size, i.e. 0.1
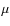 m, introduces spurious signals
stronger than
m, introduces spurious signals
stronger than
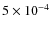 .
.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8154fig1.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg11.png) |
Figure 1: Fractional linear polarization Q/I (solid line) and normalized intensity (dotted line, right scale), around the Ba II D2 line (4554 Å) at 1 arcsec off the solar disk. The positive Q direction is along the slit and parallel to the solar limb. There is an emission Fe I line at 4555.8 Å. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8154fig2.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg12.png) |
Figure 2: As for Fig. 1 but for 0.5 arcsec on the solar disk from the limb, with profiles averaged over 30 arcsec along the slit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8154fig3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg13.png) |
Figure 3: As in Fig. 1 but for 0.5 arcsec on the solar disk from the limb. Profiles averaged over 3 arcsec along the slit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8154f4a.ps}\includegraphics[width=8.8cm,clip]{8154f4b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg14.png) |
Figure 4: Ratios of the amplitudes of the three spectral features of Stokes Q. The legends in the top left corner of both plots identify what ratio of peak amplitudes is depicted by which symbol. In the left plot, the ratios are measured on profiles from observations off-limb (illustrated by the profile in Fig. 1). In the right plot, the ratios are measured on profiles from observations inside the solar disk illustrated in the profiles of Figs. 2 and 3. The strong field shown in Fig. 3 corresponds to the right region (beyond 30 arcsec) of this right plot. The vertical lines draw the limits of the 3 bars in the observing mask. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18.2cm,clip]{8154fig5.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa8154-07/Timg15.png) |
Figure 5: As Figs. 1-3 ( uppermost, middle, and lowermost panels, respectively), but for Stokes U ( leftmost panels) and circular polarization Stokes V ( rightmost panels). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


