| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 619 - 631 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200911794 | |
| Published online | 19 May 2009 | |
Cosmic-ray ionization of molecular clouds
M. Padovani1,2 - D. Galli2 - A.E. Glassgold3
1 - Dipartimento di Astronomia e Scienza dello Spazio, Università di Firenze, Largo E. Fermi 2, 50125 Firenze, Italy
2 -
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
3 -
University of California at Berkeley, Berkeley, CA, 94720, USA
Received 4 February 2009 / Accepted 24 April 2009
Abstract
Context. Low-energy cosmic rays are a fundamental source of ionization for molecular clouds, influencing their chemical, thermal, and dynamical evolution.
Aims. The purpose of this work is to explore the possibility that a low-energy component of cosmic rays, not directly measurable from the Earth, can account for the discrepancy between the ionization rate measured in diffuse and dense interstellar clouds.
Methods. We collected the most recent experimental and theoretical data on the cross sections for the production of H2+ and He+ by electron and proton impact and discuss the available constraints on the cosmic-ray fluxes in the local interstellar medium. Starting from different extrapolations at low energies of the demodulated cosmic-ray proton and electron spectra, we computed the propagated spectra in molecular clouds in the continuous slowing-down approximation taking all the relevant energy loss processes into account.
Results. The theoretical value of the cosmic-ray ionization rate as a function of the column density of traversed matter agrees with the observational data only if the flux of either cosmic-ray electrons or of protons increases at low energies. The most successful models are characterized by a significant (or even dominant) contribution of the electron component to the ionization rate, in agreement with previous suggestions. However, the large spread of cosmic-ray ionization rates inferred from chemical models of molecular cloud cores remains to be explained.
Conclusions. Available data combined with simple propagation models support the existence of a low-energy component (below ![]() 100 MeV) of cosmic-ray electrons or protons responsible for the ionization of molecular cloud cores and dense protostellar envelopes.
100 MeV) of cosmic-ray electrons or protons responsible for the ionization of molecular cloud cores and dense protostellar envelopes.
Key words: ISM: cosmic rays - ISM: clouds - atomic processes - molecular processes
1 Introduction
Cosmic rays (CRs) play a key role in the chemistry and dynamics of the
interstellar medium (ISM). First, CR particles are a primary source of
ionization, competing with stellar UV photons (absorbed in a thin layer
of ![]() 4 mag of visual extinction, McKee 1999) and X-rays
produced by embedded young stellar objects (Krolik & Kallman 1983;
Silk & Norman 1983). The ionization fraction in turn drives the
chemistry of molecular clouds and controls the coupling of the gas with
the Galactic magnetic field. For a good review of the chemistry
that occurs in the ISM in response to CR ionization see
Dalgarno (2006). Second, CRs represent an important source of heating
for molecular clouds because the energy of primary and secondary
electrons produced by the ionization process is in large part converted
into heat by inelastic collisions with ISM atoms and molecules.
4 mag of visual extinction, McKee 1999) and X-rays
produced by embedded young stellar objects (Krolik & Kallman 1983;
Silk & Norman 1983). The ionization fraction in turn drives the
chemistry of molecular clouds and controls the coupling of the gas with
the Galactic magnetic field. For a good review of the chemistry
that occurs in the ISM in response to CR ionization see
Dalgarno (2006). Second, CRs represent an important source of heating
for molecular clouds because the energy of primary and secondary
electrons produced by the ionization process is in large part converted
into heat by inelastic collisions with ISM atoms and molecules.
In general, the CR ionization rate in the interstellar gas depends on
the relative amount of H, H2, and He (Dalgarno et al. 1999).
The first theoretical determination of the CR ionization rate was
performed for clouds made only by atomic hydrogen by Hayakawa,
Nishimura & Takayanagi (1961). They assumed a proton specific
intensity (hereafter, for simplicity, spectrum) proportional to
the proton energy ![]() for
for
![]() and
computed
and
computed
![]() s-1. Spitzer &
Tomasko (1968) determined a value (actually a lower limit) of
s-1. Spitzer &
Tomasko (1968) determined a value (actually a lower limit) of
![]() s-1 for HI clouds,
assuming a CR proton spectrum declining below
s-1 for HI clouds,
assuming a CR proton spectrum declining below
![]() MeV, and
an upper limit of
MeV, and
an upper limit of
![]() s-1, taking into account an additional flux of
s-1, taking into account an additional flux of ![]() 2 MeV protons produced by supernova explosions. To obtain the CR
ionization rate of molecular hydrogen,
2 MeV protons produced by supernova explosions. To obtain the CR
ionization rate of molecular hydrogen,
![]() ,
a useful approximation is
,
a useful approximation is
![]() (Glassgold & Langer 1974), giving
(Glassgold & Langer 1974), giving
![]() s-1, in agreement with the lower limit on
s-1, in agreement with the lower limit on
![]() of Spitzer & Tomasko (1968). This value of
of Spitzer & Tomasko (1968). This value of
![]() is often referred to the ``standard'' CR ionization rate in molecular clouds.
is often referred to the ``standard'' CR ionization rate in molecular clouds.
A major problem in determining the CR ionization rate is that
low-energy CRs are prevented from entering the heliosphere by the solar
wind and the interplanetary magnetic field (solar modulation). In
practice, Earth-based measurements of CR fluxes give no information on
the interstellar spectrum of protons and heavy nuclei for energies
below ![]() 1 GeV/nucleon. Solar modulation also suppresses the flux
of low-energy CR electrons, that already shows considerable fluctuations
at energies of 10-100 GeV (see e.g. Casadei & Bindi 2004).
Since the cross section for ionization of molecular hydrogen by
collisions with protons and electrons has a maximum at
1 GeV/nucleon. Solar modulation also suppresses the flux
of low-energy CR electrons, that already shows considerable fluctuations
at energies of 10-100 GeV (see e.g. Casadei & Bindi 2004).
Since the cross section for ionization of molecular hydrogen by
collisions with protons and electrons has a maximum at ![]() 10 keV
and
10 keV
and ![]() 50 eV, respectively (see Sect. 2), it is
clear that a knowledge of CR spectrum at low energies is an important
limiting factor for any accurate calculation of the ionization rate in
the ISM. A direct measurement of the shape of the CR spectrum at these
energies will be possible only when spacecrafts such as Pioneer and Voyager are well beyond the heliopause, the
outermost boundary for solar modulation effects, believed to lie at
100-150 AU from the Sun (at present, both Voyagers have already
crossed the solar wind termination shock at 85-95 AU from the Sun).
50 eV, respectively (see Sect. 2), it is
clear that a knowledge of CR spectrum at low energies is an important
limiting factor for any accurate calculation of the ionization rate in
the ISM. A direct measurement of the shape of the CR spectrum at these
energies will be possible only when spacecrafts such as Pioneer and Voyager are well beyond the heliopause, the
outermost boundary for solar modulation effects, believed to lie at
100-150 AU from the Sun (at present, both Voyagers have already
crossed the solar wind termination shock at 85-95 AU from the Sun).
Over the past three decades, several values of
![]() ranging
from a few 10-17 s-1 to a few 10-16 s-1 have been
obtained in diffuse interstellar clouds from measurements of the
abundances of various chemical species, in particular OH (Black &
Dalgarno 1977; Hartquist et al. 1978; Black et al. 1978) and HD (van Dishoeck & Black 1986; Federman et al. 1996). However, the derived rates are sensitive to several model assumptions, e.g. the value of specific chemical reaction rates and the intensity of the UV background. In dense molecular clouds, determining the CR ionization rate is made even more uncertain by the sensitivity of molecular abundances to the level of depletion of the various species and the role of small and large grains
in the chemical network. The values of
ranging
from a few 10-17 s-1 to a few 10-16 s-1 have been
obtained in diffuse interstellar clouds from measurements of the
abundances of various chemical species, in particular OH (Black &
Dalgarno 1977; Hartquist et al. 1978; Black et al. 1978) and HD (van Dishoeck & Black 1986; Federman et al. 1996). However, the derived rates are sensitive to several model assumptions, e.g. the value of specific chemical reaction rates and the intensity of the UV background. In dense molecular clouds, determining the CR ionization rate is made even more uncertain by the sensitivity of molecular abundances to the level of depletion of the various species and the role of small and large grains
in the chemical network. The values of
![]() derived by Caselli et al. (1998) in a sample of 23 molecular cloud cores (column density
derived by Caselli et al. (1998) in a sample of 23 molecular cloud cores (column density
![]() cm-2 ) through DCO+ and HCO+ abundance ratios span a range of about two orders of magnitudes from
cm-2 ) through DCO+ and HCO+ abundance ratios span a range of about two orders of magnitudes from ![]() 10-17 s-1 to
10-17 s-1 to ![]() 10-15 s-1, with a
scatter that may in part reflect intrinsic variations of the CR flux from core to core. Finally, values of
10-15 s-1, with a
scatter that may in part reflect intrinsic variations of the CR flux from core to core. Finally, values of
![]() of a few times 10-17 s-1 have been obtained in clouds of higher column density (
of a few times 10-17 s-1 have been obtained in clouds of higher column density (
![]() -1024 cm-2) like the
envelopes surrounding massive protostellar sources (van der Tak & van
Dishoeck 2000; Doty et al. 2002).
-1024 cm-2) like the
envelopes surrounding massive protostellar sources (van der Tak & van
Dishoeck 2000; Doty et al. 2002).
The discovery of significant abundances of H3+ in diffuse clouds
(McCall et al. 1998), confirmed by follow-up detections (Geballe et al. 1999; McCall et al. 2003; Indriolo et al. 2007), has led to values
of
![]() larger by about one order of magnitude than both
the ``standard'' rate and previous estimates based on the abundance of
OH and HD in dense clouds. Given the relative simplicity of the
chemistry of H3+, it is now believed that diffuse clouds are
characterized by CR ionization rates
larger by about one order of magnitude than both
the ``standard'' rate and previous estimates based on the abundance of
OH and HD in dense clouds. Given the relative simplicity of the
chemistry of H3+, it is now believed that diffuse clouds are
characterized by CR ionization rates
![]() s-1 or larger. This high value of
s-1 or larger. This high value of
![]() in the diffuse interstellar gas can be reconciled with the lower values
measured in cloud cores and massive protostellar envelopes by
invoking various mechanisms of CR screening in molecular clouds due to
either self-generated Alfvén waves in the plasma (Skilling & Strong 1976; Hartquist et al. 1978; Padoan & Scalo 2005) or to
magnetic mirror effects (Cesarsky & Völk 1978; Chandran 2000). An
alternative explanation, based on the possible existence of a
low-energy flux of CR particles, is that they can penetrate (and
ionize) diffuse clouds but not dense clouds, as recently proposed by
McCall et al. (2003), see also Takayanagi (1973) and Umebayashi &
Nakano (1981). This latter scenario is explored quantitatively in the
present paper.
in the diffuse interstellar gas can be reconciled with the lower values
measured in cloud cores and massive protostellar envelopes by
invoking various mechanisms of CR screening in molecular clouds due to
either self-generated Alfvén waves in the plasma (Skilling & Strong 1976; Hartquist et al. 1978; Padoan & Scalo 2005) or to
magnetic mirror effects (Cesarsky & Völk 1978; Chandran 2000). An
alternative explanation, based on the possible existence of a
low-energy flux of CR particles, is that they can penetrate (and
ionize) diffuse clouds but not dense clouds, as recently proposed by
McCall et al. (2003), see also Takayanagi (1973) and Umebayashi &
Nakano (1981). This latter scenario is explored quantitatively in the
present paper.
In this paper, we concentrate on molecular clouds, where hydrogen is
present mostly in molecular form and we can ignore ionization of atomic
hydrogen. In Sect. 8 we then apply our results to
diffuse clouds, where the fraction of hydrogen in molecular form
![]() has a mean value
has a mean value
![]() (Indriolo et al. 2007), implying that
the column densities of H and H2 are almost equal. This is justified
because the quantity directly measured (or estimated) in the diffuse
clouds examined in Sect. 8 is the ionization rate of
H2 as derived from the measured abundance of H3+.
(Indriolo et al. 2007), implying that
the column densities of H and H2 are almost equal. This is justified
because the quantity directly measured (or estimated) in the diffuse
clouds examined in Sect. 8 is the ionization rate of
H2 as derived from the measured abundance of H3+.
The organization of the paper is the following. In Sects. 2-4 we examine the ionization reactions of CR protons and electrons incident on H2 and He and other channels of electron production; in Sect. 5 we discuss the assumed interstellar spectra of CR protons and electrons; in Sect. 6 we discuss the energy loss mechanisms for CRs; in Sect. 7 we compute the ionization rate as a function of the column density in a cloud; in Sect. 8 we compare our results with the available estimates of the CR ionization rate in diffuse and dense clouds; finally, in Sect. 9 we summarize our conclusions.
Table 1: CR reactions in molecular clouds.
2 CR reactions with H2
CR particles (electrons, protons, and heavy nuclei) impact with atoms and
molecules of the ISM producing ions and electrons. Table 1 lists
the main CR ionization reactions involving H2 and He. In molecular
clouds, a large majority of CR-H2 impacts leads to the formation
of H2+ via the ionization reaction
where
with cross section
where jk(Ek) is the number of CR particles of species k per unit area, time, solid angle and per energy interval (hereafter, we will refer to jk(Ek) simply as the spectrum of particle k),
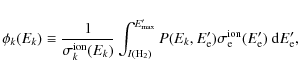 |
(4) |
where
In the following subsections we summarize the available data for
the ionization cross sections for proton and electron impact and for
the electron capture cross section. The ionization of H2 by CR
heavy-nuclei (![]() )
is computed in the Bethe-Born approximation as
described in Appendix A.
)
is computed in the Bethe-Born approximation as
described in Appendix A.
2.1 Ionization of H2 by proton impact:
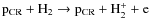
The avalaible experimental data for proton-impact ionization of H2 have
been summarized by Rudd et al. (1985). The cross section has a maximum
at
![]() keV and is considerably uncertain below
keV and is considerably uncertain below ![]() 1 keV.
The data were fitted by Rudd et al. (1985) with expressions appropriate
to the high- and low-energy regions,
1 keV.
The data were fitted by Rudd et al. (1985) with expressions appropriate
to the high- and low-energy regions,
where
with
 |
Figure 1:
Cross sections for proton impact on H2: ionization cross
section
|
| Open with DEXTER | |
2.2 Ionization of H2 by electron impact:

The experimental data for electron-impact ionization of H2 have been
reviewed by Liu & Shemansky (2004). The absolute cross sections for
electron-impact ionization of H2 measured by Straub et al. (1996) in
the energy range
![]() eV to
eV to
![]() keV represent the currently
recommended experimental values (Lindsay & Mangan 2003). Analytic
expressions and fitting formulae for the ionization cross section have
been derived by Rudd (1991), Kim & Rudd (1994) and Liu &
Shemansky (2004). Here we adopt the semi-empirical model by
Rudd (1991) that gives an analytical expression valid up to
relativistic velocities based on the theoretical results of
Mott (1930),
keV represent the currently
recommended experimental values (Lindsay & Mangan 2003). Analytic
expressions and fitting formulae for the ionization cross section have
been derived by Rudd (1991), Kim & Rudd (1994) and Liu &
Shemansky (2004). Here we adopt the semi-empirical model by
Rudd (1991) that gives an analytical expression valid up to
relativistic velocities based on the theoretical results of
Mott (1930),
where
with
 |
Figure 2:
Cross sections for electron impact on H2: ionization cross
section
|
| Open with DEXTER | |
2.3 Electron capture ionization of H2:

In this charge-exchange process, a high-energy CR proton picks up an
electron from the H2 molecule and emerges as a neutral H atom.
The electron capture cross section has been fit by Rudd et al. (1983)
with the expression
where
3 Additional reactions of CR electrons and protons with H2
Additional ionization reactions that produce electrons are
the dissociative ionization of H2,
with cross section
with cross section
In the following subsection we examine the cross sections of these two processes for electron impact reactions, whereas for proton impact we assume cross sections equal to the corresponding cross sections for electrons of equal velocity,
 |
(14) |
and
 |
(15) |
As shown below, the cross sections of these processes are smaller by at least one order of magnitude than the corresponding ionization cross section, and the relative contribution of dissociative ionization and double ionization to the total electron production rate is expected to be small.
3.1 Dissociative ionization of H2 by electron impact:

Absolute partial cross sections for dissociative ionization of H2 by
electron impact (threshold
![]() eV) have been
measured by Straub et al. (1996) for incident electron energies ranging
from
eV) have been
measured by Straub et al. (1996) for incident electron energies ranging
from
![]() eV to
eV to
![]() keV (see also Lindsay & Mangan 2003).
Their results are in agreement with the reanalysis of Van Zyl &
Stephen (1994) of the experimental results of Rapp et al. (1965) and Krishnakumar & Srivastava (1994).
For
keV (see also Lindsay & Mangan 2003).
Their results are in agreement with the reanalysis of Van Zyl &
Stephen (1994) of the experimental results of Rapp et al. (1965) and Krishnakumar & Srivastava (1994).
For
![]() ,
the cross section has been measured by Takayanagi
& Suzuki (1978). These measurements represent the currently
recommended experimental values (Liu & Shemansky 2004). The data of
Straub et al. (1996) and a polynomial fit of the data are shown in
Fig. 2. The coefficients of the polynomial fit
,
the cross section has been measured by Takayanagi
& Suzuki (1978). These measurements represent the currently
recommended experimental values (Liu & Shemansky 2004). The data of
Straub et al. (1996) and a polynomial fit of the data are shown in
Fig. 2. The coefficients of the polynomial fit
![]() ,
valid for
,
valid for
![]() keV, are given in Table 2.
keV, are given in Table 2.
Table 2: Fit coefficients for the dissociative ionization and double ionization cross sections of H2 by electron impact.
3.2 Double ionization of H2 by electron impact:

The energy threshold for this reaction is
![]() eV.
The cross section for this reaction is highly uncertain: the
measurements by Edwards et al. (1988) and Kossmann et al. (1990) disagree by a factor of
eV.
The cross section for this reaction is highly uncertain: the
measurements by Edwards et al. (1988) and Kossmann et al. (1990) disagree by a factor of ![]() 8. Here we adopt the
latter set of measurements (shown in Fig. 2). The
coefficients of a polynomial fit of these data
(see Sect. 3.1), valid for
8. Here we adopt the
latter set of measurements (shown in Fig. 2). The
coefficients of a polynomial fit of these data
(see Sect. 3.1), valid for
![]() keV, are given in Table 2.
keV, are given in Table 2.
4 CR reactions with He
The CR production rate of He+ (per He atom) is
where
4.1 Ionization of He by proton impact:

Experimental measurements of He ionization by proton impact have been
collected and fitted by Rudd et al. (1985). The cross section has a
maximum at
![]() keV and is considerably uncertain below
keV and is considerably uncertain below
![]() 10 keV. Figure 3 shows the available experimental
data. We adopt the fitting formula of Rudd et al. (1985) given by
Eqs. (5) and (6) with parameters A=0.49,
B=0.62, C=0.13, D=1.52.
10 keV. Figure 3 shows the available experimental
data. We adopt the fitting formula of Rudd et al. (1985) given by
Eqs. (5) and (6) with parameters A=0.49,
B=0.62, C=0.13, D=1.52.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg116.png) |
Figure 3:
Cross sections for proton impact on He: ionization cross
section
|
| Open with DEXTER | |
4.2 Ionization of He by electron capture:

The cross section for this charge transfer reaction has been measured
by Welsh et al. (1967) and Shah & Gilbody (1985). The cross section
has a maximum at
![]() keV, where it is about one order of
magnitude larger than the ionization cross section
keV, where it is about one order of
magnitude larger than the ionization cross section
![]() (see Fig. 3). Total ionization cross sections
(
(see Fig. 3). Total ionization cross sections
(
![]() have been reported by
DuBois et al. (1984).
have been reported by
DuBois et al. (1984).
4.3 Ionization of He by electron impact:

Accurate experimental measurements of the cross section for
He ionization by electron impact are available (see Fig. 4)
and are in good agreement with theoretical calculations (Pindzola &
Robicheaux 2000; Colgan et al. 2006). Here we adopt the fitting formula
of Rudd (1991) given in Eqs. (7)-(9) with N=2,
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig4.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg123.png) |
Figure 4:
Cross section for He ionization by electron impact
|
| Open with DEXTER | |
5 Local interstellar spectra
From a theoretical point of view, if one assumes a uniform distribution (in space and time) of CR sources characterized by a given ``source spectrum'' (usually a power-law in rigidity), CR propagation models can generate steady-state local interstellar (LIS) spectra resulting from a number of processes affecting the CR transport in the Galactic disk, like nuclear interactions, ionization energy loss, radioactive decay, escape from the Galaxy, etc. (see e.g. Berezinsky et al. 1990). These LIS spectra, in turn, can be used as input for solar modulation calculations to reproduce the CR spectrum and the relative abundances of CR particles measured at the Earth. The LIS spectra obtained in this way are clearly not uniquely defined, and a considerable range of LIS spectral shapes can be shown to be consistent with the measured CR flux with appropriate choices of parameters of the transport model (see e.g. Mewaldt et al. 2004, especially their Fig. 1).
It is generally assumed that the LIS spectrum characterizes the energy
distribution of CR everywhere in the Galactic disk, as long as the ISM
properties do not depart from the uniform conditions assumed in the
propagation model. With this assumption, Webber (1998) adopted LIS
spectra for protons and heavy nuclei of energy greater than 10 MeV
and electrons of energy greater than 2 MeV and combined them with data
from Voyager and Pioneer spacecraft measurements out to
60 AU from the Sun to obtain a CR ionization rate
![]() s-1. This is 5-6 times the
``standard'' rate of Spitzer & Tomasko (1968) for atomic hydrogen.
s-1. This is 5-6 times the
``standard'' rate of Spitzer & Tomasko (1968) for atomic hydrogen.
It is very uncertain, however, whether LIS spectra are really
representative of the whole galactic disk, especially because the Solar
System resides in a low-density (![]() 10-3 cm-3) region
produced by
10-3 cm-3) region
produced by ![]() 10 supernovae exploded over the past 10 Myr (the
``Local Bubble''). In addition, to compute reliable CR ionization
rates, the demodulated spectra need to be extrapolated down to
10 supernovae exploded over the past 10 Myr (the
``Local Bubble''). In addition, to compute reliable CR ionization
rates, the demodulated spectra need to be extrapolated down to ![]() keV energies where the ionization cross sections have a maximum
(see Sects. 2-4). Given these uncertainties, we discuss in the
remainder of the paper the consequences for the CR ionization rate of
making different assumptions about the low-energy behavior of CR
spectra. In particular, we consider for both protons and electrons a
``minimum'' and ``maximum'' LIS spectrum compatible with the available
observational constraints, and we compute the resulting ionization
rates with the objective of comparing them with existing data for
diffuse and dense clouds.
keV energies where the ionization cross sections have a maximum
(see Sects. 2-4). Given these uncertainties, we discuss in the
remainder of the paper the consequences for the CR ionization rate of
making different assumptions about the low-energy behavior of CR
spectra. In particular, we consider for both protons and electrons a
``minimum'' and ``maximum'' LIS spectrum compatible with the available
observational constraints, and we compute the resulting ionization
rates with the objective of comparing them with existing data for
diffuse and dense clouds.
5.1 Proton local interstellar spectrum
We consider two determinations of the proton LIS spectrum: Webber (1998, ``minimum'') and Moskalenko et al. (2002, ``maximum''), labeled respectively W98 and M02. Their characteristics are the following.
- (i)
- W98 estimated the LIS proton spectrum down to
 10 MeV, starting from an injection spectrum parametrized as a
power-law in rigidity, propagated according to the model of
Webber (1987) and accounting for solar modulation following
Potgieter (1995). The effects of solar modulation were refined using
data from the Voyager and Pioneer spacecraft, then at distances of
10 MeV, starting from an injection spectrum parametrized as a
power-law in rigidity, propagated according to the model of
Webber (1987) and accounting for solar modulation following
Potgieter (1995). The effects of solar modulation were refined using
data from the Voyager and Pioneer spacecraft, then at distances of
 60-70 AU from the Sun. The predicted LIS proton spectrum of
W98 has a turnover around
60-70 AU from the Sun. The predicted LIS proton spectrum of
W98 has a turnover around
 MeV because of the dominant
effect of ionization losses at low energies in the Galactic propagation
model. Our extrapolation at low energies is a power-law in energy
with exponent 0.95.
MeV because of the dominant
effect of ionization losses at low energies in the Galactic propagation
model. Our extrapolation at low energies is a power-law in energy
with exponent 0.95.
- (ii)
- The adopted LIS spectrum of M02 (their ``best-fitting''
case) reproduces the observed spectrum of protons, antiprotons, alphas,
the B/C ratio and the diffuse
 -ray background. It is obtained
from an injection spectrum which is a double power-law in rigidity with
a steepening below 20 GeV, and a flattening of the diffusion
coefficient below 4 GeV to match the B/C ratio at
-ray background. It is obtained
from an injection spectrum which is a double power-law in rigidity with
a steepening below 20 GeV, and a flattening of the diffusion
coefficient below 4 GeV to match the B/C ratio at
 MeV.
At low energies, our extrapolation follows a power-law in energy
with exponent -1.
MeV.
At low energies, our extrapolation follows a power-law in energy
with exponent -1.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig5.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg130.png) |
Figure 5: Proton LIS spectra of M02 and W98 (upper and lower solid curves, respectively). The dashed curves represent our power-law extrapolations of the spectra. For comparison, the cross sections for ionization of H2 by proton impact, electron capture, and total ionization are also shown (in arbitrary units). |
| Open with DEXTER | |
5.2 Electron local interstellar spectrum
CR electrons (and positrons), although constituting a small percentage
of the corpuscular radiation, provide important information regarding
interstellar propagation. This happens because CR electrons are more
sensitive probes of ISM conditions than CR nuclei. In fact, electrons
interact with: (i) the ISM, producing bremßtrahlung
responsible for the largest part of galactic background at
![]() -frequencies; (ii) radiation fields, generating
radiation by inverse Compton scattering at X- and
-frequencies; (ii) radiation fields, generating
radiation by inverse Compton scattering at X- and ![]() -frequencies;
(iii) magnetic fields, producing synchrotron emission at radio
frequencies. The electromagnetic radiation emitted by the interaction
of CR electrons with other components of the ISM makes it possible to
establish a relation between the observed radiation spectra and the
energy distribution of the electrons. In particular, observations of
the
-frequencies;
(iii) magnetic fields, producing synchrotron emission at radio
frequencies. The electromagnetic radiation emitted by the interaction
of CR electrons with other components of the ISM makes it possible to
establish a relation between the observed radiation spectra and the
energy distribution of the electrons. In particular, observations of
the ![]() -ray background in the 10 keV-100 MeV range, combined with
measurements of the Galactic synchrotron spectral index in the
frequency range 10 MHz-10 GHz, provide indirect constraints on the LIS
electron spectrum down to energies of
-ray background in the 10 keV-100 MeV range, combined with
measurements of the Galactic synchrotron spectral index in the
frequency range 10 MHz-10 GHz, provide indirect constraints on the LIS
electron spectrum down to energies of ![]() 100 MeV. As for the proton
spectrum, we extrapolate the LIS electron spectra to lower energies
with power-laws to reach the peak of the ionization cross section at
100 MeV. As for the proton
spectrum, we extrapolate the LIS electron spectra to lower energies
with power-laws to reach the peak of the ionization cross section at
![]() 0.1 keV. Here we consider two different estimates of the LIS
electron spectrum, both derived by Strong et al. (2000).
0.1 keV. Here we consider two different estimates of the LIS
electron spectrum, both derived by Strong et al. (2000).
- (i)
- The first spectrum, labeled C00, corresponds to the
``conventional'' model C of Strong et al. (2000), and is mostly derived
from radio observations. It reproduces the spectrum of electrons,
protons and alphas above
 10 GeV, satisfies the limits imposed by
positrons and antiprotons and the constraints on the synchrotron
spectrum, but fails to account for the
10 GeV, satisfies the limits imposed by
positrons and antiprotons and the constraints on the synchrotron
spectrum, but fails to account for the  -ray background,
especially for photon energies below
-ray background,
especially for photon energies below  30 MeV and above
30 MeV and above  1 GeV. At low-energies, we have adopted a power-law dependence of the electron spectrum as
1 GeV. At low-energies, we have adopted a power-law dependence of the electron spectrum as
 .
.
- (ii)
- The second spectrum, labeled E00, corresponds to the
model SE
of Strong et al. (2000). It reproduces the
 observations at
photon energies below
observations at
photon energies below  30 MeV by a combination of bremß
trahlung and inverse Compton emission, assuming a steepening of the
electron spectrum below
30 MeV by a combination of bremß
trahlung and inverse Compton emission, assuming a steepening of the
electron spectrum below  200 MeV to compensate for the growth of
ionization losses. The resulting increase in the synchrotron spectrum
occurs at frequencies below 10 MHz, where the radio spectrum decreases
abruptly due to the onset of free-free absorption. To fit OSSE data
would require a LIS electron even steeper than E00, but the excess
200 MeV to compensate for the growth of
ionization losses. The resulting increase in the synchrotron spectrum
occurs at frequencies below 10 MHz, where the radio spectrum decreases
abruptly due to the onset of free-free absorption. To fit OSSE data
would require a LIS electron even steeper than E00, but the excess
 emission at
emission at  MeV energies may be due to a
population of unresolved point sources (Strong et al. 2000). At
low energies, we have adopted a power-law extrapolation of the spectrum
as
MeV energies may be due to a
population of unresolved point sources (Strong et al. 2000). At
low energies, we have adopted a power-law extrapolation of the spectrum
as
 .
.
5.3 CR ionization rate for the local interstellar spectra
The values of
![]() ,
,
![]() and
and
![]() per H2 molecule and He atom, respectively, obtained from
numerical integration of Eqs. (3), (13) and (16), with the jk(Ek) taken to be the adopted LIS
spectra, are listed in Table 3. We have assumed a mixture of
H2 and He with
per H2 molecule and He atom, respectively, obtained from
numerical integration of Eqs. (3), (13) and (16), with the jk(Ek) taken to be the adopted LIS
spectra, are listed in Table 3. We have assumed a mixture of
H2 and He with
![]() and
and
![]() ,
corresponding to a He/H ratio of 0.1. We also list in
Table 3 the energy density of each CR component, defined as
,
corresponding to a He/H ratio of 0.1. We also list in
Table 3 the energy density of each CR component, defined as
where jk(Ek) is the particle's LIS spectrum and vk(Ek)=c(Ek2/mk2c4+2Ek/mkc2)1/2/(1+Ek/mkc2) is the velocity of particle k with kinetic energy Ek. We compute the total energy density of CR as
- (i)
- protons and heavy nuclei (plus secondary electrons) can
produce ionization rates ranging from
 10-17 s-1
(in the case of the the spectrum W98, decreasing below
10-17 s-1
(in the case of the the spectrum W98, decreasing below
 MeV)
to
MeV)
to  10-14 s-1 (spectrum M02, increasing below
10-14 s-1 (spectrum M02, increasing below
 MeV). The contribution of CR electrons to the
ionization rate is negligible if the LIS electron spectrum flattens
below
MeV). The contribution of CR electrons to the
ionization rate is negligible if the LIS electron spectrum flattens
below
 MeV (spectrum C00), but can become dominant if
the spectrum increases at low energies. In practice, the ionization
rate is proportional to the flux of CR particles in the energy range
where the contribution to the integrals in Eqs. (3),
(13) and (16) is larger (see
Sect. 7 and Fig. 14);
MeV (spectrum C00), but can become dominant if
the spectrum increases at low energies. In practice, the ionization
rate is proportional to the flux of CR particles in the energy range
where the contribution to the integrals in Eqs. (3),
(13) and (16) is larger (see
Sect. 7 and Fig. 14);
- (ii)
- the ratio of the CR ionization rate of He and H2depends on the shape and absolute value of the assumed spectra. For CR
protons, the ratio
 varies
between 0.15 (spectrum M02) and 0.64 (spectrum W98), whereas for
electrons it varies between 0.38 (spectrum E00) and 0.65 (spectrum
C00). In general, since the ionization cross section for He decreases
faster than that of H2 below the maximum, CR spectra rising with
decreasing energy result in a lower value of
varies
between 0.15 (spectrum M02) and 0.64 (spectrum W98), whereas for
electrons it varies between 0.38 (spectrum E00) and 0.65 (spectrum
C00). In general, since the ionization cross section for He decreases
faster than that of H2 below the maximum, CR spectra rising with
decreasing energy result in a lower value of
 .
Given the sensitivity of modeled steady-state
abundances of species like C, O2, H2O, H3+ in dense clouds to
the value of
.
Given the sensitivity of modeled steady-state
abundances of species like C, O2, H2O, H3+ in dense clouds to
the value of
 (Wakelam et al. 2006),
it might be possible to constrain this ratio from a careful combination
of molecular line observations and chemical model predictions;
(Wakelam et al. 2006),
it might be possible to constrain this ratio from a careful combination
of molecular line observations and chemical model predictions;
- (iii)
- as anticipated, the CR production rate of electrons in
molecular clouds
 is dominated by the CR ionization of H2(Sect. 2) and He (Sect. 4). The
contributions of dissociative ionization and double ionization to
is dominated by the CR ionization of H2(Sect. 2) and He (Sect. 4). The
contributions of dissociative ionization and double ionization to
 are small, about 5.5% and 0.32% of the rate of production
of electrons by single ionization of H2, respectively, independent
of the adopted spectrum;
are small, about 5.5% and 0.32% of the rate of production
of electrons by single ionization of H2, respectively, independent
of the adopted spectrum;
- (iv)
- the production rate of electrons,
 ,
is
generally larger than (but close to) the production rate of H2+.
For the W98 proton spectrum, the C00 and E00 electron spectra,
,
is
generally larger than (but close to) the production rate of H2+.
For the W98 proton spectrum, the C00 and E00 electron spectra,
 .
However, since we
have included in the expression for
.
However, since we
have included in the expression for
 the electron
capture reaction (2) whose cross section peaks at a lower
energy than the ionization reaction (1) as shown in
Fig. 1, a CR proton spectrum rising at low energies may
result in
the electron
capture reaction (2) whose cross section peaks at a lower
energy than the ionization reaction (1) as shown in
Fig. 1, a CR proton spectrum rising at low energies may
result in
 ,
as in the case of the M02
spectrum;
,
as in the case of the M02
spectrum;
- (v)
- with our assumed LIS spectra, the total CR energy density
varies from a minimum of 0.970 eV cm-3 (W98 plus C00) and a
maximum of 1.80 eV cm-3 (M02 plus E00), corresponding to an
equipartition magnetic field of 6.2
 G and 8.5
G and 8.5  G,
respectively. These equipartition values are compatible with the
``standard'' value of the magnetic field of
G,
respectively. These equipartition values are compatible with the
``standard'' value of the magnetic field of

 G in the
cold neutral medium of the Galaxy (Heiles & Troland 2005). They have
interesting consequences for the location of the solar wind termination
shock (see discussion in Webber 1998).
G in the
cold neutral medium of the Galaxy (Heiles & Troland 2005). They have
interesting consequences for the location of the solar wind termination
shock (see discussion in Webber 1998).
Table 3:
CR ionization rates
![]() and
and
![]() ,
electron production rate
,
electron production rate
![]() ,
and energy densities
,
and energy densities
![]() of CR protonsa (p) and electrons (e).
of CR protonsa (p) and electrons (e).
It is important to stress that the CR ionization rates listed in Table 3 have been obtained by integrating the spectra and the cross sections down to the ionization threshold of H2 and He, and they must therefore be considered as upper limits on the ionization rate. This is especially true for the electron spectrum E00, which results in ionization rates exceeding the observed values by more than three orders of magnitude (see Sect. 8). In the past, LIS spectra have been used to compute the CR ionization rate in the ISM assuming an appropriate lower cut-off in the CR energy (e.g. Nath & Biermann 1994; Webber 1998). In this work, we use the LIS spectra to define the energy distribution of CR particles incident on the surface of the cloud. As we show in Sects. 6 and 7, the low-energy tail of the CR spectrum is strongly (and rapidly) modified by various energy loss processes when the particles propagate in a medium denser than the local ISM.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig6.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg159.png) |
Figure 6: Electron LIS spectra of E00 and C00 (upper and lower solid curves, respectively). The dashed curves represent our extrapolations of the spectra. For comparison, the cross section for ionization of H2 by electron impact is also shown (in arbitrary units). |
| Open with DEXTER | |
6 Energy losses of CRs in the ISM
The penetration of primary CR and secondary particles in interstellar
clouds was studied by Takayanagi (1973) and more in detail by
Umebayashi & Nakano (1981). In this paper we adopt the LIS spectra
discussed in Sect. 5 to characterize the incident spectra
and we follow the propagation of CR particles inside a molecular cloud
with the so-called continuous-slowing-down approximation
(hereafter CSDA)![]() . In this
approximation, the ``degradation spectrum'' of the CR component kresulting from the energy loss of the incident particles and the
generation of secondary particles is proportional to the inverse of the
energy loss function, defined by
. In this
approximation, the ``degradation spectrum'' of the CR component kresulting from the energy loss of the incident particles and the
generation of secondary particles is proportional to the inverse of the
energy loss function, defined by
where
In the following we consider CR propagation in molecular clouds
assuming a plane-parallel geometry. It is convenient to introduce the
column density of molecular hydrogen
![]() ,
,
 |
(19) |
and to rewrite the energy loss function (Eq. (18)) as
Let us then define jk(Ek,N) as the spectrum of CR particles of species k at depth
where Rk(Ek) is the range, defined as
Conservation of the number of CR particles of each species implies
| (23) |
where, for a given value of
(we ignore here that electron capture reactions of CR protons with H2 and He do not conserve the number of CR protons). Thus, the relation between the incident spectrum jk(Ek,0,0) and the spectrum jk(Ek,N) at depth
The energy loss functions for electrons and protons in H2 are shown in Fig. 7. Some energy loss processes are common to CR protons and electrons, like Coulomb interactions, inelastic collisions and ionization; others are peculiar to protons (elastic collisions, pion production and spallation), others to electrons (bremßtrahlung, synchrotron emission and inverse Compton scattering). These processes are briefly reviewed in the following subsections.
6.1 Energy loss of protons colliding with H2
To determine the energy loss function of protons we have used the
results collected by Phelps (1990) for energies in the range from
10-1 eV to 104 eV. For higher energies, between 1 keV and
10 GeV, we have used data from the NIST Database![]() for atomic hydrogen
multiplied by a factor of 2 to obtain the corresponding values for
collisions with molecular hydrogen (NIST data do not include pion
production at energies higher than about 0.5 GeV, that we computed
following Schlickeiser 2002). The resulting energy loss function is
shown in Fig. 7. The broad peak in
for atomic hydrogen
multiplied by a factor of 2 to obtain the corresponding values for
collisions with molecular hydrogen (NIST data do not include pion
production at energies higher than about 0.5 GeV, that we computed
following Schlickeiser 2002). The resulting energy loss function is
shown in Fig. 7. The broad peak in
![]() at
at
![]() eV is due to elastic collisions and to the
excitation of rotational and vibrational levels, the peak at
eV is due to elastic collisions and to the
excitation of rotational and vibrational levels, the peak at
![]() keV to ionization, and the rapid increase at energies
above
keV to ionization, and the rapid increase at energies
above ![]() 1 GeV is due to pion production. For the low ionization
levels characteristic of molecular clouds, the energy loss for Coulomb
interactions of CRs with ambient electrons can be neglected at energies
above
1 GeV is due to pion production. For the low ionization
levels characteristic of molecular clouds, the energy loss for Coulomb
interactions of CRs with ambient electrons can be neglected at energies
above ![]() 1 eV (dashed line in Fig. 7).
1 eV (dashed line in Fig. 7).
In Fig. 8 we show the quantity
![]() ,
obtained
with a numerical integration of Eq. (22), compared with data
from the NIST Database at energies from 1 keV to 10 GeV. We also show the
fit adopted by Takayanagi (1973) in a limited range of energies and the
results of Cravens & Dalgarno (1978). As one can see, except for energies
higher than
,
obtained
with a numerical integration of Eq. (22), compared with data
from the NIST Database at energies from 1 keV to 10 GeV. We also show the
fit adopted by Takayanagi (1973) in a limited range of energies and the
results of Cravens & Dalgarno (1978). As one can see, except for energies
higher than ![]() 100 MeV, where the NIST data do not include energy
losses by pion production, the agreement between our results and the
NIST data is very good.
100 MeV, where the NIST data do not include energy
losses by pion production, the agreement between our results and the
NIST data is very good.
6.2 Energy loss of electrons colliding with H2
To determine the electron energy loss function we have adopted the
results of Dalgarno et al. (1999) for
![]() and those of Cravens et al. (1975) for
and those of Cravens et al. (1975) for
![]() keV. For higher energies,
keV. For higher energies,
![]() ,
we have adopted the loss function for electron-H
collisions from the NIST Database multiplied by a factor of 2. The
resulting energy loss function is also shown in
Fig. 7. The first peak in
,
we have adopted the loss function for electron-H
collisions from the NIST Database multiplied by a factor of 2. The
resulting energy loss function is also shown in
Fig. 7. The first peak in
![]() is due to the
excitation of vibrational levels, the second to the excitation of the
electronic levels and ionization, while at higher energies the energy
loss function is dominated by bremßtrahlung. As in the case of CR
protons, we can neglect the contribution of Coulomb interactions for
electrons at energies above
is due to the
excitation of vibrational levels, the second to the excitation of the
electronic levels and ionization, while at higher energies the energy
loss function is dominated by bremßtrahlung. As in the case of CR
protons, we can neglect the contribution of Coulomb interactions for
electrons at energies above ![]() 1 eV. In Fig. 8, we show
the range for electrons in H2, obtained as in the case of CR
protons, compared with data from the NIST Database for
1 eV. In Fig. 8, we show
the range for electrons in H2, obtained as in the case of CR
protons, compared with data from the NIST Database for
![]() .
.
 |
Figure 7:
Energy loss functions
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig8.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg180.png) |
Figure 8:
Range
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig9.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg182.png) |
Figure 9:
Dashed curve, LIS proton spectrum W98 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
7 CR ionization rate in diffuse and dense clouds
To compute the CR ionization rate in the ISM as a function of the column
density
![]() of traversed matter, we follow the method of
Takayanagi (1973). First, varying Ek and Ek,0 from 0.1 eV to
100 GeV, we determine the column density from the difference between
Rk(Ek,0) and Rk(Ek). Second, tracing the level contours of
the surface
N(Ek,0,Ek) at different values of
of traversed matter, we follow the method of
Takayanagi (1973). First, varying Ek and Ek,0 from 0.1 eV to
100 GeV, we determine the column density from the difference between
Rk(Ek,0) and Rk(Ek). Second, tracing the level contours of
the surface
N(Ek,0,Ek) at different values of
![]() ,
we obtain the relation between the energy of the incident CR particle,
Ek,0, and the residual energy Ek, when the particle has covered
a path inside the cloud corresponding to a given value of the column
density. We then fit the resulting Ek,0 vs. Ek relation at fixed
,
we obtain the relation between the energy of the incident CR particle,
Ek,0, and the residual energy Ek, when the particle has covered
a path inside the cloud corresponding to a given value of the column
density. We then fit the resulting Ek,0 vs. Ek relation at fixed
![]() with the expression
with the expression
where Ek and Ek,0 are in eV, N and N0 in cm-2, b and c are non-dimensional.
In Figs. 9-12 we
show the CR spectrum obtained from Eqs. (25) and (26)
for protons and electrons at values of
![]() ranging from
1019 cm-2 to 1026 cm-2, inside a molecular cloud
for the two incident spectra of protons and electrons described in
Sect. 5. One can notice the correspondence between the
shape of the proton spectra shown in Figs. 9 and 10, and the energy loss function
ranging from
1019 cm-2 to 1026 cm-2, inside a molecular cloud
for the two incident spectra of protons and electrons described in
Sect. 5. One can notice the correspondence between the
shape of the proton spectra shown in Figs. 9 and 10, and the energy loss function
![]() shown in
Fig. 7. In fact, the relative minimum at about 10 eV
in the attenuated spectrum corresponds to the energy loss peak due to
elastic interactions and excitation of roto-vibrational levels, and the
minimum at about 100 keV corresponds to the energy loss peak due to
ionization. The same correspondence can be seen between electron
spectra (Figs. 11 and 12) and the energy loss
function
shown in
Fig. 7. In fact, the relative minimum at about 10 eV
in the attenuated spectrum corresponds to the energy loss peak due to
elastic interactions and excitation of roto-vibrational levels, and the
minimum at about 100 keV corresponds to the energy loss peak due to
ionization. The same correspondence can be seen between electron
spectra (Figs. 11 and 12) and the energy loss
function
![]() (Fig. 7): the minima in the
spectrum at about 1 eV and 100 eV are caused by the energy loss due to
the excitation of vibrational levels, and to the excitation of
electronic levels and ionization, respectively. This is a well-known
property of the CSDA, where one approximately obtains
(Fig. 7): the minima in the
spectrum at about 1 eV and 100 eV are caused by the energy loss due to
the excitation of vibrational levels, and to the excitation of
electronic levels and ionization, respectively. This is a well-known
property of the CSDA, where one approximately obtains
![]() independent on the column density if
independent on the column density if
![]() (see Eq. (26)).
(see Eq. (26)).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig10.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg186.png) |
Figure 10:
Dashed curve, LIS proton spectrum M02 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig11.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg187.png) |
Figure 11:
Dashed curve, LIS electron spectrum C00 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig12.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg188.png) |
Figure 12:
Dashed curve, LIS electron spectrum E00 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig13.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg189.png) |
Figure 13:
CR ionization rate
|
| Open with DEXTER | |
We are now able to calculate the CR ionization rate inside a molecular
cloud as a function of the column density, with the attenuated spectra
given by Eq. (25). We compute the CR ionization rate for
![]() between 1019 cm-2 and 1025 cm-2, and we
show the results for the four incident LIS spectra in Fig. 13.
between 1019 cm-2 and 1025 cm-2, and we
show the results for the four incident LIS spectra in Fig. 13.
As a result of the detailed treatment of CR propagation, the
decrease of the ionization rate with increasing penetration in the
cloud at column densities in the range ![]() 1020-1025 cm-2 is characterized by a power-law behavior, rather than exponential attenuation, and can be approximated as
1020-1025 cm-2 is characterized by a power-law behavior, rather than exponential attenuation, and can be approximated as
We have fitted this expression to the numerical results shown in Fig. 13. The coefficients
where
Table 4: Fitting coefficients for Eq. (27) for CR protons (p, also including heavy nuclei) and electrons (e).
Table 5: Fitting coefficients for Eq. (28) for CR protons (p, also including heavy nuclei) and electrons (e).
It is important to stress that a large contribution to the
ionization of H2 comes from low-energy protons and electrons
constantly produced (in our steady-state model) by the slowing-down of
more energetic particles loosing energy by interaction with the ambient
H2. In Fig. 14 we show the differential contribution of CR
protons and electrons to the ionization rate at a depth of
![]() cm-2, corresponding to the typical column density
of a dense cloud. For protons and heavy nuclei, the bulk of the
ionization is provided by CR in the range 1 MeV-1 GeV and by a
``shoulder'' in the range 1-100 keV produced by slowed-down protons.
This low-energy tail is produced during the propagation of CR protons
in the cloud even when the incident spectrum is devoid of low-energy
particles (as shown in Fig. 9 for the W98 spectrum). The
largest contribution of CR electrons to the ionization is distributed
over energies in the range 10 keV-10 MeV, again reflecting the
distribution of electrons in the propagated spectra (see
Figs. 11 and 12). Thus, the ionization rate at any
depth in a cloud cannot be calculated by simply removing from the
incident spectrum particles with energies corresponding to ranges below
the assumed depth.
cm-2, corresponding to the typical column density
of a dense cloud. For protons and heavy nuclei, the bulk of the
ionization is provided by CR in the range 1 MeV-1 GeV and by a
``shoulder'' in the range 1-100 keV produced by slowed-down protons.
This low-energy tail is produced during the propagation of CR protons
in the cloud even when the incident spectrum is devoid of low-energy
particles (as shown in Fig. 9 for the W98 spectrum). The
largest contribution of CR electrons to the ionization is distributed
over energies in the range 10 keV-10 MeV, again reflecting the
distribution of electrons in the propagated spectra (see
Figs. 11 and 12). Thus, the ionization rate at any
depth in a cloud cannot be calculated by simply removing from the
incident spectrum particles with energies corresponding to ranges below
the assumed depth.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig14.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg211.png) |
Figure 14:
Differential contribution to the ionization rate
|
| Open with DEXTER | |
8 Comparison with observations
To obtain the total CR ionization rate in molecular clouds, we sum the
ionization rates of protons (corrected for heavy nuclei as in
Appendix A) and electrons. With two possible spectra
for each component, we obtain four possible profiles of
![]() .
These are shown in Fig. 15 as a function of
.
These are shown in Fig. 15 as a function of
![]() ,
compared with a compilation of empirical determinations of
,
compared with a compilation of empirical determinations of
![]() in diffuse and dense clouds. Our data sample
includes: (i) diffuse clouds with
in diffuse and dense clouds. Our data sample
includes: (i) diffuse clouds with
![]() from
1020 cm-2 to 1022 cm-2 (14 detections and 15 upper
limits, from Indriolo et al. 2007; including previous data of McCall et al. 2002) and for the
from
1020 cm-2 to 1022 cm-2 (14 detections and 15 upper
limits, from Indriolo et al. 2007; including previous data of McCall et al. 2002) and for the ![]() Per line-of-sight (Shaw et al. 2008); (ii) molecular cloud cores with
Per line-of-sight (Shaw et al. 2008); (ii) molecular cloud cores with
![]() from
1021 cm-2 to 1022 cm-2 (data for low-mass cores
from Caselli et al. 1998; Williams et al. 1998; and for the prestellar
core B68 from Maret & Bergin 2007); (iii) massive protostellar
envelopes with
from
1021 cm-2 to 1022 cm-2 (data for low-mass cores
from Caselli et al. 1998; Williams et al. 1998; and for the prestellar
core B68 from Maret & Bergin 2007); (iii) massive protostellar
envelopes with
![]() from 1022 cm-2 to
1023 cm-2 (see Table 6 and references therein).
from 1022 cm-2 to
1023 cm-2 (see Table 6 and references therein).
Table 6: CR ionization rate toward massive protostellar envelopes.
The observational value of
![]() in diffuse clouds is
obtained from the steady-state abundance of H3+, produced by the CR
ionization of H2 followed by a fast charge exchange reaction with
H2 and destroyed mainly by electron recombination. The situation
for dense molecular clouds and protostellar envelopes is more
complicated. In the dense molecular gas, H3+ is removed by
reactions with other molecules and atoms of the gas, e.g., by reaction
with CO to form HCO+ and with O to form OH+. Thus
in diffuse clouds is
obtained from the steady-state abundance of H3+, produced by the CR
ionization of H2 followed by a fast charge exchange reaction with
H2 and destroyed mainly by electron recombination. The situation
for dense molecular clouds and protostellar envelopes is more
complicated. In the dense molecular gas, H3+ is removed by
reactions with other molecules and atoms of the gas, e.g., by reaction
with CO to form HCO+ and with O to form OH+. Thus
![]() can be determined from the measured abundance of a variety of
molecular ions such as HCO+, DCO+ and N2H+ (see e.g Caselli
et al. 1998; van der Tak & van Dishoeck 2000; Doty et al. 2002). The
resulting rates are nonetheless very uncertain, as they depend on the
depletion of elemental C and O from their cosmic abundances, especially
for clouds with a low degree of ionization, and are generally sensitive
to the adopted chemical model. Here we adopt the values of
can be determined from the measured abundance of a variety of
molecular ions such as HCO+, DCO+ and N2H+ (see e.g Caselli
et al. 1998; van der Tak & van Dishoeck 2000; Doty et al. 2002). The
resulting rates are nonetheless very uncertain, as they depend on the
depletion of elemental C and O from their cosmic abundances, especially
for clouds with a low degree of ionization, and are generally sensitive
to the adopted chemical model. Here we adopt the values of
![]() derived by Caselli et al. (1998) with the data of
Butner et al. (1995) and the chemical model of Leung et al. (1984). We view the range of values of
derived by Caselli et al. (1998) with the data of
Butner et al. (1995) and the chemical model of Leung et al. (1984). We view the range of values of
![]() obtained for different depletion factors as an indication of the
associated uncertainties in the model determinations. In contrast with
the study of Caselli et al. (1998); Williams et al. (1998) analyze
molecular line data for a sample of low-mass cores using the chemical
models of Bergin et al. (1995) and Bergin &
Langer (1997). They conclude that a single value (or a narrow range of
values) of
obtained for different depletion factors as an indication of the
associated uncertainties in the model determinations. In contrast with
the study of Caselli et al. (1998); Williams et al. (1998) analyze
molecular line data for a sample of low-mass cores using the chemical
models of Bergin et al. (1995) and Bergin &
Langer (1997). They conclude that a single value (or a narrow range of
values) of
![]() can reproduce reasonably well the
observations for the majority of cores in their sample.
can reproduce reasonably well the
observations for the majority of cores in their sample.
The comparison between model results and observational data shown
in Fig. 15 should be taken as indicative and interpreted in a
statistical sense, as also suggested by the large spread of values of
![]() at each value of
at each value of
![]() .
First, the observational
.
First, the observational
![]() is the entire column density through the
cloud, whereas the model
is the entire column density through the
cloud, whereas the model
![]() is the column traversed
by CRs incident over the cloud's surface. The exact relation between
the quantities depend on factors like the cloud geometry and
orientation with respect to the line-of-sight, and the variation of CR
ionization rate with depth within the cloud. In addition, for the
cloud cores of Caselli et al. (1998) we adopted the H2 column
density estimated by Butner et al. (1995) from measurements of
C18O multiplied by a factor of 2, to account for depletion of CO
onto grains (Caselli et al. 1998). In fact, at the time of the study by
Caselli et al. (1998), the almost complete disappearance of CO from the
gas phase in cloud cores was still unknown. Second, many of
the sight-lines where
is the column traversed
by CRs incident over the cloud's surface. The exact relation between
the quantities depend on factors like the cloud geometry and
orientation with respect to the line-of-sight, and the variation of CR
ionization rate with depth within the cloud. In addition, for the
cloud cores of Caselli et al. (1998) we adopted the H2 column
density estimated by Butner et al. (1995) from measurements of
C18O multiplied by a factor of 2, to account for depletion of CO
onto grains (Caselli et al. 1998). In fact, at the time of the study by
Caselli et al. (1998), the almost complete disappearance of CO from the
gas phase in cloud cores was still unknown. Second, many of
the sight-lines where
![]() has been determined in
diffuse clouds may have multiple cloud components, which would reduce
the column density of a single cloud. It is probably safe to conclude that
the observational column density is an upper limit to the
column density traversed by CRs incident on each cloud, and therefore
the data shown in Fig. 15 should probably be shifted to the
left by a factor or 2 or so. We will address the problems relative to
cloud geometry and the effects of magnetic fields in a
subsequent work. At any rate, from the comparison with observational
data, shown in Fig. 15, we can draw the following
conclusions:
has been determined in
diffuse clouds may have multiple cloud components, which would reduce
the column density of a single cloud. It is probably safe to conclude that
the observational column density is an upper limit to the
column density traversed by CRs incident on each cloud, and therefore
the data shown in Fig. 15 should probably be shifted to the
left by a factor or 2 or so. We will address the problems relative to
cloud geometry and the effects of magnetic fields in a
subsequent work. At any rate, from the comparison with observational
data, shown in Fig. 15, we can draw the following
conclusions:
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig15.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg230.png) |
Figure 15:
Total CR ionization rate
|
| Open with DEXTER | |
- (i)
- Although the gas column density of the object is by no
means the only parameter controlling the CR ionization rate, the data
suggest a decreasing trend of
 with increasing
with increasing
 ,
compatible with our models M02+C00, W98+E00, W98+C00.
However, the measured values of
,
compatible with our models M02+C00, W98+E00, W98+C00.
However, the measured values of
 are very uncertain,
especially in dense environments. Part of the large spread in the
sample of cloud cores may be due to a poor understanding of the
chemistry.
are very uncertain,
especially in dense environments. Part of the large spread in the
sample of cloud cores may be due to a poor understanding of the
chemistry.
- (ii)
- The highest values of
 ,
measured in
diffuse clouds sight lines, could be explained if CR electrons are
characterized by a rising spectrum with decreasing energy. The E00
spectrum represents an extreme example of this kind, and it results in
values of
,
measured in
diffuse clouds sight lines, could be explained if CR electrons are
characterized by a rising spectrum with decreasing energy. The E00
spectrum represents an extreme example of this kind, and it results in
values of
 somewhat in excess of the diffuse clouds
observations. The same spectrum accounts simultaneously for the CR
ionization rates measured in most protostellar envelopes of much higher
column density. Conversely, a spectrum of protons and heavy nuclei
rising with decreasing energy, like the M02 spectrum, can provide alone
a reasonable lower limit for the CR ionization rate measured in diffuse
clouds.
somewhat in excess of the diffuse clouds
observations. The same spectrum accounts simultaneously for the CR
ionization rates measured in most protostellar envelopes of much higher
column density. Conversely, a spectrum of protons and heavy nuclei
rising with decreasing energy, like the M02 spectrum, can provide alone
a reasonable lower limit for the CR ionization rate measured in diffuse
clouds.
- (iii)
- Without a significant low-energy (below
 100 MeV)
component of electrons and/or protons and heavy nuclei, it is
impossible to reproduce the large majority of observations. The
combination of the C00 spectrum for electrons with the W98 spectrum for
protons and heavy nuclei clearly fails over the entire range of column
densities. Finally, a few molecular cloud cores and one dense envelope
characterized by
100 MeV)
component of electrons and/or protons and heavy nuclei, it is
impossible to reproduce the large majority of observations. The
combination of the C00 spectrum for electrons with the W98 spectrum for
protons and heavy nuclei clearly fails over the entire range of column
densities. Finally, a few molecular cloud cores and one dense envelope
characterized by
 s-1 can only be
explained by invoking the CR suppression mechanisms mentioned in
Sect. 1 not considered in this work.
s-1 can only be
explained by invoking the CR suppression mechanisms mentioned in
Sect. 1 not considered in this work.
9 Conclusions
The comparison between our models and the observational data available
for diffuse clouds, dense cores and massive protostellar envelopes
indicates that good agreement between theory and observations can be
obtained for the CR ionization rate of the ISM by including CR
electrons with an energy spectrum increasing towards low energies, as
also suggested by Webber (1998). In order to draw more stringent
conclusions, it is necessary to use observational constraints derived
from the ionization rates of diffuse clouds, as seen in
Fig. 15 where the models differ mainly at low column
densities. Our study points out the current limits towards a more
accurate understanding of the ionization due to cosmic rays. There are
essentially two limits: (1) the uncertainty in the CR spectrum at
energies below ![]() 1 GeV, and (2) the uncertainties in the
empirically determined values of
1 GeV, and (2) the uncertainties in the
empirically determined values of
![]() in diffuse and
dense molecular clouds. The estimates of the ionization rate depend
sensitively on the complex set of chemical reactions governing the
chemistry of the ISM, particularly on the so-called depletion processes
that transfer molecules and ions from the gas phase to the solid phase.
Despite these observational uncertainties, several important
conclusions clearly emerge from our study:
in diffuse and
dense molecular clouds. The estimates of the ionization rate depend
sensitively on the complex set of chemical reactions governing the
chemistry of the ISM, particularly on the so-called depletion processes
that transfer molecules and ions from the gas phase to the solid phase.
Despite these observational uncertainties, several important
conclusions clearly emerge from our study:
- (i)
- Values of
 measured in diffuse clouds
are greater on average by an order of magnitude than those ones
measured in dense molecular clouds. If confirmed, these data imply the
presence of a CR proton and/or CR electron spectrum which increases at
low energies. Thus, a combination of the spectra W98 and C00 for
protons and electrons, respectively, is excluded by this set of
observations.
measured in diffuse clouds
are greater on average by an order of magnitude than those ones
measured in dense molecular clouds. If confirmed, these data imply the
presence of a CR proton and/or CR electron spectrum which increases at
low energies. Thus, a combination of the spectra W98 and C00 for
protons and electrons, respectively, is excluded by this set of
observations.
- (ii)
- Values of
 measured in dense molecular
clouds span a range of about two orders of magnitude and are subject to
considerable uncertainty. It is difficult to establish how much of the
observed spread is due to variations in the CR ionization rate. It is
likely that in dense clouds the effects of magnetic fields on the
propagation of CR particles cannot be neglected. In addition, it might
be necessary to take into account the density distribution inside each
cloud.
measured in dense molecular
clouds span a range of about two orders of magnitude and are subject to
considerable uncertainty. It is difficult to establish how much of the
observed spread is due to variations in the CR ionization rate. It is
likely that in dense clouds the effects of magnetic fields on the
propagation of CR particles cannot be neglected. In addition, it might
be necessary to take into account the density distribution inside each
cloud.
- (iii)
- The values of
 measured in massive
protostellar envelopes are somewhat higher than the predictions of our
models at the corresponding column densities. This seems to suggest the
presence of further ionization sources in these objects, as, for
example, X-ray emission from the young stellar objects.
measured in massive
protostellar envelopes are somewhat higher than the predictions of our
models at the corresponding column densities. This seems to suggest the
presence of further ionization sources in these objects, as, for
example, X-ray emission from the young stellar objects.
- (iv)
- The exponential attenuation of the CR ionization rate
assumed in many studies is only established for column densities larger
than
 1025 cm-2. For the lower column densities
considered in this work, the ionization rate decreases as
1025 cm-2. For the lower column densities
considered in this work, the ionization rate decreases as
 with
with
 -0.8 for the
spectra that best reproduce the observational data.
-0.8 for the
spectra that best reproduce the observational data.
Acknowledgements
M.P. and D.G. acknowledge support from the Marie-Curie Research Training Network ``Constellation'' (MRTN-CT-2006-035890). A.E.G. acknowledges support from NSF grant AST-0507423 and NASA grant NNG06GF88G. We thank Malcolm Walmsley for useful discussions and comments on the manuscript and an anonymous referee for insightful comments that helped to improve our paper.
Appendix A: Approximated corrections for heavy-nuclei
In the Bethe-Born approximation, the cross section for the collisional
ionization of an atom or molecule depends only on the charge Zk and
the velocity vk of the incident particle. If Ak is the number of
nucleons in the incident particle, the ionization cross section is
![]() ,
where
,
where
![]() is the kinetic energy per nucleon and
is the kinetic energy per nucleon and
![]() is the same
for all particle's species. If, in addition, the spectra of CR protons
and heavy nuclei can be approximately described by a single function
is the same
for all particle's species. If, in addition, the spectra of CR protons
and heavy nuclei can be approximately described by a single function
![]() such that
such that
![]() ,
with fk representing the fractional abundance by number
of species k, it is possible to reduce the calculation of the
ionization rate by heavy-nuclei impact to that of protons, as
,
with fk representing the fractional abundance by number
of species k, it is possible to reduce the calculation of the
ionization rate by heavy-nuclei impact to that of protons, as
![$\displaystyle {
\sum_{k\ge 1}\int_{I({\rm H}_2)}^{E_{\rm max}}
j_k(E_k)[1+\phi_k(E_k)]\sigma_k^{\rm ion}(E_k)~{\rm d}E_k\approx}$](/articles/aa/full_html/2009/26/aa11794-09/img243.png) | |||
![$\displaystyle (1+\eta)\int_{I({\rm H}_2)}^{E_{\rm max}} j_{\rm p}(E_{\rm p})[1+\phi_{\rm p}(E_{\rm p})]
\sigma_{\rm p}^{\rm ion}(E_{\rm p})~{\rm d}E_{\rm p},$](/articles/aa/full_html/2009/26/aa11794-09/img244.png) |
(A.1) | ||
where
 |
(A.2) |
Similarly, the correction factor to account for the energy density of heavy nuclei (Eq. (17)) is given by
 |
(A.3) |
Assuming for the CR abundance of heavy nuclei the standard solar abundance (Anders & Grevesse 1989), we obtain
References
- Afrosimov, V. V., Il'in, R. N., & Fedorenko, N. V. 1958, Zh. Eksp. Teor. Fiz., 34, 1398 [Sov. Phys.-JETP, 7, 968] (In the text)
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [NASA ADS] [CrossRef] (In the text)
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., Ginzburg, V. L., & Ptuskin, V. S. 1990, Astrophysics of Cosmic Rays (North-Holland) (In the text)
- Bergin, E. A., Langer, W. D., & Goldsmith, P. F. 1995, ApJ, 441, 222 [NASA ADS] [CrossRef] (In the text)
- Bergin, E. A., & Langer, W. D. 1997, ApJ, 486, 316 [NASA ADS] [CrossRef] (In the text)
- Bethe, H. 1933, Handbuch der Physik (Berlin: Springer), Pt. 1, 24, 491
- Black, J. H., & Dalgarno, A. 1977, ApJS, 34, 405 [NASA ADS] [CrossRef] (In the text)
- Black, J. H., Hartquist, T. W., & Dalgarno, A. 1978, ApJ, 224, 448 [NASA ADS] [CrossRef] (In the text)
- Butner, H. M., Lada, E. A., & Loren, R. B. 1995, ApJ, 448, 207 [NASA ADS] [CrossRef] (In the text)
- Casadei, D., & Bindi, V. 2004, ApJ, 612, 262 [NASA ADS] [CrossRef] (In the text)
- Caselli, P., Walmsley, C. M., Terzieva, R., & Herbst, E. 1998, ApJ, 499, 234 [NASA ADS] [CrossRef] (In the text)
- Cecchi-Pestellini, C., & Aiello, S. 1992, MNRAS, 258, 125 [NASA ADS] (In the text)
- Cesarski, C. J., & Völk, H. J. 1978, A&A, 70, 367 [NASA ADS] (In the text)
- Chandran, B. D. G. 2000, ApJ, 529, 513 [NASA ADS] [CrossRef] (In the text)
- Colgan, J., Pindzola, M. S., Childers, G., & Khakoo, M. A. 2006, Phys. Rev. A, 73, 042710 [NASA ADS] [CrossRef] (In the text)
- Cravens, T. E., & Dalgarno, A. 1978, ApJ, 219, 750 [NASA ADS] [CrossRef] (In the text)
- Cravens, T. E., Victor, G. A., & Dalgarno, A. 1975, Plan. Space Sci., 23, 1059 [NASA ADS] [CrossRef] (In the text)
- Curran, R., Donahue, T. M., & Kasner, W. H. 1959, Phys. Rev., 114, 490 [NASA ADS] [CrossRef] (In the text)
- Dalgarno, A. 2006, Publ. Nat. Acad. Sci., 103, 12269 [NASA ADS] [CrossRef] (In the text)
- Dalgarno, A., Yan, M., & Liu, W. 1999, ApJS, 125, 237 [NASA ADS] [CrossRef] (In the text)
- de Boisanger, C., Helmich, F. P., & van Dishoeck, E. F. 1996, ApJ, 463, 181 [CrossRef]
- deHeer, F. J., Schutten, J., & Moustafa, H. 1966, Physica, 32, 1766 [NASA ADS] [CrossRef] (In the text)
- Doty, S. D., van Dishoeck, E. F., van der Tak, F. F. S., & Bonnman, A. M. S. 2002, A&A, 389, 446 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- DuBois, R. D., Toburen, L. H, & Rudd, M. E. 1984, Phys. Rev. A, 29, 70 [NASA ADS] [CrossRef] (In the text)
- Edwards, A. K., Wood, R. M., Beard, A. S., & Ezell, R. L. 1988, Phys. Rev. A, 37, 3697 [NASA ADS] [CrossRef] (In the text)
- Federman, S. R., Weber, J., & Lambert, D. L. 1996, ApJ, 463, 181 [NASA ADS] [CrossRef] (In the text)
- Geballe, T. R., McCall, B. J., Hinkle, K. H., & Oka, T. 1999, ApJ, 510, 251 [NASA ADS] [CrossRef] (In the text)
- Gilbody, H. B., & Hasted, J. B. 1957, Proc. Roy. Soc. (London) A240, 382 (In the text)
- Glassgold, A. E., & Langer, W. D. 1973a, ApJ, 179, L147 [NASA ADS] [CrossRef]
- Glassgold, A. E., & Langer, W. D. 1973b, ApJ, 186, 859 [NASA ADS] [CrossRef] (In the text)
- Glassgold, A. E., & Langer, W. D. 1974, ApJ, 193, 73 [NASA ADS] [CrossRef] (In the text)
- Hartquist, T. W., Black, J. H., & Dalgarno, A. 1978a, MNRAS, 185, 643 [NASA ADS] (In the text)
- Hartquist, T. W., Doyle, H. T., & Dalgarno, A. 1978b, A&A, 68, 65 [NASA ADS] (In the text)
- Hayakawa, S., Nishimura, S., & Takayanagi, T. 1961, PASJ, 13, 184 [NASA ADS] (In the text)
- Heiles, C., & Troland, T. H. 2005, ApJ, 624, 773 [NASA ADS] [CrossRef] (In the text)
- Hezareh, T., Houde, M., McCoey, C., Vastel, C., & Peng, R. 2008, ApJ, 684, 1221 [NASA ADS] [CrossRef] (In the text)
- Hooper, J. W., McDaniel, E. W., Martin, D. W., & Harmer, D. S. 1961, Phys. Rev., 121, 1123 [NASA ADS] [CrossRef] (In the text)
- Indriolo, N., Geballe, T. R., Oka, T., & McCall, B. J. 2007, ApJ, 671, 1736 [NASA ADS] [CrossRef] (In the text)
- Indriolo, N., Fields, B. D., & McCall, B. J. 2009, ApJ, 694, 257 [NASA ADS] [CrossRef] (In the text)
- Kim, Y.-K., & Rudd, M. E. 1994, Phys. Rev. A, 50, 3954 [NASA ADS] [CrossRef] (In the text)
- Kossmann, H., Schwarzkopf, O., & Schmidt, V. 1990, J. Phys. B, 23, 301 [NASA ADS] [CrossRef] (In the text)
- Krishnakumar, E., & Srivastava, S. K. 1994, J. Phys. B, 27, L251 [NASA ADS] [CrossRef] (In the text)
- Krolik, J. H., & Kallman, T. R. 1983, ApJ, 267, 610 [NASA ADS] [CrossRef] (In the text)
- Leung, C. M., Herbst, E., & Huebner, W. F. 1984, ApJS, 56, 231 [NASA ADS] [CrossRef] (In the text)
- Lindsay, B. G., & Mangan, M. A. 2003, in Landolt-Börnstein, 1/17C: Photon and Electron Interacytions with Molecules: Ionization and Dissociation, ed. Y. Itikawa (Berlin: Springer), 5 (In the text)
- Liu, X., & Shemansky, D. E. 2004, ApJ, 614, 1132 [NASA ADS] [CrossRef] (In the text)
- Maret, S., & Bergin, E. A. 2007, ApJ, 664, 956 [NASA ADS] [CrossRef] (In the text)
- McCall, B. J., Geballe, T. R., Hinke, K. H., & Oka, T. 1998, Science, 279, 1910 [NASA ADS] [CrossRef] (In the text)
- McCall, B. J., Huneycutt, A. J., Saykally, R. J., et al. 2003, Nature, 422, 500 [NASA ADS] [CrossRef] (In the text)
- McClure, G. W. 1966, Phys. Rev., 148, 47 [NASA ADS] [CrossRef] (In the text)
- McKee, C. F. 1989, ApJ, 345, 782 [NASA ADS] [CrossRef]
- Mewaldt, R. A., Wiedenbeck, M. E., Scott, L. M., et al. 2004, Physics of the Outer Heliosphere, AIP Conf. Proc., 719, 127 (In the text)
- Montague, R. G., Harrison, M. F. A., & Smith, A. C. H. 1984, J. Phys. B, 17, 3295 [NASA ADS] [CrossRef] (In the text)
- Moskalenko, I. V., Strong, A. W., Ormes, J. F., & Potgieter, M. S. 2002, ApJ, 565, 280 [NASA ADS] [CrossRef] (In the text)
- Mott, N. F. 1930, Proc. R. Soc. London, 126, 259 [CrossRef] (In the text)
- Nakano, T., & Tademaru, E. 1972, ApJ, 173, 87 [NASA ADS] [CrossRef] (In the text)
- Nath, B. B., & Biermann, L. 1994, MNRAS, 267, 447 [NASA ADS]
- Padoan, P., & Scalo 2005, ApJ, 624, L97 [NASA ADS] [CrossRef] (In the text)
- Phelps, A. V. 1990, J. Phys. Chem. Ref. Data, 19, 3 (In the text)
- Pindzola, M. S., & Robicheaux, F. J. 2000, Phys. Rev. A., 61, 052507 [NASA ADS] [CrossRef] (In the text)
- Pivovar, L. I., & Levchenko, Y. Z. 1967, Zh. Eksp. Teor. Fiz., 52, 42 [Sov. Phys. JETP, 25, 27] (In the text)
- Potgieter, M. S. 1995, Adv. Space Res., 16 (9), 191 (In the text)
- Puckett, L. J., & Martin, D. W. 1970, Phys. Rev. A, 1, 1432 [NASA ADS] [CrossRef] (In the text)
- Ramaty, R., & Lingenfelter, R. E. 1975, in Solar Gamma-, X-, and EUV Radiation, IAU Symp., 68, 363
- Ramaty, R., Kozlovsky, B., & Lingenfelter, R. E. 1996, ApJ, 456, 525 [NASA ADS] [CrossRef]
- Rapp, D., & Englander-Golden, P. 1965, J. Chem. Phys., 43, 1464 [NASA ADS] [CrossRef] (In the text)
- Rapp, D., Englander-Golden, P., & Briglia, D. D. 1965, J. Chem. Phys., 42, 4082 [NASA ADS] [CrossRef]
- Rudd, M. E., DuBois, R. D., Toburen, L. H., Ratcliffe, C. A., & Goffe, C. W. 1983, Phys. Rev. A, 28, 3244 [NASA ADS] [CrossRef] (In the text)
- Rudd, M. E., Kim, Y.-K., Madison, D. H., & Gallagher, J. W. 1985, Rev. Mod. Phys., 57, 965 [NASA ADS] [CrossRef] (In the text)
- Rudd, M. E. 1991, Phys. Rev. A, 44, 1644 [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R. 2002, in Cosmic Ray Astrophysics (Berlin: Springer) (In the text)
- Shah, M. B., & Gilbody, H. B. 1985, J. Phys. B. 18, 899 (In the text)
- Shah, M. B., Elliott, D. S., McCallion, P., & Gilbody, H. P. 1988, J. Phys. B, 21, 2751 [NASA ADS] [CrossRef] (In the text)
- Shaw, G., Ferland, G. J., Srianand, R., et al. 2008, ApJ, 675, 405 [NASA ADS] [CrossRef] (In the text)
- Silk, J., & Norman, C. 1983, ApJ, 272, L49 [NASA ADS] [CrossRef] (In the text)
- Skilling, J., & Strong, A. W. 1976, A&A, 53, 253 [NASA ADS] (In the text)
- Spitzer, L., & Tomasko, M. G. 1968, ApJ, 152, 971 [NASA ADS] [CrossRef] (In the text)
- Straub, H. C., Renault, P., Lindsay, B. G., Smith, K. A., & Stebbings, R. F. 1996, Phys. Rev. A, 54, 2146 [NASA ADS] [CrossRef] (In the text)
- Strong, A. W., Moskalenko, I. V., & Reimer, O. 2000, ApJ, 537, 763 [NASA ADS] [CrossRef] (In the text)
- Takayanagi, M. 1973, PASJ, 25, 327 [NASA ADS] (In the text)
- Takayanagi, K., & Suzuki, H. 1978, Cross sections for atomic processes, Vol. I (Nagoya: Institute of Plasma Physics) (In the text)
- Toburen, L. H., & Wilson, W. E. 1972, Phys. Rev. A, 5, 247 [NASA ADS] [CrossRef] (In the text)
- Umebayashi, T., & Nakano, T. 1981, PASJ, 33, 617 [NASA ADS] (In the text)
- Umebayashi, T., & Nakano, T. 2009, ApJ, 690, 69 [NASA ADS] [CrossRef] (In the text)
- van Dishoeck, E. F., & Black, J. H. 1986, ApJS, 62, 109 [NASA ADS] [CrossRef] (In the text)
- van der Tak, F. F. S., & van Dishoeck, E. F. 2000, A&A, 358, L79 [NASA ADS] (In the text)
- van der Tak, F. F. S., van Dishoeck, E. F., Evans, N. J., II, & Blake, G. A. 2000, ApJ, 537, 283 [NASA ADS] [CrossRef]
- Van Zyl, B., & Stephen, T. M. 1994, Phys. Rev. A, 50, 3164 [NASA ADS] [CrossRef] (In the text)
- Wakelam, V., Herbst, E., Selsis, F., & Massacrier, G. 2006, A&A, 459, 813 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Webber, W. R. 1987, A&A, 179, 277 [NASA ADS] (In the text)
- Webber, W. R. 1998, ApJ, 506, 329 [NASA ADS] [CrossRef] (In the text)
- Welsh, L. M., Berkner, K. H., Kaplan, S. N., & Pyle, R. V. 1967, Phys. Rev., 158, 85 [NASA ADS] [CrossRef] (In the text)
- Williams, J. P., Bergin, E. A., Caselli, P., Myers, P. C., & Plume, R. 1998, ApJ, 503, 689 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... CSDA)
![[*]](/icons/foot_motif.png)
- In the astrophysical literature this approximation is often referred to as the continuous energy loss regime, and when the propagation is dominated by these losses, it is often known as the thick target approximation (see e.g. Ramaty & Lingenfelter 1975; Ramaty et al. 1996).
- ... Database
![[*]](/icons/foot_motif.png)
- http://physics.nist.gov/PhysRefData/Star/Text
All Tables
Table 1: CR reactions in molecular clouds.
Table 2: Fit coefficients for the dissociative ionization and double ionization cross sections of H2 by electron impact.
Table 3:
CR ionization rates
![]() and
and
![]() ,
electron production rate
,
electron production rate
![]() ,
and energy densities
,
and energy densities
![]() of CR protonsa (p) and electrons (e).
of CR protonsa (p) and electrons (e).
Table 4: Fitting coefficients for Eq. (27) for CR protons (p, also including heavy nuclei) and electrons (e).
Table 5: Fitting coefficients for Eq. (28) for CR protons (p, also including heavy nuclei) and electrons (e).
Table 6: CR ionization rate toward massive protostellar envelopes.
All Figures
 |
Figure 1:
Cross sections for proton impact on H2: ionization cross
section
|
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
Cross sections for electron impact on H2: ionization cross
section
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg116.png) |
Figure 3:
Cross sections for proton impact on He: ionization cross
section
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig4.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg123.png) |
Figure 4:
Cross section for He ionization by electron impact
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig5.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg130.png) |
Figure 5: Proton LIS spectra of M02 and W98 (upper and lower solid curves, respectively). The dashed curves represent our power-law extrapolations of the spectra. For comparison, the cross sections for ionization of H2 by proton impact, electron capture, and total ionization are also shown (in arbitrary units). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig6.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg159.png) |
Figure 6: Electron LIS spectra of E00 and C00 (upper and lower solid curves, respectively). The dashed curves represent our extrapolations of the spectra. For comparison, the cross section for ionization of H2 by electron impact is also shown (in arbitrary units). |
| Open with DEXTER | |
| In the text | |
 |
Figure 7:
Energy loss functions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig8.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg180.png) |
Figure 8:
Range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig9.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg182.png) |
Figure 9:
Dashed curve, LIS proton spectrum W98 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig10.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg186.png) |
Figure 10:
Dashed curve, LIS proton spectrum M02 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig11.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg187.png) |
Figure 11:
Dashed curve, LIS electron spectrum C00 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig12.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg188.png) |
Figure 12:
Dashed curve, LIS electron spectrum E00 incident on the
cloud's surface; solid curves, attenuated proton spectra
at increasing depth in the cloud labeled by values of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig13.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg189.png) |
Figure 13:
CR ionization rate
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig14.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg211.png) |
Figure 14:
Differential contribution to the ionization rate
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1794fig15.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa11794-09/Timg230.png) |
Figure 15:
Total CR ionization rate
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle 4\pi \sum_k
\int_{I({\rm H}_2)}^{E_{\rm max}} j_k(E_k)[1+\phi_k(E_k)]
\sigma_k^{\rm ion.}(E_k)~{\rm d}E_k$](/articles/aa/full_html/2009/26/aa11794-09/img62.png)


![\begin{displaymath}\sigma_{\rm l}=4\pi a_0^2 C x^D, \qquad \sigma_{\rm h}=4\pi a_0^2[A\ln(1+x)+B]x^{-1},
\end{displaymath}](/articles/aa/full_html/2009/26/aa11794-09/img77.png)
![\begin{displaymath}\sigma_{\rm e}^{\rm ion}=4\pi a_0^2 N\left[\frac{I({\rm H})}{I({\rm H}_2)}\right]^2
F(t)G(t),
\end{displaymath}](/articles/aa/full_html/2009/26/aa11794-09/img83.png)

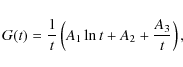
![\begin{displaymath}\sigma_{\rm p}^{\rm e.c.}=4\pi a_0^2 AN \left[\frac{I({\rm H})}{I({\rm H}_2)}\right]^2
\frac{x^2}{C+x^B+Dx^F},
\end{displaymath}](/articles/aa/full_html/2009/26/aa11794-09/img92.png)
![$\displaystyle 4\pi \sum_k
\int_{I({\rm H}_2)}^{E_{\rm max}} j_k(E_k)[1+\phi_k(E_k)]
\sigma_k^{\rm ion}(E_k)~{\rm d}E_k$](/articles/aa/full_html/2009/26/aa11794-09/img99.png)
![$\displaystyle +4\pi \sum_k\int_{E^{\rm diss~ion}}^{E_{\rm max}} j_k(E)[1+\phi_k(E_k)]
\sigma_k^{\rm diss~ion}(E_k)~{\rm d}E_k$](/articles/aa/full_html/2009/26/aa11794-09/img100.png)
![$\displaystyle +8\pi \sum_k\int_{E^{\rm doub~ion}}^{E_{\rm max}} j_k(E_k)[1+\phi_k(E_k)]
\sigma_k^{\rm doub~ion}(E_k)~{\rm d}E_k.$](/articles/aa/full_html/2009/26/aa11794-09/img101.png)
![$\displaystyle 4\pi \sum_k
\int_{I({\rm He})}^{E_{\rm max}} j_k(E_k)[1+\phi_k(E_k)]
\sigma_k^{\rm ion}(E_k)~{\rm d}E_k$](/articles/aa/full_html/2009/26/aa11794-09/img112.png)



![\begin{displaymath}N({\rm H}_2)=-\int_{E_{k,0}}^{E_k}\frac{{\rm d}E_k}{L_k(E_k)}
=n({\rm H}_2)[R_k(E_{k,0})-R_k(E_k)],
\end{displaymath}](/articles/aa/full_html/2009/26/aa11794-09/img166.png)




![\begin{displaymath}\zeta_k^{{\rm H}_2}\approx
\zeta_{0,k}\left[\frac{N({\rm H}_2)}{10^{20}~\mbox{cm$^{-2}$ }}\right]^{-a}\cdot
\end{displaymath}](/articles/aa/full_html/2009/26/aa11794-09/img190.png)
