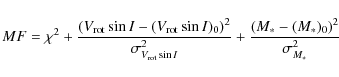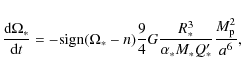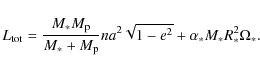Discovery and characterization of WASP-6b, an inflated sub-Jupiter mass planet transiting a solar-type star

M. Gillon; D. R. Anderson; A. H. M. J. Triaud; C. Hellier; P. F. L. Maxted; D. Pollaco; D. Queloz; B. Smalley; R. G. West; D. M. Wilson; S. J. Bentley; A. Collier Cameron; B. Enoch; L. Hebb; K. Horne; J. Irwin; Y. C. Joshi; T. A. Lister; M. Mayor; F. Pepe; N. Parley; D. Segransan; S. Udry; P. J. Wheatley

doi:10.1051/0004-6361/200911749

Free Access

Issue		A&A Volume 501, Number 2, July II 2009


Page(s)		785 - 792
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200911749
Published online		13 May 2009

Discovery and characterization of WASP-6b, an inflated sub-Jupiter mass planet transiting a solar-type star^,

M. Gillon^1,2 - D. R. Anderson³ - A. H. M. J. Triaud² - C. Hellier³ - P. F. L. Maxted³ - D. Pollaco⁴ - D. Queloz² - B. Smalley³ - R. G. West⁵ - D. M. Wilson³ - S. J. Bentley³ - A. Collier Cameron⁶ - B. Enoch⁶ - L. Hebb⁶ - K. Horne⁶ - J. Irwin⁷ - Y. C. Joshi⁴ - T. A. Lister⁸ - M. Mayor² - F. Pepe² - N. Parley⁵ - D. Segransan² - S. Udry² - P. J. Wheatley⁹

1 - Institut d'Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août 17, Bât. B5C, Liège 1, Belgium
2 - Observatoire de Genève, Université de Genève, 51 Chemin des Maillettes, 1290 Sauverny, Switzerland
3 - Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK
4 - Astrophysics Research Centre, School of Mathematics & Physics, Queen's University, University Road, Belfast, BT7 1NN, UK
5 - Department of Physics and Astronomy, University of Leicester, Leicester, LE1 7RH, UK
6 - School of Physics and Astronomy, University of St. Andrews, North Haugh, Fife, KY16 9SS, UK
7 - Department of Astronomy, Harvard University, 60 Garden Street, MS 10, Cambridge, Massachusetts 02138, USA
8 - Las Cumbres Observatory, 6740 Cortona Dr. Suite 102, Santa Barbara, CA 93117, USA
9 - Department of Physics, University of Warwick, Coventry, CV4 7AL, UK

Received 29 January 2009 / Accepted 4 May 2009

Abstract
We report the discovery of WASP-6b, an inflated sub-Jupiter mass planet transiting every $3.3610060^{\rm + 0.0000022 }_{- 0.0000035 }$ days a mildly metal-poor solar-type star of magnitude V=11.9. A combined analysis of the WASP photometry, high-precision followup transit photometry and radial velocities yield a planetary mass $M_{\rm p} = 0.503^{+0.019}_{-0.038}$ $M_{\rm J}$ and radius $R_{\rm p} = 1.224^{+0.051}_{-0.052}$ $R_{\rm J}$ , resulting in a density $\rho_{\rm p} = 0.27 \pm 0.05$ $\rho_{\rm J}$ . The mass and radius for the host star are $M_\ast = 0.88^{+0.05}_{-0.08}$ $M_\odot$ and $R_\ast = 0.870^{+0.025}_{-0.036}$ $R_\odot$ . The non-zero orbital eccentricity e = 0.054^+0.018_-0.015 that we measure suggests that the planet underwent a massive tidal heating $\sim$ 1 Gyr ago that could have contributed to its inflated radius. High-precision radial velocities obtained during a transit allow us to measure a sky-projected angle between the stellar spin and orbital axis $\beta = 11^{+14}_{-18}$ deg. In addition to similar published measurements, this result favors a dominant migration mechanism based on tidal interactions with a protoplanetary disk.

Key words: binaries: eclipsing - stars: individual: WASP-6 - planetary systems - techniques: photometric - techniques: radial velocities - techniques: spectroscopic

1 Introduction

Transiting planets play an important role in our understanding of the nature of the extrasolar planetary objects. They are the only exoplanets for which an accurate measurement of the mass and radius is available. The deduced density is a key parameter to constrain theoretical models for the formation, evolution and structure of planets (e.g. Fortney et al. 2007; Liu et al. 2008). For the brightest transiting systems, a study of the atmospheric composition and physics is possible, even with existing instruments like HST or Spitzer (e.g. Charbonneau et al. 2008; Swain et al. 2008). The discovery rate of transiting planets has increased recently thanks mainly to the efficiency of the CoRoT space-based survey (Baglin et al. 2006) and of a handful of ground-based wide-field surveys targeting rather bright stars (V < 13): HATNet (Bakos et al. 2004), WASP (Pollaco et al. 2006), TrES (O'Donovan et al. 2006), and XO (McCullough et al. 2005).

The $\sim$ 50 transiting planets known at the time of writing show a broad range of mass and radius. Their masses go from 23 $M_\oplus$ for the hot Neptune GJ 436b (Butler et al. 2004; Gillon et al. 2007) to more than 10 $M_{\rm J}$ for XO-3 (Johns-Krull et al. 2008). Many planets have a size in agreement with basic models of irradiated planets (e.g. Burrows et al. 2007; Fortney et al. 2007), some of them like HD 149026 b (Sato et al. 2005) appearing to be very rich in heavy elements. Nevertheless, a few planets like HD 209458 b (Charbonneau et al. 2000; Henry et al. 2000) are ``anomalously'' large. Several hypothesis have been proposed to explain this radius anomaly, most importantly tides (Bodenheimer et al. 2001; Jackson et al. 2008b), tides with atmospheric circulation (Guillot & Showman 2002) and enhanced opacities (Guillot et al. 2006; Burrows et al. 2007). The existence of several correlations between parameters of transiting systems has been proposed, for instance between the planet mass and the orbital period (Mazeh et al. 2005; Gaudi et al. 2005) and between the heavy-element content of the planet and the stellar metallicity (Guillot et al. 2006; Burrows et al. 2007). The astrophysics supporting these correlations has still to be fully understood.

It is highly desirable to detect and characterize thoroughly many more bright short period transiting systems to improve our understanding of the highly irradiated gaseous planets and to constrain the structure and evolution models for these objects. With its very high detection efficiency, the WASP transit survey is making a large contribution to this goal. It is the only transit survey operating in both hemispheres: it uses an instrument named WASP-North and located at La Palma to search for planets from the Northern hemisphere and a twin instrument named WASP-South and located at Sutherland to do the same from the Southern hemisphere. Each of these instruments covers a huge field of view of 482 square degrees per pointing, allowing them to search for transiting planets in a large portion of the sky. Due to the brightness of the host stars, planets detected by WASP are very good targets for high-precision followup observations. For instance, it is possible to measure for most of them the alignment between the stellar rotation axis and the planetary orbital axis via the observation of the Rossiter-McLaughlin effect (RM; Queloz et al. 2000). The measured value for this spin-orbit angle is a strong constraint for inward planetary migration models (see Winn 2008, and references therein).

We report here the discovery and characterization of WASP-6b, a new sub-Jupiter mass planet transiting a mildly metal-poor solar-type star of magnitude V=11.9. We present in Sect. 2 the WASP discovery photometry plus high precision followup transit photometry and radial velocity measurements confirming the planetary nature of WASP-6b and including the observation of a spectroscopic transit. Section 3 presents the determination of the host star parameters. Our determination of the system parameters is presented in Sect. 4. These parameters are discussed in Sect. 5.

2 Observations

2.1 WASP photometry

The host star 1SWASP J231237.75-224026.1 (=USNO-B1.0 0673-1077008 = 2MASS 23123773-2240261; hereafter WASP-6) was observed by WASP-South during the 2006 and 2007 observing seasons, covering the intervals 2006 May 07 to 2006 November 12 and 2007 July 05 to 2007 November 13 respectively. The 9630 pipeline-processed photometric measurements were de-trended and searched for transits using the methods described in Collier Cameron et al. (2006). The selection process (Collier Cameron et al. 2007) elected WASP-6 as a high priority candidate presenting a periodic transit-like signature with a period of 3.361 days. A total of 18 transits are observed in the data. Figure 1 presents the WASP photometry folded with the best-fit period.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig1.ps} \end{figure}$	Figure 1: WASP photometry of WASP-6 phase-folded with the best-fit period from the transit search algorithm presented in Collier Cameron et al. (2006).
Open with DEXTER

2.2 High-S/N transit photometry

Followup transit photometry was obtained on 2007 October 13 using the $2048\times 2048$ pixels camera HawkCam2 (Wilson et al. 2008; Anderson et al. 2008) on the 2.0-m Faulkes Telescope South (FTS) at Siding Spring Observatory . The camera has a scale of 0.135 arcsec/pixel and a field of view of $\sim$ $4.6\times4.6$ arcmin². We observed the target field using the SDSS i' band in the $2\times 2$ bin mode to improve the duty cycle. We acquired 247 frames of 60 s exposure during the run. The telescope was sufficiently defocussed to keep the stellar flux within the linear range of the CCD. The images were bias subtracted and flat-field corrected with a master bias and twilight flat field images using IRAF. DAOPHOT aperture photometry (Stetson 1987) was performed around the target and comparison stars. We substracted a linear fit from the differential magnitudes as a function of airmass to correct for the different colour dependance of the extinction for the target and comparison stars. The linear fit was calculated from the out-of-transit (OOT) data and applied to all the data. The corresponding fluxes were then normalized using the OOT part of the photometry. We discarded the first 17 measurements because they were obtained during twilight. Figure 2 shows the resulting lightcurve folded on the best-fit orbital period and the residuals obtained after removing the best-fit transit model (see Sect. 4). Their rms is $1.67 \times 10^{-3}$ . This can be compared to $9.54 \times 10^{-4}$ , the mean theoretical error bar taking into account photon, read-out, scintillation and background noises.

High precision transit observations of WASP-6 were also carried out using the $1024\times 1024$ pixels thermoelectrically cooled frame transfer CCD camera RISE mounted on the 2-m Liverpool Telescope (LT) in La Palma (Steele et al. 2008). The camera has a scale of 0.55 arcsec/pixel and a total field of view of $\sim$ $9.4\times 9.4$ arcmin². We observed the target field using a single broad band V+R filter in the $2\times 2$ bin mode. We acquired 4200 frames of 3 s exposure on the night of 2008 July 25 and 2880 frames of 5 s exposure on the night of 2008 August 11. The telescope was, here too, defocussed. A similar reduction procedure as for the FTS photometry was used. The resulting normalized light curves of WASP-6 folded with the best-fit orbital period are shown in Fig. 2. The rms of the residuals is respectively 0.54% and 0.5% for the first and second run, while their mean theoretical error bar are 0.51% and 0.40%.

As can be seen in Fig. 2, our three high-S/N transit photometric time-series, and especially the FTS one, show a significant level of correlated noise. We could not identify the origin of this noise, but we take it into account in our derivation of the system parameters (see Sect. 4).

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig2.ps}\vspace*{1.5mm} \includegraphics[width=9cm,clip]{1749fig3.ps} \end{figure}$	Figure 2: FTS i'-band (top) and LT/RISE V+R (bottom) transit photometry for WASP-6 and residuals after subtraction of the best-fit transit curve (superimposed in blue).
Open with DEXTER

2.3 Spectroscopy

As soon as WASP-6 was identified as a high priority target, spectroscopic measurements were obtained using the CORALIE spectrograph mounted on the Euler Swiss telescope (La Silla, Chile) to confirm the planetary nature of the eclipsing body and measure its mass. WASP-6 was observed from 2007 September 16 to 2007 October 26 and from 2008 September 11 to 2008 September 25. Radial velocities (RV) were computed by weighted cross-correlation (Baranne et al. 1996; Pepe et al. 2005) with a numerical G2-spectral template. RV variations of semi-amplitude $\sim$ 75 m s^-1 were detected consistent with a planetary-mass companion whose period closely matches that from the WASP transit detections.

44 additional spectroscopic measurements were obtained with the HARPS spectrograph (Mayor et al. 2003) based on the 3.6-m ESO telescope (La Silla, Chile) in the context of the programs 082.C-0040(E) and 082.C-0608(E). These programs aim to improve the characterization of WASP transiting planets. As CORALIE, HARPS is a cross-dispersed, fiber-fed, echelle spectrograph dedicated to high-precision Doppler measurements. HARPS data were reduced with a pipeline very similar to the CORALIE one. In addition to several measurements covering the whole orbital phase, high-cadence measurements of a spectroscopic transit were obtained with HARPS on 2008 October 08 in order to determine the sky-projected angle between the planetary orbital axis and the stellar rotation axis and included two points taken the night before, a point as far as possible from the transit on the transit night and a point the night after. This strategy aims to determine the systematic RV with greater accuracy than if the RM effect was taken on its own, assuming that stellar activity is the same over the three nights.

Our RV measurements are shown phase-folded and over-plotted with the best-fitting orbital+RM model in Fig. 3.

To exclude that the RV signal shown in Fig. 3 is due to spectral line distortions caused by a blended eclipsing binary, the CORALIE and HARPS cross-correlation functions were analyzed using the line-bisector technique described in Queloz et al. (2001). No evidence for a correlation between the bisector spans and the RV variations was found (Fig. 4). The most likely cause for the periodic signal observed in photometry and RV measurements and for the RM effect observed on 2008 October 08 is thus the presence of a giant planet transiting the star WASP-6 every 3.36 days.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig4.ps}\vspace*{1.5mm} \includegraphics[width=9cm,clip]{1749fig5.ps} \end{figure}$	Figure 3: Top: the RV measurements of WASP-6 obtained with CORALIE (red triangles) and HARPS (green squares). The systematic velocity has been subtracted. The solid line is the MCMC solution (see Sect. 4); it includes the RM effect. Bottom: zoom on the transit phase showing the RM effect.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig6.ps}\vspace*{1.5mm} \includegraphics[width=9cm,clip]{1749fig7.ps} \end{figure}$	Figure 4: Bisector versus RV measured from all the observed CORALIE ( top) and HARPS ( bottom) spectra. We adopt uncertainties of twice the RV uncertainty for all bisector measurements. There is no correlation between these two parameters indicating the RV variations are not caused by stellar activity or line-of-sight binarity.
Open with DEXTER

3 WASP-6 stellar parameters

The individual CORALIE and HARPS spectra are relatively low signal-to-noise, but when co-added into 0.01 Å steps they give a S/N of in excess of 100:1 which is suitable for a photospheric analysis of WASP-6. The standard pipeline reduction products were used in the analysis.

The analysis was performed using the UCLSYN spectral synthesis package (Smith 1992; Smalley et al. 2001) and ATLAS9 models without convective overshooting (Castelli et al. 1997). The H $_\alpha$ line was used to determine the effective temperature ( $T_{\rm eff}$ ), while the Na I D and Mg I b lines were used as surface gravity ( $\log g$ ) diagnostics. The parameters obtained from the analysis are listed in Table 1.

Table 1: Stellar parameters derived for WASP-6.

The equivalent widths of several clean and unblended lines were measured. Atomic line data was mainly taken from the Kurucz & Bell (1995) compilation, but with updated van der Waals broadening coefficients for lines in Barklem et al. (2000) and $\log gf$ values from Gonzalez & Laws (2000), Gonzalez et al. (2001) or Santos et al. (2004). A value for microturbulence ( $\xi_{\rm t}$ ) was determined from Fe I using Magain's (1984) method. The ionization balance between Fe I and Fe II and the null-dependence of abundance on excitation potential were used as an additional the $T_{\rm eff}$ and $\log g$ diagnostics (Smalley 2005).

We have determined the elemental abundances of several elements (listed in Table 1) from their measured equivalent widths. The quoted error estimates include that given by the uncertainties in $T_{\rm eff}$ , $\log g$ and $\xi_{\rm t}$ , as well as the scatter due to measurement and atomic data uncertainties. In our spectra the Li I 6708 Å line is not detected (EW < 2 mÅ), allowing us to derive an upper-limit on the Lithium abundance of $\log n({\rm Li/H}) + 12 < 0.5$ . The lack of lithium implies an age in excess of $\sim$ 3 Gyr (Sestito & Randich 2005).

Projected stellar rotation velocity ( $V_{\rm rot} \sin I$ ) was determined by fitting the profiles of several unblended Fe I lines in the HARPS spectra. We used a value for macroturbulence ( $v_{\rm mac}$ , see Gray 2008) of 2 km s^-1 and an instrumental FWHM of $0.060 \pm 0.005$ Å, determined from the telluric lines around 6300 Å. A best fitting value of $V_{\rm rot}\sin I = 1.4 \pm 1.0$ km s^-1 was obtained. If, however, mactroturbulence is lower, then higher rotation values are found, with $V_{\rm rot} \sin I = 3.0 \pm 0.5$ km s^-1 obtained for $v_{\rm mac}$ = 0 km s^-1. If, on the other hand, $v_{\rm mac}$ is slightly higher than 2 km s^-1, then $V_{\rm rot} \sin I$ could be undetectable.

In addition to the spectral analysis, we have also used broad-band photometry from TYCHO-2, USNO-B1.0 R-mag, CMC14 r', DENIS and 2MASS to estimate the total observed bolometric flux. The Infrared Flux Method (Blackwell & Shallis 1977) was then used with 2MASS magnitudes to determine $T_{\rm eff}$ and stellar angular diameter ( $\theta$ ). This gives $T_{\rm eff}$ = $5470 \pm 130$ K, which is in close agreement with that obtained from the spectroscopic analysis and implies a spectral type of G8V (Gray 2008).

4 Derivation of the system parameters

We derived stellar and planetary parameters for the system by fitting simultaneously the WASP, FTS and LT/RISE photometry with the CORALIE and HARPS RVs. These data were used as input into the Markov Chain Monte Carlo (MCMC, Ford 2006) code described in Gillon et al. (2008) and Triaud et al. (in prep.). MCMC is a Bayesian inference method based on stochastic simulations and provides the a posteriori probability distribution of adjusted parameters for a given model. Here the model is based on a star and a transiting planet on a keplerian orbit about their center of mass. Specifically, we used the photometric transit model of Mandel & Agol (2002) and the spectroscopic transit model of Giménez (2006) in addition to a classical Keplerian model for the orbital part of the RV variations. To model the transit lightcurves, a quadratic limb darkening law was assumed, with coefficients interpolated from Claret's tables (2000, 2004) for the appropriate photometric filters. For the RISE broad band filter, the average from V and R bands was taken to be our theoretical limb darkening parameters.

We used 16 jump parameters in our MCMC simulations: the orbital period P, the time of minimum light T₀, the transit depth D, the total transit width W, the impact parameter b, the stellar mass $M_\ast$ , the orbital RV semi-amplitude K, a systematic radial velocity $\gamma$ for each spectroscopic instrument (HARPS and CORALIE), the parameters $e\cos \omega$ and $e\sin\omega$ where e is the orbital eccentricity and $\omega$ is the argument of periastron, the products $V_{\rm rot} \sin I \cos \beta$ and $V_{\rm rot} \sin I \sin \beta$ where $V_{\rm rot} \sin I$ is the projected stellar rotational velocity and $\beta$ is the spin-orbit angle (see Giménez 2006), and a normalization factor for each of the 4 light curves (assuming the same normalization for the whole SW photometry). As explained in the now abundant literature on the application of MCMC to perform Bayesian inference for transiting planets (see e.g. Collier Cameron et al. 2007, and references therein), each MCMC simulation is composed of a large number of consecutive steps for which the jump parameters are randomly modified or not depending of the result of a test on the merit function (MF). The MF used here is the sum of the $\chi^2$ for all the data with respect to the models added to a Bayesian prior on $V_{\rm rot} \sin I$ and $M_\ast$ representing our constraints on these parameters from spectroscopy:

$\begin{displaymath} MF = \chi^2 + \frac{(V_{\rm rot} \sin I - (V_{\rm rot} \sin ... ...sin I}^2} + \frac{(M_\ast - (M_\ast)_0)^2}{\sigma_{M_\ast}^2} \end{displaymath}$

(1)

where $(V_{\rm rot} \sin I)_0 = 1.4$ km s^-1, $\sigma_{V_{\rm rot} \sin I} = 1$ km s^-1, $M_\ast = 0.87$ and $\sigma_{M_\ast} = 0.08$ . These last two values were obtained by interpolation of Girardi stellar evolution models (Girardi et al. 2000) in order to find the mass and age that best match the spectroscopic parameters. We notice that our data do not constrain strongly $M_\ast$ and that it is a free parameter under the control of a Bayesian prior in our simulations only to propagate its uncertainty to the other physical parameters.

A first MCMC run was performed and led to a refined value for the stellar density. We converted it to $R_\ast/M_\ast^{1/3}$ in solar units, and compared this property and the stellar temperature to the Girardi models interpolated at -0.2 metallicity. The quantity, $R_\ast/M_\ast^{1/3}$ , depends only on the observed transit properties (duration, depth, impact parameter, and orbital period) and is independent of the measured temperature. We generated the same property from the mass and log g values in the models, and then interpolated the models in the R/M^1/3- $T_{\rm eff}$ plane to determine a mass and age for WASP-6. We interpolated linearly along two consecutive mass tracks to generate an equal number of age points between the zero-age main sequence and the evolutionary state where the star reaches the end of core hydrogen burning. We then interpolated between the mass tracks along equivalent evolutionary points to find the mass and age from the models that best match the stellar density derived from the MCMC and the effective temperature. In this way, we obtained a value for the stellar mass of, $M_\ast =0.83^{+0.07}_{-0.09}$ $M_\odot$ and a derived age for the system of $11 \pm 7$ Gyr (see Fig. 5).

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig8.ps} \end{figure}$

Figure 5:

R/M^1/3 (in solar units) versus effective temperature for WASP-6 compared to the theoretical stellar stellar evolutionary models of Girardi et al. (2000). The labeled mass tracks are for 0.8, 0.9 and 1.0 $M_\odot$ and the isochrones are 100 Myr (solid), 1 Gyr (dashed), 5 Gyr (dot-dashed), 10 Gyr (dotted). We have interpolated the tracks at -0.2 metallicity and have included the uncertainty on the metallicity (+-0.1) in the overall uncertainties on the mass and the age. According to the models, the host star has an age of $11 \pm 7$ Gyr.

Open with DEXTER

The best-fitting model found in the first MCMC run was used to estimate the level of correlated noise in each photometric time-series and a jitter noise in the RV time series. For each photometric time-series, the red noise was estimated as described in Gillon et al. (2006), by comparing the rms of the unbinned and binned residuals. We used a bin size corresponding to a duration of 25 min, similar to the timescale of the ingress/egress of the transit. For the SW data, the red noise was estimated to be negligible when compared to the theoretical error bar of the measurements and it was thus neglected. The deduced red noise values (Table 2) were added quadratically to the theoretical uncertainties of each corresponding time-series. No jitter is detected in the CORALIE data. For the HARPS data, a significant jitter is obtained, but it seems to be originating mostly from the residuals of the RM effect and is probably more due to lower-than-usual S/N on the spectra and a worsening of airmass (reaching 1.8 at the end of the sequence) than stellar activity. For this reason, no jitter noise was added to the RV uncertainties.

Using the updated value of the stellar mass as initial value, a second MCMC run was then performed. This chain allowed a large safety burn-in period of discarded 50 000 steps followed by a simulation of 500 000 steps allowing a robust determination of the a posteriori probability distributions for the jumped parameters. The parameter set (jump + deduced parameters) corresponding to the lowest MF was considered as the best solution, and for each parameter upper and lower 1- $\sigma$ error bars were obtained from respectively the 68.3% larger and smaller values. Best-fitting jump + physical parameters are shown in Table 3. The reduced $\chi^2$ of the best-fitting solution is 0.86.

Table 2: Deduced values for the photometric red noise (top), and the RV jitter and systematic velocities (bottom).

Table 3: Values and 1- $\sigma$ error limits derived in this work for the jump and physical parameters of the WASP-6 system.

5 Discussion

With half of the mass of Jupiter and a radius significantly larger, WASP-6b appears too large for basic models of irradiated planets (Burrows et al. 2007a; Fortney et al. 2007), even if an absence of core is assumed. For instance, tables presented in Fortney et al. (2007) predict a maximum radius of $\sim$ 1.1 $R_{\rm J}$ for a 0.5 Jupiter-mass planet orbiting at 0.045 AU of a 4.5 Gyr solar-type star. WASP-6 is smaller, cooler and probably older than the Sun, so 1.2 $R_{\rm J}$ is clearly too large for these models. In this context, it is worth noticing the non-null eccentricity that we infer for its orbit ( $e = 0.054^{\rm + 0.018 }_{- 0.015}$ ). The fact that the planetary orbit is still not circularized despite the large age of the system indicates that the tidal evolution of WASP-6b probably played an important role in its energy budget. As outlined by Jackson et al. (2008b), tidal heating could have been large enough for many close-in planets to explain at least partially the large radius of some of them. To assess the past and future tidal evolution of WASP-6b, we integrated the equations for da/dt and de/dt presented in Jackson et al. (2008a) and computed at each step the tidal heating rate H using the formula presented in Jackson et al. (2008b). We assumed values of $Q_{\rm p}' = 10^{\rm 6.5}$ and $Q_\ast' = 10^{5.5}$ for respectively the planetary and stellar tidal dissipation parameters. These values were found by Jackson et al. (2008a) to conciliate the eccentricity distribution of close-in planets before their tidal evolution to the one of the planets detected further from their star. We also took into account the evolution of the stellar rotation period due to the tide raised by the planet using (Goldreich & Soter 1966):

$\begin{displaymath} \frac{{\rm d}\Omega_\ast}{{\rm d}t} = -{\rm sign}(\Omega_\as... ...R_\ast^3}{\alpha_\ast M_\ast Q_\ast'} \frac{M_{\rm p}^2}{a^6}, \end{displaymath}$

(2)

where G is the gravitational constant, n is the mean orbital motion, $\Omega_\ast$ is the stellar spin angular rate and $\alpha_\ast$ = $I_\ast/(M_\ast R_\ast^2)$ with $I_\ast$ being the moment of inertia though the spin axis of the star. For $\alpha_\ast$ , we assumed a value of 0.07 (Pätzold et al. 2004). To assess the reliability limits of the model, we also computed the evolution of the total angular momentum of the system (assuming a negligible contribution of the planet rotation):

$\begin{displaymath} L_{\rm tot} = \frac{M_\ast M_{\rm p}}{M_\ast + M_{\rm p}} n a^2 \sqrt{1 - e^2} + \alpha_\ast M_\ast R_\ast^2 \Omega_\ast . \end{displaymath}$

(3)

Neglecting the possible decrease due stellar wind (Dobbs-Dixon et al. 2004), $L_{\rm tot}$ should be a conserved quantity during the whole tidal evolution of the system.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig9.ps} \end{figure}$

Figure 6:

Tidal evolution for WASP-6b computed using the method described in Jackson et al. (2008b) . Top left: evolution of the semi-major axis. The dashed line shows the Roche limit of the system. Top right: evolution of the eccentricity. Middle left: evolution of the tidal heating rate. Middle right: evolution of the total angular momentum. Bottom: evolution of the orbital ( left) and star rotational ( right) period. For each parameter, the solid line shows the evolution computed with the best-fitting present eccentricity and semi-major axis while the red dotted lines assume the maximum and minimum tidal heating consistent with their 1- $\sigma$ error bars.

Open with DEXTER

Figure 6 shows the obtained evolution for a, e, H, $L_{\rm tot}$ and the orbital and stellar rotation period from 2 Gyr ago to 5 Gyr in the future. Interestingly, the model predicts (1) that the eccentricity and semi-major axis of WASP-6b were significantly larger in the past; (2) that the orbit will be fully circularized 1 Gyr from now; and (3) that the planet will continue to slowly approach the star until finally reaching its Roche limit. This last results agrees well with the fact that the ratio $L_{\rm tot}/L_{\rm c}$ , where $L_{\rm c}$ is critical angular momentum (see Levrard et al. 2009), has a value of $\sim$ 0.6, implying that the system is tidally unstable and will ultimately merge. Levrard et al. (2009) showed that all the other transiting systems, except HAT-P-2, are in the same case.

Under this tidal evolution model, WASP-6b was brought to a distance >0.05 AU of its host star in the very early life of the system, then its orbital evolution has been totally dominated by tides until now. This evolution does not consider the possible influence of one or more other planets able to pump the eccentricity of WASP-6b (Mardling 2007), but our RV data do not reveal the presence of another planet so it seems reasonable at this stage to assume that the orbital evolution of WASP-6b was not dominated by planet-planet interactions. The model assumes also a constant radius for the planet during the whole tidal evolution, which is not very likely (Liu et al. 2008). Furthermore, Fig. 6 shows that it does not conserve $L_{\rm tot}$ for $e >\sim 0.3$ and during the final runaway merging of the planet with the star. Considering as valid only the part of the tidal evolution for which $L_{\rm tot}$ is conserved at the 1-% level, we can nevertheless conclude from Fig. 6 that WASP-6b experienced 0.6-1.2 Gyr ago a large tidal heating rate of 5- $10 \times 10^{19}$ W. Such a large heating rate in the past should have modified drastically the thermal history of the planet and could have contributed significantly to the measured inflated radius.

It is worth exploring the influence of the assumed values of $Q_{\rm p}'$ and $Q_\ast '$ on the future tidal evolution of the planet. $Q_{\rm p}'$ is found to be of order 10⁵-10⁶ for Jupiter (Golreich & Soter 1966; Yoder & Peale 1981). It is unknown for extrasolar planets, but the theoretical analysis of Ogilvie & Lin (2004) suggests that its most probable value should be of order $5\times10^6$ . WASP-6b is not a good case to constrain this parameter, because its small mass makes negligible the tides that it raises on the star: the tidal history that we compute does not change for any value of $Q_{\rm p}'$ ranging from 10⁵-10⁹. Most studies assume $Q_\ast '$ to be around 10⁵-10⁶, but values up to 10⁹ are still considered as plausible (Eggleton et al. 1998). We computed the tidal evolution of the system for $Q_\ast '$ values ranging from 10⁵ to 10⁹. As can be seen in Fig. 7, we cannot constrain $Q_\ast '$ either: even with a value for $Q_\ast '$ of 10⁵, the future lifetime of the planet would still remain a significant fraction of its age and its detection would not have been an extremely improbable event. We can only conclude from Fig. 7 that for the smallest $Q_\ast$ values WASP-6b could fall on its host star before this latter leaves the main sequence.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1749fig10.ps} \end{figure}$	Figure 7: Future tidal evolutions for WASP-6b computed with different values for $Q_\ast '$ (see text for details). The labeled evolutions correspond to $Q_\ast ' = 10^5$ , 10^5.5 and 10⁶.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{1749fig11.ps}\vspace*{1.5mm} \includegraphics[width=8cm,clip]{1749fig12.ps} \end{figure}$	Figure 8: Mass-radius diagrams for the transiting gaseous giant planets less massive than 4 $M_{\rm J}$ . The error bars are shown only for WASP-6 (red dot) for the sake of clarity. In the top panel, the filled circles indicate the planets for which the host-star metallicity is sub-solar, while in the bottom panel they indicate the planets receiving a stellar insolation <10⁹ erg s^-1 cm^-2.
Open with DEXTER

The large radius of WASP-6b ( $\sim$ $1.2~R_{\rm J}$ ) and the metal deficiency of its host star seem to strengthen the existence of a correlation between the heavy-element content of giant planets and the stellar metallicity (Guillot et al. 2006; Burrows et al. 2007). Still, this proposed correlation is not obvious at all in a planetary mass-radius diagram presenting separately the planets for which the host star has a sub-solar metallicity (see Fig. 8, top panel): both populations seem well mixed without any hint of a smaller density for planets orbiting around metal-poor stars. On the other side, the division of transiting planets into two well separated groups in the mass-radius diagram seems clearer when the level of irradiation is considered (Fig. 8, bottom panel). This apparent correlation density-irradiation does not necessarily indicate a direct influence of the incoming stellar flux on the planet size, it could also be explained by a more indirect action. For instance, the most irradiated planets are the ones being the closest to their host star, so the ones for which tidal heating should be the largest.

With a stellar irradiation $\sim$ $4.7 \times 10^8$ erg s^-1 cm^-2, WASP-6b belongs to the theoretical pL planetary class proposed by Fortney et al. (2008; see also Burrows et al. 2008). Under this theory, Ti and V-bearing compounds should mostly be condensed in the planetary atmosphere and occultation measurements at different wavelengths should not reveal any stratospheric thermal inversion. Such occultation observations would not only constrain atmospheric models of giant close-in planets, they would also constrain the eccentricity of the orbit and thus the tidal thermal history of the planet.

The value that we determine for the sky-projected angle between the stellar spin and the planetary orbital axis is compatible with zero ( $\beta = 11^{+14}_{-18}$ deg). This good alignment was observed for ten other close-in giant planets (see Winn 2008, and references therein), while a misalignment was observed only for the planet XO-3 (Hébrard et al. 2008; Winn et al. 2009). Together, these results favor migration via tidal interactions with a protoplanetary disk (Lin et al. 1996) as the dominant mechanism of planetary migration, because it should preserve spin-orbit alignement (Ward & Hahn 1994) contrary to migration via planet-planet scattering (Rasio & Ford 1996) or Kozai cycles (Fabrycky & Tremaine 2007).

Acknowledgements

We thank the ESO La Silla staff for their support during the CORALIE and HARPS observations. The HARPS consortium is gratefully acknowledged for contributing to some of the observations presented here.

References

Anderson, D. R., Gillon, M., Hellier, C., et al. 2008, MNRAS, 387, L4 [NASA ADS] (In the text)
Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in COSPAR, Plenary Meeting, 36th COSPAR Scientific Assembly, 36, 3749 (In the text)
Bakos, G. A., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] (In the text)
Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Barklem, P. S., Piskunov, N., & O'Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] (In the text)
Bodenheimer, P., Lin, D. N. C., & Mardling, R. A. 2001, ApJ, 548, 466 [NASA ADS] [CrossRef] (In the text)
Butler, R. P., Marcy, G. W., & Fischer, D. A. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] (In the text)
Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] (In the text)
Burrows, A., Budaj, J., & Hubeny, I. 2008, ApJ, 678, 1436 [NASA ADS] [CrossRef] (In the text)
Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A 318, 841 (In the text)
Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] (In the text)
Charbonneau, D., Knutson, H. A., & Barman, T. 2008, ApJ, 686, 1341 [NASA ADS] [CrossRef] (In the text)
Claret, A. 2000, A&A, 363, 1081 [NASA ADS]
Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences]
Collier Cameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] (In the text)
Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] (In the text)
Dobbs-Dixon, I., Lin, D. N. C., & Mardling, R. A. 2004, ApJ, 610, 464 [NASA ADS] [CrossRef] (In the text)
Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] (In the text)
Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] (In the text)
Ford, E. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] (In the text)
Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] (In the text)
Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] (In the text)
Gaudi, B. S., Seager, S., & Mallén-Ornelas, G. 2005, ApJ, 623, 472 [NASA ADS] [CrossRef] (In the text)
Gillon, M., Pont, F., & Moutou, C. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gillon, M., Demory, B.-O., Barman, T., et al. 2007, A&A, 471, L51 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gillon, M., Triaud, A. H. M. J., Mayor, M., et al. 2008, A&A, 485, 871 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Giménez 2006, ApJ, 650, 408 [NASA ADS] [CrossRef] (In the text)
Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [NASA ADS] [CrossRef] (In the text)
Gonzalez, G., & Laws, C. 2000, AJ 119, 390 (In the text)
Gonzalez, G., Laws, C., Tyagi, S., & Reddy, B. E. 2001, AJ, 121, 432 [NASA ADS] [CrossRef] (In the text)
Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres, 3rd edition (CUP), 507 (In the text)
Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hébrard, G., Bouchy, F., Pont, F., et al. 2008, A&A, 488, 763 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Henry, G. W., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2000, ApJ, 529, L41 [NASA ADS] [CrossRef] (In the text)
Jackson, B., Greenberg, R., & Barnes, R. 2008a, ApJ, 678, 1396 [NASA ADS] [CrossRef] (In the text)
Jackson, B., Greenberg, R., & Barnes, R. 2008b, ApJ, 681, 1631 [NASA ADS] [CrossRef] (In the text)
Johns-Krull, Christopher, M., & McCullough, P. R. 2008, ApJ, 677, 657 [NASA ADS] [CrossRef] (In the text)
Kurucz, R. L., & Bell, B. 1995, Kurucz CD-ROM 23: Atomic Line List, SAO, Cambridge, USA (In the text)
Levrard, B., Winidoerffer, C., & Chabrier, G. 2009, to appear in ApJ[arXiv:0901.2048] (In the text)
Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] (In the text)
Liu, X., Burrows, A., & Abgui, L. 2008, ApJ, 687, 1191 [NASA ADS] [CrossRef] (In the text)
Magain, P. 1984, A&A, 134, 189 [NASA ADS]
Mandel, K., & Agol., E. 2002, ApJ, 5802, L171 [NASA ADS] [CrossRef] (In the text)
Mardling, R. A. 2007, MNRAS, 382, 1768 [NASA ADS] (In the text)
Mayor, M., Pepe, F., & Queloz, D. 2003, The Messenger, 114, 20 [NASA ADS] (In the text)
Mazeh, T., Zucker, S., & Pont, F. 2005, MNRAS, 356, 955 [NASA ADS] [CrossRef] (In the text)
McCullough, P. R., Stys, J., Valenti, J., et al. 2005, PASP, 117, 783 [NASA ADS] [CrossRef] (In the text)
O'Donovan, F. T., Francis, T., Charbonneau, D., et al. 2006, ApJ, 651, L61 [NASA ADS] [CrossRef] (In the text)
Ogilvie, G., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] (In the text)
Pätzold, M., Carone, L., & Rauer, H. 2004, A&A, 427, 1075 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Pepe, F., Queloz, D., Mayor, M., et al. 2005, The Messenger, 120, 22 [NASA ADS] (In the text)
Pollacco, D. L., Skillen, I., Cameron, A. C., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef]
Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] (In the text)
Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] (In the text)
Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Sato, B., Fischer, D. A., & Henry, G. W. 2005, ApJ, 633, 465 [NASA ADS] [CrossRef] (In the text)
Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Smalley, B. 2005, MSAIS, 8, 130 [NASA ADS] (In the text)
Smalley, B., Smith, K. C., & Dworetsky, M. M. 2001, UCLSYN Userguide (In the text)
Smith, K. C. 1992, Ph.D. Thesis, University of London (In the text)
Steele, I. A., Bates, S. D., Gibson, N., et al. 2008, Proc. SPIE, 7014, 70146 (In the text)
Stetson, P. B. 1987, PASP, 99, 111 [NASA ADS] [CrossRef] (In the text)
Swain, M. R., Vasisht, G., Tinetti, G., et al. 2009, ApJL, 690, 114 [NASA ADS] [CrossRef]
Ward, W. R., & Hahn, J. M. 1994, Icarus, 110, 95 [NASA ADS] [CrossRef] (In the text)
Winn, J. N. 2008, IAU 253 Transiting Planets, ed. F. Pont, Cambridge, USA, [arXiv:0807.4929] (In the text)
Winn, J. N., Johnson, J. A., Fabrycky, D., et al. 2009, ApJ, submitted,[arXiv:0902.3461] (In the text)
Wilson, D. M., Gillon, M., Hellier, C., et al. 2008, ApJ, 675, L113 [NASA ADS] [CrossRef] (In the text)
Yoder, C. F., & Peale, S. J. 1981, Icarus, 47, 1 [NASA ADS] [CrossRef] (In the text)

Footnotes

... star: Based on data collected with the HARPS spectrograph at ESO La Silla Observatory in the programs 082.C-0040(E) and 082.C-0608.
...: The photometric time-series and radial velocities (Tables 4, 5) used in this work are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/501/785
... IRAF: IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
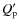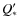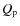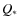... parameters: We use here the same convention as Jackson et al. (2008a): the coefficients $Q_{\rm p}'$ and $Q_\ast '$ used here are equal to the actual tidal dissipation parameters $Q_{\rm p}$ and $Q_\ast$ multiplied by the ratio 3/2k where k is the Love number.

All Tables