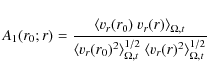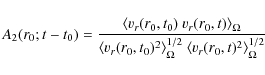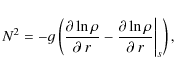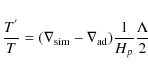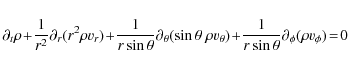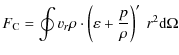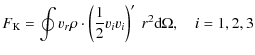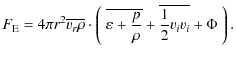| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 659 - 677 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811414 | |
| Published online | 13 May 2009 | |
The core helium flash revisited
II. Two and three-dimensional hydrodynamic simulations
M. Mocák1,2 - E. Müller1 - A. Weiss1 - K. Kifonidis1
1 - Max-Planck-Institut für Astrophysik, Postfach 1312, 85741 Garching, Germany
2 -
Institut d'Astronomie et d'Astrophysique, Université Libre de
Bruxelles, CP 226, 1050 Brussels, Belgium
Received 25 November 2008 / Accepted 3 April 2009
Abstract
Context. We study turbulent convection during the core helium flash close to its peak by comparing the results of two and three-dimensional hydrodynamic simulations.
Aims. In a previous study we found that the temporal evolution and the properties of the convection inferred from two-dimensional hydrodynamic studies are similar to those predicted by quasi-hydrostatic stellar evolutionary calculations. However, as vorticity is conserved in axisymmetric flows, two-dimensional simulations of convection are characterized by incorrect dominant spatial scales and exaggerated velocities. Here, we present three-dimensional simulations that eliminate the restrictions and flaws of two-dimensional models and that provide a geometrically unbiased insight into the hydrodynamics of the core helium flash. In particular, we study whether the assumptions and predictions of stellar evolutionary calculations based on the mixing-length theory can be confirmed by hydrodynamic simulations.
Methods. We used a multidimensional Eulerian hydrodynamics code based on state-of-the-art numerical techniques to simulate the evolution of the helium core of a 1.25 ![]() Pop I star.
Pop I star.
Results. Our three-dimensional hydrodynamic simulations of the evolution of a star during the peak of the core helium flash do not show any explosive behavior. The convective flow patterns developing in the three-dimensional models are structurally different from those of the corresponding two-dimensional models, and the typical convective velocities are lower than those found in their two-dimensional counterparts. Three-dimensional models also tend to agree more closely with the predictions of mixing length theory. Our hydrodynamic simulations show the turbulent entrainment that leads to a growth of the convection zone on a dynamic time scale. In contrast to mixing length theory, the outer part of the convection zone is characterized by a subadiabatic temperature gradient.
Key words: stars: evolution - hydrodynamics - convection - stars: interiors
1 Introduction
The core helium flash is the most violent event in the life of a star with an initial mass between approximately 0.7 ![]() and 2.2
and 2.2 ![]() (Sweigart & Gross 1978). Electron degeneracy in the helium core at the time of the flash leads to a thermonuclear runaway that at its peak produces large amounts of energy (
(Sweigart & Gross 1978). Electron degeneracy in the helium core at the time of the flash leads to a thermonuclear runaway that at its peak produces large amounts of energy (
![]() )
within the stellar core over a very short period of time (
)
within the stellar core over a very short period of time (![]() days). The temperature rises up to several 108 Kelvins until the degeneracy of the electron gas is eventually lifted. Nevertheless, the event does not seem to be catastrophic for the star. It only results in a slow expansion of the helium core (typically with a few
days). The temperature rises up to several 108 Kelvins until the degeneracy of the electron gas is eventually lifted. Nevertheless, the event does not seem to be catastrophic for the star. It only results in a slow expansion of the helium core (typically with a few
![]() ), since
energy transport by turbulent convection, heat conduction, and radiation seems to be able to deliver most of the flash energy quiescently from the stellar interior to the outer stellar layers. However, computations of the flash have a confusing history of predicting either severe explosions
(Deupree 1984a; Wickett 1977; Deupree 1984b; Cole et al. 1985; Deupree & Cole 1983; Cole & Deupree 1980; Zimmermann 1970; Edwards 1969; Cole & Deupree 1981; Villere 1976)
or quiescent behavior (Lattanzio et al. 2006; Dearborn et al. 2006; Deupree 1996).
), since
energy transport by turbulent convection, heat conduction, and radiation seems to be able to deliver most of the flash energy quiescently from the stellar interior to the outer stellar layers. However, computations of the flash have a confusing history of predicting either severe explosions
(Deupree 1984a; Wickett 1977; Deupree 1984b; Cole et al. 1985; Deupree & Cole 1983; Cole & Deupree 1980; Zimmermann 1970; Edwards 1969; Cole & Deupree 1981; Villere 1976)
or quiescent behavior (Lattanzio et al. 2006; Dearborn et al. 2006; Deupree 1996).
Previous two-dimensional (2D) hydrodynamic simulations of turbulent convection within the helium core during the peak of the core helium flash (Mocák et al. 2008) support a quiescent scenario in agreement with stellar evolutionary calculations. However, they also show that the convection zone, powered by helium burning, is characterized by convective velocities that are roughly four times higher than those predicted by mixing-length theory, and the width of the convection zone grows on a dynamical timescale. This may lead to mixing of hydrogen into the helium core as known from one-dimensional simulations of extremely metal-poor stars (Campbell & Lattanzio 2008; Cassisi et al. 2003; Fujimoto et al. 1990; Schlattl et al. 2001; Weiss et al. 2004a; Hollowell et al. 1990).
Table 1: Some properties of the initial model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg21.eps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{1414fg22.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg66.png) |
Figure 1:
Left panel: temperature (in units of
|
| Open with DEXTER | |
It is well known that two-dimensional hydrodynamic simulations of turbulence are seriously biased due to the imposed symmetry restrictions. Opposite to three-dimensional (3D) flows, the turbulent kinetic energy increases from small to large scales in 2D simulations, i.e., the energy cascade to smaller length scales characteristic of turbulent flows is not reproduced (Canuto 2000; Bazan & Arnett 1998). Hence, the mean convective velocities, the amount of overshooting, and the size of turbulent structures are too large. Thus, as pointed out already by e.g., Muthsam et al. (1995) and Bazan & Arnett (1998), three-dimensional simulations are required to validate the predictions of two-dimensional simulations.
With increasing computational capabilities, the importance of multidimensional hydrodynamic simulations in stellar evolution studies grows rapidly because they are essentially ``parameter free''. In contrast, canonical one-dimensional stellar evolutionary calculations involve free parameters like the mixing length or the overshooting distance (Böhm-Vitense 1958; Canuto & Mazzitelli 1991), which are chosen in an appropriate manner to fit observational data (Montalbán et al. 2004). Comparison of the results obtained with both approaches is crucial, because it allows one to constrain, validate or disprove the free parameters used in stellar evolutionary calculations, and because it can provide a clue to the applicability limits of the canonical (1D) treatment (Herwig et al. 2006; Meakin & Arnett 2007b; Arnett et al. 2007; Meakin & Arnett 2006; Dearborn et al. 2006; Asida & Arnett 2000; Kercek et al. 1999,1998; Bazan & Arnett 1998).
In the following we present an investigation of the core helium flash by means of two and three-dimensional hydrodynamic simulation using state-of-the-art numerical techniques, a detailed equation of state, and a time-dependent gravitational potential. Our hydrodynamic models are characterized by a convectively unstable layer (the convection zone) embedded in between two stable layers composed of several chemical nuclear species and of a partially degenerate electron gas. Similar systems were studied in the past by many authors e.g., Hurlburt et al. (1994,1986), Muthsam et al. (1995), Singh et al. (1995,1998) and Brummell et al. (2002) assuming, however, that the stellar matter is composed of a single ideal Boltzmann gas. This gives extra relevance to our simulations because they allow us to study, e.g., the dependence of turbulent entrainment and the structure of convective boundary layers on the composition of the stellar gas, and on the composition gradients present in the stellar model.
We introduce the stellar model used as input for our multidimensional simulations in the next section. We then briefly describe our hydrodynamics code in Sect. 3, and discuss and compare the results of the two and three-dimensional simulations in Sect. 4. In particular, we compare the temporal evolution, the kinetic energy density, the power spectra, the thermodynamic fluctuation amplitudes, the stability of the flow structures, and the turbulent entrainment at the convective boundaries of our models. We discuss our results in the context of the predictions of mixing-length theory in Sect. 5. Finally, we present a high resolution 2D simulation covering almost 1.5 days of core helium flash evolution in Sect. 6, partially described by Mocák et al. (2008). We end with a summary of our findings and some conclusions in Sect. 7.
2 Initial model
The initial model was obtained with the stellar evolution code Garstec (Weiss & Schlattl 2000,2007). Some of its properties are listed in Table 1, and the distributions of temperature, density and composition are displayed in
Fig. 1. The model possesses a white dwarf like degenerate structure with an off-center temperature maximum resulting from plasma and photo-neutrino cooling. Its central density is
![]()
![]() 105 g cm-3. At the outer edge of the isothermal region in the center of the helium core the temperature jumps up to
105 g cm-3. At the outer edge of the isothermal region in the center of the helium core the temperature jumps up to
![]()
![]() 108 K, and the adjacent convection zone has a superadiabatic temperature gradient. The core is predominantly composed of 4He (mass fraction X(4He) > 0.98), and some small amounts of 1H, 3He, 12C, 13C, 14N, 15N and 16O, respectively. For our hydrodynamic simulations we adopt the abundances of 4He, 12C and 16O as the triple-
108 K, and the adjacent convection zone has a superadiabatic temperature gradient. The core is predominantly composed of 4He (mass fraction X(4He) > 0.98), and some small amounts of 1H, 3He, 12C, 13C, 14N, 15N and 16O, respectively. For our hydrodynamic simulations we adopt the abundances of 4He, 12C and 16O as the triple-![]() reaction dominates the nuclear energy production during the flash. The remaining composition is assumed to be adequately represented by a gas with a mean molecular weight equal to that of 20Ne.
reaction dominates the nuclear energy production during the flash. The remaining composition is assumed to be adequately represented by a gas with a mean molecular weight equal to that of 20Ne.
As our multidimensional hydrodynamics code Herakles (see next section) utilizes an Eulerian computational grid, our initial data for the hydrodynamic simulations are obtained by polynomial interpolation from the stellar model which was computed on a Lagrangian grid. The initial hydrodynamics model obtained in this way is not in hydrostatic equilibrium, because the equation of state of Timmes & Swesty (2000) implemented in our hydrodynamics code differs from that of Rogers et al. (1996) implemented in the Garstec code (for a given density and temperature in the initial stellar model, the pressure differs by about 1%). Stabilization of this initial hydrodynamics model resulted in a small decrease of the temperature compared to the stellar model (Fig. 1).
3 Hydrodynamics code
The hydrodynamic simulations were performed with an enhanced version of the grid-based code Herakles (Mocák et al. 2008). The adopted mathematical model implemented in the code consists of the Euler
equations in spherical coordinates (![]() ,
and
,
and ![]() ;
see Appendix A) coupled to the source terms describing thermal transport, self-gravity, and nuclear burning. The hydrodynamic equations are integrated using the PPM reconstruction scheme (Colella & Woodward 1984), and a Riemann solver for real gases according to Colella & Glaz (1984). The chemical species are evolved by a set of additional coupled continuity equations (Plewa & Müller 1999). Source terms in the momentum and energy equations due to self-gravity and nuclear burning are treated by means of operator splitting at the end of every integration step. The gravitational potential is approximated by a one-dimensional Newtonian
potential which is obtained from the spherically averaged mass distribution. The stiff nuclear reaction network is integrated using the semi-implicit Bader-Deuflhard method, (Press et al. 1992; Bader & Deuflhard 1983) which allows for large time integration steps.
;
see Appendix A) coupled to the source terms describing thermal transport, self-gravity, and nuclear burning. The hydrodynamic equations are integrated using the PPM reconstruction scheme (Colella & Woodward 1984), and a Riemann solver for real gases according to Colella & Glaz (1984). The chemical species are evolved by a set of additional coupled continuity equations (Plewa & Müller 1999). Source terms in the momentum and energy equations due to self-gravity and nuclear burning are treated by means of operator splitting at the end of every integration step. The gravitational potential is approximated by a one-dimensional Newtonian
potential which is obtained from the spherically averaged mass distribution. The stiff nuclear reaction network is integrated using the semi-implicit Bader-Deuflhard method, (Press et al. 1992; Bader & Deuflhard 1983) which allows for large time integration steps.
In Herakles, a program cycle consists of two hydrodynamic time steps and proceeds as follows (in 2D simulations step (3) is omitted):
- 1.
- The hydrodynamic equations are integrated in r-direction (r-sweep) for one time step including the effects of heat conduction. The time averaged gravitational forces are computed, and the momentum and the total energy are updated to account for the respective source terms. Subsequently, the equation of state is called to update the thermodynamic state due to the change of the total energy.
- 2.
- Step (1) is repeated in
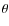 -direction (
-direction (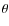 -sweep).
-sweep).
- 3.
- Step (1) is repeated in
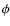 -direction (
-direction ( -sweep).
-sweep).
- 4.
- The nuclear reaction network is solved in all zones with significant nuclear burning (i.e., where
T > 108 K), and then the equation of state is called to update the pressure and the
temperature.
- 5.
- In the subsequent time step, the order of Step (1)-(3) is reversed to guarantee second-order accuracy of the time integration, and Step (4) is repeated with the updated state quantities.
- 6.
- The size of the time step for the next cycle is determined.
Table 2:
Some properties of the two and three-dimensional simulations: number of grid points in r (Nr), ![]() (
(
![]() )
and,
)
and, ![]() (
(![]() ) direction, spatial resolution in r (
) direction, spatial resolution in r (![]() in 106 cm),
in 106 cm), ![]() (
(
![]() ), and
), and ![]() (
(
![]() ) direction, characteristic velocity
) direction, characteristic velocity ![]() (in 10
(in 10
![]() )
of the flow, expansion
velocity at temperature maximum
)
of the flow, expansion
velocity at temperature maximum
![]() (in
(in
![]() ), typical convective turnover timescale
), typical convective turnover timescale
![]() (in s) and maximum evolutionary time
(in s) and maximum evolutionary time
![]() (in s), respectively.
(in s), respectively.
4 Hydrodynamic simulations
We performed two two-dimensional and one three-dimensional simulation whose properties are summarized in Table 2![]() . The simulations hefl.2d.a and hefl.3d cover 9500 s and 6000 s of evolutionary time during the peak of the core helium flash, respectively, and were computed on a computational grid spanning a wedge of
. The simulations hefl.2d.a and hefl.3d cover 9500 s and 6000 s of evolutionary time during the peak of the core helium flash, respectively, and were computed on a computational grid spanning a wedge of
![]() in angular directions centered at the equator. The grid had a radial resolution of
in angular directions centered at the equator. The grid had a radial resolution of
![]()
![]() 106 cm, and an angular resolution of
106 cm, and an angular resolution of
![]() .
The rather wide angular grid appeared to be necessary for the three-dimensional simulations, due to the size of the largest vortices (
.
The rather wide angular grid appeared to be necessary for the three-dimensional simulations, due to the size of the largest vortices (![]() 40
40![]() )
found in previous two-dimensional simulations (Mocák et al. 2008).
)
found in previous two-dimensional simulations (Mocák et al. 2008).
The 2D model hefl.2d.b was evolved for roughly 36 h (130 000 s) on a grid covering the full
![]() angle in
angle in ![]() direction. It was simulated at almost twice the resolution as the other models. The properties of model hefl.2d.b and its evolution are discussed in Sect. 6, and to some extent also in Sect. 4. We used reflective boundary
conditions in every coordinate direction and for all models, except model hefl.2d.a. For this model, it turned out to be necessary to impose periodic boundary conditions in angular direction, because
reflective boundaries together with the 120
direction. It was simulated at almost twice the resolution as the other models. The properties of model hefl.2d.b and its evolution are discussed in Sect. 6, and to some extent also in Sect. 4. We used reflective boundary
conditions in every coordinate direction and for all models, except model hefl.2d.a. For this model, it turned out to be necessary to impose periodic boundary conditions in angular direction, because
reflective boundaries together with the 120 ![]() wedge size affect the large scale convective flow adversely leading to higher convection velocities.
wedge size affect the large scale convective flow adversely leading to higher convection velocities.
We are limited with our explicit hydrodynamics code by the CFL condition which is most restrictive near the center of the spherical grid. Therefore, we cut off the inner part of the grid at a radius of 2 ![]() 108 cm that is still sufficiently far away from the radius of the temperature inversion at
108 cm that is still sufficiently far away from the radius of the temperature inversion at ![]()
![]() 108 cm. To trigger convection, we imposed a random flow field
with a maximum (absolute) velocity of
108 cm. To trigger convection, we imposed a random flow field
with a maximum (absolute) velocity of
![]() ,
and a random density perturbation
,
and a random density perturbation
![]() .
Imposing some explicit non-radial perturbations is necessary, because a spherically symmetric model evolved with Herakles on a grid in spherical coordinates will remain spherically symmetric forever. This is different from the study of Asida & Arnett (2000), who did not perturb the initial model by an artificial random flow, as instabilities were growing from round-off errors. The different perturbation techniques seem not to influence the final thermally
relaxed steady state (Meakin & Arnett 2007b).
.
Imposing some explicit non-radial perturbations is necessary, because a spherically symmetric model evolved with Herakles on a grid in spherical coordinates will remain spherically symmetric forever. This is different from the study of Asida & Arnett (2000), who did not perturb the initial model by an artificial random flow, as instabilities were growing from round-off errors. The different perturbation techniques seem not to influence the final thermally
relaxed steady state (Meakin & Arnett 2007b).
Because thermal transport of energy by conduction and radiation is roughly seven orders of magnitude smaller than the convective energy flux, it has been neglected in our simulations. Most of the liberated nuclear energy is carried away by convection. All computed models are non-rotating, because rotation seems not to play an important role during the core helium flash (Lattanzio et al. 2006).
4.1 Important timescales
A major disadvantage of multidimensional hydrodynamic simulations of stars today is related to the fact, that stars evolve on a nuclear timescale which is typically of the order of 109 years and even with the best supercomputers nowadays, we are not able to cover more than a day of hydrodynamic stellar evolution (Mocák et al. 2008; Herwig et al. 2006; Meakin & Arnett 2007b). Nevertheless, hydrodynamic simulations are an important tool for studying the evolution of stars. Let us first define three major timescales, which one can associate with nuclear burning and hydrodynamic flow.
- Nuclear timescale
 :
an e-folding time,
:
an e-folding time,
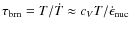 ,
where
,
where
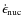 is the energy release rate of the nuclear processes, T is the temperature, and cV is the specific heat.
is the energy release rate of the nuclear processes, T is the temperature, and cV is the specific heat.
- Sound crossing timescale
 :
a time, during which a region of a radius
:
a time, during which a region of a radius 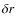 reacts to any pressure imbalance. Such a reaction occurs with the local sound speed
reacts to any pressure imbalance. Such a reaction occurs with the local sound speed 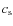 and therefore the sound crossing time scale is
and therefore the sound crossing time scale is
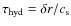 (
(
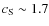
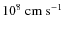 in center of our models).
in center of our models).
- Convective turnover timescale
 :
a time, which a convective element needs to cross the convection zone of width
:
a time, which a convective element needs to cross the convection zone of width
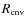 with a velocity
with a velocity
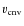 ,
i.e.,
,
i.e.,
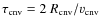 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg41.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg101.png) |
Figure 2:
Temporal evolution of the total nuclear energy production rate E of models hefl.3d (solid) and hefl.2d.a (dotted), respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg42.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg102.png) |
Figure 3:
Temporal evolution of the total kinetic energy |
| Open with DEXTER | |
4.2 Temporal evolution
The 3D model hefl.3d and the corresponding 2D model hefl.2d.a evolve initially (t < 1200 s) similarly. Convection sets in after roughly 1000 s, and hot rising bubbles appear in the region where helium burns in a thin shell (![]()
![]() 108 cm). After another
108 cm). After another ![]() s, the bubbles cover the complete height of the convection zone (R
s, the bubbles cover the complete height of the convection zone (R ![]() 4.7
4.7 ![]() 108 cm). The flow eventually approaches a quasi-steady state after roughly 2000 s consisting of several upstreams (or plumes). The total nuclear energy production (Fig. 2) during the quasi-steady state is about 10% higher in the 3D model due to the strong dependence of the triple-
108 cm). The flow eventually approaches a quasi-steady state after roughly 2000 s consisting of several upstreams (or plumes). The total nuclear energy production (Fig. 2) during the quasi-steady state is about 10% higher in the 3D model due to the strong dependence of the triple-![]() reaction rate on temperature which is slightly higher in the 3D model. Its evolution is correlated with the total kinetic energy (Fig. 3) mainly during the onset of convection when the value of the total kinetic energy rises from 1039 erg to 1045 erg, i.e., hot gas near the position of temperature maximum begins to move and carries the liberated nuclear energy off the burning region, thereby inhibiting a thermonuclear runaway.
reaction rate on temperature which is slightly higher in the 3D model. Its evolution is correlated with the total kinetic energy (Fig. 3) mainly during the onset of convection when the value of the total kinetic energy rises from 1039 erg to 1045 erg, i.e., hot gas near the position of temperature maximum begins to move and carries the liberated nuclear energy off the burning region, thereby inhibiting a thermonuclear runaway.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1414fg43.eps}\par\includegraphics[width=8.5cm,clip]{1414fg44.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg105.png) |
Figure 4:
Temporal evolution of a log10 of the angular averaged kinetic energy density (in
|
| Open with DEXTER | |
The kinetic energy density (Fig. 4) shows small fluctuations in the fully evolved convection zone, and is by an order of magnitude larger in model hefl.2d.a than in model hefl.3d. This is in agreement with other studies, as it is well know that two-dimensional turbulence
is more intensive (Muthsam et al. 1995). The convection zone in the Fig. 4 is characterized by the strip of large kinetic energy density and the adjacent convectively stable
layers by waves induced by convection. The region of high kinetic energy density appearing at
![]() s in the bottom layer in model hefl.3d (see top panel of Fig. 4) is an
artifact caused by the proximity of the reflective inner radial boundary (at 2
s in the bottom layer in model hefl.3d (see top panel of Fig. 4) is an
artifact caused by the proximity of the reflective inner radial boundary (at 2 ![]() 108 cm) of the computational grid.
108 cm) of the computational grid.
We observe buoyancy driven gravity waves in the convectively stable layers (Figs. 4, 11) (Hurlburt et al. 1994,1986; Meakin & Arnett 2007b; Zahn 1991), but we do not discuss these waves any further here, because their properties are likely biased by the reflective boundaries (Asida & Arnett 2000). We only point out that the differences in amplitude seen in Fig. 4 are physical, i.e., gravity waves have a lower amplitude in 3D than in 2D, although the energy carried by them is likely similar (Kiraga et al. 1999).
Table 3: Root mean square fluctuation amplitudes within the convection zone.
4.3 Structure of the convective flow
Fully evolved convection (t > 2000 s) in the 3D model hefl.3d differs significantly from that in the corresponding 2D model hefl.2d.a. The convective flow is dominated in the 2D model by vortices having (angular) diameters ranging from 30![]() to 50
to 50![]() (Fig. 5), and an aspect ratio of close to one. The vortices are qualitatively similar to those found in other two-dimensional simulations (Hurlburt et al. 1994,1986; Bazan & Arnett 1998; Porter & Woodward 1994). This vortex structure of 2D turbulence is quite typical, and arises from the
self-organization of the flow (Fornberg 1977; McWilliams 1984).
(Fig. 5), and an aspect ratio of close to one. The vortices are qualitatively similar to those found in other two-dimensional simulations (Hurlburt et al. 1994,1986; Bazan & Arnett 1998; Porter & Woodward 1994). This vortex structure of 2D turbulence is quite typical, and arises from the
self-organization of the flow (Fornberg 1977; McWilliams 1984).
The convective flow in the 3D model hefl.3d consists of column-shaped plumes (Figs. 5, 11), and contrary to the 2D model hefl.2d.a, it does not show any dominant angular mode. The typical angular size of turbulent features ranges from 10![]() to 30
to 30![]() (Fig. 5). The power spectra of angular velocity fluctuations show that turbulent elements have an almost time-independent characteristic angular size of 30
(Fig. 5). The power spectra of angular velocity fluctuations show that turbulent elements have an almost time-independent characteristic angular size of 30![]() -50
-50![]() in case of the 2D model, while the spectra computed for the 3D model change with time and exhibit no dominant angular mode.
in case of the 2D model, while the spectra computed for the 3D model change with time and exhibit no dominant angular mode.
We find turbulent flow features across the whole convection zone resulting from the interaction of convective up and downflows. Close to the edges of the convective zone we observe the smallest turbulent flow features that form when compact turbulent plumes are decelerated and break-up (Brummell et al. 2002). Shear instabilities likely play an important role in the development of the turbulent flow as well (Cattaneo et al. 1991).
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{1414f45a.eps}\hspace*{0.5c...
...ps}\hspace*{1.5cm}
\includegraphics[width=7.9cm,clip]{1414f45e.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg115.png) |
Figure 5:
Upper panels: snapshots taken at
|
| Open with DEXTER | |
Tables 3 and 4 provide time-averaged (over a time period of about 2500 s) root mean square fluctuation amplitudes of various variables of the convective flow inside the convection zone![]() and near its edges, respectively for models hefl.3d and hefl.2d.a. The temperature and density fluctuation amplitudes are 30-40% larger in the 2D model than in the 3D one. This is expected, because vortices are stable in 2D flows but decay in 3D ones (Fig. 5). The fluctuation amplitudes in the composition (4He and 12C) are larger by 10-30% in the 3D model which is a result of more ``broken'' and hence more non-uniform mixing of chemical elements than in the 2D one. The temperature and density fluctuation amplitudes are a factor of 2-3 larger near the inner edge than near the outer edge
and near its edges, respectively for models hefl.3d and hefl.2d.a. The temperature and density fluctuation amplitudes are 30-40% larger in the 2D model than in the 3D one. This is expected, because vortices are stable in 2D flows but decay in 3D ones (Fig. 5). The fluctuation amplitudes in the composition (4He and 12C) are larger by 10-30% in the 3D model which is a result of more ``broken'' and hence more non-uniform mixing of chemical elements than in the 2D one. The temperature and density fluctuation amplitudes are a factor of 2-3 larger near the inner edge than near the outer edge![]() of the convective layer. At both edges are the fluctuation amplitudes by a factor of 2-4 larger in 2D than in 3D models. The fluctuation amplitudes in the composition (4He and 12C) in both models differ close to the convective boundaries as well, by up to a factor of 2.
of the convective layer. At both edges are the fluctuation amplitudes by a factor of 2-4 larger in 2D than in 3D models. The fluctuation amplitudes in the composition (4He and 12C) in both models differ close to the convective boundaries as well, by up to a factor of 2.
Table 4: Root mean square fluctuation amplitudes at the edges of the convection zone (see Table 3).
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{1414f46a.eps}\hspace*{0.2c...
...s}\hspace*{0.2cm}
\includegraphics[width=5.9cm,clip]{1414f46i.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg118.png) |
Figure 6:
Cuts through the 3D model hefl.3d at t = 4815 s showing the angular variation of temperature (in units of 108 K; left panels), 12C mass fraction (in units of 10-3; middle panels), and radial velocity (in units of
|
| Open with DEXTER | |
Cuts through the 3D model hefl.3d at t = 4815 s showing the angular variation of temperature, 12C mass fraction, and radial velocity at three different radii (Fig. 6) demonstrate that the helium core at the peak of the core helium flash is a very turbulent environment at all heights of the convection zone. The bottom of the convection zone contains hot filaments of gas where the temperature exceeds that of the environment by about 1%. The filaments contain ashes from helium burning, i.e., 12C and 16O, and they move across the whole bottom of the convection zone in a random way. The filaments are correlated with upflows, as the hot gas of burned matter is forced by buoyancy to rise towards the top of the convection zone.
The apparent turbulent nature of the convective flow indicated by our simulations implies that the treatment of mixing in stars as a diffusive process may lead to inaccurate or even incorrect results. Convective flows are rather advective, as pointed out by Woodward et al. (2008).
4.4 Stability of flow structures
To analyze the size and the stability of the vortices we introduce an auto-correlation function of the radial velocity
that measures the radial extent of flow patterns at a given radius r0, or equivalently the radial size of vortices. The notation
provides a measure of the lifetime of flow patterns at radius r0, beyond time t0. Here, we average only over angles. Both correlation functions have the properties
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg47.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg123.png) |
Figure 7:
Auto-correlation function
A1(r0;r) measuring the radial extent of flow patterns (see Eq. (1)) at different radii r0 (4.8 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg48.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg124.png) |
Figure 8:
Auto-correlation function
A2(r0;t-t0) measuring the lifetime of flow patterns (see Eq. (2)) at two different epochs for the 3D model hefl.3d (solid:
|
| Open with DEXTER | |
Figure 7 displays the radial auto-correlation for models hefl.2d.a and hefl.3d and confirms the extension of the convective flow across the whole convective region as determined by the Schwarzschild criterion in the initial stellar model. The broad plateaus with
![]() corresponding to the 2D model hefl.2d.a bear eveidence of the axial symetry imposed in the two-dimensional case which leads to pronouced circular vortices. In the three-dimensional case, the
distributions of A1 tend to differ from unity at nearly all radii.
corresponding to the 2D model hefl.2d.a bear eveidence of the axial symetry imposed in the two-dimensional case which leads to pronouced circular vortices. In the three-dimensional case, the
distributions of A1 tend to differ from unity at nearly all radii.
Figure 8 shows the temporal auto-correlations with two typical results for different t0. The three-dimensional model always shows the typical behaviour of a decrease of the function value to 0.5 within 200-250 s. From this we conclude that the flow pattern fluctuates always in the same way. This is different in the two-dimensional model, where A2 can keep high values for a much longer time implying rather persistent structure (the vortices) of the convective flow.
4.5 Turbulent entrainment and the width of the convection zone
Convection may induce mixing in convectively stable layers adjacent to convectively unstable regions. Following Meakin & Arnett (2007b), we prefer to call this process turbulent entrainment (or mixing), a term also known in oceanography, see e.g., Fernando (1991). The commonly used term (convective) overshooting accounts only for localized ascending or descending plumes crossing the edge of the convection zone. If the filling factor of these plumes or their crossing frequency is high, they can change the entropy in convectively stable regions surrounding convection zones, a process that is known as penetration (Brummell et al. 2002). Turbulent entrainment accounts for both overshooting and penetration.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1414f49a.eps}\vspace*{5mm}...
....eps}\vspace*{5mm}
\includegraphics[width=7.4cm,clip]{1414f49c.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg126.png) |
Figure 9:
Carbon mass fraction X(12C) ( top), entropy S ( middle),
and entropy gradient |
| Open with DEXTER | |
Contrary to Hurlburt et al. (1994) we determine the depth of the entrainment neither by the radius where the kinetic energy carried into the stable layers is zero, nor by the radius where the kinetic energy has dropped to a certain fraction of its maximum value (Brummell et al. 2002). We find both conditions insufficient, because the kinetic energy flux becomes ``zero'' much faster than the convective flux (Fig. 12), which is another possible indicator of the depth of the
entrainment (see next Sect. 4.6). Instead, we rather use the 12C mass fraction, as it is low outside the convection zone during the flash (X(12C) < 2 ![]() 10-3), and as it can rise there only due to turbulent entrainment.
10-3), and as it can rise there only due to turbulent entrainment.
In this study, we use the condition X(12C) = 2 ![]() 10-3 to define the edges of the convection zone. Due to the turbulent entrainment, these edges are pushed towards the stellar center and surface (Fig. 9). Hence, the width of the convection zone increases on the dynamic timescale, which is in contradiction with the predictions of one-dimensional hydrostatic stellar modeling, where the width of the convection zone is determined by the local Schwarzschild or Ledoux criterion. However, the criterion for the width of the convection zone cannot be a local one due to turbulent entrainment caused by convection.
10-3 to define the edges of the convection zone. Due to the turbulent entrainment, these edges are pushed towards the stellar center and surface (Fig. 9). Hence, the width of the convection zone increases on the dynamic timescale, which is in contradiction with the predictions of one-dimensional hydrostatic stellar modeling, where the width of the convection zone is determined by the local Schwarzschild or Ledoux criterion. However, the criterion for the width of the convection zone cannot be a local one due to turbulent entrainment caused by convection.
The speed, at which the radius of the outer edge of the convection zone increases with time due to entrainment, is estimated for models hefl.2d.a and hefl.3d to be at most 14
![]() .
The radius of the inner edge of the convection zone changes at a much smaller rate (Meakin & Arnett 2007b; Bazan & Arnett 1998), as the region interior to the convection zone is more stable against convection and has a higher density than the region exterior to the convection zone (Singh et al. 1995). The entrainment at the bottom of the convection zone also leads to a heating of the cool interior layers (Cole et al. 1985; Deupree & Cole 1983). This seems to be a robust
feature of convection zones driven by nuclear burning, and is observed in other studies too (e.g., Asida & Arnett 2000).
.
The radius of the inner edge of the convection zone changes at a much smaller rate (Meakin & Arnett 2007b; Bazan & Arnett 1998), as the region interior to the convection zone is more stable against convection and has a higher density than the region exterior to the convection zone (Singh et al. 1995). The entrainment at the bottom of the convection zone also leads to a heating of the cool interior layers (Cole et al. 1985; Deupree & Cole 1983). This seems to be a robust
feature of convection zones driven by nuclear burning, and is observed in other studies too (e.g., Asida & Arnett 2000).
The region just interior to the convection zone shows less entrainment (Meakin & Arnett 2007b; Bazan & Arnett 1998), as the square of the Brunt-Väisälä frequency is almost ten times larger there than that in the region just outside the outer edge of the convection zone.
The Brunt-Väisälä frequency is a good stability indicator since it is related to the behavior of convective elements within a convection zone, a fact also pointed out by Hurlburt et al. (1994). The Brunt-Väisälä frequency can be written as (Meakin & Arnett 2007b):
where g,
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414f410.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg128.png) |
Figure 10: Square of the Brunt-Väisälä buoyancy frequency as a function of radius for the 3D model hefl.3d at t = 4638 s. |
| Open with DEXTER | |
The Brunt-Väisälä frequency differs in the 2D and 3D simulations slightly, and has on average a very small negative value inside the convection zone: N2 = -4.4 ![]() 10-6 rad
10-6 rad
![]() in the 2D model hefl.2d.a, and N2 = -1.2
in the 2D model hefl.2d.a, and N2 = -1.2 ![]() 10-6 rad
10-6 rad
![]() in the 3D model hefl.3d. Just outside (inside) the inner (outer) edge of the convection zone of the 2D model hefl.2d.a we find N2 = 0.580 rad
in the 3D model hefl.3d. Just outside (inside) the inner (outer) edge of the convection zone of the 2D model hefl.2d.a we find N2 = 0.580 rad
![]() (0.053 rad
(0.053 rad
![]() ), and N2 = 0.583 rad
), and N2 = 0.583 rad
![]() (0.052 rad
(0.052 rad
![]() )
for the 3D model hefl.3d, respectively (Fig. 10). In the 2D model hefl.2d.b, these frequencies are higher by about a factor of two.
)
for the 3D model hefl.3d, respectively (Fig. 10). In the 2D model hefl.2d.b, these frequencies are higher by about a factor of two.
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm,clip]{1414iso1.eps}\includ...
...ps}\hspace{2.5cm}
\includegraphics[width=6cm,clip]{1414iso4.eps} }\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg131.png) |
Figure 11:
Different views of isosurfaces of the velocity field for the 3D model hefl.3d at t = 3000 s. The blue isosurface corresponds to radial downflows with
vr = -6 |
| Open with DEXTER | |
Due to its high stability, the radius of the bottom edge of the convection zone did not change during the time covered by our simulations hefl.2d.a and hefl.3d, except for an initial jump inwards over one radial grid zone, when it was touched by convective downflows for the first time. However, entrainment may move the edge further towards the stellar center later in the evolution. The
entrainment rate (i.e., the velocity at which the convective boundary moves) is lower by a factor of ![]() 6 at the bottom of the convection zone in our 2D simulation hefl.2d.b (see Sect. 6) as compared to that at the outer boundary (
6 at the bottom of the convection zone in our 2D simulation hefl.2d.b (see Sect. 6) as compared to that at the outer boundary (
![]() ;
see above). Similar behavior was also observed in 3D simulations of oxygen burning shell (Meakin & Arnett 2007b). It implies that the
entrainment rate at the inner edge of the convection zone is
;
see above). Similar behavior was also observed in 3D simulations of oxygen burning shell (Meakin & Arnett 2007b). It implies that the
entrainment rate at the inner edge of the convection zone is
![]() in our core helium flash simulations. The corresponding change in radius is only
in our core helium flash simulations. The corresponding change in radius is only ![]() 1.4 (2.2)
1.4 (2.2) ![]() 106 cm or about a third of the width of a radial zone during the time covered by the simulations hefl.3d (hefl.2d.a), and hence too small to be seen. As these estimates are resolution dependent, the values presented should be considered as order of magnitude estimates, only.
106 cm or about a third of the width of a radial zone during the time covered by the simulations hefl.3d (hefl.2d.a), and hence too small to be seen. As these estimates are resolution dependent, the values presented should be considered as order of magnitude estimates, only.
The entrainment is more efficient in the 2D model hefl.2d.a than in the 3D model hefl.3d. In 2D, the observed convective flow structures are large and fast rotating vortices that due to the imposed axisymmetry are actually tori (Bazan & Arnett 1998). They have a high filling factor near the edge of the convection zone where they overshoot or penetrate (Brummell et al. 2002). 3D structures crossing the edge of the convection zones are smaller (localized) plumes with a lower filling factor and smaller velocities.
-1mm
We studied convective stability in detail only for the layer above the convection zone, where the gas is only weakly degenerate, and we are thus able to compare our results with those of similar systems simulated in 3D at high Reynolds numbers (
![]() )
by Brummell et al. (2002). According to these authors, a stable layer allows for more ``overshooting'', if its entropy gradient is smaller. We found that the turbulent entrainment lowers the entropy gradient at the outer edge of the convection zone in our simulations (Fig. 9). Hence, the stability of the exterior stable layer decreases with time, allowing for more turbulent entrainment.
)
by Brummell et al. (2002). According to these authors, a stable layer allows for more ``overshooting'', if its entropy gradient is smaller. We found that the turbulent entrainment lowers the entropy gradient at the outer edge of the convection zone in our simulations (Fig. 9). Hence, the stability of the exterior stable layer decreases with time, allowing for more turbulent entrainment.
Contrary to Brummell et al. (2002), who studied only single fluid flow, our simulations involve a mixture of different fluids of different composition. This complicates the above argumentation, as in a multi-fluid flow a shallow entropy gradient does not necessarily imply that the layer is less stable against turbulent entrainment. We plan to address this issue in more detail elsewhere. We have not analyzed the stability of the region below the inner edge of the convection zone, because it is highly degenerate and appears to be very stable. No significant entrainment of 12C was observed there during the entire simulation of models hefl.2d.a and hefl.3d, respectively. Simulations covering longer periods of time are therefore needed (see Sect. 6). The analysis of the energy fluxes inside the convection zone and near the outer edge of the convection zone, which will be discussed in the next subsection, will provide more information about the phenomenon of the turbulent entrainment.
4.6 Energy fluxes
Energy fluxes are a useful tool for understanding convective flows (Hurlburt et al. 1994; Brummell et al. 2002; Hurlburt et al. 1986; Muthsam et al. 1995; Meakin & Arnett 2007b; Chan & Sofia 1986). They allow one to discriminate the energy transport due to different processes and mechanisms (e.g., due to convection, heat conduction, etc.). We thus analyzed various energy fluxes and source terms that are defined in Appendix B. All energy fluxes and source terms (see, Fig. 12) are averaged over several convective turnover timescales, as they change considerably with time due to the appearance of plumes (Muthsam et al. 1995).
The convective energy flux is mainly positive as heat is mostly transported upwards by convection. It is larger in the 2D model hefl.2d.a, as in 2D the convective flow structures are more laminar
and ordered, and thus experience less dissipation. The smaller value of ![]() in the 3D model hefl.3d is a result of a less ordered flow throughout the whole convection zone. This is in agreement with Table 3 which shows that the fluctuations in temperature and density are smaller in the 3D model.
in the 3D model hefl.3d is a result of a less ordered flow throughout the whole convection zone. This is in agreement with Table 3 which shows that the fluctuations in temperature and density are smaller in the 3D model.
A kinetic energy flux arises from deviations from the mean convective flow (i.e., mainly from the upflow-downflow asymmetry). Typically it is largest in the most turbulent regions of the flow, where on top of the kinetic flux due to the up- and down-flow asymmetry, there is also a significant contribution due to the asymmetry of localized turbulent (convective) elements. Directly connected to this is the offset between the maxima of the kinetic and the convective flux (see Fig. 12), which reflects the fact that the convective flow decays more efficiently when the flow becomes strongly turbulent.
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm]{1414flx1.eps}\includegrap...
...=8.8cm]{1414flx3.eps}\includegraphics[width=8.8cm]{1414flx4.eps} }\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg135.png) |
Figure 12:
Various energy fluxes and source terms as a function of radius averaged (from 2000 s to 6000 s) over about four convective turnover timescales. Panel a) shows the convective flux |
| Open with DEXTER | |
The work done by buoyancy forces is positive in the whole region of dominant nuclear burning (see Fig. 12) indicating either less dense and hot gas moving upwards or more dense and cooler gas moving downwards. A negative value of the work done by buoyancy forces implies the opposite situation, i.e., less dense and hot gas flowing downward or denser and cooler gas flowing upward. The latter is known as buoyancy braking leading to a deceleration of the flow motion (Brummell et al. 2002), and to the unusual situation that hot matter tends to sink, and cool matter is likely to rise.
The gas should expand while rising up through the convection zone, i.e., the work done by buoyancy (PA) and by volume changes (PP) should always be anti-correlated. The anti-correlation is clearly seen only in the 2D model hefl.2d.a, whereas in the 3D model hefl.3d the quantities are on average anti-correlated only in the central region of the convection zone. At the inner edge of the convection zone, buoyancy drives gas upwards which is on average simultaneously compressed, probably by the broad downflows. At the outer edge where buoyancy braking occurs, the gas on average expands. Hence, it must expand faster than the upflows cool and are being compressed (a situation observed for the 2D model hefl.2d.a).
All the fluxes discussed here agree qualitatively well with those of our previous high-resolution 2D simulations (Mocák et al. 2008). They are also qualitatively very similar to those of the high-resolution 3D simulations of Brummell et al. (2002) who investigated a stratified model with a convectively stable region located on top of a convectively unstable region both consisting of an ideal gas with a very high Reynolds number (
![]() ). The angular and time averaged radial distributions of the kinetic and convective fluxes seem to be robust in the convectively unstable region, as our 3D results are qualitatively similar to those obtained in several other
3D studies (Hurlburt et al. 1994; Brummell et al. 2002; Meakin & Arnett 2007b).
). The angular and time averaged radial distributions of the kinetic and convective fluxes seem to be robust in the convectively unstable region, as our 3D results are qualitatively similar to those obtained in several other
3D studies (Hurlburt et al. 1994; Brummell et al. 2002; Meakin & Arnett 2007b).
The outer part of the convection zone, where buoyancy braking occurs, resembles the overshooting region due to active penetration of plumes described by Hurlburt et al. (1994,1986) and Brummell et al. (2002). Note, however, that this region is convectively stable at the beginning of their simulations, i.e., buoyancy braking takes already place inside the convection zone in our models.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414ve2d.eps}\hspace*{1cm}
\includegraphics[width=8cm,clip]{1414ve3d.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg136.png) |
Figure 13:
Radial distributions of the time (from 2000 s to 4000 s) and angle-averaged velocity components (vr, |
| Open with DEXTER | |
The distribution of the kinetic flux (Fig. 12) exhibits structural differences in the convection zone between 2D and 3D flows. The typical evolved 2D flow contains well defined vortices
(Fig. 5) whose central parts never interact with the region of dominant nuclear burning. This results in a reduced kinetic energy flux at
![]()
![]() 108 cm, as this region corresponds to the central region of the vortices, which do not experience any strong radial motion. On the other hand, the distribution of the kinetic energy flux in the 3D model hefl.3da is rather smooth as a result of the column-shaped flow structures (Fig. 11).
108 cm, as this region corresponds to the central region of the vortices, which do not experience any strong radial motion. On the other hand, the distribution of the kinetic energy flux in the 3D model hefl.3da is rather smooth as a result of the column-shaped flow structures (Fig. 11).
The convective flux changes sign in stable layers since the downflows or upflows penetrating into the stable zones are suddenly too hot or cold compared to the surrounding gas. The penetration continues until the momentum of the convective elements is used up or diffusion smooths out the perturbations, and the convective flux approaches zero (Brummell et al. 2002). This fingerprint of turbulent entrainment is clearly present at both convective boundaries of our models (Fig. 12). It is less pronounced at the inner convective boundary in the 3D model hefl.3d, because the simulation cover only a short period of time and the boundary was not weakened enough for the entrainment to be sufficiently visible by a negative convective flux.
The convective energy flux is relatively strong even in regions where the kinetic energy flux is almost zero. Therefore, the ``zero'' kinetic flux criterion (Brummell et al. 2002; Hurlburt et al. 1994) seems to be a bad indicator of entrainment which may extend well beyond the location where the kinetic flux becomes small.
In fact, what is happening at the convective boundaries is an exchange between the potential energy of the stratification given by the buoyancy jump
![]() and the kinetic energy of the turbulence. Turbulence looses its kinetic energy by doing work against gravity, which leads to a reduction of the buoyancy jump, and hence to stability weakening of the stable boundary layer to the effects of the turbulent entrainment. The buoyancy jump
and the kinetic energy of the turbulence. Turbulence looses its kinetic energy by doing work against gravity, which leads to a reduction of the buoyancy jump, and hence to stability weakening of the stable boundary layer to the effects of the turbulent entrainment. The buoyancy jump ![]() is a direct measure of the stability of the boundary layer. To mix gas into the boundary layer the buoyancy must be reduced. This is accomplished through the buoyancy flux
is a direct measure of the stability of the boundary layer. To mix gas into the boundary layer the buoyancy must be reduced. This is accomplished through the buoyancy flux
![]() ,
which is related to the temporal variation of the buoyancy jump by
,
which is related to the temporal variation of the buoyancy jump by
![]() ,
where PA and
,
where PA and ![]() are the sink/source term of the kinetic energy due to buoyancy forces and the density, respectively.
are the sink/source term of the kinetic energy due to buoyancy forces and the density, respectively.
The convective flux can directly be related to the buoyancy flux that is a function of PA by a linear relation
![]() described in more detail by Meakin & Arnett (2007b).
Figure 12 shows that this agrees well with what we observe in our simulations. It also supports our previous conclusion that entrainment is well indicated by the convective flux and the related buoyancy flux which via the equation
described in more detail by Meakin & Arnett (2007b).
Figure 12 shows that this agrees well with what we observe in our simulations. It also supports our previous conclusion that entrainment is well indicated by the convective flux and the related buoyancy flux which via the equation
![]() leads to the decrease of the buoyancy jump in the stable layer. This in turn reduces the convective stability of that layer.
leads to the decrease of the buoyancy jump in the stable layer. This in turn reduces the convective stability of that layer.
The properties of the entrainment at the outer convective boundary differs in models hefl.2d.a and hefl.3d (see Fig. 12). In the 2D model entrainment is reaching deeper into the stable layer due to a more active convection zone with higher typical velocities (Fig. 13) than in the 3D model. The radial distribution of the work done by buoyancy PA is qualitatively similar in both the 2D and 3D models, i.e., it is negative indicating buoyancy braking.
Nevertheless, the work done by gas compression or expansion PP is different. In the 2D model hefl.2d.a the gas on average is compressed (PP is positive), while in the 3D model hefl.3d the gas is expanding at the boundary. This again confirms that 2D and 3D convective flows are qualitatively different.
4.7 The flow within the convection zone
The velocities in the 3D model hefl.3d match those predicted by mixing-length theory better than in the 2D model hefl.2d.a, where they are about a factor of ![]() 3 larger. This behavior was also observed in other hydrodynamic simulations of convective flows; see e.g., Muthsam et al. (1995); Meakin & Arnett (2007b). The radial velocities in the regions above and below the convection zone are smaller than the angular velocities in both models, which is a typical feature of
gravity waves (Asida & Arnett 2000).
3 larger. This behavior was also observed in other hydrodynamic simulations of convective flows; see e.g., Muthsam et al. (1995); Meakin & Arnett (2007b). The radial velocities in the regions above and below the convection zone are smaller than the angular velocities in both models, which is a typical feature of
gravity waves (Asida & Arnett 2000).
In the 3D model hefl.3d, the flow in the convectively stable layer beneath the convection zone exhibits some numerical artefacts due to the proximity of the inner grid boundary (see Fig. 13). The radial distributions of the time and angle-averaged components of
the velocity field and of the density fluctuations show pronounced maxima at ![]()
![]() 108 cm and a sharp cut-off at r = 2.5
108 cm and a sharp cut-off at r = 2.5 ![]() 108 cm (Figs. 13, 14). The sharp cut-off is caused by the artificial damping we had to apply to the velocity field in the innermost grid zones to prevent numerical instabilities from
spreading limitless to the convection zone.
108 cm (Figs. 13, 14). The sharp cut-off is caused by the artificial damping we had to apply to the velocity field in the innermost grid zones to prevent numerical instabilities from
spreading limitless to the convection zone.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414f414.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg144.png) |
Figure 14: Radial distributions of the time (from 2800 s to 4800 s) and angle-averaged density fluctuations in the 3D model hefl.3d (solid red line). The panels also show the angular variation of the respective quantity at a given radius (gray shaded region). The dotted vertical lines mark the edges of the convection zone as determined by the Schwarzschild criterion. |
| Open with DEXTER | |
Although, the flow velocities in the 3D model match those predicted by mixing-length theory very well, one should keep in mind that with increasing resolution the flow velocities will likely increase due to the reduced numerical viscosity. This trend is confirmed by the velocities obtained for the high-resolution 2D model hefl.2d.b that are higher than in the low-resolution model hefl.2d.a (Table 2).
Near both edges of the convective zone there are large narrow peaks visible in the radial distributions of the time and angle-averaged density fluctuations (Fig. 14). These peaks are not caused by compression or expansion, but they are a result of the density discontinuities at the edges of the convection zone (Arnett et al. 2007; Meakin & Arnett 2007a), because any angle-dependent radial perturbation will cause large angular variations of density at these discontinuities. The same holds also for the temperature discontinuities at the convective borders.
The temperature fluctuations within the convection zone are rather uniformly distributed, but they are more intense near the outer edge of the convection zone, where they are only weakly correlated with the radial velocity (Fig. 6). At the top of the convection zone the emerging rising plumes are embedded in an environment which sinks down (Fig. 6, bottom panels). This situation is similar to the sinking down-drafts with upwelling centers found in simulations by Nordlund & Dravins (1990) and Cattaneo et al. (1991).
4.8 Upflow-downflow asymmetry
The 2D and 3D simulations share the common property of an upflow-downflow asymmetry (Brummell et al. 2002; Hurlburt et al. 1994; Muthsam et al. 1995). The downflows cover a much larger volume fraction of the convection zone than the upflows (Fig. 15). The filling factor of the downflows increases with decreasing depth (Rast et al. 1993; Meakin & Arnett 2007b) across most of the convection zone, and the downflows are more dominant in the 3D model hefl.3d than in the 2D models. In the model hefl.3d (hefl.2d.a, hefl.2d.b) we find that the absolute velocities are about 40% (15%, 4%) higher in the upflows than in the downflows. Hence, the downflows in the convection zone of a star at the peak of the core helium flash are slower and broader than the faster and narrower upflows.
5 Mixing length theory and simulations
Mixing length theory (or MLT) commonly used for treating convection in stellar evolutionary calculations relies on assumptions and parameters that are often chosen based on convenient ad-hoc arguments about the convective flow, like e.g., the value of the mixing length, the amount of upflow-downflow symmetry or the position where, within the convection zone, convective elements start to rise (Kippenhahn & Weigert 1990; Weiss et al. 2004b).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414f415.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg145.png) |
Figure 15:
Fractional volume occupied by upflow streams
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1414adg1.eps}\vspace*{0.5cm}
\includegraphics[width=7.8cm,clip]{1414adg2.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg146.png) |
Figure 16:
Upper panel: radial distributions of the adiabatic temperature
gradient
|
| Open with DEXTER | |
MLT assumes that the temperature of a convective element (blob) is the same as that of the ambient medium surrounding it when it starts to rise. However, as a blob will not rise until it is hotter than the surroundings, this MLT assumption is contradictory. MLT further assumes that once the blobs begin to rise they carry their surplus of heat lossless over a distance given by the mixing length before they release it to the surrounding gas instantaneously at the end of their path. These assumptions are also not fulfilled in general. Our simulations show that convective elements typically start their rise deep inside the star from the region of dominant nuclear burning where they are accelerated by buoyant forces. The assumptions of MLT that convective blobs form and begin their motion at different depths of the convection zone, and that the average convective blob propagates a distance equal to half of the assumed mixing length before dissolving with the surrounding gas (Kippenhahn & Weigert 1990), therefore do not hold. MLT finally also assumes a perfect correlation between the thermodynamic variables and the velocity of the flow in a convection zone. However, the results of our simulations falsify this assumption (Fig. 6).
According to MLT, the temperature fluctuations in a convection zone are directly proportional to the mixing length and to the deviation of the temperature gradient of the model
![]() from the adiabatic one
from the adiabatic one
![]() :
:
where
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{1414vl1.eps}\hspace*{5mm}
...
...s}\hspace*{5mm}
\includegraphics[width=5.7cm,clip]{1414vl3.eps}
\par\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg151.png) |
Figure 17:
Snapshots of the spatial distribution of the velocity modulus |v| (in units of
|
| Open with DEXTER | |
Since T'/T and
![]() can directly be obtained from our simulations, we attempted to test MLT in a qualitative manner. Our simulations show that in the outer part of the convection zone, i.e., in the region where the buoyancy force is getting smaller (Fig. 12, panel b), the temperature gradient of the models
can directly be obtained from our simulations, we attempted to test MLT in a qualitative manner. Our simulations show that in the outer part of the convection zone, i.e., in the region where the buoyancy force is getting smaller (Fig. 12, panel b), the temperature gradient of the models
![]() becomes subadiabatic (see lower panel of Fig. 16). Equation (4) which was derived for the adiabatic rise of convective bubbles would then imply that the temperature of convective elements should be lower than that of the surrounding gas (hence no convection) in the outer part of the convection zone, or that the value of
becomes subadiabatic (see lower panel of Fig. 16). Equation (4) which was derived for the adiabatic rise of convective bubbles would then imply that the temperature of convective elements should be lower than that of the surrounding gas (hence no convection) in the outer part of the convection zone, or that the value of ![]() should be negative. However, convective elements do not rise adiabatically in our hydrodynamic simulations and the subadiabatic gradient means only that the convective elements start to cool faster than their surroundings. It does not imply necessarily that the elements are already cooler than the surrounding gas which would prevent
the gas from being convectively active. Note that initially, the temperature gradient is superadiabatic in the whole convection zone (see upper panel of Fig. 16), because the stellar evolutionary model used as initial input for our simulations is computed under the
assumptions of the MLT.
should be negative. However, convective elements do not rise adiabatically in our hydrodynamic simulations and the subadiabatic gradient means only that the convective elements start to cool faster than their surroundings. It does not imply necessarily that the elements are already cooler than the surrounding gas which would prevent
the gas from being convectively active. Note that initially, the temperature gradient is superadiabatic in the whole convection zone (see upper panel of Fig. 16), because the stellar evolutionary model used as initial input for our simulations is computed under the
assumptions of the MLT.
6 Long-term evolution
Two-dimensional simulations are biased due to the imposed symmetry restriction which tend to overestimate the activity in the convection zone, but qualitative similarities with geometrically unconstrained 3D models exists. Moreover, many phenomena that we observe in 2D models happen also in the 3D ones, just slower. Hence, we think it is justified to explore the long-term evolution (i.e., covering a few tens of hours instead of a few hours) of our initial core helium flash models by performing cost-effective 2D instead of very costly 3D simulations.
In the following we describe the long-term evolution of the 2D model hefl.2d.b whose early evolution, covering 8 h, was discussed in detail by Mocák et al. (2008). The model is characterized by a very dynamic flow involving typical convective velocities of ![]()
![]()
![]() .
Our long-term hydrodynamic simulation of this model covering 36 h (see Figs. 17, 18) has revealed that the global and angle-averaged maximum temperatures continue to rise at the initial rate of
.
Our long-term hydrodynamic simulation of this model covering 36 h (see Figs. 17, 18) has revealed that the global and angle-averaged maximum temperatures continue to rise at the initial rate of
![]() that is 60% lower than the rate predicted by stellar evolutionary calculations. As a consequence, the typical convective velocities increase by about 50% and reach a level of
that is 60% lower than the rate predicted by stellar evolutionary calculations. As a consequence, the typical convective velocities increase by about 50% and reach a level of ![]()
![]()
![]() at the end of the simulation (Fig. 17).
at the end of the simulation (Fig. 17).
Hydrodynamic simulations of convection driven by nuclear burning covering several convective turnover timescales show a rapid growth of the convection zone due to the turbulent entrainment
(Meakin & Arnett 2007b). An analysis of our simulations based on a tracing of the radial position of the convective boundaries (defined by the condition X(12C) = 2 ![]() 10-3; see
Sect. 4.5), shows a similar behavior.
10-3; see
Sect. 4.5), shows a similar behavior.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg62.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg158.png) |
Figure 18:
Temporal evolution of the horizontally averaged temperature maximum
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{1414f63a.eps}\includegrap...
...8.5cm]{1414f63c.eps}\includegraphics[width=8.5cm]{1414f63d.eps} }\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg161.png) |
Figure 19:
Upper panels: angular averaged 12C mass fraction as a function of radius near the inner ( left) and outer edge ( right) of the convection zone in the long-term 2D model hefl.2d.b at
|
| Open with DEXTER | |
Turbulent motion near the upper edge of the convection zone pumps material into the convectively stable layer at an entrainment rate of roughly 14
![]() without any significant slowdown over the whole duration of the simulation (Fig. 19) covering
without any significant slowdown over the whole duration of the simulation (Fig. 19) covering ![]() 130 000 s (or more than 250 convective turnover timescales). The entrainment rate at the inner convective boundary is about a factor of six smaller (
130 000 s (or more than 250 convective turnover timescales). The entrainment rate at the inner convective boundary is about a factor of six smaller (![]() 2.3
2.3
![]() )
and increasing during the second half of the
simulation (
t > 60 000; see Fig. 19). These entrainment rates have to be considered as upper limits because of the imposed axisymmetry which leads to exaggerated convective velocities and large filling factors for the penetrating plumes. The turbulent entrainment causes a growth of the convection zone on a dynamic timescale, in agreement with the hydrodynamic models of oxygen shell burning (Meakin & Arnett 2007b).
)
and increasing during the second half of the
simulation (
t > 60 000; see Fig. 19). These entrainment rates have to be considered as upper limits because of the imposed axisymmetry which leads to exaggerated convective velocities and large filling factors for the penetrating plumes. The turbulent entrainment causes a growth of the convection zone on a dynamic timescale, in agreement with the hydrodynamic models of oxygen shell burning (Meakin & Arnett 2007b).
Both interfaces at the edges of the convection zone remain sharp during the whole length of the simulation (Fig. 19). The entrainment is correlated with a decrease of the temperature at the outer edge of the convection zone due to the decreasing entropy (Fig. 9). At the inner edge of the convection zone the entrainment leads to heating of the cold region at r < 4.72 ![]() 108 cm that is cooled by neutrinos (Fig. 19). Contrary to the finding of Asida & Arnett (2000), the heating does not penetrate deeper into the star than the mixing of 12C and the other nuclear ashes.
108 cm that is cooled by neutrinos (Fig. 19). Contrary to the finding of Asida & Arnett (2000), the heating does not penetrate deeper into the star than the mixing of 12C and the other nuclear ashes.
Due to the growth of the convection zone and due to nuclear burning the mean 4He, 12C and 16O mass fractions change in the convection zone at rates listed in Table 5. The mean value of the 12C mass fraction in the convection zone decreases at a rate of
![]()
![]()
![]() until
until
![]() s to a value of X(12C) = 5.2
s to a value of X(12C) = 5.2 ![]() 10-3. Then it begins to increase again at roughly the same (absolute) rate
10-3. Then it begins to increase again at roughly the same (absolute) rate
![]()
![]()
![]() .
The 12C mass fraction decreases at the beginning, because the volume of the convection zone grows initially almost discontinuously due to the sudden start of the entrainment. Hence, nuclear reactions are for a start unable to produce enough carbon to compensate for the volume increase. At
.
The 12C mass fraction decreases at the beginning, because the volume of the convection zone grows initially almost discontinuously due to the sudden start of the entrainment. Hence, nuclear reactions are for a start unable to produce enough carbon to compensate for the volume increase. At
![]() s the 12C mass fraction has risen again to its initial value of
Xi (12C)
s the 12C mass fraction has risen again to its initial value of
Xi (12C) ![]() 5.5
5.5 ![]() 10-3, and at the end of
the simulation at
t = 130 000 s the
Xf (12C)
10-3, and at the end of
the simulation at
t = 130 000 s the
Xf (12C) ![]() 5.9
5.9 ![]() 10-3, a value that is 7% higher than the initial one.
10-3, a value that is 7% higher than the initial one.
Table 5:
Rate of change of the mean mass fractions of 4He, 12C, and 16O in the 2D model hefl.2d.b within the first 40 000 s (Ri; in units of
![]() ), and within the time interval
), and within the time interval
![]() (Rf; in units of
(Rf; in units of
![]() )
with the initial Xi and final Xf mass fractions (in units of 10-3), respectively.
)
with the initial Xi and final Xf mass fractions (in units of 10-3), respectively.
The mean 16O mass fraction shows a similar trend as that of 12C as its production depends directly on the 12C mass fraction. The mass fraction of 4He rises within the first 40 000 s because convection is dredging up fresh 4He from the convectively stable layers. Later in the evolution the mass fraction of 4He decreases, as it is being constantly burned.
7 Summary
We performed, analyzed and compared 2D axisymmetric and 3D hydrodynamic simulations of the core helium flash. In agreement with our previous study of 2D hydrodynamic models of the core helium flash we find that the core helium flash in three dimensions neither rips the star apart, nor that it significantly alters its structure.
The evolved convection of the 3D models differs qualitatively from that of the axisymmetric ones. The typical convective structure in the 2D simulations is a vortex with a diameter roughly equal to the width of convection zone, whereas the 3D structures are smaller in extent and have a plume-like shape. The typical convective velocities are much higher in the 2D models than in the 3D ones. In the latter models the convective velocities tend to fit those predicted by the mixing length theory better. Both 2D and 3D models are characterized by an upflow-downflow asymmetry, where downflows occupy larger volume fraction but the upflows are faster.
The upper part of the evolved convection zone is characterized by a subadiabatic temperature gradient, where buoyancy braking takes places, i.e., rising convective plumes start to slow down in this region and eventually descend back into deeper layers of the star. Convection should not exist in that mass layer according to mixing length theory.
Our hydrodynamic simulations show the presence of turbulent entrainment at both the inner and outer edge of the convection zone, which results in a growth of the convection zone on a dynamic timescale. While entrainment occurs at an almost constant speed at the outer boundary of the convection zone, it tends to accelerate at the inner one. The entrainment rates are higher at the outer edge than at the inner edge of the convection zone, as the latter is more stable against entrainment. In essence, these findings show that the extent of the inner convection zone powered by helium burning during the flash predicted by the canonical stellar evolution theory is not correct.
The fast growth of the convection zone due to the entrainment has some potentially interesting implications. As the entrainment is not considered in canonical stellar evolutionary calculations, stars evolving towards the core helium flash may never reach a state as the one given by our initial stellar model. Hence, this may influence the growth of the convection zone observed in our hydrodynamic simulations, as the thermodynamic conditions at the edges of the convection zone may differ.
If a rapid growth of the convection zone indeed occurs, the main core helium flash studied here will never be followed by subsequent mini-flashes, as convection will lift the electron degeneracy in the helium core in less than one month. In addition, the helium core will likely experience an injection of hydrogen from the stellar envelope within 10 days and undergo a violent nuclear burning phase powered by the CNO cycle. However, the growth of the convection zone within the core that is simulated in our models does not have to continue until it will reach the outer convection zone extending up to the surface of the star. Hence, mixing of nuclear ashes to the stellar atmosphere (or a dredge-up) does not necessarily take place. But a fast dynamic growth of the inner convection zone will lead to a change of the composition of the stellar core, and consequently of the luminosities of low-mass stars on the horizontal branch.
The possibility of a dredge-up during the core helium flash explains perhaps early R-stars (Izzard et al. 2007) that are carbon enriched and show evidence of s-process elements. Their production could be triggered by hydrogen injection to the helium core. Mixing of these s-process elements together with carbon from the helium and CNO burning layers to the stellar atmosphere may produce signatures typical for the early R-stars.
We find significant differences between the properties and the evolution of 2D and 3D models having a convection zone powered by (semi-)degenerate helium burning. However, as our 3D models are likely not yet fully converged and as they cover only a relatively short period of evolutionary time, long-term 3D simulations using a higher grid resolution are needed to obtain a better and more reliable understanding of the hydrodynamics of the core helium flash. Long-term 3D simulations are especially important, as it is unclear, whether the upper boundary of the helium powered convection zone will be able to reach or even penetrate to the hydrogen envelope, hence a secondary CNO flash and the possible mixing of ash from the helium layer to the upper atmosphere may not occur.
Acknowledgements
The simulations were performed at the Leibniz-Rechenzentrum of the Bavarian Academy of Sciences & Humanities on the SGI Altix 4700 system. The authors want to thank Frank Timmes for some of his publicly available Fortran subroutines which we used in the Herakles code, and Kurt Achatz whose unpublished hydrodynamic simulations of the core helium flash performed during his diploma work in 1995 inspired this work. We are indebted to Casey Meakin for several enlightening discussions and helpful comments. The authors are grateful to an anonymous referee for his/her comments which helped to improve this manuscript.
Appendix A: Hydrodynamic equations in spherical polar coordinates
The hydrodynamic equations of a non-viscous multi-component reactive gas subject to a gravitational potential ![]() and having a heat conductivity K are given in spherical polar coordinates (
and having a heat conductivity K are given in spherical polar coordinates (
![]() ) by
) by
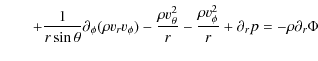 |
(A.2a) |
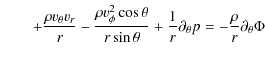 |
(A.2b) |
| (A.4) |
where ![]() ,
vr,
,
vr,
![]() ,
,
![]() ,
p, e, T,
,
p, e, T,
![]() ,
Xk, and
,
Xk, and ![]() are the density, the radial velocity, the
are the density, the radial velocity, the ![]() -velocity, the rotation velocity, the
pressure, the total specific energy, the temperature, the energy generation rate per mass due to reactions, the mass fraction of species k, and the change of this mass fraction due to reactions,
respectively.
-velocity, the rotation velocity, the
pressure, the total specific energy, the temperature, the energy generation rate per mass due to reactions, the mass fraction of species k, and the change of this mass fraction due to reactions,
respectively.
![]() is the number of species the gas is composed of.
is the number of species the gas is composed of.
Appendix B: Energy fluxes
The various contributions to the total energy flux (Hurlburt et al. 1986; Achatz 1995) can be obtained by first integrating the hydrodynamic energy equation given in Appendix A over the angular coordinates ![]() and
and ![]() .
Then, one decomposes both the specific enthalpy
.
Then, one decomposes both the specific enthalpy
![]() (where
(where
![]() is the specific thermal energy) and the specific kinetic energy vivi/2 into a horizontal mean and a perturbation,
is the specific thermal energy) and the specific kinetic energy vivi/2 into a horizontal mean and a perturbation,
![]() ,
and obtains
,
and obtains![]()
where
Here, the gravitational potential
In a similar way one can also formulate a conservation equation for the mean horizontal kinetic energy that provides further insight into the effects of convective motions. Using the other hydrodynamic equations (Eqs. (A.1) to (A.2c)), and the relation
![]() ,
one finds
,
one finds
With
where the Pi are source or sink terms of the kinetic energy. They are separated into the effect of buoyancy forces (PA), and the work due to density fluctuations (PP, volume changes). By analyzing the various Pi one can determine what causes the braking or acceleration of the convective flow. The acoustic flux, FP, describes the vertical transport of density fluctuations.
References
- Achatz, K. 1995, in Master thesis, Technical University München
- Almgren, A. S., Bell, J. B., Rendleman, C. A., & Zingale, M. 2006, ApJ, 637, 922 [NASA ADS] [CrossRef]
- Arnett, D., Meakin, C., & Young, P. A. 2007, in IAU Symp., ed. F. Kupka, I. Roxburgh, & K. Chan, 239, 247
- Asida, S. M., & Arnett, D. 2000, ApJ, 545, 435 [NASA ADS] [CrossRef]
- Bader, G., & Deuflhard, P. 1983, Numer. Math., 41, 373 [CrossRef]
- Bazan, G., & Arnett, D. 1998, ApJ, 496, 316 [NASA ADS] [CrossRef]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS]
- Brummell, N. H., Clune, T. L., & Toomre, J. 2002, ApJ, 570, 825 [NASA ADS] [CrossRef] (In the text)
- Campbell, S. W., & Lattanzio, J. C. 2008, in First Stars III, ed. B. W. O'Shea, & A. Heger, Am. Inst. Phys. Conf. Ser., 990, 315
- Canuto, V. M. 2000, A&A, 357, 177 [NASA ADS]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef]
- Cassisi, S., Schlattl, H., Salaris, M., & Weiss, A. 2003, ApJ, 582, L43 [NASA ADS] [CrossRef]
- Cattaneo, F., Brummell, N. H., Toomre, J., Malagoli, A., & Hurlburt, N. E. 1991, ApJ, 370, 282 [NASA ADS] [CrossRef] (In the text)
- Chan, K. L., & Sofia, S. 1986, ApJ, 307, 222 [NASA ADS] [CrossRef] (In the text)
- Chan, K. L., Sofia, S., & Wolff, C. L. 1982, ApJ, 263, 935 [NASA ADS] [CrossRef] (In the text)
- Cole, P. W., & Deupree, R. G. 1980, ApJ, 239, 284 [NASA ADS] [CrossRef]
- Cole, P. W., & Deupree, R. G. 1981, ApJ, 247, 607 [NASA ADS] [CrossRef]
- Cole, P. W., Demarque, P., & Deupree, R. G. 1985, ApJ, 291, 291 [NASA ADS] [CrossRef]
- Colella, P., & Glaz, H. H. 1984, J. Comp. Phys., 59, 264 [NASA ADS] [CrossRef] (In the text)
- Colella, P., & Woodward, P. R. 1984, J. Comp. Phys., 54, 174 [NASA ADS] [CrossRef] (In the text)
- Dearborn, D. S. P., Lattanzio, J. C., & Eggleton, P. P. 2006, ApJ, 639, 405 [NASA ADS] [CrossRef]
- Deupree, R. G. 1984a, ApJ, 282, 274 [NASA ADS] [CrossRef]
- Deupree, R. G. 1984b, ApJ, 287, 268 [NASA ADS] [CrossRef]
- Deupree, R. G. 1996, ApJ, 471, 377 [NASA ADS] [CrossRef]
- Deupree, R. G., & Cole, P. W. 1983, ApJ, 269, 676 [NASA ADS] [CrossRef]
- Edwards, A. C. 1969, MNRAS, 146, 445 [NASA ADS]
- Fernando, H. 1991, Ann. Rev. Fluid Mech., 23, 455 [NASA ADS] [CrossRef] (In the text)
- Fornberg, B. 1977, J. Comp. Phys., 25, 1 [NASA ADS] [CrossRef]
- Fujimoto, M. Y., Iben, I. J., & Hollowell, D. 1990, ApJ, 349, 580 [NASA ADS] [CrossRef]
- Herwig, F., Freytag, B., Hueckstaedt, R. M., & Timmes, F. X. 2006, ApJ, 642, 1057 [NASA ADS] [CrossRef]
- Hollowell, D., Iben, I. J., & Fujimoto, M. Y. 1990, ApJ, 351, 245 [NASA ADS] [CrossRef]
- Hurlburt, N. E., Toomre, J., & Massaguer, J. M. 1986, ApJ, 311, 563 [NASA ADS] [CrossRef]
- Hurlburt, N. E., Toomre, J., Massaguer, J. M., & Zahn, J.-P. 1994, ApJ, 421, 245 [NASA ADS] [CrossRef]
- Izzard, R. G., Jeffery, C. S., & Lattanzio, J. 2007, A&A, 470, 661 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kercek, A., Hillebrandt, W., & Truran, J. W. 1998, A&A, 337, 379 [NASA ADS]
- Kercek, A., Hillebrandt, W., & Truran, J. W. 1999, A&A, 345, 831 [NASA ADS]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution, XVI (Berlin, Heidelberg, New York: Springer-Verlag), 468, also Astronomy and Astrophysics Library (In the text)
- Kiraga, M., Zahn, J.-P., Stepien , K., et al. 1999, in Stellar Structure: Theory and Test of Connective Energy Transport, ed. A. Gimenez, E. F. Guinan, & B. Montesinos, ASP Conf. Ser., 173, 269 (In the text)
- Kuhlen, M., Woosley, W. E., & Glatzmaier, G. A. 2003, in 3D Stellar Evolution, ed. S. Turcotte, S. C. Keller, & R. M. Cavallo, ASP Conf. Ser., 293, 147 (In the text)
- Lattanzio, J., Dearborn, D., Eggleton, P., & Dossa, D. 2006 [arXiv:astro-ph/0612147]
- McWilliams, J. 1984, J. Fluid. Mech., 146, 21 [NASA ADS] [CrossRef]
- Meakin, C. A., & Arnett, D. 2006, ApJ, 637, L53 [NASA ADS] [CrossRef]
- Meakin, C. A., & Arnett, D. 2007a, ApJ, 665, 690 [NASA ADS] [CrossRef] (In the text)
- Meakin, C. A., & Arnett, D. 2007b, ApJ, 667, 448 [NASA ADS] [CrossRef]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2008, A&A, 490, 265 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Montalbán, J., D'Antona, F., Kupka, F., & Heiter, U. 2004, A&A, 416, 1081 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Muthsam, H. J., Goeb, W., Kupka, F., Liebich, W., & Zoechling, J. 1995, A&A, 293, 127 [NASA ADS] (In the text)
- Nordlund, A., & Dravins, D. 1990, A&A, 228, 155 [NASA ADS] (In the text)
- Plewa, T., & Müller, E. 1999, A&A, 342, 179 [NASA ADS] (In the text)
- Porter, D. H., & Woodward, P. R. 1994, ApJS, 93, 309 [NASA ADS] [CrossRef]
- Press, W. H., Tukolsky, S. A., Vetterling, W. T., & Flannery, F. B. 1992, in Numerical Recipes in FORTRAN, The Art of Scientific Computing, Second Edition (Cambridge: Cambridge University Press), 1
- Rast, M. P., Nordlund, A., Stein, R. F., & Toomre, J. 1993, ApJ, 408, L53 [NASA ADS] [CrossRef]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] (In the text)
- Schlattl, H., Cassisi, S., Salaris, M., & Weiss, A. 2001, ApJ, 559, 1082 [NASA ADS] [CrossRef]
- Schneider, T., Botta, N., Geratz, K. J., & Klein, R. 1999, J. Comp. Phys., 155, 248 [NASA ADS] [CrossRef]
- Singh, H. P., Roxburgh, I. W., & Chan, K. L. 1995, A&A, 295, 703 [NASA ADS]
- Singh, H. P., Roxburgh, I. W., & Chan, K. L. 1998, A&A, 340, 178 [NASA ADS]
- Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] (In the text)
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] (In the text)
- Turkel, E. 1999, Ann. Rev. Fluid Mech., 31, 385 [NASA ADS] [CrossRef]
- Villere, K. R. 1976, Ph.D. Thesis, AA, California Univ., Santa Cruz
- Weiss, A., & Schlattl, H. 2000, A&AS, 144, 487 [NASA ADS] [CrossRef] [EDP Sciences]
- Weiss, A., & Schlattl, H. 2007, Ap&SS, 341
- Weiss, A., Schlattl, H., Salaris, M., & Cassisi, S. 2004a, A&A, 422, 217 [NASA ADS] [CrossRef] [EDP Sciences]
- Weiss, A., Hillebrandt, W., Thomas, H.-C., & Ritter. 2004b, Cox and Giuli's Principles of Stellar Structure (Gardners Books)
- Wickett, A. J. 1977, in Problems of Stellar Convection, ed. E. A. Spiegel, & J.-P. Zahn, Lecture Notes in Physics (Berlin: Springer Verlag), 71, 284
- Woodward, P., Herwig, F., Porter, D., et al. 2008, in First Stars III, AIP Conf. Ser., 990, 300 (In the text)
- Zahn, J.-P. 1991, A&A, 252, 179 [NASA ADS]
- Zimmermann, R. 1970, Ph.D. Thesis, University of California at Los Angeles
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- We simulated another 3D model at lower resolution than model hefl.3d (using a wedge of 90
 80
80  80 zones centered at the equator with
80 zones centered at the equator with
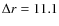
 106 cm and
106 cm and
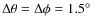 ), but we do not discuss this model here any further, because of its larger numerical viscosity and its almost 50% smaller convective velocities.
), but we do not discuss this model here any further, because of its larger numerical viscosity and its almost 50% smaller convective velocities.
- ... zone
![[*]](/icons/foot_motif.png)
- Extension of the convection zone in radius r is according to the Schwarzschild criterion: 4.72
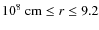
 108 cm.
108 cm.
- ... edge
![[*]](/icons/foot_motif.png)
- Inner and outer edge of the convection zone is located
at r = 4.72
 108 cm and r = 9.2
108 cm and r = 9.2  108 cm, respectively.
108 cm, respectively.
- ... otherwise
![[*]](/icons/foot_motif.png)
- The Brunt-Väisälä frequency is related to the bulk Richardson number known from oceanography, which is a more direct measure of the stability of the edges of a convection zone in the presence of a turbulent flow (Meakin & Arnett 2007b).
- ... obtains
![[*]](/icons/foot_motif.png)
- Note that the equations given in Mocák et al. (2008) that correspond to Eqs. (B.2), (B.6) and (B.8) contain some small typographical errors.
All Tables
Table 1: Some properties of the initial model.
Table 2:
Some properties of the two and three-dimensional simulations: number of grid points in r (Nr), ![]() (
(
![]() )
and,
)
and, ![]() (
(![]() ) direction, spatial resolution in r (
) direction, spatial resolution in r (![]() in 106 cm),
in 106 cm), ![]() (
(
![]() ), and
), and ![]() (
(
![]() ) direction, characteristic velocity
) direction, characteristic velocity ![]() (in 10
(in 10
![]() )
of the flow, expansion
velocity at temperature maximum
)
of the flow, expansion
velocity at temperature maximum
![]() (in
(in
![]() ), typical convective turnover timescale
), typical convective turnover timescale
![]() (in s) and maximum evolutionary time
(in s) and maximum evolutionary time
![]() (in s), respectively.
(in s), respectively.
Table 3: Root mean square fluctuation amplitudes within the convection zone.
Table 4: Root mean square fluctuation amplitudes at the edges of the convection zone (see Table 3).
Table 5:
Rate of change of the mean mass fractions of 4He, 12C, and 16O in the 2D model hefl.2d.b within the first 40 000 s (Ri; in units of
![]() ), and within the time interval
), and within the time interval
![]() (Rf; in units of
(Rf; in units of
![]() )
with the initial Xi and final Xf mass fractions (in units of 10-3), respectively.
)
with the initial Xi and final Xf mass fractions (in units of 10-3), respectively.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg21.eps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{1414fg22.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg66.png) |
Figure 1:
Left panel: temperature (in units of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg41.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg101.png) |
Figure 2:
Temporal evolution of the total nuclear energy production rate E of models hefl.3d (solid) and hefl.2d.a (dotted), respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg42.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg102.png) |
Figure 3:
Temporal evolution of the total kinetic energy |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1414fg43.eps}\par\includegraphics[width=8.5cm,clip]{1414fg44.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg105.png) |
Figure 4:
Temporal evolution of a log10 of the angular averaged kinetic energy density (in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{1414f45a.eps}\hspace*{0.5c...
...ps}\hspace*{1.5cm}
\includegraphics[width=7.9cm,clip]{1414f45e.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg115.png) |
Figure 5:
Upper panels: snapshots taken at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{1414f46a.eps}\hspace*{0.2c...
...s}\hspace*{0.2cm}
\includegraphics[width=5.9cm,clip]{1414f46i.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg118.png) |
Figure 6:
Cuts through the 3D model hefl.3d at t = 4815 s showing the angular variation of temperature (in units of 108 K; left panels), 12C mass fraction (in units of 10-3; middle panels), and radial velocity (in units of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg47.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg123.png) |
Figure 7:
Auto-correlation function
A1(r0;r) measuring the radial extent of flow patterns (see Eq. (1)) at different radii r0 (4.8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg48.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg124.png) |
Figure 8:
Auto-correlation function
A2(r0;t-t0) measuring the lifetime of flow patterns (see Eq. (2)) at two different epochs for the 3D model hefl.3d (solid:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1414f49a.eps}\vspace*{5mm}...
....eps}\vspace*{5mm}
\includegraphics[width=7.4cm,clip]{1414f49c.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg126.png) |
Figure 9:
Carbon mass fraction X(12C) ( top), entropy S ( middle),
and entropy gradient |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414f410.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg128.png) |
Figure 10: Square of the Brunt-Väisälä buoyancy frequency as a function of radius for the 3D model hefl.3d at t = 4638 s. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm,clip]{1414iso1.eps}\includ...
...ps}\hspace{2.5cm}
\includegraphics[width=6cm,clip]{1414iso4.eps} }\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg131.png) |
Figure 11:
Different views of isosurfaces of the velocity field for the 3D model hefl.3d at t = 3000 s. The blue isosurface corresponds to radial downflows with
vr = -6 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm]{1414flx1.eps}\includegrap...
...=8.8cm]{1414flx3.eps}\includegraphics[width=8.8cm]{1414flx4.eps} }\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg135.png) |
Figure 12:
Various energy fluxes and source terms as a function of radius averaged (from 2000 s to 6000 s) over about four convective turnover timescales. Panel a) shows the convective flux |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414ve2d.eps}\hspace*{1cm}
\includegraphics[width=8cm,clip]{1414ve3d.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg136.png) |
Figure 13:
Radial distributions of the time (from 2000 s to 4000 s) and angle-averaged velocity components (vr, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414f414.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg144.png) |
Figure 14: Radial distributions of the time (from 2800 s to 4800 s) and angle-averaged density fluctuations in the 3D model hefl.3d (solid red line). The panels also show the angular variation of the respective quantity at a given radius (gray shaded region). The dotted vertical lines mark the edges of the convection zone as determined by the Schwarzschild criterion. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414f415.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg145.png) |
Figure 15:
Fractional volume occupied by upflow streams
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1414adg1.eps}\vspace*{0.5cm}
\includegraphics[width=7.8cm,clip]{1414adg2.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg146.png) |
Figure 16:
Upper panel: radial distributions of the adiabatic temperature
gradient
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{1414vl1.eps}\hspace*{5mm}
...
...s}\hspace*{5mm}
\includegraphics[width=5.7cm,clip]{1414vl3.eps}
\par\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg151.png) |
Figure 17:
Snapshots of the spatial distribution of the velocity modulus |v| (in units of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1414fg62.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg158.png) |
Figure 18:
Temporal evolution of the horizontally averaged temperature maximum
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{1414f63a.eps}\includegrap...
...8.5cm]{1414f63c.eps}\includegraphics[width=8.5cm]{1414f63d.eps} }\end{figure}](/articles/aa/full_html/2009/26/aa11414-08/Timg161.png) |
Figure 19:
Upper panels: angular averaged 12C mass fraction as a function of radius near the inner ( left) and outer edge ( right) of the convection zone in the long-term 2D model hefl.2d.b at
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.