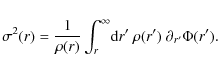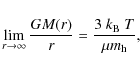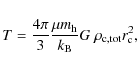| Issue |
A&A
Volume 501, Number 1, July I 2009
|
|
|---|---|---|
| Page(s) | 189 - 206 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200911734 | |
| Published online | 05 May 2009 | |
The dynamical and chemical evolution of dwarf spheroidal galaxies![[*]](/icons/foot_motif.png)
Y. Revaz1 - P. Jablonka1,2 - T. Sawala3 - V. Hill4 - B. Letarte5 - M. Irwin6 - G. Battaglia7 - A. Helmi8 - M. D. Shetrone9 - E. Tolstoy8 - K. A. Venn10
1 - Laboratoire d'Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), 1290 Sauverny, Switzerland
2 -
University of Geneva, Observatory, 1290 Sauverny, Switzerland; on leave from CNRS, UMR 8111
3 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei München, Germany
4 -
Observatoire de la Côte d'Azur, CNRS UMR 6202, BP 4229, 06304 Nice Cedex 4, France
5 -
California Institute of Technology, MC105-24, Pasadena, CA 91125, USA
6 -
Institute of Astronomy, Madingley Road, Cambridge CB03 0HA, UK
7 -
European Southern Observatory, Karl-Schwarzschild-Straße 1, 85748 Garching bei München, Germany
8 -
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
9 -
McDonald Observatory, University of Texas, Fort Davis, TX 79734, USA
10 -
Department of Physics & Astronomy, University of Victoria, Elliott Building, 3800 Finnerty Road, Victoria, BC, V8P 5C2, Canada
Received 27 January 2009 / Accepted 17 April 2009
Abstract
Context. We present a large sample of fully self-consistent hydrodynamical Nbody/Tree-SPH simulations of isolated dwarf spheroidal galaxies (dSphs). It has enabled us to identify the key physical parameters and mechanisms at the origin of the observed variety in the Local Group dSph properties. The initial total mass (gas + dark matter) of these galaxies is the main driver of their evolution. Star formation (SF) occurs in series of short bursts. In massive systems, the very short intervals between the SF peaks mimic a continuous star formation rate, while less massive systems exhibit well separated SF bursts, as identified observationally. The delay between the SF events is controlled by the gas cooling time dependence on galaxy mass. The observed global scaling relations, luminosity-mass and luminosity-metallicity, are reproduced with low scatter. We take advantage of the unprecedentedly large sample size and data homogeneity of the ESO Large Programme DART, and add to it a few independent studies, to constrain the star formation history of five Milky Way dSphs, Sextans, LeoII, Carina, Sculptor and Fornax. For the first time, [Mg/Fe] vs. [Fe/H] diagrams derived from high-resolution spectroscopy of hundreds of individual stars are confronted with model predictions. We find that the diversity in dSph properties may well result from intrinsic evolution. We note, however, that the presence of gas in the final state of our simulations, of the order of what is observed in dwarf irregulars, calls for removal by external processes.
Key words: galaxies: dwarf - galaxies: evolution - galaxies: formation
1 Introduction
Understanding the dominant physical processes at the origin of the dynamical and chemical properties of dwarf spheroidal galaxies (dSphs) is challenging. The binding energy of the interstellar medium of these low mass systems, at the faint end of the galaxy luminosity function, is weak. The injection of energy, due to violent explosions of supernovae (Mori et al. 2002,1997; Hensler et al. 2004; Mac Low & Ferrara 1999; Ricotti & Gnedin 2005; Dekel & Silk 1986; Murakami & Babul 1999; Kawata et al. 2006), or the cosmic UV background during reionization (Efstathiou 1992; Bullock et al. 2000; Mayer et al. 2006; Barkana & Loeb 1999) may leave dSphs totally devoid of gas and consequently quench their star formation. In this picture, the majority of the dSphs are fossils of the reionization epoch and are characterized by an old stellar population (Ricotti & Gnedin 2005).
However, observations offer evidence for more complex star formation
histories and reveal a clear variety of dwarf galactic systems
(Mateo 1998; Dolphin 2002). The spread in stellar chemical
abundances, and in particular the low [![]() /Fe] values compared to
Galactic halo stars at equal metallicity, are hardly compatible with an
early termination of star formation at the epoch of reionization
(e.g., Geisler et al. 2005; Shetrone et al. 2001; Koch et al. 2008; Tolstoy et al. 2003; Shetrone et al. 1998,2003; Harbeck et al. 2001, examples taken in relation to the galaxies studied in
this work). Whilst
some dSphs are indeed consistent with rather short star formation
episodes, such as Sextans (Lee et al. 2003) or Sculptor
(Babusiaux et al. 2005), others are characterized by much more extended
periods, like Carina
(Smecker-Hane et al. 1996; Hurley-Keller et al. 1998) or Fornax (Coleman & de Jong 2008).
/Fe] values compared to
Galactic halo stars at equal metallicity, are hardly compatible with an
early termination of star formation at the epoch of reionization
(e.g., Geisler et al. 2005; Shetrone et al. 2001; Koch et al. 2008; Tolstoy et al. 2003; Shetrone et al. 1998,2003; Harbeck et al. 2001, examples taken in relation to the galaxies studied in
this work). Whilst
some dSphs are indeed consistent with rather short star formation
episodes, such as Sextans (Lee et al. 2003) or Sculptor
(Babusiaux et al. 2005), others are characterized by much more extended
periods, like Carina
(Smecker-Hane et al. 1996; Hurley-Keller et al. 1998) or Fornax (Coleman & de Jong 2008).
Long durations of the star formation were early advocated by purely chemical evolution models constrained by the dwarf metallicity distributions and color-magnitude diagrams (Lanfranchi & Matteucci 2004; Ikuta & Arimoto 2002). Subsequent simulations of dwarf galaxies introduced the role of the dark matter coupled to the stellar feedback (Ferrara & Tolstoy 2000), and later the full dynamical physics of the gas and dark matter, by means of N-Body+SPH treatment (Carraro et al. 2001). Along this line, Marcolini et al. (2008,2006) concluded that a prolonged (compared to instantaneous) star formation requires an external cause for gas removal, which cannot be due to galactic winds. Intermittent episodes of star formation were at the focal point of the analysis by Stinson et al. (2007). They naturally arose from the alternation between feedback and cooling of the systems. Valcke et al. (2008) confirmed their self-regulated form. These authors also found a gradual shift of the star formation towards the inner galactic regions. Kawata et al. (2006) had looked for evidence of spatial variation as well, in the form of metallicity gradients, but had to stop their simulations at redshift 1. Likewise, considering a cosmological box as initial conditions instead of individual halos, Read et al. (2006) stopped their simulations early, and focused on the smallest and most metal-poor dwarf galaxies.
In all these works, gas remains at the end of the dSph evolutions. The resolution of this problem constitutes a challenge. Mayer et al. (2006) performed simulations of gas-rich dwarf galaxy satellites orbiting within a Milky Way-sized halo and studied the combined effects of tides and ram pressure. They showed that while tidal stirring produces objects whose stellar structure and kinematics resemble that of dSphs, ram-pressure stripping is needed to entirely remove their gas. Salvadori et al. (2008) proposed a semi-analytical treatment in a hierarchical galaxy formation framework and achieved the smallest final gas fraction.
Despite real limitations, such as scarce comparisons with observations, incomplete time-evolution, or ad hoc parameterizations, we are witnessing a rapid convergence toward understanding the formation and evolution of dSphs. A critical step forward must be undertaken with a large set of simulations to be confronted with an equally broad sample of data. In particular, the chemical imprints resulting from different hypotheses have not yet been fully capitalized on.
The VLT/FLAMES instrument, with fiber links to the GIRAFFE and UVES spectrographs, has enabled a revolution in spectroscopic studies of resolved stellar populations in nearby galaxies. It is now possible to measure the abundances of a wealth of chemical elements for more than 100 stars at once. Our ESO-Large Programme DART (Dwarf Abundances and Radial velocity Team) is dedicated to the measure of abundances and velocities for several hundred individual stars in a sample of three nearby dSph galaxies: Sculptor, Fornax, and Sextans. We have used the VLT/FLAMES facility in the low resolution mode to obtain CaII triplet metallicity estimates, as well as accurate radial velocities out to the galaxies' tidal radii (Battaglia et al. 2008b,2006; Helmi et al. 2006; Battaglia et al. 2008a; Tolstoy et al. 2004). Each of the three galaxies has also been observed at high resolution for about 80 stars in their central regions, to obtain detailed abundances for a range of interesting elements such as Mg, Ca, O, Ti, Na, Eu (Letarte et al. 2007; Venn & Hill 2005, Hill et al in preparation; Letarte et al. in preparation).
In the following, we take advantage of the statistically significant
DART sample and data homogeneity, and include some recent independent
studies, to constrain the star formation history of five Milky Way
dSphs, Sextans, LeoII, Carina, Sculptor, and Fornax. For the first
time, populated [![]() /Fe] vs. [Fe/H] diagrams can be confronted
with model predictions. Our first goal is to establish how well one
can reproduce the apparent diversity of dSph star formation histories
in a common scheme. We choose to model galaxies in isolation, as this
is the only way to control the effect of all parameters at play, and
to understand the dominant physical processes. We will try to see if
a complex star formation history may result from intrinsic evolution
or if external processes are necessary. We have performed an
unprecedentedly large number of simulations. Not only do they account
for the gravity of the dark matter and baryons, but they also contain
a large number of additional physical mechanisms: metal-dependent gas
cooling above and below
/Fe] vs. [Fe/H] diagrams can be confronted
with model predictions. Our first goal is to establish how well one
can reproduce the apparent diversity of dSph star formation histories
in a common scheme. We choose to model galaxies in isolation, as this
is the only way to control the effect of all parameters at play, and
to understand the dominant physical processes. We will try to see if
a complex star formation history may result from intrinsic evolution
or if external processes are necessary. We have performed an
unprecedentedly large number of simulations. Not only do they account
for the gravity of the dark matter and baryons, but they also contain
a large number of additional physical mechanisms: metal-dependent gas
cooling above and below
![]() ,
star formation, SNIa and SNII
energy feedback and chemical evolution. We focus on the luminosity,
star formation history and metallicity properties of dSphs, rather
than on their dynamical properties, which turn out to be less
constraining.
,
star formation, SNIa and SNII
energy feedback and chemical evolution. We focus on the luminosity,
star formation history and metallicity properties of dSphs, rather
than on their dynamical properties, which turn out to be less
constraining.
The paper is organized as follows: the code and the implementation of physical processes are described in Sect. 2. The initial conditions are detailed in Sect. 3. The presentation of the results is split in three parts: Sect. 4 focuses on the global evolution of the galaxies and discusses the main driving parameters, while Sect. 5 is devoted to the scaling relations. The detailed analysis of the chemical properties of Sextans, Leo II, Carina, Sculptor, and Fornax are treated in Sect. 6. Section 7 offers a physical interpretation of the results. Section 8 summarizes our work.
2 The code
We have adapted the code treeAsph originally developed by Serna et al. (1996), with further developments presented in Alimi et al. (2003). The chemical evolution was introduced by Poirier et al. (2003, Poirier, Ph.D. Thesis) and Poirier et al. (2002). For the sake of simplicity, we recall below the main features and the general philosophy of the algorithms.
2.1 Dynamics
All gravitational forces are computed under the tree algorithm
proposed by Barnes & Hut (1986) (see also Hernquist 1987). This
technique is based on a hierarchical subdivision of space into cubic
cells. One approximates the forces due to a cluster of particles
contained in a cubic cell and acting on a particle i by a
quadrupolar expansion of the cluster gravitational potential. This is
done under the condition that the size of the cubic cell is small
compared to its distance to the particle i. The ratio between size
and distance must be smaller than a tolerance parameter, ![]() ,
fixed to 0.7 in our simulations (Hernquist 1987). Indeed, under
this condition, the internal distribution of the particles within
cells can be neglected. Consequently, the number of operations needed
to compute the gravitational forces between N particles scales as
,
fixed to 0.7 in our simulations (Hernquist 1987). Indeed, under
this condition, the internal distribution of the particles within
cells can be neglected. Consequently, the number of operations needed
to compute the gravitational forces between N particles scales as
![]()
![]() ,
instead of
,
instead of ![]() N2 if one were to consider each
individual pair of particles.
N2 if one were to consider each
individual pair of particles.
The hydrodynamics of the gas is followed in the Lagrangian Smooth Particle Hydrodynamics (SPH) scheme. Its allows to describe an arbitrarily shaped continuous medium with a finite number of particles (Lucy 1977; Gingold & Monaghan 1977), see Monaghan (1992) and Price (2005) for reviews. Each gas particle has its mass spatially smeared out by a smoothing kernel W (here a spline function).
Unlike the gravitational forces, which are determined from the interactions with all other particles in the system, the hydrodynamical forces result from the contributions of a modest number of neighbors. The spatial resolution is determined by the smoothing length hi associated with the particle i, computed through the requirement that a sphere of radius hi centered on particle icontains 32 neighbors.
The integration scheme is the symplectic leapfrog used with adaptative time-steps.
2.2 Cooling
At temperatures lower than
![]() ,
cooling in primordial gas
is dominated by the molecule
,
cooling in primordial gas
is dominated by the molecule ![]() .
Galli & Palla (1998) have shown that
the cooling efficiency of
.
Galli & Palla (1998) have shown that
the cooling efficiency of ![]() is determined by its mass fraction
is determined by its mass fraction
![]() .
Unfortunately, an accurate computation of
.
Unfortunately, an accurate computation of
![]() is difficult and requires to take into account the complex processes
of the formation and destruction of
is difficult and requires to take into account the complex processes
of the formation and destruction of ![]() .
Following Maio et al. (2007),
we instead fix
.
Following Maio et al. (2007),
we instead fix
![]() to 10-5. Once the gas is enriched
with metals, these are important to the cooling properties. We
consider oxygen, carbon, silicon and iron (Maio et al. 2007), since they
are the most-abundant heavy atoms released during stellar evolution,
particularly by the SNe II and SNe Ia, that we follow in our
simulations. We set the density of the free electrons over that of
hydrogen, (
to 10-5. Once the gas is enriched
with metals, these are important to the cooling properties. We
consider oxygen, carbon, silicon and iron (Maio et al. 2007), since they
are the most-abundant heavy atoms released during stellar evolution,
particularly by the SNe II and SNe Ia, that we follow in our
simulations. We set the density of the free electrons over that of
hydrogen, (
![]() )
to
)
to
![]() .
.
Above
![]() ,
the cooling function is calculated following the
metallicity dependent prescription of Sutherland & Dopita (1993). The full
normalized cooling function is shown in Fig. 1, for
a large range of metallicities.
,
the cooling function is calculated following the
metallicity dependent prescription of Sutherland & Dopita (1993). The full
normalized cooling function is shown in Fig. 1, for
a large range of metallicities.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=0]{11734Fig01.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg35.png) |
Figure 1: Normalized cooling function as a function of temperature and metallicity. |
| Open with DEXTER | |
A more detailed modeling of the gas cooling is not necessary, as long as simulations are limited in spatial resolution. Indeed, the cooling of the gas is directly dependent on its density. Therefore, a limited resolution smoothes the density fluctuations of the interstellar medium.
2.3 Chemical evolution and stellar feedback
The chemical enrichment of the interstellar medium (ISM) depends on the interplay between different physical processes. It requires us to follow the rate at which stars form, the amount of newly synthesized chemical elements, the mass and energy released during the different stellar phases, and, finally, the mixing of the metal-enriched stellar outflows with the ISM. The computation of this cycle is done by implementing the original equations of chemical evolution formalized by Tinsley (1980), as closely as possible.
2.4 Star formation
We adopt the now classical recipe of Katz (1992) and
Katz et al. (1996). A gas particle becomes eligible for star formation if
it is i) collapsing (negative velocity divergence); and ii)
its density is higher than a threshold of
![]() .
However, we do not require the dynamical time
to be shorter than the sound crossing time (Jeans instability).
.
However, we do not require the dynamical time
to be shorter than the sound crossing time (Jeans instability).
The gas particles, which satisfy the above criteria, form stars
at a rate expressed by:
which mimics a Schmidt law (Schmidt 1959).
For a given time interval ![]() ,
a gas particle of mass
,
a gas particle of mass
![]() has a probability
has a probability ![]() to form a stellar particle
of mass
to form a stellar particle
of mass ![]() ,
where
,
where ![]() is defined by:
is defined by:
The new stellar particle is initially assigned the position and velocity of its gas progenitor. Subsequently, gas and stellar velocities are modified in order to conserve both energy and momentum.
Each stellar particle represent a cluster of stars, sharing the same
age and metallicity, whose initial mass function (IMF) ![]() is
described by a Salpeter law (Salpeter 1955):
is
described by a Salpeter law (Salpeter 1955):
![\begin{displaymath}\Phi(m) = \left[ \frac{x+1}{ m_u^{x+1} - m_l^{x+1}} \right] m^x,
\end{displaymath}](/articles/aa/full_html/2009/25/aa11734-09/img45.png) |
(3) |
with x=-1.35,
2.5 Ejecta
We neglect stellar winds, since they contribute little to the evolution of the chemical elements that we consider (magnesium and iron), and because the injection power to the ISM is dominated by SN explosions (Leitherer et al. 1992).
The amount of energy, mass and metals ejected by a stellar particle
during a time interval ![]() is calculated by considering the mass
of stars exploding between t and
is calculated by considering the mass
of stars exploding between t and
![]() .
The dependency of
the stellar lifetimes on metallicity is taken into account following
Kodama & Arimoto (1997, private communication).
.
The dependency of
the stellar lifetimes on metallicity is taken into account following
Kodama & Arimoto (1997, private communication).
Hence, the feedback energy released by a stellar particle in the time
interval
![]() is:
is:
| (4) |
where
With
![]() and
and
![]() being the lowest and highest masses
of stars exploding as SNe II, and m(t) being the mass of stars with
lifetime t, we can express
being the lowest and highest masses
of stars exploding as SNe II, and m(t) being the mass of stars with
lifetime t, we can express
![]() as:
as:
![\begin{displaymath}n_{\rm {II}}(t) = \int_{\max[m(t+\Delta t),m_{\rm {II},l}]}^{\min[m(t),m_{\rm {II},u}]}\frac{\Phi(m)}{m}~{\rm d}m.
\end{displaymath}](/articles/aa/full_html/2009/25/aa11734-09/img59.png) |
(5) |
To calculate
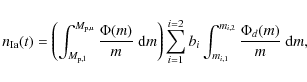 |
(6) |
with
The supernova feedback energy is released in the form of thermal energy only at the
end of each dynamical time-step. This procedure avoids the thermal energy
to be dissipated instantaneously by the strong cooling above
![]() ,
and mimics the blast wave shocks of supernovae (Stinson et al. 2006).
,
and mimics the blast wave shocks of supernovae (Stinson et al. 2006).
The ejected gas mass fraction due to SNe Ia is given by:
| (7) |
with
The mass of each chemical element k ejected by a stellar particle is:
| (8) |
where:
| |
= | ![$\displaystyle \int^{m(t)}_{\max[m(t+\Delta t),m_{\rm {II},l}]} p_{k,\rm {II}}(m) ~ \Phi(m)~{\rm d}m$](/articles/aa/full_html/2009/25/aa11734-09/img72.png) |
(9) |
![$\displaystyle + z_{k} \int^{m(t)}_{\max[m(t+\Delta t),m_{\rm {II},l}]} \left( 1- \omega(m) - p_{k,\rm {II}}(m) \right)~ \Phi(m)~{\rm d}m$](/articles/aa/full_html/2009/25/aa11734-09/img73.png) |
and
| (10) |
Since the stellar particles correspond to star clusters, we use the single stellar population mass-to-light ratios of Maraston (1998,2005) to calculate their luminosities in V-band. The effects of metallicity and age are taken into account.
3 Initial conditions
3.1 Mass distribution
We consider dSphs in isolation. Gas and dark matter are
initially represented by pseudo-isothermal spheres:
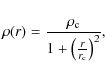 |
(11) |
where r is the radius,
As the the total mass inside a radius
![]() is linearly
dependent on the central density, there is a proportionality relation
between the fraction of baryonic matter,
is linearly
dependent on the central density, there is a proportionality relation
between the fraction of baryonic matter,
![]() ,
and the central
densities:
,
and the central
densities:
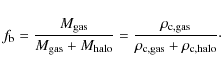 |
(12) |
In the following, we will use
| |
= | ||
| = | (13) |
Similarly to the gas, the dark matter halo evolves under the laws of gravity.
We consider a core in the initial dark model profile. Whilst cosmological simulations predict the formation of cuspy dark halos (Navarro et al. 1997; Springel et al. 2008; Moore et al. 1998; Fukushige & Makino 1997, and the references therein), our choice is motivated by observational evidences found in normal, low brightness and dwarf galaxies (Swaters et al. 2003; de Blok & Bosma 2002; de Blok et al. 2008; Gentile et al. 2005; Blais-Ouellette et al. 2001; de Blok 2005; Spano et al. 2008; Spekkens et al. 2005; Gentile et al. 2004). Measuring the inner slope of the dSph profiles is very challenging, nevertheless, Battaglia et al. (2008a) show that the observed velocity dispersion profiles of the Sculptor dSph are best fitted by a cored dark matter halo.
3.2 Velocities and temperature
The initial velocities are obtained by assuming
equilibrium, free of any rotation. For a spherical distribution, we
can assume that the velocity dispersion is isotropic. It can be
derived from the the second moment of the Jeans equation
(Binney & Tremaine 1987; Hernquist 1993). In spherical coordinates, one writes:
The halo velocities are randomly generated in order to fit the velocity dispersion
The temperature T of the gas is deduced from the virial equation:
leading, for a pseudo-isothermal sphere, to:
where
3.3 Initial parameters
All simulations start with an initial radius of
![]() ,
distance at which the gas and dark matter densities are
about 1/1000 of the central ones. We consider two different core
radii,
,
distance at which the gas and dark matter densities are
about 1/1000 of the central ones. We consider two different core
radii,
![]() ,
of 0.5 and 1 kpc. The choice of the central
total density
,
of 0.5 and 1 kpc. The choice of the central
total density
![]() (dark matter + gas) uniquely
determines the initial total mass of the system, Mi, which we vary
over a range of
(dark matter + gas) uniquely
determines the initial total mass of the system, Mi, which we vary
over a range of
![]() to
to
![]() .
We
investigate the effect of the initial baryonic mass fraction,
.
We
investigate the effect of the initial baryonic mass fraction,
![]() ,
by varying it from 0.1 to 0.2. Indeed, this helps in
disentangling the influence of the total gravitational potential from
that of the gas mass. The masses of the gas and halo particles remain
constant at
,
by varying it from 0.1 to 0.2. Indeed, this helps in
disentangling the influence of the total gravitational potential from
that of the gas mass. The masses of the gas and halo particles remain
constant at
![]() and
and
![]() ,
respectively. The corresponding gravitational
softening lengths are 0.1 and
,
respectively. The corresponding gravitational
softening lengths are 0.1 and
![]() .
As a consequence,
the simulations start with 4000 to 20 000 particles. The
variation in number of particles is therefore at most a factor 5,
hence a factor of 1.7 in spatial resolution, which justifies the
choice of fixed softening lengths. The star formation
parameter
.
As a consequence,
the simulations start with 4000 to 20 000 particles. The
variation in number of particles is therefore at most a factor 5,
hence a factor of 1.7 in spatial resolution, which justifies the
choice of fixed softening lengths. The star formation
parameter ![]() is varied from 0.01 to 0.3. The initial mass of the
stellar particles is
is varied from 0.01 to 0.3. The initial mass of the
stellar particles is
![]() ,
corresponding to about one
tenth of the initial mass of the gas particles.
,
corresponding to about one
tenth of the initial mass of the gas particles.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig02.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg106.png) |
Figure 2:
Time evolution of the star formation rate, |
| Open with DEXTER | |
4 Models
We performed 166 simulations to understand the role of each
parameter at play, and to identify a series of generic models
reproducing the observations. The complete list of the simulations is
given in Tables A.1. The models have been run for
![]() .
.
4.1 Modes
As mentioned in Sect. 3, the initial sphere of DM+gas is
in equilibrium under adiabatic conditions. At the onset of the
simulations, the energy loss due to cooling causes the gas to sinks in
the potential well and contract. The total potential is deepen not
only due to the central increase in gas density, but also as a
consequence of the halo adiabatic contraction. Despite the large
increase in density, the gas temperature is kept nearly constant due
to the strong hydrogen recombination cooling above
![]() (see
Fig. 1). Therefore, the gravitational energy
recovered from the deepening of the potential well is dissipated
nearly instantaneously. For densities above
(see
Fig. 1). Therefore, the gravitational energy
recovered from the deepening of the potential well is dissipated
nearly instantaneously. For densities above
![]() ,
the
evolution of the model depends on supernova heating, directly linked
to the star formation rate.
,
the
evolution of the model depends on supernova heating, directly linked
to the star formation rate.
Besides this general description common to all simulations, we
identify three different major regimes. We refer to them as ``full gas
consumption'', ``outflow'' and ``self-regulation''.
For each of them, Fig. 2 presents the evolution with time
of the star formation rate (SFR), the central gas density, the central
gravitational potential and the mass of the gas within
![]() from the
galaxy center.
from the
galaxy center.
4.1.1 Full gas consumption
In cases where ![]() is low for a given
is low for a given
![]() ,
the energy
released by the supernova explosions is unable to counterbalance the
radiative cooling. As a consequence, the gas keeps on sinking in the
galaxy inner regions and reaches very high densities. Stars are
formed continuously and at high rate. The model #647
(
,
the energy
released by the supernova explosions is unable to counterbalance the
radiative cooling. As a consequence, the gas keeps on sinking in the
galaxy inner regions and reaches very high densities. Stars are
formed continuously and at high rate. The model #647
(
![]() and
and
![]() )
in
Fig. 2 provides a clear example of this regime: steep
rise in star formation rate and central gas density. The chemical
enrichment of the resulting systems is rapid, and their metallicities
quickly exceed the highest ones measured in dSphs. These models were
not investigated further.
)
in
Fig. 2 provides a clear example of this regime: steep
rise in star formation rate and central gas density. The chemical
enrichment of the resulting systems is rapid, and their metallicities
quickly exceed the highest ones measured in dSphs. These models were
not investigated further.
4.1.2 Outflow
Stars can be formed at slightly lower densities by
increasing ![]() at a given initial mass, or by decreasing the initial mass
at fixed
at a given initial mass, or by decreasing the initial mass
at fixed ![]() .
This is sufficient to stop the drastic
accumulation of gas at the center. Nevertheless, the gas density is
still high, and star formation is very efficient. When SNe explode, a
huge amount of energy is deposited in the gas, which in turn is
expelled from the galaxie's central regions. In parallel, the central
potential increases (it is negative), primarily due to the ejection of
the the gas, but also due to the ensuing DM halo expansion. The final
consequence is a strong outflow.
A large fraction of the total gas mass is ejected beyond a radius of
.
This is sufficient to stop the drastic
accumulation of gas at the center. Nevertheless, the gas density is
still high, and star formation is very efficient. When SNe explode, a
huge amount of energy is deposited in the gas, which in turn is
expelled from the galaxie's central regions. In parallel, the central
potential increases (it is negative), primarily due to the ejection of
the the gas, but also due to the ensuing DM halo expansion. The final
consequence is a strong outflow.
A large fraction of the total gas mass is ejected beyond a radius of
![]() ,
chosen
to be large enough compared to the stellar extent of the systems.
For clarity, we illustrate this
regime with M#519 in Fig. 2, in which the outflow occurs
early in the galaxy evolution: after
,
chosen
to be large enough compared to the stellar extent of the systems.
For clarity, we illustrate this
regime with M#519 in Fig. 2, in which the outflow occurs
early in the galaxy evolution: after ![]()
![]() ,
there is
virtually no gas left.
,
there is
virtually no gas left.
4.1.3 Self-regulation
Dwarf galaxies are formed in a regime of self-regulation, characterized by successive periods of cooling and feedback. Such intermittent star formation episodes occurring spontaneously in hydrodynamical simulations have been mentioned by Stinson et al. (2007) and Valcke et al. (2008).
M#576 in Fig. 2 offers the example of an intermediate mass
self-regulated system (
![]() ).
As usual, the first contraction of the gas leads to a peak in star
formation (
).
As usual, the first contraction of the gas leads to a peak in star
formation (
![]() ). The gas expelled by the supernova
feedback is diluted at densities below
). The gas expelled by the supernova
feedback is diluted at densities below
![]() ,
and the star
formation stops. As the gas particles cool, they become eligible to
star formation again, forming a new burst. Star formation occurs at
high frequency in M#576 (periods between 100 and
,
and the star
formation stops. As the gas particles cool, they become eligible to
star formation again, forming a new burst. Star formation occurs at
high frequency in M#576 (periods between 100 and
![]() ).
It produces a flat distribution of stellar ages, mimicking a nearly
continuous star formation rate (see Fig. 3). We will
show later that the corresponding chemical signatures are also very
homogeneous.
).
It produces a flat distribution of stellar ages, mimicking a nearly
continuous star formation rate (see Fig. 3). We will
show later that the corresponding chemical signatures are also very
homogeneous.
Contrary to what has been observed by Stinson et al. (2007), the
fluctuation of the SF is not strictly periodic. However, we confirm
the influence of the total mass
![]() on the duration of the
quiescent periods (Valcke et al. 2008). Lower mass systems (
on the duration of the
quiescent periods (Valcke et al. 2008). Lower mass systems (
![]() )
are generally characterized
by star formation episodes separated by longer intervals, up to a few
Gyr. These systems exhibit inhomogeneous stellar populations.
)
are generally characterized
by star formation episodes separated by longer intervals, up to a few
Gyr. These systems exhibit inhomogeneous stellar populations.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{11734Fig03.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg116.png) |
Figure 3:
The distributions of stellar ages between 0 and
|
| Open with DEXTER | |
4.2 Driving parameters
![\begin{figure}
\par\includegraphics[width=17cm,clip]{11734Fig04.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg117.png) |
Figure 4: The effect of variation of the model initial parameters. The full sample of simulations is shown. Each circle or triangle stands for one model. The circle size is proportional to the final galaxy luminosity (see the top of the figure), while colors code the final stellar metallicity (median of the metallicity distribution function), following the scale given at the right hand side of the diagrams. Each panel encompasses simulations of identical baryonic fraction and initial core radius. The black triangles identify cases of full gas consumption. |
| Open with DEXTER | |
The description of the different regimes of star formation histories
already points out the importance of both the initial total mass,
![]() ,
and the star formation parameter,
,
and the star formation parameter, ![]() .
Figure 3 presents the stellar age histograms for models with
.
Figure 3 presents the stellar age histograms for models with
![]() and
and
![]() .
From bottom to top,
.
From bottom to top, ![]() increases by a factor 6. From left to right,
increases by a factor 6. From left to right,
![]() increases
by a factor 3. The highest mass systems are characterized by a strong
predominance of the old stellar populations. Decreasing the initial total
mass extends the period of star formation, passing
progressively from a continuous to a discrete distribution of stellar
ages. The role of
increases
by a factor 3. The highest mass systems are characterized by a strong
predominance of the old stellar populations. Decreasing the initial total
mass extends the period of star formation, passing
progressively from a continuous to a discrete distribution of stellar
ages. The role of ![]() appears secondary, distributing slightly
differently the different peaks of star formation (position
and strength).
appears secondary, distributing slightly
differently the different peaks of star formation (position
and strength).
Figure 4 summarizes the 166 simulations in a diagram
of ![]() and
and
![]() ,
for different core radii
,
for different core radii
![]() and baryonic fractions
and baryonic fractions
![]() .
Colors code the final galaxy
stellar metallicity
.
Colors code the final galaxy
stellar metallicity
![]() ,
computed as the median of the distribution,
since it best traces the position of the metallicity peaks in the
observations. The size of the circles is proportional to the final
stellar luminosity in the V-band,
,
computed as the median of the distribution,
since it best traces the position of the metallicity peaks in the
observations. The size of the circles is proportional to the final
stellar luminosity in the V-band,
![]() .
The small black triangles indicate the simulations that lead to
full gas consumption and have been stopped. As described earlier,
the latters result from a too small
.
The small black triangles indicate the simulations that lead to
full gas consumption and have been stopped. As described earlier,
the latters result from a too small ![]() .
It can be avoided, for our
purpose, by increasing
.
It can be avoided, for our
purpose, by increasing ![]() or decreasing
or decreasing
![]() .
Self-regulated systems with limited outflow are found for
smaller
.
Self-regulated systems with limited outflow are found for
smaller
![]() .
These tendencies do not dependent on
.
These tendencies do not dependent on
![]() and
and
![]() ,
which can only slightly modify the interval of mass in
which a particular regime is valid. For a given
,
which can only slightly modify the interval of mass in
which a particular regime is valid. For a given ![]() ,
,
![]() increases with
increases with
![]() and similarly, for a given
and similarly, for a given
![]() ,
,
![]() increases with
increases with ![]() .
At very low mass, however,
.
At very low mass, however,
![]() is
only weakly influenced by
is
only weakly influenced by ![]() .
On the contrary, the larger the
mass, the smaller
.
On the contrary, the larger the
mass, the smaller ![]() increase is needed to raise
increase is needed to raise
![]() .
.
The left and middle panels of Fig. 5 display the final
galaxy stellar metallicity and stellar V-luminosity, respectively,
as a function of
![]() .
The Local Group dSphs luminosities
(Grebel et al. 2003; Mateo 1998) and mean metallicities (DART) are indicated
with horizontal dotted red lines. The most outstanding result is that
changing
.
The Local Group dSphs luminosities
(Grebel et al. 2003; Mateo 1998) and mean metallicities (DART) are indicated
with horizontal dotted red lines. The most outstanding result is that
changing
![]() by a factor 4 translates to a change in
by a factor 4 translates to a change in
![]() by a factor 100.
by a factor 100.
![]() is varied by a factor
is varied by a factor ![]() 3.
By comparison, the influence of
3.
By comparison, the influence of ![]() on the galaxy properties
appears small. In any case, increasing
on the galaxy properties
appears small. In any case, increasing ![]() will also help
increasing both
will also help
increasing both
![]() and
and
![]() .
The consequence of
varying
.
The consequence of
varying
![]() is not linear. At low initial mass, a small increase in
mass is sufficient to strongly increase
is not linear. At low initial mass, a small increase in
mass is sufficient to strongly increase
![]() and
and
![]() ,
while at
larger initial mass, the relations saturate and a larger step in mass
is necessary. The mass-luminosity and metallicity-luminosity relations
will be discussed in the next section.
,
while at
larger initial mass, the relations saturate and a larger step in mass
is necessary. The mass-luminosity and metallicity-luminosity relations
will be discussed in the next section.
The right panel of Fig. 5 presents the relation between
the galaxy's mean stellar age and
![]() .
The influence
of
.
The influence
of ![]() looks more linear than previously on
looks more linear than previously on
![]() and
and
![]() .
As a matter of fact, we have seen in Fig. 3 that it
plays a role in the stellar age distribution. At a given initial mass,
.
As a matter of fact, we have seen in Fig. 3 that it
plays a role in the stellar age distribution. At a given initial mass,
![]() determines the length of the star formation periods as well
as the interval between them.
determines the length of the star formation periods as well
as the interval between them.
As a conclusion, the above analyses stress the primordial impact
of the initial total mass of the systems. Moreover, one can clearly
identify the range of possible
![]() leading to the formation
of the Local Group dSphs as we observed them today. This range is
narrow, e.g., a factor 2 centered on
leading to the formation
of the Local Group dSphs as we observed them today. This range is
narrow, e.g., a factor 2 centered on
![]() .
.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[angle=0]{11734Fig05.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg120.png) |
Figure 5:
The metallicity,
|
| Open with DEXTER | |
5 Global relations
dSph galaxies follow luminosity-mass and luminosity-metallicity relations that are considered as cornerstones to understanding their formation and evolution (Gilmore et al. 2007; Geha et al. 2008; Mateo 1998; Kirby et al. 2008; Strigari et al. 2008; Wilkinson et al. 2006).
In the following discussion, we calculate all physical quantities
(luminosities, masses, abundances) within the radius
![]() defined as the radius containing 90% of a galaxy's total
luminosity. This choice is guided by the wish to reproduce as closely
as possible the observational conditions under which these quantities
are measured. The classical dSphs (as opposed to newly discovered
faint ones) surrounding the Milky Way have tidal radii in the range
defined as the radius containing 90% of a galaxy's total
luminosity. This choice is guided by the wish to reproduce as closely
as possible the observational conditions under which these quantities
are measured. The classical dSphs (as opposed to newly discovered
faint ones) surrounding the Milky Way have tidal radii in the range
![]()
![]() to
to
![]() (Irwin & Hatzidimitriou 1995). Fixing a
constant small aperture for all dSphs would underestimate both light
and mass of the largest systems. Since dark matter does not
necessarily follow light, this would also bias the results. The
observational estimates of the dSph total masses are based on stellar
velocity dispersions measured at galactocentric radii as large as
possible, thereby directly linked to the limits of the visible matter.
Although the farthest measurements do not always reach the galaxies'
tidal radii, their location is determined by severe drops in stellar
density, ensuring that the bulk of the galaxies' light is
enclosed. Consequently, we compare our models to the masses derived at
the outermost velocity dispersion profile point
(e.g., Walker et al. 2007; Kleyna et al. 2004; Battaglia et al. 2008a). Ursa Minor is the
only exception to this rule. Its mass has been derived from its
central velocity dispersion (Mateo 1998).
(Irwin & Hatzidimitriou 1995). Fixing a
constant small aperture for all dSphs would underestimate both light
and mass of the largest systems. Since dark matter does not
necessarily follow light, this would also bias the results. The
observational estimates of the dSph total masses are based on stellar
velocity dispersions measured at galactocentric radii as large as
possible, thereby directly linked to the limits of the visible matter.
Although the farthest measurements do not always reach the galaxies'
tidal radii, their location is determined by severe drops in stellar
density, ensuring that the bulk of the galaxies' light is
enclosed. Consequently, we compare our models to the masses derived at
the outermost velocity dispersion profile point
(e.g., Walker et al. 2007; Kleyna et al. 2004; Battaglia et al. 2008a). Ursa Minor is the
only exception to this rule. Its mass has been derived from its
central velocity dispersion (Mateo 1998).
Figures 6 and 7 display the relations of the
galaxies' mass-to-light ratios
![]() and the median of the
stellar metallicity distributions
and the median of the
stellar metallicity distributions
![]() ,
together with the total
luminosity of the model galaxies.
The observations are represented in red, with squares for the Milky
Way satellites and crosses for the others. In general, the values of
,
together with the total
luminosity of the model galaxies.
The observations are represented in red, with squares for the Milky
Way satellites and crosses for the others. In general, the values of
![]() are taken from Mateo (1998) when available or from
Grebel et al. (2003) otherwise. The mean metallicities of Carina, Fornax,
Sculptor, and Sextans are calculated from their metallicity
distributions (Battaglia et al. 2006; Helmi et al. 2006; Battaglia et al. 2008a).The mean
metallicity of Leo II is derived from the metallicity distribution of
Bosler et al. (2007). The luminosities are taken from Grebel et al. (2003),
with the exception of Draco (Martin et al. 2008). The masses of Carina,
Fornax, Draco, Leo I and Leo II are computed by Walker et al. (2007)
inside
are taken from Mateo (1998) when available or from
Grebel et al. (2003) otherwise. The mean metallicities of Carina, Fornax,
Sculptor, and Sextans are calculated from their metallicity
distributions (Battaglia et al. 2006; Helmi et al. 2006; Battaglia et al. 2008a).The mean
metallicity of Leo II is derived from the metallicity distribution of
Bosler et al. (2007). The luminosities are taken from Grebel et al. (2003),
with the exception of Draco (Martin et al. 2008). The masses of Carina,
Fornax, Draco, Leo I and Leo II are computed by Walker et al. (2007)
inside
![]() .
The mass of Sextans corresponds to the upper
limit of Kleyna et al. (2004), while the mass of Ursa Minor comes from
Mateo (1998). Sculptor's
.
The mass of Sextans corresponds to the upper
limit of Kleyna et al. (2004), while the mass of Ursa Minor comes from
Mateo (1998). Sculptor's
![]() is taken from
Battaglia et al. (2008a).
is taken from
Battaglia et al. (2008a).
Both
![]() and
and
![]() show very clear log-linear
relations with
show very clear log-linear
relations with
![]() :
:
and
Despite differences in
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[angle=0]{11734Fig06.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg125.png) |
Figure 6:
The galaxies' mass-to-light ratios,
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig07.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg126.png) |
Figure 7:
The median of the galaxies' metallicity distributions,
|
| Open with DEXTER | |
To allow deeper insight into the building up of the
![]() relation, Fig. 8 distinguishes
between dark matter (DM), stars and gas. Colors encode the three
different initial baryonic fractions that we have considered,
relation, Fig. 8 distinguishes
between dark matter (DM), stars and gas. Colors encode the three
different initial baryonic fractions that we have considered,
![]() (yellow),
(yellow),
![]() (green) and
(green) and
![]() (blue).
(blue).
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig08.eps}}\par
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg128.png) |
Figure 8:
The relation between galaxy mass and V-band luminosity for the
the dark matter, the stars and the gas.
The lower panel displays the gas over stars mass ratio.
Colors encode the three different baryonic fractions that we have considered,
|
| Open with DEXTER | |
Very naturally, stellar mass scales with the luminosity. At fixed
luminosity, the dispersion in stellar mass is of the order of
![]()
![]() .
In fact, a more appropriate way to look at
this panel is to consider the dispersion in luminosity at fixed
stellar mass, since the dispersion in luminosity is a direct
consequence of various distributions in stellar ages and
metallicities. This dispersion, of the order of
.
In fact, a more appropriate way to look at
this panel is to consider the dispersion in luminosity at fixed
stellar mass, since the dispersion in luminosity is a direct
consequence of various distributions in stellar ages and
metallicities. This dispersion, of the order of
![]() .
It increases slightly for larger masses, for
which star formation can last longer, inducing a larger number of
possible age/metallicity combinations.
.
It increases slightly for larger masses, for
which star formation can last longer, inducing a larger number of
possible age/metallicity combinations.
As already discussed in Fig. 5, whilst
![]() spans nearly 3 orders of magnitude, the mass of dark matter varies
little. This variation is much less than one order of magnitude
inside
spans nearly 3 orders of magnitude, the mass of dark matter varies
little. This variation is much less than one order of magnitude
inside
![]() and is mostly due to the dispersion among the
models. A common mass scale (inside
and is mostly due to the dispersion among the
models. A common mass scale (inside
![]() ), around
), around
![]() ,
for the dSph total masses seems also favored by
the observations, although an exact value for this limit is difficult
to ascertain, given the large uncertainties of the mass estimates in
general (Gilmore et al. 2007; Mateo 1998; Strigari et al. 2008).
,
for the dSph total masses seems also favored by
the observations, although an exact value for this limit is difficult
to ascertain, given the large uncertainties of the mass estimates in
general (Gilmore et al. 2007; Mateo 1998; Strigari et al. 2008).
Interestingly, one can now witness the effect of varying the initial
baryonic fraction. Galaxies with
![]() exhibit identical DM halo masses, whatever
exhibit identical DM halo masses, whatever
![]() ,
while for larger luminosities, the models of lowest
,
while for larger luminosities, the models of lowest
![]() require larger halo masses in order to generate a similar
quantity of stars. For
require larger halo masses in order to generate a similar
quantity of stars. For
![]() ,
the DM halo mass is
constant over the whole luminosity range. This demonstrates that
while dark matter plays a crucial role in confining the gas, the
amount of the latter is also important for the most massive dSphs: it
must reach a critical amount to enable their formation.
,
the DM halo mass is
constant over the whole luminosity range. This demonstrates that
while dark matter plays a crucial role in confining the gas, the
amount of the latter is also important for the most massive dSphs: it
must reach a critical amount to enable their formation.
The third panel of Fig. 8 displays the mass of residual gas
after
![]() .
It constitutes a very small fraction of the
total mass, and is therefore undetectable at the level of the scaling
relations. Quite interestingly, its amount is of the order of the HI
mass observed in dwarf irregular galaxies (dIs) (Grebel et al. 2003) and
is weakly dependent on the total luminosity. Nevertheless, there is a
non-intuitive tendency for the most luminous galaxies (>
.
It constitutes a very small fraction of the
total mass, and is therefore undetectable at the level of the scaling
relations. Quite interestingly, its amount is of the order of the HI
mass observed in dwarf irregular galaxies (dIs) (Grebel et al. 2003) and
is weakly dependent on the total luminosity. Nevertheless, there is a
non-intuitive tendency for the most luminous galaxies (>
![]() )
to exhibit less gas than the rest of the systems
on the sequence. However, the most massive galaxies succeed in
retaining most of their gas despite the supernova explosions. Less
than 60% of their gas is ejected, while this fraction lies between 70% and 90% for less massive systems, in agreement with the results
of Valcke et al. (2008). However, the star formation efficiency is also
higher in more massive galaxies. As a result, the gas consumption
counterbalances the presence of the large gas reservoir. We will come
back to this in Sect. 7.
)
to exhibit less gas than the rest of the systems
on the sequence. However, the most massive galaxies succeed in
retaining most of their gas despite the supernova explosions. Less
than 60% of their gas is ejected, while this fraction lies between 70% and 90% for less massive systems, in agreement with the results
of Valcke et al. (2008). However, the star formation efficiency is also
higher in more massive galaxies. As a result, the gas consumption
counterbalances the presence of the large gas reservoir. We will come
back to this in Sect. 7.
Since the gas mass is very much constant at around
![]() ,
the smallest galaxies have proportionally more
gas than the massive ones (see bottom panel of Fig. 8).
Below
,
the smallest galaxies have proportionally more
gas than the massive ones (see bottom panel of Fig. 8).
Below
![]() ,
galaxies have more gas left than they have formed stars. Their gas to
stellar mass ratios reach 100 at the faint end of the dSph model
sequence. Meanwhile, stars dominate over gas by a factor 5 for the
most luminous galaxies.
,
galaxies have more gas left than they have formed stars. Their gas to
stellar mass ratios reach 100 at the faint end of the dSph model
sequence. Meanwhile, stars dominate over gas by a factor 5 for the
most luminous galaxies.
As a conclusion, the lessons to be taken from Fig. 8 are twofold: i) all dSphs are clearly dominated by dark matter. The lower the mass of the system, the lower the final baryonic fraction; ii) all model galaxies present an excess of gas at the end of their evolution, as found in similar studies (Marcolini et al. 2008,2006; Stinson et al. 2007; Valcke et al. 2008). As demonstrated earlier, dSphs cannot originate from smaller amounts of gas (for a given final luminosity, metallicity and age). It is necessary to initiate the star formation in the observed proportions. However, it is not yet clear how much of this gas must be kept in the subsequent phases of the galaxy evolution. It is clear that the excess of gas, observed in models in isolation, must in reality have been stripped some time during the galaxy evolution.
The quantity of gas falls in the range of HI mass observed in dIs, always found further away than dSphs from their parent galaxies, thereby bringing another piece of evidence for the role that interactions might play in its removal. It might also be achieved in a hierarchical formation framework, for which the gravitational potentials are initially weaker.
As we have just shown, the global scaling relations are reproduced by our model with impressive ease. In turn, this conveys the idea that the global scaling relations do not form a very precise set of constraints. They do not reflect the diversity in star formation histories that we have illustrated. In order to understand the individual histories of the Local Group dSphs, one definitely needs to go one step further and consider their chemical abundance patterns, as well as the information that color-magnitude diagrams provide on the stellar age distributions.
6 Generic models
We will now select and discuss a series of generic models reproducing the properties of four Milky Way dwarf spheroidals, Carina, Fornax, Sculptor and Sextans. The choice of these models is based on four observational constraints:
- 1)
- the dSph total luminosity, which scales with the total amount of matter involved in the galaxy star formation history;
- 2)
- the metallicity distribution which traces the star formation efficiency;
- 3)
- the chemical abundance patterns, in particular that of the
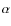 -elements, that determines the length and efficiency of the
star formation period together with its homogeneity. We use
magnesium for the
-elements, that determines the length and efficiency of the
star formation period together with its homogeneity. We use
magnesium for the 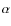 -elements. [Fe/H] and [Mg/H] are
derived from high resolution spectroscopy in the central regions of
the galaxies (Hill et al., in preparation; Letarte et al., in
preparation; Letarte et al. 2007; Venn & Hill 2005; Koch et al. 2008; Shetrone et al. 2003);
-elements. [Fe/H] and [Mg/H] are
derived from high resolution spectroscopy in the central regions of
the galaxies (Hill et al., in preparation; Letarte et al., in
preparation; Letarte et al. 2007; Venn & Hill 2005; Koch et al. 2008; Shetrone et al. 2003);
- 4)
- the stellar age distributions. They complement the above constraints with information on possible series of bursts (Coleman & de Jong 2008; Smecker-Hane et al. 1996; Hurley-Keller et al. 1998).
Figures 11, 12 and 13 display the stellar
metallicity distribution, the [Mg/Fe] vs. [Fe/H] diagrams and the
stellar age histograms, respectively, after
![]() of
evolution. Figure 14 shows the stellar age-metallicity relations.
of
evolution. Figure 14 shows the stellar age-metallicity relations.
We do not try to match exactly all properties of our target dSphs.
Instead, we select the four most satisfying models in our sample of
166. More specifically, we allow a freedom of a factor 2 in
luminosity and a shift of a few tenths of dex in peak [Fe/H]. It is
beyond doubt that we could fine-tune
![]() ,
,
![]() ,
,
![]() and
and
![]() to exactly reproduce the
observations. However, this is beyond our scope, which remains to test
the hypothesis of a formation framework common to all dSphs. The
dependence of the results on the model parameters is illustrated in
Figs. 9 and 10. We selected 6 models at low
(
to exactly reproduce the
observations. However, this is beyond our scope, which remains to test
the hypothesis of a formation framework common to all dSphs. The
dependence of the results on the model parameters is illustrated in
Figs. 9 and 10. We selected 6 models at low
(
![]() )
and high
(
)
and high
(
![]() )
luminosities. The
baryonic fraction is fixed each time, and only
)
luminosities. The
baryonic fraction is fixed each time, and only ![]() and
and
![]() vary. One sees that around a given fixed core of observed
characteristics (e.g., luminosity, metallicity), we could run the
models on a finer grid of parameters in order to match the galaxy
properties in all details. This means, for example, to exactly reflect
the stellar age distribution, or the spread in abundance ratios.
vary. One sees that around a given fixed core of observed
characteristics (e.g., luminosity, metallicity), we could run the
models on a finer grid of parameters in order to match the galaxy
properties in all details. This means, for example, to exactly reflect
the stellar age distribution, or the spread in abundance ratios.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig09.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg145.png) |
Figure 9:
The variation in [Mg/Fe] vs. [Fe/H], [Fe/H] distribution
and stellar age distribution for 3 models of similar luminosities
(
|
| Open with DEXTER | |
Table 1: Initial parameters of the five generic models.
Table 2: Final properties of the five selected generic models.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig10.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg155.png) |
Figure 10:
Same as Fig. 9 but for a brighter set of model
galaxies (
|
| Open with DEXTER | |
6.1 Global evolution
Figures 16 and 17 show the stellar surface
density, the gas surface density and the gas temperature between 0and
![]() for our four selected generic models. Not only do
these reproduce the properties of Carina, Fornax, Sculptor and Sextans
individually, but they also depict the full spectrum of evolutions
seen in our models. The size of each panel is
for our four selected generic models. Not only do
these reproduce the properties of Carina, Fornax, Sculptor and Sextans
individually, but they also depict the full spectrum of evolutions
seen in our models. The size of each panel is
![]() .
.
All gas particles initially share the same temperatures, corresponding
to the galaxy virial temperature, as given by Eq. (16). As
soon as the simulations start, the gas looses energy by radiative
cooling. Consequently, the gas density increases in the galaxy
central regions. Red areas in the gas density maps identify densities
larger than
![]() ,
i.e., they mark regions where gas
particles may be eligible for star formation. When this is indeed the
case, the newly formed stars are traced by their high brightness in
the stellar density maps.
,
i.e., they mark regions where gas
particles may be eligible for star formation. When this is indeed the
case, the newly formed stars are traced by their high brightness in
the stellar density maps.
The SN explosions induce temperature inhomogeneities. Indeed, the
heated central gas expands and generates a wave propagating outwards.
If the SN feedback dominates the cooling, the gas is diluted and the
red color vanishes from the center of the gas density maps: star
formation is quenched. Such quiescent periods are characterized by a
nearly constant and homogeneous central temperature ![]()
![]() ,
the temperature at which the radiative cooling
counterbalances the adiabatic heating. When gas has sufficiently
cooled, it can condense again, and star formation is induced again.
These periods of star formation and quiescence alternate at low or
high frequency, depending on the mass of the galaxy. For low-mass
systems, the cooling time is of the order of several Gyr, it is much
shorter for more massive ones. We will now see how each of these cases
translate into dSph stellar population properties.
,
the temperature at which the radiative cooling
counterbalances the adiabatic heating. When gas has sufficiently
cooled, it can condense again, and star formation is induced again.
These periods of star formation and quiescence alternate at low or
high frequency, depending on the mass of the galaxy. For low-mass
systems, the cooling time is of the order of several Gyr, it is much
shorter for more massive ones. We will now see how each of these cases
translate into dSph stellar population properties.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig11.eps}} \end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg157.png) |
Figure 11: The stellar [Fe/H] distributions of the four generic models reproducing Carina, Sextans, Sculptor and Fornax. The model outputs are shown in black and the observations with red dashed lines. The stellar fraction is defined as the number of stars in each bin divided by the total number of stars. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig12.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg158.png) |
Figure 12: The stellar [Mg/Fe] vs. [Fe/H] diagrams for the four generic models reproducing Carina, Sextans, Sculptor and Fornax. The observations are sketched with black dots. Their error bars are shown. Colors encode the fraction of stars as indicated by the bar at the top. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig13.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg159.png) |
Figure 13: The stellar age distributions of the four generic models. The stellar fraction is defined as the number of stars in each bin divided by the total number of stars. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig14.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg160.png) |
Figure 14: The age-metallicity relations of the four generic models. Each dot corresponds to a stellar particle. |
| Open with DEXTER | |
6.2 Sextans
The stellar population of Sextans is dominated by stars older than
![]() (Lee et al. 2003). With its mean metallicity
(Lee et al. 2003). With its mean metallicity
![]() and a V-band total luminosity of
and a V-band total luminosity of
![]() ,
it falls exactly on our
luminosity-metallicity relation (Fig. 7), and its properties
are reproduced by the model #590 (
,
it falls exactly on our
luminosity-metallicity relation (Fig. 7), and its properties
are reproduced by the model #590 (
![]() ,
,
![]() ) that experiences an outflow.
Sextans' evolution is dominated by an early period of star formation
lasting about
) that experiences an outflow.
Sextans' evolution is dominated by an early period of star formation
lasting about
![]() .
The gas surface density map of
Fig. 17 shows the dense central region at the origin of
the star formation burst (
.
The gas surface density map of
Fig. 17 shows the dense central region at the origin of
the star formation burst (
![]() ). At that time, a small
but bright stellar system is already formed. After this period, the
gas is expelled and diluted. No star can form until the last
). At that time, a small
but bright stellar system is already formed. After this period, the
gas is expelled and diluted. No star can form until the last
![]() ,
when the gas has sufficiently cooled down to fulfill the
star formation criteria. This last episode of star formation is an
artifact of the gas retained by our model, as discussed in
Sect. 5. It is however negligible compared to
the bulk of the population and does not influence Sextans' properties.
,
when the gas has sufficiently cooled down to fulfill the
star formation criteria. This last episode of star formation is an
artifact of the gas retained by our model, as discussed in
Sect. 5. It is however negligible compared to
the bulk of the population and does not influence Sextans' properties.
Figure 12 shows that the bulk of Sextans model stars are
located at [Mg/Fe] ![]() 0.3, with however a noticeable dispersion
at lower values. The dispersion originates from the uneven
intensities of the star formation peaks. They create regions with
diverse levels of chemical enrichment. When the intensity of star
formation rises again after a period of semi-quiescence, the ejecta of
new SNe II are mixed with material of low
0.3, with however a noticeable dispersion
at lower values. The dispersion originates from the uneven
intensities of the star formation peaks. They create regions with
diverse levels of chemical enrichment. When the intensity of star
formation rises again after a period of semi-quiescence, the ejecta of
new SNe II are mixed with material of low ![]() -element abundance.
Refinement of the model would require a larger sample of observed
stars at high resolution, particularly to estimate the statistical
significance of the dispersion in [Mg/Fe].
-element abundance.
Refinement of the model would require a larger sample of observed
stars at high resolution, particularly to estimate the statistical
significance of the dispersion in [Mg/Fe].
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig15.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg170.png) |
Figure 15: The [Mg/Fe] vs. [Fe/H] diagram, the stellar [Fe/H] distribution, the age-metallicity relation and the global stellar age distribution of the model #587, compared to the observations of Leo II. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[angle=0,clip]{11734Fig16.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg174.png) |
Figure 16:
Stellar, gas and temperature evolution of the models #575 (Fornax) and
#630 (Sculptor) as a function of time.
Each model is illustrated with three columns:
the first column presents the stellar surface brightness in log scale, between 0 and
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[angle=0,clip]{11734Fig17.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg175.png) |
Figure 17: Same as Fig. 16 but for the models #590 (Sextans) and #533 (Carina). |
| Open with DEXTER | |
6.3 Carina
Carina seems to have experienced a complex evolution characterized by
episodic bursts of star formation, with at least three major episodes
at around 15, 7 and
![]() ,
and a period of
quiescence between 7 and
,
and a period of
quiescence between 7 and
![]() (Smecker-Hane et al. 1996; Hurley-Keller et al. 1998).
Our set of simulations reveal that episodic bursts of star formation are
intrinsic features of the self-regulated low initial masses
systems (
(Smecker-Hane et al. 1996; Hurley-Keller et al. 1998).
Our set of simulations reveal that episodic bursts of star formation are
intrinsic features of the self-regulated low initial masses
systems (
![]() ,
see
Fig. 3). Shortly after a star formation episode,
supernovae explode, gas is heated and expands. Because its density is
low, its cooling time is of the order of several Gyr.
This series of well spaced-out SF peaks translate into dispersion in
[Mg/Fe] at fixed [Fe/H]. This spread is more accentuated than for
Sextans, due to the extended star formation and the longer intervals
between bursts.
,
see
Fig. 3). Shortly after a star formation episode,
supernovae explode, gas is heated and expands. Because its density is
low, its cooling time is of the order of several Gyr.
This series of well spaced-out SF peaks translate into dispersion in
[Mg/Fe] at fixed [Fe/H]. This spread is more accentuated than for
Sextans, due to the extended star formation and the longer intervals
between bursts.
Figure 7 shows that Carina, with
![]() and
and
![]() ,
falls above the relation [Fe/H]-
,
falls above the relation [Fe/H]-
![]() defined by our models. As already mentioned, we give priority to
constraints provided by the spectroscopic data, and allow some
flexibility in
defined by our models. As already mentioned, we give priority to
constraints provided by the spectroscopic data, and allow some
flexibility in
![]() .
Under these conditions, model #533
(
.
Under these conditions, model #533
(
![]() )
provides a very
reasonable fit to Carina's properties. The three major SF episodes
are reproduced: 45% of the stars have ages between 9 and
)
provides a very
reasonable fit to Carina's properties. The three major SF episodes
are reproduced: 45% of the stars have ages between 9 and
![]() ,
29% have 4 to
,
29% have 4 to
![]() and 22% are younger
than
and 22% are younger
than
![]() .
Whilst Carina is somewhat less luminous than
Sextans, its mean metallicity is higher. This is due to a lower
initial mass, locking less matter in stars, but a longer period of
star formation, obtained by a slightly higher star formation
parameter, which avoids outflows.
.
Whilst Carina is somewhat less luminous than
Sextans, its mean metallicity is higher. This is due to a lower
initial mass, locking less matter in stars, but a longer period of
star formation, obtained by a slightly higher star formation
parameter, which avoids outflows.
6.4 Sculptor
The Sculptor dSph has formed stars early, over a period of a few Gyr.
No significant intermediate age population has been found, hence
excluding star formation within the last ![]()
![]() .
The
evidence for low
.
The
evidence for low ![]() -element enhancement agrees with an extended
star formation and self-enrichment over a period of at least
-element enhancement agrees with an extended
star formation and self-enrichment over a period of at least
![]() (e.g. Tolstoy et al. 2003; Shetrone et al. 2003; Babusiaux et al. 2005).
(e.g. Tolstoy et al. 2003; Shetrone et al. 2003; Babusiaux et al. 2005).
Sculptor's properties are well reproduced by model #630 (
![]() ,
,
![]() ).
The outstanding feature of Sculptor, as compared to the two previous
dSph, is the small dispersion in the [Mg/Fe] vs. [Fe/H] diagram
(Fig. 12). This is guaranteed by a strong initial star
formation, followed by subsequent episodes of lower, but smoothly
decreasing intensities, ensuring the chemical homogeneity of the
interstellar medium.
).
The outstanding feature of Sculptor, as compared to the two previous
dSph, is the small dispersion in the [Mg/Fe] vs. [Fe/H] diagram
(Fig. 12). This is guaranteed by a strong initial star
formation, followed by subsequent episodes of lower, but smoothly
decreasing intensities, ensuring the chemical homogeneity of the
interstellar medium.
6.5 Fornax
Fornax is obviously the most challenging case of dSphs. It is the most luminous of all (
Fornax is nicely reproduced by the self-regulated model #575. Stars
are formed in a high frequency series of short bursts, lasting
between 200 and
![]() .
The amplitude of these bursts
progressively decreases with time, until
.
The amplitude of these bursts
progressively decreases with time, until ![]()
![]() .
Thereafter, part of the gas that had been expelled by previous SN
explosions, has sufficiently cooled to restore star formation, at
.
Thereafter, part of the gas that had been expelled by previous SN
explosions, has sufficiently cooled to restore star formation, at ![]()
![]() ,
similar to what is observed. The succession of the
short bursts of similar intensities mimics a continuous star formation
and leads to an efficient and homogeneous chemical enrichment
(
,
similar to what is observed. The succession of the
short bursts of similar intensities mimics a continuous star formation
and leads to an efficient and homogeneous chemical enrichment
(
![]() ).
).
We reach a luminosity
![]() ,
slightly
below the observation of Fornax. However, just as in the case of
Carina, the exact value of the V-band luminosity is very sensitive
to the exact amount of stars formed in the last Gyr and may easily
vary. Stars form up to the end of the simulation. This is consistent
with the observational evidence of a small number of
,
slightly
below the observation of Fornax. However, just as in the case of
Carina, the exact value of the V-band luminosity is very sensitive
to the exact amount of stars formed in the last Gyr and may easily
vary. Stars form up to the end of the simulation. This is consistent
with the observational evidence of a small number of
![]() stars (Coleman & de Jong 2008).
stars (Coleman & de Jong 2008).
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig18.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg190.png) |
Figure 18: The stars (blue circles) and dark halo (red triangles) density profiles for the four generic models. Each profile is fitted by a Plummer model. The positions of the core radii are indicated by the dashed lines. Their values are given in the left bottom corner of each panel. |
| Open with DEXTER | |
Figure 14 show the stellar age-metallicity relations of our four generic models. In all cases, we are far from a one to one correspondence between age and metallicity, although below [Fe/H] = -2.5(but more safely below [Fe/H] = -3), stars are generally older than 10 Gyr. The dispersion in metallicity is in the range 0.5 to 1 dex at ages younger than 10 Gyr.
6.6 Leo II
While writing up our results, the abundance ratios in a sample of 24 stars in Leo II have been published (Shetrone et al. 2009). We keep Leo II separated from the other individual case analyses, since its abundance ratios have been obtained from lower resolution spectra and therefore have larger uncertainties.
Figure 15 illustrates how model #587 can reproduce the star
formation history of Leo II. The observed metallicity distribution,
derived from ![]() 100 stars, is taken from Bosler et al. (2007), and
[Mg/Fe] from Shetrone et al. (2009). Leo II has a luminosity similar to
that of Sextans, but unlike Sextans, Leo II sustained a low but
constant star formation rate, leading to an important intermediate age
stellar population (Koch et al. 2007; Mighell & Rich 1996). The reason for a
continuous (low) star formation in Leo II's model is found in the
slightly smaller initial total mass for the same star formation
parameter as Sextans; it prevents the gas outflow. Carina and Leo II
have about the same mean metallicities. They probably have
experienced a very similar evolution, as indeed seen in
Table 2 for their mean properties. However, the two
galaxies indeed differ: i) by the periods of quiescence which are
longer in Carina; and ii) by the extent of the star formation peaks,
which are between 2 to 3 times longer in Leo II, at intermediate ages.
Model #587 produced a higher final luminosity than observed, due to
the presence of residual gas and therefore recent star formation, as
in all the models. It is important to recall that we do not aim at
reproducing Leo II properties in fine details, but instead check
whether its main features exist in the series of models we ran. In
this respect, model #587 demonstrates that a low level of rather
continuous star formation is indeed achievable.
100 stars, is taken from Bosler et al. (2007), and
[Mg/Fe] from Shetrone et al. (2009). Leo II has a luminosity similar to
that of Sextans, but unlike Sextans, Leo II sustained a low but
constant star formation rate, leading to an important intermediate age
stellar population (Koch et al. 2007; Mighell & Rich 1996). The reason for a
continuous (low) star formation in Leo II's model is found in the
slightly smaller initial total mass for the same star formation
parameter as Sextans; it prevents the gas outflow. Carina and Leo II
have about the same mean metallicities. They probably have
experienced a very similar evolution, as indeed seen in
Table 2 for their mean properties. However, the two
galaxies indeed differ: i) by the periods of quiescence which are
longer in Carina; and ii) by the extent of the star formation peaks,
which are between 2 to 3 times longer in Leo II, at intermediate ages.
Model #587 produced a higher final luminosity than observed, due to
the presence of residual gas and therefore recent star formation, as
in all the models. It is important to recall that we do not aim at
reproducing Leo II properties in fine details, but instead check
whether its main features exist in the series of models we ran. In
this respect, model #587 demonstrates that a low level of rather
continuous star formation is indeed achievable.
The extension of the sample of stars with spectroscopic data allowing measurements of abundance ratios would greatly help the precise identification of Leo II model. This is particularly true at [Fe/H] >-1.6 which would confirm or not the apparent plateau in [Mg/Fe]. Even more decisive and more general, one needs to observationally confirm or disprove the dispersion in [Mg/Fe] at low and moderate metallicities in low mass dSphs, as it signals the discrete nature of star formation as advocated by contemporary models.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig19.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg194.png) |
Figure 19:
Top: the Virial temperature as a function of the total
initial mass computed from Eq. (16), with
|
| Open with DEXTER | |
Table 1 gives the fraction of very-metal poor ([Fe/H] < -3)
stellar particles in the generic models. The general trend of our
series of 166 models is that the more extended the star formation
period, the smaller this fraction. This is clearly illustrated by the
models of Carina and Fornax, as compared to those of Sextans and
Fornax. Although the tail of very metal-poor stars is small
(from ![]() 1 to 6%), it is still larger than suggested by the
observations to date (Helmi et al. 2006). In order to properly address
this particular issue, one needs i) to investigate the impact of more
sophisticated IMFs, such as the one of Kroupa et al. (1993), for which the
number of low-mass stars is smaller than for a Salpeter IMF; and ii)
to introduce the peculiar features of star formation at zero
metallicity. The conditions of transition between population III and
population II star formation depends on the galaxy halo masses, and so
is the galaxy metallicity floor (Wise & Abel 2008). This opens a
independent new field of investigation. For the time being, we check
our model predictions against population II properties. Interestingly,
the outflows generated by these very first generation of stars offers
an alternative solution to get rid of the final excess of gas.
1 to 6%), it is still larger than suggested by the
observations to date (Helmi et al. 2006). In order to properly address
this particular issue, one needs i) to investigate the impact of more
sophisticated IMFs, such as the one of Kroupa et al. (1993), for which the
number of low-mass stars is smaller than for a Salpeter IMF; and ii)
to introduce the peculiar features of star formation at zero
metallicity. The conditions of transition between population III and
population II star formation depends on the galaxy halo masses, and so
is the galaxy metallicity floor (Wise & Abel 2008). This opens a
independent new field of investigation. For the time being, we check
our model predictions against population II properties. Interestingly,
the outflows generated by these very first generation of stars offers
an alternative solution to get rid of the final excess of gas.
6.7 Mass profiles and velocity dispersions
Although our primary goal is not to match the morphology of the
dSphs, we have considered the shape of the final modeled dSph profiles
within
![]() .
Figure 18 displays the mass density
profiles of the stellar and dark components for our four main targets.
Each model is successfully fitted by a Plummer model, revealing a flat
inner profile, in agreement with the observations. The ratio between
the stellar and dark core radii
.
Figure 18 displays the mass density
profiles of the stellar and dark components for our four main targets.
Each model is successfully fitted by a Plummer model, revealing a flat
inner profile, in agreement with the observations. The ratio between
the stellar and dark core radii
![]() ranges between 0.2 and 0.5, indicating a spatial segregation of
the stars relative to the dark halo, as discussed in
Peñarrubia et al. (2008). Additionally, the line-of-sight stellar velocity
dispersion profiles are flat in the region enclosed within the core radii,
with 6 to
ranges between 0.2 and 0.5, indicating a spatial segregation of
the stars relative to the dark halo, as discussed in
Peñarrubia et al. (2008). Additionally, the line-of-sight stellar velocity
dispersion profiles are flat in the region enclosed within the core radii,
with 6 to
![]() ,
corresponding to the least and the most massive
dSph, respectively, hence well within the observed range
(Muñoz et al. 2006; Walker et al. 2006b,a; Battaglia et al. 2008a).
,
corresponding to the least and the most massive
dSph, respectively, hence well within the observed range
(Muñoz et al. 2006; Walker et al. 2006b,a; Battaglia et al. 2008a).
7 Discussion
We have shown that the total initial mass
![]() and
and ![]() are the two driving parameters for the evolution of dSphs. Our models
which describe galaxies in isolation, i.e., not yet taking into
account interactions or accretions that inevitably occur in a
are the two driving parameters for the evolution of dSphs. Our models
which describe galaxies in isolation, i.e., not yet taking into
account interactions or accretions that inevitably occur in a
![]() CDM Universe, already lead to the observed variety of star
formation histories. Decreasing the initial total mass of the galaxies
separates the periods of star formation.
CDM Universe, already lead to the observed variety of star
formation histories. Decreasing the initial total mass of the galaxies
separates the periods of star formation.
The marked differences found between high- and low mass systems is a key point in understanding the formation of dSphs. In order to illustrate our findings, we now focus on cooling time and gas temperature. The top panel of Fig. 19 displays the galaxy's virial temperature as a function of its initial mass (Eq. (16)).
The green horizontal band indicates the temperature at which the
cooling time of the gas is equal to
![]() ,
for two threshold
densities,
,
for two threshold
densities,
![]() and
and
![]() that are
representative of the range in gas density observed in the course of
our simulations. The value of
that are
representative of the range in gas density observed in the course of
our simulations. The value of
![]() is chosen to be short
compared to the galaxy lifetimes. The lower border of the green band
corresponds to
is chosen to be short
compared to the galaxy lifetimes. The lower border of the green band
corresponds to
![]() while the upper ones correspond to
while the upper ones correspond to
![]() .
The intersection between the green band
and the curves corresponds to a total mass ranging between 3 and
.
The intersection between the green band
and the curves corresponds to a total mass ranging between 3 and
![]() ,
delimiting two regimes distinguished by
long and short cooling times, as can be measured in the bottom panel
of Fig. 19. The cooling times of
,
delimiting two regimes distinguished by
long and short cooling times, as can be measured in the bottom panel
of Fig. 19. The cooling times of
![]() and
and
![]() as a function of the
galaxy initial masses are shown in solid and dashed lines,
respectively, in the bottom panel of the figure. They are calculated
by taking the virial temperature of the corresponding galaxy mass.
The gas contained in galaxies of total masses larger than
as a function of the
galaxy initial masses are shown in solid and dashed lines,
respectively, in the bottom panel of the figure. They are calculated
by taking the virial temperature of the corresponding galaxy mass.
The gas contained in galaxies of total masses larger than
![]() ,
with corresponding virial temperatures larger
than
,
with corresponding virial temperatures larger
than
![]() is characterized by a short cooling time
(
is characterized by a short cooling time
(![]() Myr) at all densities. This short cooling time is
due to the strong radiative cooling induced by the recombination of
hydrogen above
Myr) at all densities. This short cooling time is
due to the strong radiative cooling induced by the recombination of
hydrogen above
![]() .
A galaxy which is in this cooling
regime will see its gas loosing a huge amount of energy, sinking in
its central regions and inducing star formation. This is precisely
what happens in the model #575 where stars are continuously formed,
generating a metal-rich Fornax-like system. By decreasing the total
mass from 4 to
.
A galaxy which is in this cooling
regime will see its gas loosing a huge amount of energy, sinking in
its central regions and inducing star formation. This is precisely
what happens in the model #575 where stars are continuously formed,
generating a metal-rich Fornax-like system. By decreasing the total
mass from 4 to
![]() ,
the virial temperature
falls below the peak of hydrogen ionization. As a consequence, the
cooling function drops and the cooling time is increased by nearly
three orders of magnitude. Below
,
the virial temperature
falls below the peak of hydrogen ionization. As a consequence, the
cooling function drops and the cooling time is increased by nearly
three orders of magnitude. Below
![]() ,
the
cooling time is long, since the loss of energy by radiative cooling is
strongly diminished. In this regime, star formation can only occur in
episodic bursts, separated by periods corresponding to the mean
cooling time. Carina gives a clear example of such a case. For even
lower mass systems (
,
the
cooling time is long, since the loss of energy by radiative cooling is
strongly diminished. In this regime, star formation can only occur in
episodic bursts, separated by periods corresponding to the mean
cooling time. Carina gives a clear example of such a case. For even
lower mass systems (
![]() ), the cooling
time is longer than
), the cooling
time is longer than
![]() ,
and therefore no stars are
expected to form.
,
and therefore no stars are
expected to form.
From our simulations, a total mass of ![]()
![]() leads to a luminosity of
leads to a luminosity of ![]()
![]() .
Not surprisingly, this luminosity
corresponds to the critical one found in
Sect. 5, below which the galaxies have more gas
left than they have formed stars.
The sharp cutoff of the cooling function below
.
Not surprisingly, this luminosity
corresponds to the critical one found in
Sect. 5, below which the galaxies have more gas
left than they have formed stars.
The sharp cutoff of the cooling function below
![]() explains very nicely why a small decrease in mass
induces a large drop in luminosity, seen in the middle panel of
Fig. 5. A direct consequence is the constancy of galaxy
masses within
explains very nicely why a small decrease in mass
induces a large drop in luminosity, seen in the middle panel of
Fig. 5. A direct consequence is the constancy of galaxy
masses within
![]() (
(![]()
![]() )
over the wide range of dSph luminosities, as discussed in
Sect. 5 (Fig. 8) and suggested by
Mateo (1998), Gilmore et al. (2007) and Strigari et al. (2008).
)
over the wide range of dSph luminosities, as discussed in
Sect. 5 (Fig. 8) and suggested by
Mateo (1998), Gilmore et al. (2007) and Strigari et al. (2008).
The next step in simulating the formation and evolution of dSph
galaxies is to study the impact of external processes resulting from
a ![]() CDM complex environment, like tidal mass stripping, ram
stripping, dark matter and gas accretion, as well as reionization and
self-shielding. Peñarrubia et al. (2008) show that tidal mass stripping
strongly depends on the spatial distribution of stars relative to the
dark halo extent. If stars are very concentrated in large halos,
dSphs will be more resilient to tidal disruption. Dwarf spheroidal
galaxies may need to loose nearly
CDM complex environment, like tidal mass stripping, ram
stripping, dark matter and gas accretion, as well as reionization and
self-shielding. Peñarrubia et al. (2008) show that tidal mass stripping
strongly depends on the spatial distribution of stars relative to the
dark halo extent. If stars are very concentrated in large halos,
dSphs will be more resilient to tidal disruption. Dwarf spheroidal
galaxies may need to loose nearly ![]() of their mass before their
star formation and therefore chemical evolution start to be affected.
Mayer et al. (2006) tackle all the above listed questions and show how
their mechanisms can be interlaced. As an example, in their models
gravitational tides help ram pressure stripping by diminishing the
overall potential of the dwarf, but tides induce bar formation making
subsequent stripping more difficult. Reionization prevent star
formation, but self-shielding helps cooling. Clearly, understanding
the impact of these physical processes on our specific modeling
requires dedicated simulations.
of their mass before their
star formation and therefore chemical evolution start to be affected.
Mayer et al. (2006) tackle all the above listed questions and show how
their mechanisms can be interlaced. As an example, in their models
gravitational tides help ram pressure stripping by diminishing the
overall potential of the dwarf, but tides induce bar formation making
subsequent stripping more difficult. Reionization prevent star
formation, but self-shielding helps cooling. Clearly, understanding
the impact of these physical processes on our specific modeling
requires dedicated simulations.
8 Summary
We have investigated the formation and evolution of dSph galaxies, which form a specific class among dwarf systems. Indeed, they reach the highest metallicities at fixed luminosity and are devoid of gas.
We performed 166 self-consistent Nbody/Tree-SPH simulations of systems initially consisting of dark matter and primordial gas. We have only considered galaxies in isolation. This has enabled us to identify the dominant physical ingredients at the origin of the observed variety in dSph properties. It has also allowed us to distinguish which of those are due to the galaxy intrinsic evolution and for which interactions are required. The diversity of star formation histories of the Milky Way dSphs, Carina, Leo II, Sextans, Sculptor and Fornax have been successfully reproduced in a single formation scheme.
- The crucial parameter driving the dSph evolution is the
total initial mass (gas + dark matter). To a smaller extent the star
formation parameter,
 ,
influences the final galaxy
properties. In particular, it governs the stellar age distribution by
modifying the time intervals at which star formation occurs. Since
there is no physical reason for changing
,
influences the final galaxy
properties. In particular, it governs the stellar age distribution by
modifying the time intervals at which star formation occurs. Since
there is no physical reason for changing  from galaxy to
galaxy, we understand its variation, if needed to reproduce the
observations, as an indirect evidence for different interaction
histories. In a hierarchical galaxy formation scheme, our initial
masses correspond to the halo masses that must be reached along the
merger tree before ignition of the bulk of the star
formation. Besides, the chemical abundance ratios constrain the
timescale of these halo mergers. For example, we have shown that
Fornax could not be formed without a high initial total mass. This
could in principle mean an already long accretion history.
Nonetheless, its chemical homogeneity requests that this should be
achieved at a very early epoch, before star formation in independent
smaller halos could have widened its abundance patterns.
from galaxy to
galaxy, we understand its variation, if needed to reproduce the
observations, as an indirect evidence for different interaction
histories. In a hierarchical galaxy formation scheme, our initial
masses correspond to the halo masses that must be reached along the
merger tree before ignition of the bulk of the star
formation. Besides, the chemical abundance ratios constrain the
timescale of these halo mergers. For example, we have shown that
Fornax could not be formed without a high initial total mass. This
could in principle mean an already long accretion history.
Nonetheless, its chemical homogeneity requests that this should be
achieved at a very early epoch, before star formation in independent
smaller halos could have widened its abundance patterns.
- Star formation occurs in series of short periods (a few
hundreds of Myr long). A high frequency SF mode is analogous to a
continuous star formation, while a low frequency SF mode produces well
separated bursts, easily identified observationally as in the case of
Carina. The period between the star formation events is governed by
the mass of the systems. It is caused by the dependence of the gas
cooling time on the galaxy mass: the more massive, the shorter it is.
This mass dependency is explained by the drop of the cooling function
below
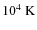 .
Systems less massive than
.
Systems less massive than
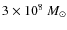 have a virial temperature below
have a virial temperature below
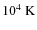 and
are characterized by weak cooling. Only episodic periods of star
formation are expected. On the contrary, massive systems
(
and
are characterized by weak cooling. Only episodic periods of star
formation are expected. On the contrary, massive systems
(
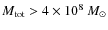 )
have a virial
temperature above
)
have a virial
temperature above
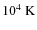 .
They are expected to form stars
continuously and generate more metal-rich dSphs.
.
They are expected to form stars
continuously and generate more metal-rich dSphs.
- The dSph scaling relations ([Fe/H], M/L) are reproduced and
exhibit very low scatter. We have shown that there is a constant final
total galaxy mass over the wide range of dSph luminosity, which
appears as a direct consequence of the cooling time -mass
relationship.
- The
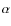 -elements were traced by magnesium. The
dispersion in the [Mg/Fe] vs. [Fe/H] diagrams is negligible for
continuous and/or efficient star formation. It is enhanced when the
star formation occurs in bursts separated by periods of quiescence, or
when the star formation occurs in peaks of uneven intensities.
Therefore, it is observed in galaxies as different as Sextans and
Carina. Our study strengthens the need for large and homogeneous
samples of stellar spectra obtained at high resolution, that are
necessary to constrain and improve the models. They call for large
observing programs dedicated to the chemical signatures at low
metallicities in order to establish the level of homogeneity of the
interstellar medium in the early phases of the galaxy evolution.
-elements were traced by magnesium. The
dispersion in the [Mg/Fe] vs. [Fe/H] diagrams is negligible for
continuous and/or efficient star formation. It is enhanced when the
star formation occurs in bursts separated by periods of quiescence, or
when the star formation occurs in peaks of uneven intensities.
Therefore, it is observed in galaxies as different as Sextans and
Carina. Our study strengthens the need for large and homogeneous
samples of stellar spectra obtained at high resolution, that are
necessary to constrain and improve the models. They call for large
observing programs dedicated to the chemical signatures at low
metallicities in order to establish the level of homogeneity of the
interstellar medium in the early phases of the galaxy evolution.
- The fraction of very metal-poor stars in our generic models
ranges from
 1 to 6%. Although this is a rather small amount,
it is still larger than suggested by the observations. In order to
properly address this particular issue, one needs to carefully
investigate the effect of more sophisticated IMFs and the peculiar
features of star formation at zero metallicity.
1 to 6%. Although this is a rather small amount,
it is still larger than suggested by the observations. In order to
properly address this particular issue, one needs to carefully
investigate the effect of more sophisticated IMFs and the peculiar
features of star formation at zero metallicity.
- Gas is found in all our model galaxies after
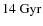 (
(
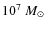 ). It clearly points to the need for
interactions that would strip the gas in the course of the dSph
evolution. The possibility that gas is gradually expelled as halos
merge in a hierarchical formation scenario also deserves careful
consideration.
). It clearly points to the need for
interactions that would strip the gas in the course of the dSph
evolution. The possibility that gas is gradually expelled as halos
merge in a hierarchical formation scenario also deserves careful
consideration.
Acknowledgements
We thank the anonymous referee for his constructive comments. As to the simulations, the data reduction and galaxy maps have been performed using the parallelized Python pNbody package (http://obswww.unige.ch/~revaz/pNbody/). This work was supported by the Swiss National Science Foundation.
References
- Alimi, J.-M., Serna, A., Pastor, C., & Bernabeu, G. 2003, J. Comp. Phys., 192, 157 [NASA ADS] [CrossRef] (In the text)
- Babusiaux, C., Gilmore, G., & Irwin, M. 2005, MNRAS, 359, 985 [NASA ADS] [CrossRef] (In the text)
- Barkana, R., & Loeb, A. 1999, ApJ, 523, 54 [NASA ADS] [CrossRef]
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] (In the text)
- Battaglia, G., Tolstoy, E., Helmi, A., et al. 2006, A&A, 459, 423 [NASA ADS] [CrossRef] [EDP Sciences]
- Battaglia, G., Helmi, A., Tolstoy, E., et al. 2008a, ApJ, 681, L13 [NASA ADS] [CrossRef]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008b, MNRAS, 383, 183 [NASA ADS]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton, NJ: Princeton University Press), 747
- Blais-Ouellette, S., Amram, P., & Carignan, C. 2001, AJ, 121, 1952 [NASA ADS] [CrossRef]
- Bosler, T. L., Smecker-Hane, T. A., & Stetson, P. B. 2007, MNRAS, 378, 318 [NASA ADS] [CrossRef] (In the text)
- Bullock, J. S., Kravtsov, A. V., & Weinberg, D. H. 2000, ApJ, 539, 517 [NASA ADS] [CrossRef]
- Carraro, G., Chiosi, C., Girardi, L., & Lia, C. 2001, MNRAS, 327, 69 [NASA ADS] [CrossRef] (In the text)
- Coleman, M. G., & de Jong, J. T. A. 2008, ApJ, 685, 933 [NASA ADS] [CrossRef] (In the text)
- de Blok, W. J. G. 2005, ApJ, 634, 227 [NASA ADS] [CrossRef]
- de Blok, W. J. G., & Bosma, A. 2002, A&A, 385, 816 [NASA ADS] [CrossRef] [EDP Sciences]
- de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef]
- Dolphin, A. E. 2002, MNRAS, 332, 91 [NASA ADS] [CrossRef]
- Efstathiou, G. 1992, MNRAS, 256, 43P [NASA ADS]
- Ferrara, A., & Tolstoy, E. 2000, MNRAS, 313, 291 [NASA ADS] [CrossRef] (In the text)
- Fukushige, T., & Makino, J. 1997, ApJ, 477, L9 [NASA ADS] [CrossRef]
- Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS] (In the text)
- Geha, M., Willman, B., Simon, J. D., et al. 2008, ArXiv e-prints
- Geisler, D., Smith, V. V., Wallerstein, G., Gonzalez, G., & Charbonnel, C. 2005, AJ, 129, 1428 [NASA ADS] [CrossRef]
- Gentile, G., Salucci, P., Klein, U., Vergani, D., & Kalberla, P. 2004, MNRAS, 351, 903 [NASA ADS] [CrossRef]
- Gentile, G., Burkert, A., Salucci, P., Klein, U., & Walter, F. 2005, ApJ, 634, L145 [NASA ADS] [CrossRef]
- Gilmore, G., Wilkinson, M. I., Wyse, R. F. G., et al. 2007, ApJ, 663, 948 [NASA ADS] [CrossRef]
- Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375 [NASA ADS]
- Grebel, E. K., Gallagher, III, J. S., & Harbeck, D. 2003, AJ, 125, 1926 [NASA ADS] [CrossRef]
- Harbeck, D., Grebel, E. K., Holtzman, J., et al. 2001, AJ, 122, 3092 [NASA ADS] [CrossRef]
- Helmi, A., Irwin, M. J., Tolstoy, E., et al. 2006, ApJ, 651, L121 [NASA ADS] [CrossRef]
- Hensler, G., Theis, C., & Gallagher, J. S. 2004, A&A, 426, 25 [NASA ADS] [CrossRef] [EDP Sciences]
- Hernquist, L. 1987, ApJS, 64, 715 [NASA ADS] [CrossRef] (In the text)
- Hernquist, L. 1993, ApJS, 86, 389 [NASA ADS] [CrossRef]
- Hurley-Keller, D., Mateo, M., & Nemec, J. 1998, AJ, 115, 1840 [NASA ADS] [CrossRef]
- Ikuta, C., & Arimoto, N. 2002, A&A, 391, 55 [NASA ADS] [CrossRef] [EDP Sciences]
- Irwin, M., & Hatzidimitriou, D. 1995, MNRAS, 277, 1354 [NASA ADS] (In the text)
- Katz, N. 1992, ApJ, 391, 502 [NASA ADS] [CrossRef] (In the text)
- Katz, N., Weinberg, D. H., & Hernquist, L. 1996, ApJS, 105, 19 [NASA ADS] [CrossRef] (In the text)
- Kawata, D., Arimoto, N., Cen, R., & Gibson, B. K. 2006, ApJ, 641, 785 [NASA ADS] [CrossRef]
- Kirby, E. N., Simon, J. D., Geha, M., Guhathakurta, P., & Frebel, A. 2008, ApJ, 685, L43 [NASA ADS] [CrossRef]
- Kleyna, J. T., Wilkinson, M. I., Evans, N. W., & Gilmore, G. 2004, MNRAS, 354, L66 [NASA ADS] [CrossRef]
- Kobayashi, C., Tsujimoto, T., & Nomoto, K. 2000, ApJ, 539, 26 [NASA ADS] [CrossRef] (In the text)
- Koch, A., Grebel, E. K., Kleyna, J. T., et al. 2007, AJ, 133, 270 [NASA ADS] [CrossRef]
- Koch, A., Grebel, E. K., Gilmore, G. F., et al. 2008, AJ, 135, 1580 [NASA ADS] [CrossRef]
- Kodama, T., & Arimoto, N. 1997, A&A, 320, 41 [NASA ADS] (In the text)
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] (In the text)
- Lanfranchi, G. A., & Matteucci, F. 2004, MNRAS, 351, 1338 [NASA ADS] [CrossRef]
- Lee, M. G., Park, H. S., Park, J.-H., et al. 2003, AJ, 126, 2840 [NASA ADS] [CrossRef] (In the text)
- Leitherer, C., Robert, C., & Drissen, L. 1992, ApJ, 401, 596 [NASA ADS] [CrossRef] (In the text)
- Letarte, B., Hill, V., & Tolstoy, E. 2007, in EAS Publ. Ser. 24, ed. E. Emsellem, H. Wozniak, G. Massacrier, J.-F. Gonzalez, J. Devriendt, & N. Champavert, 33
- Lucy, L. B. 1977, AJ, 82, 1013 [NASA ADS] [CrossRef]
- Mac Low, M.-M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef]
- Maio, U., Dolag, K., Ciardi, B., & Tornatore, L. 2007, MNRAS, 379, 963 [NASA ADS] [CrossRef] (In the text)
- Maraston, C. 1998, MNRAS, 300, 872 [NASA ADS] [CrossRef]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef]
- Marcolini, A., D'Ercole, A., Battaglia, G., & Gibson, B. K. 2008, MNRAS, 386, 2173 [NASA ADS] [CrossRef]
- Marcolini, A., D'Ercole, A., Brighenti, F., & Recchi, S. 2006, MNRAS, 371, 643 [NASA ADS] [CrossRef]
- Martin, N. F., de Jong, J. T. A., & Rix, H.-W. 2008, ApJ, 684, 1075 [NASA ADS] [CrossRef] (In the text)
- Mateo, M. L. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef]
- Mayer, L., Mastropietro, C., Wadsley, J., Stadel, J., & Moore, B. 2006, MNRAS, 369, 1021 [NASA ADS] [CrossRef]
- Mighell, K. J., & Rich, R. M. 1996, AJ, 111, 777 [NASA ADS] [CrossRef]
- Monaghan, J. J. 1992, ARA&A, 30, 543 [NASA ADS] [CrossRef] (In the text)
- Moore, B., Governato, F., Quinn, T., Stadel, J., & Lake, G. 1998, ApJ, 499, L5 [NASA ADS] [CrossRef]
- Mori, M., Yoshii, Y., Tsujimoto, T., & Nomoto, K. 1997, ApJ, 478, L21 [NASA ADS] [CrossRef]
- Mori, M., Ferrara, A., & Madau, P. 2002, ApJ, 571, 40 [NASA ADS] [CrossRef]
- Muñoz, R. R., Majewski, S. R., Zaggia, S., et al. 2006, ApJ, 649, 201 [NASA ADS] [CrossRef]
- Murakami, I., & Babul, A. 1999, MNRAS, 309, 161 [NASA ADS] [CrossRef]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef]
- Peñarrubia, J., McConnachie, A. W., & Navarro, J. F. 2008, ApJ, 672, 904 [NASA ADS] [CrossRef] (In the text)
- Poirier, S., Jablonka, P., & Alimi, J.-M. 2002, Ap&SS, 281, 315 [NASA ADS] [CrossRef] (In the text)
- Poirier, S., Jablonka, P., & Alimi, J.-M. 2003, Ap&SS, 284, 849 [NASA ADS] [CrossRef] (In the text)
- Price, D. 2005, ArXiv Astrophysics e-prints (In the text)
- Read, J. I., Pontzen, A. P., & Viel, M. 2006, MNRAS, 371, 885 [NASA ADS] [CrossRef] (In the text)
- Ricotti, M., & Gnedin, N. Y. 2005, ApJ, 629, 259 [NASA ADS] [CrossRef]
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
- Salvadori, S., Ferrara, A., & Schneider, R. 2008, MNRAS, 386, 348 [NASA ADS] [CrossRef] (In the text)
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] (In the text)
- Serna, A., Alimi, J.-M., & Chieze, J.-P. 1996, ApJ, 461, 884 [NASA ADS] [CrossRef] (In the text)
- Shetrone, M., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [NASA ADS] [CrossRef]
- Shetrone, M. D., Bolte, M., & Stetson, P. B. 1998, AJ, 115, 1888 [NASA ADS] [CrossRef]
- Shetrone, M. D., Côté, P., & Sargent, W. L. W. 2001, ApJ, 548, 592 [NASA ADS] [CrossRef]
- Shetrone, M. D., Siegel, M. H., Cook, D. O., & Bosler, T. 2009, AJ, 137, 62 [NASA ADS] [CrossRef] (In the text)
- Smecker-Hane, T. A., Stetson, P. B., Hesser, J. E., & Vandenberg, D. A. 1996, in From Stars to Galaxies: the Impact of Stellar Physics on Galaxy Evolution, ed. C. Leitherer, U. Fritze-von-Alvensleben, & J. Huchra, ASP Conf. Ser., 98, 328
- Spano, M., Marcelin, M., Amram, P., et al. 2008, MNRAS, 383, 297 [NASA ADS]
- Spekkens, K., Giovanelli, R., & Haynes, M. P. 2005, AJ, 129, 2119 [NASA ADS] [CrossRef]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [NASA ADS] [CrossRef]
- Stinson, G., Seth, A., Katz, N., et al. 2006, MNRAS, 373, 1074 [NASA ADS] [CrossRef] (In the text)
- Stinson, G. S., Dalcanton, J. J., Quinn, T., Kaufmann, T., & Wadsley, J. 2007, ApJ, 667, 170 [NASA ADS] [CrossRef] (In the text)
- Strigari, L. E., Bullock, J. S., Kaplinghat, M., et al. 2008, Nature, 454, 1096 [NASA ADS] [CrossRef]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] (In the text)
- Swaters, R. A., Madore, B. F., van den Bosch, F. C., & Balcells, M. 2003, ApJ, 583, 732 [NASA ADS] [CrossRef]
- Tinsley, B. M. 1980, Fundamentals of Cosmic Physics, 5, 287 [NASA ADS] (In the text)
- Tolstoy, E., Venn, K. A., Shetrone, M., et al. 2003, AJ, 125, 707 [NASA ADS] [CrossRef]
- Tolstoy, E., Irwin, M. J., Helmi, A., et al. 2004, ApJ, 617, L119 [NASA ADS] [CrossRef]
- Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] (In the text)
- Valcke, S., de Rijcke, S., & Dejonghe, H. 2008, MNRAS, 389, 1111 [NASA ADS] [CrossRef] (In the text)
- Venn, K. A., & Hill, V. 2005, in From Lithium to Uranium: Elemental Tracers of Early Cosmic Evolution, ed. V. Hill, P. François, & F. Primas, IAU Symp., 228, 513
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2006a, AJ, 131, 2114 [NASA ADS] [CrossRef]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2006b, ApJ, 642, L41 [NASA ADS] [CrossRef]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2007, ApJ, 667, L53 [NASA ADS] [CrossRef]
- Wilkinson, M. I., Kleyna, J. T., Wyn Evans, N., et al. 2006, in EAS Publ. Ser. 20, ed. G. A. Mamon, F. Combes, C. Deffayet, & B. Fort, 105
- Wise, J. H., & Abel, T. 2008, ApJ, 685, 40 [NASA ADS] [CrossRef] (In the text)
Online Material
Appendix A: Simulation list and parameters
Table A.1: Model parameters for the complete set of simulations.
Footnotes
- ... galaxies
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
All Tables
Table 1: Initial parameters of the five generic models.
Table 2: Final properties of the five selected generic models.
Table A.1: Model parameters for the complete set of simulations.
All Figures
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=0]{11734Fig01.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg35.png) |
Figure 1: Normalized cooling function as a function of temperature and metallicity. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig02.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg106.png) |
Figure 2:
Time evolution of the star formation rate, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{11734Fig03.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg116.png) |
Figure 3:
The distributions of stellar ages between 0 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{11734Fig04.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg117.png) |
Figure 4: The effect of variation of the model initial parameters. The full sample of simulations is shown. Each circle or triangle stands for one model. The circle size is proportional to the final galaxy luminosity (see the top of the figure), while colors code the final stellar metallicity (median of the metallicity distribution function), following the scale given at the right hand side of the diagrams. Each panel encompasses simulations of identical baryonic fraction and initial core radius. The black triangles identify cases of full gas consumption. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[angle=0]{11734Fig05.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg120.png) |
Figure 5:
The metallicity,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[angle=0]{11734Fig06.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg125.png) |
Figure 6:
The galaxies' mass-to-light ratios,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig07.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg126.png) |
Figure 7:
The median of the galaxies' metallicity distributions,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig08.eps}}\par
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg128.png) |
Figure 8:
The relation between galaxy mass and V-band luminosity for the
the dark matter, the stars and the gas.
The lower panel displays the gas over stars mass ratio.
Colors encode the three different baryonic fractions that we have considered,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig09.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg145.png) |
Figure 9:
The variation in [Mg/Fe] vs. [Fe/H], [Fe/H] distribution
and stellar age distribution for 3 models of similar luminosities
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig10.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg155.png) |
Figure 10:
Same as Fig. 9 but for a brighter set of model
galaxies (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig11.eps}} \end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg157.png) |
Figure 11: The stellar [Fe/H] distributions of the four generic models reproducing Carina, Sextans, Sculptor and Fornax. The model outputs are shown in black and the observations with red dashed lines. The stellar fraction is defined as the number of stars in each bin divided by the total number of stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig12.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg158.png) |
Figure 12: The stellar [Mg/Fe] vs. [Fe/H] diagrams for the four generic models reproducing Carina, Sextans, Sculptor and Fornax. The observations are sketched with black dots. Their error bars are shown. Colors encode the fraction of stars as indicated by the bar at the top. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig13.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg159.png) |
Figure 13: The stellar age distributions of the four generic models. The stellar fraction is defined as the number of stars in each bin divided by the total number of stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig14.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg160.png) |
Figure 14: The age-metallicity relations of the four generic models. Each dot corresponds to a stellar particle. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig15.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg170.png) |
Figure 15: The [Mg/Fe] vs. [Fe/H] diagram, the stellar [Fe/H] distribution, the age-metallicity relation and the global stellar age distribution of the model #587, compared to the observations of Leo II. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[angle=0,clip]{11734Fig16.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg174.png) |
Figure 16:
Stellar, gas and temperature evolution of the models #575 (Fornax) and
#630 (Sculptor) as a function of time.
Each model is illustrated with three columns:
the first column presents the stellar surface brightness in log scale, between 0 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[angle=0,clip]{11734Fig17.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg175.png) |
Figure 17: Same as Fig. 16 but for the models #590 (Sextans) and #533 (Carina). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig18.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg190.png) |
Figure 18: The stars (blue circles) and dark halo (red triangles) density profiles for the four generic models. Each profile is fitted by a Plummer model. The positions of the core radii are indicated by the dashed lines. Their values are given in the left bottom corner of each panel. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{11734Fig19.eps}}
\end{figure}](/articles/aa/full_html/2009/25/aa11734-09/Timg194.png) |
Figure 19:
Top: the Virial temperature as a function of the total
initial mass computed from Eq. (16), with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



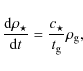
![\begin{displaymath}p_{\star} = \frac{m_{\rm {g}}}{m_{\star}}\left[ 1-\exp\left( -\frac{c_\star}{t_{\rm {g}}}\Delta t \right) \right].
\end{displaymath}](/articles/aa/full_html/2009/25/aa11734-09/img43.png)